| Issue |
A&A
Volume 640, August 2020
|
|
|---|---|---|
| Article Number | A33 | |
| Number of page(s) | 25 | |
| Section | Catalogs and data | |
| DOI | https://doi.org/10.1051/0004-6361/202037822 | |
| Published online | 07 August 2020 | |
First apsidal motion and light curve analysis of 162 eccentric eclipsing binaries from LMC⋆
1
Astronomical Institute, Charles University, Faculty of Mathematics and Physics, V Holešovičkách 2, 180 00 Praha 8, Czech Republic
e-mail: zasche@sirrah.troja.mff.cuni.cz
2
Astronomical Institute, Academy of Sciences, Fričova 298, 251 65 Ondřejov, Czech Republic
3
Research Centre for Theoretical Physics and Astrophysics, Institute of Physics, Silesian University in Opava, Bezručovo nám. 13, 746 01 Opava, Czech Republic
4
Institute of Physics, Faculty of Science, P. J. Šafárik University, Park Angelinum 9, 040 01 Košice, Slovakia
5
Department of Theoretical Physics and Astrophysics, Masaryk University, Kotlářská 2, 611 37 Brno, Czech Republic
Received:
26
February
2020
Accepted:
14
May
2020
We present an extensive study of 162 early-type binary systems located in the LMC galaxy that show apsidal motion and have never been studied before. For the ample systems, we performed light curve and apsidal motion modelling for the first time. These systems have a median orbital period of 2.2 days and typical periods of the apsidal motion were derived to be of the order of decades. We identified two record-breaking systems. The first, OGLE LMC-ECL-22613, shows the shortest known apsidal motion period among systems with main sequence components (6.6 years); it contains a third component with an orbital period of 23 years. The second, OGLE LMC-ECL-17226, is an eccentric system with the shortest known orbital period (0.9879 days) and with quite fast apsidal motion period (11 years). Among the studied systems, 36 new triple-star candidates were identified based on the additional period variations. This represents more than 20% of all studied systems, which is in agreement with the statistics of multiples in our Galaxy. However, the fraction should only be considered as a lower limit of these early-type stars in the LMC because of our method of detection, data coverage, and limited precision of individual times of eclipses.
Key words: binaries: eclipsing / stars: fundamental parameters / stars: early-type / Magellanic Clouds
The time series data are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/cat/J/A+A/640/A33
© ESO 2020
1. Introduction
The use of eclipsing binaries (EBs) for the precise derivation of the physical parameters of their components, such as masses and radii, still represents the most powerful method for deriving these quantities (see e.g. Southworth 2012). And thanks to these parameters we are able to improve and calibrate the existing models of stellar structure and evolution (Torres et al. 2010). We can also use the EBs as independent distance indicators, even outside of our Galaxy (e.g. Hilditch et al. 2005 or Vilardell et al. 2010).
Moreover, the eccentric EBs with detectable apsidal motion are important objects for studies of the internal structure constants and also to test the general relativity (Claret & Giménez 1993). For the systems, where the presence of an additional third body was detected, the more interesting dynamical interactions were also studied by Borkovits et al. (2015), among others. A large compilation of 623 galactic eccentric EBs was presented by Kim et al. (2018). The authors showed that about 5% of the systems they analysed also have a third unseen component (only based on eclipse timing variations, hereafter ETV). Finally, the effects like orbital circularisation (Zahn 2008) can also be studied by means of distribution of systems in the period-eccentricity diagram (see e.g. Kiminki & Kobulnicky 2012 or Meibom & Mathieu 2005).
Several similar studies were published on this topic, focusing on the eccentric EBs in the LMC and SMC and yielding the apsidal motion parameters, but the present study is the most extensive one. The studies that use a similar method of analysing the photometry and yield the apsidal motion, and that contain three or more systems from the LMC and/or SMC, are summarised in Table 1.
Compilation of papers studying LMC/SMC eccentric binaries.
2. Method of analysis
The selection of potential apsidal motion systems was a byproduct of our analysis of the whole LMC catalogue of EBs scanned for doubly eclipsing systems. We identified several hundreds of prospective eccentric systems for a more detailed analysis, but only a small part of them were found to fit our criteria. With these limitations we mainly mean the apsidal motion period, which has to be shorter than 200 years (principal limit due to a typical data coverage, see below). This was the strictest criterion because a large portion of the systems show apsidal motion but with very long periods. Other criteria were the data coverage of the light curve (LC) and its photometric amplitude (depth of minima), but also good coverage of the apsidal motion in the O − C diagram, where the apsidal motion should be unambiguously detectable.
For our whole analysis we only used the photometric data. Databases like OGLE and MACHO were used when available, while for some systems new photometry from the Danish 1.54 m telescope (hereafter DK154) was also obtained1. MACHO data (Alcock et al. 1997) cover the period 1992−2000, while the OGLE experiment (Udalski et al. 1992) was run in several parts: OGLE II in 1997−2000, OGLE III 2001−2009, and OGLE IV 2010−2014 for both Magellanic Clouds. The Photometric Data Retriever PDR (Zejda et al. 2019) was used for some systems to obtain the data.
The LC analysis using the PHOEBE 0.32SVN code (Prša & Zwitter 2005) (which is based on the Wilson-Devinney algorithm Wilson & Devinney 1971) was routinely used for the analysis of all systems in our sample. However, when there was no spectroscopy, several assumptions had to be made: the mass ratio was fixed at q = 1.0, and the coefficients of albedo A, limb-darkening x, and gravity brightening g were kept fixed at their suggested values for hot stars. The quality of LCs does not usually allow us to also fit these second-order parameters.
A necessary input parameter is the primary temperature, which was estimated from the de-reddened photometric index (B − V)0, which was derived following the procedure by Johnson (1958) using the values of photometric indices (B − V) and (U − B). The use of this method is substantiated because we deal here only with hot stars (of spectral types O-B-A), for which this presented (B − V)0 transformation works. These values are given below in Table A.1. The primary temperature was derived from the (B − V)0 photometric index using the assumption of main-sequence components and the tables by Pecaut & Mamajek (2013) and its later updates available online2.
This procedure of T1 estimation was used for majority of stars, but for 27 systems from our sample this resulted in rather dubious results. From these 27 systems, 19 systems were found with very low values of their indices (B − V)0 < −0.31. Normal O-type stars should have the index in the range −0.32 to −0.31, but here we deal with almost all systems having much lower unrealistic values of this photometric index. Therefore, we decided to skip this colour information completely. Moreover, four systems have unavailable indices from Massey (2002) and Zaritsky et al. (2002); two systems have unrealistically high values of (B − V)0 > 0; and finally two systems have values of their (B − V)0 indices that are too different from those of Massey (2002) and Zaritsky et al. (2002). For these 27 systems we only roughly estimated their effective temperatures from their apparent magnitudes (and this magnitude-temperature relation was constructed using the other systems with realistic (B − V)0 values). These stars are flagged in Table A.1 with asterisks. According to this temperature estimation it seems that all of the stars have effective temperatures below 32 000 K, hence none of our stars is an O-type star.
From the complete LC analysis, we constructed an LC template, which was later used to derive the times of eclipses via our AFP method (see Zasche et al. 2014). For the sake of brevity, all the figures of the LCs given here were plotted during a shorter time interval to avoid phase smearing due to change of argument of periastron ω (and using mostly only OGLE III data in the I filter).
At this point it would be useful to explain our method step by step. First, we only roughly estimated the orbital period and the eccentricity. With this assumption, we made the LC template and performed a preliminary period analysis resulting in better estimation of the true eccentricity and the period. With these values of eccentricity and period, we constructed a better LC fit. With the new LC template we were able to perform better apsidal motion analysis. With this iterative procedure we were able to get the final solution, which is the one presented in Table A.2. It should also be mentioned that for the LC analysis we used the photometric data phased only for some shorter time interval (typically one or two OGLE seasons only, i.e. 1 or 2 years) to eliminate the effect of apsidal motion causing the change of duration and depth of the LC for the template. For systems where the apsidal motion is fast, we constructed several such templates and used them separately for certain time intervals of our photometric data. The rate of apsidal motion was derived from the eclipse times, which we found is better than that derived from the LC fits. The apsidal motion analysis uses the standard technique of least-squares minimisation, as introduced by Gimenez & Garcia-Pelayo (1983) and Giménez & Bastero (1995), among others.
3. Results
Due to the very large number of individual systems, we cannot focus on each of the stars analysed in our sample. We would thus like to focus only on the most interesting results and systems that deserve our attention, and to encourage future observers and investigators to consider these particular systems.
All of our results are divided into several parts. First, the classical LC modelling and its results are given below in Table A.2 and the plots in Figs. 1 and A.1. Second, the apsidal motion parameters are given in Table A.2, while the fits can be seen in Figs. 2 and A.2. These figures show the apparent period variations of the particular stars via the eclipse timing variation together with the fits. Finally, the systems where some additional variations in the times of eclipses were detected and showed unambiguous period variability were additionally fitted assuming the light-time effect hypothesis (Mayer 1990). This hypothesis assumes a third body orbiting the inner eccentric eclipsing binary around a common barycentre. However, the potential detectability of any such body is highly dependent on the third body’s mass, its orbit, orientation, period, etc. Therefore, the number of systems detected with our method should be considered a lower limit, and any definite conclusions about the multiplicity fraction are still rather speculative because the incompleteness fraction would be rather high (see discussion in Sect. 5). Altogether 36 such systems were found for which the residuals after the apsidal motion fits were successfully fitted with the light-time effect hypothesis. All of these are shown in Figs. 3 and A.3, while five parameters of these fits are given in Table A.3.
 |
Fig. 1. Sample of plots of the light curves, full set of figures is in appendix section. |
 |
Fig. 2. Sample of plots of the O − C diagrams, full set of figures is in appendix section. Final fits of the apsidal motion are plotted as black and blue curves (for primary and secondary minima), while the individual points represent the times of eclipses. The larger the symbol, the higher the weight (which was assigned according to its uncertainty). New observations with DK154 are shown in red. In cases where an additional third body was found, the final fit is plotted (solid lines) together with only the apsidal motion fits (dashed lines). |
 |
Fig. 3. Sample of plots of the O − C diagrams after subtraction of apsidal motion fits. The LTE variations are plotted as red curves. Full set of figures is in appendix section. |
At this point it would be useful to recall some basic equations of the light-time effect and also our analysis approach. The observed deviation of individual minima in the O − C diagram can be described by
where the particular minimum JDi at epoch E is being compared with its theoretical prediction also taking into account the light-time effect term (O − C)LTE and the apsidal motion term (O − C)AM. The light-time effect can be expressed as
where A is the semi-amplitude, e3 is the eccentricity of the third body orbit, ω3 its argument of periastron, and ν its true anomaly. The mass function of this third-body orbit can be expressed as
where i stands for the inclination between the mutual orbit and the plane of the sky, and m1, m2, m3 are the masses of the primary, secondary, and tertiary components, respectively. For the second expression it is necessary to input the units of the outer period P3 in years and the semi-amplitude A in days. With this mass function we can at least make some preliminary estimates about the third body’s mass. However, for some more reliable derivation precise masses and also the inclination are needed. We also note that in a triple system, there is in principle a much more complicated influence of the third perturbing body on the apsidal motion of the eccentric inner pair (see e.g. Borkovits et al. 2015 or Borkovits et al. 2019) in addition to the classical tidal and the relativistic contributions.
The total ETV component due to the action of a third body is composed in principle of several contributions. Here we assume only the most dominant one, the classical geometrical light-time effect term. However, in general there are also other dynamical terms. In principle, these effects can be large or even dominate over the classical light-time effect. In our sample, where we deal with quite short orbital periods of the inner pairs and quite long periods of the outer bodies, we can state that for the majority of systems the light-time effect is certainly the dominant one. In Rappaport et al. (2013) a physical delay due to the third body is introduced, which has its amplitude proportional to the ratio (P2/P3). Hence, for majority of our systems third-body period that is too long makes the amplitude of this physical delay too small. On the other hand, there are also other longer-period perturbations (see e.g. Rappaport et al. 2013, Sect. 4.2), which have typical periods of the order of 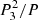 , and that cause for example the orbital precession and change in the eclipse depths. In our sample the timescales of the longer-period perturbations are typically longer than a human lifetime. Both these ratios P2/P3, and
, and that cause for example the orbital precession and change in the eclipse depths. In our sample the timescales of the longer-period perturbations are typically longer than a human lifetime. Both these ratios P2/P3, and 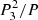 are given in the last columns of Table A.3.
are given in the last columns of Table A.3.
The question arises of whether these systems show some concordance with the systems with a detected third light contribution. However, we note that this link is not so unambiguous. For some of the potential triple systems the third bodies should have only negligibly low luminosities. On the other hand, for some systems, the detection of a third light could also be explained by an unbound star along the same line of sight. This situation is nothing novel in these very dense stellar fields in the LMC. However, mostly the detection of the light-time effect agrees with the non-zero value of the third light for a particular system. A typical example would be OGLE LMC-ECL-15664, which was identified as a system showing the largest mass function, as well as the largest value of the third light in the LC solution.
The quality of the apsidal motion fits in Figs. 2 and A.2 is mostly reasonable, but strongly depends on the value of eccentricity of the orbit (i.e. the amplitude of apsidal motion in the O − C diagram), and its apsidal motion rate (i.e. the period of apsidal advance, because longer periods only have small parts covered with data). The quality of the individual times of eclipses is comparable for different systems (usually of the order of 0.001−0.0001 d), only those with shallow eclipses and/or longer orbital periods have less precise times of eclipse.
The most interesting definitely seem to be those systems with third bodies and with a very rapid apsidal motion. Stars that have very fast apsidal motion usually have very short orbital periods. Among these, there was discovered a record-breaking system, OGLE LMC-ECL-17226, which has an eccentric orbit despite its short period (P = 0.9879314 day). This is, as far as we know, the shortest eccentric main sequence star ever discovered (the previous record of about 1.016 days belongs to the star V456 Oph located in our Galaxy; see Wolf et al. 2017). The apsidal motion of OGLE LMC-ECL-17226 is also rather fast (about 12 yr), while its eccentricity is very low (about 0.037).
Among other stars (in addition to OGLE LMC-ECL-17226), additional systems having a very rapid apsidal motion of about ten years or even faster were also found: OGLE LMC-ECL-06837 (U = 9.9 yr), #17774 (U = 7.2 yr), -22613 (U = 6.6 yr), -23298 (U = 12.2 yr), -25047 (U = 10.8 yr). To date, the system with the fastest apsidal advance in our Galaxy is V490 Cyg (Zasche & Wolf 2011) having U = 18.6 yr, while out of our Galaxy, it is the star from the SMC named OGLE SMC-ECL-2194 having U = 7.1 yr (Hong et al. 2015). For the list of all our analysed systems and their results, see Table A.2. It is important to note that the ephemerides given in Table A.2 are not always suitable for planning future observations. They represent only the value O − C = 0 in the diagrams in Figs. 2 and A.2. Hence for eclipse predictions, corrections are needed, especially in cases where the eccentricity is high and the apsidal motion amplitude significant.
Another interesting group of stars is the one where the third-body contribution to ETV caused by the light-time effect is even larger than the contribution from the apsidal motion itself. These are: OGLE LMC-ECL-10302, -16320, -17267, -20860, and -22613. The dominance of the light-time effect can be caused by two different phenomena: a very massive third body causing large amplitude of ETV, or in some systems only very low eccentricity of the inner orbit. In our cases shown here, both of these explanations play a role together.
4. Properties of the sample
First we look at the distribution of the orbital periods of the stars in our sample. Obviously, these are influenced by a strong selection effect, mainly due to our method of selection. Only those systems having an adequately short orbital period (usually P ≲ 3 d) can be studied using our methods (and having enough data for such an analysis). For this reason the plot in Fig. 4 shows a vast majority of systems from 1 to 3 days. Shorter-period systems are usually circular, while the longer-period ones usually have too slow apsidal motion to show a significant change over two decades, which is the typical time span of our data.
 |
Fig. 4. Histogram of orbital periods of the analysed systems. |
Another diagram in Fig. 5 shows how the apsidal motion period depends on the orbital period of the binary. Longer-period systems usually also have slower apsidal motion, while the fastest apsidal motion should preferably be detected for shorter orbital periods.
 |
Fig. 5. Apsidal motion period vs orbital period. |
In Fig. 6 we show the distribution of the relative radii resulting from our light curve analysis (for the primary and secondary components). It is clearly seen that preferentially those systems having relative radii between 0.15 and 0.25 were usually studied. This is again a selection effect of our method. Systems having too distant components usually have too slow apsidal motion (> 200 yr) to be detectable with our approach, and systems closer to each other were already circularised.
 |
Fig. 6. Histogram of relative radii of all systems for both eclipsing components. |
In Fig. 7 we plotted the eccentricity versus orbital period. For comparison we also added other compilations and apsidal motion studies from LMC/SMC from Table 1, and the apsidal motion systems published in the catalogue of Kim et al. (2018), who studied galactic systems. It is clearly seen that our present sample incorporates mainly the shorter-period systems (mostly below 4 days), but the overall tendency to detect the higher eccentricities only with longer periods is obvious. Hence, the circularisation in more compact systems is also much faster in the LMC galaxy (see e.g. Tassoul 1988).
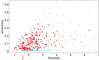 |
Fig. 7. Distribution of eccentricities vs orbital periods for eclipsing binaries. The red dots are our new data from the present paper, which are being compared with the other LMC/SMC systems. The blue dots are taken from our previous analyses, and the cyan dots are taken from publications by Hong et al. (see table in Sect. 1 for reference). A comparison with galactic eclipsing binaries as published in the catalogue of Kim et al. (2018) are plotted in black. Circularisation in shorter periods is clearly visible here. |
5. Discussion and conclusions
Our new analysis of 162 eccentric eclipsing binaries in LMC presents the largest sample studied to date in one paper (both of the LC and apsidal motion) and provide us with unique material for comparison with other results.
Because we have limited information about the stars, and no spectroscopy for these targets, the inferred parameters are only relative ones (like the relative radii), and the masses are completely unknown. The uncertainties of masses inferred from the photometric indices are too large, hence they cannot easily be used to derive the internal structure constants. Only future spectroscopic monitoring would help us in this aspect.
The ETVs due to the light-time effect term are usually rather small, which also yielded small mass function values (with only a few exceptions). The other ETV effects are negligible, or would be very slow (see the last columns of Table A.3). Hence, for instance we cannot hope to find any dynamical indication of these third bodies, for example via changing the inclination angle through eclipse depth variations (only one system has the typical period of this nodal regression below 1000 years).
On the other hand, the presented study of residuals and fitting of the light-time effect (see Figs. 3 and A.3) is only one part of the whole sample. Other systems were found to show additional variation, but they are still not well-covered, have too long periods, or too low amplitudes. For these reasons the variation is visible, but for a proper analysis we need more data spanning a longer time interval or better data to reduce the scatter. This is why we only briefly mention these systems in Figs. 8 and A.4, where the residuals after the subtraction of the apsidal motion are plotted, but no light-time effect fit is given yet. This should encourage observers to collect new data for these systems to prove or reject the hypothesis of the third body.
 |
Fig. 8. Sample of plots of the O − C diagrams after subtraction of apsidal motion fits for cases where there appears to be some variation of residuals, but it is still rather questionable. More data are needed. Full set of figures is in appendix section. |
If we take into account the proved 36 systems with the light-time effect fits in Figs. 3 and A.3 and add the 19 suspected ones from Figs. 8 and A.4, then the total fraction of potential triples in our sample grows from 20% to about 34%. We are aware that our preprocessing and selection of suitable systems for this analysis can provide some bias towards these potential triples. However, as was already stated in Sect. 2, for most of the discarded systems the criterion was the slow rate of apsidal motion. This is probably not directly connected with the multiplicity, hence its role should be small. However, what should play a role is that the stars with very small photometric amplitude (shallow eclipses) were also neglected. These systems might also be triples because the high value of the third light makes the eclipses shallower. Hence, we would probably miss these potential triples rather than overestimate their fraction in the LMC eclipsing sample. Such a large fraction of potential triples is several times more than what was found in their sample by Kim et al. (2018). However, they studied the stars in our Galaxy, where the field stars are of much later spectral type; hence, the multiplicity fraction is much lower (Duchêne & Kraus 2013). Therefore, our number should only be compared with the suggested number of multiples in the early-type population in LMC. According to Duchêne & Kraus (2013), the probability of a star to be a multiple for these massive stars should be very high and reach almost 100% for the O and B stars. Hence, our rough estimation of 1/3 should be considered a lower limit due to the methodology incompleteness limitations (e.g. long periods and short periods cannot be detected with our method; masses and inclinations play a crucial role for a light-time effect to emerge in our residuals).
Acknowledgments
We are thankful to an anonymous referee for the critical suggestions greatly improving the quality of the whole manuscript. This work was supported by the grant MSMT INGO II LG15010, grant GA ČR 18-05665S, and grant Primus/SCI/17. Marek Skarka acknowledges the OP VVV project Postdoc@MUNI (No. CZ.02.2.69/0.0/0.0/16027/0008360). We would like to thank J. Liška, K. Hornoch, L. Pilarčík, and J. Vraštil for obtaining some of the photometric data. We also do thank the OGLE and MACHO teams for making all of the observations easily public available. We are also grateful to the ESO team at the La Silla Observatory for their help in maintaining and operating the Danish telescope. This research has made use of the SIMBAD and VIZIER databases, operated at CDS, Strasbourg, France and of NASA Astrophysics Data System Bibliographic Services.
References
- Alcock, C., Allsman, R. A., Alves, D., et al. 1997, ApJ, 486, 697 [NASA ADS] [CrossRef] [Google Scholar]
- Borkovits, T., Rappaport, S., Hajdu, T., et al. 2015, MNRAS, 448, 946 [NASA ADS] [CrossRef] [Google Scholar]
- Borkovits, T., Forgács-Dajka, E., & Rappaport, S. A. 2019, EAS Publ. Ser., 99 [CrossRef] [EDP Sciences] [Google Scholar]
- Claret, A., & Giménez, A. 1993, A&A, 277, 487 [Google Scholar]
- Duchêne, G., & Kraus, A. 2013, ARA&A, 51, 269 [Google Scholar]
- Gimenez, A., & Garcia-Pelayo, J. M. 1983, Ap&SS, 92, 203 [NASA ADS] [CrossRef] [Google Scholar]
- Giménez, A., & Bastero, M. 1995, Ap&SS, 226, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Graczyk, D., Soszyński, I., Poleski, R., et al. 2011, Acta Astron., 61, 103 [Google Scholar]
- Hilditch, R. W., Howarth, I. D., & Harries, T. J. 2005, MNRAS, 357, 304 [NASA ADS] [CrossRef] [Google Scholar]
- Hong, K., Kim, S.-L., Lee, J. W., et al. 2015, AJ, 150, 1 [CrossRef] [Google Scholar]
- Hong, K., Lee, J. W., Kim, S.-L., Koo, J.-R., & Lee, C.-U. 2016, MNRAS, 460, 650 [NASA ADS] [CrossRef] [Google Scholar]
- Hong, K., Lee, J. W., Kim, S.-L., et al. 2019, AJ, 158, 185 [CrossRef] [Google Scholar]
- Johnson, H. L. 1958, Lowell Obs. Bull., 4, 37 [Google Scholar]
- Kim, C.-H., Kreiner, J. M., Zakrzewski, B., et al. 2018, ApJS, 235, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Kiminki, D. C., & Kobulnicky, H. A. 2012, ApJ, 751, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Massey, P. 2002, ApJS, 141, 81 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Mayer, P. 1990, Bull. Astron. Inst. Czech., 41, 231 [Google Scholar]
- Meibom, S., & Mathieu, R. D. 2005, ApJ, 620, 970 [NASA ADS] [CrossRef] [Google Scholar]
- Pawlak, M., Soszyński, I., Udalski, A., et al. 2016, Acta Astron., 66, 421 [Google Scholar]
- Pecaut, M. J., & Mamajek, E. E. 2013, ApJS, 208, 9 [Google Scholar]
- Prša, A., & Zwitter, T. 2005, ApJ, 628, 426 [NASA ADS] [CrossRef] [Google Scholar]
- Rappaport, S., Deck, K., Levine, A., et al. 2013, ApJ, 768, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Southworth, J. 2012, Orbital Couples: Pas de Deux in the Solar System and the Milky Way, 51 [Google Scholar]
- Tassoul, J.-L. 1988, ApJ, 324, L71 [NASA ADS] [CrossRef] [Google Scholar]
- Torres, G., Andersen, J., & Giménez, A. 2010, A&ARv, 18, 67 [Google Scholar]
- Udalski, A., Szymanski, M., Kaluzny, J., Kubiak, M., & Mateo, M. 1992, Acta Astron., 42, 253 [NASA ADS] [Google Scholar]
- Vilardell, F., Ribas, I., Jordi, C., Fitzpatrick, E. L., & Guinan, E. F. 2010, A&A, 509, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wilson, R. E., & Devinney, E. J. 1971, ApJ, 166, 605 [NASA ADS] [CrossRef] [Google Scholar]
- Wolf, M., Zasche, P., Kučáková, H., et al. 2017, Acta Astron., 67, 257 [Google Scholar]
- Zahn, J.-P. 2008, EAS Publ. Ser., 29, 67 [CrossRef] [Google Scholar]
- Zaritsky, D., Harris, J., Thompson, I. B., Grebel, E. K., & Massey, P. 2002, AJ, 123, 855 [NASA ADS] [CrossRef] [Google Scholar]
- Zasche, P., & Wolf, M. 2011, A&A, 527, A43 [CrossRef] [EDP Sciences] [Google Scholar]
- Zasche, P., & Wolf, M. 2013, A&A, 558, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zasche, P., & Wolf, M. 2019, AJ, 157, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Zasche, P., Wolf, M., Vraštil, J., et al. 2014, A&A, 572, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zasche, P., Wolf, M., Vraštil, J., & Pilarčík, L. 2015, AJ, 150, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Zejda, M., Skýba, O., Krajčovič, M., Gajdoš, P., & Fedurco, M. 2019, Contrib. Astron. Obs. Skal. Pleso, 49, 132 [NASA ADS] [Google Scholar]
Appendix A: Additional tables and figures
Relevant information for the analysed systems.
Parameters of the light curve fits and the apsidal motion.
Third-body orbit parameters of the individual systems.
 |
Fig. A.1. Light curves. |
 |
Fig. A.1. continued. |
 |
Fig. A.1. continued. |
 |
Fig. A.1. continued. |
 |
Fig. A.1. continued. |
 |
Fig. A.1. continued. |
 |
Fig. A.2. O − C diagrams. |
 |
Fig. A.2. continued. |
 |
Fig. A.2. continued. |
 |
Fig. A.2. continued. |
 |
Fig. A.2. continued. |
 |
Fig. A.2. continued. |
 |
Fig. A.3. O − C diagrams after subtraction of apsidal motion fits. The LTE variations are plotted as red curves. |
 |
Fig. A.4. O − C diagrams after subtraction of apsidal motion fits for cases where there appears to be some variation of residuals, but it is still rather questionable. More data are needed. |
All Tables
All Figures
 |
Fig. 1. Sample of plots of the light curves, full set of figures is in appendix section. |
| In the text | |
 |
Fig. 2. Sample of plots of the O − C diagrams, full set of figures is in appendix section. Final fits of the apsidal motion are plotted as black and blue curves (for primary and secondary minima), while the individual points represent the times of eclipses. The larger the symbol, the higher the weight (which was assigned according to its uncertainty). New observations with DK154 are shown in red. In cases where an additional third body was found, the final fit is plotted (solid lines) together with only the apsidal motion fits (dashed lines). |
| In the text | |
 |
Fig. 3. Sample of plots of the O − C diagrams after subtraction of apsidal motion fits. The LTE variations are plotted as red curves. Full set of figures is in appendix section. |
| In the text | |
 |
Fig. 4. Histogram of orbital periods of the analysed systems. |
| In the text | |
 |
Fig. 5. Apsidal motion period vs orbital period. |
| In the text | |
 |
Fig. 6. Histogram of relative radii of all systems for both eclipsing components. |
| In the text | |
 |
Fig. 7. Distribution of eccentricities vs orbital periods for eclipsing binaries. The red dots are our new data from the present paper, which are being compared with the other LMC/SMC systems. The blue dots are taken from our previous analyses, and the cyan dots are taken from publications by Hong et al. (see table in Sect. 1 for reference). A comparison with galactic eclipsing binaries as published in the catalogue of Kim et al. (2018) are plotted in black. Circularisation in shorter periods is clearly visible here. |
| In the text | |
 |
Fig. 8. Sample of plots of the O − C diagrams after subtraction of apsidal motion fits for cases where there appears to be some variation of residuals, but it is still rather questionable. More data are needed. Full set of figures is in appendix section. |
| In the text | |
 |
Fig. A.1. Light curves. |
| In the text | |
 |
Fig. A.1. continued. |
| In the text | |
 |
Fig. A.1. continued. |
| In the text | |
 |
Fig. A.1. continued. |
| In the text | |
 |
Fig. A.1. continued. |
| In the text | |
 |
Fig. A.1. continued. |
| In the text | |
 |
Fig. A.2. O − C diagrams. |
| In the text | |
 |
Fig. A.2. continued. |
| In the text | |
 |
Fig. A.2. continued. |
| In the text | |
 |
Fig. A.2. continued. |
| In the text | |
 |
Fig. A.2. continued. |
| In the text | |
 |
Fig. A.2. continued. |
| In the text | |
 |
Fig. A.3. O − C diagrams after subtraction of apsidal motion fits. The LTE variations are plotted as red curves. |
| In the text | |
 |
Fig. A.4. O − C diagrams after subtraction of apsidal motion fits for cases where there appears to be some variation of residuals, but it is still rather questionable. More data are needed. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



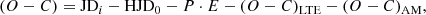
![$$ \begin{aligned} (O-C)_{\rm LTE} = \frac{A}{\sqrt{1-e_3^2\cos ^2\omega _{3}}} \left[ {{ \frac{(1-e_3^2)\sin (\nu + \omega _{3})}{1+e_3 \cos \nu }+ e_3 \sin \omega _{3}}} \right]\!, \end{aligned} $$](/articles/aa/full_html/2020/08/aa37822-20/aa37822-20-eq2.gif)
![$$ \begin{aligned} f(m_3) = \frac{(m_3 \sin i)^3}{(m_1+m_2+m_3)^2} = \frac{1}{P_3^2} \cdot {\left[ \frac{173.15 \cdot A}{\sqrt{1-e_3^2\cos ^2\omega _3}} \right]^3}, \end{aligned} $$](/articles/aa/full_html/2020/08/aa37822-20/aa37822-20-eq3.gif)