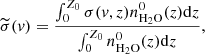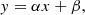| Issue |
A&A
Volume 639, July 2020
|
|
|---|---|---|
| Article Number | A29 | |
| Number of page(s) | 7 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/201834621 | |
| Published online | 03 July 2020 | |
Method for retrieval of atmospheric water vapor using OH airglow for correction of astronomical observations
1
State Key Laboratory of Space Weather, National Space Science Center, Chinese Academy of Sciences, 100190 Beijing, PR China
e-mail: xujy@nssc.ac.cn
2
Key Laboratory of Middle Atmosphere and Global Environment Observation (LAGEO), Institute of Atmospheric Physics, Chinese Academy of Sciences, 100029 Beijing, PR China
3
University of Chinese Academy of Sciences, 100049 Beijing, PR China
4
College of Mathematics and Information Science, Henan Normal University, 453007 Xinxiang, PR China
Received:
11
November
2018
Accepted:
10
May
2020
Context. Water vapor in the atmosphere undergoes quick spatial and temporal variations. This has a serious impact on ground-based astronomical observations from the visible band to the infrared band resulting from water vapor attenuation and emission.
Aims. We seek to show how the sky spectrum of an astronomical observation can be used to determine the amount of precipitable water vapor (PWV) along the line of sight toward the science target.
Methods. In this work, we discuss a method to retrieve the PWV from the OH(8-3) band airglow spectrum. We analyzed the influences of the pressure and temperature of the atmosphere and the different water vapor vertical distributions on the PWV retrieval method in detail. Meanwhile, the accuracy of the method was analyzed via Monte Carlo simulations. To further verify the method of PWV retrieval, we carried out cross comparisons between the PWV retrieved from OH airglow and PWV from the standard star spectra of UVES using equivalent widths of telluric absorption lines observed from 2000 to 2016 at Cerro Paranal in Chile.
Results. The Monte Carlo tests and the comparison between the two different methods prove the availability the PWV retrieval method from OH airglow. These results show that using OH airglow spectra in astronomical observations, PWVs along the same line of sight as the astronomical observations can be retrieved in real time.
Conclusions. We provide a quick and economical method for retrieving the water vapor along the same line of sight of astronomical observation in the real time. This is especially helpful to correcting the effect of water vapor on astronomical observations.
Key words: atmospheric effects / instrumentation: spectrographs / radiative transfer / methods: data analysis / techniques: spectroscopic
© ESO 2020
1. Introduction
Precipitable water vapor (PWV) in the atmosphere seriously affects ground-based astronomic observation in a wide optical waveband, from the visible to the infrared bands. This effect occurs because water vapor attenuates light from astronomical sources (Naylor et al. 2002; Querel et al. 2008; Smette et al. 2007, 2015; Kausch et al. 2015). In addition, water vapor emission also increases the background, which reduces the observation sensitivity, especially at infrared wavelengths larger than 16 μm (Radomski et al. 2010). Because water vapor undergoes rapid variations over time, both in different directions and at different locations, and because the line of sight of astronomical targets constantly changes with time, the water vapor along the line of sight of the optical path significantly influences astronomical observations. Therefore, locally, along the line of sight, real-time monitoring of water vapor is necessary for correction on astronomic observations.
Because water vapor is mainly distributed in the troposphere and the low stratosphere and has important effects on astronomical observations, various methods for measuring vertical column content of PWV in millimeter (Li et al. 2003) have been proposed by astronomers. For instance, astronomers used an Infrared Radiometer for Millimeter Astronomy (IRMA) to measure the emission of rotational transitions of water vapor in a narrow spectral region of approximately 20 μm and to retrieve the PWV (Naylor et al. 2002). Querel et al. (2008) used the Magellan Inamori Kyocera Echelle (MIKE) optical spectrograph at Las Campanas Observatory to measure the absorption lines in spectra of telluric standard stars and retrieved the PWV.
OH airglow has a series of emission bands in the visible and infrared part of the spectrum. It is therefore widely considered to be an annoying contaminant in astronomical spectra (Osterbrock et al. 1996; Franzen et al. 2017). OH airglow originates in the mesopause region within a layer located at a peak altitude of about 87 km (Xu et al. 2012; von Savigny et al. 2012). Chadney & Whiter (2018) note the wavelength coincidences of some OH emission lines, such as the P1(4.5) double lines in the OH(8-3) band and water vapor absorption lines. Therefore, these ground-based observed OH airglow emission lines originating in the mesopause region are attenuated by the presence of water vapor located in the troposphere. This effect may be the cause of the only partial success of methods of OH sky subtraction developed by many researchers (Davies 2007; Noll et al. 2014; Soto et al. 2016). However, Chadney & Whiter (2018) took advantage of these coincidences, for an atmospheric study, and developed a method to determine the amount of water vapor using auroral and OH airglow emissions in the polar region and evaluated the uncertainties of the retrieval method theoretically.
In this paper, we propose a method, based on the Chadney & Whiter (2018) method, to retrieve the PWV from astronomical spectra. The purpose of the method is to give the water vapor along the line of sight of the astronomical observation in the real time. First, we provide a theoretical development that give us an estimate of the uncertainty of this method. Then we apply this approach on archival Ultraviolet and Visual Echelle Spectrograph (UVES) data taken since April 2000. This data set allows a direct comparison between the values obtained by the Chadney & Wither method and the PWV retrieved from UVES standard star spectra (Querel et al. 2008, 2011).
This paper is organized as follows. Section 2 introduces the method of PWV retrieval from OH(8-3) band spectra (herein and after called OH(8-3) PWV) and evaluates the influence of the atmospheric pressure, temperature, and initial water vapor vertical profiles on PWV retrieval. Theoretical verification of the method using Monte Carlo tests is presented in Sect. 3. Section 4 provides comparisons between the retrieved PWV using OH(8-3) airglow and that from UVES standard star spectra (herein and after called STAR PWV) to further prove the reliability of this method. The choice and candidate OH airglow spectral lines for PWV retrieval, besides OH(8-3), are discussed in Sect. 5. Conclusions are given in Sect. 6.
2. Method of PWV retrieval from OH airglow
2.1. Water vapor absorption on ground-based observation of OH(8-3) spectrum
OH airglow is emitted by vibrationally excited OH(v) in an atmosphere layer near 87 km with a thickness of approximately 8 km (Baker & Stair 1988). Under local thermodynamic equilibrium (LTE) conditions, the line intensities of the OH(v′−v″) band obey the Boltzmann distribution as follows:
where j is the rotational level; I(j) represents the line intensity; A(j) is the Einstein coefficient; Nv′ is the density of OH molecules in the vibrational level v′; Qv′ is the total partition function of the vibrational level v′; E(j) is the rotational term value; Trot is the rotational temperature; and k, h, and c are the Boltzmann constant, Planck constant, and speed of light, respectively.
In principle, the intensity of every emission line in one band can be fitted by adjusting the rotational temperature Trot using the Boltzmann distribution (see Eq. (1)). However, ground-based observations of some OH airglow emission lines are affected by water vapor absorption between the airglow layer and the ground. Figure 1 gives distributions of OH(8-3) band P1(4.5) line emission spectra and water vapor transmission spectra with PWVs of 5 mm, 10 mm, and 20 mm. From Fig. 1, we can see that the water vapor has obvious absorption at the P1e(4.5) line of the OH(8-3) band, while there are very weak water vapor absorptions at adjacent lines P1(2.5), P1(3.5), and P1(5.5). Therefore, we used the three OH emission lines to calculate the rotational temperature by means of Eq. (1). The theoretical line intensity of P1(4.5), 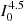 , without absorption by water vapor is obtained, as shown in Fig. 2 (the asterisk). Owing to the absorption by water vapor, the ground-based observed P1(4.5) line is weaker than that without water vapor absorption. The observed P1(4.5) line with absorption by water vapor is also given in Fig. 2. Therefore, we can use this difference to retrieve the amount of water vapor.
, without absorption by water vapor is obtained, as shown in Fig. 2 (the asterisk). Owing to the absorption by water vapor, the ground-based observed P1(4.5) line is weaker than that without water vapor absorption. The observed P1(4.5) line with absorption by water vapor is also given in Fig. 2. Therefore, we can use this difference to retrieve the amount of water vapor.
 |
Fig. 1. Water vapor absorption spectra for multiple water vapor levels. Shown are 5 mm, 10 mm, and 20 mm PWVs, parameters from HITRAN2016, and the OH(8-3) band P1(4.5) double lines with Doppler broadening. |
 |
Fig. 2. Observation of UVES on March 19, 2008 example. The linear line is fitted using P1(2.5), P1(3.5), and P1(5.5) line intensities in the OH(8-3) band. The P1(4.5) emission line without absorption by water vapor is indicated with an asterisk. The error bars are the uncertainties of intensities, which are estimated by the S/N given in the UVES dataset. |
In this work, the PWV retrieval process is similar to that from Chadney & Whiter (2018). The OH airglow emission that passes through the atmosphere and reaches the ground can be given by the Beer-Lambert law (Chadney et al. 2017) as follows:
where I(v) is the observed airglow intensity at wavenumber v, I0(v) is the airglow emission intensity in the source region, σ(v, z) is the absorption cross section of H2O at the wavenumber v, and nH2O(z) is the number density of H2O. The atmospheric transmission spectrum from water vapor can be expressed as ![$ T_v(v)=\exp\left[-\int_0^{Z_0} \sigma(v,z)n_{{\rm H}_2{\rm O}}(z){\rm d}z\right] $](/articles/aa/full_html/2020/07/aa34621-18/aa34621-18-eq4.gif) . For the zenith observation, z is the altitude, and Z0 is the altitude of the OH emission region.
. For the zenith observation, z is the altitude, and Z0 is the altitude of the OH emission region.
The instrument function of the observation system is wavelength dependent, so we calculated the integral intensity of each line. Since the width of the OH airglow emission lines and water vapor absorption lines are small compared to the instrument function, we calculated the theoretical integral transmittance of atmosphere between the OH layer and the ground for the doublet as follows (Espy & Hammond 1995):
where I(v − v1) and I(v − v2) are line spectra of Λ-doublet components at wavelength of v1 and v2, respectively, and Tv(v) is the atmospheric transmission spectrum due to water vapor. Therefore, the observed transmittance of atmosphere between the mesopause and the ground at the wavelength of the P1(4.5) line of the OH(8-3) band,  , is determined by the observed line intensity and the theoretical intensity without water vapor.
, is determined by the observed line intensity and the theoretical intensity without water vapor.
2.2. Retrieved PWV from the OH(8-3) band transmission spectrum
The absorption from the ground-based zenith observation is due to the total water vapor in the light path, and thus we can obtain the total water vapor column content. For this purpose, an effective absorption cross section is defined as
where 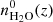 is a known priori vertical distribution of H2O.
is a known priori vertical distribution of H2O.
The absorption cross section of water vapor σ(v, z) is dominated by pressure broadening in the lower atmosphere and Doppler broadening in the upper atmosphere, and can therefore be represented by Voigt function. Therefore, when the absorption cross section of water vapor is calculated, the vertical distributions of the temperature and pressure must be considered.
In addition to the temperature and pressure, the effective cross-section calculation also requires the initial water vapor profile as the weighting function. To evaluate the effect of the temperature, pressure, and water vapor vertical distribution on PWV retrieval, the atmosphere profiles (pressure, temperature, and water vapor) from the US standard atmosphere 1976 model and mid-latitude summer and winter in MODTRAN (MODerate resolution atmospheric TRANsmission) model were used. These three pressure and temperature distributions are very similar (see Fig. 3). The total water vapor contents are 5.8 × 1022 cm−2,1.2 × 1023 cm−2 and 3.4 × 1022 cm−2, respectively, for the above water vapor density profiles. However, as the weighting functions for the effective absorption cross-section calculation, these profiles have similar normalized distributions. The effective absorption cross sections of water vapor are very similar over the spectral range of the P1(4.5) double lines of the OH(8-3) band (see Fig. 3(d)). The results show that the relative differences between the effective cross sections calculated from the three atmosphere profiles are less than 5%.
 |
Fig. 3. Atmospheric pressure (panel a), temperature (panel b), and water vapor density (panel c) profiles of the US standard atmosphere 1976 and MODTRAN mid-latitude summer and winter atmosphere models, and effective absorption cross sections of water vapor and relative differences among them (panel d). |
The absolute water vapor profiles are greatly different, but they have similar normalized distributions as the weighting function. In addition, the temperature and pressure below about 10 km do not vary greatly in different seasons. Moreover, the effective cross sections of water vapor in different seasons are weakly influenced by the atmosphere profiles. Therefore, we propose a simple and effective method for calculating the effective absorption cross section of water vapor by means of the water vapor profile from the US standard atmosphere 1976 model and parameters from HITRAN2016 (Gordon et al. 2017). Once the effective absorption cross section is calculated, the transmission spectrum Tv(v) can be written as ![$ T_v(v)=\exp[-\widetilde{\sigma}(v)\cdot N_{\mathrm{H}_2\mathrm{O}}] $](/articles/aa/full_html/2020/07/aa34621-18/aa34621-18-eq9.gif) , where NH2O is the total water vapor column content. A series of theoretical transmittances
, where NH2O is the total water vapor column content. A series of theoretical transmittances 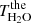 can be calculated by means of the OH spectra I(v) and water vapor transmission spectrum Tv(v) with different PWV values (see Eq. (3)). The true PWV can be estimated by comparing the observed TH2O with
can be calculated by means of the OH spectra I(v) and water vapor transmission spectrum Tv(v) with different PWV values (see Eq. (3)). The true PWV can be estimated by comparing the observed TH2O with 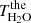 estimates for different PWV values.
estimates for different PWV values.
3. Theoretical verification of the PWV retrieval method
Transmissions of P1 branch lines for multiple PWV values are calculated (see Fig. 4) for the OH(8-3) band. The transmission of the P1e(4.5) line is still approximately 0.3 for 50 mm PWV, so the effect of water vapor absorption saturation on the PWV retrieval can be ignored for PWV of less than 50 mm. In addition, the P1(2.5) and P1(3.5) lines are also slightly absorbed by water vapor. When the water vapor absorption effects on the other lines except P1(4.5) are not taken into account the rotational temperature obtained using P1(2.5), P1(3.5) and P1(5.5) lines are slightly higher than the true value and the retrieved PWV is slightly lower than the true value. The deviation can be corrected as follows: We used the first calculated PWV to correct the absorption on all the lines and then calculated a new PWV using corrected line intensities. After a few interactions, any improvement becomes negligible. Finally, the corrected PWV was retrieved using the corrected P1(2.5), P1(3.5), and P1(5.5) lines and the original P1(4.5) line.
 |
Fig. 4. Water vapor transmission of OH(8-3) P1 branch lines varying with PWV. |
To evaluate the accuracy of the PWV inversion approach, we performed Monte Carlo simulations. For each Monte Carlo trial, we first gave a true PWV value and simulated a series of ‘observed’ spectra of the OH(8-3) band with a resolving resolution power of 43 000 corresponding to the UVES night-sky emission spectrum with slits of 1.0″(see below). The noise was added to the simulated spectra with S/N = S/σN = 20. The S is the maximum observed in the CCD analog-to-digital unit (adu) and σN is the standard deviation of the Gaussian white noise in the same units. Next, we applied the above algorithm to retrieve the PWV from the simulated OH(8-3) band spectra and then compared that with the original values.
We performed two tests: first, the simulations do not consider that the P1(2.5), P1(3.5) and P1(5.5) lines are affected by water vapor absorption. Second, the effects of water vapor absorption on P1(2.5), P1(3.5), and P1(5.5) lines were taken into account and corrected. Each simulation run of 200 trials are shown in Fig. 5. The relative deviation of calculated PWV is less than 5% for uncorrected PWV in simulations. When the absorptions of P1(2.5), P1(3.5), and P1(5.5) lines are corrected, the retrieved PWV is in good agreement with the artificially true values. For the Gaussian, white noise was added to the signal, the retrieved PWVs from the simulated spectra also have Gaussian distribution, and the derived uncertainty of PWVs is the standard deviation of simulations for each given PWV value. The low PWV values have approximate 2 mm uncertainties, because the S/N = 20 is used for all given PWV values. The signal-to-noise ratio (S/N) of some measurements of OH line intensities are much higher than 20, and then the uncertainty of retrieved PWV is smaller.
 |
Fig. 5. Retrieved PWV for 200 simulated measurements for each true value PWV. The error bars are the standard deviation of each simulation. The comparison of the PWV retrieval not considering water absorption in P1(2.5), P1(3.5), and P1(5.5) lines (left panel) and correcting for the effect (right panel). |
4. Validation of the method of PWV retrieval with other observations
The availability of a new method should be verified via a comparison with existing techniques. To validate our results, we compared our results of the PWV retrieved from OH(8-3) airglow with the PWV measured by other methods.
4.1. Datasets
The UVES has provided sky emission spectra including OH airglows since April 2000. The high-resolution spectra were produced by the so-called Phase 3 data products from the ESO Science Archive Facility. The spectra in Phase 3 data products are 1-D wavelength-calibrated for astronomical targets and night-sky emissions. The OH(8-3) band was observed by the UVES red arm with an 860 nm setup with resolving power R = 43 000 for a slit width of 1.0″. However, the sky data are not flux-calibrated. To correct the instrument response effect, six response curves were identified for the wavelength. Noll et al. (2017) indicate that the average shape correction for all covered wavelengths is 1.2% and the differences in the flux calibration for lines of the same OH band are even smaller. In addition, only the relative line intensities of the OH(8-3) band are used in this work, and the relative differences of the six response curves are less than 3% during the wavelength range. Thus, the average response curve of the six curves is used for all the selected spectra.
After the response calibration, the intensity of the OH(8-3) band lines is calculated as follows. First, the segments of sky continuum excluding the OH lines in the wavelength range from 730 nm to 742 nm are selected and the sky continuum is determined by a linear fit to these lines. Then derived continuum is subtracted from the spectrum. The intensity of OH lines is obtained by integrating the spectrum in wavelength range with a width of ±0.04 nm.
Kerber et al. (2010, 2012) analyzed and compared PWV monitored by various instruments at the Cerro Paranal Observatory. The optical and IR instruments, such as CRIRES, UVES, X-shooter (Smette et al. 2015; Kausch et al. 2015), and VISIR (Smette et al. 2007) extracted PWV from absorption or emission line spectra through the atmospheric radiative transfer model. The PWV from UVES standard star spectra was retrieved from the telluric absorption lines in the UVES flux-calibrated spectra by fitting an atmospheric radiative transfer model (Querel et al. 2011). There are 2657 STAR PWV measurements obtained during the period of 2000–2016 that can be compared with PWV from OH(8-3) band. The STAR PWV can be publicly obtained from ESO website1.
The OH(8-3) band emissions in UVES data taken from 2000 to 2016 were used in our study (see Fig. 6). To guarantee enough resolution and S/N, the spectra with a minimum exposure time of 500 s and slits between 0.3″ and 2.0″ were considered. Then, we obtained a sample of 1953 spectra according to the selection criteria. To quantitatively verify OH airglow method to retrieve the PWV, we compared OH(8-3) PWV with STAR PWV. When comparing the PWV values retrieved from the two methods we note that the two observations are not in the same time. If the time difference between the two observation methods is larger than three hours, it is not used as a sample for the quantitative comparison. In accordance with this condition, we obtained 419 pairs of samples from 2000 to 2016, which are shown in the left panel of Fig. 7.
 |
Fig. 6. OH(8-3) band from UVES Phase 3 data sample with a slit 1.0 and exposure time 1800 s measured on March 19, 2008. Intensity without flux-calibrated is given in adu. The P1 branch lines used in this work are also labeled. |
 |
Fig. 7. Comparison between the PWV values derived from OH(8-3) airglow and STAR PWV from 2000 to 2016 (left), and the scatter plots and fitting lines of the two observations (right). |
4.2. Comparison of PWV values from OH(8-3) and UVES
Because the UVES instrument is located on Cerro Paranal station, which is at 2635 m altitude, the weighted altitude range of the effective cross section is considered. The UVES sky emission data was obtained from the astronomical target observations, thus the retrieved PWV is in the same time and line of sight as the targets, which makes it convenient to correct for the effect of water vapor on targets.
The PWV values of two observations from 2000 to 2016 are shown in Fig. 8. It is shown that the PWV values derived from the two different observations have similar seasonal variations. From Fig. 8, we can see that there is a pronounced seasonal variation in the PWV, for example, maximum water vapor in southern summers and very minimal water vapor in southern winters.
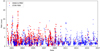 |
Fig. 8. Comparison of PWV values derived from OH(8-3) band and that from UVES standard star spectrum on Cerro Paranal from 2000 to 2016. |
The averaged difference between OH(8-3) and STAR PWV is 0.66 ± 1.17 mm. We used linear regression to fit these samples by the following formula:
where, y and x are the OH(8-3) PWV and STAR PWV, respectively, and α is the slope of the regression line. If the PWV values of the two observation methods are absolutely consistent, α should be 1. The scatter plots and regression result are given in the right panel of Fig. 7. The regression result indicates that the slope α = 1.06 ± 0.03. It is interesting that β = 0.51 ± 0.09 is larger than 0, which means that the OH(8-3) PWV values are systematically larger than the STAR PWV. This may be explained by the systematic differences of OH Einstein coefficient values provided by various researchers (Liu et al. 2015). We also calculated the correlation coefficient between these two observation methods and obtain r = 0.87, which means they are highly consistent.
In addition, we also calculated the PWV using the OH(8-3) band spectra observed by the airglow spectrometer of the Chinese Meridian Project from 2012 to 2016 at Xinglong Observatory in China (40.4° N, 117.6° E), and compared the PWV with that measured by the radiosonde nearby. The slope of the regression is α = 0.98 ± 0.02. This result further confirmed the reliability of the method.
5. Candidate OH airglow spectral bands for PWV retrieval
OH airglow emission lines and water vapor absorption lines have very wide spectral distribution, from the visible to infrared region. Therefore, besides the OH(8-3) band, there are some other OH airglow emission bands can be used for water vapor retrieval. In this work, we discuss candidates of OH airglow emission bands in the visible and near-infrared region, which is from 600 nm to 1000 nm. As a candidate OH airglow emission band for water vapor retrieval, some conditions are needed. First, there should be relative strong radiation intensity to improve the S/N of the measurement. Second, there should be an OH emission line has absorption by water vapor in the band. Finally, the spectral band does not overlap and is not contaminated by other radiation lines.
In the visible and near-infrared region, the OH(7-3) band has some lines with strong absorption by water vapor. However, the P2(1.5) line overlaps with Q1e(4.5) in the OH(7-3) band (Fig. 26 in Osterbrock et al. 1996). The intensity of Q1e(4.5) line is about 11% of P2(1.5). These lines are separated by only 0.026 nm, which is hard to be distinguished by the present observation. This contamination affects the retrieval of water vapor. The UVES sky emission spectra dataset also contains Q and R branch lines of OH airglow, but this dataset is not suitable for PWV retrieval. For the Q branch lines, the line intensities decrease quickly with the rotational levels. Only two lines have high intensity, and the third line usually has low intensity. For the R branch lines, the lines are dense and the strong lines are always blended with some weak lines. Thus, the Q and R branch lines are not considered.
Through screening, we obtained four candidate OH airglow radiation bands that can be used for water vapor inversion. Table 1 lists these bands of OH airglow with absorption more than 4% by water vapor for some lines in the band (labeled in red) under the condition of 5.0 mm PWV. For convenience, Table 1 gives these candidates according to the strength of water vapor absorption. From Table 1 we can see that the water vapor absorption on the P1e(4.5) line in the OH (8-3) band is the strongest, which reach to about 12% for 5 mm PWV.
Four candidates of OH airglow bands in the region from 600 nm to 1000 nm for PWV retrieval.
Figure 9 gives water vapor absorptivities of lines in the four candidate OH bands in Table 1 for different PWV values. From the figure we can see that the OH(8-3) and OH(7-2) bands are more sensitive to water vapor than the OH(5-1) and OH(8-2) bands for small moisture content. However, when the PWV increases to 60 mm, the absorptions of the OH(8-3) and OH(7-2) bands increase to 50%, and intensities of these lines are weak owing to absorption by water vapor. Water vapor retrieval is easily affected by the observation noise. Thus, for the location of large water vapor, the OH(8-2) band is suitable for the retrieval of PWV.
 |
Fig. 9. Variations of water vapor absorptivities of absorption lines in OH(8-3), OH(7-2), OH(5-1), and OH(8-2) bands with different PWV values. |
Generally speaking, astronomical observation stations are located in high altitude areas, which are relatively dry, so it is most advantageous to use OH (8-3) and OH (7-2) to retrieve water vapor. However, for areas with large water vapor, it is more advantageous to use the OH airglow spectral bands of weak water vapor absorption, such as the OH(8-2) band, to retrieve water vapor.
6. Conclusions
Water vapor in the atmosphere, which undergoes large spatial and temporal variations, has a serious impact on ground-based astronomical observations during the night owing to water vapor attenuation and emission, from the visible band to the infrared band. The sky subtractions from astronomical targets are also affected by water vapor emission or absorption lines (Davies 2007; Noll et al. 2014; Soto et al. 2016). Therefore, measurements of water vapor locally, in real-time, and along the line of sight of astronomical observations are very important for removing the effects of water vapor.
In this work, we give a method for retrieving the PWV from the OH(8-3) airglow spectrum from ground-based astronomical observations, which is based on the method of Chadney & Whiter (2018) which uses auroral and airglow emissions to study the polar atmosphere. The effects of the temperature, pressure, and various water vapor vertical distributions of the atmosphere on the cross section of water vapor absorption lines are analyzed in detail. The results indicate that if the pressure, temperature, and water vapor from three conditions (mid-latitude summer and winter in MODTRAN and the US standard atmosphere 1976 model) are used for the calculation of the cross section, the relative differences of the effective cross sections are less than 5%. This means that there is also less than 5% difference between the PWV values retrieved from the effective cross sections. Therefore, we provide a quick and effective method for calculating effective absorption cross sections from profiles of the US standard atmosphere 1976 model. This is because these vertical distributions are not available in the actual observation.
A Monte Carlo simulation is performed to analyze the accuracy of uncertainty, which has validated the PWV retrieval method. Furthermore, the correctness of any method should be verified by a cross comparison of multiple observation methods. Therefore, we compared the retrieved water vapor content from OH airglow with the PWV derived by the standard star absorption spectra. The results show that these two observations agree with each other. The slope of the linear regression is α = 1.06, which shows that the two methods have good consistency.
Besides the OH(8-3) band, other candidates of OH airglow emission bands for PWV retrieval in the visible and near-infrared region are given. The OH emission band with strong water vapor absorption is suitable for water vapor inversion in dry areas, while the weak water vapor absorbed OH band is more favorable for PWV inversion in humid areas.
In summary, airglow emissions inevitably exist in astronomical observations and the method of retrieving the PWV from ground-based OH airglow spectrum observations can provide water vapor locally, in real-time, and along the line of sight of ground-based astronomical observation. This method is especially adapted for water vapor correction of astronomical observations.
Acknowledgments
This work was supported by the National Natural Science Foundation of China (41831073 and 41704151), the Open Research Project of Large Research Infrastructures of CAS – “Study on the interaction between low/mid-latitude atmosphere and ionosphere based on the Chinese Meridian Project” and the Chinese Meridian Project. This project made use of the ESO Science Archive Facility. UVES Phase 3 spectra from different observing programs of the period from April 2000 to December 2016 were analyzed. Moreover, we thank Dr. Alain Smette for his detailed and very helpful comments, especially the suggestion of using the UVES sky emission data set.
References
- Baker, D. J., & Stair, A. T. 1988, Phys. Scr., 37, 611 [Google Scholar]
- Chadney, J. M., & Whiter, D. K. 2018, Geosci. Instrum. Method. Data Syst., 7, 317 [CrossRef] [Google Scholar]
- Chadney, J. M., Whiter, D. K., & Lanchester, B. S. 2017, Ann. Geophys., 35, 481 [CrossRef] [Google Scholar]
- Davies, R. I. 2007, MNRAS, 375, 1099 [NASA ADS] [CrossRef] [Google Scholar]
- Espy, P., & Hammond, M. 1995, J. Quant. Spectr. Rad. Transf., 54, 879 [CrossRef] [Google Scholar]
- Franzen, C., Hibbins, R. E., Espy, P. J., & Djupvik, A. A. 2017, Atmos. Meas. Tech., 10, 3093 [CrossRef] [Google Scholar]
- Gordon, I., Rothman, L., Hill, C., et al. 2017, J. Quant. Spectr. Rad. Transf., 203, 3 [Google Scholar]
- Kausch, W., Noll, S., Smette, A., et al. 2015, A&A, 576, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kerber, F., Querel, R. R., Hanuschik, R. W., et al. 2010, in Ground-based and Airborne Telescopes III, eds. L. M. Stepp, R. Gilmozzi, H. J. Hall, et al., Int. Soc. Opt. Photonics (SPIE), 7733, 579 [Google Scholar]
- Kerber, F., Rose, T., Chacón, A., et al. 2012, in Ground-based and Airborne Instrumentation for Astronomy IV, eds. I. S. McLean, S. K. Ramsay, H. Takami, et al., Int. Soc. Opt. Photonics (SPIE), 8446, 1248 [Google Scholar]
- Li, Z., Muller, J.-P., & Cross, P. 2003, J. Geophys. Res.: Atmos., 108, 4651 [CrossRef] [Google Scholar]
- Liu, W., Xu, J., Smith, A. K., & Yuan, W. 2015, J. Geophys. Res.: Space Phys., 120, 10069 [CrossRef] [Google Scholar]
- Naylor, D. A., Chapman, I. M., & Gom, B. G. 2002, in Atmospheric Radiation Measurements and Applications in Climate, ed. J. A. Shaw, Int. Soc. Opt. Photonics (SPIE), 4815, 36 [CrossRef] [Google Scholar]
- Noll, S., Kausch, W., Kimeswenger, S., et al. 2014, A&A, 567, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Noll, S., Kimeswenger, S., Proxauf, B., et al. 2017, JASTP, 163, 54 [Google Scholar]
- Osterbrock, D. E., Fulbright, J. P., Martel, A. R., et al. 1996, PASP, 108, 277 [NASA ADS] [CrossRef] [Google Scholar]
- Querel, R. R., Naylor, D. A., Thomas-Osip, J., Prieto, G., & McWilliam, A. 2008, in Ground-based and Airborne Instrumentation for Astronomy II, eds. I. S. McLean, & M. M. Casali, Int. Soc. Opt. Photonics (SPIE), 7014, 1805 [Google Scholar]
- Querel, R. R., Naylor, D. A., & Kerber, F. 2011, PASP, 123, 222 [NASA ADS] [CrossRef] [Google Scholar]
- Radomski, J., Trancho, G., Fuhrman, L., et al. 2010, in Observatory Operations: Strategies, Processes, and Systems III, eds. D. R. Silva, A. B. Peck, B. T. Soifer, et al., Int. Soc. Opt. Photonics (SPIE), 7737, 445 [Google Scholar]
- Smette, A., Horst, H., & Navarrete, J. 2010, in The 2007 ESO Instrument CalibrationWorkshop, eds. A. Kaufer, & F. Kerber, 433 [Google Scholar]
- Smette, A., Sana, H., Noll, S., et al. 2015, A&A, 576, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Soto, K. T., Lilly, S. J., Bacon, R., Richard, J., & Conseil, S. 2016, MNRAS, 458, 3210 [NASA ADS] [CrossRef] [Google Scholar]
- von Savigny, C., McDade, I. C., Eichmann, K.-U., & Burrows, J. P. 2012, Atmos. Chem. Phys., 12, 8813 [Google Scholar]
- Xu, J., Gao, H., Smith, A. K., & Zhu, Y. 2012, J. Geophys. Res.: Atmos., 117, D24106 [Google Scholar]
All Tables
Four candidates of OH airglow bands in the region from 600 nm to 1000 nm for PWV retrieval.
All Figures
 |
Fig. 1. Water vapor absorption spectra for multiple water vapor levels. Shown are 5 mm, 10 mm, and 20 mm PWVs, parameters from HITRAN2016, and the OH(8-3) band P1(4.5) double lines with Doppler broadening. |
| In the text | |
 |
Fig. 2. Observation of UVES on March 19, 2008 example. The linear line is fitted using P1(2.5), P1(3.5), and P1(5.5) line intensities in the OH(8-3) band. The P1(4.5) emission line without absorption by water vapor is indicated with an asterisk. The error bars are the uncertainties of intensities, which are estimated by the S/N given in the UVES dataset. |
| In the text | |
 |
Fig. 3. Atmospheric pressure (panel a), temperature (panel b), and water vapor density (panel c) profiles of the US standard atmosphere 1976 and MODTRAN mid-latitude summer and winter atmosphere models, and effective absorption cross sections of water vapor and relative differences among them (panel d). |
| In the text | |
 |
Fig. 4. Water vapor transmission of OH(8-3) P1 branch lines varying with PWV. |
| In the text | |
 |
Fig. 5. Retrieved PWV for 200 simulated measurements for each true value PWV. The error bars are the standard deviation of each simulation. The comparison of the PWV retrieval not considering water absorption in P1(2.5), P1(3.5), and P1(5.5) lines (left panel) and correcting for the effect (right panel). |
| In the text | |
 |
Fig. 6. OH(8-3) band from UVES Phase 3 data sample with a slit 1.0 and exposure time 1800 s measured on March 19, 2008. Intensity without flux-calibrated is given in adu. The P1 branch lines used in this work are also labeled. |
| In the text | |
 |
Fig. 7. Comparison between the PWV values derived from OH(8-3) airglow and STAR PWV from 2000 to 2016 (left), and the scatter plots and fitting lines of the two observations (right). |
| In the text | |
 |
Fig. 8. Comparison of PWV values derived from OH(8-3) band and that from UVES standard star spectrum on Cerro Paranal from 2000 to 2016. |
| In the text | |
 |
Fig. 9. Variations of water vapor absorptivities of absorption lines in OH(8-3), OH(7-2), OH(5-1), and OH(8-2) bands with different PWV values. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



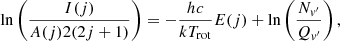
![$$ \begin{aligned} I(v)=I_0(v)\exp \left[-\int _0^{Z_0} \sigma (v,z)n_{\mathrm{H}_2\mathrm{O}}(z)\mathrm{d}z\right], \end{aligned} $$](/articles/aa/full_html/2020/07/aa34621-18/aa34621-18-eq3.gif)
![$$ \begin{aligned} T_{\mathrm{H}_2\mathrm{O}}^\mathrm{the}=\frac{\int [I(v-v_1)+I(v-v_2)]T_v(v)\mathrm{d}v}{\int [I(v-v_1)+I(v-v_2)]\mathrm{d}v} ,\end{aligned} $$](/articles/aa/full_html/2020/07/aa34621-18/aa34621-18-eq5.gif)