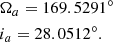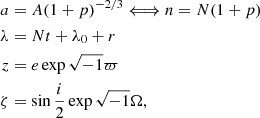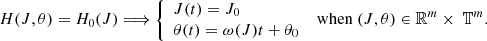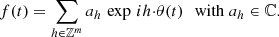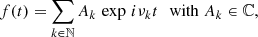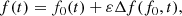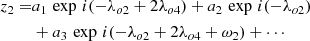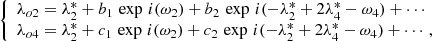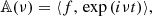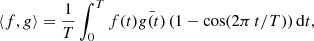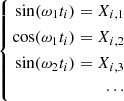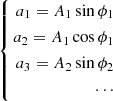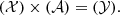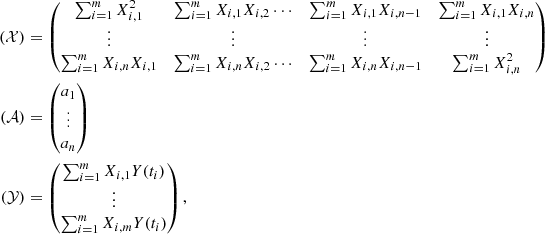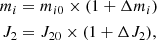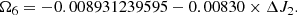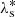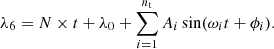| Issue |
A&A
Volume 635, March 2020
|
|
|---|---|---|
| Article Number | A91 | |
| Number of page(s) | 10 | |
| Section | Celestial mechanics and astrometry | |
| DOI | https://doi.org/10.1051/0004-6361/201937148 | |
| Published online | 12 March 2020 | |
Analytical representation for ephemeride with short time spans
Application to the longitude of Titan
1
National Time Service Centre (NTSC), Chinese Academy of Sciences, PO Box 18, Lintong, Shaanxi 710600, PR China
2
IMCCE, Observatoire de Paris, PSL Research University, CNRS, UPMC Univ. Paris 06, Paris, France
e-mail: Xiaojin.Xi@obspm.fr
3
Université de Lille, Observatoire de Lille, 59000 Lille, France
e-mail: alain.vienne@univ-lille.fr
Received:
20
November
2019
Accepted:
15
January
2020
Context. The ephemerides of natural satellites resulting from numerical integration have a very good precision on the fitting to recent observations, in a limited interval. Meanwhile, synthetic ephemerides like the Théorie Analytique des Satellites de Saturne (TASS) by Vienne and Duriez describe in detail the dynamical system by a representation based on the combinations of the proper frequencies. Some theoretical studies need to have both advantages. For example, to study the rotation of Titan, one needs to know the representation of its longitude.
Aims. We aim to use these two types of ephemerides in order to rebuild a long-lasting and high-precision ephemeris with proper frequencies based on the numerical integration ephemeris. The aim is to describe the numerical ephemerides with formulas similar to analytical ones.
Methods. We used the representation of the orbital elements from the TASS ephemeris analysed over 10 000 years as a reference template. We obtained the proper frequencies with both numerical and the TASS ephemeris over 1000 years only. A least-square procedure allowed us to get the analytical representation of an orbital element in this limited interval.
Results. We acquire the representation of the mean longitude of Titan from JPL ephemeris over 1000 years. For almost all components, the corresponding amplitudes and phases are similar to the relative terms from TASS. The biggest difference between our representation and the mean longitude of Titan of JPL is less than 100 km over 1000 years, and the standard deviation is about 26 km.
Key words: ephemerides / celestial mechanics / planets and satellites: individual: Titan / methods: numerical
© X. J. Xi and A. Vienne 2020
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1. Introduction
Numerical ephemeris of natural satellites, which is widely used in research and space projects and conveniently available for download from the online service, based on the recent observations, is highly precise. Meanwhile, due to the limited span of numerical epheremeris, the study of the motions could not benefit from the good precision of numerical ephemeris. Otherwise, theory ephemeris includes all the details of the system motion in the representation with the proper frequencies. It is helpful in the research of the influences between the different satellites in the planetary system.
We envision making a connection between these two kinds of ephemerides. The aim is to represent numerical ephemeris in the form of a representation with the proper frequencies. We attempt to obtain the proper frequencies of the system in a limited time span of numerical ephemeris and repeat the similar representation of itself.
In this paper, we take the JPL ephemeris (Giorgini et al. 1996) for experiment and the Théorie Analytique des Satellites de Saturne (TASS) ephemeris (Vienne & Duriez 1995) as the template. TASS is available at the ftp service of IMCCE1, and the Jet Propulsion Laboratory Horizons On line Ephemeris System (JPL) is available on its website2. It provides access to key solar system data and flexible production of highly accurate ephemeris for solar-system objects (HORIZONS 2018). This includes 715 000+ asteroids, 3420 comets, 178 natural satellites, all planets, the Sun, 99 spacecraft, several dynamical points such as Earth-Sun L1 to L5 equilibriums, and system barycentres. For its Saturn satellite ephemeris, the official published precision is about 10km. Therefore, JPL ephemeris is the better choice for our work.
We compared the difference between JPL and TASS in the ephemerides of Titan in Cartesian coordinates. The difference is small enough (about 2600 km over 1000 years, and no more than 200 km in the last 100 years) for us to suppose it is possible to find a similar representation of the mean longitude of Titan in JPL.
All motions are referred to the Saturnicentric equatorial plane in which the origin corresponds to the node with the mean ecliptic J2000. The node and the inclination referred to the equinox, and ecliptic J2000 system are defined as:
Each orbit of the satellites located in this system is described by the osculating ecliptic elements p, λ, z, and ζ. The definition of those variables are:
where a, e, i, Ω, ϖ, and λ are the classical elliptic elements.
n is the osculating mean motion, and N is the mean mean motion, in such a way that r has no linear component in time (r has only the quasi-periodic parts). All the classical elliptic elements correspond to the constant GMs(1 + m/Ms) (G is the Gaussian constant of gravitation, Ms and m are the masses of the planet and its satellites).
On the website, the Horizon system presents ephemeris in classical orbital elements (a, e, i, ω, ϖ, M) in the ecliptic plane. It is the normal form of ephemeris, but different from the one we used. In our work, we transferred the ephemeris into four orbital elements that form in the ring plane of Saturn with the values given in Eq. (1).
In short, we give the abbreviations of some important concepts in this paper, which are mentioned repeatedly. We name TASS-t (Sect. 2) as the template of TASS, which includes the representation of mean longitude of Titan and all the proper frequencies of Saturnian system involved in the representation, and we take TASS-s (Sect. 4) as the experiment results, consisting of the obtained representation of mean longitude of Titan and the proper frequencies of the limited interval.
FA is the abbreviation of the frequency analysis (Sect. 2), LSM means the least-square method (Sect. 3).
2. Frequencies and synthetic representation of motion
We know that a conservative dynamical system can be described by its frequencies (Laskar et al. 1992), and the stability of its orbits can be studied by the frequency analysis (Laskar 1993). For regular motions, the frequencies description has the advantage of giving rise to an analytical representation of the solutions. Generally speaking, it is important to determine the frequencies that influence the orbital elements of a dynamical system: in Saturn’s system, it can be helpful to study the resonances between satellites in detail. To this aim, we use the method based on a refined numerical search for a quasi-periodic approximation of its solutions over a finite timespan (Laskar 1993).
2.1. Integrable system, quasi-periodic series and proper frequencies
Considering an integrable Hamilton system with m degree of freedom based on Hamiltonian H, if the system evolves within the hypothesis of the Arnold-Liouville theorem, some coordinates called action-angles (J, θ) exist, with which the description dynamics of the system is quite simple:
The dynamics of the system can be described by the variable Jj exp iθj(t): the motion takes place on a m dimension torus, around Jj, with the constant angular velocities ωj. Unfortunately, we have no way of knowing the possible coordinate modification of those variables: this is the difficulty of analytical theories. However, the action-angle coordinates are intrinsic of the system, in other words, even though a system is written by “bad” variables, it should still evolve with its proper frequencies ωj.
We assume a function f(t) describing a mechanical system. For example, f(t) may stand for one of the variables in Eq. (2). The previous properties allow us to write f(t) as a Fourier series of θ:
By developing the scalar product h ⋅ θ(t), we then obtain a series in the form:
where the νj is integer combination of the proper frequencies ωj.
Suppose that we have a dynamics solution f(t) by the numerical integration of equations, to make a frequency analysis in the form of Eq. (5), but with a finite sum of the major terms, allowing us to determine the amplitude Ak and the frequencies νk of the expansion of f(t). In order to complete this step, we only need to identify the νk as a integer combinations further to have the proper frequencies.
In the following, we assume that the system is integrable, or at least, close to an integrable system.
2.2. Some particularities in the arguments of TASS
With TASS, we performed the analytic resolution of each satellite to find the solution of this form (Vienne & Duriez 1991, 1995):
where f(t) represents generically p, r, z or ζ. f0 describes the secular evolution of the variables, εΔf is the oscillatory motion with a small amplitude (ε is a small parameter). Then, the Lagrange equations are expanded in Taylor series around f0(t) and separated into the long-period terms and the short-period terms. The integration of short-period Lagrange equations is done analytically and term by term (at the first order of the masses, i and e are assumed constant): the solution we get is Δf(f0; t). Independently, the secular part is obtained through frequency analysis of numerical integration and leads to the solution f0(t).
Concretely, TASS supplies the solutions f0(t) and Δf(t) in the form of a trigonometric series. However, the description is ambiguous: Δf(t) depends implicitly on f0(t). The complete solution f(t) should behave like a trigonometric series as Eq. (4), but the amplitudes and frequencies are not written explicitly. For example, here is the preliminary expansion of z2 the variable z of Enceladus which is given in TASS:
The amplitudes ak are given explicitly in TASS, but the components λo are described as:
with ω2,  ,
,  and ω4 the proper angles, as explained in Sect. 2.1. Here and in the following, the subscript means that the argument corresponds to the proper frequency (roughly, the frequency of the main term in the frequency analysis of the corresponding element).
and ω4 the proper angles, as explained in Sect. 2.1. Here and in the following, the subscript means that the argument corresponds to the proper frequency (roughly, the frequency of the main term in the frequency analysis of the corresponding element).
2.2.1. A frequency analysis: FA and TASS-t
The short period terms in TASS have not formed as the series with exact proper frequencies. To avoid this particularity, we performed a frequency analysis of all the elements of Titan given by TASS (over 10 000 years) in order to make an explicit series such as Eq. (4). These can then be compared with other ephemerides like JPL or the ones named NOE (Lainey et al. 2004a,b).
The numerical analysis programme is implemented in C language (FA for short). The elements could be represented as the combinations following the D’Alembert rule. The software is made by Saillenfest (2014). The method is based on the works of Laskar et al. (1992) and Laskar (1993). The purpose is to reconstruct the quasi-periodic function f(t) like Eq. (5) (with a finite sum), from a series of points over the interval [0; T]. To find the first frequency ν1, we have to find the maximum of the function |𝔸(ν)| where
with
in which 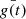 is the complex conjugate of g(t).
is the complex conjugate of g(t).
We suppose that f(t) is tabulated with a step small enough to neglect the aliasing and the numerical errors in the quadrature. In practice, we first performed a fast Fourier transform (FFT) in order to approximatively situate this maximum. The other frequencies are determined in the same way.
The elements corresponding to f(t) could be represented as the combinations following the D’Alembert rule as seen in Eq. (4).
The representation of TASS-t (template of TASS), is used as the template in the following. TASS-t is given in Tables A.1–A.4 for Titan. For better understanding of the paper, we also give the series for elements of Iapetus z8 and ζ8 (Tables A.5 and A.6). Their main terms influence the solution of Titan. All the elements used are in the ring plane (defined by Eq. (1)). It should be noted that the 10 000-year time span corresponds to an extrapolation in such a way that TASS and TASS-t have the same precision.
3. Extension of the frequency analysis (FA) via the least-squares method (LSM)
The difference between JPL and TASS in the ephemeris of Titan is so tiny that we sufficiently find a similar representation of the mean longitude of Titan in JPL. Our problem lies in determining the long-period terms similar to what we found in TASS-t, such as:
where Y(t) is one of the elements of TASS-t and nt corresponds to the number of the terms. In the case of the mean longitude, we have to add the main slope N × t + λ0.
Unfortunately, we cannot use FA to directly obtain the amplitudes and phases of these nt terms. Worse still, we know nothing about these frequencies of JPL ephemeris. Therefore, the solution has to be done separately in two steps. Firstly, we set all the proper frequencies involved in the representation with fixed values, which we do in Sect. 4 and present in Table 3. Then, we get the amplitude and phase of every component through the LSM.
With a step of 0.6 days over 1000 years, we have m = 607800 the number of equations for the mean longitude of Titan. If we note
We easily see that the equations are:
Here,
(𝒳) is the [m × n] matrix of equations, and (𝒜) as a one-dimensional unknown matrix. n is equal to the number of parameters, which is two times nt the number of terms. For every ti, the frequency of phase and amplitude of the components do not change, the difference between every equation depends on the time and Y(t).
We take Eq. (14) to find the representation Eq. (11) of mean longitude of Titan with JPL.
4. Determination of the proper frequencies
With the limited interval, such as 1000 years of the JPL, it is difficult to make distinguish between all the components with FA. Therefore, we use the least-squares method described in the previous section. However, in this procedure, we need to know the values of the set of proper frequencies. We validate our method using TASS itself, but over 1000 years only, and estimate the accuracy of the method by comparing the obtained solution, named TASS-s, with TASS-t.
Focusing on the mean longitude of Titan, the proper frequencies involved in its representation are:
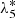 (N5) proper frequency of the mean longitude of Rhea.
(N5) proper frequency of the mean longitude of Rhea.
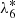 (N6) proper frequency of the mean longitude of Titan.
(N6) proper frequency of the mean longitude of Titan.
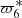 proper frequency of the pericentre of Titan.
proper frequency of the pericentre of Titan.
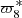 proper frequency of the pericentre of Iapetus.
proper frequency of the pericentre of Iapetus.
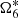 proper frequency of the ascending node of Titan.
proper frequency of the ascending node of Titan.
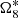 proper frequency of the ascending node of Iapetus.
proper frequency of the ascending node of Iapetus.
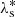 (Ns) proper frequency of mean longitude of the Sun.
(Ns) proper frequency of mean longitude of the Sun.
Λ6 undefined frequency used in TASS.
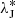 (NJ) proper frequency of mean longitude of Jupiter.
(NJ) proper frequency of mean longitude of Jupiter.
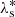 (NS) proper frequency of mean longitude of Saturn.
(NS) proper frequency of mean longitude of Saturn.
4.1. The main slope in mean longitude: N and λ0
The main slope is computed using two methods. The first is a simple least-squares method, or more specifically in this case, a least-squares regression. The second one is using FA on 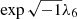 .
.
The mean mean motion N. The mean longitude of Titan λ6 is a quasi-periodic variable with a cycle of about 16 days. The mean mean motion compute with 1000 years λ6 in TASS-s is called NT1 for short. Similarly, NT10 is the mean mean motion of 10 000 years λ6 in TASS-t. The biggest difference among NT10 (FA), NT10 (LSM), and NT1 (LSM) in the position is about 25 km over 1000 years, presented in Table 1. It is not a big one, hence we take into account that both methods could find the system value of the short period components, no matter the interval or the ephemeris.
Mean motion N and phase λ0 of TASS in different intervals.
Hereinafter, when we talk about the mean mean motion of Titan in TASS-t, we use the value of NT10 = 143.924047849167 radian per year from FA. Reasonably, we take NJ1 = 143.924045534754 radian per year from FA as the parameter of mean mean motion of Titan in JPL.
The choice of phase λ0. The choice of phase in the mean longitude of Titan, λ0 (in Table 1) is important. Table 2 shows the solution of λ6 with phase of 1000 years JPL, marked as JP. Correspondingly, in the same table, we also give the solution with phase from TASS-t. Obversely, a bad choice of the phase yields a large error in three major components 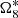 ,
, 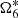 , and Λ6. Moreover, it also affects the amplitude of
, and Λ6. Moreover, it also affects the amplitude of 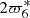 . If we do not have TASS-t as a reference to think about the difference in λ0 of different intervals, it would be impossible to detect those mistakes with only the statistical indicators of the residuals.
. If we do not have TASS-t as a reference to think about the difference in λ0 of different intervals, it would be impossible to detect those mistakes with only the statistical indicators of the residuals.
Comparison of the solutions of the mean longitude of Titan from JPL with different values of λ0.
4.2. Obtained proper frequencies of the limited interval ephemeris: TASS-s and JPL
In Table 3, we list the frequencies of TASS and JPL in used. We explain how to obtain them in subsequent section.
Proper frequencies from TASS-t, TASS-s and JPL, (the selected values are marked with ⋆).
4.2.1. Mean longitude of Rhea: 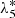 and mean longitude of the Sun:
and mean longitude of the Sun: 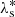
With the results above, the proper frequencies of these short-period terms (and also the mean longitude of Jupiter) are similar: the value obtained with FA over 1000 years can be considered as the system value. They are given in Table 3. The following discussion is based on many experiments in the thesis of Xi (Xi 2018). More details can be found through this reference. We just talk about the main experiments and their conclusions in this paper.
4.2.2. Longitude of the pericentre of Titan: 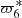
The difference in 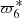 between TASS-t and TASS-s corresponds to 0, 17 years in the period and about 79.03 km in the position after 1000 years. This difference is acceptable. For JPL, we are confident of the value determined by FA of z6 over 1000 years. In Table 3, we take 0.008931618591 radian per year as
between TASS-t and TASS-s corresponds to 0, 17 years in the period and about 79.03 km in the position after 1000 years. This difference is acceptable. For JPL, we are confident of the value determined by FA of z6 over 1000 years. In Table 3, we take 0.008931618591 radian per year as 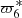 for TASS-s and 0.008922847882 radian per year for JPL.
for TASS-s and 0.008922847882 radian per year for JPL.
4.2.3. Longitude of the ascending node of Titan: 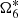
The 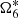 is present as the major component in the variable ζ6 equals to
is present as the major component in the variable ζ6 equals to 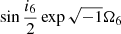 . In Table A.4, we see a constant term for which we do not know the value for JPL. In Xi (2018), the many experiments we did show that the value of
. In Table A.4, we see a constant term for which we do not know the value for JPL. In Xi (2018), the many experiments we did show that the value of 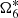 is well-correlated with the constant term. The best choice is to remove the constant term of TASS-t then compute the value of
is well-correlated with the constant term. The best choice is to remove the constant term of TASS-t then compute the value of 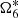 of JPL by FA. By extending our tests, we prefer to use the formula given in Vienne (1991) here. In this work, the values of the physical parameters are included numerically in each coefficient of the development, but the trace of the physical parameters is analytically preserved by the use of numerical partial derivatives:
of JPL by FA. By extending our tests, we prefer to use the formula given in Vienne (1991) here. In this work, the values of the physical parameters are included numerically in each coefficient of the development, but the trace of the physical parameters is analytically preserved by the use of numerical partial derivatives:
where
mi, is the mass of the satellite i. J2 is the main coefficient of the oblateness perturbation, whereas mi0 and J20 are the initial values of the parameters. The influence of Δm5 and Δm8 are negligible. Furthermore, the nominal value of Ω6, −0.0089306 radian per year, was obtained before the fitting of TASS on observations. So it is better to use the TASS-t value. The equation we use is:
We take ΔJ2 = −0.00046, computed from the comparison of J2 used in Vienne & Duriez (1995) and in the website of JPL (HORIZONS 2018). We obtain 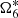 = 0.008935057595 radian per year in our following calculations. We note that we did not use the partial derivatives with respect to the initial conditions. We point out that the difference in
= 0.008935057595 radian per year in our following calculations. We note that we did not use the partial derivatives with respect to the initial conditions. We point out that the difference in 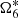 coming from the different initial conditions from TASS and JPL are supposed to be negligible.
coming from the different initial conditions from TASS and JPL are supposed to be negligible.
4.2.4. Longitude of the pericentre of Iapetus: 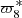
The period of 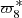 is about 3200 years, so the pericentre can not finish its cycle even once in the limited interval. An FA of
is about 3200 years, so the pericentre can not finish its cycle even once in the limited interval. An FA of 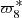 over 1000 years gives 0.001801807851 radian per year for TASS-s, and 0.001816807217 radian per year for JPL. Both are far away from 0.001974690829 radian per year of TASS-t but close to each other. As JPL and TASS describe the same dynamical system, we cannot be confident in the value determined by FA of
over 1000 years gives 0.001801807851 radian per year for TASS-s, and 0.001816807217 radian per year for JPL. Both are far away from 0.001974690829 radian per year of TASS-t but close to each other. As JPL and TASS describe the same dynamical system, we cannot be confident in the value determined by FA of 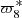 over 1000 years. So for TASS-s and JPL, we chose the value of TASS-t (Table 3): 0.001974690829 radian per year. We also note that this value gives better results than the one obtained from the formula in Vienne (1991) similar to Eq. (15).
over 1000 years. So for TASS-s and JPL, we chose the value of TASS-t (Table 3): 0.001974690829 radian per year. We also note that this value gives better results than the one obtained from the formula in Vienne (1991) similar to Eq. (15).
4.2.5. Longitude of the ascending node of Iapetus: 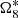
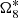 is the biggest component in the representation of the mean longitude of Titan, that the accuracy of its proper frequency has a significant influence on our final solution.
is the biggest component in the representation of the mean longitude of Titan, that the accuracy of its proper frequency has a significant influence on our final solution.
The main part of the longitude of the ascending node of Iapetus in JPL is pleasantly surprising as −0.001957029522 radian per year. With constants of their own, the two frequencies over 1000 years for TASS and JPL obtained with the LSM are similar. It leads to a departure of 30.83 km in the position over 1000 years, and no more than 0.14 years in the period. We cannot be confident of the value obtained over 1000 years for JPL. We prefer the value of −0.001925543543 radian per year of TASS-t as the proper frequency of the ascending node of Iapetus of JPL. We prefer to keep the value −0.001946457996 radian per year of TASS-s as an alternative to experiment with it.
4.2.6. Resonance 2:5 between Jupiter and Saturn: Λ6
In TASS, several possible combinations with similar values exist: 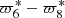 ,
, 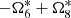 , or
, or 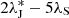 . The time interval required to separate
. The time interval required to separate 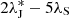 of the others would be 80 000 years and 600 000 years to separate
of the others would be 80 000 years and 600 000 years to separate 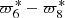 and
and 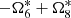 . The authors of TASS take it as
. The authors of TASS take it as 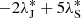 as an indirect perturbation of Jupiter. In JPL, Λ6 is not clearly identified.
as an indirect perturbation of Jupiter. In JPL, Λ6 is not clearly identified.
We do not know the exact combination in JPL. Therefore, we tested all these values and compared the means and standard deviations of the corresponding residuals (Table 4). We conclude that the distributions of residuals are almost the same, except the last line, which is mentioned as (TASS, PHASE) in Table 4. The choice of Λ6 made no difference, so we preferred to take the one from TASS-t.
Mean and standard deviation of the residuals for different uses of all the possible values of Λ6.
4.3. Proper frequencies involved: system values and obtained values
Now we have all the involved values of the proper frequencies for rewriting the representation of mean longitude of Titan. Table 3 shows the group of proper frequencies in TASS-t, the homologous values obtained over 1000 years, and those we adopted to determine the representation of JPL. The ones marked with ⋆ are not the ones obtained from the limited interval ephemeris, but the selected values after our comparison of the results. A group of frequencies is used to examine the precision of the LSM, and the error coming from the inaccurate proper frequency of the selected group. Finally, we took the JPL column to get the amplitudes and phases in the representation of mean longitude of Titan with JPL, which is our ultimate purpose.
4.4. Determination of the short period and semi-long period terms
In the mean longitude of Titan (Table A.2), there are three terms involving the mean longitude of the Sun, which turns hundreds or thousands of times in 1000 years, hence their amplitudes and phases being easier to find. It is more convenient to remove these short period and semi-long period terms before we consider all the other terms with the LSM. We made a small modification of FA in order to find the amplitude and phase of a peak which is close to a given frequency.
The obtained values for TASS-s are given in Table 5. Compared with the corresponding lines of Table A.2, there are some differences in frequency, amplitude, and phase, but the disparities are not big.
TASS-s: representation of λ6 for TASS over 1000 years with the obtained proper frequencies by the least-squares method.
For JPL, as we did with TASS, we found the short-period terms involving 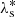 by FA. We show them in the corresponding lines of the final Table 7. These three terms are well-removed to simplify the following calculations (see Fig. 1).
by FA. We show them in the corresponding lines of the final Table 7. These three terms are well-removed to simplify the following calculations (see Fig. 1).
 |
Fig. 1. Periodic part of the mean longitude r and its residuals after removing the short-period terms in the JPL. The red curve is the mean longitude of Titan from which we have removed the linear part. The blue one represents the follow-up results when taking out the short-period components involving |
5. Test of the method: TASS-s
We tested our method with TASS over 1000 years to focus on the long-period terms. In representation TASS-t, 2Ω8 is slowly changing with a tiny amplitude (12 km) and is correlated with 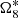 in the limited interval, which yields the failure to solve the equation. Therefore, we ignored 2Ω8 and took the other five terms in total into the calculation. They are
in the limited interval, which yields the failure to solve the equation. Therefore, we ignored 2Ω8 and took the other five terms in total into the calculation. They are 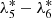 ,
, 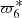 ,
, 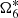 ,
, 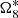 , and Λ6.
, and Λ6.
The result of TASS-s is given in Table 5. For each component, we show the frequency, the solution of amplitude and phase, the corresponding period, and the argument (like in Table A.2) for TASS-t.
The global comparison between TASS-s and TASS-t shows that: the mean of residuals of TASS-s is about −58 m, and the deviation of residuals of TASS-s is about 16 km. The result from −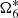 has a deviation of about 70 km. It influences the near component Λ6 to absorb it (68 km difference in amplitude).
has a deviation of about 70 km. It influences the near component Λ6 to absorb it (68 km difference in amplitude).
We carried out another test using the TASS-t system proper frequencies. Of course, the comparison is better: The biggest difference between the amplitudes is smaller than 5 km, the mean of the residuals is no more than 1 m, and the deviation of the residuals is also 16 km. The major error of the LSM is the truncation error. The solution of the LSM is credible for our following work. The disparities from phase are so small that they can be ignored. More details of these comparisons can be found in Xi’s thesis (Xi 2018).
The representation TASS-s have a limited truncation error of 10 km. All these results support our theory that the same method should work well to obtain the representation of the mean longitude of Titan with JPL.
6. Representation of the mean longitude in JPL
After these tests, we are confident in our LSM applied in the JPL ephemerides. Now, we have prepared everything to focus on the long period terms of the mean longitude of Titan in JPL. Similarly, 2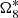 are ignored, and only these five terms are considered:
are ignored, and only these five terms are considered: 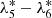 ,
, 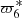 ,
, 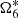 ,
, 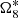 , and Λ6.
, and Λ6.
The representation of 1000 years JPL is given in Table 6, mentioned as JPL in the second line. For an easy comparison, the line mentioned as TASS-t is the exact TASS system value. For every component, we show its identification in the first column along with its frequency. After that, there are the amplitudes, both in radians and kilometres, then their phase in radians.
Comparisons of the representation of mean longitude of Titan between TASS-t and JPL.
From the comparison between TASS-t and the experiment with TASS-s, we can conclude that:
– The difference in amplitude of 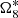 is about 74 km, which corresponded to the system disparity of both ephemerides.
is about 74 km, which corresponded to the system disparity of both ephemerides.
– Because of the uncertain proper frequency 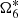 (obtained value), the error in amplitude of the LSM is more than 100 km. As in TASS-s, it influenced the amplitude of component Λ6.
(obtained value), the error in amplitude of the LSM is more than 100 km. As in TASS-s, it influenced the amplitude of component Λ6.
– When we use the theoretical value of 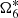 in the calculation, the difference between the amplitude of
in the calculation, the difference between the amplitude of 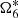 reduced to no more than 4 km, along with the influence to Λ6, disappeared.
reduced to no more than 4 km, along with the influence to Λ6, disappeared.
– Except the system difference in the major component 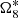 , the other results from JPL are very similar to TASS-t.
, the other results from JPL are very similar to TASS-t.
Figure 2 gives the residuals. They correspond to the mean longitude of Titan in JPL when all the obtained components of “JPL” are removed. So, they are the residuals between real ephemeris and our representation. We can find that the curve scatters much more in the period away from J2000.0. We cannot explain what causes such behaviour. Using FA on the residuals gives no more information. The mean of these residuals is about −13.27 m, and the standard deviation is about 25.59 km. The biggest difference is no more than 100 km over 1000 years.
 |
Fig. 2. Residuals of our representation of the mean longitude of Titan of JPL. |
Figure 3 gives an image of the consistency of our solutions. We take different numbers of terms into the LSM programme: one term for the first time, two terms for the second time, and so on, to make sure that we get the best solution. From the distribution of curves, we find that the solution of five terms is better than of four terms, and both solutions are consistent and stable. Here, we note that the residuals in Fig. 3 are not calculated with the final choice of the proper frequencies in our solution, but with the obtained proper frequencies in our initial experiment. That is why the blue curve in Fig. 3 is not the same as, or as good as in Fig. 2.
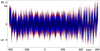 |
Fig. 3. Residuals of our representation of the mean longitude of Titan of JPL using five terms or only four terms. The red curve corresponds to the residuals when we take four terms in the calculation, and the blue one corresponds to the residuals of five terms. |
7. Conclusion
Our final solution is gathered in Table 7. It means that we can obtain the mean longitude of Titan in JPL at any time with our formula:
Mean longitude of Titan in JPL as the form: 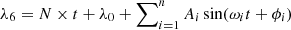 .
.
We attempt to establish a connection between theoretical ephemerides and ephemerides resulting from numerical integration. If we manage to avoid the shortcoming of the limited interval, we obtain the characteristics of the system like the proper frequencies. This task is very useful for theoretical studies, for example, the study of natural satellite rotation.
In the case of orbital motion, we can expand the perturbing function as a function of the osculating elements, in order to use the Lagrange equations or their equivalent in Hamiltonian form. Moreover, the proper frequencies for a complex system can be obtained with an approximate motion. Therefore, we possibly obtain the proper frequencies and the representation of a numerical ephemeris. We use both the FA and the LSM in our calculations.
The limited interval influences the proper frequency values. In summary, long period terms such as −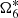 , −
, −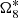 , −
, −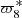 , and −
, and −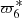 , are more affected, while short period terms like
, are more affected, while short period terms like 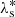 ,
, 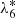 , and
, and 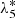 are almost unaffected. So, we choose the corresponding values obtained for the LSM to get TASS-s only.
are almost unaffected. So, we choose the corresponding values obtained for the LSM to get TASS-s only.
Finally, we repeat our work with the JPL, and obtain the proper frequencies and the representation in mean longitude of Titan. The difference between our results and ephemeris itself is less than 100 km over 1000 years. Therefore, from now on, our formula works well to accurately estimate the value of the mean longitude of Titan, for example, for the study of its rotation.
We intend to complete our work with a similar analysis of the other orbital elements from JPL ephemerides, in order to have a complete ephemeris of Titan. Our method could also be applied to other Saturnian satellites, and moreover, using other numerical ephemerides like NOE (Lainey et al. 2004a,b).
Acknowledgments
The authors want to thank N. Rambaux from IMCCE for many fruitful discussions. Thank also to Melaine Saillenfest for the use of his software of frequency analysis. The authors are indebted to all participants of the Encelade WG, supported by the International Space Science Institute (ISSI). X. J. Xi acknowledges support from the China Scholarship Council (CSC) (2014-3026) as well as financial support from the National Science Foundation of China (NSFC) (11573029 and 11603029).
References
- Giorgini, J. D., Yeomans, D. K., Chamberlin, A. B., et al. 1996, BAAS, 28, 1158 [Google Scholar]
- HORIZONS 2018, HORIZONS Web-Interface, https://ssd.jpl.nasa.gov/?horizons/ [Google Scholar]
- Laskar, J. 1993, Phys. D: Nonlinear Phenom., 67, 257 [NASA ADS] [CrossRef] [Google Scholar]
- Laskar, J., Froeschlé, C., & Celletti, A. 1992, Phys. D: Nonlinear Phenom., 56, 253 [NASA ADS] [CrossRef] [Google Scholar]
- Lainey, V., Arlot, J. E., & Vienne, A. 2004a, A&A, 420, 1171 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lainey, V., Duriez, L., & Vienne, A. 2004b, A&A, 427, 371 [Google Scholar]
- Saillenfest, M. 2014, Représentation Synthétique du Mouvement des Satellites de Saturn, Report of Paris Observatory [Google Scholar]
- Vienne, A. 1991, Théorie Analytique des Satellites de Saturne, Thesis [Google Scholar]
- Vienne, A., & Duriez, L. 1991, A&A, 246, 619 [NASA ADS] [Google Scholar]
- Vienne, A., & Duriez, L. 1995, A&A, 297, 588 [NASA ADS] [Google Scholar]
- Xi, X. J. 2018, Analytical Representation for Ephemeris with Short Time Span: Application to the Longitude of Titan, Thesis [Google Scholar]
Appendix A: Additional tables
Mean motion of Titan p6.
Mean longitude of Titan in the ring plane of Saturn, λ6 = N × t + λ0 + r6.
Eccentricity and the pericentre of Titan: 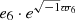 .
.
Inclination and the ascending node of Titan: 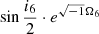 .
.
Eccentricity and the pericentre of Iapetus: 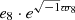 .
.
Inclination and the ascending node of Iapetus: 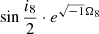 .
.
All Tables
Comparison of the solutions of the mean longitude of Titan from JPL with different values of λ0.
Proper frequencies from TASS-t, TASS-s and JPL, (the selected values are marked with ⋆).
Mean and standard deviation of the residuals for different uses of all the possible values of Λ6.
TASS-s: representation of λ6 for TASS over 1000 years with the obtained proper frequencies by the least-squares method.
Comparisons of the representation of mean longitude of Titan between TASS-t and JPL.
All Figures
 |
Fig. 1. Periodic part of the mean longitude r and its residuals after removing the short-period terms in the JPL. The red curve is the mean longitude of Titan from which we have removed the linear part. The blue one represents the follow-up results when taking out the short-period components involving |
| In the text | |
 |
Fig. 2. Residuals of our representation of the mean longitude of Titan of JPL. |
| In the text | |
 |
Fig. 3. Residuals of our representation of the mean longitude of Titan of JPL using five terms or only four terms. The red curve corresponds to the residuals when we take four terms in the calculation, and the blue one corresponds to the residuals of five terms. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.