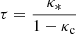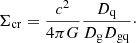| Issue |
A&A
Volume 633, January 2020
|
|
|---|---|---|
| Article Number | A107 | |
| Number of page(s) | 14 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201936462 | |
| Published online | 20 January 2020 | |
The signature of primordial black holes in the dark matter halos of galaxies
Institute for Astronomy (IfA), University of Edinburgh, Royal Observatory, Blackford Hill, Edinburgh EH9 3HJ, UK
e-mail: mrsh@roe.ac.uk
Received:
5
August
2019
Accepted:
17
October
2019
Aims. The aim of this paper is to investigate the claim that stars in the lensing galaxy of a gravitationally lensed quasar system can always account for the observed microlensing of the individual quasar images.
Methods. A small sample of gravitationally lensed quasar systems was chosen where the quasar images appear to lie on the fringe of the stellar distribution of the lensing galaxy. As with most quasar systems, all the individual quasar images were observed to be microlensed. The surface brightness of the lensing galaxy at the positions of the quasar images was measured from Hubble Space Telescope frames, and converted to stellar surface mass density. The surface density of smoothly distributed dark matter at the image positions was obtained from lensing models of the quasar systems and applied to the stellar surface mass density to give the optical depth to microlensing. This was then used to assess the probability that the stars in the lensing galaxy could be responsible for the observed microlensing. The results were supported by microlensing simulations of the star fields around the quasar images combined with values of convergence and shear from the lensing models.
Results. Taken together, the probability that all the observed microlensing is due to stars was found to be ∼3 × 10−4. Errors resulting from the surface brightness measurement, the mass-to-light ratio, and the contribution of the dark matter halo do not significantly affect this result.
Conclusions. It is argued that the most plausible candidates for the microlenses are primordial black holes, either in the dark matter halos of the lensing galaxies, or more generally distributed along the lines of sight to the quasars.
Key words: dark matter / gravitational lensing: micro / galaxies: halos
© ESO 2020
1. Introduction
The identification of the material making up the dark matter component of the Universe remains one of the most significant unsolved problems in cosmology. So far, most of the effort has gone into the search for elementary particle candidates, but with little success to date. The limits on dark matter particles come from a wide variety of sources, including direct detection (Aprile et al. 2012; Akerib et al. 2014), annihilation signals (Ackermann et al. 2014) and cosmic microwave background (CMB) measurements (Madhavacheril et al. 2014). The search for dark matter in other forms has received little attention, and has largely been confined to the Galactic halo (Alcock et al. 2000; Tisserand et al. 2007; Wyrzykowski et al. 2011), with inconclusive and apparently contradictory results (Hawkins 2015). In these searches, the idea is to detect a population of compact bodies in the halo of the Milky Way by observing the rate at which stars in the background Magellanic Clouds are microlensed. The detection of gravitational waves from a black hole merger (Abbott et al. 2016) has again brought into prominence the possibility (Hawkins 1993, 2011) that dark matter may be in the form of compact bodies, which would most plausibly be solar mass primordial black holes (Bird et al. 2016; Sasaki et al. 2016).
One of the most interesting predictions of the theory of general relativity is the creation of multiple images by gravitational lensing (Einstein 1936). A massive galaxy close to the line of sight to a quasar typically splits the image into two or four observable components. This phenomenon was first observed by Walsh et al. (1979) where the image of the quasar Q0957+561 was split into two components by a massive foreground galaxy. This led to the interesting prediction (Chang & Refsdal 1979) that stars along the light paths to each image could cause significant flux changes on a timescale of a few years. Gott (1981) used this microlensing effect to propose a method to determine whether the dark halos of galaxies were composed of compact bodies. Microlensing can be distinguished from intrinsic variations of the quasar where the changes in brightness in each image are the same, and separated by a short time interval to reflect the difference in light travel time to the observer. For microlensing variations, the individual images change in brightness independently of each other, typically on a timescale of a few years. This is due to the different trajectories of the light rays to each image that are microlensed by different magnification patterns corresponding to the distributions of compact bodies through which they have passed. Microlensing was first definitively observed by Schild & Smith (1991), where the two images of Q0957+561 were seen to vary independently of each other. Since then microlensing has been observed in most quasar systems which have been photometrically monitored over a period of a few years. At first sight this would appear to be a powerful argument for a cosmological distribution of compact bodies acting as microlenses. Given that every line of sight appears to be microlensed, this population of compact bodies would be sufficient to make up the dark matter component of the Universe (Press & Gunn 1973). There is however a problem with this conclusion. Lensed quasars from their nature must have a massive galaxy along the line of sight, and it has generally been assumed that the stellar population in these galaxies is responsible for the observed microlensing (Schild 1990; Falco et al. 1991; Kundić & Wambsganss 1993). However, casual inspection of some well-studied lensed quasar systems seems to cast doubt on this hypothesis, the images appearing to lie well clear of the main light concentration of the lensing galaxy. A good example of this is the double image quasar system HE1104−1805, shown in Fig. 1.
 |
Fig. 1. Hubble Space Telescope image in F555W band of lensed quasar HE1104−1805 showing lensing galaxy. |
The question of the proportion of dark matter in lenses for multiple quasar systems has been addressed by a number of groups (e.g. Mediavilla et al. 2009; Pooley et al. 2012). The approach used in these papers is to evaluate the likelihood of microlensing measurements using frequency distributions obtained from simulated microlensing magnification maps for different values of the fraction of mass in compact objects. They find that maximum likelihood tests favour a mass fraction of less than 10%, which is consistent with the stellar populations of the lensing galaxies. The samples of quasars used in these surveys are quite large, and mostly comprise systems where the quasar images are deeply embedded in the lensing galaxies, and where there is no reason to doubt that the stellar population can account for the observed microlensing.
In this paper we approach the problem of identifying the objects responsible for the microlensing events by starting with observations of the stellar population of the lensing galaxy. We investigate whether the optical depth to microlensing τ associated with these stars is sufficient to produce the observed microlensing. There are several well-studied quasar systems for which the stellar population of the lensing galaxy provides a plausible source for the microlenses. In the Einstein Cross quadruple system Q2237+0305 which has been extensively used for microlensing studies the four images lie close to the centre of the lensing galaxy, and there seems to be little doubt that the stars can be responsible for the observed microlensing. Similarly, image B of Q0957+561 lies deep inside the lensing galaxy, and again the microlensing could plausibly be produced by the stars. There are however a number of systems where the quasar images are being microlensed, but due to the alignment and redshifts of the source and lens, and the mass and compactness of the lensing galaxy, the quasar images lie on the fringe of the stellar distribution. In such cases it is not clear that the optical depth to microlensing of the stars is sufficient to produce the observed microlensing. Complicating factors in the calculation of τ include the possible presence of caustic-induced features that start to appear at moderate optical depth (Kofman et al. 1997; Lee et al. 1997), and the effect of any smoothly distributed dark matter in the halo, which increases the effective optical depth to microlensing due to stars or any other compact bodies (Wambsganss 1992; Schechter & Wambsganss 2002).
This study is based on four gravitational lens systems where the image of a quasar is split into two or four components by a massive galaxy, and the images appear to lie on the fringe of the stellar distribution. All four systems have well-sampled light curves which show large amplitude uncorrelated variations between the quasar images that are attributed to microlensing. The procedure we adopt is to measure the surface brightness of the lensing galaxies as a function of galactocentric distance from Hubble Space Telescope (HST) frames, and convert this to stellar surface mass density. To obtain the total mass profile, and hence the dark matter distribution, we use lens models based on the software of Keeton (2001). This also gives values for convergence and shear at the image positions. Assuming the dark matter to be smoothly distributed, this can then be used to convert stellar surface brightness to optical depth to microlensing. To assess the effects of shear on the microlensing probability we generate simulated microlensing magnification maps. These simulations also provide a way of checking the validity of microlensing probabilities derived from the optical depth measures. An additional correction is needed to account for the finite size of the quasar source. For this purpose we use the most recent values from the literature.
The results of this analysis imply that the probability of the observed microlensing in any one quasar system being due to the stellar population of the lensing galaxy is quite small. We are however mainly interested in the probability that the microlensing in at least one system is not due to stars. We thus ask what is the probability that the microlensing in all the quasar systems in our sample can be attributed to stars, and find the probability to be very small, of the order of 3 × 10−4. For the lensing galaxies to be the source of the microlensing objects, a large part of the dark matter halo must be in the form of stellar mass compact bodies. We conclude that either the dark matter content of the galaxy halos is made up of non-stellar compact bodies, or that there is a more general near-critical density distribution of compact bodies along the line of sight to the quasar, which would make up the dark matter content of the Universe.
If stars in the lensing galaxy are not responsible for the observed microlensing and the variations are attributed to a cosmological distribution of lenses, this raises the question of what the compact bodies really are. If they make up the dark matter then baryonic candidates, including stars and their evolutionary products such as white dwarfs, are ruled out on the basis of baryon synthesis constraints (Smith et al. 1993). A number of non-baryonic candidates have been proposed during the last 30 years or so but we argue that among these, primordial black holes are the only objects for which a plausible case can be made that they make up the dark matter. Throughout the paper we assume ΩM = 0.27, ΩΛ = 0.73 and H0 = 71 km s−1 Mpc−1 for cosmological calculations.
2. The quasar sample
The criteria for the selection of the sample of quasar systems used in this study were designed to choose systems where the images lie on the outskirts of the observable part of the lensing galaxy. In gravitationally lensed quasar systems, several factors determine the position of the images relative to the stellar distribution in the galaxy. The separation of the images on the sky is proportional to the deflecting mass, and their angular distance from the galaxy centre depends on the true angular separation of the source and lens, and their redshifts (Schneider et al. 1992). The compactness of the lensing galaxy also clearly affects the extent to which the quasar images lie within the stellar distribution. The parent sample for the selection of quasar systems to be used in this study was the CASTLES1 database. The criteria for inclusion were that the size estimate as given by CASTLES should be greater than 2.0 arcsec, and that the I magnitude of the lensing galaxy should be less than 20.0. The first of these criteria was to maximise the likelihood that the quasar images lie clear of the stellar distribution of the lensing galaxy, and the second to enable accurate photometry of the stellar population. This resulted in a sample of six quasar sytems. The second criterion was that there should be well sampled light curves available, typically covering around seven years or more. Of the preliminary sample five comfortably passed this test, but the available photometric data for PG1115+080 were fragmentary and inadequate for our programme. Of the remaining five systems, although Q0957+561 satisfied the criteria to be included in the sample, image B is deeply embedded in the lensing galaxy with a measured optical depth to microlensing τ ∼ 0.6 from the stars alone. For this system there is no reason to believe that the stars are not responsible for the microlensing and so it was not included in the analysis. The final sample of four systems is shown in Table 1, together with some basic parameters. zq and zd are the redshifts of the lensed quasar and the lensing galaxy respectively, mI is the apparent magnitude of the lensing galaxy in the I-band from CASTLES measurements, and MI the associated absolute magnitude. Also shown in Table 1 is the core radius Rc containing half the observed light and the Einstein radius RE for a 0.2 M⊙ compact body.
Basic data for lensed quasar systems.
Evidence for microlensing has been found in most gravitationally lensed quasar systems which have been studied in detail. There are basically two ways in which microlensing has been detected. Monitoring of lensed quasar systems shows that the individual images usually vary in an uncorrelated way, which is generally accepted to be the result of microlensing by compact bodies along the line of sight. Much effort has been been put into monitoring brightness changes, notably by the COSMOGRAIL collaboration. This project was primarily motivated by the challenge of measuring time delays between intrinsic brightness changes in the quasar images of a lensed system for the purpose of estimating the value of the Hubble constant (Eigenbrod et al. 2005). However, the light curves produced by the group form an excellent database for measuring the effects of microlensing (Tewes et al. 2013b). An alternative approach is to compare the luminosity of the accretion disc which is small enough to be microlensed by solar mass bodies with flux from less compact regions where little or no microlensing would be expected. A good example is the broad line region which is generally taken to be too large for microlensing by stellar mass objects to produce significant changes in brightness. The ratio of broad line fluxes in the quasar images is used to provide a datum for variations in continuum flux, enabling a single epoch measurement of microlensing (Motta et al. 2012; Sluse et al. 2012). An alternative approach is to use flux ratios of the quasar images in the infrared on the assumption that they originate from an area too large to be microlensed (Blackburne et al. 2011; Sluse et al. 2012). One of the shortcomings of measuring microlensing from differential flux in the component images is that it does not provide an absolute measurement of the resulting change in flux ratio. This problem can be largely overcome by using the single epoch measures of microlensing as described above to provide a datum for the non-microlensed image brightness ratios (Sluse et al. 2012).
All of the quasar systems in our sample in Table 1 have been the subject of extensive optical monitoring programmes for the purpose of measuring time delays in light travel time between the images. For HE1104−1805, early work by Gil-Merino et al. (2002) showed clear evidence for differential variation between the two images over a period of around 3 years. This was followed by longer runs of closely sampled data (Schechter et al. 2003; Ofek & Maoz 2003; Poindexter et al. 2007) to give photometry covering some 8 years. The first light curves for HE0435−1223 covered 2 years (Kochanek et al. 2006) and already showed clear signs of microlensing in the differential variation of the images. This work was followed by a large monitoring programme undertaken by the COSMOGRAIL collaboration spanning 7 years (Courbin et al. 2011) which we use here. RXJ1131−1231 is another target monitored by COSMOGRAIL (Tewes et al. 2013a), and shows the largest microlensing amplitude in our sample, of more than a magnitude. The final member of our sample, WFI2033−4723, was monitored by COSMOGRAIL for three years after which they found no evidence for microlensing (Vuissoz et al. 2008). However, after extending the observations to 8 years (Tewes 2013) a variation of around 0.2 mag was detected. The presence of microlensing was confirmed by differences between the flux ratios of broad band and emission line measures, which implied a microlensing signal of ∼0.5 mag.
Figure 2 shows difference light curves for images of the lensed quasar systems listed in Table 1. The references below the table are for the monitoring data on which the difference curves are based. For the purpose of uniform comparison, and to highlight the long timescale of the microlensing variations, the original data are plotted as half-yearly weighted means. The image pairs corresponding to the difference curves in Fig. 2 (as named in the references to the light curves) are given as F1/F2 in Table 1, and the zeropoints for the flux ratios in the absence of microlensing are shown as magnitude difference Δ0. These zeropoints are derived from the flux ratios of the broad emission line region or from infrared photometry where the emission region is supposed to be too large to be significantly microlensed by stellar mass objects. The zeropoint for HE1104−1805 is taken from Motta et al. (2012), and for the remainder from Sluse et al. (2012) (spectroscopic data) and Blackburne et al. (2011) (infrared photometry). In all cases zeropoints from the two methods are in good agreement. All four systems show distinctive microlensing variations on a variety of timescales, consistent with the statistics of recent surveys for microlensing (Motta et al. 2012; Sluse et al. 2012). The light curves of HE1104−1805 and WFI2033−4723 are dominated by long timescale variations of at least 20 years, while HE0435−1223 and RXJ1131−1231 contain complete events with a timescale of around 10 years. Adopting the conventionally assumed mean transverse velocity of 600 km s−1 for the microlenses, this corresponds to lens masses of around 0.3 M⊙. The amplitude Δm of the light curves in magnitudes is also given in Table 1.
 |
Fig. 2. Difference light curves for images of gravitationally lensed quasars. The differential variations of the images are attributed to microlensing. The derivation of the zeropoints is described in the text. |
3. The lensing galaxies
In order to test the idea that the stellar population of the lensing galaxy is responsible for the observed microlensing, we built up a mass distribution for the lensing galaxy by sticking as far as possible to observations. We started by converting galaxy surface brightness measurements to stellar surface mass density, and hence to optical depth to microlensing τ. For large values of τ a complex network of caustics is formed, resulting in a non-linear amplification pattern for the source. However, for low values, τ is essentially the probability that the trajectory of a light ray is significantly amplified by the gravitational lensing effect of a compact body along the line of sight. A criterion for this low optical depth regime is that τ ≲ 0.1 (Kofman et al. 1997; Lee et al. 1997). τ depends on the surface mass density of both the compact lensing bodies and the more smoothly distributed matter (Schneider et al. 1992), and is defined by:
where κ* and κc are the surface mass densities in compact bodies and smoothly distributed matter respectively, in units of the critical surface mass density Σcr, and
Dg, Dq, and Dgq are the angular diameter distances to the lensing galaxy, to the quasar, and from the galaxy to the quasar respectively. To calculate τ we need values for κ* and κc.
3.1. Surface brightness
To evaluate κ*, we first measured the surface brightness profiles of the lensing galaxies. For this purpose we used HST frames taken with the F160W filter, close to the H-band, for the four systems in Table 1. Working in the infrared, as opposed to the optical, provides a much more favourable contrast between the quasar images which are typically blue, and the redshifted lensing galaxies which are bright in the infrared. Standard IRAF routines were used to measure the F160W flux as a function of distance from the galaxy centre. To recover the undistorted profile of the lensing galaxy, IRAF image analysis routines were used to subtract the flux from the contaminating quasar images and derive the underlying galaxy surface brightness. Most lensing galaxies are symmetric across diagonals, and this feature was used to evaluate the flux contribution from the quasar images to be subtracted from the contaminated galaxy image, and interpolate across spurious small features to provide a clean galaxy profile. These flux measurements were then converted to surface brightness using the appropriate HST photometric zeropoints. In order to check the accuracy of this procedure, the results were compared with similar work from the literature. No surface brightness profiles for the four systems in Table 1 have so far been published, but Bernstein et al. (1997) have measured the profile of the heavily contaminated galaxy in the well-known binary system Q0957+561. This system has not been used for the present study because image B lies close to the centre of the lensing galaxy, and could plausibly be microlensed by the stellar population. However it makes a good test bed for image subtraction techniques. Figure 3 shows the surface brightness profile of the lensing galaxy of Q0957+561 from an HST frame as measured by Bernstein et al. (1997), together with measurements of the same frame using the methods employed for this paper. The agreement is satisfactory, and any discrepancies are small compared with other uncertainties in the evaluation of τ.
 |
Fig. 3. Surface brightness profile for the lensing galaxy of Q0957+561 from a WFPC2 image in the F555W band. Open circles show measures obtained using point spread function subtraction of the quasar images from Bernstein et al. (1997), and filled circles are from the present work. |
3.2. Mass-to-light ratio
To convert the surface brightness into surface mass density, K and evolutionary corrections from Poggianti (1997) were applied to the surface brightness measures to provide a zero redshift galaxy profile in units of stellar luminosity in the H-band. To convert this into surface mass density it is necessary to estimate the mass-to-light ratio of the stellar population in the lensing galaxy. Direct measurement of the stellar mass-to-light ratio in galaxies is not easy due to the uncertain contribution of dark matter, but for an early type galaxy typical of the lensing galaxies in this sample, an appropriate mass-to-light ratio is that measured for globular clusters with similar metallicity. Observations of the mass-to-light ratio of globular clusters in the Milky Way (McLaughlin & van der Marel 2005) and M 31 (Strader et al. 2011) are shown in Fig. 4, plotted against metallicity. The left hand panel is based on a catalogue of dynamical masses for Milky Way globular clusters published by McLaughlin & van der Marel (2005), who use V-band photometry to derive values of M/LV for the clusters in their sample. Some 30 of these objects have been observed in the near infrared bands by Cohen et al. (2007), who also list values for [Fe/H]. We have used this photometry to convert the values of M/LV to M/LH, which are shown plotted against [Fe/H] in Fig. 4. The data show no significant trend with metallicity, and the weighted mean of the globular cluster mass-to-light ratios is M/LH = 0.56 ± 0.21, where we take the dispersion as a measure of uncertainty.
 |
Fig. 4. M/LH versus [Fe/H] for Milky Way globular clusters based on measures of M/LV from McLaughlin & van der Marel (2005) and photometry from Cohen et al. (2007) (left hand panel), and M/LK versus [Fe/H] for M 31 globular clusters from Strader et al. (2011) (right hand panel). |
The right hand panel of Fig. 4 shows measures of M/LK for M 31 globular clusters from Strader et al. (2011). The mass-to-light ratio is calculated from direct measures of velocity dispersion and near infrared photometry, and the data show some trend with metallicity as pointed out by Strader et al. (2011). This is especially true for low values of [Fe/H] where the data are relatively sparse. The weighted mean for the mass-to-light ratio is M/LK = 0.53 ± 0.24, which after a small correction to convert to the H-band using data from Cohen et al. (2007) gives M/LH = 0.57 ± 0.26 for the M 31 globular clusters. In spite of the difference in average metallicity and the trend in [Fe/H] versus M/LK for the M 31 globular clusters, the weighted means for the two samples in Fig. 4 are very similar. On this basis we shall adopt a value of M/LH = 0.56 ± 0.21 which we apply to the surface brightness profile to evaluate κ* as a function of galactocentric distance. Error bars are derived from errors in the measurement of surface brightness. Values of κ* at the image positions of the quasars listed in Table 1 together with errors resulting from uncertainty in the value of M/LH are given in Table 2. Also shown is R, the distance of the quasar image from the centre of the lensing galaxy.
Microlensing optical depth for galaxy halos.
Although it is not feasible to make direct measurements of the stellar mass-to-light ratio of early-type galaxies due to the presence of dark matter, stellar population synthesis (SPS) models provide an alternative approach to estimating it. Conroy & van Dokkum (2012) analyse the spectra of 34 elliptical galaxies combined with a Kroupa IMF to model the stellar mass-to-light ratio in the K-band. They obtain an average value of M/LK = 0.70 ± 0.11, which converts to M/LH = 0.75 ± 0.12. This is a little larger than, but consistent with, the values obtained from direct measurements of M/LH for the globular cluster samples.
3.3. Dark matter halo
To obtain the effective optical depth to microlensing for the stars in the lensing galaxy, we also need values for κc, the surface mass density in smoothly distributed dark matter, at the positions of the quasar images. For this purpose we start with the values of total convergence κ at the quasar image positions from the mass models of Mediavilla et al. (2009) and Pooley et al. (2012), based on the software of Keeton (2001). They use a singular isothermal sphere plus external shear model (SIS + γe) to estimate the total values of projected matter density κ and shear γ at the location of the images. In the case of WFI2033−4723 a small improvement was obtained to the values of κ and γ by including a faint companion in the model (Blackburne et al. 2011). We have verified these models using Keeton’s software, and find that the values of κ and γ are relatively insensitive to the exact dark matter profile of the lensing galaxy as is well illustrated by the work of Wong et al. (2017) in their modelling of HE0435−1223. They use 12 different models for the mass profile, and find that the resulting values for κ and γ only vary by a few percent. κc is then the difference between the values of κ from the mass models and κ* from the stellar surface brightness measuremants.
The optical depth to microlensing τ for stars as a function of galactocentric distance can now be calculated from Eq. (1) for the four quasar systems, and are shown as filled circles in Fig. 5. Also shown as a solid line is the dark matter contribution κc from the SIS + γe profile. The positions of the quasar images are indicated by arrows, and the corresponding values of κc and τ are given in Table 2. Errors on τ based on those for κ* are also shown. The resulting values of τ put the stellar populations of the lensing galaxies in the low optical depth regime (Kofman et al. 1997; Lee et al. 1997), and imply a low probability that stars in the lensing galaxies can produce the strong microlensing features seen in Fig. 2.
 |
Fig. 5. Optical depth to microlensing τ as a function of radial distance for the lensing galaxies of four gravitationally lensed quasars. The solid line shows the surface mass density in smoothly distributed matter as discussed in the text, and the filled circles show the optical depth to microlensing for the stellar population of the lensing galaxy. The arrows indicate the positions of the quasar images listed in Table 2. |
4. Microlensing simulations
In this section we make use of microlensing simulations to illustrate the optical depth regimes relevant to this paper, and then estimate the probability that the amplitudes of the observed light curves can be achieved by microlensing from simulated star fields appropriate to the line of sight to the quasar images. The first studies of microlensing in gravitationally lensed quasar systems were based on the quadruple Q2237+0305 (Irwin et al. 1989; Wambsganss et al. 1990), also known as the Einstein Cross. Due to the overall configuration of this system, and in particular the very low redshift of the lensing galaxy (z = 0.0394) the four quasar images lie within a kiloparsec of the galaxy centre. This results in a high optical depth to microlensing for the stellar population (τ ≳ 0.6), which proved very useful for microlensing studies (Wyithe et al. 2000; Anguita et al. 2008). These values of τ are in the high optical depth regime defined by Kofman et al. (1997), where strong caustic-induced features dominate the magnification pattern. The top left panel of Fig. 6 shows a simulated magnification pattern for a point source with stellar surface density κ* = 0.6 and γ = 0.6, similar to that found for Q2237+0305 (Wyithe et al. 2000). The simulation was carried out using the code of Wambsganss (1999), freely available on the internet. The yellow lines show tracks in the source plane of the same length as the light curves in Fig. 2, using redshifts for the systems from Table 1, and assuming a transverse velocity of 600 km s−1. The tracks have random position and orientation, and illustrate the high probability that quasar images are microlensed by such a large optical depth of lenses. The red line in Fig. 7 shows the light curve corresponding to the longest track in the top left panel of Fig. 6, and it is seen that the image fluctuates in brightness by more than two magnitudes.
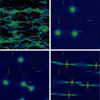 |
Fig. 6. Microlensing magnification patterns for a population of 0.2 M⊙ bodies, assuming a point source. The frames consist of 10002 pixels and have a side length of 18 Einstein radii in the source plane. The parameter values are κ* = 0.6, κc = 0, γ = 0.6 (top left), κ* = 0.04, κc = 0, γ = 0 (top right), κ* = 0.04, κc = 0.4, γ = 0 (bottom left) and κ* = 0.04, κc = 0.4, γ = 0.4 (bottom right). Yellow lines indicate tracks across the amplification pattern for the length of the four light curves in Fig. 2, and a net transverse velocity of 600 km s−1 is assumed. The position and orientation of the tracks is random. |
The top right hand panel of Fig. 6 shows a simulated magnification pattern for a population of 0.2 M⊙ compact bodies with a surface density of κ* = 0.04, typical of the values for the quasar sample in Table 2. These parameters put the value of τ in the low optical depth regime (Kofman et al. 1997), where strong caustic-induced features do not form. The simulation assumes a point source to highlight the fine structure of the magnification pattern, and shows well-separated lenses with clearly defined impact parameters and little sign of distortion. The bottom left hand panel shows the effect of the presence of smoothly distributed matter with κc = 0.4, similar to the values for the dark matter halos in Table 2. The addition of dark matter to the simulations results in the appearance of new images, in line with the value of τ from Eq. (1), but there is still little sign of caustic features. The bottom right hand panel shows the effect of including a shear term in the simulation, equal in size to κc. It is seen that the magnification pattern is smeared out in the direction of the shear, reducing the maximum magnification somewhat. Similar tracks to those in the top left hand panel are superimposed on the amplification patterns to provide a visual illustration of the implications of the low values of τ from Table 2, and the likelihood of a microlensing event in the observed light curves. All the tracks lie well clear of any lensing feature, and the fluctuations in their light curves are negligible.
The probability that the quasars in the sample are microlensed with the observed amplitude difference by stars in the lensing galaxies can be estimated by enlarging the simulated area to contain more lenses, and using the parameters for κ* and κc from Table 2 to provide a simulation for each of the eight quasar images. As an illustrative example, the left hand panel of Fig. 8 shows a simulated magnification pattern for an area 16 times larger in the source plane than for Fig. 6, using typical values for κ* and κc from Table 2. To enable a realistic estimate of the probability of microlensing we must take into account the finite size of the continuum disc of the quasar. Jimenéz-Vicente et al. (2015a) use a microlensing study of a large sample of lensed quasars to obtain a value of 7.9 light days for the half-light radius of the accretion disc at 1736 Å for an average quasar. This figure is a factor of two larger than their earlier result (Jimenéz-Vicente et al. 2012) and consistent with the compilation by Mosquera et al. (2013). It also appears to be consistent with the reverberation mapping results of Mudd et al. (2017) for quasars. Given the sensitivity of the microlensing amplitude to the source size we shall conservatively adopt the 2σ lower bound of 4 lt-day or 1016 cm from Jimenéz-Vicente et al. (2015a). Combining this with values for the Einstein radius RE from Table 1 gives a disc radius of around 0.5RE which we use in the simulation in Fig. 8. The sensitivity of our results to source size is discussed further in Sect. 8. Yellow tracks corresponding to the length of the light curves in Fig. 2, but in random position and orientation, are also plotted as for Fig. 6. The simulation in the right hand panel of Fig. 8 is as for the left hand panel, but with the addition of a shear term equal to κc. The effect of shear is basically to smear the magnification pattern along a preferred axis in such a way that small magnifications become slightly more frequent, and high magnifications are less likely to be achieved. As Schneider et al. (1992) point out, in many applications the effect of the shear is neglected for simplicity, but we include the right hand panel of Fig. 8 to clarify the point.
 |
Fig. 8. Microlensing magnification patterns for a population of 0.2 M⊙ bodies with parameter values κ* = 0.04, κc = 0.4, γ = 0 (left hand panel) and κ* = 0.04, κc = 0.4, γ = 0.4 (right hand panel). Each frame consists of 10002 pixels and has a side length of 72 Einstein radii in the lens plane. The tracks are as for Fig. 6. The plots have been convolved with a source size of 0.5RE. |
For each of the quasars in Table 1 two simulations were run, one for each image, with appropriate values for κ* and κc. In the first instance κ* and κc were set equal to the values given for the two corresponding images in Table 2, together with a source of half-light radius 4 lt-day. Tracks corresponding to the length of the light curve for that quasar were placed on the two simulations in random positions and orientations, and the magnitudes from the amplification patterns subtracted to give the difference light curve. The amplitude Δ of this difference light curve was then compared with the observed amplitude Δm from Table 1. By repeating this procedure a number of times, the frequency with which Δ exceeded Δm was counted, and hence the probability that the observed value of Δm was the result of microlensing by the simulated star field corresponding to the lensing galaxy was estimated. The results of this process are given in the first line of data for each quasar in Table 3. The first seven columns identify the quasar system and give the parameters used in the simulation for each of the two associated images. Subsequent columns give the number of runs with random placing of the light curves, the number of times N(Δ > Δm) that the amplitude of the simulated difference light curve exceeded the observed amplitude, and the consequent probability P(Δm) that it is the result of microlensing. Due to the large number of trials, the Poisson error on this probability is quite small, less than 0.0003 in all cases. The second lines of data in Table 3 show the results for simulations with the same parameters as for the first line, but with the addition of a shear term from the mass models used to estimate the convergence at the image positions.
Microlensing probabilities.
In order to estimate the probability that all four quasar systems would be found to be microlensed as observed, we combined the four sets of simulations in Table 3 and counted the number of times that all four quasars simultaneously exceeded the amplitude of their light curves in Fig. 2. This figure was found to be zero, with or without a shear contribution. Given that RXJ1131−1231 was observed to vary with a very large amplitude which may be a statistical fluke, we also counted the number of times that all but one of the quasars exceeded their observed amplitude. In this case for the runs with shear set to zero, and for the non-zero values of γ from Table 3, the numbers were 111 and 318 respectively. We discuss the significance of these results in Sect. 5.
5. Results
The results of this paper are basically summarised in Tables 2 and 3, and the data in each table may be used to estimate the probability that the microlensing observed in the four quasar systems in Table 1 can be attributed to stars in the lensing galaxies. To put it another way, we take as a statistical hypothesis that the observed microlensing in at least one quasar system is not caused by stars in the lensing galaxy. This is the question of interest, as it measures the probability that there is some other population of compact bodies along the line of sight. In Table 2 the values for τ are in the low optical depth regime and effectively measure the probability of microlensing by a star in the lensing galaxy. Given that the light path to each quasar image is different, and hence the values of τ are independent, they can be combined in a straightforward way to give the probability that all four systems are being simultaneously microlensed by stars in the lensing galaxies, or equivalently that at least one system is not. Using the data for the images which become brighter gives a probability of 1 × 10−5 that all the quasars are microlensed by stars. As we discuss below, there is a case to be made that RXJ1131−1231 is in some way untypical of lensing systems due to its very low value for τ. If we allow RXJ1131−1231 to be excluded by requiring only 3 systems to be microlensed, this increases the probability to 3 × 10−4.
The results from the microlensing simulations in Table 3 provide an alternative way of estimating the probability that a stellar distribution similar to the one seen in the lensing galaxies can produce the observed microlensing. For each quasar system the first line in Table 3 shows microlensing simulations using values for convergence from lenses κ* and smoothly distributed matter κc equal to the values in Table 2 for the lensing galaxies at the positions of the quasar images. The source size was set to 4 lt-day, as discussed in Sect. 4. As might be expected, light curves with larger amplitudes are less likely to be produced in the simulations as can be seen in Table 3, especially for RXJ1131−1231. If RXJ1131−1231 is included in a probability calculation as for Table 2, the probabilty of all systems being microlensed by stars is neglibly small (< 10−6). However, there is some reason to believe that RXJ1131−1231 may have an unusually large amplitude (Pooley et al. 2012), and so to make a more conservative estimate of the probability that the stars are responsible for the microlensing we have repeated the calculation excluding RXJ1131−1231. In this case the probability that all three of the remaining systems are microlensed by the stars is 1 × 10−4, of the same order as the result for the data in Table 2. For the simulations including shear terms, the probability increases to 3 × 10−4. This is close to the result of the simulation counting the number of times at least 3 systems were simultaneously microlensed, where the 318 coincidences in 106 trials give a probability of 3 × 10−4.
RXJ1131−1231 has stood out in our analysis as anomolous, with an exceptionally small value of τ and a large change in brightness, resulting in a very low probability for microlensing from the observed stellar population. This system has already been identified by Pooley et al. (2012) as an outlier in their analysis, and we feel it safest to exclude it from our main result, as its inclusion heavily weights our conclusion against the possibility that the stellar population can cause the observed microlensing. The most obvious explanation is that the lensing galaxy contains a large component of dark microlensing mass, but to follow this up would be beyond the scope of the present paper.
6. Comparison with other work
An alternative approach to estimating the likelihood that stars in the lensing galaxies are responsible for the observed microlensing comes from simulating microlensing patterns for a range of values for the fraction of mass in compact objects. A maximum likelihood or Bayesian analysis is then used to determine the most likely mass fraction to be responsible for the observed microlensing amplitude (Mediavilla et al. 2009; Pooley et al. 2012). These two studies find a most likely overall mass fraction in compact objects to replicate the observed microlensing of less than 10%, which in general would be compatible with the size of the stellar population of the lensing galaxies. For comparison with the analysis in this paper we have listed our values for the mass fraction in stars at the quasar image locations in Table 2. They are quite similar to the values from Mediavilla et al. (2009) and Pooley et al. (2012), and in fact if they are plotted against the data in Fig. 6 of Jimenéz-Vicente et al. (2015b) they follow the line of their composite model with a small negative offset of about 20%. From this we deduce that any difference in our conclusions is not due to differing values for the mass fraction, but depends on whether the resulting surface density of stars can actually produce the observed microlensing. As has been discussed in Sect. 4, microlensing amplitudes are strongly dependent on the size of the quasar source. Mediavilla et al. (2009) assume a source size of 1 lt-day, which is much less than the value we have used and could well account, at least in part, for the apparent difference in our results. Pooley et al. (2012) base their analysis on X-ray microlensing, and feel justified in assuming a point source. In this case it is not so easy to make a direct comparison with our results as there is considerable uncertainty as to the actual size of the X-ray emitting region.
It is important to note that the samples of quasar systems used in the two approaches are very different. The samples chosen by Mediavilla et al. (2009) and Pooley et al. (2012) are much larger than the one in this paper, and mostly composed of small separation systems where the quasar images are deeply embedded in the lensing galaxies, and can plausibly be microlensed by stars. By contrast, the sample we use here has been specifically chosen so that the quasar images lie clear of the bulk of the stellar distribution. The significance of this is made clear in Fig. 12 of Pooley et al. (2012) where wide separation lenses (including most of our sample) have a very different probability distribution to their sample as a whole, with a much higher likelihood of a dark matter component consisting of compact objects.
Looking at the probability distributions in more detail raises some interesting questions. In Fig. 7 of Pooley et al. (2012) the histograms for most objects are quite flat, with probabilities in each bin ranging from about 5% to 10%. An interesting exception is RXJ1131−1231 which shows a steady increase in probability to high values of stellar mass fraction. The histogram for HE0435−1223 is not easy to interpret, as it shows two almost equal maxima at 2% and 100% stellar mass fraction.
It is worth emphasising that the Bayesian analysis and the procedure in this paper are essentially measuring different things. The question we have addressed is the likelihood that microlensing by the observed stellar population can always reproduce features of the observed difference light curves, and this means that the stellar component is not treated as a free parameter. By contrast, the Bayesian analysis is measuring the most likely mass fraction in compact bodies. Given that the two samples of lensed systems are quite different, an extensive catalogue of mostly compact systems compared with the small number of known wide separation systems, it is perhaps to be expected that the results are different, but not necessarily contradictory.
7. The identity of the lenses
The idea that dark matter is in the form of compact bodies has a long history. In an early review of dark matter, Trimble (1987) considered such bodies as plausible candidates alongside various elementary particles. Hawkins (1993) proposed that there was observational evidence for a cosmological distribution of compact bodies which betrayed their presence by microlensing quasars, and the evidence for this has recently been reviewed and consolidated (Hawkins 2011). The case for compact bodies as dark matter received a severe setback with the publication of results from microlensing surveys in the Galactic halo (Alcock et al. 2000; Tisserand et al. 2007; Wyrzykowski et al. 2011), which put limits on any population of solar mass compact bodies. However, more recent measures of the structure of the Galactic halo, and reassessment of other aspects of the surveys, have now thrown doubt on the reliability of the limits on dark matter in the form of compact bodies set by these groups (Hawkins 2015; Green 2017; Calcino et al. 2018).
If dark matter is indeed made up of compact bodies, then there are several strong constraints on the form it can take. Combining measurements of light element abundances with the photon density from the CMB gives a fairly robust limit of Ωb < 0.03 (Smith et al. 1993) which effectively rules out baryonic objects as dark matter candidates. This of course includes stars and planets as well as later products of stellar evolution such as white dwarfs, neutron stars and stellar black holes. A second constraint comes from the timescale of microlensing events, which constitute much of the evidence for compact bodies as dark matter. Both the MACHO events in the galactic halo and the microlensing events observed in multiple quasar systems of the type discussed here point to a lens mass of around a solar mass, with an uncertainty of at least a factor of 10 either way. This is nonetheless sufficient to rule out a wide range of candidates, which we discuss below. A final constraint is compactness. Again, since much of the evidence for a cosmological distribution of compact bodies comes from microlensing, dark matter bodies must be compact enough to act as lenses in the configuration in which they are observed.
In her review of the nature of dark matter, Trimble (1987) lists quark nuggets, cosmic strings and primordial black holes as non-baryonic non-particle candidates. Quark nuggets have some virtue as dark matter candidates (Alam et al. 1999), but as their mass is limited to around 10−8 M⊙ they cannot be the objects detected in the microlensing experiments. The possibility that cosmic strings might betray their presence by the microlensing of distant quasars has been investigated in some detail by Kuijken et al. (2008). Their motivation is to establish a method for detecting the presence of cosmic strings, and they estimate that a typical microlensing event would last about 20 years. This fits in well with other microlensing signatures, but the problem they face is that such events would be extremely rare. The optical depth to microlensing for cosmic strings derived by Kuijken et al. (2008) is of the order τ ∼ 10−8 which completely rules them out as the source of the microlensing seen in multiple quasar systems.
An interesting idea proposed by Walker & Wardle (1998) suggesting that extreme radio scattering events might be caused by cold self-gravitating gas clouds has been investigated by Rafikov & Draine (2001) with a view to establishing whether such clouds could be detected by microlensing searches. The clouds are predicted to have masses of around 10−3 M⊙ and radii of ∼10 AU, and would make up a significant fraction of the mass in galaxy halos. Rafikov & Draine (2001) concluded that although strongly constrained by MACHO microlensing searches, such clouds could not be definitively ruled out as the dark matter component of the Galaxy halo. However, as an explanation for the microlensing seen in multiple quasar systems they can be ruled out on the basis of their low proposed mass, and also the fact that they are essentially baryonic and so cannot make up the dark matter on cosmological scales.
The steady improvement in numerical simulations of the formation of large-scale structure from primordial perturbations culminating in the discovery of a universal profile for dark matter halos (Navarro et al. 1995) has raised the question of the nature of their internal strucure on small scales. An ambitious programme to solve this problem was undertaken by the Aquarius Project (Springel et al. 2008) which focussed on simulating the evolution of individual galaxy halos with unprecedented resolution. The two main results of this and other similar simulations were that galaxy halos have cuspy dark matter profiles, and that there should be a very large population of dark matter subhalos. At first sight these subhalos might seem attractive candidates for microlensing quasars, but their structure as described by Springel et al. (2008) imply that they would not be compact enough to act as microlenses for the accretion discs of distant quasars, even if subhalos as small as a solar mass can form.
The objects which have received the most attention as candidates for dark matter in the form of compact bodies are primordial black holes. They satisfy the basic constraints mentioned above in that they are non-baryonic, very compact and can in principle form over a wide range of masses, including those relevant to quasar microlensing. The recent detection of gravitational waves from a black hole merger (Abbott et al. 2016) also supports the idea that dark matter may be in the form of primordial black holes, although there is still debate as to whether the gravitational wave detections should be attributed to black holes of stellar origin. The question of whether primordial black holes in the right mass range can actually be created is the subject of ongoing debate (see for example Clesse & Garcia-Bellido 2015 and references therein), but as things stand they appear to be the only plausible candidates for dark matter in the form of compact bodies. Additional support for this conclusion comes from recent work (Byrnes et al. 2018) using new lattice computations to give an accurate QCD equation of state. The softening of the equation of state during the QCD phase transition implies an enhancement in the production of primordial black holes peaking at around 0.7 M⊙.
8. Discussion
This paper sets out to examine the assumption that the microlensing observed in multiple quasar systems can always be accounted for by the stellar population of the lensing galaxy. The investigation was prompted by the observation that in some such systems the quasar images appear to lie well clear of the lensing galaxy, raising the question of the probability of them being microlensed by the lensing galaxy stars. To assess this probability, the four systems analysed here were chosen specifically because the quasar images were distant from the lensing galaxy. As for nearly all such systems which have been adequately monitored, the individual quasar images were strongly microlensed. The calculation of the optical depth to microlensing was not modelled, but based on direct measurement of the starlight, and hence of the surface density of stars along the line of sight, together with values for total convergence from lens models. The surface brightness measures were made in the near infrared H-band to optimise the contrast between galaxy and quasar light. Measurement of the surface brightness profiles of the lensing galaxies was made more complicated by the distorting effects of the superimposed quasar images, but in practice it turned out to be quite easy to remove the contribution of the star-like quasar images to obtain a good estimate of the underlying galaxy surface brightness. After careful normalisation, clean featureless profiles were obtained which in all cases closely followed the de Vaucouleurs r1/4 law. The good agreement with the work of Bernstein et al. (1997) illustrated in Fig. 3 gives further confidence that the surface brightness profiles are fair measures of the starlight in the lensing galaxies.
One of the advantages of working in the near infrared H-band is the small dispersion in the stellar mass-to-light ratio (M*/LH) for different stellar populations. The pervasive presence of dark matter severely limits the systems which are suitable for direct measurements of M*/LH, and effectively confines the candidates to globular clusters. We have used samples of globular clusters from the Milky Way and M 31 to estimate the stellar mass-to-light ratio of our sample of lensing galaxies. Despite significant differences in the relationship between [Fe/H] and M/LH for the two samples, the mean and dispersion of M/LH were very similar. The reliability with which these values of mass-to-light ratio can be used to estimate M/LH for the lensing galaxies is supported by the evidence for a universal IMF. In a comprehensive review covering a wide range of stellar environments from local stellar populations to distant galaxies Bastion et al. (2010) conclude that “there is no clear evidence that the IMF varies strongly and systematically”. There have nonetheless been claims of evidence for a “bottom heavy” IMF in massive early-type galaxies (van Dokkum & Conroy 2010) where the strength of spectral lines associated with low mass stars in a small sample of elliptical galaxies were argued to be inconsistent with a universal IMF. This conclusion is tentatively supported by Treu et al. (2010) from a study of 56 early-type galaxies using a variety of techniques to obtain the absolute normalisation of the IMF. However, Smith et al. (2015) showed that not all such galaxies have IMFs differing significantly from that of the Milky Way.
These inconsistencies seem to have been largely removed with the availabilty of high spatial resolution spectra, which appear to show a deficit of low mass stars in the central cores of some giant elliptical galaxies (Martín-Navarro et al. 2015). This results in an atypical IMF in the galactic centre, for reasons which are still not properly understood, but throughout the rest of the galaxy the IMF is consistent with that of the Milky Way. This then supports the use of a universal IMF in the calculation of the stellar surface density at the positions of the lensed quasar images which are invariably well clear of the core regions of the lensing galaxies. In addition, recent work by Shanahan & Gieles (2015) has provided an explanation for the small values of M/LK at high metallicities, and confirms the value we have adopted from Fig. 4. Further support for a low mass-to-light ratio in the near infrared is presented by Into & Portinari (2013), who show that taking into account the role of the asymptotic giant branch results in lower estimates of stellar mass in galaxies.
An alternative approach to estimating the mass-to-light ratios of galaxies comes from SPS modelling of stellar populations. The values of M/LH derived from the models of Conroy & van Dokkum (2012) applied to their observations of 34 late-type galaxies are consistent with the dynamically based values from globular clusters in the Galaxy and M 31. The small discrepancies between these two independent methods of estimating the mass-to-light ratio are not large enough to significantly affect the conclusions of this paper.
It is seen from Table 2 that the probability for any individual quasar image in our sample to be microlensed by a star is in the range 2%−12%. The uncertainties in these figures come from three different sources. The first of these is the assumed value for the H-band mass-to-light ratio. The errors given in Table 2 are based on dispersion in large samples of Galactic and M 31 globular clusters, and the very few available direct measures of mass-to-light ratios in early-type galaxies are within these bounds. The second source of uncertainty arises from the contribution of the dark matter halo to the value of τ. The values of κc we have used come directly from models of the lensing configuration, and are relatively insensitive to the assumed mass profile. In fact it is seen from Eq. (1) that for values of κc ≲ 0.5, small changes in κc have only a small effect on the value of τ. The third source of error is from the measurement of surface brightness from the HST frames. These are less than 5% in the value of τ, and small compared with the other sources of error.
Although there has been widespread interest in simulating magnification patterns for large optical depths to microlensing where caustic networks dominate, simulations for low optical depth distributions of lenses have received less attention. In order to provide illustrations of the probability of microlensing at optical depths appropriate to the quasar images in our sample, we have carried out microlensing simulations to show the effect of parameters such as κc and γ in low surface mass distributions. The sparse distribution of lenses and the minimal presence of caustic features can be compared with the widespread caustic network and consequent high probability of microlensing for the optical depth appropriate to the inner regions of a galaxy.
Taken together, the values of τ in Table 2 imply that the probability that most or all of the quasar images are being microlensed by stars in the lensing galaxy is vanishingly small. There is perhaps still some uncertainty over the value of M/LH, in the event that the lensing galaxies in our sample are not typical of the overall population of giant ellipticals, although in the case of one of our sample members HE0435−1223, direct modelling by Wong et al. (2017) gives a value for M/LH that is close to our adopted value. Overall, the errors and uncertainties discussed above do not significantly change this conclusion. In presenting our results we have conservatively excluded RXJ1131−1231 which has a very low surface mass density of stars in the quasar image positions, and a very large amplitude of variation due to microlensing. Inclusion of this system strongly weights our results against the possibility that the stars in the lensing galaxy can be responsible for the observed microlensing. RXJ1131−1231 requires further investigation to determine whether there is a large component of unseen microlensing mass associated with the lensing galaxy.
The probability that the quasar images are being microlensed by stars in the lensing galaxies can also be put on a quantitative footing by the analysis of magnification maps from microlensing simulations. This was achieved by counting the frequency with which randomly generated difference light curves are microlensed by star fields and smoothly distributed dark matter components equal to the values for the lensing galaxies at the positions of the quasar images from Table 2. The simulated light curves were assigned a length corresponding to the time for which each quasar was monitored, and the criterion for being microlensed was that the amplitude of the microlensing simulation exceeded that of the observed light curve. The results listed in Table 3 confirm the low probability that the amplitudes of the quasar light curves are the result of microlensing by the stellar population of the lensing galaxies. In addition to simulations based on the values for κ* and κc from Table 2, we have also carried out simulations to show the effect of shear on our results. It is seen from Table 3 that, as expected, the microlensing probabilities are mostly increased, but still too low to plausibly account for the observed microlensing variations.
The effect of source size on microlensing amplitudes has been discussed in Sect. 4, and it is a source of uncertainty in the microlensing simulations. The effect of increasing the size of a source in microlensing simulations is well illustrated by the figures from Kayser et al. (1986). This is put on a more quantitative footing by Refsdal & Stabell (1991) and Witt & Mao (1994), who derive analytical expressions to describe the decrease in amplitude with increasing source size. We have used a disc with half-light radius of 4 lt-days, which on the basis of recent measurements in the literature would appear to be the smallest plausible size. The actual profile of the source has been shown by Mortonson et al. (2005) to be unimportant compared with the half-light radius in determining the microlensing amplitude.
Over the last decade or more there have been a number of studies designed to use microlensing to measure the mass fraction of stars or compact bodies in galaxy halos. In Sect. 6 we have discussed in some detail two well-known analyses (Mediavilla et al. 2009; Pooley et al. 2012) which conclude that the observed microlensing variations can best be explained by a relatively small proportion of compact bodies, consistent with a plausible stellar component. This result has been supported by a number of other studies adopting slightly different approaches (for example Mediavilla et al. 2017), but resting on a number of assumptions. These include the structure of the dark matter halo, the size of the quasar accretion disc, the mass function of the microlensing bodies and the extent to which the halo is clumpy. In some cases these unknowns are treated as free parameters in a Bayesian analysis, but more direct measurements have turned out to be very illuminating. For example recent studies of stellar dynamics in the Milky Way (Green 2017; Calcino et al. 2018) have illustrated the uncertainties on microlensing constraints from broadening the mass distribution or allowing spatial clustering for the population of microlenses. The effect on microlensing at cosmological distances is still unclear. However, as we have pointed out in Sect. 6, our values for the mass fraction of stars are quite similar to these earlier studies. The main difference between these studies and our approach is that we have confined our sample to widely separated systems where the quasar images lie well clear of the bulk of the stellar distribution. We then directly estimate the probability that the observed surface density of stars can be responsible for the microlensing. These wide-separation systems tend to give atypical results in the large samples used for Bayesian analysis.
If stars in the lensing galaxies are not the primary source of the lenses responsible for the observed microlensing, the question of the true identity of the lenses must be addressed. Although a number of non-particle dark matter candidates have been proposed over the years, our analysis concludes that the only plausible objects consistent with the most fundamental constraints are primordial black holes. In this case the cosmological distribution of dark matter along the line of sight to the quasar would also contribute to the optical depth to microlensing. Whether or not this provides an adequate explanation for the observed microlensing requires further investigation and more detailed modelling, but following the general argument of Press & Gunn (1973) one can say that there is a plausible case that dark matter in the form of compact bodies would be sufficient to account for the observed microlensing in multiply-lensed quasar systems. The recent detection of gravitational waves from a black hole merger (Abbott et al. 2016) provides further support for the idea that primordial black holes make up the dark matter (Bird et al. 2016; Sasaki et al. 2016; Byrnes et al. 2018), although there is still ongoing debate as to whether such mergers are between stellar or primordial black holes.
9. Conclusions
The idea behind this paper is to test the hypothesis that stars in the lensing galaxy of a multiply lensed quasar system can account for the observed microlensing of quasar images. This was achieved by measuring the surface brightness of starlight at the positions of the quasar images and converting this into stellar surface mass density. The surface mass density in smoothly distributed dark matter was estimated from lensing models of the quasar systems, and applied to the surface mass density in stars to obtain the optical depth to microlensing τ. Providing τ is below a critical value, this is a direct measure of the probability that a quasar image is microlensed by the stars in the lensing galaxy. A sample of four gravitationally lensed quasar systems were selected for the test, where the quasar images lie on the fringe of the stellar distribution of the lensing galaxy. Photometric monitoring programmes have shown that in each system the images are varying independently by substantial amounts, implying microlensing by a population of compact objects. For all of these systems the optical depth τ was found to be below the limiting value where caustic features form, thus allowing a straightforward estimate of the probability of microlensing. The hypothesis that we wish to test is that in at least one of the systems in our sample the observed microlensing is not caused by stars in the lensing galaxy, and so by some other population of compact bodies. The probability that each system was being microlensed by stars was calculated to be in the range 2%−12%, implying a probability of around 10−6 that all four systems were microlensed by stars. Uncertainties in the assumed mass-to-light ratio and dark halo structure do not significantly affect this conclusion. There is reason to believe that RXJ1131−1231 may be untypical in its microlensing properties, and so if we conservatively exclude it from our results the probability of the stellar population producing the observed microlensing increases to 3 × 10−4.
Computer simulations of the magnification pattern of lensing galaxy star fields with the observed light curve tracks superimposed support the conclusion that the observed microlensing is very unlikely to be produced by stars. The results from these simulations, again excluding RXJ1131−1231, imply a probability of 3 × 10−4 that the observed microlensing is due to stars in the lensing galaxy, similar to the result from the analysis of optical depth to microlensing. The main uncertainty in the results from the computer simulations is the assumed size of the quasar accretion disc, and so we have accordingly adopted a very conservative value.
We have argued that the most plausible candidates for dark matter in the form of compact bodies are primordial black holes, and the recent detection of gravitational waves attributed to a black hole merger supports this idea. It is possible that dark matter in the form of primordial black holes in the lensing galaxy halos are responsible for the observed microlensing, but it is not clear that they would constitute a sufficiently large optical depth to microlensing. A more plausible possibility is that the microlensing is the result of a cosmological distribution of dark matter primordial black holes along the line of sight to the quasar images.
References
- Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2016, Phys. Rev. Lett., 116, 061102 [Google Scholar]
- Ackermann, M., Albert, A., Anderson, B., et al. 2014, Phys. Rev. D, 89, 042001 [NASA ADS] [CrossRef] [Google Scholar]
- Akerib, D. S., Araújo, H. M., Bai, X., et al. 2014, Phys. Rev. Lett., 112, 091303 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Alam, J., Raha, S., & Sinha, B. 1999, ApJ, 513, 572 [NASA ADS] [CrossRef] [Google Scholar]
- Alcock, C., Allsman, R. A., Alves, D. R., et al. 2000, ApJ, 542, 281 [NASA ADS] [CrossRef] [Google Scholar]
- Anguita, T., Schmidt, R. W., Turner, E. L., et al. 2008, A&A, 480, 327 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aprile, E., Alfonsi, M., Arisaka, K., et al. 2012, Phys. Rev. Lett., 109, 181301 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Bastion, N., Covey, K. R., & Meyer, M. R. 2010, ARA&A, 48, 339 [NASA ADS] [CrossRef] [Google Scholar]
- Bernstein, G., Fischer, P., Tysdon, J. A., & Rhee, G. 1997, ApJ, 483, L79 [NASA ADS] [CrossRef] [Google Scholar]
- Bird, S., Cholis, I., Muñoz, J. B., et al. 2016, Phys. Rev. Lett., 117, 201301 [NASA ADS] [CrossRef] [Google Scholar]
- Blackburne, J. A., Pooley, D., Rappaport, S., & Schechter, P. L. 2011, ApJ, 729, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Byrnes, C. T., Hindmarsh, M., Young, S., & Hawkins, M. R. S. 2018, JCAP, 08, 041 [NASA ADS] [CrossRef] [Google Scholar]
- Calcino, J., Garcia-Bellido, J., & Davis, T. M. 2018, MNRAS, 479, 2889 [NASA ADS] [CrossRef] [Google Scholar]
- Chang, K., & Refsdal, S. 1979, Nature, 282, 561 [Google Scholar]
- Clesse, S., & Garcia-Bellido, J. 2015, Phys. Rev. D, 92, 023524 [NASA ADS] [CrossRef] [Google Scholar]
- Cohen, J. G., Hsieh, S., Metchev, S., Djorgovski, S. G., & Malkan, M. 2007, AJ, 133, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Conroy, C., & van Dokkum, P. G. 2012, ApJ, 760, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Courbin, F., Chantry, V., Revaz, Y., et al. 2011, A&A, 536, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eigenbrod, A., Courbin, F., Vuissoz, C., et al. 2005, A&A, 436, 25 [Google Scholar]
- Einstein, A. 1936, Science, 84, 506 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Falco, E. E., Wambsganss, J., & Schneider, P. 1991, MNRAS, 251, 698 [NASA ADS] [CrossRef] [Google Scholar]
- Gil-Merino, R., Wisotzki, L., & Wambsganss, J. 2002, A&A, 381, 428 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gott, J. R. 1981, ApJ, 243, 140 [NASA ADS] [CrossRef] [Google Scholar]
- Green, A. M. 2017, Phys. Rev. D, 96, 043020 [NASA ADS] [CrossRef] [Google Scholar]
- Hawkins, M. R. S. 1993, Nature, 366, 242 [NASA ADS] [CrossRef] [Google Scholar]
- Hawkins, M. R. S. 2011, MNRAS, 415, 2744 [NASA ADS] [CrossRef] [Google Scholar]
- Hawkins, M. R. S. 2015, A&A, 575, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Into, T., & Portinari, L. 2013, MNRAS, 430, 2715 [NASA ADS] [CrossRef] [Google Scholar]
- Irwin, M. J., Webster, R. L., Hewett, P. C., Corrigan, R. T., & Jedrzejewski, R. I. 1989, AJ, 98, 1989 [NASA ADS] [CrossRef] [Google Scholar]
- Jimenéz-Vicente, J., Mediavilla, E., Munoõz, J. A., & Kochanek, C. S. 2012, ApJ, 751, 106 [NASA ADS] [CrossRef] [Google Scholar]
- Jimenéz-Vicente, J., Mediavilla, E., Kochanek, C. S., & Munoõz, J. A. 2015a, ApJ, 799, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Jimenéz-Vicente, J., Mediavilla, E., Kochanek, C. S., & Munoõz, J. A. 2015b, ApJ, 806, 251 [NASA ADS] [CrossRef] [Google Scholar]
- Kayser, R., Refsdal, S., & Stabell, R. 1986, A&A, 166, 36 [NASA ADS] [Google Scholar]
- Keeton, C. R. 2001, ArXiv e-prints [arXiv:astro-ph/0102340] [Google Scholar]
- Kochanek, C. S., Morgan, N. D., Falco, E. E., McLeod, B. A., & Winn, J. N. 2006, ApJ, 640, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Kofman, L., Kaiser, N., Lee, M. H., & Babul, A. 1997, ApJ, 489, 508 [NASA ADS] [CrossRef] [Google Scholar]
- Kuijken, K., Siemans, X., & Vachaspati, T. 2008, MNRAS, 384, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Kundić, T., & Wambsganss, J. 1993, ApJ, 404, 455 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, M. H., Babul, A., Kofman, L., & Kaiser, N. 1997, ApJ, 489, 522 [NASA ADS] [CrossRef] [Google Scholar]
- Madhavacheril, M. S., Sehgal, N., & Slatyer, T. R. 2014, Phys. Rev. D, 89, 103508 [NASA ADS] [CrossRef] [Google Scholar]
- Martín-Navarro, I., La Barbera, F., Vazdekis, A., Falcón-Barroso, J., & Ferreras, I. 2015, MNRAS, 447, 1033 [NASA ADS] [CrossRef] [Google Scholar]
- McLaughlin, D. E., & van der Marel, R. P. 2005, ApJS, 161, 304 [NASA ADS] [CrossRef] [Google Scholar]
- Mediavilla, E., Muñoz, J. A., Falco, E., et al. 2009, ApJ, 706, 1451 [NASA ADS] [CrossRef] [Google Scholar]
- Mediavilla, E., Jiménez-Vicente, J., Muñoz, J. A., et al. 2017, ApJ, 836, L18 [NASA ADS] [CrossRef] [Google Scholar]
- Mosquera, A. M., Kochanek, C. S., Chen, B., et al. 2013, ApJ, 769, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Mortonson, M. J., Schechter, P. L., & Wambsganss, J. 2005, ApJ, 628, 594 [NASA ADS] [CrossRef] [Google Scholar]
- Motta, V., Mediavilla, E., Falco, E., & Muñoz, J. A. 2012, ApJ, 755, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Mudd, D., Martini, P., Zu, Y., et al. 2017, ApJ, 862, 123 [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1995, ApJ, 462, 563 [Google Scholar]
- Ofek, E. O., & Maoz, D. 2003, ApJ, 594, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Poggianti, B. M. 1997, A&AS, 122, 399 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Poindexter, S., Morgan, N., Kochanek, C. S., & Falco, E. E. 2007, ApJ, 660, 146 [Google Scholar]
- Pooley, D., Rappaport, S., Blackburne, J. A., Schechter, P. L., & Wambsganss, J. 2012, ApJ, 744, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Press, W. H., & Gunn, J. E. 1973, ApJ, 185, 397 [NASA ADS] [CrossRef] [Google Scholar]
- Rafikov, R. R., & Draine, B. T. 2001, ApJ, 547, 207 [NASA ADS] [CrossRef] [Google Scholar]
- Refsdal, S., & Stabell, R. 1991, A&A, 250, 62 [NASA ADS] [Google Scholar]
- Sasaki, M., Suyama, T., Tanaka, T., & Yokoyama, S. 2016, Phys. Rev. Lett., 117, 061101 [NASA ADS] [CrossRef] [Google Scholar]
- Schechter, P. L., & Wambsganss, J. 2002, ApJ, 580, 685 [NASA ADS] [CrossRef] [Google Scholar]
- Schechter, P. L., Udalski, A., Szymański, M., et al. 2003, ApJ, 584, 657 [NASA ADS] [CrossRef] [Google Scholar]
- Schild, R. E. 1990, AJ, 100, 1771 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schild, R. E., & Smith, R. C. 1991, AJ, 101, 813 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, P., Ehlers, J., & Falco, E. E. 1992, Gravitational Lenses (Springer: New York) [Google Scholar]
- Shanahan, R. L., & Gieles, M. 2015, MNRAS, 448, L94 [NASA ADS] [CrossRef] [Google Scholar]
- Sluse, D., Hutsemékers, D., Courbin, F., et al. 2012, A&A, 544, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Smith, M. S., Kawano, L. H., & Malaney, R. A. 1993, ApJS, 85, 219 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, R. J., Lucey, J. R., & Conroy, C. 2015, MNRAS, 449, 3441 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V., Wang, J., Vogelsberger, M., et al. 2008, MNRAS, 391, 1685 [NASA ADS] [CrossRef] [Google Scholar]
- Strader, J., Caldwell, N., & Seth, A. C. 2011, AJ, 142, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Tewes, M. 2013, PhD Thesis, École Polytechnique Fédérale de Lausanne, Switzerland [Google Scholar]
- Tewes, M., Courbin, F., Meylan, G., et al. 2013a, A&A, 556, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tewes, M., Courbin, F., & Meylan, G. 2013b, A&A, 553, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tisserand, P., Le Guillou, L., Alfonso, C., et al. 2007, A&A, 469, 387 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Treu, T., Auger, M. W., Koopmans, L. V. E., et al. 2010, ApJ, 709, 1195 [NASA ADS] [CrossRef] [Google Scholar]
- Trimble, V. 1987, ARA&A, 25, 425 [NASA ADS] [CrossRef] [Google Scholar]
- van Dokkum, P. G., & Conroy, C. 2010, Nature, 468, 940 [NASA ADS] [CrossRef] [Google Scholar]
- Vuissoz, C., Courbin, F., Sluse, D., et al. 2008, A&A, 488, 481 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Walker, M., & Wardle, M. 1998, ApJ, 498, L125 [NASA ADS] [CrossRef] [Google Scholar]
- Walsh, D., Carswell, R. F., & Weymann, R. J. 1979, Nature, 279, 381 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Wambsganss, J. 1999, J. Sci. Comm., 109, 353 [Google Scholar]
- Wambsganss, J. 1992, ApJ, 392, 424 [NASA ADS] [CrossRef] [Google Scholar]
- Wambsganss, J., Paczyński, B., & Schneider, P. 1990, ApJ, 358, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Witt, H. J., & Mao, S. 1994, ApJ, 430, 505 [NASA ADS] [CrossRef] [Google Scholar]
- Wong, K. C., Suyu, S. H., Auger, M. W., et al. 2017, MNRAS, 465, 4895 [NASA ADS] [CrossRef] [Google Scholar]
- Wyithe, J. S. B., Webster, R. L., & Turner, E. L. 2000, MNRAS, 315, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Wyrzykowski, L., Kozłowski, S., Skowron, J., et al. 2011, MNRAS, 413 493 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1. Hubble Space Telescope image in F555W band of lensed quasar HE1104−1805 showing lensing galaxy. |
| In the text | |
 |
Fig. 2. Difference light curves for images of gravitationally lensed quasars. The differential variations of the images are attributed to microlensing. The derivation of the zeropoints is described in the text. |
| In the text | |
 |
Fig. 3. Surface brightness profile for the lensing galaxy of Q0957+561 from a WFPC2 image in the F555W band. Open circles show measures obtained using point spread function subtraction of the quasar images from Bernstein et al. (1997), and filled circles are from the present work. |
| In the text | |
 |
Fig. 4. M/LH versus [Fe/H] for Milky Way globular clusters based on measures of M/LV from McLaughlin & van der Marel (2005) and photometry from Cohen et al. (2007) (left hand panel), and M/LK versus [Fe/H] for M 31 globular clusters from Strader et al. (2011) (right hand panel). |
| In the text | |
 |
Fig. 5. Optical depth to microlensing τ as a function of radial distance for the lensing galaxies of four gravitationally lensed quasars. The solid line shows the surface mass density in smoothly distributed matter as discussed in the text, and the filled circles show the optical depth to microlensing for the stellar population of the lensing galaxy. The arrows indicate the positions of the quasar images listed in Table 2. |
| In the text | |
 |
Fig. 6. Microlensing magnification patterns for a population of 0.2 M⊙ bodies, assuming a point source. The frames consist of 10002 pixels and have a side length of 18 Einstein radii in the source plane. The parameter values are κ* = 0.6, κc = 0, γ = 0.6 (top left), κ* = 0.04, κc = 0, γ = 0 (top right), κ* = 0.04, κc = 0.4, γ = 0 (bottom left) and κ* = 0.04, κc = 0.4, γ = 0.4 (bottom right). Yellow lines indicate tracks across the amplification pattern for the length of the four light curves in Fig. 2, and a net transverse velocity of 600 km s−1 is assumed. The position and orientation of the tracks is random. |
| In the text | |
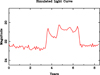 |
Fig. 7. Light curve corresponding to the longest track in the top left panel of Fig. 6. |
| In the text | |
 |
Fig. 8. Microlensing magnification patterns for a population of 0.2 M⊙ bodies with parameter values κ* = 0.04, κc = 0.4, γ = 0 (left hand panel) and κ* = 0.04, κc = 0.4, γ = 0.4 (right hand panel). Each frame consists of 10002 pixels and has a side length of 72 Einstein radii in the lens plane. The tracks are as for Fig. 6. The plots have been convolved with a source size of 0.5RE. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.