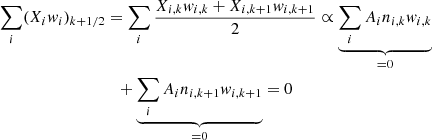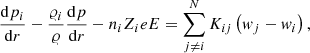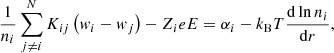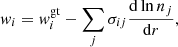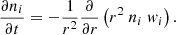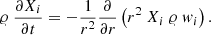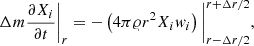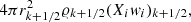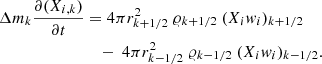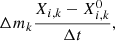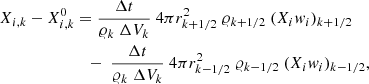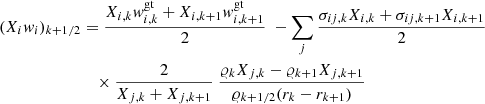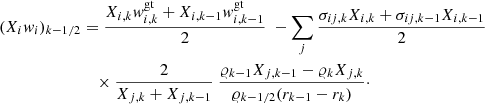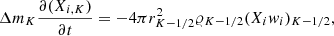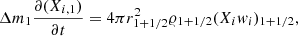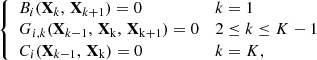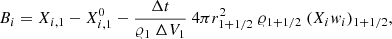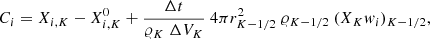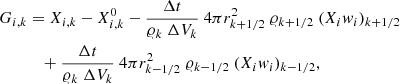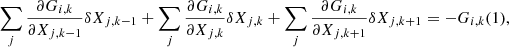| Issue |
A&A
Volume 633, January 2020
|
|
|---|---|---|
| Article Number | A20 | |
| Number of page(s) | 13 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201936346 | |
| Published online | 23 December 2019 | |
About the existence of warm H-rich pulsating white dwarfs
1
Grupo de Evolución Estelar y Pulsaciones. Facultad de Ciencias Astronómicas y Geofísicas, Universidad Nacional de La Plata, Paseo del Bosque s/n, 1900, La Plata, Argentina
e-mail: althaus@fcaglp.unlp.edu.ar
2
IALP – CONICET, Argentina
3
Instituto de Física y Astronomía, Universidad de Valparaiso, Gran Bretaña 1111, Playa Ancha, Valparaíso 2360102, Chile
4
Uniwersytet Pedagogiczny, Obserwatorium na Suhorze, ul. Podchorżych 2, 30-084 Kraków, Poland
5
DIRAC Institute, Department of Astronomy, University of Washington, Seattle, WA 98195-1580, USA
6
Instituto de Física, Universidade Federal do Rio Grande do Sul, 91501-900 Porto-Alegre, RS, Brazil
7
INAF – Osservatorio Astrofisico di Torino, Strada dell’Osservatorio 20, 10025 Pino Torinese, Italy
Received:
19
July
2019
Accepted:
6
November
2019
Context. The possible existence of warm (Teff ∼ 19 000 K) pulsating DA white dwarf (WD) stars, hotter than ZZ Ceti stars, was predicted in theoretical studies more than 30 yr ago. These studies reported the occurrence of g-mode pulsational instabilities due to the κ mechanism acting in the partial ionization zone of He below the H envelope in models of DA WDs with very thin H envelopes (MH/M⋆ ≲ 10−10). However, to date, no pulsating warm DA WD has been discovered, despite the varied theoretical and observational evidence suggesting that a fraction of WDs should be formed with a range of very low H content.
Aims. We re-examine the pulsational predictions for such WDs on the basis of new full evolutionary sequences. We analyze all the warm DAs observed by the TESS satellite up to Sector 9 in order to search for the possible pulsational signal.
Methods. We computed WD evolutionary sequences of masses 0.58 and 0.80 M⊙ with H content in the range −14.5 ≲ log(MH/M⋆)≲ − 10, appropriate for the study of pulsational instability of warm DA WDs. Initial models were extracted from progenitors that were evolved through very late thermal pulses on the early cooling branch. We use LPCODE stellar code into which we have incorporated a new full-implicit treatment of time-dependent element diffusion to precisely model the H–He transition zone in evolving WD models with very low H content. The nonadiabatic pulsations of our warm DA WD models were computed in the effective temperature range of 30 000 − 10 000 K, focusing on ℓ = 1 g modes with periods in the range 50 − 1500 s.
Results. We find that traces of H surviving the very late thermal pulse float to the surface, eventually forming thin, growing pure H envelopes and rather extended H–He transition zones. We find that such extended transition zones inhibit the excitation of g modes due to partial ionization of He below the H envelope. Only in the cases where the H–He transition is assumed much more abrupt than predicted by diffusion do models exhibit pulsational instability. In this case, instabilities are found only in WD models with H envelopes in the range of −14.5 ≲ log(MH/M⋆)≲ − 10 and at effective temperatures higher than those typical for ZZ Ceti stars, in agreement with previous studies. None of the 36 warm DAs observed so far by TESS satellite are found to pulsate.
Conclusions. Our study suggests that the nondetection of pulsating warm DAs, if WDs with very thin H envelopes do exist, could be attributed to the presence of a smooth and extended H–He transition zone. This could be considered as indirect proof that element diffusion indeed operates in the interior of WDs.
Key words: stars: evolution / white dwarfs / stars: oscillations
© ESO 2019
1. Introduction
The existence of various types of pulsating white dwarf (WD) stars characterized by multiperiodic luminosity variations due to g(gravity)-mode pulsations is well established and is supported by both theoretical and observational evidence (Winget & Kepler 2008; Fontaine & Brassard 2008; Althaus et al. 2010a). During their lives, WDs experience at least one stage of pulsational instability, during which peak-to-peak amplitudes between 0.1 mmag and 0.4 mag in optical light curves are expected. Among the different types of observed pulsating WDs (Córsico et al. 2019) we mention the most abundant ones: (i) the hydrogen (H)-rich variables ZZ Ceti or DAVs (Landolt 1968) at low effective temperatures and high gravities (10 400 K ≲ Teff ≲ 12 400 K and 7.5 ≲ log g ≲ 9.1); (ii) the variables V777 Her or DBVs, with almost pure helium (He) atmospheres, spanning a range in effective temperature and surface gravity of 22 400 K ≲ Teff ≲ 32 000 K and 7.5 ≲ log g ≲ 8.3, theoretically predicted by Winget et al. (1982a) before their discovery (Winget et al. 1982b; iii) the “hot DAVs” (Teff ∼ 30 000 K, 7.3 ≲ log g ≲ 7.8; Kurtz et al. 2008, 2013), whose existence was anticipated by the theoretical calculations of Shibahashi (2005) and Shibahashi et al. (2007; iv) the pulsating PG1159 stars or GW Vir variable stars, after the prototype of the class, PG 1159−035 (McGraw et al. 1979), rich in He, carbon (C), and oxygen (O), being the hottest known class of pulsating WDs and pre-WDs (80 000 K ≲ Teff ≲ 180 000 K and 5.5 ≲ log g ≲ 7.5); (v) the H-rich extremely low-mass variable WDs (ELMVs) with 7800 K ≲ Teff ≲ 10 000 K and 6 ≲ log g ≲ 6.8 (Hermes et al. 2012), and (vi) the He/H-atmosphere pre-ELMVs (8000 K ≲ Teff ≲ 13 000 K and 4 ≲ log g ≲ 5), the probable precursors of ELMVs (Maxted et al. 2013).
In addition to these pulsating WDs, early theoretical calculations predicted the existence of pulsating DA WDs hotter than ZZ Ceti stars, hereinafter warm DAVs, expected to be found at effective temperatures comparable to those of the cool edge of the DBV instability strip. In fact, theoretical investigations carried out by Winget et al. (1982a); see also Winget (1982) led to the discovery of g-mode pulsational instability due to κ-mechanism operating in the partial ionization zone of He below the H envelope in models of DA WDs harboring very thin H envelopes (MH/M⋆ ≲ 10−10), for effective temperatures of ∼19 000 K. A relevant aspect of this finding was related to the possibility of constraining the mass of the residual H envelope left in a WD by eventually observing pulsating WDs near this temperature (Winget et al. 1982a).
The existence of WDs with such very thin H envelopes is not discarded either by the theory of stellar evolution or by observations. From the observational point of view, nearly 80% of the spectroscopically identified WDs are characterized by H-rich atmospheres. Systematic spectroscopic and asteroseismological studies indicate that between 15 and 20% of such WDs are expected to harbor thin H envelopes with MH ≲ 10−6 M⊙ (see Tremblay & Bergeron 2008; Castanheira & Kepler 2009; Romero et al. 2012). On the other hand, single stellar evolution theory predicts that usually WDs should be formed with a total H content of about MH ∼ 10−3 − 10−5 M⊙, depending on the stellar mass and metallicity of the progenitor (Althaus et al. 2015). However, certain evolutionary scenarios predict the formation of DA WDs with thin H envelopes. One such scenario involves the occurrence of very late thermal pulses (VLTP) that take place when the WD progenitor experiences its last thermal pulse on the early WD cooling branch. In this case, the H-rich envelope is ingested by the He-shell flash convective zone, where H is burnt in the hot interior of the star (Iben et al. 1995; Herwig et al. 1999). Recent full evolutionary calculations of the event by Miller Bertolami et al. (2017) predict the formation of DA WDs with H content of MH ≲ 10−7 M⊙. In line with this, if the last thermal pulse happens during the horizontal evolution of the post-asymptotic giant branch (AGB) star in the Hertzsprung–Russell diagram, a scenario termed late thermal pulse (LTP) occurs (Blöcker 2001). Here, the H-rich envelope is not burnt but diluted by the deepening of the convective envelope once the star evolves back to the AGB after the LTP. As shown by Althaus et al. (2005a), the H diluted into the deeper parts of the envelope is later burned as the H-deficient star contracts again to the WD cooling track, leading to the formation of WDs with a low H-content (MH ≲ 10−6 − 10−7 M⊙). For the case of VLTP remnants of masses MWD ≳ 0.6 M⊙, Miller Bertolami et al. (2017) obtained DA WDs with H content of the order of 10−11 M⊙. On the other hand, the existence of WDs with extremely thin H envelopes (of the order of MH ≲ 10−14 M⊙) has been invoked in the context of the spectral evolution that some WDs experience as they evolve; see Fontaine & Wesemael (1987), Shibahashi et al. (2007). A more recent study by Cunningham et al. (2019) indicates that 60% of WDs must have a H mass larger than MH/M⋆ = 10−10, another 25% have masses in the range MH/M⋆ = 10−14 − 10−10, and 15% have less H than MH/M⋆ = 10−14. Finally, additional observational evidence supporting the picture that a fraction of DA WDs could harbor thin H envelopes is provided by a new dynamical mass determination of WD 40 Eri B, for which a fractional H envelope mass of ≈10−10 has recently been inferred by Bond et al. (2017); see also Romero et al. (2019). All this evidence suggests that WDs could be formed with H envelopes orders of magnitude less massive than the canonical value of MH ≈ 10−4 M⊙.
In view of these considerations, and despite the numerous discoveries of pulsating WD stars in the last decade, both from the ground and from space, it is surprising that no warm DAV WD has yet been detected. Ground-based observations, particularly carried out with the spectral observations of the Sloan Digital Sky Survey (SDSS; York et al. 2000), have increased the number of known WDs by a factor of 15 (Kleinman et al. 2013; Kepler et al. 2016, 2019; Kepler & Romero 2017; Gentile Fusillo et al. 2019) and the number of pulsators by a factor of 4 (Mukadam et al. 2004; Mullally et al. 2005; Castanheira et al. 2006, 2013; Voss et al. 2007; Nitta et al. 2009). On the other hand, the Kepler satellite observations, both main mission (Borucki et al. 2010) and K2 (two-wheel operation, Howell et al. 2014), increased the number of known WD pulsators by a factor of two (Hermes et al. 2017). The fact that no warm DAV has emerged from the various surveys has prompted us to re-examine the pulsational properties of warm DAV WDs on the basis of detailed WD evolutionary sequences that incorporate a full implicit treatment of time-dependent element diffusion, appropriate for modeling the formation of the H-rich envelope and H–He transition in WDs with very thin H envelopes resulting from post-VLTP remnants. In this study, we also examine the light curves provided by the TESS satellite Ricker et al. (2014) to search for possible candidates of warm DAV WDs.
The paper is organized as follows. In Sect. 2 we present null results in the search for warm DAVs on the basis of a sample of DA WDs with effective temperatures between ∼17 500 K and ∼22 500 K observed with TESS. In Sect. 3 we briefly describe some details of our stellar and pulsational codes, and evolutionary sequences, and present in detail our treatment of time-dependent element diffusion. In Sect. 4 we present the predictions of our evolution and pulsation analyses. Finally, in Sect. 5 we summarize the main findings of the paper, and we elaborate on our conclusions.
2. Observational insights from TESS
We searched for pulsations in warm DA WDs observed by the recent NASA Space Mission of Transiting Exoplanet Survey Satellite (TESS; Ricker et al. 2014). To this end, we cross-checked the targets from the Montreal White Dwarf Database (MWDD)1; Dufour et al. (2017), which provides information about all known WDs, with the targets observed with TESS. We found 36 objects matching our criteria of Teff between 17 500 and 22 500 K. They are listed in Table A.12.
We used the short-cadence (SC) observations sampled every 2 min, which allows us to analyze the frequency range up to the Nyquist frequency at around 4167 μHz. We downloaded all available data (sector 1–13) from the Barbara A. Mikulski Archive for Space Telescopes (MAST)3. The data are in the FITS format which includes all the photometric information, which have been already processed with the Pre-Search Data Conditioning Pipeline (Jenkins et al. 2016) to remove common instrumental trends. From the FITS file, first we extracted times in barycentric corrected Julian days (BJD – 245700), and fluxes (PDCSAP FLUX). In order to increase the signal-to-noise ratio (S/N) of the data in the Fourier space, we detrended the light curves after σ clipping, removing the outliers that vary significantly from the local standard deviation (σ) by applying a running 4σ clipping mask. The fluxes were then normalized and transformed to amplitudes in units of parts-per-thousand (ppt; (ΔI/I − 1) × 1000).
In order to search for periodicity, we assessed the Fourier Spectrum of each light curve. We then calculated the median noise level of each data set (σ) and used 5σ as the detection threshold (Baran et al. 2015). The amplitude spectra of all DA WDs analyzed are presented in Fig. A.1, where the blue line represents the 5σ threshold. As can be seen, none of the 36 DA WDs depicted in Fig. A.1 have any signal above the threshold in the frequency region of interest. Therefore, we conclude that this sample of DA WDs observed with TESS (in sectors 1–9) does not show any signs of pulsations up to the Nyquist frequency at 4200 μHz.
3. Evolutionary and pulsational models and numerical inputs
Our pulsation calculations are based on full WD evolutionary models of different stellar masses. Initial models were extracted from progenitor star models that were evolved from the ZAMS to the thermally pulsing AGB phase and through the VLTP occurring at the beginning of the cooling branch (Miller Bertolami & Althaus 2006). The VLTP is one of the most plausible single-evolution scenarios that predicts the formation of hydrogen-poor WDs (see Córsico et al. 2019, for recent discussion). To encompass the range of H envelope mass that should be expected in warm DAV WDs, the H content of our post VLTP sequence has been artificially reduced, mimicking a more efficient hydrogen mixing and burning during the VLTP. Specifically, we concentrate on warm DAV WD models of masses of 0.58 and 0.80 M⊙ with H content in the range −14.5 ≲ log(MH/M⋆) ≲ − 10.
We use our stellar evolutionary code, LPCODE, to follow the evolution of our selected post-VLTP remnants from the very early stages of WD evolution down to an effective temperature of 10 000 K, well below the expected domain of warm DAV WDs. LPCODE is a well tested and calibrated stellar code; see Althaus et al. (2003, 2005b, 2015) and Miller Bertolami (2016) for details. LPCODE has been widely used to study the evolution of low-mass and WD stars; see Miller Bertolami et al. (2008, 2011); García-Berro et al. (2010), Althaus et al. (2010b, 2013); Renedo et al. (2010), Wachlin et al. (2011), Córsico et al. (2012), and Miller Bertolami (2016).
We compute the non-adiabatic pulsations of our warm DA WD models in the effective-temperature range 30 000 − 10 000 K, amply covering the region where warm DAV WDs should be expected. We have focused on ℓ = 1 g modes with periods in the range 50 − 1500 s. To this end, we employ the nonadiabatic version of the LP-PUL pulsation code, which is described in Córsico et al. (2006).
After the violent proton burning and mixing during the VLTP episode, only tiny vestiges of H remain, extending from the surface down to as deep as 3 × 10−4 M⊙. As WD evolves along the cooling branch, such traces of H will float to the surface as a result of gravitational settling, thus forming an increasingly pure (and thin) H envelope. We have explored two situations: a discontinuous H–He transition separating the pure H envelope from the underlying pure He buffer, and a H–He interface as predicted by element diffusion. We have implemented a new treatment for time-dependent element diffusion, details of which can be found in Appendix B.
As an illustrative example of the performance of our new treatment of element diffusion, in Fig. 1 we show the abundances by mass (Xi) of selected chemical species in terms of the external fractional mass, for a DA WD model with M⋆ = 0.584 M⊙, Teff = 19 000 K, and log(MH/M⋆) = − 13.3. The upper panel shows the abundances on a linear scale, emphasizing the dominant species, while the lower panel shows the abundances on a logarithmic scale, making it possible to clearly visualize the less abundant species. In the lower panel, the black and red dashed lines are associated to the initial profiles of H and He, respectively. Element diffusion predicts a wide and smooth H–He transition zone. We note the tail of H digging into deeper layers as a result of element diffusion. The imprints on the chemical abundance distribution left by the violent H burning during VLTP are visible, in particular the high abundance of 13C. We note also the presence of a thick intershell rich in He and carbon, left by the convection zone driven by the last He thermal pulses.
 |
Fig. 1. Upper panel: fractional abundance by mass of selected nuclear species in terms of the outer mass fraction, corresponding to a DA WD model characterized by M⋆ = 0.584 M⊙, Teff = 19 000 K and log(MH/M⋆) = − 13.3. Lower panel: same as in the upper panel, but with a logarithmic scale for the chemical abundances. In this panel, the black and red dashed lines correspond to initial fractional abundances of H and He, respectively. |
4. Evolutionary and pulsational results
In the upper panel of Fig. 2 we depict the chemical profiles of 16O, 12C, 4He, H, and the Rosseland opacity as a function of the coordinate −log(1 − Mr/M⋆) for a template model with M⋆ = 0.584 M⊙, log(MH/M⋆) = − 11.8, and Teff = 19 000 K. As in the situation analyzed in Fig. 1, we also find that element diffusion leads to an extended H–He transition region, with the tail of the H profile reaching layers well below the point at which XHe = XH = 0.5. We note the presence of bumps in the Rosseland opacity corresponding to the second ionization of He (log T ∼ 5.3) and the ionization of H (log T ∼ 4.58). In particular, the HeII/HeIII bump is quite pronounced (note that what is shown is the logarithm of κ); however, it is unable to generate a convective zone. In the lower panel of Fig. 2 we depict the normalized4 differential work function, dW/d log q (q = 1 − Mr/M⋆), corresponding to a selected g mode with radial order k = 16 and period Π = 800 s. The differential work is negative at the region of the HeII/HeIII opacity bump, therefore this zone contributes to the damping of the mode. In this way, this mode turns out to be pulsationally stable. The same goes for all the g modes analyzed for this model. In Fig. 3 we depict the periods of unstable ℓ = 1 modes vs. Teff corresponding to the same sequence of WD models (M⋆ = 0.584 M⊙, log(MH/M⋆) = − 11.8). Also shown is the e-folding time (in years) of each unstable mode, which is defined as τe = 1/|ℑ(σ)|, ℑ(σ), with σ being the imaginary part of the complex eigenfrequency. This is an estimate of the time it would take a given mode to reach amplitudes large enough to be observable. Notably, our results indicate that all g modes are pulsationally stable at high effective temperatures, so they do not appear in the plot. As the model cools, g modes become unstable due to the κ mechanism acting at the partial ionization zone of H for effective temperatures lower than ∼11 500 K, at the instability domain of the ZZ Ceti stars. We conclude that, when the H–He interface is shaped by element diffusion, there is no excitation of g modes at high effective temperatures due to the partial ionization of He.
 |
Fig. 2. Upper panel: inner chemical profiles of 16O, 12C, 4He and H, and the logarithm of the Rosseland opacity (κ) vs. the outer mass fraction coordinate, corresponding to a DA WD model with M⋆ = 0.584 M⊙, log(MH/M⋆) = − 11.8, and Teff = 19 000 K. The H–He interface is shaped by element diffusion. The bumps in κ due to the second ionization of He and the ionization of H are evident. Lower panel: normalized differential work function corresponding to a stable g mode with k = 16 and period Π = 800 s. |
 |
Fig. 3. Unstable ℓ = 1 g-mode periods (Π) in terms of effective temperature for the sequence of DA WD models with M⋆ = 0.584 M⊙ and log(MH/M⋆) = − 11.8. Color coding indicates the value of the logarithm of the e-folding time (τe) of each unstable mode (right scale). Only unstable modes for effective temperatures characteristic of the ZZ Ceti stage (Teff ≲ 11 500 K) are found. |
In the upper panel of Fig. 4, we display the chemical profiles and the Rosseland opacity for the same WD model, but in this case the H–He transition region is not modeled by element diffusion, but is assumed to have a step-like shape. Here, opacity exhibits a sharp peak at the region of the H–He chemical interface, resulting in the formation of a narrow convection zone (marked as a gray vertical strip in the figure) immediately below the H–He chemical interface. The peak in κ is due to the absence of H below the chemical transition of H–He. We point out that the presence of H in this chemical transition when the interface is wide (Fig. 2) has the effect of reducing the total opacity and suppressing convection. This is because, at the He/H transition region, H is fully ionized and its opacity is much lower than that produced by He, which is partially ionized there (see, e.g., Tassoul et al. 1990). Hence, when H is absent, the opacity reaches much higher values locally (Fig. 4). In the lower panel of Fig. 4 we depict the normalized differential work function for the k = 16 g mode shown in the lower panel of Fig. 2. In this case, the differential work has negative values below the HeII/HeIII opacity peak, contributing to the damping of the mode, and large positive values at the opacity peak, strongly promoting the driving of the mode. Since driving overcomes damping, the mode is globally unstable. The excitation of the mode is due to the κ − γ mechanism, in which the existence of large gradients in the opacity is essential for operation (see, e.g., Aerts et al. 2010). This is clearly seen in the opacity profile shown in the upper panel of Fig. 4. Figure 5 shows the period range of excited dipole modes in terms of the effective temperature for models with step-like shape H–He interface. At variance with the case depicted in Fig. 3, here we find g modes with a wide range of periods excited in a broad interval of high effective temperatures (50 000 K ≳ Teff ≳ 17 000 K), apart from g modes excited at low temperatures in the ZZ Ceti domain. The e-folding time has to be compared with the evolutionary timescale (τevol), which represents the time that the WD spends evolving in the regime of interest. For our models, τevol ∼ 1.5 × 108 yr. This is the time it takes for the model to cool from Teff ∼ 23 000 K to Teff ∼ 15 000 K. It is much longer than the e-folding times of the excited pulsation modes: τe ≲ 103 yr. This ensures that the modes have enough time to get excited while the WD models are in the temperature range of interest. For most of the excited modes (specifically, for Π ≳ 200 s) the inequality τe ≪ τevol is satisfied, which ensures that the modes can reach observable amplitudes as the models are slowly evolving in that range of effective temperatures.
 |
Fig. 4. Upper panel: same as in Fig. 2, but for the extreme case in which the H–He interface is assumed to be discontinuous (step-like shape). The vertical gray strip marks the convection zone driven by the second ionization of He. Lower panel: differential work function for an unstable g mode with k = 16 and period Π = 803 s. |
 |
Fig. 5. Same as Fig. 3, but for the case in which the H–He interface has a step-like shape (see Fig. 4). Here, g modes with a wide range of periods are excited at high effective temperatures. |
Our results confirm the early findings of Winget et al. (1982a) that in DA WD models with very thin H envelopes, log(MH/M⋆) ≤ − 10, He is able to drive g-mode pulsations at effective temperatures Teff ∼ 19 000 K. Two other relevant works carried out almost at the same time as the analysis by Winget et al. (1982a), namely the studies by Dolez & Vauclair (1981) and Dziembowski & Koester (1981), reported pulsational instability due to the κ mechanism acting at the partial ionization region of the He in models with very thin H envelopes. Nevertheless, the pulsational instabilities they found appear at lower effective temperatures (Teff ≲ 13 500 K), compatible with the instability strip of ZZ Ceti stars.
Figure 6 is similar to Fig. 4, but for the case in which log(MH/M⋆) = − 12.8 and a step-like H–He interface. The unstable ℓ = 1 g-mode periods in terms of Teff for this case are illustrated in Fig. 7. The results shown in this figure are qualitatively similar to the case displayed in Fig. 5 for log(MH/M⋆) = − 11.8, that is, g modes are driven by the κ mechanism due to the partial ionization of He for effective temperatures higher than those characterizing ZZ Ceti stars. We also analyzed the case in which these models harbor a smooth H–He interface modeled by element diffusion. Again, in this case, we do not find unstable modes at high effective temperatures. We also explored the predictions of an even thinner H envelope: log(MH/M⋆) = − 14.5 with an abrupt H–He transition region. This is the thinnest H envelope considered in this work. Our results for this sequence indicate pulsational instability, but only for Teff ≲ 15 000 K. Hence, we consider the thickness of this envelope as the lower limit for instability pulsation to occur in warm DA WDs.
 |
Fig. 6. Upper panel: same as in Fig. 4, but for the case in which log(MH/M⋆) = − 12.8. Lower panel: normalized differential work function corresponding to an unstable g mode with k = 16 and period Π = 819 s. |
 |
Fig. 7. Same as Fig. 5 but for log(MH/M⋆) = − 12.8. Again, in this case, a lot of g modes are excited at high effective temperatures, apart from the excited modes at the ZZ Ceti phase. |
Figure 8 displays the case of a sequence of models with the same stellar mass, M⋆ = 0.584 M⊙, but with a thick H envelope of log(MH/M⋆) = − 10.2 and a step-like shaped H–He transition region. We find only marginal mode driving of low-order g modes (k ≤ 6) at high effective temperatures. Indeed, the e-folding time of these modes is extremely large, as emphasized by the black color for the period of these modes in Fig. 8; they therefore have no chance to reach observable amplitudes while the star is evolving at that stage (τe > τevol). On the other hand, we again obtain the unstable g modes at the ZZ Ceti stage driven by the partial ionization zone of H via the κ mechanism. In practical terms, we can consider that there is no excitation of g modes at high effective temperatures in DA WD models with this H envelope thickness. We have repeated the stability analysis for models with the same thickness of the H envelope but with the H–He transition modeled by diffusion. Again, we do not find excitation of g modes at high effective temperatures. We conclude that this value of MH/M⋆ constitutes an upper limit for the H envelope thickness, in such a way that for thicker H envelopes there is no mode driving at high effective temperatures, even in the case in which the H–He transition is characterized by a quasi discontinuous form (step-like shape).
 |
Fig. 8. Same as Fig. 5 but for log(MH/M⋆) = − 10.2. Here, a few low-order modes (k = 1, …, 6) are marginally unstable apart from the unstable g modes at the effective temperatures of ZZ Ceti stars. |
Finally, we examined the case of a more massive DA WD model sequence, characterized by M⋆ = 0.80 M⊙ and log(MH/M⋆) = − 12. The results of our stability analysis for the case of an abrupt H–He transition are illustrated in Fig. 9. Visibly, for this stellar mass there is also excitation in many g modes for models at high effective temperatures. We also find the instability of g modes in the phase of the ZZ Ceti stars. As in the cases analyzed above, we do not find excitation of modes at high effective temperatures when the H–He chemical transition is the result of element diffusion (not shown).
 |
Fig. 9. Same as Fig. 5, but for M⋆ = 0.80 M⊙. Also for these high-mass WD models, many g modes are excited at high effective temperature. |
5. Summary and conclusions
The existence of a new class of pulsating DA WDs hotter than ZZ Ceti stars (warm DAV WDs) was suggested a long time ago by Winget et al. (1982a), who reported the occurrence of g-mode pulsational instability due to κ mechanism acting in the partial ionization zone of He below the H envelope in models of DA WDs with very thin H envelopes (MH/M⋆ ≲ 10−10), for effective temperatures of ∼19 000 K. However, to date, no such warm DAV WDs have been found, despite the large number of pulsating WDs of different types discovered in the last decade both from ground- and space-based observational surveys. The discovery of warm DAV WDs would constitute a clear demonstration of the existence of DA WDs with very low H content, thus shedding light on the evolutionary processes that lead to WD formation in general, particularly the occurrence of late thermal pulses, the most viable scenario to form WDs with H content lower than 10−7 M⊙. The existence of such WDs cannot be discarded despite the fact that no warm DAV WD has been observed; on the contrary, different pieces of theoretical and observational evidence suggest that a fraction of WDs should be formed with a range of very low H content.
Our paper has been conducted with the aim of exploring the impact of element diffusion on the stability pulsational properties of warm DAV WDs. We concentrated on full WD evolutionary sequences of masses 0.80 and 0.58 M⊙ with H content in the range MH ∼ 10−10 − 10−14M⋆, appropriate for the study of pulsational instability of warm DAV WDs. To this end, we used a new full-implicit treatment for time-dependent element diffusion that maintains the sum of the chemical abundances almost constant over large time integrations. This treatment allows us to model the evolution of the chemical distribution in the outer layer in WDs emerging from VLTP episodes with very low H content in a realistic way, and constitutes a substantial improvement over the semi-implicit treatment considered previously in LPCODE. Initial models were extracted from progenitor star models that were evolved from the ZAMS, to the thermally pulsing AGB phase, and through the VLTP occurring at the beginning of the cooling branch (Miller Bertolami & Althaus 2006). We find that as WD evolution proceeds, traces of H surviving the VLTP float to the surface, eventually forming thin (and increasing) pure H envelopes and rather extended H–He transition zones.
We conducted a search for pulsating warm DA WDs among the stars observed by TESS. We found that 36 DA WD stars with effective temperatures in the range [17 500 − 22 500 K] have been observed with TESS in sectors 1–9, and we analyzed them to search for any signs of pulsation. After examining their amplitude spectra, we conclude that none of the 36 warm DA WD stars observed by TESS show any significant frequency above the 5σ threshold in the frequency domain of interest. Therefore, our search gives null results for pulsating warm DA WDs currently observed by TESS up to the Nyquist frequency at 4200 μHz.
Nonadiabatic pulsations of our warm DAV WD models were computed in the effective temperature range of 30 000 − 10 000 K. The driving mechanism that can excite pulsations in DA WDs in this regime is the κ mechanism due to opacity bumps resulting from He ionization zone below the H envelope or the H ionization zone, or both (see the pioneer works by Dolez & Vauclair 1981; Dziembowski & Koester 1981; Winget et al. 1982a). The stability analysis carried out in this work was focused on ℓ = 1 g modes with periods in the range 50 − 1500 s. Two possibilities were considered regarding the shape of the H–He chemical interface. In one instance, we considered this chemical transition as resulting from element diffusion. In this case, the transition is smooth and wide. In another, we assumed this transition to be extremely narrow and abrupt. Our nonadiabatic results indicate that in order to have pulsational instability due to the κ mechanism acting at the partial ionization zone of He, it is necessary that the H–He chemical transition region be very narrow and abrupt (see Figs. 4 and 5). Our computations indicate also that the thickest H envelope for which this kind of mode excitation happens is log(MH/M⋆)∼ − 10, and the thinnest one is log(MH/M⋆)∼ − 14.5. On the other hand, if the chemical transition is smooth and extended as element diffusion predicts (see Figs. 2 and 3), then there is no excitation of modes at higher effective temperatures than those characteristic of ZZ Ceti stars, irrespective of the thickness of the H envelope.
We conclude that, assuming the existence of DA WDs with very low H content, the nondetection of warm DAVs could be attributed to the fact that element diffusion produces a smooth and extended H–He interface, which inhibits the excitation of g modes due to the partial ionization of the He at effective temperatures larger than those typical of ZZ Ceti stars. In this sense, our findings could be considered as indirect evidence that element diffusion indeed operates in the interiors of WDs. However, it cannot be discarded that the lack of detected pulsations in the TESS data could be attributed to the fact that few or none of the warm DA WDs observed in Sectors 1–9 have very thin H envelopes, or that some pulsate with amplitudes below the significance thresholds.
Acknowledgments
We thank the anonymous referee for his/her valuable suggestions that improved the content and presentation of the paper. This paper includes data collected with the TESS mission, obtained from the MAST data archive at the Space Telescope Science Institute (STScI). Funding for the TESS mission is provided by the NASA Explorer Program. STScI is operated by the Association of Universities for Research in Astronomy, Inc., under NASA contract NAS 5–26555. Part of this work was supported by AGENCIA through the Programa de Modernización Tecnológica BID 1728/OC-AR, by the PIP 112-200801-00940 grant from CONICET, by MINECO grant AYA2014-59084-P, by grant G149 from University of La Plata, and by the AGAUR. MU acknowledges financial support from CONICYT Doctorado Nacional No. 21190886. ASB gratefully acknowledges financial support from the Polish National Science Center under project No. UMO-2017/26/E/ST9/00703. KJB is supported by an NSF Astronomy and Astrophysics Postdoctoral Fellowship under award AST-1903828. This research has made use of NASA Astrophysics Data System.
References
- Aerts, C., Christensen-Dalsgaard, J., & Kurtz, D. W. 2010, Asteroseismology (Berlin: Springer Science & Business Media) [Google Scholar]
- Althaus, L. G., Serenelli, A. M., Córsico, A. H., & Montgomery, M. H. 2003, A&A, 404, 593 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Althaus, L. G., Miller Bertolami, M. M., Córsico, A. H., García-Berro, E., & Gil-Pons, P. 2005a, A&A, 440, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Althaus, L. G., Serenelli, A. M., Panei, J. A., et al. 2005b, A&A, 435, 631 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Althaus, L. G., Córsico, A. H., Isern, J., & García-Berro, E. 2010a, A&ARv, 18, 471 [NASA ADS] [CrossRef] [Google Scholar]
- Althaus, L. G., Córsico, A. H., Bischoff-Kim, A., et al. 2010b, ApJ, 717, 897 [NASA ADS] [CrossRef] [Google Scholar]
- Althaus, L. G., Miller Bertolami, M. M., & Córsico, A. H. 2013, A&A, 557, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Althaus, L. G., Camisassa, M. E., Miller Bertolami, M. M., Córsico, A. H., & García-Berro, E. 2015, A&A, 576, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baran, A. S., Koen, C., & Pokrzywka, B. 2015, MNRAS, 448, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Blöcker, T. 2001, Ap&SS, 275, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Bond, H. E., Bergeron, P., & Bédard, A. 2017, ApJ, 848, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Borucki, W. J., Koch, D., Basri, G., et al. 2010, Science, 327, 977 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Burgers, J. M. 1969, Flow Equations for Composite Gases (New York: Academic Press) [Google Scholar]
- Castanheira, B. G., & Kepler, S. O. 2009, MNRAS, 396, 1709 [NASA ADS] [CrossRef] [Google Scholar]
- Castanheira, B. G., Kepler, S. O., Mullally, F., et al. 2006, A&A, 450, 227 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Castanheira, B. G., Kepler, S. O., Kleinman, S. J., Nitta, A., & Fraga, L. 2013, MNRAS, 430, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Córsico, A. H., Althaus, L. G., & Miller Bertolami, M. M. 2006, A&A, 458, 259 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Córsico, A. H., Althaus, L. G., Miller Bertolami, M. M., et al. 2012, MNRAS, 424, 2792 [NASA ADS] [CrossRef] [Google Scholar]
- Córsico, A. H., Althaus, L. G., Miller Bertolami, M. M., & Kepler, S. O. 2019, A&ARv, 27, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Cunningham, T., Tremblay, P. E., Gentile Fusillo, N. P., Hollands, M., & Cukanovaite, E. 2019, MNRAS, submitted [arXiv:1911.00014] [Google Scholar]
- Dolez, N., & Vauclair, G. 1981, A&A, 102, 375 [NASA ADS] [Google Scholar]
- Dufour, P., Blouin, S., Coutu, S., et al. 2017, ASP Conf. Ser., 509, 3 [NASA ADS] [Google Scholar]
- Dziembowski, W., & Koester, D. 1981, A&A, 97, 16 [NASA ADS] [Google Scholar]
- Fontaine, G., & Brassard, P. 2008, PASP, 120, 1043 [NASA ADS] [CrossRef] [Google Scholar]
- Fontaine, G., & Wesemael, F. 1987, in IAU Colloq. 95: Second Conference on Faint Blue Stars, eds. A. G. D. Philip, D. S. Hayes, & J. W. Liebert, 319 [Google Scholar]
- García-Berro, E., Torres, S., Althaus, L. G., et al. 2010, Nature, 465, 194 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Gentile Fusillo, N. P., Tremblay, P.-E., Gänsicke, B. T., et al. 2019, MNRAS, 482, 4570 [NASA ADS] [CrossRef] [Google Scholar]
- Henyey, L. G., Forbes, J. E., & Gould, N. L. 1964, ApJ, 139, 306 [NASA ADS] [CrossRef] [Google Scholar]
- Hermes, J. J., Montgomery, M. H., Winget, D. E., et al. 2012, ApJl, 750, L28 [NASA ADS] [CrossRef] [Google Scholar]
- Hermes, J. J., Gänsicke, B. T., Kawaler, S. D., et al. 2017, ApJS, 232, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Herwig, F., Blöcker, T., Langer, N., & Driebe, T. 1999, A&A, 349, L5 [NASA ADS] [Google Scholar]
- Howell, S. B., Sobeck, C., Haas, M., et al. 2014, PASP, 126, 398 [NASA ADS] [CrossRef] [Google Scholar]
- Iben, Jr., I., & MacDonald, J. 1985, ApJ, 296, 540 [NASA ADS] [CrossRef] [Google Scholar]
- Iben, Jr., I., & MacDonald, J. 1995, Lect. Notes Phys., 443, 48 [NASA ADS] [Google Scholar]
- Jenkins, J. M., Twicken, J. D., McCauliff, S., et al. 2016, Proc. SPIE, 9913, 99133E [Google Scholar]
- Kepler, S. O., & Romero, A. D. 2017, Eur. Phys. J. Web Conf., 152, 01011 [CrossRef] [Google Scholar]
- Kepler, S. O., Pelisoli, I., Koester, D., et al. 2016, MNRAS, 455, 3413 [NASA ADS] [CrossRef] [Google Scholar]
- Kepler, S. O., Pelisoli, I., Koester, D., et al. 2019, MNRAS, 486, 2169 [NASA ADS] [Google Scholar]
- Kleinman, S. J., Kepler, S. O., Koester, D., et al. 2013, ApJS, 204, 5 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Kurtz, D. W., Shibahashi, H., Dhillon, V. S., Marsh, T. R., & Littlefair, S. P. 2008, MNRAS, 389, 1771 [NASA ADS] [CrossRef] [Google Scholar]
- Kurtz, D. W., Shibahashi, H., Dhillon, V. S., et al. 2013, MNRAS, 432, 1632 [NASA ADS] [CrossRef] [Google Scholar]
- Landolt, A. U. 1968, ApJ, 153, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Maxted, P. F. L., Serenelli, A. M., Miglio, A., et al. 2013, Nature, 498, 463 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- McGraw, J. T., Starrfield, S. G., Liebert, J., & Green, R. 1979, in IAU Colloq. 53: White Dwarfs and Variable Degenerate Stars, eds. H. M. van Horn, & V. Weidemann, 377 [Google Scholar]
- Miller Bertolami, M. M. 2016, A&A, 588, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miller Bertolami, M. M., & Althaus, L. G. 2006, A&A, 454, 845 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miller Bertolami, M. M., Althaus, L. G., Unglaub, K., & Weiss, A. 2008, A&A, 491, 253 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miller Bertolami, M. M., Rohrmann, R. D., Granada, A., & Althaus, L. G. 2011, ApJ, 743, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Miller Bertolami, M. M., Althaus, L. G., & Córsico, A. H. 2017, ASP Conf. Ser., 509, 435 [NASA ADS] [Google Scholar]
- Mukadam, A. S., Mullally, F., Nather, R. E., et al. 2004, ApJ, 607, 982 [NASA ADS] [CrossRef] [Google Scholar]
- Mullally, F., Thompson, S. E., Castanheira, B. G., et al. 2005, ApJ, 625, 966 [NASA ADS] [CrossRef] [Google Scholar]
- Nitta, A., Kleinman, S. J., Krzesinski, J., et al. 2009, ApJ, 690, 560 [NASA ADS] [CrossRef] [Google Scholar]
- Paquette, C., Pelletier, C., Fontaine, G., & Michaud, G. 1986, ApJS, 61, 177 [NASA ADS] [CrossRef] [Google Scholar]
- Renedo, I., Althaus, L. G., Miller Bertolami, M. M., et al. 2010, ApJ, 717, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Ricker, G. R., Winn, J. N., Vanderspek, R., et al. 2014, Proc. SPIE, 9143, 914320 [Google Scholar]
- Romero, A. D., Córsico, A. H., Althaus, L. G., et al. 2012, MNRAS, 420, 1462 [Google Scholar]
- Romero, A. D., Kepler, S. O., Joyce, S. R. G., Lauffer, G. R., & Córsico, A. H. 2019, MNRAS, 484, 2711 [NASA ADS] [Google Scholar]
- Shibahashi, H. 2005, EAS Pub. Ser., 17, 143 [CrossRef] [Google Scholar]
- Shibahashi, H. 2007, AIP Conf. Ser., 948, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Tassoul, M., Fontaine, G., & Winget, D. E. 1990, ApJS, 72, 335 [Google Scholar]
- Tremblay, P.-E., & Bergeron, P. 2008, ApJ, 672, 1144 [NASA ADS] [CrossRef] [Google Scholar]
- Voss, B., Koester, D., Østensen, R., et al. 2007, ASP Conf. Ser., 372, 583 [NASA ADS] [Google Scholar]
- Wachlin, F. C., Miller Bertolami, M. M., & Althaus, L. G. 2011, A&A, 533, A139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Winget, D. E. 1982, PhD Thesis, The University of Rochester, USA [Google Scholar]
- Winget, D. E., & Kepler, S. O. 2008, ARA&A, 46, 157 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Winget, D. E., van Horn, H. M., Tassoul, M., et al. 1982a, ApJ, 252, L65 [NASA ADS] [CrossRef] [Google Scholar]
- Winget, D. E., Robinson, E. L., Nather, R. D., & Fontaine, G. 1982b, ApJ, 262, L11 [NASA ADS] [CrossRef] [Google Scholar]
- York, D. G., Adelman, J., Anderson, Jr., J. E., et al. 2000, AJ, 120, 1579 [CrossRef] [Google Scholar]
Appendix A: A sample of warm DA WDs from TESS
Here, we show the Fourier transforms of the sample of 36 warm DA WDs observed with TESS mission. Table A.1 lists the complete sample of stars analyzed in this paper including the spectral types, effective temperatures, and surface gravities (taken from the MWDD Catalog), along with the TESS magnitudes, observed sector, average noise level and the adopted threshold (5σ). In Fig. A.1 depict the Fourier Transforms of the stars listed in Table A.1. As can be seen, none of the analyzed stars exhibit signals of intrinsic variability in the frequency range of expected pulsation. The peaks seen in few stars at very low frequencies that are above 5σ threshold (TIC 408015814, TIC 054636377, TIC 237313550, TIC 000682778) are low-frequency systematic noise that has been reported in some of the TESS data. The only exception is the star TIC 439917321. This is a member of WD+dM (M dwarf) binary system, with a period of 12.98 h. In the FT of TIC 439917321, the peaks f1 and f2 (see Table A.2) are signatures of binarity. After pre-whitening the orbital frequency and its harmonic (f1 and f2), there is no other periodic signal detected above the threshold (5σ = 1.9432) and we conclude that TIC 439917321 does not show any signs of pulsation.
Complete set of 36 warm DA WD targets observed with TESS (Sectors 1–9) including three different sets of information along with their names (Cols. 1 and 2).
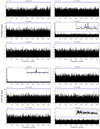 |
Fig. A.1. Amplitude spectra of warm DA WDs. The blue dashed horizontal line indicates the threshold (5σ). The inset is a blow-up of the amplitude spectra at the low-frequency regime for the few stars where some frequencies are above 5σ, as discussed in the text. |
 |
Fig. A.1. continued. |
 |
Fig. A.1. continued. |
Frequencies detected in TIC 439917321.
Appendix B: Numerical treatment of time-dependent element diffusion
Under the influence of gravity, partial pressure, and induced electric fields, the diffusion velocities in a multicomponent plasma satisfy the set of N − 1 independent equations (Burgers 1969):
where, pi, 𝜚i, ni, Zi, and wi denote, respectively, the partial pressure, mass density, number density, mean charge, and diffusion velocity for chemical species i. N is the number of ionic species plus electrons. The unknown variables are wi and the electric field E. Resistance coefficients Kij are from Paquette et al. (1986). This set of equations is solved together with the equations for no net mass flow ∑i Ainiwi = 0 and no electrical current ∑i Ziniwi = 0. In the evolutionary sequences computed in this work, thermal diffusion has been neglected. This does not change the conclusions of the paper. We verify this by including thermal diffusion in the computation of the M⋆ = 0.584 M⊙ sequence with log(MH/M⋆) = − 11.8. Although the inclusion of thermal diffusion leads to a thicker pure H envelope and a steeper H–He transition region, no excitation is found of g modes at high effective temperatures due to the partial ionization of He; see text.
Following Iben & MacDonald (1985), Eq. (B.1) can be rearranged to obtain (for the ions)
where αi = −AimHg − kBT (dlnT/dr), being g the gravitational acceleration. wi can be written
where 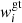 stands for the velocity component due to gravity and temperature gradient (gravitational settling component). The components due to gradients in number density are referred to as chemical diffusion components. The summation is done for the ions only. This equation, together with the conditions for no net mass flow and electrical current, can be solved using matrix inversion to find
stands for the velocity component due to gravity and temperature gradient (gravitational settling component). The components due to gradients in number density are referred to as chemical diffusion components. The summation is done for the ions only. This equation, together with the conditions for no net mass flow and electrical current, can be solved using matrix inversion to find 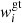 and σij, which finally are employed to follow the evolution of the number density of ionic species i:
and σij, which finally are employed to follow the evolution of the number density of ionic species i:
For numerical purposes, we write this equation in terms of the abundance by mass Xi of species i, given by Xi = 𝜚i/𝜚:
We multiply this equation by 4πr2 and integrate over the radial coordinate r from r − Δr/2 to r + Δr/2, to obtain
where 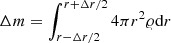 (we assume Δr small enough for ∂Xi/∂t to be constant over Δr). Equation (B.6) simply states that the difference of flux of mass of element i between the two borders of a spherical shell is equal to the time variation of the mass of element i in the shell. We discretize this equation with respect to time and space by dividing the star into K mesh points, with the lagrangian mass coordinate of the kth mesh point being mk (the mass inside the sphere of radius rk). In what follows, all the quantities with an indice k are evaluated at the mesh point k. The mesh points are numbered from 1 at the surface to K at the centre. The mass of element i removed from mesh point k + 1 and added to mesh point k per unit time becomes:
(we assume Δr small enough for ∂Xi/∂t to be constant over Δr). Equation (B.6) simply states that the difference of flux of mass of element i between the two borders of a spherical shell is equal to the time variation of the mass of element i in the shell. We discretize this equation with respect to time and space by dividing the star into K mesh points, with the lagrangian mass coordinate of the kth mesh point being mk (the mass inside the sphere of radius rk). In what follows, all the quantities with an indice k are evaluated at the mesh point k. The mesh points are numbered from 1 at the surface to K at the centre. The mass of element i removed from mesh point k + 1 and added to mesh point k per unit time becomes:
where the subscript k + 1/2 means that quantities are evaluated at the midpoint between the mesh points k + 1 and k. For instance, rk + 1/2 = (rk + rk + 1)/2. We have a similar expression for the mass of element i removed from mesh point k and added to mesh point k − 1. Denoting with Xi, k the abundance by mass of element i evaluated at the mesh point k and considering that 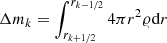 , we have
, we have
The left hand term of this equation is discretized as
where 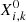 corresponds to the abundance by mass of element i at mesh point k evaluated at the beginning of time step Δt, and Xi, k the abundance of the same element at k at the end of the time step. We note that we are considering the average of the product Xiwi (specifically,
corresponds to the abundance by mass of element i at mesh point k evaluated at the beginning of time step Δt, and Xi, k the abundance of the same element at k at the end of the time step. We note that we are considering the average of the product Xiwi (specifically, 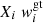 and Xiσij) between two adjacent mesh points and not the product of the averages of Xi and wi. In this way, mass conservation is guaranteed in Eq. (B.8), as we imposed the condition of no net mass flow at each mesh point k at calculating the diffusion velocities5.
and Xiσij) between two adjacent mesh points and not the product of the averages of Xi and wi. In this way, mass conservation is guaranteed in Eq. (B.8), as we imposed the condition of no net mass flow at each mesh point k at calculating the diffusion velocities5.
Taking Δmk = 𝜚kΔVk, with 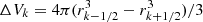 we obtain
we obtain
where (from Eq. (B.3))
and
We have a set of difference equations at each mesh point k, the solution of which will give us Xi, k for all species i at each k. The boundary conditions at the center, k = K, and at the surface, k = 1, are respectively
for which we proceed as above. Eqs. (B.10)–(B.14) can be written in a compact form as
where Xk means Xl, k {l = 1, …, Nions} with Nions the number of chemical species. Here, Bi, Gi, k, and Ci are given by
where (Xiwi)1 + 1/2 is given by Eq. (B.11) with k = 1,
where (XKwi)K − 1/2 is given by Eq. (B.12) with k = K, and
where (Xiwi)k + 1/2 and (Xiwi)k − 1/2 are given by Eqs. (B.11) and (B.12), respectively.
To solve this set of nonlinear equations we use an iterative full implicit method, in which an initial solution is gradually improved by applying successive simultaneous corrections to all variables at all mesh points. Implicit methods, in constrast with semi-implicit methods, are usually preferred because of the superior stability characteristics. In addition, they maintain the sum of Xi to be almost constant over large time integrations. This is a relevant issue, since in this work we are interested in the formation and evolution of H envelopes less massive than 10−10 M⊙. The treatment present here is an improvement over that presented in Althaus et al. (2003), based on the semi-implicit method described in Iben & MacDonald (1985).
Let X1 be a first approximation to the set of Eq. (B.15), which as a first guess we take it as the solution at the previous time t − Δt. Clearly, since this is only an approximation to the solution, then Bi(1) ≠ 0, Gi, k(1) ≠ 0, and Ci(1) ≠ 0. Let δX the corresponding corrections to all variables at all mesh points; we get a second approximation X2 = X1 + δX, so that now Bi(2) = 0, Gi, k(2) = 0, and Ci(2) = 0. If corrections are small, a first-order Taylor expansion leads to
and similarly for Bi and Ci. The derivatives are assessed at the first approximation. From here, the corrections δX are found by inverting a band-type matrix with nonvanishing coefficients only in blocks near the diagonal (because difference equations depend only on variables at adjacent points) by following the elimination procedure of Henyey et al. (1964). After several iterations (diffusion velocities are re-calculated at each iteration), the approximate solution is improved until the absolute value of all corrections drops below a given limit or the difference equations are satisfied to a given accuracy.
This implicit procedure for solving the time-dependent diffusion equations is efficient and stable. In particular, for our sequences with MH = 10−11 M⊙, the total mass of the H content changes by less than 0.01% after 108 yr of evolution. After the convergence of a stellar model, the chemical abundance changes due to element diffusion and then due to convection (and nuclear reactions if any) for the next evolutionary time step are evaluated, and then the next stellar model is computed by solving the full set of stellar structure and evolution equations.
All Tables
Complete set of 36 warm DA WD targets observed with TESS (Sectors 1–9) including three different sets of information along with their names (Cols. 1 and 2).
All Figures
 |
Fig. 1. Upper panel: fractional abundance by mass of selected nuclear species in terms of the outer mass fraction, corresponding to a DA WD model characterized by M⋆ = 0.584 M⊙, Teff = 19 000 K and log(MH/M⋆) = − 13.3. Lower panel: same as in the upper panel, but with a logarithmic scale for the chemical abundances. In this panel, the black and red dashed lines correspond to initial fractional abundances of H and He, respectively. |
| In the text | |
 |
Fig. 2. Upper panel: inner chemical profiles of 16O, 12C, 4He and H, and the logarithm of the Rosseland opacity (κ) vs. the outer mass fraction coordinate, corresponding to a DA WD model with M⋆ = 0.584 M⊙, log(MH/M⋆) = − 11.8, and Teff = 19 000 K. The H–He interface is shaped by element diffusion. The bumps in κ due to the second ionization of He and the ionization of H are evident. Lower panel: normalized differential work function corresponding to a stable g mode with k = 16 and period Π = 800 s. |
| In the text | |
 |
Fig. 3. Unstable ℓ = 1 g-mode periods (Π) in terms of effective temperature for the sequence of DA WD models with M⋆ = 0.584 M⊙ and log(MH/M⋆) = − 11.8. Color coding indicates the value of the logarithm of the e-folding time (τe) of each unstable mode (right scale). Only unstable modes for effective temperatures characteristic of the ZZ Ceti stage (Teff ≲ 11 500 K) are found. |
| In the text | |
 |
Fig. 4. Upper panel: same as in Fig. 2, but for the extreme case in which the H–He interface is assumed to be discontinuous (step-like shape). The vertical gray strip marks the convection zone driven by the second ionization of He. Lower panel: differential work function for an unstable g mode with k = 16 and period Π = 803 s. |
| In the text | |
 |
Fig. 5. Same as Fig. 3, but for the case in which the H–He interface has a step-like shape (see Fig. 4). Here, g modes with a wide range of periods are excited at high effective temperatures. |
| In the text | |
 |
Fig. 6. Upper panel: same as in Fig. 4, but for the case in which log(MH/M⋆) = − 12.8. Lower panel: normalized differential work function corresponding to an unstable g mode with k = 16 and period Π = 819 s. |
| In the text | |
 |
Fig. 7. Same as Fig. 5 but for log(MH/M⋆) = − 12.8. Again, in this case, a lot of g modes are excited at high effective temperatures, apart from the excited modes at the ZZ Ceti phase. |
| In the text | |
 |
Fig. 8. Same as Fig. 5 but for log(MH/M⋆) = − 10.2. Here, a few low-order modes (k = 1, …, 6) are marginally unstable apart from the unstable g modes at the effective temperatures of ZZ Ceti stars. |
| In the text | |
 |
Fig. 9. Same as Fig. 5, but for M⋆ = 0.80 M⊙. Also for these high-mass WD models, many g modes are excited at high effective temperature. |
| In the text | |
 |
Fig. A.1. Amplitude spectra of warm DA WDs. The blue dashed horizontal line indicates the threshold (5σ). The inset is a blow-up of the amplitude spectra at the low-frequency regime for the few stars where some frequencies are above 5σ, as discussed in the text. |
| In the text | |
 |
Fig. A.1. continued. |
| In the text | |
 |
Fig. A.1. continued. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.