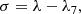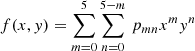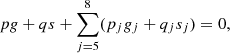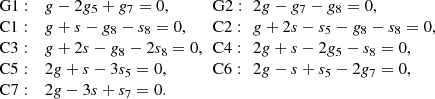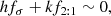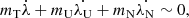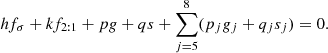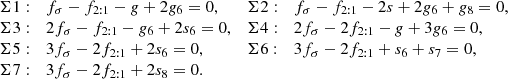| Issue |
A&A
Volume 633, January 2020
|
|
|---|---|---|
| Article Number | A153 | |
| Number of page(s) | 13 | |
| Section | Celestial mechanics and astrometry | |
| DOI | https://doi.org/10.1051/0004-6361/201936332 | |
| Published online | 23 January 2020 | |
Systematic survey of the dynamics of Uranus Trojans
1
School of Astronomy and Space Science, Nanjing University, 163 Xianlin Avenue, Nanjing 210046, PR China
e-mail: zhouly@nju.edu.cn
2
Key Laboratory of Modern Astronomy and Astrophysics in Ministry of Education, Nanjing University, Nanjing 210046, PR China
3
Institute of Space Astronomy and Extraterrestrial Exploration (NJU & CAST), PR China
4
Universitätssternwarte Wien, Türkenschanzstr. 17, 1180 Wien, Austria
Received:
17
July
2019
Accepted:
21
December
2019
Context. The discovered Uranus Trojan (UT) 2011 QF99 and several candidate UTs have been reported to be in unstable orbits. This implies that the stability region around the triangular Lagrange points L4 and L5 of Uranus should be very limited.
Aims. In this paper, we aim to locate the stability region for UTs and find out the dynamical mechanisms responsible for the structures in the phase space. The null detection of primordial UTs also needs to be explained.
Methods. Using the spectral number as the stability indicator, we constructed the dynamical maps on the (a0, i0) plane. The proper frequencies of UTs were determined precisely with a frequency analysis method that allows us to depict the resonance web via a semi-analytical method. We simulated radial migration by introducing an artificial force acting on planets to mimic the capture of UTs.
Results. We find two main stability regions: a low-inclination (0° −14°) and a high-inclination regime (32° −59°). There is also an instability strip in each of these regions at 9° and 51°, respectively. These strips are supposed to be related with g − 2g5 + g7 = 0 and ν8 secular resonances. All stability regions are in the tadpole regime and no stable horseshoe orbits exist for UTs. The lack of moderate-inclined UTs is caused by the ν5 and ν7 secular resonances, which could excite the eccentricity of orbits. The fine structures in the dynamical maps are shaped by high-degree secular resonances and secondary resonances. Surprisingly, the libration centre of UTs changes with the initial inclination, and we prove it is related to the quasi 1:2 mean motion resonance (MMR) between Uranus and Neptune. However, this quasi-resonance has an ignorable influence on the long-term stability of UTs in the current planetary configuration. About 36.3% and 0.4% of the pre-formed orbits survive fast and slow migrations with migrating timescales of 1 and 10 Myr, respectively, most of which are in high inclination. Since low-inclined UTs are more likely to survive the age of the solar system, they make up 77% of all such long-life orbits by the end of the migration, making a total fraction up to 4.06 × 10−3 and 9.07 × 10−5 of the original population for fast and slow migrations, respectively. The chaotic capture, just like depletion, results from secondary resonances when Uranus and Neptune cross their mutual MMRs. However, the captured orbits are too hot to survive until today.
Conclusions. About 3.81% UTs are able to survive the age of the solar system, among which 95.5% are on low-inclined orbits with i0 < 7.5°. However, the depletion of planetary migration seems to prevent a large fraction of such orbits, especially for the slow migration model. Based on the widely adopted migration models, a swarm of UTs at the beginning of the smooth outward migration is expected and a fast migration is favoured if any primordial UTs are detected.
Key words: celestial mechanics / minor planets, asteroids: general / planets and satellites: individual: Uranus / methods: miscellaneous
© ESO 2020
1. Introduction
Trojan asteroids are a set of celestial bodies sharing the orbit with their parent planet. These objects reside around two triangular Lagrange equilibrium points L4 and L5 with their orbits locked in the 1:1 mean motion resonance (MMR) with the parent planet, forming two swarms leading and trailing the planet by 60°, respectively. Although the triangular Lagrange points are dynamically stable for all planets of the solar system in the circular restricted three-body model (see e.g. Murray & Dermott 1999), the perturbations from other planets make the dynamical behaviour of Trojans complicated in the realistic model. Since the first discovery of a Jupiter Trojan (588 Achilles) in 1906 (Wolf 1907), more than 7000 Trojans have been detected around both L4 and L5 of Jupiter. At the same time, there have been 22 Neptune Trojans confirmed according to the Minor Planet Center1 (MPC) database. The Trojan cloud of Neptune is believed to be the second largest reservoir of asteroids larger than 50 km in radius in the solar system, only after the Kuiper belt (Chiang & Lithwick 2005; Sheppard & Trujillo 2006, 2010). To the contrary, the only discovery of Uranus Trojan (UT) 2011 QF99 around L4 (Alexandersen et al. 2013a) listed in the MPC database indicates a smaller stability window for Trojans of Uranus. Nesvorný & Dones (2002) showed that the Trojan region of Uranus is mostly unstable, although a few stability windows may exist (Dvorak et al. 2010). Compared with other giant planets in the solar system, Uranus has the smallest stability region, according to Marzari et al. (2003a).
2011 QF99 (for orbital elements; see e.g. Asteroids-Dynamic Site2, AstDyS-2) is deemed to be a Centaur temporarily captured into the Trojan region recently (Alexandersen et al. 2013b). In fact, Centaurs could be a significant supply of temporary UTs (Horner & Evans 2006). Specifically, Alexandersen et al. (2013b) find that at any time 0.4% of the a < 34 AU Centaur population supplied from scattering trans-Neptunian objects (TNOs) is in co-orbital motion with Uranus.
In addition, 2014 YX49 is identified as the second UT, which is temporarily on a high-inclined (i = 25.5°) tadpole orbit around L4 (de la Fuente Marcos & de la Fuente Marcos 2017). Moreover, it was reported that there exist several possible Uranus companions such as 83982 (Crantor), 2002 VG131, 2010 EU65, and 2015 DB216, which are supposed to be on the transient horseshoe, quasi-satellite, or even recurring co-orbital orbits (Gallardo 2006; de la Fuente Marcos & de la Fuente Marcos 2013, 2014, 2015). A detailed analysis of the dynamical evolution of these objects show that ephemeral multi-body MMRs could trigger the capture, ejection, and switching between resonant co-orbital states of transient Uranus companions. Meanwhile, Jupiter and Neptune have been found to render the long-term stability of Uranus companions (de la Fuente Marcos & de la Fuente Marcos 2013, 2014, 2015, 2017). The specific mechanisms behind these objects are different from each other, indicating complicated dynamical properties of Uranus co-orbital regions.
For a more general investigation, Dvorak et al. (2010) explore the stability regions of UTs for a range of inclinations up to 60°. They find four stability windows of initial inclinations in the ranges (0° ,7° ), (9° ,13° ), (31° ,36° ), and (38° ,50° ), where the most stable orbits could survive the age of the solar system. Counter-intuitively, high-inclined UTs may be more stable than those with low inclinations even though some instability strips caused by secular resonances rise in the high-inclination regime. In addition, the apsidal secular resonances with Jupiter and Uranus are proven to be responsible for the instability gap around i0 = 20°. Although some similar mechanisms had been identified earlier by Marzari et al. (2003a), these authors claimed that there are no stable UTs with low libration amplitudes owing to indirect perturbations from other planets.
Observational surveys of UTs are not only challenging because of their far distance from the Sun, but also discouraged by their low survival fractions over the age of the solar system (about 1% as predicted by previous theoretical investigations). For an initial density resembling the present Trojans of Jupiter, the present population of 10 km radii UTs was estimated to be less than a few tens (Nesvorný & Dones 2002).
The early dynamical evolution of the outer solar system is believed to be involved with planetary migration (Fernández & Ip 1984; Malhotra 1995; Hahn & Malhotra 1999), which could play an important role in the depletion of primordial UTs. Evaluating the influence of planetary migration on the orbital behaviour of UTs may in turn assess the proposed scenarios of the early evolution of the solar system. During the migration, the possible 1:2 MMR crossing between Jupiter and Saturn could develop great instability on their pre-formed Trojans and even empty the co-orbital region (Gomes 1998; Michtchenko et al. 2001; Morbidelli et al. 2005; Nesvorný & Vokrouhlický 2009). For Neptune Trojans, it turns out that only 5% of an initial population could survive the early stage of the solar system if a slow radial migration is taken into consideration (Kortenkamp et al. 2004). Inferred from the observed high-inclined orbits, the present population of Jovian Trojans and Neptune Trojans is probably the result of the chaotic capture from a primordial disc during migration (Morbidelli et al. 2005; Nesvorný & Vokrouhlický 2009; Lykawka et al. 2009; Lykawka & Horner 2010; Parker 2015). The influence of planetary migration on potential UTs deserves an investigation.
This paper provides detailed dynamical maps of UTs on the (a0, i0) plane where the long-term dynamical properties can be reflected with a relatively short integration time. A thorough investigation of the resonance mechanisms is needed to explain the complex structure of the phase space. Although orbits surviving the age of the solar system have been proven to be present (Dvorak et al. 2010), for the sake of observations it is still necessary to carry out a comprehensive search for the stability regions in the phase space in which possible primordial UTs reside. We urgently need to find out why primordial UTs have not been detected since they exist. The formation and evolution of the early solar system may provide an explanation, and in turn, the detection or null detection of UTs from subsequent observations can also restrict the theory of the early stage of the solar system.
The remainder of this paper is organised as follows. In Sect. 2, we briefly introduce the dynamical model alongside with the methods used for further analysis. In Sect. 3, we present the dynamical map on the (a0, i0) plane and determine the stability regions. Furthermore, we try to explain the excitation of the orbits and the displacement of libration centres. The resonance web is depicted in Sect. 4 with the help of a frequency analysis method. Owing to a long time integration of orbits, Sect. 5 shows the long-term stability of UTs. We then discuss the influence of planetary migration on the depletion of primordial UTs in Sect. 6. Finally, Sect. 7 presents the conclusions and discussions.
2. Model and method
In this paper, we evaluate the orbital stability of UTs via numerical simulations and spectral analysis. Then we try to locate the resonances responsible for the structures in the dynamical map with the help of a frequency analysis method. The tools and methods adopted are very similar to those used in our investigation of Earth Trojans (Zhou et al. 2019). We first provide a brief introduction.
2.1. Dynamical model and initial conditions
The outer solar system model consisting of the Sun (with the mass of inner planets added onto), four giant planets, and massless fictitious UTs is adopted in our numerical simulations. Many studies for UTs and Neptune Trojans have verified the reliability of this model (see e.g. Dvorak et al. 2010; Zhou et al. 2009, 2011). Since the phase spaces around L4 and L5 are dynamically symmetrical to each other (see e.g. Nesvorný & Dones 2002; Marzari et al. 2003a; Zhou et al. 2009, 2019), we just focus on L4 in this paper.
We initialised the model with a planetary configuration at epoch of JD 2457400.5. The orbital elements of planets are taken from JPL HORIZONS system3 (Giorgini et al. 1996). The fictitious UTs were initially put around L4 sharing the same eccentricity e (0.04975), longitude of the ascending node Ω (73.93°), and mean anomaly M with Uranus. We set the initial argument of perihelion of all fictitious UTs as ω0 = ω7 + 60°4, so that the resonant angle of fictitious UTs, which is defined as
where λ = ω + Ω + M is the mean longitude, is fixed at 60° at the beginning of simulations. It is worth noting that the locations of L4 and L5 could be displaced from σ = ±60° owing to the presence of the eccentricity and inclination (Namouni & Murray 2000; Kinoshita & Nakai 2007), but in our case the deviation is not remarkable (< 5°). To investigate the stability regions on the (a0, i0) plane, a grid of initial conditions was considered with 271 initial values of semi-major axes and 131 values of inclinations equally spaced in the domain, where a0 ranges from 19.08 AU to 19.35 AU and i0 ranges from 0° to 65° (35 501 test particles in total).
We performed two primary sets of numerical simulations in our investigation; one set integrated the whole system for 3.4 × 107 yr, while the other set integrated for the age of the solar system (4.5 Gyr). Adopting a Lie-series integrator (Hanslmeier & Dvorak 1984), the short time simulation was carried out to construct the dynamical map and locate the involved resonances. At the same time, a long time simulation is expected to check the existence of primordial UTs with the help of the hybrid symplectic integrator in the MERCURY6 software package (Chambers 1999). The orbits of planets remain stable in the long time run, and specifically for Uranus, the maximum eccentricity during the simulation is lower than 0.08. The same integrator including an artificial force was also implemented to simulate the radial migration of planets. We note that the results from these two numerical tools are verified to be consistent with each other.
2.2. Spectral analysis and frequency analysis method
It is necessary to apply a spectral analysis method in the short time simulation to reduce the amount of output data and remove short-period terms, which may cause some difficulties in the following frequency analysis.
Concretely, we made use of an on-line low-pass digital filter to smooth the output of the integration (Michtchenko & Ferraz-Mello 1995; Michtchenko et al. 2002) and resampled the data with an interval of Δ = 256 yr. For the whole integration time of 3.4 × 107 yr, we obtained N = 217(= 131 072) lines of data for each orbit. Using the fast Fourier transform (FFT), we calculated the frequency spectra for each orbit and then recorded the spectral number (SN), which is defined as the number of peaks above a specific threshold in a spectrum. The SN is an appropriate indicator of orbital regularity carrying abundant information of the dynamical behaviour (Zhou et al. 2009, 2011, 2019). Obviously, the smaller the SN, the more regular the orbit. In most cases, regularity could reflect stability or even predict stability. The Nyquist frequency is fNyq = 1/(2Δ) = 1.95 × 10−3 2π yr−1 while the spectral resolution is fres = 1/(NΔ) = 2.98 × 10−8 2π yr−1. All secular fundamental frequencies in the outer solar system except the nodal precession rate of Jupiter (see Sect. 4.1) are covered in the range of these two frequencies.
In order to locate the resonances responsible for the dynamical behaviour of UTs with a semi-analytical method (see Sect. 4), we have to determine precisely the proper frequencies for each orbit with a frequency analysis method proposed by Laskar (1990). A brief introduction to the numerical algorithm is provided in Zhou et al. (2019).
3. Dynamical map
Indicators such as the maximum Lyapunov characteristic exponent, diffusion rate in the frequency space, maximum eccentricity, libration amplitude, and escape time are all well used in the study of orbital stability (see e.g. Nesvorný & Dones 2002; Marzari et al. 2003a; Dvorak et al. 2010). In this paper, we adopt the SN of cosσ to construct a more detailed dynamical map.
3.1. Stability region
We present the dynamical maps around L4 of Uranus on the (a0, i0) plane in Fig. 1, where the colour represents the base-10 logarithm of SN. The results for two different integration times (4.25 × 106 yr and 3.4 × 107 yr) are shown separately. The red regions in which the orbits comprise large values of SN indicate a poor regularity while blue regions are the opposite. Based on our test runs we regard the orbits that dissatisfy 18.62 AU ≤ a ≤ 19.82 AU at any time during the integration as escaping from the co-orbital region of Uranus; these are excluded from the map.
 |
Fig. 1. Dynamical maps around the L4 point of Uranus on the (a0, i0) plane. The colour indicating the regularity of orbits represents the base-10 logarithm of SN of cosσ. Orbits escape from the 1:1 MMR with Uranus during the integration time are not included in these maps. The libration centres for different i0 are depicted by the dark line. Left panel: result for 4.25 × 106 yr; right panel: result for 3.4 × 107 yr, which is eight times the former. |
In the explored region, stability islands are confined at two small regions on the (a0, i0) plane (Fig. 1), of which one is at low inclination (0°–14°) while the other is at high inclination (32°–59°). Two nearly horizontal strips around 9° and 51° are found lying in these two stability regions, respectively, dividing each of these regions into two regimes. For the low-inclined orbits, the stability region could extend to the range between 19.224 ± 0.108 AU, while it shrinks to 19.21 ± 0.07 AU at high inclination. Obviously, the most stable orbits (in blue) whose SN is smaller than 200 reside mostly in the low-inclination regime. The subsequent long time integration (see Sect. 5) proves that these orbits have a great chance to survive the age of the solar system. It is worth noting that the centre island of the high-inclination window can also hold these kinds of stable orbits, even though the high-inclined orbits are less stable than the low-inclined orbits overall because the former possess larger SN.
It can also be seen from the right panel in Fig. 1 that abundant horizontal fine structures appear in the stability regions, implying plenty of high-degree resonances hiding in the phase space. However, some high-degree resonances causing the patterns in the dynamical map may have a weak strength that can hardly affect the long-term stability of UTs. Yet they still have a remarkable influence on the regularity of orbits and in turn, the fine structures could point us towards a way to locate the related resonances (see Sect. 4).
By the end of the whole integration time (3.4 × 107 yr), most orbits have escaped, leaving a large area of the (a0, i0) plane blank. To explore these uninformative regions, we constructed a dynamical map with the output of a shorter time simulation (4.25 × 106 yr), where the integration time is only one-eighth of the previous simulation (the left panel in Fig. 1). Owing to a much shorter evolution time, the smaller SN is expected in this dynamical map as some long-term instabilities have not worked on the orbits yet. The instability gaps around 9° and 51° are absent, implying that the corresponding timescale of the resonance mechanism is longer than 4.25 × 106 yr. On the contrary, the lack of orbits in moderate inclination suggests that the resonances residing between 15° and 30° are of shorter timescales. The formation of the cyclic structures apparently seen in the low-inclination regime is believed to be involved with short-period mechanisms such as some secondary resonances or three-body resonances (see Sect. 4.2). However, these resonance mechanisms do not contribute to the long-term stability because the cyclic structures disappear after a period of time (see the right panel in Fig. 1) and cause no escape of orbits there.
3.2. Excitation of the eccentricity and inclination
The variations of eccentricity and inclination can also provide some clues about related dynamical mechanisms. Since the variations of eccentricity and inclination are more dependent on initial inclination rather than initial semi-major axes, we show the amplitudes5 of eccentricity (Δe) and inclination (Δi) against initial inclinations (i0) in Fig. 2. We find the maximum eccentricity of surviving orbits can hardly exceed 0.14, except those in the region from i0 = 9° to 40° and around i0 = 51°, where the eccentricity could reach 0.24 or even higher (top panel in Fig. 2). The inclination of surviving orbits above i0 = 30° mainly vary within 5° while that of orbits around the instability gap at i0 = 9° could be excited to 11.8° (the bottom panel in Fig. 2). Besides, a peak of Δi up to 6.5° stands around i0 = 4°. We note there also exist some orbits diffusely distributed in Fig. 2, especially in the high-inclination regime. These orbits are close to the boundary of the stability region and on the way of losing their stability. These orbits with higher eccentricity and inclination are very likely to have left the tadpole region of L4. In our simulations we find that once an object escapes from the tadpole cloud, it obtains a very large libration amplitude (> 300°, mainly in horseshoe configuration) if it is still trapped in the 1:1 MMR (see e.g. the phase portrait in Kinoshita & Nakai 2007; Robutel & Pousse 2013). We also note that no orbits are of libration amplitudes between 180° and 300° in our simulations.
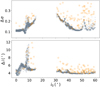 |
Fig. 2. Variations of the eccentricity and inclination for orbits with different initial inclinations surviving the integration time of 3.4 × 107 yr. The initial eccentricity is 0.04975 for all orbits. There might be many orbits with different initial semi-major axes for each initial inclination. The orange squares indicate orbits whose libration amplitude (Δσ) is larger than 300° while black crosses indicate those which have never left the tadpole region around L4 during the integration time (Δσ < 180°). |
As we know, the apsidal and nodal secular resonances are supposed to be responsible for the regional excitation of the eccentricity and inclination, respectively, according to the linear theory of secular perturbation (see e.g. Murray & Dermott 1999; Li et al. 2006), so that Fig. 2 could help us refine the search for the related resonances. The secular resonances inducing the instabilities between 14° and 32° are most probably involved with the perihelion precession, since Fig. 2 infers that Δe in this region is very large. Furthermore, these apsidal secular resonances should have large width as orbits with a large range of inclinations are affected (see the top panel of Fig. 2). The orbits close enough to the secular resonances are able to be excited to e > 0.25 and then lose their stability. Another apsidal secular resonance is found around 51° with a much narrower width. It can drive the eccentricity up to ∼0.21.
We monitor the orbital evolution and find that the most important secular resonances dominating the moderate-inclination regime are ν5 and ν7, while ν8 dominates the high-inclination regime (Fig. 3). In accordance with practice, we denote the apsidal and nodal secular resonances with the jth planet as νj and ν1j, respectively. These resonances occur when g = gj and s = sj, where g and s indicate the precession rate of perihelion and ascending node, respectively. It is worth noting that the resonances around i0 = 7.5° are able to influence both the eccentricity and inclination (Fig. 2), implying that they involve the precession of both the perihelion longitudes and ascending nodes. The inclination that can be excited up to ∼20° experiences a secular variation with a period of tens of millions of years. A large portion of orbits around i0 = 7.5° have escaped and the surviving orbits near the resonances leave the 1:1 MMR with Uranus sooner or later. For lower inclinations, the orbits are strongly influenced by other nodal secular resonances.
 |
Fig. 3. Orbital evolution of two fictitious Trojans over some period at the end of the integration (except the top right plot). The orbits in the left and right panels are initialised with (a0, i0) = (19.225 AU, 56.5° ) and (19.317 AU, 5° ), respectively. We illustrate the temporal evolution of the eccentricity e, inclination i, and resonant angle of the 1:1 MMR with Uranus σ for both orbits. The semi-major axis ratio of the UT and Uranus a/aU, resonant angle of the 1:2 MMR with Neptune σ1 : 2 and apsidal difference with Neptune Δϖ8 are also shown in the left panel, while the apsidal differences with Jupiter Δϖ5 and Uranus Δϖ7 over the last few million years (bottom right) and the whole integration time (top right) are shown in the right panel, respectively. The vertical dashed lines in the left panel indicate the time 3.2716 × 107 yr, 3.2762 × 107 yr and 3.2922 × 107 yr, when the UT enters and leaves the quasi-satellite orbit, and is captured by the Kozai mechanism. |
The close encounter with Uranus when UTs are on large-amplitude horseshoe or quasi-satellite orbits could excite the eccentricity sporadically. The Kozai mechanism inside the co-orbital resonance (Namouni 1999; Giuppone & Leiva 2016) is also likely to pump up the eccentricity of high-inclined orbits by trading the inclination and in turn the inclination can also be driven up. These two mechanisms could also work together to excite orbits. There are few orbits surviving the whole integration time under the influence of these mechanisms; even if these orbits survive, they are expected to leave the co-orbital region of Uranus soon.
The orbits denoted in orange square in Fig. 2 undergoing huge variations in resonant angles (Δσ > 300°) are mainly excited by these two mechanisms in addition to secular resonances. We arbitrarily present one such example in the left panel of Fig. 3. The orbit is initialised with (a0, i0) = (19.225 AU, 56.5° ) and is of a Δe of 0.371. As we can see, at 3.2716 × 107 yr, the orbit transforms from the tadpole orbit around L5 to quasi-satellite orbit as the resonant angle begins to librate around 0°. The eccentricity ends the periodic variation which is a result of the secular resonances (not shown in the figure) and undergoes a remarkable growth due to close encounters with Uranus. From 3.2922 × 107 yr, the orbit has been trapped in the Kozai mechanism because the argument of perihelion librates around ±90° with the eccentricity and inclination coupled to each other. This leads to a further increase in eccentricity up to 0.371. In addition, the apsidal difference between Trojans and Neptune Δϖ8 is found in oscillation all the time, which means the ν8 secular resonance governs the variations of the eccentricity before the orbits are dominated by the Kozai mechanism. We note that the semi-major axis could librate around 18.94 AU (a/aU ≈ 0.986), where the 1:2 MMR with Neptune is located. We check the resonant angle σ1 : 2 = λ − 2λ8 + ϖ and find it oscillates around 0° at that time. The resonance overlap between the 1:1 MMR with Uranus and 1:2 MMR with Neptune could induce chaos (Chirikov 1979).
Some orbits with large libration amplitudes may maintain their relatively low eccentricity and inclination for a long time, just like the orbit in the right panel in Fig. 3, whose initial semi-major axis and inclination are 19.317 AU and 5°, respectively. The amplitude of the eccentricity is only 0.124. We arbitrarily choose one orbit as the example since the evolutions of these kinds of orbits are very similar to each other. Reflected in the oscillation of Δϖ5 and Δϖ7 over the integration time, these orbits are supposed to be under the control of apsidal resonances with Jupiter (ν5) and Uranus (ν7) all the time. The rate of the apsidal precession of such UTs in fact changes little in a wide range of initial orbital elements, implying that many orbits could be dominated by the same secular resonances (see Fig. 5). Although neither close encounter nor Kozai mechanism occurs to excite the eccentricity and inclination during the integration time, the large libration amplitude coming from the chaotically recurring transformations between tadpole and horseshoe orbits will most probably lead to close encounter with Uranus and depletion from the resonance region in the future.
3.3. Libration centre
In the planar circular restricted three-body model, test particles with low eccentricity are supposed to be on tadpole orbits if the radial separation from the secondary mass is less than (8μ/3)1/2a, where μ and a denote the mass fraction and semi-major axis of the secondary mass (Murray & Dermott 1999). This criterion gives the Sun-Uranus system the maximum radial separation of tadpole orbits about 0.21 AU. Although this range shrinks as the eccentricity increases, it is still wide enough to cover all stability regions shown in Fig. 1, given that UTs with long-term stability are limited to e < 0.1 (Nesvorný & Dones 2002). This is consistent with the conclusion that horseshoe orbits of Uranus lose their stability on short time spans because of the instabilities induced by the overlap of the 1:1 MMR with high-degree first-order MMRs (Nesvorný & Dones 2002). We show in Fig. 4 the libration amplitudes of surviving orbits on the (a0, i0) plane. Most of the orbits in the stability region remain in the tadpole cloud around L4 all through the integration time. But there still exist some temporary horseshoe orbits with large libration amplitudes. These orbits keep switching between different co-orbital states (see e.g. orbits in Fig. 3) and that is why there is a lack of orbits whose Δσ are between 180° and 300°.
 |
Fig. 4. Libration amplitudes of surviving orbits (in different colours) during the orbital integration of 3.4 × 107 yr on the (a0, i0) plane. The solid line implies the libration centres for different i0. Dozens of orbits whose libration amplitudes Δσ are larger than 300° are ignored for better visibility. Because of the scarcity of numbers, we indicate the orbits with libration amplitude Δσ above 120° with the same colour. The dashed line is the same as the solid line, but for the integration where Neptune is initially placed further away from the 2:1 MMR with Uranus (see text). |
It is unexpected that the libration centre shifts significantly with inclinations (see Fig. 4) since this feature is absent for Earth Trojans and Neptune Trojans according to our previous investigations (Zhou et al. 2009, 2011, 2019). We note that the libration centre is defined in this work as the initial semi-major axis of the orbit whose libration amplitude is the smallest among the orbits with the same initial inclination. To depict the displacement, we numerically fit the libration centre ac as a function of the initial inclination i0 and show it in Fig. 4 as well as in the dynamical maps (Fig. 1). Apparently, as the inclination increases, the libration centre shifts towards smaller semi-major axis. This displacement is speculated to be involved with the quasi 2:1 MMR between Uranus and Neptune (in current orbital configuration the orbital period ratio is 1.962). To confirm this, we initially placed Neptune at different distances from the exact location of the 2:1 MMR with Uranus. The simulations indicate that the displacement would gradually disappear when Neptune gets further away from the 2:1 MMR with Uranus (see e.g. the dashed line in Fig. 4 for the case with period ratio of 1.945). In cases in which Neptune is close enough to the 2:1 MMR, the overlap between the 1:1 MMR with Uranus and 1:2 MMR with Neptune could induce great chaos, destabilising the UTs in a short time.
As we can also see from Fig. 4, UTs with the smallest libration amplitudes are found in the high-inclination regime, where the SN is a bit larger than low-inclined UTs. This proves that the most stable UTs are of relatively larger libration amplitudes. The lack of low libration UTs in the low-inclination regime is due to the cumulative effect of indirect perturbations from other planets (Marzari et al. 2003a). The libration amplitude experiences a slight growth around i0 = 12° before decreasing. Hence the stability island there by and large hosts the tadpole orbits of the largest libration amplitudes (∼52° at the libration centre). In fact, the secondary resonances (see Sect. 4.2) could pump up the libration amplitude (Tittemore & Wisdom 1990; Malhotra & Dermott 1990; Kortenkamp et al. 2004). These resonances, alongside other important resonant mechanisms, are figured out and located in next section with the frequency analysis method.
4. Frequency analysis
4.1. Dynamical spectrum
The frequency spectrum contains a lot of valuable information that can reflect the dynamical properties of orbits. Many significant components appear in the frequency spectrum of orbital variables, including the proper frequencies, forced frequencies, their harmonics, and combinations thereof. These frequencies can be computed precisely utilising the method proposed by Laskar (1990). We then picked out the proper frequencies via dynamical spectra, where several of the most important frequencies for each orbit are plotted against the initial semi-major axes or inclinations. Figure 5 presents three arbitrary examples of dynamical spectra to illustrate the determination of the proper frequencies fσ, g, and s for the orbital variables cosσ, e cos ϖ, and i cos Ω, respectively. Apparently, the proper frequencies vary with the initial orbital elements while the forced frequencies remain unchanged. Their harmonics and combinations are also present.
 |
Fig. 5. Dynamical spectra of icosΩ (top panel), ecosϖ (middle panel), and cosσ (bottom panel). The five most significant frequencies of the highest peaks in the power spectra, which are denoted by red open circles, black open inverted triangles, squares, triangles, and diamonds respectively, are plotted against their initial inclinations (top two panels) or semi-major axes (bottom panel). The proper frequencies which vary continuously with the initial semi-major axis and inclination are indicated by arrows. The initial semi-major axis for orbits in the top two panels is 19.22 AU while the initial inclination for orbits in the bottom panel is 4°. The dashed lines indicate the forced frequencies which are identified to be involved with the frequency of the quasi 1:2 MMR between Uranus and Neptune f2 : 1 or the fundamental frequencies in the outer solar system. In the bottom panel the frequencies 2f, 2f − f2 : 1, and f2 : 1 − f are also labelled. The precession rates of the ascending node for orbits in the top panel, along with s7, are all negative. Hence, the absolute values of these frequencies are plotted. |
The precession rates of the perihelion (g) and ascending node (s) of Trojans are obscured by the forced frequencies which are identified to be associated with the fundamental secular frequencies in the outer solar system (Table 1). The s7 is found in the frequency spectra of i cos Ω for low-inclined orbits, while 2g5 − g7, g5 and g7 are present in the frequency spectra of e cos ϖ. We note that the precession rate may be negative, just like the nodal precession rate of the orbits shown in Fig. 5 alongside the giant planets (see Table 1). In the dynamical spectrum of cosσ, the forced frequency is certified as the frequency of the quasi 1:2 MMR between Uranus and Neptune, which is denoted by f2 : 1 = 2.3238 × 10−4 2π yr−1 and corresponds to a period of 4303 yr.
Fundamental secular frequencies in the outer solar system.
In the case of these three examples, the proper frequencies (indicated by arrows) often have the largest amplitudes (red open circles). However, this is not always the case and it is not necessary. The intersections of the proper and forced frequency are the exact locations at which the secular resonances or secondary resonances take place (Milani 1994; Marzari et al. 2003b; Zhou et al. 2009, 2011, 2019). The corresponding proper frequencies nearby are affected and mired in a certain degree of confusion. For the same reason, the proper frequencies in the instability region are difficult to be identified. As we can see from Fig. 5, the apsidal secular resonances with Jupiter and Uranus occupy the moderate-inclination regime. The nodal secular resonance with Uranus ν17 and apsidal secular resonance g = 2g5 − g7 could dominate the motion of low-inclined orbits. As we mentioned before in Sect. 3.3, the quasi 1:2 MMR between Uranus and Neptune could have some influence on the dynamical properties of UTs.
4.2. Resonance web
Marzari et al. (2003a) obtained the expression for the proper frequencies of UTs as functions of the proper orbital elements (eccentricity, inclination, and libration amplitude). However, the dynamical maps in this paper are constructed in osculating orbital elements space, which offers every convenience for the application of the maps by direct comparison with the observational data. Hence, instead of the proper elements, we numerically fit fσ, g, and s as functions of a0 and i0 (initial osculating elements) so that we can locate the resonances on the (a0, i0) plane. The quintic polynomial
is adopted to fit the frequencies fσ, g, and s, where pmn are the undetermined coefficients. The quantities x and y represent normalised (a0 − ac) and sin(i0), where ac(i0) is the libration centre (see Sect. 3.3). We note that the proper frequencies in chaotic areas are difficult to be determined, therefore the fitting formula may have some deviations in the margin area because the extrapolation may be relatively rough there. A rough comparison shows that the values of proper frequencies obtained by Marzari et al. (2003a) and in this work are in similar ranges, especially in stability regions.
For a more intuitive and comprehensive understanding of the dynamics in the phase space, we display the resonances related to the orbital stability on the (a0, i0) plane. The secular resonances can be located by solving the equation
where p, q, pj, and qj are integers to be solved. The d’Alembert rule 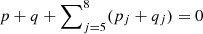 has to be satisfied and
has to be satisfied and 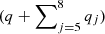 must be even. The value of
must be even. The value of 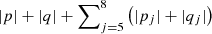 is the degree of the secular resonance.
is the degree of the secular resonance.
After a comprehensive search, we show the significant secular resonances in Fig. 6. Linear secular resonances are the most important mechanisms shaping the stability region. The ν5 and ν7 are depicted in the moderate-inclination regime, clearing the orbits from 14° to 32°. As mentioned in Sect. 3.2, these two secular resonances have large widths on the (a0, i0) plane. The UTs close to these secular resonances can be excited to high-eccentric orbits. The overlap between them can also induce chaos. The secular resonance ν8 could give rise to the instability strip around 51°. Although the exact locations of ν17 and ν18 are far from the stability region, they are still involved with the low-inclined and high-inclined orbits in the stability region, controlling the variation of the inclination.
 |
Fig. 6. Locations of secular resonances for Trojans around L4 on the (a0, i0) plane. The resonances are labelled (see text for the meaning) along the curves. The solid lines indicate the linear and fourth-degree secular resonances; the dashed lines indicate the higher order secular resonances. The C2 resonance is shown in red for better visibility. |
Following the classification of Zhou et al. (2019), we name the higher degree secular resonances only involving the apsidal precession (g) “G” type and those only involving nodal precession (s) “S” type. The rest is called “C” type in the name of “combined”. The meaning of these resonances shown in Fig. 6 is explained as follows:
The G-type resonance g − 2g5 + g7 = 0 (G1) is supposed to be responsible for the instability gap around i0 = 9°. At the same time, C4 resides in the similar location. Marzari et al. (2003a) found that the forced frequency 2g7 − g5 could be commensurate with the apsidal precession rate g for high-inclined orbits. In fact, G2 and g − 2g7 + g5 = 0 are almost located in the same position because (g7 + g8)/2 ≃ 2g7 − g5. Therefore, it should be noted that many resonances could share the same location on the (a0, i0) plane and they can act together on the orbits. We classify these resonances into the same resonance family and just show some representative resonances in Fig. 6. Sometimes, the strength of the resonances belonging to the same family differs greatly. Then the motion is dominated by the strongest resonance. In other cases, these resonances are of similar strength, which may lead to instability as a result of the resonance overlap. The horizontal fine structures are related to the high-degree secular resonances such as C1, G2, and C6. Secular resonances in C2 family are believed to control the variation of the inclination for low-inclined orbits, causing the structure around i0 = 7.5° in the bottom panel of Fig. 2. In addition, C3-like resonances could shape the outline of the stability region in the low-inclination regime.
Following the terminology used by Malhotra & Dermott (1990), the secondary resonances for UTs are those resonances that arise when the libration frequency of the resonant angle for the 1:1 MMR (fσ) is commensurate with the circulation frequency of the resonant angle for the quasi 1:2 MMR between Uranus and Neptune (f2 : 1). They can be expressed as
where h and k are integers. Three-body resonances involving UTs, Uranus, and Neptune are defined by the relation
where mT, mU, and mN are integers and λ, λU, and λN are the mean longitudes of UTs, Uranus, and Neptune, respectively. We can find that for UTs, three-body resonances are almost equivalent to secondary resonances if we could rewrite the resonant angle of three-body resonances as m (λ − λU)+n (λU − 2λN), where m and n are integers. It is valid because both fσ and f2 : 1 are small so that Eq. (6) can be satisfied.
We search secondary resonances by solving
The d’Alembert rule requires 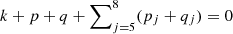 in this case. We note that Eq. (7) is consistent with Eq. (5) because the terms involving the secular precessions are much smaller than those involving fσ and f2 : 1. Representative secondary resonances shown in Fig. 7 are listed as follows:
in this case. We note that Eq. (7) is consistent with Eq. (5) because the terms involving the secular precessions are much smaller than those involving fσ and f2 : 1. Representative secondary resonances shown in Fig. 7 are listed as follows:
 |
Fig. 7. Same as Fig. 6 but for examples of secondary resonances. The dynamical map behind the resonances represents the integration of 4.25 × 106 yr. The Σ4 resonance is shown in red for better visibility. |
Since the shapes match well, the cyclic structures in the low-inclination regime are speculated to be caused by those secondary resonances. We show in Fig. 7 only one corresponding resonance (Σ4) for the cyclic structures, which are caused by plenty of such high-order secondary resonances. Since they involve fσ and f2 : 1 whose timescales are relatively short, the secondary resonances are expected to affect the motion in relatively short term. In fact, the cyclic structures in the low-inclination regime can be found only in the dynamical map of short integration time (4.25 × 106 yr) but not in the long-term integration (see Fig. 1).
The secondary resonances or three-body resonances can affect the stability of Trojans in the outer solar system to varying degrees (Marzari et al. 2003b,a; Zhou et al. 2009, 2011). Studies of the Uranian satellite system indicate that orbits captured in the secondary resonances may experience an amplification of the libration amplitude of the primary resonance (Tittemore & Wisdom 1990; Malhotra & Dermott 1990; Kortenkamp et al. 2004), which in our case is the 1:1 MMR with Uranus. The amplification eventually leads to the escape from the co-orbital region, implying the secondary resonances could destabilise the orbits. However, our investigation suggests that the secondary resonances associated with f2 : 1 have no significant effect on the long-term stability of UTs in the current planetary configuration, although they could pump up the libration amplitude mainly in the low-inclination regime (see Fig. 4). This is different from Neptune because MMRs exterior to a planet (1:2 MMR of Uranus) are supposed to be wider than MMRs interior to it (2:1 of Neptune), just like the different influence of the quasi 2:5 MMR between Jupiter and Saturn (the Great Inequality) on Jupiter Trojans and Saturn Trojans (Nesvorný & Dones 2002). As a result, the quasi 1:2 MMR between Uranus and Neptune could modify the structure of the phase space on short time spans rather than affecting the long-term stability of UTs. Páez et al. (2016) and Páez & Efthymiopoulos (2018) developed the ‘basic Hamiltonian model’ to analytically determine the centre and boundary of secondary resonances in the space of proper elements for co-orbital motion and demonstrate that the innermost boundary of the most conspicuous secondary resonance could delimit the effective stability region for Trojans.
5. Long-term stability
To assess the long-term stability of UTs, we integrated all the 35 501 fictitious Trojans on the (a0, i0) plane (see Sect. 2.1) to the age of the solar system (4.5 Gyr). For each of these fictition Trojans, the time when the orbit escapes from the co-orbital region of Uranus is recorded as its lifespan. Figure 8 presents the lifespans of all orbits on the (a0, i0) plane. The orbits of long lifespan form similar structures as the dynamical maps (Fig. 1). The cap structure around 60° that is only obvious in the dynamical map for short time integration (see the left panel of Fig. 1) appears again. This may be related to the C7-like secular resonance. The fine structures which could help us locate the resonances are absent in Fig. 8. This is because the SN characterises the regularity of the orbit and is not exactly equivalent to the lifespan in co-orbital region. Lifespan can intuitively describe the stability of orbits but SN can better reflect the characteristics of motion.
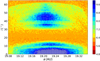 |
Fig. 8. Lifespans of fictitious UTs around the L4 point on the (a0, i0) plane. The colour indicates the base-10 logarithm of the lifespans. The white points indicate the orbits surviving the age of the solar system (4.5 Gyr). |
Among all fictitious UTs, about 3.81% orbits survive the integration time. These stable orbits mostly (95.5%) gather in the low-inclination regime around the libration centre (i0 < 7.5° , 19.164 AU < a < 19.288 AU), which is consistent with the stability region in which the orbits with the smallest SN reside. The rest (4.5%) surviving orbits are in the high-inclination regime from 42° to 48°. Some UTs with inclination up to 60° could reside in the tadpole cloud around L4 for 108 yr. This is consistent with the analysis of periodic orbits around L4 in Giuppone & Leiva (2016). Nesvorný & Dones (2002) suggested that dynamical instabilities in the long-term evolution over 4 Gy could cause a 99% depletion of primordial UTs and Saturn Trojans, while this value is only 50% for Neptune Trojans. The survival ratio (3.81%) we obtain is larger than their result (1%) because they only sampled i0 = 0°, 5°, 10°, 15°, 20°, and 25° and the stability regions only exist for the first two conditions according to Fig. 1.
To guide the search for primordial UTs, we calculated the normalised sky densities making use of the orbital evolution over the age of the solar system. All surviving orbits are taken into account. The sky positions are referred to the instantaneous orbital plane of Uranus. Then we computed the relative longitudes (Δθ) and latitude (Δϕ) for all orbits. The sky densities are obtained by calculating the time proportion that all orbits spend in each 1° ×1° segment of the sky. This is equivalent to the probability of UTs appearing in each segment at a certain time.
The result is shown in Fig. 9. Considering the high-inclined orbits (i0 ∈ [42° ,48° ]) are much fewer than the low-inclined orbits (i0 < 7.5°, see Fig. 8), we presented their sky densities separately. However, both of these are still normalised by the total residence time of all orbits. Thus the resulting sky densities are very different from each other, as indicated by the colour bars with significantly different values in Fig. 9. Apparently, for low-inclined orbits, most of primordial UTs gather in the interval of ±5° of the orbital plane of Uranus and they are most likely to be found on the coplanar orbits, especially where the L4 point locates (Δθ, Δϕ) = (60° ,0° ). For high-inclined orbits, the highest densities occur within a region of ∼480 deg2 around (Δθ, Δϕ) = (55° ,0° ). Besides, (Δθ, Δϕ) = (72° , ± 40° ) is a good choice for observations dedicated to high-inclined primordial UTs. We note that the sky density in Fig. 9 is different from that obtained by Nesvorný & Dones (2002) mainly because they have much fewer samples (only 14 orbits) with different distribution of orbital elements.
 |
Fig. 9. Normalised sky densities computed from the orbits surviving the age of the solar system. Top panel: low-inclined orbits; bottom panel: high-inclined orbits. The colour represents the proportion of the residence time in each 1° ×1° segment of the sky with respect to the instantaneous orbital plane of Uranus. The black cross denotes the position of the L4 point. |
6. Influence of planetary migration
6.1. Pre-formed UTs
Although the null detection of stable UTs may be related to the detection capacity, so far this null detection may still imply extra mechanisms destabilising Uranus companions. Nesvorný & Dones (2002) suggested that the significant depletion of the pre-formed population of primordial Trojans results from the MMRs in the radial migration of planets. Hence, we numerically studied the dynamical behaviour of pre-formed UTs during the early evolution of the outer solar system.
Even though the Nice model (Gomes et al. 2005; Morbidelli et al. 2005; Tsiganis et al. 2005) depicts a more realistic planetary migration process, we still refer to radial migration in our simulations, where Jupiter migrates slightly inward while the other three giant planets migrate outward (Fernández & Ip 1984, 1996; Hahn & Malhotra 1999; Zhou et al. 2002). This simplified model is appropriate for the purpose of investigating the survivability of primordial UTs in this paper and it requires only limited computing resources. This process can be conveniently simulated via an artificially constructed force instead of the interaction with the planetesimal disc. An exponential migration is adopted so that the semi-major axes of the planets could evolve according to
where aj(t) is the semi-major axis of the jth planet after time t, δaj is the desired amount of the total radial migration, and τ is the e-folding time determining the rate of migration (Fernández & Ip 1984, 1996; Hahn & Malhotra 1999; Zhou et al. 2002). Following the initial planetary configuration and δaj (−0.2, 0.8, 3.0, and 7.0 AU for four giant planets, respectively) adopted in Kortenkamp et al. (2004), we reproduced fast and slow migration in our simulations with τ = 1 Myr and 10 Myr, respectively.
Because no significant asymmetry is found between L4 and L5 during radial migration (Parker 2015), we consider that an initial swarm of massless planetesimals formed near Uranus and were trapped in the tadpole region around L4 while Uranus was growing before planetary migration. We use the same strategy as previously described in Sect. 2.1 to produce the initial orbital elements of pre-formed UTs. Since the disc may be pre-heated before the final stage of planetary migration (Parker 2015), we choose an initial inclination distribution of pre-formed UTs that is wide enough (0°–65°). After some test runs, a total of 392 initial semi-major axes are evenly distributed from 16.060 to 16.451 AU around the initial position of Uranus (16.316 AU), and finally 51 352 (= 392 × 131) pre-formed UTs are set. By checking the libration amplitude during the first 25 000 years, we verify that most of the sampled orbits are bound to the 1:1 MMR with Uranus initially. For fast and slow migration, there are 35 691 and 36 607 such orbits in total, respectively, and we use these orbits as the original population. Then the whole system is integrated for 5τ, when the migration is 99.33% complete.
The final distributions of the orbits that have never left the co-orbital region are shown in Fig. 10. Compared to slow migration (0.4%), many more orbits (36.3%) apparently survive fast migration. At the same time, high-inclined orbits have a much greater chance of surviving the migrations. The same instability gap as in the dynamical maps induced by ν5 and ν7 (see Fig. 6), especially the later in this case, appears for both migration rates, occupying the moderate-inclination regime from ∼10° to ∼30°.
 |
Fig. 10. Final distributions of orbits that never left the 1:1 MMR region of Uranus during planetary migration. Left and right panels: final inclination i against the final semi-major axis a and initial inclination i0, respectively. The black dots indicate the orbits surviving fast migration with the final eccentricity e lower than 0.1; the other dots indicate the orbits surviving slow migration, of which the blue and orange points represent those with e < 0.1 and e ≥ 0.1, respectively. The dashed line in the right panel depicts the equality of i and i0; the solid line depicts the best fit for slow migration. For a clear comparison with the stability regions (see Figs. 1 and 8), the same range in semi-major axis is shown in the left panel at the cost of abandoning a small part of orbits. In the right panel only data for slow migration is shown for better visibility. |
Recalling the stability regions and the orbits surviving the long-term evolution (Figs. 1 and 8), we estimate the probability of the orbits residing in the regions where they can survive the age of the solar system at the end of the migrations. The probability is obtained by calculating the product of the proportion of migratory orbits ending up in the regions enclosed by the stable orbits (two rectangles on the (a, i) plane that tightly cover the white points in Fig. 8: one for high inclination and the other for low inclination) and the proportion of area occupied by the stable orbits in those regions in current planetary configuration (i.e. ratio of number of white points to the total number of points in the corresponding rectangle). The results are 6.69 × 10−3 and 1.16 × 10−4 for fast and slow migrations, respectively. As mentioned before, the eccentricity of long-term stable UTs should be lower than 0.1 and under this constraint, the corresponding probabilities drop to 4.06 × 10−3 and 9.07 × 10−5, of which 77% is contributed by the low-inclined orbits for both kinds of migrations. However, it should be noted that the final configuration of both fast and slow migrations cannot exactly match the current configuration, which is used to construct the dynamical maps.
Figure 10 also presents the relation between the initial (i0) and final inclinations (i) of orbits surviving slow migration. In general, the surviving orbits end up with inclinations slightly smaller than their original values. We numerically fit the relation with a linear equation which is close to i = i0. This follows the results from Parker (2015), in which the inclinations change little for captured Neptune Trojans from the planetesimal disc. The similar relation also applies to fast migration. If there remain any high-inclined UTs at the end of the migration, this comes from the original inclinations, instead of the stirring from the migration process as the migration does not heat the Trojans, and even marginally cools them in the migration models adopted by us. The capture process also prefers the high-inclined orbits (Parker 2015), just as the pre-formed UTs with high inclinations have a larger chance of surviving the migration.
The decay curve of the Trojan population shown in Fig. 11 illustrates that most pre-formed UTs are depleted in the first 107 yr of slow migration. During this period, Neptune and Uranus have crossed their mutual MMRs, such as the 7:4, 9:5, and 11:6 MMRs. Concretely, every time the ice giants approach one of these MMRs, the secondary resonances associated with the MMR period and the libration period of UTs arise, inducing instabilities on the companions of Uranus (Kortenkamp et al. 2004). The evolution of the period ratio of Neptune and Uranus reveals the moments when the ice giants cross the important MMRs (Fig. 11). Obviously, the turning point of the decay curve at 0.22 τ results from the crossing of the 7:4 MMR between Neptune and Uranus. As these two planets get far from the 11:6 MMR from 0.80 τ, the depletion rate of the UT population slumps. Since then, the approach of Neptune and Uranus to the 1:2 MMR and other weaker MMRs may have contributed to the loss of UTs. For fast migration, the depletion rate is much smaller owing to shorter durations in the secondary resonances except the period from 0.70 τ to 1.08 τ, when the ice giants are moving from 11:6 MMR to 15:8 MMR.
 |
Fig. 11. Orbital period ratio of Neptune and Uranus PN/PU (top panel) and survival ratio of the original population (bottom panel) during fast (orange) and slow (blue) migrations. The orbital period ratio of which the short-period terms are eliminated by the low-pass filter is indicated by the red line. The horizontal lines indicate the locations of the 15:8, 11:6, 9:5, 7:4, and 5:3 MMRs between Neptune and Uranus. Two important moments for fast migration, 0.70 τ and 1.08 τ, and two important moments for slow migration, 0.22 τ and 0.80 τ, are indicated by the vertical lines. Only the period ratio for slow migration is shown in the top panel, and that for fast migration is almost the same. |
6.2. Chaotic capture
As the dynamical evolution of a gravitating system is a time-reversible process, asteroids can enter the co-orbital region when the instability drives the Trojans out. Hence the instabilities induced by the secondary resonances during the migration also paves the way for the so-called chaotic capture, which means Trojans could be captured when Uranus and Neptune cross their mutual MMRs (Morbidelli et al. 2005; Nesvorný & Vokrouhlický 2009; Lykawka & Horner 2010). Therefore, in our simulations, at moments such as 0.22 τ, 0.80 τ, and 1.08 τ, when the ice giants cross the 7:4, 11:6, and 15:8 MMRs (see Fig. 11), many objects in the disc would be captured to supplement the co-orbital region of Uranus. Once the planets get far away from these MMRs, the co-orbital regions become temporarily stable until they approach the next MMR. In the end, there are always some Trojans left, trapped in the co-orbital region.
Besides those planetesimals shown in Fig. 10 that have never left the co-orbital region, many more objects have escaped during the migration. Many of these may enter into the co-orbital region again later, and such recapture must be comparable to the chaotic capture from the planetesimal disc. Many objects are found to have been recaptured at least once in our simulations. Of course, the depletion and recapture would compete with each other, adjusting the amount of the UT population. By the end of the migration, there are a certain number of such recaptured objects in the co-orbital region, but we only count those that stay in the co-orbital region for more than 1 Myr after being recaptured. The orbital distribution of the final swarm of captured UTs is shown in Fig. 12. Again, more orbits can be recaptured during fast migration. Compared to the pre-formed UTs surviving the migrations, much fewer orbits end up being recaptured. Almost none of these orbits fall in the stability region in the low-inclination regime (i < 7.5°). The other stability region for the high-inclined UTs hold most of the recaptured orbits in slow migration. However, only one of these has a small chance to survive the age of the solar system (42° < i < 48°, e < 0.1). In consideration of the low survival probability for high-inclined UTs, we speculate that it is nearly impossible to detect the recaptured orbits nowadays.
 |
Fig. 12. Distribution of orbits recaptured as UTs at the end of the simulations. The blue crosses indicate fast migration (τ = 1 Myr); the orange squares indicate slow migration (τ = 10 Myr). The critical eccentricity for stable UTs (e = 0.1) is depicted by a vertical line. The horizontal lines indicate the critical inclinations for the long-life UTs, which are 7.5°, 42°, and 48° (see Fig. 8). The shaded areas indicate the stable regions. |
In view of the large amount and different orbital distribution of the planetesimals, the realistic chaotic capture from the disc could be more efficient. Lykawka & Horner (2010) investigated the capture of Trojans from the planetesimal disc by Uranus with different migration rates and different disc models. These authors obtain capture efficiency between 10−5 and 10−4. Although the capture efficiency is sensitive to the model of the planetesimal disc, it is still plausible that the chaotic capture could produce some survivors. Nevertheless, the orbital distribution of the captured UTs also suggests that their orbits are kind of hot and they are unlikely to survive the age of the solar system (Lykawka & Horner 2010).
Although there is no definitive evidence yet, some studies have shown a preference for slow migration with τ ∼ 10 Myr. High inclinations of plutinos support a migration timescale of about 10 Myr (Malhotra 1998). In addition, Lykawka et al. (2009) demonstrate that slow migration in which Neptune migrates over a large distance (from 18.1 AU to its current location) could produce an orbital distribution of Neptune Trojans, which matches the known distribution better than fast migration. The process of how the planets migrate during the early stage of the solar system only determines the original population of UTs rather than the stability in the current planetary configuration.
The Nice model suggests that Jupiter and Saturn have crossed the 1:2 MMR before smooth migration that can be approximated by our migration model, but with possibly different timescales τ (Gomes & Nesvorný 2016). The 1:2 MMR crossing of Jupiter and Saturn would cause global instability, which could empty the pre-formed UTs as a consquence of a violent change of the orbit of Uranus. This further reduces the possibility of observing primordial UTs nowadays. But in turn, according to current well-adopted migration models, if any primordial UTs are observed in the future, this will suggest that there may be a swarm of pre-formed UTs at the beginning of the smooth outward migration of Uranus, and the migration is more likely to have a short timescale.
7. Conclusions and discussion
Uranus is one of the five planets in the solar system which are verified to hold Trojan asteroids. However, confirmed UTs and candidates detected so far are all temporarily captured. In this paper, we investigate the stability of UTs via numerical simulations. Detailed dynamical maps were constructed on the (a0, i0) plane with the SN as the stability indicator. Besides a stability region at low inclination (0°–14°), stable UTs can also reside in the stability window (32°–59°) in the high-inclination regime (see Fig. 1). Two instability gaps appear around 9° and 51°, dividing both stability regions into two. Abundant fine structures are still present in the dynamical maps. These instability gaps block the possible route of Trojans achieving high inclination through dynamical diffusion in the phase space.
In order to locate the resonances shaping the structure of the phase space, we implemented a frequency analysis method to portray the resonance web on the (a0, i0) plane. The apsidal secular resonances with Jupiter (ν5) and Uranus (ν7), located at moderate inclination, are the strongest mechanisms destabilising UTs (see Fig. 6). These secular resonances could significantly excite the eccentricity of orbits, and help clean the moderate-inclined UTs. Two instability gaps around 9° and 51° are believed to be involved with the apsidal resonances g − 2g5 + g7 = 0 and ν8. High-degree secular resonances and secondary resonances could shape the outline of the stability region and carve the fine structures.
The orbits are mainly excited by secular resonances in both eccentricity and inclination. Combined secular resonances such as g + 2s − s5 − g8 − s8 = 0 could pump up the inclination with an amplitude up to ∼12°. This does not form a high-inclined UT population because the involved orbits are not stable, but it may contribute to the excitation of Centaurs’ inclination since they generally spend a portion of their lifespan on the temporary Trojan orbits (Alexandersen et al. 2013b).
The Kozai mechanism plays an important role in controlling the variation of eccentricity and inclination. It is also worth noting that UTs experience close encounters with the parent planet when they are on large-amplitude horseshoe or quasi-satellite orbits, leading to a huge increase in eccentricity (see Fig. 3). Actually, UTs with eccentricity higher than 0.1 lose their stability sooner or later.
Although some high-inclined UTs within the stability region have small libration amplitudes of the resonant angle, the most stable UTs at low inclination are of relatively larger libration amplitudes (see Fig. 4). All orbits that have ever left the tadpole cloud around L4 have a libration amplitude larger than 300°. They keep switching between different co-orbital states after leaving the tadpole orbit and we confirm that there is a lack of stable horseshoe orbits for UTs (see Fig. 3).
The libration centre at which the libration amplitude is the smallest varies with the initial inclination (see Fig. 4). It is related to the quasi 1:2 MMR between Uranus and Neptune as the displacement disappears if Uranus and Neptune is further away from the 1:2 MMR. However, the secondary resonances involving the frequency of the quasi 1:2 MMR seem to have no effect on the long-term stability of UTs (see Fig. 7).
A long time simulation up to the age of the solar system (4.5 Gyr) reveals the residence of possible primordial UTs. These UTs are close to the libration centre (see Fig. 8). About 3.81% of UTs can survive the integration, of which 95.5% are on low-inclined orbit. Another 4.5% orbits are distributed in the range of i0 = 42°–48°. The sky densities show that the primordial UTs are most likely to be detected on coplanar orbit of Uranus, but for high-inclined UTs, the region where the relative longitude and latitude with respect to the instantaneous orbital plane of Uranus are 72° and ±40° could be an alternative (see Fig. 9).
In spite of a nonzero survival ratio, no primordial UTs have been found in observation so far. de la Fuente Marcos & de la Fuente Marcos (2017) demonstrate that ephemeral multi-body MMRs may lead to the depletion of primordial UTs in the early evolution of the solar system. In our study, we consider radial migration which could destabilise the primordial UTs before the formation of the current planetary configuration.
Planetary migration with timescales τ = 1 and 10 Myr is adopted. For fast migration, 36.3% of the pre-formed orbits survive migration to 5 τ, while it is only 0.4% for slow migration (see Fig. 10). In general, the surviving orbits are of inclinations slightly smaller than their initial values, implying that the migration process cannot excite the inclinations. In spite of a relatively small amount, low-inclined orbits still contribute 77% of the orbits that can survive the age of the solar system after the migration. These stable orbits occupy 4.06 × 10−3 and 9.07 × 10−5 of the origin population for fast and slow migrations, respectively.
The depletion of the pre-formed UTs result from the MMR crossing of Uranus and Neptune. Once they approach the mutual MMR, the related secondary resonances would destabilise the UTs (see Fig. 11). Nevertheless, the orbits outside the co-orbital region can be captured at the same time. The orbital distributions from both our simulations and the chaotic capture of the planetesimals (Lykawka & Horner 2010) support that the captured orbits are unlikely to survive to today (see Fig. 12).
The final state of the migration depends on the parameters of the migration model, including the migration rate and initial planetary configuration, especially the locations of Uranus and Neptune. It is suggested that increasing migration timescale (τ) could reduce the survival ratio over planetary migration (Kortenkamp et al. 2004). Morbidelli et al. (2014) demonstrate that Neptune may have undergone migration with a much longer migration timescale (∼100 Myr). Some simulations of radial migrations also include the eccentricity damping since a high eccentricity of Neptune may be necessary at the beginning of the smooth outward migration (Dawson & Murray-Clay 2012; Wolff et al. 2012; Parker 2015).
Compared to the radial migration we use, the Nice model in which the migration is a natural result of the gravitational interaction between the planets and planetesimals is more realistic and promising. Its most significant difference from our model is the instability phase when Jupiter and Saturn crossed the mutual 1:2 MMR before smooth migration. This MMR crossing could make a great change to the orbits of Uranus and Neptune, causing a severe depletion of their pre-formed Trojans. The stirring of the planets owing to the instability phase can be relieved afterwards by the dynamical friction from the planetesimal disc (Tsiganis et al. 2005). But our model could approximate the migration after the instability phase in the Nice model and the mechanisms of the depletion and chaotic capture then are not different at all (Lykawka et al. 2009; Nesvorný & Vokrouhlický 2009; Lykawka & Horner 2010; Gomes & Nesvorný 2016).
In the Nice model, Neptune may have been further away from the Sun before the end of the migration, which means Uranus could be closer to the 1:2 MMR with Neptune than it is today (Gomes & Nesvorný 2016). We investigate the orbital behaviour of UTs with a further location of Neptune and find that the 1:2 MMR between Uranus and Neptune greatly destabilise the UTs, driving most of them out of the co-orbital region in a short time. In other words, if Uranus and Neptune had been closer to the 1:2 MMR in the past, we could hardly observe any primordial UTs today.
Acknowledgments
Our sincere appreciations go to the anonymous referee, whose comments are very helpful in improving this paper. This work has been supported by the National Natural Science Foundation of China (NSFC, Grants No. 11473016, Nos. 11933001 and 11973027) and National Key R&D Program of China (2019YFA0706601). R. Dvorak wants to acknowledge the support from the FWF project S11607/N16.
References
- Alexandersen, M., Kavelaars, J., Petit, J., & Gladman, B. 2013a, Minor Planet Electronic Circulars, 19 [Google Scholar]
- Alexandersen, M., Gladman, B., Greenstreet, S., et al. 2013b, Science, 341, 994 [NASA ADS] [CrossRef] [Google Scholar]
- Chambers, J. E. 1999, MNRAS, 304, 793 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Chiang, E. I., & Lithwick, Y. 2005, ApJ, 628, 520 [NASA ADS] [CrossRef] [Google Scholar]
- Chirikov, B. V. 1979, Phys. Rep., 52, 263 [NASA ADS] [CrossRef] [Google Scholar]
- Dawson, R. I., & Murray-Clay, R. 2012, ApJ, 750, 43 [NASA ADS] [CrossRef] [Google Scholar]
- de la Fuente Marcos, C., & de la Fuente Marcos, R. 2013, A&A, 551, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de la Fuente Marcos, C., & de la Fuente Marcos, R. 2014, MNRAS, 441, 2280 [NASA ADS] [CrossRef] [Google Scholar]
- de la Fuente Marcos, C., & de la Fuente Marcos, R. 2015, MNRAS, 453, 1288 [NASA ADS] [CrossRef] [Google Scholar]
- de la Fuente Marcos, C., & de la Fuente Marcos, R. 2017, MNRAS, 467, 1561 [NASA ADS] [Google Scholar]
- Dvorak, R., Bazsó, Á., & Zhou, L.-Y. 2010, Celest. Mech. Dyn. Astron., 107, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Fernández, J. A., & Ip, W.-H. 1984, Icarus, 58, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Fernández, J. A., & Ip, W.-H. 1996, Planet. Space Sci., 44, 431 [NASA ADS] [CrossRef] [Google Scholar]
- Gallardo, T. 2006, Icarus, 184, 29 [Google Scholar]
- Giorgini, J. D., Yeomans, D. K., & Chamberlin, A. B. 1996, in AAS/Division for Planetary Sciences Meeting Abstracts, Bull. Am. Astron. Soc., 28, 1158 [Google Scholar]
- Giuppone, C. A., & Leiva, A. M. 2016, MNRAS, 460, 966 [NASA ADS] [CrossRef] [Google Scholar]
- Gomes, R. S. 1998, AJ, 116, 2590 [NASA ADS] [CrossRef] [Google Scholar]
- Gomes, R., & Nesvorný, D. 2016, A&A, 592, A146 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gomes, R., Levison, H. F., Tsiganis, K., & Morbidelli, A. 2005, Nature, 435, 466 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Hahn, J. M., & Malhotra, R. 1999, AJ, 117, 3041 [NASA ADS] [CrossRef] [Google Scholar]
- Hanslmeier, A., & Dvorak, R. 1984, A&A, 132, 203 [NASA ADS] [Google Scholar]
- Horner, J., & Evans, N. W. 2006, MNRAS, 367, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Kinoshita, H., & Nakai, H. 2007, Celest. Mech. Dyn. Astron., 98, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Kortenkamp, S. J., Malhotra, R., & Michtchenko, T. 2004, Icarus, 167, 347 [NASA ADS] [CrossRef] [Google Scholar]
- Laskar, J. 1990, Icarus, 88, 266 [NASA ADS] [CrossRef] [Google Scholar]
- Li, J., Zhou, L.-Y., & Sun, Y.-S. 2006, A&A, 6, 588 [Google Scholar]
- Lykawka, P. S., & Horner, J. 2010, MNRAS, 405, 1375 [NASA ADS] [Google Scholar]
- Lykawka, P. S., Horner, J., Jones, B. W., & Mukai, T. 2009, MNRAS, 398, 1715 [NASA ADS] [CrossRef] [Google Scholar]
- Malhotra, R. 1995, AJ, 110, 420 [NASA ADS] [CrossRef] [Google Scholar]
- Malhotra, R. 1998, in Lunar and Planetary Inst. Technical Report, Lunar and Planetary Science Conference, 29 [Google Scholar]
- Malhotra, R., & Dermott, S. F. 1990, Icarus, 85, 444 [NASA ADS] [CrossRef] [Google Scholar]
- Marzari, F., Tricarico, P., & Scholl, H. 2003a, A&A, 410, 725 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marzari, F., Tricarico, P., & Scholl, H. 2003b, MNRAS, 345, 1091 [NASA ADS] [CrossRef] [Google Scholar]
- Michtchenko, T. A., & Ferraz-Mello, S. 1995, A&A, 303, 945 [NASA ADS] [Google Scholar]
- Michtchenko, T. A., Beaugé, C., & Roig, F. 2001, AJ, 122, 3485 [NASA ADS] [CrossRef] [Google Scholar]
- Michtchenko, T. A., Lazzaro, D., Ferraz-Mello, S., & Roig, F. 2002, Icarus, 158, 343 [NASA ADS] [CrossRef] [Google Scholar]
- Milani, A. 1994, in Asteroids, Comets, Meteors 1993, eds. A. Milani, M. di Martino, & A. Cellino, IAU Symp., 160, 159 [CrossRef] [Google Scholar]
- Morbidelli, A., Levison, H. F., Tsiganis, K., & Gomes, R. 2005, Nature, 435, 462 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Morbidelli, A., Gaspar, H. S., & Nesvorny, D. 2014, Icarus, 232, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Murray, C. D., & Dermott, S. F. 1999, Solar System Dynamics (Cambridge: Cambridge University Press) [Google Scholar]
- Namouni, F. 1999, Icarus, 137, 293 [NASA ADS] [CrossRef] [Google Scholar]
- Namouni, F., & Murray, C. D. 2000, Celest. Mech. Dyn. Astron., 76, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Nesvorný, D., & Dones, L. 2002, Icarus, 160, 271 [NASA ADS] [CrossRef] [Google Scholar]
- Nesvorný, D., & Vokrouhlický, D. 2009, AJ, 137, 5003 [NASA ADS] [CrossRef] [Google Scholar]
- Nobili, A. M., Milani, A., & Carpino, M. 1989, A&A, 210, 313 [NASA ADS] [Google Scholar]
- Páez, R. I., & Efthymiopoulos, C. 2018, Celest. Mech. Dyn. Astron., 130, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Páez, R. I., Locatelli, U., & Efthymiopoulos, C. 2016, Celest. Mech. Dyn. Astron., 126, 519 [NASA ADS] [CrossRef] [Google Scholar]
- Parker, A. H. 2015, Icarus, 247, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Robutel, P., & Pousse, A. 2013, Celest. Mech. Dyn. Astron., 117, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Sheppard, S. S., & Trujillo, C. A. 2006, Science, 313, 511 [NASA ADS] [CrossRef] [Google Scholar]
- Sheppard, S. S., & Trujillo, C. A. 2010, ApJ, 723, L233 [NASA ADS] [CrossRef] [Google Scholar]
- Tittemore, W. C., & Wisdom, J. 1990, Icarus, 85, 394 [NASA ADS] [CrossRef] [Google Scholar]
- Tsiganis, K., Gomes, R., Morbidelli, A., & Levison, H. F. 2005, Nature, 435, 459 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Wolf, M. 1907, Astron. Nachr., 174, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Wolff, S., Dawson, R. I., & Murray-Clay, R. A. 2012, ApJ, 746, 171 [NASA ADS] [CrossRef] [Google Scholar]
- Zhou, L.-Y., Sun, Y.-S., Zhou, J.-L., Zheng, J.-Q., & Valtonen, M. 2002, MNRAS, 336, 520 [NASA ADS] [CrossRef] [Google Scholar]
- Zhou, L.-Y., Dvorak, R., & Sun, Y.-S. 2009, MNRAS, 398, 1217 [NASA ADS] [CrossRef] [Google Scholar]
- Zhou, L.-Y., Dvorak, R., & Sun, Y.-S. 2011, MNRAS, 410, 1849 [NASA ADS] [Google Scholar]
- Zhou, L., Xu, Y.-B., Zhou, L.-Y., Dvorak, R., & Li, J. 2019, A&A, 622, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
All Figures
 |
Fig. 1. Dynamical maps around the L4 point of Uranus on the (a0, i0) plane. The colour indicating the regularity of orbits represents the base-10 logarithm of SN of cosσ. Orbits escape from the 1:1 MMR with Uranus during the integration time are not included in these maps. The libration centres for different i0 are depicted by the dark line. Left panel: result for 4.25 × 106 yr; right panel: result for 3.4 × 107 yr, which is eight times the former. |
| In the text | |
 |
Fig. 2. Variations of the eccentricity and inclination for orbits with different initial inclinations surviving the integration time of 3.4 × 107 yr. The initial eccentricity is 0.04975 for all orbits. There might be many orbits with different initial semi-major axes for each initial inclination. The orange squares indicate orbits whose libration amplitude (Δσ) is larger than 300° while black crosses indicate those which have never left the tadpole region around L4 during the integration time (Δσ < 180°). |
| In the text | |
 |
Fig. 3. Orbital evolution of two fictitious Trojans over some period at the end of the integration (except the top right plot). The orbits in the left and right panels are initialised with (a0, i0) = (19.225 AU, 56.5° ) and (19.317 AU, 5° ), respectively. We illustrate the temporal evolution of the eccentricity e, inclination i, and resonant angle of the 1:1 MMR with Uranus σ for both orbits. The semi-major axis ratio of the UT and Uranus a/aU, resonant angle of the 1:2 MMR with Neptune σ1 : 2 and apsidal difference with Neptune Δϖ8 are also shown in the left panel, while the apsidal differences with Jupiter Δϖ5 and Uranus Δϖ7 over the last few million years (bottom right) and the whole integration time (top right) are shown in the right panel, respectively. The vertical dashed lines in the left panel indicate the time 3.2716 × 107 yr, 3.2762 × 107 yr and 3.2922 × 107 yr, when the UT enters and leaves the quasi-satellite orbit, and is captured by the Kozai mechanism. |
| In the text | |
 |
Fig. 4. Libration amplitudes of surviving orbits (in different colours) during the orbital integration of 3.4 × 107 yr on the (a0, i0) plane. The solid line implies the libration centres for different i0. Dozens of orbits whose libration amplitudes Δσ are larger than 300° are ignored for better visibility. Because of the scarcity of numbers, we indicate the orbits with libration amplitude Δσ above 120° with the same colour. The dashed line is the same as the solid line, but for the integration where Neptune is initially placed further away from the 2:1 MMR with Uranus (see text). |
| In the text | |
 |
Fig. 5. Dynamical spectra of icosΩ (top panel), ecosϖ (middle panel), and cosσ (bottom panel). The five most significant frequencies of the highest peaks in the power spectra, which are denoted by red open circles, black open inverted triangles, squares, triangles, and diamonds respectively, are plotted against their initial inclinations (top two panels) or semi-major axes (bottom panel). The proper frequencies which vary continuously with the initial semi-major axis and inclination are indicated by arrows. The initial semi-major axis for orbits in the top two panels is 19.22 AU while the initial inclination for orbits in the bottom panel is 4°. The dashed lines indicate the forced frequencies which are identified to be involved with the frequency of the quasi 1:2 MMR between Uranus and Neptune f2 : 1 or the fundamental frequencies in the outer solar system. In the bottom panel the frequencies 2f, 2f − f2 : 1, and f2 : 1 − f are also labelled. The precession rates of the ascending node for orbits in the top panel, along with s7, are all negative. Hence, the absolute values of these frequencies are plotted. |
| In the text | |
 |
Fig. 6. Locations of secular resonances for Trojans around L4 on the (a0, i0) plane. The resonances are labelled (see text for the meaning) along the curves. The solid lines indicate the linear and fourth-degree secular resonances; the dashed lines indicate the higher order secular resonances. The C2 resonance is shown in red for better visibility. |
| In the text | |
 |
Fig. 7. Same as Fig. 6 but for examples of secondary resonances. The dynamical map behind the resonances represents the integration of 4.25 × 106 yr. The Σ4 resonance is shown in red for better visibility. |
| In the text | |
 |
Fig. 8. Lifespans of fictitious UTs around the L4 point on the (a0, i0) plane. The colour indicates the base-10 logarithm of the lifespans. The white points indicate the orbits surviving the age of the solar system (4.5 Gyr). |
| In the text | |
 |
Fig. 9. Normalised sky densities computed from the orbits surviving the age of the solar system. Top panel: low-inclined orbits; bottom panel: high-inclined orbits. The colour represents the proportion of the residence time in each 1° ×1° segment of the sky with respect to the instantaneous orbital plane of Uranus. The black cross denotes the position of the L4 point. |
| In the text | |
 |
Fig. 10. Final distributions of orbits that never left the 1:1 MMR region of Uranus during planetary migration. Left and right panels: final inclination i against the final semi-major axis a and initial inclination i0, respectively. The black dots indicate the orbits surviving fast migration with the final eccentricity e lower than 0.1; the other dots indicate the orbits surviving slow migration, of which the blue and orange points represent those with e < 0.1 and e ≥ 0.1, respectively. The dashed line in the right panel depicts the equality of i and i0; the solid line depicts the best fit for slow migration. For a clear comparison with the stability regions (see Figs. 1 and 8), the same range in semi-major axis is shown in the left panel at the cost of abandoning a small part of orbits. In the right panel only data for slow migration is shown for better visibility. |
| In the text | |
 |
Fig. 11. Orbital period ratio of Neptune and Uranus PN/PU (top panel) and survival ratio of the original population (bottom panel) during fast (orange) and slow (blue) migrations. The orbital period ratio of which the short-period terms are eliminated by the low-pass filter is indicated by the red line. The horizontal lines indicate the locations of the 15:8, 11:6, 9:5, 7:4, and 5:3 MMRs between Neptune and Uranus. Two important moments for fast migration, 0.70 τ and 1.08 τ, and two important moments for slow migration, 0.22 τ and 0.80 τ, are indicated by the vertical lines. Only the period ratio for slow migration is shown in the top panel, and that for fast migration is almost the same. |
| In the text | |
 |
Fig. 12. Distribution of orbits recaptured as UTs at the end of the simulations. The blue crosses indicate fast migration (τ = 1 Myr); the orange squares indicate slow migration (τ = 10 Myr). The critical eccentricity for stable UTs (e = 0.1) is depicted by a vertical line. The horizontal lines indicate the critical inclinations for the long-life UTs, which are 7.5°, 42°, and 48° (see Fig. 8). The shaded areas indicate the stable regions. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.