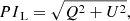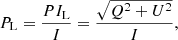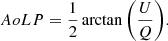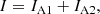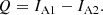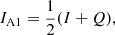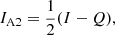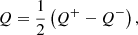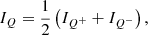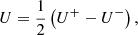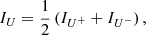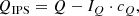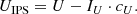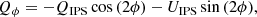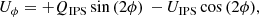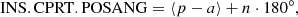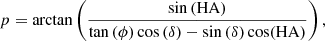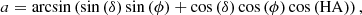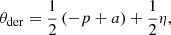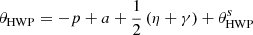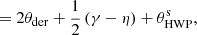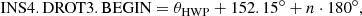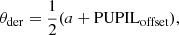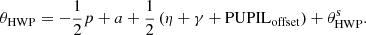| Issue |
A&A
Volume 633, January 2020
|
|
|---|---|---|
| Article Number | A63 | |
| Number of page(s) | 17 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/201834989 | |
| Published online | 14 January 2020 | |
Polarimetric imaging mode of VLT/SPHERE/IRDIS
I. Description, data reduction, and observing strategy⋆
1
Leiden Observatory, Universiteit Leiden, PO Box 9513, 2300 Leiden, The Netherlands
e-mail: deboer@strw.leidenuniv.nl
2
CRAL, UMR 5574, CNRS, Université de Lyon, Ecole Normale Supérieure de Lyon, 46 allée d’Italie, 69364 Lyon Cedex 07, France
3
Aix Marseille Univ, CNRS, CNES, LAM, Marseille, France
4
European Southern Observatory (ESO), Alonso de Córdova 3107, Casilla 19001, Santiago, Chile
5
Space Telescope Science Institute, 3700 San Martin Drive, Baltimore, MD 21218, USA
6
Univ. Grenoble Alpes, CNRS, IPAG, 38000 Grenoble, France
7
Anton Pannekoek Instituut, Universiteit van Amsterdam, Science Park 904, 1098 Amsterdam, The Netherlands
8
Faculty of Aerospace Engineering, Delft University of Technology, Kluyverweg 1, 2629 Delft, The Netherlands
9
European Southern Observatory (ESO), Karl-Schwarzschild-Str. 2, 85748 Garching, Germany
10
ETH Zurich, Institute for Particle Physics and Astrophysics, Wolfgang-Pauli-Strasse 27, 8093 Zurich, Switzerland
11
LESIA, CNRS, Observatoire de Paris, Université Paris Diderot, UPMC, 5 place J. Janssen, 92190 Meudon, France
12
Université Côte d’Azur, OCA, CNRS, Lagrange, France
13
Geneva Observatory, Univ. of Geneva, Chemin des Maillettes 51, 1290 Versoix, Switzerland
14
NOVA Optical Infrared Instrumentation Group, Oude Hoogeveensedijk 4, 7991 Dwingeloo, The Netherlands
15
ONERA, 29 avenue de la Division Leclerc, 92322 Chatillon Cedex, France
16
Max Planck Institute for Astronomy, Königstuhl 17, 69117 Heidelberg, Germany
17
INAF-Osservatorio Astronomico di Padova, Vicolo dell’ Osservatorio 5, 35122 Padova, Italy
Received:
28
December
2018
Accepted:
23
October
2019
Context. Polarimetric imaging is one of the most effective techniques for high-contrast imaging and for the characterization of protoplanetary disks, and it has the potential of becoming instrumental in the characterization of exoplanets. The Spectro-Polarimetric High-contrast Exoplanet REsearch (SPHERE) instrument installed on the Very Large Telescope (VLT) contains the InfraRed Dual-band Imager and Spectrograph (IRDIS) with a dual-beam polarimetric imaging (DPI) mode, which offers the capability of obtaining linear polarization images at high contrast and resolution.
Aims. We aim to provide an overview of the polarimetric imaging mode of VLT/SPHERE/IRDIS and study its optical design to improve observing strategies and data reduction.
Methods. For H-band observations of TW Hydrae, we compared two data reduction methods that correct for instrumental polarization effects in different ways: a minimization of the “noise” image (Uϕ), and a correction method based on a polarimetric model that we have developed, as presented in Paper II of this study.
Results. We use observations of TW Hydrae to illustrate the data reduction. In the images of the protoplanetary disk around this star, we detect variability in the polarized intensity and angle of linear polarization that depend on the pointing-dependent instrument configuration. We explain these variations as instrumental polarization effects and correct for these effects using our model-based correction method.
Conclusions. The polarimetric imaging mode of IRDIS has proven to be a very successful and productive high-contrast polarimetric imaging system. However, the instrument performance is strongly dependent on the specific instrument configuration. We suggest adjustments to future observing strategies to optimize polarimetric efficiency in field-tracking mode by avoiding unfavorable derotator angles. We recommend reducing on-sky data with the pipeline called IRDAP, which includes the model-based correction method (described in Paper II) to optimally account for the remaining telescope and instrumental polarization effects and to retrieve the true polarization state of the incident light.
Key words: polarization / techniques: polarimetric / techniques: high angular resolution / techniques: image processing / protoplanetary disks
© ESO 2020
1. Introduction
Imaging planets and protoplanetary disks in the visible and near-infrared (NIR) requires the observer to account for the large contrasts between bright stars and their faint surroundings. Polarimetry has proven to be a powerful tool for high-contrast imaging, for instance, with the Near-Infrared Camera and Multi-Object Spectrometer (NICMOS) onboard the Hubble Space Telescope (Perrin et al. 2009), the High-Contrast Instrument for the Subaru Next-Generation Adaptive Optics (HiCIAO) at the Subaru telescope (Mayama et al. 2012) and the NAOS-CONICA (NACO) instrument at the Very Large Telescope (VLT; Quanz et al. 2011). When starlight is scattered by circumstellar material, it becomes polarized. Therefore it is possible to distinguish this scattered light from the predominantly unpolarized stellar speckle halo by computing the difference between two images that are recorded in two orthogonal polarization states. This high-contrast imaging technique is known as polarimetric differential imaging (PDI; Kuhn et al. 2001). With the aid of adaptive optics (AO), polarimetric imaging has been successful in detecting faint circumstellar disks down to very small separations (∼0.1″; e.g., Quanz et al. 2013; Garufi et al. 2016). Compared to alternative high-contrast imaging techniques such as angular differential imaging (ADI; Marois et al. 2006), PDI is especially well suited to image disks that are seen close to face-on, such as TW Hydrae (seen at ∼7° inclination; Rapson et al. 2015; van Boekel et al. 2017). While ADI suffers from self-subtraction of signal from a disk with a low inclination, PDI remains sensitive to its scattered light. PDI will remove unpolarized stellar and disk signal alike, which makes this technique only less suitable for detecting disks with very low degrees of polarization due to unfavorable scattering angles (close to 0° or 180°) or grain sizes much larger than the wavelength (Hansen & Travis 1974). Fortunately, the scattering surfaces of protoplanetary disks predominantly contain submicron-sized grains (i.e., smaller than the typical wavelengths at which high-contrast imaging instruments operate), while the single-scattering angles in most regions of any circumstellar disk will not be close to 0° or 180°.
In addition to being an effective high-contrast imaging technique, polarimetry offers the potential of characterizing scattering particles in circumstellar disks and in the atmospheres of exoplanets. Radiative-transfer modeling of disks is heavily plagued by degeneracies when the models are based on the spectral energy distribution (SED) alone (e.g., Andrews et al. 2011; Dong et al. 2012). Perrin et al. (2015) and Ginski et al. (2016) have used the resolved polarimetric surface brightness to determine the scattering phase function for the debris disk around HR 4796A (see also Milli et al. 2015) and HD 97048, respectively. The scattering phase function will be instrumental in the unambiguous characterization of micron-sized dust particles.
Young self-luminous giant exoplanets or companion brown dwarfs can also be polarized at NIR wavelengths because their thermal emission is scattered by cloud and haze particles in the outer atmospheres of the companions or by dust particles surrounding the companions (Sengupta & Marley 2010; de Kok et al. 2011; Marley & Sengupta 2011; Stolker et al. 2017). Substellar companions are observed as point sources and only produce a significant (integrated) polarization signal if the shapes of these companions projected on the image plane deviate from circular symmetry. When a polarization signal from a companion is measured, this confirms the presence of a scattering medium (e.g., clouds) and can trace the cloud morphology (e.g., horizontal bands), rotational flattening, the projected spin-axis orientation, and the shape and orientation of a disk around the companion.
In 2014, the Spectro Polarimetric High-contrast Exoplanet REsearch (SPHERE; Beuzit et al. 2019) instrument was commissioned at Unit Telescope 3 (UT3) of the VLT. This instrument contains the extreme-AO system SAXO (SPHERE AO for eXoplanet Observation; Fusco et al. 2006, 2016), which consists, among other components, of a high-order deformable mirror (DM) with 41 × 41 actuators and a Shack–Hartmann wavefront sensor that can operate up to 1200 Hz (Fusco et al. 2016). The wavefront sensor records in the visible regime and performs best for stars of R = 9 − 10 mag, where it typically yields a Strehl ratio of ≥90%. Up to the magnitude limit of R = 14 − 15 mag, the AO system still improves the performance with a factor of ∼5 (Beuzit et al. 2019). This extreme-AO system supports three scientific subsystems: the (visible-light) Zurich IMaging POLarimeter (ZIMPOL; Schmid et al. 2018), the (NIR) Integral Field Spectrograph (IFS; Claudi et al. 2008), and the (Near) InfraRed Dual-band Imager and Spectrograph (IRDIS; Dohlen et al. 2008).
IRDIS is primarily designed to detect planets in differential-imaging modes combined with pupil tracking, where the telescope pupil remains fixed on the detector and the image rotates with the parallactic angle. This rotation of the image during observations allows the removal of the stellar speckle halo by performing ADI. A beam splitter ensures that the star is imaged twice on the detector. Wideband, broadband, or narrowband filters can be inserted in a common filter wheel upstream from the beam splitter to allow what is called “classical imaging”. Downstream from the beam splitter, another wheel is present with which we can introduce two different filters for the separate beams. Observations in two different color filters allow the detection of planets (e.g., by observing methane absorption in their atmosphere) with dual-band imaging (DBI; e.g., Rosenthal et al. 1996; Racine et al. 1999; Marois et al. 2000; Vigan et al. 2010).
The inclusion of orthogonal linear polarization filters (polarizers) in this second filter wheel makes IRDIS a polarimeter. In this dual-beam polarimetric imaging (hereafter DPI or IRDIS/DPI; Langlois et al. 2014) mode, a rotatable half-wave retarder is inserted into the common path of SPHERE to modulate between the linear polarization components. IRDIS/DPI is currently offered in field and pupil tracking. The requirements for DBI contrast have provided high image quality from which DPI benefits as well. In particular, DPI benefits from the high image stability, which is essential for coronagraphy (Boccaletti et al. 2008; Carbillet et al. 2011; Guerri et al. 2011), and most importantly, from the very low differential wave-front error between the two beams (Dohlen et al. 2016). Since IRDIS/DPI was first offered to the community during the science verification of SPHERE in December 2014, it has proven to be a very successful and productive mode for high-contrast imaging of circumstellar disks (e.g., Benisty et al. 2015; Stolker et al. 2016; Garufi et al. 2017; Avenhaus et al. 2018; Pinilla et al. 2018), but it also shows great promise for the characterization of polarized substellar companions. van Holstein et al. (2017) have used IRDIS/DPI to search for a polarization signal in the companions around HR 8799 and PZ Tel, similar to the attempts made with the Gemini Planet Imager (GPI) for HD 19467 B by Jensen-Clem et al. (2016) and β Pic b by Millar-Blanchaer et al. (2015). Although van Holstein et al. (2017) did not detect a polarization signal for the companions of either star, they presented stringent upper limits on the polarization of ∼0.1% for PZ Tel B, and ∼1% for the much fainter planets around HR 8799. Furthermore, they presented a polarized contrast of ∼10−7 at 0.5″ separation from the primary star HR 8799.
Because the SPHERE instrument is complex and has many reflecting surfaces, the polarimetric performance is strongly dependent on the specific instrumental setup. Each optical component in the telescope and instrument can cause instrumental polarization effects, which we group into two categories: (1) the introduction of polarization, and (2) the mixing of polarization states in the light beam, which we call instrumental polarization (hereafter IP, to avoid confusion with the overarching term “instrumental polarization effects”) and polarimetric crosstalk, respectively. IP can give the false impression of a detection of polarization when no true polarization signal is incident on the telescope. Crosstalk can change incident polarization into a state that is not measured by the instrument (e.g., linear to circular polarimetry, see Sect. 2). Therefore, crosstalk can decrease the polarimetric efficiency: the fraction of measured polarization over the incident polarization. Unlike the polarimetric mode of ZIMPOL, no hard requirements were defined for the polarimetric performance of IRDIS because the initial science priority of this mode was determined to be low. Lower instrumental polarization effects were expected in the NIR than in the visible. Furthermore, because of the difficulty of the system analysis that is required to predict and correct for these effects beforehand, the choice was made to rely on an a posteriori characterization of the DPI mode whenever possible.
This work forms Paper I of a larger study describing the polarimetric imaging mode of SPHERE/IRDIS. In Paper I we present an overview: we focus on the description of the instrument and the data reduction, and we make suggestions for observing strategies to maximize the polarimetric performance of the instrument in field-tracking mode. Field tracking, where the image of the star remains fixed on the detector, is the default mode for DPI and therefore is the tracking mode we use for this paper. In van Holstein et al. (2020, hereafter Paper II), we will describe the polarimetric instrument model that we have developed, based on calibration measurements using unpolarized stars and SPHERE’s internal light-source. Furthermore, in Paper II we will describe a correction method based on this model to account for the instrumental polarization effects and will compute the true polarization signal incident on the telescope. This correction method is included in a new data-reduction pipeline called IRDIS data reduction for accurate polarimetry (IRDAP), which we will make public (see Paper II).
Paper I begins with a general description of polarization and dual-beam polarimetric imaging in Sect. 2. We describe the optical components encountered by the light beam in Sect. 3. In Sect. 4 we explain the basic principles behind the data reduction, which we apply in Sect. 5.1 to the TW Hydrae observations of van Boekel et al. (2017). In the reduced data of TW Hydrae, we detect a variation in the polarization signal that depends on the instrument configuration. We use this to illustrate the polarimetric performance of IRDIS/DPI. In the remainder of Sect. 5 we describe the instrumental polarization effects of SPHERE/IRDIS with the use of the polarimetric instrument model of Paper II. These instrumental polarization effects enable us to explain the variations in TW Hydrae that depend on the instrument configuration. In Sect. 6 we apply the correction method described in Paper II to account for the instrumental polarization effects and obtain the true polarization state for TW Hydrae. We compare the results of the IRDAP reduction (with the model-based correction method) with the results of the best “conventional” data reduction, where we apply an empirical correction method. Based on our analysis, we propose recommendations for future observations and possible SPHERE upgrades to enhance the polarimetric performance in Sect. 7. In Sect. 8 we compare SPHERE/IRDIS/DPI and major contemporary AO-assisted polarimetric imagers in the NIR. We complete Paper I with our conclusions and recommendations in Sect. 9.
2. Dual-beam polarimetric imaging
2.1. Polarization conventions and definitions
Elliptical polarization (partial and full) is conveniently described by Stokes (1851) with what is known as the Stokes vector:
where I is the total intensity of the beam of light, Q and U describe the two linear polarization contributions, and V describes circular polarization. In the literature, the +Q direction is often aligned with the local meridian (e.g., Witzel et al. 2011). In Sect. 4 we use this convention for +Q. Although this choice of reference frame is arbitrary, it is the convention adopted by the International Astronomical Union. As illustrated in Fig. 1, we used the following conventions for the remaining orientations: For a beam propagating along the z-axis (in the direction of increasing z) in a right-handed x, y, z coordinate system, let +Q describe linear polarization with a preferred oscillation in the ±x direction (which we align with our frame of reference, e.g., the meridian); −Q then oscillates in the ±y direction; +U describes linear polarization oscillating at an angle of +45° from the x-axis (rotated in counterclockwise direction for an observer looking at the source, and −45° from the y-axis); while −U polarized light oscillates at an angle of −45° (or +135°) with respect to the x-axis. When the observer faces the −z direction, +V describes circular polarization where the peak of the electric field rotates clockwise (i.e., moving from +x to −y) and −V describes counterclockwise rotation.
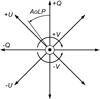 |
Fig. 1. Orientation of the Stokes vector components of Eq. (1), where the beam propagates out of the sketch, toward the observer. When the vertical axis (+Q) is aligned with a preferred orientation (usually the meridian on-sky), the remaining Stokes vector components are oriented accordingly. The AoLP (Eq. (4)) is also measured with respect to the +Q direction in counterclockwise direction. |
IRDIS/DPI is designed to measure linear polarization alone, which is expected to be the dominant polarization component caused by scattering at the surface layers of protoplanetary disks and substellar companions. From the Stokes vector components, we can determine the linearly polarized intensity (PIL) and the degree and angle of linear polarization (DoLP or PL and AoLP, respectively) according to
2.2. Polarimetric imager
Although ideal polarimeters do not exist, such a hypothetical instrument is helpful when we describe the general principles of PDI. In addition to mirrors and lenses, the main components of this ideal polarimeter are two (in case of a dual beam) analyzers and detectors (or detector halves). The analyzers can either be two separate polarizers (which require an additional preferably non-polarizing beam splitter upstream) with orthogonal polarization (also called transmission) axes or a polarizing beam splitter. We set the polarization axis of one analyzer (A1) so that it was aligned with the +Q direction, and the other analyzer (A2) so that it was aligned with −Q. We can retrieve (or “indirectly measure”) the first two components of Eq. (1) by adding and subtracting the measured intensity of both beams (IA1/A2) of light,
We can rephrase Eqs. (5) and (6) to describe the transmission of the analyzers:
where for an ideal polarimeter, I and Q are equal to their counterparts incident on the telescope (Iin and Qin, respectively).
To retrieve U, we either need to rotate the analyzers by 45° or introduce an optical component that can rotate the polarization direction with the same angle. A half-wave (λ/2) plate (HWP) retards light that is polarized in the direction orthogonal to its fast axis with λ/2 compared to light that is polarized in alignment with its fast axis. Therefore, an HWP upstream from the beam splitter can be used to rotate the measured polarization angle by ΔAoLP by placing the fast axis of the HWP at an angle of ΔAoLP/2 with respect to the polarization axes of the analyzers (Appenzeller 1967). It is possible to retrieve U by placing the HWP at an angle θHWP = 22.5° with respect to the polarization axis of A1, which changes Eqs. (7) and (8) into IA1/A2 = (I ± U)/2, and Eq. (6) yields U instead of Q. This shows why the Stokes vector notation is convenient: its components are easily retrieved from the observables of an ideal polarimeter, which “measures” a Stokes vector that is unaltered by the telescope and instrument (i.e., S = Sin, where Sin is the incident Stokes vector).
Real polarimeters are never ideal: instrumental polarization effects depend on the specific instrument configuration used during observations. For complex instruments, the main instrumental polarization effect is typically the introduction of IP caused by the large number of reflections in the telescope and instrument. We can correct for any IP created downstream of the HWP by recording Q for two HWP angles: θHWP = 0° and 45° (see, e.g., Tinbergen 1996; Witzel et al. 2011; Canovas et al. 2011). The second θHWP changes the signs of the original Q component of the beam, but leaves the IP created downstream from the HWP unaltered. For non-ideal polarimeters we therefore change the notation of the single-difference computations described by Eq. (6) to measure Q+ = Q + IP for θHWP = 0°, and Q− = −Q + IP for θHWP = 45°. Similarly, we rename the single-sum total intensities determined with Eq. (5) for θHWP = 0° and 45° with IQ+ and IQ−, respectively. We then apply the double-difference method to obtain the linear Stokes parameters corrected for IP created downstream of the HWP and the corresponding total-intensity images with the double sum:
where U+ = U + IP and IU+ are measured with θHWP = 22.5°, while θHWP = 67.5° yields U− = −U + IP and IU−.
The double difference does not remove IP caused by the telescope and instrument mirrors upstream from the HWP, nor does it remove the most important crosstalk contributions. Correcting for these instrumental polarization effects requires that we determine the polarimetric response function for the polarimetric imager, as we do in Sect. 5.2.1 for the polarimetric mode of VLT/SPHERE/IRDIS.
3. Design of the polarimetric mode IRDIS/DPI
In this section we describe the optical components of VLT/UT3, SPHERE’s Common Path and Infrastructure (CPI) and IRDIS that are most important because they either create instrumental polarization effects, are useful for calibrations, or can be changed to modify the observational sequence or strategy. These optical components are illustrated in the schematic overview of the telescope and instrument in Fig. 2. Especially reflections at high angles of incidence are highlighted because larger angles are more prone to introducing instrumental polarization effects.
 |
Fig. 2. Schematic overview of the telescope and SPHERE/IRDIS, showing the optical components that are relevant for the polarimetric imaging mode. The curved arrows indicate components that rotate during an observation block. Reflections at angles of incidence ≥45° in the instrument are represented with similarly large incidence reflections in the figure. The green beam shows the starlight before color filters are applied, blue represents visible light, and red and orange represent NIR light (the orange beam toward the IFS shows the shorter wavelengths). |
3.1. Telescope and SPHERE common path and infrastructure
SPHERE is installed on the Nasmyth platform of the alt-azimuth Unit Telescope 3. After the axi-symmetric (and therefore non-polarizing) reflections of the primary and secondary mirrors (M1 and M2), the third mirror (M3) of UT3 is used to direct the light toward the Nasmyth focus. M3 introduces the first reflection that breaks axisymmetry with a 45° angle of incidence.
Shortly after the beam enters SPHERE, we reach focal plane 1 (FP1), where a calibration light source can be inserted. The first reflection in the light path within SPHERE is the pupil tip-tilt mirror (PTTM or M4, with a 45° incidence angle), which is the only mirror in SPHERE that is coated with aluminum1. The remaining mirrors of SPHERE are all coated with protected silver for its higher reflectivity. A calibration polarizer with a fixed polarization angle can be inserted into the light path, just before the beam encounters HWP2, the only HWP available for IRDIS/DPI. In field-tracking mode, HWP2 can be rotated for two reasons. The first reason is to switch between four angles (HWP switch angles 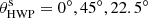 and 67.5°, where the superscript “s” is used to distinguish between switch angles and the true angle of HWP2) to measure Q± and U± with IRDIS. The second reason is to account for field rotation in order to keep the source polarization angle fixed relative to the analyzer for a given HWP2 switch angle in a polarimetric cycle. The next optical component downstream is the image derotator, composed of three mirrors that together form a “K”-shape (therefore also called K-mirror, with the subsequent angles of incidence of 55°, 20°, and 55°). The derotator rotates around the optical axis to stabilize either the field or the pupil on the detector. In Appendix A we include a detailed description of the tracking laws for HWP2 and the derotator in both field-stabilized and pupil-stabilized mode.
and 67.5°, where the superscript “s” is used to distinguish between switch angles and the true angle of HWP2) to measure Q± and U± with IRDIS. The second reason is to account for field rotation in order to keep the source polarization angle fixed relative to the analyzer for a given HWP2 switch angle in a polarimetric cycle. The next optical component downstream is the image derotator, composed of three mirrors that together form a “K”-shape (therefore also called K-mirror, with the subsequent angles of incidence of 55°, 20°, and 55°). The derotator rotates around the optical axis to stabilize either the field or the pupil on the detector. In Appendix A we include a detailed description of the tracking laws for HWP2 and the derotator in both field-stabilized and pupil-stabilized mode.
Multiple reflective surfaces with small angles of incidence follow in the AO common path, including the image tip-tilt mirror (ITTM), the 41 × 41 actuator high-order DM, and three toric mirrors (Hugot et al. 2012). A dichroic beam splitter separates the light into a visible and a NIR arm just after focal plane 2 (FP2). An additional focal plane exists between FP1 and FP2. However, we adopt the nomenclature that is commonly used in the literature, such as the SPHERE manual. The visible light is reflected by the dichroic beam splitter and sent to SAXO’s wavefront sensor and also to ZIMPOL, when required (ZIMPOL is currently not offered simultaneously with IRDIS or IFS). The NIR beam is transmitted by the dichroic beam splitter and is then corrected for atmospheric dispersion, which is determined by the airmass during the observations. Because the angles of incidence (≤2.17°) on the prisms of the atmospheric dispersion corrector (ADC) are low, it is assumed not to cause significant instrumental polarization effects. The validity of this assumption is left for future investigation. The beam then goes through the apodizer wheel (which allows apodization of the pupil in combination with Lyot coronagraphs) and is sent to a beam splitter, which transmits 2% of the H band to a differential tip-tilt sensor (DTTS) and reflects the remaining light at 45° angle of incidence. The (main) reflected beam then encounters the wheel that contains NIR coronagraph (focal) masks (Boccaletti et al. 2008; Martinez et al. 2009) in FP3 and the neutral density (ND) filter wheel, before it reaches the final 45° angle reflection that directs the beam toward IRDIS. For this reflection, a dichroic beam splitter is selected when we use IRDIS in concert with IFS. For modes that only use IRDIS, which is currently the case for polarimetry, a mirror is selected instead.
3.2. SPHERE/IRDIS
IRDIS is described in detail by Dohlen et al. (2008). In this subsection and in Fig. 2, we summarize the optical components for a better understanding of the polarimetric performance of the system and for reference later in this paper. The optical components of IRDIS are located within a cryostat that is cooled to 100 K to reduce thermal background emission. The first optical component inside IRDIS is a common filter wheel (FW1). The filters of FW1 are the only color filters that we can insert for the polarimetric mode because FW2 contains the polarizer pair. In addition to narrowband and spectroscopy filters, FW1 contains four broadband filters that are offered for DPI (see Table 1).
Central wavelength (λc), bandwidth (Δλ), and pixel scale for the SPHERE/IRDIS broadband filters that are available in FW1.
Next, the beam encounters a Lyot stop wheel that also includes a mask for the pupil obscuration by M2 and its support structure (the “spider”). Directly downstream from the Lyot stop wheel, the beam is split by the non-polarizing beam splitter plate (NBS). The beam transmitted by the NBS is reflected by an additional mirror in the direction parallel with the beam reflected by the NBS (and therefore with the same angle of incidence as the reflected beam: 45°). The beams are finally reflected by two identical spherical camera mirrors that focus the beams on the detector (not shown in Fig. 2).
The second filter wheel (FW2) hosting the wire-grid polarizer pairs (P0-90 and P45-135) is located between the camera mirrors and the detector. Finally, the beam reaches the Hawaii-2RG detector, which is mounted on a dither stage and has 2048 × 2048 pixels with 18 μm pitch. Each of the two orthogonally polarized beams is focused on a separate quadrant (1024 × 1024 pixels) of the detector, which results in a field of view (FoV) of ∼11″ × 12.5″ and the filter-dependent pixel scales listed in Table 1 (Maire et al. 2016, 2018).
3.3. Wire-grid polarizer pairs and beam splitter
The P0-90 polarizer set in FW2 filters the light with polarization angles perpendicular to and aligned with the plane of the Nasmyth platform: the plane in which all reflections downstream from the derotator occur. The P45-135 set polarizes at angles of 45° and 135° with respect to this plane. Measurements recorded with P45-135 are highly sensitive to crosstalk introduced by all reflections in this plane. We therefore limit the study in Papers I and II to the use of the P0-90 polarizer pair, while using HWP2 to switch between Q± and U± measurements, which is the default setup for DPI.
The non-polarizing beam splitter is not perfectly non-polarizing, which is corrected for when we use the double difference. Therefore we can use the first-order approximation that it does not introduce new polarization to the beam. Astrophysical objects in the field of high-contrast imaging typically have a very low degree of polarization when the total beam is integrated because this beam is dominated by the central predominantly unpolarized star. The polarizers will only transmit one polarization state each, which means that both beams will loose ∼50% of their photons.
4. Polarimetric data reduction
In this section we describe the basic steps of the polarimetric data reduction for the IRDIS/DPI mode. In Sect. 5 we apply this to the data of TW Hydrae as published by van Boekel et al. (2017), and use the results to analyze the polarimetric performance of the system. Because these observations were recorded before we had performed polarimetric calibrations, we encountered unexpected instrumental polarization effects that depend on the specific instrument configuration and vary during the observing sequence. We describe and explain these effects in detail based on the polarimetric instrument model of Paper II. In Sect. 6 we compare the reduction of these data after a data-driven correction for instrumental polarization effects with a data reduction after a correction based on the polarimetric instrument model.
To promote general understanding of the underlying principles of the polarimetric data reduction and because our analysis of the data in the subsequent sections required non-standard tests, we did not use the official data reduction and handling (DRH; Pavlov et al. 2008) pipeline, but our own custom data reduction routines described below. However, the preprocessing (background subtraction, flat fielding, and centering) is very similar to what is done by DRH and is therefore described in Appendix B.
4.1. Post-processing: polarimetric differential imaging
The single-difference images (Q+, Q−, U+, and U−) are determined frame by frame for the HWP angles: 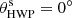 , 45°, 22.5°, and 67.5°, respectively. The single-difference images obtained from the four frames of each file (per HWP angle) are median combined. Q and U are computed with the double-difference method of Eqs. (9) and (11) for each polarimetric cycle (also called “HWP cycles”, containing the four switch angles of HWP2:
, 45°, 22.5°, and 67.5°, respectively. The single-difference images obtained from the four frames of each file (per HWP angle) are median combined. Q and U are computed with the double-difference method of Eqs. (9) and (11) for each polarimetric cycle (also called “HWP cycles”, containing the four switch angles of HWP2: 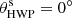 , 45°, 22.5°, and 67.5°). Accordingly, the corresponding single-sum total-intensity images are created with Eq. (5) for each HWP angle. With these single-sum images, we create the double-sum total-intensity IQ and IU images with Eqs. (10) and (12), respectively, for each HWP cycle.
, 45°, 22.5°, and 67.5°). Accordingly, the corresponding single-sum total-intensity images are created with Eq. (5) for each HWP angle. With these single-sum images, we create the double-sum total-intensity IQ and IU images with Eqs. (10) and (12), respectively, for each HWP cycle.
A residual of the read-out columns (see feature c in Fig. B.1) remains visible in the double-difference images. Similar to how Avenhaus et al. (2014) removed noise across detector rows from NACO images, we remove these artifacts from the double-difference images by taking the median over the top and bottom 20 pixels (to avoid including signal from the star) on the image per individual pixel column (not the 64-pixel-wide read-out column), and subtract this median value from the entire pixel column.
We perform a first-order correction for IP created upstream from HWP2 (i.e., by the telescope and M4) on the Q and U images of each polarimetric cycle. This correction method (as described by Canovas et al. 2011) is based on the assumption that the direct stellar light is unpolarized. We take the median of the Q/I signal over an annulus centered around the star (excluding the coronagraph mask) to obtain the scalar cQ (likewise, we determine cU with U/I), multiply this scalar with I, and subtract this from the Q image. Hence, the IP-subtracted linear stokes components are
The size and location of the annulus over which to measure cQ and cU can be adjusted to suit a particular dataset. Ideally, the annulus should lie in a region that should only contain non-scattered starlight, with high signal in the IQ and IU images. Therefore, the size and location of the annulus depends on the brightness of the central star and on the size and shape of the circumstellar material that has been observed.
We now use the possible user-specific derotator offset angle that can be found from the FITS header keyword INS4.DROT2.POSANG, together with the true-north correction of −1.7° (Maire et al. 2018) to apply a software derotation in order to align all IQ/U and Q/UIPS with north up and east left on the detector.
4.2. Azimuthal Stokes parameters
To create the final polarization image, we have two choices. In the first and most straightforward method, we compute the polarized intensity PIL according to Eq. (2) for each HWP cycle and median combine these to create a final (less noisy) PIL image. The problem with this method is that the squares taken in Eq. (2) boost the noise in each image. For example, artifacts seen as a bright positive or negative feature detected at a point in the QIPS image where the signal should be ∼0 (on the diagonal “null” lines separating the positive from the negative signal in the QIPS images) or a strong positive signal in a region where QIPS ought to be negative, will be indistinguishable from true disk signal in the PIL image. This is actually a general problem that we encounter when we compute PIL, but it is an even greater problem for images resulting from short integration times, such as the double-difference results from individual HWP cycles.
Instead, we used a second option to combine the HWP cycles and create the cleanest image by computing the azimuthal Stokes parameters (Schmid et al. 2006),
where ϕ describes the azimuth angle, which can be computed for each pixel (or x, y coordinate) as
The x and y positions of the central star in the image are described by xstar and ystar, respectively. We can use ϕ0 to give the azimuth angle an offset if the measured polarization angle is not aligned azimuthally. ϕ0 is therefore referred to as the polarization angle offset.
In contrast to Eqs. (15) and (16), Schmid et al. (2006) used the notation Qr and Ur, which have flipped signs compared to Qϕ and Uϕ, respectively. Schmid et al. (2006) chose their conventions to describe scattered-light observations of the planets Uranus and Neptune, where the polarization angle is oriented in radial direction relative to the center of the planet. However, in protoplanetary disks, we expect scattered light to produce predominantly azimuthally oriented polarization, which has motivated our choice of signs in Eqs. (15) and (16). Polarization oriented in azimuthal direction (with respect to the position of the star) will be measured as a positive Qϕ signal, radial polarization will show up as a negative Qϕ, and polarization angles oriented at ±45° with respect to azimuthal will result in ±Uϕ signal. Disks that have a high inclination or where multiple scattering is expected to produce a significant part of the scattered light can contain a significant signal in Uϕ (Canovas et al. 2015). However, for low-inclination disks, we can expect all scattering polarization to be in azimuthal direction. This means that Qϕ will de facto show us PIL, with the benefit that we do not square the noise, which results in cleaner images. The Uϕ image should ideally show no signal at all in this case, which makes it a suitable metric for the quality of our reduction.
5. Instrument-configuration dependence in polarimetric efficiency and polarization angle
5.1. Polarimetric observations of TW Hydrae
We have observed TW Hydrae during the night of 31 March 2015 with IRDIS/DPI. This dataset was recorded before we became aware of the most severe instrumental polarization effects for SPHERE/IRDIS. Therefore, these data have been recorded without taking recommendations (Sect. 7) into account that optimize the polarimetric efficiency of DPI observations. Furthermore, the near face-on orientation of this disk (inclination = 7°, Qi et al. 2008) allows us to assume azimuthal polarization after scattering, which makes this object an ideal test case to illustrate how instrumental polarization effects alter the incident polarized signal.
The data have been recorded in H band (see Table 1) using field-stabilized mode, while an apodized pupil Lyot coronagraph (Carbillet et al. 2011; Guerri et al. 2011) with a focal plane mask with radius of 93 mas was used. We performed the observations using a detector integration time (DIT) of 16 s per frame, four frames per file, during 25 polarimetric cycles. This adds up to a total exposure time of 106.7 min. After creating the double-difference images, we removed five HWP cycles with bad seeing and/or AO corrections. The final dataset we used for this analysis therefore contains 20 sets of Q, U, IQ, and IU images.
Figure 3 shows the I = (IQ + IU)/2, QIPS, and UIPS images for four polarimetric cycles observed with increasing parallactic angle for each subsequent panel row. While each QIPS and UIPS panel displays the typical “butterfly” signal of an approximately face-on and axisymmetric disk, strong variations occur between the polarimetric cycles: the butterflies appear to rotate in clockwise direction and the signal in the QIPS and UIPS images decreases with increasing parallactic angle. Because the observations were taken in field-tracking mode, the image of the disk itself does not rotate on the detector. Instead, the AoLP (Eq. (4)) changes between the polarimetric cycles. We do not expect either the incident (“true”) degree or angle of linear polarization to vary with parallactic angle. I remains roughly constant in Fig. 3, therefore a decrease in measured PIL can only be explained by a decrease in PL. The changes in PL and AoLP must therefore be caused by instrumental polarization effects that depend on the specific telescope and instrument configuration, which varies with the parallactic and altitude angle of the observed star.
 |
Fig. 3. Each row shows the I, QIPS and UIPS images (from left to right) for polarimetric cycles with increasing parallactic angle from top to bottom. The on-sky orientation is the same for all panels: north is up, and east is left. However, the measured polarization angle (Eq. (4)) changes with derotator angle (θder), which is visible in the rotation of the butterfly pattern in clockwise direction. Furthermore, the polarimetric efficiency decreases with θder further removed from 180°, which is visible by the decreasing signal-to-noise ratio in the QIPS and UIPS images. |
5.2. Instrumental polarization effects
The calibrations of instrumental polarization effects and the analysis toward a complete Mueller matrix model of the instrument are described in detail in Paper II. In this section we briefly summarize how we have derived the model from calibration measurements, and describe the instrumental polarization effect of each set of optical components. Here we consider optical components to form a “set” when they share a fixed reference frame, that is, a common rotation of the set of components. For the last set of components (CPI + IRDIS components downstream of the derotator), we only fit the diattenuation because crosstalk is absent: all reflections are aligned with the analyzers.
In Sect. 5.3 we use this polarimetric instrument model to explain variations detected in the degree and angle of linear polarization in the data of TW Hydrae. Based on the polarimetric instrument model, we have devised a correction method in Paper II. In Sect. 6 of this paper we apply this correction method to retrieve the true incident polarization for the observations of TW Hydrae.
5.2.1. From calibrations to polarimetric instrument model
In Paper II we have used the internal light source with a calibration polarizer to create 100% polarized light and measured the linear Stokes parameters for a wide range of instrumental configurations. We then defined the measured degree of linear polarization for the 100% polarized incident light to be equal to the polarimetric efficiency for this configuration. For each set of optical components including and downstream of the HWP, we fit the measured Stokes parameters to the wavelength-dependent retardance of this set of components. Similarly, we calibrated the diattenuation of these sets of optical components with the internal light source, this time without a calibration polarizer to insert nearly unpolarized incident light.
We calibrated the diattenuation of the telescope and M4 (both located upstream from the HWP) by observing unpolarized stars at various altitude angles of the telescope. The retardances of these optical components were determined analytically using the Fresnel equations and literature values for the complex refractive index of the coating material. With the diattenuation and retardance, we computed the wavelength-dependent 4 × 4 Mueller matrices for each set of optical components that share a reference frame. The combination of the Mueller matrices for all optical components forms our polarimetric instrument model.
5.2.2. Derotator and HWP2
The left-hand panel of Fig. 4 shows the polarimetric efficiency curves against derotator angle (θder) for the four broadband filters of IRDIS. The solid lines show the polarimetric efficiency derived from the Mueller matrix model for the optical system for 90° ≤θder ≤ 180°, and the green dashed line shows this for 0° ≤θder ≤ 90° in H band alone. These green solid and dashed curves clearly do not overlap, and the same is true for the other filters (not shown). This asymmetry across θder = 90° in the polarimetric efficiency curve is caused by a non-ideal behavior of HWP2, that is, the retardance ≠λ/2 (see Paper II). A dramatic decrease in polarimetric efficiency is seen for θder ≈ 45° and 135° in the H- and Ks-band filters, while Y-band and especially the J-band filters show a much better polarimetric efficiency curve.
 |
Fig. 4. Left: polarimetric efficiency as a function of derotator angle for all broadband filters listed in Table 1. The green squares show the H-band polarimetric efficiencies measured for TW Hydrae scaled to the model curves (Sect. 5.3). The green dashed curve shows the model polarimetric efficiency for the range 0° ≤θder ≤ 90° in H band. This filter shows the strongest asymmetry around θder = 90°, which is caused by the non-ideal retardance of HWP2. Right: model polarization angle offset plotted against θder for the same filters (solid and dashed lines; as before, the dashed line covers the range 0° ≤θder ≤ 90°). In the ideal case, the polarization angle offset would remain 0°. However, there is a clear dependency on θder for H and Ks band, and to a lesser extent, for Y band, while the J band remains close to ideal. The polarization angle offsets measured as ϕ0 for TW Hydrae are plotted as green squares. The deviation of the on-sky data from the model curves is caused by the crosstalk contribution of other optical components. |
The right-hand panel of Fig. 4 shows how the polarization angle offsets oscillate around 0° (which would be the value in the ideal case of no crosstalk) for the model (solid and dashed lines) and the data (green squares). While this oscillation is only marginally visible for J band, with a maximum deviation from ideal < 4°, it is < 11° in Y, and can reach up to 34° in H. For Ks band, the polarization angle offset does not even return to its equilibrium and continues to rotate beyond ±90° (where a rotation of +90° is indistinguishable from −90°).
The strong dependence of the polarization angle offset and polarimetric efficiency on θder in H and Ks band are predominantly caused by crosstalk induced by the retardance of the derotator, which is close to that of a quarter-wave (λ/4) plate at these wavelengths. With these retardances, the derotator causes a strong linear to circular polarization crosstalk. This crosstalk means that when we use an unfavorable observing strategy, we can lose up to 95% of incident linearly polarized signal, which is ultimately the information carrier we aim to measure. Because other optical components (e.g., HWP2) contribute to this loss of polarization signal as well, we list the polarimetric efficiencies for the least favorable instrumental configuration in Table 2.
Lowest polarimetric efficiencies reached at the least favorable instrumental setup.
5.2.3. Telescope and SPHERE’s first mirror
On 16 April 2017, the M1 and M3 of UT3 have been recoated, which resulted in a more effective cancellation of IP when M3 and M4 are in crossed configuration (when the telescope is pointed at or close to zenith). Therefore, we present the lowest and highest IP values for each broadband filter as measured before and after recoating in Table 3.
IP (in percent of the total intensity) induced by the telescope mirrors and M4 before and after recoating of M1 and M3.
5.3. Explaining TW Hydrae data with the instrument model
During the observation of the 20 HWP cycles, the derotator has rotated from θder = 173.2° to θder = 152.6° (Δθder = −20.6°). To account for the variation of the measured AoLP between the HWP cycles, we determined the correct value for the polarization angle offset ϕ0 for each cycle separately, based on the assumption that the polarization is oriented in azimuthal direction, and therefore Uϕ should be 0. We achieved this by computing the sum over the absolute signals measured for the pixels in a centered annulus in the Uϕ image for a range of ϕ0 values: cUϕ(ϕ0). We selected the ϕ0 value that yielded the lowest cUϕ(ϕ0). We derived the relative polarimetric efficiency by measuring the absolute signal over an annulus in the Qϕ image for each cycle and dividing these values by that of the highest (coincidentally the first) HWP cycle. During the observing sequence of TW Hydrae, the polarimetric efficiency has decreased with ∼40%.
The green squares in Fig. 4 represent the relative polarimetric efficiency (left panel) and the polarization angle offset (right panel) for the TW Hydrae measurements. For this dataset we know neither the incident nor the measured PL (instead, we measure Qϕ ≈ PIL and do not know I of the disk) to determine the absolute value of the polarimetric efficiency. However, during the observations, Qϕ is expected to be linearly proportional to the polarimetric efficiency. Therefore, we measured for each HWP cycle the mean Qϕ in a fixed annulus around the star and scaled the images such that the highest mean value (from the first HWP cycle) matched the model polarimetric efficiency in H.
Although the polarimetric efficiency is rather well explained with the H-band model curve (green solid line), the polarization angle offset deviates from the model. The models shown in Fig. 4 are created for the simplest configuration, where all instrument settings were kept constant except for θder, while during the on-sky observations, many optical components have changed position due to their field-tracking laws, such as HWP2 and the telescope altitude angle.
To account for these additional changes in configuration, we used the instrument model to compute the polarimetric efficiency and polarization angle offset for the same instrument configuration as was used during the observations of TW Hydrae. We compare the predicted polarimetric efficiencies and polarization angle offsets with on-sky observation polarimetric efficiencies in Fig. 5 and the polarization angle offsets in Fig. 6.
 |
Fig. 5. Top: polarimetric efficiency modeled (solid line) for the same derotator and HWP2 angles as used during the observation of TW Hydrae (squares). The polarimetric efficiencies measured for the HWP cycles of TW Hydrae are only determined relative to the other HWP cycles. We therefore scaled all data points such that the first cycle (red square, with the highest polarimetric efficiency) matches the value of the model. Bottom: residuals between the model and the polarimetric efficiencies obtained for TW Hydrae. |
 |
Fig. 6. Top: expected polarization angle offsets of the same model (solid line) as used in Fig. 5 and the polarization angle offset angles (ϕ0 of Eq. (17)) of TW Hydrae (squares) with respect to azimuthal polarization. Bottom: residuals between the model polarization angle offsets and ϕ0 retrieved for TW Hydrae. |
The model predictions are very successful at explaining the changes in polarimetric efficiency and polarization angle. We see some clear outliers in both Figs. 5 and 6 at θder ≈ 159°, which are most likely caused by a poor fit of ϕ0 for these HWP cycles. This shows that our comparison is limited by the accuracy of the polarimetric efficiency measurement in the data and not by that of the model.
6. Comparison between data reduction with Uϕ minimization and model-based correction
After Sect. 5.1 we paused our post-processing of the data to analyze the instrumental polarization effects that cause the detected variations in PL and AoLP for TW Hydrae in Sects. 5.2 and 5.3. We have successfully implemented these lessons to create a detailed polarimetric instrument model and a model-based correction method for the instrumental polarization effects (see Paper II). In this section we compare post-processing based on this correction method with the best post-processing we performed without using the correction method, where we corrected for residual IP empirically by minimizing signal in Uϕ. We continue with the empirical correction method from where we stopped in Sect. 5.1.
6.1. Refining the reduction by minimizing Uϕ
We determined ϕ0 as described in Sect. 5.3. Then we improved our centering by shifting the QIPS and UIPS images with a range of x and y steps to find the minimum cUϕ(x, y) value. Because the improved centering affects the minimization process with which we found ϕ0, we repeated the minimization of cUϕ(ϕ0) on the centered data and found ϕ0 with increasing values between 6° ≤ϕ0 ≤ 25° for the 20 HWP cycles. A final Uϕ minimization was performed to enhance our IP correction: we determined the minimum of cUϕ by searching a grid of constants 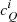 and
and 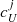 with which we replaced cQ and cU in Eqs. (13) and (14) to compute QIPS and UIPS, respectively. For each point (i, j) in the grid, we computed Uϕ with Eq. (16) and adopted the
with which we replaced cQ and cU in Eqs. (13) and (14) to compute QIPS and UIPS, respectively. For each point (i, j) in the grid, we computed Uϕ with Eq. (16) and adopted the 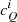 and
and 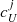 values that yield the smallest value of cUϕ.
values that yield the smallest value of cUϕ.
The Uϕ minimizations were performed and Qϕ and Uϕ were computed for each HWP cycle. At this stage we determined the polarimetric efficiency as described in Sect. 5.3. The final Qϕ and Uϕ images shown in Fig. 7 were created by median combining the 20 Qϕ and Uϕ images determined for each cycle, respectively.
 |
Fig. 7. Final Qϕ (left) and Uϕ (right) images of TW Hydrae. Qϕ and Uϕ are displayed with identical linear scale, and either unscaled (top) or scaled with r2 (bottom) to compensate for the decrease in stellar flux with distance. All four panels are shown with north up and east to the left for the same FoV of 4.9″ × 4.9″ or up to a separation of r = 2.45″ from the star in both RA (−x-axis) and Dec (+y-axis). |
6.2. Correcting observations with the instrument model
In Sect. 5.3 we show that the polarimetric instrument model can explain the variations in PL and AoLP that are measured in the data very well as instrumental polarization effects. In Paper II, we present a highly automated data-reduction pipeline (IRDAP) that contains a correction method based on this instrument model. We reduced the TW Hydrae data with IRDAP without any prior correction for instrumental polarization effects (i.e., we did not apply Eqs. (13) and (14) or Uϕ minimization). For illustrative purposes, we also applied the model correction to three individual polarimetric cycles with θder = 169.7° ,162.0°, and 154.1° of this dataset. Figure 8 shows the images as reduced with the method described in Sect. 6.1 and the result of the IRDAP corrections. The QIPS images of these three HWP cycles reduced with Uϕ minimization are shown in panels a1, a2, and a3, and the final Qϕ and Uϕ images of this reduction method are shown in panels b1 and b2, respectively. The Q images for the same HWP cycles of panel a are shown after the correction method was applied in panels c1, c2 and c3, and the final IRDAP-reduced Qϕ and Uϕ images are shown in panels d1 and d2, respectively.
 |
Fig. 8. a1, a2, and a3: QIPS images of three HWP cycles with θder = 169.7° ,162.0°, and 154.1°. These images are created with the Uϕ minimization method (Sect. 6.1). The butterfly patterns clearly rotate in clockwise direction and the signal decreases from left to right. b: when we use the assumption of azimuthal polarization, we can find the correct ϕ0 for each HWP cycle and compute the final r2-scaled Qϕ (b1) and Uϕ (b2) images (Sect. 6.1). Because we used the assumption that we know the angle of linear polarization at each point, we cannot claim to have determined the AoLP in this image. c: when we apply the correction method to the Q and U images, we retrieve the best approximation of the incident Q and U images (Sect. 6.2). The displayed Q images (for the same θder as in panel a) contain the ideal orientation of the butterflies and are corrected for the reduced polarimetric efficiency. However, the latter does not improve the signal-to-noise ratio (illustrated by the increased noise in panel c3). d1 and d2: IRDAP-corrected Qϕ and Uϕ image. Because we no longer need the assumption that we know the AoLP a priori, we can use Q and U after the correction method to determine the AoLP in our final reduction. |
6.3. Comparison of reduction methods
While the QIPS images of Fig. 8a show the butterfly rotation (ϕ0 ≠ 0) caused by crosstalk, the corrected Q images of panel c are clearly oriented such that ϕ0 ≈ 0°. Although the IRDAP-corrected Q images display a surface brightness that is approximately the same for all three images in panel c, the loss of polarization signal in the three QIPS images (from a1 to a3) is still visible as a decrease of the signal-to-noise ratio when we compare panel c3 with c1.
The azimuthal direction of the true polarization angle was used as an assumption in our reduction of Qϕ in Sect. 6.1. Therefore, we cannot claim to have derived the angle of linear polarization in panel b1. However, because we do not need to assume a priori knowledge about AoLP to compute the final Qϕ image of panel d1, we can confidently claim to have determined the AoLP. As a result, the Uϕ image of panel d2, created with ϕ0 = 0°, is even cleaner (especially at small separations) than the Uϕ image of panel b2.
Although the Qϕ images produced with both methods (Fig. 8b1 and d1) to a large degree show the same disk structures, the correction method will always produce more accurate polarization measurements than reduction methods without a model-based correction. When the aim of the observation is to perform a qualitative analysis of the data, such as describing the large-scale morphology of disks, a more conventional reduction method may suffice for a face-on disk such as TW Hydrae. However, the loss of polarization signal as displayed between panels a1, a2, and a3 illustrates that our combination of data from multiple polarimetric cycles will result in very poorly constrained polarimetric intensity measurements. More importantly, when we observe disks at larger inclination, especially in H or Ks band, even a qualitative analysis of the data is likely to become skewed when the instrumental polarization effects are not corrected properly. In Paper II we illustrate that the shape of Qϕ and especially Uϕ images of the disk around T Cha look much more reliable (i.e., more similar to radiative-transfer model predictions, Pohl et al. 2017) after the correction method is applied.
7. Recommendations for IRDIS/DPI
7.1. Observing strategy to optimize the polarimetric performance
Previous publications (e.g., Garufi et al. 2017) have demonstrated that the polarimetric mode of IRDIS is a very effective tool for imaging the scattering surface of protoplanetary and debris disks. However, the analysis of the TW Hydrae data presented in this paper illustrated that the polarimetric efficiency can be negatively affected when the instrument configuration is not optimized. When IRDIS/DPI is used in field-tracking mode, we recommend the following adjustments to the observing strategy to avoid a loss of polarized signal:
-
When no strict wavelength requirements are present and the disk surface brightness is expected to be gray in the NIR: use J band to achieve a > 90% polarimetric efficiency, which is nearly independent of the remaining instrumental setup.
-
However, most young stars are red, causing their disks to scatter more light in H than in J band. If the previous recommendation to use J band cannot be met and the Y-, H-, or Ks-band filters are used, avoid the use of derotator angles 22.5 ≲ |θder|≲67.5° +n ⋅ 90°, with n ∈ ℤ.
The latter recommendation ensures a polarimetric efficiency ≥70%. This constraint on θder can be achieved with two simple steps:
-
Within ESO’s Phase 2 Proposal Preparation tool (P2PP or P2), split the total observation within an observing block (OB) into parts (templates) where the difference between p and a does not vary by more than 90°, resulting in |Δθder|< 45°, because θder ∝ (a − p)/2.
-
For each template, the θder constraint can be determined by finding the average parallactic and altitude angles and applying a derotator (position angle) offset of
with n ∈ ℤ, and ⟨⟩ indicating the average values.
The parallactic and altitude angle can be determined by
where ϕ = −24.6° is the latitude of the VLT at the Paranal observatory, δ is the declination of the star, and HA is the hour angle of the star = local sidereal time (LST) – right ascension (RA).
The required derotator offset is strongly dependent on the exact start of the observation template. During visitor mode observations, where the observer is present at the observatory, the optimal derotator offset can be included in the OBs just before the start of the observations. During remote service mode observations, the observer does not know at what time the observation will start and therefore does not know the optimal value for INS.CPRT.POSANG. This problem can be solved by either including a list of LST values and the corresponding derotator position angle offsets to the README file of the OB, or by providing LST constraints and a corresponding optimal derotator offset to the OB, preferably for a time when the parallactic angle does not change too much during the observation.
When the optimal value for INS.CPRT.POSANG is used, the mean θder lies at either 0° or 90°, which orients the derotator horizontal or vertical with respect to the Nasmyth platform. This orientation will cause little or no crosstalk and therefore limited loss of polarized signal and a close to ideal polarization angle.
Figure 9 shows the polarimetric efficiency mapped for p and a without a derotator offset. Given the path traveled by TW Hydrae during our observations, shown with the black solid line (⟨p⟩≈90° ,⟨a⟩≈50°), we could have avoided the loss of polarization signal by providing a derotator position angle offset of INS.CPRT.POSANG = 90 − 50 = 40°, which would have rotated the derotator by 20°. We did not apply this derotator offset because we were not aware of the strong crosstalk for IRDIS/DPI at the time of these observations.
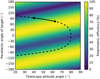 |
Fig. 9. Polarimetric efficiency in H band as a function of the parallactic angle and altitude angle when the derotator is in field-tracking mode without an additional derotator offset. The dashed line shows the parallactic and altitude angle of TW Hydrae across the sky, with the solid line showing the angles during the SPHERE observation. Default derotator settings (north is up on the detector) clearly yield mediocre polarimetric efficiencies. |
7.2. SPHERE design upgrades
7.2.1. HWPs 1 and 3 to reduce instrumental polarization effects
The most thorough way to reduce instrumental polarization effects for IRDIS would be to introduce two more HWPs in the optical path. A HWP1 at the same location as for ZIMPOL, in between M3 and M4, can keep the IP induced by both mirrors perpendicular so that they cancel out. We then use HWP2 in a slightly different fashion: rather than aligning the to-be-measured polarization angles with the analyzers, it aligns the desired polarization with the reflection plane of the derotator, as it does for ZIMPOL (Schmid et al. 2018). Similar to ZIMPOL, this new rotation law for HWP2 requires that we install a third HWP to align the desired polarization angle with the transmission axes of the IRDIS polarizers. We recommend to install this HWP3 directly downstream of the derotator to completely remove all crosstalk.
We are aware that the diverging beam downstream of the derotator is relatively large, which might make it difficult to produce an HWP that is large enough. The feasibility of this recommendation is yet to be determined. Alternatively, as for ZIMPOL, HWP3 could be installed farther down the optical path when the beam starts to become smaller (e.g., between the apodizer wheel and the DTTS beam splitter, before large incidence-angle reflections are encountered by the beam).
7.2.2. Recoating of the derotator to reduce retardance
As we described in Sect. 5.2.2, because of its unfavorable retardance (nearly λ/4 in H and Ks), the derotator is by far the largest contributor of crosstalk and hence loss of polarimetric efficiency. Therefore, an alternative recommendation to reduce the loss of polarimetric efficiency for IRDIS is to recoat the three mirrors of the derotator with a coating that yields a total retardance of the derotator close to λ/2 in all filters. We are currently investigating whether it is possible to apply a coating to the derotator that yields ∼λ/2 retardance over the very broad wavelength range required by ZIMPOL and IRDIS combined. Whether HWP3 is still desired after recoating depends on how close the retardance of the new coating is to the ideal value for the full wavelength range covered by IRDIS.
7.2.3. Polarizing beam splitter to increase throughput
The throughput of the combination of non-polarizing beam splitter plate and wire-grid polarizers is ∼50%, as discussed in Sect. 3.3. Replacing the non-polarizing plate with a polarizing beam-splitter plate will immediately increase the throughput by a factor ∼2. An additional result of this upgrade will also be that polarimetry is offered “for free” for any observation performed with IRDIS. Polarimetry-for-free will allow a substantial boost of the science output of the instrument by serendipitous discoveries of polarized circumstellar disks during planet-hunting surveys. The observer can choose whether to use full HWP cycles if polarimetry is not the primary objective. However, at least cycling two HWP angles set 45° apart (e.g., Q±) should always be considered, especially for DBI to avoid confusing polarized signal for a spectral feature. This necessity of the HWP requires that we need to investigate whether including this optical component affects the contrast of DBI, classical imaging, but also IFS observations.
7.2.4. IRDIS polarimetry and IFS observations simultaneously
An important first test for the desirability of IRDIS polarimetry-by-default is to do combined IRDIS/DPI + IFS observations. Although this combination is currently not offered, it does not require any changes in design, only software (new observing templates). The instrumental polarization effects of inserting a dichroic beam splitter instead of a mirror (to fold the beam towards IRDIS) is expected to be negligible, because it would cancel after the double difference. The largest unknown will be the effect of the HWP for IFS observations. This test is valuable, not only to investigate if a polarizing beam splitter should be installed in IRDIS. If the outcome is indeed that IRDIS/DPI observations do not affect the IFS and vice versa, we again open a new window for increased science output for each observation that can be used almost immediately. This new mode would be very helpful for substellar companion searches close to stars that are surrounded by disks, or disk-searches while characterizing substellar companions.
8. IRDIS/DPI compared to contemporary AO-assisted imaging polarimeters
In this section we briefly compare the polarimetric mode of SPHERE/IRDIS and the main contemporary AO-assisted high-contrast polarimetric imagers operating in the NIR: GPI, and NACO. The designs of both GPI and SPHERE are primarily focused on the minimization of wavefront errors (Macintosh et al. 2014; Beuzit et al. 2019), which is crucial for the detection of planets at high contrasts and small separation from the central star. Polarimetry had a much lower priority in the design choices, which resulted in designs that are suboptimal for the polarimetric performance of both instruments.
However, the extreme AO systems of both GPI (Poyneer et al. 2014) and SPHERE (Fusco et al. 2006) are clearly crucial for their polarimetric imaging modes. Although a detailed comparison between the performance of these AO systems and the previous-generation Nasmyth Adaptive Optics System (NAOS; Rousset et al. 2003) of NACO lies beyond the scope of this study, the reported performances of these systems allow for some obvious conclusions. The AO systems of SPHERE and GPI can both run at ∼1 kHz and control a high-order DM containing 41 × 41 and 64 × 64 actuators, respectively, while NAOS can control its DM with 185 active actuators at either 444 Hz or 178 Hz for its visible light or NIR wavefront sensor, respectively. The resulting point spread functions reach high Strehl ratios (≳90% in H band) and remain very stable for extended periods of time for both SPHERE and GPI, while NACO reaches typical Strehl ratios of ≳50% in Ks band and ≳30% in H band. Another important characteristic of the three AO systems is the limiting magnitude at which these systems can still operate. These magnitude limits are I ≈ 10 mag for GPI (Macintosh et al. 2014), R ≈ 15 mag for SPHERE (Beuzit et al. 2019), and V ≈ 16 mag and K ≈ 14 mag for NACO (Rousset et al. 2003). These limits make SPHERE and NACO particularly well suited to perform polarimetric imaging observations of relatively faint objects, such as most nearby T Tauri stars.
There are many differences in the designs of the polarimetric modes of NACO, GPI, and SPHERE/IRDIS. SPHERE is mounted on the Nasmyth platform of the telescope and employs an internal image derotator to stabilize the field or pupil. NACO is also mounted at the Nasmyth focus, but in contrast to SPHERE, it is attached to the derotator flange of the telescope support structure (Lenzen et al. 2003). This Nasmyth derotator rotates the complete instrument to track either field or pupil, although pupil tracking is rarely used for the polarimetric imaging mode of NACO. The GPI is mounted at the telescope Cassegrain focus, which avoids the need of a tertiary telescope mirror. It has no image derotator, which allows only pupil stabilized imaging, not field tracking.
The three instruments contain many internal reflections before the light beam reaches the detector. Because the double difference removes the IP produced by the optical components downstream of the HWP, the location of the HWP is important for the polarimetric performance of the instruments. While HWP2 of SPHERE/IRDIS is situated early in the optical train, directly after the first internal reflection within the instrument (between M4 and the derotator, see Fig. 2), the HWPs for GPI and NACO are installed after many reflective surfaces (Perrin et al. 2010; Witzel et al. 2011, respectively).
As a result of these design choices, the IP of SPHERE originates only from the telescope and M4 and therefore varies with telescope altitude angle (see Table 3). The IP of NACO is produced by the telescope and the reflections in the NAOS AO system. Because NACO rotates with respect to the telescope in field-tracking mode, its IP also depends on the telescope altitude angle. Millar-Blanchaer et al. (in prep.) measure the IP of NACO in pupil-tracking (most favorable instrument configuration) in H band, and determine the IP to be comparable to that of SPHERE/IRDIS at low altitude angles (worst configuration). The IP of GPI originates primarily from the reflections in the instrument upstream from the HWP. Millar-Blanchaer et al. (2016) measured average IP values that are very comparable to SPHERE/IRDIS.
The crosstalk of SPHERE/IRDIS is predominantly caused by the derotator and HWP2, which can result in a large decrease in polarimetric efficiency (Sect. 5.2.2). Since GPI does not have an image derotator and has all reflections aligned in a single plane, the retardance of the instrument is very small (Millar-Blanchaer et al. 2014) compared to SPHERE/IRDIS. In NACO, the crosstalk is predominantly caused by M3 and the optical components of NAOS. Because the HWP is located downstream of these components, the resulting polarimetric efficiency differs between measurements of Stokes Q and U, when Q is aligned with the optical axes of the polarizing beam splitter. Avenhaus et al. (2014) determined the polarimetric efficiency of Stokes U to be ∼60% relative to Stokes Q for NACO. Although a similar effect may be expected for GPI because of the location of the HWP, to the best of our knowledge, no differences in polarimetric efficiency between Q and U have been reported in literature.
Both Millar-Blanchaer et al. (2016) and van Holstein et al. (2017) showed for GPI and SPHERE/IRDIS, respectively, that the polarized contrast at separations ≳0.3″ is dominated by the photon and readout noise and therefore scales with the square root of the exposure time. Both papers report very similar polarized contrasts of 10−6 − 10−7 at a separation of 0.4″, while de Juan Ovelar (in prep.) has measured a polarized contrast of ∼ 10−6 at a separation of 1″ for NACO. We can therefore conclude that the polarimetric performances of GPI and SPHERE/IRDIS are very similar for relatively bright stars (R ≈ 6 mag). Because of their extreme AO systems and small differential wavefront errors, SPHERE/IRDIS and GPI reach much higher polarized contrasts than NACO at subarcsecond separations from the star.
9. Conclusions
The polarimetric mode of SPHERE/IRDIS has been very successful at imaging protoplanetary disks at resolutions and polarized contrasts close to the star that were not attainable with the previous generation of polarimetric imagers. Because the design was mainly driven by non-polarimetric requirements, its performance is strongly dependent on the observing strategy, as we have illustrated with the observations of TW Hydrae. When the observing strategy is not optimized, polarimetric crosstalk can cause the efficiency to drop toward ∼5% in H and Ks band; the polarimetric efficiency remains above 54% in Y band and above 89% in J band. Low polarimetric efficiency means that we lose polarization signal, which is what we aim to detect in DPI mode. Crosstalk also causes a polarization angle offset up to ∼30° in H- and more in Ks. We have demonstrated that the polarimetric instrument model described in Paper II can be used to explain and correct for the variations in polarimetric efficiency and polarization angle offset due to crosstalk observed in the TW Hydrae data.
The work presented in Papers I and II shows that instrumental polarization effects are significant, but also that this a posteriori work allows a very high-quality data product, which is above expectations given the loose constraints on the design requirements. Optimal results can be obtained from IRDIS/DPI observations when two important considerations are taken into account: (1) The observing strategy needs to be adjusted beforehand, as described in Sect. 7.1, to minimize a decrease in polarimetric efficiency. (2) The correction method described in Paper II and included in the IRDAP pipeline needs to be applied to correct the data for instrumental polarization effects.
This coating gives M4 similar reflective properties as M3 of UT3, which is most useful for ZIMPOL. SPHERE contains a visible-light HWP (HWP1) between M3 and M4 that keeps the angle of the polarization induced by M3 crossed with the angle of polarization induced by M4, which effectively cancels both their contributions. Unfortunately, no HWP1 is installed for the NIR in SPHERE. This decision was made because the instrumental polarization effects of these mirrors are smaller in the NIR and the requirements for the polarimetric performance of IRDIS are less stringent than those for ZIMPOL.
Acknowledgments
A significant part of this work was performed when JdB, RGvH and JHG were affiliated to ESO. JdB and RGvH thank ESO for the studentship at ESO Santiago during which this project was started. Many thanks go out to the SPHERE team and the instrument scientists and operators of the ESO Paranal observatory for their support during the calibration measurements. The research of JdB and FS leading to these results has received funding from the European Research Council under ERC Starting Grant agreement 678194 (FALCONER). SPHERE is an instrument designed and built by a consortium consisting of IPAG (Grenoble, France), MPIA (Heidelberg, Germany), LAM (Marseille, France), LESIA (Paris, France), Laboratoire Lagrange (Nice, France), INAF – Osservatorio di Padova (Italy), Observatoire de Genève (Switzerland), ETH Zurich (Switzerland), NOVA (Netherlands), ONERA (France), and ASTRON (Netherlands) in collaboration with ESO. SPHERE was funded by ESO, with additional contributions from the CNRS (France), MPIA (Germany), INAF (Italy), FINES (Switzerland) and NOVA (Netherlands). SPHERE also received funding from the European Commission Sixth and Seventh Framework Programs as part of the Optical Infrared Coordination Network for Astronomy (OPTICON) under grant number RII3-Ct-2004-001566 for FP6 (2004–2008), grant number 226604 for FP7 (2009–2012), and grant number 312430 for FP7 (2013-2016).
References
- Andrews, S. M., Wilner, D. J., Espaillat, C., et al. 2011, ApJ, 732, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Appenzeller, I. 1967, PASP, 79, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Avenhaus, H., Quanz, S. P., Schmid, H. M., et al. 2014, ApJ, 781, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Avenhaus, H., Quanz, S. P., Garufi, A., et al. 2018, ApJ, 863, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Benisty, M., Juhasz, A., Boccaletti, A., et al. 2015, A&A, 578, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beuzit, J. L., Vigan, A., Mouillet, D., et al. 2019, A&A, 631, A155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boccaletti, A., Abe, L., Baudrand, J., et al. 2008, in Adaptive Optics Systems, Proc. SPIE, 7015, 70151B [Google Scholar]
- Canovas, H., Rodenhuis, M., Jeffers, S. V., Min, M., & Keller, C. U. 2011, A&A, 531, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Canovas, H., Ménard, F., de Boer, J., et al. 2015, A&A, 582, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carbillet, M., Bendjoya, P., Abe, L., et al. 2011, Exp. Astron., 30, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Claudi, R. U., Turatto, M., Gratton, R. G., et al. 2008, in Ground-based and Airborne Instrumentation for Astronomy II, Proc. SPIE, 7014, 70143E [Google Scholar]
- de Kok, R. J., Stam, D. M., & Karalidi, T. 2011, ApJ, 741, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Dohlen, K., Langlois, M., Saisse, M., et al. 2008, in Ground-based and Airborne Instrumentation for Astronomy II, Proc. SPIE, 7014, 70143L [Google Scholar]
- Dohlen, K., Vigan, A., Mouillet, D., et al. 2016, in Ground-based and Airborne Instrumentation for Astronomy VI, Proc. SPIE, 9908, 99083D [Google Scholar]
- Dong, R., Rafikov, R., Zhu, Z., et al. 2012, ApJ, 750, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Fusco, T., Rousset, G., Sauvage, J.-F., et al. 2006, Opt. Express, 14, 7515 [NASA ADS] [CrossRef] [Google Scholar]
- Fusco, T., Sauvage, J. F., Mouillet, D., et al. 2016, in Adaptive Optics Systems V, Proc. SPIE, 9909, 99090U [NASA ADS] [CrossRef] [Google Scholar]
- Garufi, A., Quanz, S. P., Schmid, H. M., et al. 2016, A&A, 588, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Garufi, A., Benisty, M., Stolker, T., et al. 2017, The Messenger, 169, 32 [NASA ADS] [Google Scholar]
- Ginski, C., Stolker, T., Pinilla, P., et al. 2016, A&A, 595, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guerri, G., Daban, J.-B., Robbe-Dubois, S., et al. 2011, Exp. Astron., 30, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Hansen, J. E., & Travis, L. D. 1974, Space Sci. Rev, 16, 527 [NASA ADS] [CrossRef] [Google Scholar]
- Hugot, E., Ferrari, M., El Hadi, K., et al. 2012, A&A, 538, A139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jensen-Clem, R., Millar-Blanchaer, M., Mawet, D., et al. 2016, ApJ, 820, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Kuhn, J. R., Potter, D., & Parise, B. 2001, ApJ, 553, L189 [NASA ADS] [CrossRef] [Google Scholar]
- Langlois, M., Dohlen, K., Vigan, A., et al. 2014, in Ground-based and Airborne Instrumentation for Astronomy V, Proc. SPIE, 9147, 91471R [Google Scholar]
- Lenzen, R., Hartung, M., Brandner, W., et al. 2003, in Astronomical Telescopes and Instrumentation, eds. M. Iye, & A. F. M. Moorwood, SPIE, 944 [Google Scholar]
- Macintosh, B., Graham, J. R., Ingraham, P., et al. 2014, Proc. Natl. Acad. Sci., 111, 12661 [Google Scholar]
- Maire, A.-L., Langlois, M., Dohlen, K., et al. 2016, Proc. SPIE, 9908, 990834 [CrossRef] [Google Scholar]
- Maire, A. L., Rodet, L., Lazzoni, C., et al. 2018, A&A, 615, A177 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marley, M. S., & Sengupta, S. 2011, MNRAS, 417, 2874 [NASA ADS] [CrossRef] [Google Scholar]
- Marois, C., Doyon, R., Racine, R., & Nadeau, D. 2000, PASP, 112, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Marois, C., Lafrenière, D., Doyon, R., Macintosh, B., & Nadeau, D. 2006, ApJ, 641, 556 [Google Scholar]
- Martinez, P., Dorrer, C., Aller-Carpentier, E., et al. 2009, The Messenger, 137, 18 [NASA ADS] [Google Scholar]
- Mayama, S., Hashimoto, J., Muto, T., et al. 2012, ApJ, 760, L26 [NASA ADS] [CrossRef] [Google Scholar]
- Millar-Blanchaer, M., Wiktorowicz, S. J., Perrin, M. D., et al. 2014, in Exploring the Formation and Evolution of Planetary Systems, eds. M. Booth, B. C. Matthews, & J. R. Graham, IAU Symp., 299, 58 [NASA ADS] [Google Scholar]
- Millar-Blanchaer, M. A., Graham, J. R., Pueyo, L., et al. 2015, ApJ, 811, 18 [Google Scholar]
- Millar-Blanchaer, M. A., Perrin, M. D., Hung, L.-W., et al. 2016, Proc. SPIE, 9908, 990836 [CrossRef] [Google Scholar]
- Milli, J., Mawet, D., Pinte, C., et al. 2015, A&A, 577, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pavlov, A., Möller-Nilsson, O., Feldt, M., et al. 2008, in Advanced Software and Control for Astronomy II, Proc. SPIE, 7019, 701939 [NASA ADS] [CrossRef] [Google Scholar]
- Perrin, M. D., Graham, J. R., Larkin, J. E., et al. 2010, Proc. SPIE, 7736, 77365R [CrossRef] [Google Scholar]
- Perrin, M. D., Schneider, G., Duchene, G., et al. 2009, ApJ, 707, L132 [NASA ADS] [CrossRef] [Google Scholar]
- Perrin, M. D., Duchene, G., Millar-Blanchaer, M., et al. 2015, ApJ, 799, 182 [Google Scholar]
- Pinilla, P., Benisty, M., de Boer, J., et al. 2018, ApJ, 868, 85 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Pohl, A., Sissa, E., Langlois, M., et al. 2017, A&A, 605, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Poyneer, L. A., De Rosa, R. J., Macintosh, B., et al. 2014, in Adaptive Optics Systems IV, Proc. SPIE, 9148, 91480K [Google Scholar]
- Qi, C., Wilner, D. J., Aikawa, Y., Blake, G. A., & Hogerheijde, M. R. 2008, ApJ, 681, 1396 [NASA ADS] [CrossRef] [Google Scholar]
- Quanz, S. P., Schmid, H. M., Geissler, K., et al. 2011, ApJ, 738, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Quanz, S. P., Avenhaus, H., Buenzli, E., et al. 2013, ApJ, 766, L2 [NASA ADS] [CrossRef] [Google Scholar]
- Racine, R., Walker, G. A. H., Nadeau, D., Doyon, R., & Marois, C. 1999, PASP, 111, 587 [NASA ADS] [CrossRef] [Google Scholar]
- Rapson, V. A., Kastner, J. H., Millar-Blanchaer, M. A., & Dong, R. 2015, ApJ, 815, L26 [NASA ADS] [CrossRef] [Google Scholar]
- Rosenthal, E. D., Gurwell, M. A., & Ho, P. T. P. 1996, Nature, 384, 243 [NASA ADS] [CrossRef] [Google Scholar]
- Rousset, G., Lacombe, F., Puget, P., et al. 2003, in Astronomical Telescopes and Instrumentation, eds. P. L. Wizinowich, & D. Bonaccini, SPIE, 140 [Google Scholar]
- Schmid, H. M., Joos, F., & Tschan, D. 2006, A&A, 452, 657 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schmid, H. M., Bazzon, A., Roelfsema, R., et al. 2018, A&A, 619, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sengupta, S., & Marley, M. S. 2010, ApJ, 722, L142 [NASA ADS] [CrossRef] [Google Scholar]
- Stokes, G. G. 1851, Trans. Cambridge Phil. Soc., 9, 399 [NASA ADS] [Google Scholar]
- Stolker, T., Dominik, C., Avenhaus, H., et al. 2016, A&A, 595, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stolker, T., Min, M., Stam, D. M., et al. 2017, A&A, 607, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tinbergen, J. 1996, Astronomical Polarimetry (Cambridge: Cambridge University Press) [CrossRef] [Google Scholar]
- van Boekel, R., Henning, T., Menu, J., et al. 2017, ApJ, 837, 132 [NASA ADS] [CrossRef] [Google Scholar]
- van Holstein, R. G., Girard, J. H., de Boer, J., et al. 2020, A&A, 633, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Holstein, R. G., Snik, F., Girard, J. H., et al. 2017, Ser., 10400, 1040015 [Google Scholar]
- Vigan, A., Moutou, C., Langlois, M., et al. 2010, MNRAS, 407, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Witzel, G., Eckart, A., Buchholz, R. M., et al. 2011, A&A, 525, A130 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: Tracking laws for HWP2 and the derotator
A.1. Field-tracking
A.1.1. Derotator
Field-tracking is the default setting for the polarimetric imaging mode of IRDIS. In this setting, the derotator control law keeps the image with north up on the detector (except for the true-north offset described in Sect. 4.1), which is given by
with θder the derotator angle, p the parallactic angle of the astronomical object (FITS header keyword: TEL.PARANG.START), and a the altitude angle of the Unit Telescope (TEL.ALT). The user-defined position angle offset η of the image (INS4.DROT2.POSANG) can be altered by changing the value of INS.CPRT.POSANG in the Observing Block (OB), as described in Sect. 7. The header value of the derotator angle is computed as
with n ∈ ℤ.
A.1.2. Half-wave plate
The HWP2 control law for field-tracking with IRDIS/DPI (implemented in March 2015) keeps the polarization direction aligned with the analyzers, and is given by
where θHWP is the HWP angle, and γ a position angle offset of the linear polarization direction due to a user-defined HWP2 offset (INS4.DROT3.GAMMA, to be changed by adjusting SEQ.POL.OFFSET.GAMMA in the OB). 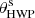 is the switch angle used during HWP cycles as described in Sect. 3.1. When SEQ.IRDIS.POL.STOKES is set to “QU” in the OB,
is the switch angle used during HWP cycles as described in Sect. 3.1. When SEQ.IRDIS.POL.STOKES is set to “QU” in the OB, 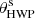 cycles through the angles 0° , 45° , 22.5°, and 67.5°, but only through 0° an 45° if SEQ.IRDIS.POL.STOKES is set to “Q”. The latter setting is not recommended for polarimetric measurements. The header value of HWP2 angle is computed as
cycles through the angles 0° , 45° , 22.5°, and 67.5°, but only through 0° an 45° if SEQ.IRDIS.POL.STOKES is set to “Q”. The latter setting is not recommended for polarimetric measurements. The header value of HWP2 angle is computed as
with n ∈ ℤ.
A.2. Pupil-tracking
A.2.1. Derotator
The derotator control law for pupil-tracking with IRDIS keeps the pupil fixed, which causes the image to rotate over the detector with the parallactic angle. This tracking law is given by
with PUPILoffset = 135.99 ± 0.11° (SPHERE Manual) the position angle offset of the image required to align the telescope pupil with the spider mask in the Lyot stop within IRDIS, in order to mask the diffraction pattern caused by the M2 support structure (spiders). The header value of the derotator angle is computed as
with n ∈ ℤ. This means that the header value of the derotator angle does not include PUPILoffset, and therefore does not represent the true derotator angle, as is the case with the header value in field-tracking (Eq. (A.2)).
A.2.2. Half-wave plate
The pupil-tracking law for HWP2 (implemented in January 2019) keeps the polarization direction aligned with the analyzers. Therefore, we can simply median combine the Q- and U-images after software-derotating them (the conventional data-reduction method). This way the polarization direction is also kept constant during integration and does not smear (however, the image, especially at large separations from the star, does smear out on the detector during long integrations due to the rotation of the field with parallactic angle). The following HWP2 control law is implemented:
The header value of HWP2 can still be determined using Eq. (A.5).
Appendix B: Data preprocessing
Raw IRDIS frames consist of 2048 by 1024 pixels in the x and y directions, respectively. The two beams separated by the beam splitter (see Sect. 3.2) are centered roughly on the left and right detector halves, while a field mask avoids leakage of signal from one half to the other.
We median combine all dark plus background observations taken with DIT = 16 s to create a master-dark image. From internal light source (flat-field) measurements, we create a (dark-subtracted) master-flat image: we take median over two regions of 800 × 800 centered on the left half ([x, y] = [512, 512]) and the right half ([x, y] = [1536,512]) and use this value to normalize. To avoid emphasizing dead pixels or pixels masked by the field mask, we change all pixel values < 0.1 into 1000. The final master-flat is shown in Fig. B.1. The master-flat still contains a vertical read-out pattern (features c in Fig. B.1). It is difficult to distinguish between the flat signal and this pattern, and polarimetry requires that we maintain the different transmission ratios of the two detector halves in our master-flat (hence the single normalization earlier). Therefore, we chose to leave the master-flat uncorrected for this pattern and removed these read-out columns at a later stage in the post-processing (Sect. 4.1).
 |
Fig. B.1. Normalized IRDIS master-flat image in H band. The illuminated detector halves are surrounded by the field mask {a}. The masked regions (and all pixels with value < 0.1) are set to 1000 and shown as white in this image. This enhances several clusters of dead and hot pixels (e.g., {b} around [x, y]≈[400, 400]). A time-varying read-out signature of the detector is visible as columns of 64 pixels wide (e.g., {c}). |
To correct for background signal, we would have preferred to used “SKY” observations: observations taken with the same DIT as the science (or “OBJECT”) frames, recorded on-sky with the star moved out of the detector FoV. Such SKY images contain background emission from possible interstellar origin (e.g., from nearby nebulosity), the Earth atmosphere, the optical system, and the detector dark current. Because no SKY images were recorded for these observations, we corrected for instrument background emission by subtracting the master-dark from each science frame recorded of TW Hydrae. Subsequently, we divided the science frames by the master-flat to correct for flat-field errors. Next, we cropped the frames to separate the left (1 ≤ x ≤ 1024) from the right (1025 ≤ x ≤ 2048) detector half.
To align the central star with the center of the image one could use the “CENTER” frames, where the SPHERE DM has created satellite spots around the star center. However, because alignment between individual frames is a crucial element of PDI, we opted for an alternative multi-stage approach. We determined the centers of the star in the left and right frames by cross-correlation with a two-dimensional Moffat function, where the central pixels within a radius of six pixels are set to zero to account for the coronagraph mask. We determined I according to Eq. (5), and median combined the images of all HWP cycles to create a template image. To enhance our frame-to-frame alignment, we repeat the cross correlation for all frames, this time using the template image. Because of irregular diffraction patterns close to the edge of the coronagraph mask, we cannot guarantee with the two centering steps described above that the star center lies at the center of the image. However, it does place the star close to the center of the image, and accurately aligns all frames with respect to each other. The latter is crucial to perform the single- and double-difference subtractions. A more advanced centering is performed at a later stage.
All Tables
Central wavelength (λc), bandwidth (Δλ), and pixel scale for the SPHERE/IRDIS broadband filters that are available in FW1.
Lowest polarimetric efficiencies reached at the least favorable instrumental setup.
IP (in percent of the total intensity) induced by the telescope mirrors and M4 before and after recoating of M1 and M3.
All Figures
 |
Fig. 1. Orientation of the Stokes vector components of Eq. (1), where the beam propagates out of the sketch, toward the observer. When the vertical axis (+Q) is aligned with a preferred orientation (usually the meridian on-sky), the remaining Stokes vector components are oriented accordingly. The AoLP (Eq. (4)) is also measured with respect to the +Q direction in counterclockwise direction. |
| In the text | |
 |
Fig. 2. Schematic overview of the telescope and SPHERE/IRDIS, showing the optical components that are relevant for the polarimetric imaging mode. The curved arrows indicate components that rotate during an observation block. Reflections at angles of incidence ≥45° in the instrument are represented with similarly large incidence reflections in the figure. The green beam shows the starlight before color filters are applied, blue represents visible light, and red and orange represent NIR light (the orange beam toward the IFS shows the shorter wavelengths). |
| In the text | |
 |
Fig. 3. Each row shows the I, QIPS and UIPS images (from left to right) for polarimetric cycles with increasing parallactic angle from top to bottom. The on-sky orientation is the same for all panels: north is up, and east is left. However, the measured polarization angle (Eq. (4)) changes with derotator angle (θder), which is visible in the rotation of the butterfly pattern in clockwise direction. Furthermore, the polarimetric efficiency decreases with θder further removed from 180°, which is visible by the decreasing signal-to-noise ratio in the QIPS and UIPS images. |
| In the text | |
 |
Fig. 4. Left: polarimetric efficiency as a function of derotator angle for all broadband filters listed in Table 1. The green squares show the H-band polarimetric efficiencies measured for TW Hydrae scaled to the model curves (Sect. 5.3). The green dashed curve shows the model polarimetric efficiency for the range 0° ≤θder ≤ 90° in H band. This filter shows the strongest asymmetry around θder = 90°, which is caused by the non-ideal retardance of HWP2. Right: model polarization angle offset plotted against θder for the same filters (solid and dashed lines; as before, the dashed line covers the range 0° ≤θder ≤ 90°). In the ideal case, the polarization angle offset would remain 0°. However, there is a clear dependency on θder for H and Ks band, and to a lesser extent, for Y band, while the J band remains close to ideal. The polarization angle offsets measured as ϕ0 for TW Hydrae are plotted as green squares. The deviation of the on-sky data from the model curves is caused by the crosstalk contribution of other optical components. |
| In the text | |
 |
Fig. 5. Top: polarimetric efficiency modeled (solid line) for the same derotator and HWP2 angles as used during the observation of TW Hydrae (squares). The polarimetric efficiencies measured for the HWP cycles of TW Hydrae are only determined relative to the other HWP cycles. We therefore scaled all data points such that the first cycle (red square, with the highest polarimetric efficiency) matches the value of the model. Bottom: residuals between the model and the polarimetric efficiencies obtained for TW Hydrae. |
| In the text | |
 |
Fig. 6. Top: expected polarization angle offsets of the same model (solid line) as used in Fig. 5 and the polarization angle offset angles (ϕ0 of Eq. (17)) of TW Hydrae (squares) with respect to azimuthal polarization. Bottom: residuals between the model polarization angle offsets and ϕ0 retrieved for TW Hydrae. |
| In the text | |
 |
Fig. 7. Final Qϕ (left) and Uϕ (right) images of TW Hydrae. Qϕ and Uϕ are displayed with identical linear scale, and either unscaled (top) or scaled with r2 (bottom) to compensate for the decrease in stellar flux with distance. All four panels are shown with north up and east to the left for the same FoV of 4.9″ × 4.9″ or up to a separation of r = 2.45″ from the star in both RA (−x-axis) and Dec (+y-axis). |
| In the text | |
 |
Fig. 8. a1, a2, and a3: QIPS images of three HWP cycles with θder = 169.7° ,162.0°, and 154.1°. These images are created with the Uϕ minimization method (Sect. 6.1). The butterfly patterns clearly rotate in clockwise direction and the signal decreases from left to right. b: when we use the assumption of azimuthal polarization, we can find the correct ϕ0 for each HWP cycle and compute the final r2-scaled Qϕ (b1) and Uϕ (b2) images (Sect. 6.1). Because we used the assumption that we know the angle of linear polarization at each point, we cannot claim to have determined the AoLP in this image. c: when we apply the correction method to the Q and U images, we retrieve the best approximation of the incident Q and U images (Sect. 6.2). The displayed Q images (for the same θder as in panel a) contain the ideal orientation of the butterflies and are corrected for the reduced polarimetric efficiency. However, the latter does not improve the signal-to-noise ratio (illustrated by the increased noise in panel c3). d1 and d2: IRDAP-corrected Qϕ and Uϕ image. Because we no longer need the assumption that we know the AoLP a priori, we can use Q and U after the correction method to determine the AoLP in our final reduction. |
| In the text | |
 |
Fig. 9. Polarimetric efficiency in H band as a function of the parallactic angle and altitude angle when the derotator is in field-tracking mode without an additional derotator offset. The dashed line shows the parallactic and altitude angle of TW Hydrae across the sky, with the solid line showing the angles during the SPHERE observation. Default derotator settings (north is up on the detector) clearly yield mediocre polarimetric efficiencies. |
| In the text | |
 |
Fig. B.1. Normalized IRDIS master-flat image in H band. The illuminated detector halves are surrounded by the field mask {a}. The masked regions (and all pixels with value < 0.1) are set to 1000 and shown as white in this image. This enhances several clusters of dead and hot pixels (e.g., {b} around [x, y]≈[400, 400]). A time-varying read-out signature of the detector is visible as columns of 64 pixels wide (e.g., {c}). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$$ \begin{aligned} \boldsymbol{S} = \left[ \begin{array}{c} I \\ Q \\ U \\ V \end{array}\right], \end{aligned} $$](/articles/aa/full_html/2020/01/aa34989-18/aa34989-18-eq1.gif)