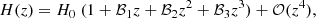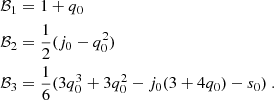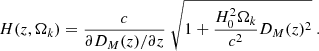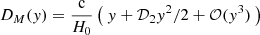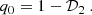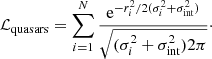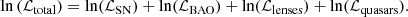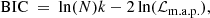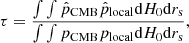| Issue |
A&A
Volume 632, December 2019
|
|
|---|---|---|
| Article Number | A91 | |
| Number of page(s) | 6 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201935972 | |
| Published online | 09 December 2019 | |
Low-redshift measurement of the sound horizon through gravitational time-delays
DARK, Niels Bohr Institute, University of Copenhagen, Lyngbyvej 2, 2100 Copenhagen, Denmark
e-mail: nikki.arendse@nbi.ku.dk, adriano.agnello@nbi.ku.dk, radek.wojtak@nbi.ku.dk
Received:
28
May
2019
Accepted:
4
October
2019
Context. The matter sound horizon can be infered from the cosmic microwave background within the Standard Model. Independent direct measurements of the sound horizon are then a probe of possible deviations from the Standard Model.
Aims. We aim at measuring the sound horizon rs from low-redshift indicators, which are completely independent of CMB inference.
Methods. We used the measured product H(z)rs from baryon acoustic oscillations (BAO) together with supernovae Ia to constrain H(z)/H0 and time-delay lenses analysed by the H0LiCOW collaboration to anchor cosmological distances (∝ H0−1). Additionally, we investigated the influence of adding a sample of quasars with higher redshift with standardisable UV-Xray luminosity distances. We adopted polynomial expansions in H(z) or in comoving distances so that our inference was completely independent of any cosmological model on which the expansion history might be based. Our measurements are independent of Cepheids and systematics from peculiar motions to within percent-level accuracy.
Results. The inferred sound horizon rs varies between (133 ± 8) Mpc and (138 ± 5) Mpc across different models. The discrepancy with CMB measurements is robust against model choice. Statistical uncertainties are comparable to systematics.
Conclusions. The combination of time-delay lenses, supernovae, and BAO yields a distance ladder that is independent of cosmology (and of Cepheid calibration) and a measurement of rs that is independent of the CMB. These cosmographic measurements are then a competitive test of the Standard Model, regardless of the hypotheses on which the cosmology is based.
Key words: gravitational lensing: strong / cosmological parameters / distance scale / early Universe
© ESO 2019
1. Introduction
The sound horizon is a fundamental scale that is set by the physics of the early Universe and is imprinted on the clustering of dark and luminous matter of the Universe. The most precise measurements of the sound horizon are obtained from observations of the acoustic peaks in the power spectrum of the cosmic microwave background (CMB) radiation, although the inference partially depends on the underlying cosmological model. In particular, the recent Planck satellite mission yielded a sound horizon scale (at the end of the baryonic drag epoch) of rs = 147.09 ± 0.26 Mpc. This was based on the spatially flat six-parameter Λ cold dark matter (ΛCDM) model, which provides a satisfactory fit to all measured properties of the CMB (Planck Collaboration VI 2019), and on the Standard Model of particle physics.
The sound horizon remains fixed in the comoving coordinates since the last scattering epoch and its signature can be observed at low redshifts as an enhanced clustering of galaxies. This feature is referred to as baryon acoustic oscillations (BAO). When we assume that the sound horizon is calibrated by the CMB, BAO observations can be used to measure distances and the Hubble parameter at the corresponding redshifts. The resulting BAO constraints can then be extrapolated to z = 0, for instance, using type Ia supernovae (SNe), in order to determine the present-day expansion rate H0. However, this inverse distance ladder procedure depends on the choice of cosmological model and on the strong assumption that the current standard cosmological model provides an accurate and sufficient description of the Universe at the lowest and highest redshifts. The robustness of the standard cosmological model has recently been questioned on the grounds of a strong and unexplained discrepancy between the local H0 measured from SNe with distances calibrated by Cepheids and its CMB-based counterpart (currently a 4.4σ difference; Riess et al. 2019). The inverse distance ladder calibrated on the CMB should therefore be taken with caution. Recently, Macaulay et al. (2019) performed an inverse-distance-ladder measurement of H0 adopting the baseline rs from Planck, and therefore their inferred H0 agrees with CMB predictions, as expected.
Observations of BAO alone only constrain a combination of the sound horizon and a distance or the expansion rate at the corresponding redshift, that is1, rs/D(z) and rsH(z). Using SNe, we can propagate BAO observables to redshift z = 0 and obtain constraints on rsH0 that are fully independent of the CMB (L’Huillier & Shafieloo 2017; Shafieloo et al. 2018). The extrapolation to low redshifts can be performed using various cosmographic techniques, so that the final measurement is essentially independent of cosmological model. Furthermore, combining BAO constraints with a low-redshift absolute calibration of distances or the expansion history, we can break the intrinsic degeneracy of the BAO between rs and H(z) and thus can determine the sound horizon scale. The resulting measurement is based solely on low-redshift observations, and it is therefore an alternative based on the local Universe to the sound horizon inferred from the CMB.
Several different calibrations of distances or the expansion history have been used to obtain independent low-redshift measurements of the sound horizon. The main results include the calibration of H(z) estimated from cosmic chronometers (Heavens et al. 2014; Verde et al. 2017), the local measurement of H0 from SNe with distances calibrated with Cepheids (Bernal et al. 2016), angular diameter distances to lens galaxies (Jee et al. 2016; Wojtak & Agnello 2019), and adopting the Hubble constant from time-delay measurements (Aylor et al. 2019), although the last measurement is based on cosmology-dependent modelling (Birrer et al. 2019). Currently, the sound horizon is most precisely constrained by a combination of BAO measurements from the Baryon Oscillations Spectroscopic Survey (BOSS; Alam et al. 2017), with a calibration from the Supernovae and H0 for the Equation of State of dark energy project (SH0ES; Riess et al. 2019). A significantly higher local value of the Hubble constant than its CMB-inferred counterpart implies a substantially smaller sound horizon scale than its analogue inferred from the CMB under the assumption of the standard ΛCDM model (Aylor et al. 2019). The discrepancy in H0 and rs may indicate a generic problem of distance scale at lowest and highest redshifts within the flat ΛCDM cosmological model (Bernal et al. 2016).
Here, we present a self-consistent inference of H0 and rs from BAO, SNe Ia, and time-delay likelihoods released by the H0LiCOW collaboration (Suyu et al. 2010, 2014, 2017; Wong et al. 2017; Birrer et al. 2019). We examine flat-ΛCDM models as a benchmark and different classes of cosmology-free models. Our approach allows us to determine the local sound horizon scale in a model-independent manner. A similar method was employed by Taubenberger et al. (2019), who used SNe to extrapolate constraints from time-delays to redshift z = 0, and thus to obtain a direct measurement of the Hubble constant that depends rather weakly on the adopted cosmology.
This paper is organised as follows. The datasets, models, and inference are outlined in Sect. 2. Results are given in Sect. 3, and their implications are discussed in Sect. 4.
Throughout this work, comoving distances, luminosity distances, and angular diameter distances are denoted by DM, DL, and DA, respectively. We also adopt the distance duality relations DM(z1 < z2) = DL(z1 < z2)/(1 + z2), DA(z1 < z2) = DM(z1 < z2)/(1 + z2), which should hold in all generality and whose validity with current datasets has been tested (Wojtak & Agnello 2019).
2. Datasets, models, and inference
We used a combination of different low-redshift probes to set different distance measurements and different models for the expansion history. All models inferred the following set of parameters: H0, rs, M1 (normalisation of the SN distance moduli), and coefficients parametrising the expansion history or distance as a function of redshift. Curvature Ωk is left as a free parameter in some models. The sample of high-redshift quasars introduces two additional free parameters: the normalisation M2 and the intrinsic scatter σint of the quasar distance moduli.
2.1. Models
The first model, for homogeneity with previous literature, adopted a polynomial expansion of H(z) in z:
where the coefficients are related to the standard kinematical parameters, that is, the deceleration q0, jerk j0, and snap s0, in the following way (Xu & Wang 2011; Weinberg 2008; Visser 2004):
Model distances were computed through direct integration of 1/H(z). This is preferred over a corresponding expansion in distances (as chosen e.g. by Macaulay et al. 2019) in order to ensure sub-percent accuracy in the model distances (Arendse et al., in prep.).
In our second chosen model family, H(z) was expanded as a polynomial in x = log(1 + z):
Plugging the Taylor expansion of z = 10x − 1 into Eq. (1) and grouping the new terms by order, we find the following mapping between coefficients Ci and the kinematical parameters:
Here, distances were also computed through direct numerical integration of 1/H(z).
In our third model choice, comoving distances were computed through expansion in y = z/(1 + z), and H(z) was obtained through a general relation (Li et al. 2019),
When a polynomial expansion
is adopted, then the second-order coefficient 𝒟2 is related to the deceleration parameter q0 through
Adopting multiple families of parametrisations, for H(z) and/or for model distances allowed us to quantify the systematics due to different ways of extrapolating the given distance measurements down to z = 0. This is equivalent to another common choice of adopting different cosmologies to extend the CDM model, but with the important difference that our chosen parametrisations are completely agnostic about what the underlying cosmological model should be.
Lastly, for the sake of comparison with widely adopted models, we also adopted a ΛCDM model class, with a uniform prior Ωk = [ − 1.0, 1.0] on curvature, and with the constraint that ΩΛ + Ωm + Ωk = 1. A discrepancy in flat-ΛCDM (Ωk = 0) between CMB measurements and our low-redshift measurements would then indicate that more general model families are required, that is, possible departures from concordance cosmology, or that the Standard Model needs to be extended.
2.2. Datasets
Our measurement relies on the complementarity of different cosmological probes. BAO observations constrain rsH(z) at several different redshifts and independently of the CMB. Standard candles play the role of the inverse distance ladder, by means of which the BAO constraints can be extrapolated to redshift z = 0. Finally, gravitational lensing time-delays place constraints on H0, thus breaking the degeneracy between H0 and rs in the inverse distance ladder of BAO and standardisable candles.
In our study, we used pre-reconstruction (independent of cosmological model) consensus measurements of the BAO from the Baryon Oscillations Spectroscopic Survey (Alam et al. 2017). For the relative luminosity distances, we employed binned distance moduli of SNe Ia from the Pantheon sample (Scolnic et al. 2018). We excluded possible changes due to the choice of SN sample by re-running our inference on distance moduli from JLA (Betoule et al. 2014), and with the current quality of data, there is no appreciable change in the results. Finally, we used constraints on time-delays of four strongly lensed quasars observed by the H0LiCOW collaboration (see Suyu et al. 2017; Birrer et al. 2019, and references therein). Results from a fifth lens have recently been communicated by H0LiCOW (Rusu et al. 2019). We currently use only results that have been reviewed, validated, and released.
As an option that provides more precise distance indicators at high redshifts, we used distance moduli estimated from a relation between UV and X-ray luminosity quasars, which was proved to be an alternative standard candle at high redshift (Risaliti & Lusso 2019). Risaliti & Lusso (2019) reported that quasar distances at high redshift show a deviation from ΛCDM; however, the lack of any corroborative pieces of evidence does not allow us to conclude if this deviation is a genuine cosmological anomaly or an unaccounted-for systematic effect. For this reason, we dismissed the quasar data at redshifts z > 1.8, which is the highest redshift of lensed quasars in our sample.
2.3. Inference
The best-fit parameters and credibility ranges of the different expansion models were obtained by sampling the posterior using affine-invariant Monte Carlo Markov chains (Goodman & Weare 2010), and in particular with the python module emcee (Foreman-Mackey et al. 2013). For the BAO and SN data set, the uncertainties are given by a covariance matrix C. The likelihood is obtained by
where r corresponds to the difference between the value predicted by the expansion and the observed data.
The high-redshift quasar sample contains significant intrinsic scatter, σint, which has to be modelled as an additional free parameter. The total uncertainty on each quasar data point is the sum of σi, the uncertainty of that data point, and σint. This leads to the following formula of the likelihood:
The likelihoods of the lensed quasars HE0435, RXJ1131, and B1608 of the H0LiCOW collaboration were given as skewed log-normal distributions of their time-delay distances DΔt = (1 + zl)DA, lDA, s/DA, ls. For the lensed quasar J1206, both the angular diameter distance and the time delay distance were available in the form of a sample drawn from the model posterior distribution. A Gaussian kernel density estimator (KDE) was used to interpolate a smooth distribution between the posterior points.
The final log-likelihood that was sampled by emcee is a sum of the separate likelihoods of the SN, BAO, lensed quasars, and high-redshift quasars,
We note that the high-redshift quasar likelihood is optional in our study. For all cosmographic models used in our work, parameter inference is carried out with or without quasar data, and both results are consistently reported.
A uniform prior was used for all the free parameters, except when the high-redshift quasar sample was used. In that case, the intrinsic scatter σint was also constrained to be larger than zero. This choice of priors does not seem to bias the inference according to current data and tests on flat-ΛCDM mocks.
To choose the right order of expansion for each model, the Bayesian information criterion (BIC) indicator was used,
where N is the number of data points, k is the number of free parameters and ℒm.a.p. is the maximum a posteriori likelihood (i.e. evaluated where the posterior is maximised). The BIC score expresses how well a model describes the data, with a lower score corresponding to a better agreement. It also introduces a penalty term for added complexity in a model. Table 1 displays the number of free parameters, maximum a posteriori likelihood, and the BIC score for four increasing orders of expansion. The expansion order with five free parameters provides the lowest BIC score. When more complexity is added to the model, the BIC value continuously increases, which supports the conclusion that higher expansion orders will be ruled out as well. When the high-redshift quasar sample was added to the data collection, it changed the preferred order of expansion of model 3 from third to second order.
Overview of the number of free parameters, maximum a posteriori likelihood, and BIC score for different expansion orders for cosmographic models 1, 2, and 3.
3. Results and discussion
The inferred values from our inference are given in Tables 2 and 3. For the sake of compactness, we report only the inferred values for each model that correspond to the lowest BIC scores (and to a ΔBIC > 2). Figure 1 shows the change in H0 as inferred by different expansion orders. Plots of marginalised posteriors on selected cosmological parameters are given in Figs. 2 and 3.
Inference on the cosmological parameters from BAO+SNe+lenses in our four model classes, with or without imposed flatness.
 |
Fig. 1. Inferred Hubble constant H0 (in km s−1 Mpc−1) vs. the chosen model family and expansion truncation. The fiducial values from each expansion model (displayed as squares) are chosen by considering the change in BIC score and in lnℒm.a.p. vs. the change in degrees of freedom. The upper dashed line corresponds to the local measurement value of H0 = 74.0 km s−1 Mpc−1 with a Cepheid calibration, and the lower dashed line corresponds to the Planck value of H0 = 67.4 km s−1 Mpc−1. The shaded grey regions show the error bars. |
 |
Fig. 2. Inference on cosmological parameters, including the Hubble constant H0 and sound horizon rs, for the baseline case of flat-ΛCDM models using time-delay lenses, SN Ia, and BAO as late-time indicators. The outermost credibility contour contains 95% of the marginalised posterior probability, and the innermost contour contains 68%. |
 |
Fig. 3. Inference on the Hubble constant H0 and sound horizon rs for different models (at fiducial truncation order for models 1–3), with free Ωk, using time-delay lenses, SN Ia, and BAO. While the inferred parameters can change among models and among truncation choices, the relative discrepancy with CMB measurements remains the same. The credibility contours contain 95% of the marginalised posterior probability. The grey point corresponds to the Planck value of H0 and rs and to a flat Universe. |
The inferred values of the Hubble constant from Table 1, both its maximum a posteriori and uncertainty, vary between (73.0 ± 2.7) km s−1 Mpc−1 and (76.0 ± 4.0) km s−1 Mpc−1. They are in full agreement with current results form the H0LiCOW and SH0ES collaborations, even despite the choice of general and agnostic models in our method. This indicates that the discrepancy between Cepheid-calibrated H0 and that inferred from CMB measurements is not due to (known and unknown) systematics in the very low redshift range. The inferred sound horizon rs varies between (133 ± 8) Mpc and (138 ± 5) Mpc. The largest discrepancy with the value from CMB and Standard Model predictions (147.09 ± 0.26 Mpc) is more significant for models that are agnostic to the underlying cosmology.
The systematic uncertainties, due to different model choices, are still within the range allowed by statistical uncertainties. However, they may become dominant in future measurements aiming at percent-level precision. Adding UV-Xray standardisable quasars generally raises the inferred value of H0 (and correspondingly lowers the inferred rs), even though the normalisation of their Hubble diagram is treated as a nuisance parameter. The addition of the quasar sample also results in lower values of Ωk. This suggests that the behaviour of distance modulus with redshift has sufficient constraining power on auxiliary cosmological parameters that in turn are degenerate with H0 in the time-delay lensing standardisation. For all cosmographic models, the intrinsic scatter in quasar distance moduli found in our analysis is 1.45 mag, which is fully consistent with the estimate reported in Risaliti & Lusso (2019).
We quantified the tension with CMB measurements through the two-dimensional inference on H0 and rs. Following Verde et al. (2013), we estimated the odds that both measurements are consistent by computing the following ratio:
where p is the marginalised probability distribution for rs and H0 from the CMB (Planck Collaboration VI 2019) or our study (in both cases approximated by Gaussians), while 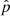 is a distribution shifted to a fixed arbitrary point so that both measurements have the same posterior probability means. A more intuitive scale representing the discrepancy between two measurements is a number-of-sigma tension, which can be derived from the odds ratio. This is done by calculating the probability enclosed by a contour such that
is a distribution shifted to a fixed arbitrary point so that both measurements have the same posterior probability means. A more intuitive scale representing the discrepancy between two measurements is a number-of-sigma tension, which can be derived from the odds ratio. This is done by calculating the probability enclosed by a contour such that 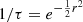 . The number of sigma tension can then be calculated from the probability by means of the error function. We list the logarithm of the odds and the number of sigma tension in Tables 2 and 3.
. The number of sigma tension can then be calculated from the probability by means of the error function. We list the logarithm of the odds and the number of sigma tension in Tables 2 and 3.
The tension with Planck measurements from CMB is approximately at a 2σ level. While the uncertainties from some model families are larger, the corresponding H0 (rs) optimal values are also higher (lower), and the tension remains the same. The curvature Ωk slightly alleviates the tension through larger H0 uncertainties, but the current data do not yield any evidence of a departure from flatness.
4. Conclusions and outlook
Current data enable a ≈3% determination of key cosmological parameters, in particular, the Hubble constant H0 and the sound horizon rs, resulting in a ≈2σ Gaussian tension with predictions from CMB measurements and the Standard Model. While this tension is robust against the choice of model family and is therefore independent of the underlying cosmology, the systematics due to different model choices are currently comparable to the statistical uncertainties and may dominate percent-level measurements of H0. A simple estimate based on recent SH0ES measurements (Riess et al. 2019) and very recent five-lens measurements by H0LiCOW (Rusu et al. 2019) indicates a ≈5σ tension with CMB measurements within a flat-ΛCDM model.
Our study also demonstrated the potential of constraining the curvature of the Universe solely based on low-redshift observations and in a cosmology-independent manner. The current precision of 0.20 is insufficient to test possible minimum departures from flatness, mainly due to the accuracy in H0 from a small sample of well-studied lenses. Samples of lenses with suitable ancillary data are already being assembled (see e.g. Shajib et al. 2019). Future measurements of gravitational time-delays from the Large Synoptic Survey Telescope can reach percent-level precision (Liao et al. 2015), making this method a highly competitive probe (Denissenya et al. 2018).
Acknowledgments
The authors were supported by a grant from VILLUM FONDEN (project number 16599). This project is partially funded by the Danish Council for independent research under the project “Fundamentals of Dark Matter Structures”, DFF–6108-00470. We are grateful for the public release of the time-delay distance likelihoods by the H0LiCOW collaboration, and interesting conversations with S. H. Suyu, F. Courbin and T. Treu. We thank Guido Risaliti for sharing distance moduli measured from high-redshift quasars. We also thank the anonymous referee for constructive comments which helped improve our work.
References
- Alam, S., Ata, M., Bailey, S., et al. 2017, MNRAS, 470, 2617 [NASA ADS] [CrossRef] [Google Scholar]
- Aylor, K., Joy, M., Knox, L., et al. 2019, ApJ, 874, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Bernal, J. L., Verde, L., & Riess, A. G. 2016, J. Cosmology Astropart. Phys., 10, 019 [Google Scholar]
- Betoule, M., Kessler, R., Guy, J., et al. 2014, A&A, 568, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Birrer, S., Treu, T., Rusu, C. E., et al. 2019, MNRAS, 484, 4726 [NASA ADS] [CrossRef] [Google Scholar]
- Denissenya, M., Linder, E. V., & Shafieloo, A. 2018, J. Cosmology Astropart. Phys., 3, 041 [NASA ADS] [CrossRef] [Google Scholar]
- Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [CrossRef] [Google Scholar]
- Goodman, J., & Weare, J. 2010, Appl. Math. Comput. Sci., 5, 65 [Google Scholar]
- Heavens, A., Jimenez, R., & Verde, L. 2014, Phys. Rev. Lett., 113, 241302 [NASA ADS] [CrossRef] [Google Scholar]
- Jee, I., Komatsu, E., Suyu, S. H., & Huterer, D. 2016, J. Cosmology Astropart. Phys., 2016, 031 [Google Scholar]
- L’Huillier, B., & Shafieloo, A. 2017, J. Cosmol. Astropart. Phys., 2017, 015 [CrossRef] [Google Scholar]
- Li, E. K., Du, M., & Xu, L. 2019, ArXiv e-prints [arXiv:1903.11433] [Google Scholar]
- Liao, K., Treu, T., Marshall, P., et al. 2015, ApJ, 800, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Macaulay, E., Nichol, R. C., Bacon, D., et al. 2019, MNRAS, 486, 2184 [NASA ADS] [CrossRef] [Google Scholar]
- Planck Collaboration VI. 2019, A&A, submitted [arXiv:1807.06209] [Google Scholar]
- Riess, A. G., Casertano, S., Yuan, W., Macri, L. M., & Scolnic, D. 2019, ApJ, 876, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Risaliti, G., & Lusso, E. 2019, Nat. Astron., 3, 272 [NASA ADS] [CrossRef] [Google Scholar]
- Rusu, C. E., Wong, K. C., Bonvin, V., et al. 2019, MNRAS, submitted [arXiv:1905.09338] [Google Scholar]
- Scolnic, D. M., Jones, D. O., Rest, A., et al. 2018, ApJ, 859, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Shafieloo, A., L’Huillier, B., & Starobinsky, A. A. 2018, Phys. Rev. D, 98, 083526 [NASA ADS] [CrossRef] [Google Scholar]
- Shajib, A. J., Birrer, S., Treu, T., et al. 2019, MNRAS, 483, 5649 [NASA ADS] [CrossRef] [Google Scholar]
- Suyu, S. H., Marshall, P. J., Auger, M. W., et al. 2010, ApJ, 711, 201 [NASA ADS] [CrossRef] [Google Scholar]
- Suyu, S. H., Treu, T., Hilbert, S., et al. 2014, ApJ, 788, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Suyu, S. H., Bonvin, V., Courbin, F., et al. 2017, MNRAS, 468, 2590 [Google Scholar]
- Taubenberger, S., Suyu, S. H., Komatsu, E., et al. 2019, A&A, 628, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Verde, L., Protopapas, P., & Jimenez, R. 2013, Phys. Dark Universe, 2, 166 [Google Scholar]
- Verde, L., Bernal, J. L., Heavens, A. F., & Jimenez, R. 2017, MNRAS, 467, 731 [NASA ADS] [Google Scholar]
- Visser, M. 2004, Class. Quant. Grav., 21, 2603 [NASA ADS] [CrossRef] [Google Scholar]
- Weinberg, S. 2008, Cosmology (Oxford University Press: Oxford, UK) [Google Scholar]
- Wojtak, R., & Agnello, A. 2019, MNRAS, 486, 5046 [NASA ADS] [CrossRef] [Google Scholar]
- Wong, K. C., Suyu, S. H., Auger, M. W., et al. 2017, MNRAS, 465, 4895 [NASA ADS] [CrossRef] [Google Scholar]
- Xu, L., & Wang, Y. 2011, Phys. Lett. B, 702, 114 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Overview of the number of free parameters, maximum a posteriori likelihood, and BIC score for different expansion orders for cosmographic models 1, 2, and 3.
Inference on the cosmological parameters from BAO+SNe+lenses in our four model classes, with or without imposed flatness.
All Figures
 |
Fig. 1. Inferred Hubble constant H0 (in km s−1 Mpc−1) vs. the chosen model family and expansion truncation. The fiducial values from each expansion model (displayed as squares) are chosen by considering the change in BIC score and in lnℒm.a.p. vs. the change in degrees of freedom. The upper dashed line corresponds to the local measurement value of H0 = 74.0 km s−1 Mpc−1 with a Cepheid calibration, and the lower dashed line corresponds to the Planck value of H0 = 67.4 km s−1 Mpc−1. The shaded grey regions show the error bars. |
| In the text | |
 |
Fig. 2. Inference on cosmological parameters, including the Hubble constant H0 and sound horizon rs, for the baseline case of flat-ΛCDM models using time-delay lenses, SN Ia, and BAO as late-time indicators. The outermost credibility contour contains 95% of the marginalised posterior probability, and the innermost contour contains 68%. |
| In the text | |
 |
Fig. 3. Inference on the Hubble constant H0 and sound horizon rs for different models (at fiducial truncation order for models 1–3), with free Ωk, using time-delay lenses, SN Ia, and BAO. While the inferred parameters can change among models and among truncation choices, the relative discrepancy with CMB measurements remains the same. The credibility contours contain 95% of the marginalised posterior probability. The grey point corresponds to the Planck value of H0 and rs and to a flat Universe. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.