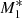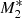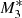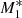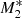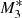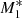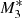| Issue |
A&A
Volume 631, November 2019
|
|
|---|---|---|
| Article Number | A13 | |
| Number of page(s) | 10 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201935917 | |
| Published online | 11 October 2019 | |
Bondi accretion for adiabatic flows onto a massive black hole with an accretion disc
The one dimensional problem
1
Environmental Physics Laboratory (EPHYSLAB), Facultad de Ciencias, Campus de Ourense, Universidad de Vigo, Ourense 32004, Spain
e-mail: josem.ramirez@gmail.com
2
School of Physical Sciences and Nanotechnology, Yachay Tech University, 100119 Urcuqui, Ecuador
3
Área de Física de Procesos Irreversibles, Departamento de Ciencias Básicas, Universidad Autónoma Metropolitana-Azcapotzalco (UAM-A), Av. San Pablo 180, 02200 Ciudad de México, Mexico
4
Instituto de Ciencias Básicas e Ingenierías, Universidad Autónoma del Estado de Hidalgo (UAEH), Ciudad Universitaria, Carretera Pachuca-Tulancingo km. 4.5 s/n, Colonia Carboneras, Mineral de la Reforma, CP 42184 Hidalgo, Mexico
5
Departamento de Física, Instituto Nacional de Investigaciones Nucleares (ININ), Carretera México-Toluca km. 36.5, La Marquesa, 52750 Ocoyoacac, Estado de México, Mexico
Received:
19
May
2019
Accepted:
5
September
2019
We present the classical Bondi accretion theory for the case of non-isothermal accretion processes onto a supermassive black hole (SMBH), including the effects of X-ray heating and the radiation force due to electron scattering and spectral lines. The radiation field is calculated by considering an optically thick, geometrically thin, standard accretion disc as the emitter of UV photons and a spherical central object as a source of X-ray emission. In our analysis, the UV emission from the accretion disc is assumed to have an angular dependence, and the X-ray radiation from the central object is assumed to be isotropic. This allows us to build streamlines in any angular direction. The influence of both types of radiation is evaluated for different flux fractions of the X-ray and UV emissions with and without the effects of spectral line driving. We find that the radiation emitted near the SMBH interacts with the infalling matter and modifies the accretion dynamics. In the presence of line driving, a transition takes place from pure type 1 and 2 to type 5 solutions, which takes place regardless of whether the UV emission dominates the X-ray emission. We computed the radiative factors at which this transition occurs, and discard type 5 solution from all our models. We also provide estimated values of the accretion radius and accretion rate in terms of the classical Bondi values. The results are useful for constructing proper initial conditions for time-dependent hydrodynamical simulations of accretion flows onto SMBHs at the centre of galaxies.
Key words: accretion / accretion disks / black hole physics / gravitation / hydrodynamics / line: formation / radiation: dynamics
© ESO 2019
1. Introduction
The spherically symmetric Bondi solution (Bondi 1952) has become a reference model for interpreting the observations of mass accretion onto supermassive black holes (SMBHs) in the centre of galaxies. This is so because SMBHs at the centre of elliptical galaxies are likely to accrete primarily from the surrounding hot, quasi-spherical interstellar medium, suggesting that accretion rates can be simply estimated using the Bondi accretion theory. Studies on mass accretion were first considered in the framework of Newtonian gravity (Bondi & Hoyle 1944; Bondi 1952; Hoyle & Lyttleton 1939) and then they were generalized by Michel (1972) to curved space-time. Quantum corrections to the general relativistic accretion have also been proposed (Yang 2015; Contreras et al. 2019). In recent years, the accretion onto SMBHs has been the subject of intense research because of its role in the co-evolution of SMBHs and their host galaxies. In particular, the number of these studies down to the parsec scale in the centre of galaxies has significantly increased with the advances in instrumental and computational capabilities (one example is given by the Event Horizon Telescope Collaboration 2019). On the other hand, fully analytical solutions on isothermal Bondi-like accretion including radiation pressure and the gravitational potential of the host galaxy have started to appear recently (Korol et al. 2016; Ciotti & Pellegrini 2017; Ciotti & Ziaee Lorzad 2018, hereafter KCP16, CP17 and CZ18). Moreover, recent detailed numerical calculations on Bondi accretion (Ramírez-Velasquez et al. 2018), using advanced consistent smoothed particle hydrodynamics (SPH) techniques (Gabbasov et al. 2017; Sigalotti et al. 2018), suggest that it would be possible to push these studies further to cover the sub-parsec scales in active galactic nuclei (AGNs), including the effects of radiation pressure due to spectral lines (Ramírez-Velasquez et al. 2016, 2017).
Accretion onto compact objects is now recognized to be a major influence on the environment surrounding SMBHs in the centre of galaxies (e.g. Salpeter 1964; Fabian 1999; Barai 2008; Germain et al. 2009). In the study of the several properties governing the evolution of the system, that is, Bondi quantities such as the accretion rate and the solution of the hydrodynamical equations, it is a quite common assumption to prescribe values of temperature, pressure, and density at infinity and use them as the “true” boundary conditions for the solution of the equations, even when the problem at hand needs sub-parsec resolution scales as in the case of AGNs, for instance. However, this resolution is never achieved in observational and numerical studies (Pellegrini 2005), introducing under- and over-estimations of the physical quantities (CP17). The outflow phenomenon is believed to play a major role in the feedback processes invoked by modern cosmological models (i.e. Λ-cold dark matter) to explain the possible relationship between the SMBH and its host galaxy (e.g. Magorrian et al. 1998; Gebhardt et al. 2000) as well as in the self-regulating growth of the SMBH. The problem of accretion onto an SMBH has been studied through hydrodynamical simulations of galaxy evolution (e.g. Ciotti & Ostriker 2001; Di Matteo et al. 2005; Li et al. 2007; Ostriker et al. 2010; Novak et al. 2011). For example, in numerical studies of galaxy formation, spatial resolution permits resolving scales from kiloparsecs to parsecs, while the sub-parsec scales of the Bondi radius are not resolved. This is why a prescribed sub-grid physics is often employed to solve this lack of resolution. With sufficiently high X-ray luminosities, the falling material will have the correct opacity, developing outflows that originate at sub-parsec scales (e.g. Ramírez 2013). Therefore, calculations of the processes involving accretion onto SMBH have become of primary importance (e.g. Proga 2000, 2003, 2007; Proga et al. 2000; Proga & Kallman 2004; Ostriker et al. 2010). In order to provide a robust and reliable methodology for the production of initial conditions (ICs) for the numerical calculations of mass accretion onto SMBHs, we have combined the geometric effects and assumptions employed by Proga (2007, hereafter P07) to compute the radiation field from the disc and central object with the analytical solution procedure provided by KCP16 and CP17.
In particular, P07 reported axisymmetric time-dependent hydrodynamical calculations of gas flow under the influence of the gravity of black holes in quasars by taking into account X-ray heating and the radiation force due to electron scattering and spectral lines. He found that for an SMBH with a mass of 108 M⊙ with an accretion luminosity of 0.6 times the Eddington luminosity, the flow settles into a steady state and has two components: an equatorial inflow and a bipolar inflow and outflow with the outflow leaving the system along the rotational axis of the disc and the inflow being a realization of a Bondi-like accretion flow. To calculate the radiation field, an optically thin accretion disc was considered as a source of UV photons and a spherical central object as a source of X-rays. In contrast, KCP16 generalized the classical Bondi accretion theory, including the radiation pressure feedback due to electron scattering in the optically thin approximation and the effects of a general gravitational potential due to a host galaxy. In particular, they presented a full analytical discussion for the case of a Hernquist galaxy model. An extension of this analytical solution was reported by CP17 in terms of the Lambert-Euler W-function for isothermal accretion in Jaffe and Hernquist galaxies with a central SMBH. They found that the flow structure is sensitive to the shape of the mass profile of the host galaxy, and that for the Jaffe and Hernquist galaxies the value of the critical accretion parameter can be calculated analytically.
We here derive radiative non-isothermal (γ ≠ 1) angular-dependent streamline solutions for use as initial conditions in numerical simulations of mass accretion flows onto massive compact objects. To do so, we introduce a radiation force term due to a non-isothermal extended source in the momentum equation as in P07 and develop a semi-analytical solution for the non-isothermal accretion onto an SMBH at the centre of galaxies using a procedure similar to that developed by KCP16 and CP17, with no assumption about the Bernoulli equation, but radially integrating the equations of motion. The effects of the gravitational potential due to the host galaxy are ignored here, and they are left for a further analysis. In Sect. 2 we introduce the mathematical methodology and the fundamental equations, and Sect. 3 contains the analysis of the results. Section 4 presents the theoretical prediction of absorption lines. Section 5 provides a general analysis of the bias in the estimates of the Bondi radius and mass accretion rate and discusses the importance of using the semi-analytical solution as true initial conditions for numerical simulations of accretion flows. Finally, Sect. 6 contains the relevant conclusions.
2. Bondi accretion for a non-isothermal flow
Under the assumption of spherical symmetry, the classical Bondi solution describes a purely adiabatic accretion flow onto a point mass for the case of a gas at rest at infinity and free of self-gravity. Detailed numerical calculations of the classical Bondi accretion flow onto a stationary SMBH were performed by Ramírez-Velasquez et al. (2018), using a mathematically consistent SPH method. In real situations, however, the accretion flow is affected by the emission of radiation near the SMBH. The radiation emitted near the SMBH interacts with the inflowing matter and modifies the accretion dynamics. The radiation effects can be strong enough to stop the accretion and shut off the central object. Here we follow the recipe of P07 to model the radiation field from the disc and central object, where a radiation force term is added as a source in the momentum equation. In this formulation, the disc is assumed to be flat, Keplerian, geometrically thin, and optically thick. The structure and evolution of a flow irradiated by a central compact object can be described by the continuity and momentum equations,
where ρ is the mass density, v = (vr, vθ = 0, vϕ = 0) is the velocity vector, p is the gas pressure, g is the gravitational acceleration due to the central object, Frad = (Fr, Fθ = 0, Fϕ = 0) is the total radiation force per unit mass, and d/dt = ∂/∂t + v ⋅ ∇. Under the assumption that vθ = vϕ = 0, Eq. (2) reduces to a single equation for the radial velocity component, which in spherical coordinates takes the form
where C is a constant whose value is given by the physical parameters of the system, while ψgrav = (GMBH)/r and ψrad = −C/r are the gravitational and radiation1 potentials, respectively. The opposite signs in the potentials indicate that the radiative and gravitational forces act in opposite directions. In this analysis we study the 1D problem, where vr(r, θ, ϕ) = vr(r, θ0) = vr, for a fixed angle θ0, and p(r, θ, ϕ) = p(r, θ0) = p. With these assumptions, Eq. (3) can be written in the more convenient form
where
is the so-called Bernoulli function ℋ(r), which we use below to radially integrate Eq. (4). In Eqs. (4) and (5), the gas pressure is related to the mass density by the equation
where kB is the Boltzmann constant, T is the gas temperature, μ is the mean molecular weight, mp is the proton mass, 1 < γ ≤ 5/3 is the polytropic index, and 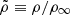 , where p∞ and ρ∞ are the values of the pressure and density at infinity, respectively. The polytropic sound speed is given by
, where p∞ and ρ∞ are the values of the pressure and density at infinity, respectively. The polytropic sound speed is given by
The radiative acceleration on the right-hand side of Eq. (3) is composed of two parts: one due to electron scattering, which was first studied for the isothermal case by KCP16, CP17, and CZ18, and the other due to the radiation pressure produced by the spectral lines, which is here designed using the same strategy as P07. The disc luminosity Ldisc and the central object luminosity L⋆ are expressed in terms of the total accretion luminosity L. That is, Ldisc = fdiscL and L⋆ = f⋆L = (1 − fdisc)L. As in P07, the disc is assumed to emit only in the UV (i.e. fdisc = fUV), while the central object is assumed to emit only X-rays (i.e. f⋆ = fX). In this way, the central object only contributes to the radiation force due to electron scattering, while the disc contributes to the radiation force due to both electron scattering and spectral lines. For simplicity, only the radiation force along the radial direction is considered, which for an optically thin gas is approximated by the relation
where c is the speed of light, σT/mp is the mass scattering coefficient for free electrons, θ0 is some fixed and constant polar angle measured from the rotational axis of the disc, τ is the optical depth, and M(τ) is the so-called force multiplier (Castor et al. 1975), which defines the numerical factor that parameterizes by how much spectral lines increase the scattering coefficient. Following P07, we use the following prescriptions for the force multiplier
where k is a factor proportional to the total number of lines, α(= 0.6) is the ratio of optically thick to optically thin lines, τmax = τηmax and ηmax is a parameter that determines the maximum value 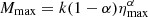 . The parameters k and ηmax are given by the following relations (Stevens & Kallman 1990):
. The parameters k and ηmax are given by the following relations (Stevens & Kallman 1990):
and
where ξ is the photoionization parameter. As in P07, the photoionization parameter is calculated as ξ = 4πℱX/n, where ℱX is the local X-ray flux and n is the number density of the gas given by n = ρ/(mpμ), with μ = 1. The local X-ray flux, corrected for the effects of optical depth, is defined by
where τX is the X-ray optical depth, which can be estimated by the integral
between the central source (r = 0) and a point r in the accreting flow, where κX is the absorption coefficient. Here the attenuation of the X-rays is calculated using κX = 0.4 g−1 cm2 for all ξ.
We introduce the normalized quantities
where
is the Bondi radius, 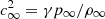 , G is the Newtonian gravitational constant, MBH is the mass of the black hole, and ℳ is the Mach number, and assuming a steady-state motion (i.e. ∂vr/∂t = 0). Now Eqs. (4) and (5) can be combined to give
, G is the Newtonian gravitational constant, MBH is the mass of the black hole, and ℳ is the Mach number, and assuming a steady-state motion (i.e. ∂vr/∂t = 0). Now Eqs. (4) and (5) can be combined to give
where 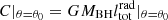 . The above integral is easily evaluated as follows:
. The above integral is easily evaluated as follows:
where ℳ∞ → 0 and r∞ → ∞. Integration of Eq. (16) leads to
for the steady-state radial non-isothermal (γ > 1) gravitational accretion, including the effects of radiation emission due to electron scattering and spectral discrete lines with appropriate boundary conditions at infinity, where
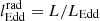 , LEdd = 4πcGMBHmp/σT is the Eddington luminosity, σT = 6.6524 × 10−25 cm2 is the Thomson cross section, and frad|θ = θ0 is the radiative force parameter given by
, LEdd = 4πcGMBHmp/σT is the Eddington luminosity, σT = 6.6524 × 10−25 cm2 is the Thomson cross section, and frad|θ = θ0 is the radiative force parameter given by
Although the force multiplier depends on the gas temperature through the parameter k, as shown by Eq. (17) of P07 based on detailed photoionization calculations performed with the XSTAR code (Kallman 2006, priv. comm.), here we adopt the temperature-independent relation given by their Eq. (12) and leave the corrections for the temperature effects for future numerical work (e.g. when an energy equation accompanied by the net heating and cooling function developed by Ramírez-Velasquez et al. 2016, 2017 is used; see also Dannen et al. 2019). The temperature correction for a fixed ionization parameter ξ is explained in detail in P07, but here we provide a brief qualitative explanation. The dependence of the force multiplier on both ξ and T is an extremely complex problem, in part due to the amount and participation of the ∼104 different atomic transitions given by neutral and ionized species from H to Fe. It is worth exploring these relationships in detail. However, we know that r ∼ 10 pc is a good place to start2 such a study because of the number of UV absorption transitions that are available for spectral line acceleration (Kashi et al. 2013; Higginbottom et al. 2014; Ramírez-Velasquez et al. 2016, 2017) and is suitable for the comparison we propose here. We computed the radiative factor for a ξ10 pc = ξ(r = 10 pc) without temperature corrections even though the hydrodynamical variables were taken to be temperature dependent. For instance, the dependence on temperature and ionization can be taken into account using the detailed tables of Ramírez-Velasquez et al. (2017). Equation (20) must be solved coupled to the continuity Eq. (1), which in terms of the above assumptions and normalized parameters can be written as
where
is the dimensionless accretion parameter that determines the accretion rate for given MBH and boundary conditions. In Eq. (24), 4πfsolid = ∫sinθdθdϕ is the solid angle covered by the streamline at the polar angle θ0. When fsolid = 1 (full solid angle), we recover the classical accretion parameter. However, for the case of a θ0-dependent force, fsolid < < 1. This dependence is important only for the final calculation of 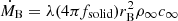 , which is fixed once the value of θ0 is chosen. Using Eq. (23) to eliminate
, which is fixed once the value of θ0 is chosen. Using Eq. (23) to eliminate 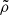 from Eq. (20), the Bondi problem reduces to solving the equation
from Eq. (20), the Bondi problem reduces to solving the equation
where 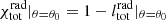 , λ is set equal to the critical value of the accretion parameter, defined as
, λ is set equal to the critical value of the accretion parameter, defined as 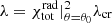 , and
, and
Although Eq. (25) together with the definitions (26)–(28) looks the same as those derived by KCP16 and CP17, there are some differences that we describe below. On the other hand, it is clear from Eq. (25) that all physical quantities can be expressed in terms of the radial Mach number profile.
Compared to the previous analyses performed by KCP16 and CP17, the new feature of our model is the angular dependence of the UV emission of the accretion disc, while it is assumed that the central X-ray radiation object does not change with θ0. For an incident angle of θ0 = 0, the particles experience maximum intensity. As θ0 increases towards the equator, it follows from Eq. (22) that the radiation flux from the accretion disc becomes weaker until it vanishes for θ0 = π/2. Consequently, the ratio between the X-ray and the UV flux increases with increasing θ0. Thus, for large θ0 pure gravitational accretion (type 1 solution)3 takes place until a critical angle θphase develops for which radiation dominates gravity and type 5 solutions result. In Fig. 1 we plot this feature of the solutions for three different flux fractions of the X-ray and UV emissions with and without the force multiplier. For instance, models M1, M2, and M3 have f⋆ = 0.5 and fdisc = 0.5, f⋆ = 0.2 and fdisc = 0.8, and f⋆ = 0.05 and fdisc = 0.95, respectively, with M(τ) = 0 so that we can evaluate the influence of both types of radiation in detail. Models 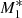 ,
, 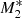 , and
, and 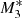 are identical to models M1, M2, and M3, respectively, but with M(τ)≠0 and a radially varying ionization parameter given by
are identical to models M1, M2, and M3, respectively, but with M(τ)≠0 and a radially varying ionization parameter given by
 |
Fig. 1. Angular dependence of the radiative force parameter for models M1, M2, and M3 (when M(τ) = 0; thin dashed lines) and models |
where the total accretion luminosity is set to be L = 7.45 × 1045 erg s−1, which is appropriate for an SMBH of 108 M⊙, at a distance r = 10 pc that accretes at an efficiency of 8%. The gas density is nH = 1010 cm−3 and the optical depth is set to τ = 0.3. The physical parameters employed for all these models are listed in Table 1. For all models we set 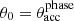 4 and γ = 1.1. The exploration of different values of the polytropic index γ is a very complex topic. For instance, the mirror problem, Parker’s winds, with 3/2 < γ < 5/3, and their spherical properties change when angular momentum is added to the flow equations (Waters & Proga 2012). Moreover, γ = 3/2 is the critical adiabatic index that separates the solution space from their transonic behaviour. We therefore study the γ < 3/2 and γ > 3/2 solutions, which lead to accelerating and decelerating Parker winds, respectively. The values of f⋆ and fdisc listed in Table 1 are the same as were employed by P07 and are guided by the observational results from Zheng et al. (1997) and Laor et al. (1997).
4 and γ = 1.1. The exploration of different values of the polytropic index γ is a very complex topic. For instance, the mirror problem, Parker’s winds, with 3/2 < γ < 5/3, and their spherical properties change when angular momentum is added to the flow equations (Waters & Proga 2012). Moreover, γ = 3/2 is the critical adiabatic index that separates the solution space from their transonic behaviour. We therefore study the γ < 3/2 and γ > 3/2 solutions, which lead to accelerating and decelerating Parker winds, respectively. The values of f⋆ and fdisc listed in Table 1 are the same as were employed by P07 and are guided by the observational results from Zheng et al. (1997) and Laor et al. (1997).
Parameters of the generalized Bondi accretion models.
Models M1, M2, and M3 represent non-isothermal accretion models that only include the effect of electron scattering as in KCP16, CP17, and CZ18. Figure 1 shows that for model M1, where the X-ray and UV emitters each add the same (50%) to the radiation emission, type 5 solutions are not produced at any angle. Model M1 represents a pure accretion process in which the force of gravity close to θ0 = 0 nearly cancels and where the radiative force parameter, 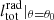 , is always below unity. In contrast, model
, is always below unity. In contrast, model 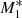 with M(τ)≠0 and θphase ≈ 0.51 undergoes a transition from pure accretion to a type 5 solution with
with M(τ)≠0 and θphase ≈ 0.51 undergoes a transition from pure accretion to a type 5 solution with 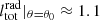 at θ0 ≈ 0. Similarly, models M2 and M3 have values of θphase for which there will be non-physical solutions around ≈0.4 − 0.5, and models
at θ0 ≈ 0. Similarly, models M2 and M3 have values of θphase for which there will be non-physical solutions around ≈0.4 − 0.5, and models 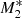 and
and 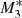 develop type 5 solutions (Frank et al. 2002) for values of ≈0.82 − 0.90. We explore these numerical solutions separately below in more detail.
develop type 5 solutions (Frank et al. 2002) for values of ≈0.82 − 0.90. We explore these numerical solutions separately below in more detail.
3. Analysis of the results
Figure 2 shows the radial Mach number profiles of the inflow (solid lines) and type 2 (dotted lines) solutions (which we include in the discussion and call outflow from now on) of Eq. (25) for models 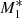 ,
, 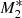 , and
, and 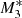 . The supersonic inflow (ℳ > 1) solution is depicted in orange, while the subsonic (ℳ < 1) solution is given by the blue lines. For model
. The supersonic inflow (ℳ > 1) solution is depicted in orange, while the subsonic (ℳ < 1) solution is given by the blue lines. For model 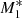 , X-ray heating is the strongest (i.e. f⋆ = fdisc = 0.5). In this case, the solution predicts a transition from pure accretion (i.e. θ0 > θphase) to a type 5 flow with a critical radius xcrit ≈ 0.0090, where the supersonic and subsonic flows combine to produce a full transonic flow. For model
, X-ray heating is the strongest (i.e. f⋆ = fdisc = 0.5). In this case, the solution predicts a transition from pure accretion (i.e. θ0 > θphase) to a type 5 flow with a critical radius xcrit ≈ 0.0090, where the supersonic and subsonic flows combine to produce a full transonic flow. For model 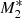 , X-ray heating by the central object (f⋆ = 0.2) is smaller than the UV emission from the accretion disc (fdisc = 0.8) and we observe two important differences compared to model
, X-ray heating by the central object (f⋆ = 0.2) is smaller than the UV emission from the accretion disc (fdisc = 0.8) and we observe two important differences compared to model 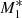 . First, the critical point occurs at a larger radius (xcrit ≈ 0.034) and so the flow becomes supersonic at a distance from the SMBH about four times larger than for model
. First, the critical point occurs at a larger radius (xcrit ≈ 0.034) and so the flow becomes supersonic at a distance from the SMBH about four times larger than for model 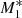 . Second, at an inner radius of ≈0.001, the inflow for model
. Second, at an inner radius of ≈0.001, the inflow for model 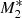 reaches ℳ ≈ 8.1 against ≈4.1 for model
reaches ℳ ≈ 8.1 against ≈4.1 for model 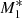 .
.
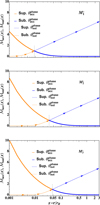 |
Fig. 2. Mach number of the inflow (solid lines) and outflow (dotted lines) solutions of Eq. (20) with M(τ)≠0. The supersonic part of the inflow solutions is depicted in orange, and the subsonic part is given in blue. In contrast, the supersonic outflow solution is depicted in blue and the subsonic one in orange. The vertical lines in each frame mark the position of the sonic radius. When radiation dominates, the gas will escape from the gravitational potential of the accretor. Upper, middle, and bottom frames: models with fdisc = 0.5, 0.8, and 0.95, respectively (see Table 1). |
For the 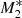 model, the winds are developed farther away from the centre, that is, around x ≈ 0.034 compared to model
model, the winds are developed farther away from the centre, that is, around x ≈ 0.034 compared to model 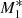 , where the thermal outflows are produced closer to the central object at x ≈ 0.01. Therefore, at larger distances from the SMBH, that is, at x ≈ 3, faster winds are developed for model
, where the thermal outflows are produced closer to the central object at x ≈ 0.01. Therefore, at larger distances from the SMBH, that is, at x ≈ 3, faster winds are developed for model 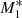 (ℳ(x = 3) ≈ 6.2) than for model
(ℳ(x = 3) ≈ 6.2) than for model 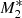 , for which ℳ(x = 3) ≈ 4.4. In all plots, the flows escaping supersonically from the gravitational potential of the SMBH are indicated by arrows. When only 5% of the heating from the central object contributes to the radiation factor, as in model
, for which ℳ(x = 3) ≈ 4.4. In all plots, the flows escaping supersonically from the gravitational potential of the SMBH are indicated by arrows. When only 5% of the heating from the central object contributes to the radiation factor, as in model 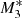 , xcrit ≈ 0.046, and mass accretion proceeds supersonically below this radius with ℳ ≈ 10 at x = 0.001, while supersonic outflows are produced for x ≳ 0.046. The numerical simulations of P07 for f⋆ = fdisc = 0.5 (his run case A) shows that a strong X-ray heating can accelerate the outflow to maximum velocities of 700 km s−1 with the outflow collimation by the infall increasing with increasing radius. When f⋆ = 0.2 and fdisc = 0.8, line driving is seen to accelerate the outflow to higher velocities (up to 4000 km s−1), while the outflow collimation becomes very strong for f⋆ = 0.05 and fdisc = 0.95, that is, when the X-ray heating is the lowest, which corresponds to our model
, xcrit ≈ 0.046, and mass accretion proceeds supersonically below this radius with ℳ ≈ 10 at x = 0.001, while supersonic outflows are produced for x ≳ 0.046. The numerical simulations of P07 for f⋆ = fdisc = 0.5 (his run case A) shows that a strong X-ray heating can accelerate the outflow to maximum velocities of 700 km s−1 with the outflow collimation by the infall increasing with increasing radius. When f⋆ = 0.2 and fdisc = 0.8, line driving is seen to accelerate the outflow to higher velocities (up to 4000 km s−1), while the outflow collimation becomes very strong for f⋆ = 0.05 and fdisc = 0.95, that is, when the X-ray heating is the lowest, which corresponds to our model 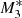 . In this case, the gas outflow is confined within a very narrow channel along the equatorial axis of the accretion disc, while most of the computational volume is occupied by the inflow.
. In this case, the gas outflow is confined within a very narrow channel along the equatorial axis of the accretion disc, while most of the computational volume is occupied by the inflow.
The density profiles for models 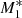 ,
, 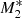 , and
, and 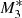 are shown in Fig. 3. As the UV emission intensity from the accretion disc becomes stronger, the gas density close to the SMBH becomes higher. This is counter-intuitive because we would have expected the radiation to push the gas away from the centre, resulting in decreasing density close to the SMBH. This is in fact the case. As the radiation intensity increases, it pushes the critical radius farther away from the SMBH, and consequently, the gas becomes supersonic at larger radial distances. As the supersonic flow occupies a larger central volume, the density close to the SMBH increases by factors as large as ≈10 from fdisc = 0.5 to fdisc = 0.95.
are shown in Fig. 3. As the UV emission intensity from the accretion disc becomes stronger, the gas density close to the SMBH becomes higher. This is counter-intuitive because we would have expected the radiation to push the gas away from the centre, resulting in decreasing density close to the SMBH. This is in fact the case. As the radiation intensity increases, it pushes the critical radius farther away from the SMBH, and consequently, the gas becomes supersonic at larger radial distances. As the supersonic flow occupies a larger central volume, the density close to the SMBH increases by factors as large as ≈10 from fdisc = 0.5 to fdisc = 0.95.
 |
Fig. 3. Density profiles of the radiative non-isothermal models with M(τ)≠0. The vertical lines mark the position of the sonic radius for each model. As the UV emission becomes stronger, the accreting gas becomes supersonic at larger radial distances from the SMBH, and the density becomes higher for x ≲ 0.5. |
The Mach number profiles for models M1, M2, and M3 with no force multiplier are shown in Fig. 4. In the absence of line driving and strong X-ray heating (model M1), no type 5 flows are developed regardless of the incidence angle. In this case, the critical point occurs at x ≈ 0.12 and close to the SMBH at x = 0.001 the Mach number reaches values as high as ≈20. As the UV emission intensity increases over the X-ray intensity (models M2 and M3), the critical point and the outflows occur at smaller radii from the SMBH than in models 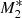 and
and 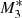 . On the other hand, at radii sufficiently far from the SMBH, that is, at x = 3 the outflows become more supersonic than for models
. On the other hand, at radii sufficiently far from the SMBH, that is, at x = 3 the outflows become more supersonic than for models 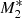 and
and 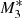 , as we may see by comparing Figs. 2 and 4. These results clearly show that radial velocities can differ from system to system depending on the details of the radiative processes dominating the source.
, as we may see by comparing Figs. 2 and 4. These results clearly show that radial velocities can differ from system to system depending on the details of the radiative processes dominating the source.
 |
Fig. 4. Mach number of the inflow (solid lines) and outflow (dotted lines) solutions of Eq. (20) with M(τ) = 0. The supersonic part of the inflow solutions are depicted in orange, and the subsonic part is given in blue. In contrast, the supersonic outflow solution is depicted in blue and the subsonic one in orange. The vertical lines in each frame mark the position of the sonic radius. When the radiation dominates, the gas escapes from the gravitational potential of the accretor. With no force multiplier, no winds are developed for f⋆ = fdisc = 0.5 (model M1). |
For our choice of 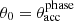 , Fig. 5 shows the density profiles for models M1, M2, and M3. Model M1 reaches a density as high as ≈3000 at x = 0.001, which is about 30 times higher than for model
, Fig. 5 shows the density profiles for models M1, M2, and M3. Model M1 reaches a density as high as ≈3000 at x = 0.001, which is about 30 times higher than for model 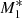 . This result implies that when X-ray emission is strong enough, the accretion rate also increases by the same factor and the accretion lifetime decreases for systems with the same gas reservoirs. In contrast, as the UV emission intensity dominates the X-ray emission, the effects of line driving are those of increasing the density close to the SMBH. In particular, when we compare Figs. 3 and 5, the density at x = 0.001 is from 10 to 5 times higher for models
. This result implies that when X-ray emission is strong enough, the accretion rate also increases by the same factor and the accretion lifetime decreases for systems with the same gas reservoirs. In contrast, as the UV emission intensity dominates the X-ray emission, the effects of line driving are those of increasing the density close to the SMBH. In particular, when we compare Figs. 3 and 5, the density at x = 0.001 is from 10 to 5 times higher for models 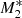 and
and 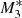 than for models M2 and M3.
than for models M2 and M3.
 |
Fig. 5. Density profiles of the radiative non-isothermal models with M(τ) = 0. The vertical lines mark the position of the sonic radius for each model. As the UV emission becomes stronger, the accreting gas becomes supersonic at larger radial distances from the SMBH, while the density becomes higher for x ≲ 0.2. These trends apply only to models M2 and M3, while model M1, having an arbitrary θ0 and weaker UV emission, becomes supersonic at a much larger distance from the SMBH and achieves a much higher central densities than models M2 and M3. |
4. Predicted spectral line shape for pure absorption
A very important prediction of these models is the symmetry in shape of absorption spectral lines as seen by an observer far away from the system. To show this, we assume an atom falling onto the black hole as predicted by model 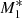 . This atom has a hypothetical transition that would absorb photons emitted by the inner region at 10 Å in the rest-frame (λ0). Then we use the Doppler-shift formula (Rybicki & Lightman 1979),
. This atom has a hypothetical transition that would absorb photons emitted by the inner region at 10 Å in the rest-frame (λ0). Then we use the Doppler-shift formula (Rybicki & Lightman 1979),
where w is the angular frequency (measured by the observer) of an emitted photon with rest-frame frequency w0. Here γL is the Lorentz factor, v(x) is the velocity of the absorbing atom, and ϕ is the angle between the streamline and the line of sight towards the observer, which we have set to ϕ = 0. For falling particles we use v(x) = − ℳ(x)cs, where cs is given by Eq. (7)5, for a value of ≈345 km s−1. The simplest absorption model to describe the absorption spectrum is
where ν0λ0 = (w0/2π)λ0 = c and σ is a representative width given by 0.1%λ(x). We set A(x) = ρ(x)/ρmax to model the intensity of the absorption taken from the density profile of each model, 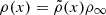 and
and 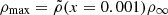 . As the particle approaches the SMBH, the density increases and the final shape tends to be shifted more deeply towards the red. Figure 8 shows that the most asymmetrical line has f⋆ = 0.05 (bottom panel, solid red line), for which the high-energy radiation is weaker, which leaves the particle to reach higher velocities and a stronger asymmetry. On the other hand, we do not discuss the outflow profile (type 2 solution) because the boundary conditions are not located at the base of the wind, as we mentioned earlier. An in-depth discussion of the shape of the asymmetrical absorption line is beyond the scope of this work. An observational treatment in the Seyfert galaxy NGC 3783 can be found in Ramírez et al. (2005). We leave the detailed description of infalling and outflowing real atoms and ionized species, such as O VII, O VIII, and Fe XXV, for future work. They are very important for our understanding of BHs.
. As the particle approaches the SMBH, the density increases and the final shape tends to be shifted more deeply towards the red. Figure 8 shows that the most asymmetrical line has f⋆ = 0.05 (bottom panel, solid red line), for which the high-energy radiation is weaker, which leaves the particle to reach higher velocities and a stronger asymmetry. On the other hand, we do not discuss the outflow profile (type 2 solution) because the boundary conditions are not located at the base of the wind, as we mentioned earlier. An in-depth discussion of the shape of the asymmetrical absorption line is beyond the scope of this work. An observational treatment in the Seyfert galaxy NGC 3783 can be found in Ramírez et al. (2005). We leave the detailed description of infalling and outflowing real atoms and ionized species, such as O VII, O VIII, and Fe XXV, for future work. They are very important for our understanding of BHs.
5. Estimated Bondi radius and application of mass accretion
An important application of our analysis is to quantify the differences between the true (rB) and estimated (re) Bondi radius as well as the true (Ṁrad) and estimated (Ṁe) accretion rate when the instrumental resolution is limited or the numerical resolution is inadequate at the sub-parsec scales. Following KCP16 and CP17, these differences as a function of radial distance from the central source are defined by the relations
for the radius and
for the accretion rate, where 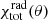 is the angle-dependent radiative factor we used. In Fig. 6 we show the estimated values of the Bondi radius for all models. For comparison the solid black line is the estimated Bondi radius for the classical Bondi accretion problem. At small radii, that is, at x = 0.001, model
is the angle-dependent radiative factor we used. In Fig. 6 we show the estimated values of the Bondi radius for all models. For comparison the solid black line is the estimated Bondi radius for the classical Bondi accretion problem. At small radii, that is, at x = 0.001, model 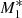 has an estimated Bondi radius of ≈0.64rB compared to model
has an estimated Bondi radius of ≈0.64rB compared to model 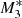 , which has re/rB ≈ 0.51 when the UV emission from the accretion disc dominates the radiation field. These values are somewhat lower than those resulting for models M2 and M3 with no spectral line driving, which have re/rB ≈ 0.68 and ≈0.6, respectively. Moreover, comparing the asymptotic behaviour of re/rB for the pure gravitational case (solid black line) given by re(x)/rB ∼ x3(γ − 1)/2 when x → 0+ (see Eq. (22) of KCP16), we find differences of ≈10%−40% between the classical and current generalized Bondi models. In addition, for models M1, M2, and
, which has re/rB ≈ 0.51 when the UV emission from the accretion disc dominates the radiation field. These values are somewhat lower than those resulting for models M2 and M3 with no spectral line driving, which have re/rB ≈ 0.68 and ≈0.6, respectively. Moreover, comparing the asymptotic behaviour of re/rB for the pure gravitational case (solid black line) given by re(x)/rB ∼ x3(γ − 1)/2 when x → 0+ (see Eq. (22) of KCP16), we find differences of ≈10%−40% between the classical and current generalized Bondi models. In addition, for models M1, M2, and 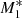 the ratio re/rB → 1 at x ≈ 0.1, while at larger radii all models have values of re/rB close to unity, as shown in Fig. 6 for x = 3.
the ratio re/rB → 1 at x ≈ 0.1, while at larger radii all models have values of re/rB close to unity, as shown in Fig. 6 for x = 3.
 |
Fig. 6. Estimated Bondi radius for all models. Models with M(τ)≠0 are represented by the solid lines, while models with M(τ) = 0 are depicted by the dashed lines. For comparison, the black solid line displays the asymptotic behaviour for the pure gravitational case. In the limit when x → ∞, re → rB. |
The estimated accretion rates for all models are displayed in Fig. 7 as compared with the asymptotic behaviour of the pure gravitational accretion at small radii given by Ṁe(x)/ṀB ∼ x−3(5−3γ)/4 (see Eq. (23) of KCP16). The radiative effects lead to an overestimation of the accretion rates. In particular at x = 0.001, models M2 and M3 with M(τ) = 0 have accretion rates that are from 2 to 5 times higher than those of models 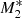 and
and 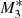 . The differences between these models grow up to a factor of 10 at x ≈ 3. The degree to which the accretion rates are overestimated compared to the classical Bondi problem is lower when the effects of line driving are ignored (in M1).
. The differences between these models grow up to a factor of 10 at x ≈ 3. The degree to which the accretion rates are overestimated compared to the classical Bondi problem is lower when the effects of line driving are ignored (in M1).
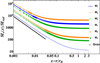 |
Fig. 7. Estimated accretion rate for all models. Models with M(τ)≠0 are represented by the solid lines, and models with M(τ) = 0 are depicted by the dashed lines. For comparison, the black solid line displays the asymptotic behaviour for the pure gravitational case. |
 |
Fig. 8. Predicted accretion absorption line shape for models |
Figure 9 shows the estimated values of the Bondi radius for models 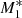 ,
, 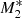 , and
, and 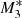 for the inflow solutions (alone). For the type 5 solutions the limit of re/rB when x → ∞ is no longer one, but deviates from it by about 10%. This occurs because rB looses its meaning for
for the inflow solutions (alone). For the type 5 solutions the limit of re/rB when x → ∞ is no longer one, but deviates from it by about 10%. This occurs because rB looses its meaning for 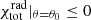 , which is precisely the case here. For completeness, Fig. 10 displays the accretion rates as a function of the radial distance from the SMBH (with y-linear scale). The accretion rates associated with the type 5 flows are close to those associated with the infalling material; the differences do not exceed about 3%.
, which is precisely the case here. For completeness, Fig. 10 displays the accretion rates as a function of the radial distance from the SMBH (with y-linear scale). The accretion rates associated with the type 5 flows are close to those associated with the infalling material; the differences do not exceed about 3%.
 |
Fig. 9. Estimated Bondi radius for all models with M(τ)≠0. The solid line shows |
 |
Fig. 10. Estimated accretion rate for all models with M(τ)≠0. The solid line shows |
A further important application of these semi-analytical models is the construction of proper initial conditions for studying the stability of the Bondi accretion flow (Foglizzo et al. 2005). In most simulations of accretion flows the accretor is assumed to be stationary. Small-scale density and velocity gradients that develop near it, which are the result of non-linear amplification of numerical noise, may lead to different flow patterns as the resolution is increased. This noise arises because mutually repulsive pressure forces do not cancel in all directions simultaneously, giving rise to non-radial velocities whose magnitudes are larger near the accretor. On the other hand, the use of standard artificial viscosity with a constant coefficient leads to spurious angular momentum advection in the presence of vorticity. However, the intrinsic noise generated by numerical effects is not sufficient to make the flow unstable at parsec scales, while it may become prominent in the proximity of the accretor at sub-parsec scales. On the other hand, the strength and type of the instability may also depend on the size of the accretor (Blondin & Raymer 2012), the Mach number, and the polytropic index γ. Understanding how these parameters can influence noise amplification at sub-parsec scales will shed light on the instability production mechanisms and the accretion rate for long-stage accretion systems.
6. Summary and conclusions
We have presented the classical Bondi accretion theory for the case of non-isothermal accretion processes onto an SMBH, including the effects of X-ray heating and the radiation force due to electron scattering and spectral lines. The radiation field was modelled following the recipe of P07, where an optically thick, geometrically thin, standard accretion disc is considered as a source of UV photons and a spherical central object as a source of X-ray emission. A semi-analytical solution for the radiative non-isothermal accretion onto an SMBH at the centre of galaxies was obtained using a procedure similar to that developed by Korol et al. (2016) (KCP16). A novel feature of our analysis is the angular dependence of the UV emission from the accretion disc, while the X-ray radiation from the central object was assumed to be isotropic. The influence of both types of radiation was evaluated for different flux fractions of the X-ray/central object radiation (f⋆) and the UV emission from the disc (fdisc) with and without the effects of spectral line driving for an incident angle 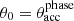 .
.
The main conclusions can be summarized as follows:
-
The ratio between the X-ray and the UV flux increases with increasing θ0. For θ0 = π/2, the radiation flux from the accretion disc vanishes and only the X-ray emission therefore contributes to the radiation flux.
-
When the radiation force due to spectral lines does not contribute to the heating, pure gravitational accretion onto the SMBH occurs when the X-ray emission intensity is strongest and participates to the same degree as the UV emission (i.e. f⋆ = fdisc = 0.5). As long as the UV emission dominates the X-ray heating, a transition from pure accretion to mathematical but non-trivial physical type 5 flows occurs.
-
When the radiation force due to spectral lines is taken into account, a transition from pure accretion to outflows always takes place independently of the intensity of the X-ray emission. However, as the UV emission dominates the X-ray heating, the angle of incidence for which the transition from pure accretion to outflow occurs and the radial distance from the SMBH for which the inflow and the outflow becomes supersonic both increase.
-
As the UV emission becomes stronger, the gas density close to the centre becomes higher. The same trend also applies to the cases where line driving is not considered, except when the X-ray luminosity is strong enough to suppress the outflow. In this case, only pure accretion takes place, and the central density achieves much higher values than the other models.
-
For our radiative non-isothermal Bondi accretion model, we also provide the exact formula for the Bondi radius bias re/rB as a function of the radial distance from the central accretor, the Mach number, the critical accretion parameter, and the total radiation luminosity. The exact formula for the mass accretion bias Ṁe/ṀB is also given in terms of re/rB.
-
The estimated values of the Bondi radius re are between ≈0.2 and ≈0.68 times the classical Bondi radius rB close to the accretor, and re → rB at large distances from the accretor (r ≳ 3rB).
-
The radiative effects produce an overestimation of the estimated accretion rates compared to the classical Bondi accretion rates. However, the degree of overestimation is lower when the effects of line driving are ignored for the M1 models.
-
Under the effects of line driving, the limit of re/rB (for
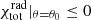 ) at large distances from the central accretor is no longer one, but deviates from unity by about 10%. On the other hand, the accretion rates associated with
) at large distances from the central accretor is no longer one, but deviates from unity by about 10%. On the other hand, the accretion rates associated with 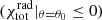 flows are close to those associated with the accreting material, with differences of ≲3%.
flows are close to those associated with the accreting material, with differences of ≲3%. -
The prediction of asymmetric pure absorption lines as seen in the line of sight of a distant observer serves as platform to construct more complex scenarios by adding emission components and/or including ionization structure to the interacting gas. This is interesting in light of the new-generation telescopes that are able to image galaxy centres, as well as for the spectroscopy of galaxy centres and the new developments in our understanding of black holes.
-
We have computed the radiative factor for a ξ10 pc = ξ(r = 10 pc) without temperature corrections although the hydrodynamical variables were taken to be temperature dependent. A future work will consider the temperature and ionization dependence.
We conclude by emphasizing that our results are useful for modelling proper initial conditions for time-dependent simulations of accretion flows onto massive black holes at galaxy centres. A further important application of our semi-analytical solutions is the stability of the Bondi accretion flow at sufficiently close distances from the accretor, where the stability of the flow is expected to be affected by the growth of low-density and velocity fluctuations. As a further step in this line of research, we plan to include the additional effects of the gravitational potential of the host galaxy (Korol et al. 2016) for Hernquist and Jaffe galaxy models (Ciotti & Pellegrini 2017), which are applicable to early-type galaxies.
For ultraluminous X-ray sources (ULXs) L ∼ 1046, nH ∼ 10(7 − 9) and ξ ∼ (1 − 10), r ∼ (1 − 10) pc (Pinto et al. 2019). Physically, this distance seems to be a plausible location for super-Eddington outflows to take place given the relationship between the hardness ratio and the ionization parameter as well as the role that radiation pressure might be playing in these objects.
The type 2 transonic solution exists but the boundary conditions are imposed for an accretion flow (i.e. at infinity Waters & Proga 2012).
Acknowledgments
JMRV thanks D. Proga for an in-depth discussion of the X-type solutions of the Bondi problem. J.K. acknowledges financial support by the Consejo Nacional de Ciencia y Tecnología (CONACyT), Mexico, under grant 283151. We are greatly indebted to the anonymous referee, who has raised a number of suggestions that have improved and clarified the content of the manuscript. IMPETUS is a collaboration project between the ABACUS-Centro de Matemática Aplicada y Cómputo de Alto Rendimiento of Cinvestav-IPN, the School of Physical Sciences and Nanotechnology, Yachay Tech University, and the Área de Física de Procesos Irreversibles of the Departamento de Ciencias Básicas of the Universidad Autónoma Metropolitana–Azcapotzalco (UAM-A) aimed at the SPH modelling of astrophysical flows. This work has been partially supported by Yachay Tech under the project for the use of the supercomputer QUINDE I and by UAM-A through internal funds. We are also grateful for the support from Cinvestav-Abacus, where part of this work was done.
References
- Barai, P. 2008, ApJ, 682, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Blondin, J. M., & Raymer, E. 2012, ApJ, 752, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Bondi, H. 1952, MNRAS, 112, 195 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Bondi, H., & Hoyle, F. 1944, MNRAS, 104, 273 [NASA ADS] [CrossRef] [Google Scholar]
- Castor, J. I., Abbott, D. C., & Klein, R. I. 1975, ApJ, 195, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Ciotti, L., & Ostriker, J. P. 2001, ApJ, 551, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Ciotti, L., & Pellegrini, S. 2017, ApJ, 848, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Ciotti, L., & Ziaee Lorzad, A. 2018, MNRAS, 473, 5476 [NASA ADS] [CrossRef] [Google Scholar]
- Contreras, E., Rincón, Á., & Ramírez-Velásquez, J. M. 2019, Eur. Phys. J. C, 79, 53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dannen, R. C., Proga, D., Kallman, T. R., & Waters, T. 2019, ApJ, 882, 99 [Google Scholar]
- Di Matteo, T., Springel, V., & Hernquist, L. 2005, Nature, 433, 604 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Event Horizon Telescope Collaboration (Akiyama, K., et al.) 2019, ApJ, 875, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Fabian, A. C. 1999, MNRAS, 308, L39 [NASA ADS] [CrossRef] [Google Scholar]
- Foglizzo, T., Galletti, P., & Ruffert, M. 2005, A&A, 435, 397 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Frank, J., King, A., & Raine, D. J. 2002, Accretion Power in Astrophysics: Third Edition (Cambridge University Press), 398 [Google Scholar]
- Gabbasov, R., Sigalotti, L. D. G., Cruz, F., Klapp, J., & Ramírez-Velasquez, J. M. 2017, ApJ, 835, 287 [NASA ADS] [CrossRef] [Google Scholar]
- Gebhardt, K., Bender, R., Bower, G., et al. 2000, ApJ, 539, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Germain, J., Barai, P., & Martel, H. 2009, ApJ, 704, 1002 [NASA ADS] [CrossRef] [Google Scholar]
- Higginbottom, N., Proga, D., Knigge, C., et al. 2014, ApJ, 789, 19 [Google Scholar]
- Hoyle, F., & Lyttleton, R. A. 1939, Proc. Camb. Philos. Soc., 35, 405 [Google Scholar]
- Kashi, A., Proga, D., Nagamine, K., Greene, J., & Barth, A. J. 2013, ApJ, 778, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Korol, V., Ciotti, L., & Pellegrini, S. 2016, MNRAS, 460, 1188 [NASA ADS] [CrossRef] [Google Scholar]
- Laor, A., Fiore, F., Elvis, M., Wilkes, B. J., & McDowell, J. C. 1997, ApJ, 477, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Li, Y., Hernquist, L., Robertson, B., et al. 2007, ApJ, 665, 187 [NASA ADS] [CrossRef] [Google Scholar]
- Magorrian, J., Tremaine, S., Richstone, D., et al. 1998, AJ, 115, 2285 [NASA ADS] [CrossRef] [Google Scholar]
- Michel, F. C. 1972, Ap&SS, 15, 153 [Google Scholar]
- Novak, G. S., Ostriker, J. P., & Ciotti, L. 2011, ApJ, 737, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Ostriker, J. P., Choi, E., Ciotti, L., Novak, G. S., & Proga, D. 2010, ApJ, 722, 642 [NASA ADS] [CrossRef] [Google Scholar]
- Pellegrini, S. 2005, MNRAS, 364, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Pinto, C., Mehdipour, M., Walton, D. J., et al. 2019, MNRAS, submitted [arXiv:1903.06174] [Google Scholar]
- Proga, D. 2000, ApJ, 538, 684 [NASA ADS] [CrossRef] [Google Scholar]
- Proga, D. 2003, ApJ, 592, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Proga, D. 2007, ApJ, 661, 693 [NASA ADS] [CrossRef] [Google Scholar]
- Proga, D., & Kallman, T. R. 2004, ApJ, 616, 688 [Google Scholar]
- Proga, D., Stone, J. M., & Kallman, T. R. 2000, ApJ, 543, 686 [NASA ADS] [CrossRef] [Google Scholar]
- Ramírez, J. M. 2013, A&A, 551, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ramírez, J. M., Bautista, M., & Kallman, T. 2005, ApJ, 627, 166 [NASA ADS] [CrossRef] [Google Scholar]
- Ramírez-Velasquez, J. M., Klapp, J., Gabbasov, R., Cruz, F., & Sigalotti, L. D. G. 2016, ApJS, 226, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Ramírez-Velasquez, J. M., Klapp, J., Gabbasov, R., Cruz, F., & Sigalotti, L. D. G. 2017, Communications in Computer and Information Science (Cham: Springer), 697, 374 [CrossRef] [Google Scholar]
- Ramírez-Velasquez, J. M., Sigalotti, L. D. G., Gabbasov, R., Cruz, F., & Klapp, J. 2018, MNRAS, 477, 4308 [NASA ADS] [CrossRef] [Google Scholar]
- Rybicki, G. B., & Lightman, A. P. 1979, Radiative Processes in Astrophysics (New York: Wiley-Interscience) [Google Scholar]
- Salpeter, E. E. 1964, ApJ, 140, 796 [CrossRef] [Google Scholar]
- Sigalotti, L. D. G., Cruz, F., Gabbasov, R., Klapp, J., & Ramírez-Velasquez, J. 2018, ApJ, 857, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Stevens, I. R., & Kallman, T. R. 1990, ApJ, 365, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Waters, T. R., & Proga, D. 2012, MNRAS, 426, 2239 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, R. 2015, Phys. Rev. D, 92, 084011 [NASA ADS] [CrossRef] [Google Scholar]
- Zheng, W., Kriss, G. A., Telfer, R. C., Grimes, J. P., & Davidsen, A. F. 1997, ApJ, 475, 469 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1. Angular dependence of the radiative force parameter for models M1, M2, and M3 (when M(τ) = 0; thin dashed lines) and models |
| In the text | |
 |
Fig. 2. Mach number of the inflow (solid lines) and outflow (dotted lines) solutions of Eq. (20) with M(τ)≠0. The supersonic part of the inflow solutions is depicted in orange, and the subsonic part is given in blue. In contrast, the supersonic outflow solution is depicted in blue and the subsonic one in orange. The vertical lines in each frame mark the position of the sonic radius. When radiation dominates, the gas will escape from the gravitational potential of the accretor. Upper, middle, and bottom frames: models with fdisc = 0.5, 0.8, and 0.95, respectively (see Table 1). |
| In the text | |
 |
Fig. 3. Density profiles of the radiative non-isothermal models with M(τ)≠0. The vertical lines mark the position of the sonic radius for each model. As the UV emission becomes stronger, the accreting gas becomes supersonic at larger radial distances from the SMBH, and the density becomes higher for x ≲ 0.5. |
| In the text | |
 |
Fig. 4. Mach number of the inflow (solid lines) and outflow (dotted lines) solutions of Eq. (20) with M(τ) = 0. The supersonic part of the inflow solutions are depicted in orange, and the subsonic part is given in blue. In contrast, the supersonic outflow solution is depicted in blue and the subsonic one in orange. The vertical lines in each frame mark the position of the sonic radius. When the radiation dominates, the gas escapes from the gravitational potential of the accretor. With no force multiplier, no winds are developed for f⋆ = fdisc = 0.5 (model M1). |
| In the text | |
 |
Fig. 5. Density profiles of the radiative non-isothermal models with M(τ) = 0. The vertical lines mark the position of the sonic radius for each model. As the UV emission becomes stronger, the accreting gas becomes supersonic at larger radial distances from the SMBH, while the density becomes higher for x ≲ 0.2. These trends apply only to models M2 and M3, while model M1, having an arbitrary θ0 and weaker UV emission, becomes supersonic at a much larger distance from the SMBH and achieves a much higher central densities than models M2 and M3. |
| In the text | |
 |
Fig. 6. Estimated Bondi radius for all models. Models with M(τ)≠0 are represented by the solid lines, while models with M(τ) = 0 are depicted by the dashed lines. For comparison, the black solid line displays the asymptotic behaviour for the pure gravitational case. In the limit when x → ∞, re → rB. |
| In the text | |
 |
Fig. 7. Estimated accretion rate for all models. Models with M(τ)≠0 are represented by the solid lines, and models with M(τ) = 0 are depicted by the dashed lines. For comparison, the black solid line displays the asymptotic behaviour for the pure gravitational case. |
| In the text | |
 |
Fig. 8. Predicted accretion absorption line shape for models |
| In the text | |
 |
Fig. 9. Estimated Bondi radius for all models with M(τ)≠0. The solid line shows |
| In the text | |
 |
Fig. 10. Estimated accretion rate for all models with M(τ)≠0. The solid line shows |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



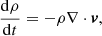
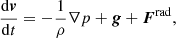
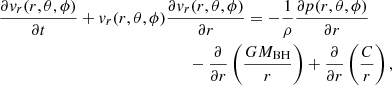
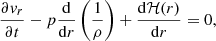
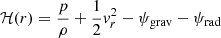
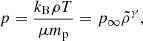
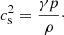
![$$ \begin{aligned} F_{r}^\mathrm{rad}(r)|_{\theta =\theta _{0}}=\frac{\sigma _{\rm T}L}{4\pi r^{2}cm_{\rm p}} \left[f_{\star }+2\cos \theta _{0}f_{\rm disc}(1+M(\tau ))\right], \end{aligned} $$](/articles/aa/full_html/2019/11/aa35917-19/aa35917-19-eq9.gif)
![$$ \begin{aligned} M(\tau )=k\tau ^{-\alpha }\left[\frac{(1+\tau _{\rm max})^{(1-\alpha )}-1}{\tau _{\rm max}^{(1-\alpha )}}\right], \end{aligned} $$](/articles/aa/full_html/2019/11/aa35917-19/aa35917-19-eq10.gif)
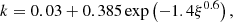
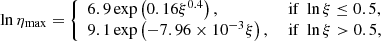
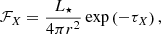
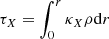
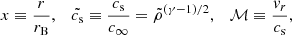
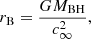
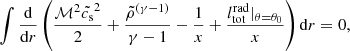
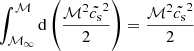
![$$ \begin{aligned}&\int _{\rho _{\infty }}^{\rho } \mathrm{d}\left[\frac{\tilde{\rho }^{(\gamma -1)}}{\gamma -1}\right]= \frac{1}{\gamma -1}\left[\tilde{\rho }^{(\gamma -1)}-1\right]\end{aligned} $$](/articles/aa/full_html/2019/11/aa35917-19/aa35917-19-eq22.gif)
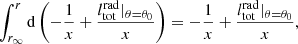
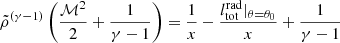
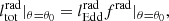
![$$ \begin{aligned} f^\mathrm{rad}|_{\theta =\theta _0}=f_{\star }+2\cos \theta _{0}f_{\rm disc}[1+M(\tau )]. \end{aligned} $$](/articles/aa/full_html/2019/11/aa35917-19/aa35917-19-eq27.gif)
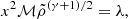
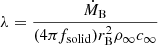
![$$ \begin{aligned} { g}(\mathcal{M} )=\Lambda f(x), \quad \mathrm{with}\quad \Lambda =\left[\chi _{\rm tot}^\mathrm{rad} |_{\theta =\theta _0}^{2}\lambda _{\rm cr}\right]^{2(1-\gamma )/(\gamma +1)}, \end{aligned} $$](/articles/aa/full_html/2019/11/aa35917-19/aa35917-19-eq32.gif)
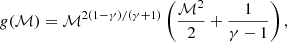
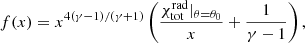
![$$ \begin{aligned}&\lambda _{\rm cr}=\frac{1}{4}\left(\frac{2}{5-3\gamma }\right)^{(5-3\gamma )/[2(\gamma -1)]}. \end{aligned} $$](/articles/aa/full_html/2019/11/aa35917-19/aa35917-19-eq37.gif)
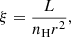
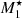
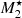

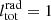
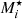
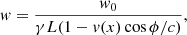
![$$ \begin{aligned} F_{\lambda }(x)=\exp \left[-A(x)\exp \left(-\frac{(\lambda (x)-\lambda _{0})^2}{\sigma ^2}\right)\right], \end{aligned} $$](/articles/aa/full_html/2019/11/aa35917-19/aa35917-19-eq90.gif)
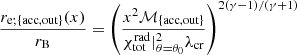
![$$ \begin{aligned} \frac{\dot{M}_{\mathrm{e};\{\mathrm{acc},\mathrm{out}\}}(x)}{\dot{M}_{\rm rad}}= \frac{1}{\chi _{\rm tot}^\mathrm{rad}|_{\theta =\theta _0}^2}\left[\frac{r_{\mathrm{e};\{\mathrm{acc},\mathrm{out}\}}(x)}{r_{\rm B}}\right]^{-(5-3\gamma )/[2(\gamma -1)]} \end{aligned} $$](/articles/aa/full_html/2019/11/aa35917-19/aa35917-19-eq94.gif)