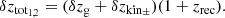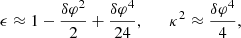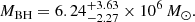| Issue |
A&A
Volume 662, June 2022
|
|
|---|---|---|
| Article Number | L9 | |
| Number of page(s) | 6 | |
| Section | Letters to the Editor | |
| DOI | https://doi.org/10.1051/0004-6361/202243653 | |
| Published online | 24 June 2022 | |
Letter to the Editor
A general relativistic estimation of the black hole mass-to-distance ratio at the core of TXS 2226–184
1
Instituto de Física Luis Rivera Terrazas, Benemérita Universidad Autónoma de Puebla, CP 72570 Puebla, Mexico
e-mail: aherrera@ifuap.buap.mx
2
Instituto de Física y Matemáticas, Universidad Michoacana de San Nicolás de Hidalgo, Edificio C–3, Ciudad Universitaria, CP 58040 Morelia, Michoacán, Mexico
Received:
28
March
2022
Accepted:
7
June
2022
In this work we make use of a general relativistic method to estimate the mass-to-distance ratio M/D = 3.54−0.18+0.20 × 104 M⊙ Mpc−1 of the black hole hosted at the core of the active galactic nucleus of TXS 2226–184, along with its right ascension offset and the recession redshift (velocity) of the galaxy. Our statistical fit is based on the frequency shift of photons emitted by water masers and their orbital positions when circularly revolving around the black hole center within the accretion disk of the active galactic nucleus. By taking a previously reported distance to the galaxy into account, we compare the result of the black hole mass fit to an estimate based on a mass-luminosity correlation. We find that the black hole mass at the core of TXS 2226–184 obtained with the aid of the statistical fit using the general relativistic method, M = 3.67−0.18+0.20 × 106 M⊙, is approximately 0.6 times the black hole mass, MBH = 6.24−2.27+3.63 × 106 M⊙, which was computed with the mass–luminosity correlation.
Key words: black hole physics / masers / galaxies: high-redshift / galaxies: kinematics and dynamics / galaxies: nuclei / galaxies: luminosity function / mass function
© A. Villalobos-Ramírez et al. 2022
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe-to-Open model. Subscribe to A&A to support open access publication.
1. Introduction
Over 100 years ago, Albert Einstein published his theory of general relativity (Einstein 1915). Two months later, Karl Schwarzschild published a solution to Einstein’s field equations (Schwarzschild 1916), describing the gravitational field outside a spherically symmetric and static body. This solution is useful to describe the spacetime curvature generated by astrophysical objects such as stars and it was later understood to describe a black hole (BH). A BH is a region of spacetime where the gravitational field is so strong that not even light can escape beyond the event horizon. A Schwarzchild BH is fully characterized by its mass. In 1963, Kerr constructed a solution that describes the gravitational field of a rotating BH (Kerr 1963), which is completely characterized by its mass and angular momentum.
In recent years, there has been important observational evidence of the existence of BHs. For instance, the observation of the stars orbiting with a very short period around Sgr A* in the center of our galaxy indicates the presence of a supermassive BH Ghez et al. (1998, 2008), Genzel et al. (1997, 2010), Do et al. (2019), and Abuter et al. (2020), the detection of gravitational waves produced by the merger of BHs by LIGO-Virgo Collaborations Abbott et al. (2016, 2020a,b), and the imaging of the M 87 and SgrA* BH shadows by the EHT collaboration Event Horizon Telescope Collaboration (2019, 2022).
Since BHs do not emit electromagnetic radiation, one way to study these enigmatic entities consists in observing their influence on stars, accretion disks, gas particles, etc. that orbit them. For certain astrophysical systems, the positions of the orbiting bodies and the redshift and blueshift of the photons they emit are available and can be measured. For this reason, several models that relate these observational quantities of the orbiting objects to the mass and the mass-to-distance ratio of the BH have been developed.
Water megamasers, emitting at 22 GHz, are astrophysical objects that have been found within active galactic nuclei (AGNs), where they orbit central BHs (Claussen et al. 1984). The prefix “mega” refers to the intense luminosity emitted by the water maser in the AGN (L > 10 L⊙) compared to the luminosity of galactic masers (L < L⊙), which are associated with star-forming regions (Genzel & Downes 1977).
Very long baseline interferometry (VLBI) is an accurate technique for observing the positions and displacements of these maser features, as it gives us appropriate submilliarcsecond resolution for objects at (sub)parsec distances from the center of active galaxies. Telescopes, such as the Green Bank Telescope, the NRAO Very Long Baseline Array (VLBA)1, the European VLBI Network (EVN)2, and the Effelsberg 100 m one Reid et al. (2009), Braatz et al. (2010), and Kuo et al. (2011), provide us with observational data of positions and redshifts associated with the megamasers that allow us to estimate the mass of their central BH within an appropriate model.
In Herrnstein et al. (2005), the authors used a dynamic Keplerian model with relativistic corrections for maser features to fit the mass of the BH hosted at the core of the NGC 4258 galaxy. This modeling related the radial velocity of water megamasers to the observed redshift of the emitted photons by making use of the optical definition of the redshift. The Newtonian approach works accurately when the object is far enough from the gravitational source, but when the orbiting objects get close enough to the BH event horizon, the general relativistic effects become stronger and relevant. Thus, when this happens, the redshift of the photons begins to have important general and special relativistic contributions.
A model for test particles orbiting a Kerr BH was presented in Herrera-Aguilar & Nucamendi (2015). In this formalism, the influence of the BH on the curvature of spacetime was taken into account, and therefore the so-called gravitational redshift was included in the total redshift of photons emitted by particles orbiting the BH.
In Nucamendi et al. (2021), the authors used a simplified version of the latter model and considered a Schwarzschild BH with water megamasers orbiting the AGN of NGC 4258. The authors estimated the mass-to-distance ratio of the BH at the galactic core of this galaxy as well as its peculiar redshift using a general relativistic approach. The peculiar redshift is related to the peculiar velocity of the galaxy with respect to the distant observer using the same optical definition.
Another way to estimate the BH mass without using a model based on gravity relies on a correlation between the mass of the BH and the bulge luminosity MBH − Lbulge of the host galaxy (Kormendy & Ho 2013). It is important to note that this correlation uses the K band in the near-infrared instead of the visible spectrum. This correlation was initially based on the study of disk galaxies, but it also works for elliptical galaxies because they are morphologically equivalent to the bulge of disk galaxies.
One of the brightest known H2O maser sources was discovered in the AGN of the TXS 2226–184 galaxy using the Effelsberg telescope (Koekemoer et al. 1995). The isotropic luminosity associated with this water maser is so large, L = 6100 ± 900 L⊙ (Koekemoer et al. 1995), that it is called a “gigamaser”. The distance to TXS 2226–184 is D = 103.8571 ± 0.2606 Mpc3 as a result of applying Hubble’s law to the reported systemic velocity Vlsr, radio = 7270 ± 18.24 km s−1 in Taylor et al. (2002) and Surcis et al. (2020) and assuming H0 = 70 km s−1 Mpc−1 Kuo et al. (2018, these authors did not report uncertainties taken into account for the Hubble constant value). TXS 2226–184 has been optically classified as an elliptical galaxy (Koekemoer et al. 1995).
In Ball et al. (2005), the authors observed with the VLBA seven H2O maser emission clusters in TXS 2226–184. The clusters were linearly distributed from the northeast to the southwest with the position angle = +25°. The observational maser data have five redshifted maser features and two blueshifted maser features, where only one blueshifted maser was along the linear distribution (the most southwest maser feature), and the other one was about 7 mas southeast of the linear distribution. Given these features, the authors associated the distribution of the maser clusters with a parsec-scale, rotating disk, where the farthest blueshifted maser was situated completely outside the disk. However, the data reported in Ball et al. (2005) did not provide absolute positions of the maser features.
In Surcis et al. (2020), the authors made new observations of the H2O gigamaser in TXS 2226–184 with the VLBA (one epoch) and the EVN (two epochs). The authors detected six maser features in epoch 2017.45 (VLBA), one in epoch 2017.83 (EVN), and two in epoch 2018.44 (EVN). In the data corresponding to epoch 2017.45 (VLBA), only one blueshifted maser feature was detected, while the other five maser features were redshifted with respect to the systemic velocity of TXS 2226–184. In addition, the authors provided absolute positions of the maser features.
Most of the masers located in the accretion disks of supermassive BHs are megamasers. Estimates of BH masses using megamaser dynamics are on the order of 106 − 107 M⊙. So far, no estimate of the mass of central BHs in galaxies hosting a gigamaser has been made, leaving the question open of whether the high luminosity of the maser is related to a central BH mass of magnitude greater than 106 − 107 M⊙. New observations of the gigamaser made with the VLBA have been published in Surcis et al. (2020) and, in principle, they give us the opportunity to investigate whether there is a connection between its intense luminosity and the mass of the central BH.
2. General relativistic model
Here we assume a static and spherically symmetric spacetime. Thus, we used the Schwarzschild metric (in natural units):
where m = GM/c2 and M is the BH mass.
The general relativistic model which we used was developed in Nucamendi et al. (2021). We consider that massive test particles (photon sources such as stars, masers, and other bodies) follow a geodesic path. The geodesic motion of massive test particles is described by the four-velocity Uμ = (Ut, Ur, Uθ, Uφ) normalized to unity UμUμ = −1.
From this relation, we obtain an equation similar to the conservation law of energy for a nonrelativistic particle with energy E2/2. For the special case of equatorial and circular orbits, the expression for the four-velocity components simplifies since Ur = 0 = Uθ. Therefore,
where the ± signs correspond to the angular velocity direction of the orbiting object.
The photons emitted by the test particles have a four-momentum kμ = (kt, kr, kθ, kφ). These photons move along null and equatorial geodesics (kμkμ = 0), so that the emitted and detected frequencies can be written in terms of the parameters of the metric.
Emitted photons experience a Schwarzschild redshift or blueshift on their way from the source bodies toward a static observer, which stands far away from the BH (Uμ|d = (1, 0, 0, 0)|d; rd → ∞), and read as follows:
where the subscripts (1/2) correspond to (+/−), the subscript (e) refers to the emitter, (d) refers to the detector, and ω is the photon frequency. Here, b∓ is the light bending (deflection) parameter to the right and left of the line of sight; zg and zkin± represent the gravitational and kinematic redshifts, respectively, and are expressed as follows:
where the ± signs in Eq. (5) correspond to an approaching and receding object with respect to a far away observer, yielding the kinematic redshift zkin+ and blueshift zkin−.
Hereinafter we use the approximation Θ ≈ re/D for the angular distance between a given maser and the BH position, where rd = D is the distance from the detector to the BH. Then the gravitational and kinematic redshift become the following:
For a full description of realistic systems, we must take into account the recession redshift zrec given by the composition of the peculiar redshift, zp, related to the peculiar velocity of the galaxy with respect to the observer, and the cosmological redshift, zcosm, associated with the expansion of the universe when the galaxy is within the Hubble flow. Both of these redshifts have a different nature. Thus the total redshift is given by the following composition (Davis & Scrimgeour 2014):
Strictly speaking, one should consider a Schwarzschild-Friedmann-Robertson-Walker metric in order to take into account the expansion of the universe in the BH geometry that generates the cosmological redshift. However, we do not have the expression for the redshift for such a metric at hand, and as a first approximation we made use of the Schwarzschild background.
The peculiar redshift is defined through the special relativistic boost (Rindler 1982)
where vp ≡ c zp and vpcosα is the radial component of the peculiar velocity of the galaxy with respect to the observer (see Fig. 1). Thus, in principle the α angle encodes the transversal motion of the galaxy with respect to the line of sight.
 |
Fig. 1. Motion of the galaxy hosting the BH with respect to a distant observer. The galaxy has a peculiar velocity vp and a cosmological one vcosm. The composition of the corresponding redshifts yields the observed recession redshift related to the velocity vrec. |
3. Mass–luminosity correlation
Increased availability in BH mass demography has led to the observation that there appears to be a close correlation between the BH mass and the bulge properties of the host galaxy. The most studied correlations of bulge properties with BH masses are given by the mass-velocity dispersion correlation MBH − σ*Gebhardt et al. (2000) and Ferrarese & Merritt (2000) and the mass–luminosity correlation MBH − LbulgeDressler et al. (1989), Kormendy & Richstone (1995), and Marconi & Hunt (2003). In Kormendy & Richstone (1995), the authors found that the BH masses show a correlation with the absolute blue luminosity of the host bulge for eight galaxies. In Marconi & Hunt (2003), luminosity was taken in the K band centered on 2.2 μm (in the near-infrared 136 THz range) instead of the blue luminosity because the scatter in the first band is smaller than in the second one.
For an overview of the MBH − Lbulge correlation, followed by a larger sample of galaxies of a different type and distinct BH masses hosted at their center, readers can refer to Sect. 6 in Kormendy & Ho (2013). In the case of elliptical galaxies, we must consider their total luminosity because these galaxies are morphologically equivalent to the bulge component of disk galaxies. The next equation shows the correlations of MBH with LK, bulge (Kormendy & Ho 2013):
where LK, bulge is the bulge luminosity and LK⊙ is the solar luminosity in the K band.
4. Observation of the H2O gigamaser in TXS 2226–184
In this Letter, we consider the VLBI observations of gigamaser features in the AGN of TXS 2226–184. We use the data reported by Taylor et al. (2002) and Surcis et al. (2020). The latter authors measured the redshift of photons emitted at the points of maximum emission and their absolute positions with errors lesser than 1 milliarcsecond. According to these authors, the TXS 2226–184 galaxy is located at a distance D = 103.85 ± 0.26 Mpc with an adopted center at  ,
, 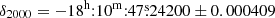 , with peculiar velocity Vlsr, radio = 7270 ± 18.24 km s−1. We used the observations of redshift and masers positions corresponding to VLBA data epoch 2017.45 on June 12, 2017. The VLBA provides an angular resolution of 0.2 miliarcsec (mas) and spectral resolution of 1 km s−1 at 22 GHz. The observational data of the maser were sparse, with only six maser features reported, five redshifted, and only one blueshifted. Despite the minimal quantity of data, we still can perform a statistical fit to estimate the mass-to-distance ratio of the central BH of this galaxy.
, with peculiar velocity Vlsr, radio = 7270 ± 18.24 km s−1. We used the observations of redshift and masers positions corresponding to VLBA data epoch 2017.45 on June 12, 2017. The VLBA provides an angular resolution of 0.2 miliarcsec (mas) and spectral resolution of 1 km s−1 at 22 GHz. The observational data of the maser were sparse, with only six maser features reported, five redshifted, and only one blueshifted. Despite the minimal quantity of data, we still can perform a statistical fit to estimate the mass-to-distance ratio of the central BH of this galaxy.
5. Statistical fit with our general relativistic model
The observations indicate that a set of water maser clouds is allocated on the accretion disk of a central BH hosted at the AGN of the galaxy TXS 2226–184. These features lie on the equatorial plane since we see the disk edge-on, and we shall assume that their motion is circular around the BH. Therefore we can make use of Eq. (7) to model their total redshifts and blueshifts, which are directly observed.
To fit the parameters, we used the least-squares estimation χ2 by a Bayesian statistical fit based on the Markov–chain Monte Carlo scheme applied to the maser data using the general relativistic formalism. We emphasize that we applied our fits to directly measured general relativistic invariant quantities.
The parameters we fit are the mass-to-distance ratio M/D, the right ascension (RA) offset x0 of the BH, and the recession redshift of the galaxy zrec. The position data of the maser features reported in Surcis et al. (2020) are presented by considering the brightest maser as a reference. Instead of using a reference maser, we propose a new reference origin at the geometric center of the maser system (see Fig. 2), so that the fitted BH position will be estimated with a reference to that point. However, by varying y0 within the observed height of the disk, we see that the estimate of M/D changes at the third significant figure after the decimal point in comparison to the estimation with y0 = 0 mas. This change is well behind the M/D uncertainty and reveals the thin character of the disk, implying that y0 does not influence the estimation of this quantity. Indeed we shall assume that masers do not lie completely along the midline, but that they are uniformly scattered about it with a scattering angle δφ and that the disk inclination θ0 is parameterized by the polar angle toward the equatorial plane.
 |
Fig. 2. View of the rotated H2O maser system in TXS 2226–184. The star indicates the origin, the blue dot corresponds to the blueshifted maser, and red dots indicate the redshifted masers (Surcis et al. 2020). |
Now, we present the χ2 of the general relativistic model based on Herrnstein et al. (2005) and Nucamendi et al. (2021):
where the first term in the numerator refers to the observed redshift and the remaining terms are related to our model. In the denominator, 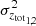 is the error associated with the total redshift. This quantity is |δztot1, 2|2 and means the variation of the total redshift as shown in Nucamendi et al. (2021) is as follows:
is the error associated with the total redshift. This quantity is |δztot1, 2|2 and means the variation of the total redshift as shown in Nucamendi et al. (2021) is as follows:
Following the latter work, we considered the redshift errors caused by the errors in the positions so that ![$ \delta z_{\mathrm{g}} = \left(1+z_{\mathrm{g}}\right)^{3}\left[\dfrac{-3M}{2r^2}\right]\delta r $](/articles/aa/full_html/2022/06/aa43653-22/aa43653-22-eq18.gif) and
and ![$ \delta z_\mathrm{kin_{\pm}} = \epsilon \sin{\theta_0}\left(z_\mathrm{kin_{\pm}}\right)^{3}\left[\dfrac{6M^2-r^2}{2Mr^2}\right]\delta r $](/articles/aa/full_html/2022/06/aa43653-22/aa43653-22-eq19.gif) , where
, where  and (xi, yi) is the position of the ith megamaser on the sky and δx and δy are their respective errors. The quantities ϵ and κ refer to the spread of the maser features by the azimuth angle (Herrnstein et al. 2005)
and (xi, yi) is the position of the ith megamaser on the sky and δx and δy are their respective errors. The quantities ϵ and κ refer to the spread of the maser features by the azimuth angle (Herrnstein et al. 2005)
where the first expansion corresponds to the cosine function of the azimuthal angle φ and κ denotes the induced uncertainties of the maser scattering under the assumption that φ ≪ 1 and φ ∼ δφ. The observed data were rotated by an angle of −87° to fit the positions on the horizontal axis, and we considered an error propagation related to the rotation, according to the following formula:
where xrot, yrot are the rotated positions, σx, y are the nonrotated uncertainties, and σxrot, yrot are the rotated ones.
6. Results
We have obtained two different estimates for the mass of the BH in TXS 2226–184 based on two different approaches being consistent between them. The estimate based on the motion of the masers and the frequency shift of the photons they emit is more precise. It is the first reliable estimate of the mass-to-distance ratio of the central BH of this galaxy.
6.1. General relativistic model
This method allowed us to make a statistical fit with good accuracy of the mass-to-distance ratio (see Table 1) despite the fact that there are few pieces of data from the masers. We also find that our model provides a good fit to the data, yielding a value of the reduced  with a maser scattering angle δφ = 0.35 rad and assuming a completely edge-on view of the accretion disk (θ0 = π/2 rad). Table 1 shows the values for the best fit and the uncertainties with 1σ confidence associated with each of the estimated parameters. In Fig. 3 we present the posterior distribution of the general relativistic Bayesian fit with flat priors for the parameters of the central BH at the core of TXS 2226–184.
with a maser scattering angle δφ = 0.35 rad and assuming a completely edge-on view of the accretion disk (θ0 = π/2 rad). Table 1 shows the values for the best fit and the uncertainties with 1σ confidence associated with each of the estimated parameters. In Fig. 3 we present the posterior distribution of the general relativistic Bayesian fit with flat priors for the parameters of the central BH at the core of TXS 2226–184.
Posterior parameters for the BH located at the core of TXS 2226–184.
 |
Fig. 3. Posterior distribution of the general relativistic Bayesian fit. Here the BH mass-to-distance ratio M/D is expressed in ×104 M⊙ Mpc−1, x0 is expressed in mas, and vrec is in km s−1. Contour levels correspond to 1σ and 2σ confidence regions. We have considered flat priors for M/D : [0, 200] × 104 M⊙ Mpc−1, x0 : [−1.5, 1.5] mas, and zrec : [0, 0.03] (vrec : [0, 9000] km s−1). |
In Table 1 we also display the most probable value of the redshift zrec (and its associated velocity vrec) that is related with the recessional motion of the galaxy. The recession velocity we obtain is consistent with the systemic velocity of the galaxy previously reported in Taylor et al. (2002). In fact, what the statistical fit estimates is the recession redshift, which is the composition of the cosmological and the peculiar redshifts, despite the fact that these quantities have a very different nature. Since both of these redshifts do not depend on the position of the masers, they are degenerate and cannot be estimated separately.
If we use the distance to the BH reported in Taylor et al. (2002)D = 103.85 ± 0.26 Mpc, we get the following BH mass estimate:
We can also use this model to calculate the gravitational redshift of each maser. Below in Table 2 we display the gravitational redshift for the two closest masers to the BH.
Gravitational redshift for the masers closest to the central BH.
6.2. BH mass–luminosity correlation
In Koekemoer et al. (1995), the authors measured the luminosity of the TXS 2226–184 galaxy in the K band; the adopted luminosity is LK = 2.5 × 109 L⊙ with no reported uncertainties. In this framework, we accordingly substituted this reported luminosity into Eq. (8), thus, the BH mass estimate reads as follows:
Using the mass–luminosity method, we get a mass of the same order of magnitude as the estimate using the method of general relativity. However, we get a substantial uncertainty compared to that estimate, which is in fact an order of magnitude larger. Thus, by comparing these results, we see that a fit based on the redshift of the particles is more precise and reliable than using estimates based on the galaxy properties such as luminosity.
7. Conclusions and discussion
Our general relativistic approach provides estimates for the mass-to-distance ratio of the BH hosted at the AGN of TXS 2226–184 ( Mpc−1) as well as for its RA offset, the recession redshift of the host galaxy, and its associated velocity. Furthermore, this model also allowed us to quantify the gravitational redshift of each of the maser features; we calculated it for the two closest masers to the central BH of this galaxy. The gravitational redshift obtained for each of the gigamasers is one order of magnitude smaller than the detector sensitivity, implying that this quantity cannot be currently detected in an unambiguous manner in this astrophysical system.
Mpc−1) as well as for its RA offset, the recession redshift of the host galaxy, and its associated velocity. Furthermore, this model also allowed us to quantify the gravitational redshift of each of the maser features; we calculated it for the two closest masers to the central BH of this galaxy. The gravitational redshift obtained for each of the gigamasers is one order of magnitude smaller than the detector sensitivity, implying that this quantity cannot be currently detected in an unambiguous manner in this astrophysical system.
Starting from our estimate of the mass-to-distance ratio of the BH located at the core of TXS 2226–184 and the distance to this galaxy based on a previous work (Taylor et al. 2002), we obtain  . Therefore, TXS 2226–184 hosts a BH with a mass of the same order expected for BHs hosted in galaxies associated with megamaser emission. This result allows us to conclude that the high luminosity of the gigamaser is not related to a more massive central BH.
. Therefore, TXS 2226–184 hosts a BH with a mass of the same order expected for BHs hosted in galaxies associated with megamaser emission. This result allows us to conclude that the high luminosity of the gigamaser is not related to a more massive central BH.
By comparing the results obtained for the mass of the BH hosted in TXS 2226–184 (see Eqs. (12) and (13)), we find that the mass obtained from the MBH − LK, bulge correlation is approximately 1.6 times the mass obtained from the statistical fit using the general relativistic method. Finally, we note that the accuracy of the results differs by an order of magnitude, with the relativistic fit being the most accurate. However, these results are not mutually exclusive due to the uncertainties of the estimate based on the mass–luminosity correlation. Although less accurate, the MBH − Lbulge correlation is a good first approximation for systems for which there is no relevant data to make use of the general relativistic model.
Among the possible systematic errors of our modeling, one could consider modifications of the edge-on view and a warped disk, in particular. By performing small variations to the inclination disk parameter θ0 (up to 5°)4, the M/D estimation changes on the order of 1%, which is well behind the uncertainty of this ratio. According to Eq. (9), the warping of a disk is correlated with the M/D parameter. By considering a linear inclination warping along the radius of the disk, and performing variations in the inclination gradient (up to 0.04 rad/mas based on the masers distribution), the M/D estimation is altered around 5% and the corresponding reduced  .
.
The European VLBI Network (EVN) is a network of radio telescopes located primarily in Europe and Asia, with additional antennas in South Africa and Puerto Rico. Support for proposal preparation, scheduling, and correlation of EVN projects is provided by the Joint Institute for VLBI ERIC (JIVE); ERIC stands for the European Research Infrastructure Consortium.
In Kuo et al. (2018), the reported distance to TXS 2226–184 is D = 107.1 Mpc; however, since this distance has no associated uncertainties, we cannot use this result to estimate the value of the BH mass with properly propagated errors.
According to Kuo et al. (2011) and Darling (2017), if a thin disk is inclined by more than ∼5° from an edge-on view, the masers will be no longer beamed toward us.
Acknowledgments
The authors are grateful to D.E. Villaraos-Serés for fruitful discussions and to FORDECYT-PRONACES-CONACYT for support under grant No. CF-MG-2558591; U.N. also was supported under grant CF-140630. A.H.-A. and U.N. thank SNI and PROMEP-SEP and were supported by grants VIEP-BUAP No. 122 and CIC-UMSNH, respectively. O.G.-R. and A.V.-R. acknowledge financial assistance from CONACYT through PhD grants No. 885032 and No. 1007718, respectively.
References
- Abbott, B. P., Abbott, R., Abbott, T., et al. 2016, Phys. Rev. Lett., 116, 061102 [CrossRef] [PubMed] [Google Scholar]
- Abbott, R., Abbott, T., Abraham, S., et al. 2020a, Phys. Rev. Lett., 125, 101102 [Google Scholar]
- Abbott, R., Abbott, T., Abraham, S., et al. 2020b, Phys. Rev. D, 102, 043015 [NASA ADS] [CrossRef] [Google Scholar]
- Abuter, R., Amorim, A., Bauböck, M., et al. 2020, A&A, 636, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ball, G. H., Greenhill, L. J., Moran, J. M., Zaw, I., & Henkel, C. 2005, in Future Directions in High Resolution Astronomy, eds. J. Romney, & M. Reid, ASP Conf. Ser., 340, 235 [NASA ADS] [Google Scholar]
- Braatz, J., Reid, M., Humphreys, E., et al. 2010, ApJ, 718, 657 [NASA ADS] [CrossRef] [Google Scholar]
- Claussen, M., Heiligman, G., & Lo, K. 1984, Nature, 310, 298 [NASA ADS] [CrossRef] [Google Scholar]
- Darling, J. 2017, ApJ, 837, 100 [NASA ADS] [CrossRef] [Google Scholar]
- Davis, T. M., & Scrimgeour, M. I. 2014, MNRAS, 442, 1117 [NASA ADS] [CrossRef] [Google Scholar]
- Do, T., Hees, A., Ghez, A., et al. 2019, Science, 365, 664 [Google Scholar]
- Dressler, A., Osterbrock, D., & Miller, J. 1989, IAU Symp., 134, 217 [NASA ADS] [Google Scholar]
- Einstein, A. 1915, Deutsche Akademie der Wissenschaften zu Berlin, Berlin, 844 [Google Scholar]
- Event Horizon Telescope Collaboration (Akiyama, K., et al.) 2019, ApJ, 875, L1 [Google Scholar]
- Event Horizon Telescope Collaboration (Akiyama, K., et al.) 2022, ApJ, 930, L14 [NASA ADS] [CrossRef] [Google Scholar]
- Ferrarese, L., & Merritt, D. 2000, ApJ, 539, L9 [Google Scholar]
- Gebhardt, K., Bender, R., Bower, G., et al. 2000, ApJ, 539, L13 [Google Scholar]
- Genzel, R., & Downes, D. 1977, A&AS, 30, 145 [NASA ADS] [Google Scholar]
- Genzel, R., Eckart, A., Ott, T., & Eisenhauer, F. 1997, MNRAS, 291, 219 [NASA ADS] [CrossRef] [Google Scholar]
- Genzel, R., Eisenhauer, F., & Gillessen, S. 2010, Rev. Mod. Phys., 82, 3121 [Google Scholar]
- Ghez, A. M., Klein, B., Morris, M., & Becklin, E. 1998, ApJ, 509, 678 [NASA ADS] [CrossRef] [Google Scholar]
- Ghez, A. M., Salim, S., Weinberg, N., et al. 2008, AJ, 689, 1044 [NASA ADS] [CrossRef] [Google Scholar]
- Herrera-Aguilar, A., & Nucamendi, U. 2015, Phys. Rev. D, 92, 045024 [NASA ADS] [CrossRef] [Google Scholar]
- Herrnstein, J., Moran, J. M., Greenhill, L. J., & Trotter, A. S. 2005, ApJ, 629, 719 [NASA ADS] [CrossRef] [Google Scholar]
- Kerr, R. P. 1963, Phys. Rev. Lett., 11, 237 [Google Scholar]
- Koekemoer, A. M., Henkel, C., Greenhill, L. J., et al. 1995, Nature, 378, 697 [NASA ADS] [CrossRef] [Google Scholar]
- Kormendy, J., & Ho, L. C. 2013, ARA&A, 51, 511 [Google Scholar]
- Kormendy, J., & Richstone, D. 1995, ARA&A, 33, 581 [Google Scholar]
- Kuo, C., Braatz, J., Condon, J., et al. 2011, ApJ, 727, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Kuo, C., Constantin, A., Braatz, J., et al. 2018, ApJ, 860, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Marconi, A., & Hunt, L. K. 2003, ApJ, 589, L21 [Google Scholar]
- Nucamendi, U., Herrera-Aguilar, A., Lizardo-Castro, R., & López-Cruz, O. 2021, ApJ, 917, L14 [NASA ADS] [CrossRef] [Google Scholar]
- Reid, M., Braatz, J., Condon, J., et al. 2009, ApJ, 695, 287 [NASA ADS] [CrossRef] [Google Scholar]
- Rindler, W. 1982, Introduction to Special Relativity (Oxford: Oxford University Press) [Google Scholar]
- Schwarzschild, K. 1916, Sitzungsberichte der Königlich Preußischen Akademie der Wissenschaften Berlin, 189 [Google Scholar]
- Surcis, G., Tarchi, A., & Castangia, P. 2020, A&A, 637, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Taylor, G. B., Peck, A. B., Henkel, C., et al. 2002, ApJ, 574, 88 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1. Motion of the galaxy hosting the BH with respect to a distant observer. The galaxy has a peculiar velocity vp and a cosmological one vcosm. The composition of the corresponding redshifts yields the observed recession redshift related to the velocity vrec. |
| In the text | |
 |
Fig. 2. View of the rotated H2O maser system in TXS 2226–184. The star indicates the origin, the blue dot corresponds to the blueshifted maser, and red dots indicate the redshifted masers (Surcis et al. 2020). |
| In the text | |
 |
Fig. 3. Posterior distribution of the general relativistic Bayesian fit. Here the BH mass-to-distance ratio M/D is expressed in ×104 M⊙ Mpc−1, x0 is expressed in mas, and vrec is in km s−1. Contour levels correspond to 1σ and 2σ confidence regions. We have considered flat priors for M/D : [0, 200] × 104 M⊙ Mpc−1, x0 : [−1.5, 1.5] mas, and zrec : [0, 0.03] (vrec : [0, 9000] km s−1). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.





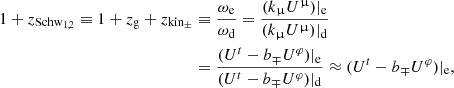
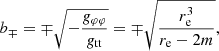
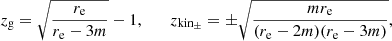
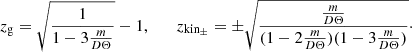



![$$ \begin{aligned} \chi ^2 = \sum _{k=1} \frac{\left[\frac{v_{k,\mathrm{obs}}}{c}-(1+z_{\rm g}+ \epsilon {\sin {\theta _0}}\; z_{\rm kin_{\pm }}){(1+z_{\rm rec})}+1\right]^2}{\sigma _{z_{\rm tot_{1,2}}}^{2} + {{\kappa }}^{2} z_{\rm kin_{\pm }}^{2} \sin ^{2}{\theta _0}{(1+z_{\rm rec})^2}}, \end{aligned} $$](/articles/aa/full_html/2022/06/aa43653-22/aa43653-22-eq15.gif)