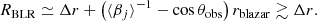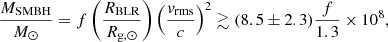| Issue |
A&A
Volume 631, November 2019
|
|
|---|---|---|
| Article Number | A4 | |
| Number of page(s) | 8 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201935904 | |
| Published online | 11 October 2019 | |
Long-term optical spectroscopic variations in blazar 3C 454.3
1
Nicolaus Copernicus Astronomical Center, Polish Academy of Sciences, Bartycka 18, 00-716 Warsaw, Poland
e-mail: knalew@camk.edu.pl
2
Aryabhatta Research Institute of Observational Sciences (ARIES), Manora Peak, Nainital 263002, India
3
Key Laboratory for Research in Galaxies and Cosmology, Shanghai Astronomical Observatory, Chinese Academy of Sciences, Shanghai 200030, PR China
4
University of Chinese Academy of Sciences, 19A Yuquanlu, Beijing 100049, PR China
Received:
16
May
2019
Accepted:
1
September
2019
Aims. Characterisation of the long-term variations in the broad line region in a luminous blazar, where Comptonisation of broad-line emission within a relativistic jet is the standard scenario for production of γ-ray emission that dominates the spectral energy distribution.
Methods. We analysed ten years of optical spectroscopic data from the Steward Observatory for the blazar 3C 454.3, as well as γ-ray data from the Fermi Large Area Telescope (LAT). The optical spectra are dominated by a highly variable non-thermal synchrotron continuum with a prominent Mg II broad emission line. The line flux was obtained by spectral decomposition including significant contribution from the Fe II pseudo-continuum. Three methods were used to characterise variations in the line flux: (1) stacking of the continuum-subtracted spectra, (2) subtracting the running mean light curves calculated for different timescales, and (3) evaluating potential time delays via the discrete correlation function (DCF).
Results. Despite very large variations in the γ-ray and optical continua, the line flux changes only moderately (<0.1 dex). The data suggest that the line flux responds to a dramatic change in the blazar activity from a very high state in 2010 to a deep low state in 2012. Two interpretations are possible: either the line flux is anti-correlated with the continuum or the increase in the line luminosity is delayed by ∼600 days. If this time delay results from the reverberation of poorly constrained accretion disc emission in both the broad-line region (BLR) and the synchrotron emitting blazar zone within a relativistic jet, we would obtain natural estimates for the BLR radius RBLR, MgII ≳ 0.28 pc and for the supermassive black hole mass MSMBH ∼ 8.5 × 108 M⊙. We did not identify additional examples of short-term “flares” of the line flux, in addition to the previously reported case observed in 2010.
Key words: galaxies: active / quasars: emission lines / quasars: individual: 3C 454.3
© ESO 2019
1. Introduction
The cores of active galaxies exhibit a complex mixture of energetic physical phenomena (for review see Madejski & Sikora 2016, and references therein). Supermassive black holes (MSMBH ∼ 109 M⊙) accrete surrounding gas, often forming radiatively efficient accretion discs that produce intense radiation fields (quasar emission; Ldisc ∼ 1046 erg s−1) that ionise the surrounding gas, resulting in emission lines broadened by rapid gas motions (v > 1000 km s−1). In some cases, magnetic flux accumulated on the black hole produces a pair of relativistic collimated outflows called jets that produce non-thermal radiation beams (blazar emission), the luminosity of which can be greatly enhanced (by a factor of ∼104 to Ljet ∼ 1048 erg s−1) by special-relativistic effects for observers located along one of the jets. A class of active galaxies called flat spectrum radio quasars (FSRQs) combines the characteristics of blazars, where broad non-thermal spectral components dominate the radio, infrared, optical, X-ray, and gamma-ray bands, and those of quasars, where thermal emission of accretion disc peak in the rest-frame UV, and broad emission lines (BELs) produced in so-called broad line region (BLR) contribute to the rest-frame optical and/or UV. The BELs constitute an important source of soft radiation that strongly interacts with relativistic jets, with the potential of producing the bulk of observed γ-ray emission by inverse Compton (IC) scattering off ultra-relativistic electrons (Sikora et al. 1994), and of absorbing a part of the γ-ray spectrum in the process of photon-photon pair production (Blandford & Levinson 1995). The understanding of the BLR properties, especially its geometry and dynamics, while essential for making a self-consistent picture of FSRQs, is still rather basic (Tavecchio & Ghisellini 2008, 2012; Czerny & Hryniewicz 2011; Janiak et al. 2015).
A primary example of an FSRQ of exceptional gamma-ray luminosity (up to 1050 erg s−1 Abdo et al. 2011) and large-amplitude time variability is 3C 454.3 (z = 0.859). It has been a target of multiple dedicated multi-wavelength observational campaigns (Hartman et al. 1993; Fuhrmann et al. 2006; Pian et al. 2006; Villata et al. 2006; Giommi et al. 2006; Raiteri et al. 2007, 2008; Jorstad et al. 2010), especially in the context of high-energy gamma-ray observations by AGILE (Vercellone et al. 2008, 2009, 2010, 2011; Donnarumma et al. 2009) and by Fermi LAT (Abdo et al. 2009; Bonning et al. 2009; Ackermann et al. 2010; Bonnoli et al. 2011; Raiteri et al. 2011; Wehrle et al. 2012; Gaur et al. 2012; Jorstad et al. 2013; Kushwaha et al. 2017; Gupta et al. 2017).
As one of the brightest gamma-ray blazars of the Fermi era, 3C 454.3 was selected for regular optical spectroscopic monitoring by the Steward Observatory (Smith et al. 2009). Based on a part of this dataset (2008–2011), a flare-like variability of the Mg II broad emission line flux in 2010 November (MJD ∼ 55512) was reported by León-Tavares et al. (2013). However, independent optical spectroscopic survey by the SMARTS Consortium over a very similar period but with relatively sparse cadence found variations in the Mg II flux at the level of 2σ, in addition to more significant variations in the Hγ line (Isler et al. 2013, 2015). Here, we analyse ten years of spectroscopic data from Steward Observatory comprising 564 observations, an unprecedented dataset in terms of long-term regular and frequent monitoring. We find a hint (statistical significance of ∼1.5σ) of modulation in the Mg II line luminosity on a timescale of about two years in response to large-amplitude variability of the optical and gamma-ray continua that were not noticed by previous studies. The line luminosity is either anti-correlated with the optical continuum luminosity or delayed by ∼300 source-frame days. This would be only the second case of reverberation mapping in a blazar after the case of 3C 273 (PG 1226+023; z = 0.1583) included in the sample studied by Kaspi et al. (2000), with a recent analysis based on the Steward survey (Zhang et al. 2019).
2. Data
2.1. Steward Observatory
Regular optical photometric and spectropolarimetric observations of a sample of gamma-ray bright blazars are performed by the team of the University of Arizona Steward Observatory as support programme for the Fermi Gamma-Ray Space Telescope1. Moderate-resolution (R ∼ 300−1000) optical spectra were obtained in the spectral range of λobs = (4000−7600) Å with the SPOL spectropolarimeter and calibrated to the V magnitudes of nearby standard stars. Technical details of the instrument and data reduction procedures are described in Smith et al. (2009).
We analysed all 564 photometrically calibrated spectroscopic observations over the period of ten years (2008–2018; MJD = 54743−58306). The observed spectra were corrected for Galactic extinction using the map of Schlegel et al. (1998) and the extinction curve from Cardelli et al. (1989) with the following parameters: A(V) = 0.33 mag and E(B − V) = 0.105 mag with RV = 3.1.
The main spectral feature seen in all spectra is the Mg II broad emission line (λsrc = 2800 Å redshifted to λobs = 5200 Å. It is imposed on a continuum consisting of non-thermal synchrotron emission component of the blazar and of thermal accretion disc emission component of the quasar, as well as an Fe II pseudo-continuum. As the primary analysis method, we performed spectral decomposition of the Mg II line complex following the approach of Shen et al. (2011). The Mg II emission was modelled with up to three Gaussian components, with the Fe II template adopted after (Vestergaard & Wilkes 2001), and the continuum was fitted within the source-frame spectral windows of (2200−2700) Å and (2900−3090) Å. The centroids of the three Gaussians were treated as free parameters, and their values show stochastic variations without a systematic long-term trend. Sorting the Gaussians according to their centroids (low, medium, high), the median source-frame centroid values are 2764 Å, 2797 Å, and 2820 Å, with the standard deviations of 14Å, 3 Å, and 12 Å, respectively. The observed full width at half maximum FWHMobs of the Mg II line was calculated from the superposed profiles of the fitted Gaussian components, and it was corrected for instrumental line broadening using 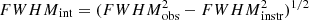 with the adopted source-frame instrumental resolution of FWHMinstr ≃ 1150 km s−1. In order to estimate observational flux uncertainty, we calculated the rms value of the spectra over the source-frame spectral window of (3000−3100) Å after subtracting a second-order polynomial function. To estimate uncertainties of the measured spectral parameters, we generated samples of 100 mock spectra by adding a random Gaussian noise to the observed spectrum using the flux density error and calculating the rms of the obtained distributions of measured parameters. A more accurate theoretical template for the Fe II pseudo-continuum, with independent Fe II multiplets taken from Kovačević-Dojčinović & Popović (2015) and Popović et al. (2019), was fitted to the mean line profile; however, it was not used to model individual observations.
with the adopted source-frame instrumental resolution of FWHMinstr ≃ 1150 km s−1. In order to estimate observational flux uncertainty, we calculated the rms value of the spectra over the source-frame spectral window of (3000−3100) Å after subtracting a second-order polynomial function. To estimate uncertainties of the measured spectral parameters, we generated samples of 100 mock spectra by adding a random Gaussian noise to the observed spectrum using the flux density error and calculating the rms of the obtained distributions of measured parameters. A more accurate theoretical template for the Fe II pseudo-continuum, with independent Fe II multiplets taken from Kovačević-Dojčinović & Popović (2015) and Popović et al. (2019), was fitted to the mean line profile; however, it was not used to model individual observations.
We also perform a simplified spectral analysis in order to verify that the inferred modulation of the Mg II line flux is not affected by uncertainties in the Fe II pseudo-continuum template and its separation from both the Mg II line or from the actual non-thermal continuum. In this approach, the continuum is evaluated as a power law fitted over two narrow source-frame spectral windows of (2650−2680) Å and (3010−3070) Å in which the Fe II template of Vestergaard & Wilkes (2001) shows significant local minima. This continuum is subtracted from the observed spectra, and the residual is integrated over the wavelength range of (2650−3070) Å to approximate the Mg II + Fe II flux. Individual spectra are then stacked with weights proportional to the exposure time of each observation.
The quality of individual residual spectra is evaluated by the rms function calculated over the continuum fitting spectral windows. These rms values were found to be in the range of (1−25)×10−17 erg s−1 cm−2 Å−1. After analysing the strongest outlier values among estimates of the Mg II + Fe II line flux, we decided to introduce an upper limit to the rms value: rmsmax = 7 × 10−17 erg s−1 cm−2 Å−1. Applying this criterion, we rejected 107 (19%) of the most noisy individual photometric spectra from further analysis. This selection was also applied to the results of spectral decomposition analysis.
2.2. Fermi LAT
Gamma-ray data from the Fermi LAT (Atwood et al. 2009) were extracted from the region of interest (ROIs) of radius 10° centred on the position of 3C 454.3. We used the ScienceTools software package, version v11r5p3, to perform the maximum likelihood analysis, fitting a PowerLaw2 spectral model over the energy range 100 MeV–100 GeV, using the P8R2_SOURCE_V6 response function, maximum zenith angle of 100°, and a source model including all background sources from the 3FGL catalogue (Acero et al. 2015) up to the angular separation of 25°, with the detection criteria of TS > 10 and Npred > 32. The light curve was obtained over the period of MJD ≃ 54683−58234 with uniform time bins of 10 days.
3. Results
Figure 1 shows γ-ray and optical light curves of 3C 454.3 over the period of 10 years (2008–2018; MJD 54700–58300). The γ-ray data show large-amplitude (factor ∼100) variations that can be broadly characterised as two periods of high activity (2009.5–2011.0 and 2013.5–2018) separated by a particularly quiescent period of 2011.0–2013.5. Due to the relatively long binning timescale (10 days), short-scale variations (detected down to the timescale of ≃5 h; Nalewajko 2017) with peak fluxes reaching the level of f(E > 100 MeV)≃8 × 10−5 ph s−1 cm−2 on MJD 55520 (Abdo et al. 2011) are not included here. However, taking them into account, the overall variability amplitude exceeds a factor of 1000.
 |
Fig. 1. Light curves of blazar 3C 454.3. From the top, the first panel shows the γ-ray photon flux for photon energies above 100 MeV obtained from the Fermi LAT data in 10-day bins; the second panel shows the optical continuum at source-frame 3000 Å, obtained independently using two analysis methods (spectral decomposition, blue circles; simplified power-law fit, red/grey crosses); the third panel shows the corresponding values of the spectral index α such that fλ ∝ λα; the fourth panel shows estimates of the spectrally integrated Mg II line flux, either separated from the Fe II continuum (decomposition method) or not (simplified method); the fifth panel shows the source-frame FWHM width of Mg II line obtained in the decomposition method and corrected for instrumental broadening; the sixth panel shows the rms of continuum subtracted spectra calculated over the continuum fitting spectral windows, with the limiting value of 7 × 10−17 erg s−1 cm−2 Å−1 indicated with the dashed line. Results reported in León-Tavares et al. (2013; Steward) and Isler et al. (2013; SMARTS) are indicated in the second and fourth panels. Periods of interest for spectral stacking are marked with vertical stripes or lines. |
Simultaneous variations in the optical continuum are roughly correlated with the γ-ray signal (cf. Bonning et al. 2009; Gaur et al. 2012; Kushwaha et al. 2017; Gupta et al. 2017), but with significantly lower amplitude (a factor of ∼20). It has been noticed before that the γ-ray flux scales in at least quadratic relation to the optical continuum (Bonnoli et al. 2011). This is confirmed by the scatter diagram of γ-ray photon flux versus optical flux density shown in the top left panel of Fig. 2. In the lowest gamma-ray state at MJD ∼ 56000, for γ-ray fluxes <10−7 ph s−1 cm−2, the optical λsrc = 3000 Å continuum flux density does not decrease below 10−15 erg s−1 cm−2 Å, or the level at which contribution of the thermal accretion disc emission is expected to become dominant. The optical spectral index α (defined as fλ ∝ λα) is generally lower during the low γ-ray and optical state (see the middle left panel of Fig. 2), which means a redder-when-brighter trend consistent with the presence of accretion disc component (also known as the big blue bump, e.g. Gu et al. 2006; Villata et al. 2006; Raiteri et al. 2007; Bonning et al. 2009), although the value of α remains highly variable.
 |
Fig. 2. Scatter diagrams between γ-ray photon flux, γ-ray photon index, optical continuum flux density, optical spectral index, and integrated Mg II + Fe II line flux measured simultaneously within ±5 days. The colour-coding indicates the observation date, as in the top panel of Fig. 1. |
We present two different estimates of the optical continuum; one is based on the spectral decomposition (blue circles in Fig. 1) including the spectral template for Fe II emission and the other is a simplified approach (red crosses in Fig. 1) in which Fe II emission is not separated from the Mg II emission. The normalisations of the optical continuum at λsrc = 3000 Å and the spectral indices α obtained with these two methods are consistent. On the other hand, the fluxes of the broad Mg II emission line integrated over λobs appear discrepant in the fourth panel of Fig. 1 because of the inclusion of Fe II in simplified measurements. However, for the initial period (MJD < 55800) we compare them with the values for Mg II and Mg II + Fe II obtained from the same Steward spectra and reported in Table 1 in León-Tavares et al. (2013) 3. We find that our decomposition results are consistent with the Mg II fluxes of León-Tavares et al. (2013), and that our simplified results are consistent with their Mg II + Fe II fluxes. On the other hand, the Mg II flux measurements based on the SMARTS observations, as reported by Isler et al. (2013, 2015), are systematically lower (a factor of ∼3) than the Mg II fluxes obtained from the Steward data. A comparison of these two datasets is discussed in Isler et al. (2013, 2015); however, the relative spectral calibration between these two instruments has not been fully explained.
The Mg II line flux light curve reveals several outliers with respect to the typical values, and occasional differences with the results of León-Tavares et al. (2013). Observation at MJD 54771 yields both the line fluxes (either decomposed Mg II or simplified Mg II + Fe II) and the continuum level that are a factor of ∼3 higher than several other observations taken within the same week (with consistent line FWHM and continuum index); a corresponding systematic difference is also seen in the photometric spectrum. A similar outlier can be seen at MJD 56308, with continuum and line fluxes increased by factor ∼1.5; unlike the case of MJD 54771, this spectrum is affected by noise despite the same exposure time (960 s). Several observations around MJD 55295 suggest line fluxes lower than the typical values, and also lower than the results of León-Tavares et al. (2013); these observations are characterised by relatively short exposure times (320 s), and hence high statistical flux uncertainty.
3.1. Short-term variations
León-Tavares et al. (2013) reported an episode of short-term variation (flare) in the Mg II line flux (and in the Fe II emission) during an optical flare centred at MJD 55512. This epoch is indicated in Fig. 1 by the green dotted lines. We confirm that both Mg II and Mg II + Fe II line fluxes are elevated during the week-long window centred at MJD 55512, compared with neighbouring windows. Because of wide gaps in the observations, the variability timescale is uncertain: it could be closer to weekly than daily. However, all individual spectra obtained over that period are relatively noisy; their rms values are above our adopted upper limit rmsmax (see bottom panel of Fig. 1). We searched for more examples of such flares beyond MJD 55900, and we have not found any. Around MJD 56832, there was an even brighter flare of the optical continuum (Kushwaha et al. 2017), but it was not accompanied by any clear increase in the Mg II line flux (and the individual spectra obtained over that week are even more noisy than those around MJD 55512).
In Fig. 3, we present stacked continuum-subtracted spectra evaluated over two short observational windows (without any selection for the rms values): MJD = 55512 ± 10 (green line) and MJD = 56832 ± 10 (magenta line). These line profiles are compared with a ten-year average4 (thick black line). Differences between short-term stacked spectra and the ten-year average are shown in the lower panel of Fig. 3. We performed two-sample Kolmogorov–Smirnov (K–S) tests for the difference between stacked spectra. This test suggests that the line profile stacked during the MJD 55512 flare reported by León-Tavares et al. (2013) is clearly different from the ten-year average (p ∼ 10−9; 6σ), while the line profile stacked during the second optical continuum flare around MJD 56832 is only different at the level of 2σ (p ≃ 0.04).
 |
Fig. 3. Upper panel: observed source-frame spectra stacked over different observational periods after subtraction of power-law continuum. Middle panel: differences between spectra stacked over limited observational periods and the spectrum stacked over all available observations (line styles correspond to those in the upper panel). Lower panel: model for the spectral decomposition of the Mg II line and theoretical Fe II pseudo-continuum template. The spectral windows for continuum evaluation are indicated with grey stripes. |
3.2. Long-term variations
The left panel of Fig. 4 shows again the light curve of Mg II line luminosity obtained from the spectral decomposition method (corresponding to the blue circles shown in the fourth panel of Fig. 1, we take the logarithm and subtract the mean value). Due to our selection for rms < rmsmax, the short-term variations discussed in the previous subsection are largely excluded. We suggest that this light curve shows a systematic modulation on long timescales (∼100 days). A power spectral density (PSD) analysis showed that variations in the Mg II line luminosity are consistent with the red noise, with no sign of quasi-periodic oscillations (QPOs).
 |
Fig. 4. Left panel: light curve of Mg II line luminosity log10LMgII obtained with the spectral decomposition method, with the mean value subtracted (blue); running mean calculated for the minimum timescale of 100 d (red). Right panel: residual of the light curve shown in the left panel with the running mean subtracted. Periods of interest for spectral stacking are marked with vertical stripes or lines (cf. Fig. 1). |
In order to evaluate the significance of this long-term modulation, we calculate a running mean light curve using uniform time bins of fixed timescale τ. As an example, in the left panel of Fig. 4, we show the running mean light curve for τ = 100 d (solid red line), and in the right panel of that figure we show the measured Mg II luminosities after subtracting the running mean. We then perform a series of two-sample K–S tests between the measured and running mean subtracted Mg II light curves for a wide range of running mean timescales τ. Figure 5 shows the dependence of the p-values for the null hypothesis (that subtracting a running mean does not modify the distribution of Mg II luminosities) on the running mean timescale τ. The basic result is that p < 0.1 for τ < 200 d, hence long-term variations have only moderate statistical significance (1.5σ).
 |
Fig. 5. Probability of rejecting the hypothesis that subtracting a running mean does not affect the distribution of Mg II line luminosities calculated from two-sample K–S tests between the measured light curve of log LMgII (left panel of Fig. 4) and the running mean subtracted light curve (right panel of Fig. 4) as function of the running mean timescale. |
We also calculated the discrete correlation functions (DCF; Edelson & Krolik 1988) in order to estimate the characteristic time lags between partially correlated signals5. Noting the fundamentally different nature of variations in the Mg II line luminosity (moderate departures from the mean value) and the optical continuum (large-amplitude–order of magnitude variations without a clear mean value), we cross-correlated the logarithms of measured flux values using the time lag bins of 40 days. As a reference, we first calculated the DCF between the γ-ray and optical continua (left panel of Fig. 6). This DCF has a clear positive peak of DCF ≃ 0.73 at Δt ≃ 0. In order to estimate the most likely value of time lag, we fitted a Gaussian function over a limited range of time lags (red dotted lines), finding a centroid of Δt0 = 60 ± 41 d and dispersion of σ(Δt) = 178 ± 42 d. The right panel of Fig. 6 shows the DCF calculated between the Mg II line luminosity and the optical λsrc = 3000 Å continuum. This DCF shows broad negative and positive peaks of DCF ≃ −0.76 and 0.68 at Δt ≃ 0 and Δt ≃ 600 d, respectively. A Gaussian fit to the negative peak yields the centroid of Δt0 = −65 ± 44 d and dispersion of σ(Δt) = 222 ± 48 d; a fit to the positive peak yields the centroid of Δt0 = 621 ± 45 d and dispersion of σ(Δt) = 221 ± 50 d. This allows for two alternative interpretations: (1) that the Mg II luminosity is anti-correlated with the optical continuum (as can be seen in the bottom left panel of Fig. 2), or (2) that the Mg II luminosity lags behind the optical continuum by Δt ≃ 600 days. The two interpretations are discussed in Sect. 4.
 |
Fig. 6. Discrete correlation functions calculated between the logarithms of the (>100 MeV) γ-ray photon flux and the optical continuum flux density (left panel), and between the logarithms of the Mg II line flux and the optical continuum (right panel). |
Looking at the Mg II light curve more subjectively, we can distinguish two periods of interest: a period of reduced Mg II luminosity at MJD ≃ 55070−55315 and a period of enhanced Mg II luminosity at MJD ≃ 55690−55980 (see Figs. 1 and 4). The midpoints of these periods are separated by 640 days. We use these periods to calculate another continuum-subtracted stacked spectra presented in Fig. 3. From a two-sample K–S test between these two stacked spectra, we find a probability p ≃ 5 × 10−4 (confidence level of 3.5σ) that these spectra are consistent with each other.
3.3. Modelling the mean line profile
In Fig. 3, we show an example of an accurate model for the decomposition of the stacked continuum-subtracted spectrum into an Mg II line represented by three Gaussian components (e.g. Adhikari et al. 2018) with the FWHM of 1607, 8390, and 2239 km s−1, and a theoretical Fe II pseudo-continuum with independent multiplets of 60–63, 78, and I Zw 1 (Kovačević-Dojčinović & Popović 2015; Popović et al. 2019) with kinematic broadenings in the range 2400−3600 km s−1.
4. Discussion
In many non-blazar AGNs, variations in the BEL flux are observed to be correlated with the optical continuum (typically interpreted as accretion disc emission) with time delays of Δt ∼ (10−1000) days (e.g. Kaspi et al. 2000, 2007; Peterson et al. 2004). Measuring this time delay allows us to estimate the characteristic radius RBLR of the BLR; this technique is known as reverberation mapping (Blandford & McKee 1982).
In the case of 3C 454.3, which is both a blazar and a quasar, we have a more complex situation (see Fig. 7). The optical continuum is a combination of highly variable synchrotron emission produced in a blazar zone located in a relativistic jet up to a parsec in front of the nucleus (SMBH), and of thermal emission produced in the accretion disc. It is not possible to confidently separate these two components. In the traditional picture of BLR being concentrated and slightly flattened around the equatorial plane of the AGN (e.g. Tavecchio & Ghisellini 2012; Nalewajko et al. 2014; Janiak et al. 2015; Sturm et al. 2018), it is this unknown accretion disc emission (rather than the jet emission that is relativistically beamed away from the equatorial plane) that is reprocessed into the BEL. Observation of a correlation between synchrotron light curve produced in a foreground jet and BEL light curve produced in the background BLR requires that both are correlated with the underlying poorly constrained accretion disc emission. While the reverberation of accretion disc emission in the BLR can be explained purely by light-travel effects, correlation of the synchrotron emission requires consideration of perturbations originating in the inner accretion disc and propagating along the jet to the blazar zone.
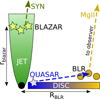 |
Fig. 7. Schematic illustration of an AGN being both a quasar (luminous thermal emission from the accretion disc) and a blazar (even more luminous non-thermal emission from the relativistic jet), i.e. an FSRQ like 3C 454.3. It is assumed here that the BLR is concentrated along the accretion disc plane at characteristic distance RBLR from the SMBH. The optical continuum is dominated by the synchrotron radiation produced in a blazar zone located within the jet at characteristic distance rblazar, and the Mg II BEL is produced in the BLR. |
We should note that the DCF presented in the right panel of Fig. 6, between the Mg II line luminosity and the optical continuum, shows a broad negative peak around zero time lag, suggesting that these two light curves could be anti-correlated. This anti-correlation would be difficult to explain in the traditional models of BLR geometry, such as the one depicted in Fig. 7. It could be possibly accommodated in a variant of the extended BLR scenario, with the BLR clouds concentrated along the relativistic jets and ionised by their relativistically boosted non-thermal radiation, as advocated by León-Tavares et al. (2013). Instead of having short-scale flares of line luminosity, positively correlated with the optical continuum flares, increasing luminosity of jet emission could have a destructive effect on such extended BLRs by inducing too strong ionisation of the surrounding gas. The main difficulty of such a scenario would be to explain a much longer variability timescale (∼1 month) of the BEL.
Assuming that the observed time delay of Δtobs ≃ (621 ± 45) days between the optical continuum light curve and the Mg II light curve is due to reverberation of the thermal accretion disc emission, the corresponding additional path distance that should be travelled by reverberated light in the source frame is Δr = cΔtobs/(1 + z)≃(0.28 ± 0.02) pc. For a blazar observer located at small viewing angle 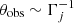 measured from the jet axis, the relative distance measured along the line of sight between the blazar zone and the BLR zone is rblazar cos θobs, where rblazar ∼ 0.1−1 pc (Nalewajko et al. 2014) is the distance along the jet of the synchrotron emitting blazar zone. Considering that at t = 0, a perturbation in the inner accretion disc produces a flare in the quasar continuum emission, and triggers a perturbation (e.g. internal shock) propagating along the jet with velocity ⟨βj⟩=⟨vj⟩/c. The continuum flare illuminates the BLR zone at ctBLR ≃ RBLR, while the jet perturbation reaches the blazar zone at ctblazar ≃ rblazar/⟨βj⟩. We can thus express the additional reverberation path distance as Δr = rblazar cos θobs + ctBLR − ctblazar = RBLR − rblazar(⟨βj⟩−1− cos θobs). With this, we can attempt to constrain the BLR radius:
measured from the jet axis, the relative distance measured along the line of sight between the blazar zone and the BLR zone is rblazar cos θobs, where rblazar ∼ 0.1−1 pc (Nalewajko et al. 2014) is the distance along the jet of the synchrotron emitting blazar zone. Considering that at t = 0, a perturbation in the inner accretion disc produces a flare in the quasar continuum emission, and triggers a perturbation (e.g. internal shock) propagating along the jet with velocity ⟨βj⟩=⟨vj⟩/c. The continuum flare illuminates the BLR zone at ctBLR ≃ RBLR, while the jet perturbation reaches the blazar zone at ctblazar ≃ rblazar/⟨βj⟩. We can thus express the additional reverberation path distance as Δr = rblazar cos θobs + ctBLR − ctblazar = RBLR − rblazar(⟨βj⟩−1− cos θobs). With this, we can attempt to constrain the BLR radius:
Since ⟨βj⟩−1 ≳ 1 ≳ cos θobs and rblazar ∼ Δr, the second term in the above equation is not important. This corresponds to an independent estimate of the black hole mass,
where vrms ≃ (3170 ± 410) km s−1 is measured from the mean FWHM of the Mg II line and f ∼ 1.3 is a geometrical form factor (Sturm et al. 2018). The obtained value is very reasonable and corresponds well to the previous estimates 5−45 × 108 M⊙, based mostly on the empirical relation between line widths and continuum luminosities (Gu et al. 2001; Woo & Urry 2002; Liu et al. 2006; Bonnoli et al. 2011; Sbarrato et al. 2012; Gupta et al. 2017). In the case of a blazar with the jet oriented close to the line of sight, a BLR that is concentrated along the AGN equatorial plane should be oriented close to the plane of the sky, largely eliminating the uncertainty on the BLR inclination angle.
Our claim for delayed correlation between optical continuum and broad line luminosity is based in the first place on the modulation of the line luminosity as presented in Fig. 4. While we identified two periods of interest in the line luminosity light curve, their connection to the structure of the continuum light curve is not obvious. The period of enhanced line luminosity at MJD ≃ 55690−55980 could be related to the continuum flare peaking at MJD ≃ 55150 (corresponding to a time delay of ∼690 days) or to the following continuum flare peaking at MJD ≃ 55520 (with a delay of ∼320 days). On the other hand, the period of reduced line luminosity at MJD ≃ 55070−55315 could be related to the continuum dip at MJD ≃ 54900 (with delay of ∼290 days), while a longer delay of 600−700 days would point to the period of MJD ≃ 54500−54600, which coincides with a seasonal gap in the optical photometric data from the GASP-WEBT project (Vercellone et al. 2010). Finally, the historical minimum in the continuum light curve at MJD ∼ 56000 does not have a corresponding decrease in line luminosity, which we would expect at MJD ∼ 56600−56700. Unlike the case of 3C 273 (Zhang et al. 2019), this tentative reverberation measurement should be treated with caution, and should also be confirmed by future spectroscopic monitoring campaigns.
The (1 + z)3K-correction was applied to the line fluxes reported by León-Tavares et al. (2013); here its effect is removed for the green symbols shown in Fig. 1.
Very similar results were obtained with the ZDCF algorithm of Alexander (1997).
Acknowledgments
We thank the referee for helpful suggestions, and Marek Sikora and Bożena Czerny for discussions. We used data from the Steward Observatory spectropolarimetric monitoring project that has been supported by Fermi Guest Investigator grants NNX08AW56G, NNX09AU10G, NNX12AO93G, and NNX15AU81G. We also used public data acquired by the Fermi LAT created by NASA and DoE (USA) in collaboration with institutions from France, Italy, Japan, and Sweden. KN was supported by the Polish National Science Centre grant 2015/18/E/ST9/00580. The work of ACG is partially supported by Indo-Poland project no. DST/INT/POL/P19/2016 funded by the Department of Science and Technology (DST) of the Government of India, and by the Chinese Academy of Sciences (CAS) President’s International Fellowship Initiative (PIFI) grant no. 2016VMB073. KH acknowledges the support of the Polish National Science Centre grant 2015/17/B/ST9/03422. MFG was supported by the National Science Foundation of China (grants 11873073 and U1531245). ML was supported by the National Science Foundation of China (grants 11773056 and U1831138).
References
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2009, ApJ, 699, 817 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2011, ApJ, 733, L26 [NASA ADS] [CrossRef] [Google Scholar]
- Acero, F., Ackermann, M., Ajello, M., et al. 2015, ApJS, 218, 23 [Google Scholar]
- Ackermann, M., Ajello, M., Baldini, L., et al. 2010, ApJ, 721, 1383 [NASA ADS] [CrossRef] [Google Scholar]
- Adhikari, T. P., Hryniewicz, K., Różańska, A., et al. 2018, ApJ, 856, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Alexander, T. 1997, Astron. Time Ser., 218, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Atwood, W. B., Abdo, A. A., Ackermann, M., et al. 2009, ApJ, 697, 1071 [NASA ADS] [CrossRef] [Google Scholar]
- Blandford, R. D., & Levinson, A. 1995, ApJ, 441, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Blandford, R. D., & McKee, C. F. 1982, ApJ, 255, 419 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonning, E. W., Bailyn, C., Urry, C. M., et al. 2009, ApJ, 697, L81 [NASA ADS] [CrossRef] [Google Scholar]
- Bonnoli, G., Ghisellini, G., Foschini, L., Tavecchio, F., & Ghirlanda, G. 2011, MNRAS, 410, 368 [NASA ADS] [CrossRef] [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Czerny, B., & Hryniewicz, K. 2011, A&A, 525, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Donnarumma, I., Pucella, G., Vittorini, V., et al. 2009, ApJ, 707, 1115 [NASA ADS] [CrossRef] [Google Scholar]
- Edelson, R. A., & Krolik, J. H. 1988, ApJ, 333, 646 [NASA ADS] [CrossRef] [Google Scholar]
- Fuhrmann, L., Cucchiara, A., Marchili, N., et al. 2006, A&A, 445, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaur, H., Gupta, A. C., & Wiita, P. J. 2012, AJ, 143, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Giommi, P., Blustin, A. J., Capalbi, M., et al. 2006, A&A, 456, 911 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gu, M., Cao, X., & Jiang, D. R. 2001, MNRAS, 327, 1111 [NASA ADS] [CrossRef] [Google Scholar]
- Gu, M. F., Lee, C.-U., Pak, S., et al. 2006, A&A, 450, 39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gupta, A. C., Mangalam, A., Wiita, P. J., et al. 2017, MNRAS, 472, 788 [NASA ADS] [CrossRef] [Google Scholar]
- Hartman, R. C., Bertsch, D. L., Dingus, B. L., et al. 1993, ApJ, 407, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Isler, J. C., Urry, C. M., Coppi, P., et al. 2013, ApJ, 779, 100 [NASA ADS] [CrossRef] [Google Scholar]
- Isler, J. C., Urry, C. M., Bailyn, C., et al. 2015, ApJ, 804, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Janiak, M., Sikora, M., & Moderski, R. 2015, MNRAS, 449, 431 [NASA ADS] [CrossRef] [Google Scholar]
- Jorstad, S. G., Marscher, A. P., Larionov, V. M., et al. 2010, ApJ, 715, 362 [NASA ADS] [CrossRef] [Google Scholar]
- Jorstad, S. G., Marscher, A. P., Smith, P. S., et al. 2013, ApJ, 773, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Kaspi, S., Smith, P. S., Netzer, H., et al. 2000, ApJ, 533, 631 [NASA ADS] [CrossRef] [Google Scholar]
- Kaspi, S., Brandt, W. N., Maoz, D., et al. 2007, ApJ, 659, 997 [NASA ADS] [CrossRef] [Google Scholar]
- Kovačević-Dojčinović, J., & Popović, L. Č. 2015, ApJS, 221, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Kushwaha, P., Gupta, A. C., Misra, R., et al. 2017, MNRAS, 464, 2046 [NASA ADS] [CrossRef] [Google Scholar]
- León-Tavares, J., Chavushyan, V., Patiño-Álvarez, V., et al. 2013, ApJ, 763, L36 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, Y., Jiang, D. R., & Gu, M. F. 2006, ApJ, 637, 669 [NASA ADS] [CrossRef] [Google Scholar]
- Madejski, G. M., & Sikora, M. 2016, ARA&A, 54, 725 [NASA ADS] [CrossRef] [Google Scholar]
- Nalewajko, K. 2017, Galaxies, 5, 100 [NASA ADS] [CrossRef] [Google Scholar]
- Nalewajko, K., Begelman, M. C., & Sikora, M. 2014, ApJ, 789, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Peterson, B. M., Ferrarese, L., Gilbert, K. M., et al. 2004, ApJ, 613, 682 [NASA ADS] [CrossRef] [Google Scholar]
- Pian, E., Foschini, L., Beckmann, V., et al. 2006, A&A, 449, L21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Popović, L. Č., Kovačević-Dojčinović, J., & Marčeta-Mandić, S. 2019, MNRAS, 484, 3180 [NASA ADS] [CrossRef] [Google Scholar]
- Raiteri, C. M., Villata, M., Larionov, V. M., et al. 2007, A&A, 473, 819 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Raiteri, C. M., Villata, M., Larionov, V. M., et al. 2008, A&A, 491, 755 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Raiteri, C. M., Villata, M., Aller, M. F., et al. 2011, A&A, 534, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sbarrato, T., Ghisellini, G., Maraschi, L., et al. 2012, MNRAS, 421, 1764 [NASA ADS] [CrossRef] [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Shen, Y., Richards, G. T., Strauss, M. A., et al. 2011, ApJS, 194, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Sikora, M., Begelman, M. C., & Rees, M. J. 1994, ApJ, 421, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, P. S., Montiel, E., Rightley, S., et al. 2009, 2009 Fermi Symposium, eConf Proceedings C091122 [arXiv:0912.3621] [Google Scholar]
- Sturm, E., Dexter, J., Pfuhl, O., et al. 2018, Nature, 563, 657 [Google Scholar]
- Tavecchio, F., & Ghisellini, G. 2008, MNRAS, 386, 945 [NASA ADS] [CrossRef] [Google Scholar]
- Tavecchio, F., & Ghisellini, G. 2012, ArXiv e-prints [arXiv:1209.2291] [Google Scholar]
- Vercellone, S., Chen, A. W., Giuliani, A., et al. 2008, ApJ, 676, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Vercellone, S., Chen, A. W., Vittorini, V., et al. 2009, ApJ, 690, 1018 [NASA ADS] [CrossRef] [Google Scholar]
- Vercellone, S., D’Ammando, F., Vittorini, V., et al. 2010, ApJ, 712, 405 [NASA ADS] [CrossRef] [Google Scholar]
- Vercellone, S., Striani, E., Vittorini, V., et al. 2011, ApJ, 736, L38 [NASA ADS] [CrossRef] [Google Scholar]
- Vestergaard, M., & Wilkes, B. J. 2001, ApJS, 134, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Villata, M., Raiteri, C. M., Balonek, T. J., et al. 2006, A&A, 453, 817 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wehrle, A. E., Marscher, A. P., Jorstad, S. G., et al. 2012, ApJ, 758, 72 [NASA ADS] [CrossRef] [Google Scholar]
- Woo, J.-H., & Urry, C. M. 2002, ApJ, 579, 530 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, Z.-X., Du, P., Smith, P. S., et al. 2019, ApJ, 876, 49 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1. Light curves of blazar 3C 454.3. From the top, the first panel shows the γ-ray photon flux for photon energies above 100 MeV obtained from the Fermi LAT data in 10-day bins; the second panel shows the optical continuum at source-frame 3000 Å, obtained independently using two analysis methods (spectral decomposition, blue circles; simplified power-law fit, red/grey crosses); the third panel shows the corresponding values of the spectral index α such that fλ ∝ λα; the fourth panel shows estimates of the spectrally integrated Mg II line flux, either separated from the Fe II continuum (decomposition method) or not (simplified method); the fifth panel shows the source-frame FWHM width of Mg II line obtained in the decomposition method and corrected for instrumental broadening; the sixth panel shows the rms of continuum subtracted spectra calculated over the continuum fitting spectral windows, with the limiting value of 7 × 10−17 erg s−1 cm−2 Å−1 indicated with the dashed line. Results reported in León-Tavares et al. (2013; Steward) and Isler et al. (2013; SMARTS) are indicated in the second and fourth panels. Periods of interest for spectral stacking are marked with vertical stripes or lines. |
| In the text | |
 |
Fig. 2. Scatter diagrams between γ-ray photon flux, γ-ray photon index, optical continuum flux density, optical spectral index, and integrated Mg II + Fe II line flux measured simultaneously within ±5 days. The colour-coding indicates the observation date, as in the top panel of Fig. 1. |
| In the text | |
 |
Fig. 3. Upper panel: observed source-frame spectra stacked over different observational periods after subtraction of power-law continuum. Middle panel: differences between spectra stacked over limited observational periods and the spectrum stacked over all available observations (line styles correspond to those in the upper panel). Lower panel: model for the spectral decomposition of the Mg II line and theoretical Fe II pseudo-continuum template. The spectral windows for continuum evaluation are indicated with grey stripes. |
| In the text | |
 |
Fig. 4. Left panel: light curve of Mg II line luminosity log10LMgII obtained with the spectral decomposition method, with the mean value subtracted (blue); running mean calculated for the minimum timescale of 100 d (red). Right panel: residual of the light curve shown in the left panel with the running mean subtracted. Periods of interest for spectral stacking are marked with vertical stripes or lines (cf. Fig. 1). |
| In the text | |
 |
Fig. 5. Probability of rejecting the hypothesis that subtracting a running mean does not affect the distribution of Mg II line luminosities calculated from two-sample K–S tests between the measured light curve of log LMgII (left panel of Fig. 4) and the running mean subtracted light curve (right panel of Fig. 4) as function of the running mean timescale. |
| In the text | |
 |
Fig. 6. Discrete correlation functions calculated between the logarithms of the (>100 MeV) γ-ray photon flux and the optical continuum flux density (left panel), and between the logarithms of the Mg II line flux and the optical continuum (right panel). |
| In the text | |
 |
Fig. 7. Schematic illustration of an AGN being both a quasar (luminous thermal emission from the accretion disc) and a blazar (even more luminous non-thermal emission from the relativistic jet), i.e. an FSRQ like 3C 454.3. It is assumed here that the BLR is concentrated along the accretion disc plane at characteristic distance RBLR from the SMBH. The optical continuum is dominated by the synchrotron radiation produced in a blazar zone located within the jet at characteristic distance rblazar, and the Mg II BEL is produced in the BLR. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.