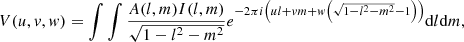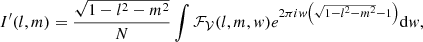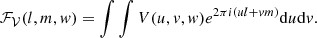| Issue |
A&A
Volume 631, November 2019
|
|
|---|---|---|
| Article Number | A12 | |
| Number of page(s) | 12 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/201935722 | |
| Published online | 11 October 2019 | |
Precision requirements for interferometric gridding in the analysis of a 21 cm power spectrum
1
Netherlands Institute for Radio Astronomy (ASTRON), 7991 PD Dwingeloo, The Netherlands
e-mail: offringa@astron.nl
2
Kapteyn Astronomical Institute, University of Groningen, PO Box 800, 9700 AV Groningen, The Netherlands
3
School of Earth and Space Exploration, Arizona State University, 781 Terrace Mall, Tempe, AZ 85287, USA
Received:
17
April
2019
Accepted:
27
August
2019
Context. Experiments that try to observe the 21 cm redshifted signals from the epoch of reionisation (EoR) using interferometric low-frequency instruments have stringent requirements on the processing accuracy.
Aims. We analyse the accuracy of radio interferometric gridding of visibilities with the aim to quantify the power spectrum bias caused by gridding. We do this ultimately to determine the suitability of different imaging algorithms and gridding settings for an analysis of a 21 cm power spectrum.
Methods. We simulated realistic Low-Frequency Array (LOFAR) data and constructed power spectra with convolutional gridding and w stacking, w projection, image-domain gridding, and without w correction. These were compared against data that were directly Fourier transformed. The influence of oversampling, kernel size, w-quantization, kernel windowing function, and image padding were quantified. The gridding excess power was measured with a foreground subtraction strategy, for which foregrounds were subtracted using Gaussian progress regression, as well as with a foreground avoidance strategy.
Results. Constructing a power spectrum with a significantly lower bias than the expected EoR signals is possible with the methods we tested, but requires a kernel oversampling factor of at least 4000, and when w-correction is used, at least 500 w-quantization levels. These values are higher than typically used values for imaging, but they are computationally feasible. The kernel size and padding factor parameters are less crucial. Of the tested methods, image-domain gridding shows the highest accuracy with the lowest imaging time.
Conclusions. LOFAR 21 cm power spectrum results are not affected by gridding. Image-domain gridding is overall the most suitable algorithm for 21 cm EoR power spectrum experiments, including for future analyses of data from the Square Kilometre Array (SKA) EoR. Nevertheless, convolutional gridding with tuned parameters results in sufficient accuracy for interferometric 21 cm EoR experiments. This also holds for w stacking for wide-field imaging. The w-projection algorithm is less suitable because of the requirements for kernel oversampling, and a faceting approach is unsuitable because it causes spatial discontinuities.
Key words: dark ages / reionization / first stars / methods: data analysis / methods: observational / techniques: interferometric / instrumentation: interferometers
© ESO 2019
1. Introduction
The epoch of reionisation (EoR) is a pivotal era in the evolution of our Universe. In this era, which is expected to have started approximately 500 million years after the Big Bang, the very first objects in our Universe heated and ionised the intergalactic medium. One of the most promising ways to analyse this process is through detection of the redshifted 21 cm line emission of neutral hydrogen (Iliev et al. 2002; Morales 2005; Furlanetto et al. 2006; McQuinn et al. 2006; Pritchard & Loeb 2012; Park et al. 2019). Current constraints indicate that the EoR has taken place at a redshift of approximately z = 6 − 10, implying that the 21 cm signals from the EoR are detectable in the frequency range of approximately 130–200 MHz. Several low-frequency instruments have been built or are planned for which the detection of these signals is one of their key science goals (Parsons et al. 2012; van Haarlem et al. 2013; Tingay et al. 2013; Dewdney et al. 2013; DeBoer et al. 2017; Fialkov et al. 2018).
Interferometric experiments aim to detect the EoR signals through power spectrum analysis (Paciga et al. 2013; Beardsley et al. 2016; Patil et al. 2017; Trott et al. 2016). Such an analysis can combine a large field of view and several megahertz of bandwidth to decrease the uncertainty due to the thermal noise of the instrument to ultimately detect the signals from the EoR in a statistical manner. Recently, the LOFAR EoR project has worked on interferometric upper limits from ten observation nights (Mertens et al., in prep.). Direct imaging of the EoR is probably not feasible until the Square Kilometre Array (SKA; Dewdney et al. 2013) is functional (Zaroubi et al. 2012).
It is often necessary to average visibility measurements together that observe (almost) the same modes on the sky in order to process the enormous volume of visibilities that are produced by modern telescopes. One method to do this is by gridding the visibilities on a regular 2D grid in Fourier (uv) space, a step that is also part of making images from interferometric data. This step leads to small errors. Gridding can be avoided in some specific power spectrum methodologies, such as by making use of redundancy (Parsons & Backer 2009) or using different transforms based on spherical harmonics or m-mode analysis (Carozzi 2015; Ghosh et al. 2018; Eastwood et al. 2018).
Several 21 cm power spectrum pipelines use gridded uv-cubes or image cubes (the third dimension being frequency), such as CHIPS (Trott et al. 2016), a pipeline that constructs a fully invariance-weighted power spectrum; the ϵPPSILON pipeline (Jacobs et al. 2016; Barry et al. 2019), which makes use of the fast holographic deconvolution software for imaging (FHD; Sullivan et al. 2012); and the image-based tapered gridded estimater (ITGE; Choudhuri et al. 2018). In this paper we make use of the two LOFAR 21 cm power spectrum pipelines described in Offringa et al. (2019), which use WSCLEAN (Offringa et al. 2014) for imaging the data. During calibration or source subtraction, gridded model images are sometimes used to forward-predict (continuous) model visibilities. This requires the reverse action of gridding, sometimes referred to as de-gridding, and like gridding, this is also subject to small errors.
In typical scenarios gridding decreases the number of data samples by several orders of magnitude. In addition to decreasing the data volume, gridding may also have some other benefits:
– By imaging only the most sensitive part of the primary beam, emission that falls outside the imaged area is removed. Side lobes of off-axis emission are not removed. Off-axis emission is often harder to model and calibrate, and removing this emission can therefore be a benefit. In the context of power spectrum analysis, this might come at the cost of no longer being able to measure the largest scales and increasing the sample variance (Choudhuri et al. 2016). Alternatively, visibility-based filters exist that allow some degree of primary beam shaping without gridding (Offringa et al. 2012; Parsons et al. 2016; Atemkeng et al. 2016), but these are more limited than what is provided by a gridding anti-aliasing filter or by trimming or windowing in image space.
– During gridding, projection algorithms for correcting direction-dependent effects can be included, such as the w term, the primary beam, and the ionosphere (Cornwell et al. 2008; Bhatnagar et al. 2008, 2013; Tasse et al. 2013).
– The output of the gridding algorithm can be stored as a standardized product (e.g. a FITS image cube), which improves the overall modularity of a pipeline, which facilitates analysing and comparing with different gridders or power spectrum pipelines. This can help in localizing the cause of excess power (such as foreground sources that have not been subtracted properly) and allows using code from regular imaging software that is rigorously tested.
Separating the redshifted 21 cm signals from the Galactic and extra-galactic foregrounds requires a high dynamic range: whereas the foregrounds have a brightness temperature of a few thousand kelvin, the expected 21 cm signals are only a few millikelvin. In order to use an approach that includes gridding, the gridding algorithm needs to have a high accuracy to avoid biasing the power spectrum measurements, while it is at the same time necessary to process large data volumes within a reasonable time. In this paper, we analyse the influence of gridding on the accuracy of the 21 cm power spectrum. We investigate the magnitude at which the power spectrum is affected by the gridding, and analyse the minimum required conditions that keep the power spectrum bias sufficiently small so that the 21 cm signals from the EoR or cosmic dawn with their expected signal strength can be detected.
In Sect. 2 we describe gridding methods and list their accuracy trade-offs. Section 3 describes the method we used to calculate power spectra from gridded images. The simulated data are described in Sect. 4, and the gridding accuracy test results are presented in Sect. 5. In Sect. 6 we discuss the results and draw conclusions.
2. Gridding
To understand the effects caused by interferometric gridding, we start by describing some of the foundations of gridding. An interferometer samples the complex visibility function,
where u, v, w specifies a baseline coordinate in the coordinate system of the array, A is the primary-beam function, I is the sky function, and l, m specifies a cosine sky coordinate. The visibility function V is the result of interferometric observing and calibration. We here ignore any errors that might occur during this process.
In polarimetry, V, A, and I become 2 × 2 matrices. Without loss of generality, we ignore polarisation and treat imaging as a scalar problem. We do not cover gridding with the element beam either and instead assume A to be unity. Application of the element beam during gridding potentially improves the sensitivity of the power spectrum because this allows including the primary-beam weighted full field of view into the power spectrum. However, the improvement in power spectrum sensitivity of gridding with the beam is small because most of the sensitivity is achieved by the central part of the beam. Using only the most sensitive part of the beam avoids parts of the beam that are less well modelled, and this has therefore been the LOFAR EoR approach in practice (Patil et al. 2017).
Imaging consists of solving I from V, thereby inverting Eq. (1). Part of imaging consists of calculating the point spread function (PSF) convolved (dirty) image I′,
with N a normalization constant that corrects for the uv coverage and ℱ𝒱 the inverse 2D Fourier transform of visibilities V with the same w value,
We do not consider deconvolution in this paper. It is common to subtract bright sources before the gridding step (Beardsley et al. 2016; Patil et al. 2017; Trott et al. 2016).
Gridding consists of discretising the non-uniformly sampled u, v, w values. We considered gridding with and without w-term correction, and investigated the accuracy that different w-term correcting methods achieve. The simplest method of gridding is to add the value of each visibility to the closest uv grid point (nearest-neighbour gridding) and ignoring its w value. Such gridding introduces two types of errors:
1. Aliasing: Visibilities and the uv sampling function might have frequencies beyond the corresponding Nyquist rate of the uv grid (i.e. they are not band limited at the resolution of the uv grid). In other words, sources and side lobes might exist outside the imaging field of view. Structures outside the field of view are aliased; they appear as ghost structures within the imaging field of view.
2. Discretisation of u, v, and w values: The true continuous uv value of the sample is discretised to match the regular uv grid. This causes smearing and decorrelation of emission. Similarly, any non-coplanarity of the array causes visibilities with different w terms to be averaged together, which also leads to smearing and decorrelation.
Visibilities can be band limited by low-pass filtering the visibilities, thereby avoiding aliasing. The common method to do this is by convolving the visibilities with a smoothing kernel, the so-called anti-aliasing kernel (Brouw 1975; Schwab 1980). Gridding with the element beam A (see Eq. (1)) can act as a natural anti-aliasing kernel (Bhatnagar et al. 2008). When the convolution kernel is a continuous function (such as a sinc function), convolutional gridding has the additional benefit that the contribution of the continuous visibilities can be evaluated precisely at each discretised uv position, which solves the second inaccuracy (i.e. point 2 listed above) for u and v. The w term can be corrected for by one of several w-correction methods, such as convolving each visibility with a w-correction term that projects it onto the w = 0 plane (Cornwell et al. 2008).
By convolving each visibility with the combination of an anti-alias kernel and a w-term correction kernel, it is theoretically possible to perform gridding that matches the accuracy of a direct Fourier transform. In practice, gridders apply further simplifications for various reasons:
– To reduce the computational cost of the convolution, the spatial anti-aliasing low-pass kernel is windowed to a typical size of seven uv cells. The prolate spheroidal wave function is commonly used as a compact low-pass filtering kernel and has several beneficial properties for gridding (Brouw 1975). It is sometimes approximated by the Kaiser-Bessel function, which is easier to evaluate (e.g. Offringa et al. 2014).
– The kernels are pre-calculated and interpolated to avoid evaluation of a computationally expensive function for each visibility. This requires discretisation of the uv space in which it can be evaluated; this in turn results in errors. It is possible to sample the kernel more finely and thereby reduce the error. We refer to the factor by which the kernel is increased as the oversampling factor.
– Because of the pre-calculation of kernels, the w values are discretised as well. The number of w-discretisation levels can strongly affect the computational performance.
– To limit the size of the kernel in the case of w projection, the w kernel is trimmed at a point at which its power is a small fraction (e.g. 1%) of its peak power. This error is not made in a pure w-stacking algorithm because the w term is applied in the full image domain.
In this paper, we use WSCLEAN as a gridding and imaging platform, which implements several gridding engines: a w-stacking gridder (Sect. 2.1), an image-domain gridder (Sect. 2.2), and inversion using a direct Fourier transform. The latter implements an imaging operation that is computationally the most expensive but accurate up to the floating-point precision, and is used as the ground truth in this work. We use WSCLEAN version 2.6, released on 11 June 2018. WSCLEAN is an open-source program1. Even though we use a specific gridder implementation, we analyse generic gridding parameters that are applicable to most imaging algorithms. We include an analysis of standard convolutional gridding by turning w stacking off. These results are therefore applicable to any standard (e.g. prolate-spheroidal based) gridding implementation, such as the implementation in CASA. Additionally, because WSCLEAN does not implement w projection, we include an analysis of the w-projection implementation in CASA (McMullin et al. 2007).
2.1. w-stacking gridding
In the w-stacking algorithm, visibilities are gridded on a number of w planes, each corresponding to a certain range of w values. All planes are separately Fourier transformed to the image domain, and the w term is subsequently corrected for by applying multiplication of the images by the spatially varying w term. The standard gridding engine of WSCLEAN applies the w-stacking algorithm to correct for w terms (Offringa et al. 2014). We used this gridder to investigate the influence of gridding settings on the power spectrum. Configurable gridding parameters that we investigated are listed below.
– Anti-aliasing kernel size. The width of the convolution kernel in number of uv cells. The WSCLEAN default for this setting is 7, which indicates that the kernel covers 7 × 7 uv cells.
– Kernel oversampling factor. For performance reasons, the kernel is tabulated beforehand and is not directly evaluated. When a value is gridded on the uv plane, the nearest tabulated kernel is selected. Other interpolation methods such as linear interpolation help to reduce the error, but increase the per-visibility cost and are not implemented in WSCLEAN. In WSCLEAN, the default is to oversample the kernel 63 times, which implies a pre-computed table of size 7 × 63.
– Gridding function. By default, WSCLEAN uses a sinc function windowed by a Kaiser-Bessel function (Kaiser & Schafer 1980), which approximates a discrete prolate spheroidal sequence (DPSS).
– Padding factor. Factor by which the image size is increased beyond the field of interest to avoid edge issues. By default, WSCLEAN uses a factor of 1.2.
– Number of w layers. Discrete number of w values. Visibilities are moved to their nearest w value. By default, WSCLEAN uses a number of w values such that the maximum phase decorrelation, which occurs at the edge pixels of the image, is 1 radian.
In the w-stacking implementation, all calculations are performed with 64-bit (IEEE 754-2008) double-precision floating-point values.
2.2. Image-domain gridding
Image-domain gridding (IDG; van der Tol et al. 2018) is a method that calculates the contribution of visibilities in image space. Visibilities are grouped into slightly overlapping uv subgrids, each covering a small part of the uv plane (typically 322 to 1282 cells). The contribution of the visibilities in their subgrid is then calculated by directly evaluating the image-domain (lm space) contribution using a direct Fourier transform, taking into account the offset of the subgrid in uv space. After the contribution of all visibilities within the subgrid is calculated, a fast Fourier transform (FFT) is used to transform each subgrid from image domain to uv space, and the contributions of all the subgrids are added to the global uv plane. Finally, the full uv plane is transformed into the image using an FFT.
While this method performs more computations than convolutional gridding, it can be executed in parallel and is highly efficient when graphics processing units (GPUs) are used, resulting in a high gridding throughput. IDG has been shown to speed up the gridding by an order of magnitude compared to traditional gridding algorithms (Veenboer et al. 2017).
When IDG is used, anti-aliasing and w-term corrections are applied in image space and are evaluated directly. This implies that IDG is not affected by some of the errors made in traditional gridding algorithms, such as the discretisation of w values and the discretised gridding kernel. When IDG is used to predict visibilities, it has been shown that IDG has a higher per-visibility accuracy than the w-stacking algorithm of WSCLEAN (van der Tol et al. 2018). Most of the calculations within IDG are calculated with 32-bit single-precision floating-point values (IEEE 754-2008).
The IDG implementation allows additional gridding terms, such as w terms, primary-beam terms (a terms), and other direction-dependent effects. Unlike the a-projection algorithm (Bhatnagar et al. 2008, 2013; Tasse et al. 2013), the kernels are applied as multiplications in image space. Primary-beam corrections could be important in the context of EoR experiments, in particular to correct for instrumental polarization leakage (Asad et al. 2015; Jagannathan et al. 2017). This is critical in power spectrum estimation (Jelić et al. 2008) and for tomography with the SKA (Mellema et al. 2015). Full a correction also allows per-station beam weighting during imaging. This allows an optimally weighted integration of the data. We do not focus on the errors associated with including such corrections, and instead limit the scope of this article to the gridding errors involved in the calculation of w-term corrected images without other direction-dependent effects.
IDG is open source and available under the GNU General Public License v3.02, and has been integrated into WSCLEAN. Therefore, IDG can be combined with the deconvolution algorithms implemented in WSCLEAN, such as the auto-masked multi-scale multi-frequency deconvolution algorithm (Offringa & Smirnov 2017).
We used the IDG default settings, which include an optimised anti-aliasing kernel as described in van der Tol et al. (2018). For our setup, IDG selected a subgrid size of 40 × 40 elements. IDG employs w stacking to keep the size of the kernel, trimmed at the 1% level, within the subgrid size. There is no oversampling parameter in IDG because IDG always calculates the contribution of a visibility in real space, which implies that the uv kernel is not discretised.
2.3. w-projection gridding
The w-projection algorithm applies the w correction as a convolution in uv space (Cornwell et al. 2008). To apply the w-projection algorithm, we used the tclean task in CASA version 5.1.1-5 (McMullin et al. 2007). The w-projection algorithm shares many of the configurable parameters of w stacking, such as oversampling, anti-aliasing kernel size, and padding, but these are not exposed in the tclean interface, and we therefore used the default values: a prolate spheroidal kernel of 3 × 3, oversampling of a factor of 4, and a padding factor of 1.2. As with w stacking, the w direction needs to be discretised for w projection in order to pre-calculate a limited set of the w kernels, and this leads to a similar parameter that sets the number of discretised w values (the wprojplanes parameter in CASA). In our analysis, we used wprojplanes=256. Furthermore, w projection limits the w kernel to a specific size, typically to the size at which the power sinks below 1% of the peak power (Cornwell et al. 2008).
3. Power spectra
The 21 cm power spectra quantify the spatial and spectral fluctuations found in the data. We calculated the power spectrum values from image cubes. The calculations follow those described in Offringa et al. (2019), and consist of the following steps: (i) spatial Fourier transformation; (ii) normalisation of the uv values by dividing out the instrumental uv response and converting them into kelvin; (iii) a generalised inverse-variance weighted (with a diagonal matrix) least-squares Fourier transform along the line-of-sight direction; and (iv) cylindrical or spherical averaging. We analysed the data in two ways, as described below.
– Using a foreground-avoidance strategy. We measured the power bias caused by gridding inside the foreground-free EoR window of a cylindrically averaged power spectrum. In this approach, the modes inside the foreground wedge are not used.
– Using a foreground-removal strategy. We used Gaussian process regression (GPR; Mertens et al. 2018) to remove residual foregrounds after gridding, and analysed the resulting full power spectra.
A Blackman-Harris window was used both during the spatial Fourier transform and during the least-squares inversion along the line of sight. We calculated the power spectra for baseline sizes of 50–250λ, corresponding to k⊥-values of approximately 0.05–0.3 h Mpc−1. These same settings are used in the analysis of LOFAR EoR observations (Patil et al. 2017; Mertens et al., in prep.).
4. Simulated data
To analyse the gridding accuracy, we simulated a typical EoR observation with point sources drawn from a realistic population distribution. We used a distribution determined from low-frequency (154 MHz) observations (Franzen et al. 2016):
Using this distribution, we predict sources with intrinsic (i.e. before applying the primary beam) flux densities between 1 mJy and 10 Jy in an area with a diameter of 90°, resulting in a model of approximately one million sources. We assumed that all sources with an apparent flux density (i.e. after multiplying each source with the corresponding primary beam response) of at least 100 mJy can be subtracted from the visibilities before gridding, which is realistic for LOFAR observations: in LOFAR EoR observations, the residual peak flux after direction-dependent subtraction of bright sources, imaged with a maximum baseline of 250λ, is about 70 mJy in the NCP field (Yatawatta et al. 2013) and 150 mJy in the 3C 196 field (Offringa et al., in prep.). Therefore we evaluated the average LOFAR primary beam value for each source and removed sources with an apparent brightness > 100 mJy. To further limit the number of sources to be predicted, we also removed sources with an apparent flux density < 500 μJy, resulting in a model with ∼15 000 sources that are distributed out to 45° away from the phase centre. The spectral index of each source was drawn from a normal distribution with an average spectral index of α = −0.8 (with α defined by S(ν) = S0(ν/ν0)α) and a standard deviation of 0.2. These distribution parameters match those of the weakest sources found by Hurley-Walker et al. (2017). We did not specifically simulate flattening of fainter (starburst) galaxies or special classes of sources such as ultra-steep spectrum sources, compact steep spectrum sources or gigahertz-peaked sources sources that can have steep or curved spectra at the frequencies of interest (see Callingham et al. 2017 for an overview).
The standard LOFAR software tool DPPP3 was used to predict fully accurate visibilities from the model by analytical evaluation of the visibility function and primary-beam model. The observing time, phasing centre, and antenna positions were taken from a 6 h night-time 3C 196 observation. In addition to gridding, several other processing steps can cause excess power, such as missing data due to radio-frequency interference excision (Offringa et al. 2019) and calibration with an incomplete model (Patil et al. 2016; Barry et al. 2016; Mouri Sardarabadi & Koopmans 2018). We limited ourselves here to the effects of gridding, and therefore predict perfect data without flags or calibration errors. We did include missing channels in our simulation, however, which are unavoidable in LOFAR data because of channel aliasing at the sub-band edges. The same effect is also the reason for the loss of the sub-band edge channels of the Murchison Widefield Array (MWA; Tingay et al. 2013) (Offringa et al. 2015). In LOFAR EoR processing, two 3 kHz channels at each side of the sub-band were removed before averaging, leaving 60 of 64 channels in the data for each 195 kHz sub-band. These data were averaged by a factor of 12 in frequency and 6 in time, resulting in 12 s time steps and 5 channels per sub-band, with gaps between the sub-bands. The decorrelation caused by averaging is ≪1%. We here directly forward-predict the averaged data, and are therefore not affected by time or frequency smearing. We simulated data between 115–134 MHz, that is, 94 sub-bands in total, each with 5 channels.
5. Results
To assess the effects of gridding, we independently imaged each of the 470 frequency channels of our simulated data (Sect. 4) using WSCLEAN, and constructed 21 cm power spectra from the resulting image cube. These power spectra were compared to ground-truth power spectra that were made from the direct-Fourier transformed images.
The images cover 3° by 3° on the sky with 360 × 360 pixels. Our limited imaging field of view implies that only the most sensitive part of the primary beam is used. In the corners of the images, the beam has a gain of approximately 75%.
5.1. Foreground-avoidance results
We started by investigating a foreground-avoidance strategy. In this scenario, the modes that are dominated by foregrounds are not used in the final power spectra, and we therefore did not perform Gaussian progress regression to remove the wedge. Before we performed the k∥ transform, a third-order polynomial fit in frequency direction was subtracted from the uv cube separately from the real and imaginary parts. This removed both EoR and foreground power from the low k∥-modes inside the wedge. This decreased the dynamic range requirements of the generalized k∥ Fourier transform, thereby avoiding some artefacts that are not the focus of this paper, without biasing the power spectrum in the parts that we measured.
Figure 1 shows cylindrically averaged power spectra for various gridding methods to provide an overview of the artefacts that each method produces. The foreground wedge structure is clearly visible. Power under the wedge is saturated in the colour scale used in these plots. The strongest modes within the wedge have values of 1011 mK2h−3 Mpc3, which implies a dynamic range of over ten orders of magnitude between contaminated and uncontaminated modes. A horizontal line at k = 2.4 h Mpc−1 (delay of 5 μs) is caused by the spectral gap between sub-bands. Figure 1 demonstrates that gridding can cause different artefacts in the 2D power spectra: excess power that is strongest at low k∥-values (nearest-neighbour gridding), a uniform level of excess power (default WSCLEAN settings: w stacking with 32 w layers, kernel size of 7, 1.2× padding, 63× oversampling), and excess power at the longest baselines (limited w sampling).
 |
Fig. 1. Cylindrically averaged power spectra for various gridding settings. From left to right, top to bottom: direct FT inversion, nearest-neighbour gridding (no oversampling), default settings for WSCLEAN, default settings for IDG, increased oversampling and kernel size settings for WSCLEAN without w correction and including w correction, but with a low number of w layers. Nearest-neighbour gridding results are drawn with a different colour scale. Black dashed line: horizon wedge. Pink dashed line: same with additional space for the windowing function. Blue dashed line: primary beam (5°) wedge. Gridding parameters are abbreviated as follows: o = oversampling factor, s = gridding kernel size, nwl = number of w-layers, and p = padding factor. |
An overview of the effect of various settings in a spherically averaged power spectrum is given in Fig. 2. Only modes outside the wedge were integrated. We added a delay of 0.6 μs to the theoretical horizon wedge line to also exclude the convolution kernel size resulting from the windowing in the k∥ transform; this is shown by the pink dashed line in Fig. 1. When the different methods are compared by their excess power above the wedge, nearest-neighbour gridding results in strong excess power, with an excess of about 100 mK. The w-projection implementation in CASA shows an excess of ∼20−50 mK. Both exceed nearly all 21 cm EoR models. With the default WSCLEAN settings, this decreases to 1 mK at low k-values and to 10 mK at high k-values. Gridding with IDG results in very accurate results with the least excess power (1 to 10 μK) of all tests.
 |
Fig. 2. Spherically averaged foreground-avoidance power spectra errors (absolute difference) without GPR foreground subtraction, compared to the directly Fourier transformed data. k values that fall under the wedge are excluded. Gridding parameters are abbreviated as follows: o = oversampling factor, s = gridding kernel size, nwl = number of w-layers, and p = padding factor. |
Figure 3 shows various foreground-avoiding power spectra, each visualising the result of changing the value of one parameter while the other parameters are fixed to a setting that reflects a high accuracy for that parameter. For each parameter, we determined the least computationally expensive setting that would still allow a detection of the 21 cm signals from the EoR. The 21 cm signals are expected to have a brightness of a few millikelvin (e.g. Greig & Mesinger 2015; Ghara et al. 2018), and we therefore required that less than 0.1 mK power is added in the range of k = 0.5–1 h Mpc−1. The parameter settings are summarised in Table 1.
 |
Fig. 3. Effect of gridding accuracy for several gridding parameters: (a) kernel oversampling (Sect. 5.1.1), (b) kernel size (Sect. 5.1.2), (c) the number of w-discretisation levels (Sect. 5.1.3), (d) gridding kernel function and IDG comparison (Sects. 5.1.4 and 5.1.5), and (e) padding (Sect. 5.1.6). The plots describe the absolute error of spherically averaged power spectrum measurements using a foreground-avoidance strategy. The direct FT results are used as ground truth. Each plot shows the dependency on one parameter, and the other parameters are kept at their highest accuracy setting (see Table 1). |
Gridding parameter values.
5.1.1. Oversampling
The results indicate that the oversampling factor is the most crucial parameter for avoiding gridding excess power. Figure 3a shows that the default setting of 63 for WSCLEAN adds a few millikelvin excess power. Therefore, the default settings do not meet the minimum accuracy. Oversampling with a factor of 4 × 103 limits the excess noise below 0.1 mK (34 μK at k = 1 h Mpc−1). With an oversampling of approximately 8 × 103 times, the excess power is no longer reduced by increasing the oversampling further, indicating that the error due to sampling of the kernel is no longer the limiting factor. The added computational cost of increasing the oversampling factor is relatively small because the gridding kernel is pre-calculated. Increasing the oversampling from 63 to 8 × 103 increases the imaging time by less than 10%. The need for large oversampling factors also explains why the w-projection result in Fig. 2, for which an oversampling factor of 4 was used, shows a high level of excess power.
5.1.2. Kernel size
As shown in Fig. 3b, a kernel size of 3 is enough to limit the excess noise below 0.1 mK at k = 1 h Mpc−1. This implies that the default size of 7 can be decreased for EoR experiments. However, decreasing the kernel size from 7 to 3 does not improve gridding speed (Offringa et al. 2014).
5.1.3. w layers
The bottom left figure of Fig. 1 shows the result of applying no w-term correction. This demonstrates that w correction is not strictly required to avoid excess noise. However, the lack of w correction causes some decorrelation to occur, which in turn reduces sensitivity. The amount of decorrelation is dependent on the image size, baseline length, and array configuration. When the w-term correction was disabled, we measured a root mean square error of 9% over the full image, and an average loss of 8% in source strength at 1.5° distance for our imaging configuration (3° × 3° FOV, LOFAR baselines up to 250λ). Figure 3c shows that using a small number of w layers of 16, for example, causes more excess power than using no w layers at all. This can be explained by how w stacking works: it groups visibilities with similar w terms and uses a constant w correction for them. Because the w term depends on frequency, whereas the maximum w term (and therefore the Δw step size) is limited by the baseline length threshold (250λ), this causes fluctuations over frequency. To avoid significant decorrelation and excess noise, at least 300 w layers are necessary. Using 300 w layers increases the imaging time by a factor of 3 compared to no w correction.
5.1.4. Kernel function
Figure 3d shows the results for gridding with different kernel functions: a truncated sinc-function, the Kaiser-Bessel function, and a sinc windowed by a truncated Gaussian, Kaiser-Bessel, and Blackman-Nutall function. Windows with stronger side-lobe suppression cause less excess power. This underlines that kernels with discontinuities at the border will cause spectral fluctuations.
5.1.5. IDG
In addition to different kernel functions, Fig. 3d also shows the IDG results with CPU and GPU, which both show a low excess power of a few μK over most of the measured k range. The two results show slightly different results, which might be caused by different implementations of the sin and cos functions or the use of a different FFT library.
5.1.6. Padding
Padding mitigates edge effects in the image domain. As demonstrated by Fig. 3e, padding has no significant effect on the gridding excess power in an analysis of 21 cm data. This can be explained by the fact that the edge effects do not cause spectral fluctuations.
5.1.7. Numerical precision
We compared a direct Fourier transform performed with single-precision floats and with double-precision floats, and observed no significant differences between the two results. This suggests that gridding with single-precision floating point calculations is accurate enough for EoR experiments. In general, adding a large number of values together can result in a loss of precision, and with 2.6 × 109 visibilities, this might seem inevitable. A reason why in practice we see no difference between single- and double-precision floats is that values in image space grow with the square root of the number of samples. In uv space, values are naturally dispersed because they are gridded in different uv bins.
5.2. Foreground-subtraction results
In this section we discuss the results of applying GPR to the data to remove the emission in the wedge, and subsequently including the foreground-contaminated modes in the power spectra. GPR has the potential to cause some bias of the signal (Mertens et al. 2018). A full quantisation of this bias is beyond the scope of this paper, but we made a simple simulation to test the performance of GPR with the settings and foregrounds that are used in this paper. This simulation consisted of the predicted foregrounds with the most accurate gridding settings, a noise equivalent to 100 nights of 12 h, and a realistic system-equivalent flux density for LOFAR of 4000 Jy per station, and a 21 cm signal covering a wide range of variances and frequency coherence scales.
For each of these signal strengths and coherence-scales, ten realizations of noise and signal were generated, and GPR was performed on the summed images. The ratio of input over recovered signal power-spectra was computed for three different ranges of scales. We find biases in the range 0.7–2.5, and overall similar results to what was found in Mertens et al. (2018).
We continued by applying GPR to the foreground-only image cubes with different gridding settings, and constructed power spectra from the GPR residuals. Figure 4 shows the cylindrically averaged power spectra after the foregrounds were removed with GPR. In the direct Fourier transform (FT) result, the residual foreground power is about 2 mK2h−3 Mpc3, which is a factor of ∼1011 lower than the unsubtracted results. GPR also successfully removes the horizontal band of power at 5 μs that is caused by the sub-band gaps.
 |
Fig. 4. Residual cylindrically averaged power spectra after applying GPR. From left to right, top to bottom: direct FT inversion, nearest-neighbour gridding (no oversampling), default settings for WSCLEAN, default settings for IDG, increased oversampling and kernel size settings for WSCLEAN, and the same, but with a high number of w layers. To highlight the excess power, not all power spectra use the same colour maps. Black dashed line: Horizon wedge. Pink dashed line: Same with additional space for the windowing function. Blue dashed line: primary beam (5°) wedge. Gridding parameters are abbreviated as follows: o = oversampling factor, s = gridding kernel size, nwl = number of w-layers, and p = padding factor. |
Figure 5 shows the spherically averaged power spectra that include all modes (including foreground modes) after foreground removal. Foreground removal allows the use of the low-k foreground modes, down to k = 0.07 h Mpc−1. LOFAR is much more sensitive at these scales and compared to foreground avoidance, it requires less observing time to achieve comparable EoR constraints.
 |
Fig. 5. Spherically averaged foreground-subtraction power spectra errors (absolute difference) after foreground removal with GPR. The ground truth (power spectrum from directly Fourier transformed data) was subtracted from each resulting power spectrum. All k values are included. Gridding parameters are abbreviated as follows: o = oversampling factor, s = gridding kernel size, nwl = number of w layers, and p = padding factor. |
From the results, it is clear that GPR cannot fully remove the excess gridding power introduced by nearest-neighbour gridding or insufficient sampling of the kernel, although even in these cases, it reduces the wedge power considerably. The default WSCLEAN settings show an excess of 0.1 mK at low-k values of 0.07 h Mpc−1 up to approximately 10 mK at high-k values of 0.9 h Mpc−1. We define an acceptable excess power in the foreground-subtraction strategy to be at most 0.1 mK at k = 0.1 h Mpc−1. With this requirement, the default settings do not result in sufficient accuracy. To reach this level of accuracy, the only parameter that requires tuning is the oversampling factor. This is in contrast to the foreground-avoidance strategy, where increased w quantisation and oversampling factor are required to reach an acceptable level of excess power. GPR is able to remove excess power caused by w quantisation, making it possible to use the default of 32 w layers. The GPR results with IDG as gridding algorithm meet the required accuracy, with an excess power of 3 μK at k = 0.1 h Mpc−1 and, similar to the foreground avoidance results, this overall shows the best accuracy.
5.3. Required w-stacking settings
The last column of Table 1 lists the minimum (least expensive) w-stacking gridding settings that are required to achieve a maximum excess power of 0.1 mK at k = 1 h Mpc−1 and 0.1 h Mpc−1 in the case of foreground avoidance and foreground subtraction, respectively. Compared to the default settings, constraining the excess power requires increasing the oversampling factor and the number of w layers, while the kernel size and padding can be decreased.
5.4. Computational requirements
In this section we report the computational requirements for the default and minimum gridding settings as listed in Table 1. We compare this to the performance of IDG and a direct FT. We used 15 compute nodes from the LOFAR EoR “Dawn” cluster, which each have the following specifications: two Intel Xeon E5-2670v3 CPUs (for a total of 24 physical cores), 128 GB of memory, and four NVIDIA Tesla K40 GPUs (unless noted otherwise, we used only one GPU in our experiments). The CPUs provide a combined peak performance of 2.0 TFlop/s (single precision, using FMA and AVX2 instructions), while one Tesla K40 GPU has a single-precision peak performance of 5.0 TFlop/s. The imaging was performed in parallel on the 15 nodes.
We measured the run time for an imaging task that consisted of creating the PSF and the four Stokes images (I, Q, U, V) for each of the 94 sub-bands, with a total of 2.6 × 109 visibilities. We report the results in Table 2. We did not include the calculation of the LOFAR primary beam in the run-time measurement.
Imaging runtime on the “Dawn” cluster, using both CPU sockets of each of the 15 compute nodes.
These results illustrate that a direct transform takes too much time in practice. w projection is significantly faster (more than 84 times faster than the direct transform), and w stacking is even faster. The difference in runtime for w stacking with a larger kernel is explained as follows: (1) the number of w layers is increased from 16 to 300 (this increases run time); (2) the padding factor is reduced from 1.2 to 1.0 (no padding, this reduces run time). Using kernels smaller than 7 pixels (in case of w stacking or w projection) does not significantly reduce run time (Offringa et al. 2014), and we therefored use 7 pixels. The CPU version of IDG is about as fast as w stacking with a kernel size of 7, while the GPU version of IDG is much faster. The accuracy of the CPU and GPU versions of IDG is the same.
Veenboer et al. (2017) reported that the performance of IDG is not bound by the number of (floating-point) operations alone. They used throughput, measured as the number of visibilities processed per second as a (floating-point) operation-agnostic performance metric. Throughput therefore provides a meaningful way to express imaging performance, and we used it to compare the performance of the different imaging algorithms.
Given the imaging parameters and the run-time measurements, we computed the achieved imaging throughput per node. It is listed in the rightmost column of Table 2. We note that our visibility count considers the Stokes parameters separately, while Veenboer et al. (2017) considered the four parameters as a single visibility. Taking this into account, and correcting for the faster GPU (GeForce GTX 1080, 9.2 TFLOP/s) in their measurements, we achieve only 5% of the throughput that they report. The difference is mainly caused by the overhead of applying the IDG gridder kernel as part of a larger application (WSCLEAN) with all associated practical overheads, such as disk access and reordering of visibilities.
To place these results in perspective, we also measured the calibration run time with SAGECAL-CO (Kazemi et al. 2011; Yatawatta 2016), which on the same compute nodes (using 15 nodes with all four GPUs) requires several days. The required imaging time is therefore not a bottleneck in the full LOFAR EoR data processing pipeline (Patil et al. 2017). Nevertheless, fast imaging is very useful for analysis.
6. Discussion and conclusions
We have shown the bias that is induced by gridding visibilities on a regular grid with various settings, using traditional convolutional gridding and IDG. If the brightest sources are removed before gridding, the gridding excess power resulting from traditional convolution gridding of LOFAR data sets ranges from approximately 100 mK with simple gridding settings to 10 μK with tuned gridding settings. IDG has a superior accuracy and requires no tuning in accuracies of 2 μK at k = 0.07 h Mpc−1 in a foreground-removal approach up to at most 30 μK for all measured k values in either a foreground-removal or foreground-avoidance approach. The expected strength of the redshifted 21 cm signal is a few millikelvin, therefore the excess power caused by either gridding method can be limited to an insignificant level well below the noise level. This also shows that the SKA will not be limited by gridding noise even in extremely deep integrations. The improved uv coverage of the SKA over LOFAR is likely to lower the gridding noise further.
The two parameters that are crucial for 21 cm experiments are the oversampling rate of the kernel and the quantisation in the w direction. The reason for this is that the discretisation of u, v, and w causes frequency-dependent errors. These spectral fluctuations make it harder to separate the astronomical foreground from the 21 cm signals. For the LOFAR EoR case, where the field of view is 3° × 3° and a maximum baseline of 250λ is used, the kernel is required to be at least oversampled by a factor of 4000, implying a table of at least 28 000 values in the case of a gridding kernel of size 7. The w direction is required to have at least 500 quantisation levels. Alternatively, using an algorithm without w correction also produces good power spectrum results, but leads to a decorrelation loss of ∼8% for the LOFAR field of view.
The current LOFAR EoR results of Δ2 < (79.6 mK)2 at k = 0.053 h Mpc−1 (one night; Patil et al. 2017) and Δ2 < (72.4 mK)2 at k = 0.075 h Mpc−1 (ten nights; Mertens et al., in prep.) are not significantly affected by gridding noise. These results use foreground subtraction and different kernel oversampling settings. In both cases a higher kernel oversampling setting was used than in the default WSCLEAN setting. The default settings would have resulted in a contribution of approximately 0.1 mK to the spherically averaged power spectrum measurements (Fig. 5).
We here focussed on the imaging accuracy. A related operation that is required during calibration is the prediction of model visibilities from a sky model. The prediction accuracy has a reciprocate relation to the imaging accuracy, and our results therefore imply that visibility prediction using gridding algorithms can be made to have sufficient accuracy for 21 cm EoR data calibration. This is crucial for calibration with models that have very many sources, as will be required for the SKA.
Our results imply that the use of the w-projection algorithm (Cornwell et al. 2008) as a w-term correcting algorithm is likely not an option for EoR experiments because oversampling the gridding kernel is inherently difficult in w projection because very many w-value kernels need to be tabulated. For example, to oversample 4095 times, the memory cost for the two-dimensional w kernels increases by a factor of 40952. With an average kernel size of 322 pixels and 512 w-projection planes, this would require 33 terabyte of memory. Barry et al. (2019) showed that for a homogenous array and a beam that is separable in the direction on the sky, large oversampling is possible using FHD. The IDG algorithm is an interesting alternative, in particular when ionospheric or beam terms are necessary during gridding. Faceted imaging has shown to be an effective approach for high-quality low-frequency observations (Kogan & Greisen 2009; Weeren et al. 2016; Tasse et al. 2018), and is used for example in the LOFAR Two-metre Sky Survey (Shimwell et al. 2017). However, faceted imaging causes discontinuities in image space and is therefore unsuitable for 21 cm power spectra in which the Fourier modes of the image are measured.
The high accuracy and speed of IDG, combined with its possibility for beam and ionospheric corrections, makes IDG an attractive option for experiments that try to detect the 21 cm signals from the EoR. These properties will in particular be important for processing of the future SKA EoR observations.
The WSCLEAN software is available at http://wsclean.sourceforge.net/
The IDG software is available at https://gitlab.com/astron-idg/idg
DPPP is available at https://github.com/lofar-astron/DP3
Acknowledgments
We thank W. Brouw for useful comments. F. Mertens and L. V. E. Koopmans would like to acknowledge support from an SKA-NL Roadmap grant from the Dutch ministry of OCW. S. van der Tol was supported by the Astronomy ESFRI and Research Infrastructure Cluster, part of the European Union’s Horizon 2020 research and innovation programme, under grant agreement No 653477.
References
- Asad, K. M. B., Koopmans, L. V. E., Jelić, V., et al. 2015, MNRAS, 451, 3709 [NASA ADS] [CrossRef] [Google Scholar]
- Atemkeng, M. T., Smirnov, O. M., Tasse, C., Foster, G., & Jonas, J. 2016, MNRAS, 462, 2542 [NASA ADS] [CrossRef] [Google Scholar]
- Barry, N., Hazelton, B., Sullivan, I., Morales, M. F., & Pober, J. C. 2016, MNRAS, 461, 3135 [NASA ADS] [CrossRef] [Google Scholar]
- Barry, N., Beardsley, A. P., Byrne, R., et al. 2019, PASA, 36, e026 [NASA ADS] [CrossRef] [Google Scholar]
- Beardsley, A. P., Hazelton, B. J., Sullivan, I. S., et al. 2016, ApJ, 833, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Bhatnagar, S., Cornwell, T. J., Golap, K., & Uson, J. M. 2008, A&A, 487, 419 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bhatnagar, S., Rau, U., & Golap, K. 2013, ApJ, 770, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Brouw, W. N. 1975, Meth. Comput. Phys., 14, 131 [Google Scholar]
- Callingham, J. R., Ekers, R. D., Gaensler, B. M., et al. 2017, ApJ, 836, 174 [NASA ADS] [CrossRef] [Google Scholar]
- Carozzi, T. D. 2015, MNRAS, 451, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Choudhuri, S., Bharadwaj, S., Chatterjee, S., et al. 2016, MNRAS, 463, 4093 [NASA ADS] [CrossRef] [Google Scholar]
- Choudhuri, S., Dutta, P., & Bharadwaj, S. 2018, MNRAS, 483, 3910 [NASA ADS] [CrossRef] [Google Scholar]
- Cornwell, T. J., Golap, K., & Bhatnagar, S. 2008, IEEE J. Sel. Top. Signal Process., 2, 647 [NASA ADS] [CrossRef] [Google Scholar]
- DeBoer, D. R., Parsons, A. R., Aguirre, J. E., et al. 2017, PASP, 129, 045001 [NASA ADS] [CrossRef] [Google Scholar]
- Dewdney, P. E., Turner, W., Millenaar, R., et al. 2013, SKA-TEL-SKO-DD-001 [Google Scholar]
- Eastwood, M. W., Anderson, M. M., Monroe, R. M., et al. 2018, AJ, 156, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Fialkov, A., Tong, E., Garsden, H., et al. 2018, MNRAS, 478, 4193 [NASA ADS] [Google Scholar]
- Franzen, T. M. O., Jackson, C. A., Offringa, A. R., et al. 2016, MNRAS, 459, 3314 [NASA ADS] [CrossRef] [Google Scholar]
- Furlanetto, S. R., Oh, S. P., & Briggs, F. H. 2006, Phys. Rep., 433, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Ghara, R., Mellema, G., Giri, S. K., et al. 2018, MNRAS, 476, 1741 [NASA ADS] [CrossRef] [Google Scholar]
- Ghosh, A., Mertens, F. G., & Koopmans, L. V. E. 2018, MNRAS, 474, 4552 [NASA ADS] [CrossRef] [Google Scholar]
- Greig, B., & Mesinger, A. 2015, MNRAS, 449, 4246 [NASA ADS] [CrossRef] [Google Scholar]
- Hurley-Walker, N., Callingham, J. R., Hancock, P. J., et al. 2017, MNRAS, 464, 1146 [NASA ADS] [CrossRef] [Google Scholar]
- Iliev, I. T., Shapiro, P. R., Ferrara, A., & Martel, H. 2002, ApJ, 572, L123 [NASA ADS] [CrossRef] [Google Scholar]
- Jacobs, D. C., Hazelton, B. J., Trott, C. M., et al. 2016, ApJ, 825, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Jagannathan, P., Bhatnagar, S., Rau, U., & Taylor, A. R. 2017, AJ, 154, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Jelić, V., Zaroubi, S., Labropoulos, P., et al. 2008, MNRAS, 389, 1319 [NASA ADS] [CrossRef] [Google Scholar]
- Kaiser, J., & Schafer, R. 1980, IEEE Trans. Acoust. Speech Signal Process., 28, 105 [CrossRef] [Google Scholar]
- Kazemi, S., Yatawatta, S., Zaroubi, S., et al. 2011, MNRAS, 414, 1656 [NASA ADS] [CrossRef] [Google Scholar]
- Kogan, L., & Greisen, E. W. 2009, AIPS Memo 113 [Google Scholar]
- McMullin, J. P., Waters, B., Schiebel, D., Young, W., & Golap, K. 2007, in Astronomical Data Analysis Software and Systems XVI, ASP Conf. Ser., 376, 127 [NASA ADS] [Google Scholar]
- McQuinn, M., Zahn, O., Zaldarriaga, M., Hernquist, L., & Furlanetto, S. R. 2006, ApJ, 653, 815 [NASA ADS] [CrossRef] [Google Scholar]
- Mellema, G., Koopmans, L., Shukla, H., et al. 2015, Proc. Adv. Astrophys. SKA, 10 [Google Scholar]
- Mertens, F. G., Ghosh, A., & Koopmans, L. V. E. 2018, MNRAS, 478, 3640 [NASA ADS] [Google Scholar]
- Morales, M. F. 2005, ApJ, 619, 678 [NASA ADS] [CrossRef] [Google Scholar]
- Mouri Sardarabadi, A., & Koopmans, L. V. E. 2018, MNRAS, 483, 5480 [NASA ADS] [CrossRef] [Google Scholar]
- Offringa, A. R., & Smirnov, O. 2017, MNRAS, 471, 301 [NASA ADS] [CrossRef] [Google Scholar]
- Offringa, A. R., de Bruyn, A. G., & Zaroubi, S. 2012, MNRAS, 422, 563 [NASA ADS] [CrossRef] [Google Scholar]
- Offringa, A. R., McKinley, B., Hurley-Walker, N., et al. 2014, MNRAS, 444, 606 [NASA ADS] [CrossRef] [Google Scholar]
- Offringa, A. R., Wayth, R. B., Hurley-Walker, N., et al. 2015, PASA, 32, e008 [NASA ADS] [CrossRef] [Google Scholar]
- Offringa, A. R., Mertens, F., & Koopmans, L. V. E. 2019, MNRAS, 484, 2866 [NASA ADS] [CrossRef] [Google Scholar]
- Paciga, G., Albert, J. G., Bandura, K., et al. 2013, MNRAS, 433, 639 [NASA ADS] [CrossRef] [Google Scholar]
- Park, J., Mesinger, A., Greig, B., & Gillet, N. 2019, MNRAS, 484, 933 [NASA ADS] [CrossRef] [Google Scholar]
- Parsons, A. R., & Backer, D. C. 2009, AJ, 138, 219 [NASA ADS] [CrossRef] [Google Scholar]
- Parsons, A. R., Pober, J., McQuinn, M., Jacobs, D., & Aguirre, J. 2012, ApJ, 753, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Parsons, A. R., Liu, A., Ali, Z. S., & Cheng, C. 2016, ApJ, 820, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Patil, A. H., Yatawatta, S., Zaroubi, S., et al. 2016, MNRAS, 463, 4317 [NASA ADS] [CrossRef] [Google Scholar]
- Patil, A. H., Yatawatta, S., Koopmans, L. V. E., et al. 2017, ApJ, 838, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Pritchard, J. R., & Loeb, A. 2012, Rep. Prog. Phys., 75, 086901 [NASA ADS] [CrossRef] [Google Scholar]
- Schwab, F. R. 1980, VLA Sci. Memo., 132, 1 [Google Scholar]
- Shimwell, T. W., Röttgering, H. J. A., Best, P. N., et al. 2017, A&A, 598, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sullivan, I. S., Morales, M. F., Hazelton, B. J., et al. 2012, ApJ, 759, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Tasse, C., van der Tol, S., van Zwieten, J., van Diepen, G., & Bhatnagar, S. 2013, A&A, 553, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tasse, C., Hugo, B., Mirmont, M., et al. 2018, A&A, 611, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tingay, S. J., Goeke, R., Bowman, J. D., et al. 2013, PASA, 30, e007 [NASA ADS] [CrossRef] [Google Scholar]
- Trott, C. M., Pindor, B., Procopio, P., et al. 2016, ApJ, 818, 139 [NASA ADS] [CrossRef] [Google Scholar]
- van der Tol, S., Veenboer, B., & Offringa, A. R. 2018, A&A, 616, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Haarlem, M. P., Wise, M. W., Gunst, A. W., et al. 2013, A&A, 556, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Veenboer, B., Petschow, M., & Romein, J. W. 2017, 2017 IEEE International Parallel and Distributed Processing Symposium (IPDPS), 545 [CrossRef] [Google Scholar]
- Weeren, R. J. T., Williams, W. L., Hardcastle, M. J., et al. 2016, ApJS, 223, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Yatawatta, S. 2016, Proc. of EUSIPCO-2016 (EURASIP) [Google Scholar]
- Yatawatta, S., de Bruyn, A. G., Brentjens, M. A., et al. 2013, A&A, 550, A136 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zaroubi, S., de Bruyn, A. G., Harker, G., et al. 2012, MNRAS, 425, 2964 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Imaging runtime on the “Dawn” cluster, using both CPU sockets of each of the 15 compute nodes.
All Figures
 |
Fig. 1. Cylindrically averaged power spectra for various gridding settings. From left to right, top to bottom: direct FT inversion, nearest-neighbour gridding (no oversampling), default settings for WSCLEAN, default settings for IDG, increased oversampling and kernel size settings for WSCLEAN without w correction and including w correction, but with a low number of w layers. Nearest-neighbour gridding results are drawn with a different colour scale. Black dashed line: horizon wedge. Pink dashed line: same with additional space for the windowing function. Blue dashed line: primary beam (5°) wedge. Gridding parameters are abbreviated as follows: o = oversampling factor, s = gridding kernel size, nwl = number of w-layers, and p = padding factor. |
| In the text | |
 |
Fig. 2. Spherically averaged foreground-avoidance power spectra errors (absolute difference) without GPR foreground subtraction, compared to the directly Fourier transformed data. k values that fall under the wedge are excluded. Gridding parameters are abbreviated as follows: o = oversampling factor, s = gridding kernel size, nwl = number of w-layers, and p = padding factor. |
| In the text | |
 |
Fig. 3. Effect of gridding accuracy for several gridding parameters: (a) kernel oversampling (Sect. 5.1.1), (b) kernel size (Sect. 5.1.2), (c) the number of w-discretisation levels (Sect. 5.1.3), (d) gridding kernel function and IDG comparison (Sects. 5.1.4 and 5.1.5), and (e) padding (Sect. 5.1.6). The plots describe the absolute error of spherically averaged power spectrum measurements using a foreground-avoidance strategy. The direct FT results are used as ground truth. Each plot shows the dependency on one parameter, and the other parameters are kept at their highest accuracy setting (see Table 1). |
| In the text | |
 |
Fig. 4. Residual cylindrically averaged power spectra after applying GPR. From left to right, top to bottom: direct FT inversion, nearest-neighbour gridding (no oversampling), default settings for WSCLEAN, default settings for IDG, increased oversampling and kernel size settings for WSCLEAN, and the same, but with a high number of w layers. To highlight the excess power, not all power spectra use the same colour maps. Black dashed line: Horizon wedge. Pink dashed line: Same with additional space for the windowing function. Blue dashed line: primary beam (5°) wedge. Gridding parameters are abbreviated as follows: o = oversampling factor, s = gridding kernel size, nwl = number of w-layers, and p = padding factor. |
| In the text | |
 |
Fig. 5. Spherically averaged foreground-subtraction power spectra errors (absolute difference) after foreground removal with GPR. The ground truth (power spectrum from directly Fourier transformed data) was subtracted from each resulting power spectrum. All k values are included. Gridding parameters are abbreviated as follows: o = oversampling factor, s = gridding kernel size, nwl = number of w layers, and p = padding factor. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.