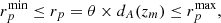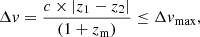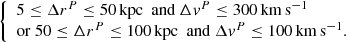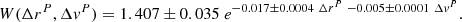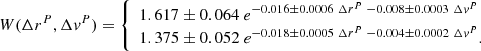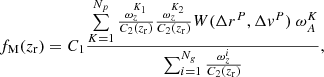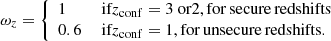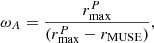| Issue |
A&A
Volume 631, November 2019
|
|
|---|---|---|
| Article Number | A87 | |
| Number of page(s) | 18 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201935597 | |
| Published online | 25 October 2019 | |
New criteria for the selection of galaxy close pairs from cosmological simulations: evolution of the major and minor merger fraction in MUSE deep fields⋆, ⋆⋆
1
Institut de Recherche en Astrophysique et Planétologie (IRAP), Université de Toulouse, CNRS, UPS, 31400 Toulouse, France
e-mail: thierry.contini@irap.omp.eu
2
Univ. Lyon, Univ. Lyon1, Ens de Lyon, CNRS, Centre de Recherche Astrophysique de Lyon UMR5574, 69230 Saint-Genis-Laval, France
3
Aix Marseille Univ., CNRS, CNES, LAM, Marseille, France
4
Instituto de Astrofísica e Ciências do Espaço, Universidade do Porto, CAUP, Rua das Estrelas, 4150-762 Porto, Portugal
5
Leiden Observatory, Leiden University, PO Box 9513, 2300, RA Leiden, The Netherlands
6
Hiroshima Astrophysical Science Center, Hiroshima University, 1-3-1 Kagamiyama, Higashi-Hiroshima, Hiroshima 739-8526, Japan
7
GEPI, Observatoire de Paris, PSL Université, CNRS, 5 Place Jules Janssen, 92190 Meudon, France
8
Leibniz-Institut für Astrophysik Potsdam (AIP), An der Sternwarte 16, 14482 Potsdam, Germany
Received:
2
April
2019
Accepted:
6
September
2019
It remains a challenge to assess the merger fraction of galaxies at different cosmic epochs in order to probe the evolution of their mass assembly. Using the ILLUSTRIS cosmological simulation project, we investigate the relation between the separation of galaxies in a pair, both in velocity and projected spatial separation space, and the probability that these interacting galaxies will merge in the future. From this analysis, we propose a new set of criteria to select close pairs of galaxies along with a new corrective term to be applied to the computation of the galaxy merger fraction. We then probe the evolution of the major and minor merger fraction using the latest Multi-Unit Spectroscopic Explorer (MUSE) deep observations over the Hubble Ultra Deep Field, Hubble Deep Field South, COSMOS-Gr30, and Abell 2744 regions. From a parent sample of 2483 galaxies with spectroscopic redshifts, we identify 366 close pairs spread over a large range of redshifts (0.2 < z < 6) and stellar masses (107 − 1011M⊙). Using the stellar mass ratio between the secondary and primary galaxy as a proxy to split the sample into major, minor, and very minor mergers, we found a total of 183 major, 142 minor, and 47 very minor close pairs corresponding to a mass ratio range of 1:1–1:6, 1:6–1:100, and lower than 1:100, respectively. Due to completeness issues, we do not consider the very minor pairs in the analysis. Overall, the major merger fraction increases up to z ≈ 2−3 reaching 25% for pairs where the most massive galaxy has a stellar mass M⋆ ≥ 109.5 M⊙. Beyond this redshift, the fraction decreases down to ∼5% at z ≈ 6. The major merger fraction for lower-mass primary galaxies with M⋆ ≤ 109.5 M⊙ seems to follow a more constant evolutionary trend with redshift. Thanks to the addition of new MUSE fields and new selection criteria, the increased statistics of the pair samples allow us to significantly shorten the error bars compared to our previous analysis. The evolution of the minor merger fraction is roughly constant with cosmic time, with a fraction of 20% at z < 3 and a slow decrease to 8−13% in the redshift range 3 ≤ z ≤ 6.
Key words: galaxies: evolution / galaxies: high-redshift / galaxies: interactions
Full Tables B.1 and B.2 are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/cat/J/A+A/631/A87
© E. Ventou et al. 2019
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1. Introduction
Understanding the processes behind the mass assembly of galaxies in dark matter halos remains one of the most outstanding issues of modern astrophysics. Thanks to the development of more and more sophisticated cosmological models and simulations as well as new data coming from deep and wide photometric and spectroscopic surveys, much progress has been made both on the theoretical and observational side of galaxy evolution. Several mechanisms, such as cold gas accretion and galaxy mergers, contribute to the build-up of galaxies along cosmic time (e.g., Anglès-Alcàzar et al. 2017). In the first scenario, fresh gas is supplied to the galaxy from cold filaments following the cosmic web of large-scale structure. While direct observational evidence of this phenomenon has been difficult to obtain, indirect arguments such as evidence from internal kinematics, expected absorption features along background quasar sight lines, and chemical evolution models with the well-known G-dwarf problem have been accumulating over the past decade (Chiappini 2001; Caimmi 2008; Sancisi et al. 2008; Bournaud et al. 2011; Stewart et al. 2011; Bouché et al. 2016; Zabl et al. 2019). In comparison, many examples of colliding and merging galaxies have been observed and studied in the local universe. Galaxy mergers are known to not only enhance star formation and fuel starbursts (Joseph & Wright 1985; Di Matteo et al. 2007; Kaviraj 2014) but also to strongly affect galaxy morphologies and dynamics (Bell et al. 2008; Perret et al. 2014; Borlaff et al. 2014; Lagos et al. 2018).
The relative contribution and efficiency of these processes to the mass growth of galaxies is still unclear. Cosmological simulations suggest that a large fraction of cold gas can be accreted by galaxies and smooth gas accretion may dominate galaxy assembly, at least for low-mass galaxies hosted by halos below the virial shock mass threshold (Murali et al. 2002; Kereš et al. 2005; Williams et al. 2011; L’Huillier et al. 2012; van de Voort et al. 2012; Conselice et al. 2013). The efficiency of smooth accretion onto halos seems to be more efficient at high redshift and increases slowly with halo mass (e.g., Kereš et al. 2005; Ocvirk et al. 2008; van de Voort et al. 2011). The same redshift dependence is seen in simulations for the cold gas accretion onto galaxies, but the dependence on halo mass is not constant and peaks around (Mh ∼ 1011−12 M⊙). However, the relative importance of both phenomena (cold accretion and mergers) remains uncertain, since the total amount of mass accretion onto galaxies by merging is still poorly constrained, especially in the early epoch of galaxy evolution due to difficulties in observing these events at high redshift.
Several methods have been used to investigate merging activity across cosmic time, for instance by identifying mergers through perturbations in galaxy morphologies (Le Fèvre et al. 2000; Conselice et al. 2003, 2008; Conselice 2006; Kampczyk et al. 2007; Heiderman et al. 2009; Bluck et al. 2012; Casteels et al. 2014). However, such approaches are limited by the poor spatial resolution of broadband observations, by the insufficient depth of better-resolution data necessary to identify low-surface-brightness features such as tidal tails, and by the lack of near-infrared (NIR) observations for large samples of high-redshift galaxies. In addition, morphological disturbances are not necessarily related to merger events (e.g., Cibinel et al. 2015; Förster Schreiber et al. 2009, 2011). Kinematical studies and numerical simulations have shown that a rotating disk can quickly (< 1 Gyr) rebuild after a merger at high redshift and that the signatures of a merger event are usually only visible during a period of a few hundred million years (e.g., Perret 2014; Cibinel et al. 2015; Hung et al. 2016; Simons et al. 2019). It has been shown that identifying mergers based on kinematics only is not straightforward and depends on the method used (e.g., Neichel et al. 2008; Shapiro et al. 2008; Epinat et al. 2012). The most secure way to study merging activity is therefore to identify close pairs based on their kinematics.
At high redshift (z ≥ 2), studies have focused on the close pair counts method to probe merger abundance. These close pairs are gravitationally bound systems of two galaxies and are expected to merge within an estimated timescale of about 1 Gyr (Kitzbichler & White 2008; Jian et al. 2012; Moreno et al. 2013) for nearly equal-mass galaxies (major merger with a mass ratio between the two galaxies greater than 1:4).
Several photometric and spectroscopic surveys have found that the major merger fraction and rate increase with redshift up to z ∼ 1 (Lin et al. 2008; Bundy et al. 2009; de Ravel et al. 2009; López-Sanjuan et al. 2012). Only a few estimates of this fraction and rate have been attempted for z ≥ 1.5 and the conclusions reached on their evolution across cosmic time depend strongly on the adopted selection method. Flux-ratio-selected major pairs based on photometric studies reveal that the major merger rate increases steadily up to z ∼ 2−3 (Bluck et al. 2009; Man et al. 2012, 2016; López-Sanjuan et al. 2015; Mundy et al. 2017; Duncan et al. 2019 but see Mantha et al. 2018 for a contradictory result), whereas spectroscopic and mass-ratio-selected pairs from recent surveys found that beyond z ≥ 2, the incidence of major mergers remains constant or decreases at early times (López-Sanjuan et al. 2013; Tasca et al. 2014; Ventou et al. 2017). This discrepancy could be explained by the contamination of photometric samples by a large number of minor mergers, with a mass ratio lower than 1:4 (Lotz et al. 2011; Mantha et al. 2018). The large scatter between measurements using the same selection method can also be attributed to the wide range of companion selection criteria used in previous surveys. While it would be more accurate to identify close pairs of galaxies based on their true (i.e., in real space) physical separation, it is not applicable directly to the observed datasets. Thereby various criteria have been considered.
The first analyses of galaxy pairs formulated a criterion mostly relying on apparent angular separation and the angular diameter of the galaxies (Turner 1976; Peterson 1979). In more recent studies (Patton et al. 2000; de Ravel et al. 2009; Tasca et al. 2014; Man et al. 2016; Ventou et al. 2017) close pairs of galaxies are frequently defined as two galaxies within a limited projected angular separation and line-of-sight relative velocity. For spectroscopic surveys, a relative velocity difference of ΔV ≤ 300−500 km s−1 is often applied, which offers a good compromise between contamination by chance pairing, that is, pairs which will satisfy the selection criteria but are not gravitationally bound, and pair statistics (Patton et al. 2000; Lin et al. 2008). The projected separation criterion however varies a lot in the literature, 0−10 ≤ rp ≤ 25−50 h−1 kpc, which makes direct comparisons difficult (Patton et al. 2000; de Ravel et al. 2009; López-Sanjuan et al. 2013; Tasca et al. 2014; Ventou et al. 2017; Mantha et al. 2018). Furthermore, recent studies based on the Sloan Digital Sky Survey have shown that the effect of galaxy interactions can be detected in galaxy pairs with separation greater than 50 h−1 kpc. Star formation rate (SFR) enhancements, for example, are present out to projected separations of 150 h−1 kpc (Scudder et al. 2012; Patton et al. 2013). This shows the need to investigate and better refine companion selection criteria for close-pair count studies.
While major mergers are relatively easy to identify, minor mergers are more frequent in the nearby universe and may also be an important driver of galaxy evolution (Naab et al. 2009; McLure et al. 2013; Kaviraj 2014). However, the cosmic evolution of the minor merger fraction and rate of galaxies is almost unconstrained, with very few attempts so far (e.g., López-Sanjuan et al. 2011, 2012).
In the present paper, we aim to provide new selection criteria for close pair count analysis. We make use of the ILLUSTRIS cosmological simulation project to investigate the relation between close pair selection criteria, that is, separation distance and relative velocity, and whether the two galaxies will finally merge by z = 0. Following the analysis of Ventou et al. (2017), we apply these new criteria to Multi-Unit Spectroscopic Explorer (MUSE; Bacon et al. 2010) deep observations performed over four regions: the Hubble Deep Field South, the Hubble Ultra Deep Field, the galaxy cluster Abell 2744, and the COSMOS-Gr30 galaxy group, in order to better constrain the cosmic evolution of the merger fraction. Thanks to its large field-of-view, MUSE allows the user to explore the close environment of galaxies and thus to probe the evolution of the major and minor merger fraction over a wide range of stellar masses and redshift domains.
This paper is organized as follows: in Sect. 2, we introduce the ILLUSTRIS simulation and we detail in Sect. 3 the analysis performed on the companion-selection criteria and its results. The MUSE data sets used to detect close pairs of galaxies as well as the final close pairs sample, are described in Sect. 4.1. Finally, we provide an estimate of the major and minor merger fraction evolution up to z ∼ 6 in Sect. 5. A summary and conclusion are given in Sect. 6.
Throughout this work, we use a standard ΛCDM cosmology with H0 = 100 h km s−1 Mpc−1, h = 0.7, Ωm = 0.3, ΩΛ = 0.7. Magnitudes are given in the AB system.
2. ILLUSTRIS simulation
The ILLUSTRIS cosmological simulation project (Vogelsberger et al. 2014; Genel et al. 2014; Nelson et al. 2015), is a series of N-body/hydrodynamical simulations reproducing the formation and evolution of galaxies across cosmic time over a large volume of 106.5 Mpc3. The simulations use the moving-mesh code AREPO (Springel 2010) and include many ingredients for galaxy evolution such as primordial and metal-line cooling with self-shielding corrections, stellar evolution, stellar feedback, galactic-scale outflows with an energy-driven kinetic wind scheme, chemical enrichment, super-massive black hole growth, and feedback from active galactic nuclei (Vogelsberger et al. 2013).
Merger trees were constructed from the main ILLUSTRIS-1 simulation using the SUBLINK algorithm, which identifies a unique sub-halo descendant from the next snapshot using a merit function that takes into account the binding energy rank of each particle to discriminate between the potential sub-halo candidates (see Rodriguez-Gomez et al. 2015 for more details on the creation of merger trees of sub-halos and galaxies). The ILLUSTRIS-1 simulation has already been used in previous works related to galaxy mergers. These analyses suggest that major pair fractions change little or decrease with increasing redshift for z > 1 (Snyder et al. 2017), which is in agreement with recent surveys, and that 50(20)% of the ex-situ stellar mass in nearby elliptical galaxies comes from major(minor) mergers (Rodriguez-Gomez et al. 2016).
For this analysis, mock catalogs were created from six snapshots of the ILLUSTRIS-1 simulation, corresponding to six different redshifts: z = 0.5, 1, 1.5, 3, 4, and 5. For each of them, merger tree information was generated. The simulation produces galaxies spread over a large range of stellar masses, 108 ≤ M⋆ ≤ 1011.5 M⊙ (see Fig. 1). The lower mass cut of 108 M⊙ is about two orders of magnitude higher than the nominal baryonic mass resolution of the ILLUSTRIS-1 simulation. The number of galaxies in these mocks decreases with redshift, from ∼75 000 at z = 0.5 to ∼9000 at z = 5. This variation in the number of galaxies is reflected in Figs. 2 and 3, where the sample size decrease at high redshift. Since mock data are versions of the real simulation in which the geometry and selection effects of observational surveys are reproduced, they can be analyzed using similar methods, which is a powerful advantage for comparisons between theory and observations.
 |
Fig. 1. Stellar mass distribution of galaxies in the ILLUSTRIS simulation for six snapshots corresponding to redshifts z = 0.5, 1, 1.5, 3, 4 and 5. The total number of galaxies and the median stellar mass are indicated in each panel. |
 |
Fig. 2. (a) Galaxy pair velocity-separation distance diagram from the ILLUSTRIS-1 simulation for six snapshots at different redshifts, color-coded with respect to the fraction of future mergers within the pair sample. (b) Same diagram as (a) but with projected velocity-separation distances. The two red boxes correspond to the new criteria introduced in Sect. 3.2.3. |
 |
Fig. 3. Influence of the galaxy mass ratio in the pair on the velocity-separation distance diagram (zoomed into a box of 200 kpc × 200 km s−1) and the probability that the pair will merge for different redshifts. Top: major merger distribution, with a mass ratio between the primary galaxy and its companion within 1:1 and 1:6. Bottom: minor merger distribution with a mass ratio in the pair lower than 1:6. |
3. New criteria for the selection of galaxy close pairs
A close pair of galaxies is defined as two galaxies with a small rest-frame relative velocity and projected separation distance in the sky plane. These selection parameters are respectively computed as follows in most observational surveys:
where θ is the angular distance between the two galaxies, dA(zm) is the angular scale (in kpc arcsec−1), and zm is the mean redshift of the two galaxies, and:
where z1 and z2 are the redshifts of each galaxy in the pair and c is the speed of light.
For each of these two criteria, a wide range of values can be found in the literature (see Sect. 1). In the following sections, we try to improve these parameters by analyzing the relation between the velocity-distance relative separation of a close pair of galaxies and the probability that this pair will merge in the future.
3.1. Galaxy pairs identification
For each of the six mock catalogs created from ILLUSTRIS-1 simulation (see Sect. 2), we applied selection techniques that are commonly used in observational surveys. Knowing the position and velocity of each galaxy in real space, we detect pairs of galaxies with a difference in relative velocity amplitude Δv ≤ 500 km s−1, since most studies have shown that pairs with Δv > 500 km s−1 are not likely to be gravitationally bound (Patton et al. 2000; De Propris et al. 2007), and a separation distance, Δr ≤ 500 kpc, which allows us to explore a large range of values for the separation distance criterion. From the merger trees, we can then follow the descendant branch information for each sub-halo in the subsequent snapshot, and so on, until z = 0 and thus identify which of the galaxy pairs become a true merger in the future.
3.2. Results
3.2.1. Projection effect
Figure 2a shows the relation between the true velocity-distance separation of the galaxy pairs in real space and their probability to merge for the different redshifts. As expected the probability that a pair will merge decreases both with the separation distance, Δr, and with the velocity difference, Δv, of the galaxy pair. The decrease is slower for Δv than for Δr. Thus, a galaxy pair within a separation distance of Δr ≤ 50 kpc and velocity difference of Δv ≤ 200 km s−1 has between 100 and 80% chance of merging by z = 0. For the highest-redshift snapshots, z = 4 and 5, statistical effects due to much lower numbers of pairs begin to appear for Δv ≥ 400 km s−1.
However, true, unprojected velocity differences and physical separation distances are not available in observations. Therefore, we use projected values of the relative velocity and distance which reflect the projected separation distance in the sky plane and the rest-frame velocity difference in redshift space from observations. The probability for a galaxy pair to merge as a function of its position in the projected velocity-distance diagram (ΔvP vs. ΔrP) is shown in Fig. 2b. Using projected values clearly affects the probability of a pair to merge because of contamination effects, dropping the probability to 70% for a pair with ΔrP ≤ 25 kpc and ΔvP ≤ 100 km s−1. In the projected space, pairs with ΔvP ≥ 300 km s−1 have less than 10% chance of ending up as a merging system.
3.2.2. Dependence on stellar mass
Interacting galaxies can end up in a merging system if the two colliding galaxies do not have enough momentum to overcome the gravitational hold they have on one another and continue their courses after the collision. Velocities, angles of the collision, sizes, relative composition, and masses are all parameters that can affect the result of two colliding galaxies. The more massive the primary galaxy, the more gravitational pull it will have and the harder it will be for its companion to liberate itself from this holding force.
An attempt to study the influence of the mass ratio on the relation between the velocity-separation distance diagram of the galaxy pairs and their probability of merging is shown in Fig. 3. The influence of the primary galaxy stellar mass on this relation is shown in Fig. 4.
 |
Fig. 4. Influence of the stellar mass of the primary galaxy on the merger velocity-separation distance diagram. A constant stellar mass limit of 109.5 M⊙ is chosen to distinguish low-mass from massive primary galaxies within the major (top) and the minor (bottom) pair samples at z = 1. |
First, we use the mass ratio between the two galaxies to discriminate between the pairs. Figure 3 shows the relation between the projected velocity-distance separation of the pair and their probability of merging for major close pairs, with a stellar mass ratio higher than 1:6 (as adopted in Ventou et al. 2017), and minor close pairs, that is, with stellar mass ratio lower than 1:6. The main difference seen in Fig. 3 between the two samples comes from the rest-frame relative velocity condition. For a fixed projected separation distance ΔrP ≤ 25 kpc, ∼70% of the major close pairs will merge if their rest-frame relative velocity ΔvP is lower than ∼50 km s−1 (see Fig. 3, top panels), whereas the same fraction of mergers will be reached by minor close pairs with ΔvP up to 100 km s−1 (see the bottom panels of Fig. 4).
We further separate our sample into two regimes using the stellar mass of the primary galaxy, that is, the most massive galaxy of the pair, as a limit. In Fig. 4 we distinguish, for the z = 1 snapshot, between low-mass and massive galaxies within the major and minor close pair samples by applying a separation limit of 109.5 M⊙, similar to the limit adopted in Ventou et al. (2017).
As for the major-minor discrimination, the stellar mass separation affects mainly the condition on the rest-frame velocity. For a primary galaxy with a stellar mass, M⋆ > 109.5 M⊙, a pair within ΔrP ≤ 25 kpc and ΔvP ≤ 150 km s−1 has between 75 and 60% chance of merging, for a major and minor close pair, respectively. However, for pairs with a lower-mass primary galaxy, M⋆ ≤ 109.5 M⊙, and for the same probability of merging, the threshold in relative velocity is smaller: ΔrP ≤ 25 kpc and ΔvP ≤ 75 km s−1. Similar results are obtained for the other redshift snapshots, showing that these conditions have almost no dependance on redshift.
To summarize, the stellar mass of the galaxies involved in the pair will mostly have an impact on the rest-frame relative velocity selection criterion. Massive primary galaxies with their strong gravitational pull are better able than lower-mass galaxies to retain satellite galaxies where the difference in relative velocity is larger.
3.2.3. New criteria for pair selection and weighting scheme
From this analysis we propose new criteria for the selection of close pairs of galaxies. We define a close pair as two galaxies within a limited projected separation distance in the sky plane and a rest-frame relative velocity of:
With these parameters, all close pairs with at least 30% chance of merging are considered, regardless of the mass ratio or stellar mass of the primary galaxy (see red boxes in lower left panel of Fig. 2). We choose this threshold of 30% as the fraction of mergers converges below this value. This is illustrated in Fig. 5 where we show the major merger fraction computed in the Hubble Ultra Deep Field for three redshift intervals as a function of five different values of merging probability threshold (10, 20, 30, 55, and 80%). Adding pairs with a probability to merge below the 30% threshold would increase the major merger fraction by a few percent only.
 |
Fig. 5. Major merger fraction of close pairs selected in MUSE deep observations over the Hubble Ultra Deep Field (so-called UDF-mosaic) for three redshift bins and five values of merging probability threshold (10, 20, 30, 55, and 80%). The choice of a 30% threshold is motivated by the convergence of the merger fraction below this value. |
The limit 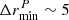 kpc comes from the limitation in spatial resolution of the MUSE data (see Ventou et al. 2017). Indeed, two galaxies within an angular separation of θ ≤ 0.7″ which corresponds approximately to
kpc comes from the limitation in spatial resolution of the MUSE data (see Ventou et al. 2017). Indeed, two galaxies within an angular separation of θ ≤ 0.7″ which corresponds approximately to 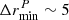 h−1kpc at z ∼ 1, are nearly impossible to distinguish and would appear as a blended object. Further in the analysis, a corrective term is applied to the expression of the merger fraction to account for the missing pairs. We note that these values are similar to those applied by Scudder et al. (2012) and Patton et al. (2013) in their SDSS-based study of the SFR enhancement in pairs of interacting galaxies.
h−1kpc at z ∼ 1, are nearly impossible to distinguish and would appear as a blended object. Further in the analysis, a corrective term is applied to the expression of the merger fraction to account for the missing pairs. We note that these values are similar to those applied by Scudder et al. (2012) and Patton et al. (2013) in their SDSS-based study of the SFR enhancement in pairs of interacting galaxies.
Based on a least-squares fit to the simulated datasets shown in Fig. 2b with a nonlinear regression, a new weighting scheme can be applied to the merger fraction that takes into account the probability that the galaxy pair will merge as a function of their relative velocity (in kpc) and projected separation (in km s−1) distances (see Appendix A for more details):
If we further divide the sample by the stellar mass of the primary galaxy (see Fig. 4), we propose the following two equations for galaxies with a stellar mass above or below M⋆ = 109.5 M⊙, respectively:
This new corrective term allows us to give an estimate of the close pair fraction that reflects more accurately the true merger fraction. The following sections present the application of these new selection criteria and weighting scheme on MUSE deep fields in order to derive the evolution of the major and minor galaxy pair fractions over the last 13 Gyr.
4. Data description
The analysis presented in this paper is based on MUSE observations obtained during the last commissioning run of the instrument in August 2014 and 1.5 years of MUSE Guaranteed Time Observations (GTO) from September 2014 to February 2016.
4.1. Parent sample
For this analysis, a large spectroscopic sample of 2483 galaxies is constructed from MUSE deep observations over four different regions of the southern sky, the Hubble Deep Field South (HDF-S; Bacon et al. 2015), the Hubble Ultra Deep Field (HUDF; Bacon et al. 2017), the lensing cluster Abell 2744 (Mahler et al. 2018), and the galaxy group COSMOS-Gr30 at z ∼ 0.7 (Epinat et al. 2018). The two first MUSE datasets in HDFS and HUDF are already described in Ventou et al. (2017). In the following sections, we describe the additional MUSE datasets in Abell 2744 and COSMOS-Gr30.
4.1.1. Abell 2744
Abell 2744 was observed as part of a GTO program aimed at probing the highly magnified regions of massive lensing clusters (PI: J. Richard). The resulting data cube is a 2′×2′ mosaic centered around α = 00h14′20.95″ and δ = −30 ° 23′53.88″ with exposure times ranging from 4 h to 7 h. Instrumental setup was similar to HUDF observations. Sources were extracted using three complementary detection methods described in Mahler et al. (2018): spectral extraction at the location of known faint sources in the deep Hubble Frontier Field images, emission line detection based on narrow-band filtering in the MUSE data cube using the software MUSELET1, and finally manual extraction for sources found by visual inspection and not detected with the previous methods. Overall the spectroscopic redshift of 514 sources was measured, with 414 new identifications (Mahler et al. 2018). For this study, we kept one galaxy only for all the confirmed multiple-image systems. The source positions were corrected for lensing effects and estimated in the source plane (Mahler et al. 2018). However, lensing does not affect the redshift and velocity differences measured in the MUSE data.
4.1.2. COSMOS-Gr30
The deep observations of the galaxy group COSMOS-Gr30 at z ∼ 0.7 are part of a large GTO program that aims to study how the environment has affected galaxy evolution over the past 8 Gyr (PI: T. Contini). A single field of 1 × 1 arcmin2 and 10h exposure time was obtained, comprising 40 exposures of 900 seconds. The data cube presents the same spatial and spectral sampling characteristics as for the HUDF and Abell 2744. The seeing was estimated to be around 0.68″ at 7000 Å (Epinat et al. 2018). As for the UDF-Mosaic, sources were selected from the COSMOS2015 photometric catalog (Laigle et al. 2016), complemented by emission-line detection using ORIGIN software (Bacon et al. 2017). A customized version of the redshift finding code MARZ (Hinton et al. 2016) was used to assess the spectroscopic redshift of the sources. The final catalog consists of 208 spectroscopic redshifts.
4.1.3. Redshift and stellar masses
By combining the catalogs associated with each of the four surveys, we built a parent sample of 2483 galaxies with spectroscopic redshift up to z ∼ 6. Each redshift measurement is assigned a confidence level based mostly on the detected spectral features (see details in Inami et al. 2017). Confidences 3 and 2 signify secure redshifts based on several spectral features, such as strong emission lines, or a clearly identified single feature (mainly [O II] λλ3726,3729 and Lyα), or strong absorption features. Confidence 1 signifies a tentative redshift with uncertainties on the nature of the feature from the line profile: most of the time Lyα versus [O II] λλ3726,3729. This redshift confidence is later taken into account in the merger fraction estimate, and a weight is thus applied to distinguish between secure galaxy pairs involving two galaxies with a confidence level of 3 or 2, and unsecure ones involving at least one galaxy with confidence 1. As in a previous paper (Ventou et al. 2017), we used the empirical relation between the velocity shift of the Lyα emission peak relative to the systemic velocity and the FWHM of the line (Verhamme et al. 2018) to compute the systemic redshift of all the Lyα emitters.
Stellar masses were derived using FAST (Fitting and Assessment of Synthetic Templates), a code that fits stellar population synthesis templates to broadband photometry and spectra (Kriek et al. 2009). We assume for all four fields a Chabrier (2003) initial mass function, an exponentially declining star formation history, and the dust attenuation law from Calzetti et al. (2000). As described in Ventou et al. (2017), extended UV-to-NIR ACS and WFC3 photometric measurements (Rafelski et al. 2015) were used for the UDF-Mosaic, with the addition of mid-infrared (MIR) IRAC photometry from the GOODS Re-ionization Era wide-Area Treasury from Spitzer program to better constrain the stellar mass of high-redshift galaxies (z ≥ 3). The optical-NIR photometric bands used for the HDF-S are also listed in Ventou et al. (2017). As described in Epinat et al. (2018), the photometric measurements for COSMOS-Gr30 come from the extensive dataset available in the COSMOS field (Scoville et al. 2007) and are summarized in the COSMOS2015 catalog (Laigle et al. 2016). This catalog includes infrared (IR) and far-infrared (FIR) photometry from Spitzer and Herschel, radio data from the VLA, UV-to-IR from HST-ACS, SDSS, VIRCAM/VISTA camera, WIRCam/CFHT, and MegaCam/CFHT camera, as well as HSC/Subaru Y band and SuprimeCam/Subaru, near- and far-ultraviolet measurements from the Galaxy Evolution Explorer, Chandra, and XMM observations for X-ray data (see Epinat et al. 2018 for details). For the lensing cluster A2744, seven HST bands (ACS; F435W, F606W, F814W and WFC3; F105W, F125W, F140W, F160W) were used. A median boxcar subtraction was applied to these images in order to better estimate the stellar masses of faint background galaxies, which can be contaminated by the light of the cluster galaxies. Results are all corrected for lensing magnification effects.
The final parent galaxy sample assembled from the four MUSE deep surveys probes a large domain in stellar mass, from ∼ 107 − 1011 M⊙, distributed over a large redshift range 0.2 ≤ z ≤ 6.8 (see Fig. 6). We note that no stellar mass has been derived for the few Lyα emitters in the UDF-Mosaic which are not detected in deep HST images (see Inami et al. 2017). These galaxies are not considered further in the analysis.
 |
Fig. 6. Stellar mass as a function of redshift for the parent sample of 2483 galaxies drawn from MUSE deep observations in HUDF (gray dots), HDFS (blue dots), A2744 (red dots), and CGR30 (green dots). Thanks to the high sensitivity of MUSE, star-forming galaxies are identified with a secure spectroscopic redshift up to z ∼ 6 over a large range of stellar masses (∼ 107 − 1011 M⊙), except in the so-called “redshift desert” (z ∼ 1.5−2.8) where galaxies in the low-mass regime (M⋆ ∼ 107 − 108 M⊙) are detected behind the A2744 lensing cluster only. |
Figure 7 (top) shows the spectroscopic redshift distribution of the parent galaxy sample for all individual fields. Peaks in the histograms account for particular structures detected in each data cube. In the UDF-Mosaic, an over-dense structure is detected around z ≈ 1 (see Inami et al. 2017). The peak at z ≈ 0.3 in A2744 corresponds to the galaxy cluster and overall the redshifts of 156 cluster members were measured from MUSE observations over this region (Mahler et al. 2018). The green peak around z ≈ 0.7 represents the galaxy group Gr30 in COSMOS. The dearth of spectroscopic redshifts in the range 1.5 ≤ z ≤ 2.8 is expected, as it covers the well-known redshift desert interval for optical instruments such as MUSE. Due to the absence of bright emission lines in this range (in between Lyα and [O II] λλ3726,3729), the redshifts are measured mainly on absorption features or the [C III] λλ1907,1909 emission-line doublet.
 |
Fig. 7. Top: spectroscopic redshift distribution of the parent galaxies in the four MUSE data cubes used in this analysis. Bottom: redshift histogram of the close pairs sample showing the contribution of major (black), minor (red), and very minor close pairs (blue). |
4.2. Close pair sample
Applying the criteria defined in Sect. 3.2.3 to the MUSE data set, a total of 366 close pairs of galaxies were identified. About 44% of them were detected in the UDF-Mosaic, 40% in A2744, 9% in COSMOS-Gr30, and 7% in HDF-S. As mentioned in Sect. 4.1.3, we do not include in this sample the few z > 3 pairs detected in the UDF-Mosaic (∼1.8% of the total pair sample) of one or two Lyα emitters without a HST counterpart, and thus without any stellar mass estimate.
The mass ratio, defined as the ratio between the stellar mass of the companion and that of the primary galaxies, is used as a proxy to divide this sample into major mergers, with a mass ratio of 1:1−1:6 as chosen in Ventou et al. (2017), minor mergers (1:6−1:100), and very minor mergers with a mass ratio lower than 1:100. In this last regime the primary galaxy is so much more massive than its companion that it is getting closer to the regime of smooth gas accretion than to a galaxy merger. The secondary galaxy is completely stripped and absorbed by the massive one.
Within our sample, we thus identify a total of 179 major close pairs, 140 minor and 47 very minor close pairs, distributed over a broad range of redshift 0.2 ≤ z ≤ 6 (see Fig. 7, bottom). As stated before, the peaks around z ≈ 0.3 and z ≈ 0.7 in the redshift distributions are due to the lensing cluster and galaxy group, respectively. More than 30(32) major(minor) close pairs are detected at high redshift z ≥ 3. Examples of close pairs in each mass ratio regime are displayed in Fig. 8. The first two rows correspond to a very minor pair and a minor pair at z ∼ 3 and z ∼ 0.15, respectively. The last two rows are both major close pairs at z ∼ 1 and z ∼ 5, respectively. The catalogs of major and minor pairs are listed in Tables B.1 and B.2, respectively.
 |
Fig. 8. Examples of close pairs of galaxies, at different redshifts and with various mass ratios in the UDF-Mosaic field. From left to right: HST image in the F775W filter with the redshift of the primary galaxy, MUSE reconstructed white light image, narrow-band image of one of the brightest emission lines of the pair, and the zoomed spectra of the two galaxies around this line (red for the primary galaxy and blue for its companion) with the labeled MUSE ID, mass ratio, relative velocity difference, and projected separation distance. Images are 10″ in linear size and centered around the primary galaxy, circled in white. The green circle indicates the location of its companion. The first two close pairs correspond to the very minor and minor regimes, and the last two are major close pairs at low and high redshift. |
Figures 9 and 10 reveal the mass ratio and stellar mass domain of our samples. With deep-enough MUSE observations, we manage to probe galaxy pairs with very-low-mass ratios (down to 1:104; see Fig. 9) at any redshift, except for the “redshift desert” interval. Pairs with a mass ratio lower than 1:100 are considered as very minor, close to the smooth accretion regime. Likewise the stellar mass range of the primary galaxies extends over 4 dex, from ∼107 to 1011 M⊙ (see Figs. 6 and 10). Within this mass range, the major close pair sample has a good level of stellar-mass completeness, as already discussed in Ventou et al. (2017). Three of the four MUSE datasets used in this analysis (HUDF, A2744 and CGR30) have a similar exposure time of 10 h, leading to a homogeneous stellar mass completeness down to ∼107 M⊙ up to redshift z ∼ 6. However, as can be seen in Fig. 6, a significant number of galaxies identified in the A2744 field have very low stellar masses thanks to the lensing cluster magnification allowing to unveil star-forming galaxies down to ∼106 M⊙. Even if the MUSE observations in the HDFS are significantly deeper (30 h) than in other fields, we do not reach galaxies with lower stellar masses, still keeping a homogeneous completeness over the four datasets. This is likely due to HDFS data being taken during commissioning when the calibration sequence was not fully established and with a slightly older data reduction procedure. However, due to the extended mass ratio range down to 1:100 considered for the minor close pairs, the low-mass threshold must be reduced to retain a relatively good mass completeness for this regime. Therefore, for the minor close pair sample, we adopt a low-mass cut of 109 M⊙. This effect is even more dramatic for very minor pairs. In this regime, the mass completeness is too poor for the sample to be useful. We therefore focus the remainder of the analysis on the major and minor samples, within their corresponding mass ranges, and estimate the associated fractions.
 |
Fig. 9. Stellar mass ratio and redshift distribution of the whole close pairs sample from the combined analysis of the four MUSE deep fields. Symbols are color-coded with respect to the stellar mass of the primary galaxy. The dashed lines indicate the mass ratio (primary over companion galaxy) limits chosen to distinguish major close pairs (limit of 6, blue dashed line and colored area) from minor (between a mass ratio limit of 6 and 100, red dashed line and colored area) and very minor pairs (mass ratio greater than 100). |
 |
Fig. 10. Stellar mass of the primary galaxy as a function of redshift for our major (top) and minor (bottom) close pair samples. Right pointing triangles correspond to close pairs in the HDF-S, other triangles to close pairs in the COSMOS-Gr30 field, squares are pairs from A2744, and circles from the UDF-Mosaic. Symbols are color-coded with respect to the weight, Wp described in Sect. 3.2.3, used for the computation of merger fractions. Darker pairs have a higher probability of merging by z = 0 and will thus have a higher contribution on the estimated merger fraction. Except in the redshift desert (z ∼ 1.5−2.8), we have a relatively good stellar mass completeness level for major close pairs down to a primary galaxy stellar mass of ≈107 M⊙. However, for the minor close pairs sample, a lower mass limit of 109 M⊙ must be applied to keep a reasonable level of completeness for the merger fraction estimates. |
In Fig. 10, the weighting scheme described in Eq. (3) is also shown, differentiating between pairs with a high probability of merging (darkest symbols) and the others, which will have a lower contribution to the merger fractions estimated in the following section.
5. Evolution of the galaxy major and minor merger fraction up to z≈ 6 in MUSE deep fields
In order to probe the evolution of the galaxy merger fraction along cosmic time, the redshift range is divided into different bins containing enough pairs to be statistically significant. We follow the division adopted in Ventou et al. (2017), with the lowest redshift bin corresponding to the interval 0.2 ≤ zr < 1, then 1 ≤ zr < 1.5 which ends up with the loss of the [O II] λλ3726,3729 emission-line in the MUSE spectral range, following the redshift desert domain 1.5 ≤ zr < 2.8 and two more bins 2.8 ≤ zr < 4 and 4 ≤ zr ≤ 6 for the highest-redshift close pairs.
5.1. Major merger fraction
To obtain a merger fraction from a close pair count study, for each redshift bin zr, the number of galaxy pairs, Np, must be divided by the number of primary galaxies in the parent sample, Ng, and corrected from all selection effects. Indeed, observations are limited in volume and luminosity and this must be taken into account and corrected in the fraction estimates (e.g., de Ravel et al. 2009).
The expression from Ventou et al. (2017) is used to define the major merger fraction with the addition of the new weighting scheme described in Sect. 3.2.3:
where K is the running number attributed to a pair, K1 and K2 correspond to the primary and companion galaxy in the pair, respectively. Here, C1 accounts for the missing companions due to our limit in spatial resolution at small radii (Sect. 3.2.3) and is defined as 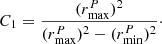 The redshift confidence weight, ωz, represents the confidence level associated to the spectroscopic redshift measurement:
The redshift confidence weight, ωz, represents the confidence level associated to the spectroscopic redshift measurement:
The area weight takes into account the missing companion galaxy for primary galaxies on the border of the MUSE field:
where 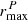 is the radius corresponding to the projected distance limit, and rMUSE the radius available in MUSE observations. Here, W(ΔrP, ΔvP), defined in Eq. (4), is the new weight corresponding to the probability of the close pair merging by z = 0 based on their relative velocity and projected separation distance. The parameter C2(zr) corrects for redshift incompleteness. To compute this value we use the same method as described in Ventou et al. (2017) for the UDF-Mosaic and HDF-S and applied to the two other fields. Assuming that photometric redshift measurements are uniformly representative of the real redshift distribution, the number of spectroscopic redshifts is divided by the number of photometric redshifts for each bin. Photometric redshift measurements for the UDF-Mosaic field are estimated in Brinchmann et al. (2017) and reported in the COSMOS2015 catalog (Laigle et al. 2016) for the COSMOS-Gr30 field. Photometric redshifts for A2744 were estimated using the spectral energy distribution (SED) fitting code HyperZ (Bolzonella et al. 2000) based on photometry from the publicly available Hubble Frontier Field images of A2744 in seven filters (ACS; F435W, F606W, F814W and WFC3; F105W, F125W, F140W, F160W; Lotz et al. 2017). A constant star formation history, a Chabrier (2003) initial mass function, a Calzetti et al. (2000) extinction law, and templates from the Bruzual & Charlot (2003) stellar library were used as input parameters.
is the radius corresponding to the projected distance limit, and rMUSE the radius available in MUSE observations. Here, W(ΔrP, ΔvP), defined in Eq. (4), is the new weight corresponding to the probability of the close pair merging by z = 0 based on their relative velocity and projected separation distance. The parameter C2(zr) corrects for redshift incompleteness. To compute this value we use the same method as described in Ventou et al. (2017) for the UDF-Mosaic and HDF-S and applied to the two other fields. Assuming that photometric redshift measurements are uniformly representative of the real redshift distribution, the number of spectroscopic redshifts is divided by the number of photometric redshifts for each bin. Photometric redshift measurements for the UDF-Mosaic field are estimated in Brinchmann et al. (2017) and reported in the COSMOS2015 catalog (Laigle et al. 2016) for the COSMOS-Gr30 field. Photometric redshifts for A2744 were estimated using the spectral energy distribution (SED) fitting code HyperZ (Bolzonella et al. 2000) based on photometry from the publicly available Hubble Frontier Field images of A2744 in seven filters (ACS; F435W, F606W, F814W and WFC3; F105W, F125W, F140W, F160W; Lotz et al. 2017). A constant star formation history, a Chabrier (2003) initial mass function, a Calzetti et al. (2000) extinction law, and templates from the Bruzual & Charlot (2003) stellar library were used as input parameters.
Finally, uncertainties due to the cosmic variance and statistical errors on the estimated fractions are taken into account in the error budget on the merger fractions. The computed total cosmic variance for the four fields follows the recipes of Moster et al. (2011). A purely statistical error was derived as a confidence interval from a Bayesian approach (see e.g., Cameron 2011).
Compared to Ventou et al. (2017), we improve our results with smaller error bars due to the increased number of galaxies in the parent and close pair samples thanks to the addition of two new observed fields A2744 and COSMOS-Gr30, as well as the new selection criteria. At first glance, it could be surprising to find similar pair fractions compared with our previous study. Indeed, in Ventou et al. (2017) we made the (strong) assumption that all the selected close pairs will merge by z = 0 and thus we did not apply any weight for those pairs in the fraction estimates. With our new selection criteria, we indeed found a lower probability (between ∼30% and 80%) for the pairs to merge and applied a corresponding weight in the fraction estimate. However, the expected decrease of the pair fractions due to the lower probability of merging is compensated by the higher number of selected close pairs, even with a probability of merging as low as 30%.
Figure 11 shows the cosmic evolution of the major merger fraction up to z ≈ 6 for a variety of primary galaxy stellar mass ranges. Results are summarized in Table 1 for each redshift bin and mass range.
 |
Fig. 11. Evolution of the galaxy major merger fraction up to z ∼ 6 from MUSE deep fields. Left: blue diamonds, green circles, yellow stars, and purple triangles are estimates of the fraction from the UDF-mosaic, Abell 2744, HDF-S, and COSMOS-Gr30 regions, respectively, whereas red squares correspond to the fraction for the combined analysis of the MUSE data. For the lowest redshift bin, fractions were computed without (filled symbols) and with (open symbols) members of the galaxy cluster A2744 and galaxy group COSMOS-Gr30. Right: evolution of the major merger fraction for two ranges of stellar mass, assuming first a constant separation limit of M⋆ = 109.5 M⊙ (grey and yellow circles show the MUSE estimates for low-mass and massive galaxies, respectively), then taking the median mass of the parent sample in each redshift bin as the limit (orange and purple triangles). As for the combined fraction of the left panel, the fractions were computed without taking into account the cluster and group members. The median stellar mass estimated in the range 107 − 1011 M⊙ for each redshift intervals are listed in Table 1. |
Major merger fractions up to z ≈ 6 from MUSE deep observations for different redshift and stellar mass intervals.
We first estimate the fractions for each field individually as well as for the combined data set for major close pairs with a stellar mass primary galaxy in the range 107 − 1011 M⊙ (Fig. 11, left panel). Although the measurements are in good agreement within the error bars for the majority of the redshift bins, the impact of the environment on these estimates is clearly seen for the lowest redshift bin, 0.2 ≤ zr < 1. Due to the presence of the galaxy cluster Abell 2744 at z ≈ 0.3 and the galaxy group in the COSMOS area at z ≈ 0.7, we observe an enhancement of the close pair counts and hence the merger fraction for these two fields compared to the UDF-Mosaic estimate. Whereas we measure a major merger fraction of 21% in A2744 and 25% in COSMOS Gr30, which is about twice the value estimated in the UDF-Mosaic for this redshift bin, these fractions drop to 5% and 9%, respectively, if we remove the members belonging to the galaxy cluster and to the galaxy group.
In the subsequent analysis and discussion of the merger fraction, we restrict the samples of close pairs in the low-redshift bins by excluding those belonging to these massive structures. Indeed, galaxy clusters and groups provide high-density environments where near neighbors are common. However, the high velocity dispersion of low-z virialized clusters and groups (∼500−1000 km s−1) is not conducive to active merging among galaxies (see Mihos 2004 for a review). Indeed, measurements of the merger rate in low-redshift galaxy clusters do not generally exceed 2−3% (Adams et al. 2012; Cordero et al. 2016). Nonetheless, recent studies of high-redshift proto-clusters have shown evidence of enhanced merger rates, suggesting that merging in dense environments may play an important role in galaxy mass assembly in the early universe (Lotz et al. 2013; Hine et al. 2016).
Assuming a constant stellar mass separation of 109.5 M⊙ for the primary galaxy, we push this analysis further and split the sample into two mass bins. Figure 11 (right panel) shows the resulting evolution of the major merger fraction for massive and low-mass galaxies separately, using different merging probabilities W(ΔrP, ΔvP) computed from Eq. (4). We observe an increase in the fraction of major mergers for the high-mass sample up to 25% at z ≈ 2 where it reaches its maximum, followed by a decrease down to 4-5% in the redshift range 3 ≤ z ≤ 6. The evolution of the fraction of major mergers in the low-mass sample is less pronounced with a nearly flat trend, with an almost constant fraction of 8–13% over the whole redshift range probed by our MUSE sample. Similar results are found if we consider the median mass of the parent sample in each redshift bin as the separation limit (see right panel of Fig. 11), as was done in Ventou et al. (2017).
These evolutionary trends of the major merger fractions are in fairly good agreement with those derived from previous spectroscopic analyses (see Fig. 12), where authors claim that beyond z ≥ 2, the incidence of major mergers remains constant or turns over at early times (López-Sanjuan et al. 2013; Tasca et al. 2014; Ventou et al. 2017). A comparison of the major pair fractions can also be made with recent estimates derived from the full photometric redshift probability distributions, a probabilistic approach first introduced by López-Sanjuan et al. (2010). Our estimates are in very good agreement with the pair fractions derived up to z ∼ 1.5 in the ALHAMBRA survey (López-Sanjuan et al. 2015) and up to z ∼ 3.5 in a combined analysis of UDS, VIDEO, COSMOS, and GAMA surveys (Mundy et al. 2017) and recently extend to CANDELS fields (Duncan et al. 2019). All these analyses, which are based on photometric redshifts of large samples of galaxies, find a constant evolution of the major pair fraction with redshift as (1 + z)n, with a power-law index n in the range n ∼ 1 − 3 which is almost independent of galaxy stellar masses. The comparison at higher redshift (z > 3) is more difficult. Duncan et al. (2019) estimate the major pair fraction up to z ∼ 6 for massive galaxies only, with log(M⋆ / M⊙) > 10.3, and find a constant rise of this fraction reaching ∼37% at z ∼ 6. This is clearly in contradiction with our estimates (∼10% of pairs at z ∼ 4 − 6) but we need to keep in mind that the stellar mass range of galaxies probed with our MUSE deep fields is wider, extending down to much lower masses than the photometric sample used in Duncan et al. (2019).
 |
Fig. 12. Major merger fraction compared to previous close pairs count studies and recent simulations. Combined major merger fractions from this work (red squares) are compared to previous estimates from MUSE observations (black squares: Ventou et al. 2017) and other surveys (light blue symbols: de Ravel et al. 2009; Xu et al. 2012; López-Sanjuan et al. 2013; Tasca et al. 2014). The purple and orange solid lines show the predictions from the EAGLE simulations for two different mass ranges (see Qu et al. 2017 for details). Green triangles correspond to the major pair fractions estimated in the ILLUSTRIS simulation (Snyder et al. 2017). Finally, the predictions of pair fractions up to z ∼ 6 with a lower stellar mass cut-off of 109.5 M⊙ from the EMERGE simulations (O’Leary et al., in prep.) are shown with the brown line. |
As discussed in Ventou et al. (2017), predictions from cosmological simulations, such as HORIZON-AGN (Kaviraj et al. 2015), EAGLE (Qu et al. 2017), and ILLUSTRIS (Snyder et al. 2017), show a broadly good agreement with the cosmic evolution of the major merger fraction up to z ∼ 2 − 3 (see Fig. 12). However, none of these simulations makes a prediction above a redshift of z ∼ 3. We therefore compare our results to new predictions from simulations in Fig. 12 (brown line; O’Leary et al., in prep.) which extend up to z ∼ 6. These simulations employ the empirical model EMERGE (Moster et al. 2018) to populate dark matter halos with galaxies. The EMERGE model utilizes a cosmological dark-matter-only N-body simulation in a periodic box with side lengths of 200 Mpc. The simulations are constrained such that a suite of observations are reproduced; for example, galaxy catalogs out to high redshift (z ∼ 6), making it an ideal environment to study the evolving pair fraction of galaxies. Mock observations are produced from these simulated data, producing a pair fraction for each simulation snapshot. The agreement between our measurements of major pair fractions above z ∼ 3 and these new simulations is very good. We note however that EMERGE predicts lower values by a factor of approximately two for the major pair fractions in the redshift range z ∼ 1 − 3 compared to those measured in the MUSE deep fields.
5.2. Minor merger fraction
We derive the minor merger fraction from the number count of close pairs of galaxies with stellar mass ratios between 1:6 and 1:100 using the same expression (Eq. (5)) as for the major merger fraction. In order to retain a relatively good mass completeness in our sample, the fractions are estimated for a stellar mass range of 109 − 1011 M⊙ for the primary galaxy.
Figure 13 shows the individual fractions for each field (left panel) and the combined data set (right panel). For A2744 and COSMOS-Gr30, only the estimates for the lowest-redshift bins are shown as smaller sample sizes for these two fields at higher redshift intervals hamper a robust statistical analysis. For the merger fraction estimated from the combined MUSE fields, we excluded minor pairs belonging to the cluster A2744 and to the group COSMOS-Gr30 from the computations.
 |
Fig. 13. Evolution of the galaxy minor merger fraction up to z ∼ 6 from MUSE deep fields, for primary galaxies with a stellar mass range of ∼ 109 − 1011 M⊙. Left: as in Fig. 11; different symbols show the results from the four regions individually. Right: red squares are estimates of the combined minor merger fraction from the whole MUSE data set and over the whole stellar mass range ∼ 109 − 1011 M⊙. Using the median value of stellar mass in each redshift bin as a separation limit (∼ 1010 M⊙, see Table 2), the purple and golden triangles correspond to the minor merger fraction for low-mass and massive galaxies, respectively. As in Fig. 11, filled and open symbols correspond to the fractions computed without and with galaxy members of the cluster and group for 0.2 ≤ z ≤ 1, respectively. Cyan points are estimates from previous spectroscopic minor pair counts (López-Sanjuan et al. 2011, 2012). |
The minor merger fraction shows little evolution in the redshift range 0.2 ≤ z ≤ 1.5 with a roughly constant fraction of 20%. Beyond z ≈ 3, we observe a slight decrease of the fraction down to 8 − 13% in this high-redshift range. Fraction estimates for the combined MUSE data set are listed in Table 2.
Minor merger fractions up to z ≈ 6 from MUSE deep observations for different redshift and stellar mass intervals.
An attempt was made to separate the minor merger sample into two stellar mass ranges, as was done for the major close pair in Sect. 5.1. We took the median stellar mass in the range 109 − 1011 M⊙ of the parent sample reported in Table 2 as the separation limit. For statistical reasons it was only computed for the two first redshift bins. For massive primary galaxies in the range 10 ≤ log(M⋆ / M⊙) ≤ 11, the minor merger fraction is roughly constant around 18% at z ∼ 0.2 − 1.5 and around 6 − 9% for the low-mass sample, that is, with 9 ≤ log(M⋆)< 10.
A comparison to the few previous estimates of the minor merger fraction from spectroscopic pair counts is made in Fig. 13 (right panel). López-Sanjuan et al. (2012) computed the minor fraction for a mass ratio range of 1:4–1:10 and a projected separation of 10 ≤ rP ≤ 30 h−1 kpc. These latter authors found a fraction of around 4.5 − 6% for z ∼ 0.29 − 0.86. Since their selection criteria on the minor merger sample, which were based on projected distance and mass ratio range, are narrower compared to ours, it is not surprising that our estimates of ∼20% are higher for the same redshift interval. In López-Sanjuan et al. (2011), a minor merger fraction for bright galaxies within 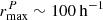 kpc and a luminosity ratio in the B-band of 1:4−1:10 is reported. Their projected separation distance is more similar to that of this work, and their estimated fractions of 25% and 21% at z = 0.5 and z = 0.8, respectively, are in good agreement with our results.
kpc and a luminosity ratio in the B-band of 1:4−1:10 is reported. Their projected separation distance is more similar to that of this work, and their estimated fractions of 25% and 21% at z = 0.5 and z = 0.8, respectively, are in good agreement with our results.
A comparison of our minor merger fraction with recent cosmological simulations is not straightforward as the latter usually focus on the major merger fraction only and/or use different mass ratio limits to discriminate between major and minor mergers. However, we found that on average the minor merger fraction is higher than the major one by a factor of approximately four, which is in relatively good agreement with the HORIZON-AGN simulations (Kaviraj et al. 2015) which predict a difference of a factor of 2.5 − 3 between minor and major merger fractions. The difference between these two values can be explained by the different mass ratio limits to separate minor mergers from major ones.
6. Summary and conclusion
Using the ILLUSTRIS cosmological simulation project, we investigated the relation between the velocity-distance relative separation of galaxies in a close pair and the probability that these galaxies will merge by z = 0. We propose a new set of selection criteria for galaxy close pair counts, along with a new weighing scheme to be applied to the merger fraction. This takes into account the probability of merging for the pair derived from their relative velocity and projected separation distance.
We found that combining constraints on the projected separation distance in the sky plane and the rest-frame relative velocity of ΔrP ≤ 50 kpc with ΔvP ≤ 300 km s−1 and 50 ≤ ΔrP ≤ 100 kpc with ΔvP ≤ 100 km s−1 allows the selection of all close pairs with a probability of merging of at least 30%.
Deep MUSE observations in the HUDF, HDF-S, A2744, and COSMOS-Gr30 fields are used to construct a large spectroscopic sample of 2483 galaxies. Applying the new selection criteria, 366 secure close pairs of galaxies spread over a large range of redshift (0.2 < z < 6) and stellar masses (107 − 1011 M⊙) were identified. We used stellar masses derived from SED fitting to distinguish between major, minor, and very minor close pairs using their mass ratios as a proxy. We end up with a sample of 183 major, 140 minor, and 47 very minor close pairs with a respective galaxy mass ratio limit of 1:6, 1:100, and lower than 1:100.
Splitting the redshift domain into five intervals, we probed the evolution of the major and minor merger fractions up to z ≈ 6. We left out the very minor close pairs which are close to the regime of smooth gas accretion. We observe an increase of the major pair fraction in A2744 and COSMOS-Gr30 with respect to lower-density fields (HUDF and HDF-S) at z < 1 due to the presence of the cluster (z ∼ 0.3) and galaxy group (z ∼ 0.7) at these redshifts. The pairs found in these two dense structures were then removed for the analysis of the merger fractions.
The sample was further divided into two ranges of stellar masses using a constant separation limit of 109.5 M⊙. Estimates for the high-mass galaxy sample show an increase of the major merger fraction up to z ≈ 2 − 3 reaching a fraction of 21% and a decrease at high redshift dropping to ∼5% at z ≈ 6. The fraction for lower mass primary galaxies (M∗ ≤ 109.5 M⊙) seems to follow a more constant evolutionary trend along cosmic time. Similar trends are found for a median stellar mass separation.
Although we trace the merger fraction more accurately with the new criteria, the results are similar to our previous analysis over the HUDF and HDF-S fields (Ventou et al. 2017), especially taking into account the error bars. However, error bars are smaller due to the increased number of galaxies in the parent and close-pair samples. The comparison of the major merger fraction with new predictions from the EMERGE simulations (O’Leary et al., in prep.) shows a very good agreement at high redshift (z ∼ 3 − 6).
The evolution of the minor merger fraction is roughly constant around 20% for z < 1.5 and decreases slightly for z ≥ 3 with a fraction of 8 − 13%. The ratio between minor and major merger fractions is in good agreement with the predictions of HORIZON-AGN simulations (Kaviraj et al. 2015), taking into account the different mass ratio limits used to discriminate minor pairs from major ones.
MUSELET is an analysis software released by the consortium as part of the MPDAF suite http://mpdaf.readthedocs.io/en/latest/muselet.html
Acknowledgments
We thank the referee for providing useful and constructive comments which helped to improve the quality of this paper. We warmly thank Shy Genel for giving us access to mock catalogs of galaxies generated in the ILLUSTRIS-1 simulations, which are the basis of this publication. We also acknowledge Joseph O’Leary for providing us with new results from EMERGE simulations in advance of publication. This work has been carried out thanks to the support of the ANR FOGHAR (ANR-13-BS05-0010-02), the OCEVU Labex (ANR-11-LABX-0060), and the A*MIDEX project (ANR-11-IDEX-0001-02) funded by the “Investissements d’avenir” French government programme. BE acknowledges financial support from “Programme National de Cosmologie et Galaxies” (PNCG) of CNRS/INSU, France. JB acknowledges support by FCT/MCTES through national funds by this grant UID/FIS/04434/2019 and through the Investigador FCT Contract No. IF/01654/2014/CP1215/CT0003.
References
- Adams, S. M., Zaritsky, D., Sand, D. J., et al. 2012, AJ, 144, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Anglès-Alcàzar, D., Faucher-Giguère, C.-A., Kereš, D., et al. 2017, MNRAS, 470, 4698 [NASA ADS] [CrossRef] [Google Scholar]
- Bacon, R., Accardo, M., Adjali, L., et al. 2010, in Ground based and Airborne Instrumentation for Astronomy III, Proc. SPIE, 7735, 773508 [CrossRef] [Google Scholar]
- Bacon, R., Brinchmann, J., Richard, J., et al. 2015, A&A, 575, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bacon, R., Conseil, S., Mary, D., et al. 2017, A&A, 608, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bell, E. F., Zucker, D. B., Belokurov, V., et al. 2008, ApJ, 680, 295 [NASA ADS] [CrossRef] [Google Scholar]
- Bluck, A. F. L., Conselice, C. J., Bouwens, R. J., et al. 2009, MNRAS, 394, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Bluck, A. F. L., Conselice, C. J., Buitrago, J., et al. 2012, ApJ, 747, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Bolzonella, M., Miralles, J.-M., & Pelló, R. 2000, A&A, 363, 476 [NASA ADS] [Google Scholar]
- Borlaff, A., Eliche-Moral, M. C., Rodríguez-Pèrez, C., et al. 2014, A&A, 570, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bouché, N., Finley, H., Schroetter, I., et al. 2016, ApJ, 820, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Bournaud, F., Dekel, A., Teyssier, R., et al. 2011, ApJ, 741, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Brinchmann, J., Inami, H., Bacon, R., et al. 2017, A&A, 608, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- Bundy, K., Fukugita, M., Ellis, R. S., et al. 2009, ApJ, 697, 1369 [NASA ADS] [CrossRef] [Google Scholar]
- Caimmi, R. 2008, New A, 13, 314 [NASA ADS] [CrossRef] [Google Scholar]
- Calzetti, D., Armus, L., Bohlin, R. C., et al. 2000, ApJ, 533, 682 [NASA ADS] [CrossRef] [Google Scholar]
- Cameron, E. 2011, PASA, 28, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Casteels, K. R. V., Conselice, C. J., Bamford, S. P., et al. 2014, MNRAS, 445, 1157 [NASA ADS] [CrossRef] [Google Scholar]
- Chabrier, G. 2003, PASP, 115, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Chiappini, C. 2001, Rev. Mex. Astron. Astrofis. Conf. Ser., 11, 171 [NASA ADS] [Google Scholar]
- Cibinel, A., Le Floc’h, E., Perret, V., et al. 2015, ApJ, 805, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Conselice, C. J. 2006, ApJ, 638, 686 [NASA ADS] [CrossRef] [Google Scholar]
- Conselice, C. J., Bershady, M. A., Dickinson, M., & Papovich, C. 2003, AJ, 126, 1183 [NASA ADS] [CrossRef] [Google Scholar]
- Conselice, C. J., Rajgor, S., & Myers, R. 2008, MNRAS, 386, 909 [NASA ADS] [CrossRef] [Google Scholar]
- Conselice, C. J., Mortlock, A., Bluck, A. F. L., Grützbauch, R., & Duncan, K. 2013, MNRAS, 430, 1051 [NASA ADS] [CrossRef] [Google Scholar]
- Cordero, J. P., Campusano, L. E., De Propris, R., et al. 2016, ApJ, 817, L6 [NASA ADS] [CrossRef] [Google Scholar]
- De Propris, R., Conselice, C. J., Liske, J., et al. 2007, ApJ, 666, 212 [NASA ADS] [CrossRef] [Google Scholar]
- de Ravel, L., Le Févre, O., Tresse, L., et al. 2009, A&A, 498, 379 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Di Matteo, P., Combes, F., Melchior, A.-L., & Semelin, B. 2007, A&A, 468, 61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Duncan, K., Conselice, C. J., Mundy, C., et al. 2019, ApJ, 876, 110 [NASA ADS] [CrossRef] [Google Scholar]
- Epinat, B., Tasca, L., Amram, P., et al. 2012, A&A, 539, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Epinat, B., Contini, T., Finley, H., et al. 2018, A&A, 609, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Förster Schreiber, N. M., Genzel, R., Bouchè, N., et al. 2009, ApJ, 706, 1364 [NASA ADS] [CrossRef] [Google Scholar]
- Förster Schreiber, N. M., Shapley, A. E., Erb, D. K., et al. 2011, ApJ, 731, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Genel, S., Vogelsberger, M., Springel, V., et al. 2014, MNRAS, 445, 175 [Google Scholar]
- Heiderman, A., Jogee, S., Marinova, I., et al. 2009, in Galaxy Evolution: Emerging Insights and Future Challenges, eds. S. Jogee, I. Marinova, L. Hao, G. A. Blanc, et al., ASP Conf. Ser., 419, 257 [NASA ADS] [Google Scholar]
- Hine, N. K., Geach, J. E., Alexander, D. M., et al. 2016, MNRAS, 455, 2363 [NASA ADS] [CrossRef] [Google Scholar]
- Hinton, S. R., Davis, T. M., Lidman, C., Glazebrook, K., & Lewis, G. F. 2016, Astron. Comput., 15, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Hung, C.-L., Hayward, C. C., Smith, H. A., et al. 2016, ApJ, 816, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Inami, H., Bacon, R., Brinchmann, J., et al. 2017, A&A, 608, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jian, H.-Y., Lin, L., & Chiueh, T. 2012, ApJ, 754, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Joseph, R. D., & Wright, G. S. 1985, MNRAS, 214, 87 [NASA ADS] [Google Scholar]
- Kampczyk, P., Lilly, S. J., Carollo, C. M., et al. 2007, ApJS, 172, 329 [NASA ADS] [CrossRef] [Google Scholar]
- Kaviraj, S. 2014, MNRAS, 437, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Kaviraj, S., Devriendt, J., Dubois, Y., et al. 2015, MNRAS, 452, 2845 [NASA ADS] [CrossRef] [Google Scholar]
- Kereš, D., Katz, N., Weinberg, D. H., & Davè, R. 2005, MNRAS, 363, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Kitzbichler, M. G., & White, S. D. M. 2008, MNRAS, 391, 1489 [NASA ADS] [CrossRef] [Google Scholar]
- Kriek, M., van Dokkum, P. G., Labbè, I., et al. 2009, ApJ, 700, 221 [NASA ADS] [CrossRef] [Google Scholar]
- Lagos, C. D. P., Stevens, A. R. H., Bower, R. G., et al. 2018, MNRAS, 473, 4956 [NASA ADS] [CrossRef] [Google Scholar]
- Laigle, C., McCracken, H. J., Ilbert, O., et al. 2016, ApJS, 224, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Le Fèvre, O., Abraham, R., Lilly, S. J., et al. 2000, MNRAS, 311, 565 [NASA ADS] [CrossRef] [Google Scholar]
- L’Huillier, B., Combes, F., & Semelin, B. 2012, A&A, 544, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lin, L., Patton, D. R., Koo, D. C., et al. 2008, ApJ, 681, 232 [NASA ADS] [CrossRef] [Google Scholar]
- López-Sanjuan, C., Balcells, M., Pèrez-Gonzàlez, P. G., et al. 2010, A&A, 518, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- López-Sanjuan, C., Le Fèvre, O., de Ravel, L., et al. 2011, A&A, 530, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- López-Sanjuan, C., Le Fèvre, O., Ilbert, O., et al. 2012, A&A, 548, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- López-Sanjuan, C., Le Fèvre, O., Tasca, L. A. M., et al. 2013, A&A, 553, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- López-Sanjuan, C., Cenarro, A. J., Varela, J., et al. 2015, A&A, 576, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lotz, J. M., Jonsson, P., Cox, T. J., et al. 2011, ApJ, 742, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Lotz, J. M., Papovich, C., Faber, S. M., et al. 2013, ApJ, 773, 154 [NASA ADS] [CrossRef] [Google Scholar]
- Lotz, J. M., Koekemoer, A., Coe, D., et al. 2017, ApJ, 837, 97 [Google Scholar]
- Mahler, G., Richard, J., Clèment, B., et al. 2018, MNRAS, 473, 663 [NASA ADS] [CrossRef] [Google Scholar]
- Man, A. W. S., Toft, S., Zirm, A. W., Wuyts, S., & van der Wel, A. 2012, ApJ, 744, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Man, A. W. S., Zirm, A. W., & Toft, S. 2016, ApJ, 830, 89 [NASA ADS] [CrossRef] [Google Scholar]
- McLure, R. J., Pearce, H. J., Dunlop, J. S., et al. 2013, MNRAS, 428, 1088 [NASA ADS] [CrossRef] [Google Scholar]
- Mantha, K. B., McIntosh, D. H., Brennan, R., et al. 2018, MNRAS, 475, 1549 [NASA ADS] [CrossRef] [Google Scholar]
- Mihos, J. C. 2004, Clusters of Galaxies: Probes of Cosmological Structure and Galaxy Evolution, 277 [Google Scholar]
- Moreno, J., Bluck, A. F. L., Ellison, S. L., et al. 2013, MNRAS, 436, 1765 [NASA ADS] [CrossRef] [Google Scholar]
- Moster, B. P., Somerville, R. S., Newman, J. A., & Rix, H.-W. 2011, ApJ, 731, 113 [Google Scholar]
- Moster, B. P., Naab, T., & White, S. D. M. 2018, MNRAS, 477, 1822 [NASA ADS] [CrossRef] [Google Scholar]
- Mundy, C. J., Conselice, C. J., Duncan, K. J., et al. 2017, MNRAS, 470, 3507 [NASA ADS] [CrossRef] [Google Scholar]
- Murali, C., Katz, N., Hernquist, L., Weinberg, D. H., & Davè, R. 2002, ApJ, 571, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Naab, T., Johansson, P. H., & Ostriker, J. P. 2009, ApJ, 699, L178 [NASA ADS] [CrossRef] [Google Scholar]
- Neichel, B., Hammer, F., Puech, M., et al. 2008, A&A, 484, 159 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nelson, D., Pillepich, A., Genel, S., et al. 2015, Astron. Comput., 13, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Ocvirk, P., Pichon, C., & Teyssier, R. 2008, MNRAS, 390, 1326 [NASA ADS] [Google Scholar]
- Patton, D. R., Carlberg, R. G., Marzke, R. O., et al. 2000, ApJ, 536, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Patton, D. R., Torrey, P., Ellison, S. L., Mendel, J. T., & Scudder, J. M. 2013, MNRAS, 433, L59 [NASA ADS] [CrossRef] [Google Scholar]
- Perret, V. 2014, Thesis, Aix-Marseille Université, France [Google Scholar]
- Perret, V., Renaud, F., Epinat, B., et al. 2014, A&A, 562, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Peterson, S. D. 1979, ApJS, 40, 527 [NASA ADS] [CrossRef] [Google Scholar]
- Qu, Y., Helly, J. C., Bower, R. G., et al. 2017, MNRAS, 464, 1659 [NASA ADS] [CrossRef] [Google Scholar]
- Rafelski, M., Teplitz, H. I., Gardner, J. P., et al. 2015, AJ, 150, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Rodriguez-Gomez, V., Genel, S., Vogelsberger, M., et al. 2015, MNRAS, 449, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Rodriguez-Gomez, V., Pillepich, A., Sales, L. V., et al. 2016, MNRAS, 458, 2371 [NASA ADS] [CrossRef] [Google Scholar]
- Sancisi, R., Fraternali, F., Oosterloo, T., & van der Hulst, T. 2008, A&A Rev., 15, 189 [CrossRef] [Google Scholar]
- Scoville, N., Aussel, H., Brusa, M., et al. 2007, ApJS, 172, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Scudder, J. M., Ellison, S. L., Torrey, P., Patton, D. R., & Mendel, J. T. 2012, MNRAS, 426, 549 [NASA ADS] [CrossRef] [Google Scholar]
- Shapiro, K. L., Genzel, R., Förster Schreiber, N. M., et al. 2008, ApJ, 682, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Simons, R. C., Kassin, S. A., Snyder, G. F., et al. 2019, ApJ, 874, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Snyder, G. F., Lotz, J. M., Rodriguez-Gomez, V., et al. 2017, MNRAS, 468, 207 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V. 2010, MNRAS, 401, 791 [NASA ADS] [CrossRef] [Google Scholar]
- Stewart, K. R., Kaufmann, T., Bullock, J. S., et al. 2011, ApJ, 735, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Tasca, L. A. M., Le Fèvre, O., Lòpez-Sanjuan, C., et al. 2014, A&A, 565, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Turner, E. L. 1976, ApJ, 208, 20 [NASA ADS] [CrossRef] [Google Scholar]
- van de Voort, F., Schaye, J., Booth, C. M., Haas, M. R., & Dalla Vecchia, C. 2011, MNRAS, 414, 2458 [NASA ADS] [CrossRef] [Google Scholar]
- van de Voort, F., Schaye, J., Altay, G., & Theuns, T. 2012, MNRAS, 421, 2809 [NASA ADS] [CrossRef] [Google Scholar]
- Ventou, E., Contini, T., Bouchè, N., et al. 2017, A&A, 608, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Verhamme, A., Garel, T., Ventou, E., et al. 2018, MNRAS, 478, L60 [NASA ADS] [CrossRef] [Google Scholar]
- Vogelsberger, M., Genel, S., Sijacki, D., et al. 2013, MNRAS, 436, 3031 [NASA ADS] [CrossRef] [Google Scholar]
- Vogelsberger, M., Genel, S., Springel, V., et al. 2014, MNRAS, 444, 1518 [NASA ADS] [CrossRef] [Google Scholar]
- Williams, R. J., Quadri, R. F., & Franx, M. 2011, ApJ, 738, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Xu, C. K., Shupe, D. L., Bèthermin, M., et al. 2012, ApJ, 760, 72 [NASA ADS] [CrossRef] [Google Scholar]
- Zabl, J., Bouchè, N. F., Schroetter, I., et al. 2019, MNRAS, 485, 1961 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: A new weighting scheme for the merger fraction
In Fig. A.1 we compare, for the six redshift snapshots, the projected velocity-separation distance diagrams obtained in Sect. 3 to the least-squares fits of an exponential function using a nonlinear regression to the simulated datasets. The redshift evolution of the parameter estimates is shown in Fig. A.2. We decided to use the median of the parameter estimates in the final expression of the probability weight, W(ΔrP, ΔvP), effective for all redshifts (see Eq. (3)), since there is little evolution of the different parameters with redshift.
 |
Fig. A.1. From left to right: for each redshift, the projected velocity-separation distance diagram, the approximate function from the nonlinear regression, and the residual of their subtraction from one another. |
 |
Fig. A.1. continued. |
 |
Fig. A.2. Redshift evolution of the regression parameter estimates with the reported approximate function. The error bars represent the computed 1σ errors on the parameters. |
Appendix B: Catalogs of close pairs of galaxies detected in MUSE fields
Sample of major (mass ratio of 1:1−1:6) close pairs of galaxies identified in the four MUSE fields.
Sample of minor (mass ratio of 1:6−1:100) close pairs of galaxies identified in the four MUSE fields.
All Tables
Major merger fractions up to z ≈ 6 from MUSE deep observations for different redshift and stellar mass intervals.
Minor merger fractions up to z ≈ 6 from MUSE deep observations for different redshift and stellar mass intervals.
Sample of major (mass ratio of 1:1−1:6) close pairs of galaxies identified in the four MUSE fields.
Sample of minor (mass ratio of 1:6−1:100) close pairs of galaxies identified in the four MUSE fields.
All Figures
 |
Fig. 1. Stellar mass distribution of galaxies in the ILLUSTRIS simulation for six snapshots corresponding to redshifts z = 0.5, 1, 1.5, 3, 4 and 5. The total number of galaxies and the median stellar mass are indicated in each panel. |
| In the text | |
 |
Fig. 2. (a) Galaxy pair velocity-separation distance diagram from the ILLUSTRIS-1 simulation for six snapshots at different redshifts, color-coded with respect to the fraction of future mergers within the pair sample. (b) Same diagram as (a) but with projected velocity-separation distances. The two red boxes correspond to the new criteria introduced in Sect. 3.2.3. |
| In the text | |
 |
Fig. 3. Influence of the galaxy mass ratio in the pair on the velocity-separation distance diagram (zoomed into a box of 200 kpc × 200 km s−1) and the probability that the pair will merge for different redshifts. Top: major merger distribution, with a mass ratio between the primary galaxy and its companion within 1:1 and 1:6. Bottom: minor merger distribution with a mass ratio in the pair lower than 1:6. |
| In the text | |
 |
Fig. 4. Influence of the stellar mass of the primary galaxy on the merger velocity-separation distance diagram. A constant stellar mass limit of 109.5 M⊙ is chosen to distinguish low-mass from massive primary galaxies within the major (top) and the minor (bottom) pair samples at z = 1. |
| In the text | |
 |
Fig. 5. Major merger fraction of close pairs selected in MUSE deep observations over the Hubble Ultra Deep Field (so-called UDF-mosaic) for three redshift bins and five values of merging probability threshold (10, 20, 30, 55, and 80%). The choice of a 30% threshold is motivated by the convergence of the merger fraction below this value. |
| In the text | |
 |
Fig. 6. Stellar mass as a function of redshift for the parent sample of 2483 galaxies drawn from MUSE deep observations in HUDF (gray dots), HDFS (blue dots), A2744 (red dots), and CGR30 (green dots). Thanks to the high sensitivity of MUSE, star-forming galaxies are identified with a secure spectroscopic redshift up to z ∼ 6 over a large range of stellar masses (∼ 107 − 1011 M⊙), except in the so-called “redshift desert” (z ∼ 1.5−2.8) where galaxies in the low-mass regime (M⋆ ∼ 107 − 108 M⊙) are detected behind the A2744 lensing cluster only. |
| In the text | |
 |
Fig. 7. Top: spectroscopic redshift distribution of the parent galaxies in the four MUSE data cubes used in this analysis. Bottom: redshift histogram of the close pairs sample showing the contribution of major (black), minor (red), and very minor close pairs (blue). |
| In the text | |
 |
Fig. 8. Examples of close pairs of galaxies, at different redshifts and with various mass ratios in the UDF-Mosaic field. From left to right: HST image in the F775W filter with the redshift of the primary galaxy, MUSE reconstructed white light image, narrow-band image of one of the brightest emission lines of the pair, and the zoomed spectra of the two galaxies around this line (red for the primary galaxy and blue for its companion) with the labeled MUSE ID, mass ratio, relative velocity difference, and projected separation distance. Images are 10″ in linear size and centered around the primary galaxy, circled in white. The green circle indicates the location of its companion. The first two close pairs correspond to the very minor and minor regimes, and the last two are major close pairs at low and high redshift. |
| In the text | |
 |
Fig. 9. Stellar mass ratio and redshift distribution of the whole close pairs sample from the combined analysis of the four MUSE deep fields. Symbols are color-coded with respect to the stellar mass of the primary galaxy. The dashed lines indicate the mass ratio (primary over companion galaxy) limits chosen to distinguish major close pairs (limit of 6, blue dashed line and colored area) from minor (between a mass ratio limit of 6 and 100, red dashed line and colored area) and very minor pairs (mass ratio greater than 100). |
| In the text | |
 |
Fig. 10. Stellar mass of the primary galaxy as a function of redshift for our major (top) and minor (bottom) close pair samples. Right pointing triangles correspond to close pairs in the HDF-S, other triangles to close pairs in the COSMOS-Gr30 field, squares are pairs from A2744, and circles from the UDF-Mosaic. Symbols are color-coded with respect to the weight, Wp described in Sect. 3.2.3, used for the computation of merger fractions. Darker pairs have a higher probability of merging by z = 0 and will thus have a higher contribution on the estimated merger fraction. Except in the redshift desert (z ∼ 1.5−2.8), we have a relatively good stellar mass completeness level for major close pairs down to a primary galaxy stellar mass of ≈107 M⊙. However, for the minor close pairs sample, a lower mass limit of 109 M⊙ must be applied to keep a reasonable level of completeness for the merger fraction estimates. |
| In the text | |
 |
Fig. 11. Evolution of the galaxy major merger fraction up to z ∼ 6 from MUSE deep fields. Left: blue diamonds, green circles, yellow stars, and purple triangles are estimates of the fraction from the UDF-mosaic, Abell 2744, HDF-S, and COSMOS-Gr30 regions, respectively, whereas red squares correspond to the fraction for the combined analysis of the MUSE data. For the lowest redshift bin, fractions were computed without (filled symbols) and with (open symbols) members of the galaxy cluster A2744 and galaxy group COSMOS-Gr30. Right: evolution of the major merger fraction for two ranges of stellar mass, assuming first a constant separation limit of M⋆ = 109.5 M⊙ (grey and yellow circles show the MUSE estimates for low-mass and massive galaxies, respectively), then taking the median mass of the parent sample in each redshift bin as the limit (orange and purple triangles). As for the combined fraction of the left panel, the fractions were computed without taking into account the cluster and group members. The median stellar mass estimated in the range 107 − 1011 M⊙ for each redshift intervals are listed in Table 1. |
| In the text | |
 |
Fig. 12. Major merger fraction compared to previous close pairs count studies and recent simulations. Combined major merger fractions from this work (red squares) are compared to previous estimates from MUSE observations (black squares: Ventou et al. 2017) and other surveys (light blue symbols: de Ravel et al. 2009; Xu et al. 2012; López-Sanjuan et al. 2013; Tasca et al. 2014). The purple and orange solid lines show the predictions from the EAGLE simulations for two different mass ranges (see Qu et al. 2017 for details). Green triangles correspond to the major pair fractions estimated in the ILLUSTRIS simulation (Snyder et al. 2017). Finally, the predictions of pair fractions up to z ∼ 6 with a lower stellar mass cut-off of 109.5 M⊙ from the EMERGE simulations (O’Leary et al., in prep.) are shown with the brown line. |
| In the text | |
 |
Fig. 13. Evolution of the galaxy minor merger fraction up to z ∼ 6 from MUSE deep fields, for primary galaxies with a stellar mass range of ∼ 109 − 1011 M⊙. Left: as in Fig. 11; different symbols show the results from the four regions individually. Right: red squares are estimates of the combined minor merger fraction from the whole MUSE data set and over the whole stellar mass range ∼ 109 − 1011 M⊙. Using the median value of stellar mass in each redshift bin as a separation limit (∼ 1010 M⊙, see Table 2), the purple and golden triangles correspond to the minor merger fraction for low-mass and massive galaxies, respectively. As in Fig. 11, filled and open symbols correspond to the fractions computed without and with galaxy members of the cluster and group for 0.2 ≤ z ≤ 1, respectively. Cyan points are estimates from previous spectroscopic minor pair counts (López-Sanjuan et al. 2011, 2012). |
| In the text | |
 |
Fig. A.1. From left to right: for each redshift, the projected velocity-separation distance diagram, the approximate function from the nonlinear regression, and the residual of their subtraction from one another. |
| In the text | |
 |
Fig. A.1. continued. |
| In the text | |
 |
Fig. A.2. Redshift evolution of the regression parameter estimates with the reported approximate function. The error bars represent the computed 1σ errors on the parameters. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.