EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 630 (October 2019) A&A, 630 (2019) A93 Full HTML
Free Access
Issue
A&A
Volume 630, October 2019
Article Number A93
Number of page(s) 7
Section Celestial mechanics and astrometry
DOI https://doi.org/10.1051/0004-6361/201935379
Published online 27 September 2019

© ESO 2019

1. Introduction

The International VLBI Service for Geodesy and Astrometry (IVS) Working Group on Galactic Aberration (WG8) was established by the IVS Directing Board at its meeting in November 2015 with the work to begin in 2016. The purpose of the group was to investigate the issues related to incorporating the effect of Galactic aberration in IVS analysis. By “Galactic aberration”, we are referring in this report to the change in aberration over decade time scales due to the rotation of the galaxy. Other names for this effect are also used in the literature, such as aberration in proper motions (Kovalevsky 2003), secular aberration drift (Titov et al. 2011), and glide (Mignard & Klioner 2012). We should note that the static effect of Galactic aberration Θ0/c for a circular rotation speed Θ0 = 240 km s−1 is 8 × 10−4 radians or 165 arcsec, which is huge compared to the change in aberration. Because of the extreme length of the Galactic rotation period, it has been standard practice to absorb this large, nearly constant effect into the reported source positions. Based on this investigation, WG8 was tasked to formulate a recommendation for an aberration correction to be applied in IVS data analysis and to be provided to the ICRF3 working group (Jacobs et al. 2012). This effect is not currently included in our standard VLBI analysis. Estimates of the size of this effect indicate that it is important that secular aberration drift be accounted for in order to maintain an accurate celestial reference frame and allow astrometry at the several microarcsecond level.

Secular aberration drift is caused by the acceleration of the solar system barycenter (SSB). It is mainly due to the rotation of the barycenter about the center of the Milky Way galaxy with a period of about 200 million years. One of the goals of our analysis was to establish this fact but also to determine an upper bound on the non-Galactic center component of the acceleration of the SSB. This motion induces an apparent proper motion of extragalactic objects observed by VLBI. Proper motion due to Galactocentric acceleration was predicted theoretically to have a systematic dipolar structure with an amplitude of 4–6 μas yr−1 (see e.g., Fanselow 1983; Bastian 1995; Gwinn et al. 1997; Sovers et al. 1998; Mignard 2002; Kovalevsky 2003, and Kopeikin & Makarov 2006).

A number of papers have been written using different observation data and analysis methods to determine the distance R0 to the Galactic center and the circular rotation speed Θ0 at the distance R0. For instance, by using measured trigonometric parallaxes and proper motions of masers in massive star-forming regions, many investigators have determined the values Θ0 and R0. Using these values, one can determine an aberration constant of dipole proper motion . Estimates of this dipole proper motion amplitude based on recent Galactic astronomy measurements are discussed in Sect. 4.

Figure 1 shows the proper motion induced by Galactic aberration where the galactocentric aberration constant is 5.8 μas yr−1, which is the value recommended by WG8. The proper motion vectors stream away from the anti-Galactic center towards the Galactic center in a dipolar pattern where the maximum proper motion occurs for sources that are 90° away from the Galactic center (αG = 266.4°, δG = −29.0°).

thumbnail Fig. 1.

Aberration proper motion field for an aberration constant of 5.8 μas yr−1.

The effect of secular aberration drift is to cause apparent source positions to change over time. Several studies in recent years, which we discuss in Sect. 5, have shown that aberration drift can be estimated from VLBI geodetic data. The VLBI estimates of the galactocentric aberration constant AG are in the range 5.1–6.4 μas yr−1. These estimates are reasonably close to independently determined estimates of 4.8–5.4 μas yr−1 that can be derived from recent astrometric measurements of proper motions and parallaxes of masers in the Milky Way galaxy. Although the effect of aberration drift is small, it is not negligible in terms of future micro-arcsecond astrometry. The systematic drift due to an aberration drift of 5 μas yr−1 would lead to a dipole systematic error of 100 μas after 20 years. One of the effects of applying an aberration model in a solution is to change the source position estimates for a given reference epoch. If the reference epoch of the aberration model is 2015.0, when the correction is defined to be zero, the changes in estimated radio source positions due to applying the aberration correction are as large as 30–40 μas depending on the source coordinates (see Sect. 3). This arises from the distribution of the median epochs of observation of the sources observed by VLBI over the last three decades. The correction for a given source increases as the temporal difference between the median epoch of observation of the source and the reference epoch increases. Malkin (2014) discussed this in some detail as well as the effect of Galactic aberration on the CRF in general. Liu et al. (2012) investigated the impact of Galactic aberration on the ICRF and on EOP.

From our VLBI solutions, we determine global acceleration estimates that could include contributions other than galactocentric acceleration. There are several possible contributions.

One contribution is the aberration drift due to the oscillation of the solar system about the Galactic plane as the solar system rotates around the Galactic center. The amplitude of this motion is 49–93 pc and with a period of 52–74 Myr (Bahcall & Bahcall 1985). Kopeikin & Makarov (2006) derive harmonic expressions expressions for the peculiar acceleration components of the Sun’s oscillation. In the vertical direction, the maximum acceleration would be 0.40–0.57 μas yr−1. Titov & Lambert (2013) find a similar result. Majaess et al. (2009) estimated that 3 Myr ago the solar system passed through the Galactic plane and is now about 26 pc above it. Based on this, we estimate that the current vertical acceleration contribution is 0.12–0.18 μas yr−1. The maximum peculiar acceleration contribution in the direction of rotation about the Galactic center is 0.35 μas yr−1 and 0.19 μas yr−1 in the Galactic center direction using the expressions in Kopeikin & Makarov (2006).

Another possible contribution to acceleration could be due to attraction of the Milky Way Galaxy by distant galaxies or clusters of galaxies. Virgo with a mass of 1.2 × 1015 solar mass at a distance of 15.4 Mpc (Fouqué et al. 2001) leads to a maximum aberration proper motion of 0.015 μas yr−1. Andromeda with a mass of 1.3 × 1012 solar mass (Evans & Wilkinson 2000) at a distance of 0.778 Mpc (Karachentsev et al. 2004) would lead to an aberration proper motion of only 0.006 μas yr−1. Distant clusters, for instance the Shapley cluster with a mass of 1.0 × 1016 solar mass and distance of 200 Mpc yields only 0.0008 μas yr−1. These contributions are too small to detect in our VLBI observations.

The primary objective of the WG was to determine a value of the galactocentric constant AG to be applied in an a priori model of aberration. The application of an a priori model of aberration will most importantly account for the systematic error that is committed without the model. Clearly the dipole systematic due to aberration is significant compared to the Celestial Reference Frame (CRF) noise floor, which in the case of ICRF3 is 30 μas. Preliminary results of WG8 were first reported in MacMillan et al. (2018).

The ICRF realizes the International Celestial Reference System (ICRS) by the positions of a set of defining sources that are assumed to have no measurable proper motion. An underlying issue is that applying apparent proper motion corrections due to aberration in VLBI analysis could require a redefinition of the ICRS. By definition, an inertial reference frame has no rotation and no acceleration of the reference point. A quasi-inertial reference frame has no rotation, but acceleration is permitted. As the ICRS is quasi-inertial, the introduction of the Galactic acceleration to the solar system barycentre is allowed. In any case, a redefinition of the ICRS is not something that the IVS can do as it would have to be done by the International Astronomical Union (IAU). The working group found that it was not necessary to redefine the ICRS. We can simply apply an aberration proper motion correction in VLBI analysis by a procedure that is similar to that followed in VLBI analysis to account for other effects like precession or annual aberration (see Sect. 3). For non-VLBI applications requiring source positions at an epoch other than the reference epoch of the aberration model, one would need to apply the Galactic aberration model proper motions with that reference epoch to the source positions given in a catalog generated with the model.

In Sect. 2, we begin by considering the observed proper motion field and the parameters of aberration. Then in Sect. 3, we consider the effects on estimated source positions that result when an aberration model is applied in a VLBI CRF solution. In Sects. 4 and 5, we consider possible choices of the model aberration constant: (1) a value determined from recent parallax and proper motion measurements of Galactic masers, or (2) a geodetic VLBI determined value. Section 6 gives our recommendation for a model to apply for the IAU ICRF3 solution. Section 7 is a discussion of geodetic solution results. Here we also discuss placing an upper bound on non-Galactic center acceleration of the SSB based on our estimates of the secular aberration drift vector.

2. Proper motion field and aberration parameters

To give a sense of the range of apparent proper motion, we start by looking at the raw picture of estimated source proper motions. Figure 2 shows the proper motion field computed from source position time series where the RA and Dec rate uncertainties were better than 50 μas yr−1, which for the most part depend on how frequently a given source has been observed. These position time series were estimated (by D. Gordon) with Calc/Solve using the data from 1979 to 2018. The precision and number of proper motion estimates for Southern declinations below −40° to −50° is poorer than at higher declinations because there are fewer geodetic antennas in the Southern hemisphere compared to the Northern hemisphere. These observed proper motions can be as large as a few hundred μas yr−1, which are likely due to apparent motion caused by source structure effects. In contrast, Galactic aberration proper motions in Fig. 1 are less than 6 μas yr−1, but they are systematic.

thumbnail Fig. 2.

Proper motion field computed from source position time series (RA an Dec rate uncertainties better than 50 μas yr−1).

Source structure variations are known to be correlated with variations in the apparent position as measured by VLBI (see e.g., Petrov et al. 2018; Titov & Lopez 2018). For the bulk of the sources we observe, we have not determined the apparent linear source position motions arising from source structure variations that could in turn affect Galactic aberration estimates. Determining the effect of source structure for the large number of sources in our VLBI solutions would require significant effort, which is something that should be done in the future. Xu et al. (2016) used delay observables for detection of source structure effects. Anderson & Xu (2018) demonstrated that structure effects are a major error source in geodetic VLBI. Xu et al. (2019) quantified the structure effect magnitudes for 3417 sources by analyzing phases and amplitudes in historical geodetic VLBI observations. Based on this and future additional work, source structure effects could be corrected for a large fraction of geodetic sessions and specifically for Calc/Solve analysis to estimate aberration drift. However, for the VLBI geodetic solutions discussed here, estimation of systematic aberration drift assumed that source structure effects were random over the sky.

A change in the source direction away from the nominal direction s0 due to the aberration acceleration vector A in the BCRS frame (A1, A2, A3) in a time interval Δt can be expressed by the classical expression (see e.g., Kovalevsky (2003)) for aberration since the SSB velocity is much less than the speed of light

(1)

(2)

where A is the magnitude of A and αA and δA are the equatorial coordinates of the vector direction.

The components of the aberration proper motion Δs/Δt for a source with equatorial coordinates in right ascension and declination (α, δ) are

(3)

(4)

3. Application of aberration in geodetic VLBI solutions

In this section, we discuss how the aberration correction should be applied for a given acceleration vector A to determine a new ICRF catalog. One can simply run a solution with an aberration correction that has a reference epoch of t0. The estimated positions will then be self-consistent with the correction. The aberration contributions to the a priori source positions are

(5)

(6)

where the aberration proper motions (Δμα cos δ, Δμδ) are given above in Eqs. (2) and (3). For non-VLBI applications requiring positions at epoch t, the catalog positions at t0 would be corrected by applying the Galactic aberration model correction.

We have investigated what is the effect of the aberration on estimated source positions. Figures 3–6 show the Calc/Solve differences in source positions (RA, Dec) versus RA and Dec for an aberration constant AG of 5.8 μas yr−1, which is the value we recommended for the IAU ICR3 solution as discussed below in Sect. 6. The variation (scatter) of the differences at RA or Dec in these plots is due to the fact that the difference in the mean epochs from the chosen reference epoch 2015.0 vary significantly over the set of sources. The source position differences range over ±30–40 μas.

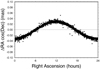thumbnail Fig. 3.

Change in right ascension due to aberration versus right ascension with an aberration constant of 5.8 μas yr−1 and reference epoch of 2015.0.

thumbnail Fig. 4.

Change in right ascension due to aberration versus declination with an aberration constant of 5.8 μas yr−1 and reference epoch of 2015.0.

thumbnail Fig. 5.

Change in declination due to aberration versus right ascension with an aberration constant of 5.8 μas yr−1 and reference epoch of 2015.0.

thumbnail Fig. 6.

Change in declination due to aberration versus declination with an aberration constant of 5.8 μas yr−1 and a reference epoch of 2015.0.

4. Estimates derived from Galactic astronomy measurements

Aberration can also be derived from recent (2009–2017) Galactic astronomy measurements (e.g., Reid et al. 2014; Rastorguev et al. 2017; Brunthaler et al. 2011). These measurements are trigonometric parallaxes and proper motions of masers in high-mass star-forming regions in the Milky Way galaxy. The measurements were made using the Very Long Baseline Array (VLBA), the European VLBI network (EVN), and the Japanese VLBI Exploration of Radio Astronomy Project (VERA). The most recent investigation noted here (Rastorguev et al. 2017), used a maser sample of 136 sources. Using these parallax and proper motion measurements, different investigators have derived models of the galaxy. Among the parameters of these models are the radial distance R0 (kpc) to the Galactic center and circular rotation speed Θ0 (km s−1) of the solar system barycenter around the Galactic center, which is located at a position with right ascension and declination of αG = 266.4° and δG = −29.0° (Reid & Brunthaler 2004). To determine an aberration constant, we just consider the effect of the Local Standard of Rest (LSR) circular revolution with speed Θ0 around the Galactic center. We note that there could be a small pecular acceleration an order of magnitude less than galactocentric acceleration due to solar motion with respect to the LSR as discussed in the introduction.

Based on the estimated parameters R0 and Θ0 and their uncertainties from each investigator, one can determine the acceleration vector amplitude of (see Kovalevsky 2003) and its uncertainty assuming a circular orbit. This can be converted to an aberration constant of dipole proper motion . Table 1 shows the resulting estimates of the aberration constant AG. Based on the uncertainties of R0 and Θ0, the formal uncertainties of AG are in the range 0.30−0.8 μas yr−1. The uncertainties have improved over the period 2009–2016, because more maser data became available. This also had the effect of reducing correlations between the Galactic model parameters that were being estimated. Malkin (2014) averaged estimates of R0 and Θ0 from 2010 to 2014 and obtained an average AG of 5.0 ± 0.3 μas yr−1, which is consistent with the values in Table 1. To apply a model based on an aberration constant derived in this way, technically one would need to transform source motion in the Galactic coordinate system to the equatorial system (Murray 1983), but Malkin (2014) noted that errors induced by these matrix transformations are less than 0.04 μas yr−1.

Table 1.

Galactic astronomy derived estimates of the aberration constant.

5. Geodetic VLBI solutions

Over the last several years, several groups that include WG8 members have made solutions for the secular aberration vector A using Calc/Solve (Ma et al. 1990) or VieVS (Böhm et al. 2018), where it was not assumed that it was in the Galactic center direction. Table 2 shows the estimates and uncertainties of the secular aberration vector components: Galactic center component AG = AX, the component AY in the direction of motion around the Galactic center, and the component AZ toward the Galactic pole, and the direction of the vector that was estimated for each solution. These solutions include published solutions as well as solutions done as part of the WG8 study. Calc/Solve global parameter estimate uncertainties are usually inflated by a factor of 1.5, which was derived in decimation studies (e.g., Fey et al. 2015). In Table 2, the uncertainties of the Calc/Solve global parameter (Method 1) estimates were all scaled up by this factor and the uncertainties of the other solutions are the uncertainties given in the referenced publications.

Table 2.

Geodetic VLBI aberration estimates.

The solutions reported in Table 2 were performed using all or most of the geodetic VLBI observations from 1979 to as late as 2018. For these solutions, site positions and velocities, and radio source positions were estimated along with Earth Orientation parameters (polar motion, UT1 and nutation). The site position estimates were constrained via no net translation and rotation constraints to ITRF2008 or ITRF2014 and the source positions via no net rotation constraints to a priori ICRF2 positions (Fey et al. 2015). Station clocks, wet zenith troposphere delay and troposphere gradient parameters were estimated as piecewise linear functions. Post-seismic position changes following Earthquakes at Concepcion (Chile) in January 2010, Tsukuba (Japan) in May 2011, Fairbanks (Alaska) in September 2002 were accounted for by either estimating post-seismic positions for these sites for each 24-h session in which they appeared or by applying the ITRF2014 (Altamimi et al. 2016) coseismic and postseismic models.

The global Calc/Solve solutions (Xu et al. 2012 and Xu 2017 priv. com. MacMillan 2014 and MacMillan 2017 priv. com.) and the VieVS solution (Titov & Krásná 2018) estimated the components of A as additional global parameters (Method 1). For the Calc/Solve “time series” solutions (Method 2; Titov et al. 2011 and Titov & Lambert 2013), A was estimated in three steps: (1) estimate source position time series in Calc/Solve solutions, (2) estimate source apparent proper motions from these time series, and (3) estimate A from these proper motions. The big advantage of estimation of A globally is that all global TRF and CRF parameters are estimated in the same solution which means that they are self-consistent and covariances between them are preserved. However, the advantage of the Titov and Lambert type of solution is that they can address the problem of source position scatter and large proper motion more directly for each source by removing sources altogether or by removing outliers in the source position time series.

For the “scale” solution (Method 3), Titov & Krásná (2018) expanded Eq. (1) so that the aberration delay becomes

(7)

(8)

A global scale factor parameter F was estimated for each source using only the second term in Eq. (7) and A was then derived from the estimated scale factor parameters for all sources using the expression above for F. In the Calc/Solve and VieVS global solutions (Method 1), no such separation was made and A was estimated essentially from the proper motions of all the sources. An advantage of the “scale” method is that it allows one to estimate A from different subsets of all sources and thereby remove poorly determined sources from the estimation. The scale solution in Table 2 required that a source have a minimum of 50 observations to be included in the aberration estimate.

Most of the VLBI estimates of A have relatively small components (less than 25% of |A|) not in the Galactic center direction. An exception is the first solution of Xu et al. (2012), where the component of the acceleration A perpendicular to the Galactic plane was 46% of |A|. They suggested several hypothetical mechanisms that could explain this estimate, for example, a companion star orbiting the Sun. A second solution of Xu et al. made in 2017 has significantly smaller components not in the direction of the Galactic center. Further investigation of possible physical means for producing non-Galactic center acceleration components could provide a bound for the VLBI estimates of these components. WG8 investigated whether this could be due to how VLBI analysis is performed. For the recommended model, we just consider the Galactic center component AG of the estimates of the aberration acceleration vector.

6. IAU ICRF3 recommendation

Possible options for the IVS working group recommendation for the aberration constant AG are: (1) VLBI weighted mean of 5.6 ± 0.13 μas yr−1, (2) Galactic astronomy weighted mean of 4.9 ± 0.17 μas yr−1, or (3) the average of (1) and (2). However, we recommended that the IAU ICRF3 working group should use a geodetic VLBI value of AG when a Galactic aberration contribution is to be applied. The rationale is that since the correction was derived via geodetic VLBI solutions, it should be applied in the analysis of geodetic VLBI sessions and specifically for the ICRF3 solution, in order to be self-consistent. Since none of the solutions reported in the upper section of Table 2 used all of the available data, a new Calc/Solve global solution was run using all of the data that was to be used for the ICRF3 solution (from 1979 through May 2018) with a reference epoch of 2015.0. The reasons for this choice are (1) it is close to the current time so the effect aberration is small for current applications that do not have the ability to model the effect and (2) it is close to the Gaia DR2 reference epoch of 2015.5 so that even though Gaia does not yet model Galactic aberration, one can compare VLBI and Gaia source positions without much error since the VLBI solution models the decades long effect of aberration. The resulting estimated aberration constant of 5.8 ± 0.3 μas yr−1 is not significantly different from the solutions in Table 2 that used data from the period 1979 to 2016. This aberration constant was taken to be the final recommended value.

7. Discussion of results

In this section, we consider several sensitivities involving Galactic aberration based on solutions using the ICRF3 Calc/Solve solution setup. The issues investigated are (1) the dependence of aberration estimates on the set of VLBI sessions included in the solution, (2) dependence of aberration estimates on the radio sources included, (3) comparison of Gaia DR2 positions and VLBI radio source positions estimated with a range of applied aberration constants, and (4) effects of applying aberration on EOP estimates and the estimated terrestrial reference frame.

Geodetic VLBI sessions have been observed from 1980 to the present with a wide variety of observing networks. Before 1990, networks were relatively small (3–6 antennas) and the set of sources observed was also relatively small and the sources observed were generally strong sources (flux >  1 Jy) some of which have significant source structure. As a result of these factors, the quality of sessions before 1990 is not as good as from sessions after 1990 when network size and observing source catalogs grew. To test the effect of data before 1990, we ran a Calc/Solve solution that estimates AG just from data after 1990. The estimated aberration constant was 6.0 ± 0.3 μas yr−1, which is close to the recommended constant.

Alternatively, we also ran a session decimation test to determine the sensitivity of results to the sessions used throughout the 1980–present time period. The VLBI 24-h sessions were ordered chronologically for each session network type. By doing this, we ensure that each type of networks observing similar sources is represented uniformly in each decimation group. These session groups were each divided by even and odd session. All of the odd-numbered sessions then comprised the 1st decimation group of the sessions and the even-numbered sessions the 2nd decimation group. The estimated aberration constants estimate for the two groups were 5.7 ± 0.4 μas yr−1 and 5.9 ± 0.4 μas yr−1.

From Fig. 2, it is clear that the observed apparent proper motion field contains a large range of motion extending to several hundred μas yr−1 which most likely is due to source structure. In the presence of such large effects, estimation of systematic Galactic acceleration requires that source structure effects occur randomly over the sky. One test that can be done is to remove sources with large apparent proper motions from the estimation. We removed the contribution to AG estimation from sources with large apparent proper motion. There were 1620 sources with apparent proper motion magnitude greater than 50 μas yr−1 out of a total of 3338 sources for which proper motions could be reliably determined from source position time series. Estimating aberration including sources with proper motion less than 50 μas yr−1 yielded an aberration constant of vector 5.80 ± 0.30 μas yr−1 that is insignificantly different from including all sources (5.75 ± 0.30 μas yr−1).

We investigated the sensitivity of glide transformation parameters between the positions of sources in ICRF3 solutions and positions from Gaia DR2 on the choice of aberration constant applied in the VLBI solution. Figure 7 shows that the glide parameter differences Di vary significantly over the range of 3–9 μas yr−1. However, between 5 and 6 μas yr−1 where most of the VLBI estimates lie, the differences vary by at most 2–3 μas. The glide parameter transformations (e.g., Mignard & Klioner 2012) have the same dependences on declination and right ascension as the aberration proper motion given in Eqs. (3) and (4). D2 and D3 are sensitive to AG, whereas, D1 is insensitive to AG.

thumbnail Fig. 7.

Glide transformation parameters between ICRF3 positions from solutions with range of applied aberration constants and the Gaia positions.

(9)

(10)

Based on Calc/Solve solutions, Table 3 shows that the effect of the applying aberration in a TRF/CRF solution on EOP (offsets of polar motion, UT1, and celestial pole) estimates is not significant. The effect on TRF scale and scale rate is only −0.044 ± 0.004 ppb and −0.0048 ± 0.0003 ppb yr−1. It causes offsets and rates of TRF translation less than 0.2 mm and less than 0.01 mm yr−1. Offsets and rates of rotation are less than 2.0 μas and 0.5 μas yr−1, respectively.

Table 3.

EOP with aberration minus without aberration.

The recommended WG model just consists of the galactocentric component of the VLBI estimated aberration drift vector. Although we have not determined the source of the non-Galactic center components of the estimated vector, we can at least provide an upper bound on the magnitude of the non-Galactic center components. Based on working group solutions that used data through 2016, the average estimate of the component in the direction of motion around the Galactic center is 0.8 ± 0.2 μas yr−1, where the uncertainty is the standard deviation of the estimates. In the direction perpendicular to the Galactic plane, the estimates are less consistent and the average is 0.2 ± 0.6 μas yr−1. The difference between estimates of Galactic center component AG from geodetic VLBI and maser astronomy is 0.9 ± 0.5 μas yr−1. This could be due in part to acceleration not caused by rotation of the galaxy as well as possible systematic errors in the Galactic astronomy estimates or in our VLBI estimates.

8. Conclusions

The working group recommended a galactocentric aberration constant AG derived only from geodetic VLBI data analysis in order to be consistent with geodetic VLBI solutions (and specifically for the ICRF3 solution) rather than averaging geodetic solution estimates and estimates based on Galactic astronomy measurements. The ICRF3 solution was to be derived using data from 1979 to May 2018, which is two years more data than any of the previous VLBI solutions given in Table 1. For this reason, the working group ran a new solution using the ICRF3 data set to determine the aberration constant to be used in the final ICRF3 solution.

The recommended aberation constant value of 5.8 μas yr−1 of the component of the aberration vector in the direction of the Galactic center is reasonably close to estimates derived from Galactic astronomy measurements. Future work should be done to understand why the two estimates differ.

An issue that remains to be studied further is to understand the cause of non-Galactic center components of the aberration vector estimates from the different WG solutions although their magnitudes are generally less than 25% of |A|. This could be due to non-galactocentric acceleration, unmodeled source structure effects, or possibly how the VLBI analysis was done.

Acknowledgments

D. S. MacMillan, J. M. Gipson, and D. Gordon acknowledge support from NASA contracts NNG12HP00C and NNG17HS00C. C. S. Jacobs acknowledges support for work done at Jet Propulsion Laboratory, California Institute of Technology under contract with NASA. H. Krásná is supported by the Austrian Science Fund (FWF): T697-N29. The work of Z. Malkin was partly supported by the Russian Government Program of Competitive Growth of Kazan Federal University. Figures were produced using the Generic Mapping Tools package (Wessel et al. 2013). Results in this paper were based on data from the IVS and its international member organizations.

References

  1. Altamimi, Z., Rebischung, P., Métivier, L., & Collilieux, X. 2016, J. Geophys. Res., 121, 6109 [Google Scholar]
  2. Anderson, J. M., & Xu, M. H. 2018, J. Geophys. Res., 123, 10162 [NASA ADS] [CrossRef] [Google Scholar]
  3. Bahcall, J. N., & Bahcall, S. 1985, Nature, 316, 706 [NASA ADS] [CrossRef] [Google Scholar]
  4. Bastian, U. 1995, in Proc. RG0-ESA Workshop on Future Possibilities for Astrometry in Space, eds. M. A. Perryman, & F. Van Leeuwen, ESA SP-379, 99 [Google Scholar]
  5. Böhm, J., Böhm, S., Boisits, J., et al. 2018, PASP, 130, 044503 [NASA ADS] [CrossRef] [Google Scholar]
  6. Brunthaler, A., Reid, M. J., Menten, K. M., et al. 2011, Astron. Nachr., 332, 461 [NASA ADS] [CrossRef] [Google Scholar]
  7. Evans, N. W., & Wilkinson, M. I. 2000, MNRAS, 316, 929 [NASA ADS] [CrossRef] [Google Scholar]
  8. Fanselow, J. L. 1983, Observation Model and Parameter Partials for the JPL VLBI Parameter Estimation Software "MASTERFIT-v1.0." (JPL Publication), 83 [Google Scholar]
  9. Fey, A. L., Gordon, D., Jacobs, C. S., et al. 2015, AJ, 150, 58 [NASA ADS] [CrossRef] [Google Scholar]
  10. Fouqué, P., Solanes, J. M., Sanchis, T., & Balkowski, C. 2001, A&A, 375, 770 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Gwinn, C. R., Eubanks, T. M., Pyne, T., et al. 1997, ApJ, 485, 87 [NASA ADS] [CrossRef] [Google Scholar]
  12. Honma, M., Nagayama, T., Ando, K., et al. 2012, PASJ, 64, 136 [Google Scholar]
  13. Jacobs, C., Arias, F., Boboltz, D., et al. in ICRF-3: Roadmap to the next generation ICRF, ed. N. Capitaine, Proceedings of the Journées 2013 "Systèmes de référence spatio-temporels", Observatoire de Paris, 16–18 September 2013, 51 [Google Scholar]
  14. Karachentsev, I. D., Karachentseva, V. E., Huchtmeier, W. K., & Makarov, D. I. 2004, AJ, 127, 2031 [Google Scholar]
  15. Kopeikin, S. M., & Makarov, V. V. 2006, AJ, 131, 1471 [NASA ADS] [CrossRef] [Google Scholar]
  16. Kovalevsky, J. 2003, A&A, 404, 743 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Liu, J.-C., Capitaine, N., Lambert, S. B., et al. 2012, A&A, 548, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Ma, C., Sauber, J. M., Bell, L. J., et al. 1990, J. Geophys. Res., 95, 21991 [NASA ADS] [CrossRef] [Google Scholar]
  19. MacMillan, D. S. 2014, in Determination of Galactic Aberration from VLBI Measurements and Its Effect on VLBI Reference Frames and Earth Orientation Parameters, AGU Meeting Abstracts, San Francisco, CA [Google Scholar]
  20. MacMillan, D. S., Fey, A., Gipson, J., et al. 2018, in Galactic Aberration in VLBI Analysis: Findings of IVS WG8, 2018 IVS General Meeting Proceedings, Longyearbyen, Spitsbergen, Norway, 3–9 June 2018 [Google Scholar]
  21. Majaess, D. J., Turner, D. G., & Lane, D. J. 2009, MNRAS, 398, 263 [Google Scholar]
  22. Malkin, Z. 2014, MNRAS, 445, 845 [NASA ADS] [CrossRef] [Google Scholar]
  23. Mignard, F. 2002, in Gaia: A European Space Projet, eds. O. Bienayme, & C. Turon, EAS Publ. Ser., 2, 327 [Google Scholar]
  24. Mignard, F., & Klioner, S. 2012, A&A, 547, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Murray, Z. 1983, Vectorial Astrometry (Bristol: Adam Hilger) [Google Scholar]
  26. Petrov, L., Kovalev, Y. Y., & Plavin, A. V. 2018, MNRAS, 482, 3023 [Google Scholar]
  27. Rastorguev, A. S., Utkin, N. D., Zabolotskikh, M. V., et al. 2017, Astrophys. Bull., 72, 122 [NASA ADS] [CrossRef] [Google Scholar]
  28. Reid, M. J., & Brunthaler, A. 2004, ApJ, 616, 772 [Google Scholar]
  29. Reid, M. J., Menten, K. M., Zheng, X. W., et al. 2009, ApJ, 700, 137 [NASA ADS] [CrossRef] [Google Scholar]
  30. Reid, M. J., Menten, K. M., Brunthaler, A., et al. 2014, ApJ, 783, 130 [Google Scholar]
  31. Sovers, O. J., Fanselow, J. L., & Jacobs, C. S. 1998, Rev. Mod. Phys., 70, 1393 [NASA ADS] [CrossRef] [Google Scholar]
  32. Titov, O., & Krásná, H. 2018, A&A, 610, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  33. Titov, O., & Lambert, S. 2013, A&A, 559, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  34. Titov, O., Lambert, S., & Gontier, A.-M. 2011, A&A, 529, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  35. Titov, O. A., & Lopez, Y. R. 2018, Astron. Lett., 44, 139 [NASA ADS] [CrossRef] [Google Scholar]
  36. Wessel, P., Smith, W. H. F., Sharroo, R., et al. 2013, EOSTr, 94, 409 [NASA ADS] [Google Scholar]
  37. Xu, M. H., Wang, G. L., & Zhao, M. 2012, A&A, 544, A135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  38. Xu, M. H., Heinkelmann, R., Anderson, J. M., et al. 2016, AJ, 152, 151 [NASA ADS] [CrossRef] [Google Scholar]
  39. Xu, M. H., Anderson, J. M., Heinkelmann, R., et al. 2019, ApJS, 242, 5 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1.

Galactic astronomy derived estimates of the aberration constant.

In the text
Table 2.

Geodetic VLBI aberration estimates.

In the text
Table 3.

EOP with aberration minus without aberration.

In the text

All Figures

thumbnail Fig. 1.

Aberration proper motion field for an aberration constant of 5.8 μas yr−1.
In the text
thumbnail Fig. 2.

Proper motion field computed from source position time series (RA an Dec rate uncertainties better than 50 μas yr−1).
In the text
thumbnail Fig. 3.

Change in right ascension due to aberration versus right ascension with an aberration constant of 5.8 μas yr−1 and reference epoch of 2015.0.
In the text
thumbnail Fig. 4.

Change in right ascension due to aberration versus declination with an aberration constant of 5.8 μas yr−1 and reference epoch of 2015.0.
In the text
thumbnail Fig. 5.

Change in declination due to aberration versus right ascension with an aberration constant of 5.8 μas yr−1 and reference epoch of 2015.0.
In the text
thumbnail Fig. 6.

Change in declination due to aberration versus declination with an aberration constant of 5.8 μas yr−1 and a reference epoch of 2015.0.
In the text
thumbnail Fig. 7.

Glide transformation parameters between ICRF3 positions from solutions with range of applied aberration constants and the Gaia positions.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.