| Issue |
A&A
Volume 630, October 2019
|
|
|---|---|---|
| Article Number | A148 | |
| Number of page(s) | 10 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201834715 | |
| Published online | 10 October 2019 | |
Influence of the Yarkovsky force on Jupiter Trojan asteroids
Institute of Planetary Research, German Aerospace Center (DLR), Rutherfordstr 2, 12489 Berlin, Germany
e-mail: stephan.hellmich@dlr.de
Received:
24
November
2018
Accepted:
4
September
2019
Aims. We investigate the influence of the Yarkovsky force on the long-term orbital evolution of Jupiter Trojan asteroids.
Methods. Clones of the observed population with different sizes and different thermal properties were numerically integrated for 1 Gyr with and without the Yarkovsky effect. The escape rate of these objects from the Trojan region as well as changes in the libration amplitude, eccentricity, and inclination were used as a metric of the strength of the Yarkovsky effect on the Trojan orbits.
Results. Objects with radii R ≤ 1 km are significantly influenced by the Yarkovsky force. The effect causes a depletion of these objects over timescales of a few hundred million years. As a consequence, we expect the size-frequency distribution of small Trojans to show a shallower slope than that of the currently observable population (R ≳ 1 km), with a turning point between R = 100 m and R = 1 km. The effect of the Yarkovsky acceleration on the orbits of Trojans depends on the sense of rotation in a complex way. The libration amplitude of prograde rotators decreases with time while the eccentricity increases. Retrograde rotators experience the opposite effect, which results in retrograde rotators being ejected faster from the 1:1 resonance region. Furthermore, for objects affected by the Yarkovsky force, we find indications that the effect tends to smooth out the differences in the orbital distribution between the two clouds.
Key words: methods: numerical / minor planets, asteroids: general
© ESO 2019
1 Introduction
Jupiter shares its orbit with a large number of asteroids, called Jupiter Trojan asteroids, that populate the regions around the L4 and L5 Lagrangian points in the Sun-Jupiter system. It is still debated how these objects were emplaced into their current orbits. However, it was demonstrated that a large part of the known population is indeed stable over the age of the solar system (Erdi 1988) and detailed maps describing the stable regions around the Lagrangian points have been created (Levison et al. 1997; Tsiganis et al. 2005). An interesting peculiarity of the Jupiter Trojans is that the two swarms significantly differ in the number of objects. As of August 2019, the Minor Planet Center lists 4603 numbered, multi-, and single-opposition Trojans in the leading (around L4) but only 2476 in the trailing cloud (around L5). It can be excluded that this asymmetry originates from an observational bias (Grav et al. 2011). Although the gravitational stability for orbits around either of the Lagrangian points is similar (Marzari 2002), it was found in long-term integrations of the known Trojan population that the fraction of escaping particles from the L5 cloud is larger than that from L4 (Di Sisto et al. 2019). However, Di Sisto et al. (2019) also concluded that the difference in escaping objects alone cannot explain the asymmetry in the Trojan clouds that is observed today. A theory capable of describing both orbital distribution and asymmetry is the jump capture scenario proposed by Nesvorný et al. (2013). According to this model, the Trojans originate from more distant objects, initially located between 5 and 30 au, which were scattered inward during a phase of orbital chaos in the early solar system and eventually became trapped in resonance when Jupiter and Saturn reached their current orbits. In this model, the asymmetry is explained by the influence of Uranus, Neptune, or a hypothetical ice giant (now ejected from the solar system) that may have moved through one of the Trojan clouds and wiped out a large number of objects. By simulating the early phase of the solar system, Pirani et al. (2019) recently showed that particles in the gaseous protoplanetary disk can be captured around the Lagrange points of Jupiter while the growing planets migrate through the disk. Because the drift is directed inward, the process of particle capture naturally favors tadpole orbits around L4, and the resulting asymmetry after migration and planet formation is compatible with the observed asymmetry. However, their model fails to explain the inclination distribution of the known Trojans.
Only very little is known about the physical properties of the Jupiter Trojans. Using infrared observations carried out with the Wide-field Infrared Survey Explorer (WISE) space telescope, a low mean geometric albedo of 0.07 ± 0.03 was determined for a sample of about 3000 objects (Grav et al. 2011). Density estimates exist for only two Jupiter Trojans: for (624) Hektor and (617) Patroclus. For (617) Patroclus, several studies report low bulk densities ranging from 0.8 (Marchis et al. 2006) to 1.3 g cm−3 (Merline et al. 2002), with 0.88 g cm−3 (Buie et al. 2015) being the most recent result. Densities found for (624) Hektor vary from 1.0 g cm−3 (Marchis et al. 2014)to 2.48 g cm−3 (Lacerda & Jewitt 2007). Thermal properties are also measured for only a few Trojans. Ferrari (2018) suggested that thermal inertia decreases with increasing heliocentric distance and reported a thermal inertia of 10 J K−1 m−2 s−0.5 and lower for objects beyond Saturn, to which the Trojans might be linked due to their dynamical history. In general, it is expected that Jupiter Trojans have very low thermal inertia of about 5 J K−1 m−2 s−0.5 (Dotto et al. 2008). Using thermo-physical modeling from infrared observation data, a thermal inertia of 6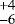 J K−1 m−2 s−0.5 has been determined for (624) Hektor (Hanuš et al. 2015), while for (1173) Anchises, a higher value in the range of 25 to 100 J K−1 m−2 s−0.5 was reported (Horner et al. 2012). By examining temperature changes on the surface of (617) Patroclus during mutual events caused by its moon Menoetius, a thermal inertia of 20 ± 15 J K−1 m−2 s−0.5 was determined (Müller et al. 2010). Fernández et al. (2003) placed upper limits on the thermal inertia for (2363) Cebriones and (3063) Makhaon of 14 and 30 J K−1 m−2 s−0.5, respectively.
J K−1 m−2 s−0.5 has been determined for (624) Hektor (Hanuš et al. 2015), while for (1173) Anchises, a higher value in the range of 25 to 100 J K−1 m−2 s−0.5 was reported (Horner et al. 2012). By examining temperature changes on the surface of (617) Patroclus during mutual events caused by its moon Menoetius, a thermal inertia of 20 ± 15 J K−1 m−2 s−0.5 was determined (Müller et al. 2010). Fernández et al. (2003) placed upper limits on the thermal inertia for (2363) Cebriones and (3063) Makhaon of 14 and 30 J K−1 m−2 s−0.5, respectively.
The stability regions around the L4 and L5 Lagrangian points of theSun-Jupiter system are well known. The main parameter controlling the orbital stability of Jupiter Trojans is their libration amplitude D, which defines the maximum excursion in mean longitude λ with respectto Jupiter (Tsiganis et al. 2005),
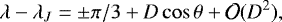 (1)
(1)
where θ is the phase of libration, as well as their eccentricity and inclination. For L4 Trojans, the difference in mean longitude is positive, while it is negative for L5 Trojans. Tsiganis et al. (2005) characterized the residence time of objects around the Lagrangian points of Jupiter as a function of libration amplitude, eccentricity, and inclination. They provided detailed stability maps and found that in general, the residence time increases with decreasing libration amplitude and eccentricity. Inclination affects the long-term behavior to a lesser degree (see Figs. 2–5 in Tsiganis et al. 2005).
The Yarkovsky effect describes a nongravitational force that is caused by diurnal heating and asymmetric reradiation of energy received from the Sun (Hartmann et al. 1999). Depending on the asteroid’s rotational parameters and the physical properties of its surface material, the effect can lead to a secular change in the orbital semimajor axis. In the main belt, the Yarkovsky effect is the dominant mechanism that drives asteroids toward unstable resonance regions where they are eventually ejected from the belt (Farinella et al. 1998). It also causes dynamical spreading of collisional asteroid families (Bottke et al. 2001).
Many studies have been carried out to answer the questions about the origin and dynamical evolution of Jupiter Trojans. Some authors argued that due to the large heliocentric distance of Jupiter Trojans, the Yarkovsky force is too weak to remove them from the stable region inside the resonance (Yoshida & Nakamura 2005; Di Sisto et al. 2014). Others concluded that at least for the smaller bodies, the Yarkovsky force may become important for their long-term orbital evolution (Tsiganis et al. 2005; Karlsson 2011). So far, the only orbital evolution studies of Trojans that incorporated the Yarkovsky effect were performed by Wang & Hou (2017) and Hou et al. (2016). They used a simplified model for the Yarkovsky force and demonstrated in numerical experiments considering the Sun, Jupiter, Saturn, and a single meter-sized Trojan asteroid that the Yarkovsky force causes the oscillation in semimajor axis to increase, with the object escaping the Trojan region after a few tens of million years.
This study is intended to address the question of the size at which the Yarkovsky force starts to affect the population of Jupiter Trojans. We also study whether it is able to significantly influence their orbits on timescales of hundreds of million years.
2 Methods
2.1 Creating a synthetic population of Trojans
For the purpose of explaining certain dynamical properties of the Trojans such as the difference in escaping particles from each cloud, the population of currently known Trojans is too small. Moreover, some objects have been observed during a single opposition only, which means that their orbits may not be known with sufficient accuracy. Therefore, when the long-term evolution is investigated, only the orbital elements of the numbered and unnumbered multi-opposition Trojans should be used, which shrinks the set of available orbits even more. Considering only those particles for our numerical study would not allow usto draw statistically meaningful conclusions. Therefore, a large synthetic population of Trojans was created by cloning the orbits of the numbered and unnumbered multi-opposition Trojans. Because the long-term stability of the Trojans is very sensitive to their orbital distribution, care should be taken that cloning does not change the long-term dynamical behavior of the orbits. On that account, the variations in orbital elements for each clone were computed based on the accuracy of the astrometric positions from which the orbit of the real object is calculated. The uncertainties for each orbit are published in form of a covariance matrix on the AstDyS website1. Using that covariance matrix, we can express the uncertainty Δq in the orbital elements vector q as
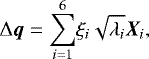 (2)
(2)
where ξi are Gaussian-distributed random variables with a standard deviation of unity and zero mean, λi are the eigenvalues of the covariance matrix, and Xi are the normalized eigenvectors. This cloning technique was used to generate a total number of 98 304 Trojan particles. Because only precisely determined orbits were chosen for cloning and each clone is a realization of its parent orbit within the 1σ range of the observational data, the long-term orbital evolution of the cloned population is expected to be representative of the current population.
The clones were generated from numbered and multi-opposition Trojan orbits, consisting of 3642 L4 and 1925 L5 objects. In order to create a population that contains an equal amount of L4 and L5 Trojans, the cloned population incorporates the real orbits plus 13–14 clones for L4 Trojans and 25–26 clonesfor L5 Trojans. Forefficiency reasons, the population of clones was split into groups of 32 768 particles, and we started an individual simulation for each group. In order to determine whether the Yarkovsky force influences the long-term orbital behavior of this population, we conducted simulations with and without the Yarkovsky effect. To provide a good baseline against which the results from the Yarkovsky run could be compared with, the full sample of 98 304 particles was used for the non-Yarkovsky run, while for the Yarkovsky run a smaller number of 32 768 particles was simulated. For the Yarkovsky run, the subpopulations of the two clouds were further subdivided into 16 groups of particles with different physical properties and sizes each. We defined four size classes with radii of 10 m, 100 m, 1 km, and 10 km. The object density and thermal inertia were split into two categories each, set to the upper and lower bounds of the values reported in the literature (see Table 1). This subdivision resulted in 1024 particles for each category, size, and cloud. The spin-axis orientation was uniformly distributed over the celestial sphere and the spin period (in seconds) was set to five times the body’s radius (in meters) (Farinella & Vokrouhlický 1999). Geometric albedo (pv) and infrared emissivity (ϵ) for all objects were fixed to 0.07 and 0.9, respectively (Grav et al. 2011). To compute the Bond albedo (A), which is relevant for the Yarkovsky force, the relation A ≈ qpv with the phase integral q = 0.290 + 0.68G (Bowell et al. 1989)and a slope parameter G = 0.15 was used.
We caution that the orbital distribution of the cloned population is based on the currently known population. This consists of large objects and might be different for the actual population of Trojans that are smaller than a few kilometer in radius.
Combinations of thermo-physical properties used for the Yarkovsky effect.
2.2 Collisional lifetime of the Jupiter Trojans
On the one hand, under the gravitational influence alone, the orbits of a large number of Jupiter Trojan asteroids can survive the age of the solar system (about 4.5 Gyr). On the other hand, the lifetime of asteroids is also limited by mutual collisions that are not resolvedby the integration method used in this work. Therefore, the integration interval should not exceed the expected collisional lifetime of the involved bodies. To choose a realistic integration interval, we therefore estimated the collisional lifetime of Jupiter Trojans.
Here, the collisional lifetime of a minor body is considered as the mean time until the object is destroyed by a catastrophic disruption. Such an event is defined as a collision in which the size of the largest remnant is smaller than or equal to half the size of the original body, and the fragments are dispersed (Benz & Asphaug 1999). The relevant parameters for the collisional lifetime are size and density of the colliding bodies as well as the intrinsic collision probability Pi, average impact velocity vi, and size distribution of the collisional interacting population. The physical parameters and impact velocity of the bodies are relevant for determining the energy per unit mass that causes a catastrophic disruption of the target body (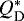 ). The intrinsic collision probability, which defines the flux of impactors per area and time, is a geometric property, and can be combined with the object size distribution to estimate how frequently catastrophic disruption events occur.
). The intrinsic collision probability, which defines the flux of impactors per area and time, is a geometric property, and can be combined with the object size distribution to estimate how frequently catastrophic disruption events occur.
The average impact velocities and the intrinsic collision probability for Jupiter Trojans have been determined in several studies (Marzari et al. 1996; dell’Oro et al. 1998). However, providing a good estimate for 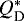 is not easy. By simulating collisions using hydrocode and performing high-velocity impact experiments, several methods for modeling
is not easy. By simulating collisions using hydrocode and performing high-velocity impact experiments, several methods for modeling 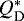 were proposed. The most recent study reporting a method for the evaluation of
were proposed. The most recent study reporting a method for the evaluation of 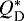 for Jupiter Trojans was carried out by Wong et al. (2014). They simulated the collisional evolution of the Jupiter Trojans by adjusting the scaling law for
for Jupiter Trojans was carried out by Wong et al. (2014). They simulated the collisional evolution of the Jupiter Trojans by adjusting the scaling law for 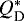 of main belt asteroids proposed by Durda et al. (1998) to fit it to the low-diameter end of the debiased size-frequency distribution of Trojans down to about 10 km. Because the composition of Trojans is believed to be different from main belt asteroids and much smaller objects are studied in this work, their approach is not applicable here. Instead, a scaling law introduced by Benz & Asphaug (1999), which is valid down to centimeter-sized objects, is used to determine
of main belt asteroids proposed by Durda et al. (1998) to fit it to the low-diameter end of the debiased size-frequency distribution of Trojans down to about 10 km. Because the composition of Trojans is believed to be different from main belt asteroids and much smaller objects are studied in this work, their approach is not applicable here. Instead, a scaling law introduced by Benz & Asphaug (1999), which is valid down to centimeter-sized objects, is used to determine 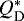 :
:
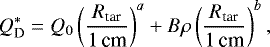 (3)
(3)
where Rtar and ρ denote radius and density of the target body, respectively. The advantage of this model is that it uses the density as a parameter and that it is capable of describing 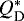 both in the strength regime (small objects) where fragmentation of the target body is the dominant factor, and in the gravity-dominated regime (large objects) where the target body is fragmented and the fragments must also be dispersed in order to cause a catastrophic disruption. Benz and Asphaug used a smoothed-particle hydrodynamics code to simulate collisions of different materials and impact velocities and provided
both in the strength regime (small objects) where fragmentation of the target body is the dominant factor, and in the gravity-dominated regime (large objects) where the target body is fragmented and the fragments must also be dispersed in order to cause a catastrophic disruption. Benz and Asphaug used a smoothed-particle hydrodynamics code to simulate collisions of different materials and impact velocities and provided 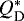 fits for each parameter set. For icy material and an impact velocity of vi = 3 km s−1, conditions closest to those in this work, the remaining parameters in Eq. (3) are Q0 = 1.6 J g−1, B = 1.2 × 10−7 J cm3 g−2, a = −0.39, and b = 1.26. To obtain a lower limit for the collisional lifetime, the density of the weakest bodies (0.8 g cm−3) was used to evaluate
fits for each parameter set. For icy material and an impact velocity of vi = 3 km s−1, conditions closest to those in this work, the remaining parameters in Eq. (3) are Q0 = 1.6 J g−1, B = 1.2 × 10−7 J cm3 g−2, a = −0.39, and b = 1.26. To obtain a lower limit for the collisional lifetime, the density of the weakest bodies (0.8 g cm−3) was used to evaluate 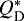 . Knowing
. Knowing 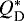 , the radius for an impactor Rdis capable of disrupting a target body of a certain radius Rtar can be calculated as in Bottke et al. (2005),
, the radius for an impactor Rdis capable of disrupting a target body of a certain radius Rtar can be calculated as in Bottke et al. (2005),
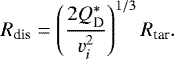 (4)
(4)
Finally, given the size distribution of the collisionally interacting bodies, the collisional lifetime (τdis) of an object with radius Rtar is (Farinella et al. 1998)
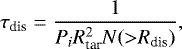 (5)
(5)
where N(> Rdis) is the number of objects with radii R > Rdis. Pi was set to the highest value reported, which is 7.79 × 10−18 yr−1km−2 for L4 versus L4 Trojans (Davis et al. 2002). Other populations such as short-period comets or Hildas also collisionally interact with Jupiter Trojans (Dell’Oro et al. 2001). However, the intrinsic impact probability between these populations and the Trojans is orders of magnitude lower than the Trojan’s mutual impact probability, and the total number of objects of the collisionally interacting populations is much smaller thanthe number of Trojans. Their influence on the collisional lifetime of Trojans is therefore negligible for this experiment.
We know only very little about the size distribution of R < 1 km Jupiter Trojans, which we need to calculate N(≥Rdis). By observing and debiasing L4 Trojans using the 8.2 m Subaru Telescope at the Mauna Kea Observatory on Hawaii, Yoshida & Terai (2017) found the size distribution of objects between absolute magnitude 12 < H < 17.5 (roughly corresponding to 1 < R < 10 km) to follow a broken power law. According to their work, the cumulative size distribution of L4 Trojans is
![\begin{equation*} \sum(H)=\begin{cases} 10^{\alpha_1(H-H_0)}, & \text{for $H<H_{\textrm{b}}$}\\[4pt] 10^{\alpha_2H+(\alpha_1-\alpha_2)H_{\textrm{b}}-\alpha_1H_0}, & \text{for $H \geq H_{\textrm{b}}$}, \end{cases} \end{equation*}](/articles/aa/full_html/2019/10/aa34715-18/aa34715-18-eq17.png) (6)
(6)
with the break magnitude Hb = 13.56 mag, corresponding to an approximate radius of 5 km, and power-law slopes α1 and α2 of 0.50 and 0.37 mag−1, respectively.
Adding all this together, an estimation of the collisional lifetime of Jupiter Trojans can be made. For the size ranges considered in this experiment, the collisional lifetimes are given in Table 2. Figure 1 shows the cumulative size distribution we used to estimate the number of targets and impactors as well as the resulting estimate for the collisional lifetime of L4 Trojans. Although this estimation is calculated based on the size distribution of L4 Trojans, it represents a lower limit for the collisional lifetime of Jupiter Trojans in general because the L5 Trojans are expected to be fewer in numbers and thus should have even longer collisional lifetimes than L4 Trojans. The integration interval for investigating the influence of the Yarkovsky effect was therefore set to 1 Gyr.
We note that the collisional lifetime of small Trojans calculated by de Elía & Brunini (2007) is significantly shorter than the estimate presented here. The authors considered catastrophic disruptions as collisions where the objects are shattered but not necessarily dispersed. Furthermore, they used a primordial population of Trojans that was eight times more massive than the debiased population found by Jewitt et al. (2000). The focus in this work is on the dynamical evolution of the already evolved population rather than the collisional evolution of the primordial population. Even for a population containing ten times more objects, the collisional lifetime for R = 100 m objects would still be in the order of several 100 Myr.
 |
Fig. 1 Left panel: cumulative size distribution of L4 Trojans. Orange: known population; red dots: Trojan population after Yoshida & Terai (2017); red line: broken power law Yoshida & Terai (2017) fit to their observations; dashed gray line: extrapolation of the power law down to R = 100 m objects. Right panel: collisional lifetime of L4 Trojans according to this work. |
Radii of target and projectile capable of causing a catastrophic disruption of the target body as well as the number projectiles in the L4 cloud and the resulting collisional lifetime for the target body.
2.3 Estimation of the libration amplitude
Another quantity needed to interpret the results of this work is the libration amplitude because it is an important indicator for the long-term orbital stability of Trojans. The libration amplitudes of Jupiter Trojans typically lies in the range between a few degrees to about 35°. A convenient way to determine the libration amplitude is to apply a frequency map analysis on the output of the numerical integration in order to identify periodic variations in the orbital elements and the resonant argument (Marzari et al. 2003). To estimate thelibration amplitudes for the population of clones used in our study, a simpler approach was employed. The libration amplitudes were calculated from a short (200 kyr) integration. In order to remove the short-period variations from the orbital elements, which would modulate the libration, a digital low-pass filter was used. The parameters were chosen such that periods shorter thanthe libration period lie in the stop band, while the libration period (about 145 yr or longer) lies in the pass band and is very little affected by the filter. Using the filtered elements, we computed the amplitude of the oscillation in semimajor axis (d) as the mean of the maximum excursion in semimajor axis (a − aJ) in 2 kyr intervals over the 200 kyr of integration,
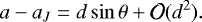 (7)
(7)
For our estimation, the higher order terms described by 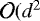 are omitted. Finally, the oscillation amplitude in semimajor axis was translated into the libration amplitude (D) in mean longitude using an approximation by Erdi (1988),
are omitted. Finally, the oscillation amplitude in semimajor axis was translated into the libration amplitude (D) in mean longitude using an approximation by Erdi (1988),
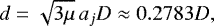 (8)
(8)
where μ is the ratio of the mass of Jupiter to the total mass of the system.
In order to test this procedure, the libration amplitudes of the numbered and multi-opposition Trojans were calculated and compared with those available on AstDyS2. The estimated amplitudes agree well. The average error is 0.61 ± 0.01°, and only a few objects with very large libration amplitudes or very long libration periods show larger errors.
2.4 cuSwift
The numerical experiments described in this paper place high demands on computing power. In total, 131 072 particles were integrated for 1 Gyr. It was decided to use the WHM integrator (Wisdom & Holman 1991) with an extension for the Yarkovsky effect introduced by Brož (2006). With the traditional implementation, however, the calculations would either require expensive supercomputer time, or the problem would need to be split and distributed over an impractical number of workstation computers to achieve results in acceptable computation time. In order to circumvent these obstacles, the original integration methods were redesigned in order to exploit the enormous computational power of multicore processors and modern graphics processing units (GPUs). The newly implemented integration methods are written in C/CUDA and follow the implementations in SWIFT3 and Swifter4. To ensure correctness and consistency, extensive tests were carried out and test results were carefully compared with the original methods (Hellmich 2017). Our integration package, which we call cuSwift, can produce output in the same format as Swifter. Simulations with Swifter and the CPU version of cuSwift with the same initial conditions produce exactly the same results. Because of slight differences in the implementation of some mathematical operations on GPUs, results obtained with the GPU version of cuSwift may differ from those obtained with SWIFT/Swifter. However, the tests revealed that these differences do not influence the overall accuracy. Some mathematical expressions evaluated on the GPU produce even more accurate values than on the CPU.
On a 2014 workstation PC, equipped with a 3.40 GHz Intel i7 Processor and two Nvidia GeForce GTX Titan Black GPUs, the WHM implementation in cuSwift outperforms the original implementation by a factor of about 100. Using that workstation, the main integrations of 98 304 orbits with and 32 768 orbits without inclusion of the Yarkovsky effect over 1 Gyr took about 65 days in total.
3 Results and discussion
We ran a simulation including all planets from Earth to Neptune, with the population of Trojans as described in Sect. 2.1 considered as massless particles. During the simulation we flagged all particles when their heliocentric distance became smaller than 3 au, exceeded 8 au, or when the particles approached Jupiter closer than twice the planet’s Hill radius. Such particles were excluded from further processing and considered escaped from the Trojan region. Figure 2 shows the fraction of particles escaping from the Trojan clouds over 1 Gyr. Each line for the non-Yarkovsky run corresponds to 49 152 initial particles, while each line for the Yarkovsky run represents a group of 16 384 initial particles with radii from 10 m to 10 km and with physical properties as described in Table 1. Transparent areas represent the 1σ confidence region, assuming the number of ejected particles follows a Poisson distribution.
The Yarkovsky effect on our synthetic Trojan population is striking. After 1 Gyr, significantly more particles were ejected from the Trojan region than without the Yarkovsky effect.
3.1 Influence of the physical properties
In order to explore the influence of the physical properties of the objects on the magnitude of the Yarkovsky-induced change in fraction of ejected particles, we separately monitored the escaping fraction for each category and size. Figure 3 shows that smaller objects are more likely to be ejected from the Trojan region. Here, each line corresponds to a group of 2048 initial particles, and the colored transparent areas in the plots represent the 1σ confidence region for each category and size. The gray area in each plot is the confidence region for the non-Yarkovsky run. Because the initial number of particles for each category and size in the Yarkovsky run was 2048 and the number of particles in the non-Yarkovsky run was 98 304, the 1σ confidence region for the non-Yarkovsky run is accordingly narrower than the region corresponding to the subpopulations of the Yarkovsky run. While for objects of R = 1 km and R = 10 km no significant difference in the escaping fractions due to the Yarkovsky effect was detected, for objects with radii of 10 and 100 m, low thermal inertia, and low density, more than 7 and 1.5 times as many particles were ejected over the integration interval of 1 Gyr of the Yarkovsky run than during the non-Yarkovsky run, respectively. Moreover, the fraction of escaped particles with low thermal inertia and high density and the fraction for the objects with high thermal inertia and low density are clearly above the confidence region of the non-Yarkovsky run. The consequences of this finding reach far. The efficient removal of small Trojans through the Yarkovsky effect implies that below a radius of 100 m these objects are increasingly depleted, and might even be entirely removed at very small sizes. As a consequence, we expect that the size-frequency distribution of Trojans shows a shallower slope at smaller radii, with a turning point between R = 100 m and R = 1 km, just below the size regime observed by Yoshida & Terai (2017). The shape of this size-frequency distribution is expected to be imprinted on the cratering record of Trojans.
An interesting feature for the particles with R = 10 m, low density, and low thermal inertia is that the rate of ejected particles per unit time increases after about the first 250 Myr. If the initial orbital distribution were in a steady state, as can be assumed for an evolved population like the Jupiter Trojans, we would expect the escape rates to be constant over time for each size and category of physical properties. A possible explanation for the rate change is that the initial orbital distribution of the test particles for this experiment reflects the distribution of the currently known Jupiter Trojans. This distribution is based on objects much larger than 1 km in radius, which are less strongly influenced by the Yarkovsky effect. Most of them have very long dynamical lifetimes (fewer than 5% of all particles were ejected during the non-Yarkovsky run), that is, they are on very stable orbits. The reason for the suddenly increasing escape rate would be that it takes some time until the Yarkovsky force moves the much smaller particles we considered in this experiment from their stable initial orbits to less stable regions from which they are eventually ejected. For small particles this is expected to occur faster than for larger particles because they are more strongly affected by the Yarkovsky force. The same effect becomes visible for the R = 100 m objects. Except for objects with high thermal inertia and high density, the escape rate increases after about 500 Myr of integration. The change in slope implies that the initial conditions for this experiment may not represent the steady-state orbital distribution for Trojans smaller than 1 km in radius and suggests that the actual number of escaped particles could be higher. It is understood that the details of the change in slope will depend on the actual distribution of the physical and rotational properties of the particles, especially obliquity. However, we expect the general trend to remain.
 |
Fig. 2 Fraction of escaped particles with and without the Yarkovsky effect over 1 Gyr. |
 |
Fig. 3 Fraction of escaped particles for the different sizes and physical properties of the particles. |
3.2 Ratio between escaped L4 and L5 Trojans
The asymmetry between the two Trojan clouds is observed on the known population, which consists of objects with radii of tens to some hundred kilometers. Because these bodies are hardly influenced by the Yarkovsky effect, the latter cannot explain the asymmetry at large sizes. Furthermore, Hou et al. (2016) demonstrated that in the case of a restricted three-body problem containing the Sun, Jupiter, and a Trojan asteroid, the influence of the Yarkovsky force is slightly different for the two Lagrangian regions, suggesting that their long-term orbital stability might also differ. It is therefore meaningful to examine whether the effect may influence the ratio of escaping particles between L5 and L4 for small objects in a more realistic scenario where perturbations from the other planets are considered as well. In Fig. 2 the escaping fractions are separately monitored for the two clouds. For the non-Yarkovsky run, the ratio between escaped L5 and L4 particles after 1 Gyr was 1.106 ± 0.026, which shows that L5 objects are indeed depleted at a faster pace than L4 Trojans, although not fast enough to explain the currently observed asymmetry. This value, which appears to be roughly constant as the system evolves, agrees well with the ratio of 1.11 ± 0.08 that was computed using the escape rates reported by Di Sisto et al. (2019), who integrated the numbered Jupiter Trojans for 4.5 Gyr without the Yarkovsky effect.
When the Yarkovsky effect is activated, the overall fraction of the escaping particles from L4 and L5 is virtually identical. Figure 2 shows no trend of more particles escaping from either of the two clouds. Grading the particles according to radius suggests that the ratio of escaped particles between L5 and L4 decreases with size, although the uncertainty is too large to allow a significant conclusion. In order to verify whether the Yarkovsky effect indeed causes the L5 /L4 escape ratio to decrease with size, an additional integration incorporating 32 768 R = 10 m particles with low density and low thermal inertia (category 1 in Table 1) over 1 Gyr was performed. For these bodies, the influence of the Yarkovsky force is greatest. The L5 /L4 escape ratio for this run is 0.985 ± 0.016, meaning that the L5 and L4 escape rates are indistinguishable with our sample size. The fact that the L5 /L4 escape ratio becomes unity for the Yarkovsky run including only bodies with R = 10 m, low density, and low thermal inertia supports the notion that the Yarkovsky effect causes the orbital distribution in the two clouds to become more homogeneous.
 |
Fig. 4 Initial amplitude and escape time for the escaped particles during the non-Yarkovsky run (left panel) and the Yarkovsky run (right panel). The small gray dots represent the survivors. |
3.3 Libration amplitude
To understand better how the Yarkovsky force changes the long-term orbital evolution of the Trojans, the initial libration amplitudes and eccentricities of the particles ejected during both runs were compared. In general, orbits with a low libration amplitude, eccentricity, and inclination tend to be more stable. Figure 4 shows that objects with high eccentricity or libration amplitude were ejected early during the simulation, while those with lower eccentricity or libration amplitude remained for a longer time span. The figure also shows that more particles were ejected that were initially located in the low libration amplitude regime during the Yarkovsky run as during the non-Yarkovsky run. The average initial libration amplitude for the particles ejected during the non-Yarkovsky run was 21.75 ± 0.12° for L4 and 20.85 ± 0.10° for L5 Trojans. For the Yarkovsky run, these values slightly decreased to 20.19 ± 0.17° and 19.51 ± 0.17° for L4 and L5 Trojans, respectively. Although the difference is not very large, it is significant, and it indicates that the Yarkovsky effect causes objects that initially were on stable orbits to leave the Trojan region. This trend should also be reflected in the distribution of the libration amplitudes and eccentricities of the survivors at the end of the integration. If the initial population is not in steady state, we would expect more objects with higher amplitudes and eccentricities after 1 Gyr integration including the Yarkovsky effect than there are in the non-Yarkovsky run. Thus, the libration amplitudes of the surviving particles at the end of each simulation were computed and compared. Figure 5 shows histograms of libration amplitude and eccentricity at the end of the integration. Because the Yarkovsky force has the strongest effect on objects with 10 m radius, only these objects are plotted as histograms for the Yarkovsky run. There clearly is an abundance of large libration amplitude and high-eccentricity orbits in the Yarkovsky run. The differences decrease with increasing size. While for R = 10 m to R = 1 km objects, a two-dimensional Kolmogorov-Smirnoff non-parametric test rejected the null-hypothesis (that D and e after the Yarkovsky run and the non-Yarkovsky run follow the same distribution) with a significance level lower than 0.01, the test was unable to distinguish between distributions for 10 km objects.
The Yarkovsky effect did not increase the libration amplitudes and eccentricities for all objects: Fig. 5 clearly shows that there is also an abundance of low amplitude and low-eccentricity objects after 1 Gyr of integration, which indicates that the Yarkovsky effect tends to increase the dynamical lifetime for some of the small objects. The same trend was also present when we considered either of the Trojan clouds separately, suggesting that both clouds are affected in the same way. The drift in semimajor axis caused by the diurnal component of the Yarkovsky force depends on the sense of the object’s rotation. In general, the Yarkovsky effect leads to an increase in the semimajor axis of prograde rotators and decreases the semimajor axis of retrograde rotators.
Trojans are in a 1:1 mean-motion resonance with Jupiter, and their semimajor axes are coupled with that of the gas giant. For these objects, the Yarkovsky effect causes a secular change in the oscillation amplitude of the semimajor axis. The libration cycle of Trojans typically lasts about 150 yr. An object spends about half of that time on an orbit with a semimajor axis smaller than that ofJupiter and the other half on an orbit with a semimajor axis larger than that of the gas giant. Assuming prograde rotation, a Trojan would be pushed toward the libration center during the first half of the libration cycle and dragged away from it during the second half. Because the magnitude of the Yarkovsky force changes proportionally to 1∕r, where r is the distance to the Sun, the force pushing the object toward the libration center is slightly stronger than that dragging it away from it, which results in a secular decrease of the oscillation amplitude. Retrograde rotation would result in the opposite effect. This mechanism was also shown by Wang & Hou (2017) in an idealized experiment employing the circular restricted three-body and a simplified model for the Yarkovsky effect. They found that under the influence of the Yarkovsky force, prograde rotators experience an exponential decrease of the oscillation amplitude and that the amplitude is exponentially increased for retrograde rotators. The eccentricity changes in the opposite direction (decreasing for retrograde rotators and increasing for prograde rotators), but the inclination remains unaffected. They further showed that when the gravitational influence of Saturn is included, the oscillation in semimajor axis for prograde rotators at some point also increases because the eccentricity becomes so high that the influence of Saturn dominates the orbital evolution.
In order to verify if indeed a prograde rotation causes the observed abundance of low-amplitude objects in our experiment, libration amplitude and eccentricity were analyzed separately for prograde and retrograde rotators. Figure 6 shows histograms of libration amplitude and eccentricity for prograde versus retrograde rotators after 1 Gyr of integration for objects of R = 10 m and R = 100 m. While there are more prograde rotators in the low libration amplitude regime (implying longer dynamical lifetime), there are also more prograde rotators in the high-eccentricity regime (implying shorter dynamical lifetime). The average values are listed in Table 3.
We again applied the two-dimensional Kolmogorov-Smirnoff test. This showed that libration amplitudes and eccentricities of prograde and retrograde rotator objects with R = 10 m and R = 100 m do not follow the same distribution with a significance level lower than 0.001. For larger objects, the test was unable to distinguish between the two distributions. The fraction of escaping particles also shows that the destabilizing influence of the Yarkovsky effect is greater for retrograde than for prograde rotators. In total, there were 8272 prograde and 8112 retrograde objects with R = 10 m and R = 100 m of which after 1 Gyr, 929 (11.2%) and 1533 (18.9%) were ejected, respectively. The fact that at the end of the simulation we found more prograde rotators with both small libration amplitude and high eccentricity can be explained as follows: during the phase when the eccentricity is still low, the libration amplitude decreases, but when the eccentricity becomes so high that the gravitational influence of Saturn dominates, the libration amplitude increases rather fast, which eventually causes the particles to be ejected from the Trojan region.
The finding that the Yarkovsky effect causes small retrograde rotators to be ejected faster than prograde rotators is expected to be reflected in the obliquity distribution of the small Jupiter Trojans, which currently is unknown, however. The influence of the Yarkovsky force on the obliquity distribution of Jupiter Trojans might therefore be confirmed by observations in the future.
We found no impact of the Yarkovsky effect on the inclination. The distributions of the inclination resulting from the two simulations for each cloud and size do not differ significantly.
 |
Fig. 5 Comparison of the histograms of libration amplitudes (left) and eccentricities (right) of particles that remained in the Trojan region over the complete integration time span in the Yarkovsky and non-Yarkovsky run after 1 Gyr (10 m radius objects only). |
3.4 Caveats
In order to assess the significance of the results of this work, we list three main caveats. First of all, the physical and thermal propertiesof the test particles were set to values obtained for rather large objects and might be different for smaller bodies considered in this experiment. The parameters for the scaling law by Benz & Asphaug (1999) we used to determine 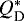 are valid for icy bodies and an impact velocity of 3 km s−1. However, there is no evidence so far that Trojans are indeed icy bodies, and the impact velocity lies between 4.5 and 5 km s−1 (Davis et al. 2002). Second, the particles were assumed to be perfect spheres, as for most studies modeling the dynamical evolution of a huge number of bodies under the Yarkovsky effect. This simplification might have an influence on the magnitude of the Yarkovsky effect, especially for small bodies, which can have very irregular shapes. Moreover, the YORP effect, which changes the rotational properties, was not considered in this study. Over long timescales, the YORP effect tends to drive the obliquity toward 0° and 180° for prograde and retrograde rotators, respectively (Vokrouhlický et al. 2003), resulting in a bimodal rather than uniform distribution of spin vector orientations. Obliquities close to 0 or 180° cause the diurnal component of the Yarkovsky effect to become stronger, and because for Trojans this component is dominant, a bimodal distribution of spin vectors would lead to a stronger Yarkovsky effect. Last but not least, the smaller the objects, the greater theirnumber, and consequently, the higher the frequency of their collisions that, when not disruptive, change the spin-axis orientation and spin rate of the object. This in turn results in a random Yarkovsky-drift direction over very long timescales.
are valid for icy bodies and an impact velocity of 3 km s−1. However, there is no evidence so far that Trojans are indeed icy bodies, and the impact velocity lies between 4.5 and 5 km s−1 (Davis et al. 2002). Second, the particles were assumed to be perfect spheres, as for most studies modeling the dynamical evolution of a huge number of bodies under the Yarkovsky effect. This simplification might have an influence on the magnitude of the Yarkovsky effect, especially for small bodies, which can have very irregular shapes. Moreover, the YORP effect, which changes the rotational properties, was not considered in this study. Over long timescales, the YORP effect tends to drive the obliquity toward 0° and 180° for prograde and retrograde rotators, respectively (Vokrouhlický et al. 2003), resulting in a bimodal rather than uniform distribution of spin vector orientations. Obliquities close to 0 or 180° cause the diurnal component of the Yarkovsky effect to become stronger, and because for Trojans this component is dominant, a bimodal distribution of spin vectors would lead to a stronger Yarkovsky effect. Last but not least, the smaller the objects, the greater theirnumber, and consequently, the higher the frequency of their collisions that, when not disruptive, change the spin-axis orientation and spin rate of the object. This in turn results in a random Yarkovsky-drift direction over very long timescales.
4 Conclusions
By simulating the orbital evolution of a synthetic population of Trojan asteroids under the influence of the Yarkovsky effect over 1 Gyr, we obtained the following results: (1) We proved that small objects up to the size of 1 km in radius can be affected by the Yarkovsky force, depending on their thermo-physical properties. Compared with a purely gravitational orbital evolution, the Yarkovsky effect leads to a significant shortening of the residence time. (2) Owing to the Yarkovsky effect, objects with R ≤ 1 km are expected to exhibit a distinct orbital distribution from the currently observable population of larger objects. In particular, purely gravitational models predict that more particles are ejected from L5 than from L4. When the Yarkovsky force is considered, the escape rates from both clouds become equal, suggesting a more homogeneous orbital distribution in both clouds for small objects. (3) The experiment thereby confirmed that the difference in the number of Trojans that escape from L4 and L5 cannot be explained by the Yarkovsky effect and must be caused by the different preexisting orbital distributions of each group. (4) The Yarkovsky effect causes the residence time in Trojan orbits to decrease with decreasing object radius. Therefore fewer Trojans with R ≤ 1 km are expected to exist than is predicted by purely dynamical and collisional models. (5) The residence time of small objects in the Trojan region depends on their sense of rotation. For retrograde rotators, the Yarkovsky effect shortens the residence time in the Trojan clouds because the libration amplitude increases. For prograde rotators, the permanence time is also reduced, but to a lesser extent, as a result of the increase in eccentricity.
Some of our findings implicitly assume that small Trojans have the same size-frequency distribution slope as larger bodies. To which extent this assumption is justified is currently unknown. The recently selected Lucy space mission (Levison et al. 2017) may providevaluable insights into this. During its 12-yr mission, the spacecraft will fly by five Trojans and deliver high-resolution images of their surfaces. From the cratering records on these bodies it will be possible to measure the size-frequency distribution of the impacting bodies down to a size of 5 m, which may reveal the signature of the Yarkovsky effect on Trojans that we found here.
 |
Fig. 6 Distribution of libration amplitudes and eccentricities of objectse with 10 and 100 m radii that survive 1 Gyr of integration under the influence of the Yarkovsky force. |
Average values for libration amplitudes after 1 Gyr integration considering the Yarkovsky effect.
Acknowledgements
The authors are grateful to Tilman Spohn for the continuous support and to Jürgen Oberst and Enrico Mai for the useful discussions. The authors are indebted to David Nesvorny and Tim Holt for their thorough review, which contributed to improving this paper.
References
- Benz, W., & Asphaug, E. 1999, Icarus, 142, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Bottke, W. F., Vokrouhlický, D., Brož, M., Nesvorný, D., & Morbidelli, A. 2001, Science, 294, 1693 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Bottke, W., Durda, D., Nesvorny, D., et al. 2005, Icarus, 179, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Bowell, E., Hapke, B., Domingue, D., et al. 1989, in Asteroids II, eds. R. P. Binzel, T. Gehrels, & M. S. Matthews (Tucson: University of Arizona Press), 524 [Google Scholar]
- Brož, M. 2006, PhD Thesis, Charles University, Faculty of Mathematics and Physics Astronomical Institute, Praha, Czech Republic [Google Scholar]
- Buie, M. W., Olkin, C. B., Merline, W. J., et al. 2015, AJ, 149, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Davis, D. R., Durda, D. D., Marzari, F., Campo Bagatin, A., & Gil-Hutton, R. 2002, Collisional Evolution of Small-Body Populations (Tucson: University of Arizona Press), 545 [Google Scholar]
- de Elía, G. C., & Brunini, A. 2007, A&A, 475, 375 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- dell’Oro, A., PAolicchi, F., Marzari, P., Dotto, E., & Vanzani, V. 1998, A&A, 339, 272 [NASA ADS] [Google Scholar]
- Dell’Oro, A., Marzari, F., Paolicchi, P., & Vanzani, V. 2001, A&A, 366, 1053 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Di Sisto, R. P., Ramos, X. S., & Beaugé, C. 2014, Icarus, 243, 287 [NASA ADS] [CrossRef] [Google Scholar]
- Di Sisto, R. P., Ramos, X. S., & Gallardo, T. 2019, Icarus, 319, 828 [NASA ADS] [CrossRef] [Google Scholar]
- Dotto, E., Emery, J. P., Barucci, M. A., Morbidelli, A., & Cruikshank, D. P. 2008, The Solar System Beyond Neptune (Tucson: University of Arizona Press), 383 [Google Scholar]
- Durda, D. D., Greenberg, R., & Jedicke, R. 1998, Icarus, 135, 431 [NASA ADS] [CrossRef] [Google Scholar]
- Erdi, B. 1988, Celest. Mech., 43, 303 [NASA ADS] [CrossRef] [Google Scholar]
- Farinella, P., & Vokrouhlický, D. 1999, Science, 283, 1507 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Farinella, P., Vokrouhlický, D., & Hartmann, W. K. 1998, Icarus, 132, 378 [NASA ADS] [CrossRef] [Google Scholar]
- Fernández, Y. R., Sheppard, S. S., & Jewitt, D. C. 2003, AJ, 126, 1563 [NASA ADS] [CrossRef] [Google Scholar]
- Ferrari, C. 2018, Space Sci. Rev., 214, 22 [CrossRef] [Google Scholar]
- Grav, T., Mainzer, A. K., Bauer, J., et al. 2011, ApJ, 742, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Hanuš, J., Delbó, M., Ďurech, J., & Alí-Lagoa, V. 2015, Icarus, 256, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Hartmann, W. K., Farinella, P., Vokrouhlický, D., et al. 1999, Meteorit. Planet. Sci., 34, A161 [NASA ADS] [CrossRef] [Google Scholar]
- Hellmich, S. 2017, PhD Thesis, Westfälische Wilhelms-Universität Münster, Germany [Google Scholar]
- Horner, J., Müller, T. G., & Lykawka, P. S. 2012, MNRAS, 423, 2587 [NASA ADS] [CrossRef] [Google Scholar]
- Hou, X., Scheeres, D. J., & Liu, L. 2016, Celest. Mech. Dyn. Astron., 125, 451 [NASA ADS] [CrossRef] [Google Scholar]
- Jewitt, D. C., Trujillo, C. A., & Luu, J. X. 2000, AJ, 120, 1140 [NASA ADS] [CrossRef] [Google Scholar]
- Karlsson, O. 2011, Astron. Nachr., 332, 562 [NASA ADS] [CrossRef] [Google Scholar]
- Lacerda, P., & Jewitt, D. C. 2007, AJ, 133, 1393 [NASA ADS] [CrossRef] [Google Scholar]
- Levison, H. F., Shoemaker, E. M., & Shoemaker, C. S. 1997, Nature, 385, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Levison, H., Olkin, C., Noll, K., & Marchi, S. 2017, Lucy: Surveying the diversity of Trojans (Riga, Latvia: European Planetary Science Congress), 11 [Google Scholar]
- Marchis, F., Hestroffer, D., Descamps, P., et al. 2006, Nature, 439, 565 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Marchis, F., Durech, J., Castillo-Rogez, J., et al. 2014, ApJ, 783, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Marzari, F. 2002, Icarus, 159, 328 [NASA ADS] [CrossRef] [Google Scholar]
- Marzari, F., Scholl, H., & Farinella, P. 1996, Icarus, 119, 192 [NASA ADS] [CrossRef] [Google Scholar]
- Marzari, F., Tricarico, P., & Scholl, H. 2003, MNRAS, 345, 1091 [NASA ADS] [CrossRef] [Google Scholar]
- Merline, W. J., Weidenschilling, S. J., Durda, D. D., et al. 2002, Asteroids III (Tucson: University of Arizona Press), 289 [Google Scholar]
- Müller, M., Marchis, F., Emery, J. P., et al. 2010, Icarus, 205, 505 [NASA ADS] [CrossRef] [Google Scholar]
- Nesvorný, D., Vokrouhlický, D., & Morbidelli, A. 2013, ApJ, 768, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Pirani, S., Johansen, A., Bitsch, B., Mustill, A. J., & Turrini, D. 2019, A&A, 623, A169 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tsiganis, K., Varvoglis, H., & Dvorak, R. 2005, A Comparison of the Dynamical Evolution of Planetary Systems (Berlin: Springer Science & Business Media), 71 [CrossRef] [Google Scholar]
- Vokrouhlický, D., Nesvorný, D., & Bottke, W. F. 2003, Nature, 425, 147 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Wang, X., & Hou, X. 2017, MNRAS, 471, 243 [NASA ADS] [CrossRef] [Google Scholar]
- Wisdom, J., & Holman, M. 1991, AJ, 102, 1528 [NASA ADS] [CrossRef] [Google Scholar]
- Wong, I., Brown, M. E., & Emery, J. P. 2014, AJ, 148, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Yoshida, F., & Nakamura, T. 2005, AJ, 130, 2900 [NASA ADS] [CrossRef] [Google Scholar]
- Yoshida, F., & Terai, T. 2017, AJ, 154, 71 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Radii of target and projectile capable of causing a catastrophic disruption of the target body as well as the number projectiles in the L4 cloud and the resulting collisional lifetime for the target body.
Average values for libration amplitudes after 1 Gyr integration considering the Yarkovsky effect.
All Figures
 |
Fig. 1 Left panel: cumulative size distribution of L4 Trojans. Orange: known population; red dots: Trojan population after Yoshida & Terai (2017); red line: broken power law Yoshida & Terai (2017) fit to their observations; dashed gray line: extrapolation of the power law down to R = 100 m objects. Right panel: collisional lifetime of L4 Trojans according to this work. |
| In the text | |
 |
Fig. 2 Fraction of escaped particles with and without the Yarkovsky effect over 1 Gyr. |
| In the text | |
 |
Fig. 3 Fraction of escaped particles for the different sizes and physical properties of the particles. |
| In the text | |
 |
Fig. 4 Initial amplitude and escape time for the escaped particles during the non-Yarkovsky run (left panel) and the Yarkovsky run (right panel). The small gray dots represent the survivors. |
| In the text | |
 |
Fig. 5 Comparison of the histograms of libration amplitudes (left) and eccentricities (right) of particles that remained in the Trojan region over the complete integration time span in the Yarkovsky and non-Yarkovsky run after 1 Gyr (10 m radius objects only). |
| In the text | |
 |
Fig. 6 Distribution of libration amplitudes and eccentricities of objectse with 10 and 100 m radii that survive 1 Gyr of integration under the influence of the Yarkovsky force. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


