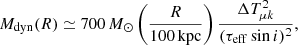| Issue |
A&A
Volume 629, September 2019
|
|
|---|---|---|
| Article Number | A87 | |
| Number of page(s) | 5 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201936327 | |
| Published online | 10 September 2019 | |
Rotating baryonic dark halos
1
Department of Mathematics and Physics “E. De Giorgi”, University of Salento, Via per Arnesano, 73100 Lecce, Italy
e-mail: dePaolis@le.infn.it
2
INFN, Sezione di Lecce, Via per Arnesano, 73100 Lecce, Italy
3
Sainsbury Laboratory, University of Cambridge, Bateman Street, Cambridge CB2 1LR, UK
4
Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Wilberforce Road, Cambridge CB3 0WA, UK
5
Center for Cosmology and Astrophysics, Alikhanian National Laboratory and Yerevan State University, Yerevan, Armenia
6
SIA, Sapienza University of Rome, Rome, Italy
7
Fellow of the Pakistan Academy of Sciences, Constitution Avenue, G-5, Islamabad, Pakistan
8
Physik-Institut, Universität Zürich, Winterthurerstrasse 190, 8057 Zürich, Switzerland
9
Department of Physics, School of Natural Sciences, National University of Sciences and Technology, Islamabad, Pakistan
Received:
16
July
2019
Accepted:
16
August
2019
Galactic halos are of great importance for our understanding of both the dark matter nature and primordial non-Gaussianity in the perturbation spectrum, a powerful discriminant of the physical mechanisms that generated the cosmological fluctuations observed today. In this paper we analyze Planck data towards the galaxy M 104 (Sombrero) and find an asymmetry in the microwave temperature which extends up to about 1° from the galactic center. This frequency-independent asymmetry is consistent with that induced by the Doppler effect due to the galactic rotation and we find a probability of less than about 0.2% that it is due to a random fluctuation of the microwave background. In addition, Planck data indicate the relatively complex dynamics of the M 104 galactic halo, and this appears to be in agreement with previous studies. In view of our previous analysis of the dark halos of nearby galaxies, this finding confirms the efficiency of the method used in revealing and mapping the dark halos around relatively nearby edge-on galaxies.
Key words: galaxies: general / galaxies: individual: M 104 / galaxies: halos
© ESO 2019
1. Introduction
As is well known, baryons contribute about 5% of our universe, but observations show that at least 40−50% of the baryons in the local universe are undetected. The question therefore arises as to what form they take. Indeed, most of these baryons must be in a form that is difficult to detect. Cosmological simulations suggest that these baryons have been ejected from galaxies into the intergalactic medium and are present in the form of a warm-hot medium around galaxies (Cen & Ostriker 1999, 2006; Gupta et al. 2012; Fraser-McKelvie et al. 2011) at temperatures of about 105 − 107 K. A non-negligible fraction of these baryons might also lie in a very cold form in clouds in the galactic halos. This possibility, previously suggested in De Paolis et al. (1995a,b), Gerhard & Silk (1995), was more recently directly evidenced by the detection of the so-called Herschel cold clouds (see Nieuwenhuizen et al. 2012 and references therein). Indeed, observations by Herschel-SPIRE towards the Large and Small Magellanic Clouds reveal the presence of thousands of gas clouds with temperatures of about 15 K, and it has been calculated that the full population of these clouds might constitute a non-negligible fraction of the Galactic halo dark matter.
We also remark here that galactic halos are on the one hand the least studied substructures of galaxies, and on the other are of particular importance for understanding large-scale structure formation. First, the parameters of galactic halos are sensitive to the non-Gaussianity in the primordial cosmological perturbation spectrum (Schmidt & Kamionkowski 2010), second, halos are probes for the mysterious nature of the dark matter (Bertone 2013; Somerville et al. 2018), and third, halos determine the properties of the disks and the spheroidal structures of galaxies (Kravtsov 2013; Gurzadyan 2019).
The primordial non-Gaussianity can be imprinted even in the profiles of the galactic halos (Moradinezhad Dizgah et al. 2013), thus linking the latter to the inflationary phase of the Universe (An et al. 2017). Halo properties can thus be probes for the nature of perturbations; for example, even though we presently possess no observable evidence of non-adiabatic (iso-curvature) perturbations, we have strong constraints on their possible resistance and it was shown that during re-ionization the iso-curvature modes are transferred to adiabatic ones (Weinberg 2004).
In a series of papers we have used the cosmic microwave background (CMB) data, first that of WMAP and then that of Planck, to trace the halos of certain nearby galaxies (De Paolis et al. 2011, 2014, 2015, 2016; Gurzadyan et al. 2015, 2018). The main aim was to test if the microwave data show a substantial temperature asymmetry of one side with respect to the other about the rotation axis of the galactic disks, as first suggested in De Paolis et al. (1995c) as due to the possible presence of a substantial amount of cold baryons in the galactic halos. Another motivation is that at the scales of galaxy clusters, the kinetic Sunyaev–Zeldovich (SZ) effect due to the cluster rotation is expected to induce temperature asymmetry in microwave data (see, e.g., Chluba & Mannheim 2002; Baxter et al. 2019). The same could in principle also happen for galaxies, provided they have a very hot gas halo component.
Among the considered objects were the M 31 galaxy, the active radio galaxy Centaurus A, M 82, the largest galaxy in the M 81 Group, the M 33 galaxy, where we found a substantial temperature asymmetry with respect to its minor axis up to about 3° from the galactic center and which correlates well with the HI velocity field at 21 cm, at least within about 0.5° (De Paolis et al. 2016), and the M 81 galaxy. In those galaxies we detected a clear temperature asymmetry of one side with respect to the other (as predicted for a Doppler shift) with ΔT/T values of typically about 2−3 × 10−5 and extending much further than the visible part of the galaxies (typically corresponding to peak values of ΔT ≃ 60−80 μK). Moreover, this temperature asymmetry is always almost frequency independent, which is an indication of an effect due to the galaxy rotation. It was thereby shown that our method can be applied to nearby edge-on spirals to trace the halo bulk dynamics on rather large scales in a model-independent way. In other words, the method is revealing the dark halos through the regular motion of either a cold gas component (De Paolis et al. 1995c; for the possible modelling of the gas clouds and their distribution in galaxies we refer to, e.g., Pfenniger et al. 1994; Fabian & Nulsen 1994; De Paolis et al. 1998; Draine 1998; Walker & Wardle 1998), or a hot ionized gas component (for a discussion of hot ionized gas through the thermal and kinetic Sunyaev–Zeldovich effect we refer the reader to, e.g., Lim et al. 2017).
Along with the studies of the mentioned galaxies, we note that other galaxies, namely M 63, M 64, M 65, and M 66, analyzed in a similar manner, either do not show any significant microwave temperature asymmetry (for the first three galaxies) or the apparent asymmetry is frequency dependent (the M 66 galaxy), and therefore has to be attributed, in this specific case at least, to a nonDoppler type signature (Gurzadyan 2018).
Here we continue those studies on the microwave mapping of dark halos, analyzing the Planck data on a nearly edge-on Sa type spiral galaxy M 104 known by its remarkable internal dynamics (see, e.g., Jardel et al. 2011), and draw some conclusions on the baryonic dark matter content of its halo.
The outline of the paper is the following: after a short presentation of the M 104 galaxy, the analysis of Planck data is discussed in Sect. 2, while in Sect. 3 we present our main conclusions.
2. The M 104 Sombrero galaxy
2.1. M 104: generalities
The galaxy M 104, also known as the Sombrero galaxy (or NGC 4594), is a majestic galaxy located in the Virgo constellation at a distance of about 9.55 Mpc from Earth (see Fig. 1 for a view in the optical band). The luminous bulge and the prominent dust lane give this galaxy its name. This dust lane is the site of star formation in the galaxy and a rich system of globular clusters (GCs) characterize the M 104 halo. The estimated number of these GCs is about 2 × 103, about ten times larger than the number of GCs in the Milky Way. It is the brightest nearby spiral galaxy and is inclined at an angle of only about 7° to our line of sight and appears edge-on (its inclination angle is therefore i = 83°). It is visible with binoculars and small telescopes, but only appears as a small patch of light. The large bulge of the Sombrero galaxy and the super-massive black hole at its core make it a popular target for study. The galaxy, at coordinates RA: 12h39m59.4s, Dec: −11 ° 39′23″ (the galactic coordinates are l = 298.46055° and b = 51.14929°), has major and minor diameters of about 8.6′ and 4.2′, corresponding to about 24 kpc and 9.7 kpc, respectively (at the M 104 distance 1′ corresponds to about 2.78 kpc and 1° to about 167 kpc). The galaxy has a visible mass of about (22.9 ± 3.2) × 1010 M⊙ (Tempel & Tenjes 2006) and its center is thought to be home to a supermassive black hole.
 |
Fig. 1. Sombrero galaxy in the visible band. The white circle traces the distance of 0.1° around the galaxy center at coordinates RA: 12h39m59.4s, Dec: −11 ° 39′23″. |
2.2. Planck data for M 104
Following the same procedures described in our previous papers we used the publicly released Planck 2015 data1 (Adam et al. 2016) in the 70 GHz bands of the Low-Frequency Instrument (LFI), and in the bands at 100 GHz, 143 GHz, and 217 GHz of the High-Frequency Instrument (HFI). We also used the foreground-corrected SMICA map (indicated as SmicaH), which should display the lowest contamination by the galactic foreground. We notice here that the resolution of Planck is 13.2′, 9.6′, 7.1′, and 5′ in terms of FHWM (full width at half maximum) at 70, 100, 143, and 217 GHz bands, respectively, and the frequency maps by Ade et al. (2016) are provided in CMB temperature at a resolution corresponding to Nside = 2048 in the HEALPix scheme (Górski et al. 2005). We also note that in the CMB maps we consider, the monopole and dipole contributions have been removed.
In Fig. 2 the Sombrero galaxy in the 143 GHz Planck band is shown. The optical extension of the M 104 galaxy is shown, as indicated by the inner ellipse. Spectroscopic observations in the optical band and radio observations at 21 cm show that the galaxy disk has an asymptotic rotation velocity of 376 ± 12 km s−1 (Jardel et al. 2011). Also, the globular cluster system around the M 104 galaxy shows a global rotation with an estimated speed of about 100 km s−1 (Bridges et al. 1997), with the eastern part moving towards Earth. To study the CMB data toward the M 104 galaxy in the simplest way, the Planck field of the region of interest has been divided into four quadrants: A1, A2, A3, and A4.
 |
Fig. 2. Sombrero galaxy in the 143 GHz Planck band. The inner and outer circles mark the galactocentric distances of 0.1° and 1°, respectively. |
As detailed in the histograms in Figs. 3 and 4, we considered the temperature asymmetry in three radial regions about the M 104 center within 0.2°, 0.4°, 0.6°, and 1.0° (indicated as R0.2, R0.4, R0.6, and R1.0, respectively). In the upper panel of Fig. 3 we give the temperature asymmetry toward M 104 in μK (with the standard errors) of the A1+A4 region with respect to the A2+A3 region in the four considered Planck bands within the four radial distances. In the bottom panel of the figure we give the same for the 360 control fields with the same geometry (shown in Fig. 2) equally spaced at one degree distance from each other in Galactic longitude and at the same latitude as M 104. Here, we mention that we have intentionally avoided the use of CMB simulations to get the error bars. Indeed, simulations are mandatory when whole-sky CMB properties are studied (correlation functions, power spectra, etc.), while they could introduce additional uncertainties related to the modelling of foregrounds. As one can see from Fig. 3, the A1+A4 region always appears hotter than the A2+A3 region, and the temperature asymmetry increases with increasing galactocentric radius from about 25 μK (at 0.2°) to a maximum value of about 65 μK (within 0.6°). We note that SMICA_H data show a similar trend. In the lower panel of Fig. 3, the 360 control fields show a temperature asymmetry consistent with zero in all Planck bands.
 |
Fig. 3. Temperature asymmetry towards (first panel) the M 104 galaxy in μK (with the standard errors) of the Variant 1 (A2A3–A1A4), in the four considered Planck bands (see text for details) within four radial distances of 0.2° (R0.2), 0.4° (R0.4), 0.6° (R0.6), and 1° (R1.0); and (second panel) the same for the 360 control fields with the same geometry equally spaced at one degree distance from each other in Galactic longitude and at the same latitude as M 104. |
 |
Fig. 4. Temperature asymmetry toward (first panel) the M 104 galaxy in μK (with the standard errors) of the Variant 2 (A1A2–A3A4), in the four considered Planck bands (see text for details) within four radial distances of 0.2° (R0.2), 0.4° (R0.4), 0.6° (R0.6), and 1° (R1.0); and (second panel) the same for the 360 control fields with the same geometry equally spaced at one degree distance from each other in Galactic longitude and at the same latitude as M 104. |
In Fig. 4 we show the second considered variant, namely the temperature asymmetry in the four considered Planck bands of the A3+A4 region with respect to the A1+A2 one. As one can see by comparing the upper and lower panels of Fig. 4, the temperature asymmetry now has a more complicated pattern; it is almost consistent with zero within 0.4° in the 70 GHz, 100 GHz, and 143 GHz bands, while SMICA_H data indicate that the A1+A2 region is hotter than the A3+A4 one. The A3+A4 side of the external M 104 halo instead seems to be hotter than the other region in all considered bands by about 10−20 μK.
We also considered available data of the GCs in the M 104 galaxy. Bridges et al. (2007) searched for rotation of the globular cluster systems around the M 104 galaxy by considering the line of sight velocity of 108 GCs and found no evidence for global rotation. As also noticed by these latter authors, the lack of rotation is certainly surprising because there is a rotation of 300−350 km s−1 in the stellar and gas disk and, moreover, cosmological simulations of galaxy formation predict a significant amount of angular momentum in early-type galaxies. In this respect, we note that most of the GCs towards M 104 are detected relatively near to the galactic center. If one considers the 43 GCs with galactocentric distance larger than 5′ one finds a non-negligible rotation with the 95% upper limit on the rotation velocity of 250 km s−1 and a GC velocity dispersion σ of about 155 km s−1. Therefore, the obtained 95% upper limit on the value of (v/σ) is about 1.6. To further strengthen this discussion, in Fig. 5 we show the position of the eight outermost GCs (see Bridges et al. 2007, for details). Unfortunately, these GCs reside in the A3 and A4 regions in Fig. 2, and therefore they can be used at most to probe the north–south asymmetry (as in the Variant 1), but not the east–west asymmetry. We obtain that the average line-of-sight velocity of the four GCs in the A3 region (⟨vr⟩≃947 km s−1) is similar to that of the four GCs in the A4 region (⟨vr⟩≃972 km s−1), also consistent with the observed recession velocity of the M 104 galaxy of about 1024 km s−1. We note here that the two GCs with highest and lowest radial velocity are GC2200 in the A4 region and GC682 in the A3 region. These two globular clusters show a remarkable rotation about the M 104 center since the first one is moving with line-of-sight velocity ⟨vr⟩≃1524 km s−1 while GC682 is moving towards Earth with (⟨vr⟩≃681 km s−1), thus with a relative velocity of ≃343 km s−1 towards the observer. There is no doubt that an enlarged sample of GCs in the M 104 galaxy at galactocentric distances larger than 0.4° could greatly help to probe the rotation of the Sombrero galaxy halo.
 |
Fig. 5. Position of the eight outermost globular clusters observed in the M 104 galaxy (for details see Bridges et al. 2007). The inner circle traces the visible part of the Sombrero galaxy while the outer circle is at a radius of 0.4°. |
The detected temperature structure observed in the Planck microwave bands towards M 104 may indicate the absence of a regular bulk motion at various scales and complicated internal dynamics. Indeed, the presence of an internal disk and an external ellipsoid has been suggested to explain the complex dynamics of the M 104 galaxy.
We would like to emphasize that our methodology to study the temperature asymmetry towards a given target aims to be maximally model-independent and, in particular, independent of the precise knowledge of the spectrum emitted in the considered regions (due to molecular clouds or to other mechanisms such as the kinetic Sunyaev–Zeldovich effect or synchrotron emission, etc.). The temperature asymmetry signal we detect is practically frequency independent2, which is a clear signature of the Doppler effect. In fact, we find that, in the case of the first Variant, the probability that the detected signal in each of the four considered rings is due to a random fluctuation of the CMB signal is 0.30, 0.31, 0.11, 0.26, respectively, which yield, assuming independent probabilities, a cumulative probability of about 1.8 × 10−3, that is less than 0.2%, while for Variant 2, where the situation is less regular, the chance probability yields 3.1 × 10−2.
Before closing this section, we also note that the simple Doppler nature of the temperature asymmetry can be influenced by several effects such as the peculiar motion of the halo clouds, the nonuniform spectrum of the clouds due to the radiation balance and radiative transfer details, and so on. However, obviously, at this stage, those are lower-order effects with respect the global halo rotation. Moreover, since we consider M 104 as being foreground to the CMB, we note that for the maps we study (with monopole and dipole extracted) the foregrounds could also be negative due to physical processes, for example, in the case of clouds, the particular molecular energy level transitions, metastable states, two-photon emission or absorption, and so on.
3. Conclusions
Similar to the case of other galaxies of the Local Group considered previously (in particular the galaxies M 31, M 82, M 81, M 33, and Cen A have been analyzed using Planck data and a temperature asymmetry ΔT about 60−80 μK of one side with respect to the other about the rotation axis of the galactic disks has been detected in all cases), we found a consistent north–south temperature asymmetry toward the M 104 galaxy, that reaches values up to about 65 μK within 0.6° (about 100 kpc) in all considered Planck bands3, and then starts to decrease. We mention that Chandra observations in the X-ray band of the M 104 galaxy show the presence of a diffuse X-ray emission extending at least up to 30 kpc from its center (Li et al. 2011), together with hundreds of point sources which are a mixture of objects in the M 104 halo (mainly X-ray binaries) as well as background Quasars (Li et al. 2010). However, the presence of this X-ray-emitting hot gas cannot explain the temperature asymmetry detected in Planck data.
It is straightforward to show that if the cold-gas cloud model is at the origin of the detected temperature asymmetry (however, as anticipated in the previous section, other emission mechanisms may play a role in the detected signal), a lower limit to the M 104 galaxy dynamical mass is given by
where R is the considered galaxy halo radius in units of 100 kpc, ΔT is the measured temperature asymmetry (in μk), and τeff is the effective cloud optical depth (which depends on both the cloud filling factor and the averaged optical depth within a given Planck band. Expected values for τeff are about a few 10−3 (Tahir et al. 2019), meaning that the M 104 dynamical mass out to ∼100 kpc is seen to be Mdyn ≃ 3 × 1012M⊙, in agreement with other measurements (see, e.g., Tempel & Tenjes 2006). It is interesting to mention in this respect that this galactocentric distance appears close to the transonic point (at ≃126 kpc), determined recently by Igarashi et al. (2014) within the framework of the transonic outflow model in a dark matter halo applied to the Sombrero galaxy4.
The detected temperature asymmetry is, as discussed in the previous section, almost frequency-independent and indicates that the M 104 galaxy halo is rotating with respect to the major symmetry axis of the galaxy disk (Variant 1). However, the fact that a strong temperature asymmetry is detected also with respect to the minor symmetry axis of M 104 (Variant 2), is a robust indication of a relatively complex geometry and rotation patterns. We note that that several different components have been shown to contribute to the observed galaxy kinematics (see, e.g., Wagner et al. 1989). These components have different rotational velocities and velocity dispersions. In addition, they cannot be described by a single Gaussian broadening function. This complex structure may explain the observations in the different Planck bands toward the Sombrero galaxy. As a matter of fact, the Sombrero galaxy exhibits the characteristics of both disk-like and elliptical galaxies. Recent observations by the Spitzer space telescope show that M 104 is much more complex than previously thought and resembles a disk galaxy inside an elliptical one. We wish to emphasize here that the results in the present paper find strong support by Spitzer infrared vision which offers a different view of that emerging in visible light, with a glowing halo filled by old stars and a strong quantity of dust through which we observe a reddened star population. This implies that the M 104 halo has the same size and mass as those of giant elliptical galaxies. The Sombrero galaxy resembles a giant elliptical that has swallowed a disk galaxy, but this is unlikely to have taken place since the process would have completely destroyed the galactic disk structure. Following Gadotti & Sánchez-Janssen (2012), we propose that the M 104 galactic structure is the result of a giant elliptical inundated by a huge amount of gas billions of years ago. This could explain the complex dynamical morphology of the Sombrero galaxy.
Before concluding this paper, we would like to make a general remark about the use of CMB data to map various galaxy halos. Indeed, the systematic study of the mean temperature asymmetry, applied here to the Sombrero galaxy, could become a conventional tool for studying and mapping the internal motions of not-too-distant galaxies (including their halos) in the microwave band, in a complementary way with respect to other methods. As for the case of the Kolmogorov stochasticity parameter (Gurzadyan et al. 2009, 2014) and the Sunyaev–Zeldovich effect, software for an automated analysis, cross-correlating surveys in different bands with CMB data, may be developed. This is especially important in view of the next generation of CMB experiments, such as LiteBird (Hazumi et al. 2012), CMB-S4 (Abazajian et al. 2016), CORE (Cosmic Origins Explorer, Finelli et al. 2018), DeepSpace5, PIXIE (Cosmic Origins Explorer, Kogut et al. 2011), and Polarbear (The Polarbear Collaboration 2014), which will attempt to obtain measurements of the CMB that are even more precise than have been available so far and that may allow higher-resolution studies of the galaxies of the Local Group. Many of these experiments are designed to cover mainly the frequency range around 100 GHz where the relative intensity of the CMB is known to be highest and where one of the most dominant foreground components is dust emission (see, e.g., Liu et al. 2017). Understanding the properties of dust emission and distinguishing between Galactic foregrounds and extragalactic emission are important for the optimized use of the next-generation CMB experiments.
From the Planck Legacy Archive, http://pla.esac.esa.int
We remark here that we consider maps of Nside = 2048 in the HEALPix scheme, which corresponds to a pixel size ≃1.718′ (Górski et al. 2005, see also the web page https://irsa.ipac.caltech.edu/data/Planck/release_1/ancillary-data/), thus ensuring the pixel number statistics in the studied regions and the resulting error bars as in Figs. 3 and 4, and the discussion in Sect. 2.2.
See the DeepSpace website at http://deep-space.nbi.ku.dk
Acknowledgments
We acknowledge the use of Planck data in the Legacy Archive for Microwave Background Data Analysis (LAMBDA) and HEALPix (Górski et al. 2005) package. FDP, GI and AAN acknowledge the TAsP and Euclid INFN projects. PJ acknowledges support from the Swiss National Science Foundation. AQ is most grateful to the Lecce Unit of INFN for support during this work. AVG acknowledges Henrik Jönsson and is supported by the Gatsby Charitable Foundation under award GAT3395-PR4 to the Jönsson Group.
References
- Abazajian, K. N., Adshead, P., Ahmed, Z., et al. 2016, ArXiv e-prints [arXiv:1610.02743] [Google Scholar]
- Adam, R., Ade, P. A. R., Aghanim, N., et al. 2016, A&A, 594, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ade, P. A. R., Aghanim, N., Akrami, Y., et al. 2016, A&A, 594, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- An, H., McAneny, M., Ridgway, A. K., & Wise, M. B. 2017, Phys. Rev. D, 97, 123528 [NASA ADS] [CrossRef] [Google Scholar]
- Baxter, E. J., Sherwin, B. D., & Raghunathan, S. 2019, JCAP, 6, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Bertone, G. 2013, Particle Dark Matter (Cabridge, UK: Cambridge University Press) [Google Scholar]
- Bridges, T. J., Ashman, K. M., Zepf, S. E., et al. 1997, MNRAS, 284, 376 [NASA ADS] [CrossRef] [Google Scholar]
- Bridges, T. J., Rhode, K. L., Zepf, S. E., et al. 2007, ApJ, 658, 980 [NASA ADS] [CrossRef] [Google Scholar]
- Cen, R., & Ostriker, J. P. 1999, ApJ, 514, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Cen, R., & Ostriker, J. P. 2006, ApJ, 650, 560 [NASA ADS] [CrossRef] [Google Scholar]
- Chluba, J., & Mannheim, K. 2002, A&A, 396, 419 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Paolis, F., Ingrosso, G., Jetzer, Ph, & Roncadelli, M. 1995a, Phys. Rev. Lett., 74, 14 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- De Paolis, F., Ingrosso, G., Jetzer, Ph, & Roncadelli, M. 1995b, A&A, 295, 567 [NASA ADS] [Google Scholar]
- De Paolis, F., Ingrosso, G., Jetzer, Ph, et al. 1995c, A&A, 299, 647 [NASA ADS] [Google Scholar]
- De Paolis, F., Ingrosso, G., Jetzer, Ph, & Roncadelli, M. 1998, ApJ, 500, 59 [NASA ADS] [CrossRef] [Google Scholar]
- De Paolis, F., Gurzadyan, V. G., Ingrosso, G., et al. 2011, A&A, 534, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Paolis, F., Gurzadyan, V. G., Nucita, A. A., et al. 2014, A&A, 565, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Paolis, F., Gurzadyan, V. G., Nucita, A. A., et al. 2015, A&A, 580, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Paolis, F., Gurzadyan, V. G., Nucita, A. A., et al. 2016, A&A, 593, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Draine, B. T. 1998, ApJ, 509, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Fabian, A. C., & Nulsen, P. E. J. 1994, MNRAS, 269, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Finelli, F., Bucher, M., Achúcarro, A., et al. 2018, JCAP, 4, 16 [Google Scholar]
- Fraser-McKelvie, A., Pimbblet, K. A., Lazendic, J., et al. 2011, MNRAS, 415, 1961 [NASA ADS] [CrossRef] [Google Scholar]
- Gadotti, D. A., & Sánchez-Janssen, R. 2012, MNRAS, 423, 877 [NASA ADS] [CrossRef] [Google Scholar]
- Gerhard, O., & Silk, J. 1995, ApJ, 472, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Górski, K. M., Hivon, E., Banday, A. J., et al. 2005, ApJ, 622, 759 [NASA ADS] [CrossRef] [Google Scholar]
- Gupta, A., Mathur, S., Krongold, Y., Nicastro, F., & Galeazzi, M. 2012, ApJ, 756, L8 [NASA ADS] [CrossRef] [Google Scholar]
- Gurzadyan, A. V. 2018, Master Degree Essay, DAMTP (Cambridge: Univ. Cambridge), unpublished [Google Scholar]
- Gurzadyan, V. G. 2019, Eur. Phys. J. Plus, 134, 14 [CrossRef] [Google Scholar]
- Gurzadyan, V. G., Allahverdyan, A. E., Ghahramanyan, T., et al. 2009, A&A, 497, 343 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gurzadyan, V. G., Kashin, A. L., Khachatryan, H., et al. 2014, A&A, 566, A135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gurzadyan, V. G., De Paolis, F., Nucita, A., et al. 2015, A&A, 582, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gurzadyan, V. G., De Paolis, F., Nucita, A., et al. 2018, A&A, 609, A131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hazumi, M., Borrill, J., Chinone, Y., et al. 2012, Proc. SPIE, 8442, 844219 [CrossRef] [Google Scholar]
- Igarashi, A., Mori, M., & Nitta, S. 2014, MNRAS, 444, 1177 [NASA ADS] [CrossRef] [Google Scholar]
- Jardel, J. R., Gebhardt, K., Fabricius, M., & Drory, N. 2011, ApJ, 739, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Kogut, A., Fixsen, D. J., Chuss, D. T., et al. 2011, JCAP, 7, 25 [Google Scholar]
- Kravtsov, A. V. 2013, ApJ, 764, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Li, Z., Spitler, L. R., Jones, C., et al. 2010, ApJ, 721, 1368 [NASA ADS] [CrossRef] [Google Scholar]
- Li, Z., Jones, C., Forman, W. R., et al. 2011, ApJ, 730, 84 [NASA ADS] [CrossRef] [Google Scholar]
- Lim, S., Mo, H., Wang, H., & Yang, X. 2017, MNRAS, submitted [arXiv:1712.08619] [Google Scholar]
- Liu, H., von Hausyger, S., & Naselsky, P. 2017, Phys. Rev. D, 95, 103517 [NASA ADS] [CrossRef] [Google Scholar]
- Moradinezhad Dizgah, A., Dodelson, S., & Riotto, A. 2013, Phys. Rev. D, 88, 063513 [NASA ADS] [CrossRef] [Google Scholar]
- Nieuwenhuizen, T. M., van Heusden, E. F. G., & Liska, M. T. P. 2012, Phys. Scr., 151, 014085 [CrossRef] [Google Scholar]
- Pfenniger, D., Combes, F., & Martinet, L. 1994, A&A, 285, 79 [NASA ADS] [Google Scholar]
- Schmidt, F., & Kamionkowski, M. 2010, Phys. Rev. D, 82, 103002 [NASA ADS] [CrossRef] [Google Scholar]
- Somerville, R. S., Behroozi, P., Pandya, V., et al. 2018, MNRAS, 473, 2714 [NASA ADS] [CrossRef] [Google Scholar]
- Tahir, N., De Paolis, F., Qadir, A., & Nucita, A. A. 2019, IJMPD, 28, 1950088 [NASA ADS] [CrossRef] [Google Scholar]
- Tempel, E., & Tenjes, P. 2006, MNRAS, 371, 1269 [NASA ADS] [CrossRef] [Google Scholar]
- The Polarbear Collaboration (Ade, P. A. R., et al.) 2014, ApJ, 794, 171 [NASA ADS] [CrossRef] [Google Scholar]
- Wagner, S. J., Dettmar, R. J., & Bender, R. 1989, A&A, 215, 243 [NASA ADS] [Google Scholar]
- Walker, M., & Wardle, M. 1998, ApJ, 498, L125 [NASA ADS] [CrossRef] [Google Scholar]
- Weinberg, S. 2004, Phys. Rev. D, 70, 083522 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
All Figures
 |
Fig. 1. Sombrero galaxy in the visible band. The white circle traces the distance of 0.1° around the galaxy center at coordinates RA: 12h39m59.4s, Dec: −11 ° 39′23″. |
| In the text | |
 |
Fig. 2. Sombrero galaxy in the 143 GHz Planck band. The inner and outer circles mark the galactocentric distances of 0.1° and 1°, respectively. |
| In the text | |
 |
Fig. 3. Temperature asymmetry towards (first panel) the M 104 galaxy in μK (with the standard errors) of the Variant 1 (A2A3–A1A4), in the four considered Planck bands (see text for details) within four radial distances of 0.2° (R0.2), 0.4° (R0.4), 0.6° (R0.6), and 1° (R1.0); and (second panel) the same for the 360 control fields with the same geometry equally spaced at one degree distance from each other in Galactic longitude and at the same latitude as M 104. |
| In the text | |
 |
Fig. 4. Temperature asymmetry toward (first panel) the M 104 galaxy in μK (with the standard errors) of the Variant 2 (A1A2–A3A4), in the four considered Planck bands (see text for details) within four radial distances of 0.2° (R0.2), 0.4° (R0.4), 0.6° (R0.6), and 1° (R1.0); and (second panel) the same for the 360 control fields with the same geometry equally spaced at one degree distance from each other in Galactic longitude and at the same latitude as M 104. |
| In the text | |
 |
Fig. 5. Position of the eight outermost globular clusters observed in the M 104 galaxy (for details see Bridges et al. 2007). The inner circle traces the visible part of the Sombrero galaxy while the outer circle is at a radius of 0.4°. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.