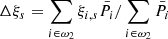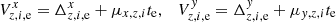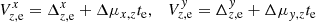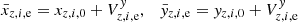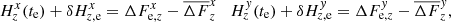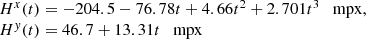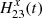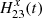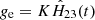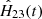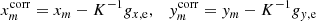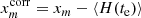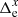| Issue |
A&A
Volume 629, September 2019
|
|
|---|---|---|
| Article Number | A113 | |
| Number of page(s) | 11 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/201936319 | |
| Published online | 12 September 2019 | |
Astrometric planet search around southern ultracool dwarfs
IV. Relative motion of the FORS2/VLT CCD chips⋆
1
Main Astronomical Observatory, National Academy of Sciences of the Ukraine, Zabolotnogo 27, 03680 Kyiv, Ukraine
e-mail: laz@mao.kiev.ua
2
Space Telescope Science Institute, 3700 San Martin Drive, Baltimore, MD 21218, USA
Received:
15
July
2019
Accepted:
8
August
2019
We present an investigation of the stability of the two chips in the FORS2 camera CCD mosaic on the basis of astrometric observations of stars in 20 sky fields, some of which were monitored for four to seven years. We detected a smooth relative shear motion of the chips along their dividing line that is well approximated by a cubic function of time with an amplitude that reaches ∼0.3 pixels (px) or ∼38 mas over seven years. In a single case, we detected a step change of ∼0.06 px that occurred within four days. In the orthogonal direction that corresponds to the separation between the chips, the motion is a factor of 5–10 smaller. This chip instability in the camera significantly reduces the astrometric precision when the reduction uses reference stars located in both chips, and the effect is not accounted for explicitly. We found that the instability introduces a bias in stellar positions with an amplitude that increases with the observation time span. When our reduction methods and FORS2 images are used, it affects stellar positions like an excess random noise with an rms of ∼0.5 mas for a time span of three to seven years when left uncorrected. We demonstrate that an additional calibration step can adequately mitigate this and restore an astrometric accuracy of 0.12 mas, which is essential to achieve the goals of our planet-search program. These results indicate that similar instabilities could critically affect the astrometric performance of other large ground-based telescopes and extremely large telescopes that are equipped with large-format multi-chip detectors if no precautions are taken.
Key words: astrometry / methods: data analysis
© ESO 2019
1. Introduction
Astrometry is a powerful technique for detecting companions to the nearby ultracool dwarfs by monitoring the induced reflex motion, provided that a measurement precision better than 1 mas can be achieved. For ground-based observations, this requires the use of 8–10 m telescopes and good observing conditions. For targets near the Galactic plane, where a large number of reference stars is available, and 0.4″ seeing, the initial estimates of Lazorenko & Lazorenko (2004) indicated an achievable astrometric accuracy of 0.01–0.06 mas for faint stars. With the Very Large Telescope (VLT) camera FORS2 (Appenzeller et al. 1998) we demonstrated a single-epoch astrometric accuracy close to 0.1 mas for 15–20 mag stars and 0.6″ atmospheric seeing (Lazorenko et al. 2009; Sahlmann et al. 2014; Lazorenko et al. 2014; Lazorenko & Sahlmann 2017). This accuracy is sufficient to detect and characterize the orbits of Jupiter-mass companions to nearby ultracool dwarfs. With this purpose, we initiated an astrometric planet search around 20 ultracool dwarfs in 2011 (Sahlmann et al. 2015a,b).
The further accuracy improvement beyond 0.1 mas, needed for the detection of Neptune- and lower-mass companions to ultracool dwarfs, is restrained by fundamental limits on the precision of photocenter determination, the atmospheric image motion caused by turbulence in the upper atmospheric layers, and by systematic errors of instrumental origin. It is expected that in the near future the achievable astrometric accuracy will be improved to 0.01–0.05 mas on 30 m class telescopes such as the European Extremely Large Telescope (ELT), primarily due to the use of adaptive optics, better signal-to-noise ratio in the stellar images, and general performance improvements of the cameras (Davies et al. 2010; Rodeghiero et al. 2018; Pott et al. 2018).
The CCD detectors in most cameras of large telescopes are formed as mosaics of CCD chips allowing for a wide field of view (FoV). However, this structure of detectors potentially affects geometric stability of the compound image when the mounting of the CCDs is not sufficiently rigid. The first evidence of the displacements in the FORS2 CCD mosaic were detected by Lazorenko et al. (2014; hereafter Paper I) from the analysis of two years of data. At that time, we discovered a relative chip motion (RCM) in the two-chip CCD mosaic with an amplitude of 0.001–0.010 px, or 0.1–1 mas. In one peculiar case, we detected a shift of nearly 0.02–0.05 px or 3–6 mas. These amplitudes were small but exceeded the astrometric accuracy of FORS2 by a factor of 10.
Relative chip motion was observed for cameras on board the Hubble Space Telescope (Anderson & King 2003, Sect. 6)1 with an amplitude of up to 3 px = 120 mas over ∼10 years. More recently, Bernstein et al. (2017) analyzed the stability of the CCD chip array of the Dark Energy Camera (DECam) and discovered surprisingly large RCM with an amplitude of 0.4 px = 100 mas occurring over only 2 weeks.
In this paper, we use newly obtained series of FORS2 observations to characterize the instability of its detector chips. We also predict how these instrumental errors can affect the astrometric performance of FORS2 and other telescopes.
2. Observational data
This study is based on observations of Ndw = 20 ultracool dwarfs obtained with the FORS2 camera of the VLT. The program of observations, reduction methods, and the first results obtained from observations in 2010–2013 are described in Sahlmann et al. (2014) and Paper I. We monitored all targets during two visibility periods, but for targets with suspected orbital signals, we followed up with additional observations. As a consequence, six fields were observed over one to one and a half years, seven fields were observed for three years, and the seven remaining fields were monitored over six to seven years. We refer to the corresponding data as the short-, medium-, and long-duration datasets.
The FORS2 detector has an exchangeable blue (E2V) and red (MIT) sensitive detector pair. We used FORS2 only in its standard configuration with an MIT detector. This detector is a mosaic of two CCD chips. With the 2 × 2 binned read-out mode we used, they are 2k × 1k pixel arrays with pixel sizes of 30 μm. The upper chip 1 and the lower chip 2 are mounted with a small gap of ∼480 μm (∼16 binned pixels). Observations were obtained with a high-resolution collimator that produces an angular pixel scale of 126.1 mas pixel. Every observation “epoch” consists of a series of 30–100 images. For the different sky fields we obtained Ne = 10…23 epochs of observations.
In every image, we measured 500–1500 star photocenters x, y of i = 1…N unsaturated reference stars. The following reduction proceeded in a coordinate system whose axes X, Y are oriented along RA, Dec. For convenience, the row y = 1000 px was aligned with the upper edge of the gap between the chips (a lower edge of the upper chip 1), thus y < 1000 px identifies stars in the bottom chip 2, and y > 1000 px corresponds to the upper chip 1.
3. Basic astrometric reduction
The observations are reduced with differential astrometric techniques as previously reported (Lazorenko et al. 2009; Paper I), where we use the effective filtration of the atmospheric image motion by the large ground-based telescope (Lazorenko & Lazorenko 2004). This technique requires a circular reference field, and the best performance is achieved at its center. For this reason, the reference field is centered on the target object. We take into consideration that the atmospheric image motion variance increases with the reference field size R while the reference frame noise decreases with R. Therefore, there is some optimal radius Ropt at which the sum of these error components is smallest. Its value is determined numerically and is 400–800 px (1–2′ for FORS2), which is typical for the sky fields near the Galactic plane.
A list of the variables that are most frequently used in the paper along with a short description is given in Table 1.
Frequently used variables and functions.
3.1. Astrometric model
All measured stars (except for the target object) are used as references to provide the best information on the geometric distortion Φ(x, y) of the field caused both by the instability of the telescope optics and its adjustment, and by the image motion. Its spatial power density is represented by an infinite expansion into series of even integer powers k = 2, 4, … in the domain of the spatial frequencies, where k is the modal index, and the mode amplitude decreases rapidly with increasing k. Over the CCD space (x, y), the image motion causes deformations of the frame of reference stars that are modeled by an expansion into a series of basic functions fi, 1 = 1, fi, 2 = xi, fi, 3 = yi, 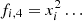 which are full bivariate polynomials of x, y and whose number N′ = 1…k(k + 2)/8 depends on k. The use of functions Φ(x, y) in the reduction model removes all first 1…k/2 − 1 modes of the image motion spectrum. Usually, k is between 4 and 16, and for this study, we set k = 10, which leads to the most stable solution. The function
which are full bivariate polynomials of x, y and whose number N′ = 1…k(k + 2)/8 depends on k. The use of functions Φ(x, y) in the reduction model removes all first 1…k/2 − 1 modes of the image motion spectrum. Usually, k is between 4 and 16, and for this study, we set k = 10, which leads to the most stable solution. The function 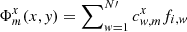 therefore includes N′×M coefficients
therefore includes N′×M coefficients 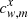 that model geometric distortions to the fourth power of x, y at the exposure number m = 1…M. Similarly,
that model geometric distortions to the fourth power of x, y at the exposure number m = 1…M. Similarly, 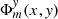 models geometric distortions along the Y-axis through the coefficients
models geometric distortions along the Y-axis through the coefficients 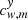 .
.
The displacement of some star i photocenter (either the target or reference star) from its initial position xi, 0, yi, 0 in the reference frame (exposure m = 0) to xi, m, yi, m in exposure m is caused by intrinsic (proper motion, parallax) and atmospheric (refraction) motion. We model it with s = 1…S astrometric parameters ξi, s: the offsets to the positions Δx0, i, Δy0, i, proper motion μx, i, μy, i, relative parallax ϖ, and two atmospheric differential chromatic parameters ρ and d, that is, S = 7. The corresponding displacement is 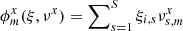 and
and 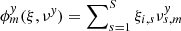 , where νx, νy are S × M coefficients (time t, parallax factors Π, etc.) valid at the time of exposure tm for the measurements along X or Y. In particular,
, where νx, νy are S × M coefficients (time t, parallax factors Π, etc.) valid at the time of exposure tm for the measurements along X or Y. In particular, 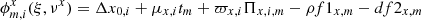 , where functions f1, f2 depend on zenith distance, parallax angle, temperature, and pressure (Sahlmann et al. 2014).
, where functions f1, f2 depend on zenith distance, parallax angle, temperature, and pressure (Sahlmann et al. 2014).
All ξ values are determined as free model parameters. Alternatively, the reduction model can be significantly simplified if some ξ values are taken from the external sources. In particular, Gaia DR2 (Lindegren et al. 2018) provides proper motions with standard uncertainties of 0.08–0.16 mas yr−1 for G = 16–17 mag stars. For our targets of comparable magnitudes with a time base of about 1.4 yr, the accuracy of FORS2 proper motions is 0.10 mas yr−1 (Paper I), which improves to 0.01–0.03 mas yr−1 for the objects monitored over 5–7 yr. Because the accuracy of differential FORS2 proper motions and parallaxes is currently better, we do not use DR2 as an external source of ξ values at this time. However, we use Gaia DR2 as an astrometric flat-field calibrator, see Sect. 6.2. The differential chromatic refraction (DCR) parameters ρ, d can be constrained using stellar spectra (e.g., Garcia et al. 2017), however for field stars these are usually unavailable.
The measured displacement of a star from the initial position x0, y0 is described by the sum of functions Φ(x, y) and ϕ(ξ, ν), or
This system is solved using reference stars i ∈ ω, where ω is the reference space that includes either chip 1 only or stars of both chips within Ropt distance from the target. Equation (1) is solved with the weights Pi, m assigned according to the measurement uncertainties σi, m of the star i in the frame m. In the context of this investigation, additional terms 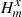 ,
, 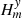 are included as the potential displacement of chip 2 relative to chip 1 along the coordinate axes in exposure m. In the primary astrometric reduction, the solution of Eq. (1) is derived assuming H = 0, and later, during the second phase of the investigation, the terms Hm are extracted by analyzing the model residuals
are included as the potential displacement of chip 2 relative to chip 1 along the coordinate axes in exposure m. In the primary astrometric reduction, the solution of Eq. (1) is derived assuming H = 0, and later, during the second phase of the investigation, the terms Hm are extracted by analyzing the model residuals 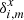 ,
, 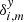 and the peculiar properties of the ξ parameters. The step function U(y)
and the peculiar properties of the ξ parameters. The step function U(y)
is introduced to limit the application of the H function to one chip only. The system Eq. (1) is solved with S × N′ conditions
on the parameters ξ in the normalizing parameter space ω*, which does not necessarily coincide with ω. When s is fixed, Eq. (3) can be understood as the formal expression of the fact that the least-squares residuals (which are recognized here as ξi) are orthogonal to each of w = 1…N′ basic functions fw of some conditional system of i = 1…N measurements obtained with the weights 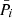 . In this interpretation, the corresponding system of conditions is
. In this interpretation, the corresponding system of conditions is 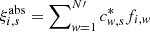 , where ξabs are the parameters given in some external (e.g., absolute) system. Consequently,
, where ξabs are the parameters given in some external (e.g., absolute) system. Consequently, 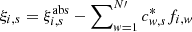 represents the fit residuals (Lazorenko et al. 2009). This establishes the relationships between the system of relative parameters ξ, the absolute parameters ξabs, fit constants c*, the weights
represents the fit residuals (Lazorenko et al. 2009). This establishes the relationships between the system of relative parameters ξ, the absolute parameters ξabs, fit constants c*, the weights 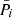 , and the functions fw.
, and the functions fw.
One property of the derived parameters ξ is that the weighted sum of differential proper motions is zero, that they do not change systematically across the FoV, and that they do not correlate with x, y, xy or any other function fw, which is expressed by 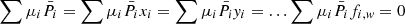 . Equation (3) is applied with arbitrary weights
. Equation (3) is applied with arbitrary weights 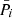 that define the system of relative parameters ξ. In practice, we set
that define the system of relative parameters ξ. In practice, we set 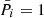 for sufficiently bright stars and
for sufficiently bright stars and 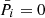 for ∼10% for fainter reference stars to exclude wildly scattered values ξ of these stars. For the standard astrometric reduction, we usually set ω* = ω, but in this investigation, ω* space can be expanded over ω, see Table 2.
for ∼10% for fainter reference stars to exclude wildly scattered values ξ of these stars. For the standard astrometric reduction, we usually set ω* = ω, but in this investigation, ω* space can be expanded over ω, see Table 2.
Summary of the spaces ω, ω*, and flags λ that specifies different modifications of astrometric reduction, and the estimated displacement of chip 2 along the X-axis from 2012.0 to 2017.5.
The model Eq. (1) with constraints Eq. (3) is solved iteratively as described in Lazorenko et al. (2009), in turn deriving cw, m within each single image m at some fixed ξi, s. With these cw, m, we then update ξi, s separately for each single reference star i. Here we omit the details of the reduction and note only that as soon as iterations converge and the geometric distortions Φm of each frame m are found, the ith star’s astrometric parameters ξi, s are derived from the subsystem of equations
where 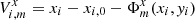 , and
, and 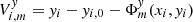 are the stellar displacements corrected for Φm. This system involves m = 1…M measurements of the star i and is solved considering both x and y data simultaneously, which also yields the residuals
are the stellar displacements corrected for Φm. This system involves m = 1…M measurements of the star i and is solved considering both x and y data simultaneously, which also yields the residuals 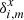 ,
, 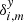 . Because
. Because 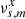 ,
, 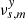 are the basic functions of the system Eq. (4) solved by the least-squares fit, the residuals
are the basic functions of the system Eq. (4) solved by the least-squares fit, the residuals 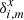 ,
, 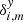 are orthogonal to these functions. In particular, they should have no linear dependence on time. Similarly, the residuals
are orthogonal to these functions. In particular, they should have no linear dependence on time. Similarly, the residuals 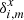 ,
, 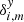 , which are orthogonal to the basic functions fi, w of Eq. (1), should have no systematic trend along X or Y. The frame residuals of reference stars, converted into the epoch residuals
, which are orthogonal to the basic functions fi, w of Eq. (1), should have no systematic trend along X or Y. The frame residuals of reference stars, converted into the epoch residuals 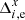 and
and 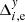 , can display some correlation pattern that is caused by systematic errors, which provides useful information on these errors. In particular, the investigation of the epoch residuals derived under the assumption that H(t) = 0 allows us to reveal the time-dependent relative chip motion.
, can display some correlation pattern that is caused by systematic errors, which provides useful information on these errors. In particular, the investigation of the epoch residuals derived under the assumption that H(t) = 0 allows us to reveal the time-dependent relative chip motion.
3.2. RF and CAL files
The principal results of the astrometric reduction are the parameters ξi, s and the epoch residuals 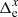 ,
, 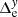 derived for the star i that is the target object. In addition, we obtain the same quantities for every reference star within a circular reference field centered on the target. These data in 20 sky fields are referred to as the reference frame (RF) files. The uncertainties of the RF dataset change across the field and are smallest at its center. At the outer boundaries, the astrometric accuracy degrades because the uncertainty of the Φ(x, y) determination increases.
derived for the star i that is the target object. In addition, we obtain the same quantities for every reference star within a circular reference field centered on the target. These data in 20 sky fields are referred to as the reference frame (RF) files. The uncertainties of the RF dataset change across the field and are smallest at its center. At the outer boundaries, the astrometric accuracy degrades because the uncertainty of the Φ(x, y) determination increases.
Stars in the RF files do not cover the full FoV for typical sizes of Ropt. For calibration purposes we need to know the astrometric parameters and the epoch residuals of all stars in the full FoV. We achieve this by repeating the basic reduction for each of i = 1…N field stars, setting it as the target object. The results are saved in the calibration (CAL) files that contain results for the single central star only. In CAL files the reference star data are disregarded because the precision is reduced. The CAL files include most stars in the FoV and therefore contain about three times more stars than RF files.
3.3. Response properties of the astrometric model
The model defined by Eqs. (1)–(3) can be treated as a filtering system that absorbs some part of a signal at its entrance because of the least-squares fit of data. Therefore we should not expect that the chip displacement H(t) that affects the measurements is fully reflected in the epoch residuals. We demonstrate this with the help of reference stars around the brown dwarf DENIS J125310.8−570924 (hereafter dw14), for which we obtained Ne = 23 epochs over about seven years. We introduced a step change U(y) = 1 in the measurements xi, e obtained on 17 February 2012 and performed our reduction process. Figure 1 shows that the computed residuals differ significantly from the introduced step change. The residuals have a discontinuity at y = 1000 px with an offset amplitude of 1 between the chips. The scatter of individual 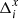 values relative to their systematic change as a function of y is related to a weak dependence of
values relative to their systematic change as a function of y is related to a weak dependence of 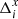 on x, and a small asymmetry relative to the detector center y = 1000 px is due to the location of the reference field center ∼73 px off the gap between the chips.
on x, and a small asymmetry relative to the detector center y = 1000 px is due to the location of the reference field center ∼73 px off the gap between the chips.
 |
Fig. 1. Simulation of the astrometric model response to a step change U(y) in the position of chip 2 for the example sky field of dw14 offset by 73 px from the detector center. Dots show the response in the epoch residuals |
The solid curves in Fig. 1 correspond to the systematic change of the residuals if the reduction is made with Pi, m = 1. The restriction Eq. (3) leads to ξ parameters that are orthogonal to the functions f with the weights 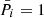 , that is, the response characteristics of ξ and Δi derived with Pi, m = 1 are exactly equivalent. In this interpretation, solid curves represent the model response WRF in ξ (e.g., in proper motions) to the step change of these parameters for all chip 2 stars by U(y). The response WRF corresponds to RF files or to the proper motions of reference stars in a field centered at the target.
, that is, the response characteristics of ξ and Δi derived with Pi, m = 1 are exactly equivalent. In this interpretation, solid curves represent the model response WRF in ξ (e.g., in proper motions) to the step change of these parameters for all chip 2 stars by U(y). The response WRF corresponds to RF files or to the proper motions of reference stars in a field centered at the target.
The dashed lines in Fig. 1 correspond to a reference field that is symmetric around the detector center y = 1000 px and with Pi, m = 1 set in Eq. (1). This option approximately corresponds to the averaging of response functions over many circular reference fields with centers that cover most of the FoV, and we therefore used it as the response function WCAL for the CAL files. This function is nearly antisymmetric relative to y = 1000 px, where it is equal to ±0.5. Below we discuss the application of the response functions to the effects in the epoch residuals and in proper motions. The above examples demonstrate that a step signal U(y) is associated with a specific discontinuity pattern in the epoch residuals or proper motions.
4. Observational evidence of the chip motion
First evidence of the FORS2 chip mosaic instability was found in the epoch residuals of reference stars within the same reference field, but located in different chips (Paper I). As an example, Fig. 2 shows the residuals 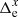 in RA of stars in the sky field of dw14. The residuals are shown separately for the stars imaged in each chip and for a few bright stars only that were measured with a single-epoch uncertainty of 0.1–0.5 mas, or about 1–3 millipixels (mpx). These residuals do not show a linear trend in time because the astrometric model includes the proper motion as a model parameter. However, a significant time-dependent variation with opposite sign in both chips is evident.
in RA of stars in the sky field of dw14. The residuals are shown separately for the stars imaged in each chip and for a few bright stars only that were measured with a single-epoch uncertainty of 0.1–0.5 mas, or about 1–3 millipixels (mpx). These residuals do not show a linear trend in time because the astrometric model includes the proper motion as a model parameter. However, a significant time-dependent variation with opposite sign in both chips is evident.
 |
Fig. 2. Epoch positional residuals |
In Paper I, Sect. 4.3.2, this effect was explained by the relative chip displacement without deformation and rotation. The motion of chips along the CCD X-axis for each epoch e was described by the quantity gx, e equal to the systematic difference
in the measured positional residuals of stars in chip 2 and chip 1 at the division line (y = 1000 px). The motion gy, e along Dec (Y-axis of CCD) was defined similarly as a difference of 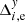 values.
values.
Figure 3 shows the typical dependence of the positional residuals 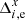 on y at the example epoch on 17 February 2012 for dw14. It has a discontinuity at y = 1000 px and is approximated by the empirical function
on y at the example epoch on 17 February 2012 for dw14. It has a discontinuity at y = 1000 px and is approximated by the empirical function
 |
Fig. 3. Individual epoch positional residuals |
where 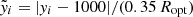 is the normalized distance from the chip gap, and a positive (negative) sign is used for stars in chip 2 (chip 1). The fit function (6) shown in Fig. 3 by solid lines nearly coincides with the response function WCAL(y) (dashed) reproduced from Fig. 1 and normalized to the offset amplitude g = 19.5 ± 0.6 mpx in the measured positional residuals. The estimates of gx, e in x and gy, e in y were derived for each epoch e = 1…Ne by a least-squares fit of function (6) to the residuals
is the normalized distance from the chip gap, and a positive (negative) sign is used for stars in chip 2 (chip 1). The fit function (6) shown in Fig. 3 by solid lines nearly coincides with the response function WCAL(y) (dashed) reproduced from Fig. 1 and normalized to the offset amplitude g = 19.5 ± 0.6 mpx in the measured positional residuals. The estimates of gx, e in x and gy, e in y were derived for each epoch e = 1…Ne by a least-squares fit of function (6) to the residuals 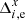 ,
, 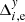 . The average uncertainty in the determination of the offset g is σg = 1.3 mpx.
. The average uncertainty in the determination of the offset g is σg = 1.3 mpx.
The change in gx, e values with time for all sky fields is shown in Fig. 4. The behavior is different for short- (one to one and a half years), medium- (three years), and long-duration (seven years) datasets, which is expected: the astrometric reduction uses the model Eq. (1), which fits the measurements of every star i by the linear change in time caused by proper motion, hence the residuals 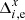 and
and 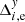 do not change linearly in time. The set of values g for each star field derived later by the least-squares fit Eq. (6) of these residuals are linear combinations of these residuals. Therefore, a set of ge values for a given star field with its observation time-span also has zero linear dependence on time within the corresponding time intervals, as seen in Fig. 4. In particular, this explains why the g values for short-duration datasets show no trend in 2010–2012, while that is not the case for the longer-duration datasets.
do not change linearly in time. The set of values g for each star field derived later by the least-squares fit Eq. (6) of these residuals are linear combinations of these residuals. Therefore, a set of ge values for a given star field with its observation time-span also has zero linear dependence on time within the corresponding time intervals, as seen in Fig. 4. In particular, this explains why the g values for short-duration datasets show no trend in 2010–2012, while that is not the case for the longer-duration datasets.
 |
Fig. 4. Change in time of chip offset gx, e for sky fields with short (filled dots, six sky fields), medium (crosses, seven fields), and long (open circles, seven fields) observation time-span. The vertical line marks the time of an event that caused a 20–50 mpx offset in gx, e for four fields observed on 20–24 November 2011 (squares). |
The vertical line in Fig. 4 marks the time of a large fluctuation on 20–24 November 2011 in four fields. This event is even more prominent in the reduced residuals (Fig. 7).
The discontinuity of WCAL(y) type is seen in all ξ parameters, for instance, in the parallaxes (cf. Paper I, Fig. 6). Figure 5 shows the distribution of the CAL dataset proper motions for the example case of dw14, which is well approximated by the WCAL(y) function with an offset amplitude of Δμ = −56.0 ± 5.0 mpx yr−1. The offset terms g and Δμ can be caused by the RCM, but the nonzero offset values for the other parameters ξ are unphysical; they represent the formal fit solution of a model with correlated parameters.
 |
Fig. 5. Same as Fig. 3, but for proper motions: the approximation of Eq. (6) (solid lines) and the model response WCAL(y) to the step change Δμ = −56.0 mpx yr−1 in the proper motions of stars in chip 2 (dashed lines). |
5. Chip motion retrieved from the calibration files
The definition in Eq. (5) means that the parameter g incorporates information on the epoch residuals of all stars near the chip gap. It is therefore convenient to represent the full star sample for a particular sky field z by one single “equivalent” star that is located right at the chip gap on chip 2 and that has the epoch residuals gx, z, e, gy, z, e. For this star, the equivalent proper motions Δμx, z, Δμy, z were derived by fitting individual stellar motions μx, z, i, μy, z, i with the function WCAL(y). The equivalent star displacement at epoch e relative to time t = 0 is
The values of V can be considered as the measurements in the right side of the model Eq. (4), therefore we rewrite this model into a system of Ne × Ndw × 2 equations,
where z = 1…Ndw is the sky field index, 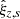 are the formal fit parameters (offsets
are the formal fit parameters (offsets 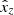 ,
, 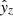 , proper motion
, proper motion 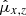 ,
, 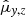 , etc.), H(te) is the smooth component of the RCM, and δHz, e are the residuals of the fit, which include the measurement errors and the irregular component of the RCM. The fit parameters
, etc.), H(te) is the smooth component of the RCM, and δHz, e are the residuals of the fit, which include the measurement errors and the irregular component of the RCM. The fit parameters 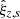 are the corrections to the ξ values in Eq. (1) derived from the primary astrometric solution with H(t) = 0. The system of Eq. (8) allows us to extract H(t). When applied to a single sky field, Eq. (8) returns the trivial solution
are the corrections to the ξ values in Eq. (1) derived from the primary astrometric solution with H(t) = 0. The system of Eq. (8) allows us to extract H(t). When applied to a single sky field, Eq. (8) returns the trivial solution 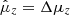 , δHz, e = gz, e, and H(te) = 0. A meaningful solution is found by applying it to all fields. For the function H(t) we adopted the low-order polynomial approximation
, δHz, e = gz, e, and H(te) = 0. A meaningful solution is found by applying it to all fields. For the function H(t) we adopted the low-order polynomial approximation
with n = 3 and n = 1 for the measurements along X and Y, respectively. To separate the fully correlated proper motion and h1 terms, we required that the sum of proper motions taken over all stars and fields is zero, that is, 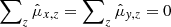 . With a similar restriction on the stellar position offsets
. With a similar restriction on the stellar position offsets 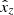 and
and 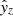 , we separated these terms and h0. Thus, the systematic position change in time is fully included in the function H(t), whereas the parameters
, we separated these terms and h0. Thus, the systematic position change in time is fully included in the function H(t), whereas the parameters 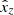 ,
, 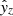 ,
, 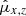 , and
, and 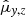 have an average value of zero.
have an average value of zero.
Figure 6 shows the unreduced displacements gx, z, e + Δμx, zte, which reveals significant changes of the position of chip 2 relative to chip 1, which reaches offset of 0.2–0.3 pixels in 2016–2018. These displacements are measured consistently in several fields and can therefore not be caused by particular stellar motions. The solution H(t) for the motion along the X-axis is derived from Eq. (8) as a cubic function of time (solid line in Fig. 6). It has an approximately linear segment between 2012 and 2017 where the rate is ∼50 mpx yr−1. Along the Y-axis, the motion is approximately linear at a rate of ∼10 mpx yr−1.
 |
Fig. 6. Motion of chip 2 along the X-axis (lower panel) relative to a reference frame defined by stars in both chips: the unreduced displacements |
Figure 7 presents the change in time of the fit residuals δHz, e for short-, medium-, and long-duration datasets. The residual distribution is approximately random with an rms of 4.3 and 3.8 mpx along the X- and Y-axes, respectively. Weak correlations and departures from the cubic model Eq. (9) can be seen, for example, close to 2017.0. In general, we did not find any strong deviations on timescales of 1–4 days, which means that the RCM is quite smooth in time.
 |
Fig. 7. Fit residuals δH between the measured and the position of chip 2 according to the model Eq. (8) relative to chip 1 for each epoch and the sky fields with a short (filled dots), medium (crosses), and long (open circles) duration of observations. An impulse jump for four fields obtained on 20–24 November 2011 is marked by squares. |
The only strong variation on timescales of days is found for four fields observed on 20, 22, and 24 November 2011. The large 20–50 mpx offsets occurred within one day because two fields had been observed on November 19 with normal results. This event was probably caused by an intervention on the instrument as part of regular maintenance. Upon our enquiry, the ESO User Support Department confirmed that the FORS2 CCDs were switched on 28 November 2011 and that the observatory records do not indicate an earthquake recovery procedure or FORS2 cryostat warm-up or cool-down cycle on 20–24 November 2011, but that the exact dates of such interventions can sometimes be uncertain.
6. Alternative measurements of the chip motion
In the past section we retrieved the best precise displacement history of RCM using extensive data collected in the calibration files (the CAL dataset derived from multiple reference frames covering all FoVs), and with a reference frame ω set by stars in both chips. In order to confirm this primary result, we investigated the RCM by making several modifications to our astrometric solution. Instead of CAL files, we now used the files of RF datasets (stars of a single reference frame ω per each sky field) and additionally restricted ω space to chip 1. The motion of chip 2 stars then evidently reproduces the RCM effect. However, we found that a robust astrometric solution requires use of the normalizing parameter space ω* expanded on both chips, in a field within Ropt distance from the dwarf. We also had to update the system of the normalizing conditions Eq. (3) by a model Eq. (10) with a flag λ that allows for two options of the normalization (for details, see Sect. 6.1.1).
Our computations confirm that the RCM does not depend significantly on the choice of the reference frame. Table 2 summarizes the results of determining the RCM with these alternative approaches.
6.1. Motion of chip 2 derived in the reference frame of chip 1
To measure the displacements of chip 2, we performed the astrometric reduction Eqs. (1)–(4) with the reference space ω limited to chip 1 by excluding its segment ω2 located on chip 2. We first also excluded ω2 from ω* (Sect. 6.1.1), and we revised this option in Sect. 6.1.2.
6.1.1. Systematic difference of proper motions between chips
The dependence of the solution coefficients ξ on y, which we illustrate in Fig. 8 for proper motions, is very different from the response function W(y) shown in Fig. 5. The amplitude of the discontinuity Δμx, however, is close to that derived with the calibration files.
 |
Fig. 8. Proper motions μx in the dw14 field derived relative to chip 1 (gray filled circles) and when the astrometric parameters are derived with Eq. (10) (open circles), which allows for a step change between the chips of Δμx = −56.0 mpx yr−1. The circle size is proportional to the stellar brightness. |
For stars in chip 2 (y < 1000 px), Fig. 8 shows a clear trend of μx, which is natural because the restrictions Eq. (4) do not apply to stars in chip 2 in this case. A flat dependence of ξ on chip 2 is obtained by expanding ω* over this chip (i.e., by including ω2 in ω*) and allowing for a Δξs step change in the model Eq. (3):
Here
is a new parameter that corresponds to the step change of ξ in chip 2. The λ ∈ [0, 1] parameter allows us to switch this addition on and off. This new model includes the offsets (Δx, Δy, Δμx, Δμy, Δρ, Δd, Δϖ) of the parameter values between chips and excludes their systematic change across the FoV.
Figure 8 shows that this approach works because the distribution of μx along Y is flat, except for the step change of Δμx = −56.0 ± 5.0 mpx yr−1, which is very similar to that obtained from the calibration files, and because the proper motions computed with Eq. (10) (open circles) and when the ω* space is restricted to chip 1 (gray circles) are nearly identical for y > 1000 px.
6.1.2. Motion of individual stars in the lower chip
With a reference frame anchored in chip 1, the space ω* expanded to both chips, and the restrictions of Eq. (10) with λ = 1, we obtained a well-behaved step change in the parameters ξ (a typical example is shown in Fig. 8 with open circles). With this model, we ran a primary reduction with Eq. (1) and computed the displacements
from the initial position of each star. Here Δz, i, e are the positional residuals, and μz, i are the proper motions of the stars i in the field z. The displacements Vz, i, e do not show any systematic trending in time for stars in the upper chip, but reveal a clear trend in the lower chip, especially in 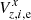 . Figure 9 shows the displacements
. Figure 9 shows the displacements 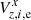 for 15 bright but not saturated stars in each field within a narrow 750 < y < 1000 px area close to the chip edge. We defined homogeneous star samples and discarded stars with proper motions μx, μy that deviated strongly from the average Δμx, Δμy values in a given field.
for 15 bright but not saturated stars in each field within a narrow 750 < y < 1000 px area close to the chip edge. We defined homogeneous star samples and discarded stars with proper motions μx, μy that deviated strongly from the average Δμx, Δμy values in a given field.
 |
Fig. 9. Motion of chip 2 relative to the reference frame of the upper chip: unreduced displacements Vz, i, e along the X- and Y-axes of 15 bright lower chip stars in each sky field at each epoch (small dots). The same after correction for the residual parameters |
The sample of data points Vz, i, e presented here directly describes the motion of stars in chip 2 relative to the reference frame anchored in chip 1. Because the displacements are synchronous in all fields, we attribute this effect to the real RCM rather than to peculiar motions of stars. We directly fit the full sample of individual stellar displacements 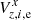 along the X-axis with a cubic function of time and obtained a function (dashed line in Fig. 9) that is similar in shape to the previous estimate of H(t) in Fig. 6.
along the X-axis with a cubic function of time and obtained a function (dashed line in Fig. 9) that is similar in shape to the previous estimate of H(t) in Fig. 6.
The values of Vz, i, e vary as a result of the intrinsic proper motions of individual stars, and therefore Fig. 9 appears noisy. To obtain clearer results, we had to mitigate the impact of proper motions. For this purpose we applied Eq. (8) as a secondary reduction model and replaced the right-hand side of the equations by 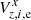 and
and 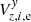 from Eq. (12). This created a system of 15 × Ne × Ndw × 2 equations with polynomial order n = 3 in Hx(t) and n = 1 in Hy(t). We solved it under the s = 1…7 restrictions of ∑z, iξz, i, s = 0. The obtained epoch displacements
from Eq. (12). This created a system of 15 × Ne × Ndw × 2 equations with polynomial order n = 3 in Hx(t) and n = 1 in Hy(t). We solved it under the s = 1…7 restrictions of ∑z, iξz, i, s = 0. The obtained epoch displacements 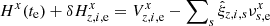 shown by the solid dots in Fig. 9 differ from the raw displacements
shown by the solid dots in Fig. 9 differ from the raw displacements 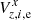 only by the single term
only by the single term 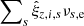 . These new estimates are tightly correlated with the direct approximation of
. These new estimates are tightly correlated with the direct approximation of 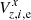 ,
, 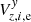 obtained from 15 bright stars (dashed lines in Fig. 9). The scatter decreased from the initial ±200 mpx in Vz, e values to ∼20 mpx in the residuals δHi, e, mainly because we subtracted individual stellar proper motions from the residuals. We found that the RCM is common for all sky fields, as expected, and that deviations from the smooth change in time are smaller than ∼20 mpx.
obtained from 15 bright stars (dashed lines in Fig. 9). The scatter decreased from the initial ±200 mpx in Vz, e values to ∼20 mpx in the residuals δHi, e, mainly because we subtracted individual stellar proper motions from the residuals. We found that the RCM is common for all sky fields, as expected, and that deviations from the smooth change in time are smaller than ∼20 mpx.
6.1.3. Chip motion based on the properties of the stellar group
To improve upon the results when 15 stars were used in the previous Section, we formed an equivalent star for each sky field z in the way described in Sect. 5. This artificial star was positioned at the edge of chip 2, represents an ensemble of stars, and is characterized by the displacements
measured relative to the reference frame of chip 1. Here, Δz, e are the positional residuals, and Δμz are the proper motions of the equivalent star in a field z. In Sect. 5, similar estimates were derived from the fit of individual stellar parameters and their variation along Y with the functions WCAL(y) and G(y). We again used a step function (Fig. 8) fit of individual stars corresponding to the parameter change along Y, derived the estimates at y = 1000 px separately for each chip, and finally obtained Δz, e and Δμz as the difference between the results in chip 2 and chip 1.
Then, using the model Eq. (8), we derived the residual fit parameters 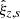 , the functions Hx(t), Hy(t), and the fit residuals
, the functions Hx(t), Hy(t), and the fit residuals 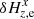 ,
, 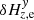 , whose rms of 10 mpx is twice smaller than when individual stars are used (Sect. 6.1.2). The instant displacements H(t)+δHz, e for each sky field and epoch are shown in Fig. 10 with open circles. The function Hx(t) (solid curve) is close to those obtained in the previous sections with 15 bright stars per field, and to Hx(t) derived using both chips as reference field (Fig. 6). The differences between the estimates of Hy(t) are small considering the uncertainty in proper motions. For both reduction versions the displacement amplitude of chip 2 is ∼0.25 px.
, whose rms of 10 mpx is twice smaller than when individual stars are used (Sect. 6.1.2). The instant displacements H(t)+δHz, e for each sky field and epoch are shown in Fig. 10 with open circles. The function Hx(t) (solid curve) is close to those obtained in the previous sections with 15 bright stars per field, and to Hx(t) derived using both chips as reference field (Fig. 6). The differences between the estimates of Hy(t) are small considering the uncertainty in proper motions. For both reduction versions the displacement amplitude of chip 2 is ∼0.25 px.
 |
Fig. 10. Motion of chip 2 along RA (lower panel) and Dec (upper panel) relative to chip 1. Each curve is the solution for H(t) derived with the models in Table 2, as indicated by the legend. The instant motion estimate H(t)+δHz, e for model 2 (open circles) shows the scatter in the RCM determination for individual fields and epochs. The step change in four fields observed on 20–24 November 2011 and derived with approaches 2 and 4 is marked by squares. |
We obtained one more estimate of H(t) with the reference frame anchored in chip 1, where we used the full FoV as a space ω* for the normalization Eqs. (10) and (11) of parameters ξ, but instead of λ = 1, we set λ = 0 (Nr.3 in Table 2). Now, the parameters ξ follow a change that is approximated by the functions WCAL(y) or G(y). Using these functions to fit the individual stellar parameters, we formed the equivalent stars for each sky field described by the group parameters Δz, e and Δμz. A subsequent reduction derived the model motion H(t) that is shown by the dash-dotted curve in Fig. 6 and ∼10 mpx for the rms of fit residuals δHz, e.
6.2. Using Gaia DR2 to estimate the chip motion
We used the Gaia DR2 catalog (Lindegren et al. 2018; Gaia Collaboration 2018) as an absolute calibrator to convert differential FORS2 astrometry into the ICRF coordinate system (ICRS). In this system, the RCM is apparent as a change in the astrometric zero-points of the CCD chips. To measure this effect, we converted FORS2 into ICRS at every observation epoch. For the seven fields with the longest time-span, we have 147 epoch measurements, thus we obtained 147 estimates of the relative chip position in 2010–2018. The CCD epoch positions
converted into ICRS are formed from the ith star position xz, i, 0, yz, i, 0 in the reference image (m = 0) and the displacements 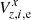 ,
, 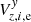 computed with Eq. (12) for each sky field z. Thus, we used Δz, e and Δμz as previously derived with the astrometric reduction based on the reference frame ω limited to chip 1, and the space ω* set to all FoVs (Nr. 4 in Table 2).
computed with Eq. (12) for each sky field z. Thus, we used Δz, e and Δμz as previously derived with the astrometric reduction based on the reference frame ω limited to chip 1, and the space ω* set to all FoVs (Nr. 4 in Table 2).
The zero-point estimates potentially depend on the exact sample of stars used at a given epoch. We mitigated this by using the stars that are common to all epochs. This common star list was derived at the first identification between FORS2 and Gaia at the epoch nearest to the Gaia reference epoch TDR2 = 2015.5. The identification procedure was similar to that described in Lazorenko & Sahlmann (2017, 2018), where we used full bivariate polynomials of the maximum power n for the transformation between catalogs. We used stars in both chips for this transformation. To take the relative displacement of chip 2 into account, we expanded these transformation functions with two additional free parameters 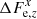 and
and 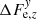 that we added to the zero-points of chip 2 only and set to zero for chip 1. This model integrates information on the relative position of the reference frames and thus on the relative motion of chips. Upon the estimation of ΔFe, z, we find the instant displacements
that we added to the zero-points of chip 2 only and set to zero for chip 1. This model integrates information on the relative position of the reference frames and thus on the relative motion of chips. Upon the estimation of ΔFe, z, we find the instant displacements
where 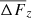 is the average offset in a field z on 2011–2012. We tested all polynomial orders n up to the maximum n = 7, and its best-fit value was found using an F-test for the rejection of insignificant coefficients as described in Lazorenko & Sahlmann (2017). We found that n = 5 fit most fields best.
is the average offset in a field z on 2011–2012. We tested all polynomial orders n up to the maximum n = 7, and its best-fit value was found using an F-test for the rejection of insignificant coefficients as described in Lazorenko & Sahlmann (2017). We found that n = 5 fit most fields best.
We set the cross-match radius to 3.3σ1, where σ1 is the model uncertainty that includes all known errors of FORS2 and Gaia DR2, and is 1–2 mas for G = 16–19 mag stars at the epochs near TDR2. In different fields we identified between 43 to 206 stars that FORS2 and DR2 had in common. For the epochs ±0.5 yr within TDR2 = 2015.5, we obtained the unbiased rms of individual differences between FORS2 and Gaia positions σF − G = 1 − 2.5 mas, which is close to the expected value of σ1. The dominant error component of σ1 is the uncertainty of Gaia proper motions of about 0.3–1 mas yr−1. For this reason, σF − G is minimum on TDR2 and increases to 4–7 mas at the 2011 and 2017 epochs.
In some fields we found fewer than expected cross-matched stars in chip 2, and the number was too low to determine ΔFe, z reliably. Better results were obtained when the common star list was created from the identification made at the first epoch of the sky field exposure (2011–2012). For these epochs, which are distant from TDR2, a higher value of σ1 and thus a wider identification window favorably increased the common star number. With this approach, the σF − G value increased slightly but the uncertainty in the determination of ΔFe, z improved significantly in some fields. Finally, we obtained the values ΔFe, z and computed the instant motion of chip 2 Hz(te) that we present in Fig. 11 with Eq. (15). These estimates can be approximated by the polynomials
 |
Fig. 11. Motion of chip 2 along RA (lower panel) and Dec (upper panel) relative to the upper chip derived using Gaia DR2: instant estimates Hz(te)+δHz, e for individual sky fields z and epochs e (open circles) and the smooth fit functions H(t). |
with uncertainties of ±0.08 and ±0.04 mpx for the linear coefficients in RA and Dec, respectively, and t is measured relative to TDR2. In 2017.5, Hx = −318 mpx and Hy = 67 mpx, which matches the estimates derived with the other approaches (Table 2) relatively well.
7. Calibration of and correction for the chip motion
The relative displacement of the chips directly affects the position of the target by adding a bias to the epoch residuals Δz, e (see Fig. 3). According to Eq. (6), the bias value G(y) depends on the amplitude g, the target distance from the division line between chips, and the reference field size Ropt. Typically, gx = 10 − 20 mpx and Ropt = 500 − 1000 px, which for a target located at y = 1100 px results in an RA bias of ≈3–6 mpx or 0.4–0.7 mas at a single epoch. This is a rough estimate for the rms variation of the bias added to the epoch residuals, which we denote as σbias and which is very large in comparison to the FORS2 astrometric uncertainty of ∼0.1 mas. In the extreme events of g ≈ 60 mpx, the bias in these epoch residuals can reach 2 mas. This bias therefore needs to be identified, modeled, and removed.
The bias can be removed in two ways: either using the discrete estimates ge derived from the calibration files, or using the analytic approximations for H(t) derived in Sects. 6.1 and 6.2. In the first case, incorrectly assuming that the RCM is a random process that is not correlated in time, we expect that H(te) = ge, so that a simple correction xm − gx, e, xm − gy, e applied to the measurements of stars in chip 2 eliminates the effect.
However, the values of H(te) are clearly correlated and reflect the mostly smooth motion of the chips. The models of H(t) derived in Sects. 5 and 6.1 are sums of the linear and nonlinear components H23(t) with quadratic and cubic (t2 and t3) terms. The linear component is included in the proper motions of stars and therefore does not affect the computation of the epoch residuals and g values. The following discussion therefore does not concern the RCM along Y, which is linear in time.
The component H23(t) produces RCM variations of ±20 − 50 mpx amplitude and correlated on a 1–2 yr timescale (Fig. 12). The astrometric reduction redistributes the H23(t) variations across the model parameters ξ and the epoch residuals. Moreover, because some sky fields are observed within a restricted time interval Δt, instead of H23(t), we detected only the remnants 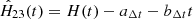 of this function after subtracting the linear fit aΔt + bΔtt over the time interval Δt specific to a field. The shape of H23(t) therefore depends on Δt, and the variation amplitude increases with Δt. Thus, H(t) is not fully reflected in the epoch residuals, and we consequently measure a reduced value of ge.
of this function after subtracting the linear fit aΔt + bΔtt over the time interval Δt specific to a field. The shape of H23(t) therefore depends on Δt, and the variation amplitude increases with Δt. Thus, H(t) is not fully reflected in the epoch residuals, and we consequently measure a reduced value of ge.
 |
Fig. 12. Nonlinear component |
This is illustrated with Fig. 13, where we compare the measured gx, z, e values derived from the CAL files for each sky field z and epoch e, and 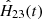 derived using Gaia DR2 and explicitly set by Eq. (16) for H(t). This graph shows that the g values are on average lower than the expected
derived using Gaia DR2 and explicitly set by Eq. (16) for H(t). This graph shows that the g values are on average lower than the expected 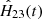 values. We find a linear dependence
values. We find a linear dependence
 |
Fig. 13. Correlation between the epoch displacements in chip 2, gx, along RA in 20 sky fields derived with the standard reduction (Nr.1 in Table 2) and the nonlinear component of the chip motion |
between these values with a slope of K = 0.63 ± 0.03. Thus, given the measured ge value, the statistical RCM is 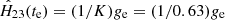 , which is close to the empirical (1/0.70)ge estimate derived in Paper I. Similar estimates for K were obtained with other models of RCM, for instance, 0.62 ± 0.03 and 0.58 ± 0.02 for solutions 2 and 3 of Table 2. With the correction
, which is close to the empirical (1/0.70)ge estimate derived in Paper I. Similar estimates for K were obtained with other models of RCM, for instance, 0.62 ± 0.03 and 0.58 ± 0.02 for solutions 2 and 3 of Table 2. With the correction
applied to the measurements of stars in chip 2, the systematic change in residuals with Y similar to that shown in Fig. 3 is removed (Paper I, Sect. 4.3.2, Fig. 5). Given the average uncertainty σg = 1.3 mpx of the g determination, the effect of RCM in the epoch residuals of targets at y0 = 1100 px decreases by one order of magnitude from the initial σbias = 3–6 mpx to σbias = K−1σgg−1G(y0) ≈ 0.6 mpx or ±0.07 mas. This residual bias is acceptable for FORS2 astrometry.
Alternatively, the RCM can be removed directly using one of the derived model functions H(t). As explained above, it is sufficient to apply these corrections for the nonlinear motion components only because the linear component (i.e., the case of Dec) does not affect the epoch residuals. In the previous sections we obtained a few estimates of H(t) whose nonlinear components H23(te) (Fig. 12) are slightly dispersed, and we formed their average ⟨H⟩ to obtain more reliable results. The rms of the individual H23(te) relative to ⟨H⟩ is 6.1 mpx, therefore the formal uncertainty of ⟨H⟩ is σ′≈3.1 mpx. We can now correct for RCM by applying the correction
to stars in chip 2. For stars at y0 = 1100 px, the bias is expected to decrease to σbias = σ′g−1G(y0) ≈ ± 0.12 mas, which is larger than the residual bias obtained when ge is used.
We verified the above estimates with the complete astrometric reduction of dw14 by including and excluding the RCM corrections Eqs. (18) and (19). We applied a reduction model based on Eqs. (1) and (3) (or, equivalently, Eq. (10) with λ = 0) using circular ω and ω* spaces of Ropt = 711 px radius centered at dw14. This is a standard model for astrometric reduction on FORS2 (Sahlmann et al. 2014; Lazorenko et al. 2014), but now we take into consideration that ω and ω* spaces are fragmented into two sections that are related to different chips.
Without the RCM correction, the astrometric reduction produced the epoch residuals 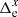 shown in Fig. 14 by gray circles for the example epoch on 17 February 2012, which can be compared to Fig. 3 at the same epoch, but based on the calibration files (Sect. 3.2). The plots are similar in shape, but the distribution of
shown in Fig. 14 by gray circles for the example epoch on 17 February 2012, which can be compared to Fig. 3 at the same epoch, but based on the calibration files (Sect. 3.2). The plots are similar in shape, but the distribution of 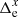 in Fig. 14 is now not exactly symmetric relative to y = 1000 px because the reference field center is 73 px off this line. Moreover, the number of stars is twice smaller than in the calibration files because of the limited Ropt size.
in Fig. 14 is now not exactly symmetric relative to y = 1000 px because the reference field center is 73 px off this line. Moreover, the number of stars is twice smaller than in the calibration files because of the limited Ropt size.
 |
Fig. 14. Epoch residuals |
The systematic value of 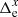 at some y is the bias in the position of the object located there, so that for dw14 at y = 1073 px the bias in the example epoch is roughly 0.28gx, e≈5 mpx or 0.6 mas. The rms value
at some y is the bias in the position of the object located there, so that for dw14 at y = 1073 px the bias in the example epoch is roughly 0.28gx, e≈5 mpx or 0.6 mas. The rms value 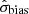 of the bias taken over all epochs is 0.55 mas. This includes the uncertainty of the fit σfit = 0.06 mas, which we subtracted quadratically and obtained σbias = 0.54 mas. This value characterizes the bias in the epoch residuals without correction of RCM (Table 3).
of the bias taken over all epochs is 0.55 mas. This includes the uncertainty of the fit σfit = 0.06 mas, which we subtracted quadratically and obtained σbias = 0.54 mas. This value characterizes the bias in the epoch residuals without correction of RCM (Table 3).
rms of additional bias σbias in the epoch residuals in mas obtained with and without RCM correction, for the short-, medium-, and long-duration datasets indicated by Δt.
The efficiency of the correction with Eq. (18) is evident from Fig. 14, which displays the new residuals 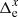 (open circles) computed with the positions
(open circles) computed with the positions 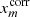 ,
, 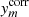 of stars in chip 2 corrected for each image m. The distribution of
of stars in chip 2 corrected for each image m. The distribution of 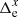 along Y is now flat. For the example epoch and objects at y = 1073 px, this calibration decreases the bias to 0.3 mpx. For all epochs, the average rms bias for the target is
along Y is now flat. For the example epoch and objects at y = 1073 px, this calibration decreases the bias to 0.3 mpx. For all epochs, the average rms bias for the target is 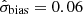 –0.07 mas; it is equally good for the two tested coefficient values of K = 0.70 and K = 0.63. By quadratically subtracting σfit, we find σbias = 0.02 mas for the correction with K = 0.63.
–0.07 mas; it is equally good for the two tested coefficient values of K = 0.70 and K = 0.63. By quadratically subtracting σfit, we find σbias = 0.02 mas for the correction with K = 0.63.
This is the best way of removing the RCM effect and reducing its impact to the noise level. We also find that for the epoch shown in Fig. 14 this calibration decreased the rms of Δe for bright 17–18 mag stars from 4.2 mpx (=0.5 mas) to 1.0 mpx (=0.12 mas), which is a typical uncertainty of the epoch residuals for FORS2 astrometry.
A significant but insufficient decrease of σbias to 0.16 mas (Table 3) was also obtained with the calibration of Eq. (19). This result indirectly suggests that the true RCM follows a smooth cubic polynomial change in time, but that the updated model of H(t) should include higher order terms in t and possibly some irregular displacements like those that took place on 20–24 November 2011. For comparison, we repeated these computations for the ultracool dwarfs 3 and 11 listed in Table 1 by Sahlmann et al. (2014), which represent short- and medium-duration datasets, respectively.
Summarizing these results, we conclude that the RCM effect is comparable for long- and medium-duration datasets and can be removed well using g values based on calibration files. For short-duration datasets, the RCM adds a small bias that does not significantly degrade the astrometric precision even when left uncorrected.
8. Conclusion
Astrometric programs often require a reference field whose size exceeds a single chip. For multi-chip detectors it is therefore natural to use stars both in the primary chip where the target object is imaged and in the adjacent chips. In the case of FORS2, the reference field partially covers the primary chip 1, but for precise astrometric reduction it is often extended to the second chip 2. The use of such multi-chip reference frames implies that the locations of the chips within a detector are known.
First signs of internal chip motions within the FORS2 detector were reported in Paper I. Here, we investigated this effect in detail using images of sky fields that were monitored over a few years (Sahlmann et al. 2014). We used several approaches: the motion of chip 2 was measured relative to chip 1 or relative to the reference frame extended over both chips, and we used the Gaia DR2 catalog. All approaches yielded concordant results in which the motion of chip 2 varied in time with an amplitude of up to ∼70 mpx yr−1. The full amplitude of the chip displacement between 2011 and 2018 is 0.3 px or 38 mas in the direction along the line that divides the chips. In the orthogonal direction (i.e., across the chip gap) the displacements is ∼0.07 px.
The dominant relative chip motion follows a cubic dependence on time in RA and changes its direction in 2011.8 from positive to negative, and it seems to invert again in 2017.5. In addition, we found significant deviations from a smooth continuous motion. For example, we detected a step-like displacement by 0.02–0.05 px (2–6 mas) that occurred on 20–24 Nov. 2011 and was likely caused by an instrument maintenance intervention. In the orthogonal direction, the relative chip motion appears linear in time.
On average, the relative chip motion adds a random component to the epoch residuals of ∼0.5 mas, thus it can significantly degrade the FORS2 astrometric performance of 0.1 mas for a single epoch if it is not corrected for. We demonstrated that the relative chip motion effect can be mitigated to the noise level at the cost of extensive computations that are needed to create special calibration files.
The relative chip motion was investigated by Bernstein et al. (2017), who analyzed the stability of a 61 CCD chip array of the Dark Energy Camera (DECam; Flaugher et al. 2015) and discovered displacements of chips with an amplitude of 0.4 px = 100 mas, or 6 μm. Although these estimates are comparable to those we obtained for FORS2, they refer to the detectors of a quite different design and linear dimensions. The DECam CCDs cover a very large ∼450 × 450 mm space, so that the displacement values are 10−5 relative to the detector size only, while we found ∼10−4 for FORS2. The motions of the DECam CCDs were found to be closely related to the warming or cooling thermal recycling, which appears as a stochastic change in time. In contrast, the motion of FORS2 chips within the MIT detector is smooth and linear in time, at least between 2012 and 2018, and does not depend much on the thermal recycling during the exchanges between the MIT and E2V mosaic detectors, which occur with a spacing of a few months. For these reasons, we consider that the relative chip motion in the case of FORS2 is of a different physical nature and potentially reflects some aging processes.
We demonstrated that chip array instabilities can seriously degrade high-precision astrometry if left uncorrected. The MICADO near-infrared camera (Davies et al. 2010) for the ELT aims at a single-epoch accuracy of ≤50 μas over an FOV of 53″ (Rodeghiero et al. 2018; Pott et al. 2018). The detector of MICADO is a 3 × 3 array, and if the reference field is expanded over the full FoV, the RCM effect can fragment it into 3 × 3 segments. In the hypothetical case that the relative chip motion of MICADO is comparable to FORS2, it can introduce biases of 50–300 μas in the target epoch positions if the reference field extends over several chips and the effect is not calibrated and corrected using dedicated methods (e.g., Rodeghiero et al. 2019).
Our findings underline that chip stability needs to be considered. Dedicated monitors for detector arrays may need to be implemented that are expected to fulfill the stringent requirements of astrometric performances.
References
- Anderson, J., & King, I. R. 2003, PASP, 115, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Appenzeller, I., Fricke, K., Fürtig, W., et al. 1998, The Messenger, 94, 1 [NASA ADS] [Google Scholar]
- Bernstein, G. M., Armstrong, R., Plazas, A. A., et al. 2017, PASP, 129, 074503 [NASA ADS] [CrossRef] [Google Scholar]
- Davies, R., Ageorges, N., & Barl, L. 2010, in Ground-based and Airborne Instrumentation for Astronomy III, Proc. SPIE, 7735, 77352A [NASA ADS] [Google Scholar]
- Flaugher, B., Diehl, H. T., Honscheid, K., et al. 2015, AJ, 150, 150 [NASA ADS] [CrossRef] [Google Scholar]
- Gaia Collaboration 2018, VizieR Online Data Catalog: I/345 [Google Scholar]
- Garcia, E. V., Ammons, S. M., Salama, M., et al. 2017, ApJ, 846, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Lazorenko, P. F., & Lazorenko, G. A. 2004, A&A, 427, 1127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lazorenko, P. F., & Sahlmann, J. 2017, A&A, 606, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lazorenko, P. F., & Sahlmann, J. 2018, A&A, 618, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lazorenko, P. F., Mayor, M., Dominik, M., et al. 2009, A&A, 505, 903 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lazorenko, P. F., Sahlmann, J., Ségransan, D., et al. 2014, A&A, 565, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lindegren, L., Hernández, J., Bombrun, A., et al. 2018, A&A, 616, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pott, J. U., Rodeghiero, G., & Riechert, H. 2018, in Ground-based and Airborne Instrumentation for Astronomy VII, SPIE Conf. Ser., 10702, 1070290 [Google Scholar]
- Rodeghiero, G., Pott, J.-U., Arcidiacono, C., et al. 2018, MNRAS, 479, 1974 [NASA ADS] [CrossRef] [Google Scholar]
- Rodeghiero, G., Sawczuck, M., Pott, J.-U., et al. 2019, PASP, 131, 054503 [NASA ADS] [CrossRef] [Google Scholar]
- Sahlmann, J., Lazorenko, P. F., Ségransan, D., et al. 2014, A&A, 565, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sahlmann, J., Burgasser, A. J., Martín, E. L., et al. 2015a, A&A, 579, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sahlmann, J., Lazorenko, P. F., Ségransan, D., et al. 2015b, A&A, 577, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Summary of the spaces ω, ω*, and flags λ that specifies different modifications of astrometric reduction, and the estimated displacement of chip 2 along the X-axis from 2012.0 to 2017.5.
rms of additional bias σbias in the epoch residuals in mas obtained with and without RCM correction, for the short-, medium-, and long-duration datasets indicated by Δt.
All Figures
 |
Fig. 1. Simulation of the astrometric model response to a step change U(y) in the position of chip 2 for the example sky field of dw14 offset by 73 px from the detector center. Dots show the response in the epoch residuals |
| In the text | |
 |
Fig. 2. Epoch positional residuals |
| In the text | |
 |
Fig. 3. Individual epoch positional residuals |
| In the text | |
 |
Fig. 4. Change in time of chip offset gx, e for sky fields with short (filled dots, six sky fields), medium (crosses, seven fields), and long (open circles, seven fields) observation time-span. The vertical line marks the time of an event that caused a 20–50 mpx offset in gx, e for four fields observed on 20–24 November 2011 (squares). |
| In the text | |
 |
Fig. 5. Same as Fig. 3, but for proper motions: the approximation of Eq. (6) (solid lines) and the model response WCAL(y) to the step change Δμ = −56.0 mpx yr−1 in the proper motions of stars in chip 2 (dashed lines). |
| In the text | |
 |
Fig. 6. Motion of chip 2 along the X-axis (lower panel) relative to a reference frame defined by stars in both chips: the unreduced displacements |
| In the text | |
 |
Fig. 7. Fit residuals δH between the measured and the position of chip 2 according to the model Eq. (8) relative to chip 1 for each epoch and the sky fields with a short (filled dots), medium (crosses), and long (open circles) duration of observations. An impulse jump for four fields obtained on 20–24 November 2011 is marked by squares. |
| In the text | |
 |
Fig. 8. Proper motions μx in the dw14 field derived relative to chip 1 (gray filled circles) and when the astrometric parameters are derived with Eq. (10) (open circles), which allows for a step change between the chips of Δμx = −56.0 mpx yr−1. The circle size is proportional to the stellar brightness. |
| In the text | |
 |
Fig. 9. Motion of chip 2 relative to the reference frame of the upper chip: unreduced displacements Vz, i, e along the X- and Y-axes of 15 bright lower chip stars in each sky field at each epoch (small dots). The same after correction for the residual parameters |
| In the text | |
 |
Fig. 10. Motion of chip 2 along RA (lower panel) and Dec (upper panel) relative to chip 1. Each curve is the solution for H(t) derived with the models in Table 2, as indicated by the legend. The instant motion estimate H(t)+δHz, e for model 2 (open circles) shows the scatter in the RCM determination for individual fields and epochs. The step change in four fields observed on 20–24 November 2011 and derived with approaches 2 and 4 is marked by squares. |
| In the text | |
 |
Fig. 11. Motion of chip 2 along RA (lower panel) and Dec (upper panel) relative to the upper chip derived using Gaia DR2: instant estimates Hz(te)+δHz, e for individual sky fields z and epochs e (open circles) and the smooth fit functions H(t). |
| In the text | |
 |
Fig. 12. Nonlinear component |
| In the text | |
 |
Fig. 13. Correlation between the epoch displacements in chip 2, gx, along RA in 20 sky fields derived with the standard reduction (Nr.1 in Table 2) and the nonlinear component of the chip motion |
| In the text | |
 |
Fig. 14. Epoch residuals |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



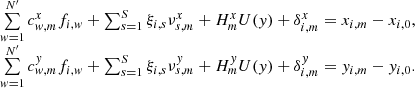
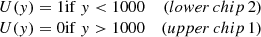
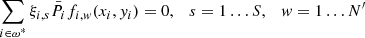
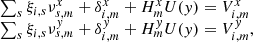
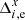
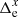
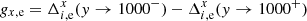
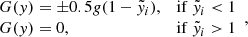
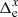
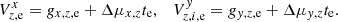
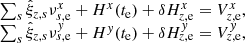
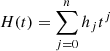
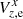
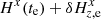
![$$ \begin{aligned} \begin{array}{l} \sum\nolimits _{i \in \omega ^*} [\xi _{i,s}- \lambda U({ y}_i) \Delta \xi _s] \bar{P}_{i} =0, \quad s=1 \ldots S, \\ \sum\nolimits _{i \in \omega ^*} \xi _{i,s} \bar{P}_{i} f_{i,{ w}}(x_i,{ y}_i) =0, \quad s=1 \ldots S, \quad { w}=2 \ldots {N^{\prime }}. \end{array} \end{aligned} $$](/articles/aa/full_html/2019/09/aa36319-19/aa36319-19-eq90.gif)