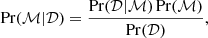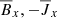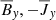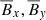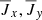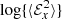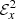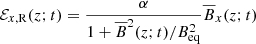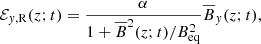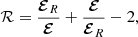| Issue |
A&A
Volume 629, September 2019
|
|
|---|---|---|
| Article Number | A89 | |
| Number of page(s) | 10 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/201935945 | |
| Published online | 10 September 2019 | |
Exploring helical dynamos with machine learning: Regularized linear regression outperforms ensemble methods
1
Department of Space, Earth and Environment, Chalmers University, 41296 Gothenburg, Sweden
e-mail: naumanf@chalmers.se
2
Nordita, KTH Royal Institute of Technology and Stockholm University, Roslagstullsbacken 23, 10691 Stockholm, Sweden
e-mail: joonas.nattila@su.se
Received:
24
May
2019
Accepted:
12
August
2019
We use ensemble machine learning algorithms to study the evolution of magnetic fields in magnetohydrodynamic (MHD) turbulence that is helically forced. We perform direct numerical simulations of helically forced turbulence using mean field formalism, with electromotive force (EMF) modeled both as a linear and non-linear function of the mean magnetic field and current density. The form of the EMF is determined using regularized linear regression and random forests. We also compare various analytical models to the data using Bayesian inference with Markov chain Monte Carlo (MCMC) sampling. Our results demonstrate that linear regression is largely successful at predicting the EMF and the use of more sophisticated algorithms (random forests, MCMC) do not lead to significant improvement in the fits. We conclude that the data we are looking at is effectively low dimensional and essentially linear. Finally, to encourage further exploration by the community, we provide all of our simulation data and analysis scripts as open source IPYTHON notebooks.
Key words: dynamo / magnetohydrodynamics (MHD) / turbulence
© ESO 2019
1. Introduction
Large scale magnetic fields are observed on the Earth, the Sun, galaxies. Understanding the origin and sustenance of these magnetic fields is the subject of dynamo theory. Magnetic fields observed in the galaxies are thought to have their origin in the early phases of cosmological evolution (Subramanian 2019). On relatively smaller scales, magnetic fields likely play a significant role in star (Wurster & Li 2018) and planet formation (Ercolano & Pascucci 2017). For the Sun, a long standing question has been to understand the origin of the cyclical behavior of the magnetic North and South poles (Brun & Browning 2017).
A number of outstanding questions remain about dynamo theory. Classical models of dynamo theory (Krause & Steenbeck 1967; Krause & Rädler 1980) assume that the background flow is stationary and the magnetic field is too weak to feedback on the flow. This reduces the problem of magnetic field generation to a closure problem: how does the fluctuating electromotive force (EMF) depend on the mean field? Previous work on dynamo theory has often modeled the EMF as a linear function of the mean field (see Brandenburg & Subramanian 2005, for an extensive review). This approximation is reasonable in the growth (kinematic) phase in a flow-driven magnetohydrodynamic (MHD) system where the initial magnetic energy is orders of magnitude smaller than the kinetic energy of the forced fluid. But the limitations become apparent when the magnetic fields have gained enough energy to modify the background flow through the Lorentz force. To model this backreaction of the mean magnetic field on the flow, various proposals have been put forward including models where EMF is a non-linear function of the mean field (Jepps 1975; Pouquet et al. 1976; Vainshtein & Cattaneo 1992).
Two methods have been widely used in numerical simulations of dynamos to get an explicit form for the electromotive force and both are essentially linear: the test field method (Schrinner et al. 2007) and linear regression using the least squares method (Brandenburg & Sokoloff 2002). The kinematic test field method uses a set of orthogonal “test” fields that are pre-determined and can be used to compute the various coefficients in the EMF expansion corresponding to terms linear in the large scale field and its gradients. As input, the test field requires both the small and large scale velocity field and dynamically solves (on the fly) the test field equations to compute the test field coefficients. This has the advantage of retaining dynamical information (Hubbard & Brandenburg 2009; Rheinhardt & Brandenburg 2012). Linear regression, in contrast, is mostly used in post-processing to model the “inverse” problem of determining the coefficients corresponding to different terms in the linear expansion of the EMF.
Machine learning and deep learning have revolutionized image processing, object detection, natural language processing (LeCun et al. 2015). Recently there has been a surge of interest in using machine and deep learning tools in dynamical systems and computational fluid dynamics (Hennigh 2017; Kutz 2017; Brunton & Kutz 2019). Data-driven modeling is not new to fluid dynamics; in meteorology, observational data has been used for decades to guide weather predictions (see Navon 2009, for a historical overview). Considerable increase in computational power with advances in hardware (GPUs) has allowed modern optimization methods to become increasingly tractable. The end goal is to not only build predictive data-driven models but also to understand underlying complex physics that cannot be captured by simple linear regression.
The motivation to study reduced descriptions of the full 3D MHD simulations comes primarily from the extremely large, and currently numerically intractable, magnetic Reynolds number of most astrophysical systems (Rm ∼ 106 − 1012, Brandenburg & Subramanian 2005). Reduced-order modeling of dynamical systems is currently a highly active field of research that aims to provide description of physical systems in terms of the minimal possible degrees of freedom (Kutz 2013, 2017). In this paper, we attempt to build reduced-order models for MHD dynamos by applying non-linear regression tools to the widely studied α2 dynamo (Brandenburg & Subramanian 2005). In this context, we follow the best practices in machine learning that emphasize generalization by using train-validation-test splits in data. If one uses all the data to compute correlations (or use any other algorithm for that matter), it amounts to “descriptive” modeling. By separating the data into distinct training, validation and test sets, one enters into the realm of “predictive” modeling where the generalization power of different algorithms can be tested by first fitting data on the training set, and then testing it on the validation before making predictions on the test set. A high score on the training set but a poor score on validation set indicates poor generalization. This is in contrast to standard linear regression techniques employed in the dynamo literature where the entire data set is taken to be the training set with no validation set to test overfitting (Brandenburg & Sokoloff 2002).
We use data from Direct Numerical Simulations (DNS) of forced helical turbulence to construct a reduced model where the EMF is an unknown (linear and non-linear) function of the large scale field. This allows us to quantitatively assess the standard assumption of modeling EMF as linearly proportional to the mean magnetic field and current density. We employ three classes of modern statistical and machine learning models: (i) Linear regression, (ii) Random forests, (iii) Bayesian inference (with Markov chain Monte Carlo model minimization). Our selection of a well-studied systems like forced helical MHD turbulence supports our second main motivation: we can compare our results from machine learning tools against relatively well-known results in the literature. The insights gained from such a comparison could then help guide future work on more complex MHD turbulent systems such as MHD turbulence with differential rotation (Blackman & Brandenburg 2002; Charbonneau 2014).
We describe our data and numerical simulations in the next section. This is followed by a section that begins by explaining the fitting methods considered in this paper. We then apply these machine learning and statistical methods on the data. We discuss our results in Sect. 4 putting out work in the context of previous work and some caveats. Section 5 is conclusions. All of our analysis scripts and data are freely available as interactive IPYTHON notebooks1.
2. Data
We describe the equations, setup and code that was used to conduct DNS of forced turbulence in magnetized flows.
2.1. Description of DNS
We use the publicly available 6th order finite difference PENCIL-CODE (Brandenburg & Dobler 2002)2. The MHD equations are solved in a triply periodic cubic domain of size 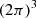 :
:
where ν is the viscosity, 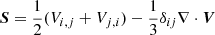 , f is the forcing function, η is the resistivity, and
, f is the forcing function, η is the resistivity, and 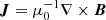 is the current density.
is the current density.
The forcing function is taken to be homogeneous and isotropic with explicit control over the fractional helicity determined by the σ parameter. It is defined as:
where the wave vectors k(t) and the phase |ϕ(t)| < π are random at each time step. The wavevectors are chosen within a band to specify a range of forcing centered around kf. The normalization factor is defined such that the forcing term matches the physical dimensions of the other terms in the Navier Stokes equation, N = f0cs(|k|cs/δt)1/2, where f0 is the forcing amplitude, cs is the sound speed, δt is the time step. The Fourier space forcing has the form (Haugen et al. 2004):
where σ is a measure of the helicity of the forcing; for positive maximum helicity, σ = 1, and 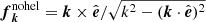 .
.
The initial velocity and density are set to zero while the magnetic field is initialized through a vector potential with a small amplitude (10−3) Gaussian noise. We define the units (Brandenburg 2001):
such that the magnetic field, B, is in the units of Alfen speed (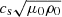 ). The domain size is L3 = (2π)3, which leads to k1 = 2π/L = 1. Moreover, we use the following dimensionless numbers:
). The domain size is L3 = (2π)3, which leads to k1 = 2π/L = 1. Moreover, we use the following dimensionless numbers:
where kf/k1 = 10 is the forcing wavemode. We provide a summary of the simulations in Table 1.
Summary of the simulations used in this paper.
2.2. Reduced model
Numerical simulations of large scale astrophysical flows with magnetic Reynolds number well in the excess of 106 are prohibitive. Moreover, state-of-the-art simulations requires 𝒪(106) CPU hours to compute for moderate Reynolds numbers. To make modeling such systems more tractable, it is therefore necessary to look for simpler surrogate models that can capture the most significant properties of the high fidelity simulations (DNS).
Large scale dynamo theory concerns itself with the evolution equation of the filtered induction equation,
where EMF is given as 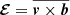 , η is the turbulent resistivity, and the overbar represents a filtered quantity. The filter could be ensemble, temporal or spatial depending on the problem. The first term on the right-hand side is typically ignored unless there is a strong non-constant mean velocity field such as in the case of galaxies (the mean differentially rotating flow for the galactic dynamo is considered in Shukurov et al. 2006). The dynamics of the velocity field (Eq. (2)) are ignored based on the assumption that the forcing term is the dominant term and it causes the velocity field to be in a steady state. This assumption is only reasonable in the “kinematic” regime where the magnetic fields are too weak to modify the velocity field dynamically.
, η is the turbulent resistivity, and the overbar represents a filtered quantity. The filter could be ensemble, temporal or spatial depending on the problem. The first term on the right-hand side is typically ignored unless there is a strong non-constant mean velocity field such as in the case of galaxies (the mean differentially rotating flow for the galactic dynamo is considered in Shukurov et al. 2006). The dynamics of the velocity field (Eq. (2)) are ignored based on the assumption that the forcing term is the dominant term and it causes the velocity field to be in a steady state. This assumption is only reasonable in the “kinematic” regime where the magnetic fields are too weak to modify the velocity field dynamically.
In keeping with previous work that has used horizontal averaging as the filter in Eq. (8) (Brandenburg 2001; Brandenburg & Subramanian 2005), our data has been averaged over the whole xy plane:
This averaging scheme has the interesting property that  since
since 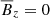 (due to incompressibility and periodic boundary conditions). We only consider the fields (let Q be an arbitrary field) reduced to 1D by furthermore averaging them in two different ways:
(due to incompressibility and periodic boundary conditions). We only consider the fields (let Q be an arbitrary field) reduced to 1D by furthermore averaging them in two different ways:
-
z averaged:
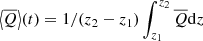 where z1, z2 are chosen such that they do not cover the entire z-domain since that will correspond to volume averaged quantities that are zero.
where z1, z2 are chosen such that they do not cover the entire z-domain since that will correspond to volume averaged quantities that are zero. -
t averaged:
![$ {\left[ \overline{Q} \right]}(z) = 1/(t_2 - t_1) \int_{t_1}^{t_2} {\overline{Q}} \mathrm{d}t $](/articles/aa/full_html/2019/09/aa35945-19/aa35945-19-eq19.gif) where t1, t2 are chosen to correspond to either the kinematic or saturation regime for different runs.
where t1, t2 are chosen to correspond to either the kinematic or saturation regime for different runs.
This leaves two independent magnetic fields and corresponding EMF components. Analytical models that use 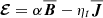 are termed α2 dynamos and have been extensively studied in the literature. Here ηt represents the turbulent resistivity.
are termed α2 dynamos and have been extensively studied in the literature. Here ηt represents the turbulent resistivity.
In Fig. 1, we show a three-dimensional phase-space visualization of ℰx vs. 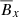 vs.
vs. 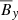 that shows the relation between the EMF and the mean magnetic fields (situation is the same when considering ℰy too). The circle in
that shows the relation between the EMF and the mean magnetic fields (situation is the same when considering ℰy too). The circle in 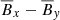 plane represents the fact that the total magnetic energy
plane represents the fact that the total magnetic energy 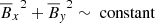 . The slight tilt with respect to the EMF (i.e., towards z direction) implies a linear correlation with the EMF. The increasing disorder with increasing Rm is characteristic of highly turbulent systems.
. The slight tilt with respect to the EMF (i.e., towards z direction) implies a linear correlation with the EMF. The increasing disorder with increasing Rm is characteristic of highly turbulent systems.
 |
Fig. 1. 3D parametric visualization of the |
3. Model fits
We describe the 1D linear and non-linear regression for temporal and vertical profiles in the following subsections. In the following, we will refer to the magnetic fields as both “fields” and “features”, and EMF as “target” interchangeably. For most of the following, we will focus on ℰx but similar results hold for ℰy since we are looking at isotropically forced MHD turbulence with no background field.
3.1. Description of algorithms considered in this paper
Ordinary Least Squares (OLS) assumes that the data is linear, features/terms are independent, variance for each point is roughly constant (homoscedasticity), features/terms do not interact with one another. Moreover, causal inference based on linear regression can be misleading (Bollen & Pearl 2013), a problem shared by all curve fitting methods. We should highlight the distinction between linearity of the regression as opposed to linearity of the features. For example, one can construct a non-linear basis (example: x, x2, x3, … or sin x, cos x, …) and do linear regression with this basis. Linear regression on non-linear data can potentially represent non-linear data well assuming that the non-linear basis terms are independent and have low variance. Constructing the correct interacting/non-linear terms requires domain expertise. For this reason, it is important to also consider non-linear regression methods such as random forests that are robust to noise and are capable of modeling interactions implicitly.
3.1.1. LASSO
Most real data have considerable variance that can lead to misleading fits from linear regression. Regularized linear regression aims to construct models that are more robust to outliers. Two of the most common regularization schemes for linear regression are (Tibshirani 1996; Hastie et al. 2015): (i) LASSO (Least Absolute Shrinkage and Selection Operator; also known simply as L1 norm), (ii) Ridge (also known as L2 norm). As opposed to ridge, LASSO has the advantage of doing feature selection by reducing coefficients of insignificant features. We will use LASSO regression in this work.
Intuitively LASSO reduces variance at the cost of introducing more bias. LASSO works better than ridge regression if the data is low dimensional (or the coefficient matrix is sparse). For high dimensional complex data, neither ridge nor LASSO do well. Because of this, the “Bet on sparsity” principle (Hastie et al. 2009) suggests trying LASSO for all datasets. Formally, LASSO optimizes for:
where y represents the target vector (in our case, ℰ), X is the feature matrix (Bx, By, … are the columns), w is coefficient vector and α is a parameter with a range between 0 and 1. The subscripts “1” and “2” represent L1 (∑ n||w||1 = |w1|+|w2|+…+|wn|) and L2 ( ) norms, respectively. A higher α penalizes outliers more strongly and shrinks coefficients of unimportant features to zero while a lower α is similar to linear regression with no regularization (OLS).
) norms, respectively. A higher α penalizes outliers more strongly and shrinks coefficients of unimportant features to zero while a lower α is similar to linear regression with no regularization (OLS).
3.1.2. Random forests
Random forests belong to the class of ensemble machine learning algorithms (Breiman 2001a; Hastie et al. 2009). A random forest consists of a large number of decision trees that each take a random subset of features with a bootstrapped sample of the data (Raschka 2018). This helps in getting rid of strong correlations among different trees but some correlations might still remain. Random forests are one of the most popular and widely used machine learning algorithms because they require little hyperparameter tuning and can handle large noisy data sets. From a computational point of view, each decision tree in the ensemble is independent and can thus be easily processed in parallel. Moreover, because of the weighted average over the ensemble, random forests are robust to strong variance in the data but a few deep decision trees can lead to strong bias.
Ensembles of decision trees (random forests and gradient boosting) are non-parametric models meaning they do not require information about the underlying data distribution. In other words, unlike in linear regression where the shape of the function that connects the independent variables to the dependent variable is fixed, the functional form is not known in random forests and is instead determined through training. This offers a different perspective on modeling, termed “algorithmic” modeling as opposed to “data” modeling (Breiman 2001b). The non-parametric nature of random forests and gradient boosting make them applicable to a wide class of problems since in most real-world situations, data distribution is not known a-priori. However, this comes at the cost of interpretability making ensembles of decision trees harder to understand than linear regression (Strobl et al. 2008).
Feature importance and selection: As opposed to linear regression, random forests do not directly measure the coefficient of the features. A single decision tree is highly interpretable but a whole ensemble of decision trees is harder to interpret (Breiman 2001b). Random forests offer some insight through feature importances (Hastie et al. 2009). We use the “mean decrease impurity” method implemented in PYTHON library SCIKIT-LEARN (Pedregosa et al. 2011; Breiman et al. 1984; Louppe 2014). With this method, the feature importance corresponds to the frequency of a particular feature appearing across different trees combined with the reduction of error corresponding to that particular feature, weighted by the fraction of samples in that particular node. One popular alternative is to randomly permute the data for a particular feature and see whether it has an effect on the mean squared error (or information gain/gini importance for classification tasks). If the mean squared error increases or remains the same, it implies that the particular feature is not important. This is termed as “permutation” importance (Breiman 2001a; Strobl et al. 2008).
3.1.3. Bayesian inference
Bayesian inference is a powerful statistical framework that presents an alternative way to perform the model parameter estimation. The main strengths of Bayesian-based approaches are their ability to quantify the uncertainty of the model and the possibility to incorporate previous a-priori knowledge into the estimation. The downside, when compared to many conventional machine learning methods, is that the model needs to be known before the fit.
Let us quickly summarize the idea behind Bayesian inference. In general, let us present our model with ℳ and our empirical (simulation) data with 𝒟. We are then interested in how well can our model describe the data, or quantitatively what is the probability that our model is valid given the data, Pr(ℳ|𝒟). By directly comparing our model and the data, what we actually get is, however, the probability of our model given the data, known as the likelihood ℒ = Pr(𝒟|ℳ). Our original question of the validity of our model, can be answered by applying the Bayes’ theorem presented as (see e.g., Grinstead & Snell 1997)
where Pr(ℳ) is our prior probability of the model and Pr(𝒟)= ∫ Pr(𝒟|ℳ)dℳ is the prior probability. Therefore, because ℒ can be computed and Pr(ℳ) is known a-priori, we can use the Bayes’ theorem to quantitatively asses the validity of, for example, our α2 dynamo models given the simulation data results.
In practice, not only are we interested in the validity of the model, but also what are the parameters Θ of the model, ℳ(Θ), that best describe the data. In Bayesian inference, these model parameters are determined using a marginal estimation where the resulting posterior parameter for model parameter Θj are obtained by integrating over the probability of all the other model parameters, Θi (i ≠ j). Then, this (one-dimensional) distribution represents the probability that the jth model parameter, Θj, will take a particular value given our data 𝒟.
Here we solve the Eq. (11) (and therefore obtain also posterior distributions for our model parameters) using Monte Carlo Markov chain (MCMC) integration techniques. To perform the MCMC fit we use the publicly available EMCEE library (Foreman-Mackey et al. 2013). We employ the affine-invariant stretch-move ensemble sampler with typically 3Nparam number of walkers (members of ensemble), where Nparam is the number of fit parameters. No prior knowledge is incorporated into the fits and so we use uniform priors for all of our model parameters.
3.2. Vertical profiles
In this subsection, we apply various methods on time averaged data that only has vertical dependence (256 grid points).
In Fig. 2, we show the linear (Pearson) correlation coefficients among the various fields. The correlation between the current densities and the magnetic fields is nearly 1 indicating they are linearly dependent. Strong linear correlation does not rule out the physical importance of a variable – it only implies that from a curve fitting point of view, it has redundant information. Since we are using helical forcing leading to a helical state, 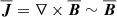 . At high Rm, one might expect that the power in the velocity and magnetic field spectrum will be distributed across multiple modes implying weaker correlations. However, Fig. 2 (right panel) indicates the correlation between
. At high Rm, one might expect that the power in the velocity and magnetic field spectrum will be distributed across multiple modes implying weaker correlations. However, Fig. 2 (right panel) indicates the correlation between 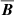 and
and 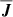 is still perfect. This means that we can eliminate current density as an independent variable. See, however, the work Tilgner & Brandenburg (2008) that suggests that the tensorial form of αij, ηij in the non-linear regime depends on
is still perfect. This means that we can eliminate current density as an independent variable. See, however, the work Tilgner & Brandenburg (2008) that suggests that the tensorial form of αij, ηij in the non-linear regime depends on  . In keeping with previous work, for linear basis we do consider the current density as an independent variable but eliminate it for the non-linear (polynomial) basis where its inclusion will lead to several redundant terms.
. In keeping with previous work, for linear basis we do consider the current density as an independent variable but eliminate it for the non-linear (polynomial) basis where its inclusion will lead to several redundant terms.
 |
Fig. 2. Heat map of correlation coefficients between the different fields: Rm = 103 (left panel), Rm = 1.5 × 104 (right panel). This analysis implies that the ℰx has a strong correlation with |
We consider two sets of basis in this subsection:
-
Linear:
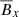 ,
, 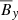 ,
, 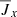 ,
, 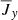 .
. -
Polynomial of O(3):
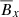 ,
, 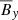 ,
, 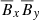 ,
, 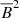 ,
, 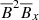 ,
, 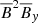 .
.
We note that for kinetically forced simulations, v2 ∼ constant, which means that the total energy conservation equation yields, 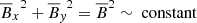 in the saturated state. This makes
in the saturated state. This makes 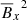 and
and  linearly dependent terms and thus we do not consider them separately. Another motivation to use
linearly dependent terms and thus we do not consider them separately. Another motivation to use 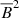 is because work on dynamo quenching often considers
is because work on dynamo quenching often considers 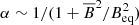 , which when expanded for the ℰ leads to cubic terms of the form
, which when expanded for the ℰ leads to cubic terms of the form 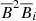 (i = x, y). We will be using the publicly available PYTHON library SCIKIT-LEARN (see Guido & Müller 2017; Géron 2017, for introductions) for modeling the data.
(i = x, y). We will be using the publicly available PYTHON library SCIKIT-LEARN (see Guido & Müller 2017; Géron 2017, for introductions) for modeling the data.
Previous work on dynamo theory has often relied on linear regression methods (Brandenburg & Sokoloff 2002; Brandenburg 2018) with some effort to incorporate non-linear effects through magnetic helicity conservation (Pouquet et al. 1976; Blackman 2015; see also non-linear test field method Rheinhardt & Brandenburg 2010). In this section, we use linear regression with a regularization term for both the linear and polynomial basis discussed previously.
In Fig. 3, we show the fits using random forests regression and LASSO. Because our data is small (only 256 points), we use two-fold cross validation to determine various hyperparameters of LASSO and random forests. We found that bootstrapping leads to spurious results so we turned it off. A similar problem was found with random train/test splits: the spatial structure of the fields is like one full sinusoidal wave and randomly picking a fraction of the points leads to strange patterns. Moreover, while deep trees can lead to overfitting, in our case we found that a maximum depth of 8 was optimal through 2-fold cross validation. The end results are still not as good as LASSO perhaps owing to the fact that the training set is only 204 entries (80% of the data) – this is too low for an algorithm like random forest to really excel. That is the key lesson we have learnt while modeling this dataset throughout: “small” datasets mean simpler algorithms will outperform more sophisticated algorithms like random forests.
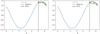 |
Fig. 3. Fits for linear basis (left panel) and polynomial basis (right panel) for random forests and LASSO. Note that the horizontal lines seen in the fits are there because of decision tree regression: decision trees set one value of the y-axis for a given range of x-axis leading to a step-function like fit. In both cases, LASSO seems to do a better job at capturing the curved shape of the vertical profiles. The black vertical dashed line presents the train-test split (80% training data). |
In Table 2, we compare the coefficients from OLS, LASSO, randomized LASSO (stability), Recursive Feature Elimination (RFE) from OLS and RFErf from random forests, Mutual Information Criterion (MIC), Pearson correlation (Corr) and the average of all these predictions in the last column. The meaning of these numbers is different. For OLS and LASSO, the numbers corresponding to the fields  represent coefficients from linear regression and can be negative or positive. For random forests, the numbers represent the relative feature importance based on “mean decrease impurity” that is only positive. These feature importance numbers are scaled to sum to unity. Stability selection is a general term that refers to checking robustness of model predictions by testing it on different random (bootstrapped) subsets of data with different hyperparameter values. In our particular application, we are using randomized LASSO that randomly varies the LASSO coefficient (Meinshausen & Bühlmann 2010)3.
represent coefficients from linear regression and can be negative or positive. For random forests, the numbers represent the relative feature importance based on “mean decrease impurity” that is only positive. These feature importance numbers are scaled to sum to unity. Stability selection is a general term that refers to checking robustness of model predictions by testing it on different random (bootstrapped) subsets of data with different hyperparameter values. In our particular application, we are using randomized LASSO that randomly varies the LASSO coefficient (Meinshausen & Bühlmann 2010)3.
Feature importances using various machine learning models and statistics.
RFE is a model-agnostic (wrapper) feature selection method that starts with a number of features and removes the most important features recursively. This is an example of “backward” feature selection (Guyon & Elisseeff 2003; Hastie et al. 2009) and we used it with OLS and random forests in this case. Maximal Information Coefficient (MIC) is a measure of mutual information between two (random) variables and is capable of accounting for non-linear relationships that the Pearson correlation coefficient cannot (example: correlation between x and x2 will be nearly zero, but MIC will yield an answer close to one). We scaled the whole set of features Xtrain using standard scaling before calculating coefficients/feature importances. Moreover, because LASSO, OLS, Corr returned negative as well as positive values and RFE returned values ranging from 1 to 6, we used minmax scaling to re-scale all values between 0–1.
Ensembles of machine learning models can lead to improved accuracy (Wolpert 1992). Here we take the simplest possible approach: we take the unweighted average of various predictors to compute the overall score for each feature. While stability selection shows that 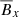 is the dominant feature, the mean of all predictors gives
is the dominant feature, the mean of all predictors gives  a slightly higher score. This could be because both
a slightly higher score. This could be because both 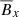 and
and  have the same sinusoidal form.
have the same sinusoidal form.
What do these results mean? Because we are dealing with low-dimensional data, constructing higher order terms from linear terms is not beneficial. LASSO is particularly well suited to identify important features in a low-dimensional model. It is, therefore, no surprise that the most important feature that (both randomized and ordinary) LASSO is picking up is the linear term 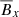 . Random forests, on the other hand, pick up
. Random forests, on the other hand, pick up 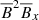 as the most significant feature and this might explain the poor prediction based on random forests seen in Fig. 3. Random forests work best for large datasets; for small data that is really low-dimensional (that is nearly linear), random forests do not perform well. Therefore, the results of Table 2 are consistent with Fig. 3.
as the most significant feature and this might explain the poor prediction based on random forests seen in Fig. 3. Random forests work best for large datasets; for small data that is really low-dimensional (that is nearly linear), random forests do not perform well. Therefore, the results of Table 2 are consistent with Fig. 3.
3.3. Time series analysis: Vertically averaged data
In contrast to the previous section, the magnetic fields and the EMF show exponential growth in time. To model this behavior, we found it convenient to do pre-processing where we took the logarithm of squared vertically averaged fields. Because of this choice, we do not consider polynomial expansions like we did before and instead focus on either the linear 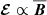 form, or the quenched form
form, or the quenched form 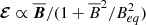 .
.
3.3.1. Preprocessing
For the vertically averaged data set, we find that the fluctuations in the EMF are quite significant (see Fig. 4). Such large fluctuations make any kind of statistical analysis quite prohibitive. In this section, we therefore decided to use the log of 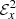 averaged over the z direction. Moreover, to reduce the fluctuations we used a moving window of size 20 (right panel of Fig. 4). This allows for cleaner fits.
averaged over the z direction. Moreover, to reduce the fluctuations we used a moving window of size 20 (right panel of Fig. 4). This allows for cleaner fits.
 |
Fig. 4. EMF evolution for Rm = 1.5 × 104. Left: ℰx component is shown without any pre-processing (z = π). Right: here we show |
3.3.2. LASSO and random forest
In Fig. 5, we show fits for the 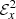 time series using LASSO and random forests. Time series data is particularly difficult to fit in the presence of fluctuations and trend as in the figure of
time series using LASSO and random forests. Time series data is particularly difficult to fit in the presence of fluctuations and trend as in the figure of  . In the kinematic phase (left panel), the random forest fit is not considerably different from LASSO fit whereas the random forest fit does poorly when the same time series is extended up to the saturation phase (right panel). This is a relatively common issue with random forests that they do not perform well when there is a “trend” present in the series. Just like the spatial profiles in last subsection, the LASSO outperforms random forests.
. In the kinematic phase (left panel), the random forest fit is not considerably different from LASSO fit whereas the random forest fit does poorly when the same time series is extended up to the saturation phase (right panel). This is a relatively common issue with random forests that they do not perform well when there is a “trend” present in the series. Just like the spatial profiles in last subsection, the LASSO outperforms random forests.
 |
Fig. 5. The fits for |
 |
Fig. 6. MCMC fits for the reconstructed ℰ2 fields. Three panel shows maximum likelihood Monte Carlo realizations of the fits (blue line) against the true ℰ2 curve (red line) for Rm = 500, 5 × 103, and 1.5 × 104. |
3.3.3. Bayesian inference
In this section we focus on reconstructing square of the “true” EMF field ℰ2 as a function of time t. As one of the simplest forms possible, we construct the reconstructed EMF, ℰR(z; t)2 = ℰx, R(z; t)2 + ℰy, R(z; t)2, from the corresponding magnetic field components as
where 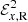 and
and 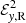 are the reconstructed x and y components of the EMF field. Here α and Beq are our model parameters to optimize. This EMF form has the nice property that in the limit Beq → ∞ it reduces to the linear model.
are the reconstructed x and y components of the EMF field. Here α and Beq are our model parameters to optimize. This EMF form has the nice property that in the limit Beq → ∞ it reduces to the linear model.
After this, we are left with the freedom to define our likelihood or score-function that describes the quality of the reconstruction. Here we define it via a simple residual function ℛ,
that penalizes the fit from over- and underestimating the reconstructed EMF. Note that other forms of the residual functions are also possible. For discrete simulation data results (defined on an array) the likelihood then simplifies to ℒq = ∑ k|ℛk|, where the summation index k is taken to be over the time dimension or the z direction, depending on the type of fit we are considering. Finally, when employing the MCMC fit note that we are actually minimizing log ∑ qℒq, as is typically done, to get a more shallow and slowly varying score-function.
Examples of the fit results are shown in Fig. 6 for three different Rm values of 500, 5 × 103, and 1.5 × 104 depicting the maximum a posteriori model. The (quenched) EMF model does reproduce the qualitative behavior of the saturating 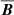 field but especially for higher Rm the fits become more worse. Most importantly, we have found that constraints on the saturation field strength Beq are always very loose. Results without using the quenching form also lead to similar fits. This gives an indirect support for the previous machine learning results: The data strongly favors isotropic α with a simplified model of
field but especially for higher Rm the fits become more worse. Most importantly, we have found that constraints on the saturation field strength Beq are always very loose. Results without using the quenching form also lead to similar fits. This gives an indirect support for the previous machine learning results: The data strongly favors isotropic α with a simplified model of 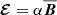 . The meaning of this “α” could be confusing since we have already eliminated the mean current density
. The meaning of this “α” could be confusing since we have already eliminated the mean current density 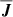 as an independent variable. The α coefficient represents the saturated value where the growth term roughly balances the dissipation term, leading to the effective expression: α ∼ k1(η + ηt).
as an independent variable. The α coefficient represents the saturated value where the growth term roughly balances the dissipation term, leading to the effective expression: α ∼ k1(η + ηt).
3.4. Results summary
For both the vertical and temporal profiles, various models suggest that 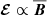 is a good description of the data. But if
is a good description of the data. But if 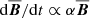 , this will lead to exponential growth without any saturation. Is there an inconsistency here? In the induction equation, the fields at time “t” are related to the fields at earlier times. The machine learning models we use here are not capable of storing long term memory. The fits shown in this paper are comparing ℰ and
, this will lead to exponential growth without any saturation. Is there an inconsistency here? In the induction equation, the fields at time “t” are related to the fields at earlier times. The machine learning models we use here are not capable of storing long term memory. The fits shown in this paper are comparing ℰ and 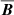 in some nearest neighbor sense and because both ℰ and
in some nearest neighbor sense and because both ℰ and 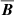 are growing exponentially before saturating at about the same time, they appear to be linearly correlated. Capturing the dynamical information requires more sophisticated algorithms that we leave for future work.
are growing exponentially before saturating at about the same time, they appear to be linearly correlated. Capturing the dynamical information requires more sophisticated algorithms that we leave for future work.
4. Discussion
4.1. Caveats
We summarize the properties of the different machine learning algorithms considered in this work in Table 3. Linear regression (both OLS and LASSO) are by definition capable of dealing with linear data only. However, they can handle some non-linear properties using a non-linear basis (for example, polynomial regression). The biggest advantage of linear models is the interpretability: the sensitivity of the target variable (EMF) with respect to the features (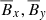 ) is as easy as determining the coefficients of these terms. Linear models are also good at dealing with data of all sizes but matrix inverses are expensive for large data. Linear models might also be able to model trends in data if the features they consider have the same trend as the target variable.
) is as easy as determining the coefficients of these terms. Linear models are also good at dealing with data of all sizes but matrix inverses are expensive for large data. Linear models might also be able to model trends in data if the features they consider have the same trend as the target variable.
Summary of the advantages and disadvantage of different models considered in this work.
Random forests are based on ensembles of decision trees. While random forests are quite robust to outliers and missing data, the feature importances computed from random forests can be misleading (Strobl et al. 2008). Moreover, random forests are not as interpretable as linear regression or single decision trees. A typical random forest fit can involve 10–100 trees implying that interpretation is difficult. But computation of feature importances and partial dependence plots help in making sense of random forest results (Breiman 2001b; Hastie et al. 2009). Random forests typically bootstrap data and use a random subset of features for each decision tree to determine which one leads to the lowest error. These two sources of randomness imply that random forests are best suited for intermediate to big data. Indeed in our “small data” case, we find that bootstrapping had to be turned off and the best fit models used less than 10 decision trees.
Bayesian methods offer an interesting complementary toolkit to various machine learning techniques. They also enable us to properly take the noisy nature of DNS into account. Here the big caveat is, that the model(s) needs to be known beforehand. This, however, further arguments in favor of our hybrid approach applied in this paper. We have used machine learning techniques to detect important features and then applied our physical knowledge to build valid models out from those. Biggest caveat here is that Bayesian model optimization becomes more and more computationally demanding with multidimensional (and often multi-modal) data. This puts a limitation on the real-life usability of the method when dealing with increasingly complex data.
The data considered in this paper is either spatially or temporally averaged reducing to O(100–1000) entries. Big data typically refers to the case where the observations/rows are ≥106. “Small” data faces problems of overfitting and is more likely to be sensitive to outliers. Because of these issues, simpler models like linear regression with regularization tend to do well. It is, therefore, no surprise that LASSO has outperformed random forests. For larger datasets with irregular non-linear patterns, random forests and gradient boosting tend to do much better (Olson et al. 2017).
4.2. Comparison with previous work
We used the simplest model: isotropic with no non-local effects in either space and/or time. While earlier work has focused primarily on linear models of dynamos where 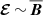 using linear regression and the test field method (Brandenburg & Subramanian 2005), non-linear models have also been considered (Rheinhardt & Brandenburg 2010). We assumed isotropy, which could be a misleading assumption in the presence of shear (see Brandenburg & Sokoloff 2002; Karak et al. 2014). Furthermore, in our model, we did not incorporate non-local effects that were considered by Brandenburg & Sokoloff (2002); Hubbard & Brandenburg (2009); Rheinhardt & Brandenburg (2012). Combining machine learning algorithms with anisotropic, local, non-linear models might lead to new insights, and we leave this for future work.
using linear regression and the test field method (Brandenburg & Subramanian 2005), non-linear models have also been considered (Rheinhardt & Brandenburg 2010). We assumed isotropy, which could be a misleading assumption in the presence of shear (see Brandenburg & Sokoloff 2002; Karak et al. 2014). Furthermore, in our model, we did not incorporate non-local effects that were considered by Brandenburg & Sokoloff (2002); Hubbard & Brandenburg (2009); Rheinhardt & Brandenburg (2012). Combining machine learning algorithms with anisotropic, local, non-linear models might lead to new insights, and we leave this for future work.
The α2 dynamo considered in this work is an idealized system but has the advantage that due to maximally helical forcing and periodic boundary conditions, magnetic helicity is both conserved and is gauge invariant (see Blackman 2015). This simplistic setup allows developing analytical theory to explain the origin and saturation of magnetic fields (Pouquet et al. 1976; Blackman & Field 2002). Numerical results seem to be consistent with theory (Brandenburg 2001; Brandenburg et al. 2012). In this work, we considered existing analytical formulations and used machine learning tools to test whether the EMF is linear or non-linear in the mean magnetic fields. Machine learning models can complement analytical theory in looking for reduced descriptions of high dimensional systems (Brunton & Kutz 2019).
5. Conclusions
Our main result can be summarized as follows: because we are in the “small” data regime and we are dealing with ordered data (high signal to noise ratio due to helically forced turbulence), regularized linear regression (LASSO) provides the best fit. For small organized data, sources of randomness such as random train/test splits, bootstrapping, cross validation with random subsets do not help. For this particular dataset, many of the features are strongly correlated with one another complicating the model fits even further. Strong correlations also imply that feature engineering to construct polynomial basis is not particularly useful.
Random forests and MCMC do better with mid-sized to big data. Moreover, these ensemble methods tend to outperform linear and regularized linear regression when the signal to noise ratio is poor (see Table 3). For the data we consider in this paper, it is therefore no surprise that LASSO provides the best fit.
What we intended to demonstrate using the example of α2 is that sophisticated machine learning algorithms can be used to analyze data from DNS of MHD turbulence thanks to the publicly available machine learning libraries. This provides an exciting opportunity to re-visit some long-standing problems in astrophysical flows where linear regression has dominated modeling efforts. For example, one can look at the full data cube without planar averaging and study whether 3D localized structures play a dominant role in the sustenance of the turbulence. Here, deep learning (Lusch et al. 2018) will be a useful alternative as it is known to outperform classical machine learning methods in image processing, voice recognition, natural language processing. One particular problem of interest is shear-driven dynamos (Tobias & Cattaneo 2013; Nauman & Blackman 2014).
Acknowledgments
We thank A. Brandenburg for several stimulating discussions and comments on an earlier draft of the paper. We also thank the anonymous referee for constructive comments that led to several improvements. The work has been performed under the Project HPC-EUROPA3 (INFRAIA-2016-1-730897), with the support of the EC Research Innovation Action under the H2020 Programme; in particular, the author gratefully acknowledges the support of Dhrubaditya Mitra (NORDITA, Stockholm) and the computer resources and technical support provided by PDC, Stockholm. We used the following python packages: NUMPY (Walt 2011), JUPYTER NOTEBOOK (Kluyver et al. 2016), MATPLOTLIB (Hunter 2007), PANDAS (McKinney 2010), SCIKIT-LEARN (Pedregosa et al. 2011), EMCEE (Foreman-Mackey et al. 2013), MINEPY (Albanese et al. 2012).
References
- Albanese, D., Filosi, M., Visintainer, R., et al. 2012, Bioinformatics, 29, 407 [CrossRef] [Google Scholar]
- Blackman, E. G. 2015, Space Sci. Rev., 188, 59 [Google Scholar]
- Blackman, E. G., & Brandenburg, A. 2002, ApJ, 579, 359 [Google Scholar]
- Blackman, E. G., & Field, G. B. 2002, Phys. Rep., 89, 265007 [Google Scholar]
- Bollen, K. A., & Pearl, J. 2013, in Eight Myths About Causality and Structural Equation Models, ed. S. L. Morgan (Dordrecht, Netherlands: Springer), 301 [Google Scholar]
- Brandenburg, A. 2001, ApJ, 550, 824 [NASA ADS] [CrossRef] [Google Scholar]
- Brandenburg, A. 2018, J. Plasma Phys., 84, 735840404 [CrossRef] [Google Scholar]
- Brandenburg, A., & Dobler, W. 2002, Comput. Phys. Commun., 147, 471 [Google Scholar]
- Brandenburg, A., & Sokoloff, D. 2002, Geophys. Astrophys. Fluid Dyn., 96, 319 [NASA ADS] [CrossRef] [Google Scholar]
- Brandenburg, A., & Subramanian, K. 2005, Phys. Rep., 417, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Brandenburg, A., Sokoloff, D., & Subramanian, K. 2012, Space Sci. Rev., 169, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Breiman, L. 2001a, Mach. Learn., 45, 5 [CrossRef] [Google Scholar]
- Breiman, L. 2001b, Statist. Sci., 16, 199 [CrossRef] [Google Scholar]
- Breiman, L., Friedman, J., Stone, C. J., & Olshen, R. A. 1984, Classification and Regression Trees (Chapman and Hall/CRC) [Google Scholar]
- Brun, A. S., & Browning, M. K. 2017, Liv. Rev. Sol. Phys., 14, 4 [Google Scholar]
- Brunton, S. L., & Kutz, J. N. 2019, Data-Driven Science and Engineering: Machine Learning, Dynamical Systems, and Control (Cambridge University Press) [CrossRef] [Google Scholar]
- Charbonneau, P. 2014, ARA&A, 52, 251 [Google Scholar]
- Ercolano, B., & Pascucci, I. 2017, R. Soc. Open Sci., 4, 170114 [Google Scholar]
- Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [CrossRef] [Google Scholar]
- Géron, A. 2017, Hands-On Machine Learning with Scikit-Learn and TensorFlow (O’Reilly Media) [Google Scholar]
- Grinstead, C., & Snell, J. 1997, Introduction to Probability, 2nd ed. (Providence, RI: American Mathematical Society) [Google Scholar]
- Guido, S., & Müller, A. C. 2017, Introduction to Machine Learning with Python (O’Reilly Media) [Google Scholar]
- Guyon, I., & Elisseeff, A. 2003, J. Mach. Learn. Res., 3, 1157 [Google Scholar]
- Hastie, T., Tibshirani, R., & Friedman, J. 2009, The Elements of Statistical Learning (Springer: New York) [Google Scholar]
- Hastie, T., Tibshirani, R., & Wainwright, M. 2015, Statistical Learning with Sparsity (Chapman and Hall/CRC) [CrossRef] [Google Scholar]
- Haugen, N. E., Brandenburg, A., & Dobler, W. 2004, Phys. Rev. E, 70, 016308 [NASA ADS] [CrossRef] [Google Scholar]
- Hennigh, O. 2017, ArXiv e-prints [arXiv:1705.09036] [Google Scholar]
- Hubbard, A., & Brandenburg, A. 2009, ApJ, 706, 712 [NASA ADS] [CrossRef] [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Jepps, S. A. 1975, J. Fluid Mech., 67, 625 [NASA ADS] [CrossRef] [Google Scholar]
- Karak, B. B., Rheinhardt, M., Brandenburg, A., Käpylä, P. J., & Käpylä, M. J. 2014, ApJ, 795, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Kluyver, T., Ragan-Kelley, B., Pérez, F., et al. 2016, in Positioning and Power in Academic Publishing: Players, Agents and Agendas, eds. F. Loizides, & B. Schmidt (IOS Press), 87 [Google Scholar]
- Krause, F., & Rädler, K. H. 1980, Mean-field Magnetohydrodynamics and Dynamo Theory [Google Scholar]
- Krause, F., & Steenbeck, M. 1967, Z. Naturforsch. Teil A, 22, 671 [NASA ADS] [CrossRef] [Google Scholar]
- Kutz, J. N. 2013, Data-Driven Modeling& Scientific Computation: Methods for Complex Systems& Big Data (New York: Oxford University Press, Inc.) [Google Scholar]
- Kutz, J. N. 2017, J. Fluid Mech., 814, 1 [Google Scholar]
- LeCun, Y., Bengio, Y., & Hinton, G. E. 2015, Nature, 521, 436 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Louppe, G. 2014, PhD Thesis, University of Liege, Belgium [Google Scholar]
- Lusch, B., Kutz, J. N., & Brunton, S. L. 2018, Nat. Commun., 9 [Google Scholar]
- McKinney, W. 2010, in Proceedings of the 9th Python in Science Conference, eds. S. van der Walt, & J. Millman, 51 [Google Scholar]
- Meinshausen, N., & Bühlmann, P. 2010, J. R. Stat. Soc. Ser. B (Stat. Method.), 72, 417 [CrossRef] [Google Scholar]
- Nauman, F., & Blackman, E. G. 2014, MNRAS, 441, 1855 [NASA ADS] [CrossRef] [Google Scholar]
- Navon, I. M. 2009, in Data Assimilation for Numerical Weather Prediction: A Review, eds. S. K. Park, & L. Xu (Berlin, Heidelberg: Springer), 21 [Google Scholar]
- Olson, R. S., Cava, W. L., Mustahsan, Z., Varik, A., & Moore, J. H. 2017, Biocomputing 2018 (World Scientific) [Google Scholar]
- Pedregosa, F., Varoquaux, G., Gramfort, A., et al. 2011, J. Mach. Learn. Res., 12, 2825 [Google Scholar]
- Pouquet, A., Frisch, U., & Leorat, J. 1976, J. Fluid Mech., 77, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Raschka, S. 2018, CoRR [arXiv:1811.12808] [Google Scholar]
- Rheinhardt, M., & Brandenburg, A. 2010, A&A, 520, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rheinhardt, M., & Brandenburg, A. 2012, Astron. Nachr., 333, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Schrinner, M., Rädler, K.-H., Schmitt, D., Rheinhardt, M., & Christensen, U. R. 2007, Geophys. Astrophys. Fluid Dyn., 101, 81 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Shukurov, A., Sokoloff, D., Subramanian, K., & Brandenburg, A. 2006, A&A, 448, L33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Strobl, C., Boulesteix, A.-L., Kneib, T., Augustin, T., & Zeileis, A. 2008, BMC Bioinf., 9, 307 [CrossRef] [Google Scholar]
- Subramanian, K. 2019, Galaxies, 7, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Tibshirani, R. 1996, J. R. Stat. Soc. Ser. B (Method.), 58, 267 [Google Scholar]
- Tilgner, A., & Brandenburg, A. 2008, MNRAS, 391, 1477 [NASA ADS] [CrossRef] [Google Scholar]
- Tobias, S. M., & Cattaneo, F. 2013, Nature, 497, 463 [NASA ADS] [CrossRef] [Google Scholar]
- Vainshtein, S. I., & Cattaneo, F. 1992, ApJ, 393, 165 [NASA ADS] [CrossRef] [Google Scholar]
- Walt, S. V. D., Colbert, S. C., & Varoquaux, G. 2011, Sci. Eng., 13, 22 [Google Scholar]
- Wolpert, D. H. 1992, Neural Netw., 5, 241 [CrossRef] [Google Scholar]
- Wurster, J., & Li, Z.-Y. 2018, Front. Astron. Space Sci., 5, 39 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Summary of the advantages and disadvantage of different models considered in this work.
All Figures
 |
Fig. 1. 3D parametric visualization of the |
| In the text | |
 |
Fig. 2. Heat map of correlation coefficients between the different fields: Rm = 103 (left panel), Rm = 1.5 × 104 (right panel). This analysis implies that the ℰx has a strong correlation with |
| In the text | |
 |
Fig. 3. Fits for linear basis (left panel) and polynomial basis (right panel) for random forests and LASSO. Note that the horizontal lines seen in the fits are there because of decision tree regression: decision trees set one value of the y-axis for a given range of x-axis leading to a step-function like fit. In both cases, LASSO seems to do a better job at capturing the curved shape of the vertical profiles. The black vertical dashed line presents the train-test split (80% training data). |
| In the text | |
 |
Fig. 4. EMF evolution for Rm = 1.5 × 104. Left: ℰx component is shown without any pre-processing (z = π). Right: here we show |
| In the text | |
 |
Fig. 5. The fits for |
| In the text | |
 |
Fig. 6. MCMC fits for the reconstructed ℰ2 fields. Three panel shows maximum likelihood Monte Carlo realizations of the fits (blue line) against the true ℰ2 curve (red line) for Rm = 500, 5 × 103, and 1.5 × 104. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



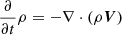
![$$ \begin{aligned} \frac{\partial }{\partial t}\boldsymbol{V}&= -\frac{1}{\rho } \left[ \boldsymbol{V}\cdot \nabla \cdot \boldsymbol{V}+ \nabla p - 2\nabla \cdot (\nu \rho \boldsymbol{S}) - \boldsymbol{J}\times \boldsymbol{B}\right] + \boldsymbol{f} \end{aligned} $$](/articles/aa/full_html/2019/09/aa35945-19/aa35945-19-eq3.gif)
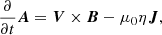
![$$ \begin{aligned} \boldsymbol{f}(t,\boldsymbol{r}) = {Re}\left\{ N\boldsymbol{f}_{\boldsymbol{k}(t)}\exp [i\boldsymbol{k}(t)\cdot \boldsymbol{x} + i\phi (t)] \right\} , \end{aligned} $$](/articles/aa/full_html/2019/09/aa35945-19/aa35945-19-eq7.gif)
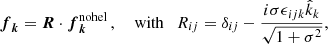
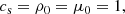
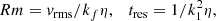
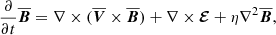
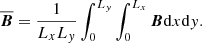
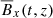
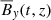
![$$ \begin{aligned} \mathrm{argmin} _{ w} \left[ || { y} - X { w} ||_2^2 + \alpha || { w} ||_1 \right], \end{aligned} $$](/articles/aa/full_html/2019/09/aa35945-19/aa35945-19-eq27.gif)