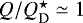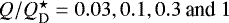| Issue |
A&A
Volume 629, September 2019
|
|
|---|---|---|
| Article Number | A122 | |
| Number of page(s) | 12 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201935690 | |
| Published online | 17 September 2019 | |
Impacts into rotating targets: angular momentum draining and efficient formation of synthetic families
1
Institute of Astronomy, Charles University, Prague,
V Holešovičkách 2,
18000
Prague 8,
Czech Republic
e-mail: sevecek@sirrah.troja.mff.cuni.cz
2
Physics Institute, University of Bern, NCCR PlanetS,
Sidlerstrasse 5,
3012
Bern,
Switzerland
Received:
13
April
2019
Accepted:
7
August
2019
About 10% of the observed asteroids have rotational periods lower than P = 3 h and seem to be relatively close to the spin barrier. Yet, the rotation has often been neglected in simulations of asteroid collisions. To determine the effect of rotation, we performed a large number of impact simulations with rotating targets. We developed a new unified smoothed particle hydrodynamics and N-body code with self-gravity, suitable for simulations of both fragmentation phase and gravitational reaccumulation. The code has been verified against previous ones, but we also tested new features, such as rotational stability, tensile stability, etc. Using the new code, we ran simulations with Dpb = 10 and 100 km monolithic targets and compared synthetic asteroid families created by these impacts with families corresponding to non-rotating targets. The rotation affects mostly cratering events at oblique impact angles. The total mass ejected by these collisions can be up to five times larger for rotating targets. We further computed the transfer of the angular momentum and determined conditions under which impacts accelerate or decelerate the target. While individual cratering collisions can cause both acceleration and deceleration, the deceleration prevails on average. Collisions thus cause a systematic spin-down of the asteroid population.
Key words: minor planets, asteroids: general / methods: numerical
© ESO 2019
1 Asteroid collisions in the main belt
The main belt of asteroids is a collisional system. The breakups of asteroids have been recorded in the form of asteroid families (Nesvorný et al. 2015; Vinogradova 2019). We can also see impact features, such as craters or boulders, on surfaces of asteroids. These features can be observed directly during a satellite flyby or even with ground-based instruments (Vernazza et al. 2018; Fétick et al. 2019).
Physical processes during asteroid collisions are rather complicated for purely analytical estimates to yield precise quantitative results, as it is necessary to model a propagation of shock wave in the target, crack growth and consequent fragmentation, gravitational reaccumulation of ejected fragments, etc. Fragmentation of targets due to hyper-velocity impacts has been studied using laboratory experiments (Nakamura & Fujiwara 1991; Morris & Burchell 2017; Wickham-Eade et al. 2018). While the experiments can produce valuable constraints, the results cannot be directly compared with the breakups of asteroids, as the sizes of targets and kinetic energies of the impact would have to be extrapolated over several orders of magnitude. Experiments also do not take into account a gravitational reaccumulation. The collisions of asteroids are therefore commonly studied using numerical methods; the experiments then provide the calibration for the respective numerical codes.
Common methods for studying the collisions can be divided into particle-based (for example the N-body code pkdgrav, see Richardson et al. 2000) and shock-physics ones, such as mesh-based methods (used by code iSALE, see Suetsugu et al. 2018), or the smoothed particle hydrodynamics (Jutzi et al. 2015), used in this work. This is a Lagrangian, gridless method, which makes it suitable for impact simulations, as the computational domain is not a priori known. Especially in a hit-and-run impact, fragments of the projectile can travel to considerable distances from the target. In the smoothed particle hydrodynamics (SPH), the distant fragments do not require any special handling (they only might affect the performance of the code). SPH is also versatile, allowing the relatively easy implementation of new physics. The model of fragmentation can be straightforwardly incorporated into SPH, but it would be a difficult task for grid-based methods.
An outcome of a collision depends on a number of parameters, namely the diameter Dpb of the target, the diameter dimp of the projectile, the specific impact energy Q, the impact angle ϕimp, but also the rotational periods of the colliding bodies, their shapes, material properties, etc. For completeness, we should also include parameters introduced by the numerical scheme, such as the spatial resolution, the time step, the artificial viscosity ΠAV, etc. The extent of this parameter space prohibits a thorough analysis of every collision as a function of all the mentioned parameters, we thus have to restrict ourselves to a particular set of simulations, varying some parameters and keeping the others constant.
Asteroidal targets have been considered non-rotating in most previous studies of asteroid families (Durda et al. 2007; Benavidez et al. 2012; Ševeček et al. 2017; Benavidez et al. 2018; Jutzi et al. 2019). Jutzi et al. (2013) considered a rotating Vesta, though rotating bodies have also been studied by Jutzi & Benz (2017). Ćuk & Stewart (2012) and Canup (2008) take the rotation into account for simulations of the Moon-forming impact and Canup (2005) for the impact event forming Pluto and Charon. Ballouz et al. (2015) used an N-body code to simulate collisions of rotating rubble-pile asteroids, while Takeda & Ohtsuki (2007, 2009) studied the angular momentum transfer for both stationary and rotating rubble-piles. In this work, we study formation of asteroid families from monolithic targets, extending the parameters of the simulation by the initial rotational period Ppb of the target, including cases close to the spin barrier.
The paper is organized as follows. In Sect. 2, we describe our numerical model. Section 3 analyzes differences between synthetic families created from parent bodies with various rotational periods. Section 4 is focusedon largest remnants, specifically on their accelerations or decelerations and the angular momentum transfer. Finally, we summarize our results in Sect. 5.
2 Numerical model
We developed a new SPH and N-body code. The code is publicly available, see Appendix C. In this section, we do not attemptto present a thorough review of the SPH method (as e.g., Cossins 2010), but instead we summarize the exact equations used in the code, emphasizing the modifications introduced in order to properly deal with rotating bodies.
2.1 Equations
The set of hydrodynamical equations is solved with a smoothed particle hydrodynamics (Monaghan 1985). The continuum is discretized into particles comoving with the continuum, with the density profile of the particles given by a kernel W, which is a cubic spline in our case:
![\begin{equation*} W(r, h) = \frac{\sigma}{h^3} \left\{\begin{array}{ll} \frac{1}{4}(2-q)^3-(1-q)^3, & 0\leq q < 1, \\[2pt] \frac{1}{4}(2-q)^3, & 1\leq q < 2 , \\[2pt] 0 & q \geq 2 , \end{array} \right. \end{equation*}](/articles/aa/full_html/2019/09/aa35690-19/aa35690-19-eq1.png) (1)
(1)
where q ≡ r∕h.
Below, we denote indices of particles with Latin subscripts (usually i, j, ...), the components of vector and tensor quantities with Greek superscripts (usually α, β, ...). We also use Einstein notation to sum over components (but not for particles).
The equation of motion for ith particle reads:
![\begin{eqnarray*} \frac{\textrm{d} v_i^{\alpha}}{\textrm{d} t} & = & \sum_j m_j \left( \frac{\sigma^{\alpha \beta}_i}{\rho_i^2} + \frac{\sigma^{\alpha \beta}_j}{\rho_j^2} + \Pi_{ij} \delta^{\alpha\beta} + \zeta^{\alpha\beta}_{ij} f^n\right) \frac{\partial W_{ij}}{\partial x^{\beta}}\nonumber \\[2pt] && +\, \nabla \Phi - \left[\bm{\omega} \times (\bm{\omega} \times \bm{r}_i)\right]^{\alpha} - \left[2\bm{\omega} \times \bm{v}_i\right] ^{\alpha} ,\end{eqnarray*}](/articles/aa/full_html/2019/09/aa35690-19/aa35690-19-eq2.png) (2)
(2)
where σαβ = −Pδαβ + Sαβ is the total stress tensor, Π is the artificial viscosity (Monaghan & Gingold 1983), ζαβfn is the artificial stress (Monaghan 2000), Φ is the gravitational potential (including both external fields and self-gravity of particles), and ω is the angular velocity of the reference frame.
The respective terms in the Eq. (2) correspond to the stress divergence, gravitational acceleration, centrifugal force, and Coriolis force. Inertial forces are only applied if the simulation is carried out in a non-inertial reference frame, corotating with the target asteroid (see Appendix B).
We used the standard artificial viscosity with linear and quadratic velocity divergence terms and coefficients αAV and βAV, respectively. This term is essential for a proper shock propagation and thus was always enabled in our simulations. Optionally, the code allows enabling the Balsara switch (Balsara 1995), which reduces the artificial viscosity in shear motions in order to reduce an unphysical angular momentum transfer. Additionally, the code includes the artificial stress term ζαβ fn, which reduces the tensile instability, meaning an unphysical clustering of particles due to negative pressure. We tested the effects of this term using the “colliding rubber cylinders” test (cf. Schäfer et al. 2016).
We used a different discretization of the equation than in Ševeček et al. (2017), as we found the above equation to be more robust, avoiding a high-frequency oscillation in the pressure field. This is a recurring problem in high-velocity impact simulations and while it can be suppressed by a larger kernel support, additional modifications of the method have been suggested to address the issue, for example the δ-SPH modification (Marrone et al. 2011). The density is evolved using the continuity equation:
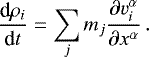 (3)
(3)
We solved the evolution equation instead of direct summation of particle masses to avoid the artificial low-density layer at the surface of the asteroid (Reinhardt & Stadel 2017). The velocity gradient at the right-hand side of Eq. (3) is computed as:
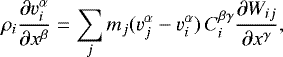 (4)
(4)
where the correction tensor Cαβ is defined as(Schäfer et al. 2016):
![\begin{equation*} C_i^{\alpha\beta} \equiv \left[ \sum_j \frac{m_j}{\rho_j} (r_j^{\alpha} - r_i^{\alpha}) \frac{\partial W_{ij}}{\partial x^{\beta}} \right]^{-1}\,.\end{equation*}](/articles/aa/full_html/2019/09/aa35690-19/aa35690-19-eq5.png) (5)
(5)
In the case the bracketed matrix was not invertible, we used the Moore–Penrose pseudo-inverse instead. The correction tensor is further set to 1 for fully damaged material.
The correction tensor has been introduced to tackle the linear inconsistency of the standard SPH formulation. It is a fundamental term in the velocity gradient that allows for a stable bulk rotation of the simulated body and significantly improves the conservation of the total angular momentum. We evolved the internal energy u using the energy equation:
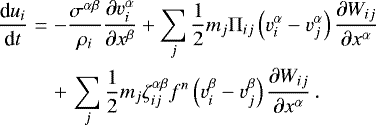 (6)
(6)
In this equation the velocity gradient is also corrected by the tensor Cαβ. While this is required for a consistent handling of rotation, the inequality of kernel gradients used in the energy equation (Eq. (6)) and in the equation of motion (Eq. (2)) implies the total energy is generally not conserved in the simulations. This is usually not an issue, as the total energy does not increase by more than 5%.
However, in some cases (e.g., weak cratering impacts or exceedingly long integration time), the energy growth can be prohibitive. For such cases, the code also offers an alternative way to evolve the internal energy, using a compatibly-differenced scheme (Owen 2014). Instead of computing the energy derivative, the energy change is computed directly from particle pair-wise accelerations 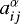 and half-step velocities
and half-step velocities 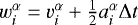 , using the equation:
, using the equation:
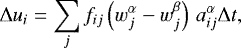 (7)
(7)
where the energy partitioning factors fij can be chosen arbitrarily, provided they fulfill constraint fij + fji = 1. With this form of SPH, the total energy can be conserved to machine precision, at a cost of performance overhead. However, this does not solve the inconsistency mentioned above.
The listed set of equations is supplemented by the Tillotson equation of state (Tillotson 1962). To close the set of equations, we have to specify the constitutive equation. We used the Hooke’s law, evolving the deviatoric stress tensor in time using:
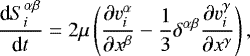 (8)
(8)
where μ denotes the shear modulus. To account for plasticity of the material, we further used the von Mises criterion, which reduces the deviatoric stress tensor by the factor:
![\begin{equation*} f = \operatorname{min}\left[ \frac{Y_0^2(1-u/u_{\textrm{melt}})^2}{\frac{3}{2} S^{\alpha\beta} S^{\alpha\beta}}, 1 \right], \end{equation*}](/articles/aa/full_html/2019/09/aa35690-19/aa35690-19-eq11.png) (9)
(9)
where Y0 is the yield stress and umelt is the specific melting energy. While more complex, pressure-dependent rheology models exist (Jutzi et al. 2015), von Mises rheology is reasonable for monolithic asteroids and still consistent with laboratory experiments (Remington et al. 2018). The effects of friction have been studied by Jutzi et al. (2015) or Kurosawa & Genda (2018) so we do not discuss such effect in this work.
Additionally, we integrated the fragmentation model to model an activation of flaws and a propagation of fractures in the material. Following Benz & Asphaug (1994), we define a scalar quantity damage D, modifying the total stress tensor as
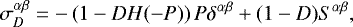 (10)
(10)
where H(x) is the Heaviside step function. A fully damaged material (D = 1) has no shear nor tensile strength, it only resists compressions.
Smoothing lengths of particles are evolved to balance the changes of particle concentration. We thus derived the equation directly from the continuity equation:
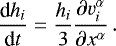 (11)
(11)
Since it is also an evolution equation, we need to specify the initial conditions for smoothing lengths:
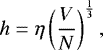 (12)
(12)
where V is the volume of the body, N is the number of particles in the body and η is a free non-dimensional parameter, which we set to η = 1.3. This corresponds to an average number of neighboring particles Nneigh ≃ 65.
2.2 Gravity
Beyond hydrodynamics, the code also computes accelerations of SPH particles due to self-gravity. To compute it efficiently (albeit approximately), we employed the Barnes-Hut algorithm (Barnes & Hut 1986). Instead of computing pair-wise interactions of particles, we first clustered the particles hierarchically and evaluated gravitational moments of particles in each node of the constructed tree. The accelerations were then computed by a tree-walk; if the evaluated node was distant enough, the acceleration could be approximated by evaluating the multipole moments up to the octupole order, otherwise we descended into child nodes. The precision of the method is controlled by an opening radius ropen. For an extensive description of the method, see Stadel (2001).
As our SPH particles are spherically symmetric, they can be replaced by point masses, provided they do not intersect each other (the corresponding kernel Wij is zero). However, it is absolutely necessary to account for softening of the gravitational potential for neighboring particles. We follow Cossins (2010) by introducing a gravitational softening kernel ϕ (associated with the SPH smoothing kernel W) using the equation:
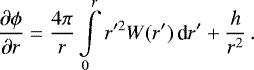 (13)
(13)
The gravitational kernel ϕ corresponding to our M4 spline kernel W is then:
![\begin{equation*} \phi(r, h) = \left\{\begin{array}{ll} \frac{2}{3} q^2 - \frac{3}{10} q^4 + \frac{1}{10} q^5 - \frac{7}{5} ,& 0 \leq q < 1 ,\\[2pt] \frac{4}{3} q^2 - q^3 + \frac{3}{10} q^4 -\frac{1}{10} q^5 \\[2pt] \hskip50pt -\frac{8}{5} + \frac{1}{15q} ,& 1 \leq q < 2 ,\\[2pt] -\frac{1}{q} , & q \geq 2, \end{array} \right.\end{equation*}](/articles/aa/full_html/2019/09/aa35690-19/aa35690-19-eq16.png) (14)
(14)
where q ≡ r∕h. However, this kernel does not have compact support.
2.3 Temporal discretization
Using derivatives computed at each time step, the equations were integrated using explicit timestepping. The scheme used in this work is the predictor-corrector, however other schemes are implemented in the code, such as the leapfrog, fourth order Runge–Kutta, or Bulirsch–Stoer.
The value of the time step is determined by the Courant–Friedrichs–Lewy (CFL) criterion:
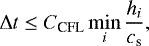 (15)
(15)
where hi is the smoothing length of ith particle, cs the local sound speed, and CCFL is the Courant number. In our simulations, we usually used CCFL = 0.25, as higher values can lead to instabilities in some cases. Moreover, we restricted the time step by the value-to-derivative ratio of all time-dependent quantities in the simulation to control the discretization errors. The upper limit of the time step is therefore:
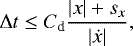 (16)
(16)
where sx is a parameter with the same dimensions as x, assigned to each quantity in order to avoid zero time step if the quantity x is zero. Constant Cd is 0.2 for all quantities.
2.4 Equilibrium initial conditions
Setting up the initial conditions for the impact simulation is not a trivial task. It is necessary to assign a particular value to the density ρ, internal energy u, and deviatoric stress tensor S to each particle, so that the configuration is stable when the impact simulation starts and the particles do not oscillate.
This problem is not restricted to simulations with rotating targets. A proper handling of initial conditions is essential in simulations of the Moon formation, collisions of planetary embryos, etc. If neglected, the initial gravitational compression would introduce macroscopic radial oscillations in the target.
For small and stationary asteroids with D ≃ 10 km, the self-gravity is much less important, in fact it was often completely neglected during the fragmentation phase (as in Ševeček et al. 2017). These asteroids are assumed to be undifferentiated, hence it was reasonable to set up a homogeneous bulk density of ρ0 = const. For these stationary targets, the stress tensor of particles is zero in equilibrium.
For rotating targets, however, such initial conditions are unstable due to the emerged centrifugal force (in the corotating frame). To prevent any unphysical fractures in the target, the configuration of particles has to be set up carefully, especially for asteroids rotating close to the critical spin rate. For this reason, we run a stabilization phase before the actual impact simulation, with an artificial damping of particle velocities:
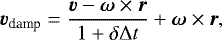 (17)
(17)
where v is the undamped velocity, ω the angular frequency of the target, r the position vector of the particle, δ an arbitrary damping coefficient (gradually being decreased during the stabilization phase), and Δt the actual time step. In this equation, we need to subtract and re-add the bulk rotation velocity, otherwise the damping would cause the target to slow down. We also did not integrate the fragmentation model during this phase, as the oscillations of the particles might damage the target prematurely.
While more general approaches for setting up the initial conditions exist (Reinhardt & Stadel 2017), the presented method is simple, robust, and sufficient for our purposes. A disadvantage of our method is a significant computational overhead, as for some simulations the time needed to converge into a stable solution is comparable to the duration of the actual impact simulation. However, here we performed many simulations with fixed target diameter Dpb and period P, so we had to precompute the initial conditions only once and then used the cached particle configuration for other runs.
2.5 Reaccumulation phase
As our numerical model contains both the hydrodynamics and the gravitational interactions, it could be used for the entire simulation – from the stabilization, pre-impact flight, fragmentation phase until the gravitational reaccumulation of all fragments. However, the time step is often severely limited by the CFL criterion (Eq. (15)).
We can increase the time step by several orders of magnitude and hence speed up the simulation considerably by changing the numerical scheme from SPH to N-body integration. This is a common approach in studies of asteroid families (Durda et al. 2007; Michel et al. 2015; Ševeček et al. 2017; Jutzi et al. 2019). Once the target is fully fractured and the fragments start to recede, we converted all SPH particles into hard spheres and replaced the complexity of hydrodynamic equations with a simple collision detection. This allows us to overcome the time step limitation.
We further optimized the simulation by merging the collided particles into larger spheres. By doing so, we lost information about the shape of the fragments; to preserve the shapes, it is necessary to either form rigid aggregates of particles instead of mergers (Michel & Richardson 2013), or simulate the entire reaccumulation using the SPH (as in Sugiura et al. 2018). Here, as we are mainly interested in distribution of sizes and rotational periods, merging the particles is thus a viable option.
Merging not only affects the shape, but also the dynamics of fragments. As it modifies the moment of inertia, the merger has a generally different rotational period than a real non-spherical fragment would have. Merging also removes higher gravitational moments, thus altering motion of near fragments. This is a slight limitation of the presented model.
Hard spheres are created directly from SPH particles. Their mass is unchanged, and the radius of the formed spheres is computed as:
![\begin{equation*} r_i = \sqrt[3]{\frac{3m_i}{4\pi\rho_i}} ,\end{equation*}](/articles/aa/full_html/2019/09/aa35690-19/aa35690-19-eq20.png) (18)
(18)
so that the volume of spheres is equal to the volume of SPH particles. As the total volume is conserved, created spheres inevitably overlap. Appendix A describes how the code handles such overlaps.
When two spheres collide, they are merged only if their relative speed is lower than the mutual escape speed
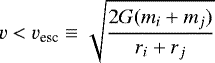 (19)
(19)
and if the rotational angular frequency of the merger does not exceed the critical frequency
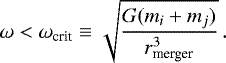 (20)
(20)
In this way we prevent formation of unphysically fast rotators. If any of these conditions is not fulfilled, particles undergo an inelastic bounce. The damping of velocities is determined by the normal ηn and tangential ηt coefficient of restitution, which we set to 0.5 and 1, respectively.
When merging the particles, we determined the mass, radius, velocity, and angular frequency of the merger, so that the total mass, volume, momentum, and angular momentum are conserved. As the tangential components of velocities are not damped by a bounce, merging is the only way to spin up fragments in our simulations.
3 Synthetic families created from rotating targets
To better understand how the rotation influences impact events, we decided to compute a matrix of simulations for various impact parameters. We ran simulations for two different target sizes, Dpb = 10 km and Dpb = 100 km, in order to ascertain the scaling of the rotational effect. We tested head-on impacts, having the impact angle ϕimp = 15°, the intermediate cases with ϕimp = 45°, and oblique impacts with ϕimp = 75°. We have to further distinguish prograde events, meaning impacts where the orbital velocity has the same direction as the impact velocity, and retrograde events, where the orbital velocity has the opposite direction. In the following, the prograde impacts have positive values of impact angles, while the retrograde impacts have negative values.
In all of our simulations, we set the impact velocity to vimp= 5 km s−1, which is close to the mean velocity for Main-belt collisions (Dahlgren 1998). The simulation matrix covers both the cratering and the catastrophic events. We ran simulations with relative impact energies 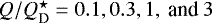 , where the critical energy
, where the critical energy 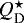 is given by the scaling law of Benz & Asphaug (1999). As
is given by the scaling law of Benz & Asphaug (1999). As 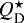 is defined as the specific impact energy (relative to mass of the target) required to eject 50% of the target’s mass as fragments, it necessarily depends on the rotational period of the target. However, we consider
is defined as the specific impact energy (relative to mass of the target) required to eject 50% of the target’s mass as fragments, it necessarily depends on the rotational period of the target. However, we consider 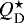 to be independentof rotation and used the same value for all performed simulations, as it provides a convenient dimensionless measure of the impact energy.
to be independentof rotation and used the same value for all performed simulations, as it provides a convenient dimensionless measure of the impact energy.
We assume that both the target and the impactor are monolithic bodies, the material parameters are summarized in Table 1. The spatial resolution of the target was approximately N = 500 000 SPH particles and the number of projectile particles was selected to match the particle density of the target. Three simulations with different periods Ppb are shown in Fig. 1.
 |
Fig. 1 Impacts into Dpb = 100 km targets without rotation (first row), rotational period Ppb = 3 h (second row), and Ppb = 2 h (third row). The period of two hours is approximately the critical period of the target. The color brightness corresponds to specific internal energy of the particles. |
Material parameters used in simulations.
3.1 Coordinate system
Due to the rotation, the impact geometry is more complex compared to the stationary case, where it was determined by a single parameter – the impact angle ϕimp between the normal at the impact point and the velocity vector of the impactor. To describe the impact into a rotating target, we first defined a coordinate system of the simulations. We placed the target at origin with zero velocity. The impactor has velocity [−vimp;0;0] and its position in x-y plane is given by ϕimp, specifically:
![\begin{equation*} \bm{r}_0 = \left[ \begin{array}{l} x_0 + 0.5 (D_{\textrm{pb}} + d_{\textrm{imp}})\cos \phi_{\textrm{imp}}, \\ 0.5 (D_{\textrm{pb}} + d_{\textrm{imp}})\sin \phi_{\textrm{imp}}, \\ 0 \end{array}\right], \end{equation*}](/articles/aa/full_html/2019/09/aa35690-19/aa35690-19-eq27.png)
where x0 is the distance of the impactor from the impact point. These initial conditions have a mirror symmetry in z.
The rotation vector ωpb of the target adds an additional three free parameters into the simulation setup. Generally, the vector does not have to be aligned with any coordinate axis. We reduced the number of free parameters and thus simplified the analysis by aligning the vector with z-axis, meaning we only consider impacts in the equatorial plane of the target. We expect these impacts will be affected by the rotation the most, as the centrifugal force is the largest on the equator. Furthermore, the angular momentum of the target is aligned with the angular momentum of the impactor. We can thus expect the largest changes in the angular momentum. These expectations have been confirmed for rubble-pile bodies by N-body simulations of Takeda & Ohtsuki (2009).
3.2 Size-frequency distributions for Dpb = 10 km targets
The first set of simulations was carried out with the target size Dpb = 10 km. The diameters of impactors were dimp = 394, 570, 850, and 1226 m, respectively. We ran a number of simulations for different Ppb, dimp, and ϕimp and compared the size-frequency distribution (SFD) of a family created by an impact into a rotating target with corresponding impact into a stationary target. The resulting distributions are plotted in Fig. 2.
At firstglance, the differences between the targets rotating with a period of Ppb = 3 h and the non-rotating targets are relatively small. The slope of the SFD is almost unchanged in most simulations, it is only shifted as more mass is ejected from the rotating target. In several simulations, like for ϕimp = −45° and dimp = 0.85 km, we can see a larger number of fragments in the middle part of the SFD for rotating targets; fragments that would reaccumulate to the largest remnant in the stationary case now escape due to the extra speed from rotation and contribute to the family.
Much larger differences in SFDs can be seen for the target with period Ppb = 2 h, which is rather expected; for ρ0 = 2700 kg m−3 the critical period is Pcrit ≃ 2.009 h, so a Ppb = 2 h target actually rotates very slightly supercritically, although it is held stable by the material strength. The difference is the most prominent for oblique ϕimp = ±75° impacts. In several cases, the rotation seems to make the SFD less steep, although this might be partially attributed to a numerical artifact, as the synthetic families of non-rotating targets are already very close to the resolution limit.
On the other hand, energetic impacts produce practically the same SFDs regardless of Ppb. In this regime, angular momentum of projectiles is larger than the rotational angular momentum of the target; for 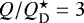 and Ppb = 2 h, the angular momentum of a projectile is five times larger. Ejection velocities are also considerably larger than orbital velocities, hence it is not surprising that the rotation does not make a substantial difference.
and Ppb = 2 h, the angular momentum of a projectile is five times larger. Ejection velocities are also considerably larger than orbital velocities, hence it is not surprising that the rotation does not make a substantial difference.
It is not probable that these differences come from different fragmentation patterns, as targets are fully damaged by the impact. In our model, such damaged material is strengthless and it essentially behaves like a fluid. Since there is no internal friction nor a mechanism to regain the material strength, this model is insufficient to determine shapes of the fragments; however, here we are only interested in size distributions and using a simplified model is therefore justified.
 |
Fig. 2 Cumulative size-frequency distributions N(>D) of synthetic families for Dpb = 10 km targets. Stationary targets are plotted in black; red and yellow plots correspond to targets with rotational period P = 3 h and P = 2 h, respectively.Columns 3–5 of the plot show prograde impacts (i.e., positive impact angles); Cols. 1 and 2 are retrograde impacts (i.e., negative impact angles). |
3.3 Size-frequency distributions for Dpb = 100 km targets
It is a priori not clear how rotation affects targets of different sizes. To preliminarily estimate the importance of initial rotation, we computed the ratio of the angular frequency ωpb of the targetand ωimp of the impactor with respect to the target:
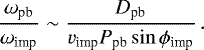 (21)
(21)
Because the ratio scales linearly with the target size Dpb, we expect that the rotation will play a bigger role for impacts into larger targets; however, this back-of-the-envelope computation is by no means definite proof and it needs to be tested.
To thispoint, we ran a set of simulations with target size Dpb = 100 km. The set is analogous to the one in Sect. 3.2: we used the same impact angles and rotational periods, the impactor diameters were dimp = 11.170, 16.110, 24.064, and 34.706 km in order to obtain the required relative energies 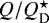 . The size-frequency distributions of the synthetic families are plotted in Fig. 3.
. The size-frequency distributions of the synthetic families are plotted in Fig. 3.
As expected, the differences between rotating and non-rotating targets are indeed substantially larger than for Dpb = 10 km. The rotation can completely change the impact regime from cratering to catastrophic; see for example the impact with ϕimp = 15° and dimp = 16.110 km, where a cratering gradually changes to a catastrophic disruption as we decrease Ppb. Focusing on Ppb = 3 h targets, they produce very shallow SFD in case of oblique prograde impacts. For ϕimp = ±45° cratering impacts, we see numerous intermediate-sized fragments (somewhat separated in the SFD) if the target is non-rotating, but the SFD becomes continuous when rotation is introduced.
The effects are even stronger for critically rotating bodies with Ppb = 2 h, of course. Generally, SFDs of formally cratering events are more similar to catastrophic ones. It also seems that oblique retrograde craterings produce more fragments than prograde ones. For the impact ϕimp = 15° and dimp = 24.064 km, the SFD is well below the non-rotating case and most of the mass is contained in the smallest fragments.
Although large (D ≫ 10 km) asteroids typically rotate much slower than smaller bodies, there are a few that rotate close to the critical spin rate for elongated bodies, such as (216) Kleopatra (Hirabayashi & Scheeres 2014). Rotation in collisional simulations of such bodies should therefore not be neglected.
3.4 Total ejected mass
While Figs. 2 and 3 clearly show the differences between the SFDs, it is quite difficult to read the total mass ejected from the target during the impact. Even when the SFDs of a rotating and a stationarytarget seem to differ only negligibly, the total integrated mass of fragments may be significantly different.
To show the effect of the initial rotation on the ejected mass clearly, we performed over 400 simulations with the target size Dpb = 10 km, various impact angles ϕimp, projectile diameters dimp, and initial periods Ppb of the target. These simulations have a lower spatial resolution compared to the simulations of family formation in previous sections, as here we do not need to resolve individual fragments in detail. The target is resolved by approximately N = 100 000 particles.
We ran simulations for ϕimp ranging from 15°–75° (both prograde and retrograde). To capture the dependence on Ppb, we selected nine different values from Ppb = Pcrit to 50 Pcrit. The impact energies of the simulations were 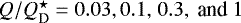 , meaning thesimulations range from cratering events to mid-energy events.
, meaning thesimulations range from cratering events to mid-energy events.
Our goal is to compute the total mass of the fragments as a function of the impact angle ϕimp, the initial rotational period Ppb and the diameter dimp. We are actually not interested in the absolute value of the ejected mass, but rather in the ejected mass relative to the mass that would be ejected if the targets were stationary. Therefore, we computed the ratio:
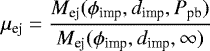 (22)
(22)
and plot the result in Fig. 4. Values μej < 1 would mean that the impact into the rotating target ejected fewer fragments, compared to the stationary target; no such result was found in the performed simulations.
Generally, the rotation amplifies the ejection by several tens of percent. However, the increase is significantly higher if the following conditions are satisfied:
-
Target rotates near the critical period. As expected, the effect of rotation decreases rapidly with the increasing period of the target.
-
The impact results in a cratering rather than a catastrophic event. While high-energy impacts eject more fragments in an absolute measure, the initial rotation does not affect the value notably in this regime.
-
The impact is oblique and has a prograde direction. Head-on impacts and the impacts in retrograde directions are not affected by the rotation to the same degree.
In extreme cases, the rotation can amplify the ejected mass by a factor of five. On the other hand, the ejection ratio μej does not exceed 1.6 for rotational periods Ppb > 2Pcrit in any of the performed simulations.
Although it is a different rheology, rubble-pile bodies also exhibit a minor effect of rotation (on 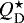 as well as μej) in this range of Ppb (Takeda & Ohtsuki 2009, see Fig. 2 therein). However, their strength is an order of magnitude lower than for monoliths of Benz & Asphaug (1999), so the comparison is not straightforward.
as well as μej) in this range of Ppb (Takeda & Ohtsuki 2009, see Fig. 2 therein). However, their strength is an order of magnitude lower than for monoliths of Benz & Asphaug (1999), so the comparison is not straightforward.
 |
Fig. 3 Cumulative size-frequency distribution for Dpb = 100 km targets. Thenotation is the same as in Fig. 2. |
 |
Fig. 4 Total mass of fragments Mej(P)∕Mej(∞) ejected by collisions, normalized by mass of fragments from corresponding collision into stationary target. The four figures correspond to different relative impact energies, from cratering (left) to mid-energy (right) events. The ejected mass is plotted as a function of the impact angle ϕimp and initial period Ppb of the target. |
 |
Fig. 5 Damage D of the target at time t = 10 s after impact for various impact angles, from left to right, ϕimp = 75°, 45°, 15°, −45°, −75°. Simulations were carried out with the impactor of size dimp = 314 m and speed vimp = 5 km s−1; target was not rotating. The red outline shows the original position of the target and the impactor. There is an undamaged cavity only for oblique impacts, otherwise the target is fully damaged by the impact. |
 |
Fig. 6 Change of spin rate Δω
of target (or largest remnant in case |
4 Embedding and draining the angular momentum
Impact into a rotating target can cause either an acceleration or a deceleration of the target’s rotation. This can be immediatelyseen from two limit cases: a stationary target is always spun by the impact, on the other hand a target rotating at the breakup limit cannot be accelerated any further and the collision thus always causes a deceleration.
It has been proposed that rotating asteroids are decelerated over time by numerous subsequent cratering collisions, as a fraction of the angular momentum is carried away by fragments. Coined the angular momentum drain (Dobrovolskis & Burns 1984), this effect could explain the excess of slow rotators in the main belt. In this section, we examine whether this effect emerges in our simulations and we determine the functional dependence of the deceleration on the impact parameters.
We analyze the angular momentum transfer as a function of impact parameters, using the set of simulations described in Sect. 3.4. The impacts range from cratering (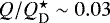 ) to mid-energy (
) to mid-energy (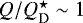 ) events. For
) events. For 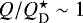 , the whole target asteroid is disintegrated by the collision and fragments with mass of about 0.5 Mpb are reaccumulated later, forming the largest remnant. This can no longer be viewed as a cratering event that merely modifies the rotational state of the target, nevertheless we can still formally compute the relation between the period of the target and the largest remnant.
, the whole target asteroid is disintegrated by the collision and fragments with mass of about 0.5 Mpb are reaccumulated later, forming the largest remnant. This can no longer be viewed as a cratering event that merely modifies the rotational state of the target, nevertheless we can still formally compute the relation between the period of the target and the largest remnant.
In a majority of performed simulations, the target is completely damaged by the impact. There remained an undamaged cavity only for the weakest oblique impacts with 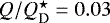 , as shown inFig. 5. Otherwise all particles of the target have damage D = 1 after the fragmentation phase.
, as shown inFig. 5. Otherwise all particles of the target have damage D = 1 after the fragmentation phase.
The change of spin rate Δω of the target is plotted in Fig. 6. We plot the change of frequency rather than period, as the period is formally infinite for anon-rotating body; a change of period is thus not a meaningful quantity.
For cratering events, the prograde events (denoted with positive ϕimp) mostly accelerate the target, while retrograde events cause deceleration. The two exceptions from this rule are:
- 1.
a prograde impact into a critically rotating body, in which case it cannot be accelerated any more and some deceleration is expected; and
- 2.
a retrograde impact to an almost stationary body.
Impacts with higher energies show a different pattern. It seems that the two regions described above expand. Prograde impacts into fast rotators actually decelerate the target, while retrograde impacts start to accelerate it. For the most energetic event we studied, 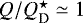 , it seems that the two regions completely swapped: most prograde impacts cause a deceleration while retrograde impacts cause an acceleration.
, it seems that the two regions completely swapped: most prograde impacts cause a deceleration while retrograde impacts cause an acceleration.
The despinning (or angular momentum draining) on rubble-piles in catastrophic disruptions was confirmed by Takeda & Ohtsuki (2009). In our simulations, the pattern is more complex, likely because the parameter space (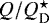 , Ppb) is significantly more extended; additionally rubble-piles cannot initially rotate critically.
, Ppb) is significantly more extended; additionally rubble-piles cannot initially rotate critically.
 |
Fig. 7 Dimensionless effectivity γ of angular momentum transfer. The other quantities are the same as in Fig. 6. |
4.1 Effectivity of the angular momentum transfer
Let us define the effectivity γ of the angular momentum transfer as:
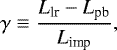 (23)
(23)
where Lpb is the rotational angular momentum of the target before the impact, Lpb is the rotational angular momentum of the largest remnant, and Limp is the angular momentum of the impactor with respect to the target. As these values are scalars, we assign a negative sign to the value Limp for retrograde impacts.
We emphasize that the effectivity γ is not necessarily in the unit interval ⟨0;1⟩. Specifically, it may be significantly larger than one for head-on impacts, as the delivered angular momentum is very low; in fact, Limp approaches zero for ϕimp = 0. The effectivity can also be a negative number for impacts to critically rotating targets, as in these cases, the target cannot accelerate over the breakup limit, so a zero or even negative values of γ are expected.
The effectivity γ as a function of the initial period Ppb, the impact angle ϕimp, and the impactor diameter dimp is plotted in Fig. 7. We can see that cratering impacts have generally higher effectivity than high-energy impacts. This result might have been expected, as the cratering impacts eject less mass and thus transfer less angular momentum to fragments, compared to the catastrophic impacts. A less expected outcome is the negative effectivity for the high-energy impacts. We predicted the negative values only for prograde impacts into critically rotating targets, but for dimp = 850 m the effectivity is negative for the majority of performed simulations.
Finally, the highest effectivity is achieved for retrograde impacts into critically rotating targets. However, this results is slightly false, because in this regime the target is always decelerated; γ can therefore exceed one as the angular momentum lost in the collision is higher than Limp (in absolute value). Impacts into slower rotators have values of γ around 0.5.
4.2 Angle-averaged ejection and momentum transfer
To express an overall effect of collisions on a rotational state of a target, it is useful to consider a large number of collisions at random impact angles and compute the average change of spin rate:
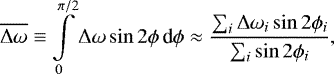 (24)
(24)
where sin2ϕ is the probability of the impact with the impact angle ϕ. The averaged change 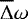 is plotted in Fig. 8, together with a plot of the relative mass ejection
is plotted in Fig. 8, together with a plot of the relative mass ejection 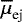 , defined in Sect. 3.4.
, defined in Sect. 3.4.
The figures show that targets are on average decelerated for both low-energy and mid-energy impacts. A target is only accelerated if it was originally a very slow rotator, since it cannot be decelerated any more. The transition between these two regimes (plotted in white) is where the target does not change its angular frequency upon the impact. It seems to depend on the energy of the impact; for 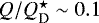 , the transition occurs at around P ~ 20Pcrit, while for
, the transition occurs at around P ~ 20Pcrit, while for 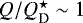 , it is shifted to around P ~ 6Pcrit.
, it is shifted to around P ~ 6Pcrit.
5 Conclusions and future work
In this paper, we showed that a fast initial rotation of targets may significantly affect resulting synthetic families. The effect is more prominent for larger target bodies and for oblique impact angles. Generally, more fragments are ejected from prograde (ϕimp > 0) compared to the retrograde (ϕimp < 0) targets.
In extreme cases, the mass ejection can be amplified by a factor five. Neglecting the rotation would therefore introduce a considerablebias. Other parameters of the simulation do introduce similar (or sometimes larger) uncertainties, for example the Weibull parameters of the fragmentation model (Ševeček et al. 2017), the rheological model of the target, etc. As shown in Jutzi &Benz (2017), the initial shape can also have a significant effect.
Throughout this paper, we assumed that both the targets and impactors are monolithic bodies. It is a priori not clear whether the rotation would be more important for rubble-pile bodies (with macro-porosity), or when a rheological model with crushing (microporosity) is used in the simulations (Jutzi et al. 2019). It should also be explored how initial shapes relate to spin rates of fragments. We postpone such studies to future works.
In the future, we also plan to determine the scaling law as a function of both Dpb and Ppb. It is clear that the critical energy 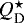 is a steep function of Ppb close to the critical spin rate. Finding a functional dependence
is a steep function of Ppb close to the critical spin rate. Finding a functional dependence 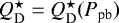 might be a valuable result for studies of main belt evolution, as it could be used to construct a combined model that includes both collisions and rotations.
might be a valuable result for studies of main belt evolution, as it could be used to construct a combined model that includes both collisions and rotations.
 |
Fig. 8 Quantities averaged over impact angles using Eq. (24) as function of period Ppb of target andimpactor diameter dimp. The left figure shows the change of spin rate Δω, the right one the total mass of fragments, normalized by the mass of fragments from corresponding collision into a stationary target. |
Acknowledgements
The work of P.Š. and M.B. has been supported by the Czech Science Foundation (GACR 18-04514J) and Charles University (GAUK 1584517). M.J. acknowledges support from the Swiss National Centre of Competence in Research PlanetS.
Appendix A Handling particle overlaps
Since we treat particles as solid spheres during the reaccumulation phase, particle overlaps are unavoidable and need to be handled by our N-body integrator. There are two main reasons why particle overlaps occur.
First, the spheres overlap initially after the hand-off (Eq. (18)). In SPH, the particles naturally overlap as they describe a continuum rather than point masses. After converting them to solid spheres, particles belonging to the same body will necessarily overlap, unless their radius is decreased significantly.
Second, overlaps occur when particles are being merged. When two spherical particles collide, they merge into a larger particle with volume equal to the sum of volumes of the colliders. This merging is an atomic operation, particles are converted into the merger in an instant rather than over several timesteps, so any other particles located close to the colliders potentially overlap the particle merger.
Our code allows for several options to resolve overlaps. One straightforward solution is to always merge the overlapping particles. While this is a simple and robust solution, it can potentially create unphysical, supercritically rotating bodies. Alternatively, we can repel the overlapping particles, so that they are in contact rather than overlap. However, this causes an “inflation” of the largest remnant after the hand-off. Even worse, the angular momentum is no longer conserved.
Another option is to abandon the 1:1 conversion of spheres and instead construct a new set of spheres inside the alpha-shape of the largest remnant (Ballouz et al. 2018). Such an approach allows the placement of spheres onto a regular grid and to thus avoid overlaps by construction. However, it is more suitable when collided particles form rigid aggregates instead of mergers. As spheres never fill the entire volume (a filling factor of hexagonal close packing is about 0.74) and the merging conserves volume, fragments would shrink considerably.
We decided to merge particles only if the spin rate of the would-be merger is lower than the critical spin rate, otherwise we allow particles to pass through each other. Of course, such handling is only applied to resolve overlaps; particles that collide are always treated as solid.
Appendix B Comparison of inertial and co-rotating reference frames
We can choose two different approaches to implementing the rotation of the target:
- 1.
rotate the particles around the center of the target, and
- 2.
perform the simulation in the coordinate system co-rotating with the target.
From a numerical point of view, the second approach is easier to handle, as the particles of the target initially have zero velocities and we thusavoid numerical problems with the bulk rotation outlined in Sect. 2.1. The rotation is taken into account by introducing inertial accelerations, meaning the last two terms of Eq. (2).
However, it only solves the issue partially. Even though the target is stationary (in the co-rotating frame) before the impact, the projectile can spin up the target and the impact can also eject rotating fragments. To properly handle rotating bodies in SPH, it is necessary to introduce the correction tensor in Eq. (5). This allows us to perform simulations in the inertial frame, which is a natural choice.
Ideally, these two approaches should produce identical results. To test it, we ran two simulations with Dpb = 200 km parent bodies rotating critically. The results are plotted in Fig. B.1. We observe some stochastic differences, but the spatial distribution of the ejected fragments is similar in both simulations. This test confirms the consistency of both approaches.
 |
Fig. B.1 Impact into Dpb = 200 km target. This was computed with a rotating target (upper row) and with a rotating coordinate frame in which the target is stationary (lower row), and plotted at times t = 40, 80, 120, and 160 min after the impact. The color scale represents the specific energy of the particles (in SI units). |
Appendix C Implementation notes
The code OpenSPH used throughout this work is open-source, available under MIT license. As of August 7, 2019, it can be downloaded1. It includes ahelpful graphic interface, allowing the user to interactively visualize the simulation (see Fig. C.1). It is also a stand-alone viewer of OpenSPH output files and potentially files generated by other particle-based codes, provided their file formats are implemented.
 |
Fig. C.1 Screenshot of graphic interface of our code. |
Our code can be used as both an SPH solver and an N-body integrator, as we separated computations of SPH derivatives and gravitational accelerations. In each time step, accelerations due to hydrodynamics and gravity are computed independently and summed up.Even though we miss some optimization possibilities with this approach, it allows us to use the same code for both the fragmentation and the reaccumulation phase; the hand-off is thus only an internal change of a solver, replacing SPH hydrodynamics with a collision detection.
We used the Barnes–Hut algorithm to evaluate gravitational accelerations (Barnes & Hut 1986). The code uses the same functionality in SPH and N-body solver. It only differs in the softening kernel ϕ; in SPH, it is defined by Eq. (14), while for N-body it corresponds to a homogeneous sphere. Our implementation uses a k-d tree, which is also used to find particle neighbors.
In the fragmentation phase, we found that the time step criterion that uses stress tensor derivatives (see Eq. (16)) is often unnecessarily restricting, as the stress tensor changes rapidly inside the projectile. However, as we are not very interested in remnants of projectiles, simulations can be thus be sped up by applying the criterion only for particles of the target. No such optimization is applied for CFL criterion, as it determines stability of the method and it is thus essential for all particles.
In the reaccumulation phase, collided particles are merged, provided their relative velocity does not exceed the escape velocity vesc (as in Eq. (19)) and the spin rate does not exceed the critical spin rate ωcrit (as in Eq. (20)). In practice, both vesc and ωcrit are multiplied by user-defined factors (i.e., a merging limit). It may be useful to tune it in such a way that a simplified N-body model of reaccumulation matches a full SPH simulation (in terms of resulting SFDs).
The total computation time needed depends on a type of simulation. Generally, catastrophic impacts take longer to compute than cratering impacts (quantities change more rapidly, hence smaller time steps are needed).For smaller targets, SPH particles are also smaller, which in turn implies smaller time steps due to the CFL criterion. The computation time is thus longer. The code is parallelized using a custom thread pool, utilizing the native C++11 threads, or optionally using the Intel Thread Building Blocks library. For Dkm = 10 km target and N = 500 000 particles, a single simulation takes about ten hours on a AMD Ryzen Threadripper 1950X 16-Core processor.
References
- Ballouz, R.-L., Richardson, D. C., Michel, P., Schwartz, S. R., & Yu, Y. 2015, Planet. Space Sci., 107, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Ballouz, R.-L., Walsh, K. J., Richardson, D. C., & Michel, P. 2018, Lunar Planet. Sci. Conf., 49, 2816 [NASA ADS] [Google Scholar]
- Balsara, D. S. 1995, J. Comput. Phys., 121, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Barnes, J., & Hut, P. 1986, Nature, 324, 446 [NASA ADS] [CrossRef] [Google Scholar]
- Benavidez, P. G., Durda, D. D., Enke, B. L., et al. 2012, Icarus, 219, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Benavidez, P. G., Durda, D. D., Enke, B., et al. 2018, Icarus, 304, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Benz, W., & Asphaug, E. 1994, Icarus, 107, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Benz, W., & Asphaug, E. 1999, Icarus, 142, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Canup, R. M. 2005, Science, 307, 546 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Canup, R. M. 2008, Icarus, 196, 518 [NASA ADS] [CrossRef] [Google Scholar]
- Cossins, P. J. 2010, PhD Thesis, University of Leicester, UK [Google Scholar]
- Ćuk, M., & Stewart, S. T. 2012, Science, 338, 1047 [NASA ADS] [CrossRef] [Google Scholar]
- Dahlgren, M. 1998, A&A, 336, 1056 [NASA ADS] [Google Scholar]
- Dobrovolskis, A. R., & Burns, J. A. 1984, Icarus, 57, 464 [NASA ADS] [CrossRef] [Google Scholar]
- Durda, D. D., Bottke, W. F., Nesvorný, D., et al. 2007, Icarus, 186, 498 [NASA ADS] [CrossRef] [Google Scholar]
- Fétick, R. J., Jorda, L., Vernazza, P., et al. 2019, A&A, 623, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hirabayashi, M., & Scheeres, D. J. 2014, ApJ, 780, 160 [NASA ADS] [CrossRef] [Google Scholar]
- Jutzi, M., & Benz, W. 2017, A&A, 597, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jutzi, M., Asphaug, E., Gillet, P., Barrat, J.-A., & Benz, W. 2013, Nature, 494, 207 [NASA ADS] [CrossRef] [Google Scholar]
- Jutzi, M., Holsapple, K., Wünneman, K., & Michel, P. 2015, in Asteroids IV, eds. P. Michel, F. E. DeMeo, & W. F. Bottke (Tucson: University of Arizona Press), 679 [Google Scholar]
- Jutzi, M., Michel, P., & Richardson, D. C. 2019, Icarus, 317, 215 [NASA ADS] [CrossRef] [Google Scholar]
- Kurosawa, K., & Genda, H. 2018, Geophys. Res. Lett., 45, 620 [NASA ADS] [CrossRef] [Google Scholar]
- Marrone, S., Antuono, M., Colagrossi, A., et al. 2011, Comput. Methods Appl. Mech. Eng., 200, 1526 [NASA ADS] [CrossRef] [Google Scholar]
- Michel, P., & Richardson, D. C. 2013, A&A, 554, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Michel, P., Richardson, D. C., Durda, D. D., Jutzi, M., & Asphaug, E. 2015, in Asteroids IV, eds. P. Michel, F. E. DeMeo, & W. F. Bottke (Tucson: University of Arizona Press), 341 [Google Scholar]
- Monaghan, J. J. 1985, Comput. Phys. Rep., 3, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Monaghan, J. J. 2000, J. Comput. Phys., 159, 290 [NASA ADS] [CrossRef] [Google Scholar]
- Monaghan, J.,& Gingold, R. 1983, J. Comput. Phys., 52, 374 [NASA ADS] [CrossRef] [Google Scholar]
- Morris, A. J. W., & Burchell, M. J. 2017, Icarus, 296, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Nakamura, A.,& Fujiwara, A. 1991, Icarus, 92, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Nesvorný, D., Brož, M., & Carruba, V. 2015, in Asteroids IV, eds. P. Michel, F. E. DeMeo, & W. F. Bottke (Tucson: University of Arizona Press), 297 [Google Scholar]
- Owen, J. M. 2014, Int. J. Numer. Methods Fluids, 75, 749 [CrossRef] [Google Scholar]
- Reinhardt, C., & Stadel, J. 2017, MNRAS, 467, 4252 [NASA ADS] [CrossRef] [Google Scholar]
- Remington, T., Owen, J. M., Nakamura, A., Miller, P. L., & Bruck Syal, M. 2018, in AAS/Division for Planetary Sciences Meeting Abstracts #50, 312.02 [Google Scholar]
- Richardson, D. C., Quinn, T., Stadel, J., & Lake, G. 2000, Icarus, 143, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Schäfer, C., Riecker, S., Maindl, T. I., et al. 2016, A&A, 590, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ševeček, P., Brož, M., Nesvorný, D., et al. 2017, Icarus, 296, 239 [NASA ADS] [CrossRef] [Google Scholar]
- Stadel, J. G. 2001, PhD Thesis, University of Washington, USA [Google Scholar]
- Suetsugu, R., Tanaka, H., Kobayashi, H., & Genda, H. 2018, Icarus, 314, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Sugiura, K., Kobayashi, H., & Inutsuka, S. 2018, A&A, 620, A167 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Takeda, T., & Ohtsuki, K. 2007, Icarus, 189, 256 [NASA ADS] [CrossRef] [Google Scholar]
- Takeda, T., & Ohtsuki, K. 2009, Icarus, 202, 514 [NASA ADS] [CrossRef] [Google Scholar]
- Tillotson, J. H. 1962, General Atomic Report, GA-3216 [Google Scholar]
- Vernazza, P., Brož, M., Drouard, A., et al. 2018, A&A, 618, A154 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vinogradova, T. A. 2019, MNRAS, 484, 3755 [NASA ADS] [Google Scholar]
- Wickham-Eade, J. E., Burchell, M. J., Price, M. C., & Harriss, K. H. 2018, Icarus, 311, 52 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Impacts into Dpb = 100 km targets without rotation (first row), rotational period Ppb = 3 h (second row), and Ppb = 2 h (third row). The period of two hours is approximately the critical period of the target. The color brightness corresponds to specific internal energy of the particles. |
| In the text | |
 |
Fig. 2 Cumulative size-frequency distributions N(>D) of synthetic families for Dpb = 10 km targets. Stationary targets are plotted in black; red and yellow plots correspond to targets with rotational period P = 3 h and P = 2 h, respectively.Columns 3–5 of the plot show prograde impacts (i.e., positive impact angles); Cols. 1 and 2 are retrograde impacts (i.e., negative impact angles). |
| In the text | |
 |
Fig. 3 Cumulative size-frequency distribution for Dpb = 100 km targets. Thenotation is the same as in Fig. 2. |
| In the text | |
 |
Fig. 4 Total mass of fragments Mej(P)∕Mej(∞) ejected by collisions, normalized by mass of fragments from corresponding collision into stationary target. The four figures correspond to different relative impact energies, from cratering (left) to mid-energy (right) events. The ejected mass is plotted as a function of the impact angle ϕimp and initial period Ppb of the target. |
| In the text | |
 |
Fig. 5 Damage D of the target at time t = 10 s after impact for various impact angles, from left to right, ϕimp = 75°, 45°, 15°, −45°, −75°. Simulations were carried out with the impactor of size dimp = 314 m and speed vimp = 5 km s−1; target was not rotating. The red outline shows the original position of the target and the impactor. There is an undamaged cavity only for oblique impacts, otherwise the target is fully damaged by the impact. |
| In the text | |
 |
Fig. 6 Change of spin rate Δω
of target (or largest remnant in case |
| In the text | |
 |
Fig. 7 Dimensionless effectivity γ of angular momentum transfer. The other quantities are the same as in Fig. 6. |
| In the text | |
 |
Fig. 8 Quantities averaged over impact angles using Eq. (24) as function of period Ppb of target andimpactor diameter dimp. The left figure shows the change of spin rate Δω, the right one the total mass of fragments, normalized by the mass of fragments from corresponding collision into a stationary target. |
| In the text | |
 |
Fig. B.1 Impact into Dpb = 200 km target. This was computed with a rotating target (upper row) and with a rotating coordinate frame in which the target is stationary (lower row), and plotted at times t = 40, 80, 120, and 160 min after the impact. The color scale represents the specific energy of the particles (in SI units). |
| In the text | |
 |
Fig. C.1 Screenshot of graphic interface of our code. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.