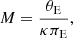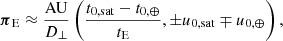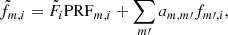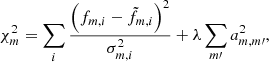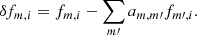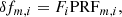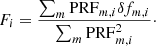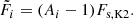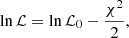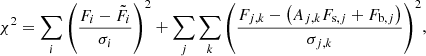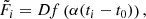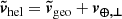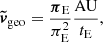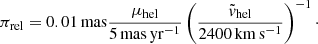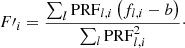| Issue |
A&A
Volume 627, July 2019
|
|
|---|---|---|
| Article Number | A54 | |
| Number of page(s) | 10 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/201834544 | |
| Published online | 02 July 2019 | |
Photometry of K2 Campaign 9 bulge data
1
Department of Astronomy, Ohio State University, 140 W. 18th Ave., Columbus, OH 43210, USA
e-mail: poleski.1@osu.edu
2
Warsaw University Observatory, Al. Ujazdowskie 4, 00-478 Warszawa, Poland
e-mail: rpoleski@astrouw.edu.pl
3
Astrophysics Science Division, NASA/Goddard Space Flight Center, Greenbelt, MD 20771, USA
4
NASA Ames Research Center, Moffett Blvd, Mountain View, CA 94035, USA
5
Bay Area Environmental Research Institute, 625 2nd St., Ste. 209, Petaluma, CA 94952, USA
6
Korea Astronomy and Space Science Institute, 776 Daedukdae-ro Yuseong-gu, Daejeon 34055, Korea
7
Max-Planck-Institute for Astronomy, Köigstuhl 17, 69117 Heidelberg, Germany
Received:
31
October
2018
Accepted:
13
May
2019
In its Campaign 9, K2 observed dense regions toward the Galactic bulge in order to constrain the microlensing parallaxes and probe for free-floating planets. Photometric reduction of the K2 bulge data poses a significant challenge due to a combination of the very high stellar density, large pixels of the Kepler camera, and the pointing drift of the spacecraft. Here we present a new method to extract K2 photometry in dense stellar regions. We extended the Causal Pixel Model developed for less-crowded fields, first by using the pixel response function together with accurate astrometric grids, second by combining signals from a few pixels, and third by simultaneously fitting for an astrophysical model. We tested the method on two microlensing events and a long-period eclipsing binary. The extracted K2 photometry is an order of magnitude more precise than the photometry from other method.
Key words: gravitational lensing: micro / methods: observational / techniques: photometric
© ESO 2019
1. Introduction
In May 2013, the original Kepler mission (Borucki et al. 2010) suffered from the failure of the second of its four reaction wheels and hence lost the ability to maintain stable pointing. To compensate for spacecraft pointing drifts, the Kepler satellite used solar radiation pressure to partially stabilize its pointing. The sacrifice of this solution is that Kepler can only look at locations near the ecliptic plane, and then only for roughly 80 days. Further, there is still a residual pointing drift with an amplitude of about one pixel over a period of 6.5 h. Thus, the photometric signals are dominated by sensitivity variations of the detector on the subpixel scale as bright stars drift across the pixels. The repurposed mission was named K2 (Howell et al. 2014) and observed Ecliptic fields in a series of ≈80-day-long campaigns. One of these was K2 Campaign 9 (K2C9), which was devoted to a microlensing experiment (Gould & Horne 2013; Henderson et al. 2016). In K2C9 almost all pixels available for downlink were selected in a nearly continuous superstamp (Henderson et al. 2016), which made K2 the first wide-field microlensing survey carried out by a satellite. The most important capability of K2C9 was to directly measure masses of microlenses without requiring target selection, which, in principle, enabled mass measurements of free-floating planets for the first time (Penny et al. 2017, see method description below). The first estimate from microlensing of an occurrence rate of a free-floating planet was very high and was based on the distribution of event timescales, meaning the occurrence rate was inferred indirectly (Sumi et al. 2011). The events of short duration can be caused not only by free-floating planets but also by planets on very wide orbits (Han et al. 2005), both of which are difficult to study and scientifically important (Poleski et al. 2014; Mróz et al. 2018). Simultaneous observations of short-timescale events from the ground and from a satellite directly constrain the lens mass (Refsdal 1966; Gould 1994a) and hence verify that the observed short-timescale events are due to planetary-mass objects. The mass is measured directly if we can measure the Einstein ring radius (θE) and the microlensing parallax (πE):
where κ = 4G/(c2AU) = 8.14 mas  . The microlensing parallax vector can be measured by comparing ground-based and satellite impact parameters (u0) and epochs of closest approach (t0):
. The microlensing parallax vector can be measured by comparing ground-based and satellite impact parameters (u0) and epochs of closest approach (t0):
where tE is Einstein timescale and D⊥ is the Earth–satellite separation projected on the sky. Measurement of lens masses in the shortest timescale events cannot be obtained by employing Spitzer, the other satellite used for microlensing parallax measurements, due to the small field-of-view of its camera and scheduling requirements (Yee et al. 2015a) that favor the observations of medium-length and longer events. During K2C9, the superstamp was intensively observed from the ground (Henderson et al. 2016) and no short-timescale events (tE < 2 d) were detected. It is possible that this is partially due to unusually bad weather during the K2C9 at Chilean observatories, which would have contributed a significant part of the microlensing data. After K2C9, Mróz et al. (2017) analyzed a few years of the high-cadence observations by the Optical Gravitational Lensing Experiment (OGLE) and demonstrated that the rate of short events is much smaller than previously claimed. A decrease in the expected number of short events significantly reduced the interest in photometric reduction of K2C9 data, which was recognized early on to be a very challenging task.
The original Kepler mission produced highly accurate photometry thanks to stable pointing and a low density of stars. There are a number of aspects that make K2 photometry of bulge fields difficult: the spacecraft pointing is not stable; the pixel scale is large; the pixel response function (PRF) is undersampled, yet is extended and varies across the field; and the bulge fields have an extremely high density of stars. A combination of all these factors produced a data set that is considerably more difficult to analyze than would be the case for a data set affected by only one of these aspects.
Here we introduce the Modified Causal Pixel Model (MCPM) for extraction of K2 bulge photometry. MCPM is a significant advance upon the Causal Pixel Model (CPM) by Wang et al. (2016), which was developed for photometry of planetary transits in less crowded K2 campaigns. The basic idea behind CPM is to remove the instrumental trends in the photometry, which are highly correlated between different pixels, see Fig. 1. A linear combination of signals observed in pixels far from the target is used to model the instrumental trends in the target pixel.
 |
Fig. 1. Raw light curves in 25 adjacent pixels centered on very bright microlensing event MOA-2016-BLG-290 (top, C9b) and significantly fainter event OGLE-2016-BLG-0795 (bottom, C9a). The Y-axis values (in e− s−1) are very precisely measured: the uncertainties are in the range 1.8−3.6 counts, i.e., invisible on the plot above. There are 2022 epochs in each panel of the top plot and 1278 in each panel of the bottom plot. The instrumental trends have patterns that are shared by different pixels. The instrumental trends are larger (and in many cases much larger) than the microlensing signal, as the microlensed source is usually not the brightest star in a K2 pixel. For OGLE-2016-BLG-0795 we extract photometry using the central pixel and three pixels adjacent to it (bottom, left, and right). |
The CPM method (Wang et al. 2016) was designed for planetary transits and takes advantage of the fact that transits last only a short period of time relative to the full span of the data, and have relatively low amplitudes. Most of the time, the target is at the baseline brightness and, therefore, there are many epochs that can be used for finding linear dependencies between signals observed in different pixels, or training the model. In contrast to planetary transits, most microlensing events show significant flux variations over long periods of time. Typical Einstein timescales are between 10 and 40 days (Wyrzykowski et al. 2015), and significant flux variations can be seen over a few tE. In most cases, the event lasts longer than the length of a single K2 subcampaign of around 40 days. Hence, only a small fraction of the events have data taken over both the baseline and the event peak during the same subcampaign. Additionally, there are very few epochs that can be used for training the model. This lacuna forces us to extract photometry and fit the astrophysical model simultaneously.
The first method of extracting K2C9 photometry was presented by Zhu et al. (2017a). They further developed the method by Huang et al. (2015), which was aimed at less crowded K2 fields. In this method, first the difference images are calculated, then the aperture photometry is extracted from the difference images, and finally this photometry is decorrelated against pointing parameters. The decorrelation is done simultaneously with microlensing model fitting. The Zhu et al. (2017a) method was later used by Zhu et al. (2017b), Ryu et al. (2018), and Zang et al. (2018). Libralato et al. (2016) have also developed a crowded-field K2 photometry technique, though it has not been applied to K2C9 as of yet.
The challenging nature of extracting K2 crowded-field photometry, and the lack of publicly available tools to do so, have almost certainly held back microlensing studies based on the K2 data. This work aims to address some of the challenges, and make the tools for photometry extraction publicly available.
In the next section we present the K2 bulge data. Our method is described in Sect. 3. In Sect. 4 we apply our method to a few examples. In Sect. 5 we discuss K2 flux calibration. We conclude in Sect. 6.
2. K2 bulge data
The K2C9 was divided into two subcampaigns (C9a and C9b), with a data downlink during the break in between, in order to increase the sky-area surveyed. This resulted in a superstamp covering 3.7 deg2 (Henderson et al. 2016), which was then selected to maximize the observed event rate (Poleski 2016). The camera field of view was slightly shifted between the subcampaigns. The cadence of K2 data was 30 min. Hence, in subcampaigns C9a and C9b there were 1290 and 2022 epochs collected, respectively. About 10% of epochs in each subcampaign are affected by spacecraft thrusters firing and we exclude these epochs from analysis. The pixel scale is 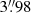 . The K2 camera is divided into channels of 1100 × 1024 pixels. The superstamp is at the edge of the camera and falls in channels numbered 30, 31, 32, 49, and 52. The entire channel 31 was within the superstamp, while only sections of the other channels were included (Henderson et al. 2016). We obtained the K2 data from the Mikulski Archive for Space Telescopes.
. The K2 camera is divided into channels of 1100 × 1024 pixels. The superstamp is at the edge of the camera and falls in channels numbered 30, 31, 32, 49, and 52. The entire channel 31 was within the superstamp, while only sections of the other channels were included (Henderson et al. 2016). We obtained the K2 data from the Mikulski Archive for Space Telescopes.
In addition to the superstamp observations, selected events detected by the ground-based microlensing surveys (mainly the OGLE Early Warning System; Udalski 2003) early in the season were scheduled for observations (these are called “late targets”; Henderson et al. 2016). Additional K2 observations of the bulge were performed in Campaign 11 (C11), but in this part of the bulge the event rate is lower. Thus, no superstamp was selected in K2C11 and only late targets were observed.
3. Method description
In order to extract the photometry from K2 data, the MCPM first assumes a model light curve, then uses this model to detrend the signal in target pixels, and finally combines the detrended signals to extract the photometry. The extracted photometry is compared to the assumed model in order to calculate χ2 for a given model. Hence, if the assumed model is different than the real signal present in the data, then the resulting χ2 is large.
In the MCPM the flux fm, i integrated in pixel m at epoch i is decomposed into the astrophysical difference flux and the instrumental trends. The astrophysical difference flux in any given pixel is the total astrophysical difference flux F̃i from the target object multiplied by the appropriate value of the PRF. The PRF(xp − x*, yp − y*) is the total flux measured in the pixel centered at (xp, yp) due to a star with centroid at (x*, y*) (Anderson & King 2000). We describe the estimation of the PRF values in detail in Sect. 3.1 and, for simplicity, index the PRF with pixel (m) and epoch (i), that is, PRFm, i. The second contribution to the signal in a given pixel comes from the instrumental trends. To model the instrumental trends the MCPM follows the CPM approach and represents these trends as a linear combination of the fluxes observed at the same epoch i but in different pixels m′, meaning, ∑m′ am, m′ fm′,i, where am, m′ are the coefficients that are found by fitting as described below and are independent of time. The number of pixels used for training (M′) is a few hundred. Finally, we derived the following equation:
where F̃m,i is the MCPM estimate of fm, i and can be thought of as the model flux for a given pixel.
There are many sets of values of am, m′ that would produce similar results in Eq. (3). We designed the MCPM so that it finds am, m′ values that describe the data well while simultaneously avoiding the danger of overfitting. The MCPM follows the approach taken by Wang et al. (2016) and regularizes the system of equations using L2 regularization, meaning the MCPM adds a term 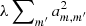 to the χ2 in order to favor values of am, m′ that are small:
to the χ2 in order to favor values of am, m′ that are small:
where λ is the regularization strength. The signal in a pixel m with instrumental trends removed is:
The 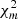 minimization is run separately for each pixel. The simplest approach for finding the astrophysical difference flux is to take the sum of the δfm, i over M pixels: ∑m δfm, i. This approach leads to acceptable results, but a more efficient approach is to perform a PRF-like photometry and assume that the δfm, i are already background-corrected. The MCPM finds Fi by minimizing the residuals of a system of equations:
minimization is run separately for each pixel. The simplest approach for finding the astrophysical difference flux is to take the sum of the δfm, i over M pixels: ∑m δfm, i. This approach leads to acceptable results, but a more efficient approach is to perform a PRF-like photometry and assume that the δfm, i are already background-corrected. The MCPM finds Fi by minimizing the residuals of a system of equations:
which leads to:
There are hundreds of nuisance parameters in the MCPM, making the model very flexible. In turn, this flexibility can affect the fitting convergence. Added to this, microlensing model fits suffer from multiple degeneracies. In particular, a continuous degeneracy exists between tE, the source flux (Fs), and u0 (Woźniak & Paczyński 1997; Han 1999). In practice, to reduce K2 data we must also simultaneously fit ground-based data for the same event in order to constrain the timescale and possibly also the source flux (Zhu et al. 2017a; Zang et al. 2018) when fitting the microlensing model to the K2 data. For the brightest and the shortest events the ground-based data may not be needed. There are multiple ground-based datasets of the K2C9 superstamp area that were collected during the campaign and some of them are public: the Korean Microlensing Telescope Network (KMTNet; Kim et al. 2018a), the United Kingdom Infrared Telescope (UKIRT; Shvartzvald et al. 2017)1, and the Canada-France-Hawaii Telescope (CFHT; Zang et al. 2018). We simultaneously fit the ground-based data and K2 data and extract the K2 photometry as part of this process.
For microlensing events, the astrophysical difference flux F̃i is the K2 source flux (Fs, K2) multiplied by the magnification Ai with source contribution at baseline (Fs, K2) subtracted:
We used MulensModel package (Poleski & Yee 2018, 2019) to evaluate magnification curves Ai. Equation (8) lacks the baseline flux, Fs, K2 + Fb, K2, where Fb, K2 is the blending flux in the K2 band. We have performed a few verification fits with a baseline flux added as a parameter. As expected, these fits resulted in zero baseline flux. This is because the training pixels contain the total flux of numerous constant stars, and the additive constant in a model (like the baseline flux) is absorbed during the decorrelation process. Thus, the MCPM ignores the baseline flux. In order to apply the method to other types of variable sources, the definition of F̃i (Eq. (8)) must be modified. It should be noted that we do not need to assume F̃i for every epoch; we can limit training to a subsample of epochs, train the model, and then extract photometry for all epochs. This approach can be used to search for short-lasting microlensing events or planetary anomalies in microlensing light curves.
We first ran the MCPM with M′ = 500 pixels used for training, and combined it with M = 4 pixels used for extracting photometry results in as many as 2000 coefficients to be fit. Most of these coefficients are close to zero and do not contribute significantly to the trend removal model, see Fig. 2. To reduce the number of model parameters, we selected M″ = 100 training pixels for which ∑m(|am, m′|∑i PRFm, i) is the largest. Here we used the absolute value of the coefficients because both positive and negative values give important information. Then, we again ran the fitting process using these 100 pixels for training.
 |
Fig. 2. Significance of each individual training pixel to detrending model. Higher values of ∑m(|am, m′|∑i PRFm, i) correspond to higher significance of a given pixel in constraining the detrending model. The three colors refer to three targets analyzed in Sect. 4. In each case, about half of the significance is contained in the top 100 pixels, and we use only these pixels in the further analysis. |
In our approach, we analyzed K2 photometry from each subcampaign separately, that is, the am, m′ coefficients are different for each subcampaign even though the parameters that define the astrophysical model are the same. For a few events, there are both K2C9 and K2C11 data, and the am, m′ coefficients are different in every subcampaign.
We note that the CPM software by Wang et al. (2016) contained the possibility to include an astrophysical model, but it was treated similarly to the signal observed in other pixels, meaning, it was multiplied by a coefficient, which in turn was subject to regularization. This is in contrast to our approach, wherein the astrophysical model is subtracted from the target pixel signal before training the model, so that the astrophysical model is not subject to regularization.
3.1. PRF and astrometry
One of the key differences between the MCPM and the CPM is the use of the PRF. Calculating the fraction of the source flux that falls on a given pixel requires a few pieces of information: prior knowledge of the source sky coordinates, astrometric grid transformation for every epoch, the PRF function, and an algorithm to interpolate the PRF function. For the events detected from the ground, the sky coordinates are known. The treatment of events not found from the ground is discussed below. The astrometric grid transformation translates sky coordinates (right ascension and declination) to (x, y) positions on the camera plane. The K2 bulge field is extremely crowded, and it is difficult to find isolated stars, which are required to find the grid transformation. For finding the grid transformation we used coordinates from the Gaia DR1 catalog (Gaia Collaboration 2016a,b). The Gaia passband is similar to the Kepler passband (Kp), which allows us to easily select the brightest objects without worrying about the highly variable extinction in the field. We measured the positions of the brightest stars using PyKE software (Vnicius et al. 2017; Still & Barclay 2012), though some very bright stars were not fit properly. Thus, the results of PyKE fitting were further cleaned based on the inspection of the centroid time series plots and astrometric scatter. We fit second-order 2D polynomials (12 coefficients in total) to transform the sky coordinates to (x, y) positions. We tried third-order polynomials and found that they did not improve the accuracy of the grids significantly. The dispersion of residuals is in the range 0.04−0.11 pix or 0.16−0.44 arcsec, which is sufficient for our purposes.
To estimate the fraction of the source flux that falls on a given pixel, the MCPM also needs the PRF function. The MCPM uses the Kepler PRF function as measured by Bryson et al. (2010) and interpolates it twice. First, the MCPM uses barycentric interpolation of the five PRFs for every channel to account for spatial changes in the PRF. Second, the MCPM uses bivariate spline interpolation to find the PRF value for every subpixel position.
3.2. Initial selection of training pixels
A selection of M′ pixels is necessary for training the model. The MCPM selects pixels that are at least 15 pixels away from the target. In order to minimize the impact of possible saturated pixels, the MCPM removes the pixels that are on the same or neighboring rows as the target, totaling three rows. It also removes the pixels that are on the same or neighboring columns as the target. To further remove the possibility of the overexposed pixels lowering the signal, the MCPM excludes the pixels for which the median signal (calculated over the whole subcampaign) is above 105 e− s−1. We note that some of the training pixels may lie very close to the intrinsically varying sources, thus decreasing the power of the model. Most importantly, Mira-type variables are bright, have large amplitudes, and number nearly 600 inside the superstamp (Soszyński et al. 2013)2. At this juncture, we did not remove pixels affected by variable stars from the training set.
3.3. Limitations
The MCPM requires prior knowledge of the astrophysical model. We do not need to know the exact model, but the prior parameter space model must include a model that adequately describes the K2 data. For microlensing events, it is possible that the source passed close to a component of the lens system as seen by K2, but the trajectory seen from the ground did not pass this component closely (Gould & Horne 2013; Poleski et al. 2016; Wang et al. 2018). Identifying such events may be problematic in photometric methods such as ours, which depend on an assumed astrophysical model.
The MCPM can be run only if we know (or assume) the celestial coordinates of the target. For events not found in the ground-based data, we do not know the coordinates, and searching multidimensional parameter space (t0, u0, tE, Fs, K2, right ascension, and declination) may seem like an extremely computing-intensive task. However, there are a few ways of simplifying the calculations. First, we may limit the search to short events because three independent, high-cadence, ground-based surveys (OGLE, KMTNet, and MOA or Microlensing Observations in Astrophysics; Bond et al. 2001) already searched their K2C9 superstamp data and all long events should have been found. Second, for the short events and assumed right ascension and declination we may exclude a few-day-long part of the light curve from training, extract the signal for the whole light curve, and then check whether the microlensing signal is present in the part excluded from training. To check for the microlensing signal, we only needed to fit four parameters: t0, u0, tE, and Fs, K2, which is a simple task. It should be noted that for event detection a very coarse grid in u0 is enough, for example, Kim et al. (2018b) used only 0 and 1. The separation of the event finding process into two independent tasks makes the effort more efficient computationally. We note that if the part excluded from training is at the beginning or end of the campaign, then extracted signals may not be reliable due to changes in the spacecraft drift pattern.
3.4. Fitting process
For fitting the microlensing model, we used the affine-invariant ensemble sampler for Markov chain Monte Carlo (called EMCEE) by Foreman-Mackey et al. (2013). We defined likelihood:
where ℒ0 is a constant. The χ2 for given model is:
where the first term is the K2 contribution and the second term is the contribution of the ground-based datasets. The index j indicates ground-based datasets and k indicates the epochs for a given dataset. The source flux Fs, j and blending flux Fb, j were found via a least-squares fit for a given model and a given dataset. The microlensing model gives Aj, k – a prediction of magnification for a given epoch. For each flux measurement Fj, k the corresponding uncertainty is σj, k.
First, we ran the fitting with M′ = 500 training pixels. These pixels contain both pixels in which instrumental trends are correlated or anticorrelated with trends observed in the target pixels as well as pixels in which instrumental trends are not correlated with target pixels. We used the first run to select training pixels that carry useful information, meaning those that are correlated or anticorrelated with trends observed in the target pixels. The acceptance rate in this run steadily decreases because the chain gets stuck in very narrow minima of χ2 produced by the large number of poorly constrained nuisance parameters. Even a small change of model parameters (as compared to parameter uncertainties) results in a significant change in χ2. The sampler is run typically for 500 steps because after that point, the acceptance rate is very low. To fully explore the parameter space, we ran many parallel walkers. The large number of walkers does not impact the acceptance rate. For every model, we stored all am, m′ nuisance parameters. We calculated the mean of the posterior distribution of am, m′ using all samples after the first 100 for each walker. We note that the acceptance rate problem is worse when the regularization is not strong enough, as in for small values of regularization constant normalized by the number of training pixels (λ′≡λ/M′).
In the second run, we limited the number of training pixels to M″ = 100 as described above. The sampler was run for thousands of steps in order to achieve stable posteriors. If a chain with a reasonable acceptance rate was produced, then we reported the results from that run. We verified that the best-fitting models from the first run were close to the best-fitting models from the second run. If the acceptance rate in the second run was also very small, then the sampler was run for the third time. This time, all the am, m″ coefficients were fixed at the mean values as found in the first 500 steps of the second run. The third run always produced a reasonable acceptance rate. We validate the uncertainties resulting from the third run in Sect. 4.2.
We multiplied the K2 flux uncertainties by a constant factor that brings χ2/d.o.f. for K2 close to unity. For the determination of the d.o.f. we took into account all the am, m″ coefficients, of which there are typically 400. Hence, the χ2 for K2 data should be ≈750 and ≈1500 for C9a and C9b, respectively. For the examples presented in Sect. 4, the K2 flux uncertainties were multiplied by 10.0, 4.48, and 4.36, respectively, relative to the fm, i uncertainties as reported by the K2 pipeline, which include all expected sources of noise.
The nuisance parameters am, m′ may be significantly affected by just a few epochs with exceptionally large residuals. The typical scatter of the MCPM photometry is in the order of 20 flux units (e− s−1; the zero-point of photometry is 25 mag). Our experience shows that in some cases removing epochs with absolute residuals > 300 (of which there are typically few) improves the model substantially.
The microlensing model fitting is subject to discrete degeneracies and, in particular, the satellite parallax measurements are affected by the four-fold degeneracy (Refsdal 1966; Gould 1994b). In some events this degeneracy can be partially or fully broken. On the other hand, the binary lens events can be affected by additional degeneracies (Dominik 1999; Skowron et al. 2011; Choi et al. 2012). In our approach, each degenerate solution gives slightly different input to the minimization process defined by Eqs. (3) and (4). Hence, the am, m′ coefficients differ and the resulting light curve is different. In practice, different degenerate models of a given event produce very similar light curves.
4. Examples
We applied our method to an eclipsing binary and two microlensing events, as discussed below. We used photometric data from ground-based microlensing surveys. For the OGLE survey data (Udalski et al. 2015), the errorbars were rescaled following Skowron et al. (2016). For other datasets the errorbars were multiplied by a constant that was chosen so that for an initial model fit, a given dataset gives χ2/d.o.f. = 1. Outlying points were removed from the ground-based data. The MCPM parameters used in the examples were: M = 4, M′ = 500, M″ = 100, and λ′ = 6000. We estimated the crowding in the vicinity of targets by calculating the number of stars I < 19 mag within two K2 pixel radii and found: 40, 28, 38, and 39, respectively for objects discussed in the following subsections. Three of these numbers are higher than the median for superstamp events of 29. The scatter of the K2 photometry extracted using the MCPM is: 17, 18, and 9.3 e− s−1 for objects presented in Sects. 4.1–4.3, respectively. For the two latter objects the Zhu et al. (2017a) method gives scatter of 110 (Zhu et al. 2017a) and 130 e− s−1 (Zang et al. 2018), respectively. Thus, our method has photometric scatter that is smaller by a factor of 6.1 and 14, respectively.
4.1. Eclipsing binary OGLE-BLG-ECL-234840
Eclipses of long-period eclipsing binaries show light curves that are similar to inverted microlensing events. Unlike microlensing events, however, the eclipses will appear the same to an observer in space as they do from Earth3. Hence, we tested our method on the bright, long-period eclipsing binary OGLE-BLG-ECL-234840 (Soszyński et al. 2016). The maximum light brightness is I = 13.753 mag and V = 16.428 mag. The orbital period is 369.2 d, and the long-term OGLE light curve predicts a primary eclipse at HJD = 2457519.862, that is, during K2C9a. We fit Chebyshev polynomial models to phased OGLE I- and V-band light curves and obtained eclipse depths of ΔI = 0.398 mag and ΔV = 0.504 mag. The I- and V-band model light curves were transformed to Kp-band using the relations presented by Zhu et al. (2017a) and interpolated to the extinction parameters for this line of sight: AI = 1.42 mag and RI = 1.22 mag (Nataf et al. 2013). We could not use multiband photometry and relations from CFHT (Zang et al. 2018) because the target star falls in the gap between CFHT camera CCD chips. The Zhu et al. (2017a) relations were derived for a single star and are quadratic functions of (V − I) color, whereas in eclipsing binaries we observe two stars with different intrinsic colors, which may cause low-level inaccuracies in the predicted model. The resulting Kp light curve has maximum light at 15.426 mag and amplitude of 0.421 mag (in flux space 6752 and 2255 e− s−1, respectively). We transformed the model curve to flux space and normalized it so that maximum light and the faintest eclipse part correspond to one and zero, respectively. This model curve is denoted as f(t). We calculated f(t) using phase-folded data, hence f(0) = 0.
After preparing the normalized eclipse light curve in Kp, we applied the MCPM to K2C9a data with a flux model defined as
where D is the eclipse depth in flux units, α is the eclipse duration stretching factor, and t0 is the epoch of the eclipse. When combined with the f(t) model from above, the only information that is fixed in this approach is the eclipse shape, and the free parameters enable us to test the model fitting process. We applied the MCPM to K2 data only and obtained: t0 = 2457519.836 ± 0.048, α = 0.9943 ± 0.0064, D = 3251 ± 27, and χ2/d.o.f. = 739.0/743. The extracted photometry and model light curve are presented in Fig. 3. The eclipse epoch and the stretching factor are consistent with the OGLE predictions within 1σ. The measured depth would be consistent with the model light curve if the maximum light were Kp = 15.03 mag, which is 0.40 mag brighter than the prediction. To verify this discrepancy, we extracted the K2 light curve with training limited to maximum light (i.e., BJD < 2457508, 283 epochs) and assumed zero flux during this time. In this way, we extracted K2 photometry that is independent from our model light curve. We present the resulting data in Fig. 4. The eclipse depth differs from the model fitting result, but the difference is not large enough to account for the 0.40 mag discrepancy found above. The general shape of the light curve is similar to Fig. 3, while the scatter of the data is larger.
 |
Fig. 3. K2 light curve (represented by red points) of eclipsing binary OGLE-BLG-ECL-234840 derived using MCPM with model light curve (indicated by a blue line) predicted using ground-based data and a three-parameter fit (Eq. (11)). The y-axis units are K2 flux units where the photometric zero point of the magnitude scale corresponds to Kp = 25 mag. Lower panel: residuals of the fit. |
 |
Fig. 4. K2 light curve of OGLE-BLG-ECL-234840 derived using MCPM. The model was trained using a flat part of the light curve only (indicated by a blue solid line; BJD < 2457508) and the full light curve was extracted. The blue dotted line reproduces the model from Fig. 3 for comparison. |
4.2. Microlensing event OGLE-2016-BLG-0795
We tested our method on the short (tE = 4.5 d) event OGLE-2016-BLG-0795 that was previously analyzed by Zang et al. (2018). We present the results of model fitting in Fig. 5 and Table 1.
 |
Fig. 5. MCPM light curve of OGLE-2016-BLG-0795. The K2 light curve (red) has amplitude of 1600 counts, see bottom part of Fig. 1 for raw data. The right-hand side of the Y axis is nonlinear and shows selected K2 flux values. Compare to Fig. 9 in Zang et al. (2018). |
OGLE-2016-BLG-0795 models.
For all plots of microlensing event light curves we scaled all the data to a common photometric system so that data from different telescopes and in different passbands can be compared to just one model curve (or two if satellite data are used). The standard method is to first translate the measured flux F to the observed magnification space: A = (F − Fb)/Fs, where Fb and Fs are the blending and source fluxes for a given photometric system. Second, the observed magnification is translated to the photometric system of a reference dataset (OGLE I-band in our case): Fref = AFs, ref + Fb, ref, where Fb, ref and Fs, ref are the blending and source fluxes for the reference dataset. All source and blending fluxes are found via linear regression.
Our K2 photometry differs from that of Zang et al. (2018), which was extracted using the Zhu et al. (2017a) approach. Our four models have peak K2 magnification (A0) in the range 11.9−12.0, or peak (A0 − 1)Fs, K2 of 1600. The four Zang et al. (2018) models have peak magnification in the range 7.6−8.0 and corresponding (A0 − 1)Fs, K2 from 550−590. This is a significant difference, and we try to verify which model is correct by running the MCPM on the Zang et al. (2018) models and with the MCPM trained on the nearly flat part of the light curve, meaning the union of BJD < 2457510 and BJD > 2457515. All four Zang et al. (2018) models result in peak fluxes of 1550, which is very close to the results from the MCPM fit on the whole light curve. We conclude that in our framework of decorrelating K2 signals against signals in other pixels, the Zang et al. (2018) model is inconsistent with the photometry extracted using the MCPM. We can imagine that the models that were fit using the two methods differ because the MCPM is overfitting. To test if this is the case, we ran the fit with a smaller number of training pixels. We found that with M′ = 6 (i.e., there are just 24 nuisance parameters) the microlensing signal is still extracted and consistent with Table 1, though with larger uncertainties. We obtained consistent results even with M′ = 5 and a single additional change (λ′ = 500). To sum up, our tests do not show signs of overfitting.
The results presented in Table 1 were obtained from the second run of the sampler with M″ = 100 and am, m″ as free parameters. We then ran the sampler a third time (i.e., am, m″ are fixed) for each of the models and compared the resulting posterior statistics. The uncertainties are on average 1.6 times larger when compared to the second run. The largest ratios are for tE and are up to 3.5 times higher. The mean values from both runs are consistent when compared to the uncertainties from the third run. We conclude that the third run returns posteriors that are consistent with the second run, though with larger uncertainties.
We also performed additional fits to check how the K2 source flux constraints affect the MCPM fitting results. We use the predictions made by Zhu et al. (2017a) where (Kp − I) was parameterized as a function of (V − I) and the extinction parameters at a given sight-line. We used AI = 1.04 mag and E(V − I) = 0.88 mag (Nataf et al. 2013). The (V − I) color was estimated using OGLE data. When the Zhu et al. (2017a) calibration is applied to the results presented in Table 1, the predicted (Kp, s − Is) color is larger by 0.366 mag than the MCPM fitting result. In our fitting routine, we added the χ2 penalty: ((Kp,s − K̃p,s)/0.02 mag)2, where K̃p,s is the K2 brightness predicted using the Zhu et al. (2017a) calibration. The χ2 penalty was calculated for every model. The resulting fits have parameters that are significantly different from those presented in Table 1 and have χ2 higher by 130. We conclude that the MCPM method gives results inconsistent with the Zhu et al. (2017a) calibration.
The measurement of πE allows an estimation of the relative heliocentric lens-source velocity projected on the observer plane (ṽhel):
where
and v⊕, ⊥ is the velocity of Earth at t0, ⊕ projected on the plane of the sky. For OGLE-2016-BLG-0795, the preferred solutions are (+, +) and (−, −) (by the so-called Rich argument, see Zang et al. 2018). The projected heliocentric velocities are (N, E): (−2428 ± 104, 435 ± 68) km s−1 for the (+, +) solution and (2347 ± 120, −645 ± 47) km s−1 for the (−, −) solution. The relative lens-source heliocentric proper motion (μhel) is related to ṽhel via: 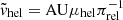 , which can be rewritten as:
, which can be rewritten as:
This suggests that πrel is small, hence, the lens is close to the source. The most likely interpretation is that the lens is located in the Galactic bulge.
4.3. Microlensing event OGLE-2016-BLG-0980
OGLE-2016-BLG-0980 was first modeled by Zhu et al. (2017a). The OGLE I-band data show a slight dependence on airmass so we removed this trend from the data. We also used KMTNet data (Kim et al. 2016, 2018a) from the Cerro Tollo Inter-American Observatory (Chile; designated C) and the South African Astronomical Observatory (South Africa; designated S). The KMTNet data from the Siding Spring Observatory (Australia; designated A) are noisy and do not contribute significantly to constraining the model; we therefore did not include them. We present the results of model fitting in Fig. 6 and Table 2. As compared to Zhu et al. (2017a) results, we note differences in t0, u0, and tE that are caused by the fact that we detrended against airmass, whereas Zhu et al. (2017a) did not. The parallax results are statistically different, but the differences are small. The differences are comparable to the parallax uncertainties measured using the annual parallax effect for other events. The scatter of the data is significantly smaller in the MCPM reduction as compared to Zhu et al. (2017a).
 |
Fig. 6. MCPM light curve of OGLE-2016-BLG-0980. Compare to Fig. 4 in Zhu et al. (2017a). |
OGLE-2016-BLG-0980 models.
From Table 2 we see that the u0 > 0 solution is clearly preferred. The projected heliocentric velocity is (520 ± 13, 264.0 ± 5.5) km s−1. Combining this value with Eq. (14), we see that the lens and source parallaxes differ significantly, which suggests that the lens is located in the Galactic disk.
4.4. Microlensing event MOA-2016-BLG-290
Zhu et al. (2017b) analyzed photometry of the microlensing event MOA-2016-BLG-290 from three different locations in the Solar System: Earth, K2, and Spitzer. They fit a parallax point-source point-lens model to the ground-based data and extracted the K2 photometry using the Zhu et al. (2017a) method. The ground-based data were from MOA and OGLE surveys, and for OGLE data, zero blending flux was assumed. Four degenerate solutions were found and were further verified using twelve epochs of Spitzer photometry that cover only the falling part of the light curve. Zhu et al. (2017b) predicted Spitzer light curves and fit the source and blending fluxes for Spitzer data. Two of the four solutions have Spitzer source fluxes that are consistent with the prediction based on a color-color relation derived using nearby stars. This allowed Zhu et al. (2017b) to break the four-fold πE degeneracy. One can also consider the source flux consistency as a strong argument showing the reliability of the Zhu et al. (2017a) method.
We tried to reduce K2 data for MOA-2016-BLG-290, but quickly arrived at a problem with fitting the ground-based data alone: The best point-source point-lens fit requires significant negative blending flux. The negative blending flux can be caused by an incorrect model, or can be naturally produced if the event occurs on a “hole” in an otherwise roughly uniform background of bulge sources (Park et al. 2004). As an example, Yee et al. (2015b) suggested that the blending flux in I-band: Fb, I > −0.2 (where the zero-point corresponds to 18 mag) can be explained this way. In other words, the uniform background would be composed of I = 19.75 mag stars. In the case of MOA-2016-BLG-290, we fit I-band data from OGLE and two overlapping fields from both KMT A and KMT S. The fit results in χ2/d.o.f. = 7569.9/7843 and the blending flux of −3.15 ± 0.50. This is equivalent to a hole in a uniform background of 16.76 mag stars, which is unlikely given the source density and luminosity function of stars toward the bulge. Thus, we conclude that the inferred blending flux is significantly more negative than can be explained using the Park et al. (2004) interpretation of a hole in a uniform background of stars. After adding a prior Fb, I, OGLE > −0.2, we obtained χ2/d.o.f. = 7612.1/7843 and the blending flux of 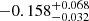 . We conclude that the negative blending flux cannot be explained as a hole in a uniform background of stars, nor can it be explained by systematic effects in the photometry because it is present in a joint fit to data from three telescopes. Hence, it is most likely caused by some second-order effect, such as: a finite source, a binary source, xallarap, or a binary lens.
. We conclude that the negative blending flux cannot be explained as a hole in a uniform background of stars, nor can it be explained by systematic effects in the photometry because it is present in a joint fit to data from three telescopes. Hence, it is most likely caused by some second-order effect, such as: a finite source, a binary source, xallarap, or a binary lens.
After considering the uniform finite-source models (Lee et al. 2009), we found χ2/d.o.f. = 7561.2/7842, ρ = 0.471 ± 0.075, and the blending flux in this case is −1.42 ± 0.48. Thus, a single additional parameter gives an improvement of Δχ2 = 8.7. In this case, the baseline object is about 1 mag brighter than the red clump and hence would have an angular source size (θ⋆) of roughly 10 μas. In this finite-source model, we can estimate physical properties: θE = θ⋆/ρ ≈ 0.022 mas and the relative lens-source geocentric proper motion μgeo = θE/tE ≈ 1.3 mas yr−1. Our preliminary extraction of K2 photometry suggests t0, K2 ≈ 7553.105 and u0, K2 ≈ u0, ⊕, that is, πE ≈ 0.17. If these values were correct, then we would infer a lens mass of 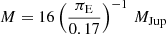 . A priori probability of such a small θE value seems to be small. We also fit the binary-source model with the Fb, I prior, resulting in χ2/d.o.f. = 7564.3/7840 or Δχ2 = 47.8 for three additional parameters. A binary companion to such a bright source also seems unlikely.
. A priori probability of such a small θE value seems to be small. We also fit the binary-source model with the Fb, I prior, resulting in χ2/d.o.f. = 7564.3/7840 or Δχ2 = 47.8 for three additional parameters. A binary companion to such a bright source also seems unlikely.
The significantly negative blending flux suggests that the correct model for MOA-2016-BLG-290 has not yet been found. In principle, the agreement between the predicted and fit Spitzer source fluxes for the small-parallax solutions in Zhu et al. (2017a) would argue that the their solutions were correct, however this agreement could be coincidental. We conclude that a more in-depth analysis of this event is needed, which is beyond the scope of this paper.
5. Flux calibration
In the previous section, we saw that there are significant differences between the flux we measured and the Kp magnitudes predicted using the Zhu et al. (2017a) and Zang et al. (2018) relations. The calibration of fluxes is important for microlensing events because microlensing models predict magnification, which is not a directly measured quantity. We can measure the magnified flux and then estimate the magnification when the source flux is constrained. However, the precise knowledge of Kp magnitudes is not needed for many other applications of Kepler and K2 data. Most importantly, in the case of planetary transits, the fundamental quantity is the relative transit depth.
The best approach to constrain the source flux is to directly measure fluxes in the K2 data for a number of isolated stars and then check how these fluxes relate to predictions. The number of truly isolated K2C9 superstamp stars is very small, because the superstamp was selected to cover high-stellar density regions. The most isolated superstamp stars are in the regions of particularly high extinction and these stars are in front of most of the dust. Hence, these objects are relatively nearby main-sequence stars and their spectral energy distributions are different from the microlensing sources. Thus, we searched for isolated red giants and supergiants, which are then less isolated than the nearby main-sequence objects. We searched the OGLE-IV photometric catalog calibrated to the standard system because it covers the superstamp fully (except small gaps between CCD chips) and the OGLE-IV data are available for almost all K2C9 microlensing events. To select isolated stars for our test, we applied a few constraints: (1) the star is not overexposed in the OGLE I-band data, meaning, I > 12 mag; (2) the other stars contribute relatively little flux in the OGLE I-band data; (3) there are no overexposed pixels in the K2C9 data; (4) the position of the star on the extinction-corrected (Nataf et al. 2013) color-magnitude diagram is consistent with red giants or supergiants; and (5) the star is relatively constant (σI < 0.025 mag in the OGLE data).
In order to estimate K2 brightness, we first estimated background flux for the given target and subcampaign. We selected a square of 5 × 5 pixels centered on the target and sorted these pixels according to the PRF contributions from the target. We ignored the top ten pixels and for each remaining pixel we took the median flux measured over a subcampaign and then took the median over the pixels, which results in the background estimate for a given subcampaign (b). To estimate the target flux, we assumed the background is properly measured which leads to the following equation for the flux estimate (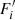 ):
):
The index l indicates five pixels with the highest PRF contribution from the given target. The resulting photometry shows trends with spacecraft pointing and changes between the two subcampaigns. We report median fluxes and their uncertainties in Table 3. Table 3 also gives Kp brightness that was estimated using the Zhu et al. (2017a) calibration and OGLE data. The last column of the table gives the difference between predicted and measured values. These differences are much larger than the uncertainties of measured flux.
Photometry of isolated stars.
There is a significant scatter of differences between measured and predicted Kp magnitudes, however, all differences have the same sign. The mean difference is ⟨ΔKp⟩ = 0.47 ± 0.13 mag and the measured value is brighter than the prediction. This difference is significant and is most probably caused by a combination of two effects: flat-field errors (which are largest at the edges of camera field of view) and the inaccurately measured zero-point of the Kp band.
In Sect. 4 we have discussed the MCPM photometry for three targets. In each case, the source was found to be brighter than the prediction based on the Zhu et al. (2017a) calibration of: 0.40 mag, 0.37 mag, and 0.19 mag, respectively. The first two of these values are close to ⟨ΔKp⟩, and the third one is 2.2σ away. We conclude that the MCPM fitting results are consistent with the Zhu et al. (2017a) calibration after correcting for ⟨ΔKp⟩.
6. Summary
We have presented a novel method for extracting photometry from highly blended K2 data. The method combines the PRF photometry with a data-driven model that removes instrumental effects. The removal of instrumental effects depends on model training that can be done on the full light curve or on only a part of the data, enabling an efficient search for very short events and short (e.g., planetary) anomalies. Our method of the removal of systematic trends in the photometry is designed in a way that preserves the intrinsic astrophysical signal.
We found that the MCPM produces photometry that is an order of magnitude more precise than the photometry extracted using the Zhu et al. (2017a) method and that some of the results differ. Both methods are based on the methods developed previously for the less crowded K2 campaigns. Both methods use an astrophysical model to decorrelate instrumental noise, but they decorrelate against different pieces of information. An important aspect of the MCPM is the direct use of the PRF, which is not employed in the Zhu et al. (2017a) method. In addition to running the MCPM on two microlensing events, we also tested the MCPM on an eclipse of a long-period binary. The inverted shape of this eclipse is comparable to the shape of a microlensing event light curve. The epoch of the eclipse and its length were measured to be consistent with the prediction based on the ground-based data. We measured the eclipse depth using two approaches within the MCPM. These approaches are roughly consistent with each other, but in order to be consistent with the predicted eclipse depth, require the object to be brighter by 0.40 mag than the prediction based on the Zhu et al. (2017a) calibration. We have also extracted photometry for ten bright and isolated stars using a method that is similar to PRF fitting. In all cases, we find these stars to be brighter than the Zhu et al. (2017a) calibration, with the mean difference similar to the brightness difference found for the eclipsing binary. We conclude that the Zhu et al. (2017a) calibration requires an additive constant. The Zang et al. (2018) and the MCPM results for OGLE-2016-BLG-0795 differ and we ran a number of tests to verify the MCPM results. These tests result in parameters that are very close to our main solution. We also find that K2 flux calibration is consistent with the correction found on isolated stars. We conclude, that the MCPM results are favored over the Zang et al. (2018) results.
We distribute the MCPM software via: https://github.com/CPM-project/MCPM. Our astrometric transformations are distributed together with the MCPM code.
See https://www.asc.ohio-state.edu/poleski.1/K2C9_var_stars/ for a list of more than 60 000 variable stars inside the superstamp that was compiled from the literature.
The parallax effect changes the epoch of eclipse, but this effect is negligible (Scharf 2007).
Acknowledgments
We thank David Hogg, Chelsea Huang, Przemek Mróz, Andrew Vanderburg, Dun Wang, Weicheng Zang, and Wei Zhu for consultation. This work was partly supported by NASA grant NNX17AF72G to R.P. OGLE project has received funding from the Polish National Science Center, grant MAESTRO 2014/14/A/ST9/00121 to A.U. The work by C.R. was supported by an appointment to the NASA Postdoctoral Program at the Goddard Space Flight Center, administered by USRA through a contract with NASA. Work by A.G. was supported by AST-1516842 from the US NSF and by JPL grant 1500811. A.G. received support from the European Research Council under the European Union’s Seventh Framework Programme (FP 7) ERC Grant Agreement n. [321035]. This research has made use of the KMTNet system operated by the Korea Astronomy and Space Science Institute (KASI) and the data were obtained at three host sites of CTIO in Chile, SAAO in South Africa, and SSO in Australia. Some of the data presented in this paper were obtained from the Mikulski Archive for Space Telescopes (MAST). STScI is operated by the Association of Universities for Research in Astronomy, Inc., under NASA contract NAS5-26555. This paper includes data collected by the Kepler mission. Funding for the Kepler mission is provided by the NASA Science Mission directorate.
References
- Anderson, J., & King, I. R. 2000, PASP, 112, 1360 [NASA ADS] [CrossRef] [Google Scholar]
- Bond, I. A., Abe, F., Dodd, R. J., et al. 2001, MNRAS, 327, 868 [NASA ADS] [CrossRef] [Google Scholar]
- Borucki, W. J., Koch, D., Basri, G., et al. 2010, Science, 327, 977 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Bryson, S. T., Tenenbaum, P., Jenkins, J. M., et al. 2010, ApJ, 713, L97 [NASA ADS] [CrossRef] [Google Scholar]
- Choi, J.-Y., Shin, I.-G., Han, C., et al. 2012, ApJ, 756, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Dominik, M. 1999, A&A, 349, 108 [NASA ADS] [Google Scholar]
- Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [CrossRef] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2016a, A&A, 595, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Prusti, T., et al.) 2016b, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gould, A. 1994a, ApJ, 421, L75 [NASA ADS] [CrossRef] [Google Scholar]
- Gould, A. 1994b, ApJ, 421, L71 [NASA ADS] [CrossRef] [Google Scholar]
- Gould, A., & Horne, K. 2013, ApJ, 779, L28 [NASA ADS] [CrossRef] [Google Scholar]
- Han, C. 1999, MNRAS, 309, 373 [NASA ADS] [CrossRef] [Google Scholar]
- Han, C., Gaudi, B. S., An, J. H., & Gould, A. 2005, ApJ, 618, 962 [NASA ADS] [CrossRef] [Google Scholar]
- Henderson, C. B., Poleski, R., Penny, M., et al. 2016, PASP, 128, 124401 [NASA ADS] [CrossRef] [Google Scholar]
- Howell, S. B., Sobeck, C., Haas, M., et al. 2014, PASP, 126, 398 [NASA ADS] [CrossRef] [Google Scholar]
- Huang, C. X., Penev, K., Hartman, J. D., et al. 2015, MNRAS, 454, 4159 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, S.-L., Lee, C.-U., Park, B.-G., et al. 2016, J. Korean Astron. Soc., 49, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, H.-W., Hwang, K.-H., Kim, D.-J., et al. 2018a, AJ, 155, 186 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, D.-J., Kim, H.-W., Hwang, K.-H., et al. 2018b, AJ, 155, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, C.-H., Riffeser, A., Seitz, S., & Bender, R. 2009, ApJ, 695, 200 [NASA ADS] [CrossRef] [Google Scholar]
- Libralato, M., Bedin, L. R., Nardiello, D., & Piotto, G. 2016, MNRAS, 456, 1137 [NASA ADS] [CrossRef] [Google Scholar]
- Mróz, P., Udalski, A., Skowron, J., et al. 2017, Nature, 548, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Mróz, P., Ryu, Y.-H., Skowron, J., et al. 2018, AJ, 155, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Nataf, D. M., Gould, A., Fouqué, P., et al. 2013, ApJ, 769, 88 [NASA ADS] [CrossRef] [Google Scholar]
- Park, B.-G., DePoy, D. L., Gaudi, B. S., et al. 2004, ApJ, 609, 166 [NASA ADS] [CrossRef] [Google Scholar]
- Penny, M. T., Rattenbury, N. J., Gaudi, B. S., & Kerins, E. 2017, AJ, 153, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Poleski, R. 2016, MNRAS, 455, 3656 [NASA ADS] [CrossRef] [Google Scholar]
- Poleski, R., & Yee, J. 2018, Astrophysics Source Code Library [record ascl:1803.006] [Google Scholar]
- Poleski, R., & Yee, J. C. 2019, Astron. Comput., 26, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Poleski, R., Skowron, J., Udalski, A., et al. 2014, ApJ, 795, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Poleski, R., Zhu, W., Christie, G. W., et al. 2016, ApJ, 823, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Refsdal, S. 1966, MNRAS, 134, 315 [NASA ADS] [CrossRef] [Google Scholar]
- Ryu, Y.-H., Yee, J. C., Udalski, A., et al. 2018, AJ, 155, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Scharf, C. A. 2007, ApJ, 661, 1218 [NASA ADS] [CrossRef] [Google Scholar]
- Shvartzvald, Y., Bryden, G., Gould, A., et al. 2017, AJ, 153, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Skowron, J., Udalski, A., Gould, A., et al. 2011, ApJ, 738, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Skowron, J., Udalski, A., Kozłowski, S., et al. 2016, Acta Astron., 66, 1 [NASA ADS] [Google Scholar]
- Soszyński, I., Udalski, A., Szymański, M. K., et al. 2013, Acta Astron., 63, 21 [NASA ADS] [Google Scholar]
- Soszyński, I., Pawlak, M., Pietrukowicz, P., et al. 2016, Acta Astron., 66, 405 [NASA ADS] [Google Scholar]
- Still, M., & Barclay, T. 2012, Astrophysics Source Code Library [record ascl:1208.004] [Google Scholar]
- Sumi, T., Kamiya, K., Bennett, D. P., et al. 2011, Nature, 473, 349 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Szymański, M. K., Udalski, A., Soszyński, I., et al. 2011, Acta Astron., 61, 83 [NASA ADS] [Google Scholar]
- Udalski, A. 2003, Acta Astron., 53, 291 [NASA ADS] [Google Scholar]
- Udalski, A., Szymański, M. K., & Szymański, G. 2015, Acta Astron., 65, 1 [NASA ADS] [Google Scholar]
- Vnicius, Z., Barentsen, G., Gully-Santiago, M., et al. 2017, KeplerGO/PyKE, DOI 10.5281/zenodo.835583 [Google Scholar]
- Wang, D., Hogg, D. W., Foreman-Mackey, D., & Schölkopf, B. 2016, PASP, 128, 094503 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, T., Calchi Novati, S., Udalski, A., et al. 2018, ApJ, 860, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Woźniak, P., & Paczyński, B. 1997, ApJ, 487, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Wyrzykowski, Ł., Rynkiewicz, A. E., Skowron, J., et al. 2015, ApJS, 216, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Yee, J. C., Gould, A., Beichman, C., et al. 2015a, ApJ, 810, 155 [NASA ADS] [CrossRef] [Google Scholar]
- Yee, J. C., Udalski, A., Calchi Novati, S., et al. 2015b, ApJ, 802, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Zang, W., Penny, M. T., Zhu, W., et al. 2018, PASP, 130, 104401 [NASA ADS] [CrossRef] [Google Scholar]
- Zhu, W., Huang, C. X., Udalski, A., et al. 2017a, PASP, 129, 104501 [NASA ADS] [CrossRef] [Google Scholar]
- Zhu, W., Udalski, A., Huang, C. X., et al. 2017b, ApJ, 849, L31 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1. Raw light curves in 25 adjacent pixels centered on very bright microlensing event MOA-2016-BLG-290 (top, C9b) and significantly fainter event OGLE-2016-BLG-0795 (bottom, C9a). The Y-axis values (in e− s−1) are very precisely measured: the uncertainties are in the range 1.8−3.6 counts, i.e., invisible on the plot above. There are 2022 epochs in each panel of the top plot and 1278 in each panel of the bottom plot. The instrumental trends have patterns that are shared by different pixels. The instrumental trends are larger (and in many cases much larger) than the microlensing signal, as the microlensed source is usually not the brightest star in a K2 pixel. For OGLE-2016-BLG-0795 we extract photometry using the central pixel and three pixels adjacent to it (bottom, left, and right). |
| In the text | |
 |
Fig. 2. Significance of each individual training pixel to detrending model. Higher values of ∑m(|am, m′|∑i PRFm, i) correspond to higher significance of a given pixel in constraining the detrending model. The three colors refer to three targets analyzed in Sect. 4. In each case, about half of the significance is contained in the top 100 pixels, and we use only these pixels in the further analysis. |
| In the text | |
 |
Fig. 3. K2 light curve (represented by red points) of eclipsing binary OGLE-BLG-ECL-234840 derived using MCPM with model light curve (indicated by a blue line) predicted using ground-based data and a three-parameter fit (Eq. (11)). The y-axis units are K2 flux units where the photometric zero point of the magnitude scale corresponds to Kp = 25 mag. Lower panel: residuals of the fit. |
| In the text | |
 |
Fig. 4. K2 light curve of OGLE-BLG-ECL-234840 derived using MCPM. The model was trained using a flat part of the light curve only (indicated by a blue solid line; BJD < 2457508) and the full light curve was extracted. The blue dotted line reproduces the model from Fig. 3 for comparison. |
| In the text | |
 |
Fig. 5. MCPM light curve of OGLE-2016-BLG-0795. The K2 light curve (red) has amplitude of 1600 counts, see bottom part of Fig. 1 for raw data. The right-hand side of the Y axis is nonlinear and shows selected K2 flux values. Compare to Fig. 9 in Zang et al. (2018). |
| In the text | |
 |
Fig. 6. MCPM light curve of OGLE-2016-BLG-0980. Compare to Fig. 4 in Zhu et al. (2017a). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.