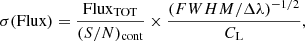| Issue |
A&A
Volume 626, June 2019
|
|
|---|---|---|
| Article Number | A9 | |
| Number of page(s) | 14 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201935062 | |
| Published online | 04 June 2019 | |
Obscured AGN at 1.5 < z < 3.0 from the zCOSMOS-deep Survey
I. Properties of the emitting gas in the narrow-line region⋆
1
INAF – Osservatorio di Astrofisica e Scienza delle Spazio di Bologna, OAS, Via Gobetti 93/3, 40129 Bologna, Italy
e-mail: marco.mignoli@inaf.it
2
Sorbonne Universités, UPMC-CNRS, UMR 7095, Institut d’Astrophysique de Paris, 75014 Paris, France
3
Université Lyon, Univ. Lyon1, Ens de Lyon, CNRS, Centre de Recherche Astrophysique de Lyon UMR 5574, 69230 Saint-Genis-Laval, France
4
SISSA, Via Bonomea 265, 34136 Trieste, Italy
5
INAF – Osservatorio Astronomico di Roma, 00040 Monteporzio Catone, Italy
6
Dipartimento di Fisica e Astronomia, Università degli Studi di Bologna, 40127 Bologna, Italy
7
Department of Physics, ETH Zurich, Wolfgang-Pauli-Strasse 27, 8093 Zurich, Switzerland
8
Aix Marseille Université, CNRS, LAM, UMR 7326, 13388 Marseille, France
9
MIT-Kavli Center for Astrophysics and Space Research, 77 Massachusetts Avenue, Cambridge, MA 02139, USA
10
Department of Physics, North Carolina State University, Raleigh, NC 27695, USA
11
Kapteyn Astronomical Institute, University of Groningen, PO Box 800, 9700 AV Groningen, The Netherlands
12
INAF – Osservatorio Astrofisico di Arcetri, Largo E. Fermi 5, 50125 Firenze, Italy
13
Institute of Astronomy, Madingley Road Cambridge, CB3 0HA Cambridge, UK
14
INAF – Istituto di Astrofisica Spaziale e Fisica Cosmica di Milano, Via Bassini 15, 20133 Milan, Italy
15
Space Telescope Science Institute, 3700 San Martin Dr., Baltimore, MD 21218, USA
16
University of Vienna, Department of Astrophysics, Tuerkenschanzstrasse 17, 1180 Vienna, Austria
17
European Southern Observatory, Karl-Schwarzschild-Str. 2, 85748 Garching bei München, Germany
18
Kavli Institute for Astronomy & Astrophysics, Peking University, 5 Yiheyuan Road, Beijing 100871, PR China
19
Instituto de Astrofisica de Andalucia, CSIC, Apartado de correos 3004, 18080 Granada, Spain
20
Kavli Institute for the Physics and Mathematics of the Universe (WPI), The University of Tokyo, Kashiwa, Chiba 277-8583, Japan
Received:
15
January
2019
Accepted:
27
March
2019
Context. The physics and demographics of high-redshift obscured active galactic nuclei (AGN) is still scarcely investigated. New samples of such objects, selected with different techniques, can provide useful insights into their physical properties.
Aims. With the goal to determine the properties of the gas in the emitting region of type 2 AGN, in particular, the gas metal content, we exploit predictions from photoionization models, including new parameterizations for the distance of gas distribution from the central source and internal microturbulence in the emitting clouds, to interpret rest-frame UV spectral data.
Methods. We selected a sample of 90 obscured (type 2) AGN with 1.45 ≤ z ≤ 3.05 from the zCOSMOS-deep galaxy sample by 5σ detection of the high-ionization C IV λ1549 narrow emission line. This feature in a galaxy spectrum is often associated with nuclear activity, and the selection effectiveness has also been confirmed by diagnostic diagrams based on utraviolet (UV) emission-line ratios. We applied the same selection technique and collected a sample of 102 unobscured (type 1) AGN. Taking advantage of the large amount of multiband data available in the COSMOS field, we investigated the properties of the C IV-selected type 2 AGN, focusing on their host galaxies, X-ray emission, and UV emission lines. Finally, we investigated the physical properties of the ionized gas in the narrow-line region (NLR) of this type 2 AGN sample by combining the analysis of strong UV emission lines with predictions from photoionization models.
Results. We find that in order to successfully reproduce the relative intensity of UV emission lines of the selected high-z type 2 AGN, two new ingredients in the photoionization models are fundamental: small inner radii of the NLR (≈90 pc for LAGN = 1045 erg s−1), and the internal dissipative microturbulence of the gas-emitting clouds (with vmicr ≈ 100 km s−1). With these modified models, we compute the gas-phase metallicity of the NLR, and our measurements indicate a statistically significant evolution of the metal content with redshift. Finally, we do not observe a strong relationship between the NLR gas metallicity and the stellar mass of the host galaxy in our C IV-selected type 2 AGN sample.
Key words: galaxies: active / galaxies: fundamental parameters / galaxies: evolution / quasars: emission lines / X-rays: galaxies / line: formation
The type 2 AGN catalog is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/626/A9
© ESO 2019
1. Introduction
There is solid observational evidence that the growth of super-massive black holes (SMBHs) at the center of galaxies is tightly connected to nuclear stellar activity and the formation of spheroids (Richstone et al. 1998). The correlation between the masses of SMBHs and the velocity dispersions and masses of their host stellar spheroids (Kormendy & Richstone 1995; Magorrian et al. 1998; Ferrarese & Merritt 2000; Gebhardt et al. 2000) suggests that the fueling of the central black hole must be linked to the spheroid growth. The star formation in the nuclear region of the galaxy is indeed predicted to contribute to the overall bulge stellar population (Schmitt et al. 1999; Cid Fernandes et al. 2001). In addition, the similar cosmic trend of the rates of star formation and central black hole accretion, both peaking around redshift ≃2 with an exponential decline at later times (Madau & Dickinson 2014; Silverman et al. 2008; Franceschini et al. 1999), further supports a coevolution of black holes and their host galaxies. Both theoretical and observational studies have been undertaken to comprehend the evolutionary link between active galactic nuclei (AGN) and their host galaxies, but the underlying mechanisms responsible for this coevolution are still far from being fully understood. In particular, spectroscopic analyses devoted to studying the properties, such as metal content, geometry, and gas dynamics, of the emitting gas in the narrow-line region of the AGN, which extends up to the kiloparsec scale (e.g., Netzer et al. 2004), are fundamental to better understand the AGN-host coevolution in terms of gas-fueling toward the central SMBH and of the impact of gravitational accretion on the gas content of the host galaxy. A representative census of AGN over a wide range of cosmic time is therefore crucial to shed light on the role of central SMBH in this symbiosis with the host.
It is now generally accepted that z ∼ 2 is a critical epoch for galaxy evolution, as both the global star formation rate (SFR) and the AGN activity peak at about this redshift (Hopkins & Beacom 2006; Richards et al. 2006a; Delvecchio et al. 2014). The chemical evolution of galaxies and active nuclei at their center in these crucial times therefore provides important clues to understand their build-up processes. AGN inhabit galaxies where the central SMBH is accreting the surrounding gas during its activity phase. The accreted gas possibly keeps the imprint of the past star formation of the bulge. By measuring the gas metallicity in regions surrounding the AGN, it could be possible to obtain indirect information on the host star formation history. In particular, given the larger spatial extent of the NLR emitting gas compared to the broad-line region (BLR), estimating the metallicity using the AGN narrow emission lines could be particularly promising as they are more suited as proxy of the host galaxy properties. A fortiori, this holds not only at low redshift, but also for the high-redshift and high-luminosity AGN samples because the spatial extent of the NLR region is larger in higher luminosity AGN, as confirmed by a strong correlation observed between the size of the NLR and the luminosity of the optical [O III] λ5007 emission line (e.g., Bennert et al. 2002; Liu et al. 2013; Sun et al. 2018; Dempsey & Zakamska 2018).
Chemical abundance indicators for the NLR have mainly been calibrated in the optical bands. Storchi-Bergmann et al. (1998) have explored two metallicity calibrations based on three emission-line ratios, namely [O III] λλ4959, 5007/Hβ, [N II] λλ6548, 84/Hα, and [O II]λ3727/[O III] λλ4959, 5007, while Castro et al. (2017) have recently proposed a metal abundance calibration of the N2O2 parameter, defined as the logarithm of the [N II] λ6584/[O II] λ3727 ratio. At z ≳ 2, current optical spectroscopic studies of AGN probe their redshifted UV emission, which prevents exploiting standard metallicity indicators. Therefore, the metal content must be estimated by comparing the ratios of strong-UV lines detected in AGN spectra with photoionization models (e.g., Groves et al. 2004; Nagao et al. 2006; Feltre et al. 2016). Recently, Dors et al. (2014) have proposed a new index based on the C IV, C III], and He II lines, that is, C43 = log[(CIV + CIII])/HeII] to study the metallicity evolution of narrow-line AGN in a wide redshift range (0 < z < 4). Moreover, UV-line ratios have been found to be a valuable alternative to the standard BPT (Baldwin et al. 1981) and Veilleux & Osterbrock (1987) optical diagnostic diagrams to distinguish between AGN and star formation activity at high redshift (e.g., Feltre et al. 2016; Nakajima et al. 2018).
In the local Universe, a strong correlation between the stellar mass and metallicity is observed in z ∼ 0.1 star-forming galaxies of the Sloan Digital Survey (SDSS; Tremonti et al. 2004). This mass-metallicity relation (MZR; Lequeux et al. 1979) shows a small dispersion (≈0.1 dex in gas-phase O/H ratio) and is relatively steep below 1010.5 M⊙, but flattens at higher stellar masses. Moving at high redshift, the MZR evolves with time in such a way that at a given stellar mass, the galaxies had a lower gas metallicity in the past. The MZR is usually assessed on samples of star-forming galaxies where AGN are removed through the exploitation of optical selection criteria, for instance, BPT diagram, the presence of broad lines in their spectra, and X-ray data constraints (e.g., Tremonti et al. 2004; Erb et al. 2006; Maiolino et al. 2008). In the literature, the MZR of AGN, its evolution with redshift, and a comparison with that of star-forming galaxies is still poorly explored. Previous studies based on rest-UV spectroscopy of AGN support no evolution of the metallicity with redshift (e.g., Nagao et al. 2006; Matsuoka et al. 2009; Dors et al. 2014). These studies are limited both in terms of line detections, as they are mainly based on line ratios of C III], C IV, He II, and in some cases N V, and the number of sources, with samples of a few tens of objects at z ∼ 2 and even lower numbers at higher redshift.
In this work, we present the largest spectroscopic sample of type 2 AGN at 1.5 < z < 3.0 drawn from the z-COSMOS deep survey (Lilly et al. 2007). We use the C IV emission line as indicator of nuclear activity and its line profile to divide the sample into unobscured (broad, type 1) and obscured (narrow, type 2) AGN. We focus on the study of the excitation properties of the NLR by comparing the ratios of the emission lines that are detected in the spectra of our sources. We also exploit the broad-band photometry available to infer the physical properties (e.g., the stellar mass) of the host galaxies. Our main goal is to determine the properties of the gas in the NLR of type 2 AGN, with particular regard to the metallicity (as traced by the gas-phase oxygen abundance, expressed in terms of 12 + log(O/H)gas). To this aim, we exploit predictions from photoionization models including new parameterizations for the distance of gas distribution from the central source and the velocity of internally microturbulent clouds. We aim at investigating the evolution with redshift of the gas metal content in the NLR and compare it with the properties of the host to study the mass-metallicity relation in type 2 AGN. This work fits into a wider project that is attempting to exploit the high-ionization narrow emission lines to select and characterize samples of obscured AGN both at low (using [O III] λ5007; Vignali et al. 2010) and intermediate redshifts (via [Ne V] λ3427 detection; Gilli et al. 2010; Mignoli et al. 2013).
The paper is structured as follows. In Sect. 2 we present the spectroscopic survey, the sample selection, and the classification into narrow- and broad-line AGN, along with the observed spectral properties. Section 3 summarizes the measurements of rest-UV emission lines and stellar masses of the host galaxies for the type 2 AGN sample. In Sect. 4 we describe the photoionization models of the AGN NLR, and we exploit diagnostic diagrams and emission-line ratios to study the nebular properties of the AGN NLR. Finally, in Sect. 5 we discuss the properties of the NLR gas in our type 2 AGN sample, the evolution with redshift of its metallicity, and the mass-metallicity relationship in our C IV-selected type 2 AGN. The summary and conclusions are presented in Sect. 6.
2. Sample selection
2.1. The zCOSMOS-deep spectroscopic survey
The Cosmic Evolution Survey (COSMOS, Scoville et al. 2007) provided high angular resolution and good depth Hubble Space Telescope (HST) imaging with single-orbit I-band ACS exposures in an equatorial field of two square degrees (Koekemoer et al. 2007), along with ground-based images in 15 photometric optical and near-infrared bands (Capak et al. 2007). The zCOSMOS survey (Lilly et al. 2007) produced spectroscopic redshifts for a large number of galaxies in the COSMOS field using VIMOS, a multislit spectrograph mounted on the 8m UT3 of the European Southern Observatory’s Very large Telescope (ESO VLT). The zCOSMOS project has been designed to efficiently use VIMOS by dividing the survey into two components: the zCOSMOS-bright is a purely magnitude-limited survey, which has collected about 20 000 redshifts for objects brighter than I = 22.5 across the full COSMOS field. This selection culls galaxies mainly in the redshift range 0.1 < z < 1.2. The second part, zCOSMOS-deep, has targeted about 10 000 B < 25 galaxies, selected using color-selection criteria to cover the redshift range 1 ≲ z ≲ 4. In this case, only the central 1 deg2 region of the COSMOS field has been observed, and the spectra of the targeted objects have been obtained using the R ∼ 200 LR-Blue grism, which provides a spectral coverage from 3700 to 6800 Å. The spectra were reduced and calibrated with the VIMOS Interactive Pipeline Graphical Interface software (VIPGI, Scodeggio et al. 2005), while the redshifts were measured by two different zCOSMOS teams, with the support of an interactive package (EZ, Garilli et al. 2010), and were then visually checked and validated. For more details about the zCOSMOS survey, we refer to Lilly et al. (2009).
2.2. The C IV-selected sample
The zCOSMOS-deep survey includes 9523 spectroscopically observed objects, but only 7635 of them (80%) have available redshift measurements. A quality flag has been assigned to account for the redshift measurement reliability: objects with flags 4 and 3 have very secure redshifts, whereas objects with flags 2 and 1 have less secure redshifts, with decreasing spectra quality; flag 9 indicates redshifts based on a single emission line. Moreover, a decimal place modifier (0.5) is added to denote the agreement with the photometric redshift (see Lilly et al. 2009, for a detailed definition of the confidence classes). In this paper we analyze galaxies with flags 4, 3, 2.5, 1.5, and 9.5 because their redshifts are either secure on their own or are confirmed by the associated photo-z. To guarantee that the C IV λ1549 emission line is included in the observed wavelength range, we limit our analysis to the redshift range 1.45 < z < 3.05. The final analyzed sample contains 4391 galaxies, and their VIMOS spectra were visually inspected and measured to select the C IV-emitting objects.
The motivation for using the C IV emission line to select high-z AGN from the zCOSMOS-deep survey is twofold: on the one hand, the high-ionization potential of the triply ionized carbon, C3+, makes it a likely signature for nuclear activity, and furthermore, the C IV emission line is the most intense AGN feature in the UV range, apart from Lyα. On the other hand, in the redshift range culled by the zCOSMOS-deep survey (1.0 < z < 3.5, see the upper panel of Fig. 1), the C IV is the most frequent spectral feature, with more than 85% of the galaxies covering the C IV wavelength range in their spectra.
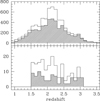 |
Fig. 1. Redshift distributions of zCOSMOS-deep galaxies with z ≥ 1. Top panel: parent galaxy sample; the hatched histogram shows the galaxies with redshift quality flag ≥1.5. Lower panel: C IV-selected AGN sample; the hatched histogram shows the type 2 sample. |
The accurate selection process consists of two main steps. First, the C IV wavelength region is visually inspected in all the galaxy spectra, within the redshift range where the line is visible, to identify possible emitter candidates. The complexity of the C IV spectral feature did not allow an automatic detection procedure, since the C IV line profile could include an AGN emission component, an absorption doublet due to the ISM, and a stellar wind feature which should display a P-Cygni shape. This preliminary analysis reduced the number of galaxies to be further examined to a few hundred, allowing a careful inspection of the one- and two-dimensional sky-subtracted spectra to eliminate spurious detections (i.e., sky-line and cosmic-ray residuals). The final pass of the selection process consists of the measurement, on the three-pixel smoothed spectra, of the putative C IV emission line using IRAF task splot: we selected as strong emitter all the objects with a C IV emission peak five times higher than the continuum rms estimated in 50 Å windows adjacent to the emission line. No C IV-emitter has been found in galaxy spectra with confidence class 1.5, probably because the presence of a strong emission line caused the assignment of a fair-to-high redshift reliability. Following this laborious but accurate selection, we identified 192 C IV-selected AGN candidates, and their redshift distribution is shown as an empty histogram in the lower panel of Fig. 1.
2.3. Spectral measurements and AGN classification
The first aim of the spectral line measurement is to classify the selected AGN candidates into narrow-line (type 2) and broad-line (type 1) objects. Because the C IV emission line is by construction ubiquitous and has an adequate signal-to-noise ratio (S/N), it was accurately fit in all spectra, assuming a linear continuum and a Gaussian profile. In order to evaluate the quality of the line profile fitting and to estimate the error in the measurements of the full width at half-maximum (FWHM), we performed four different line fits, using both the original raw and the three-pixel smoothed spectra, and adopting different wavelength regions in the continuum level determination. The results of the first set of spectral measurements are presented in Fig. 2, where the intrinsic FWHM of the C IV emission line is shown as a function of redshift. To estimate the intrinsic width of the line, the observed FWHM was deconvolved by subtracting in quadrature the instrumental resolution, FWHMinst = 1350 km s−1, as determined from sky lines. We used the width of the C IV line to carry out the classical AGN optical classification: the objects were identified as type 2 AGN if the rest-frame FWHM was less than 2000 km s−1 (to be conservative, we required that the FWHM measurement plus its associated 1σ error should be below the threshold value); otherwise, we classified them as type 1 AGN. A few objects, especially at lower redshifts, inhabit a part of the FWHM space near the separation limit, but an analysis of the spectral and morphological properties of the two AGN samples confirmed the goodness of the adopted threshold of 2000 km s−1. Out of the 192 C IV-selected AGN candidates, 90 are classified as type 2 AGN, and their redshift distribution is shown in the lower panel of Fig. 1 as the dashed histogram. The remaining 102 selected type 1 AGN were already identified as such during the zCOSMOS redshift measurement process, where broad emission-line objects were flagged, and most importantly, no object previously identified as a quasi-stellar object (QSO) was missed by our selection process in the redshift range of interest.
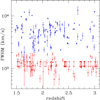 |
Fig. 2. Intrinsic rest-frame FWHMs of the C IV emission line in our sample as a function of redshift. Objects with line FWHM strictly less than 2000 km s−1 are classified as type 2 AGN (red symbols); unresolved lines are shown as downward arrows. Broad emission-line objects (with FWHM > 2000 km s−1) are classified as type 1 AGN and plotted with blue symbols. |
2.4. Spectral properties of the AGN samples
We investigated the average spectral properties of the two AGN samples by generating and analyzing their composite spectra, obtained by coadding all available zCOSMOS spectra included in each class. To create the composite, each spectrum was shifted to the rest-frame according to its redshift (with a 2.0 Å bin width, to match the instrumental pixel size at the median redshift of the sample) and normalized to a common continuum region, which is always observed in the spectral window. An identical weight was assigned to each individual spectrum to avoid biasing the final composite toward the brightest objects.
Figure 3 shows the average spectra corresponding to the type 1 (bottom blue curve) and type 2 (top red curve) AGN samples. Both spectra show the typical AGN emission lines as labeled in the figure. A summary of the main line parameters is also provided in Table 1. All the emission lines in the composite spectrum of the type 2 AGN sample are consistent with being unresolved (the upper limit of 1350 km s−1 corresponds to the spectral resolution of the zCOSMOS-deep data), with the possible exception of the N Vλ1240 line, which is apparently resolved. Comparing the equivalent widths (EW) measured in our type 1 AGN composite with the values reported in Harris et al. (2016) from the BOSS composite spectra (third and fifth column of Table 1, respectively), we observe a significant difference: the larger EWs that are measured in our C IV-selected sample can be explained to be a consequence of the Baldwin effect (Baldwin 1977) because our AGN are fainter than thoses of the BOSS survey.
 |
Fig. 3. Composite spectra of the two AGN samples with the identification of the main emission lines: the lower (in blue) and upper (in red) spectra represent the average spectra of the C IV-selected type 1 and type 2 AGN, respectively. The flux normalization is arbitrary, and the spectra are offset for clarity. |
Spectral measurements in AGN composite spectra.
2.5. X-ray properties of the AGN samples
The deepest X-ray coverage of the entire zCOSMOS-deep region is granted by the COSMOS-Legacy survey (Civano et al. 2016), a Chandra program that has observed the COSMOS field with an effective exposure of ≃160 ks over the central 1.5 deg2. Of the 192 C IV-selected AGN candidates, 147 (77%) are detected by Chandra within 2.5″ from the optical coordinates. The mean displacement between the AGN optical positions and their X-ray detected counterparts is 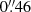 , and all of the associations are validated by the maximum likelihood technique (Marchesi et al. 2016). Furthermore, the six sources with a spatial offset larger than 1″ are the true X-ray counterparts of the C IV-selected AGN because the likelihood of finding a spectroscopic AGN in an X-ray error box is strongly increased by their low surface densities (Zamorani et al. 1999).
, and all of the associations are validated by the maximum likelihood technique (Marchesi et al. 2016). Furthermore, the six sources with a spatial offset larger than 1″ are the true X-ray counterparts of the C IV-selected AGN because the likelihood of finding a spectroscopic AGN in an X-ray error box is strongly increased by their low surface densities (Zamorani et al. 1999).
The X-ray detection rate is significantly different for the two AGN spectral classes: more than 94% (96/102) of type 1 AGN are detected by Chandra, whereas for the type 2 AGN, the fraction drops to 57% (51/92). This different behavior cannot be ascribed to a significantly different vignetting-corrected (i.e., effective) exposure time for the two populations. Vignali et al. (2014) also found a striking difference in the rate of X-ray detections for AGN selected at z ∼ 1 by the presence of the high-ionization [Ne V] line: 94% of the objects with broad lines in their optical spectra showed a Chandra X-ray counterpart, while the narrow-line AGN are detected in only one-third of the cases. To verify that this behavior is not related to the selection criteria, we investigated the X-ray detection rate in the SDSS: Pâris et al. (2014) cross-correlated the Data Release 10 Quasar (DR10Q) catalog with the second XMM-Newton Serendipitous Source Catalog (Third Data Release, 2XMMi-DR3; Watson et al. 2009). Analyzing the DR10Q catalog, we find that 92.4% of the SDSS quasars are detected in the X-rays. To perform a similar analysis for the obscured AGN, we cross-correlated the type 2 SDSS quasars presented in Reyes et al. (2008) with the third XMM-Newton Serendipitous Source Catalogue (3XMM-DR5; Rosen et al. 2016). Of the 118 type 2 SDSS quasars included in the XMM-Newton pointings, 55 match entries in the 3XMM-DR5 catalog, corresponding to an X-ray detection rate of 46.6%. These results reflect significant obscuration in the X-rays for the type 2 AGN (typically, the column density is above 1022 cm−2) and reassures us that the adopted FWHM threshold for the spectral classification effectively separates the C IV-selected AGN sample into obscured and unobscured objects. A more exhaustive analysis of the X-ray properties of the C IV-selected AGN sample will be presented in a forthcoming paper (Vignali et al., in prep.).
3. The C IV-selected type 2 AGN sample
The principal aim of this paper is to investigate the physical properties of NLR emitting gas and their connection with the properties of the host galaxy. The type 2 AGN sample is the ideal laboratory for such studies because both the broad component of the emission lines and the intense radiation from the nuclear engine are shielded by dust, allowing a better analysis of the narrow emission lines and of the spectral energy distribution (SED) of the host galaxy. In the following, we therefore focus on the properties of the narrow-line AGN and their host galaxies.
3.1. UV emission-line measurements
The selected type 2 AGN show various emission features in the rest-frame UV spectral range (see Fig. 3 and Table 1). The analysis of the line ratio diagnostic diagrams, combined with predictions from photoionization models, provides a powerful tool for probing the physical conditions within the narrow-line emitting regions of AGN.
We computed fluxes, velocity dispersions, and EWs of the emission lines by simultaneously fitting Gaussian profiles to each set of lines, assuming the same FWHM for all the lines and allowing a small shift of the central positions with respect to the systemic redshift in order to account for the well-known offset between emission-line peaks in quasars (Richards et al. 2002). Fixing the same velocity dispersion for all the profiles improves the fit for low S/N lines. This is indeed reasonable because we assumed that all lines originate from the same emitting region (i.e., the NLR), and most of them are dominated by the instrumental point spread function (PSF). The continuum level was fit, in regions free of known emissions, with a polynomial function. We used customized fitting procedures, adapted from the IRAF task splot, to measure eight emission lines: N Vλ1240 (hereinafter N V), N IV] λ1486 (N IV]), C IVλ1549 (C IV), He IIλ1640 (He II), O III] λ1663 (O III]), C III] λ1909 (C III]), C II]λ2326 (C II]), and [Ne IV] λ2423 ([Ne IV]). The Lyα emission line was excluded from the simultaneous fit because it could be severely affected by resonant scattering in the interstellar and circumgalactic medium, internal kinematics, and emissivity distribution, which would make the comparison with the outcome of the photoionization models difficult. We also avoided the line blend Si IV/O IV] at ∼1400 Å.
Errors on the flux measurements were estimated following the recipe described by Lenz & Ayres (1992):
where FluxTOT is the measured flux of the emission line, (S/N)cont is the signal-to-noise ratio of the continuum close to the line, Δλ is the spectral sampling, and CL is the coefficient computed by Lenz & Ayres (1992; see their Table 1). The computed relative flux errors are ≈10% for the brightest emission lines (flux > 5 × 10−17 erg cm−2 s−1), but they increase up to ≈30−40% for the faintest ones (with flux ≈ 2 ÷ 5 × 10−18 erg cm−2 s−1).
3.2. Stellar masses of the host galaxies
Stellar masses were computed using a two-component (AGN and galaxy) SED fitting technique. Briefly, we used a combination of AGN and host-galaxy templates to fit the large set of optical and near-infrared photometry available in the COSMOS field, using a χ2 minimization to find the best solution that reproduced the observed flux of each object at a redshift fixed to the spectroscopic one. In particular, for the AGN component, we adopted the Richards et al. (2006b) mean QSO SED as derived from the study of 259 IR-selected quasars with both SDSS and Spitzer photometry, while the galaxy component was described using a library of synthetic spectra generated from the stellar population synthesis model of Bruzual & Charlot (2003), with different star formation histories and ages and assuming a universal initial mass function (IMF) from Chabrier (2003). A more detailed description of the method can be found in Bongiorno et al. (2012). The lower panel of Fig. 4 shows the stellar mass distribution of the host galaxies for the type 2 AGN sample. We computed stellar masses for all but two of the C IV-selected type 2 AGN because the photometric data for two objects did not allow a reliable estimate: nearby objects seriously contaminate the data. The host galaxy stellar masses are in the range 8.5 × 108 − 2.2 × 1011 M⊙, with an average (median) stellar mass of 2.1 × 1010 M⊙ (3.6 × 1010 M⊙). The upper panel of Fig. 4 shows the mass distribution of the parent sample of zCOSMOS-Deep galaxies in the redshift range where the C IV line is present in the spectral coverage (empty histogram), along with that of the galaxies with spectroscopic redshift flag ≥2, represented by the shaded histogram. For the parent sample the stellar masses were computed following the recipe adopted by Bolzonella et al. (2010). We note that for our type 2 AGN sample, the stellar masses estimated by the two methods differ by less than 30% for the majority of the cases (85%), and for the galaxies with the largest mass disagreement, the higher value is often computed by the method that does not include the AGN contribution. Even when we take the different calculation methods into account, the two mass distributions are significantly different, with the type 2 AGN host galaxies peaking toward the high-mass tail. We used a two-population Kolmogorov-Smirnov (K-S) test to assess the significance of the difference between the stellar masses of the galaxy parent sample and the type 2 AGN hosts. We find that they differ at very high significance (> 6σ).
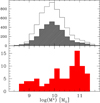 |
Fig. 4. Stellar mass distribution of zCOSMOS-Deep galaxies with 1.45 < z < 3.05. Top panel: parent galaxy sample; the hatched histogram shows the galaxies with redshift quality flag ≥2. Lower panel: stellar mass distribution of the galaxies hosting the C IV-selected type 2 AGN. For these objects the masses are derived from a two-component (AGN and galaxy templates) SED fitting. |
In order to parameterize the relative contribution of the AGN emission over the host galaxy light, we computed the dereddened luminosity of the two components in the rest-frame K band, using two distinct values (one for the galaxy and one for the active nucleus) of the dust attenuation provided by the SED fitting routine. We defined the ratio between the AGN K-luminosity and that of the host galaxy as “AGN dominance”. Reassuringly, this ratio correlates with the rest-frame EW of the C IV emission line, which is also a good indicator of the AGN prominence because the EW is the ratio between the flux of the AGN-powered emission line and the UV stellar continuum (the power-law continuum from the nuclear engine is largely shielded by dust in obscured AGN). Only five of the C IV-selected objects show an AGN contribution lower than 20%, and all of them also belong to the low tail of the C IV EW distribution; their rest-frame equivalent widths are smaller than 10 Å. Because these objects are also undetected in the X-rays, they are the prime suspects for being low-luminosity AGN, if not actually pure star-forming galaxies.
4. Comparison with photoionization models
We compared observations with predictions from photoionization models (described in Sect. 4.1) to improve our understanding of the excitation properties of the narrow-line emitting gas in AGN. We first explore diagnostic diagrams (Sect. 4.3) based on UV emission-line ratios and these diagrams confirm the efficacy of the C IV line to select AGN. We then perform a simple spectral fitting to estimate the metallicity, expressed in terms of the gas-phase oxygen abundance, of the emitting gas in our C IV-selected AGN (Sect. 4.4).
4.1. Photoionization models
The nebular emission from the NLR of AGN was modeled with single ionization-bounded gas clouds using the approach described in Feltre et al. (2016). The AGN ionizing spectrum, described as a series of broken power laws (Eq. (5) in Feltre et al. 2016), is combined with the photoionization code CLOUDY (version c13.03, last described in Ferland et al. 2013). We included dust and radiation pressure and adopted an open geometry appropriate for gas with a small covering factor, that is, the radiation from the illuminated face of the cloud toward the source of continuum radiation is allowed to escape without further interacting with the gas.
The models are parameterized in terms of
-
the UV spectral index, α, of the incident radiation field (Fν ∝ να) at the wavelength range of the ionizing photons;
-
the volume-averaged ionization parameter ⟨U⟩1, defined as the dimensionless ratio of the number density of H-ionizing photons to that of hydrogen;
-
the hydrogen gas density of the clouds, nH;
-
the interstellar (gas+dust phase) metallicity, Z;
-
the dust-to-heavy element mass ratio, ξd;
-
the mean distance from the central source of the illuminated face of the NLR gas distribution, rin, hereafter inner radius of the NLR for conciseness;
-
the internal microturbulence velocity of the gas cloud, vmicr.
The values of these parameters that we adopted in our calculations are summarized in Table 2. Exploring different values for the NLR inner radius, that is, the distance from the center, means testing different scaling relations, where the AGN luminosity is linked to the inner radius of the NLR, rin, through the scaling relation 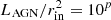 erg s−1 cm−2. For a given AGN luminosity, the value of the index p depends only on the assumed rin value. We explored two values of rin, 90 and 300 pc, and scaled the models to an AGN accretion-disk luminosity, integrated over the wavelength range between 0.001 and 10 μm (Eq. (5) in Feltre et al. 2016), of LAGN = 1045 erg s−1. To compute the transmission of the radiation through the gas cloud, we set the outer boundary of the photoionized gas distribution by stopping our calculations when the electron density fell below 1% of the number density of atoms of neutral hydrogen or the temperature fell below 100 K. The NLR emission extent of our models covers a wide range of values; the outer boundary of 68% of the models lies between ∼0.8 pc and ∼12 kpc, and the median value is ∼3.8 kpc. The median luminosity of the [O III] λ5007 lines in our models is 3.6 × 1042 erg s−1, in agreement with the empirical values shown in Fig. 15 of Storchi-Bergmann et al. (2018).
erg s−1 cm−2. For a given AGN luminosity, the value of the index p depends only on the assumed rin value. We explored two values of rin, 90 and 300 pc, and scaled the models to an AGN accretion-disk luminosity, integrated over the wavelength range between 0.001 and 10 μm (Eq. (5) in Feltre et al. 2016), of LAGN = 1045 erg s−1. To compute the transmission of the radiation through the gas cloud, we set the outer boundary of the photoionized gas distribution by stopping our calculations when the electron density fell below 1% of the number density of atoms of neutral hydrogen or the temperature fell below 100 K. The NLR emission extent of our models covers a wide range of values; the outer boundary of 68% of the models lies between ∼0.8 pc and ∼12 kpc, and the median value is ∼3.8 kpc. The median luminosity of the [O III] λ5007 lines in our models is 3.6 × 1042 erg s−1, in agreement with the empirical values shown in Fig. 15 of Storchi-Bergmann et al. (2018).
Main adjustable parameters of the photoionization models.
4.2. Microturbulent clouds and inner radius of the NLR gas
It is worth noting that the AGN NLR model grid adopted in this work is an improvement over Feltre et al. (2016) and includes two new adjustable parameters: the inner radius of the NLR, rin, and the internal microturbulence velocity of the gas cloud, vmicr. These additional terms have been introduced to explain the observed luminosity of the N V compared to C IV and He II emission lines, which is commonly underestimated by photoionization models of both broad- and narrow-line emitting regions of AGN (Davidson & Netzer 1979).
To solve the problem of high N V/C IV and N V/He II ratios observed in AGN, some authors appeal to super-solar metallicities (e.g., Hamann & Ferland 1993; Shemmer & Netzer 2002; Nagao et al. 2006), up to 10 times solar (see also Sect. 7.1.2 of Netzer 2013). However, these same high-metallicity models do not reproduce other ratios observed in the spectra of the same sources (Nagao et al. 2006; Feltre et al. 2016), such as C IV/He II and C III]/He II, which instead favored lower metal abundances. Other solutions have been proposed in the literature, such as “selectively” enhanced nitrogen abundance (Hamann & Ferland 1992, 1993) and internally microturbulent clouds (Bottorff et al. 2000; Kraemer et al. 2007). We did not consider models with an overabundance of nitrogen for two reasons: first, photoionization models agree well with the observed emission from other nitrogen ions, such as N IV] (observed in this sample), without requiring an enhanced fraction of nitrogen or highly super-solar metallicity. Second, we have computed models in which the nitrogen abundance was increased by 0.15 dex compared to that used in Feltre et al. (2016) and found no significant improvement in reproducing the observed line ratios involving N V. We note that our models already account for the secondary nucleosynthesis production of nitrogen (Eq. (11) of Gutkin et al. 2016) that results from the CNO cycle of stars that are already enriched in carbon and oxygen and are therefore important at high metallicities (e.g., Cowley 1995; Chiappini et al. 2003).
As an alternative to exotic metal abundances, we computed models with a dissipative turbulence (vmicr = 100 km s−1) internal to the clouds that converts the turbulent motion into heat, following the approach of Kraemer et al. (2007). The consequent increase of the electron temperature affects the emissivity of some emission lines, and in particular, that of the collisionally excited lines. This hypothesis is further supported because the FWHM of the N V line is wider than other high-ionization emission lines that are observed in the type 2 composite spectrum (see Table 1), although the poor resolution of the VIMOS spectra, the partial blending with the Lyα, and the doublet nature of the N V line mean that the line width difference cannot be used to constrain the microturbulence models. We also explored different scaling relations between the AGN luminosity and the distance of the inner face of the NLR gas clouds from the central source, that is, models with different values of the inner radius of the NLR emitting gas (rin = 90, 300 pc) for LAGN = 1045 erg s−1. A lower inner radius at fixed AGN luminosity translates into an increase in radiation pressure at the inner face of the gas cloud Pin (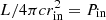 , see also Eq. (1) of Dempsey & Zakamska 2018).
, see also Eq. (1) of Dempsey & Zakamska 2018).
4.3. Diagnostic diagrams
We compared the emission-line measurements (Sect. 3.1) of the C IV-selected type 2 AGN with predictions from the photoionization models described above. Figure 5 shows four diagnostic diagrams based on UV emission-line ratios, which we found to be good diagnostics of nuclear activity versus star formation (see Sect. 4 of Feltre et al. 2016, and references therein). The C IV/He II versus C IV/C III] and C III]/He II diagrams, originally investigated by Villar-Martin et al. (1997), are shown in the two top panels of Fig. 5 (left and right, respectively), while the two bottom panels show C IV/He II versus N V/C IV and N V/He II (left and right, respectively). These line ratios are used in the literature as diagnostics of the ionizing source and to investigate the gas metallicity of type 2 AGN and z ∼ 2.5 radio galaxies (e.g., De Breuck et al. 2000; Vernet et al. 2001; Groves et al. 2004; Nagao et al. 2006; Humphrey et al. 2008).
 |
Fig. 5. Predictions of the AGN NLR models described in Sect. 4.1 in the C IV/He II vs. C IV/C III] (top left), C III]/He II (top right), N V/C IV (bottom left) and N V/He II (bottom right) diagrams. Each panel shows data measurements with error bars and upper limits (black symbols) of the C IV-selected type 2 AGN, described in Sect. 3, and AGN models (shaded areas) encompassing wide ranges in power-law index, α, ionization parameter, ⟨U⟩, gas metallicity, Z, gas density, nH, and dust-to-metal mass ratio, ξd. The purple and orange shaded areas indicate AGN models with no microturbulence velocity and an inner radius of 300 pc and models with microturbulence velocity vmicr = 100 km s−1 and an inner radius of 90 pc, respectively. Cyan stars show the predictions from photoionization models of star-forming galaxies of Gutkin et al. (2016). In each panel, the gray arrows indicate the effect of correcting the AGN data by dust attenuation for a galactic attenuation curve (Cardelli et al. 1989) and AV = 1 mag. |
The purple and orange shaded areas in each panel of Fig. 5 indicate AGN photoionization models encompassing wide ranges of model parameters: power-law index, α, ionization parameter, ⟨U⟩, gas metallicity, Z, hydrogen gas density nH, and dust-to-metal mass ratio ξd, as summarized in Table 2. Models with no internal microturbulence and an inner radius of 300 pc as in Feltre et al. (2016) are shown in purple, while models with internal microturbulence (vmicr = 100 km s−1) and smaller inner radius (rin = 90 pc) are plotted in orange. For comparison, the cyan stars indicate models of nebular emission from star-forming galaxies by Gutkin et al. (2016). AGN models, in particular those with internally microturbulent clouds and a small inner radius, predict line ratios similar to those measured in the spectra of our C IV-selected sample. Reducing the inner radius and adding the microturbulence has a similar impact on the predictions of emission-line ratios and, specifically, lead to the increase in C IV/He II and N V/He II ratios.
Only a few C IV-selected objects do not lie in the area occupied by pure AGN models in the diagnostic diagrams; in particular, four objects appear to be outliers with respect to pure AGN models in all the diagnostic diagrams. Two of the four outliers show SEDs with an AGN contribution to the rest-frame K band (see Sect. 3.2) that is lower than 10% and very low C IV EWs (< 10 Å), suggesting a non-negligible contribution from star-formation activity to the emission lines of these sources. This suggestion is supported by a blue continuum with strong absorption lines in their VIMOS spectra. The other two outliers present noisy spectra with a possible contribution from the broad component to the C III] emission line. This contribution might artificially increase the C III]/He II line ratio. The moderate S/N of the VIMOS spectra did not allow us to perform a multiple fitting (broad, narrow, and stellar components) of the emission lines, but we are confident that both the C IV-selection and the removal of the broad-line objects through FWHM thresholding provided us with a relatively clean sample of narrow-line AGN. We also studied diagnostic diagrams based on the EW of C III] and C IV lines, namely EW(C III]) versus C III]/He II (EW−C3) and EW(C IV) versus C IV/He II (EW−C4). None of the sources is classified as a star-forming galaxy when the separation criteria of Hirschmann et al. (2018) are adopted. Of the 64 objects that are covered by the C III] line, 8 lie in the composite region (i.e., intermediate between pure AGN and pure star-forming galaxy) of the EW−C3 diagram, while 15 of the C IV-selected AGN lie in the composite region of EW−C4 (see Table 1 and Fig. 5 of Hirschmann et al. 2018). All the sources except for one are classified as AGN following the separation criteria of Nakajima et al. (2018). This object is one of the two outliers that show a significant contribution from a stellar component in the spectra. That the diagnostic diagrams contain only a few outliers suggests that contaminations from the BLR and/or from the star formation (the two main sources of uncertainty in the analysis of the UV emission lines) probably do not significantly affect the measurements of the narrow-line fluxes.
4.4. Physical properties of the nebular gas
To study the excitation properties of our C IV-selected type 2 sample, we compared predictions from the photoionization models (Sect. 4) to the observations by fitting emission-line ratios. In particular, we considered ratios of any possible combination of the emission lines measured in the spectra of our C IV-selected type 2 AGN, namely N V, N IV], He II, O III], C IV, C III], C II] and [Ne IV]. We adopted a galactic attenuation curve (Cardelli et al. 1989) for consistency with the fitting procedure that was used to derive the stellar masses of the host galaxy (Sect. 3.2).
The C IV-selected type 2 sample is ideal to study the excitation properties of the AGN NLR. The simultaneous presence of several emission lines of ions such as oxygen, nitrogen, and/or carbon in the same spectra, along with the plethora of the other UV lines available, provides strong constraints on the photoionization models. We computed the likelihood of each model given the data by adopting a simple Bayesian approach, similarly to Vidal-García et al. (2017, see their Eq. (3)), where our sets of observables are emission-line ratios instead of spectral indices. We then computed the median values of the posterior distribution functions and corresponding errors (computed using the 16th and 84th percentile) of the parameters of the models (see Sect. 4 and Table 2).
The line fluxes of our C IV-selected AGN are compatible with a wide range of the volume-averaged ionization parameter, −2.8 < log⟨U⟩ < −0.65, and interstellar metallicities, 0.002 ≲ Z ≲ 0.05, (0.1 ≲ Z/Z⊙ ≲ 3.3), with median values of −1.65 and 0.008 (∼half solar), respectively. The present-day solar (photospheric) metallicity adopted in the models is Z⊙ = 0.01524 (Bressan et al. 2012).
Moreover, the median UV spectral index of the ionizing radiation field for our type 2 AGN sample is α = −1.63; here, 51% of the objects with a the median value of the posterior distribution function lie in the range −1.7 < α < −1.55. We find no preference among the different values of hydrogen gas density, nH and dust-to-metal mass ratio, ξd. Determining whether these loose constraints are due to a lack of observables connected with these parameters or to the need of a finer sampling in the models is beyond the scope of this paper. We also find that about 85% and 70% of our sample favor models with an inner radius of 90.0 pc for LAGN = 1045 erg s−1 and an internal microturbulence velocity of 100 km s−1, respectively.
From the spectral fitting we finally derive values of the gas-phase oxygen abundance, expressed as 12 + log(O/H)gas, of between 7.6 < log(O/H)gas < 9.4, with median value of 7.9. This quantity is directly linked to a photoionization model of a given interstellar metallicity, Z, and dust-to-metal mass ratio, ξd (i.e., the fraction of metals depleted onto dust grains), as outlined in Sect. 2.3.2 of Gutkin et al. (2016). For reference, the solar interstellar (dust+gas phase) and gas-phase oxygen abundances of the models are 12 + log(O/H) = 8.83 and 12 + log(O/H)gas = 8.68 for Z = Z⊙ = 0.01524 and ξd = ξd, ⊙ = 0.36 respectively. The implications of these results are discussed in the next section.
5. Discussion
5.1. Nebular properties of narrow-line AGN at z = 1.5−3
By exploiting predictions from photoionization models, we investigated the excitation properties of the ionized gas in the NLR of C IV-selected type 2 AGN. Several works have performed similar studies on other samples, even though those samples are more limited in terms of number of sources and line detections. The line ratios measured from the spectra of our C IV-selected type 2 AGN, shown in Fig. 5, are similar to those measured from the spectra of z ∼ 2 radio galaxies and X-ray selected narrow-line QSO (De Breuck et al. 2000; Vernet et al. 2001; Szokoly et al. 2004; Nagao et al. 2006; Dors et al. 2014). We review and discuss the main results from our analysis below.
Ionization parameter. Our C IV-selected AGN favor models with a relatively high volume-averaged ionization parameter (−2.8 < log⟨U⟩ < −0.65, Sect. 4.4), but this is in line with those observed in other samples of active galaxies. Nagao et al. (2006) and Dors et al. (2014) found −2.2 < log(U0) < − 1.4 and −2.5 < log(U0) < − 1.0, respectively. We note that the models of Nagao et al. (2006) and Dors et al. (2014) are parameterized in terms of the ionization parameter computed at the inner edge of the gas distribution rin (U0 = U(rin)), the values of which are not directly comparable with the volume-averaged ionization parameter considered here. For comparison purposes, we computed the ionization parameter from the C III]/C IV ratio using Eq. (1) of Dors et al. (2014) for the 62 sources of our sample in whose spectra the C III] line is detected. We obtained ionization parameters at the inner radius of the NLR in the range −2.2 < log(U0) < − 1.0. These values are similar to those found in previous works and further validate our C IV-based criteria to select type 2 AGN.
Interstellar metallicity. As discussed in Sect. 4.1, high super-solar metallicities, up to ∼6 Z⊙ (e.g., Hamann & Ferland 1993; Shemmer & Netzer 2002; Nagao et al. 2006), have been invoked to explain enhanced N V emission in both BLR and NLR of AGN. In our sample of 1.5 ≤ z ≤ 3.0 type 2 AGN we estimated a subsolar or close to solar interstellar (gas+dust phase) metallicity for 89% of our objects. In particular, only 5 of the 54 C IV-selected sources at z > 1.9, the redshift at which the N V line enters the VIMOS spectral coverage, have supersolar metallicity. This result is at odds with results presented in literature and probably arises because we measured a larger number of different emission lines and adopted a wider range of free parameters in our model grid (i.e., inner radius and internal microturbulence), which can explain the enhanced N V emission observed in AGN spectra at z ∼ 2 without invoking high supersolar metallicities.
Dors et al. (2014) calibrated the C43 index (see Introduction) to derive the AGN metallicity. This quantity is based on the strong C III], C IV, and He II emission lines that are observed in the spectra of active galaxies and does not consider the N V lines. For the 57 sources for which the C III], C IV, and He II lines are simultaneously present in the spectral range (excluding upper limits), we computed the C43 index and compared it with the metallicities inferred from our fitting. Specifically, we used the “upper branch” coefficients tabulated in Table 3 of Dors et al. (2014). We find that the C43 indicator yields a metallicity in the range 0.1 ≲ Z/Z⊙ ≲ 3.0, with Z/Z⊙ > 2.5 for only 7 of 57 galaxies. We note that the values for the metal abundances and solar metallicity adopted by Dors et al. (2014) slightly differ from those of this work. However, despite these different assumptions, which prevent a real quantitative comparison, the ranges of Z/Z⊙ obtained with the line fitting and the C43 method agree overall. The advantage of our model-dependent metallicity estimate is that it employs all of the available nebular lines rather than relying on a small subset of them, as is the case for C43.
Inner radius of the NLR. As summarized in Sect. 4.4, the majority of the line fluxes measured in our sample favor models with rin = 90 × (L45)0.5 pc, where L45 is the AGN luminosity, LAGN, expressed in units of 1045 erg s−1. A similar relation has also been found by Mor et al. (2009). A smaller inner radius for a given AGN luminosity implies higher radiation pressure at the inner edge of the cloud (Sect. 4, see also Dempsey & Zakamska 2018). This can be interpreted as UV lines originating from regions closer to the central ionizing source, where the radiation pressure is higher for a radiation field of a given intensity. This result confirms the wide range of ionization levels expected in the AGN NLR, as was also shown by some studies of the rest-optical lines of type 2 AGN (e.g., Richardson et al. 2014).
Internal microturbulence. The majority of the rest-frame UV spectra of our C IV-selected type 2 AGN are better explained by models with internally microturbulent gas. To mimic the internal microturbulence and dissipative heating, we followed Bottorff & Ferland (2002; see also Kraemer et al. 2007)2.
Our calculations were computed for a gas density of 102 < nH < 104 cm−3, that is, a lower density regime than was used in the BLR models of Bottorff & Ferland (2002) and lower than the nH = 105 cm−3 of the NLR in Kraemer et al. (2007). This implies that the dissipative heating has a small effect on the lines of interest here, whereas a major role in strengthening the intensities of high-ionization lines is played by photoexcitation.
The number of continuum photons that can be absorbed by the gas before it becomes optically thick to the incident radiation is higher when the gas is internally microturbulent. These broader absorption profiles will affect resonant transitions, such as C IV and N V, which increases the contribution from photoexcitation. This is shown in Fig. 5, where models with internal microturbulence have higher C IV/He II and N V/He II. It is worth nothing that a smaller inner radius and internal microturbulence affect the line ratios in a similar way, and a combination of the two (rin = 90 pc and vmicr = 100 km s−1) provides the highest intensities for the high-ionization C IV and N V lines. We also note that more sophisticated methods for modeling the gas turbulence exist, such as the use of hydrodynamical simulations (Gray & Scannapieco 2017). To reproduce the complex physical mechanisms associated with turbulent gas is beyond the goal of this work.
We relied on NLR properties inferred from photoionization models and rest-UV emission lines. More reliable estimates of metal abundances can be obtained by adding rest-optical lines (such as [O III] λ5007, [O III] λ4959, [O III] λ4363, [O II] 3727, 3729, and the strong hydrogen recombination lines), from which we could have direct measurements of the oxygen abundance. When models based on both the rest-UV and rest-optical emissions are combined, high-to-low ionization states of the NLR gas can also be investigated, and it can be studied how these different ionization levels correlate with the radial extent of the narrow-line emitting region. Our sample therefore represents the ideal target for near-IR spectroscopic observations, which are aimed at complementing our set of rest-UV emission lines with the rest-optical lines. A comparative study of metal abundances that are separately derived from rest-optical and rest-UV observations will be particularly relevant in the context of spectroscopy of high-z AGN, for which we have to rely mainly on strong UV lines.
5.2. Evolution with redshift of the NLR metallicity
We investigated the chemical evolution of the NLR gas with redshift, and the results are summarized in Fig. 6, where the gas-phase metallicity, expressed in terms of gas-phase oxygen abundance 12+log(O/H)gas, of the C IV-selected type 2 AGN is plotted against redshift. Despite the large scatter, our measurements indicate a moderate evolution of gas-phase metal content with redshift. A least-squares fit to the data (the dashed straight line in Fig. 6) yields a decrement in the oxygen abundance of ≈0.3 dex per unity of redshift. For the sample of 90 type 2 AGN, the Spearman rank correlation coefficient is ρ = −0.55, rejecting the hypothesis that no correlation is present at > 99.9% confidence. We also divided our sample into three redshift bins (z ≤ 1.9, 1.9 < z ≤ 2.6 and z > 2.6) that correspond to different sets of emission lines used in the comparisons with the models3 and contain 34, 33, and 23 objects, respectively. We computed the average oxygen abundance in these three redshift bins (black squares in Fig. 6) and obtained averaged values of ⟨12+log(OH)⟩ = (8.55 ± 0.04, 8.34 ± 0.06, 8.16 ± 0.04).
 |
Fig. 6. Evolution of the NLR gas-phase metallicity with redshift. The gray dots represent the individual C IV-selected type 2 AGN, while the black squares are the average oxygen abundance in three redshift bins. Lower panel: the arrows highlight the redshift intervals where the quoted emission lines are visible in the observed spectral range. |
The decline in gas-phase oxygen abundance with increasing redshift in the NLR of our type 2 AGN is further enforced by the fact that the redshift bins in which the intense N Vλ1240 line is present are those with the lowest average metallicity, while an enhanced metallicity is needed to reproduce this line with standard photoionization models (see Sect. 4.1). Moreover, the rate of the oxygen abundance decline that we measured is in good agreement with the evolution of the metallicity reported by Maiolino et al. (2008) for a sample of high-z star-forming galaxies: using their Eq. (2) and the average stellar mass of our sample (2 × 1010 M⊙), we computed a decrement in the oxygen abundance of 0.285 per unity of redshift in the interval between 2.2 < z < 3.5. This redshift range is slightly higher than but overlaps with the range considered in this work. A similar decline (0.3 dex offset between z ∼ 2 and z ∼ 3.3) was observed by Onodera et al. (2016) for a sample of 41 normal star-forming galaxies. Observations of damped Lyα absorbers (DLAs) at 0 < z < 4.5 indicate that their metallicity decreases at a rate of ∼0.26 dex per unit redshift (Prochaska et al. 2003). This rate of metallicity growth observed in DLAs is similar to the rate inferred from the observed evolution of the mass-metallicity relation (e.g., Erb et al. 2006; Henry et al. 2013).
The SFR in galaxies ensures the production of heavy elements, whose local and global abundances in galaxies are modified by feedback processes, along with galactic winds, gas inflows, and accretion. In general, the decrease in metal content of galaxies with increasing redshift is globally accounted for by chemical evolultion models (e.g., Dalcanton 2007; Calura et al. 2009; Lilly et al. 2013), reproduced by semianalytical models and cosmological hydrodynamical simulations (e.g., De Lucia et al. 2004; Ma et al. 2016; Davé et al. 2011, 2017; Torrey et al. 2019), and observed from z ∼ 0 to ∼3 in star-forming galaxies (e.g., Maiolino et al. 2008; Mannucci et al. 2010; Yuan et al. 2013). There are many reasons for this observed decrease. First of all, high-z sources are much younger and consequently less chemically evolved than present-day galaxies. In addition, higher z sources may still be accreting a significant fraction of pristine gas and may host more powerful outflows that can drive the metals outside the galaxy (e.g., Yuan et al. 2013).
To our knowledge, this is the first time that a trustworthy metallicity evolution with redshift is observed in the NLR gas of high-z type 2 AGN. Previous studies on rest-UV line ratios of type 2 AGN (e.g., Nagao et al. 2006; Matsuoka et al. 2009; Dors et al. 2014) did not show a significant evolution with redshift. The differences between our and previous results might depend on two main factors: first, our sample was extracted from one single spectroscopic survey with a uniform selection technique, while previous works were based on a mixed collection of local AGN, radio galaxies, and X-ray selected type 2 AGN (see Nagao et al. 2006). Moreover, the fact that we observe a decrease in metallicity with increasing redshift is most likely related to the different approach in inferring the NLR gas metal content, exploiting more complex photoionization models (i.e., including the microturbulence) to interpret multiple rest-UV emission lines rather than using single-line ratios.
5.3. Mass-metallicity relationship in our type 2 AGN sample
After computing both the host galaxy stellar masses and NLR gas-phase metallicities, we investigated whether the mass-metallicity relationship (MZR) also held for our sample of type 2 AGN. Figure 7 shows the mass-metallicity data for 88 C IV-selected type 2 AGN for which reliable measurements are available4 along with the MZR at z = 2.2 (red curve) and z = 3.5 (purple curve) from Eq. (2) of Maiolino et al. (2008). The vertical error bars in the figure represent the 1σ (68%) uncertainties resulting from the 16th and 84th percentiles of the posterior distribution function of the gas-phase metallicity, while the horizontal lines indicate the 1σ errors on the stellar masses computed following Bongiorno et al. (2012)5.
 |
Fig. 7. Mass-metallicity relation for the C IV-selected type 2 AGN. The filled symbols mark the 61 objects with reliable measurements (emission lines detected with S/N > 3 and the SED fit with 0.5 < |
Although our gas-phase metallicities are in the same range, at least for log(M*) higher than 9.5, as those computed by Maiolino et al. (2008) for star-forming galaxies at similar redshifts, we do not find a statistically significant MZR in our data. For the full sample of C IV-selected type 2 AGN we find in a least-squares fitting of the data a shallow slope α = 0.08 of the relationship, and the corresponding Spearman rank correlation coefficient cannot reject with high significance the null hypothesis of no correlation. In order to understand whether the estimates of both stellar mass and gas metallicity in the whole type 2 AGN sample can suffer problems due to either insufficiently precise measurements or to host galaxy contamination, we repeated the least-squares fitting to the possible MZR and its statistical evaluation in different subsamples. In all the cases the relationship is shallow and less statistically significant than in the full sample. In Table 3 we show the slope and rms of the least-squares fitting along with the correlation coefficient for 1) the global sample; 2) the subsample with good measurements (all the emission lines detected with S/N > 3 and the SED fit with 0.5 < 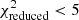 ); 3) the type 2 AGN detected in the X-rays with L2−10 keV > 6 × 1042 erg s−1; 4) the sample of type 2 AGN with intense C IV emission-line (EW0 > 15 Å); 5) the sample of type 2 AGN with relatively weak C IV emission-line (EW0 < 15 Å); 6) the sample of type 2 AGN with a photometry that requires a SED fitting with an AGN dominance > 1; and finally, 7) the sample of AGN with a relevant galaxy component in the photometry, that is, AGN dominance < 1. The values listed in Table 2 show that the mass-metallicity relationship is always extremely flat and statistically compatible with no correlation between the two quantities. Therefore, we can safely conclude that at least for our C IV-selected type 2 AGN sample, a strong relationship is not observed between the NLR gas metallicity and the stellar mass of the host galaxy.
); 3) the type 2 AGN detected in the X-rays with L2−10 keV > 6 × 1042 erg s−1; 4) the sample of type 2 AGN with intense C IV emission-line (EW0 > 15 Å); 5) the sample of type 2 AGN with relatively weak C IV emission-line (EW0 < 15 Å); 6) the sample of type 2 AGN with a photometry that requires a SED fitting with an AGN dominance > 1; and finally, 7) the sample of AGN with a relevant galaxy component in the photometry, that is, AGN dominance < 1. The values listed in Table 2 show that the mass-metallicity relationship is always extremely flat and statistically compatible with no correlation between the two quantities. Therefore, we can safely conclude that at least for our C IV-selected type 2 AGN sample, a strong relationship is not observed between the NLR gas metallicity and the stellar mass of the host galaxy.
MZR in different C IV-selected AGN samples.
The absence of the MZR could be ascribed to sample selection effects. By selecting powerful high-redshift AGN with intense emission lines, such as the C IV, we culled host galaxies that may not be representative of the global star-forming galaxy population at these redshifts. The distribution of the host galaxy masses shown in Fig. 4 already clearly shows that the distribution is strongly biased toward the tail with the highest stellar masses. Moreover, our selection required a strong high-ionization emission line in the UV range, which might have biased our sample toward objects with a strong ionization continuum, with a massive central black hole, and with mild-to-absent galactic extinction. All these properties may be connected more with an evolved and massive host galaxy bulge than with a late-type galaxy rich in dust and gas.
On the other hand, Fig. 7 shows host galaxies that even if they have stellar masses lower than 1.5 × 109 M⊙, show an NLR gas metallicity of 12+log(OH)gas > 8, and such values are expected for more massive galaxies. These objects, which keep the MZR relatively flat within the mass range explored by our sample, cannot be simply explained as due to selection effects. The MZR for star-forming galaxies has been interpreted as a consequence of the interplay between star formation efficiency, inflows of metal poor-gas, gas outflows due to galactic winds, and consequent metal depletion (e.g., Mannucci et al. 2010). Moreover, lower mass galaxies are more metal poor because their potential well is smaller (Dayal et al. 2013). The presence of an AGN could strengthen the potential well in the central part of the NLR, where most of the high-ionization emission lines are emitted (in particular the UV lines; Costantini et al. 2016), reducing the metal depletion in the NLR gas across the range of host galaxy stellar masses. Another possible explanation of the observed lack of relation between the gas-phase metallicity of the NLR and the mass of the host is that strong AGN-driven outflows can carry metal-rich gas from the BLR to radial distances of up to few kiloparsec. It is well known that the metallicity of the BLR is higher than that of the host galaxy (Xu et al. 2018; Thomas et al. 2019) and does not seem to evolve with redshift (Warner et al. 2003; Nagao et al. 2006). Even if the metal-rich gas in the NLR can be supplied by massive stars from the bulge, it could also be polluted by metals delivered by outflows emerging from the central regions of the AGN, which enhance the metallicity in the NLR and weaken the relationship with the stellar mass content of the host galaxy. A connection between the two AGN regions has also been suggested by Du et al. (2014), who found a strong correlation between NLR and BLR metallicities for 31 low-z type 1 AGN.
The lack of MZR in our sample is at odds with the relation recently found by Matsuoka et al. (2018) in high-z type-2 AGN. There can be many reasons for this discrepancy, and they include differences in terms of sample selection, mass and redshift ranges of the objects, and photoionization models. Our sample is uniformly selected and measured from the zCOSMOS-deep galaxy sample, while Matsuoka et al. (2018) collected mixed spectra of previously confirmed AGN through either radio or X-ray selection. Our C IV-selected type 2 AGN sample comprises 88 objects in a smaller redshift range compared to the 1.2 ≤ z ≤ 4.0 range of the 28 objects of the previous study. Moreover, the stellar masses of about 40% (35/88) of the C IV-selected AGN are lower than then minimum value of Matsuoka et al. (2018), that is, log(M⋆) = 10.2 M⊙. Finally, the suite of photo-ionization models used in this work differs from that of Matsuoka et al. (2018) in terms of the values of gas densities, the set of metal abundances, and the inclusion of dust physics and metal depletion. Because the two setups of the photoionization models are so different, it is difficult to perform a quantitative comparison between the metallicity values inferred with the two model grids.
6. Summary and conclusions
-
This paper presented a sample of 192 C IV-selected AGN in the redshift range 1.45 < z < 3.05, extracted from the zCOSMOS-deep survey. Ninety of them are classified as type 2 AGN on the basis of the FWHM of the emission lines (Sect. 2.3).
-
The average spectral properties in the rest-frame UV range are compatible with other (brighter) optical AGN samples. About three-quarters of the sample are detected in X-rays based on the Chandra COSMOS-Legacy survey, but the detection rate is significantly different for the two AGN spectral classes: more than 94% of type 1 AGN are detected by Chandra, while for the type 2 AGN, the fraction decreases to 57%, meaning that they are likely obscured in the X-rays (Sect. 2.5).
-
We have accurately measured fluxes and widths of eight UV emission lines in the VIMOS spectra of the type 2 AGN, and we have exploited the large set of photometric data available in the COSMOS field to estimate the stellar masses of their host galaxies using a two-component (AGN and galaxy) SED-fitting technique. The host galaxy stellar masses of the type 2 AGN are in the range 8.5 × 108−2.2 × 1011M⊙; the distribution is skewed toward high masses and peaks at ∼1011M⊙ (Sect. 3.2).
-
We find that the observed emission-line ratios involving the C IV and N V emission lines can be best explained by models with internally microturbulent clouds and an inner radius of the NLR gas distribution of rin = 90 × (L45)0.5 pc. All but four (∼95%) of the type 2 AGN lie in the regions of the UV-based emission-line ratio diagnostic diagrams occupied by these modified AGN photoionization models. This further strengthens the proposed AGN selection through strong C IV emission (Sect. 4.3).
-
We have implemented a simple spectral fitting to estimate the oxygen abundance of the NLR gas in our C IV-selected type 2 AGN, finding subsolar or solar interstellar metallicity for 89% of the sample (Sect. 4.4). At z > 1.9, only 5 of 54 type 2 AGN show super-solar metallicity, even though at this redshift the N V line enters the spectral range. We explained the observed strength of the N V emission by reducing the inner radius of the NLR and by introducing microturbulent clouds (see also Kraemer et al. 2007, for the latter), without the need of invoking highly super-solar metallicities (Sect. 5.1).
-
The gas-phase metallicity of the NLR in our type 2 AGN exhibits a statistically significant evolution with redshift in the range covered by our sample (1.5 < z < 3.0). We measure a decrement in the oxygen abundance of ≈0.3 per unity of redshift. This value is comparable to other estimates obtained in star-forming galaxies at similar redshifts (Sect. 5.2).
-
The mass-metallicity relationship is not observed in our C IV-selected sample of type 2 AGN, even when differently selected subsamples were considered (Sect. 5.3). The lack of a statistically significant MZR could be ascribed to sample selection effects because the high-ionization C IV emission line can cause culling of massive and dust-free hosts, which are not representative of the star-forming galaxy population at these redshifts. These results could also suggest that the NLR metallicity is not a good proxy of that of the host galaxy because an AGN can affect the gas supply and metal depletion in these regions.
We have adopted single-density ionization bounded models of pure AGN nebular emission to interpret the observed excitation properties of the NLR emitting gas. Future works should focus on more complex and tailored spectral decompositions accounting, in addition to the AGN component, for the contribution of star-formation to the observed SED. Moreover, the interpretation of the physical mechanisms responsible for the enhanced emission of the resonant N V line in AGN will strongly benefit from advanced models such as those based on hydrodynamical simulations of turbulent gas, as well as a proper treatment of the resonant lines by means of radiative transfer through the neutral medium. This will have relevant implications for the detection and study of potential AGN host galaxies close to the epoch of reionization, as indicated by some tentative detections at z ≳ 7 that have been presented in the literature (e.g., Laporte et al. 2017; Mainali et al. 2018). To conclude, combining the rest-UV emission of our sample with additional information from rest-optical spectra from other facilities (e.g. FMOS-COSMOS; Silverman et al. 2015) will allow us to better constrain the models and compare the physical properties inferred from the rest-optical with those from rest-UV. This is particularly important for future studies at higher redshifts with forthcoming facilities, such as the James Webb Space Telescope, which will probe both the rest-frame and optical UV emission of galaxies at z ≳ 3, and Euclid, which will unveil the rest-UV emission of the more luminous AGN at z ≳ 6.
The figures of the VIMOS spectra and the ACS images of the C IV-selected type 2 AGN, along with figures showing results from the SED fitting described in Sect. 3.2 and spectral fitting described in Sect. 4.4, are available electronically6. The data is also available at the CDS.
The models here are labeled in terms of the volume-averaged ionization parameter (see Eq. (B.6) of Panuzzo et al. 2003) instead of the ionization parameter at the edge of the Strömgren sphere US (Eq. (4) of Feltre et al. 2016). This parametrization translates into ⟨U⟩ = 9/4 US. Different choices for model-labelling have no impact on the actual CLOUDY computations, for which the input parameter is the rate of ionizing photons.
At z ≤ 1.9 the N Vλ1240 is still too blue for the spectral range, while at z > 2.6 the C III] λ1909 line moves out of the observed spectral range (see bottom panel of Fig. 6).
Two type 2 AGN do not have a good measurement of the host stellar mass, see Sect. 3.2.
Acknowledgments
We acknowledge financial support from the agreement ASI-INAF n. 2017-14-H.O. A.F. acknowledges support from the ERC via an Advanced Grant under grant agreement no. 321323-NEOGAL and no. 339659-MUSICOS. A.C. acknowledges the support from the grants PRIN-MIUR 2015 and ASI n.I/023/12/0 and ASI n.2018-23-HH.0. Y.P. acknowledges National Key R&D Program of China Grant 2016YFA0400702, and NSFC Grant No. 11773001 and 11721303.
References
- Baldwin, J. A. 1977, ApJ, 214, 679 [NASA ADS] [CrossRef] [Google Scholar]
- Baldwin, J. A., Phillips, M. M., & Terlevich, R. 1981, PASP, 93, 5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bennert, N., Falcke, H., Schulz, H., Wilson, A. S., & Wills, B. J. 2002, ApJ, 574, L105 [NASA ADS] [CrossRef] [Google Scholar]
- Bolzonella, M., Kova, K., Pozzetti, L., et al. 2010, A&A, 524, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bongiorno, A., Merloni, A., Brusa, M., et al. 2012, MNRAS, 427, 3103 [NASA ADS] [CrossRef] [Google Scholar]
- Bottorff, M., & Ferland, G. 2002, ApJ, 568, 581 [NASA ADS] [CrossRef] [Google Scholar]
- Bottorff, M., Ferland, G., Baldwin, J., & Korista, K. 2000, ApJ, 542, 644 [NASA ADS] [CrossRef] [Google Scholar]
- Bressan, A., Marigo, P., Girardi, L., et al. 2012, MNRAS, 427, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- Calura, F., Pipino, A., Chiappini, C., et al. 2009, A&A, 504, 373 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Capak, P., Aussel, H., Ajiki, M., et al. 2007, ApJS, 172, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Castro, C. S., Dors, O. L., Cardaci, M. V., & Hägele, G. F. 2017, MNRAS, 467, 1507 [NASA ADS] [Google Scholar]
- Chabrier, G. 2003, PASP, 115, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Chiappini, C., Romano, D., & Matteucci, F. 2003, MNRAS, 339, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Cid Fernandes, R., Heckman, T., Schmitt, H., et al. 2001, ApJ, 558, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Civano, F., Marchesi, S., Comastri, A., et al. 2016, ApJ, 819, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Cowley, C. R. 1995, An Introduction to Cosmochemistry (Cambridge, UK: Cambridge University Press), 502 [Google Scholar]
- Costantini, E., Kriss, G., Kaastra, J. S., et al. 2016, A&A, 595, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dalcanton, J. J. 2007, ApJ, 658, 941 [NASA ADS] [CrossRef] [Google Scholar]
- Dayal, P., Ferrara, A., & Dunlop, J. S. 2013, MNRAS, 430, 2891 [NASA ADS] [CrossRef] [Google Scholar]
- Davidson, K., & Netzer, H. 1979, Rev. Mod. Phys., 51, 715 [NASA ADS] [CrossRef] [Google Scholar]
- Davé, R., Finlator, K., & Oppenheimer, B. D. 2011, MNRAS, 416, 1354 [NASA ADS] [CrossRef] [Google Scholar]
- Davé, R., Rafieferantsoa, M. H., Thompson, R. J., & Hopkins, P. F. 2017, MNRAS, 467, 115 [NASA ADS] [Google Scholar]
- De Breuck, C., Röttgering, H., Miley, G., van Breugel, W., & Best, P. 2000, A&A, 362, 519 [NASA ADS] [Google Scholar]
- De Lucia, G., Kauffmann, G., & White, S. D. M. 2004, MNRAS, 349, 1101 [NASA ADS] [CrossRef] [Google Scholar]
- Delvecchio, I., Gruppioni, C., Pozzi, F., et al. 2014, MNRAS, 439, 2736 [NASA ADS] [CrossRef] [Google Scholar]
- Dempsey, R., & Zakamska, N. L. 2018, MNRAS, 477, 4615 [NASA ADS] [CrossRef] [Google Scholar]
- Dors, O. L., Cardaci, M. V., Hägele, G. F., & Krabbe, Â. C. 2014, MNRAS, 443, 1291 [NASA ADS] [CrossRef] [Google Scholar]
- Du, P., Wang, J.-M., Hu, C., et al. 2014, MNRAS, 438, 2828 [NASA ADS] [CrossRef] [Google Scholar]
- Erb, D. K., Steidel, C. C., Shapley, A. E., et al. 2006, ApJ, 646, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Feltre, A., Charlot, S., & Gutkin, J. 2016, MNRAS, 456, 3354 [Google Scholar]
- Ferland, G. J., Porter, R. L., van Hoof, P. A. M., et al. 2013, Rev. Mex. Astron. Astrofis., 49, 137 [Google Scholar]
- Ferrarese, L., & Merritt, D. 2000, ApJ, 539, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Franceschini, A., Hasinger, G., Miyaji, T., et al. 1999, MNRAS, 310, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Garilli, B., Fumana, M., Franzetti, P., et al. 2010, PASP, 122, 827 [NASA ADS] [CrossRef] [Google Scholar]
- Gebhardt, K., Kormendy, J., Ho, L. C., et al. 2000, ApJ, 543, 5 [Google Scholar]
- Gilli, R., Vignali, C., Mignoli, M., et al. 2010, A&A, 519, 92 [Google Scholar]
- Gray, W. J., & Scannapieco, E. 2017, ApJ, 849, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Groves, B. A., Dopita, M. A., & Sutherland, R. S. 2004, ApJS, 153, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Gutkin, J., Charlot, S., & Bruzual, G. 2016, MNRAS, 462, 1757 [NASA ADS] [CrossRef] [Google Scholar]
- Hamann, F., & Ferland, G. 1992, ApJ, 391, L53 [NASA ADS] [CrossRef] [Google Scholar]
- Hamann, F., & Ferland, G. 1993, ApJ, 418, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, D. W., Jensen, T. W., Suzuki, N., et al. 2016, ApJ, 418, 11 [Google Scholar]
- Henry, A., Scarlata, C., Domínguez, A., et al. 2013, ApJ, 776, L27 [NASA ADS] [CrossRef] [Google Scholar]
- Hirschmann, M., Charlot, S., Feltre, A., et al. 2017, MNRAS, 472, 2468 [NASA ADS] [CrossRef] [Google Scholar]
- Hirschmann, M., Charlot, S., Feltre, A., et al. 2018, MNRAS, submitted [arXiv:1811.07909] [Google Scholar]
- Hopkins, A. M., & Beacom, J. F. 2006, ApJ, 651, 142 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Humphrey, A., Villar-Martín, M., Vernet, J., et al. 2008, MNRAS, 383, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Kraemer, S. B., Bottorff, M. C., & Crenshaw, D. M. 2007, ApJ, 668, 730 [NASA ADS] [CrossRef] [Google Scholar]
- Koekemoer, A. M., Aussel, H., Calzetti, D., et al. 2007, ApJS, 172, 196 [NASA ADS] [CrossRef] [Google Scholar]
- Kormendy, J., & Richstone, D. 1995, ARA&A, 33, 581 [NASA ADS] [CrossRef] [Google Scholar]
- Laporte, N., Nakajima, K., Ellis, R. S., et al. 2017, ApJ, 851, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Lenz, D. D., & Ayres, T. R. 1992, PASP, 104, 1104 [NASA ADS] [CrossRef] [Google Scholar]
- Lequeux, J., Peimbert, M., Rayo, J. F., et al. 1979, A&A, 1979, 155 [NASA ADS] [Google Scholar]
- Lilly, S. J., Le Févre, O., Renzini, A., et al. 2007, ApJS, 172, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Lilly, S. J., Le Brun, V., Maier, C., et al. 2009, ApJS, 184, 218 [Google Scholar]
- Lilly, S. J., Carollo, C. M., Pipino, A., Renzini, A., & Peng, Y. 2013, ApJ, 772, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, G., Zakamska, N. L., Greene, J. E., Nesvadba, N. P. H., & Liu, X. 2013, MNRAS, 436, 2576 [NASA ADS] [CrossRef] [Google Scholar]
- Ma, X., Hopkins, P. F., Faucher-Giguère, C.-A., et al. 2016, MNRAS, 456, 2140 [NASA ADS] [CrossRef] [Google Scholar]
- Madau, P., & Dickinson, M. 2014, ARA&A, 52, 415 [NASA ADS] [CrossRef] [Google Scholar]
- Magorrian, J., Tremaine, S., Richstone, D., et al. 1998, AJ, 115, 2285 [NASA ADS] [CrossRef] [Google Scholar]
- Mainali, R., Zitrin, A., Stark, D. P., et al. 2018, MNRAS, 479, 1180 [NASA ADS] [Google Scholar]
- Maiolino, R., Nagao, T., Grazian, A., et al. 2008, A&A, 488, 463 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mannucci, F., Cresci, G., Maiolino, R., Marconi, A., & Gnerucci, A. 2010, MNRAS, 408, 2115 [NASA ADS] [CrossRef] [Google Scholar]
- Marchesi, S., Civano, F., Elvis, M., et al. 2016, ApJ, 817, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Matsuoka, K., Nagao, T., Maiolino, R., Marconi, A., & Taniguchi, Y. 2009, A&A, 503, 721 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Matsuoka, K., Nagao, T., Marconi, A., et al. 2018, A&A, 616, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mignoli, M., Vignali, C., Gilli, R., et al. 2013, A&A, 556, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mor, R., Netzer, H., & Elitzur, M. 2009, ApJ, 705, 298 [NASA ADS] [CrossRef] [Google Scholar]
- Nagao, T., Maiolino, R., & Marconi, A. 2006, A&A, 447, 863 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nakajima, K., Schaerer, D., Le Fèvre, O., et al. 2018, A&A, 612, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Netzer, H. 2013, The Physics and Evolution of Active Galactic Nuclei, by Hagai Netzer (Cambridge, UK: Cambridge University Press) [CrossRef] [Google Scholar]
- Netzer, H., Shemmer, O., Maiolino, R., et al. 2004, ApJ, 614, 558 [NASA ADS] [CrossRef] [Google Scholar]
- Onodera, M., Carollo, C. M., Lilly, S. J., et al. 2016, ApJ, 822, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Panuzzo, P., Bressan, A., Granato, G. L., Silva, L., & Danese, L. 2003, A&A, 409, 99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pâris, I., Petitjean, P., Aubourg, E., et al. 2014, A&A, 563, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Prochaska, J. X., Gawiser, E., Wolfe, A. M., et al. 2003, ApJ, 595, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Revalski, M., Crenshaw, D. M., Kraemer, S. B., et al. 2018, ApJ, 856, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Reyes, R., Zakamska, N. L., Strauss, M. A., et al. 2008, AJ, 136, 2373 [NASA ADS] [CrossRef] [Google Scholar]
- Richardson, C. T., Allen, J. T., Baldwin, J. A., Hewett, P. C., & Ferland, G. J. 2014, MNRAS, 437, 2376 [NASA ADS] [CrossRef] [Google Scholar]
- Richards, G. T., Vanden Berk, D. E., Reichard, T. A., et al. 2002, AJ, 124, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Richards, G. T., Strauss, M. A., Fan, X., et al. 2006a, AJ, 131, 2766 [NASA ADS] [CrossRef] [Google Scholar]
- Richards, G. T., Lacy, M., Storrie-Lombardi, L. J., et al. 2006b, ApJS, 166, 470 [NASA ADS] [CrossRef] [Google Scholar]
- Richstone, D., Ajhar, E. A., Bender, R., et al. 1998, Nature, 395, A14 [NASA ADS] [Google Scholar]
- Rosen, S. R., Webb, N. A., Watson, M. G., et al. 2016, A&A, 590, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shemmer, O., & Netzer, H. 2002, ApJ, 567, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Schmitt, H. R., Storchi-Bergmann, T., & Cid Fernandes, R. 1999, MNRAS, 303, 173 [NASA ADS] [CrossRef] [Google Scholar]
- Scodeggio, M., Franzetti, P., Garilli, B., et al. 2005, PASP, 117, 1284 [NASA ADS] [CrossRef] [Google Scholar]
- Scoville, N., Abraham, R. G., Aussel, H., et al. 2007, ApJS, 172, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Silverman, J. D., Green, P. J., Barkhouse, W. A., et al. 2008, ApJ, 679, 118 [NASA ADS] [CrossRef] [Google Scholar]
- Silverman, J. D., Kashino, D., Sanders, D., et al. 2015, ApJS, 220, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Storchi-Bergmann, T., Schmitt, H. R., Calzetti, D., & Kinney, A. L. 1998, AJ, 115, 909 [NASA ADS] [CrossRef] [Google Scholar]
- Storchi-Bergmann, T., Dall’Agnol de Oliveira, B., Longo Micchi, L. F., et al. 2018, ApJ, 868, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Sun, A.-L., Greene, J. E., Zakamska, N. L., et al. 2018, MNRAS, 480, 2302 [NASA ADS] [CrossRef] [Google Scholar]
- Szokoly, G. P., Bergeron, J., Hasinger, G., et al. 2004, ApJS, 155, 271 [NASA ADS] [CrossRef] [Google Scholar]
- Thomas, A. D., Kewley, L. J., Dopita, M. A., et al. 2019, ApJ, 874, 100 [NASA ADS] [CrossRef] [Google Scholar]
- Tremonti, C. A., Heckman, T. M., Kauffmann, G., et al. 2004, ApJ, 613, 898 [NASA ADS] [CrossRef] [Google Scholar]
- Torrey, P., Vogelsberger, M., Marinacci, F., et al. 2019, MNRAS, 484, 5587 [NASA ADS] [Google Scholar]
- Vanden Berk, D. E., Richards, G. T., Bauer, A., et al. 2001, AJ, 122, 549 [NASA ADS] [CrossRef] [Google Scholar]
- Veilleux, S., & Osterbrock, D. E. 1987, ApJS, 63, 295 [NASA ADS] [CrossRef] [Google Scholar]
- Vernet, J., Fosbury, R. A. E., Villar-Martín, M., et al. 2001, A&A, 366, 7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vidal-García, A., Charlot, S., Bruzual, G., & Hubeny, I. 2017, MNRAS, 470, 3532 [NASA ADS] [CrossRef] [Google Scholar]
- Vignali, C., Alexander, D. M., Gilli, R., & Pozzi, F. 2010, MNRAS, 404, 48 [NASA ADS] [Google Scholar]
- Vignali, C., Mignoli, M. M., Gilli, R., et al. 2014, A&A, 571, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Villar-Martin, M., Tadhunter, C., & Clark, N. 1997, A&A, 323, 21 [NASA ADS] [Google Scholar]
- Warner, C., Hamann, F., & Dietrich, M. 2003, ApJ, 596, 72 [NASA ADS] [CrossRef] [Google Scholar]
- Watson, M. G., Schröder, A. C., Fyfe, D., et al. 2009, A&A, 493, 339 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Xu, F., Bian, F., Shen, Y., et al. 2018, MNRAS, 480, 345 [NASA ADS] [CrossRef] [Google Scholar]
- Yuan, T.-T., Kewley, L. J., & Richard, J. 2013, ApJ, 763, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Zamorani, G., Mignoli, M., Hasinger, G., et al. 1999, A&A, 346, 731 [NASA ADS] [Google Scholar]
All Tables
All Figures
 |
Fig. 1. Redshift distributions of zCOSMOS-deep galaxies with z ≥ 1. Top panel: parent galaxy sample; the hatched histogram shows the galaxies with redshift quality flag ≥1.5. Lower panel: C IV-selected AGN sample; the hatched histogram shows the type 2 sample. |
| In the text | |
 |
Fig. 2. Intrinsic rest-frame FWHMs of the C IV emission line in our sample as a function of redshift. Objects with line FWHM strictly less than 2000 km s−1 are classified as type 2 AGN (red symbols); unresolved lines are shown as downward arrows. Broad emission-line objects (with FWHM > 2000 km s−1) are classified as type 1 AGN and plotted with blue symbols. |
| In the text | |
 |
Fig. 3. Composite spectra of the two AGN samples with the identification of the main emission lines: the lower (in blue) and upper (in red) spectra represent the average spectra of the C IV-selected type 1 and type 2 AGN, respectively. The flux normalization is arbitrary, and the spectra are offset for clarity. |
| In the text | |
 |
Fig. 4. Stellar mass distribution of zCOSMOS-Deep galaxies with 1.45 < z < 3.05. Top panel: parent galaxy sample; the hatched histogram shows the galaxies with redshift quality flag ≥2. Lower panel: stellar mass distribution of the galaxies hosting the C IV-selected type 2 AGN. For these objects the masses are derived from a two-component (AGN and galaxy templates) SED fitting. |
| In the text | |
 |
Fig. 5. Predictions of the AGN NLR models described in Sect. 4.1 in the C IV/He II vs. C IV/C III] (top left), C III]/He II (top right), N V/C IV (bottom left) and N V/He II (bottom right) diagrams. Each panel shows data measurements with error bars and upper limits (black symbols) of the C IV-selected type 2 AGN, described in Sect. 3, and AGN models (shaded areas) encompassing wide ranges in power-law index, α, ionization parameter, ⟨U⟩, gas metallicity, Z, gas density, nH, and dust-to-metal mass ratio, ξd. The purple and orange shaded areas indicate AGN models with no microturbulence velocity and an inner radius of 300 pc and models with microturbulence velocity vmicr = 100 km s−1 and an inner radius of 90 pc, respectively. Cyan stars show the predictions from photoionization models of star-forming galaxies of Gutkin et al. (2016). In each panel, the gray arrows indicate the effect of correcting the AGN data by dust attenuation for a galactic attenuation curve (Cardelli et al. 1989) and AV = 1 mag. |
| In the text | |
 |
Fig. 6. Evolution of the NLR gas-phase metallicity with redshift. The gray dots represent the individual C IV-selected type 2 AGN, while the black squares are the average oxygen abundance in three redshift bins. Lower panel: the arrows highlight the redshift intervals where the quoted emission lines are visible in the observed spectral range. |
| In the text | |
 |
Fig. 7. Mass-metallicity relation for the C IV-selected type 2 AGN. The filled symbols mark the 61 objects with reliable measurements (emission lines detected with S/N > 3 and the SED fit with 0.5 < |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.