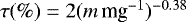| Issue |
A&A
Volume 625, May 2019
|
|
|---|---|---|
| Article Number | A106 | |
| Number of page(s) | 17 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201935203 | |
| Published online | 21 May 2019 | |
Small iron meteoroids
Observation and modeling of meteor light curves
Astronomical Institute of the Czech Academy of Sciences,
Fričova 298,
251 65
Ondřejov,
Czech Republic
e-mail: capek@asu.cas.cz
Received:
4
February
2019
Accepted:
14
March
2019
Context. A significant fraction of small meteors are produced by iron meteoroids. Their origin and the interaction with the atmosphere have not been well explained up to now.
Aims. The goals of the study are to observe faint, slow, low altitude meteors, to identify candidates for iron meteoroids among them, to model their ablation and light curves, and to determine their properties.
Methods. Double station video observations were used for the determination of atmospheric trajectories, heliocentric orbits, light curves, and spectra of meteors. Meteors with iron spectra or of suspected iron composition based on beginning heights and light curves were modeled. The immediate removal of liquid iron from the surface as a cloud of droplets with Nukiyama–Tanasawa size distribution and their subsequent vaporization was assumed as the main ablation process on the basis of our previous work. The numerical model has only five parameters: meteoroid initial velocity v∞, zenith distance z, initial mass m∞, mean drop size Ddr, and luminous efficiency τ. The theoretical light curves were compared with the observed ones.
Results. The model is able to explain the majority of the selected light curves, and meteoroid parameters that are not directly observable – m∞, Ddr, and τ – are determined. Unlike in most meteor studies, the mass and luminous efficiency are determined independently. Luminous efficiency ranges from 0.08 to 5.8%; it weakly decreases with increasing initial meteoroid mass. No simple dependency on initial velocity was found. The mean size of iron drops depends on the meteoroid velocity. Slower meteoroids can produce drops with a wide range of mean sizes, whereas faster ones are better matched with larger drops with a smaller dispersion of sizes.
Key words: meteorites, meteors, meteoroids
© ESO 2019
1 Introduction
A fraction of fainter meteoroids, which hit Earth’s atmosphere, are composed dominantly of iron (Borovička et al. 2005). These meteoroids usually have low velocities (<20 km s−1) and their orbits indicate asteroidal (in some cases Jupiter family comet) origin. The meteors mostly have unusual light curves with a rapid increase of brightness, low beginning heights, and short trajectories. This population was discovered by Borovička et al. (2005), who recorded 14 spectra of meteors with only iron lines and with the properties mentioned above. Campbell-Brown (2015) described a “low, slow population” of meteors, which is probably the same as that of Borovička. She found that the frequency of appearance of these meteors increases with decreasing meteor brightness. Specifically, they form 3% of meteors brighter than +3 and about 6% of meteors between +6 and +3 magnitudes. This population is also characterized by strong and refractory material.
Ceplecha (1967) analyzed the radiation of a meteoroid with a spectrum consistent with iron composition. He concluded that the spraying of droplets behind the meteoroid is the main ablation process in this case. Borovička et al. (2005) explain unusual light curves as being the result of sudden vaporization of a liquid iron drop when it reaches boiling temperature. However, Čapek & Borovička (2017) found that the vaporization of liquid iron on the meteoroid’s surface is too slow a process, and it cannot explain observed meteors with iron spectra (for simplicity we will use the term “iron meteors”). They showed that a sudden destruction of a liquid iron drop also does not take place. Similarly to Ceplecha (1967), the spraying of the droplets was determined to be the most probable ablation process.
In this paper we extend the work of Čapek & Borovička (2017) by developing a detailed model of the spraying and ablation of liquid droplets. We also ran a number of observational campaigns aimed at faint meteors at relatively low heights, around 80 km, in 2016–2018. The model was used to fit the observed light curves of iron meteors and to derive meteoroid masses, the sizes of the droplets, and the luminous efficiency. In order to also include very small meteoroids that produce meteors too faint for spectra to be observed, we used criteria based on light curve shapes and beginning heights to identify probable iron meteoroids.
Section 2 briefly describes our observing instruments, techniques, and data processing. It also deals with spectral observations – observing instruments, and differences between normal and iron spectra. Section 3 is devoted to the selection of iron meteors without spectra, meteoroid atmospheric trajectories, and heliocentric orbits. The model of ablation is described in Sect. 4. Section 5 deals with the application of the model to light curves and the determination of parameters of meteoroids. In Sect. 6 we discuss the ablation process, the ability of the model to describe observed light curves of iron meteors, and the luminous efficiency. Section 7 summarizes the key properties of the model and main results. The appendix contains a summary of all meteors that were successfully described by the model, and corresponding light curves.
2 Observations and data processing
2.1 Double station data
In order to detect faint meteors (including those produced by iron meteoroids), the video cameras used for many years at the Ondřejov observatory (e.g. Koten et al. 2004) were modernized and improved. The analog camera was replaced by a digital DMK23G445 GigE monochromatic camera. Using a 1/3′′ Sony CCD sensor, it provides spatial resolution of 1280 × 960 pixels, time resolution up to 30 frames per second, and dynamic range 8–12 bits. A CCTV Basler C125 F/1.8, f = 8 mm objective lens was used to read the output aperture of the image intensifier. The Mullard XX1332 image intensifier is the only part of the original camera setup that remained. The lens was changed in favor of the long focal Canon F/2, f = 135 mm lens. This configuration provides a circular field of view with a diameter of 20° and limiting magnitudes +9 (stellar) and +7 (meteor). The observations were carried out at our usual double station locations, Ondřejov (λ = 14°46′48.8″ E, φ = 49°54′36.8″ N, 524 m) and Kunžak (λ = 15°12′1.1″ E; φ = 49°6′27.3″ N, altitude = 652 m) observatories. The distance between the stations is 92.5 km and the azimuth of the southern station 340° (south = 0°). Each station was equipped with one long focal length camera; the Ondřejov station also had a spectral camera.
Dedicated software for camera control, observation planning, and video capture was written. The video was saved as 30 s long AVI sequences in eight bits. The internal computer time, synchronized using an NTP service, was written into each frame of the video. Approximately 1 TB of data was recorded and stored on the hard drive for each 8 h of observations. The sequences were searched for meteors using the automatic detection software dMaia (Koten et al. 2014) and short sequences containing meteors were saved. Time correlation was used for detection of the same events from both stations.
The observations were carried out during the new Moon periods and only under clear sky at both stations. Also, periods without significant activity of main meteor showers – with two exceptions (Perseids and Draconids 2018) – were selected. Because the aim of the experiment was to observe slow and compact meteors, the intersection point of the lines of the sight from the two stations was set to be at an altitude of 80 km. About 3000 meteors were recorded all together (Table 1). Due to the relatively small fields of view, only about 50% of meteors were double station cases.
The recorded meteors were visually inspected and cases showing a fast increase in brightness and rather slow motion were marked as potential iron candidates. This selected 72 candidates. Their records were measured using MAIAMetPho software (Koten et al. 2016). Later, the atmospheric trajectories and heliocentric orbits were calculated using standard procedures (Borovička 1990; Ceplecha 1987). Some of the candidates were found not to be true double station (each station recorded a different meteor), a few candidates were excluded because of poor solution (e.g. due to small convergence angle). Spectral records were inspected independently and meteors with iron spectra were identified (see Table 2).
The light curves of the meteors were expressed in the form of absolute brightness, that is, the brightness of the meteor at a standard distance of 100 km. The majority of meteors produce very similar light curves at both stations. However, there is a difference insome cases. Despite a careful calibration, it was impossible to obtain similar light curves. One possible explanation could be a very small angular velocity of some meteors in the field of view. Since we are interested in slow meteors, their angular velocity is usually low. According to our experience, in some cases the extremely low angular velocity causes the meteor signal to spread among only a few pixels. Then even relatively faint meteors can be easily saturated if observed with high sensitivity cameras. If the meteor is angularly faster at the second station, its signal is spread into a higher number of pixels and the signal is not saturated. This could lead to a larger difference in the light curves constructed from both stations.
Statistics of the observations.
2.2 Spectral data
Spectra were observed from Ondřejov simultaneously with the direct observations. The camera, recording software, and image intensifier were the same as for the direct observations but a Jupiter 2/85 mm lens was used. The lens was equipped with a blazed transmission grating with 600 grooves mm−1. The reason for using a lens with a shorter focal length than for direct observations was that otherwise the field of view would be too small and many spectra would be only partially recorded. The whole recorded spectrum ranges from 380 to 880 nm and its angular length is 19°. The field of view was smaller and the sensitivity and spectral dispersion were higher than in our previous program when we used a 50 mm lens and a 768× 576 pixel camera (Vojáček et al. 2019). The new circular field of view had a diameter of 27° and the dispersion was 1 nm pixel−1. The spectral resolution was ~2.5 nm in good cases, when the meteor moved nearly perpendicular to the direction of dispersion. Spectra of meteors brighter than magnitude + 2 could be recorded.This means that spectra were only obtained for a minority of the meteors observed by the direct cameras.
Figure 1 shows the spectra of two bright meteors, one having a normal spectrum, the other an iron spectrum. In normal spectra of low and medium speed meteors, the two brightest lines are the Na line (unresolved doublet at 589.0 and 589.6 nm) and the Mg line (unresolved triplet at 516.7, 517.3, and 518.4 nm) (in fast meteors the oxygen triplet near 777 nm is the brightest line). Almost all other lines visible in the spectra are due to Fe. In meteors classified as irons, the Na and Mg lines are missing. The spectrum is dominated by numerous Fe lines of multiplets 15 and 37 (multiplet numbers according to the tables of Moore 1945) at 517–546 nm. We note, however, that some Fe lines overlap with the Mg line, namely the multiplet 37 line at 516.7 nm, multiplet 36 line at 517.2 nm, and multiplet 1 lines at 516.6 and 516.9 nm. With the available spectral resolution, these lines cannot be separated from the lines of the Mg triplet. We cannot therefore exclude the presence of Mg lines in the spectrum. However, in normal spectra the Mg line at 517 nm is much brighter than the brightest Fe line at 527 nm (formed by multiplet 15 line at 527.0 nm and multiplet 37 line also at 527.0 nm). If the 517 nm line was comparable to or only slightly brighter than the 527 nm line, we considered Mg to be missing or at least significantly depleted in the meteoroid. Thermal equilibrium is not maintained in the radiating plasma due to relatively high meteor altitudes (around 80 km) and modeling the intensities of spectral lines would therefore be difficult. Lines of low transition probability (in particular Fe multiplets 1, 2, 3) are enhanced in non-equilibrium conditions (Borovička & Jenniskens 2000).
Figure 2 shows the calibrated plot of summary spectra from Fig. 1. There are many bright lines in both spectra in the blue region below 450 nm, where the sensitivity of the image intensifier (also shown in the plot) is low and the lines are therefore poorly seen in the images. Most of the blue lines belong to Fe as well. The most visible is the multiplet 41 line at 438.4 nm mixed with the 437.6 nm line of multiplet 2. Other Fe lines present mostly belong to Fe multiplets 2, 3, 41, 42, and 43 and, below 400 nm, to multiplets 4, 45 and others. A full list of spectral lines seen in meteor spectra can be found in Borovička (1994). Among these numerous Fe lines there are some lines of other elements, most notably Ca multiplet 2, Cr multiplet 1, Mn multiplet 2, and multiplet 1 of ionized Ca, but they are difficult to separate from the Fe lines under the given spectral resolution. In other parts of the spectra, there are visible Fe lines in the region 480–500 nm, where the lines of the multiplet 318 are the brightest contributors. The spectra also contain continuous radiation.
Poorer spectra of fainter iron meteors, which may also have poorer resolution (due to less favorable geometry of meteor flight), are characterized by the absence of well-defined spectral lines and the presence of just one or two diffuse bands (in fact unresolved lines) in the region 510–550 nm and possibly another band near 440 nm. If a meteor exhibited this kind of a spectrum, it was classified as iron. Examples of iron video spectra from our previous programs can be found in Borovička et al. (2005) or Vojáček et al. (2015).
There were nine meteor spectra among all the candidate meteors observed by the DMK cameras (see Sect. 2.1). All of them were iron spectra. No other spectra were found. Three meteors with iron spectra do not show a typical light curve of iron meteors – they lack a rapid increase of the brightness. These meteors were not selected as the candidates for iron, if there was no spectrum available. All of them are among the brightest meteors in our sample.
Trajectories and orbits of nine meteors with iron spectra.
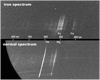 |
Fig. 1 Co-added frames of video spectra of meteors 17528031 (top) and 17527064 (bottom). Both meteors moved nearly from top to bottom. Approximate wavelengths are indicated and important spectral lines are identified. |
 |
Fig. 2 Spectra of meteors 17528031 and 17527064 averaged over all frames and calibrated using the spectral sensitivity function of the instrument (plotted as dashed line). The 17527064 spectrum has been offset vertically for clarity. Lines other than Fe are identified; that is, all non-identified lines are produced primarily by iron. |
Summary of the data of 45 iron candidate meteors.
3 Properties of the meteors without spectra
Since the population of refractory meteoroids studied by Campbell-Brown (2015) was characterized by low beginning heights (under 86 km), all meteors without spectra with beginning heights above 90 km were excluded from the sample. In the end, 45 candidates for iron meteoroids remained. The summary of their atmospheric data are given in Table 3. The maximum brightness occurred, on average, in the first third of the luminous meteor trajectory.
The initial velocities of 45 candidates were between 10.7 and 26.1 km s−1. We note that velocities of some meteors were affected by atmospheric deceleration already at their beginnings, so some observed initial velocities were below the Earth escape velocity of 11.2 km s−1. Velocities in only a few cases are higher than 20 km s−1. The distribution of the beginning heights and initial velocities is shown in Fig. 3. Velocities below 20 km s−1 prevail in this sample.
The F parameter indicates the location of the maximum brightness along the luminous trajectory of the meteor (Fleming et al. 1993). Although the spread of the values for the sample of iron candidates and meteors with iron spectra looks relatively wide – the F parameter varies between 0.02 and 0.67 – the histogram shows (Fig. 4) that the majority of the selected meteors reached their maximum brightness in the first half of the trajectory.
Another characteristic property of iron meteoroids should be a shorter luminous trajectory. The sample contains relatively short meteors with a luminous trajectory length between 3.2 and 23.1 km. The average length is 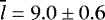 km. The heights, the F-parameters, and the trajectory lengths confirm that the initial selection of possible iron meteoroids was correct and that those meteors are good candidates for further modeling.
km. The heights, the F-parameters, and the trajectory lengths confirm that the initial selection of possible iron meteoroids was correct and that those meteors are good candidates for further modeling.
All the selected Fe candidates are sporadic meteors. The Tisserand parameter TJ with respectto Jupiter is usually used to classify orbits in the solar system into the groups of typical asteroidal orbits, Jupiter family comets (JFC) and Halley type comets (for example Weissman et al. 2002). Usually, TJ = 3 is used as the boundary between JFCs and asteroids. Borovička et al. (2005) note that there is an overlap between the two groups around TJ = 3. The Tisserand parameter TJ for the iron candidate meteors is shown in Fig. 5. Almost all iron candidates in our sample have orbits with TJ > 3; only four meteors lie slightly below this threshold.
Borovička et al. (2005) defined five groups of the heliocentric orbits. All 14 meteors with iron spectra were classified as asteroidal-chondritic (A-C) orbits in their work. Such orbits have TJ > 3 or Q < 4.5 AU. The irons are concentrated within a very small area in the perihelion-aphelion plot (q-Q plot). A similar plot for our 45 candidates is shown in Fig. 6. The majority of the meteors settles in the same area of this plot, with perihelion between 0.8 and 1.0 AU and aphelion up to 5 AU. There are only six outliers with significantly lower perihelion distances. Still, all the meteors satisfy the criteria for A-C orbits.
 |
Fig. 3 Beginning height and initial velocity distribution for Fe candidates and meteors with iron spectra. |
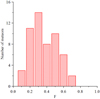 |
Fig. 4 Distribution of the F parameter for Fe candidates and meteors with iron spectra. |
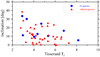 |
Fig. 5 Tisserand parameter for iron candidates (red triangles) and meteors with iron spectra (blue circles). |
 |
Fig. 6 Perihelion versus aphelion plot for iron candidates (red triangles) and meteors with iron spectra (blue circles). |
4 Model
Our aim is to describe the flight of a meteoroid through the atmosphere with as few parameters as possible. We made some simplifying assumptionsas in Čapek & Borovička (2017): meteoroids are composed of iron, and they have spherical shape. The temperature field T depends only on radial distance r and meteoroids have fast random rotation, which means that the whole surface is heated homogeneously. The meteoroid is affected by collisions with molecules of atmospheric gases that cause its deceleration and heating. The model for meteoroid flight before ablation is the same as in Čapek & Borovička (2017). The description of the ablation phase, however, differs. When the surface temperature of the meteoroid reaches the melting point of iron, ablation begins: molten material starts to be removed. In the present model its removal is also immediate, but its transformation into vapor is not. The blown-off material forms a cloud of droplets and each droplet moves and evaporates independently. Let us now describe the model in detail.
4.1 Pre-ablation phase
The meteoroid has an initial mass m∞, velocity v∞, and zenith distance z. It has constant temperature over its whole volume T(r, t = 0) = Teq, which is equal to the equilibrium temperature at Earth’s heliocentric distance. The meteoroid height h is given by
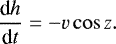 (1)
(1)
The velocity v decreases due to collisions with molecules,
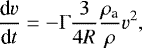 (2)
(2)
where Γ is the drag coefficient, ρa is atmospheric density, and ρ is the density of the meteoroid. The mass m and the radius R are constant during the pre-ablation stage. The temperature inside the meteoroid can be determined from the heat diffusion equation
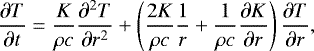 (3)
(3)
where c is the heat capacity and K is the thermal conductivity. Let us note that the thermophysical parameters ρ, c, and K depend on temperature and therefore on the radial distance r from the center of the meteoroid (see Sect. 2.3 in Čapek & Borovička 2017). The energy balance on the surface is
![\begin{equation*}\Lambda\frac{1}{2}\rho_{\textrm{a}} v^3=4\left[{\epsilon\sigma \left({T^4-T_0^4}\right) + K{\frac{\partial T}{\partial r}}}\right]_{r\,=\,R},\end{equation*}](/articles/aa/full_html/2019/05/aa35203-19/aa35203-19-eq5.png) (4)
(4)
where Λ is the heat-transfer coefficient, ɛ is emissivity of the surface of meteoroid, σ = 5.6697 × 10−8 W m−2 K−4 is the Stephan–Boltzmann constant, and T0 is the ambient temperature. The left-hand side represents the absorbed energy, the terms on the right are energy losses due to thermal radiation and heat conduction. We assume zero heat flux in the center of the body
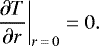 (5)
(5)
The temperature profile inside the meteoroid can therefore be determined from Eqs. (3)–(5).
4.2 Ablation phase
As soon as the surface reaches the melting temperature, ablation starts. We consider that all molten iron is immediately removed from the surface by the action of air flow. Instead of the surface boundary condition defined by Eq. (4), we have
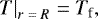 (6)
(6)
where Tf = 1811 K is the fusiontemperature of the iron. The temperature of the meteoroid during the ablation phase is therefore given by Eqs. (3), (5), and (6). The ablation rate is given by the expression
![\begin{equation*} {\frac{\textrm{d} m}{\textrm{d} t}} = \frac{1}{\ell_{\textrm{f}}}\left\{\Lambda\frac{1}{8}\rho_{\textrm{a}} v^3-\left[{\epsilon\sigma \left({T_{\textrm{f}}^4-T_0^4}\right) + K{\frac{\partial T}{\partial r}}}\right]_{r\,=\,R}\right\},\end{equation*}](/articles/aa/full_html/2019/05/aa35203-19/aa35203-19-eq8.png) (7)
(7)
where ℓf = 289 kJ kg−1 is the fusion heat of the iron. We consider that the layer of molten iron is immediately blown of by the air flow as a cloud of small droplets. Its size distribution follows the Nukiyama–Tanasawa law (e.g. Semião et al. 1996),
![\begin{equation*}\textrm{d}N = \frac{3D^2}{\left[{{D_{\textrm{dr}}}\Gamma\left(\frac{5}{3}\right)}\right]^3} \exp\left\{-\frac{D^3}{\left[{D_{\textrm{dr}}\Gamma\left(\frac{5}{3}\right)}\right]^3}\right\} \textrm{d}D,\end{equation*}](/articles/aa/full_html/2019/05/aa35203-19/aa35203-19-eq9.png) (8)
(8)
where D is the drop diameter, dN is the number of drops in the interval of ⟨D, D + dD), and Γ(5∕3) is the statistical gamma function. The size distribution expressed by Eq. (8) is widely used in engineering applications and it depends on only one parameter, the Sauter mean diameter Ddr (for simplicity we will use the term “mean diameter” or “mean size”). We assume that Ddr does not change during the flight.
Drops are released during the whole ablation phase from the height hmelt when the melting of the surface begins to the height where the original meteoroid disappears hdis. As soon as a drop i is released from the surface of meteoroid, it moves and ablates independently. Collisions with molecules of atmospheric gases cause deceleration and heating of the drop. We consider that all absorbed energy is consumed for evaporation. The height hi, velocity vi, and mass mi of the drop can be determined from equations

where A≐1.209 is the shape factor, ρd is the density of the drop, and Q = 7 115.134 kJ kg−1 is the enthalpy of vaporization of iron. At the instant of drop release, it has the same height and velocity as the parent meteoroid: hi = h ∈⟨hmelt, hdis⟩ and vd = v.
The normalized luminosity (i.e. with luminous efficiency τ equal to unity) of evaporated material from the drop i is given by
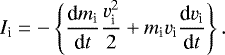 (12)
(12)
The total normalized luminosity of the meteor is given by a sum over all drops released at different times at different heights in amounts according to ablation rate (Eq. (7)) and size distribution (Eq. (8)),
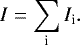 (13)
(13)
Our model neglects the oxidation of iron drops (e.g. Genge 2016). Let us compare the oxidation rate with the ablation rate for the drops. The ablation rate is given by Eq. (11), whereas the oxidation rate can be expressed as d mo∕dt = ΛρoSivi, where ρo is an atmospheric oxygen density and Si is the drop cross section. The ratio of the oxidation and ablation rates is therefore
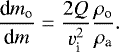 (14)
(14)
The ratio ρo∕ρa at altitudes of 70–90 km is about 0.22. For a liquid iron drop with a speed of 11.2 km s−1, Eq. (14) leads to a value of ~2.5 or ~11% for molar ratio. For faster meteoroids this ratio is even lower. If we focus on molar ratios, then for 15 km s−1 it is ~6%, and for 20 km s−1 it is ~3.5%. The velocity of the drops remains almost constant except for the terminal part of their trajectory.
The model also neglects energy losses due to the heating of drops to the boiling temperature. For the assumed drop sizes, this energy is orders of magnitude lower than the energy necessary for the evaporation of the drop, and so we neglect it.
4.3 Drag and heat transfer coefficients
When ablation starts, evaporated molecules form a cloud around the body, which affects the interaction of airflow molecules with the surface of the body. The assumption of a free molecular flow regime is not valid anymore and the dependence of drag and heat transfer coefficients on ablation rate and flow conditions must be taken into account. We adopt the results of Nelson et al. (2005), who used the direct simulation Monte Carlo method for modeling interactions between evaporated and atmospheric molecules during meteoroid entry. They found that Γ and Λ can be expressed as

where Kn is a Knudsen number far from the meteoroid and Br represents a blowing ratio, which is
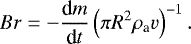 (19)
(19)
4.4 Numerical implementation of the model
There are only five free parameters in our model: (i) initial mass m∞, (ii) velocity v∞, (iii) zenith angle z, (iv) the mean diameter Ddr of drops, and (v) luminous efficiency τ. Both equations of motion and the heat diffusion problem are solved numerically as in Čapek & Borovička (2017). The integration starts at an altitude of 150 km with initial temperature T(r, t = 0) = Teq = 293.15 K. The spatial step is 0.01 mm and the time step is chosen according to velocity and the Von Neumann stability criterion. In each time step during the ablation phase the quantity of mass that is blown off from the surface of the meteoroid is determined according to Eq. (7). Next we determine the number of drops ni inside bins (which covers an appropriate size range around Ddr) according tosize distribution Eq. (8). The number of bins is 20. For each bin, Eqs. (9)–(11) are solved by a fourth order Runge–Kutta method, including the equation for normalized luminosity (Eq. (12)). The drops released in the given time step then contribute to the total normalized luminosity by d I(h) = ∑iniIi(h).
Some difficulties arise when the mean drop diameter is larger than ~250 μm and the ablation rate is low (which happens near the end of the light curve). In this case, the volume of the melt that is released during one time step can be smaller than the volume of these large drops. The number of these drops is then lower than one, and this causes artificial waves in the theoretical light curves. This phenomenon can be seen, for example, in meteor 05403028 in Fig. A.1.
4.5 Fitting the observed light curves
Each observed iron meteor is described by these quantities, which are important for our purpose: (i) velocity v∞, (ii) zenith angle z, and (iii) the light curve. Our goal is to determine the unknown parameters m∞, Ddr, and τ. We use a brute-force method: at first, a rough grid of initial masses (usually five values) and mean diameters (usually nine values from 8 to 256 μm) is chosen and for each combination a synthetic light curve is computed. Next, by comparison with observed light curves, the range of possible masses and mean diameters is narrowed and for this refined grid synthetic light curves are computed. Finally, the best fitting synthetic light curve determines m∞ and Dms, and τ. The last quantity, the luminous efficiency τ, is determined as follows. The total re-radiated energy of the observed meteor is
![\[ E_{\textrm{o}}=1500\,\int 10^{-M(t)/2.5} \textrm{d}t, \]](/articles/aa/full_html/2019/05/aa35203-19/aa35203-19-eq17.png)
where M(t) is the observed visual magnitude of the meteor (i.e. light curve). The conversion factor of 1500 W for radiative energy output of a zero magnitude meteor was taken from Ceplecha et al. (1998). Similarly, the total re-radiated energy of the synthetic light curve is
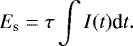 (20)
(20)
We require the equivalence of these energies, therefore
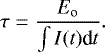 (21)
(21)
The selection of the synthetic light curve that best matches the observed one is done according to root mean square deviation (RMSD) together with the condition that the curves have the same (or similar) beginning height and similar shape. We stress that unlike most meteor studies, where the meteoroid mass is computed from the radiated energy assuming a value of luminous efficiency, our model allows us to determine the meteoroid mass and the luminous efficiency independently.
Let us note that for each meteor we have two light curves: one from the Ondřejov station and one from the Kunžak station. These light curves differ more or less due to observation errors. The derived properties of the meteoroid therefore also differ according to the stations. The resulting properties of the meteoroid are given as mean of the values, and their uncertainty is derived from the differences of the values and sampling of the parameter space (see Table A.1).
 |
Fig. 7 Examples of light curves of meteors with iron spectra. The observed light curves are black, the theoretical ones are red or blue. The dashed curves represent the radius R of the meteoroid divided by its initial value R∞. The letters A–E represents the class of the observed light curve (see the text). Here A is meteor 09820028 from Kunžak station, B is meteor 03802071 from Ondřejov station, C is meteor 08505008 from Kunžak station, D is meteor 03504018 from Ondřejov station, and E is meteor 12815084 from Kunžak station. |
5 Results
For the modeling we selected 38 meteors (including nine with iron spectra) with the best quality light curves, and added eight meteors with iron spectra from Borovička et al. (2005), and 14 meteors with iron spectra from Vojáček et al. (2019). Among these 60 meteors, we were not able to sufficiently describe three meteors with iron spectra and four meteors without spectra. The resulting parameters of light curve fits are summarized in Table A.1. The light curves and their fits can be seen in Figs. A.1–A.2.
The derived initial masses m∞ range from 6 to 900 mg. According to our model the beginning height corresponds to the beginning of fusion of the meteoroid, that is, reaching a temperature of 1811 K. This is a function of velocity, zenith distance of the radiant, and meteoroid mass. For a given meteor, the initial mass can be therefore determined from the beginning height. The mass also affects the length of the meteor. The masses of meteoroids with spectra are generally higher than those of meteoroids without spectra. This can be explained by the fact that it is more difficult to record spectra for fainter meteors.
The luminous efficiency is in the interval of 0.08–5.8% (see Fig. 8). For a given meteor it depends on initial mass; the mean diameter of the drops has only a small effect on its value.
The mean diameter of iron drops ranges from 4 to 500 μm and it affects the shape of the light curve and the length of the meteor. Small drops cause a shorter meteor with a rapid increase of brightness, whereas larger drops cause a slower increase of brightness, a shift of the maximum from the beginning, and a longer meteor. Let us recall that theoretical light curves, which correspond to iron drops larger than ~250 μm, sometimes contain waves near the end that are not real (see Sect. 4.4). The left plot of Fig. 7 shows modeled light curves (solid color curves) and the decrease of normalized radius of two meteoroids (dashed color curves). The model predicts corresponding mean drop sizes of 10 and 15 μm. Due to the small drop sizes, the kinetic energy of the melt material is quickly transformed into light and when the original meteoroid disappears, no more light isemitted. A different case can be seen in the middle plot of Fig. 7, where the model predicts a mean drop size of 235 μm. Here the transformation of kinetic energy is slower, the drops survive for a longer time, and the light is emitted more than five kilometers after the extinction of the meteoroid.
According to the shape of the observed light curve, we classified the meteors into six groups. A sudden apparition of the meteor and consequent monotonic decrease of its brightness characterizes the first group, denoted as A (see Fig. 7 left). The second group, B, contains meteors with a very rapid increase of brightness and maximum near the beginning of the light curve (Fig. 7 left). The third group, denoted as C, has a less rapid increase of brightness, more rounded shape, and longer luminous trajectory (Fig. 7 middle). Group D contains symmetrical light curves (Fig. 7 right). Group E has maximum brightness in the second half of the trajectory (Fig. 7 right). Meteors with more complicated light curves or meteors where classification was impossible belong to group F. In some cases it was difficult to decide between two neighboring groups. An example of such a case is meteor 17527052 (see Fig. A.1). We decided to classify it as A, but group B would also be possible.
The quality of the fit is described by numbers from 1 to 3. Quality 1 means that the shape of model light curve corresponds well to the observed one, and RMSD < 0.5 mag. A value 2 describes cases where the fit is also good but with RMSD in the interval ⟨0.5, 1). The worst quality, 3, corresponds to cases where (i) the synthetic light curve has a slightly different shape but RMSD ∈ ⟨0.5, 1) mag, or (ii) it has a similar shape, but RMSD > 1 mag. The model was not able to describe the light curves of four meteors without spectra. These cases are not listed in Table A.1. There are also three unsuccessful cases among meteors with iron spectra (quality 4). These meteors are the brightest ones in our sample and they exhibit symmetrical light curves without a rapid increase of brightness.
 |
Fig. 8 Histogram of luminous efficiency τ derived by the model. |
6 Discussion
6.1 Ablation process
Our simple model is able to describe most of the light curves relatively well. The best match is for class C. In these cases the ablation takes place consistently with our model, and minor differences are possibly given by deviations from idealized conditions: the meteoroid shape is not spherical, melt is removed with some delay, drops have a different size distribution function, the meteoroid is not composed of pure iron but of iron-nickel alloy, and other factors.
Meteors that belong to classes A and B are also described well, but there are some difficulties. Sometimes the model is able to fit the initial increase of brightness and the maximum (usually with small iron drops), but then the model brightness decreases more quickly than the observed one (see Fig. 7, left plot). A better fit in terms of a lower value of RMSD can be achieved with larger iron drops but in this case, the model does not fit the initial fast increase of brightness and position of brightness maximum. A possible explanation is that the assumption of immediate removal of the liquid is not valid. The liquid iron rests on the meteoroid’s surface and the amount of liquid increases until the condition for spraying drops is fulfilled. Ablation starts at this moment and the amount of removed mass is not equal to newly created liquid, but it follows laws that are more complicated. Moreover, the distribution of drop sizes may change according to flight conditions. Both these phenomena were described by Girin (2017, 2019).
The ability of our model to describe light curves of class D and E meteors is the worst, because the predicted light curves always have their maximum brightness in the first part of the luminous trajectory. Nevertheless, our model predicts similar beginning heights, maximum brightness, and length of these meteors; the light curve shape (and especially the position of the maximum) differs in about half of these cases. The reasons can be different: the ablation process may be more complicated than the assumed one (delayed removal of liquid, erosion, fragmentation), the meteoroid may have a non-iron composition, for larger meteoroids their shape and rotation may play important role, and so on. Observational errors may also be an important source of disagreement.
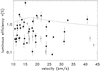 |
Fig. 9 Luminous efficiency τ as a function of meteoroid velocity. The filled symbols correspond to meteors with light curve fit quality 1 and 2. The dashed curve corresponds to the study of Becker & Friichtenicht (1971). |
6.2 Luminous efficiency and drop sizes
A detailed analysis of the dependence of τ on meteoroid parameters is beyond the scope of this article, and it will be presented in a forthcoming one. We will make only a few brief comments:
- (i)
There is no clear dependency of luminous efficiency τ on initial velocity v∞ (Fig. 9). Laboratory measurements, however, predict such a dependence for iron meteoroids: Ayers et al. (1970) studied several meteors produced by artificial iron meteoroids of masses between 0.6 and 5.7 g launched by rockets. They found a velocity dependence of τ= τ0vα, where α =1.9 ± 0.4. Becker & Friichtenicht (1971) determined τ as a function of velocity with a peak value of τ = 1.7% for 18 km s−1 for ~0.05–1 μm meteoroids under conditions of free molecular flow in a laboratory (see dotted curve in Fig. 9). A possible explanation of this mismatch is that luminous efficiency τ is not only a function of velocity, but also of other parameters such as mass and flow regime, which vary substantially across the modeled meteors. A similar spread of τ was obtained by Subasinghe & Campbell-Brown (2018) for non-iron meteors. In any case, this question will be addressed by a subsequent study that will use more data and will be focused on this problem.
- (ii)
There is only a very weakly defined dependency of luminous efficiency on initial mass (Fig. 10). If we use only light curves with fit quality 1 and 2, we find that the luminous efficiency in percent can be estimated as
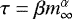 , where mass is in milligrams,
, where mass is in milligrams, 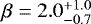 and α =−0.38 ± 0.11. Subasinghe & Campbell-Brown (2018) studied non-fragmenting, non-iron meteoroids with slightly lower masses and mostly faster speeds than our cases. They found α = −0.3647, which is similar to our value (Subasinghe & Campbell-Brown 2018, their Fig. 10, lower).
and α =−0.38 ± 0.11. Subasinghe & Campbell-Brown (2018) studied non-fragmenting, non-iron meteoroids with slightly lower masses and mostly faster speeds than our cases. They found α = −0.3647, which is similar to our value (Subasinghe & Campbell-Brown 2018, their Fig. 10, lower). - (iii)
Themean drop size Ddr as a function of initial velocity can be seen in Fig. 11. For lower velocities, there is a large dispersion of values of Ddr, from several μm to several hundreds of μm. With increasing velocity, the dispersion decreases and droplet mean size grows.
 |
Fig. 10 Luminous efficiency τ as a function of meteoroid mass. The filled symbols correspond to meteors with light curve fit quality 1 and 2. The solid curve is a function |
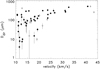 |
Fig. 11 Mean drop size Ddr as a function of meteoroid velocity. The filled symbols correspond to meteors with light curve fit quality 1 and 2. |
7 Conclusions
We developed a simple numerical model of the ablation of iron meteoroids that assumes immediate removal of liquid iron from the meteoroid surface as droplets with a Nukiyama-Tanasawa size distribution. The model was able to adequately describe most of the available light curves, including beginning height, position of maximum brightness, the length of the meteor, and its overall shape. Better results were obtained for light curves with maxima in the first half of the trajectory. The model has difficulties with symmetricallight curves and cases with maxima in the second part of the trajectory. Three meteors with iron spectra could not be modeled at all. These are in fact the three brightest meteors in our sample, all brighter than magnitude zero at maximum. We can therefore conclude that our model, assuming regular symmetric ablation and no fragmentation of the solid phase, is applicable only to small iron meteoroids causing meteors fainter than approximately magnitude zero.
For an individual faint meteor, the model allows us to estimate initial mass m∞, mean drop size Drd, and luminous efficiency τ. The fact that mass and luminous efficiency can be estimated independently is a unique property of the model. No dependence of luminous efficiency on initial velocity or mean drop size has been found, and only a weak dependence on initial mass has been suggested. Meteoroids with high velocities are fitted best with larger droplets of liquid iron, whereas those with low velocities create droplets with a wide range of mean sizes.
We can confirm previous findings that iron meteoroids are encountered primarily on asteroidal orbits with aphelia inside Jupiter’s orbit and with inclinations lower than 40°. We note, nevertheless, that Vojáček et al. (2019) found two iron meteoroids (with spectra) on Halley-type orbits, both with aphelia around 6.5 AU and inclinations of 63°. Both these meteors were analyzed here; their numbers are 05403028 and 12815084.
A natural improvement of the model will be the inclusion of the theory of Girin (2017, 2019) that predicts the mass shedding rate from the liquid surface of a meteoroid and the size distribution of drops. This kind of modification can possibly improve the agreement of the theoretical light curves with observed ones.
Acknowledgements
We are grateful to Margaret Campbell-Brown, whose comments significantly helped to improve the text. This work was supported by GAČR grant 16-00761S.
Appendix A Meteor parameters and light curves
Parameters of iron meteors.
 |
Fig. A.1 Observed light curves of meteors with iron spectra (diamond and triangle symbols) and best fit model light curves (solid curves). Blue corresponds to the Kunžak station and red to the Ondřejov station. The plots are titled with the meteor designation; v means initialvelocity, z is zenith distance. Parameters of best fit models are: initial mass m, luminous efficiency τ, and mean diameter of iron drops Ddr. The big letter (A, B, C, D, E or F) followed by a number means light curve class and quality of the fit (see Sect. 5). |
 |
Fig. A.1 continued. |
 |
Fig. A.1 continued. |
 |
Fig. A.1 continued. Meteor 17527052 has no spectra. The model was no able to describe light curves of meteors 17330039, 17528031, and 18A08052. |
 |
Fig. A.2 Observed light curves of meteors without spectra (diamond and triangle symbols) and best fit model light curves (solid curves). Blue corresponds to the Kunžak station and red to the Ondřejov station. The plots are titled with the meteor designation; v means initialvelocity, z is zenith distance. Parameters of best fit models are: initial mass m, luminous efficiency τ, and mean diameter of iron drops Ddr. The big letter (A, B, C, D, E or F) followed by a number means light curve class and quality of the fit (see Sect. 5). |
 |
Fig. A.2 continued. |
 |
Fig. A.2 continued. |
References
- Ayers, W. G., McCrosky, R. E., & Shao, C.-Y. 1970, SAO Special Report, 317 [Google Scholar]
- Becker, D. G., & Friichtenicht, J. F. 1971, ApJ, 166, 699 [NASA ADS] [CrossRef] [Google Scholar]
- Borovička, J. 1990, Bull. astr. Inst. Czechosl., 41, 391 [Google Scholar]
- Borovička, J. 1994, A&AS, 103, 83 [NASA ADS] [Google Scholar]
- Borovička, J., & Jenniskens, P. 2000, Earth Moon Planets, 82, 399 [NASA ADS] [Google Scholar]
- Borovička, J., Koten, P., Spurný, P., Boček, J., & Štork, R. 2005, Icarus, 174, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Campbell-Brown, M. 2015, Planet. Space Sci., 118, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Ceplecha, Z. 1967, Bull. astr. Inst. Czechosl., 18, 303 [NASA ADS] [Google Scholar]
- Ceplecha, Z. 1987, Bull. astr. Inst. Czechosl., 38, 222 [Google Scholar]
- Ceplecha, Z., Borovička, J., Elford, W. G., et al. 1998, Space Sci. Rev., 84, 327 [NASA ADS] [CrossRef] [Google Scholar]
- Čapek, D., & Borovička, J. 2017, Planet. Space Sci., 143, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Fleming, D. E. B., Hawkes, R. L., & Jones, J. 1993, Meteoroids and their Parent Bodies, eds. J. Stohl & I. P. Williams (Bratislavaed: Slovak Academy of Sciences), 261 [Google Scholar]
- Genge, M. J. 2016, Meteor. Planet. Sci., 51, 1063 [NASA ADS] [CrossRef] [Google Scholar]
- Girin, O. G. 2017, A&A, 606, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Girin, O. G. 2019, A&A, 621, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Koten, P., Borovička, J., Spurný, P., Betlem, H., & Evans, S. 2004, A&A, 428, 683 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Koten, P., Páta, P., Fliegel, K., & Vítek, S. 2014, Proceedings of the International Meteor Conference, Poznan, Poland, 22–25 August 2013, eds. M. Gyssens, P. Roggemans, & P. Zoladek (Hove, Belgium: International Meteor Organization), 53 [Google Scholar]
- Koten, P., Štork, R., Páta, P., Fliegel, K., & Vítek, S. 2016, Proceedings of the International Meteor Conference Egmond, the Netherlands, 2–5 June 2016, eds. A. Roggemans & P. Roggemans (Hove, Belgium: International Meteor Organization), 133 [Google Scholar]
- Moore, C. E. 1945, Contrib. Princet. Univ. Observ., 20, 1 [Google Scholar]
- Nelson, D. A., Baker, R. L., & Yee, P. P. 2005, Aerospace report no. ATR-2006(9368)-1 [Google Scholar]
- Semião, V., Andrade, P., & da Graça Carvalho, M. 1996, Fuel, 75, 1707 [CrossRef] [Google Scholar]
- Subasinghe, D., & Campbell-Brown, M. 2018, AJ, 155, 88 [NASA ADS] [CrossRef] [Google Scholar]
- Vojáček, V., Borovička, J., Koten, P., Spurný, P., & Štork, R. 2015, A&A, 580, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vojáček, V., Borovička, J., Koten, P., Spurný, P., & Štork, R. 2019, A&A, 621, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Weissman, P. R., Bottke, Jr. W. F., & Levison, H. F. 2002, Evolution of Comets into Asteroids, eds. W. F. Bottke, Jr., A. Cellino, P. Paolicchi, & R. P. Binzel (Tucson: University of Arizona Press), 669 [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Co-added frames of video spectra of meteors 17528031 (top) and 17527064 (bottom). Both meteors moved nearly from top to bottom. Approximate wavelengths are indicated and important spectral lines are identified. |
| In the text | |
 |
Fig. 2 Spectra of meteors 17528031 and 17527064 averaged over all frames and calibrated using the spectral sensitivity function of the instrument (plotted as dashed line). The 17527064 spectrum has been offset vertically for clarity. Lines other than Fe are identified; that is, all non-identified lines are produced primarily by iron. |
| In the text | |
 |
Fig. 3 Beginning height and initial velocity distribution for Fe candidates and meteors with iron spectra. |
| In the text | |
 |
Fig. 4 Distribution of the F parameter for Fe candidates and meteors with iron spectra. |
| In the text | |
 |
Fig. 5 Tisserand parameter for iron candidates (red triangles) and meteors with iron spectra (blue circles). |
| In the text | |
 |
Fig. 6 Perihelion versus aphelion plot for iron candidates (red triangles) and meteors with iron spectra (blue circles). |
| In the text | |
 |
Fig. 7 Examples of light curves of meteors with iron spectra. The observed light curves are black, the theoretical ones are red or blue. The dashed curves represent the radius R of the meteoroid divided by its initial value R∞. The letters A–E represents the class of the observed light curve (see the text). Here A is meteor 09820028 from Kunžak station, B is meteor 03802071 from Ondřejov station, C is meteor 08505008 from Kunžak station, D is meteor 03504018 from Ondřejov station, and E is meteor 12815084 from Kunžak station. |
| In the text | |
 |
Fig. 8 Histogram of luminous efficiency τ derived by the model. |
| In the text | |
 |
Fig. 9 Luminous efficiency τ as a function of meteoroid velocity. The filled symbols correspond to meteors with light curve fit quality 1 and 2. The dashed curve corresponds to the study of Becker & Friichtenicht (1971). |
| In the text | |
 |
Fig. 10 Luminous efficiency τ as a function of meteoroid mass. The filled symbols correspond to meteors with light curve fit quality 1 and 2. The solid curve is a function |
| In the text | |
 |
Fig. 11 Mean drop size Ddr as a function of meteoroid velocity. The filled symbols correspond to meteors with light curve fit quality 1 and 2. |
| In the text | |
 |
Fig. A.1 Observed light curves of meteors with iron spectra (diamond and triangle symbols) and best fit model light curves (solid curves). Blue corresponds to the Kunžak station and red to the Ondřejov station. The plots are titled with the meteor designation; v means initialvelocity, z is zenith distance. Parameters of best fit models are: initial mass m, luminous efficiency τ, and mean diameter of iron drops Ddr. The big letter (A, B, C, D, E or F) followed by a number means light curve class and quality of the fit (see Sect. 5). |
| In the text | |
 |
Fig. A.1 continued. |
| In the text | |
 |
Fig. A.1 continued. |
| In the text | |
 |
Fig. A.1 continued. Meteor 17527052 has no spectra. The model was no able to describe light curves of meteors 17330039, 17528031, and 18A08052. |
| In the text | |
 |
Fig. A.2 Observed light curves of meteors without spectra (diamond and triangle symbols) and best fit model light curves (solid curves). Blue corresponds to the Kunžak station and red to the Ondřejov station. The plots are titled with the meteor designation; v means initialvelocity, z is zenith distance. Parameters of best fit models are: initial mass m, luminous efficiency τ, and mean diameter of iron drops Ddr. The big letter (A, B, C, D, E or F) followed by a number means light curve class and quality of the fit (see Sect. 5). |
| In the text | |
 |
Fig. A.2 continued. |
| In the text | |
 |
Fig. A.2 continued. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.