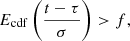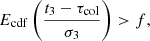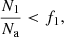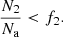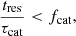| Issue |
A&A
Volume 625, May 2019
|
|
|---|---|---|
| Article Number | A98 | |
| Number of page(s) | 8 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/201834588 | |
| Published online | 20 May 2019 | |
Advanced aspects of Galactic habitability
1
Department of Astronomy, Faculty of Mathematics, University of Belgrade, Studentski Trg 16, 11000 Belgrade Serbia
e-mail: vladimir_djosovic@matf.bg.ac.rs
2
Astronomical Observatory, Volgina 7, PO Box 74 11060 Belgrade, Serbia
e-mail: bvukotic@aob.rs, mcirkovic@aob.rs
Received:
6
November
2018
Accepted:
29
March
2019
Context. Astrobiological evolution of the Milky Way (or the shape of its “astrobiological landscape”) has emerged as a key research topic in recent years. In order to build precise, quantitative models of the Galactic habitability, we need to account for two opposing tendencies of life and intelligence in the most general context: the tendency to spread to all available ecological niches (conventionally dubbed “colonization”) and the tendency to succumb to various types of existential catastrophes (“catastrophism”). These evolutionary tendencies have become objects of study in fields such as ecology, macroevolution, risk analysis, and futures studies, though a serious astrobiological treatment has so far been lacking.
Aims. Our aim is to numerically investigate the dynamics of opposed processes of expansion (panspermia, colonization) and extinction (catastrophic mechanisms) of life in the Galaxy.
Methods. We employed a new type of numerical simulation based on 1D probabilistic cellular automaton with very high temporal resolution, in order to study astrobiological dynamics.
Results. While the largest part of the examined parameter space shows very low habitability values, as expected, the remaining part has some observationally appealing features that imply, among other things, a reduction in the amount of fine-tuning necessary for resolving the Fermi paradox.
Conclusions. Advanced aspects of Galactic habitability are amenable to precision studies using massive parallel computer simulations. There are regions of the parameter space that correspond to a quasi-stationary state satisfying observable constraints and possessing viable SETI targets.
Key words: methods: numerical / Galaxy: evolution / extraterrestrial intelligence
© ESO 2019
1. Introduction: habitability and colonization
Studies of habitability – circumstellar, galactic, and cosmological – have rapidly become the main topic of astrobiological research in recent years (e.g. Chyba & Hand 2005; Javaux & Dehant 2010; Horner & Jones 2010; Lineweaver & Chopra 2012; Dayal et al. 2015). Both important theoretical insights and novel numerical models have been developed and deployed in the course of the last decade in order to obtain a better quantitative handle on the hitherto mostly intuitive concept of habitability. In particular, cosmological structure formation simulations (Vukotić et al. 2016; Forgan et al. 2017) and semi-analytic merger trees (Stanway et al. 2018) have been used successfully to that effect. Clearly, there is much work to be done in this area, with refinement of both computing resolution and empirical constraints on habitability.
There is, however, another aspect of habitability that has not yet been quantitatively studied. This is the interplay between (often intuitively assumed, but rarely explored in detail) two generalized ecological tendencies that characterize life irrespective of its exact definition: the tendency to spread to all available niches and the tendency to become extinct as a consequence of catastrophic changes in its physical environment. While intuitively generalized from our observations of terrestrial life, there is no reason whatsoever to assume that extraterrestrial life, if it exists, will be exempt from either of these two grand trends. The spread of life over various cosmic distances has been usually operationalized as either panspermia or intentional colonization by intelligent life. Since the classical study of Newman & Sagan (1981), there have been several specific studies of the modes of spreading of intelligent life through the Galaxy (e.g. Bjørk 2007; Cotta & Morales 2009; Starling & Forgan 2014). On the other hand, most of the contemporary studies of habitability take into account at least some of the astrophysical catastrophic risks, such as those from supernovae and gamma-ray bursts (e.g. Ellis & Schramm 1995; Scalo & Wheeler 2002; Galante & Horvath 2007; Ćirković & Vukotić 2008; Gowanlock 2016; Stanway et al. 2018). In fact, one could even state that the “catastrophic” aspects of the overall astrobiological evolution have been overemphasized in recent years. The very concept of habitable zones, bounded in space and time, which has emerged as the “bread and butter” of astrobiology (e.g. Gonzalez 2005), testifies to the resurgence of catastrophism as a key ingredient in any viable astrobiological theory.
In contrast, the aspect of astrobiological evolution that deals with spreading of life has thus far been largely neglected or downplayed in quantitative models (even though the philosophical justification of life’s tendency to spread and consequent implications for astrobiology is well-studied under the title of the continuity thesis; cf. Fry 2000; Ćirković 2012). Often a lip service is paid to the tendency of life to spread and fill all available ecological niches (e.g. Hanson 1998; Sagan 2000), but it is seldom analysed and modelled in detail. There are essentially two modes of spreading of life which might be co-present in the overall astrobiological landscape: panspermia (simple life) and colonization (complex life, specifically technological civilizations). The two are not entirely disjunctive, since the emergence of spacefaring civilization is accompanied by possibility of directed panspermia (Crick & Orgel 1973; Sleator & Smith 2017). Actual concerns about planetary contamination and planetary protection (e.g. Rummel 2001) testify how even a primitive technological civilization, like the present-day human one, faces this problem quite early in its spacefaring attempts. Therefore, it makes sense to discuss both these aspects of the same “spreading of life” tendency in a unified way, as we are doing in the present model; we refer to this dual tendency as “colonization”, while keeping in mind that the model parameters are actually adaptable enough to include all kinds of panspermia. (A similar dual construal is applicable on the catastrophism side of the story, where we can subsume both naturally occurring and technogenic events, such as the nuclear winter, which is capable of causing widespread ecological devastation and extinction, under the same controlling parameter.)
Therefore, trying to achieve a more complete picture is highly justified. Cellular automata approach, a grid of cells (each described with some variable called state) that evolve in discrete time steps (see Ilachinski 2001) has been shown to be a promising modelling platform for such phenomena (Vukotić & Ćirković 2012a,b). However, since life-friendly matter conditions are usually found on planetary bodies, and in particular the habitability of systems of such bodies is greatly influenced with galactic parameters, the required spatio-temporal dynamical range for such models is huge. Consequently, vast computational resources are required. Clearly, a practical difficulty in incorporating these two opposing tendencies in a single synthetic model is the discrepancy between relevant timescales in the general case. The present study seeks to address at least some of these issues, by concurrent simplification of the spatial structure and drastic increase in temporal resolution of the simulation. Our pilot study has shown that even a very simple, 1D (temporal) toy model of such phenomena is a fruitful approach (Đošović et al. 2018), and has the upper hand over the similar approach realized with 2D cellular automata (Vukotić & Ćirković 2010; Bezsudnov & Snarskii 2010; Galera et al. 2019), since the spatial aspect of the model is greatly simplified. This enables much better temporal resolution of the simulation that can model phenomena with ∼104 yr characteristic timescale during the lifespan of the Galactic disk. This is comparable to the historical span of human civilization on Earth. On the other hand, the temporal aspects of evolution of life can be studied against our empirical knowledge of the Earth’s fossil record, while even the highly successful contemporary exo-planet studies have yet to figure out the empirical signatures of life on other planets. Even with multiple modern panspermia studies (e.g. Wallis & Wickramasinghe 2004; Lingam 2016), it is still highly contentious how efficient naturally occurring panspermia is in the Galaxy (Gordon & Hoover 2007; Mcnichol & Gordon 2012). On the other hand, the efficiency of directed panspermia is not in doubt, in contrast to the frequency of the technological civilizations capable of undertaking it, which remains unknown. Therefore, it makes sense to try to model both jointly. Also, the model presented is rather conservative in that it employs the conventional notion of habitable planets and fairly gradual evolutionary processes (even if punctuated by occasional catastrophes), and it does not include a type of more radical transformative processes, in particular postbiological evolution of extraterrestrial intelligence (e.g. Dick 2003).
This paper is organized as follows. The description of code, its structure, and phenomenology included is given in Sect. 2. Sect. 3 contains the description of simulations, with the computing resources employed. The main results are presented in Sect. 4, while the discussion and prospects for further work are given in the concluding section.
2. Method
Unlike standard cellular automata approach, where spatial influence is implemented through the interaction of the cell with its neighbours, our model is simplified so that probability of colonizing (or possible panspermia seeding) of a particular spatial site is dependent on the total number of colonization capable entities (sites that have sufficiently evolved to be able to colonize other sites) in a given time step of the simulation. From the technical point of view, this can be regarded as a cellular automaton where each cell has a neighbourhood comprised of all other cells in the simulation. While this approach limits the inference on for example, modes of spatial spreading, such as simple spherical expansion vs. resource-driven percolation schemes (e.g. Galera et al. 2019), the benefits from higher resolution of temporal scales are evident. The main features of our model are as follows:
-
The habitable sites in the Galaxy are represented as entities that have a particular state which evolves over time.
-
Each site can evolve through four discrete states designated as: 0 – no life, 1 – simple life, 2 – complex life, 3 – technological civilization.
-
Each site evolves according to probabilistic evolution rules with fiducial timescales representing the Earth’s fossil record and planetary formation rate. During the course of the simulation, the sites are gradually activated to state 0 as per distribution of the Earth-like planets’ formation rate from Lineweaver (2001).
-
Each cell in state 3 can colonize only one cell in state 1 or 2 per time-step, according to a Poisson-like probability distribution.
We do not enter into complex and partially philosophical issues such as what exactly constitutes a technological civilization. Instead, we have adopted pragmatic approach of classic studies such as Newman & Sagan (1981) that technological civilization is an entity capable – unless destroyed by an existential catastrophe – of colonizing nearby habitable planetary systems, sooner or later. We also used the terrestrial values in the present proof-of-concept model as the starting point, since the Copernican assumption has served us well in both science in general and astrobiology in particular (for an extended discussion of the latter see Ćirković 2012).
2.1. Code description
At the beginning of the simulation there are no active sites. As the simulation run progresses, the 1000 simulated sites are activated to state “0” according to probability density distribution representative of cosmic Earth-like planet formation rate from Lineweaver (2001; for other works see also Zackrisson et al. 2016). We used only the most recent 10 Gyr of this distribution and normalized it in such a way as to activate all sites (in a probabilistic manner) during our simulation time span of 10 Gyr. The frequency of site activation peaks at ∼1.5 Gyr after the beginning of the run and than falls off with a shallower slope towards the end of the simulation. Also, once activated, each site is assigned the main sequence lifetime of 1010m−2.5, where m is the stellar mass selected randomly with uniform probability from [0.6 − 1.3] M⊙ mass interval. If the time from the site activation exceeds the assigned main sequence time the site is removed from the simulation.
The modelled transitions are presented in Fig. 1. Each site might preserve its state to the next time step, sites in 0–2 states can evolve to +1 higher complexity just by internal evolution, state 1 and 2 sites might be colonized to state 3, while only state 3 sites can be degraded to state 2 by catastrophic events (natural or artificial). The transitions between the states are implemented in a similar manner as in Vukotić & Ćirković (2012a). The transition probabilities in that work (arranged in a matrix for the sake of formalism and easier reference) have been calculated from the timescales describing those transitions. The main difference is that this work uses Epanechnikov instead of a Gauss kernel to calculate transition probabilities from the parameters of the relevant transition timescales (Table 1). The active site in state i can evolve to state j according to Epanechnikov kernel (Epanechnikov 1967), E(u) = 0.75(1 − u2), where |u|≤1. Epanechnikov kernel is much less computation intensive than widely used Normal distribution kernel. As explicated in our recent pilot study concerning the topic of this work (Đošović et al. 2018), at the beginning of each run, each of the simulated sites is assigned a set (one for each possible transition) of random variates from a uniform probability distribution in (0 − 1) interval (f). The state of the site is changed if the resulting cumulative density function at a time t has higher value than this pseudo-random number (we used a pseudo-random number generator SFMT, see Saito & Matsumoto 2008):
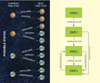 |
Fig. 1. Modelled transitions with a symbolic scheme of states (we assume that a Mars-like planet could have been habitable for simple life in at least some epochs of its history). |
Parameters of the transitions in our model.
where t is time that a site have spent in state i since activation or the last transition, if applicable, τ is a characteristic time (mean value of kernel) for transition i → j where j is the next state and σ is standard deviation, that is, width of the kernel. When the transition occurs for the particular object, a random variate for that particular transition is reinitialized. The above model is used for evolution-type transitions, where site evolution is not to be influenced by spatial spreading agents, such as colonization or panspermia. A similar equation is adopted for the calculation of probability for colonization-induced transitions:
where t3 is time that object have spent in state 3 (up to the current time step), τcol is the characteristic time of colonization while it’s standard deviation is σ3. When the state 3 object reaches a time step where the above condition is fulfilled it makes a colonization attempt and it’s t3 gets reset to zero regardless of colonization success. The colonization attempt is considered a failure if there are no objects in state 1 or 2 (at a particular time step), which is highly improbable. If there are objects in state 1 or 2 then the following conditions are tested:
The total number of objects in state 1 and 2 are represented with N1 and N2, respectively, while Na is the total number of activated objects from the beginning of the simulation run. The above conditions are tested for each colonizing (state 3) object at a given time step. Two separate random variates f1 and f2 are generated each time the conditions are tested. If the first condition is true, then the randomly selected object in state 1 is colonized. Otherwise, if the first condition is false, then the second condition is tested. If the second condition is true, the randomly selected state 2 object is colonized. In the case when the second condition is false (i.e. both conditions are false), then the corresponding colonization attempt is considered a failure. When the object in state 1 or 2 gets colonized, the random variate of the corresponding evolutionary 1 → 2 or 2 → 3 transition for that object is also reinitialized. While this might not be of practical importance for objects in state 1, objects in state 3 can be catastrophically degraded back to state 2.
The catastrophic aspect of the model is implemented with a separate 3 → 2 transition as a Poisson-like process. In each time step the object in state 3 must satisfy:
where tres is a simulation time step, τcat is a characteristic time scale for catastrophic events and fcat a uniform random variate generated each time the condition is tested. Otherwise, the object is degraded to state 2. Table 1 summarizes transitions and their parameters.
For the characteristic times from Table 1, for the emergence of life and its evolution to complex forms are according to Dodd et al. (2017) and Maloof et al. (2010), respectively. Finally, we used a figure of 600 million years for the development of intelligent life and civilization, roughly following the Copernican assumption about typicality of evolution of complex life and intelligence on Earth. The catastrophic timescale that represent high risk events such as close gamma-ray burst, supernovae, and asteroid impacts is variable in the interval indicated in Table 1. Independent of catastrophic transition, the two timescales for the colonization transitions are varied together (have equal values in each simulation). We have neglected colonization rates to sites in state 0, in order to avoid seeding of planets incapable of supporting life at given time. This makes the model more conservative and more in line with the conventional scenarios of colonizing planets possessing at least some biotic resources, usable as soil or food, as well as for other life-supporting purposes.
2.2. Simulation technical details
The simulations were run on PARADOX III super-computer at The Institute of Physics Belgrade. PARADOX III consists of 106 computing nodes. Each node has 16 CPU cores (2 × 8) Sandy Bridge Xeon 2.6GHz, with 32 GB RAM memory. All nodes are interconnected by the QDR InfiniBand network. A great deal of the required computation was also carried out at the Bibliotheca Alexandrina High-Performance Computing machine, BA-HPC C2. BA-HPC C2 consists of 98 servers (each with 128 GB of RAM memory), with a total of 1968 CPU cores and 288 TB of storage.
Each simulation covers the time span of 10 Gyr in steps of 10 kyr. The input timescales for colonization and catastrophism were different for each simulation. They were selected from an interval of 104–1010 yr on exponential scales in increments of 0.05. This gives a total of 14 641 combinations of input parameters which is also the total number of simulations performed (and the total number of the output files). We ran one simulation per core. A pseudo random number generator is seeded with the number of the simulation, that is, from (0, 14 641) interval. The results of each simulation are an average of 100 runs. The described models for colonization and catastrophism accounted for the most of the computational resources. The runs with a significant number of state 3 objects took up to a 104 s of wall-clock time, while some of the fastest were completed in a matter of 7 × 102 s. The downside of the sequential output is that it is not feasible to perform “atemporal” analysis of the model (e.g. to calculate the number of sites at a fixed state over all snapshots).
3. Results
We present the results of our simulations in Figs. 2–4. Figure 2 shows the colour coded plot of the average total number of sites in state 3 at the end of the simulation (at 10 Gyr) for each set of varied characteristic timescales. For the greater part, the plot surface shows the number of objects to be below the middle point of the colour scale (the indicated mean value is below 450). This apparent dominance of catastrophism is also evident in the prominent diagonal feature lying below the τcat = τcol line. The middle value of the colour bar settles at ≈108 = τcat = τcol. The light blue to orange region in the upper right corner of the plot with τcat = τcol > 108 is not dominated by catastrophic events. There, even if τcat < τcol, it is possible for the number of objects in state 3 to be above the average. The gradient of colour coded values in this part is also smaller than in the catastrophism dominated region. The area with τcol < 105 and τcat < 106 shows some fluctuations.
 |
Fig. 2. Number of sites in state 3 as a function of timescale for catastrophism and colonization at the end of the simulated time span (10 Gyr). Axes are designated with decadic logarithm of the relevant timescale in years. The grey colour represents pixels with exactly zero number of sites in state 3, while the numbers values higher than zero are colour-coded as displayed. The mean value of the plotted matrix is 391.90 and is indicated with the black dash on the colour bar. |
 |
Fig. 3. Number of cells in each state (colour-coded as listed in bottom right panel) as a function of time. Different plots means different initial conditions for colonization timescale (τcol) and catastrophism (τcat). The number of sites in each state after 10 Gyr is indicated at the top of each panel. |
 |
Fig. 4. Similar plot as in Fig. 3, except that it shows the standard deviation of the number of cells in each state. |
In Fig. 3 we plot how the average number of sites in each state changes with time for a selected set of variable input parameters. The standard deviation of curves from Fig. 3 is given in Fig. 4. While Fig. 2 is useful for discussion of the emerging “habitability regimes”, Figs. 3 and 4 are more suitable for grasping the underlying mechanics of the evolution timescales and their relation to different evolution scenarios.
Each data point in Figs. 2 and 3 is the mean value of 100 runs of the simulation. The first row of panels in Figs. 2 and 3 shows that catastrophism overwhelms the colonization and there are almost none of the objects in state 3 throughout the whole simulated time span. The standard deviation for all emergent curves is at a level of approximately ten which implies no sudden changes and a steady evolution.
This is very similar to the third row of panels with colonization as a dominant agent. The main difference however is a region of instability between 3 and 4 Gyr (left most and middle panel). Once the colonization starts it takes about 0.5 − 1 Gyr (for τcol = 105 up to τcol = 107, respectively) to colonize most of the objects in states 1 and 2. Once the equilibrium with catastrophism is evident in the middle panel of this row and the number of objects in state 2 is approximately ten until the end of the simulation. The panel on the right hand side shows no such behaviour and is very similar to the panels in the first row, except for existence of a significant number of state 3 objects, mostly at the expense of the population in state 2. Similar curve shapes, but with lesser number of objects in state 3 are emergent in the middle row in central and the right hand side panel, while the left most panel in this row shows a typical signature of dominant colonization.
A somewhat larger fluctuations, both in the numbers of state 3 objects and in their standard deviation is evident in the middle row (when compared to the third row). The larger values for catastrophic timescales give a smooth appearance of the curve while smaller values suppress the appearance of state 3 sites. The small number of state 3 sites in the right-hand side and in the middle panel of the middle row in Fig. 3, approximately ten, shows a slightly larger relative spread and a non-stable behaviour (Fig. 4). Apart from being of little value for making the quantitative conclusions from the statistical point of view, it also lacks credit from a methodical view point. Ćirković (2018) argues that even the discovery of a single to a few advanced civilizations would have a little power in resolving Fermi’s paradox in its stronger forms. The similar standard deviation curve for states 1 and 3 in colonization dominated cases (at 3 − 4 Gyr time interval) is due to the fact that onset of colonization happens at a rather stochastic and unpredictable pace, because small variations in the number of state 3 objects at the beginning of this phase can proliferate fast to much larger differences. This directly imprints on the state 1 curve since it is subjected to colonization at a pace dictated by the state 3 curve. A similar process should hold for state 2 curves, but this is not obvious from the presented plots as state 2 does not have enough time to build up in numbers as state 1 does.
4. Discussion
The larger part of the plot surface in Fig. 2 is grey or dark-blue-coloured, indicating that catastrophic events might play a dominant role in shaping the parameter space for the evolution of life. Even only in a mild catastrophic regime, with no 3 → 1 transitions. This might be a consequence of the 1 → 2 evolution characteristic time of 3 billion years. If life took very “little” time to appear on Earth it is somewhat contradictory that it required another 3 billion years to make complex forms. Either some form of astrobiological regulation (possibly catastrophic) might be at play or it can simply be attributed to the enormous fitness of extremophile single cell life. This fits well into our current empirical inventory: there are many planets out there, but still no perception of the advanced exo-civilizations. The dominance of catastrophism is also obvious from plot features extending along the colonization scale, which show an independence of those features from colonization and strong dependence on selected catastrophic times. Another interesting interpretation would be that cosmic catastrophes followed by mass (but not total) extinctions may indeed have a positive effect on evolution as a whole (through evo-devo mechanisms, adaptive radiations similar to the Cambrian explosion, etc.), as has been speculated, for instance, by the “rare Earth” theorists (Ward & Brownlee 2000), following an early idea of the physicist John Cramer (1986). With that interpretation, we would rather expect a U-shaped dependence, even if skewed, of the frequency of complex life on the rate of occurrence of catastrophic events.
Our model of transitions is very conservative as far as colonization is concerned, at least when compared with catastrophism. From Fig. 1, state 3 can be pumped with evolution from state 2 and colonization from states 1 and 2. At the same time it is drained only by catastrophism to state 2. The overall compendium of empirical evidence from astrophysics, biology, geology, sociology, philosophy, and even anthropology) implies that life-hazardous events have occurred in the past and are a probable threat in the future. Even our present existence on Earth, in the light of the probabilistic anthropic selection effect (Ćirković et al. 2010), is consistent with a significant underestimate of hazardous event frequency. On the other hand, we have no such empirical background in estimating relevant colonization timescales; at least without significant extrapolation to future technologies. Enforcing a certain level of handicap to interstellar colonization over naturally- or technologically-induced catastrophes should give more restrictive but reliable results as far as outlining the parameter space regions with a large number of state 3 sites is concerned. For this purpose, state 3 objects were restricted to make a colonization attempt towards only one possible target during the τcol. In addition, the success of colonization depends also on the relative number of the available targets. It is evident from Fig. 2 that at the onset of colonization, the rate of making the state 3 objects rapidly increases and then gradually decreases as the number of state 3 objects becomes larger.
Even with such restrictions the τcat = τcol > 108 region is dominated by a high number of state 3 objects. It appears that this is the consequence of setting the 2 → 3 characteristic evolution time to 3 × 108 yr. This implies that the shape of distinction pattern between colonization- and catastrophism- dominated regions is primarily determined by the ability of the habitable sites to recover from the catastrophic events. With the recovery pace being larger than the frequency of hazards, the state 3 objects clearly dominate the scene. Also, the steeper slope of this pattern in the τcat = τcol > 108 region indicates that there is less dependence on the colonization time scale, even for points in excess of 500 state 3 objects at the end of the simulation. Here, the significant number of state 3 objects should not be contributed to colonization but rather to evolution and increased life time because of the larger τcat.
The panels on the main diagonal in Fig. 3, τcat = τcol show a very interesting behaviour of state 1 curve. With respect to the results presented in Fig. 2, the catastrophism-dominated part (with both timescales at 105 or 107 yr) shows a convex shape of state 1 curve at epochs later than ∼5 Gyr, resulting in a comparable number of state 1 and state 0 objects at the end of the simulation. Figure 4 shows that, although in Fig. 3 there are no state 3 objects for τcat = τcol = 105 yr, objects in state 3 do appear during the simulation run. The shape of the state 1 curve might be explained by the colonization action of state 3 upon state 1. Some of the state 3 objects manage to colonize state 1 objects before they are catastrophically degraded to state 2. This effect reduces towards later epochs since the number of available state 1 targets gets smaller. Since the state 2 curve does not show similar features, likely because of also being catastrophically populated back from state 3, the shape of the state 1 curve might be indicative of the colonization action even in the absence of detecting (or existence) of colonizing objects themselves at the present epoch. The quantification of this effect requires further examination and fine-tuning of the colonization model.
With regard to our current ignorance of exo-civilizations, the red-coloured part of the parameter space in Fig. 2 is not of particular interest for better understanding of the Fermi’s paradox, while the yellow and light-blue regions might be very significant. In other words, all the regions of the parameter space with a very small number of state 3 objects, especially the sub-parts with smaller colonization timescales (i.e. τcol < 108 yr). The colour bar in Fig. 2 indicates that a number of colonized sites can reach up to a 20% of the total number of sites with a very steep gradient. This implies that the conventional (and perhaps naive) view of gradual, melioristic evolution towards increasing complexity – which is incompatible with our observations – should be reconsidered. Note that panels below the main diagonal in Fig. 3 exhibit the typical phase-transition behavior of the state 3 objects. Clearly, the higher resolution sampling of the parameter space is of particular importance for measuring this gradient and relating it to the adopted evolutionary timescales.
In addition to an earlier study by Schulze-Makuch et al. (2011), a recent surge of works (Kashyap Jagadeesh et al. 2018, 2017; Saha et al. 2018; Kulkarni & Desai 2018; Rodríguez-Mozos & Moya 2017; Barnes et al. 2015) demonstrates classification possibilities for the discovered population of exoplanets according to their habitability. The primary motivation for these works is advancing the field of exo-life search via expected biosignatures. However, these works also offer a prospect for advancing our understanding of Fermi’s paradox. A detailed comparison of the relative abundance of objects in different states (such as the curves in Fig. 3) and habitability classification of exo-planets might further constrain the parameter space of possible evolutionary timescales.
5. Summary
We have presented the results of our study that used a simplified version of the spatial spreading of life in the Galaxy in order to achieve higher computational efficiency for the purpose of mapping the colonization vs. catastrophic timescales parameter space. The other relevant timescales for the life evolution (biological) are tentatively taken to be adequately represented by the Earth’s fossil record, as per the Copernican principle. The emerging shape of the number of highly evolved sites shows lower than average values for the greater part of the examined parameter space, indicating the dominance of catastrophism over colonization. This fits well into our current perception of exolife and as our results have demonstrated, indicates a possibility of a fine-tuning solution to Fermi’s paradox. However, further understanding and improvements of the present model are required. Among possibilities to be considered in the course of the future work, there are both “conservative” (better theoretical models of the habitable planets’ ages, and different averaging procedures) and “radical” ones (more different discrete sites, and a wider Poissonian distribution of the transition timescales, taking into account correlated artificial disasters like large-scale wars or pandemics). In any case, the present proof-of-concept study clearly shows that discrete models of this kind are capable of capturing some of the complexity of astrobiological evolution.
Acknowledgments
We thank an anonymous referee for an extensive and insightful review that has greatly improved the overall content of the paper. Fruitful discussions with Srđa Janković, Milan Stojanović, Anders Sandberg, and John Smart have enormously contributed to the ideas presented in this paper. The authors acknowledge financial support from the Ministry of Education, Science and Technological Development of the Republic of Serbia – VĐ through the project #ON176011 “Dynamics and kinematics of celestial bodies and systems”, BV and MMĆ through the project #ON176021 “Visible and invisible matter in nearby galaxies: theory and observations”. Numerical simulations were run on the PARADOX supercomputing facility at the Scientific Computing Laboratory of the Institute of Physics Belgrade as a part of the MALAHIT project, and on the Bibliotheca Alexandrina High-Performance Computing facility (in Alexandria, Egypt) within the VI-SEEM initiative project CAT-ICE. In this regard, the authors wish to express their special gratitude to Antun Balaž, Aleksandar Bogojević, Aleksandar Belić, Dušan Vudragović, and Petar Jovanović.
References
- Barnes, R., Meadows, V. S., & Evans, N. 2015, ApJ, 814, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Bezsudnov, I., & Snarskii, A. 2010, ArXiv e-prints [arXiv:1007.2774] [Google Scholar]
- Bjørk, R. 2007, Int. J. Astrobiol., 6, 89 [CrossRef] [Google Scholar]
- Chyba, C. F., & Hand, K. P. 2005, ARA&A, 43, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Ćirković, M. 2012, The Astrobiological Landscape: Philosophical Foundations of the Study of Cosmic Life, Cambridge Astrobiology (Cambridge: Cambridge University Press) [Google Scholar]
- Ćirković, M. M. 2018, The Great Silence: Science and Philosophy of Fermi’s Paradox (Oxford, UK: Oxford University Press) [Google Scholar]
- Ćirković, M. M., & Vukotić, B. 2008, Origins Life Evol. Biosphere, 38, 535 [NASA ADS] [CrossRef] [Google Scholar]
- Ćirković, M. M., Sandberg, A., & Bostrom, N. 2010, Int. J., 30, 1495 [Google Scholar]
- Cotta, C., & Morales, Á. 2009, J. Br. Interplanet. Soc., 62, 82 [NASA ADS] [Google Scholar]
- Crick, F. H., & Orgel, L. E. 1973, Icarus, 19, 341 [NASA ADS] [CrossRef] [Google Scholar]
- Dayal, P., Cockell, C., Rice, K., & Mazumdar, A. 2015, ApJ, 810, L2 [NASA ADS] [CrossRef] [Google Scholar]
- Dick, S. J. 2003, Int. J. Astrobiol., 2, 65 [CrossRef] [Google Scholar]
- Dodd, M. S., Papineau, D., Grenne, T., et al. 2017, Nature, 543, 60 [NASA ADS] [CrossRef] [Google Scholar]
- Đošović, V., Vukotić, B., & Ćirković, M. M. 2018, Pub. Astron. Obs. Belgrad., 98, 121 [NASA ADS] [Google Scholar]
- Ellis, J., & Schramm, D. N. 1995, Proc. Nat. Acad. Sci., 92, 235 [NASA ADS] [CrossRef] [Google Scholar]
- Epanechnikov, V. A. 1967, Theory of Probability & Its Applications, 14, 153 [CrossRef] [Google Scholar]
- Forgan, D., Dayal, P., Cockell, C., & Libeskind, N. 2017, Int. J. Astrobiol., 16, 60 [CrossRef] [Google Scholar]
- Fry, I. 2000, The Emergence of Life on Earth: A Historical and Scientific Overview (New Brunswick, NJ: Rutgers University Press) [Google Scholar]
- Galante, D., & Horvath, J. E. 2007, Int. J. Astrobiol., 6, 19 [CrossRef] [Google Scholar]
- Galera, E., Galanti, G. R., & Kinouchi, O. 2019, Int. J. Astrobiol., 18, in press, DOI: 10.1017/S1473550418000101 [Google Scholar]
- Gonzalez, G. 2005, Origins Life Evol. Biosphere, 35, 555 [NASA ADS] [CrossRef] [Google Scholar]
- Gordon, R., & Hoover, R. B. 2007, in Instruments, Methods, and Missions for Astrobiology X, Proc. SPIE, 6694, 669404 [CrossRef] [Google Scholar]
- Gowanlock, M. G. 2016, ApJ, 832, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Hanson, R. 1998, Burning the cosmic commons: evolutionary strategies for interstellar colonization, http://hanson.gmu.edu/filluniv.pdf, Last accessed September 15, 2018 [Google Scholar]
- Horner, J., & Jones, B. W. 2010, Int. J. Astrobiol., 9, 273 [CrossRef] [Google Scholar]
- Ilachinski, A. 2001, Cellular Automata: A Discrete Universe (Singapore: World Scientific) [CrossRef] [Google Scholar]
- Javaux, E. J., & Dehant, V. 2010, A&ARv, 18, 383 [NASA ADS] [CrossRef] [Google Scholar]
- John Cramer, J. 1986, Analog Science Fiction & Fact Magazine, 106, 124 [Google Scholar]
- Kashyap Jagadeesh, M., Gudennavar, S. B., Doshi, U., & Safonova, M. 2017, Ap&SS, 362, 146 [NASA ADS] [CrossRef] [Google Scholar]
- Kashyap Jagadeesh, M., Roszkowska, M., & Kaczmarek, Ł. 2018, Life Sci. Space Res., 19, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Kulkarni, S., & Desai, S. 2018, Open J. Astrophys., 1, 4 [CrossRef] [Google Scholar]
- Lineweaver, C. H. 2001, Icarus, 151, 307 [NASA ADS] [CrossRef] [Google Scholar]
- Lineweaver, C. H., & Chopra, A. 2012, Annu. Rev. Earth Planet. Sci., 40, 597 [NASA ADS] [CrossRef] [Google Scholar]
- Lingam, M. 2016, MNRAS, 455, 2792 [NASA ADS] [CrossRef] [Google Scholar]
- Maloof, A. C., Porter, S. M., Moore, J. L., et al. 2010, GSA Bulletin, 122, 1731 [CrossRef] [Google Scholar]
- Mcnichol, J. C., & Gordon, R. 2012, Genesis-In The Beginning (Springer), 591 [CrossRef] [Google Scholar]
- Newman, W. I., & Sagan, C. 1981, Icarus, 46, 293 [NASA ADS] [CrossRef] [Google Scholar]
- Rodríguez-Mozos, J. M., & Moya, A. 2017, MNRAS, 471, 4628 [NASA ADS] [CrossRef] [Google Scholar]
- Rummel, J. D. 2001, Proc. Nat. Acad. Sci., 98, 2128 [NASA ADS] [CrossRef] [Google Scholar]
- Sagan, C. 2000, Carl Sagan’s Cosmic Connection: An Extraterrestrial Perspective (Cambridge: Cambridge University Press) [Google Scholar]
- Saha, S., Basak, S., Safonova, M., et al. 2018, Astron. Comput., 23, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Saito, M., & Matsumoto, M. 2008, Monte Carlo and Quasi-Monte Carlo Methods 2006 (Berlin: Springer), 607 [CrossRef] [Google Scholar]
- Scalo, J., & Wheeler, J. C. 2002, ApJ, 566, 723 [NASA ADS] [CrossRef] [Google Scholar]
- Schulze-Makuch, D., Méndez, A., Fairén, A. G., et al. 2011, Astrobiology, 11, 1041 [NASA ADS] [CrossRef] [Google Scholar]
- Sleator, R. D., & Smith, N. 2017, Sci. Prog., 100, 187 [CrossRef] [Google Scholar]
- Stanway, E. R., Hoskin, M. J., Lane, M. A., et al. 2018, MNRAS, 475, 1829 [NASA ADS] [CrossRef] [Google Scholar]
- Starling, J., & Forgan, D. H. 2014, Int. J. Astrobiol., 13, 45 [CrossRef] [Google Scholar]
- Vukotić, B., & Ćirković, M. M. 2010, Publications de l’Observatoire Astronomique de Beograd, 90, 85 [NASA ADS] [Google Scholar]
- Vukotić, B., & Ćirković, M. M. 2012a, Origins Life Evol. Biosphere, 42, 347 [NASA ADS] [CrossRef] [Google Scholar]
- Vukotić, B., & Ćirković, M. M. 2012b, Publications de l’Observatoire Astronomique de Beograd, 91, 221 [NASA ADS] [Google Scholar]
- Vukotić, B., Steinhauser, D., Martinez-Aviles, G., et al. 2016, MNRAS, 459, 3512 [NASA ADS] [CrossRef] [Google Scholar]
- Wallis, M. K., & Wickramasinghe, N. C. 2004, MNRAS, 348, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Ward, P., & Brownlee, D. 2000, Rare Earth : Why Complex Life is Uncommon in the Universe (New York: Springer) [Google Scholar]
- Zackrisson, E., Calissendorff, P., González, J., et al. 2016, ApJ, 833, 214 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1. Modelled transitions with a symbolic scheme of states (we assume that a Mars-like planet could have been habitable for simple life in at least some epochs of its history). |
| In the text | |
 |
Fig. 2. Number of sites in state 3 as a function of timescale for catastrophism and colonization at the end of the simulated time span (10 Gyr). Axes are designated with decadic logarithm of the relevant timescale in years. The grey colour represents pixels with exactly zero number of sites in state 3, while the numbers values higher than zero are colour-coded as displayed. The mean value of the plotted matrix is 391.90 and is indicated with the black dash on the colour bar. |
| In the text | |
 |
Fig. 3. Number of cells in each state (colour-coded as listed in bottom right panel) as a function of time. Different plots means different initial conditions for colonization timescale (τcol) and catastrophism (τcat). The number of sites in each state after 10 Gyr is indicated at the top of each panel. |
| In the text | |
 |
Fig. 4. Similar plot as in Fig. 3, except that it shows the standard deviation of the number of cells in each state. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.