| Issue |
A&A
Volume 625, May 2019
|
|
|---|---|---|
| Article Number | A87 | |
| Number of page(s) | 12 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201833822 | |
| Published online | 17 May 2019 | |
The evolution of ultra-massive white dwarfs⋆
1
Facultad de Ciencias Astronómicas y Geofísicas, Universidad Nacional de La Plata, Paseo del Bosque s/n, 1900 La Plata, Argentina
e-mail: camisassa@fcaglp.unlp.edu.ar
2
Instituto de Astrofísica de La Plata, UNLP-CONICET, Paseo del Bosque s/n, 1900 La Plata, Argentina
3
Instituto de Ciencias Astronómicas, de la Tierra y del Espacio (CONICET-UNSJ), Av. España Sur 1512, J5402DSP San Juan, Argentina
4
Departament de Física Aplicada, Universitat Politècnica de Catalunya, c/Esteve Terrades 5, 08860 Castelldefels, Spain
5
Institute for Space Studies of Catalonia, c/Gran Capita 2–4, Edif. Nexus 201, 08034 Barcelona, Spain
Received:
10
July
2018
Accepted:
27
January
2019
Ultra-massive white dwarfs are powerful tools used to study various physical processes in the asymptotic giant branch (AGB), type Ia supernova explosions, and the theory of crystallization through white dwarf asteroseismology. Despite the interest in these white dwarfs, there are few evolutionary studies in the literature devoted to them. Here we present new ultra-massive white dwarf evolutionary sequences that constitute an improvement over previous ones. In these new sequences we take into account for the first time the process of phase separation expected during the crystallization stage of these white dwarfs by relying on the most up-to-date phase diagram of dense oxygen/neon mixtures. Realistic chemical profiles resulting from the full computation of progenitor evolution during the semidegenerate carbon burning along the super-AGB phase are also considered in our sequences. Outer boundary conditions for our evolving models are provided by detailed non-gray white dwarf model atmospheres for hydrogen and helium composition. We assessed the impact of all these improvements on the evolutionary properties of ultra-massive white dwarfs, providing updated evolutionary sequences for these stars. We conclude that crystallization is expected to affect the majority of the massive white dwarfs observed with effective temperatures below 40 000 K. Moreover, the calculation of the phase separation process induced by crystallization is necessary to accurately determine the cooling age and the mass-radius relation of massive white dwarfs. We also provide colors in the Gaia photometric bands for our H-rich white dwarf evolutionary sequences on the basis of new model atmospheres. Finally, these new white dwarf sequences provide a new theoretical frame to perform asteroseismological studies on the recently detected ultra-massive pulsating white dwarfs.
Key words: stars: evolution / stars: interiors / white dwarfs
The evolutionary sequences are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/625/A87
© ESO 2019
1. Introduction
White dwarf stars are the most common end point of stellar evolution. Indeed, more than 97% of all stars will eventually become white dwarfs. These old stellar remnants preserve information about the evolutionary history of their progenitors, providing a wealth of information about the physical evolutionary processes of stars, the star formation history, and the characteristics of various stellar populations. Furthermore, their structure and evolutionary properties are well understood (see Fontaine & Brassard 2008; Winget & Kepler 2008, and Althaus et al. 2010a for specific reviews) to the point that the white dwarf cooling times are currently considered one of the best age indicators for a wide variety of Galactic populations, including open and globular clusters (see Winget et al. 2009; García-Berro et al. 2010; Jeffery et al. 2011; Bono et al. 2013; Hansen et al. 2013, for some applications).
The mass distribution of white dwarfs exhibits a main peak at MWD ∼ 0.6 M⊙, and a smaller peak at the tail of the distribution around MWD ∼ 0.82 M⊙ (Kleinman et al. 2013). The existence of massive white dwarfs (MWD ≳ 0.8 M⊙) and ultra-massive white dwarfs (MWD ≳ 1.10 M⊙) has been revealed in several studies (Castanheira et al. 2010, 2013; Hermes et al. 2013; Kepler et al. 2016; Curd et al. 2017). Rebassa-Mansergas et al. (2015) report the existence of a distinctive high-mass excess in the mass function of hydrogen-rich white dwarfs near 1 M⊙.
A historic interest in the study of ultra-massive white dwarfs is related to our understanding of type Ia Supernovae. It is thought that type Ia Supernovae are formed via the explosion of an ultra-massive white dwarf or the merger of two white dwarfs. Also, massive white dwarfs can act as gravitational lenses. It has been proposed that massive faint white dwarfs can be responsible for microlensing events in the Large Magellanic Cloud.
The formation of an ultra-massive white dwarf is theoretically predicted as the end product of the isolated evolution of a massive intermediate-mass star with a mass larger than 6–9 M⊙, depending on metallicity and the treatment of convective boundaries. Once the helium in the core has been exhausted, these stars reach the super asymptotic giant branch (SAGB) with a partially degenerate carbon(C)-oxygen(O) core as their less massive siblings. However, in the case of SAGB stars their cores develop temperatures that are high enough to start carbon ignition under partially degenerate conditions. The violent carbon ignition leads to the formation of an oxygen-neon core, which is not hot enough to burn oxygen or neon (Ne) (Siess 2006) and is supported by the degenerate pressure of the electron gas. If the hydrogen-rich envelope is removed by winds before electron captures begin in the O-Ne core, an electron-capture supernova is avoided and the star leaves the SAGB to form a white dwarf. As a result, ultra-massive white dwarfs are born with cores composed mainly of 16O and 20Ne, with traces of 12C, 23Na, and 24Mg (Siess 2007). In addition, massive white dwarfs with C-O cores can be formed through binary evolution channels, namely the single-degenerate channel in which a white dwarf gains mass from a nondegenerate companion, and the double-degenerate channel involving the merger of two white dwarfs (Maoz et al. 2014). The study of the predicted surface properties and cooling times of ultra-massive CO- and ONe-core white dwarfs can help to assess the relevance of different channels in the formation of these stars.
During recent years, g(gravity)-mode pulsations have been detected in many massive and ultra-massive variable white dwarfs with hydrogen-rich atmospheres (DA), also called ZZ Ceti stars (Kanaan et al. 2005; Castanheira et al. 2010, 2013; Hermes et al. 2013; Curd et al. 2017). The ultra-massive ZZ Ceti star BPM 37093 (Kanaan et al. 1992, 2005) was the first object of this kind to be analyzed in detail. The existence of pulsating ultra-massive white dwarfs opens the possibility of carrying out asteroseismological analyses of heavy-weight ZZ Ceti stars that can provide information about their origin and internal structure through the comparison between the observed periods and the theoretical periods computed for appropriate theoretical models. In particular, one of the major interests in the study of pulsating ultra-massive DA white dwarfs lies in the fact that these stars are expected to have a well-developed crystallized core. The occurrence of crystallization in the degenerate core of white dwarfs, resulting from Coulomb interactions in very dense plasmas, was first suggested by several authors about 60 years ago (see Kirzhnits 1960; Abrikosov 1961; van Horn 1968 for details, and the more recent works by Montgomery & Winget 1999; Metcalfe et al. 2004; Córsico et al. 2005; Brassard & Fontaine 2005 for discussions). However, this theoretical prediction was not observationally demonstrated until the recent studies of Winget et al. (2009) and García-Berro et al. (2010), who inferred the existence of crystallized white dwarfs from the study of the white dwarf luminosity function of stellar clusters. Since ultra-massive ZZ Ceti stars are expected to have a partially or totally crystallized core, these stars are unique objects that can be used to detect the presence of crystallization. Thus, asteroseismology of ultra-massive DA white dwarfs is expected to contribute to our understanding of the Coulomb interactions in dense plasmas. The first attempt to infer the existence of crystallization in an ultra-massive white dwarf star from the analysis of its pulsation pattern was carried out by Metcalfe et al. (2004) in the case of BPM 37093 (Kanaan et al. 2005), but the results were inconclusive (Brassard & Fontaine 2005).
Asteroseismological applications of ultra-massive DA white dwarfs require the development of detailed evolutionary models for these stars, taking into account all the physical processes responsible for interior abundance changes as evolution proceeds. The first attempts to model these stars by considering the evolutionary history of progenitor stars were the studies by García-Berro et al. (1997a) and Althaus et al. (2007). These studies, however, adopted several simplifications which should be assessed. To begin with, they consider a core chemical profile composed mainly of 16O and 20Ne, implanted to white dwarf models with different stellar masses. A main assumption made in Althaus et al. (2007; hereafter A07) is that the same fixed chemical profile during the entire evolution is assumed for all of their models. Also, phase separation during crystallization is an important missing physical ingredient in these studies. When crystallization occurs, energy is released in two different ways. First, as in any crystallization process, latent heat energy is released. Second, a phase separation of the elements occurs upon crystallization, releasing gravitational energy (Isern et al. 1997) and lengthening the cooling times of white dwarfs. This process of phase separation has been neglected in all the studies of ultra-massive white dwarfs. Finally, progress in the treatment of conductive opacities and model atmospheres has been made in recent years, and should be taken into account in new attempts to improve our knowledge of these stars.
The aim of this paper is precisely to upgrade these old white dwarf evolutionary models by taking into account the above-mentioned considerations. We present new evolutionary sequences for ultra-massive white dwarfs, appropriate for accurate white dwarf cosmochronology of old stellar systems and for precise asteroseismology of these white dwarfs. We compute four hydrogen-rich and four hydrogen-deficient white dwarf evolutionary sequences. The initial chemical profile of each white dwarf model is consistent with predictions of the progenitor evolution with stellar masses in the range 9.0 ≤ MZAMS/M⊙ ≤ 10.5 calculated in Siess (2010). This chemical structure is the result of the full evolutionary calculations starting at the zero age main sequence (ZAMS), and evolving through the core hydrogen burning, core helium burning, and the SAGB phase, including the entire thermally pulsing phase. An accurate nuclear network has been used for each evolutionary phase. Thus, a realistic O-Ne inner profile is considered for each white dwarf mass, and realistic chemical profiles and intershell masses built up during the SAGB are also taken into account. In our study the energy released during the crystallization process and the ensuing core chemical redistribution were considered by following the phase diagram of Medin & Cumming (2010) suitable for 16O and 20Ne plasmas1. We also provide accurate magnitudes and colors for our hydrogen-rich models in the filters used by the spacial mission Gaia: G, GBP, and GRP.
To the best of our knowledge, this is the first set of fully evolutionary calculations of ultra-massive white dwarfs including realistic initial chemical profiles for each white dwarf mass, an updated microphysics, and the effects of the phase separation process duration crystallization2. This paper is organized as follows. In Sect. 2 we briefly describe our numerical tools and the main ingredients of the evolutionary sequences, while in Sect. 3 we present in detail our evolutionary results and compare them with previous works. Finally, in Sect. 4 we summarize the main findings of the paper, and we elaborate on our conclusions.
2. Numerical setup and input physics
The white dwarf evolutionary sequences presented in this work were calculated using the LPCODE stellar evolutionary code (see Althaus et al. 2005, 2012, for details). This code has been well tested and calibrated and has been amply used in the study of different aspects of low-mass star evolution (see García-Berro et al. 2010; Althaus et al. 2010b; Renedo et al. 2010, and references therein). More recently, the code has been used to generate a new grid of models for post-AGB stars (Miller Bertolami 2016) and also new evolutionary sequences for hydrogen-deficient white dwarfs (Camisassa et al. 2017). In addition, the LPCODE has been tested against another white dwarf evolutionary code, and the uncertainties in the white dwarf cooling ages that result from the different numerical implementations of the stellar evolution equations were found to be below 2% (Salaris et al. 2013).
For the white dwarf regime, the main input physics of LPCODE includes the following ingredients. Convection is treated within the standard mixing length formulation, as given by the ML2 parameterization (Tassoul et al. 1990). Radiative and conductive opacities are from OPAL (Iglesias & Rogers 1996) and from Cassisi et al. (2007), respectively. For the low-temperature regime, molecular radiative opacities with varying carbon-to-oxygen ratios are used. To this end, the low-temperature opacities computed by Ferguson et al. (2005) as presented by Weiss & Ferguson (2009) are adopted. The equation of state for the low-density regime is taken from Magni & Mazzitelli (1979), whereas for the high-density regime, we employ the equation of state of Segretain et al. (1994), which includes all the important contributions for both the solid and liquid phases. We considered neutrino emission for pair, photo, and bremsstrahlung processes using the rates of Itoh et al. (1996), while for plasma processes we follow the treatment presented in Haft et al. (1994). Outer boundary conditions for both H-rich and H-deficient evolving models are provided by non-gray model atmospheres (see Rohrmann et al. 2012; Camisassa et al. 2017; Rohrmann 2018 for references). The impact of the atmosphere treatment on the cooling times becomes relevant for effective temperatures lower than 10 000 K. LPCODE considers a detailed treatment of element diffusion, including gravitational settling, and chemical and thermal diffusion. As we will see, element diffusion is a key ingredient in shaping the chemical profile of evolving ultra-massive white dwarfs, even in layers near the core.
2.1. Treatment of crystallization
A main issue in the modeling of ultra-massive white dwarfs is the treatment of crystallization. As temperature decreases in the interior of white dwarfs, the Coulomb interaction energy becomes increasingly important, until at some point they widely exceed the thermal motions and the ions begin to freeze into a regular lattice structure. Since the crystallization temperature of pure 20Ne is larger than the crystallization temperature of 16O, this crystallization process induces a phase separation. In a mixture of 20Ne and 16O the crystallized plasma will be enriched in 20Ne, and consequently 20Ne will decrease in the remaining liquid plasma. This process releases gravitational energy, thus constituting a new energy source that will impact the cooling times.
We used the most up-to-date phase diagram of dense O-Ne mixtures appropriate for massive white dwarf interiors (Medin & Cumming 2010). This phase diagram, shown in Fig. 1, yields the temperature at which crystallization occurs, as well as the abundance change at a given point in the solid phase during the phase transition. The parameter Γ is the Coulomb coupling parameter, defined as 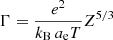 , where
, where 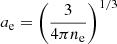 is the mean electron spacing. The value of Γcrit is set to 178.6, the crystallization value of a mono-component plasma; ΓO is the value of Γ of 16O at which crystallization of the mixture occurs, and is related to the temperature and the density through the relation
is the mean electron spacing. The value of Γcrit is set to 178.6, the crystallization value of a mono-component plasma; ΓO is the value of Γ of 16O at which crystallization of the mixture occurs, and is related to the temperature and the density through the relation 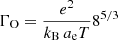 . For a given mass fraction of 20Ne, the solid red line in Fig. 1 gives us ΓO, and consequently the temperature of crystallization is obtained. Once we obtain this temperature, it can be related to the Γ of the mixture by replacing T in the formula
. For a given mass fraction of 20Ne, the solid red line in Fig. 1 gives us ΓO, and consequently the temperature of crystallization is obtained. Once we obtain this temperature, it can be related to the Γ of the mixture by replacing T in the formula 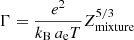 , where Zmixture is the mean ionic charge of the mixture. The Γ obtained using this procedure is larger than the value of Γ commonly used in the white dwarf evolutionary calculations, which is artificially set to 180. For a given abundance of 20Ne in the liquid phase, the solid red line predicts Γcrit/ΓO, and the corresponding value of Γcrit/ΓO at the dashed black line predicts the 20Ne abundance in the solid phase, which is slightly larger than the initial 20Ne abundance. The final result of the crystallization process is that the inner regions of the star are enriched in 20Ne, and the outer regions are enriched in 16O.
, where Zmixture is the mean ionic charge of the mixture. The Γ obtained using this procedure is larger than the value of Γ commonly used in the white dwarf evolutionary calculations, which is artificially set to 180. For a given abundance of 20Ne in the liquid phase, the solid red line predicts Γcrit/ΓO, and the corresponding value of Γcrit/ΓO at the dashed black line predicts the 20Ne abundance in the solid phase, which is slightly larger than the initial 20Ne abundance. The final result of the crystallization process is that the inner regions of the star are enriched in 20Ne, and the outer regions are enriched in 16O.
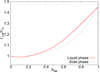 |
Fig. 1. Phase diagram of crystallization for a 16O/20Ne mixture (Medin & Cumming 2010). XNe is the 20Ne abundance. Γcrit is set to 178.6. ΓO is given by ΓO = (e2/kB aeT)85/3 (see text for details). |
The energetics resulting from crystallization processes has been self-consistently and locally coupled to the full set of equations of stellar evolution (see Althaus et al. 2010c, for details of the implementation). The local change of chemical abundance resulting from the process of phase separation at crystallization leads to a release of energy (in addition to the latent heat). The inclusion of this energy in LPCODE is similar to that described in Althaus et al. (2010c), but adapted to the mixture of 16O and 20Ne characterizing the core of our ultra-massive white dwarf models. At each evolutionary time step, we calculate the change in chemical composition resulting from phase separation using the phase diagram of Medin & Cumming (2010) for an oxygen-neon mixture. Then we evaluate the net energy released by this process during the time step. This energy is added to the latent heat contribution, which is considered to be 0.77 kBT per ion. The total energy is distributed over a small mass range around the crystallization front. This local energy contribution is added to the luminosity equation (see Althaus et al. 2010c, for details).
The increase in 20Ne abundance in the solid core as a result of crystallization leads to a Rayleigh-Taylor instability and an ensuing mixing process at the region above the crystallized core, which in turn induce the oxygen enrichment in the overlying liquid mantle (Isern et al. 1997). Thus, those layers that are crystallizing are energy sources, and the overlying unstable layers will be sinks of energy.
2.2. Initial models
As we have mentioned, an improvement of the present calculations over those published in A07 is the adoption of detailed chemical profiles that are based on the computation of all the previous evolutionary stages of their progenitor stars. This is true for both the O-Ne core and the surrounding envelope. In particular, the full computation of previous evolutionary stages allows us to assess the mass of the helium-rich mantle and the hydrogen-helium transition, which are of particular interest for the asteroseismology of ultra-massive white dwarfs. Specifically, the chemical composition of our models is the result of the entire progenitor evolution calculated in Siess (2007, 2010). These sequences correspond to the complete single evolution from the ZAMS to the thermally pulsating SAGB phase of initially MZAMS = 9, 9.5, 10, and 10.5 M⊙ sequences with an initial metallicity of Z = 0.02. Particular care was taken by Siess (2007, 2010) to precisely follow the propagation of the carbon burning flame where most carbon is burnt (Siess 2006). This is of special interest for the final oxygen and neon abundances in the white dwarf core. In addition, Siess (2010) computed in detail the evolution during the thermally pulsing SAGB phase where the outer chemical profiles and the total helium content of the final stellar remnant are determined. No extra mixing was included at any convective boundary at any evolutionary stage. The absence of core overshooting during core hydrogen- and helium-burning stages implies that, for a given final remnant mass (MWD), initial masses (MZAMS) are an upper limit of the expected progenitor masses. Considering moderate overshooting during core helium burning lowers the mass range of SAGB stars in 2 M⊙ (Siess 2007; Gil-Pons et al. 2007). It is worth noting that the initial final mass relation is poorly constrained from observations (Salaris et al. 2009) and it is highly uncertain in stellar evolution models. On the other hand, considering overshooting during the thermally pulsing SAGB, would induce third dredge-up episodes, altering the carbon and nitrogen abundances in the envelope. Finally, in this work we have not explored the impact on white dwarf cooling that could be expected from changes in the core chemical structure resulting from the consideration of extra-mixing episodes during the semi-degenerate carbon burning.
The stellar masses of our white dwarf sequences are MWD = 1.10 M⊙, 1.16 M⊙, 1.23 M⊙, and 1.29 M⊙. Each evolutionary sequence was computed from the beginning of the cooling track at high luminosities down to the development of the full Debye cooling at very low surface luminosities, log(L⋆/L⊙)= − 5.5. The progenitor evolution through the thermally pulsing SAGB provides us with realistic values of the total helium content, which is relevant for the accurate computation of cooling times at low luminosities. In particular, different helium masses lead to different cooling times. The helium mass of our 1.10 M⊙, 1.16 M⊙, 1.23 M⊙, and 1.29 M⊙ models are 3.24 × 10−4 M⊙, 1.82 × 10−4 M⊙, 0.78 × 10−4 M⊙, and 0.21 × 10−4 M⊙, respectively. By contrast, the total mass of the hydrogen envelope left by prior evolution is quite uncertain, since it depends on the occurrence of carbon enrichment on the thermally pulsing AGB phase (see Althaus et al. 2015), which in turn depends on the amount of overshooting and mass loss, and on the occurrence of late thermal pulses. For this paper, we have adopted the maximum expected hydrogen envelope of about ∼10−6 M⊙ for ultra-massive white dwarfs. Higher values of the total hydrogen mass would lead to unstable nuclear burning and thermonuclear flashes on the white dwarf cooling track.
Figure 2 illustrates the chemical profiles resulting from the progenitor evolution of our four hydrogen-rich white dwarf sequences3. The core composition is ∼55% 16O and ∼30% 20Ne, with minor traces of 22Ne, 23Na, and 24Mg. At some layers of the models, the mean molecular weight is higher than in the deeper layers, leading to Rayleigh-Taylor instabilities. Consequently, these profiles are expected to undergo a rehomogenization process on a timescale shorter than the evolutionary timescale. Thus, we have simulated the rehomogenization process assuming it to be instantaneous. The impact of this mixing process on the abundance distribution in the white dwarf core is apparent (see Fig. 3). Clearly, rehomogenization mixes the abundances of all elements at some layers of the core, erasing preexisting peaks in the abundances.
 |
Fig. 2. Initial chemical profiles before Rayleigh-Taylor rehomogenization corresponding to our four hydrogen-rich white dwarf models, as given by the nuclear history of the progenitor stars. |
 |
Fig. 3. Initial chemical profiles of our four hydrogen-rich white dwarf models once Rayleigh-Taylor rehomogenization has occurred. |
3. Evolutionary results
We present in Fig. 4 a global view of the main phases of the evolution of an ultra-massive hydrogen-rich white dwarf model during the cooling phase. In this figure, the temporal evolution of the different luminosity contributions is displayed for our 1.16 M⊙ hydrogen-rich white dwarf sequence. The cooling time is defined as zero at the beginning of the white dwarf cooling phase when the star reaches the maximum effective temperature. During the entire white dwarf evolution, the release of gravothermal energy is the dominant energy source of the star. At early stages, neutrino emission constitutes an important energy sink. In fact, during the first million years of cooling, the energy lost by neutrino emission is of about the same order of magnitude as the gravothermal energy release, remaining higher than the star luminosity until the cooling time reaches about log(t) ∼ 7. As the white dwarf cools, the temperature of the degenerate core decreases, thus neutrino emission ceases, and consequently the neutrino luminosity abruptly drops. It is during these stages that element diffusion strongly modifies the internal chemical profiles. The resulting chemical stratification is discussed below. At log(t) ∼ 8.3 crystallization sets in at the center of the white dwarf. This results in the release of latent heat and gravitational energy due to oxygen-neon phase separation. We note that as a consequence of this energy release, during the crystallization phase the surface luminosity is higher than the gravothermal luminosity. This phase lasts for 2.5 × 109 years. Finally, at log(t) ∼ 9, the temperature of the crystallized core drops below the Debye temperature, and consequently, the heat capacity decreases. Thus, the white dwarf enters the so-called Debye cooling phase, characterized by rapid cooling.
 |
Fig. 4. Temporal evolution of surface luminosity (double dotted line) and different luminosity contributions: neutrino luminosity (dashed line), gravothermal luminosity (dotted line), latent heat (dot-dot-dashed line), and phase separation energy (solid line). The arrows indicate the main physical processes responsible for the evolution at different moments. |
The cooling times for all of our white dwarf sequences are displayed in Fig. 5. These cooling times are also listed in Table 1 at some selected stellar luminosities. Our hydrogen-deficient sequences have been calculated by considering recent advancement in the treatment of energy transfer in dense helium atmospheres (see Camisassa et al. 2017; Rohrmann 2018, for details). As shown in Camisassa et al. (2017), detailed non-gray model atmospheres are needed to derive realistic cooling ages of cool, helium-rich white dwarfs. At intermediate luminosities, hydrogen-deficient white dwarfs evolve a little more slowly than their hydrogen-rich counterparts. This result is in line with previous studies of hydrogen-deficient white dwarfs (Camisassa et al. 2017), and the reason for this is that convective coupling (and the associated release of internal energy) occurs at higher luminosities in hydrogen-deficient white dwarfs, with the consequent lengthening of cooling times at those luminosities. By contrast, at low luminosities hydrogen-deficient white dwarfs evolve markedly faster than hydrogen-rich white dwarfs; at these stages the thermal energy content of the hydrogen-deficient white dwarfs is lower, and more importantly in these white dwarfs the outer layers are more transparent to radiation. We note in this sense that the 1.10 M⊙ hydrogen-rich sequence needs 8.2 Gyr to reach the lowest luminosities, while the hydrogen-deficient sequence of the same mass evolves in only 4.6 Gyr to the same luminosities. We also note that the cooling behavior of the stellar mass is different, particularly the fast cooling of the 1.29 M⊙ hydrogen-rich sequence, our most massive sequence, which reaches log(L⋆/L⊙)= − 5 in only 3.6 Gyr, which is even shorter (2.4 Gyr) in the case of the hydrogen-deficient counterpart. These short cooling times that characterize the most massive sequences reflect that, at these stages, matter in most of the white dwarf star has entered the Debye regime, with the consequent strong reduction in the specific heat of ions (see Althaus et al. 2010a, for details).
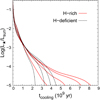 |
Fig. 5. Solid (dashed) lines indicate the cooling times for our hydrogen-rich (deficient) white dwarf sequences. At low luminosities and from left to right, stellar masses of both set of sequences are 1.29 M⊙, 1.23 M⊙, 1.16 M⊙, and 1.10 M⊙. |
Cooling times of our hydrogen-rich (HR) and hydrogen-deficient (HD) white dwarf sequences at selected luminosities.
All our hydrogen-deficient white dwarf sequences experience carbon enrichment in the outer layers as a result of convective mixing. The outer convective zone grows inward and when the luminosity of the star has decreased to log(L⋆/L⊙) ∼ − 2.5, it penetrates into deeper layers where heavy elements such as carbon and oxygen are abundant. Consequently, convective mixing dredges up these heavy elements, and the surface chemical composition changes. In particular, the surface layers are predominantly enriched in carbon. These results are in line with the predictions of Camisassa et al. (2017) for hydrogen-deficient white dwarfs of intermediate mass.
The evolution of our ultra-massive white dwarf sequences in the plane log(g) − Teff is depicted in Fig. 6 together with observational expectations taken from Mukadam et al. (2004), Nitta et al. (2016), Gianninas et al. (2011), Kleinman et al. (2013), Bours et al. (2015), Kepler et al. (2016) and Curd et al. (2017). In addition, isochrones of 0.1, 0.5, 1, 2, and 5 Gyr connecting the curves are shown. For these white dwarfs, we estimate from our sequences the stellar mass and cooling age (we select those whose surface gravities are greater than 8.8). Results are shown in Table 2. We note that for most of the observed white dwarfs, the resulting cooling age is in the range 1−4 Gyr, and many of them have stellar masses above 1.25 M⊙. We also note the change of slope of the isochrones in Fig. 6, which reflects the well-known dependence of cooling times on the mass of the white dwarf: at early stages, evolution proceeds more slowly in more massive white dwarfs, while the opposite trend is found at advanced stages.
 |
Fig. 6. Hydrogen-rich sequences in the plane log(g)−Teff. Blue solid lines display isochrones of 0.1, 0.5, 1, 2, and 5 Gyr. Crosses indicate the location of ultra-massive white dwarfs from Mukadam et al. (2004), Nitta et al. (2016), Gianninas et al. (2011), Kleinman et al. (2013), Bours et al. (2015), Kepler et al. (2016), Curd et al. (2017). |
Stellar mass (solar mass) and cooling ages (Gyr) as predicted by our sequences under the assumption that they harbor O-Ne cores for selected ultra-massive white dwarfs in the literature.
In Fig. 7 we display our hydrogen-rich sequences in the plane log(g) − Teff together with observational expectations for pulsating massive white dwarfs taken from Mukadam et al. (2004), Hermes et al. (2013), Curd et al. (2017) and Nitta et al. (2016). We also show 0, 20, 40, 60, 80, 90, 95, and 99 % of the crystallized mass of the star. We note that all of the observed pulsating white dwarfs with masses higher than 1.1 M⊙ fall in the region where more than 80% of their mass is expected to be crystallized. It is expected, as we will discuss in a forthcoming paper, that the crystallization process affects the pulsation properties of massive ZZ Ceti stars, as has also been shown by Montgomery & Winget (1999), Córsico et al. (2004, 2005) and Brassard & Fontaine (2005).
 |
Fig. 7. Hydrogen-rich sequences in the plane log(g) − Teff. Blue solid lines indicate 0, 20, 40, 60, 80, 90, 95 and 99% of crystallized mass. The symbols with error bars indicate the location of the known pulsating ultra-massive DA white dwarfs (Mukadam et al. 2004; Hermes et al. 2013; Curd et al. 2017; Nitta et al. 2016). |
The effective temperature at various percentages of crystallized mass is also listed in Table 3. We note that at the onset of crystallization the highest mass sequences exhibit a marked increase in their surface gravities. This behavior is a consequence of the change in the chemical abundances of 16O and 20Ne during the crystallization. As the abundance of 20Ne grows in the inner regions of the white dwarf, its radius decreases, and consequently its surface gravity increases. Crystallization sets in at similar luminosities and effective temperatures in a hydrogen-deficient as in a hydrogen-rich white dwarf with the same mass. Hydrogen-deficient cooling sequences are not shown in this figure since they exhibit a similar behavior, but their surface gravities are slightly higher, since their radius are relatively small.
Percentages of crystallized mass of our hydrogen-rich sequences and effective temperature at which they occur.
Element diffusion profoundly alters the inner abundance distribution from the early cooling stages of our massive white dwarf models. This is borne out by Figs. 8 and 9, which display the abundance distribution in the whole star at three selected effective temperatures for the 1.10 and 1.29 M⊙ hydrogen-rich white dwarf models, respectively. As a result of gravitational settling, all heavy elements are depleted from the outer layers. We note that initial chemical discontinuities are strongly smoothed out. But more importantly, the initial helium and carbon distribution in the deep envelope are markedly changed, particularly in the most massive models, where the initial pure helium buffer has almost vanished when evolution has reached low effective temperatures. This is quite different from the situation encountered in white dwarfs of intermediate mass. These changes in the helium and carbon profiles affect the radiative opacity in the envelope and thus the cooling times at late stages.
 |
Fig. 8. Inner abundance distribution for 1.10 M⊙ hydrogen-rich models at three selected effective temperatures, as indicated. |
The other physical process that changes the core chemical distribution during white dwarf evolution is, as we mentioned, phase separation during crystallization. The imprints of phase separation on the core chemical composition can be appreciated in the bottom panels of Figs. 8 and 9, and more clearly in Fig. 10, which illustrates the change in the abundances of 20Ne and 16O in a 1.16 M⊙ model shortly after the occurrence of crystallization (top panel) and by the time a large portion of the star has crystallized (bottom panel). The chemical abundances of 20Ne and 16O right before the crystallization sets in are plotted with thick dashed lines. For this stellar mass, crystallization starts at the center of the star at log(L⋆/L⊙) ∼ − 1.8. In the top panel (the crystallization front is at log(Mr/M⋆) ∼ − 0.4) the initial 20Ne and 16O abundances have been strongly changed by the process of phase separation and the induced mixing in the fluid layers above the core, which extends upward to log(Mr/M⋆) ∼ − 1. Other elements apart from 16O and 22Ne are not taken into account in the phase separation process, and the slight change shown in their abundances is due to element diffusion alone.
 |
Fig. 10. Change in the chemical profiles of our 1.16 M⊙ hydrogen-rich white dwarf model induced by the phase separation process during crystallization. Top (bottom) panel: chemical profile at log(Teff)=4.26(3.94). For comparison, the abundances of 16O and 20Ne right before phase separation are also plotted with thick lines in both panels. |
To properly assess the phase separation process during crystallization, it should be necessary to consider a five-component crystallizing plasma composed in our case of 12C, 16O, 20Ne,23Na, and 24Mg, which are the most abundant elements in the white dwarf core (see Fig. 3). A five-component phase diagram of this kind is not available in the literature. However, we have been provided with the final abundances in the solid phase in the center of the 1.10 M⊙ white dwarf model, considering a given five-component composition4. The abundances of 12C, 16O, 20Ne,23Na, and 24Mg at the center of this model right before crystallization occurs are listed in Table 4, together with the final abundances in the solid phase predicted by the five-component calculations, and those predicted by the phase diagram for the 16O-20Ne mixture shown in Fig. 1. The abundances of 16O and 20Ne are noticeably altered by crystallization regardless of the treatment considered. However, considering a two-component phase diagram results in a stronger phase separation of 16O and 20Ne. Nevertheless, in this treatment the abundances of trace elements 12C, 23Na, and 24Mg are not altered by the crystallization process. The sum of the abundances of these trace elements is lower than 15% in the core of all our ultra-massive white dwarf models and we do not expect this to alter the evolutionary timescales substantially. To properly assess the effects of considering a five-component phase diagram on the cooling times of white dwarfs it is necessary to calculate the evolution of the white dwarf model through the entire crystallization process, for which we would require the full phase diagram, but they were not available at the time of publication.
The phase separation process of 20Ne and 16O releases appreciable energy (see Fig. 4) that impacts the white dwarf cooling times. This can be seen in Fig. 11, which shows the cooling times for our 1.22 M⊙ hydrogen-rich sequence (upper panel) when crystallization is neglected (double-dotted line), when only latent heat is considered during crystallization (dotted line), and when both latent heat and energy from phase separation are considered during crystallization (solid line). Clearly, the energy resulting from crystallization, in particular the release of latent heat, increases substantially the cooling times of the ultra-massive white dwarfs. The inclusion of energy from phase separation leads to an additional delay in the cooling times (admittedly less than the delay caused by latent heat) at intermediate luminosities. However, below log(L⋆/L⊙) ∼ − 3.6 when most of the star has crystallized, phase separation accelerates the cooling times. At these stages, no more energy is delivered by phase separation, but the changes in the chemical profile induced by phase separation have strongly altered both the structure and thermal properties of the cool white dwarfs, impacting their rate of cooling. We note in this sense the change in the radius of the white dwarf that results from the inclusion of phase separation (bottom panel of Fig. 11). In fact, the star radius becomes smaller due to the increase in neon in the core during crystallization. As we mentioned, this explains the increase in the surface gravity of our sequences in the case of phase separation is considered (see Figs. 6 and 7).
 |
Fig. 11. Top panel: cooling times of our 1.22 M⊙ hydrogen-rich sequence when crystallization is neglected (double dotted line), when only latent heat is considered during crystallization (dotted line), and when both latent heat and energy from phase separation are considered during crystallization (solid line). Bottom panel: white dwarf radius in terms of the cooling time for these evolutionary tracks. |
The present evolutionary sequences of ultra-massive white dwarfs constitute an improvement over those presented in A07. The comparison between the evolutionary sequences of both studies is presented in Fig. 12 for the 1.10 M⊙, 1.16 M⊙, and 1.23 M⊙ hydrogen-rich sequences. There are appreciable differences in the cooling times between the two sets of sequences. In particular, the present calculations predict shorter ages at intermediate luminosities, but this trend is reversed at very low surface luminosities where our new sequences evolve much more slowly than in A07.
 |
Fig. 12. Cooling times of our hydrogen-rich white dwarf sequences with 1.10 M⊙, 1.16 M⊙, and 1.23 M⊙ (thick lines) compared with the cooling sequences of A07 of similar masses (thin lines). |
To close the paper, we attempt to trace the origin of these differences. We begin by examining the impact of the new chemical profiles compared with that used in A07 (as illustrated in Fig. 4 of Córsico et al. 2004), which is the same used for all white dwarf sequences in A07. To this end, we have computed two artificial white dwarf sequences by neglecting phase separation during crystallization. A comparison is made in Fig. 13, which shows the cooling times of a 1.16 M⊙ hydrogen-rich white dwarf model resulting from the use of the chemical profile considered in A07 (solid line) and the chemical profile employed in the current study (dotted line). The use of new chemical profiles employed in the present study (Siess 2010) predicts longer cooling times than the use of the chemical profiles of García-Berro et al. (1997b) considered in A07. This is not only due to the different core chemical stratification in both cases, but also to the different predictions for the helium buffer mass expected in the white dwarf envelopes, which affects the cooling rate of cool white dwarfs. In this sense, the full computation of the evolution of progenitor stars along the thermally pulsing SAGB constitutes an essential aspect that cannot be overlooked in any study of the cooling of massive white dwarfs.
 |
Fig. 13. Cooling times of 1.16 M⊙ hydrogen-rich white dwarf models without phase separation resulting from the use of different chemical profiles. The solid red line corresponds to the cooling sequence using our current stellar evolutionary code but implanting the chemical profile considered in A07. The black dotted line corresponds to the cooling sequence calculated using our new chemical profile (plotted in the top right panel of Fig. 3). |
Improvements in the microphysics considered in the computation of our new sequences also impact markedly the cooling times; this is particularly true regarding the treatment of conductive opacities and the release of latent heat during crystallization. Specifically, in the present sequences we make use of the conductive opacity given in Cassisi et al. (2007), in contrast to A07 where the older conductive opacities of Itoh et al. (1994) were employed. The resulting impact on the cooling time becomes apparent in Fig. 14. Here we compare the cooling times for 1.16 M⊙ white dwarf models having the same chemical composition as in A07, but adopting different microphysics. A close inspection of this figure reveals that the improvement in the microphysics considered in our current version of LPCODE compared with that used in A07, particularly the conductive opacity at intermediate luminosity and the treatment of latent heat during the crystallization phase at lower luminosities, lead to shorter cooling times. When we use the old microphysics (and the same chemical profile) we recover the results of A07.
 |
Fig. 14. Cooling times of 1.16 M⊙ hydrogen-rich white dwarf models without phase separation and considering the same chemical profiles of A07, but adopting different microphysics. The cooling sequence of A07, which is based on an old treatment of conductive opacity and latent heat, is shown as a green dotted line. The red solid line shows the cooling times calculated using our current numerical code. The dashed line shows the prediction given by our current numerical code, but with old microphysics, i.e., the same conductive opacities and treatment of latent heat as considered in A07. Left panel: amplifies the early stages of the white dwarf stage. Right panel: rest of the white dwarf cooling track. |
We conclude from Figs. 13 and 14 that the inclusion of detailed chemical profiles appropriate for massive white dwarfs resulting from SAGB progenitors and improvements in the microphysics results in evolutionary sequences for these white dwarfs much more realistic than those presented in A07. These improvements together with the consideration of the effects of phase separation of 20Ne and 16O during crystallization yield accurate cooling times for ultra-massive white dwarfs.
Finally, we present our ultra-massive white dwarf cooling tracks in Gaia photometry bands: G, GBP, and GRP. These magnitudes have been obtained using detailed model atmospheres for H-composition described in Rohrmann et al. (2012). The cooling tracks are plotted in the color-magnitude diagram in Fig. 15, together with the local sample of white dwarfs within 100 pc from our sun of Jiménez-Esteban et al. (2018) in the color range −0.52 < (GBP − GRP)< 0.80. The onset of crystallization in our cooling sequences is indicated with filled squares. Crystallization occurs at approximately the same magnitude, G + 5 + 5log(π) ∼ 12. The moment when convective coupling occurs in each white dwarf sequence is also indicated by filled triangles. Clearly, our ultra-massive white dwarf cooling tracks fall below the vast majority of the white dwarf sample. The reason for this is the mass distribution of the white dwarf sample, which exhibits a sharp peak around 0.6 M⊙ (Tremblay et al. 2019). Thus, the vast majority of white dwarfs will be characterized by higher luminosities than those present in our ultra-massive white dwarfs. However, a detailed analysis of this color-magnitude diagram is beyond the scope of the present paper and we simply present white dwarf colors for our ultra-massive white dwarfs, which are available for downloading.
 |
Fig. 15. H-rich white dwarf cooling sequences in the color-magnitude diagram in Gaia bands, together with the sample of white dwarfs within 100 pc, obtained by Jiménez-Esteban et al. (2018). The filled squares indicate the moment when crystallization begins in each white dwarf cooling sequence and the filled triangles indicate the moment when convective coupling occurs. |
4. Summary and conclusions
In this paper we studied the evolutionary properties of ultra-massive white dwarfs with 16O and 20Ne cores. For this purpose, we calculated hydrogen-rich and hydrogen-deficient white dwarf cooling sequences of 1.10, 1.16, 1.23, and 1.29 M⊙, resulting from solar metallicity progenitors with the help of the LPCODE evolutionary code. These cooling sequences are appropriate for the study of the massive white dwarf populations in the solar neighborhood resulting from the single evolution of progenitor stars. In our study we considered initial chemical profiles for each white dwarf model consistent with predictions of the progenitor evolution with stellar masses in the range 9.0 ≤ MZAMS/M⊙ ≤ 10.5, as calculated in Siess (2010). These chemical profiles are the result of the computation of full evolutionary sequences from the ZAMS through core hydrogen burning, core helium burning, and semidegenerate carbon burning during the thermally pulsing SAGB phase. Hence, not only is a realistic O-Ne inner profile considered for each white dwarf mass, but realistic chemical profiles and intershell masses built up during the SAGB are also taken into account. In particular, the evolution through the entire SAGB phase provides us with realistic values of the total helium content necessary to compute realistic cooling times at low luminosities. We have calculated both hydrogen-rich and hydrogen-deficient white dwarf evolutionary sequences. In particular our hydrogen-deficient sequences have been calculated by considering recent advancements in the treatment of energy transfer in dense helium atmospheres. Each evolutionary sequence was computed from the beginning of the cooling track at high luminosities down to the development of the full Debye cooling at very low surface luminosities, log(L⋆/L⊙)= − 5.5. We also provide colors in the Gaia photometric bands for these white dwarf evolutionary sequences on the basis of models atmospheres of Rohrmann et al. (2012).
A relevant aspect of our sequences is that we have included the release of energy and the ensuing core chemical redistribution resulting from the phase separation of 16O and 20Ne induced by the crystallization. This constitutes a major improvement as compared with previous studies on the subject, like those of A07 and Córsico et al. (2004). To this end, we incorporate the phase diagram of Medin & Cumming (2010) suitable for 16O and 20Ne plasma, which also provides us with the correct temperature of crystallization. In addition, our white dwarf models include element diffusion consistent with evolutionary processes.
The calculations presented here constitute the first set of fully evolutionary calculations of ultra-massive white dwarfs including realistic initial chemical profiles for each white dwarf mass, an updated microphysics, and the effects of phase separation process during crystallization. All these processes impact to a different extent the cooling times of ultra-massive white dwarfs. We find a marked dependence of the cooling times on the stellar mass at low luminosity and a fast cooling in our most massive sequences. In particular, our 1.29 M⊙ hydrogen-rich sequence reaches log(L⋆/L⊙)= − 5 in only 3.6 Gyr, which is even shorter (2.4 Gyr) in the case of the hydrogen-deficient counterpart. Our results also show an enrichment of carbon in the outer layers of the hydrogen-deficient sequences at intermediate luminosities. We have also investigated the effect of element diffusion, and found that these processes profoundly change the inner abundance distribution from the very early stages of white dwarf evolution. In particular, the initial helium and carbon distributions below the hydrogen-rich envelope are substantially changed when evolution reaches a low effective temperature, thus impacting the cooling times at such advanced stages of evolution.
Our new cooling sequences indicate that all pulsating white dwarfs existing in the literature with masses higher than 1.10 M⊙ should have more than 80% of their mass crystallized if they harbor O-Ne cores. This is a relevant issue since crystallization has important consequences on the pulsational properties of massive ZZ Ceti stars. This aspect has recently been thoroughly explored in De Gerónimo et al. (2019) on the basis of these new sequences, with relevant implications for the pulsational properties characterizing ultra-massive white dwarfs.
In summary, we find that the use of detailed chemical profiles as given by progenitor evolution and their time evolution resulting from element diffusion processes and from phase separation during crystallization constitute important improvements compared with existing calculations that have to be considered when assessing the cooling times and pulsational properties of ultra-massive white dwarfs. We hope that asteroseismological inferences of ultra-massive white dwarfs benefit from these new evolutionary sequences, and help shed light on the crystallization in the interior of white dwarfs.
These evolutionary sequences are available at http://evolgroup.fcaglp.unlp.edu.ar/TRACKS/ultramassive.html
Acknowledgments
This paper is dedicated to the memory of Enrique García-Berro; without his experience, talent, and passion, this work would have not been possible. We are very grateful to A. Cumming for providing us with the phase diagram, a key physical ingredient required in our investigation, and to L. Siess for the chemical profiles of his models. Part of this work was supported by AGENCIA through the Programa de Modernización Tecnológica BID 1728/OC-AR, and by the PIP 112-200801-00940 grant from CONICET. M3B is partially supported through ANPCyT grant PICT-2016-0053 and MinCyT-DAAD bilateral cooperation program through grant DA/16/07. This research has made use of NASA’s Astrophysics Data System.
References
- Abrikosov, A. A. 1961, Sov. Phys. JETP, 12, 1254 [Google Scholar]
- Althaus, L. G., Serenelli, A. M., Panei, J. A., et al. 2005, A&A, 435, 631 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Althaus, L. G., García-Berro, E., Isern, J., Córsico, A. H., & Rohrmann, R. D. 2007, A&A, 465, 249 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Althaus, L. G., Córsico, A. H., Isern, J., & García-Berro, E. 2010a, A&ARv, 18, 471 [NASA ADS] [CrossRef] [Google Scholar]
- Althaus, L. G., Córsico, A. H., Bischoff-Kim, A., et al. 2010b, ApJ, 717, 897 [NASA ADS] [CrossRef] [Google Scholar]
- Althaus, L. G., García-Berro, E., Renedo, I., et al. 2010c, ApJ, 719, 612 [NASA ADS] [CrossRef] [Google Scholar]
- Althaus, L. G., García-Berro, E., Isern, J., Córsico, A. H., & Miller Bertolami, M. M. 2012, A&A, 537, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Althaus, L. G., Camisassa, M. E., Miller Bertolami, M. M., Córsico, A. H., & García-Berro, E. 2015, A&A, 576, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bono, G., Salaris, M., & Gilmozzi, R. 2013, A&A, 549, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bours, M. C. P., Marsh, T. R., Gänsicke, B. T., et al. 2015, MNRAS, 450, 3966 [NASA ADS] [CrossRef] [Google Scholar]
- Brassard, P., & Fontaine, G. 2005, ApJ, 622, 572 [NASA ADS] [CrossRef] [Google Scholar]
- Camisassa, M. E., Althaus, L. G., Rohrmann, R. D., et al. 2017, ApJ, 839, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Cassisi, S., Potekhin, A. Y., Pietrinferni, A., Catelan, M., & Salaris, M. 2007, ApJ, 661, 1094 [NASA ADS] [CrossRef] [Google Scholar]
- Castanheira, B. G., Kepler, S. O., Kleinman, S. J., Nitta, A., & Fraga, L. 2010, MNRAS, 405, 2561 [NASA ADS] [Google Scholar]
- Castanheira, B. G., Kepler, S. O., Kleinman, S. J., Nitta, A., & Fraga, L. 2013, MNRAS, 430, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Córsico, A. H., García-Berro, E., Althaus, L. G., & Isern, J. 2004, A&A, 427, 923 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Córsico, A. H., Althaus, L. G., Montgomery, M. H., García-Berro, E., & Isern, J. 2005, A&A, 429, 277 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Curd, B., Gianninas, A., Bell, K. J., et al. 2017, MNRAS, 468, 239 [NASA ADS] [CrossRef] [Google Scholar]
- De Gerónimo, F. C., Córsico, A. H., Althaus, L. G., Wachlin, F. C., & Camisassa, M. E. 2019, A&A, 621, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ferguson, J. W., Alexander, D. R., Allard, F., et al. 2005, ApJ, 623, 585 [NASA ADS] [CrossRef] [Google Scholar]
- Fontaine, G., & Brassard, P. 2008, PASP, 120, 1043 [NASA ADS] [CrossRef] [Google Scholar]
- García-Berro, E., Isern, J., & Hernanz, M. 1997a, MNRAS, 289, 973 [NASA ADS] [CrossRef] [Google Scholar]
- García-Berro, E., Ritossa, C., & Iben, Jr., I. 1997b, ApJ, 485, 765 [NASA ADS] [CrossRef] [Google Scholar]
- García-Berro, E., Torres, S., Althaus, L. G., et al. 2010, Nature, 465, 194 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Gianninas, A., Bergeron, P., & Ruiz, M. T. 2011, ApJ, 743, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Gil-Pons, P., Gutiérrez, J., & García-Berro, E. 2007, A&A, 464, 667 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haft, M., Raffelt, G., & Weiss, A. 1994, ApJ, 425, 222 [NASA ADS] [CrossRef] [Google Scholar]
- Hansen, B. M. S., Kalirai, J. S., Anderson, J., et al. 2013, Nature, 500, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Hermes, J. J., Kepler, S. O., Castanheira, B. G., et al. 2013, ApJ, 771, L2 [NASA ADS] [CrossRef] [Google Scholar]
- Iglesias, C. A., & Rogers, F. J. 1996, ApJ, 464, 943 [NASA ADS] [CrossRef] [Google Scholar]
- Isern, J., Mochkovitch, R., García-Berro, E., & Hernanz, M. 1997, ApJ, 485, 308 [NASA ADS] [CrossRef] [Google Scholar]
- Itoh, N., Hayashi, H., & Kohyama, Y. 1994, ApJ, 436, 418 [NASA ADS] [CrossRef] [Google Scholar]
- Itoh, N., Hayashi, H., Nishikawa, A., & Kohyama, Y. 1996, ApJS, 102, 411 [NASA ADS] [CrossRef] [Google Scholar]
- Jeffery, E. J., von Hippel, T., DeGennaro, S., et al. 2011, ApJ, 730, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Jiménez-Esteban, F. M., Torres, S., Rebassa-Mansergas, A., et al. 2018, MNRAS, 480, 4505 [NASA ADS] [CrossRef] [Google Scholar]
- Kanaan, A., Kepler, S. O., Giovannini, O., & Diaz, M. 1992, ApJ, 390, L89 [NASA ADS] [CrossRef] [Google Scholar]
- Kanaan, A., Nitta, A., Winget, D. E., et al. 2005, A&A, 432, 219 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kepler, S. O., Pelisoli, I., Koester, D., et al. 2016, MNRAS, 455, 3413 [NASA ADS] [CrossRef] [Google Scholar]
- Kirzhnits, D. A. 1960, Sov. Phys. JETP, 11, 365 [Google Scholar]
- Kleinman, S. J., Kepler, S. O., Koester, D., et al. 2013, ApJS, 204, 5 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Magni, G., & Mazzitelli, I. 1979, A&A, 72, 134 [NASA ADS] [Google Scholar]
- Maoz, D., Mannucci, F., & Nelemans, G. 2014, ARA&A, 52, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Medin, Z., & Cumming, A. 2010, Phys. Rev. E, 81, 036107 [NASA ADS] [CrossRef] [Google Scholar]
- Metcalfe, T. S., Montgomery, M. H., & Kanaan, A. 2004, ApJ, 605, L133 [NASA ADS] [CrossRef] [Google Scholar]
- Miller Bertolami, M. M. 2016, A&A, 588, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Montgomery, M. H., & Winget, D. E. 1999, ApJ, 526, 976 [NASA ADS] [CrossRef] [Google Scholar]
- Mukadam, A. S., Mullally, F., Nather, R. E., et al. 2004, ApJ, 607, 982 [NASA ADS] [CrossRef] [Google Scholar]
- Nitta, A., Kepler, S. O., Chené, A.-N., et al. 2016, IAU Focus Meeting, 29, 493 [Google Scholar]
- Rebassa-Mansergas, A., Rybicka, M., Liu, X.-W., Han, Z., & García-Berro, E. 2015, MNRAS, 452, 1637 [NASA ADS] [CrossRef] [Google Scholar]
- Renedo, I., Althaus, L. G., Miller Bertolami, M. M., et al. 2010, ApJ, 717, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Rohrmann, R. D. 2018, MNRAS, 473, 457 [NASA ADS] [CrossRef] [Google Scholar]
- Rohrmann, R. D., Althaus, L. G., García-Berro, E., Córsico, A. H., & Miller Bertolami, M. M. 2012, A&A, 546, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Salaris, M., Serenelli, A., Weiss, A., & Miller Bertolami, M. 2009, ApJ, 692, 1013 [NASA ADS] [CrossRef] [Google Scholar]
- Salaris, M., Althaus, L. G., & García-Berro, E. 2013, A&A, 555, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Segretain, L., Chabrier, G., Hernanz, M., et al. 1994, ApJ, 434, 641 [NASA ADS] [CrossRef] [Google Scholar]
- Siess, L. 2006, A&A, 448, 717 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Siess, L. 2007, A&A, 476, 893 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Siess, L. 2010, A&A, 512, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tassoul, M., Fontaine, G., & Winget, D. E. 1990, ApJS, 72, 335 [Google Scholar]
- Tremblay, P.-E., Cukanovaite, E., Gentile Fusillo, N. P., Cunningham, T., & Hollands, M. A. 2019, MNRAS, 482, 5222 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Horn, H. M. 1968, ApJ, 151, 227 [NASA ADS] [CrossRef] [Google Scholar]
- Weiss, A., & Ferguson, J. W. 2009, A&A, 508, 1343 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Winget, D. E., & Kepler, S. O. 2008, ARA&A, 46, 157 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Winget, D. E., Kepler, S. O., Campos, F., et al. 2009, ApJ, 693, L6 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Cooling times of our hydrogen-rich (HR) and hydrogen-deficient (HD) white dwarf sequences at selected luminosities.
Stellar mass (solar mass) and cooling ages (Gyr) as predicted by our sequences under the assumption that they harbor O-Ne cores for selected ultra-massive white dwarfs in the literature.
Percentages of crystallized mass of our hydrogen-rich sequences and effective temperature at which they occur.
All Figures
 |
Fig. 1. Phase diagram of crystallization for a 16O/20Ne mixture (Medin & Cumming 2010). XNe is the 20Ne abundance. Γcrit is set to 178.6. ΓO is given by ΓO = (e2/kB aeT)85/3 (see text for details). |
| In the text | |
 |
Fig. 2. Initial chemical profiles before Rayleigh-Taylor rehomogenization corresponding to our four hydrogen-rich white dwarf models, as given by the nuclear history of the progenitor stars. |
| In the text | |
 |
Fig. 3. Initial chemical profiles of our four hydrogen-rich white dwarf models once Rayleigh-Taylor rehomogenization has occurred. |
| In the text | |
 |
Fig. 4. Temporal evolution of surface luminosity (double dotted line) and different luminosity contributions: neutrino luminosity (dashed line), gravothermal luminosity (dotted line), latent heat (dot-dot-dashed line), and phase separation energy (solid line). The arrows indicate the main physical processes responsible for the evolution at different moments. |
| In the text | |
 |
Fig. 5. Solid (dashed) lines indicate the cooling times for our hydrogen-rich (deficient) white dwarf sequences. At low luminosities and from left to right, stellar masses of both set of sequences are 1.29 M⊙, 1.23 M⊙, 1.16 M⊙, and 1.10 M⊙. |
| In the text | |
 |
Fig. 6. Hydrogen-rich sequences in the plane log(g)−Teff. Blue solid lines display isochrones of 0.1, 0.5, 1, 2, and 5 Gyr. Crosses indicate the location of ultra-massive white dwarfs from Mukadam et al. (2004), Nitta et al. (2016), Gianninas et al. (2011), Kleinman et al. (2013), Bours et al. (2015), Kepler et al. (2016), Curd et al. (2017). |
| In the text | |
 |
Fig. 7. Hydrogen-rich sequences in the plane log(g) − Teff. Blue solid lines indicate 0, 20, 40, 60, 80, 90, 95 and 99% of crystallized mass. The symbols with error bars indicate the location of the known pulsating ultra-massive DA white dwarfs (Mukadam et al. 2004; Hermes et al. 2013; Curd et al. 2017; Nitta et al. 2016). |
| In the text | |
 |
Fig. 8. Inner abundance distribution for 1.10 M⊙ hydrogen-rich models at three selected effective temperatures, as indicated. |
| In the text | |
 |
Fig. 9. Same as Fig. 8, but for 1.29 M⊙ models. |
| In the text | |
 |
Fig. 10. Change in the chemical profiles of our 1.16 M⊙ hydrogen-rich white dwarf model induced by the phase separation process during crystallization. Top (bottom) panel: chemical profile at log(Teff)=4.26(3.94). For comparison, the abundances of 16O and 20Ne right before phase separation are also plotted with thick lines in both panels. |
| In the text | |
 |
Fig. 11. Top panel: cooling times of our 1.22 M⊙ hydrogen-rich sequence when crystallization is neglected (double dotted line), when only latent heat is considered during crystallization (dotted line), and when both latent heat and energy from phase separation are considered during crystallization (solid line). Bottom panel: white dwarf radius in terms of the cooling time for these evolutionary tracks. |
| In the text | |
 |
Fig. 12. Cooling times of our hydrogen-rich white dwarf sequences with 1.10 M⊙, 1.16 M⊙, and 1.23 M⊙ (thick lines) compared with the cooling sequences of A07 of similar masses (thin lines). |
| In the text | |
 |
Fig. 13. Cooling times of 1.16 M⊙ hydrogen-rich white dwarf models without phase separation resulting from the use of different chemical profiles. The solid red line corresponds to the cooling sequence using our current stellar evolutionary code but implanting the chemical profile considered in A07. The black dotted line corresponds to the cooling sequence calculated using our new chemical profile (plotted in the top right panel of Fig. 3). |
| In the text | |
 |
Fig. 14. Cooling times of 1.16 M⊙ hydrogen-rich white dwarf models without phase separation and considering the same chemical profiles of A07, but adopting different microphysics. The cooling sequence of A07, which is based on an old treatment of conductive opacity and latent heat, is shown as a green dotted line. The red solid line shows the cooling times calculated using our current numerical code. The dashed line shows the prediction given by our current numerical code, but with old microphysics, i.e., the same conductive opacities and treatment of latent heat as considered in A07. Left panel: amplifies the early stages of the white dwarf stage. Right panel: rest of the white dwarf cooling track. |
| In the text | |
 |
Fig. 15. H-rich white dwarf cooling sequences in the color-magnitude diagram in Gaia bands, together with the sample of white dwarfs within 100 pc, obtained by Jiménez-Esteban et al. (2018). The filled squares indicate the moment when crystallization begins in each white dwarf cooling sequence and the filled triangles indicate the moment when convective coupling occurs. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


