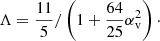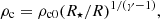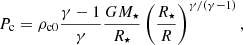| Issue |
A&A
Volume 624, April 2019
|
|
|---|---|---|
| Article Number | A31 | |
| Number of page(s) | 7 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201834580 | |
| Published online | 04 April 2019 | |
“Atlas” of numerical solutions for star-disk magnetospheric interaction
Nicolaus Copernicus Astronomical Center, Bartycka 18, 00-716 Warsaw, Poland
e-mail: miki@camk.edu.pl
Received:
5
November
2018
Accepted:
7
February
2019
Aims. I report results in numerical simulations of star-disk magnetospheric interaction. A thin accretion disk with a corona above a rotating stellar surface is simulated, and a parameter study is performed to find trends in the angular momentum flux. The results are presented for young stellar objects, but they can be rescaled to other objects with similar geometry.
Methods. I performed resistive and viscous magnetohydrodynamic simulations that reached a quasi-stationary state for cases with different parameters. I computed angular momentum fluxes in the different components of the flow to compare the results.
Results. I present the simulation results with the matter density distribution and a sample of the magnetic field lines, gathered in an “Atlas” of solutions. The torque exerted on the star is computed, together with the angular momentum flux that is expelled from the system in the cases with a conical outflow. I find trends in the components of the flow in the part of parameter space with a slowly rotating star.
Key words: stars: formation / stars: magnetic field / stars: pre-main sequence
© ESO 2019
1. Introduction
An analytical solution for a viscous accretion disk was given in Shakura & Sunyaev (1973) a few years after the first numerical solution by Prendergast & Burbidge (1968). As in many numerical and analytical models that followed, the disk structure was derived separately in radial and vertical direction. The radial structure was computed by equations averaged over the disk thickness and the vertical structure from the hydrostatic equilibrium in the vertical direction. In some models, radiative transfer was also taken into account.
Height-averaged computations were shown to be insufficient in the analytical work by Urpin (1984) and in many numerical works as well, starting with Kley & Lin (1992). In all of them, a backflow in the disk midplane occurs that is thought to be of thermal origin.
An analytical solution for a thin accretion disk in three dimensions was given in Kluzniak & Kita (2000; hereafter KK00). They derived the equations of a polytropic, viscous hydrodynamical accretion disk using the Taylor expansion in the small parameter ϵ = H/R, the disk aspect ratio. Although thermal effects were neglected, backflow is still present with the values of the viscosity parameter αv < 0.685. Such a disk accretes only at the higher latitudes, closer to the surface, and the backflow in the mid-plane occurs at a particular distance from the star. Inside this distance, matter always flows toward the star. If αv > 0.685, the disk accretes across the entire height.
When stellar magnetic field and disk resistivity are added in the model, the angular momentum transfer depends on the details of star-disk magnetospheric interaction. As first shown in Ghosh & Lamb (1979a,b), to correctly describe this interaction, it is not enough to consider the disk alone. The rotating stellar surface and corona have to be included in the model so that the interaction with the region in the disk below and beyond the corotation radius is included. Pioneering such simulations were Romanova et al. (2009, 2013) and Zanni & Ferreira (2009, 2013). As described in Zanni & Ferreira (2009; hereafter ZF09), to answer the stellar angular momentum problem, the different regimes of magnetospheric interaction need to be probed through exploration of the parameter space. Here I follow this suggestion.
In Sect. 2 I demonstrate the difference in the matter density distribution in the results with different parameters, obtained from a set of simulations sweeping through the parameter space. In Sect. 3 the results with different parameters in the simulations are compared and trends are illustrated, with conclusions listed in Sect. 4. A short but detailed technical exposition of the code setup is presented in the appendix.
2. Simulations of star-disk magnetospheric interaction
Using the PLUTO code (v.4.1; Mignone et al. 2007, 2012), I performed simulations of star-disk magnetospheric interaction (SDMI). Initial conditions in the disk and corona and boundary conditions at the edges of the computational domain closely follow ZF09. See the appendix for the details of the numerical setup.
Simulations span over 64 points in the parameter space (see Table 1), by varying stellar angular velocity Ω⋆, expressed in units of stellar breakup angular velocity 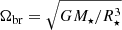 , stellar magnetic field strength B⋆, and the magnetic Prandtl number
, stellar magnetic field strength B⋆, and the magnetic Prandtl number
where αm is the resistive parameter. In the simulations presented here, the viscosity parameter was fixed to αv = 1.
Parameter space in the study presented in the “Atlas” for YSOs.
To compare the results in the different points in the parameter space, a quasi-stationary state in each of the simulations was found by computing the mass flux Ṁ and the angular momentum flux J̇. The fluxes were computed by integrating
over the corresponding surface S in the different parts of the flow.
I computed the mass and angular momentum fluxes onto the star, into the stellar wind, and across the disk height in the middle part of the disk at Rd = 12R⋆. When an outflow formed, the fluxes that contributed to it were also computed at this distance. In the angular momentum flux onto the star, the parts coming from beyond and below the corotation radius 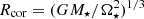 were computed separately. The sign convention is such that a positive angular momentum flux increases the total in the system and a negative decreases it. In both fluxes, the equatorial symmetry was taken into account so that they were computed in a complete meridional plane.
were computed separately. The sign convention is such that a positive angular momentum flux increases the total in the system and a negative decreases it. In both fluxes, the equatorial symmetry was taken into account so that they were computed in a complete meridional plane.
A typical example, computed in one point of the parameter space in the simulations, is presented in Fig. 1. It shows that after relaxation from the initial and boundary conditions (lasting typically for 10–50 stellar rotations), the quasi-stationary state is reached. Oscillations in the simulations, still present into the quasi-stationary state, are smoothed out by averaging over some characteristic interval; typically, an average was taken over ten stellar rotations. In the considered example the averaging interval is from 65 to 75 stellar rotations.
 |
Fig. 1. Fluxes for the case with Ω⋆ = 0.1Ωbr, B⋆ = 0.5 kG, and αm = 1. Left panel: mass flux across the disk at R = 12R⋆ (solid line), onto the star (dotted line) and into the stellar wind (dashed line) in units of |
Such an interval in which neither mass nor angular momentum fluxes varied strongly was chosen in each of the 64 simulations. I computed the average values of the angular momentum flux in the various components in the flow during that time interval.
The density distribution in each of the 64 cases can be represented by one of the three solutions from Fig. 2:
-
Disk connected with the star by an accretion column (DC).
-
Disk pushed away from the star, without an accretion column (D).
-
Conical outflow above an accretion column connecting star and disk (DCE).
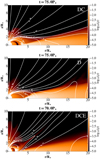 |
Fig. 2. Three different cases of geometry in the results. Top and middle panels: matter density and a sample of magnetic field lines, with the stellar magnetic field B⋆ = 1 kG and the resistivity αm = 1, in the cases with the stellar rotation rates Ω⋆ = 0.1Ωbr (top panel) where a stable accretion column is formed (DC for disk+column) and Ω⋆ = 0.15Ωbr (middle panel) in which the faster stellar rotation prevents the stable accretion column formation (D for disk only). The bottom panel shows the third case, with the stellar magnetic field B⋆ = 0.5 kG, resistivity αm = 0.1, and the rotation rate Ω⋆ = 0.1Ωbr, in which a conical outflow is formed (DCE for disk+column+ejection). |
I label the three cases obtained in the quasi-stationary state in the simulations as D, DC and DCE: D is the disk alone, DC is with disk and column, and DCE is with the disk, column, and magnetospheric ejection present in the result. This signature is used to form an “Atlas” of solutions in Table 2. The numerical values for density and exact positions of the field lines in each of the 64 simulations are different, but they qualitatively resemble the geometry of the flow components in one of the three listed cases.
Parameter space in the simulations, with an “Atlas” of solutions, where the geometry of the flow components in each case is labeled with D for disk, DC for disk+column, and DCE for disk+column+ejection.
3. Trends in the angular momentum flux
After indicating the quasi-stationary states in simulations, I proceed to compare solutions presented in the “Atlas”. In the first example, Fig. 3 shows a comparison of the density in the middle part of the disk in the simulations with an increasing stellar magnetic field. The density increases with increasing magnetic field. This trend contributes to the trends in mass and angular momentum fluxes.
 |
Fig. 3. Disk density in the simulations with Ω⋆ = 0.2Ωbr and αm = 1, measured along the disk height at R = 12R⋆. Results for B⋆ = 0.25 (solid black line), 0.5 (short dashed green line), 0.75 (dash-dotted blue line) and 1 kG (long dashed red line) are shown. There is a trend in density with increasing stellar field. The result in the simulations without a magnetic field is shown with pluses. |
In the second example, the simulations are compared with the increasing stellar rotation rate, in which the stellar magnetic field remains unchanged. Angular momentum flux from the accretion disk contributes to various components of the flow: to the star through the accretion column, to the stellar wind, and to the conical outflow when it forms.
By comparing the solutions, I find a trend in the angular momentum flux, as shown in Fig. 4. With the increase in stellar rotation rate, the spin-up of the star by the infalling matter decreases and eventually switches to a spin-down. A similar outcome is obtained in each of the cases with different stellar magnetic field strengths. This trend is expected because for slowly rotating stars the torque exerted on the star depends mostly on the stellar magnetic field at each value of the resistivity parameter. The trend changes only after a change in flow geometry.
 |
Fig. 4. Average angular momentum flux transported onto the stellar surface by the matter in-falling from the disk onto the star through the accretion column. Each panel shows a set of solutions with one stellar magnetic field strength and varying stellar rotation rate and resistivity. Results with Ω⋆/Ωbr = 0.05 (dotted), 0.1 (dashed), 0.15 (dash-dot-dotted), and 0.2 (solid) are shown in units of stellar angular momentum |
The third example of a trend in the results is in the cases with αm = 0.1, in which a conical outflow is formed. The angular momentum flux expelled from the system with such an outflow in the cases with different magnetic field strength is shown in Fig. 5.
 |
Fig. 5. Average angular momentum flux in the outflow that forms for αm = 0.1. It is computed at R = 12R⋆ for different stellar rotation rates. Normalization is the same as in Fig. 4. Fluxes in B⋆ = 0.25 (dotted), 0.5 (dash-dotted), 0.75 (dashed) and 1 kG (solid) are shown. |
The momentum flux in the outflow does not change much, except for faster stellar rotation together with a strong magnetic field, when the outflow takes away much more, about an order of magnitude, of the angular momentum from the system. The magnetospheric ejection increases with the stronger magnetic field and faster rotation.
The trends in the examples can be compared with the results in other models and simulations when they become available. If they are found to be robust, these trends can be compared with observations and can be incorporated in star formation models.
4. Conclusions
In the numerical simulations of star-disk magnetospheric interaction (SDMI), I investigated the angular momentum flux in the system. In a parameter study, stellar rotation rate, magnetic field, and the disk resistivity were varied to obtain a suite of the quasi-stationary solutions. I computed the angular momentum flux in different components of the flow to compare results in the cases with different stellar magnetic field strengths.
In a discussion of the results, I find a trend in matter density along a vertical line in the middle of the disk in the first example. The density increases with increasing stellar magnetic field in the simulation.
The second result is a trend in angular momentum flux onto the star with increasing stellar rotation rate. I find that with faster stellar rotation, the spin-up of the star decreases and eventually switches to a spin-down.
The third finding from the simulations is that for αm = 0.1 and a faster-rotating star, the angular momentum flux in the conical outflow increases significantly with high values of the stellar magnetic field. The increase is about an order of magnitude. For a low stellar magnetic field, the angular momentum in the outflow remains the same.
The results apply to disks around YSOs and can be rescaled to disks in a compact binary. I provide a table with scaling factors for different cases.
I presented here the results for a slowly rotating star. In the simulations with a stellar rotation faster than 20% of the stellar breakup rotation rate, two additional solutions are obtained, similar to Romanova et al. (2009): a fast axial outflow, and with both the conical and axial outflow. I leave them for a separate study, together with the solutions with αv < 0.685, which show a backflow in the initial disk.
I am aware of several unsuccessful attempts in repeating the ZF09 setup by experienced researchers and students in the past decade. To my knowledge, the first successful simulations following ZF09 were reported by Čemeljić et al. (2017).
Acknowledgments
MČ developed the setup of star-disk simulations while in CEA, Saclay, France, under the ANR Toupies grant with A.S. Brun. Work in NCAC Warsaw is funded by a Polish NCN grant no. 2013/08/A/ST9/00795, and collaboration with Croatian STARDUST project through HRZZ grant IP-2014-09-8656 is acknowledged. I thank IDRIS (Turing cluster) in Orsay, France, ASIAA/TIARA (PL and XL clusters) in Taipei, Taiwan and NCAC (PSK cluster) in Warsaw, Poland, for access to the Linux computer clusters I used for the high-performance computations. The PLUTO team is thanked for the possibility to use the code, in particular C. Zanni for help with the code modifications. V. Parthasarathy and F. Bartolić are acknowledged for developing the Python scripts for visualization, N. Bessolaz for the initial version of the setup, and M. Flock for useful discussions about the code.
References
- Čemeljić, M., Parthasarathy, V., & Kluźniak, W. 2017, J. Phys. Conf. Ser., 932, 012028 [CrossRef] [Google Scholar]
- Ghosh, P., & Lamb, F. K. 1979a, ApJ, 232, 259 [NASA ADS] [CrossRef] [Google Scholar]
- Ghosh, P., & Lamb, F. K. 1979b, ApJ, 234, 296 [NASA ADS] [CrossRef] [Google Scholar]
- Kley, W., & Lin, D. N. C. 1992, ApJ, 397, 600 [NASA ADS] [CrossRef] [Google Scholar]
- Kluzniak, W., & Kita, D. 2000, ArXiv e-prints [arXiv:astro-ph/0006266] [Google Scholar]
- Mignone, A., Bodo, G., Massaglia, S., et al. 2007, ApJS, 170, 228 [Google Scholar]
- Mignone, A., Zanni, C., Tzeferacos, P., et al. 2012, ApJS, 198, 7 [Google Scholar]
- Powell, K. G., Roe, P. L., Linde, T. J., Gombosi, T. I., & De Zeeuw, D. L. 1999, J. Comput. Phys., 154, 284 [NASA ADS] [CrossRef] [Google Scholar]
- Prendergast, K. H., & Burbidge, G. R. 1968, ApJ, 151, L83 [NASA ADS] [CrossRef] [Google Scholar]
- Romanova, M. M., Ustyugova, G. V., Koldoba, A. V., & Lovelace, R. V. E. 2009, MNRAS, 399, 1802 [NASA ADS] [CrossRef] [Google Scholar]
- Romanova, M. M., Ustyugova, G. V., Koldoba, A. V., & Lovelace, R. V. E. 2013, MNRAS, 430, 699 [NASA ADS] [CrossRef] [Google Scholar]
- Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
- Tanaka, T. 1994, J. Comput. Phys., 111, 381 [NASA ADS] [CrossRef] [Google Scholar]
- Urpin, V. A. 1984, Sov. Astron., 28, 50 [NASA ADS] [Google Scholar]
- Zanni, C., & Ferreira, J. 2009, A&A, 508, 1117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zanni, C., & Ferreira, J. 2013, A&A, 550, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: Numerical simulations of star-disk magnetospheric interaction
Star-disk magnetospheric interaction (SDMI) determines the angular momentum transfer in a star-disk system. Simulations including SDMI have been reported by Romanova et al. (2009, 2013) with a code that is not publicly available, and ZF09 and Zanni & Ferreira (2013) with the publicly available code PLUTO (v.3). Following ZF09, I performed simulations with the updated version of the PLUTO code (v.4.1; Mignone et al. 2007, 2012). I present a short version of the setup, amended to facilitate reproducibility1.
The equations solved in the magnetohydrodynamic (MHD) module of the PLUTO code are in the cgs system of units:
where the symbols have their usual meaning: ρ and v are the matter density and velocity vector, P is the pressure, B is the magnetic field, and ηm and τ represent the resistivity and the viscous stress tensor, respectively. Λ is the cooling source term, the gravity acceleration is g = −∇Φg, where the gravitational potential of the star with mass M⋆ is equal to Φg = −GM⋆/R. Then gR = −1.0/R2 in the code units.
Simulations were performed using the second-order piecewise linear reconstruction, with a Van Leer limiter in density and magnetic field and a minmod limiter in pressure and velocity. To enhance stability, in the subroutine plm_states, the default was set to Van Leer instead of the less diffusive monotonized central difference limiter. An approximate Roe solver (hlld in the PLUTO options) was used, with a modification in the flag_shock subroutine: flags were set to switch to more diffusive hll solver when the internal energy was lower than 1% of the total energy, instead of switching in the presence of shocks. The second-order time-stepping (RK2) was employed, and ∇ ⋅ B = 0 was maintained by the constrained transport. The magnetic field was evolved with the split-field option, so that only changes from the initial stellar magnetic field were evolved in time (Tanaka 1994; Powell et al. 1999). In version 4.1 of PLUTO the constrained transport is by default disabled to work with the background field in the resistive MHD. This is probably an artifact from the older version. To enable the background field option, the constraint was removed by changing the condition in the routine backgrnd_field, to point to some feature that will not be used, for instance, thermal conduction.
A logarithmically stretched radial grid and a uniform grid in the meridional half-plane θ = [0, π/2] in spherical coordinates were used to perform 2D axisymmetric SDMI simulations. The resolution was set to R × θ = (217 × 100) grid cells in the physical domain from the stellar surface to 30 stellar radii, as shown in Fig. A.1.
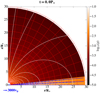 |
Fig. A.1. Initial density distribution of matter shown in a logarithmic color grading. A sample of the initial poloidal magnetic field lines is shown with solid white lines. Arrows show the initial velocity distribution in the disk, with the unit vector length measured in Keplerian velocity units indicated below the figure. The computational grid is shown in 8 × 8 blocks of cells. |
The total energy density is E = P/(γ − 1) + ρ(v ⋅ v)/2 + B ⋅ B/8π, where γ = 5/3 is the plasma polytropic index. The electric current is given by Ampère’s law J = ∇ × B/4π.
To prevent the thermal thickening of the accretion disk in simulations, following the description of ZF09, I removed the underbraces Ohmic and viscous heating terms from the PLUTO energy equation. This equals the assumption that all the heating is radiated away from the disk. To do this, lines in the code with the viscous and resistive part of the flux computation in parabolic_flux subroutine were commented out. The viscous and resistive fluxes were added in the rhs subroutine to ensure that the correct dissipative flux terms were incorporated. These simulations remain in the non-ideal MHD regime because of the viscous term in the momentum equation and the resistive term in the induction equation2.
The initial disk was set with the initial density by KK00 with a self-similar profile and the aspect ratio ϵ:
The pressure was
The capital R indicates the spherical radius, and r = Rsinθ is the cylindrical radius. The disk unit density ρd0 and Keplerian speed 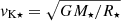 were both calculated in the disk midplane at R⋆. The initial disk was truncated about the corotation radius.
were both calculated in the disk midplane at R⋆. The initial disk was truncated about the corotation radius.
The obtained disk is a polytropic hydrodynamical solution of the viscous accretion disk in full 3D, obtained by approximate expansion up to the second order in the terms of ϵ = cs/vK, the disk aspect ratio measured on the midplane of the disk, where 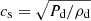 and vK are the isothermal sound speed and Keplerian speed in the disk.
and vK are the isothermal sound speed and Keplerian speed in the disk.
The viscosity and resistivity were defined explicitly in separate subroutines by a second-order finite-difference approximation for the dissipative fluxes, with checking of the time step. Both are parameterized by the Shakura-Sunyaev prescription as 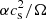 . To avoid the issues related to the backflow in the disk, I here address only the case with anomalous3 viscosity coefficient αv = 1.
. To avoid the issues related to the backflow in the disk, I here address only the case with anomalous3 viscosity coefficient αv = 1.
The viscosity was defined by the viscous stress tensor
with the dynamic viscosity ηv = ρνv given with
where νv is the kinematic viscosity. The magnetic diffusivity was assumed proportional to the viscosity, with the free parameter αm:
so that in the cgs system of units the resistivity is ηm = 4πνm.
The diffusive parameters αv and αm were defined in separate subroutines visc_nu and res_eta. A condition for including the diffusive term was in both routines defined by the β = Pmag/Phyd > 0.5, meaning that the magnetic pressure prevailed. In both subroutines, the diffusive term was taken into account only when the tracer value was unity, otherwise it was set to zero.
The initial disk velocity profile is, following KK00:
where
The initial corona is a non-rotating, polytropic corona with γ = 5/3 in hydrostatic balance. It is defined by the density and pressure, given by
where ρc0 ≪ ρd0 is the ratio between the initial coronal and disk density, set to 0.01.
The initial stellar magnetic dipole field was set with the field axis aligned with the stellar rotation axis. There is no resistivity in the magnetosphere outside of the disk. This means that the reconnection of the magnetic field is a numerical, not physical dissipation.
In the internal boundary part, which enables change in the quantities inside the computational domain in PLUTO, the density in the grid cell just above the star was corrected when it falls below some limit value (I set it to 5 × 10−8), to prevent the density near the star from becoming too low. The pressure was corrected in such a way to conserve the same sound speed in the corona. To maintain the self-consistency, velocities were also changed to conserve the momentum. Here was also ensured that the scalar tracer value was always set to zero in the corona. Around the reconnection sheet and outflows, the tracer scalar can obtain spurious values, this is prevented here.
The numerical heating in the corona was prevented by enforcing the conservation of the entropy S, to keep the values close to the initial conditions. The maximum of the entropy is on top of the star, so it was kept throughout the computational box below the value 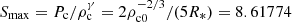 . For the minimum, the small number Smin = 0.01 was set. From this I obtained corrected values for the pressure interval in the computational box, by P = max[min(P, Smaxργ),Sminργ].
. For the minimum, the small number Smin = 0.01 was set. From this I obtained corrected values for the pressure interval in the computational box, by P = max[min(P, Smaxργ),Sminργ].
In the inner boundary conditions, the density, pressure, and toroidal components of the velocity and magnetic field were prescribed from the active zones into the boundary. The linear extrapolation was used, with Van Leer limiter in the density and the magnetic field, and minmod limiter in the pressure and velocity. For the numerical stability in the corona, in the cases with vR > 0, I introduced a correction of the pressure by a free parameter Tf in the inner radial boundary condition. It should be set to the number of order a few hundred. It adjusts the pressure ρv2 on top of the star (stellar wind) from the default 2/5 to 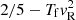 so that the pressure in the corona is given by
so that the pressure in the corona is given by 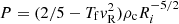 . The first term here is the coronal initial pressure
. The first term here is the coronal initial pressure 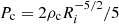 . Because P ∼ ρT in the ideal gas law, we can think of 2/5 as an effective temperature, and
. Because P ∼ ρT in the ideal gas law, we can think of 2/5 as an effective temperature, and 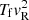 is an ad hoc correction.
is an ad hoc correction.
In the axisymmetric 2D setup, only the toroidal component of the magnetic field was set in the staggered grid because in the constrained transport method, a staggered grid is used4. I used a custom boundary condition for Bφ, in which Ωeff = Ω − vpBφ/rBp is derived from the condition for the stellar surface as a rotating perfect conductor. The magnetic torque to drive the plasma rotation on top of the star was set, with the matching measured by the comparison of the stellar angular velocity and the effective rotation rate of the field lines by the ratio Ωeff/Ω*. This prescribes rotation of the matter on top of the star and the effective rotation rate of the field lines to Ωeff, with vp and Bp standing for the poloidal velocity and magnetic field, respectively. In addition, in the constrained transport method, the subroutine ct toroidal component of the EMF was set to zero. Then in the stellar reference frame, the electric field is zero, with the flow speed parallel to the magnetic field.
I did not follow the suggestion in ZF09 to impose continuity of the speed along the field lines on the outflowing matter, nor the continuity of the axisymmetric MHD invariant k = 4πρvp/Bp on the infalling material, as it did not improve the result.
The stellar rotation rate was set with those corrections. I started the simulation with Ω⋆, not with the slower rotation of the star as described in ZF09.
In the outer boundary conditions, in the coronal part of the domain, the logarithmic extrapolation in the density and pressure was set. In the radial and meridional components of the velocity an outflow was set, and a linear extrapolation with the minmod limiter for the azimuthal velocity component and Van Leer limiter in the toroidal magnetic field component. At the disk outer radial boundary, I introduced the initial hydrodynamical values, anticipating the thickening of the disk for 25%. Because the velocity might roll back above the thickened disk, inflow to twice the initial disk height in the corona was prevented by setting the velocities to zero. The toroidal magnetic field was linearly extrapolated with a Van Leer limiter.
The simulations were stopped after 100 stellar rotations. In some cases, the simulation stopped earlier because the time step was too short. This was caused by the numerical instability in the rarefied corona, not by the disk instability.
Normalized equations were solved in the code. The unit length, velocity, and mass were chosen with the stellar radius R⋆, the Keplerian speed at the stellar surface vK⋆, and mass M⋆. The time unit was then t0 = R⋆/vK⋆. Time t in the results was measured in the number of stellar rotation periods P⋆. The mass flux rate was measured in 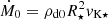 , which was the free parameter in simulation from which I determined ρd0, the disk density. The initial coronal density was defined as a free parameter in the code, ρc0 = 0.01ρd0. The magnetic field unit was defined by
, which was the free parameter in simulation from which I determined ρd0, the disk density. The initial coronal density was defined as a free parameter in the code, ρc0 = 0.01ρd0. The magnetic field unit was defined by 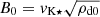 . The torque in the simulations was measured in units of
. The torque in the simulations was measured in units of 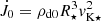 .
.
The simulations can be rescaled to different objects using the scaling coefficients from Table A.1. In the case of compact objects, the radial extension of the domain, measured from the axis of rotation, should not reach the light cylinder, RℓcΩ⋆ = c, where the azimuthal velocity equals the speed of light. This limitation was not mentioned in the previous publications with SDMI, so I list distances of the light cylinder in the different cases in Table A.2.
Typical values and scaling for different central objects.
Position of the light cylinder as a function of stellar rotation rate in some typical cases.
All Tables
Parameter space in the simulations, with an “Atlas” of solutions, where the geometry of the flow components in each case is labeled with D for disk, DC for disk+column, and DCE for disk+column+ejection.
Position of the light cylinder as a function of stellar rotation rate in some typical cases.
All Figures
 |
Fig. 1. Fluxes for the case with Ω⋆ = 0.1Ωbr, B⋆ = 0.5 kG, and αm = 1. Left panel: mass flux across the disk at R = 12R⋆ (solid line), onto the star (dotted line) and into the stellar wind (dashed line) in units of |
| In the text | |
 |
Fig. 2. Three different cases of geometry in the results. Top and middle panels: matter density and a sample of magnetic field lines, with the stellar magnetic field B⋆ = 1 kG and the resistivity αm = 1, in the cases with the stellar rotation rates Ω⋆ = 0.1Ωbr (top panel) where a stable accretion column is formed (DC for disk+column) and Ω⋆ = 0.15Ωbr (middle panel) in which the faster stellar rotation prevents the stable accretion column formation (D for disk only). The bottom panel shows the third case, with the stellar magnetic field B⋆ = 0.5 kG, resistivity αm = 0.1, and the rotation rate Ω⋆ = 0.1Ωbr, in which a conical outflow is formed (DCE for disk+column+ejection). |
| In the text | |
 |
Fig. 3. Disk density in the simulations with Ω⋆ = 0.2Ωbr and αm = 1, measured along the disk height at R = 12R⋆. Results for B⋆ = 0.25 (solid black line), 0.5 (short dashed green line), 0.75 (dash-dotted blue line) and 1 kG (long dashed red line) are shown. There is a trend in density with increasing stellar field. The result in the simulations without a magnetic field is shown with pluses. |
| In the text | |
 |
Fig. 4. Average angular momentum flux transported onto the stellar surface by the matter in-falling from the disk onto the star through the accretion column. Each panel shows a set of solutions with one stellar magnetic field strength and varying stellar rotation rate and resistivity. Results with Ω⋆/Ωbr = 0.05 (dotted), 0.1 (dashed), 0.15 (dash-dot-dotted), and 0.2 (solid) are shown in units of stellar angular momentum |
| In the text | |
 |
Fig. 5. Average angular momentum flux in the outflow that forms for αm = 0.1. It is computed at R = 12R⋆ for different stellar rotation rates. Normalization is the same as in Fig. 4. Fluxes in B⋆ = 0.25 (dotted), 0.5 (dash-dotted), 0.75 (dashed) and 1 kG (solid) are shown. |
| In the text | |
 |
Fig. A.1. Initial density distribution of matter shown in a logarithmic color grading. A sample of the initial poloidal magnetic field lines is shown with solid white lines. Arrows show the initial velocity distribution in the disk, with the unit vector length measured in Keplerian velocity units indicated below the figure. The computational grid is shown in 8 × 8 blocks of cells. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



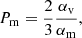
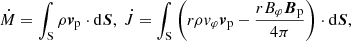
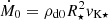
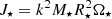
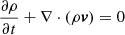
![$$ \begin{aligned}&\frac{\partial \rho \boldsymbol{v}}{\partial t}+\nabla \cdot \left[\rho \boldsymbol{v} \boldsymbol{v}+\left(P+\frac{\boldsymbol{B}\cdot \boldsymbol{B}}{8\pi }\right) \boldsymbol{I}-\frac{\boldsymbol{B}\boldsymbol{B}}{4\pi }-\boldsymbol{\tau }\right]=\rho \boldsymbol{g}\end{aligned} $$](/articles/aa/full_html/2019/04/aa34580-18/aa34580-18-eq8.gif)
![$$ \begin{aligned}&\frac{\partial E}{\partial t}+ \nabla \cdot \left[\left(E+P+\frac{\boldsymbol{B}\cdot \boldsymbol{B}}{8\pi }\right)\boldsymbol{v}-\frac{(\boldsymbol{v}\cdot \boldsymbol{B})\boldsymbol{B}}{4\pi }\right] \nonumber \\&\qquad +\nabla \cdot \left[\underbrace{\eta _{\rm m}\boldsymbol{J}\times \boldsymbol{B}/4\pi - \boldsymbol{v}\cdot \boldsymbol{\tau }}_{\rm heating\ terms}\right]= \rho \boldsymbol{g}\cdot \boldsymbol{v}-\underbrace{{\Lambda }}_{\rm cooling} \end{aligned} $$](/articles/aa/full_html/2019/04/aa34580-18/aa34580-18-eq9.gif)
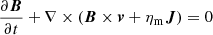
![$$ \begin{aligned} \rho _{\rm d}&=\rho _{\rm d0}\left\{ \frac{\gamma -1}{\gamma \epsilon ^2}\left[\frac{R_*}{R}-\left(1-\frac{\gamma \epsilon ^2}{\gamma -1}\right)\frac{R_\star }{R\sin \theta }\right]\right\} ^{1/(\gamma -1)} \nonumber \\&=\rho _{\rm d0}\left\{ \frac{2}{5\epsilon ^2}\left[\frac{R_\star }{R}-\left(1-\frac{5}{2}\epsilon ^2\right)\frac{R_\star }{R\sin \theta }\right]\right\} ^{3/2}\cdot \end{aligned} $$](/articles/aa/full_html/2019/04/aa34580-18/aa34580-18-eq11.gif)
![$$ \begin{aligned}&P_{\rm d}=\epsilon ^2\rho _{\rm d0}v_{\rm K\star }^2\left(\frac{\rho _{\rm d}}{\rho _{\rm d0}}\right)^\gamma =&\\ \nonumber&=\frac{\rho _{\rm d0}v_{\rm K\star }^2}{\epsilon ^3}\left\{ \frac{2}{5}\left[\frac{R_\star }{R}-\left(1-\frac{5\epsilon ^2}{2}\right)\frac{R_\star }{R\sin {\theta }}\right]\right\} ^{5/2}. \end{aligned} $$](/articles/aa/full_html/2019/04/aa34580-18/aa34580-18-eq12.gif)
![$$ \begin{aligned} \boldsymbol{\tau }=\eta _{\rm v}\left[(\nabla \boldsymbol{v})+(\nabla \boldsymbol{v})^T-\frac{2}{3}(\nabla \cdot \boldsymbol{v})\boldsymbol{I}\right], \end{aligned} $$](/articles/aa/full_html/2019/04/aa34580-18/aa34580-18-eq16.gif)
![$$ \begin{aligned} \eta _{\rm v}=\frac{2}{3}\rho \alpha _{\rm v} \left[c_{\rm s}^2(r)|_{z=0}+\frac{2}{5}\left(\frac{GM_\star }{R}-\frac{GM_\star }{r}\right)\right]\sqrt{\frac{r^3}{GM_\star }}, \end{aligned} $$](/articles/aa/full_html/2019/04/aa34580-18/aa34580-18-eq17.gif)
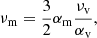
![$$ \begin{aligned} v_{Rd}&=-\alpha _{\rm v}\epsilon ^2\left[10-\dfrac{32}{3}\Lambda \alpha _{\rm v}^2-\Lambda \left(5-\dfrac{1}{\epsilon ^2\tan ^2\theta }\right)\right] \sqrt{\dfrac{GM_*}{R\sin ^3\theta }}\nonumber ,\\ v_{R\varphi }&=\left[\sqrt{1-\dfrac{5\epsilon ^2}{2}}+\dfrac{2}{3} \epsilon ^2\alpha _{\rm v}^2\Lambda \left(1-\dfrac{6}{5\epsilon ^2\tan ^2\theta }\right) \right]\sqrt{\dfrac{GM_*}{R\sin \theta }} \end{aligned} $$](/articles/aa/full_html/2019/04/aa34580-18/aa34580-18-eq19.gif)