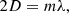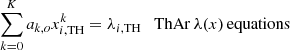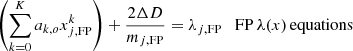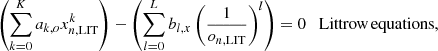| Issue |
A&A
Volume 624, April 2019
|
|
|---|---|---|
| Article Number | A122 | |
| Number of page(s) | 14 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/201833852 | |
| Published online | 24 April 2019 | |
New wavelength calibration for echelle spectrographs using Fabry-Pérot etalons
Observatoire Astronomique de l’Université de Genève, 51 Ch. des Maillettes, 1290 Versoix, Switzerland
e-mail: maria.cersullo@unige.ch, adrien.coffinet@unige.ch
Received:
13
July
2018
Accepted:
28
February
2019
Context. The study of Earth-mass extrasolar planets via the radial-velocity technique and the measurement of the potential cosmological variability of fundamental constants call for very-high-precision spectroscopy at the level of δλ/λ < 10−9. Only an accurate wavelength calibration of the spectrograph can guarantee that the aimed precision is achieved over a multi-exposure and multi-epoch data set. Wavelength accuracy is obtained by providing two fundamental ingredients: 1) an absolute and information-rich wavelength source and 2) the ability of the spectrograph and its data reduction of transferring the reference scale (wavelengths) to a measurement scale (detector pixels) in a repeatable manner.
Aims. The goal of this work is to improve the wavelength calibration accuracy of the HARPS spectrograph by combining the absolute spectral reference provided by the emission lines of a thorium-argon hollow-cathode lamp (HCL) with the spectrally rich and precise spectral information of a Fabry-Pérot-based calibration source.
Methods. On the basis of calibration frames acquired each night since the Fabry-Pérot etalon was installed on HARPS in 2011, we constructed a combined wavelength solution that fits simultaneously the thorium emission lines and the Fabry-Pérot lines. The combined fit was anchored to the absolute thorium wavelengths, which provide the “zero-point” of the spectrograph, while the Fabry-Pérot lines were used to improve the (spectrally) local precision. The obtained wavelength solution was verified for auto-consistency and tested against a solution obtained using the HARPS laser-frequency comb (LFC).
Results. The combined thorium+Fabry-Pérot wavelength solution shows significantly better performances compared to the thorium-only calibration. In both cases, the residuals of the LFC line positions to the fitted wavelength solution follow a Gaussian distribution with an rms value of about 14 m s−1 for the combined solution, and twice as large for the thorium-only solution (29 m s−1). Given these positive results, we have applied the new calibrations to scientific frames and tested the radial-velocity residual on three well-known stars: HD 10700, HD 20794, and HD 69830. In all three cases the radial-velocity (RV) scatter could be reduced compared to the measurements using the previous calibration.
Conclusions. The richness of the Fabry-Pérot spectrum helps to improve the wavelength calibration using thorium-argon lamps or extending the wavelength domain of LFCs with limited operational range. The presented techniques will therefore be used in the new HARPS and HARPS-N pipeline, and will be exported to the ESPRESSO spectrograph.
Key words: instrumentation: spectrographs / techniques: radial velocities / planets and satellites: detection / planets and satellites: general / methods: data analysis
© ESO 2019
1. Introduction
The High-Accuracy Radial-velocity Planet Searcher (HARPS; Pepe et al. 2000; Mayor et al. 2003) is a visible-wavelength high-resolution fiber-fed echelle spectrograph located at ESO’s 3.6-m telescope and is one of the most precise instruments for the measurement of radial velocities in the context of exoplanet research, reaching a precision better than 1 m s−1. New instruments aim at even better precision. The challenge for the next generation of spectrographs is to go towards the cm s−1 level of precision, for example 10 cm s−1 for Echelle SPectrograph for Rocky Exoplanets and Stable Spectroscopic Observations (ESPRESSO; Pepe et al. 2014), Gemini High Resolution Optical SpecTrograph (GHOST; Ireland et al. 2016), EXtreme PREcision Spectrograph (EXPRES; Fischer et al. 2017), and Giant Magellan Telescope (G-CLEF; Szentgyorgyi et al. 2016); 2 cm s−1 for High Resolution Spectrograph (HIRES; Marconi et al. 2016).
In order to achieve this extreme precision, these spectrographs will have to rely on accurate wavelength calibration, that is, they will have to assign to each detector pixel uniquely a wavelength that allows us to determine precisely the photocentre of a spectral line. For this purpose, one has to employ spectral sources that provide a rich spectrum of lines that can be used as absolute spectral reference.
Today, hollow-cathode thorium lamps are employed for wavelength calibration and drift measurements in most echelle spectrographs for precise radial velocities (PRV). Indeed, they offer numerous spectral features over the whole visible and near-infrared range, narrow highly symmetric line profiles, and a very stable spectrum. A large electric potential difference, applied between anode and cathode (thorium), ionizes the gas (argon) and transforms it into plasma. Under the effect of the electric field, the positive ions of the gas are accelerated towards the cathode and hit it. Following these collisions, some atoms of the cathode are sputtered and mixed with the inert gas. These atoms pass to an excited state colliding with the other particles produced during ionization and return into the ground state, then emit photons of characteristic wavelengths that are independent from the environment. By the same process also the atoms of the inert gas can emit photons at different characteristic wavelengths. The result is a rich spectrum of thorium and argon emission lines (Kerber et al. 2007).
The Atlas of the Thorium Spectrum obtained by Palmer & Engleman (1983) and more recently the thorium atlas made by Redman et al. (2014) provide a complete list of accurate thorium and argon wavelengths that are used for wavelength calibration. The wavelengths of the Atlas of the Thorium Spectrum were obtained with the McMath-Pierce 1 m Fourier Transform Spectrometer (FTS) of the National Solar Observatory at Kitt Peak. The more recent Redman et al. (2014) combines the lines measured with the 2 m FTS at the National Institute of Standards and Technology (NIST) with several other studies. Redman et al. (2014)’s list contains two sets of wavelengths: the Ritz wavelengths computed from globally optimized energy levels, and the measured wavelengths. For the same reasons as explained in Coffinet et al. (2019), we used these Ritz wavelengths as our reference.
However, several limitations hinder us reaching a precision of cm s−1 measurements such as:
-
high dynamical range of line intensities,
-
line blending in finite resolution spectrographs,
-
aging, that is, line shifts due to gas-pressure changes inside the hollow cathode lamp (HCL) over its life cycle (Kerber et al. 2007; Seemann et al. 2014),
-
flux variability and pollution by “strong” argon lines,
-
sparse coverage of the spectral range.
Because of the aforementioned limiting factors, other calibration sources are currently under development. Laser frequency combs (LFC) are undeniably the most accurate calibration source (Wilken et al. 2010; Lo Curto et al. 2012; Ravi et al. 2017). However, the current generation of LFCs still has shortcomings in term of reliability, wavelength coverage, and usability in an observatory environment. For these reasons, we proposed in the past a solution based on a Fabry-Pérot etalon (FP; Wildi et al. 2010; Chazelas et al. 2012; Cersullo et al. 2017).
These Fabry-Pérot etalons have been employed mainly for drift measurements providing nevertheless internal precision of cm s−1 and repeatability of about 10 cm s−1 over an observing night (Wildi et al. 2010). We cannot consider a passive Fabry-Pérot as an absolute calibrator, however. Indeed, the wavelength of each FP line is not known a priori, because it is related to the etalon gap (spacing of the mirrors) being a mechanical characteristic rather than anchored to fundamental physics. Therefore, an external absolute reference is necessary to anchor the spectral lines. Wildi et al. (2010) proposed linking the FP spectrum to an external absolute spectral reference such as an LFC or HCL. Bauer et al. (2015) adopted such an approach and presented algorithms that combine the HCL and the Fabry-Pérot spectra within a single wavelength calibration of echelle spectrographs. This approach has been tested on HARPS calibration spectra and eventually implemented on the Carmenes spectrograph (Caballero et al. 2016).
In the case of HARPS, the FP module guarantees nearly equally spaced spectral lines of uniform intensity over an extremely wide spectral range. The mirror coatings introduce slow variations of the phase (causing group-delay dispersion, GDD, Wildi et al. 2010). Nevertheless, we have shown in Cersullo et al. (2017) that the GDD remains stable with time and that only one global parameter, D0, the average etalon gap, must be determined by using an external absolute reference. The line separation and position being perfectly smooth and continuous in wavelength, the FP lines can be used to improve the wavelength solution, especially to determine the higher order terms of the polynomials used to describe the pixel-to-wavelength relationship (wavelength solution), which is otherwise poorly constrained by the sparse lines of hollow-cathode lamps only.
Inspired by the aforementioned works (Wildi et al. 2010, 2011; Bauer et al. 2015), we present in this paper the development of the technique to obtain a locally more accurate wavelength solution by combining the (accurate) information provided by a hollow-cathode lamp with the (precise) information given by a Fabry-Pérot etalon. Section 2 describes the characterization of the Fabry-Pérot and its main operating principles with the view of using it for wavelength calibration. In Sect. 3, we describe our concept and algorithms of wavelength calibration combining thorium and Fabry-Pérot lines. Section 4 finally presents results obtained by applying the new calibration to a few standard stars of the HARPS radial-velocity programme.
2. Characterizing the Fabry-Pérot
The HARPS Fabry-Pérot (FP) used for drift measurements consists of two flat and partially reflective parallel mirrors separated by an optical gap (cavity spacing in vacuum). HARPS’s Fabry-Pérot has a cavity of D = 7.3 mm and a measured effective finesse of 4.3. Temperature and pressure are stabilized inside a vacuum tank. Details on the employed Fabry-Pérot, its design, and its performances can be found in Wildi et al. (2010).
Multiple interferences occur and create a transmission spectrum that consists of a series of discrete peaks. At normal incidence and in a vacuum, a transmission maximum is reached every time the phase difference between the interfering waves is an integral multiple of 2π, which is equivalent to
where m is an integer number defined as the interference order and λ is the wavelength of the transmission peak. The theory and the characterization of such a kind of Fabry-Pérot is described in detail in Cersullo et al. (2017).
The Fabry-Pérot (Eq. (1)) allows us to associate a wavelength to every transmission peak of order m. If we wanted to use the Fabry-Pérot as an absolute calibrator, these wavelengths λm would have to be known with an accuracy of better than 1 m s−1. By consequence, the cavity spacing D would have to be known to better than δλ/λ = 3 × 10−9. It means that, for the FP system of HARPS, we would need to know, at each moment in time, D with an accuracy of better than 0.2 Å. In practice, the cavity spacing is known to about 1 μm, a level 10 000 times worse than needed for absolute calibration purposes. Furthermore, the used Fabry-Pérot system is fully passive, although stabilized in temperature and pressure, and may show drifts of the order of 0.2 m s−1 over 24 h.
Finally, and probably most importantly, the cavity spacing is not constant across the wavelength range of the spectrograph. This is due to the Fabry-Pérot mirrors that are coated with multi-layer dielectric films. The optical depth of the coating and thus the phase shift introduced by its reflection will result in a variable cavity spacing D(λ), which, however, we expect to be a smooth function λ and which can therefore be modelled with a low-order polynomial. If this model function was known, it could be used to assign to every transmission peak an accurate wavelength and subsequently use the Fabry-Pérot spectrum to perform the wavelength calibration of the spectrograph and obtain the corresponding wavelength solution. For this reason, the first step was to characterize the Fabry-Pérot and determine D(λ).
The initial wavelength λi of every transmission peak i of order mi of the Fabry-Pérot is determined from the calibration using the thorium spectrum. This means in practice that the spectrograph is calibrated by injecting the thorium spectrum and computing, for each spectral line and from the association of its wavelength λi with the pixel coordinate x of its photocentre and a wavelength solution λ(x), where x is the pixel coordinate of the detector. Then, the spectrograph is fed with the Fabry-Pérot spectrum. Using the previously determined thorium wavelength solution, an initial wavelength is assigned to the pixel coordinate xi of each Fabry-Pérot peak determined by a Gaussian fit on the extracted spectrum. We determine the order number mi of the peak with the formula mi = 2D0/λi, assuming a gap 2D0 = 14.6 mm and rounding to the closest integer value. Inverting this same formula and adopting the integer value for m, we determine the effective gap Di(mi) = miλi/2 of the etalon. Due to errors on the wavelength solution and the uncertainty on D0, the computed Di(mi) will be affected by errors and even discontinuities induced by misnumbering. Such a misnumbering is unlikely to happen within an echelle order of the spectrograph, since the subsequent peaks must correspond to adjacent Fabry-Pérot orders (continuous numbering). However, a discontinuity may occur at the boundary between two echelle orders, in particular if the initial D0, assumed constant, is sufficiently different from the effective Dλ at this very wavelength. On the other hand, we can assume that D(m) must be continuous and smooth. The order numbering must be corrected, if necessary, to achieve a continuous function and minimize its slope; any discontinuity or residual average slope would be an indication of a wrong order numbering. Figure 1 shows the gap variation 2Di(mi)−2D0 for each peak mi as a function of wavelength (or m). In contrast to Bauer et al. (2015), we chose to fit a polynomial function D(m) to the data pairs [Di, mi]. By comparing the Bayesian information criterion (BIC) for different degrees of the function, we concluded that the polynomial of degree nine best fits the data. The model parameters of D(m) were determined through a least-square fit. The mean effective cavity spacing that minimizes the slope and discontinuities is 2D0 = 14.6008851 mm. The rms scatter to the model is 1.85 nm, equivalent to about 38 m s−1.
 |
Fig. 1. Effective etalon gap variation 2D(λ)−2D0 as a function of wavelength as computed for each Fabry-Pérot peak using the initial thorium wavelength solution (blue line, upper panel). The green line shows the best-fit polynomial. The residuals to the fit are shown in the lower panel. |
The model function D(m) provides us with a very precise prediction of the cavity gap as a function of Fabry-Pérot order. From this function, we can determine for each Fabry-Pérot peak the precise wavelength, that is, wavelengths that are not affected by local errors of the initial wavelength solution determined using thorium lines or other local instrumental effects (e.g., pixel errors). The so-obtained wavelengths table for the Fabry-Pérot peaks can be used to construct a new wavelength solution.
3. Constructing new wavelength solutions for HARPS
3.1. Data set
HARPS has a spectral resolution of 115 000 and it covers a wavelength range from 380 to 690 nm for which we have ThAr, Fabry-Pérot, and laser frequency comb spectra. The spectral format is split between the lower, blue CCD (orders 0−43, from 378 to 530 nm) and the upper, red CCD (orders 44−71, from 533 to 690 nm). HARPS’s CCDs are made of “blocks” of 512 × 1024 pixels stitched (Wilken et al. 2010) together. The junction between these blocks is not perfect, such that the pixels at the junction may have sizes slightly different from the nominal size, producing “gaps” in the pixel coordinates and/or wavelength solution whenever the pixel number is used as the coordinate. A pixel size map is used to correct for the mismatch between pixel number and “physical” coordinate. This pixel size map has been determined on the basis of flat-field exposures (Coffinet et al. 2019). Exactly in the same way, the flat-field map (pixel sensitivity) is corrected for the effective pixel size. Hereafter we will follow the recipe described in Coffinet et al. (2019) to extract and wavelength-calibrate the spectra, and to correct them for the effect of block-stitching errors. The weighting of the equations is also the same as in Coffinet et al. (2019), with a line-dependent weight for the wavelength-solution for the Littrow equations. The only difference will consist in also using FP lines to better constrain the wavelength solution. The resulting spectra consist of gap-corrected, flat-fielded 2D spectra of 71 lines (orders of the echelle spectrum) and 4096 columns (CCD pixels along the dispersion direction).
In this section, we describe how to determine the wavelength solution of the HARPS high-resolution echelle spectrograph. We will show its architecture and configuration. The strategy starts from the wavelength frames produced by the thorium and Fabry-Pérot calibration exposures.
3.2. Wavelength-calibration plan
Every time a FP exposure is done, D(λ) is fully characterized. Whenever a FP exposure on the fiber to be calibrated is not available (e.g., in the early times of the instrument), we use the FP-line table issued from the FP exposure the closest in time and by allowing an offset for D0. In fact, we can assume that D(λ) does not change in time apart from the global D0. Therefore at each calibration only D0 is refitted in this case. The ideal (normal) calibration sequence is shown in Table 1.
HARPS calibration sequence.
The TH-TH + FP-FP exposures serve to define the FP and TH line tables for which we compute the (joint) wavelength solution. However, since the spectrograph may drift, we make an TH-FP exposure by which we define the nightly zero-point, that is, on fiber A we redetermine the wavelength solution for exposure (3), this time fitting the lines TH and FP from (2) and (3), while with fiber B we set the “zero-drift” point for exposure (3), which will serve as reference for the scientific observation (4) of the night. On this latter, possible instrumental drifts are measured by comparing the FP lines’ position on fiber B following the so-called “simultaneous-reference” concept (Baranne et al. 1996; Queloz et al. 2001). This latter concept assumes that the FP remains stable to the required instrumental precision between to the two calibration sequences, typically on timescales of 24 h.
In addition, this new method requires FP-FP exposures. The whole set of wavelength calibration is TH-TH + FP-FP + TH-FP. It is not possible to obtain a good calibration on fiber A if it has not been exposed with FP. Fiber B is much less critical, since it is used only for simultaneous reference.
3.3. Wavelength-calibration process
The diagram shown in Fig. 2 represents the structure of the new reduction process. The left part of the diagram (steps 4 to 10) corresponds to the treatment of the FP files. As described in the previous section, the goal is to obtain a model D(m) from which, by knowing the order mi of each FP line, we can compute the corresponding peak wavelength λi of the same line. The upper right part (steps 1 and 2) corresponds to the first part of the standard thorium calibration. From these two parts, we get independently (steps 11 and 3, respectively) two input tables [xi, λi, mi, Di, oi, si], where xi is the position of the line, oi the echelle order this line belongs to, and si its type (thorium or FP line). These two tables are merged in step 12 (zeros are added in the table for the mi and Di of the thorium lines simply to keep the correct number of columns, but these values are not used later) and serve as input to compute the final wavelength solution, which is obtained by a global solution (in the sense of least squares) to the ThAr, the FP, and the Littrow equations (step 13) given hereafter:
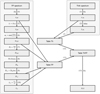 |
Fig. 2. Structure of the thorium+FP combined calibration process. |
where x is the physical (stitching-corrected) pixel coordinate along the diffraction order o of the echelle spectrograph. The weighting of the equations is the same as in Coffinet et al. (2019).
The echelle order number ranges in HARPS from 161 (blue end) to 89 (red end), but for practical reasons they are numbered from 0 to 71 in the data-reduction software and described in this way hereafter. The parameter ΔD in the second equation is used to allow for a possible temporal change in the etalon spacing, since we do not have any guarantee (and actually no requirement) that it remains stable over timescales much longer than 24 h. It is important to note that the zero-point of the calibration is locked by the thorium lines, while from the FP lines we shall use only the (spectrally) local information. Since D(m) of a given FP exposure is based on any (previously reduced) thorium exposure, the ΔD not only accounts for the actual cavity spacing but also for possible drifts of the spectrograph in the time between the previous thorium exposure and the TH-FP exposure used as the zero-point reference for the night. With this latter exposure the previously determined FP wavelengths stored in the line list are “realigned” on the absolute wavelength scale given by the thorium lines and the so-determined wavelength solution will be used for the following scientific exposures. For this reason ΔD can be redetermined independently for every wavelength solution.
The echelle spectrum consists of a number of spectral chunks (spectral orders of the echelle grating), each covering at least one free spectral range (FSR). For this reason, many of the spectral lines are present on two consecutive orders. Thanks to cross-dispersions that act perpendicularly to the main dispersion, the spectral orders are sorted by wavelength and distributed side by side across the detector. Furthermore, the Littrow equations can be used to link the wavelength solutions of the echelle orders together and give more “rigidity” to the 2D wavelength map. In fact, if we “cut” the CCD frame along the cross-dispersion direction at any arbitrary pixel coordinate, we know from the optical setup of the echelle grating (Littrow mounting) that the wavelength at that position must be inversely proportional to the echelle order number. Therefore we compute the wavelength in every echelle order for a fixed set of pixel coordinates (x = 400, 1200, 2000, 2800, and 3600). Then, we use a third-degree polynomial to describe the Littrow relation across the orders. The higher degree of the polynomial is chosen in order to include also optical aberrations and other distortions of the wavelength map. The relative weight of these equations with respect to the ThAr and FP equations is given by the number of Littrow equations, which in turn is determined by the number of “cuts” in cross-dispersion direction. In order not to over- or under-constrain the wavelength solution, we chose to adopt a number of cuts similar to the degree of the polynomial describing the wavelength scale in main-dispersion direction.
The output of the solution to the equation set given above consists of the coefficients of the wavelength solutions ak, o (four coefficients per order), the FP-gap correction ΔD (two coefficients, one for each CCD), and the coefficients of the Littrow solutions bl, x (four coefficients for each position x where these Littrow equations are computed). One has to note that the ak, o and bl, x are the same for both the thorium and Fabry-Pérot equations, while the the FP-gap correction ΔD is defined only for the FP equations. The total number of free parameters is 330 and should be compared with the more than 22 000 spectral lines (about 15 000 FP lines and more than 7000 thorium lines) used to constrain the model. The total number of parameters takes into account that the HARPS 4k4 detector is a mosaic of two mechanically independent 2k4 chips, that is, two Littrow equations.
The very first thorium calibration exposure reduced by our pipeline, a first wavelength solution based only on the thorium file, is computed. This first step is identical to the wavelength calibration process presented in Coffinet et al. (2019). The preliminary solution is then used for the Fabry-Pérot part at step 5 (see the diagram), after which we compute the combined TH+FP wavelength solution. For the thorium calibrations reduced after the first one, the preliminary wavelength solution used at step 5 is the combined TH+FP wavelength solution of the previous thorium calibration that was reduced. This additional iteration produces a more accurate wavelength solution compared to the preliminary thorium-only based solution. This new wavelength solution is used to redetermine a new model D(m), which, given the iteration, is also more accurate than the very first model based only on the thorium solution.
For practical reasons, we decided to reduce the Fabry-Pérot calibration frames inside the reduction recipe for the TH-calibration frame. The idea is to be able to use optimally, but freely, any FP calibration exposure in the computation of the combined TH+FP wavelength solution. The FP frame is nonetheless not chosen randomly. The combined solution shall use TH and FP frames taken as close in time as possible, ideally one after the other, such that possible drifts of the spectrograph are close to zero.
It must be remembered here that ΔD was not introduced to account for a possible drift of the spectrograph, but as the variable (fitted) part of the “unknown” etalon cavity spacing D0. In the frame of the proposed wavelength-calibration concept, the absolute value D of the etalon cavity spacing is not relevant, since we simply fit for it by adjusting ΔD that will take into account possible variations of D with time. Nevertheless, we cannot exclude that small drifts of the spectrograph or the CCD may occur between the time we recorded the TH exposure and the time of the FP exposure. In the proposed method, we would then interpret the spectrograph drift as a change of the FP cavity, and spectrograph drifts would simply be absorbed by the free parameter ΔD that was foreseen to fit the actual FP etalon cavity at the time of the FP calibration. In fact, a change in ΔD is strictly proportional to Δv, which in turn is proportional to a motion Δx (pixel position) of a spectral line located in the central part (at blaze) of an echelle order. On the other hand, spectrograph drifts are supposed to be approximately constant in Δx across the chip but not in Δv, mainly because along the echelle orders the linear dispersion dx/dλ varies by almost a factor of two. Therefore, a spectrograph drift is not fully modelled by a single velocity change Δv and thus by simply adjusting ΔD. For these reasons, we have finally limited the application of the presented wavelength-calibration concept to the period after 2011, from the date starting from which FP-calibration frames have started to be taken systematically on HARPS, and for which we can assume that the spectrograph drifts between the TH and the FP expsoures are small, that is, much smaller than the pixel size or typically m s−1.
Nevertheless, we would like to briefly provide an idea of how to extend this concept retro-actively to a time when FP frames were not yet available, and thus even in the presence of significant instrumental drifts. Let us assume that we have recorded at any moment of the lifetime T1 of HARPS during the same night TH-calibration spectra and stellar observations. Let us also suppose that we have taken both TH and FP calibrations at a much later time T2 > > T1, and we want to use these later FP spectra to refine the wavelength solution at T1. Then, we can use the TH spectra to determine a motion Δx(x, o) of the spectra on the CCD between T1 and T2 as a function of order o and pixel x along each order. These shifts can directly be applied to the FP line-list obtained from the FP calibration at time T2 and transposed to the time T1, such that it can be combined with the TH calibration of time T1 and so obtain a combined wavelength solution. The only assumption we made is that the “local” geometry of the detector and the spectral format did not change with time (apart from very low-order effects) and that the information of the FP frames taken later on is applicable. For clarity, we shall however again recall that this modified concept has not been applied to the tests and results presented hereafter.
3.4. Comparison with LFC data
Laser frequency combs (LFC) are the best sources for absolute wavelength calibration of astronomical spectrographs (Lo Curto et al. 2012). The spectrum of an optical LFC consists of an optical spectrum of equidistant spectral lines. Since, on the one hand, this spectrum is related to a regular train of ultra-short pulses that are synchronized with an absolute radio frequency reference such as a global positioning system (GPS) signal or atomic clock, and, on the other hand, the offset frequency is controlled by octave-spanning self-referencing, the frequencies (or wavelengths) of all spectral lines are known in absolute terms. Therefore, such a kind of absolute source, with dense and perfectly regular spectral lines, is most suitable for the accurate calibration of astronomical spectrographs.
HARPS has used an LFC since the first commissioning run held on 22 April 2015. It provides spectral emission lines with a mode spacing (i.e. repetition rate) that can be resolved by the spectrograph but dense enough to maximize the information. Typical values are of ∼20 GHz. Optical frequencies of frequency comb lines are uniquely described by the equation fn = n ⋅ frep + f0. We define the frep repetition rate as the frequency difference between two neighbouring lines and f0 as the carrier-envelope offset frequency. The frequency fn of each line is characterized by a unique integer n. Then, the nominal wavelength is derived in a standard way as λn = c/fn.
To determine these λn, a first approximate wavelength is determined based on the previous thorium-based wavelength solution. This is necessary to get the absolute wavelengths. From these approximate wavelengths, one can compute an approximate n for each LFC line based on the known frep and f0 of the laser frequency comb, f0 = 288.0598 THz et frep = 18.0 GHz (private communication with Gaspare Lo Curto). These n, which should be very close to an integer value, are then rounded to the closest integer. The theoretical LFC wavelength is then computed from this rounded n.
Given the nature of the LFC and the well-known wavelength of its lines, we decided to test our wavelength calibration method on LFC lines. The method is as follows: we calibrate the spectrograph using either the standard Data Reduction Software (DRS) (only thorium lines) or the new DRS (TH+FP). Then we measure the position of the LFC lines in pixels and apply the two wavelength solutions to transform, for each line, the pixel position in wavelength. Finally, we compare the so-obtained (measured) wavelength with the nominal wavelength of the LFC line.
Figure 3 shows the difference between the theoretical wavelengths and theose of the laser’s lines along each spectral order of HARPS covered by the LFC (orders 25th to 69th). In green we show the solution obtained after calibration of the spectra using the new DRS (combination of both thorium and Fabry-Pérot) and in blue the standard DRS (thorium only). One can remark that in all cases the residuals obtained through calibration with the new DRS are much smoother and flatter than with the standard DRS. In particular it should be remarked that the underlying wavelength solution rarely “diverges” towards the edges of the orders, which is certainly due to the much higher density of information provided by the FP lines compared to the sparse thorium lines.
 |
Fig. 3. Difference between the theoretical wavelengths of the LFC lines and the wavelengths along a subset of spectral orders for HARPS obtained after calibration with jumps gaps corrected (Coffinet et al. 2019) using the “pure” thorium-wavelength solution (blue curve) and the TH+FP wavelength solution of the new DRS (green curve). The remaining orders are shown in the Appendix A. |
In order to further illustrate that the new method is superior, we have computed the normalized distribution of the residuals on LFC line positions for the two wavelength solutions with respect to the nominal LFC wavelengths (Fig. 4). The results for the standard DRS using thorium-only (blue histogram) and the new DRS using TH+FP (green histogram) are shown and compared. As expected a simple Gaussian fit to both distributions gives nearly the same mean offset of −38.3 m s−1 and −38.0 m s−1, respectively, while the standard deviation is significantly reduced: 29.0 m s−1 for the standard DRS and 14.2 m s−1 for the new DRS. These values can be compared to the result from the LFC wavelength solution, for which a standard deviation of about 7 m s−1 was obtained (see Coffinet et al. 2019, Sect. 5.1 and Fig. 5). Both curves show the same mean offset, which is significantly different from zero. Given the fact that the offset is identical for the two wavelength solutions (using quite different algorithms), we assume that it is possibly due to a systematic offset of the wavelengths of either the thorium or the LFC-lines’ reference wavelengths. As mentioned in Coffinet et al. (2019), we suspect that the anchor frequency of the laser may be wrong by ≈100 MHz. Although admittedly not fully understood, we have to remark that, in terms of radial-velocities, this offset has no consequence.
 |
Fig. 4. Histogram of the differences in wavelengths between the theoretical and the calibrated (measured) wavelengths of the LFC spectral lines. The results obtained with the standard (blue) and the new (green) DRS are compared. The dashed plots (red and black) are the corresponding Gaussian fits. |
4. Results on verification of new calibration applied on three standard stars
Given these promising results, we decided to test the new wavelength calibration on a few “stable” stars of the HARPS long-term radial-velocity programme for which we have acquired continuous observations since the start of HARPS in October 2003. The considered objects are HD 10700 (tau Cet), probably the most observed and stable star of the HARPS programme, and HD 20794 (e Eri) and HD 69830, two quiet planet-hosting stars. Our goal was to confirm that the new implementation of the wavelength solution improves the radial velocities, that is, the rms of these stable stars is reduced in the new DRS compared to the standard and the Coffinet et al. 2019 (C19) versions of the HARPS Pipeline.
Version 3.5 of the HARPS Pipeline or data reduction software (DRS) was installed at the telescope on 20 October, 2010. All the data obtained with HARPS, including pre-2010 data, were (re-)reduced using this same version of the DRS. We shall call hereafter version 3.5 of the DRS the “standard” DRS. The C19 version of the DRS is based on DRS version 3.5 but includes a block-stitching correction map of the CCD. This change required quite a fundamental intervention in the data structure, although the algorithms of most of the data-reduction steps had not been changed. For a detailed description of the C19 DRS version, we refer to Coffinet et al. (2019). The latest version of the DRS, called “New DRS” hereafter, is similar to the C19 version, with the only exception being the wavelength calibration. Given the fact that the Fabry-Pérot was installed at the end of 2010 on HARPS, we applied the “New DRS” only on the 2011–2017 data set.
In May 2015, a new set of octagonal fibers was installed on HARPS (Lo Curto et al. 2015), which required an adaptation of the DRS since both the spectral format and the instrumental profile (IP) had slightly changed. All the DRS versions have been applied separately to the pre-6/2015 data set (before the fiber change) and on the post-6/2015 data set (after the fiber change), since they had to be treated as if they had been obtained from two different instruments (different configuration files in the DRS). As a consequence, all three versions of the DRS foresee an additional fit parameter, that is, one free offset value between pre- and post-6/2015 data.
We compare in the following the three versions of the DRS in terms of radial velocities. To do so we look at the radial-velocity dispersion after subtraction of known or well-characterized signals. Also, for all targets, the Lomb-Scargle periodograms (LSP) of the residuals and the false alarm probability (FAP) of residual signals were computed. We define a signal as statistically significant when its peak exceeds a FAP level of 10−2. A summary of the results for the three analysed stars is given in Table 2.
Comparison of the standard (std), the intermediate (C19; Coffinet et al. 2019), and the new (new) versions of the DRS.
4.1. HD 10700
The star HD 10700, or τ Ceti, is a G8V star located within 12 light-years (3.7 parsecs) of the solar system. It has a very low “raw” RV dispersion just above 1 m s−1 (Pepe et al. 2011; Tuomi et al. 2013).
Comparing the data issued from the standard and new versions of the DRS, we found a few peaks in the LSP with a FAP below 1%. For the sake of simplicity and transparency, we fitted only the most significant peak at a period of ∼240 days. This signal does not correspond to any of the planets claimed by Tuomi et al. (2013) and Feng et al. (2017a), although it could be a one-year alias of the claimed planet f at 636.13 days (or vice-versa). Since for the C19 DRS we find an unlikely value for the eccentricity e = ∼0.96 for this signal, we decided to fix e = 0 for all three data sets (standard, C19, and new DRS) in order not to penalize any of the data sets and make the most direct comparison. Table 3 provides the model parameters.
Model parameters of the Keplerian fit to the HD 10700 radial-velocity data obtained with the new DRS.
In terms of radial-velocity dispersion, after subtracting the one-planet signal, we obtain 1.13 and 1.56 m s−1 (before and after change of fibres) for the standard DRS, and 1.03 and 0.98 m s−1 for the new DRS, respectively. The two data sets, before and after the change of the fibres, are fitted jointly. The values obtained with the C19 DRS, which already includes the corrections of the CCD block-stitching error (see Coffinet et al. 2019) but not the new combined TH+FP wavelength calibration, lie in between the results of the two other DRS.
The left side of Fig. 5 shows the radial velocities of HD 10700 and the fitted one-planet model. The right side of the figure shows instead the LSP of the residuals to the fit for every version of the DRS, respectively, and FAPs of 50%, 10%, 1%, and 0.1%. In the case of the new DRS, we have a significant signal at ∼20 days, which may correspond to a signal reported by Tuomi et al. (2013) and Feng et al. (2017a) and assigned to a potential planet HD 10700 g. Similarly, the weaker signal at 51.41 days may correspond to the signal assigned to HD 10700 h. Based on the data obtained with the new DRS, we could detect other signals reported by Tuomi et al. (2013) and Feng et al. (2017a). The long-period signal around 2000−2700 days is significant but may be attributed either to stellar activity or instrumental effects. Only continued observations and additional observables (e.g., activity indicators) may discriminate between the various possibilities. This study was not pursued, however, not being the scope of this paper.
 |
Fig. 5. Left panels: HARPS RV data of HD 10700 obtained between 2011 and 2017 are shown being reduced with the standard (top), C19 (centre), and new DRS (bottom). The data set before the change of the fibres is plotted in blue while the data set after the change of the fibres is plotted in red. Right panels: respective LSP of the residuals to the fitted Keplerian model. |
4.2. HD 20794
The star HD 20794 is a bright G8 dwarf ∼20 light years away from Earth. In 2011, the discovery of two, possibly three planets orbiting this star was announced (Pepe et al. 2011). As part of our test, we re-reduced the data set taken after 2011 with the three DRS versions and compared the result.
The two signals at periods of ∼18 and ∼89 days, corresponding to planets b and d, respectively, could easily be confirmed, while the signal at a period of ∼40 days, which had been reported by Pepe et al. (2011) to be at the limit of significance, is not detected. Instead, another signal at ∼231 days appeared clearly in all the data sets. This signal may correspond to that around 250 days found by Feng et al. (2017b) and proposed to be the yearly alias of another signal at 147 days. We found, however, that fitting the 231 days signal perfectly removed residual power at other periods, while fitting the 147 days produced worse results. We adopted therefore a three-planet model with the parameters presented in Table 4. The radial-velocity dispersion, after subtracting the three-planet signal, results in 1.05 and 1.36 m s−1 (before and after change of fibres) for the standard DRS, and 1.04 and 0.96 m s−1 for the new DRS, respectively. The values obtained with the C19 DRS are slightly worse but similar to the new DRS.
Model parameters of the Keplerian fit to the HD 20794 radial-velocity data obtained with the new DRS.
The left side of Fig. 6 shows the radial velocities of HD 20794 and the fitted three-planet model. The right side of the figure shows again the LSP of the residuals to the fit for every version of the DRS, respectively, with the usual FAP levels. We would like to note that no significant signal is left in the data produced with the new DRS, and that the power distribution is amazingly uniform.
 |
Fig. 6. Left panels: HARPS RV data of HD 20794. The plotted period, the order of the different DRS, and the colour of the two different data sets (before and after the change of the fibres) is the same as in Fig. 5. Right panels: respective LSP of the residuals to the fitted Keplerian model with the two known planets at periods of 18.32 and 89.7 days and another significant signal at 230.58 days. |
4.3. HD 69830
The star HD 69830 is a yellow dwarf star located ∼41 light-years away (van Leeuwen 2007). It is a G8-K0V star with magnitude V = 5.95) harbouring three super-Earth/Neptune-mass planets (Lovis et al. 2006).
For all the versions of the DRS we fitted the planets at 8.7 and 31 day periods (planets b and c) reported by Lovis et al. (2006), while the signal at 200 days (planet d) did not appear in a significant way, most probably due to the lower number of observations in the period from 2011 to 2017. In addition, the star has become more active in recent years, showing higher stellar jitter. Therefore we remained on the two-planet model for all versions of the DRS. Again we refer to Table 5 for the model parameters.
Model parameters of the Keplerian fit to the HD 69830 radial-velocity data obtained with the new DRS.
The radial-velocity dispersion, after subtracting the two-planet signal, is 1.56 and 1.32 m s−1 (before and after change of fibres) for the standard DRS, and 1.44 and 1.35 m s−1 for the new DRS, respectively. The values obtained with C19 are slightly worse but similar to the new DRS.
The left side of Fig. 7 shows the radial velocities of HD 69830 and the fitted two-planet model. The right side of the figure shows the LSP of the residuals to the fit for every version of the DRS, respectively, with the usual FAP levels. We have to note here that the improvement with the new DRS is still significant, but much less spectacular than for the other targets. The reason might be simply that the dispersion of this star is likely to be dominated by stellar jitter (Tanner et al. 2014) rather than by “calibration noise”.
 |
Fig. 7. Left panels: HARPS RV data of HD 69830. The plotted period, the order of the different DRS, and the colour of the two different data sets (before and after the change of the fibres) is the same as in Fig. 5. Right panels: respective LSP of the residuals to the fitted Keplerian model with the two known planets at 8.67 and 31.64 day periods. |
The analysis of the three targets gives a clear indication of the improvements obtained with the new calibration strategy, although the results differ slightly depending on the star. We find, however, the following common aspects for all the targets:
-
The standard DRS shows much higher residuals on data obtained after the fiber change. This is simply due to the fact that the standard DRS had not been optimized for but rather only adapted to the new spectral format. By consequence, the initial guess for the reference wavelengths of the thorium lines had not been updated, leading by as a matter of fact to poorer calibration quality.
-
The most important improvement of the C19 and new DRS with respect to the standard DRS is obtained on post-6/2015 data. This is a direct consequence of the previous point.
-
The global dispersion is systematically lower for the C19 DRS and lowest for the new DRS.
-
Even when considering only pre-6/2015 data, the dispersion is reduced by the C19 DRS and is lowest on data obtained with the new DRS.
-
It is important to note that for the new DRS the dispersion is not only reduced but also similar in both pre- and post-6/2018 data.
5. Conclusion
Hollow-cathode thorium lamps (HCL) have successfully served for wavelength calibration and drift measurements in astronomical spectrographs despite their non-ideal characteristics. Fabry-Pérot etalons combined with HCL are good alternatives that produce regularly spaced calibration lines covering the entire spectral range of the spectrograph. Since the cavity width of the etalon is not known accurately and considering possible drifting over time, the peak wavelengths are uncertain. Therefore, Fabry-Pérot interferometers cannot be used as an absolute calibrator. The combination with HCL provides the possibility of “anchoring” the wavelength solution in absolute terms. We have developed and presented in our paper a method that allows us to combining the precision provided by the etalon with the accuracy provided by the HCL.
We demonstrated that the developed calibration method works very well if we include also the CCD block-stitching correction developed by Coffinet et al. (2019). We first tested the new wavelength solution on the HARPS LFC, demonstrating that the dispersion of difference between the LFC-lines wavelengths after calibration and their theoretical wavelengths is reduced by more than a factor of two and that the residual to the wavelength solution is flatter along the spectral orders. The measured systematic offset of 38 m s−1 of the LFC lines with respect to their nominal wavelength is not understood but at least it is identical for all versions of the DRS. We conclude that this offset arises either from the reference wavelengths of the thorium or from those of the LFC.
Finally, we applied the new wavelength calibration to three stable stars of the HARPS programme. Also this test demonstrated that the radial-velocity dispersion is reduced in all cases, although the improvement is obviously more visible on very quiet stars.
We conclude that the new DRS significantly improved the quality of the radial velocities and should be considered in future to be used as a standard pipeline for HARPS after confirming the functionalities and the performances also in statistical terms over the full HARPS data set. The use of a “calibrated” FP can be considered a less expensive alternative to broad-band LFCs for precise and accurate wavelength calibration and may be considered for existing instruments, such as HARPS-N, CORALIE, ESPRESSO, SPIRou, as well as for future instruments such as NIRPS or HIRES at the Extremely Large Telescope.
Acknowledgments
This publication makes use of the Data & Analysis Centre for Exoplanets (DACE), which is a facility based at the University of Geneva (CH) dedicated to extrasolar planets data visualization, exchange, and analysis. DACE is a platform of the Swiss National Centre of Competence in Research (NCCR) PlanetS, bringing together the Swiss expertise in exoplanet research. The DACE platform is available at https://dace.unige.ch. The NCCR are a research instrument of the Swiss National Science Foundation. We acknowledge the Swiss National Science Foundation for their continuous support through project funding.
References
- Baranne, A., Queloz, D., Mayor, M., et al. 1996, A&AS, 119, 373 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bauer, F. F., Zechmeister, M., & Reiners, A. 2015, A&A, 581, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Caballero, J. A., Guàrdia, J., López del Fresno, M., et al. 2016, Proc. SPIE, 9910, 99100E [Google Scholar]
- Cersullo, F., Wildi, F., Chazelas, B., & Pepe, F. 2017, A&A, 601, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chazelas, B., Pepe, F., & Wildi, F. 2012, Proc. SPIE, 8450, 845013 [CrossRef] [Google Scholar]
- Coffinet, A., Lovis, C., Dumusque, X., & Pepe, F. 2019, A&A, in press, DOI: 10.1051/0004-6361/201833272 [Google Scholar]
- Feng, F., Tuomi, M., Jones, H. R. A., et al. 2017a, AJ, 154, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Feng, F., Tuomi, M., & Jones, H. R. A. 2017b, A&A, 605, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fischer, D., Jurgenson, C., McCracken, T., et al. 2017, AAS Meeting Abstracts, 229, 126.04 [Google Scholar]
- Ireland, M. J., Artigau, É., Burley, G., et al. 2016, Proc. SPIE, 9908, 99087A [CrossRef] [Google Scholar]
- Kerber, F., Nave, G., Sansonetti, C. J., Bristow, P., & Rosa, M. R. 2007, ASP Conf. Ser., 364, 461 [NASA ADS] [Google Scholar]
- Lo Curto, G., Manescau, A., Avila, G., et al. 2012, Proc. SPIE, 8446, 84461W [NASA ADS] [CrossRef] [Google Scholar]
- Lo Curto, G., Pepe, F., Avila, G., et al. 2015, The Messenger, 162, 9 [NASA ADS] [Google Scholar]
- Lovis, C., Mayor, M., Pepe, F., et al. 2006, Nature, 441, 305 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Marconi, A., Di Marcantonio, P., D’Odorico, V., et al. 2016, Proc. SPIE, 9908, 990823 [CrossRef] [Google Scholar]
- Mayor, M., Pepe, F., Queloz, D., et al. 2003, The Messenger, 114, 20 [NASA ADS] [Google Scholar]
- Palmer, B. A., & Engleman, R. 1983, Atlas of the Thorium spectrum (Los Alamos: National Laboratory) [Google Scholar]
- Pepe, F., Mayor, M., Delabre, B., et al. 2000, Proc. SPIE, 4008, 582 [Google Scholar]
- Pepe, F., Lovis, C., Ségransan, D., et al. 2011, A&A, 534, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pepe, F., Molaro, P., Cristiani, S., et al. 2014, Astron. Nachr., 335, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Queloz, D., Mayor, M., Udry, S., et al. 2001, The Messenger, 105, 1 [NASA ADS] [Google Scholar]
- Ravi, A., Phillips, D. F., Beck, M., et al. 2017, J. Astron. Telesc. Instrum. Syst., 3, 045003 [NASA ADS] [CrossRef] [Google Scholar]
- Redman, S. L., Nave, G., & Sansonetti, C. J. 2014, ApJS, 211, 4 [Google Scholar]
- Seemann, U., Anglada-Escude, G., Baade, D., et al. 2014, Proc. SPIE, 9147, 91475G [CrossRef] [Google Scholar]
- Szentgyorgyi, A., Baldwin, D., Barnes, S., et al. 2016, Proc. SPIE, 9908, 990822 [CrossRef] [Google Scholar]
- Tanner, A. M., Boyajian, T. S., von Braun, K., et al. 2014, AAS Meeting Abstracts, 223, 347.27 [Google Scholar]
- Tuomi, M., Jones, H. R. A., Jenkins, J. S., et al. 2013, A&A, 551, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Leeuwen, F. 2007, Astrophys. Space Sci. Lib., 350 [Google Scholar]
- Wildi, F., Pepe, F., Chazelas, B., Lo Curto, G., & Lovis, C. 2010, Proc. SPIE, 7735, 77354X [Google Scholar]
- Wildi, F., Pepe, F., Chazelas, B., Lo Curto, G., & Lovis, C. 2011, Techniques and Instrumentation for Detection of Exoplanets V, 8151, 81511F [CrossRef] [Google Scholar]
- Wilken, T., Lovis, C., Manescau, A., et al. 2010, MNRAS, 405, L16 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Additional data
Figure 3 shows the difference between the theoretical wavelengths and the ones of the lasers lines along a subset of spectral order of HARPS covered by the LFC. In this appendix, we report the comparison between the solution obtained after calibration of the spectra using the new DRS (combination of both thorium and Fabry-Pérot) and the standard DRS (thorium only) along each spectral order of HARPS covered by the LFC (orders 25th to 69th).
 |
Fig. A.1. Difference between the theoretical wavelengths of the LFC lines and the wavelengths along the spectral orders for HARPS obtained after calibration with jumps gaps corrected (Coffinet et al. 2019) using the “pure” thorium-wavelength solution (blue curve) and the TH+FP wavelength solution of the new DRS (green curve). |
 |
Fig. A.1. continued. |
 |
Fig. A.1. continued. |
All Tables
Comparison of the standard (std), the intermediate (C19; Coffinet et al. 2019), and the new (new) versions of the DRS.
Model parameters of the Keplerian fit to the HD 10700 radial-velocity data obtained with the new DRS.
Model parameters of the Keplerian fit to the HD 20794 radial-velocity data obtained with the new DRS.
Model parameters of the Keplerian fit to the HD 69830 radial-velocity data obtained with the new DRS.
All Figures
 |
Fig. 1. Effective etalon gap variation 2D(λ)−2D0 as a function of wavelength as computed for each Fabry-Pérot peak using the initial thorium wavelength solution (blue line, upper panel). The green line shows the best-fit polynomial. The residuals to the fit are shown in the lower panel. |
| In the text | |
 |
Fig. 2. Structure of the thorium+FP combined calibration process. |
| In the text | |
 |
Fig. 3. Difference between the theoretical wavelengths of the LFC lines and the wavelengths along a subset of spectral orders for HARPS obtained after calibration with jumps gaps corrected (Coffinet et al. 2019) using the “pure” thorium-wavelength solution (blue curve) and the TH+FP wavelength solution of the new DRS (green curve). The remaining orders are shown in the Appendix A. |
| In the text | |
 |
Fig. 4. Histogram of the differences in wavelengths between the theoretical and the calibrated (measured) wavelengths of the LFC spectral lines. The results obtained with the standard (blue) and the new (green) DRS are compared. The dashed plots (red and black) are the corresponding Gaussian fits. |
| In the text | |
 |
Fig. 5. Left panels: HARPS RV data of HD 10700 obtained between 2011 and 2017 are shown being reduced with the standard (top), C19 (centre), and new DRS (bottom). The data set before the change of the fibres is plotted in blue while the data set after the change of the fibres is plotted in red. Right panels: respective LSP of the residuals to the fitted Keplerian model. |
| In the text | |
 |
Fig. 6. Left panels: HARPS RV data of HD 20794. The plotted period, the order of the different DRS, and the colour of the two different data sets (before and after the change of the fibres) is the same as in Fig. 5. Right panels: respective LSP of the residuals to the fitted Keplerian model with the two known planets at periods of 18.32 and 89.7 days and another significant signal at 230.58 days. |
| In the text | |
 |
Fig. 7. Left panels: HARPS RV data of HD 69830. The plotted period, the order of the different DRS, and the colour of the two different data sets (before and after the change of the fibres) is the same as in Fig. 5. Right panels: respective LSP of the residuals to the fitted Keplerian model with the two known planets at 8.67 and 31.64 day periods. |
| In the text | |
 |
Fig. A.1. Difference between the theoretical wavelengths of the LFC lines and the wavelengths along the spectral orders for HARPS obtained after calibration with jumps gaps corrected (Coffinet et al. 2019) using the “pure” thorium-wavelength solution (blue curve) and the TH+FP wavelength solution of the new DRS (green curve). |
| In the text | |
 |
Fig. A.1. continued. |
| In the text | |
 |
Fig. A.1. continued. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.