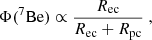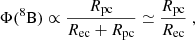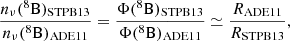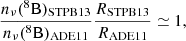| Issue |
A&A
Volume 623, March 2019
|
|
|---|---|---|
| Article Number | A126 | |
| Number of page(s) | 7 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201834993 | |
| Published online | 18 March 2019 | |
Effects of a revised 7Be e−-capture rate on solar neutrino fluxes⋆
1
Gran Sasso Science Institute, Viale Francesco Crispi, 7, 67100 L’Aquila, Italy
e-mail: diego.vescovi@gssi.it
2
INFN, Section of Perugia, Via A. Pascoli snc, 06123 Perugia, Italy
3
INAF, Observatory of Abruzzo, Via Mentore Maggini snc, 64100 Teramo, Italy
4
University of Perugia, Department of Physics and Geology, Via A. Pascoli snc, 06123 Perugia, Italy
5
INFN, Laboratori Nazionali del Gran Sasso, Via G. Acitelli, 22, Assergi, L’Aquila, Italy
6
Division of physics School of Science and Technology Università di Camerino, Italy
7
Faculty of Mathematics and Physics, Charles University, Prague, Czech Republic
8
European Centre for Theoretical Studies in Nuclear Physics and Related Areas (ECT*-FBK) and Trento Institute for Fundamental Physics and Applications (TIFPA-INFN), Trento, Italy
Received:
28
December
2018
Accepted:
4
February
2019
Context. Electron-capture on 7Be is the main production channel for 7Li in several astrophysical environments. Theoretical evaluations have to account for not only the nuclear interaction, but also the processes in the plasma in which 7Be ions and electrons interact. In recent decades several estimates were presented, pointing out that the theoretical uncertainty in the rate is in general of a few percent.
Aims. In the framework of fundamental solar physics, we consider a recent evaluation for the 7Be+e− rate, which has not been used up to now, in the estimate of neutrino fluxes.
Methods. We analyzed the effects of the new assumptions on standard solar models (SSMs) and compared the results obtained by adopting the revised 7Be+e− rate to those obtained by that reported in a widely used compilation of reaction rates (ADE11).
Results. We found that new SSMs yield a maximum difference in the efficiency of the 7Be channel of about −4% with respect to what is obtained with the previously adopted rate. This fact affects the production of neutrinos from 8B, increasing the relative flux up to a maximum of 2.7%. Negligible variations are found for the physical and chemical properties of the computed solar models.
Conclusions. The agreement with the Sudbury Neutrino Observatory measurements of the neutral current component of the 8B neutrino flux is improved.
Key words: neutrinos / nuclear reactions, nucleosynthesis, abundances / Sun: abundances / Sun: helioseismology / Sun: interior
The electron-capture table is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/623/A126
© ESO 2019
1. Introduction
Solar models and their comparisons with observations are a powerful tool for probing the solar interiors with high accuracy, describing the trend of the sound speed, and predicting how neutrinos are distributed among the various channels (see, e.g., Bahcall et al. 2001, for a review).
Solar neutrino measurements in particular those from the 8B channel (Aharmim et al. 2013; Abe et al. 2016) yielded information on fundamental neutrino properties; nowadays these properties are measured with an increasing accuracy and detailed knowledge of neutrino fluxes is also important to this aim.
Very recently the Borexino collaboration presented the first global analysis of three individual neutrino components of the proton–proton (pp) chain, namely pp, 7Be, and pep neutrinos, also putting an upper limit for those from CNO, over an energy range from 0.19 MeV to 2.93 MeV (Agostini et al. 2018).
These new data on neutrino fluxes can be used to improve our knowledge of the solar interiors (Vinyoles et al. 2017), which is still beset with problems; among these, of special relevance are those raised by the compilations of solar abundances based on 3D atmospheric models (Asplund 2005), which lead to disagreements with the measured sound speed (Bahcall et al. 2005b).
Standard solar model predictions for neutrino fluxes are then very sensitive to the reaction rates adopted, obviously including electron-captures in the plasma (which are also of great importance for several other astrophysical problems). The electron-capture rate on 7Be itself is strongly dependent on the density and temperature distribution in the stellar structure (Simonucci et al. 2013); in solar conditions, in particular, this destruction channel of 7Be dominates over proton captures (Adelberger et al. 1998). From this latter branching, through 8B-decays, further neutrinos are emitted and can be detected by experiments such as Super-Kamiokande, Sudbury Neutrino Observatory (SNO), and KamLand. The observed flux of 8B neutrinos is expected to be inversely proportional to the electron-capture rate on 7Be because the counting rate in experiments is determined by the number of proton-capture reactions occurring per unit of time (Bahcall & Moeller 1969). Despite many different estimates presented (Bahcall 1962; Bahcall & Moeller 1969; Johnson et al. 1992; Gruzinov & Bahcall 1997), the accuracy in our knowledge of the relative importance of these two channels in not yet satisfactory and improvements have been limited over the years.
In this work we make a step forward by using a new estimate of the electron-capture rate on 7Be (Simonucci et al. 2013, hereafter STPB13) to compute standard solar models (SSMs). The results are then compared with those obtained by the widely used rate by Adelberger et al. (2011; hereafter ADE11), focusing our attention on solar neutrino fluxes. We make use of a tabulated version of the decay rate by STPB13. The aforementioned table, available at the CDS, contains the following information. Column 1 lists the density over the mean molecular weight for electrons in units of g cm−3, Col. 2 gives the temperature in units of K, and Col. 3 provides the value of the electron-capture rate in units of s−1. All the quantities are expressed in logarithmic scale. We also present an analytical approximation to the electron-capture rate. Our work is organized as follows. In Sect. 2 the main features of the adopted stellar evolutionary code and of SSMs are described. Section 3 illustrates the calculation of the electron-capture rate on 7Be and presents a comparison with the previous estimate. In Sect. 4 we analyze the main characteristics of the ensuing SSM, while in Sect. 5 the impact of the adopted rate on neutrinos from the 8B channel is discussed. We summarize our results in Sect. 6.
2. Standard solar model
A SSM represents the mathematical way of fitting the present-day Sun status, provided some boundary conditions as luminosity, radius, mass, and composition are available. Other important features such as temperature, pressure, sound-speed profiles, solar photospheric abundances, and neutrino fluxes can then be predicted. Each of these quantities strictly depends on the nuclear reactions at work in the Sun’s interiors, whose main outcome is helium production by hydrogen burning. This occurs through the pp-chain (∼99%) and, to a much lesser extent, through the CN-cycle (∼1%). Although the latter is not very important for the energy production in our Sun, it is relevant for the details of the neutrino production and as a test of the correctness of the predictions. Other ingredients of the input physics, such as equation of state (EoS), opacity, and chemical composition are also crucial for predicting the solar quantities mentioned above.
The essentials of a SSM include the full evolution of a 1 M⊙ star from the pre-main sequence to the present solar age t⊙ = 4.566 Gyr, usually by considering that mass loss is negligible. In addition, a SSM is required to reproduce, once the presolar composition is fixed, the present-day solar mass M⊙, age, radius R⊙, and luminosity L⊙ as well as the observed metal-to-hydrogen ratio (Z/X)⊙ at the surface of the Sun. In order to do this, in our models we calibrated accordingly, with an iterative procedure, the initial helium and metal mass fractions Yini and Zini, respectively, as well as the mixing-length parameter (αMLT). Our solar models have been calculated with the FUll Network Stellar evolution (FUNS) code (Straniero et al. 2006; Piersanti et al. 2007; Cristallo et al. 2011). All the models assume a present solar luminosity of L⊙ = 3.8418 × 1033 erg s−1, a present solar radius R⊙ = 6.9598 × 1010 cm, and a solar mass M⊙ = 1.989 × 1033 g (Allen 1963; Bahcall et al. 2005a).
The input physics is basically the same adopted by Piersanti et al. (2007), but includes a few recent updates as listed below. We adopted the nuclear reaction rates presented in Table 1, except for the case of the 7Be electron-captures, for which we used either the rate suggested by Adelberger et al. (2011) or that computed by Simonucci et al. (2013). Concerning the mean energy loss in the individual branches of neutrino production, we used the experimental values suggested by Vissani (2018; see their Table 2). For electron screening effects in the solar plasma we adopted the Salpeter formula for the weak-screening, as recommended by Gruzinov & Bahcall (1998) and Bahcall et al. (2002). The EoS is the same as that described by Straniero (1988) for fully ionized matter, in the form updated by Prada Moroni & Straniero (2002) for log T [K] ≥ 6.0 and a Saha equation for log T [K] < 6.0. Atomic diffusion has been included, taking into account the effects of gravitational settling and thermal diffusion, by inverting the coupled set of Burgers equations (Thoul et al. 1994; Piersanti et al. 2007). For radiative opacities, we used the OPAL tables (Iglesias & Rogers 1996) for high temperatures (log T [K] ≥ 4.0) and the Ferguson et al. (2005) molecular opacities for low temperatures (log T [K] < 4.0), corresponding to the scaled-solar composition given either by Grevesse & Sauval (1998) or by Palme et al. (2014; hereafter GS98 and PLJ14, respectively). Different choices of (Z/X)⊙ correspond to different metal distributions in the solar structure, which, in their turn, change the calculated depth of the convective zone. Indeed, it was pointed out that SSMs with low metal abundances (i.e., with low (Z/X)⊙ values) disagree with the helioseismologically measured sound speed, the depth of the convective zone, and the surface helium abundance (see, e.g., Bahcall et al. 2004). Solving this disagreement, known as the “solar abundance problem”, is an issue not related to 7Be decay and is therefore beyond the scope of this work. We show that the effects of using the new rate are independent from the solar mixture assumed and can be stated in a general way.
Major reaction rates included in the SSMs presented in this paper.
Finally, we have to mention that all the analyses presented in the various cases of this work were performed by keeping all the physical parameters fixed, except for the 7Be electron-capture rate, to evaluate the specific role of this rate and to minimize the effects related to other inputs. The results obtained with the updated estimate of the 7Be electron-capture rate given by STPB13 were compared with those obtained with the evaluation given by ADE11 for the two mentioned stellar choices of the chemical composition. In principle, different assumptions for the composition, i.e., for the metal abundances, may lead to differences in the solar core temperature, hence also in the solar structure and in neutrino fluxes; see Sect. 4 for a quantitative discussion.
3. Electron-capture on 7Be
The deep stellar interiors are characterized by high densities and high temperatures. This implies that atoms are almost completely ionized; therefore, when describing the stellar core matter, it is necessary to apply the methods of plasma physics. The radioactive decay of a particular radioisotope (and its mean lifetime τ) is strongly dependent in such plasma conditions on the density ρ and temperature T of the plasma itself. In short, to provide an estimate of decay rates in stellar conditions we have to rely on accurate models for the plasma.
Many contributions, developed between the 1960s and 1980s, considered a ionized plasma, whose degree of ionization is described through the Saha equation. Free electrons, acting as a screen inside the Debye radius, are treated as a Maxwellian gas (Takahashi & Yokoi 1987). Concerning the specific case of 7Be electron-captures, the first detailed calculation from continuum states was done by Bahcall (1962). Subsequently, estimates of the bound-electron contributions were also made (Iben et al. 1967; Bahcall & Moeller 1969; Bahcall 1994). A recommended resulting rate, based on all these calculations, was proposed by Adelberger et al. (1998) and Adelberger et al. (2011). More general treatments have also been developed over the years (Gruzinov & Bahcall 1997; Brown & Sawyer 1997; Sawyer 2011), but always referring to solar core conditions and maintaining an approach resembling the Born–Oppenheimer (BO) one. In addition to this, it was recognized that the major uncertainty affecting the decay rate arises from possible deviations from a pure Debye screening. Indeed, Johnson et al. (1992) estimated these possible corrections to the Debye–Hückel (DB) approximation by means of self-consistent thermal Hartree calculations, concluding that the proposed rate was correct within an accuracy of about 2%. In this regard, it has to be remarked that the temperature at the center of the Sun (T ≃ 15.5 MK) is too high for electron degeneracy to set in. Hence, the classical approximation used, for example, by Bahcall to derive his rate is well founded for the solar conditions.
Recently, Simonucci et al. (2013) developed a first-principles approach to derive the 7Be electron-capture rate by modeling the electron-capture as a two-body scattering process 7Be-e−. To this aim, the e−-capture process is assumed to be proportional to the electronic density at the nucleus ρe(0), which is screened and modified by the presence of the surrounding particles. We notice in passing that the DB approximation used by Bahcall represents the high-temperature classical limit of the approach developed by Simonucci et al. (2013), which provides the e−-capture rate on 7Be over a range of plasma densities and temperatures definitively wider than that in the solar core conditions.
In this approach, the plasma is assumed hot and is modeled as a homogeneous Fermi gas made by 7Be atoms, surrounded by Np protons (hydrogen nuclei) and Ne electrons, at various temperatures T and densities ρ. The motion of quantum Fermi gases is ruled by the Schrödinger equation and described in a reference frame fixed on the Be nucleus. Because of the adopted non-inertial frame, the Hamiltonian of the system contains non-inertial terms, coupling the motion of particles of the different species. As Be is definitively more massive, all these terms can be safely neglected, so that a factorization of the eigenfunctions can be performed and separable eigensolutions can be found. This procedure is reminiscent of the conditions for the adiabatic theorem, and thus it represents an adiabatic approximation. In this way the many-body scattering problem is reduced to a screened two-body problem. As such, ρe(0) is computed by solving a coupled Hartree–Fock (HF) self-consistent system of equations for both protons and electrons in the electric field generated by a 7Be nucleus located at the origin of the reference frame. The HF treatment of the Coulomb repulsion is satisfactory and accurate enough to comply with the electron correlation in stellar conditions (see Simonucci et al. 2013).
The mean lifetime, resulting from this method, is in general compatible with estimates by Bahcall (1962, 1994), Bahcall & Moeller (1969), and Adelberger et al. (1998, 2011); however, the mean lifetime has values that in solar conditions are smaller by ∼3 − 4% with respect to those estimated in the mentioned works. Far from these conditions, the differences can be much more pronounced (see Fig. 1). Details of the calculations are provided in Simonucci et al. (2013). The total reaction rate λ for 7Be(e−,νe)7Li by STPB13 can also be expressed analytically in an approximate formula, as a function of temperature, density, and composition.
 |
Fig. 1. Fractional variation of the 7Be electron-capture rate, Δλ/λ[%] = 100 ⋅ (RSTPB13 − RADE11)/RADE11, as a function of ρ/μe and T, adopting the Simonucci et al. (2013) rate, as compared to that of Adelberger et al. (2011) for the PLJ14 solar composition (see Sect. 2). The solar core conditions are highlighted with the common solar symbol. |
An expression that agrees with an accuracy of 2% to the tabulated results for the rate λ [s−1], in the region of relevance for solar physics, i.e., 35 ≲ ρ/μe [g cm−3] ≲ 105 and 10 ≤ T6 [MK] ≤ 16, is written as
In this equation, μe is the mean molecular weight per electron, T6 is the temperature in units of 106 K, and ρ is the density in units of [g cm−3]. Thus, the electron density is ne = ρ/(mpμe), where mp is the proton mass. The values of the four coefficients κ, α, β, γ, whose units ensure the correct dimension of Eq. (1), are reported in Table 2. We notice that a nonlinear term in the density is present, while it was absent in Bahcall’s calculations. In fact, this term results from the Coulomb repulsion (electron screening) acted upon the electrons, which modifies the density close to the nucleus. Taking into account such a nonlinearity requires the introduction of a higher number of polynomial terms. We recall, however, that in this work we make use of a tabulated version of the decay rate by STPB13: in fact, the adopted fine resolution allows us to compute highly accurate solar models without adding further uncertainties deriving from the use of an analytical formula. We note that in our discussion, none of the nuclear reaction rates relevant for the standard solar model has been modified, so that expected variations are entirely a consequence of the new approach adopted in computing 7Be electron-capture rate. Nevertheless, the change in the electron density, due to the formalism introduced by Simonucci et al. (2013) to describe e−-capture on 7Be, might also be relevant for other charged-particle interactions, leading to a correction in the screening factor. An investigation of this possibility and the quantitative estimation of this effect deserves dedicated analyses and future work.
Coefficients for the analytical approximation to the STPB13 and ADE11 electron-capture rates.
4. Solar neutrino fluxes
Stars with initial mass M ≲ 1.2 M⊙ primarily burn hydrogen through the pp-chain. The latter has three main branches, namely the ppI-, ppII-, and ppIII-cycles. The pp, 8B β-decay, and hep reactions produce neutrino spectra with characteristic shapes and with energies from zero up to a maximum energy q. In particular, the neutrinos coming from the weak hep branch are the most energetic neutrinos produced by the Sun (q ≤ 18.773 MeV) and, thus, are observed in the SNO and Super-Kamiokande event distributions because they populate energy bins above the 8B neutrino endpoint. The electron-capture reactions p + e− + p and 7Be + e− produce, on the contrary, emission lines, possibly broadened by thermal effects. Concerning the 7Be neutrinos, they form two distinct lines, corresponding to population of both the ground state (89.5%) and the first excited state (10.5%) in 7Li (Vissani 2018).
The ppI, ppII, and ppIII contributions to solar energy generation can be determined from measurements of the pp/pep, 7Be, and 8B neutrino fluxes. Because the relative rates are very sensitive to the solar core temperature Tc, it is possible to infer important information about the physics of the solar interior from neutrino fluxes. Nowadays the pp, 7Be, and 8B fluxes are well known, while the measured pep neutrino flux is strongly model-dependent. In particular, this flux depends on the metallicity assumed for estimating the competing CNO neutrinos (Agostini et al. 2018). The solar core physics is sensitive to metallicity effects because of the free-bound/bound-free transitions in metals, which are important contributors to the opacity. This means that metallicity variations alter the solar core temperature and, in turn, the fluxes of temperature-sensitive neutrinos, such as those from 8B β-decay. Heavier metals (Mg, Si, and Fe) also affect the predicted neutrino fluxes (see Bahcall et al. 1982). Even if not very abundant, they are important opacity sources at the Sun center, as they are highly ionized. Instead, in the region just below the convective zone, at temperatures of a few millions kelvins, they are small contributors to the opacity. On the contrary, abundant, lighter, volatile heavy elemements (C, N, O, Ne, and Ar) are partially ionized there and significantly affect the radiative opacities. This is the origin of discrepancies between helioseismological measurements and the predictions made using solar compositions with low (Z/X), as discussed in Bahcall et al. (2005b) and Bahcall & Serenelli (2005). As a matter of fact, abundance variations of different metals influence different regions in the solar interior. Moreover, different CNO abundances also imply an effect on CNO burning efficiency (and corresponding neutrino fluxes) and a minor effect on the mean molecular weight and, in turn, on the thermodynamical quantities.
The net effect is that models using the GS98 compilation of abundances exhibit higher temperatures and higher densities with respect to those using that of PLJ14 (see Table 3). On the other hand, while pp and pep fluxes are only slightly modified, 7Be, 8B, 13N, 15O, and 17F neutrino fluxes are rather enhanced. Their fluxes are indeed strongly dependent on the central temperature Tc, with a power law of the form 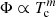 , where m = 10.0, 24.0, 24.4, 27.1, and 27.8, respectively (see Bahcall & Ulmer 1996). CNO neutrino fluxes are also enhanced because of the increased burning efficiency caused by the higher CNO abundances in the GS98 compilation. As was already mentioned, using modern solar compositions such as that of PLJ14, with low surface metal abundances, solar models have been found to be in disagreement with helioseismological measurements (see Bahcall et al. 2004, 2005a; Basu & Antia 2004; Serenelli et al. 2011; Haxton et al. 2013; Vinyoles et al. 2017). We checked that the predicted sound speed profiles of our computed SSMs are in agreement with others in the literature. We found that for the PLJ14 abundance choice the prediction disagrees with that measured (Schou et al. 1998). Instead, the choice of the older GS98 composition gives a better match.
, where m = 10.0, 24.0, 24.4, 27.1, and 27.8, respectively (see Bahcall & Ulmer 1996). CNO neutrino fluxes are also enhanced because of the increased burning efficiency caused by the higher CNO abundances in the GS98 compilation. As was already mentioned, using modern solar compositions such as that of PLJ14, with low surface metal abundances, solar models have been found to be in disagreement with helioseismological measurements (see Bahcall et al. 2004, 2005a; Basu & Antia 2004; Serenelli et al. 2011; Haxton et al. 2013; Vinyoles et al. 2017). We checked that the predicted sound speed profiles of our computed SSMs are in agreement with others in the literature. We found that for the PLJ14 abundance choice the prediction disagrees with that measured (Schou et al. 1998). Instead, the choice of the older GS98 composition gives a better match.
Main relevant quantities for the solar models adopting the ADE11 rate, as defined in the text.
We recall however that this work is not aimed at giving the best prediction for the total neutrino fluxes nor at probing the solar metallicity problem, rather we want to probe the effects induced on solar neutrino fluxes by varying the 7Be electron-capture rate alone, in the light of the mentioned evaluation by STPB13.
5. Impact of a revised 7Be + e− on the 8B neutrino flux
In this section we want to evaluate the impact of using a revised rate for the 7Be electron-capture, computed following the approach suggested by Simonucci et al. (2013), on the 8B neutrino flux. While pp neutrinos originate in a wide range of the Sun, corresponding to the main energy-producing region, 7Be and 8B neutrinos are produced in a hotter and narrower zone, ranging from the solar center to about 0.15–0.2 R⊙. The quantities RSTPB13 and RADE11 represent the electron-capture rate given by STPB13 and by ADE11, respectively. As shown in the top panel of Fig. 2, there is an appreciable variation: the new rate is lower with respect to the ADE11 choice in solar core conditions, meaning that the 7Be neutrino production channel is slightly suppressed in favor of all other channels. In particular, the solar neutrino fluxes from 7Be and 8B, Φ(7Be) and Φ(8B) are proportional to the local density of 7Be ions. The Φ(7Be) flux depends on both the electron-capture (Rec) and the proton-capture rate (Rpc) through
 |
Fig. 2. Top panel: ratio of the STPB13 electron-capture rate to that of ADE11 in the production region of 8B neutrinos. These are both computed on the solar structure resulting from the ADE11 SSM, with a PLJ14 composition. Middle panel: ratio of the neutrinos fraction produced in STPB13 SSM to that of ADE11, both computed with a PLJ14 composition. Bottom panel: product nν(8B)STPB13 ⋅ RSTPB13/(nν(8B)ADE11⋅RSTPB13) is shown; we note, in comparison with the other two panels, the much finer vertical scale. The consistency of this value with the unity means that there is practically no difference in computing a SSM with the revised STPB13 rate or applying it directly on the solar structure of a ADE11 SSM. |
where Rpc ≈ 10−3Rec (see Adelberger et al. 1998). The flux Φ(7Be) is therefore basically independent from the rates and dependent only upon the branching ratio of the reactions 3He+3He e 3He+4He. On the contrary, Φ(8B) can be written as
meaning that it is inversely proportional to the electron-capture rate Rec. This means that a variation of the Rec should have a linear effect on neutrino flux of 8B and negligible effects on other channels. Indeed, the STPB13 models present exactly the same physical and chemical features of the ADE11 models (see Table 3). If we take into account neutrinos that originate in each fraction of the solar radius (Fig. 2, middle panel), we thus deduce that the 8B neutrino production channel becomes more efficient and so Φ(8B) is increased because of the less efficient electron-capture on 7Be rate. It is also possible to see that, in correspondence of a change from negative to positive values of the variations in the electron-capture rate, the neutrino flux variation shifts from positive to negative values, thus corroborating the hypothesis of linearity between the electron-capture rate on 7Be and the 8B neutrino flux. Furthermore, if relation Eq. (3) holds, then we see that
or alternatively,
where nν(8B) is the number of neutrinos coming from the 8B decay. The bottom panel of Fig. 2 shows the product in the left-hand side of relation Eq. (5). Its value is consistent with unity at less than one part per thousand, meaning that relation Eq. (3) is indeed valid and that an increase of the Rec has the effect of linearly decreasing the flux of 8B neutrinos. Finally, variations by +2.6% and +2.7% in Φ(8B) are obtained for SSMs using a PLJ14 or a GS98 composition, respectively (see Table 4). The adoption of the STPB13 rate for electron-captures on 7Be has negligible effects on all other neutrino fluxes because it induces no variation on the physics and chemistry of the SSM itself (see Table 3).
Predicted fluxes in units of 1010 (pp), 109 (7Be), 108 (pep, 13N, 15O), 106 (8B, 17F), and 103 (hep) cm−2 s−1 for the reference ADE11 models, presented in Table 3, for the STPB13 models and relative differences.
At the present moment we cannot tag our predicted fluxes with well-defined uncertainty estimates. We should construct Monte Carlo (MC) simulations of SSMs to provide statistical errors to our results (see Bahcall et al. 2006; Serenelli et al. 2011; Vinyoles et al. 2017). Still we can estimate these uncertainties starting from known literature. Concerning the predicted 8B neutrino flux, Bahcall et al. (2006) found that the 1σ theoretical uncertainty varies from 17% to 11%, depending on the adopted composition (see their Table 15 and Fig. 6). Similar but lower values were also found by Serenelli et al. (2011) and Vinyoles et al. (2017). Then we can choose, in a conservative way, the higher value of 17% as our uncertainty on the predicted 8B neutrino flux. Similarly we can adopt an error of 10% 1σ on the 7Be neutrino flux, as predicted by Bahcall et al. (2006), which is the highest found in the literature. We also use, as correlation coefficient of the 7Be-8B neutrino fluxes, that given by Bahcall et al. (2006) for the GS98 composition. In this way we only give a rough, but still reliable, estimate of the uncertainties affecting our neutrino flux predictions, to be compared with the measured values.
The final joint fit to all SNO data gave a total flux of neutrino from 8B decays in the Sun of Φ(8B) = 5.25(1 ± 0.04) × 106 cm−2 s−1 (Aharmim et al. 2013). The latest results of the Borexino collaboration (Agostini et al. 2018) provided a total flux of 7Be neutrino flux of Φ(7Be) = 4.99(1 ± 0.03) × 109 cm−2 s−1. Such a value is somehow model-dependent, being obtained from the measured rates assuming a specific mechanism of neutrino oscillations (see Agostini et al. 2018, for details). In fact, elastic scattering measurements, such as those performed by Borexino, are mainly sensitive to νe charged-current interactions. On the contrary, the neutral-current detection channel in SNO is sensitive to all neutrino flavors and so it is a direct model-independent observation of the 8B solar neutrino flux. Figure 3 shows that adopting either the GS98 or PLJ14 compositions leads to a fair agreement with the total 8B neutrino flux measured by the SNO neutral current experiments. The use of the revised electron-capture rate RSTPB13 increases the old values of the predicted 8B neutrino fluxes with respect to the measured value. The measured value of the 8B neutrino flux is compatible with the solar model predictions for each of the two adopted solar compositions.
 |
Fig. 3. Fluxes of Φ(8B) and Φ(7Be) compared to solar values (Aharmim et al. 2013; Agostini et al. 2018). The black dot and error bars indicate solar values, while the squares and circles indicate the results obtained with the ADE11 electron-capture rate (older) and that of STPB13 (current), respectively. Ellipses denote theoretical 1σ confidence level (C.L.) for 2 degrees of freedom. |
6. Conclusions
We have presented new SSMs for two different mixtures of solar abundances, GS98 and PLJ14. We performed the simulation with the FUNS code suite. We used recent values for the cross sections in our nuclear reaction network. In particular, we adopt the e−-capture rate on 7Be provided by Simonucci et al. (2013) based on a description of the physical conditions in the solar interior that is more accurate than previous works (e.g., ADE11) and is also applicable to more general stellar environments. A tabulated version of this rate is available at the CDS. The comparison with models computed with the ADE11 widely adopted electron-capture rate shows maximum differences of about 3–4% in solar conditions. The effects on the standard solar model calculations, along with the effects on neutrino fluxes, have been discussed. We found that variations in the solar structure and in neutrino fluxes are negligible, except for the 8B neutrino flux. The estimated increase is 2.6–2.7%, depending on the composition assumed. Finally, we have also shown that the solar 8B neutrino flux is reproduced rather well, both using the GS98 and PLJ14 abundance sets.
Acknowledgments
We warmly thank the referee, S. Degl’Innocenti, for the insightful comments and suggestions that helped us to improve the manuscript.
References
- Abe, K., Haga, Y., Hayato, Y., et al. 2016, Phys. Rev. D, 94, 052010 [NASA ADS] [CrossRef] [Google Scholar]
- Adelberger, E. G., Austin, S. M., Bahcall, J. N., et al. 1998, Rev. Mod. Phys., 70, 1265 [NASA ADS] [CrossRef] [Google Scholar]
- Adelberger, E. G., García, A., Robertson, R. G. H., et al. 2011, Rev. Mod. Phys., 83, 195 [NASA ADS] [CrossRef] [Google Scholar]
- Agostini, M., Altenmüller, K., Appel, S., et al. 2018, Nature, 562, 505 [NASA ADS] [CrossRef] [Google Scholar]
- Aharmim, B., Ahmed, S. N., Anthony, A. E., et al. 2013, Phys. Rev. C, 88, 025501 [NASA ADS] [CrossRef] [Google Scholar]
- Allen, C. W. 1963, Astrophysical Quantities (London: University of London, Athlone Press) [Google Scholar]
- Angulo, C., Arnould, M., Rayet, M., et al. 1999, Nucl. Phys. A, 656, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Asplund, M. 2005, ARA&A, 43, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Bahcall, J. N. 1962, Phys. Rev., 126, 1143 [NASA ADS] [CrossRef] [Google Scholar]
- Bahcall, J. N. 1994, Phys. Rev. D, 49, 3923 [NASA ADS] [CrossRef] [Google Scholar]
- Bahcall, J. N., & Moeller, C. P. 1969, ApJ, 155, 511 [NASA ADS] [CrossRef] [Google Scholar]
- Bahcall, J. N., & Serenelli, A. M. 2005, ApJ, 626, 530 [NASA ADS] [CrossRef] [Google Scholar]
- Bahcall, J. N., & Ulmer, A. 1996, Phys. Rev. D, 53, 4202 [NASA ADS] [CrossRef] [Google Scholar]
- Bahcall, J. N., Huebner, W. F., Lubow, S. H., Parker, P. D., & Ulrich, R. K. 1982, Rev. Mod. Phys., 54, 767 [NASA ADS] [CrossRef] [Google Scholar]
- Bahcall, J. N., Pinsonneault, M. H., & Basu, S. 2001, ApJ, 555, 990 [NASA ADS] [CrossRef] [Google Scholar]
- Bahcall, J. N., Brown, L. S., Gruzinov, A., & Sawyer, R. F. 2002, A&A, 383, 291 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bahcall, J. N., Serenelli, A. M., & Pinsonneault, M. 2004, ApJ, 614, 464 [NASA ADS] [CrossRef] [Google Scholar]
- Bahcall, J. N., Basu, S., Pinsonneault, M., & Serenelli, A. M. 2005a, ApJ, 618, 1049 [NASA ADS] [CrossRef] [Google Scholar]
- Bahcall, J. N., Serenelli, A. M., & Basu, S. 2005b, ApJ, 621, L85 [NASA ADS] [CrossRef] [Google Scholar]
- Bahcall, J. N., Serenelli, A. M., & Basu, S. 2006, ApJS, 165, 400 [NASA ADS] [CrossRef] [Google Scholar]
- Basu, S., & Antia, H. M. 2004, ApJ, 606, L85 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, L. S., & Sawyer, R. F. 1997, ApJ, 489, 968 [NASA ADS] [CrossRef] [Google Scholar]
- Bruno, C. G., Scott, D. A., Aliotta, M., et al. 2016, Phys. Rev. Lett., 117, 142502 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Buckner, M. Q., Iliadis, C., Cesaratto, J. M., et al. 2012, Phys. Rev. C, 86, 065804 [NASA ADS] [CrossRef] [Google Scholar]
- Cristallo, S., Piersanti, L., Straniero, O., et al. 2011, ApJS, 197, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Di Leva, A., Scott, D. A., Caciolli, A., et al. 2014, Phys. Rev. C, 89, 015803 [NASA ADS] [CrossRef] [Google Scholar]
- Ferguson, J. W., Alexander, D. R., Allard, F., et al. 2005, ApJ, 623, 585 [NASA ADS] [CrossRef] [Google Scholar]
- Grevesse, N., & Sauval, A. J. 1998, Space Sci. Rev., 85, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Gruzinov, A. V., & Bahcall, J. N. 1997, ApJ, 490, 437 [NASA ADS] [CrossRef] [Google Scholar]
- Gruzinov, A. V., & Bahcall, J. N. 1998, ApJ, 504, 996 [NASA ADS] [CrossRef] [Google Scholar]
- Haxton, W., Robertson, R. H., & Serenelli, A. M. 2013, ARA&A, 51, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Iben, Jr., I., Kalata, K., & Schwartz, J. 1967, ApJ, 150, 1001 [NASA ADS] [CrossRef] [Google Scholar]
- Iglesias, C. A., & Rogers, F. J. 1996, ApJ, 464, 943 [NASA ADS] [CrossRef] [Google Scholar]
- Iliadis, C., Longland, R., Champagne, A. E., Coc, A., & Fitzgerald, R. 2010, Nucl. Phys. A, 841, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Indelicato, I., La Cognata, M., Spitaleri, C., et al. 2017, ApJ, 845, 19 [Google Scholar]
- Johnson, C. W., Kolbe, E., Koonin, S. E., & Langanke, K. 1992, ApJ, 392, 320 [NASA ADS] [CrossRef] [Google Scholar]
- La Cognata, M., Spitaleri, C., & Mukhamedzhanov, A. M. 2010, ApJ, 723, 1512 [NASA ADS] [CrossRef] [Google Scholar]
- Lamia, L., Spitaleri, C., La Cognata, M., Palmerini, S., & Pizzone, R. G. 2012, A&A, 541, A158 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lamia, L., Spitaleri, C., Tognelli, E., et al. 2015, ApJ, 811, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Marcucci, L. E., Schiavilla, R., & Viviani, M. 2013, Phys. Rev. Lett., 110, 192503 [NASA ADS] [CrossRef] [Google Scholar]
- Marta, M., Formicola, A., Bemmerer, D., et al. 2011, PhRvC, 83, 045804 [NASA ADS] [Google Scholar]
- Oda, T., Hino, M., Muto, K., Takahara, M., & Sato, K. 1994, At. Data Nucl. Data Tables, 56, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Palme, H., Lodders, K., & Jones, A. 2014, Solar System Abundances of the Elements, ed. A. M. Davis, 15 [Google Scholar]
- Piersanti, L., Straniero, O., & Cristallo, S. 2007, A&A, 462, 1051 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Prada Moroni, P. G., & Straniero, O. 2002, ApJ, 581, 585 [NASA ADS] [CrossRef] [Google Scholar]
- Rauscher, T., & Thielemann, F.-K. 2000, At. Data Nucl. Data Tables, 75, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Sawyer, R. F. 2011, Phys. Rev. C, 83, 065804 [NASA ADS] [CrossRef] [Google Scholar]
- Schou, J., Antia, H. M., Basu, S., et al. 1998, ApJ, 505, 390 [NASA ADS] [CrossRef] [Google Scholar]
- Serenelli, A. M., Haxton, W. C., & Peña-Garay, C. 2011, ApJ, 743, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Simonucci, S., Taioli, S., Palmerini, S., & Busso, M. 2013, ApJ, 764, 118 [NASA ADS] [CrossRef] [Google Scholar]
- Straniero, O. 1988, A&AS, 76, 157 [NASA ADS] [Google Scholar]
- Straniero, O., Gallino, R., & Cristallo, S. 2006, Nucl. Phys. A, 777, 311 [NASA ADS] [CrossRef] [Google Scholar]
- Takahashi, K., & Yokoi, K. 1987, ADNDT, 36, 375 [NASA ADS] [CrossRef] [Google Scholar]
- Thoul, A. A., Bahcall, J. N., & Loeb, A. 1994, ApJ, 421, 828 [NASA ADS] [CrossRef] [Google Scholar]
- Vinyoles, N., Serenelli, A. M., Villante, F. L., et al. 2017, ApJ, 835, 202 [NASA ADS] [CrossRef] [Google Scholar]
- Vissani, F. 2018, ArXiv e-prints [arXiv:1808.01495] [Google Scholar]
- Zhang, X., Nollett, K. M., & Phillips, D. R. 2015, Phys. Lett. B, 751, 535 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Coefficients for the analytical approximation to the STPB13 and ADE11 electron-capture rates.
Main relevant quantities for the solar models adopting the ADE11 rate, as defined in the text.
Predicted fluxes in units of 1010 (pp), 109 (7Be), 108 (pep, 13N, 15O), 106 (8B, 17F), and 103 (hep) cm−2 s−1 for the reference ADE11 models, presented in Table 3, for the STPB13 models and relative differences.
All Figures
 |
Fig. 1. Fractional variation of the 7Be electron-capture rate, Δλ/λ[%] = 100 ⋅ (RSTPB13 − RADE11)/RADE11, as a function of ρ/μe and T, adopting the Simonucci et al. (2013) rate, as compared to that of Adelberger et al. (2011) for the PLJ14 solar composition (see Sect. 2). The solar core conditions are highlighted with the common solar symbol. |
| In the text | |
 |
Fig. 2. Top panel: ratio of the STPB13 electron-capture rate to that of ADE11 in the production region of 8B neutrinos. These are both computed on the solar structure resulting from the ADE11 SSM, with a PLJ14 composition. Middle panel: ratio of the neutrinos fraction produced in STPB13 SSM to that of ADE11, both computed with a PLJ14 composition. Bottom panel: product nν(8B)STPB13 ⋅ RSTPB13/(nν(8B)ADE11⋅RSTPB13) is shown; we note, in comparison with the other two panels, the much finer vertical scale. The consistency of this value with the unity means that there is practically no difference in computing a SSM with the revised STPB13 rate or applying it directly on the solar structure of a ADE11 SSM. |
| In the text | |
 |
Fig. 3. Fluxes of Φ(8B) and Φ(7Be) compared to solar values (Aharmim et al. 2013; Agostini et al. 2018). The black dot and error bars indicate solar values, while the squares and circles indicate the results obtained with the ADE11 electron-capture rate (older) and that of STPB13 (current), respectively. Ellipses denote theoretical 1σ confidence level (C.L.) for 2 degrees of freedom. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$$ \begin{aligned} \lambda (\frac{\rho }{\mu _{\rm e}},T_6)= \frac{\rho }{\mu _{\rm e}} \frac{\kappa }{\sqrt{T_{6}}} \Big [ 1+ \alpha \, (T_6-16) + \beta \, \frac{\rho }{\mu _{\rm e}} \, \Big (1 + \gamma \, (T_6-16)\Big ) \Big ] \,. \end{aligned} $$](/articles/aa/full_html/2019/03/aa34993-18/aa34993-18-eq3.gif)