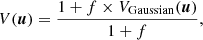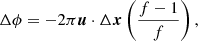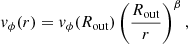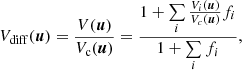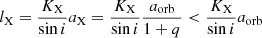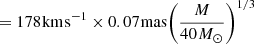| Issue |
A&A
Volume 623, March 2019
|
|
|---|---|---|
| Article Number | A47 | |
| Number of page(s) | 13 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201834746 | |
| Published online | 04 March 2019 | |
Super-Keplerian equatorial outflows in SS 433
Centrifugal ejection of the circumbinary disk⋆
1
Max Planck Institute for extraterrestrial Physics, Giessenbachstr., 85748 Garching, Germany
e-mail: idelw@mpe.mpg.de
2
Univ. Grenoble Alpes, CNRS, IPAG, 38000 Grenoble, France
Received:
29
November
2018
Accepted:
27
December
2018
Context. The microquasar SS 433 is the only known steady supercritical accretor in the Galaxy. It is well-known for its relativistic baryonic jets, but the system also drives equatorial outflows. These have been routinely detected in radio images, and components associated with a circumbinary disk have also been suggested in optical emission lines.
Aims. We aim to spatially resolve the regions producing the stationary emission lines of SS 433 to shed light on its circumbinary structure and outflows. With an estimated binary orbit size of ≲0.1 mas, this requires optical interferometry.
Methods. We use the optical interferometer VLTI+GRAVITY to spatially resolve SS 433 in the near-infrared K band at high spectral resolution (R ≈ 4000) on three nights in July 2017. This is the second such observation, after the first one in July 2016.
Results. The stationary Brγ line in the 2017 observation is clearly dominated by an extended ∼1 mas ∼ 5 AU circumbinary structure perpendicular to the jets with a strong rotation component. The rotation direction is retrograde relative to the jet precession, in accordance with the slaved disk precession model. The structure has a very high specific angular momentum and is too extended to be a stable circumbinary disk in Keplerian rotation; interpreting it as such leads to a very high enclosed mass M ≳ 400 M⊙. We instead interpret it as the centrifugal ejection of the circumbinary disk, with the implication that there must be an efficient transfer of specific angular momentum from the binary to the disk. We suggest that the equatorial outflows sometimes seen in radio images result from similar episodes of circumbinary disk centrifugal ejection. In addition to the equatorial structure, we find a very extended ∼6 mas ∼ 30 AU spherical wind component to the Brγ line: the entire binary is engulfed in an optically thin spherical line emission envelope.
Key words: techniques: interferometric / binaries: close / circumstellar matter / stars: winds / outflows / infrared: stars
© ESO 2019
1. Introduction
The extreme emission-line object SS 433 (Stephenson & Sanduleak 1977; Clark & Murdin 1978) was the first microquasar discovered, from its broad, red/blueshifted hydrogen and helium emission lines moving across its optical spectrum (Margon et al. 1979) and produced by relativistic, precessing baryonic jets moving at 0.26c (Fabian & Rees 1979; Margon 1984). The jets are also seen in emission lines of highly ionized metals in X-rays (e.g., Marshall et al. 2013) and as moving knots (e.g., Vermeulen et al. 1993) and a large-scale corkscrew structure in radio (e.g., Blundell & Bowler 2004). SS 433 is the only known Galactic manifestation of a steady super-Eddington accretion disk, which outshines its donor star at all wavelengths and drives powerful outflows, manifested not only in the jets but also in strong, broad, and complex “stationary” (in wavelength) emission lines. The estimated mass outflow Ṁ ∼ 10−4 M⊙ yr (Shklovskii 1981; Fuchs et al. 2006) establishes SS 433 as an outflow-regulated supercritically accreting system (Ṁ ∼ 500 ṀEddington for a 10 M⊙ black hole). For a review of the fascinating properties of SS 433, see Fabrika (2004).
Although famous for its jets, one of the more exotic aspects of SS 433 is its equatorial outflows. The presence of an equatorial excretion flow from the accretion disk was proposed to explain the photometric and eclipsing behavior of SS 433 by Zwitter et al. (1991), possibly fed from the Lagrangian point behind the compact object (Fabrika 1993). The equatorial outflows were later detected in high-resolution radio images as outflowing emission knots at anomalous position angles, almost perpendicular to the jets (Paragi et al. 1999). Blundell et al. (2001) later detected a smooth, extended (∼40 mas) equatorial structure in radio images, calling it the “radio ruff”. A collection of further observations (Paragi et al. 2002; Mioduszewski et al. 2004) showed that the orientation of the equatorial outflows is roughly perpendicular to the precessing jets but spans a larger angle range of ∼70° (compared to 40° for the jets; Doolin & Blundell 2009).
On the other hand, the presence of equatorial, circumbinary material has also been inferred from the double-peaked shapes that often appear in the optical emission lines. Filippenko et al. (1988) ascribed the double peaks with half-separation ≈150 km s−1 in the high-order Paschen lines to an accretion disk (deriving a rather low mass for the compact object, suggestive of a neutron star), but also recognized that the structure may instead arise in a circumbinary disk that, if in Keplerian rotation, would imply a much larger ≳40 M⊙ enclosed mass. Robinson et al. (2017) presents a similar analysis of the higher-order Brackett lines, assigning them to an accretion disk and favoring a neutron star as the compact object. On the other hand, based on decomposition of the line profiles with several different Gaussian components, Blundell et al. (2008) concluded that the Hα emission line arises from a combination of a disk wind and a circumbinary disk, the latter manifesting itself as stable Gaussian components with half-separation ≳200 km s−1. This velocity was interpreted as evidence that the total system mass must be large (≳40 M⊙) and the compact object must be a massive ≳16 M⊙ black hole. Gaussian components arising from a circumbinary disk have also been suggested in the Brγ and He I emission lines (Perez & Blundell 2009; Bowler 2010). Cherepashchuk et al. (2018) argues that the double-peaked structure must indeed arise from extended material because the wings of the line are not eclipsed (as would be expected for an accretion disk; SS 433 is an eclipsing binary). On the other hand, radial-velocity measurements, notably extremely challenging in SS 433 due to the complexity of the emission lines and lack of clear stellar signatures, tend to favor lower masses of 2 − 5 M⊙ for the compact object (Hillwig & Gies 2008; Kubota et al. 2010). The relation between the circumbinary structure detected in optical emission lines and the equatorial outflows seen in radio is not clear. It has been suggested that the former might feed the latter (Blundell et al. 2008; Doolin & Blundell 2009).
With an orbital period of Porb = 13.1 days (Goranskij 2011) and a distance of d = 5.5 kpc (Blundell & Bowler 2004), the semi-major axis of SS 433 is 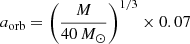 mas, where M is the total binary mass. Spatially resolving the optical emission requires sub-milliarcsecond resolution. This is beyond the capabilities of even future extremely large telescopes, but is achievable through spectro-differential optical interferometry. In Gravity Collaboration (2017b; Paper I) we presented the first such observations taken during the commissioning of the GRAVITY instrument (Gravity Collaboration 2017a) in July 2016 at the Very Large Telescope Interferometer (VLTI), which works in the near-infrared K band. These observations spatially resolved the near-infrared continuum as well as the stationary double-peaked Brγ line. The interferometric signature across the latter showed a complex structure dominated by emission in the jet direction, suggestive of a bipolar outflow.
mas, where M is the total binary mass. Spatially resolving the optical emission requires sub-milliarcsecond resolution. This is beyond the capabilities of even future extremely large telescopes, but is achievable through spectro-differential optical interferometry. In Gravity Collaboration (2017b; Paper I) we presented the first such observations taken during the commissioning of the GRAVITY instrument (Gravity Collaboration 2017a) in July 2016 at the Very Large Telescope Interferometer (VLTI), which works in the near-infrared K band. These observations spatially resolved the near-infrared continuum as well as the stationary double-peaked Brγ line. The interferometric signature across the latter showed a complex structure dominated by emission in the jet direction, suggestive of a bipolar outflow.
Here we report on a second set of observations of SS 433 with GRAVITY in July 2017, which clearly revealed equatorial emission with a strong rotation component. In Sect. 2, we summarize the observations and data reduction. The analysis of the K-band near-infrared continuum is presented in Sect. 3, whereas Sect. 4 describes the results on the stationary Brγ line. Finally, Sect. 5 presents the conclusions.
We often quote the results in milliarcseconds, as that is the measured unit. For convenience, we quote 1 mas ↔ 8.2 × 1013 cm = 1180 R⊙ = 5.5 AU, assuming a distance d = 5.5(±0.2) kpc derived from radio images using the aberration induced by the light travel-time effect between the two jets (Blundell & Bowler 2004). The Gaia DR2 distance of 4.6 ± 1.3 kpc (Luri et al. 2018) is consistent with this value.
2. Observations and data reduction
SS 433 (K ≈ 8) was observed with GRAVITY (Gravity Collaboration 2017a) with the Unit Telescopes (UT) on VLTI on three nights over a period of four days in July 2017. Half of the K band light of SS 433 itself was directed to the fringe tracker (FT), which operates at > 1000 Hz to stabilize the fringes in the science channel (SC), allowing coherent integration over detector integration times of 10s in high spectral resolution (R ≈ 4000). The FT operates in low resolution (R ≈ 20) with five channels over the K band. The data were obtained in split polarization mode. The adaptive optics (AO) was performed at visual wavelength using SS 433 itself as the AO guide star (V ≈ 14).
Table 1 summarizes the observations. The precessional phase was ≈0.9, when the disk inclination is close to its minimum value (i ≈ 60°). The orbital phases varied from ∼0.25 − 0.5, meaning that the accretion disk is not eclipsed. Figure 1 shows the uv-coverage for the second epoch, with the jet precessional axis and cone as seen in radio observations (e.g., Stirling et al. 2002). The uv coverage for the other epochs is similar, but shorter in the third observation. The imaging resolution is ≈3 mas; however, we can resolve structures at sub-milliarcsecond resolution through spectral differential visibilities.
Summary of observations.
 |
Fig. 1. The uv-coverage for Epoch 2 of the GRAVITY 2017 observations. The colors represent the six different baselines, and the coverage in the radial direction corresponds to the different wavelength channels across the K band (2 − 2.5 μm). We also show the precessional axis of the jet and its precession cone as seen on sky. The projected baselines are sensitive to both the jet and the orthogonal directions. |
The data were reduced with the standard GRAVITY pipeline (version 1.0.7, Lapeyrere et al. 2014). The interferometric calibrators used are listed in Table 1. They were also used as telluric line calibrators. We detected no significant difference in the interferometric quantities between the two polarizations in any of the three nights, either in the continuum FT or differential SC visibilities, and therefore we averaged the two polarizations. The data are also averaged in time for each of the three epochs because we do not see clear variability during each observation. We use the low-resolution FT data to study the K band continuum, and the high-resolution SC data to study the emission lines through differential visibility amplitudes and phases. Our limited uv-coverage resulting from the rather short observations did not allow for model-independent image reconstruction; therefore, we have to rely on model-independent quantities and model fitting.
3. The near-infrared K band continuum
SS 433 is known to have strong infrared excess (e.g., Allen 1979; Fuchs et al. 2006) from extended outflows. At NIR wavelengths, we expect a flux contribution from both the accretion disk and donor star (< 0.1 mas) and from more extended emission. In all observations, the continuum closure phases are very small ≲2°, pointing to symmetric structures within the spatial resolution of ≈3 mas.
In Paper I we reported a phenomenological model for the K band continuum consisting of a partially resolved source (FWHM ≲ 1 mas) embedded in a completely resolved background with ≈10% of its flux. Here we construct a slightly more involved model in face of the strong evidence for an equatorial structure in the 2017 observations. The model consists of two components: an unresolved point source representing the binary (accretion disk + donor star) and a two-dimensional elliptical Gaussian which could represent an extended disk/wind. The model parameters are:
-
The flux ratio f between the Gaussian and the point source components;
-
The FWHM θg of the Gaussian component along the major axis;
-
The disk inclination i, which gives the aspect ratio of the Gaussian cos(i);
-
The position angle (PA) of the Gaussian axis.
The model visibility is therefore:
where VGaussian is the visibility of the elliptical Gaussian and 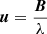 with B the baseline vector.
with B the baseline vector.
Table 2 and Fig. 2 show the results for the model fits to the continuum squared visibilities for the 2016 observation and Epoch 2 of the 2017 observations (the other epochs look similar). Because the measurement errors are dominated by systematic errors from imperfect calibration of the visibilities (which leads to large 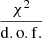 ), we estimate the parameter errors from bootstrapping over the different baselines. We also note that spectral channels with strong emission lines were not used, to avoid the biasing of continuum visibilities by the differential visibilities.
), we estimate the parameter errors from bootstrapping over the different baselines. We also note that spectral channels with strong emission lines were not used, to avoid the biasing of continuum visibilities by the differential visibilities.
K band continuum model fit results.
 |
Fig. 2. K band continuum squared visibilities of SS 433 from the GRAVITY fringe tracker for the 2016 observation (top) and Epoch 2 of the 2017 observation (bottom). The continuum is modeled by the combination of an unresolved point source representing the binary (accretion disk + donor star) and a two-dimensional elliptical Gaussian which could represent an extended disk/wind. The data is shown in color and the best fit model is shown in black. |
The model fits point to an extended structure with a FWHM ∼ 7 mas containing 10 − 30% of the flux of the central point source. The PAs are not very well-constrained, but the inclinations do not favor a symmetric Gaussian. The extended continuum structure could therefore correspond to a disk, with some possible contribution from an extended wind (both of which are seen in the Brγ line, see below). The inclination and position angle of the jets are ijet ≈ 90°, PAjet ≈ 75° in the 2016 observation (Paper I) and ijet ≈ 60°, PAjet ≈ 88° for the 2017 observations (see companion paper on the jets; Waisberg et al. 2018).
4. The stationary Brγ line
4.1. The K band spectrum
The K band spectrum of SS 433 contains both stationary emission lines (Brγ, He I 2.06 μm, He I 2.112 μm and high-order (upper levels 19–24) Pfund lines) as well as emission lines from the baryonic jets. By far the strongest stationary line is the Brγ line, which is the focus of this paper. It is a broad line with FWHM ∼ 1000 km s−1 and often shows a double-peaked structure. We note that the Brγ stationary line in our observations is partially blended with Paα emission lines from the receding jet. Figure 4 shows the relevant part of the K band spectrum for Epoch 2, with velocities centered on the Brγ line. For the complete K band spectra, we refer to the companion paper on the jets (Waisberg et al. 2018).
4.2. Model-independent results
As mentioned previously, the stationary emission lines in SS 433 have been ascribed to multiple components, including an accretion disk, extended accretion disk wind/outflow, and a circumbinary ring. Our interferometric data spatially resolve the Brγ line emission for the first time. The differential phases on most baselines show a remarkable “S-shape”, which is a typical signature of a spatial velocity gradient (Fig. 4). A comparison of the differential phases between the jet lines and the Brγ line reveals that in 2017 the latter is perpendicular to the jets, rather than along their direction as was the case in the 2016 observation (Paper I). This can be clearly visualized in a model-independent way by converting the differential phases Δϕ to centroid offsets Δx between the line and the continuum, since in the marginally resolved limit (e.g., Monnier & Allen 2013; Waisberg et al. 2017)
where 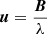 and f is the line flux in continuum-normalized units. Figure 3 shows the centroid of emission across the Brγ line for the 2016 observation (Paper I) and Epoch 2 of the 2017 observations, along with the centroid of the jet emission lines. The emission is dominated by a bipolar (jet-like) structure in the 2016 observation, as reported in Paper I (although with a substantial scatter and an apparent offset ≈0.2 mas between the jet PA and the stationary line PA), and by a clear equatorial structure in the 2017 observation.
and f is the line flux in continuum-normalized units. Figure 3 shows the centroid of emission across the Brγ line for the 2016 observation (Paper I) and Epoch 2 of the 2017 observations, along with the centroid of the jet emission lines. The emission is dominated by a bipolar (jet-like) structure in the 2016 observation, as reported in Paper I (although with a substantial scatter and an apparent offset ≈0.2 mas between the jet PA and the stationary line PA), and by a clear equatorial structure in the 2017 observation.
 |
Fig. 3. Model-independent centroid shifts across the Brγ stationary line for the 2016 observation and Epoch 2 of the 2017 observations. The dashed circle shows the binary size a ≈ 0.07 mas for a total mass M = 40 M⊙. The insets show the Brγ line spectrum with the color corresponding to the different wavelength/velocity channels. |
Figure 4 shows the interferometric data of Epoch 2 of the 2017 observations on two representative baselines (one close to perpendicular to the jets, the other close to parallel to the jets). We note the following important findings:
-
From Fig. 3, the higher-velocity part of the line is more compact than the lower-velocity part, which points to a significant rotation component rather than a radially accelerating outflow.
-
Figure 4 shows that the differential phase peaks, which are much stronger in baselines closer to perpendicular to the jets, have a half-separation of ∼250 km s−1, and extend to ≳1000 km s−1. The jet inclination in SS 433 is ≳60°, so that any disk-like component is likely to be very close to edge-on, meaning that this velocity should be close to the deprojected velocity.

Fig. 4. Main features of the data and model. We show two representative baselines (UT3-1, yellow, and UT4-3, red – see Fig. 1) for Epoch 2 and the outflow model fit. Top row: spectrum centered on the Brγ stationary line. The latter is decomposed into an equatorial outflow (dark green) and a spherical wind (lime). The former is responsible for the S-shape signatures in the differential visibility phases (middle row) for baselines which are close to perpendicular to the jet (left), and show almost no signature on baselines more aligned with the jet (right). The inset shows the position angle of the outflow from the fit as well as the baseline directions on the sky plane. Bottom row: differential visibility amplitudes. The equatorial outflow alone would lead to an increase in visibility amplitude across the Brγ line. The extended wind component can explain both the high-velocity (≳1000 km s−1) wings in the spectrum and the net decrease in visibility amplitude across the line. We note that there are two Paα emission lines from the receding jet that are blended with the Brγ stationary line on its red side, and also create strong visibility signatures. The model fits were done for all the components simultaneously, but here we show only the visibility model for the stationary line for clarity (full model is shown in the Appendix). For the jet model and results, we refer to the companion paper on the jets (Waisberg et al. 2018).
-
From Fig. 3, the centroid displacement near the line peak (where the differential phase peaks occur) is ≳0.4 mas. This is a lower limit to the size of the region associated with that intrinsic velocity because, in a disk, projection effects cause inner material to also contribute to that velocity. We also note that, if the emission line has additional components, meaning that the true f in Eq. (2) is reduced, the centroid displacement necessary to produce the same differential phase will be larger. Therefore, 0.4 mas is a lower limit to the size of the region where the velocity is ∼250 km s−1.
This clearly shows that the rotating structure is too extended to be an accretion disk, since aorb < 0.07 mas for a total binary mass M < 40 M⊙. The phase peaks ∼250 km s−1 are close in velocity to the Gaussian components that have been associated with a circumbinary ring in previous spectral decompositions (Blundell et al. 2008; Bowler 2010); however, the interferometric data show that these structures are too extended to correspond to the inner edge of a circumbinary ring at ≈2aorb. We note that the Keplerian velocity 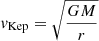 at 0.4 mas for M < 40 M⊙ is ≈130 km s−1, meaning that if in Keplerian rotation, the structure would imply a very high enclosed mass ≳150 M⊙. Alternatively, the structure may be an equatorial rotating outflow (see below).
at 0.4 mas for M < 40 M⊙ is ≈130 km s−1, meaning that if in Keplerian rotation, the structure would imply a very high enclosed mass ≳150 M⊙. Alternatively, the structure may be an equatorial rotating outflow (see below).
4.3. Models
We model the equatorial structure emitting in Brγ as a geometrically and optically thin disk-like structure, which can be either stationary in Keplerian rotation or expanding. The parameters are as follows:
-
The outer radius is Rout (mas), beyond which Brγ emission ceases.
-
The ratio of outer to inner radius, the latter demarcating the radius at which Brγ emission begins, is
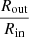 .
. -
The radial emission profile in Brγ, parametrized by I(r)∝r−α.
-
The deprojected rotational velocity at the outer radius, vϕ(Rout). The rotational velocity is given by
where β = 0.5 for Keplerian rotation and β = 1 for an expanding outflow from conservation of angular momentum.
-
The outflow velocity vr for the case β = 1. This is assumed to be constant, that is, the outflow has reached its terminal velocity by the time Brγ emission starts.
-
The inclination i of the disk.
-
The position angle PA of the disk.
-
The systematic velocity of the disk, vsys, which could include orbital motion, for example.
-
The turbulence velocity fraction, given by
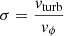 . This parameter makes the double-peaked profile, typical of disks, less pronounced.
. This parameter makes the double-peaked profile, typical of disks, less pronounced.
In addition, there is a need for an extended component, which also creates the high-velocity ( ≳ 1000 km s−1) wings of the line profile. This is because the differential visibility amplitudes decrease across the line, pointing to a net structure that is more extended than the continuum, whereas the disk alone would cause an increase in visibility amplitude if no other component were present (Fig. 4). The presence of a broad wind component has been inferred from previous spectroscopic decompositions of the stationary lines (e.g., Blundell et al. 2008; Perez & Blundell 2009). We model it as a spherically symmetric component, assumed to produce a Gaussian emission line in the spectrum and a symmetric 2D Gaussian in the image. Since it is spherically symmetric, this component does not induce differential visibility phase shifts. Its model parameters are the strength and FWHM (km s−1) of the wind line in the spectrum, FWHMwind, and the size (FWHM) of the wind image (mas), θwind. The systemic velocity is assumed to be the same as for the equatorial structure.
The errors for the science channel are estimated from the scatter in line-free regions. We fit for the spectrum and the differential visibilities simultaneously; however, because the former is sensitive to telluric correction and has very small statistical error bars, we increase the flux error bars by a factor of two. We found that this scaling led to a comparable reduced χ2 between flux and visibilities in all observations. Moreover, because of the blending with Paα emission lines from the receding jet, which also produces differential visibility signatures, it is necessary to perform simultaneous fits for the Brγ line and the jets. For the model and results for the jets we refer to the companion paper (Waisberg et al. 2018).
For the velocity-resolved interferometric model for the equatorial disk detailed above, we construct a spatial grid with velocities and fluxes determined by the model parameters, and the visibilities are then computed through a numerical 2D Fourier transform. The total differential visibility at a given spectral channel is then
where Vc is the continuum visibility (taken from the best fit continuum model, Sect. 3), and fi and Vi are the flux ratios relative to the continuum and visibilities for each component i (equatorial disk/outflow, extended wind and jets).
The fits are done through nonlinear least-squares minimization with the Levenberg-Marquardt method through the python package LMFIT1. The quoted errors correspond to the 1σ errors from the least squares fit, i.e., the estimated derivatives around the optimal solution (scaled by 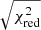 ). We caution, however, that true uncertainties are dominated by degeneracies between the many parameters, which create a complicated multi-dimensional χ2 map; systematic errors from the continuum model; and the assumptions of our simple “geometric” models, which cannot capture all the complexities likely involved. A more realistic assessment of the errors can probably be grasped from the comparison between the results of the three different epochs (barring fast variability). We note, however, that in Epoch 1 there is very severe spectral blending of the different components, meaning that its results are less robust.
). We caution, however, that true uncertainties are dominated by degeneracies between the many parameters, which create a complicated multi-dimensional χ2 map; systematic errors from the continuum model; and the assumptions of our simple “geometric” models, which cannot capture all the complexities likely involved. A more realistic assessment of the errors can probably be grasped from the comparison between the results of the three different epochs (barring fast variability). We note, however, that in Epoch 1 there is very severe spectral blending of the different components, meaning that its results are less robust.
4.4. Model results
Table 3 shows the model fit results for both the disk and outflow models. Figure 4 shows the data and best fit for the “outflow” model in Epoch 2 for two representative baselines. All the data and best fits for the three epochs for the “outflow” model are shown in the Appendix.
Stationary Brγ model fit results.
The PA of the equatorial structure is almost (although not exactly) perpendicular to the jets (the fit jet PA is 88°; Waisberg et al. 2018), confirming the results from the model-independent analysis. The inclination of the outflow is also close to the jet inclination during the observations (60°). Interestingly, the rotation direction of the equatorial outflow is retrograde relative to the jet precession (known from radio and optical observations), in agreement with the slaved disk precession model, according to which the precession is driven by gravitational torques from the compact object on the donor star with a spin axis misaligned with the binary plane (Roberts 1974; van den Heuvel et al. 1980). Modeling of the eclipses in the X-ray and optical light curves at different precessional phases had shown evidence of retrograde precession (e.g., Brinkmann et al. 1989; Leibowitz 1984); our results clearly confirm that the jets precess in a retrograde manner relative to the binary.
The “disk” and “outflow” models look very similar and cannot be distinguished from one another based on the χ2. However, we disfavor the “disk” model based on the following arguments. The resulting enclosed mass is very high, that is, ∼400 M⊙, which follows from the fact that the disk is too extended (Rout ≈ 1 mas) for its velocity (vϕ(Rout)≈260 km s−1). It would entail that SS 433 harbors an intermediate-mass black hole, which is strongly disfavored by all that is known about the object, such as the radial-velocity curves and eclipse behavior (Fabrika 2004). Even more problematic is the fact that the “disk” model is not self-consistent: for such a high mass, aorb ≈ 0.15 mas, which is larger than the resulting inner radius of the disk ≲0.1 mas, implying instability (e.g. Artymowicz & Lubow 1994).
Instead, we favor the “outflow” model. In this case, the extended equatorial structure we detect would correspond to an outflow moving out at vr ∼ 240 km s−1 but with a very significant rotation component. The inner edge of the outflow at ∼0.1 mas has a rotational velocity of ∼1500 km s−1 and the outer edge at ∼0.7 mas rotates at ∼220 km s−1. This corresponds to a very high specific angular momentum, which is ≳10 times larger than the specific orbital angular momentum of the compact object lX for a total mass of M < 40 M⊙, assuming a radial-velocity amplitude of KX = 175 km s−1 as derived from the HeII 4686 Å line (Fabrika & Bychkova 1990) and a binary inclination of i = 78° (Eikenberry et al. 2001),
where 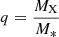 is the mass ratio. The specific angular momentum of the donor star is even smaller, since q < 1 based on radial velocities (Hillwig & Gies 2008; Kubota et al. 2010) or other estimates of the mass ratio (Cherepashchuk et al. 2018; Bowler 2018). The extended outflows therefore seem to require a mechanism for transfer of substantial specific angular momentum to the outflowing material, which requires tidal or magnetic torques. We note that the inferred expansion velocity of the outflow of ≈240 km s−1 corresponds to only ∼0.02 mas day−1, which precludes the detection of movement within the different epochs above the uncertainties.
is the mass ratio. The specific angular momentum of the donor star is even smaller, since q < 1 based on radial velocities (Hillwig & Gies 2008; Kubota et al. 2010) or other estimates of the mass ratio (Cherepashchuk et al. 2018; Bowler 2018). The extended outflows therefore seem to require a mechanism for transfer of substantial specific angular momentum to the outflowing material, which requires tidal or magnetic torques. We note that the inferred expansion velocity of the outflow of ≈240 km s−1 corresponds to only ∼0.02 mas day−1, which precludes the detection of movement within the different epochs above the uncertainties.
Because the inner radius of the outflow is ≈0.1 mas, which is ≈aorb, it appears that it is launched from circumbinary material. Alternatively, it could be launched from the outer parts of the accretion disk, but only become visible in Brγ at larger scales. Centrifugal outflows from magnetic torques in the accretion disk itself require geometrically thin disks (H ≪ R) threaded by vertical magnetic fields which dominate the pressure (Blandford & Payne 1982). Although such a mechanism is unlikely to operate in the inner parts of the SS 433 accretion disk (which are geometrically thick and dominated by radiation pressure), it could be at work in the outer parts of the disk. In fact, because the inflow timescale in the outer disk must be short (of the order of the binary period) for the jets to nutate (Begelman et al. 2006), an efficient way to remove angular momentum in the outer disk is indeed needed.
A more exotic possibility would be extraction of angular momentum from a neutron star through a magnetic propeller effect, in which transfer of angular momentum from the spinning neutron star to the flow can happen if the magnetospheric radius Rm is larger than the co-rotation radius Rco, leading the flow to be centrifugally ejected (Illarionov & Sunyaev 1975). Although the currently favored model for SS 433 is based on accretion-powered outflows from a massive stellar-mass black hole (Fabrika 2004; Cherepashchuk et al. 2018; Bowler 2018), neutron star models for SS 433 have been considered in the past (e.g., Begelman et al. 1980; Begelman & Rees 1984), including the idea that it could be a supercritical propeller (Mineshige et al. 1991). In the latter scenario, Rm is smaller than the spherization radius Rsp meaning that a thick disk could still form (Rsp is the radius within which the disk becomes geometrically thick from radiation pressure, determined from L(R > Rsp)=LEddington; Shakura & Sunyaev 1973). Our equatorial outflow model would require a launch radius ≳4 × 1010 cm for its speed not to exceed c, which is comparable to 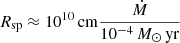 in SS 433. However, for such a large magnetospheric radius to be inside the light cylinder of a neutron star would require a spin period P ≳ 10 s, deeming a propeller mechanism very unlikely (in addition, it would require very large, i.e., ≫1015 G, surface magnetic fields).
in SS 433. However, for such a large magnetospheric radius to be inside the light cylinder of a neutron star would require a spin period P ≳ 10 s, deeming a propeller mechanism very unlikely (in addition, it would require very large, i.e., ≫1015 G, surface magnetic fields).
We instead favor a scenario where the outflow is driven from a circumbinary disk. There is strong evidence for such a disk from optical spectroscopy (Blundell et al. 2008; Bowler 2010), which appears to be in Keplerian rotation at ∼1.5aorb with a speed of ∼250 km s−1 (Bowler 2018). It is probably fed by excretion through the Lagrangian points behind the compact object, donor star, or both. We note that the specific angular momentum of such a disk is a few times higher than that available in either binary component, meaning that its formation must also involve transfer of specific angular momentum. Nevertheless, there is strong evidence that this circumbinary disk is not stable: we see no evidence for substantial equatorial material in the 2016 GRAVITY observation, where the asymmetric double-peaked Brγ line is instead mostly aligned in the jet direction. We suggest that the equatorial structure we detected in optical interferometry traces the inner part of a centrifugally ejected disk, which implies there must be an efficient transfer of specific angular momentum from the binary to the disk, making it super-Keplerian by a factor of ≲10, probably through tidal torques (e.g., Chen & Zeng 2009). It is then tempting to associate the enigmatic equatorial outflows sometimes detected in radio images to similar episodes of centrifugal ejection of the circumbinary disk. Interestingly, Goranskij (2017) reports on episodes of disappearance and reappearance of the eclipses and jets in SS 433, which they associate with the formation and ejection of a common envelope, and which could in turn be related to the formation and/or ejection of the circumbinary disk.
The feeding of the circumbinary disk removes angular momentum from the binary, and Cherepashchuk et al. (2018) recently used the stability of the orbital period reported in Goranskij (2011) to constrain the mass ratio q ≳ 0.6. The ejection of the circumbinary disk we suggest here could also have important implications on the binary evolution. However, because it is most probably a transient structure, more observations are needed to understand its cadence and behavior, and that of the outflows in SS 433 in general. The two optical interferometric observations with GRAVITY so far have revealed extremely variable spatial structure to the line emission.
Finally, we note that the spherical wind component, with FWHM ∼ 2000 km s−1, surrounds the entire binary with a FWHM size of ∼5 − 6 mas (the fit size of the wind is much smaller for Epoch 1; however, this epoch suffers from severe blending with jet emission lines, meaning that its parameters are much more degenerate and difficult to constrain). The entire SS 433 system appears to be engulfed in an optically thin line-emission envelope.
5. Conclusions
Here we present a second set of optical interferometry observations of the unique microquasar SS 433 with VLTI/GRAVITY. We have focused on the analysis of the near-infrared continuum and the Brγ stationary line. Our results can be summarized as follows.
-
The K band continuum is composed of an unresolved point source (accretion disk+donor star) and an extended structure of FWHM ∼ 7 mas. The latter is consistent with being an equatorial disk, but could also have a contribution from an extended spherical wind, both of which are seen in the Brγ stationary line.
-
The model-independent emission centroids across the Brγ line clearly point to it being dominated by an equatorial (perpendicular to the jets) structure in the 2017 observations, whereas in the previous GRAVITY observation in 2016 the emission was rather more aligned with the jets, suggestive of a bipolar outflow. The rotation direction of the outflow is retrograde relative to the jet precession, in accordance with the slaved disk precession model.
-
The equatorial structure is very extended and carries a specific angular momentum that is greater than or approximately equal to ten times that of either binary component. If interpreted as a disk in Keplerian rotation, this would imply an implausibly high enclosed mass of ∼400 M⊙. We suggest instead that it traces an outflow corresponding to the centrifugal ejection of a circumbinary disk, the existence of which has been inferred from optical spectroscopy. The nondetection of an equatorial structure in the 2016 observation suggests that such a disk can disappear. We suggest that the equatorial outflows typically seen in high-resolution radio images correspond to similar episodes of circumbinary disk ejection. The mechanism driving the specific angular momentum transfer necessary to make the disk super-Keplerian and centrifugally eject it is unclear, but is possibly associated with tidal torques from the binary components.
-
The formation and ejection of the circumbinary disk could have an important effect on the binary evolution of SS 433 depending on their cadence. Future optical and radio interferometric observations capable of spatially resolving the outflows are needed to further study them.
-
In addition to the equatorial structure, the data also suggest a line component from a symmetric and extended spherical wind ∼6 mas responsible for the high-velocity wings ≳1000 km s−1 of the line. The binary appears therefore to be engulfed in an optically thin and extended emission line envelope.
Acknowledgments
We thank the GRAVITY Co-Is, the GRAVITY Consortium, and ESO for developing and operating the GRAVITY instrument. In particular, I.W. and J.D. thank the MPE GRAVITY team, in particular F. Eisenhauer, R. Genzel, S.Gillessen, T. Ott, O. Pfhul and E. Sturm. We also thank the GRAVITY team members (W. Brandner, F. Einsenhauer, S. Hippler, M. Horrobin, T. Ott, T. Paumard, O. Pfhul, O. Straub, E. Wieprecht) and ESO staff who were on the mountain during the observations. We also thank P. Kervella for comments on the paper. POP acknowledges financial support from the CNRS High Energy National Program (PNHE). POP and GD acknowledge financial support from the CNES. This research has made use of the Jean-Marie Mariotti Center SearchCal service (available at http://www.jmmc.fr/searchcal) co-developped by LAGRANGE and IPAG, CDS Astronomical Databases SIMBAD and VIZIER (available at http://cdsweb.u-strasbg.fr/), NASA’s Astrophysics Data System Bibliographic Services, NumPy (Van Der Walt et al. 2011) and matplotlib, a Python library for publication quality graphics (Hunter 2007).
References
- Allen, D. A. 1979, Nature, 281, 284 [NASA ADS] [CrossRef] [Google Scholar]
- Artymowicz, P., & Lubow, S. H. 1994, ApJ, 421, 651 [NASA ADS] [CrossRef] [Google Scholar]
- Begelman, M. C., & Rees, M. J. 1984, MNRAS, 206, 209 [NASA ADS] [CrossRef] [Google Scholar]
- Begelman, M. C., Sarazin, C. L., Hatchett, S. P., McKee, C. F., & Arons, J. 1980, ApJ, 238, 722 [NASA ADS] [CrossRef] [Google Scholar]
- Begelman, M. C., King, A. R., & Pringle, J. E. 2006, MNRAS, 370, 399 [NASA ADS] [CrossRef] [Google Scholar]
- Blandford, R. D., & Payne, D. G. 1982, MNRAS, 199, 883 [NASA ADS] [CrossRef] [Google Scholar]
- Blundell, K. M., & Bowler, M. G. 2004, ApJ, 616, L159 [NASA ADS] [CrossRef] [Google Scholar]
- Blundell, K. M., Mioduszewski, A. J., Muxlow, T. W. B., Podsiadlowski, P., & Rupen, M. P. 2001, ApJ, 562, L79 [NASA ADS] [CrossRef] [Google Scholar]
- Blundell, K. M., Bowler, M. G., & Schmidtobreick, L. 2008, ApJ, 678, L47 [Google Scholar]
- Bowler, M. G. 2010, A&A, 521, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bowler, M. G. 2018, A&A, 619, L4 [Google Scholar]
- Brinkmann, W., Kawai, N., & Matsuoka, M. 1989, A&A, 218, L13 [NASA ADS] [Google Scholar]
- Chelli, A., Duvert, G., Bourgès, L., et al. 2016, A&A, 589, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chen, W., & Zeng, Q. 2009, Chin. Sci. Bull., 54, 711 [Google Scholar]
- Cherepashchuk, A. M., Postnov, K. A., & Belinski, A. A. 2018, MNRAS, 479, 4844 [NASA ADS] [CrossRef] [Google Scholar]
- Clark, D. H., & Murdin, P. 1978, Nature, 276, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Doolin, S., & Blundell, K. M. 2009, ApJ, 698, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Eikenberry, S. S., Cameron, P. B., Fierce, B. W., et al. 2001, ApJ, 561, 1027 [NASA ADS] [CrossRef] [Google Scholar]
- Fabian, A. C., & Rees, M. J. 1979, MNRAS, 187, 13P [NASA ADS] [CrossRef] [Google Scholar]
- Fabrika, S. N. 1993, MNRAS, 261, 241 [NASA ADS] [Google Scholar]
- Fabrika, S. 2004, Phys. Rev., 12, 1 [Google Scholar]
- Fabrika, S. N., & Bychkova, L. V. 1990, A&A, 240, L5 [NASA ADS] [Google Scholar]
- Filippenko, A. V., Romani, R. W., Sargent, W. L. W., & Blandford, R. D. 1988, AJ, 96, 242 [NASA ADS] [CrossRef] [Google Scholar]
- Fuchs, Y., Koch Miramond, L., & Ábrahám, P. 2006, A&A, 445, 1041 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goranskij, V. 2011, Peremennye Zvezdy, 31, 5 [NASA ADS] [Google Scholar]
- Goranskij, V. P. 2017, in Stars: From Collapse to Collapse, eds. Y. Y. Balega, D. O. Kudryavtsev, I. I. Romanyuk, & I. A. Yakunin, ASP Conf. Ser., 510, 466 [NASA ADS] [Google Scholar]
- Gravity Collaboration (Abuter, R., et al.) 2017a, A&A, 602, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gravity Collaboration (Petrucci, P. O., et al.) 2017b, A&A, 602, L11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hillwig, T. C., & Gies, D. R. 2008, ApJ, 676, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. & Eng., 9, 90 [Google Scholar]
- Illarionov, A. F., & Sunyaev, R. A. 1975, A&A, 39, 185 [NASA ADS] [Google Scholar]
- Kubota, K., Ueda, Y., Fabrika, S., et al. 2010, ApJ, 709, 1374 [NASA ADS] [CrossRef] [Google Scholar]
- Lapeyrere, V., Kervella, P., Lacour, S., et al. 2014, in Optical and Infrared Interferometry IV, Proc. SPIE, 9146, 91462D [Google Scholar]
- Leibowitz, E. M. 1984, MNRAS, 210, 279 [NASA ADS] [CrossRef] [Google Scholar]
- Luri, X., Brown, A. G. A., Sarro, L. M., et al. 2018, A&A, 616, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Margon, B. 1984, ARA&A, 22, 507 [NASA ADS] [CrossRef] [Google Scholar]
- Margon, B., Ford, H. C., Grandi, S. A., & Stone, R. P. S. 1979, ApJ, 233, L63 [NASA ADS] [CrossRef] [Google Scholar]
- Marshall, H. L., Canizares, C. R., Hillwig, T., et al. 2013, ApJ, 775, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Mineshige, S., Rees, M. J., & Fabian, A. C. 1991, MNRAS, 251, 555 [NASA ADS] [CrossRef] [Google Scholar]
- Mioduszewski, A. J., Rupen, M. P., Walker, R. C., et al. 2004, in AAS/High Energy Astrophysics Division #8, Bull. Am. Astron. Soc., 36, 967 [Google Scholar]
- Monnier, J. D., & Allen, R. J. 2013, in Radio and Optical Interferometry: Basic Observing Techniques and Data Analysis, eds. T. D. Oswalt, & H. E. Bond, 325 [Google Scholar]
- Paragi, Z., Vermeulen, R. C., Fejes, I., et al. 1999, A&A, 348, 910 [NASA ADS] [Google Scholar]
- Paragi, Z., Fejes, I., Vermeulen, R. C., et al. 2002, in Proc. 6th EVN Symp., eds. E. Ros, R. W. Porcas, A. P. Lobanov, & J. A. Zensus, 263 [Google Scholar]
- Perez, M. S., & Blundell, K. M. 2009, MNRAS, 397, 849 [NASA ADS] [CrossRef] [Google Scholar]
- Roberts, W. J. 1974, ApJ, 187, 575 [NASA ADS] [CrossRef] [Google Scholar]
- Robinson, E. L., Froning, C. S., Jaffe, D. T., et al. 2017, ApJ, 841, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
- Shklovskii, I. S. 1981, Sov. Astron., 25, 315 [NASA ADS] [Google Scholar]
- Stephenson, C. B., & Sanduleak, N. 1977, ApJS, 33, 459 [NASA ADS] [CrossRef] [Google Scholar]
- Stirling, A. M., Jowett, F. H., Spencer, R. E., et al. 2002, MNRAS, 337, 657 [NASA ADS] [CrossRef] [Google Scholar]
- van den Heuvel, E. P. J., Ostriker, J. P., & Petterson, J. A. 1980, A&A, 81, L7 [NASA ADS] [Google Scholar]
- Van Der Walt, S., Colbert, S. C., & Varoquaux, G. 2011, Comput. Sci. Eng., 13, 22 [CrossRef] [Google Scholar]
- Vermeulen, R. C., Schilizzi, R. T., Spencer, R. E., Romney, J. D., & Fejes, I. 1993, A&A, 270, 177 [NASA ADS] [Google Scholar]
- Waisberg, I., Dexter, J., Pfuhl, O., et al. 2017, ApJ, 844, 72 [NASA ADS] [CrossRef] [Google Scholar]
- Waisberg, I., Dexter, J., Olivier-Petrucci, P., Dubus, G., & Perraut, K. 2018, A&A, submitted [arXiv:1811.12564] [Google Scholar]
- Zwitter, T., Calvani, M., & D’Odorico, S. 1991, A&A, 251, 92 [NASA ADS] [Google Scholar]
Appendix A: Full data and model fits
Here we show the data (spectrum, differential visibility phases, and amplitudes) and best fits for the “outflow” model for the three epochs of the 2017 observations and for all baselines. The solid lines show the models without the blended jet emission lines, whereas the dashed lines show the full combined model (as the fits are done). For the jet models and results, we refer to the companion paper on the jets (Waisberg et al. 2018). The projected length and position angle of each baseline is indicated.
 |
Fig. A.1. Data and best fit “outflow” model for Epoch 1. |
 |
Fig. A.2. Data and best fit “outflow” model for Epoch 2. |
 |
Fig. A.3. Data and best fit “outflow” model for Epoch 3. |
All Tables
All Figures
 |
Fig. 1. The uv-coverage for Epoch 2 of the GRAVITY 2017 observations. The colors represent the six different baselines, and the coverage in the radial direction corresponds to the different wavelength channels across the K band (2 − 2.5 μm). We also show the precessional axis of the jet and its precession cone as seen on sky. The projected baselines are sensitive to both the jet and the orthogonal directions. |
| In the text | |
 |
Fig. 2. K band continuum squared visibilities of SS 433 from the GRAVITY fringe tracker for the 2016 observation (top) and Epoch 2 of the 2017 observation (bottom). The continuum is modeled by the combination of an unresolved point source representing the binary (accretion disk + donor star) and a two-dimensional elliptical Gaussian which could represent an extended disk/wind. The data is shown in color and the best fit model is shown in black. |
| In the text | |
 |
Fig. 3. Model-independent centroid shifts across the Brγ stationary line for the 2016 observation and Epoch 2 of the 2017 observations. The dashed circle shows the binary size a ≈ 0.07 mas for a total mass M = 40 M⊙. The insets show the Brγ line spectrum with the color corresponding to the different wavelength/velocity channels. |
| In the text | |
 |
Fig. 4. Main features of the data and model. We show two representative baselines (UT3-1, yellow, and UT4-3, red – see Fig. 1) for Epoch 2 and the outflow model fit. Top row: spectrum centered on the Brγ stationary line. The latter is decomposed into an equatorial outflow (dark green) and a spherical wind (lime). The former is responsible for the S-shape signatures in the differential visibility phases (middle row) for baselines which are close to perpendicular to the jet (left), and show almost no signature on baselines more aligned with the jet (right). The inset shows the position angle of the outflow from the fit as well as the baseline directions on the sky plane. Bottom row: differential visibility amplitudes. The equatorial outflow alone would lead to an increase in visibility amplitude across the Brγ line. The extended wind component can explain both the high-velocity (≳1000 km s−1) wings in the spectrum and the net decrease in visibility amplitude across the line. We note that there are two Paα emission lines from the receding jet that are blended with the Brγ stationary line on its red side, and also create strong visibility signatures. The model fits were done for all the components simultaneously, but here we show only the visibility model for the stationary line for clarity (full model is shown in the Appendix). For the jet model and results, we refer to the companion paper on the jets (Waisberg et al. 2018). |
| In the text | |
 |
Fig. A.1. Data and best fit “outflow” model for Epoch 1. |
| In the text | |
 |
Fig. A.2. Data and best fit “outflow” model for Epoch 2. |
| In the text | |
 |
Fig. A.3. Data and best fit “outflow” model for Epoch 3. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.