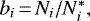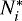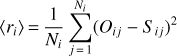| Issue |
A&A
Volume 623, March 2019
|
|
|---|---|---|
| Article Number | A103 | |
| Number of page(s) | 17 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201834680 | |
| Published online | 12 March 2019 | |
Ca line formation in late-type stellar atmospheres
I. The model atom
1
Instituto de Astrofísica de Canarias,
38205
La Laguna,
Tenerife,
Spain
e-mail: yeisson.osorio@iac.es
2
Departamento de Astrofísica, Universidad de La Laguna (ULL),
38206
La Laguna,
Tenerife,
Spain
3
Theoretical Astrophysics, Department of Physics and Astronomy, Uppsala University,
Box 516,
751 20
Uppsala,
Sweden
4
Max Plank Institute for Astronomy,
Königstuhl 17,
69117
Heidelberg,
Germany
5
Department of Physics and Astronomy, Drake University,
Des Moines,
IA
50311,
USA
Received:
19
November
2018
Accepted:
24
January
2019
Context. Departures from local thermodynamic equilibrium (LTE) distort the calcium abundance derived from stellar spectra in various ways, depending on the lines used and the stellar atmospheric parameters. The collection of atomic data adopted in non-LTE (NLTE) calculations must be sufficiently complete and accurate.
Aims. We derive NLTE abundances from high-quality observations and reliable stellar parameters using a model atom built afresh for this work, and check the consistency of our results over a wide wavelength range with transitions of atomic and singly ionised calcium.
Methods. We built and tested Ca I and Ca II model atoms with state-of-the-art radiative and collisional data, and tested their performance deriving the Ca abundance in three benchmark stars: Procyon, the Sun, and Arcturus. We have excellent-quality observations and accurate stellar parameters for these stars. Two methods to derive the LTE/NLTE abundances were used and compared. The LTE/NLTE centre-to-limb variation (CLV) of Ca lines in the Sun was also investigated.
Results. The two methods used give similar results in all three stars. Several discrepancies found in LTE do not appear in our NLTE results; in particular the agreement between abundances in the visual and infra-red (IR) and the Ca I and Ca II ionisation balance is improved overall, although substantial line-to-line scatter remains. The CLV of the calcium lines around 6165 Å can be partially reproduced. We suspect differences between our modelling and CLV results are due to inhomogeneities in the atmosphere that require 3D modelling.
Key words: line: formation / stars: abundances
© ESO 2019
1. Introduction
Calcium produced in supernovae explosions is one of the most useful elements for the quantitative analysis of stellar spectra, since it produces numerous absorption lines, many of which have accurate oscillator strengths measured in the laboratory (Smith 1988; Smith & Gallagher 1966; Smith & Raggett 1981). The Ca II IR triplet (8500–8600 Å) is one of the most extensively used spectral features to study radial velocities and metallicities of distant stars and stellar systems (Terlevich et al. 1989; Kordopatis et al. 2011), and is the target of the Radial Velocity Spectrometer on board the Gaia mission (Gaia Collaboration 2016, Sect. 3.3.7). The Ca II H and K resonance lines at ~3950 Å, on the other hand, are essentially the only metallicity indicator accessible at intermediate or low spectral resolution in extremely metal-poor stars (Christlieb et al. 2004), in addition to being an invaluable tool to probe the interstellar medium (Welsh et al. 2010) or solar and stellar chromospheres (Hall 2008; Socas-Navarro et al. 2015).
The separation of the [Ca/Fe] abundance ratios found in thin/thick-disc star sequences with metallicity is smaller compared to other α elements (see Fig. 14 of Reddy et al. 2006); a more precise and accurate determination of the calcium abundances is required in order to make this separation more clear. Calcium also has observable lines along a broad range of wavelengths in late-type stellar spectra. To ensure the consistency of the derived abundances for transitions in different parts of the spectrum is important in order to make reliable comparisons among different surveys. The Apache Point Observatory Galactic Evolution Experiment (APOGEE, Majewski et al. 2017) is part of the Sloan Digital Sky Survey (SDSS-III, Eisenstein et al. 2011) and is observing stars in the northern hemisphere in the H-band (15 090–16 990 Å). Its successor APOGEE-2, part of SDSS-IV (Blanton et al. 2017), extends the sample to the southern hemisphere. The MaSTAR program (MANGA stellar library, part of SDSS-IV) will also observe northern stars in the optical (3600–10 350 Å) while the GALAH Survey (Anguiano et al. 2014) observes stars in the southern hemisphere at optical wavelengths (4700–7890 Å); in those surveys Ca lines are observed for hundreds of thousands of stars.
Early work on non-local thermodynamic equilibrium (NLTE) effects for calcium performed in the Sun and Procyon indicated that small corrections should be expected for solar-type stars (Smith & Drake 1987), but later work has shown that this situation changes depending on the stellar spectral type and luminosity.
NLTE studies on Ca have been done since the 1970s, starting with the ground-breaking work by Linsky & Avrett (1970) on Ca II lines in the Sun. Till the mid 1980s, NLTE studies on Ca focused on the H and K Ca II lines (Mein 1971; Auer & Heasley 1976; Saliba 1985). Watanabe & Steenbock (1985) compared their NLTE calculations with observations of the Sun and Procyon, and found that Ca is more sensitive to NLTE in the latter star. Drake (1991) calculated the first grid of NLTE calculations, spanning 5400 < Teff < 6200, 1.0 < log g < 4.5, and −1 < [Fe/H] < 0, and finding enhanced NLTE effects at low log g values and found that departures from LTE in giants can significantly vary among different multiplets of Ca I lines. An important conclusion from these studies is that the thermalisation of the Ca populations in late-type stars is sensitive to inelastic collisions with hydrogen, and the over-ionisation of Ca I by UV photons.
Idiart & Thévenin (2000), in the first large-scale application of NLTE calculations for Ca, collected equivalent widths (weq) from the literature and computed NLTE differential abundances for some 250 dwarf/sub-giant stars, studying the implications for Ca and Mg in Galactic evolution.
More recently, Mashonkina et al. (2007) performed a detailed NLTE study of Ca in cool stars with a comprehensive model atom with 63 Ca I levels, 37 Ca II levels, and the ground level of Ca IIi. Energy levels were adopted from the NIST atomic spectra database. Bound–bound and bound–free radiative data were obtained from the Opacity Project available through the TOPBASE database (Cunto & Mendoza 1992). Hydrogen collisions for Ca I were included via empirically scaled rates from the Drawin formula (Drawin 1968; Steenbock & Holweger 1984). Regarding electron collisions, excitation rates from the ground level of Ca I were taken from Samson & Berrington (2001), and for Ca II, for transitions involving the seven lowest levels, from Burgess & Chidichimo (1983). For the remaining allowed and forbidden transitions the impact parameter method (IPM) from Seaton (1962) and a thermally averaged collision strength of 1.0 (Allen 1976) were adopted, respectively. Electron collisional ionisation using the Seaton formula (Seaton 1962) was also implemented in this study. Almost all later work for calcium Ca in NLTE until now used modified versions of this model atom.
Spite et al. (2012) used the same model atom from Mashonkina et al. (2007), except that they substituted the IPM for electron collisional excitation with the van Regemorter (1962) formula. They derived calcium abundances for lines in the spectrum of Procyon, finding good agreement between the results for lines of neutral and singly ionised calcium: A(Ca) = 6.25 ± 0.04 and 6.27 ± 0.06 dex from Ca I and Ca II lines respectively, in contrast with the values derived by Mashonkina et al. (2007): 6.19 ± 0.04 and 6.38 ± 0.05 dex from Cai and Ca II lines, respectively.
An important conclusion from the Mashonkina et al. (2007) study is the sensitivity of the derived Ca I/II abundance ratio to inelastic hydrogen collisions. Recently, Mashonkina et al. (2017) used an upgraded version of their model atom from 2007. This update included inelastic calcium-hydrogen collisions from Belyaev et al. (2016), avoiding the need for adopting the Drawin formula, and calcium-electron collisions for Ca II from Meléndez et al. (2007). Their results for Procyon were 6.26 ± 0.05 and 6.32 ± 0.05 dex from Ca I and Ca II lines, respectively, bringing the two average values closer than in their earlier study.
In this paper, we assembled from scratch new model atoms for neutral and singly ionised calcium suitable for the determination of Ca abundance1 in the visual and in the IR where many of the lines come from high excitation levels. We decided to perform this study to take advantage of recently published H-Ca inelastic collisional rates, electron collisional excitation rates calculated via the R-matrix method, new theoretical calculations of oscillator strengths, and, for the first time, updated methods for the treatment of hydrogen collisional excitation rates involving Rydberg levels of Ca I and electron collisional ionisation rates for Ca I. Our model atom is publicly available2. With the new model atoms, we revisit the formation of calcium lines in the photospheres of the Sun, Procyon, and Arcturus (α Boo). We confrontour calculations with ultra-high-quality observations for these stars in both the optical and the IR, comparing the inferred abundances. In order to study NLTE effects over such a wide wavelength range, we decided to focus this work on stars with reliable parameters and excellent observations; the interesting case of metal-poor stars will betreated in a forthcoming paper. In Sect. 2 we describe our new model atoms, while Sect. 3 addresses the adopted observations for the reference stars. Section 4 is devoted to the statistical equilibrium calculations, and Sect. 5 examines the impact of departures from LTE on the interpretation of the spectra of the reference stars. Section 6 summarises our main conclusions.
2. Model atom
Our model atom was built integrating radiative and collisional data mostly from the literature, and including data calculated by us. Below, we provide a description of the different radiative and collisional components adopted.
2.1. Energy levels and radiative data
For Ca I and Ca II, energy levels were obtained from the NIST database (Ralchenko et al. 2014). Bound–bound radiative data (f-values) were taken from the NIST and the VALD databases (Piskunov et al. 1995; Ryabchikova et al. 1997; Kupka et al. 1999, 2000, from which broadening parameters were also obtained). When possible, we computed Van der Waals broadening parameters from the ABO theory (Anstee & O’Mara 1995; Barklem & O’Mara 1997; Barklem et al. 1998a,b).
New ab initio relativistic calculations of radiative lifetimes of bound–bound transitions of Ca I from Yu & Derevianko (2018) include data for 811 optically allowed transitions in LS coupling. The original information in the VALD database is mainly from Kurucz (2007) for Ca I and Kurucz (2010) for Ca II, updated with f-values of 114 bb transitions (63 for Ca I and 51 for Ca II) from Drozdowski et al. (1997), Smith (1981, 1988), Shabanova (1963), Smith & Raggett (1981), Smith & O’Neill (1975), Smith &Gallagher (1966), Seaton et al. (1994) and Theodosiou (1989). NIST f-values are available for 134 Ca I and 99 Ca II transitions, compiled by Wiese et al. (1969). The preference order for the selection of f-values for transitions with multiple sources is:
- 1.
experimental values from VALD;
- 2.
Yu & Derevianko (2018; only available for Ca I);
- 3.
NIST;
- 4.
Kurucz (2007, 2010);
- 5.
TOPBASE.
We decided on the levels to be included in the final model atom based on three criteria. First, to ensure that the gap between the highest level of Ca I and the ground level of Ca II was sufficiently small to guarantee that those two levels are collisionally coupled, and thus ionisation balance between Ca I and Ca II is not affected by any artificial energy gap (similarly for the gap between Ca II and Ca IIi). Second, the fine-structure splitting of the levels is needed in order to directly compare the synthetic spectrum with the observation of lines for which fine structure produces asymmetric profiles, or that are seen as fully resolved lines. Third, the transitions used in the visual and IR to compare with observations do not come from merged levels.
Our final model atom has 127 levels in total (96 for Ca I, 30 for Ca II and the ground level of Ca IIi). For Ca I, all the triplets up to the 3d.3d(3F) levels are split into their fine structure components, except for the triplet 4s.4f(3F), which is represented by a single level. From the 4s.7s(3S) up to the 4s.8f (1F) level, triplets are merged into a single level, except for the 4s.7p(3P), 4s.8d(3D) and the 3d.5s(3D) levels. The levels with n = 6, l ≥ 4 are merged, as are those with n = 7, l ≥ 4, and n = 8, l ≥ 4. We use super levels for the levels with 9 ≤ n ≤ 15. The energies for the 3d.3d(3P) levels (also included in the final model atom with split fine-structure components) are similar to those for the n = 12 super level.
Ca II consists only of doublets. Fine-structure components were split for all levels up to 6p(2 P), except for the 4f(2F) level. The 5f(2F), 5g(2 G), 6d(2 D), and 6f(2 F) levels were also represented by one level each. For n = 6, l ≥ 4, a single level was used; weused super levels for 7 ≤ n ≤ 15. Isotopic splitting was considered for the Ca II triplet lines (wavelength shifts were taken from Leenaarts et al. 2014; Nörtershäuser et al. 1998) and using the solar-system isotope abundance ratios (Anders & Grevesse 1989; Asplund et al. 2009).
Our final model atom has 120 bound–free transitions and 1808 bound–bound transitions (1656 of Ca I and 152 of Ca II). When a level that has been merged is involved in a transition, the excitation oscillator strength fij is re-scaled as
![\[ f_{ij}' =f_{ij}\frac{g_i}{g_i'}, \]](/articles/aa/full_html/2019/03/aa34680-18/aa34680-18-eq1.png)
where 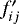 denotes the new, re-scaled, excitation oscillator strength and gi,
denotes the new, re-scaled, excitation oscillator strength and gi, 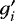 are the statistical weights of the original and the new (merged) low level of the transition, respectively. Radiative data for the most relevant transitions of Ca used in this work are shown in Table A.1. Grotrian diagrams for Ca I and Ca II are shown in Fig. 1.
are the statistical weights of the original and the new (merged) low level of the transition, respectively. Radiative data for the most relevant transitions of Ca used in this work are shown in Table A.1. Grotrian diagrams for Ca I and Ca II are shown in Fig. 1.
 |
Fig. 1 Grotrian diagram representing the Ca I (left panel) and Ca II (right panel) levels and radiative transitions (grey) used in our model atom. The horizontal black solid lines represent super levels. The dashed line in each diagram shows the ionisation limit. Only the lowest levels are labelled to ease visualisation. |
2.2. Collisional data
The main collisional perturbers in cool stars are electrons (due to their high velocity) and hydrogen atoms (due to their abundance).We consider four collisional processes, and their inverse through detailed-balance relations: electron collisional excitation and ionisation, hydrogen collisional excitation, and charge exchange with hydrogen. In the latter, an atom of Ca I transfers one of its electrons to the colliding hydrogen atom in its ground level and, as a result of this collision, an ionised atom (Ca II) and a negative hydrogen ion (H−) are produced. When levels are merged, the final transition is the sum of the transitions between the levels involved, weighted with the statistical weight of the initial levels of the transitions to merge. Below, we provide a description of the data used to represent all these processes.
2.2.1. Electron collisions
Electron collisional ionisation for all levels of Ca II and the low-lying levels of Ca I were calculated with the hydrogenic approximation presented in Cox (2000), based on the semi-empirical formulation in Bely & van Regemorter (1970) which is original from Percival (1966). For the levels above the 4s.6s(1S) level of Ca I, we used the formula from Vrinceanu (2005), suitable for electron collisional ionisation of Rydberg states of neutral atoms, and which takes into account the electronic angular momentum of the Rydberg level.
The adopted electron collisional excitation rates for Ca I are an extension of the rates calculated by Zatsarinny et al. (2006). This extension includes electron collisional excitation cross sections between the lowest levels of Ca I and 4s.8s(1S), using the B-spline R matrix (BSR) method. Electron collisional excitation of Ca II for levels up to n = 8 were taken from Meléndez et al. (2007). For higher levels, we neglected dielectronic transitions and tested both the impact parameter method (IPM, Seaton 1962 for neutral species and Burgess et al. 1977 for positive ions) and the vanRegemorter (vR) formula (Bely & van Regemorter 1970; van Regemorter 1962), finally adopting the IPM rates. The vR formula is based on the Born approximation, which is known to overestimate electron collisional cross-sections at low energies (see Seaton 1962). Our previous work on Mg (Osorio et al. 2015) also showed thatthe use of the IPM (when no quantum mechanical calculations are available) reproduces the IR Mg i emission lines observed in the Sun, but that if we used the vR formula instead, the above-mentioned lines cannot be reproduced.
We decided to neglect dielectronic transitions based on comparison between one and two electron transitions calculated for this work. Figure 2 shows the electron collisional rate coefficients at 5000 K obtained from quantum mechanical calculations (Zatsarinny et al. 2006). One-electron transitions are marked with black crosses in Fig. 2. Dielectronic transitions tend to be orders of magnitude weaker. The most clear case is with the 3d2 (3F) level, where due to its weak collisional coupling with levels with similar energies, it is the first level that shows significant departures from LTE at the deep layers of the photosphere (see Sect. 4).
Parameters adopted and results of the calculation of inferred Ca abundance.
 |
Fig. 2 Matrix with electron collisional rate coefficients at 5000 K taken from the extension of the calculations made in Zatsarinny et al. (2006) and used in this work. The colours represent the rate coefficients in a logarithmic scale. The crosses indicate one-electron transitions. Transitions involving the 4s.5g levels are not calculated and approximation formulas (valid only for one-electron transitions) are used. |
2.2.2. Hydrogen collisions
Hydrogen collisional excitation was considered for Ca I and neglected for Ca II. Apart from Mashonkina et al. (2017), previous works on NLTE calculations for Ca that studied the effects of collisions with hydrogen made use of the Drawin formula. Mashonkina et al. (2017) included detailed calculations on Ca I+H collisions by Belyaev et al. (2016) and the Drawin formula for Ca II+H collisions in their model atom. The Drawin formula is used to treat excitation of atoms due to collisions with hydrogen only for optically allowed transitions; although it has been shown that it overestimates collision rates by orders of magnitude (Barklem et al. 2011) and often an arbitrary scale-factor is used. We adopted the data from Barklem (2016, 2017), who uses a new theoretical method based on an asymptotic two-electron model of ionic-covalent interactions for the calculation of hydrogen-atom collisional excitation and charge-transfer processes. We included collisional excitation between the lowest levels of Ca I up to 4s.6s(3S), but ignoring two-electron (de)excitation processes. Charge-transfer processes with H involving the same levels of Ca I as above and the three lowest levels of Ca II were considered. Again, only transitions involving the removal of one of the valence electrons were considered. Hydrogen collisional excitations between levels above 4s.6s (3 S) were treated using the formula for Rydberg-neutral inelastic collisions from Kaulakys (1986), disregarding dielectronic transitions.
3. Reference stars
In order to test our model atom for Ca we used three benchmark stars with observations of exceptional quality and well-known parameters: the Sun, Arcturus, and Procyon. For the Sun, we adopted Teff = 5772 K, log g (cm s−2) = 4.44, and [Fe/H] = 0.0 dex, with the solar element abundances from Asplund et al. (2005) and microturbulent velocity Vmic = 1.1 km s−1. For Arcturus, we adopted Teff / log g/[Fe/H] = 4300/ 1.5/−0.5 and Vmic = 1.6 (Ramírez & Allende Prieto 2011). In the case of Procyon the parameters were Teff / log g/ [Fe/H]= 6530/4.00/0.0 and Vmic = 2.0 (Allende Prieto et al. 2002). These parameters, together with the derived calcium abundance, A(Ca), are summarised in Table 1.
Calcium lines are detectable in a wide wavelength range of the spectrum of late-type stars. The variety in strength and excitation level makes calcium a good candidate for testing various NLTE processes. The UV continuum forms in higher atmosphericlayers than the visual and near-infrared (NIR) continuum, thus lines in this region are typically affected by severe departures from LTE. Strong lines form their wings and cores at very different atmospheric depths, and therefore different NLTE effects can be at play shaping them.
For the Sun, we adopted the atlas from Kurucz et al. (1984); it covers an area from 3000 to 13 000 Å and has a resolution of R ≈ 400 000. We compared this atlas with the PEPSI solar atlas (Strassmeier et al. 2018a), which has lower resolution and therefore shallower line cores (see Fig. 4). Good agreement is however found after smoothing the higher-resolution atlas to match the PEPSI resolution.
For the NIR region we used the atlas from Livingston & Wallace (1991) that spans between 11 000 and 50 000 Å with a resolving power ≈300 000 and measures the disc-centre intensities of the Sun with telluric lines removed. In the overlap between both atlases there are two clean Ca II lines: 11 838 and 11 949 Å. Figure 3 shows part of the overlapping region around the 11 949 Ca II line.
For Arcturus, we adopted the high-resolution atlases in the visible (Hinkle et al. 2000, R ≈ 150 000), spanning between 3727 and 9300 Å, and in the IR (Hinkle et al. 1995, R ≈ 100 000), spanning between 9129 and 53 000 Å.
The Procyon observations are from PEPSI (Strassmeier et al. 2018b). The PEPSI spectrum covers wavelengths from 3800 to 9100 Å at R ≈ 220 000, therefore including the Ca II triplet. We compared them with observations from Allende Prieto et al. (2002), which span from 4560 to 7400 Å, and found excellent agreement, as illustrated in Fig. 4.
 |
Fig. 3 Comparison of the observations in part of the overlapping region between the two atlases used for the Sun: Kurucz et al. (1984) for the visual region (solid black lines) and Livingston & Wallace (1991) for the IR (red dashed lines). The latter atlas has telluric lines removed and measures the disc centre intensity of the Sun. The wavelengths were shifted in order to match the observations. |
4. Computations
The calculations of LTE/NLTE synthetic line profiles and populations were performed using the code MULTI (version 2.3; Carlsson 1986, 1992), which adopts the plane parallel approximation on its radiative transfer and statistical equilibrium calculations. The same is true for the 1D LTE model atmospheres we employ in our calculations (see Sect. 4.1).
MULTI uses the trace-element approach, where it is assumed that the departures from LTE of the level populations of the element under study do not affect the atmospheric structure or the background opacities. Therefore, atmospheric parameters and background opacities are held fixed. The latter assumption may be justified since the calcium contribution to the background opacity and the free-electron reservoir is <10% of the contribution made by more-abundant elements such as Fe, Si, or Mg. We adopted the same background line opacity data used in the MARCS grid presented in Gustafsson et al. (2008), re-sampled on 10 300 frequency points.
The radial-tangential formulation (Gray 1975) was implemented to represent macroturbulence and we allowed it to vary at the same time as the calcium abundance in order to fit the observations. The values adopted for vsini were extracted from the literature: 5.4, 1.6, and 4.0 km s−1 for Procyon (Martínez-Arnáiz et al. 2010), the Sun (Pavlenko et al. 2012), and Arcturus (Massarotti et al. 2008), respectively.
4.1. Stellar atmospheric models
In this work we used Kurucz model atmospheres computed with ATLAS9 (Kurucz 1993), using exactly the same setup described by Mészáros et al. (2012). For the centre-to-limb variation (CLV) analysis, we also tested the photospheric reference model from Maltby et al. (1986), as this is a semi-empirical model intended to represent the quiet Sun and the average thermodynamical properties of the chromosphere. We refer to this model as the MACKKL model, and its thermal structure is shown and compared with its Kurucz counterpart in Fig. 5.
MULTI accepts input depth points defined in column mass or optical depth at 5000 Å (τ5000) in the model atmosphere, but the calculations are performed in a τ5000 scale. If the input is provided in a column mass scale, the τ5000 data points are calculated by integration of the density multiplied by the absorption coefficient using the trapezoidal rule. We experimented using both τ5000 and column-mass formats in the input Kurucz model atmosphere for MULTI, and found that adopting a column mass scale for the input leads to optical depths compatible with the background opacities used in the calculations. We also found that using column mass on the input model atmosphere results in structures on an optical depth scale that are in good agreement with the MARCS models (Gustafsson et al. 2008), which were calculated with the same background opacities used in this work.
Given that the main NLTE effect visible in the stellar spectra in this study is the deepening of the core of Ca lines, and the formation ofthese cores occurs in high atmospheric layers, we decided to adopt Kurucz model atmospheres over MARCS due to their larger extent. For example, for the solar models available for the Sun, the ranges in optical depth are log10(τ5000) = (−4.9,1.8) and (−6.9,1.8) for the MARCS and Kurucz model atmospheres, respectively.
In LTE the cores of the Ca II IR-triplet lines form at the top boundary of the MARCS model atmospheres, while for the Kurucz models the same region is well under the outer limit. The NLTE calculations make this situation worse, shifting the formation of the core of these lines to log10(τ5000) approximately − 6 in the Kurucz model.
 |
Fig. 4 Comparison of the observations of the Ca I 5590 Å line between popular atlases of the three studied stars. PEPSI atlases are from Strassmeier et al. (2018a,b). IAG atlas comes from Reiners et al. (2016), NOAO atlas for Arcturus comes from Hinkle et al. (2000) and McDonald data come from Allende Prieto et al. (2002). The atlases were wavelength shifted in order to match the air wavelength of the 5590 Å Ca I line. |
4.2. NLTE populations and spectral synthesis
In order to test the impact of the electron collisional data adopted in this work, we compared our results with those obtained with standard formulae, namely those by van Regemorter (vR) and Allen (taken from Cox 2000) for electron collisional excitation and ionisation, respectively. This set of electron collisional data will be referred to as vR+A; in contrast, our default atom contains electron collisional data from quantum mechanical calculations for excitation and a more sophisticated formula (Vrinceanu 2005) for ionisation.
The use of the vR+A data tends to increase the population of the low-lying levels of Ca I at line-formation layers (which for Procyon and the Sun implies larger departures from LTE) while intermediate and high levels of Ca I tend to decrease their population when compared with NLTE calculations using updated electron collisional data. A notable case is the 3d2 (3P) levels where, as mentioned earlier, quantum mechanical calculations of electron collisional cross sections show a weak collisional coupling between this level and other levels with similar energy while the use of vR+A rates couples the 4s.4f(1F*) and 3d2 (3P) levels leaving them in relative LTE. The thick three-dot-dash lines in Fig. 6 represent the departure coefficients3 of the n = 15 super-level (bn = 15). For the Sun and Procyon, these levels couple with the ground level of Ca II (which is thermalised). In the case of Arcturus, the n = 13 level decouples from the ground level of Ca II at log τ5000 ≲−2.5 while the n = 15 level (the highest level adopted for Ca I in our model atom) remains coupled with the ground level of Ca II in most of the atmosphere, including the line-formation region, up to logτ5000 approximately − 4. In reality, the highest levels of Ca I and the continuum (i.e. the ground level of Ca II) are collisionally coupled and this must be reflected in the modelling of the populations. As mentioned earlier, this is one of the criteria used to select the levels of our final model atom.
 |
Fig. 5 Temperature structure of the two solar models used in this work. The MACKKL model includes the lower chromosphere. |
5. Comparisons with observations
We compare high-quality observations of the Sun, Arcturus, and Procyon with synthetic spectra of Ca I and Ca II lines in LTE and NLTE conditions. Due to the large number of Ca lines present in the spectra of late-type stars we can take advantage of the wide spectral range offered by the available atlases to investigate NLTE effects. Additionally, we examine the CLV in the solar spectrum, which is also a useful diagnostic for departures from LTE.
 |
Fig. 6 Departure coefficients (b = nNLTE∕nLTE) of selected levels of Ca I and the ground level of Ca II using different electron collisional data. Line symbols represent different levels; in red are the departure coefficients obtained when the vR+A data are used for electron collisions (see text), and in black are the b coefficients obtained when updated electron collisional data are used. |
5.1. Reference stars
Two methods were used here for the calculation of observed Ca abundances in each star. The first method is the so-called line-by-line method, where the abundance is calculated for individual lines. For each transition, the radial-tangential macroturbulent velocity vmac and the Ca abundance were allowed to vary, in order to obtain the best possible match to the observations. The dispersion in the inferred Ca abundances was used as an indicator of the uncertainty. In the second method, named all-lines method, the same Ca lines were analysed, but only one value of vmac and A(Ca) was allowed in order to find the best fit for all lines simultaneously. The best fit in each case was evaluated via χ2 minimisation; the error estimation for the all-lines method was determined via the confidence region in the (A(Ca),vmac) plane where χ2 < min(χ2)+2.71 (corresponding to a confidence level of 90%), following the recommendations in Press et al. (1992). The confidence regions of the fit are shown in Fig. 7.
For the Sun and Arcturus, 76 and 59 lines, respectively, were used for 3800 < λ < 22 900 Å. For Procyon, 49 lines were used in the range 3800–9100 Å. Figure 8 shows the behaviour of the derived LTE and NLTE abundances with respect to wavelength as well as line strength4. We also experimented with different values of microturbulence that basically changed the slopes shown in Fig. 8. Tuning the microturbulence does not flatten the trends of A(Ca) versus line strength and A(Ca) versus wavelength simultaneously.
In Procyon, we found a NLTE abundance correction of 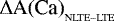 approximately − 0.07 dex in the two methods. The all-lines method shows a weak dependence of the best fit with macroturbulence since the confidence region around the best χ2 is elongated in vmac (see contours in Fig. 7). The line-by-line method shows improvement in the trend of NLTE calcium abundances versus wavelength in comparison with LTE abundances but the trends of A(Ca) versus line strength show a negative slope in NLTE (see Fig. 8) while LTE derived abundances versus line strength show a positive slope.
approximately − 0.07 dex in the two methods. The all-lines method shows a weak dependence of the best fit with macroturbulence since the confidence region around the best χ2 is elongated in vmac (see contours in Fig. 7). The line-by-line method shows improvement in the trend of NLTE calcium abundances versus wavelength in comparison with LTE abundances but the trends of A(Ca) versus line strength show a negative slope in NLTE (see Fig. 8) while LTE derived abundances versus line strength show a positive slope.
In the solar spectrum, there is a small reduction in the spread in the derived A(Ca) in NLTE with respect to LTE. The standard deviations of the derived abundances in the line-by-line method change from 0.17 (IR) and 0.10 (visual) in LTE to 0.09 (IR and visual) in NLTE. Saturated lines ( − 5.5 ≲ log (weq∕λ) ≲ −4.5) suffer the strongest departures from LTE, while weak and strong lines are less affected (mid-right panel in Fig. 8). The strengthening of the line cores in NLTE significantly improves the match with observations. A typical example of the LTE and NLTE fits of a Ca line is shown in Fig. 9. As mentioned in Mashonkina et al. (2017), we found also that NLTE effects in saturated lines are the weakening of the wings and the strengthening of the line core. The dependence of the NLTE abundance corrections with wavelength is less clear; lines with noticeable differences in LTE/NLTE abundance are spread all over the wavelength range (see left panels in Fig. 8). It is worth pointing out that the Ca lines covered by APOGEE (Wilson et al. 2010) at ~ 1.6 μm are not affected by NLTE in the Sun due to their small strength and formation depth.
In the Sun, NLTE effects are obvious in the core of strong but unsaturated lines. The derived abundances obtained from line-profile fitting or equivalent-width matching are not significantly affected by this discrepancy, but the NLTE line profiles fit the observations much better, reducing the overall discrepancy between modelled and observed spectra (see Fig. 10). For example, in Fig. 9 a χ2 test comparing the best fit and the observations leads to χ2 = 345.7, 191.3, and 160.6 for the LTE, NLTE (using the vR+A set of electron collisions), and NLTE cases, respectively5. We find consistent NLTE abundances for the visual and IR regions of the Sun (in the visual, 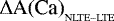 approximately−0.08 dex). We also note that the derived macroturbulent velocity is lower in LTE than in NLTE. The resulting NLTE correction is also a consequence of having vmac as a free parameter; in order to reduce the overall difference between observed and synthetic line profiles, vmac tends to decrease when A(Ca)
approximately−0.08 dex). We also note that the derived macroturbulent velocity is lower in LTE than in NLTE. The resulting NLTE correction is also a consequence of having vmac as a free parameter; in order to reduce the overall difference between observed and synthetic line profiles, vmac tends to decrease when A(Ca) increases.
increases.
In Arcturus, NLTE improves the agreement between derived abundances in the visual and the IR. When LTE is adopted, the difference of derived A(Ca) between the visual and the IR is 0.18 dex when using the all-lines method and 0.33 dex when using the line-by-line method. The derived A(Ca) in the visualand IR regions differ by 0.05 dex when using the all-lines method. The line-by-line method shows a discrepancy of A(Ca)
in the visualand IR regions differ by 0.05 dex when using the all-lines method. The line-by-line method shows a discrepancy of A(Ca) between the visual and the IR of 0.18 dex but there is no improvement in the dispersion, with respect to the LTE case, and marginal improvements in the trends with λ and line strength (see Fig. 8). Improving the agreement of derived abundances in different wavelength regimes is especially important for studies that aim to compare abundances from different surveys (Anguiano et al. 2018).
between the visual and the IR of 0.18 dex but there is no improvement in the dispersion, with respect to the LTE case, and marginal improvements in the trends with λ and line strength (see Fig. 8). Improving the agreement of derived abundances in different wavelength regimes is especially important for studies that aim to compare abundances from different surveys (Anguiano et al. 2018).
For the three cases studied here, we checked the effect of microturbulence in the derived NLTE abundances and did not find any significant improvement either in the overall fit obtained or in the dispersion of derived abundances in the line-by-line method. The trends in wavelength and line strength (see Fig. 8) observed when using the line-by-line method cannot be corrected simultaneously by tuning the microturbulent velocity.
The residuals between the synthetic and observed line profiles are improved in NLTE with respect to LTE in the three cases studied here. In Fig. 10 we compared the mean of the residuals6 of the best fit obtained for each line in LTE and NLTE using the line-by-line method. We can conclude that in general NLTE reproduces the line profiles better than LTE.
Regarding the Ca I/Ca II abundance ratio, we obtain good agreement in NLTE (see Table 2). When applying the all-lines method in the solar IR spectra we used 13 Ca I lines, and only the two Ca II lines at ~11 900 Å because the other two Ca II lines covered by the observed spectrum were too weak. When using the line-by-line method (grouping together all the lines in the visual and IR solar spectra, see Table 2) we again obtain a good agreement in the NLTE results. We obtained very similar 1D NLTE results to Scott et al. (2015), who used MARCS models (6.26 and 6.28 dex for Ca I and Ca II respectively). However, they recommend A(Ca) = 6.32 ± 0.03 dex resulting from their 3D radiative-transfer calculations combined with ⟨3D⟩ NLTE corrections.
= 6.32 ± 0.03 dex resulting from their 3D radiative-transfer calculations combined with ⟨3D⟩ NLTE corrections.
The work of Mashonkina et al. (2017) presents a reduction of the Ca I/Ca II discrepancy ΔA (Ca II, Ca I) from 0.13 dex in LTE to 0.07 dex in NLTE for the Sun. They also derived A(Ca) from the 8498 Å Ca II line, which is insensitive to NLTE effects in the Sun and with a value of A(Ca)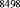 = 6.27 dex is in agreement with our NLTE results (see Table 2).
= 6.27 dex is in agreement with our NLTE results (see Table 2).
In the case of Procyon, Mashonkina et al. (2017) found good agreement between the derived Ca I and Ca II abundances already in LTE (0.03 dex) and the discrepancy slightly increases in NLTE (0.06 dex). In Table 2 we show our results (in LTE ~ 0.25 dex and NLTE ~ 0.04 dex). The reason for this difference could be due to the fact the Ca II lines used to report the Ca II abundances in Col. 3 of Table 2 do not include the Ca II triplet lines (which for Procyon and Arcturus are listed in Col. 5 of the same table).
In the three stars studied here, the wings of the Ca II IR lines are not sensitive to either NLTE or macroturbulence. In the Sun, the cores of these lines in LTE have depths similar to the observed ones but once NLTE is included the synthetic lines get deeper. When the solar model atmosphere includes chromosphere, the NLTE cores fit the observations, while the LTE cores go into emission (see Fig. 11).
 |
Fig. 7 Observed normalised flux spectra and comparison with our LTE/NLTE results. The spectra plots show the points used to calculate abundance and Vmac and the residuals with best fit in LTE and NLTE. The contours show the confidence regions corresponding to 1, 2, and 3σ (see Press et al. 1992). |
 |
Fig. 8 Line-by-line Ca abundance determination in the three observed stars. Red and black symbols denote LTE and NLTE abundances, respectively; triangles correspond to Ca I and squares/asterisks to Ca II lines. The lines show the linear fit of the LTE (red) and NLTE (black) abundances. |
 |
Fig. 9 Upper panel: comparison between observations (solid circles) and line profiles in LTE (dot-dash), NLTE using vR+A electron collisional data (dot-dash), and NLTE with updated electron collisional data of the solar Ca I 6439 Å line (A(Ca) = 6.25, Vmac = 3.0 m s−1). Lower panel: differences with observations. |
5.2. Centre-to-limb variation of solar Ca lines
Observations of the CLV of solar Ca lines were performed at the Swedish Solar Telescope (SST) in the summer of 2011. These data were used by Lind et al. (2017) who gave a detailed description of their analysis. In short, observations were performed using the TRIPPEL spectrograph (Kiselman et al. 2011), at μ = 0.2, 0.4, 0.6, 0.8 and 1.0, covering several wavelength regions with spectral resolution of ~150 000, among them the region used in this work: (6147,6159) Å; the Ca II IR triplet line at 8662 Å was also part of the observations.
The CLV observations are shown in Fig. 11. The synthetic spectra show only the Ca lines under study. The spectrum at μ = 1.0 was used to set A(Ca) and the macroturbulent velocity using the all-lines method. We obtained [A(Ca) dex, vmac m s−1] = [6.26(5), 1.9(3)] in NLTE and [6.28(5), 1.6(3)] in LTE. The values found at μ = 1.0 were used in the synthetic line profiles at μ = 0.8, 0.6, 0.4 and0.2. Figure 11 shows the comparison between the observations and the synthetic spectra for the LTE (dashed line) and NLTE (solid line) cases. The MACKKL solar model is used in this comparison. NLTE profiles are able to reproduce the depth of these lines at every μ value, while LTE profiles produce weaker cores at lower μ. As seen in Fig. 11, the depth of the NLTE cores match the observations even at low μ but the observed wings are wider than the synthetic ones. We believe the missing ingredient is atmospheric inhomogeneities; as shown by Lind et al. (2017) for the case of Fe, the observed variation of weq with μ is modelled significantly better with 3D than with 1D modelling. A more sophisticated analysis involving 3D model atmospheres and radiative transfer is expected to improve the agreement with observations near the limb.
We also tested the CLV behaviour using the Kurucz solar model atmosphere and found that the LTE/NLTE behaviour is similar in both cases for five of the lines in the 6165 Å region because those lines are formed in deep atmospheric layers. The 6162 Å line, on the other hand, has a different profile in LTE when using the MACKKL and Kurucz solar atmospheresbut the NLTE line profiles are almost identical (the line has the same depth in both cases but the core of the MACKKL profile is thinner). This is unexpected given that lines tend to form at higher layers in NLTE and this is where the two atmospheric models differ the most. We found, though, that different NLTE mechanisms are at work in the high layers of these two atmospheres: in the MACKKL model, the Planck function Bν (T) increases from log (τ5000) < −4 making Sv < Bν(T) and over-recombination of Ca I levels from the Ca II reservoir dominates. For the solar models with no chromosphere, levels of CaI tend to lower the population with respect to LTE (due to overall over-ionisation), but for the lowest levels, photon losses (particularly due to frequency redistribution from line wings) compete efficiently against over-ionisation in at high layers of the atmosphere making deeper line cores with respect to LTE, as in the case of the Ca I lines at 6165 Å.
The core of the 8662 Å Ca II triplet line forms at higher layers than the Ca I lines at ~6165 Å making the LTE-MACKKL line profile produce an emission core while the NLTE-MACKKL line profile matches the observations. The solar Kurucz model does not include the chromosphere. If this model is used, the wings of this line are almost unaffected, but the core differs considerably: at μ = 1.0 the LTE-Kurucz profile fits the observations better than the NLTE-Kurucz profile, but, as was the case for the 6162 Å line, the former becomes too weak at lower μ (see bottom panel in Fig. 11, where the long-dashed line shows the LTE-Kurucz profile). The profile for the NLTE-Kurucz model has, at every μ, deeper cores than the observations.
Derived LTE/NLTE abundances from Ca I and Ca II lines using the all-lines and the line-by-line methods for each star.
 |
Fig. 10 Comparison of the mean of residuals ⟨r⟩ between observed and synthetic spectra after fitting each line separately (i.e. using the line-by-line method) between NLTE (abscissa) and LTE (ordinate) for the three stars studied here. The diagonal lines show the 1:1 relation between the two axes. |
 |
Fig. 11 Centre-to-limb variation of the Ca lines in the [6160,6170] Å region and the 8662 Å Ca II triplet line. The atmospheric model used was MACKKL. In order to get the best fit for the observed intensity profile at μ = 1.0, calcium abundances and macroturbulent velocities were (A(Ca), vmacro) = (6.28 dex, 1.6 m s−1) for the LTE and (6.26 dex, 1.9 m s−1) for the NLTE synthetic profiles. The 8662 Å line produces an emission core in LTE due to the increase in temperature at τ approximately −4 in the MACKKL model; in order to avoid over-plotting, the emission cores at μ = 0.6 and 0.2 werecut. The Ca II triplet line was also modelled using the Kurucz solar model atmosphere. LTE-Kurucz profiles are the long dashed lines and NLTE-Kurucz profiles are the dot-dashed lines. |
6. Conclusions
We performed NLTE calculations of neutral and single-ionised calcium using state-of-the-art radiative and collisional data and improved approximation formulas for the missing collisional data. The results were tested against high-quality observations in a wide wavelength range on three benchmark stars: Procyon, Arcturus, and the Sun. Very recently Belyaev et al. (2018) presented detailed calculations on Ca II+H collisions. Unfortunately that work was too recent to be considered here but will certainly be considered in our future investigations on NLTE effects of calcium. Our analyses have lead us to the following main conclusions.
-
In Procyon, NLTE abundances are more consistent along the observed wavelength range used in this work than LTE. In the Sun, the dispersion in abundances derived for each line is slightly reduced in NLTE when compared to LTE. Removing outliers does not change the trends of derived abundances versus wavelength/line strength. In Arcturus, the average LTE abundances in the visual and the IR differ by 0.2 dex, which is reflected in a trend of derived abundance with wavelength; this trend is reduced in NLTE. The main NLTE effect in the three stars studied here is visible in the core of lines of medium strength (weq∕λ ~ 10−4).
-
The lowest states of Ca I tend to be underpopulated with respect to the LTE values in the metal-poor giant Arcturus while for the Sun and Procyon, low-lying levels of Ca I are overpopulated with respect to LTE at line-formation depths. Due to its weak electron collisional coupling (obtained from quantum mechanical calculations), the 3d2(3F) level suffers from departures from LTE at deep atmospheric layers. The weak collisional coupling can be explained using the fact that the transitions of this level with levels of similar energy require two-electron (de)excitation.
-
The LTE profile of the 6162 Å line (and other strong lines) does not reproduce the core and the wings of the line observedin the Sun. Typically, in the Sun, lines behave like the 6439 Å line, profile fitting does not give a good match to the core in LTE, and as a result the LTE abundance increases and the macroturbulent velocity decreases in order to fit the observations.
-
In the three stars studied here, the Ca I/Ca II abundance-ratio discrepancy found in LTE is reduced with our NLTE modelling, improving the agreement between the derived Ca I and Ca II abundances.
-
The CLV of the solar calcium lines is partially but not perfectly reproduced. For the lines studied here we suspect that the differences are related to the presence of inhomogeneities in the atmosphere. Strong lines such as the Ca II triplet require a chromosphere due to the fact that their cores form at layers where the temperature inversion of the upper atmosphere cannot be ignored.
-
Within the limitations of our modelling (1D, trace-element NLTE) we arrived at a solar calcium abundance that is consistent among lines over a large range of the solar spectrum and various formation depths; and also between neutral and singly ionised Ca. Nevertheless, it is important to note that our derived NLTE calcium abundance is about 0.05 dex lower than the meteoritic value (which is well within our uncertainties).
-
In the three cases studied here, NLTE line profiles fit the observations better with respect to the LTE ones for the majority of the lines used here. When all lines are fit at once, Arcturus gives slightly better results in LTE in the visual region of the spectrum, but we find a negligible abundance correction
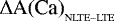 = 0.0.
= 0.0.
For these reasons, we believe that the present calculations are a step forward towards achieving more accurate determinations of the calculated calcium abundances for late-type stars.
Acknowledgements
K.L. acknowledges funds from the Alexander von Humboldt Foundation in the framework of the Sofja Kovalevskaja Award endowed by the Federal Ministry of Education and Research as well as funds from the Swedish Research Council (Grant nr. 2015-00415_3) and Marie Sklodowska Curie Actions (Cofund Project INCA 600398). P.S.B. received financial support from the Swedish Research Council and the project grant “The New Milky Way” from the Knut and Alice Wallenberg Foundation. This work has made use of the VALD database, operated at Uppsala University, the Institute of Astronomy RAS in Moscow, and the University of Vienna.
Appendix A: Table with line data
Description of the transitions used in this work for comparison with observations.
References
- Allen, C. W. 1976, Astrophysical Quantities (Athlone Press: London) [Google Scholar]
- Allende Prieto, C., Asplund, M., García López, R. J., & Lambert, D. L. 2002, ApJ, 567, 544 [NASA ADS] [CrossRef] [Google Scholar]
- Anders, E., & Grevesse, N. 1989, Geochim. Cosmochim. Acta, 53, 197 [Google Scholar]
- Anguiano, B., Freeman, K., Bland-Hawthorn, J., et al. 2014, in Setting the scene for Gaia and LAMOST, eds. S. Feltzing, G. Zhao, N. A. Walton, & P. Whitelock, IAU Symp., 298, 322 [NASA ADS] [Google Scholar]
- Anguiano, B., Majewski, S. R., Allende-Prieto, C., et al. 2018, A&A, 620, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Anstee, S. D., & O’Mara, B. J. 1995, MNRAS, 276, 859 [NASA ADS] [CrossRef] [Google Scholar]
- Asplund, M., Grevesse, N., & Sauval, A. J. 2005, in Cosmic Abundances as Records of Stellar Evolution and Nucleosynthesis, eds. T. G. Barnes, III, & F. N. Bash, ASP Conf. Ser., 336, 25 [NASA ADS] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Auer, L. H., & Heasley, J. N. 1976, ApJ, 205, 165 [NASA ADS] [CrossRef] [Google Scholar]
- Barklem, P. S. 2016, Phys. Rev. A, 93, 042705 [NASA ADS] [CrossRef] [Google Scholar]
- Barklem, P. S. 2017, Phys. Rev. A, 95, 069906 [NASA ADS] [CrossRef] [Google Scholar]
- Barklem, P. S., & O’Mara, B. J. 1997, MNRAS, 290, 102 [Google Scholar]
- Barklem, P. S., Anstee, S. D., & O’Mara, B. J. 1998a, PASA, 15, 336 [NASA ADS] [CrossRef] [Google Scholar]
- Barklem, P. S., O’Mara, B. J., & Ross, J. E. 1998b, MNRAS, 296, 1057 [Google Scholar]
- Barklem, P. S., Belyaev, A. K., Guitou, M., et al. 2011, A&A, 530, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bely, O., & van Regemorter, H. 1970, ARA&A, 8, 329 [NASA ADS] [CrossRef] [Google Scholar]
- Belyaev, A. K., Yakovleva, S. A., Guitou, M., et al. 2016, A&A, 587, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Belyaev, A. K., Voronov, Y. V., & Gadéa, F. X. 2018, ApJ, 867, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Blanton, M. R., Bershady, M. A., Abolfathi, B., et al. 2017, AJ, 154, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Burgess, A., & Chidichimo, M. C. 1983, MNRAS, 203, 1269 [NASA ADS] [CrossRef] [Google Scholar]
- Burgess, A., Summers, H. P., McWhirter, R. W. P., & Cochrane, D. M. 1977, MNRAS, 179, 275 [NASA ADS] [CrossRef] [Google Scholar]
- Carlsson, M. 1986, Uppsala Astronomical Observatory Report, 33 [Google Scholar]
- Carlsson, M. 1992, in Cool Stars, Stellar Systems, and the Sun, eds. M. S. Giampapa, & J. A. Bookbinder, ASP Conf. Ser., 26, 499 [NASA ADS] [Google Scholar]
- Christlieb, N., Gustafsson, B., Korn, A. J., et al. 2004, ApJ, 603, 708 [NASA ADS] [CrossRef] [Google Scholar]
- Cox, A. N. 2000, Allen’s Astrophysical Quantities (Berlin: Springer Science & Business Media) [Google Scholar]
- Cunto, W., & Mendoza, C. 1992, Rev. Mex. Astron. Astrofis., 23, 107 [NASA ADS] [Google Scholar]
- Drake, J. J. 1991, MNRAS, 251, 369 [NASA ADS] [CrossRef] [Google Scholar]
- Drawin, H.-W. 1968, Z. Phys., 211, 404 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Drozdowski, R., Ignaciuk, M., Kwela, J., & Heldt, J. 1997, Z. Phys. D. Atom. Mol. Clusters, 41, 125 [CrossRef] [Google Scholar]
- Eisenstein, D. J., Weinberg, D. H., Agol, E., et al. 2011, AJ, 142, 72 [Google Scholar]
- Gaia Collaboration (Prusti, T., et al.) 2016, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gray, D. F. 1975, ApJ, 202, 148 [NASA ADS] [CrossRef] [Google Scholar]
- Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hall, J. C. 2008, Liv. Rev. Sol. Phys., 5, 2 [Google Scholar]
- Hinkle, K., Wallace, L., & Livingston, W. 1995, PASP, 107, 1042 [NASA ADS] [CrossRef] [Google Scholar]
- Hinkle, K., Wallace, L., Valenti, J., & Harmer, D. 2000, Visible and Near Infrared Atlas of the Arcturus Spectrum 3727-9300 A (San Francisco: ASP) [Google Scholar]
- Idiart, T., & Thévenin, F. 2000, ApJ, 541, 207 [NASA ADS] [CrossRef] [Google Scholar]
- Kaulakys, B. P. 1986, J. Exp. Theor. Phys., 91, 391 [Google Scholar]
- Kiselman, D., Pereira, T. M. D., Gustafsson, B., et al. 2011, A&A, 535, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kordopatis, G., Recio-Blanco, A., de Laverny, P., et al. 2011, A&A, 535, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kupka, F., Piskunov, N., Ryabchikova, T. A., Stempels, H. C., & Weiss, W. W. 1999, A&AS, 138, 119 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [PubMed] [Google Scholar]
- Kupka, F. G., Ryabchikova, T. A., Piskunov, N. E., Stempels, H. C., & Weiss, W. W. 2000, Balt. Astron., 9, 590 [NASA ADS] [Google Scholar]
- Kurucz, R. 1993, ATLAS9 Stellar Atmosphere Programs and 2 km/s grid. Kurucz CD-ROM No. 13, Cambridge, MA: Smithsonian Astrophysical Observatory, 13 [Google Scholar]
- Kurucz, R. L. 2007, Online database of observed and predicted atomic transitions [Google Scholar]
- Kurucz, R. L. 2010, Online database of observed and predicted atomic transitions [Google Scholar]
- Kurucz, R., Furenlid, I., Brault, J., & Testerman, L. 1984, Solar flux atlas from 296 to 1300 nm [Google Scholar]
- Leenaarts, J., de la Cruz Rodríguez, J., Kochukhov, O., & Carlsson, M. 2014, ApJ, 784, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Lind, K., Amarsi, A. M., Asplund, M., et al. 2017, MNRAS, 468, 4311 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Linsky, J. L., & Avrett, E. H. 1970, PASP, 82, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Livingston, W., & Wallace, L. 1991, An atlas of the solar spectrum in the infrared from 1850 to 9000 cm-1 (1.1 to 5.4 micrometer) [Google Scholar]
- Majewski, S. R., Schiavon, R. P., Frinchaboy, P. M., et al. 2017, AJ, 154, 94 [NASA ADS] [CrossRef] [Google Scholar]
- Maltby, P., Avrett, E. H., Carlsson, M., et al. 1986, ApJ, 306, 284 [Google Scholar]
- Martínez-Arnáiz, R., Maldonado, J., Montes, D., Eiroa, C., & Montesinos, B. 2010, A&A, 520, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mashonkina, L., Korn, A. J., & Przybilla, N. 2007, A&A, 461, 261 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mashonkina, L., Sitnova, T., & Belyaev, A. K. 2017, A&A, 605, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Massarotti, A., Latham, D. W., Stefanik, R. P., & Fogel, J. 2008, AJ, 135, 209 [NASA ADS] [CrossRef] [Google Scholar]
- Mein, P. 1971, Sol. Phys., 20, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Meléndez, M., Bautista, M. A., & Badnell, N. R. 2007, A&A, 469, 1203 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mészáros, S., Allende Prieto, C., Edvardsson, B., et al. 2012, AJ, 144, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Nörtershäuser, W., Blaum, K., Icker, K., et al. 1998, Eur. Phys. J. D, 2, 33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Olsen, K. H., Routly, P. M., & King, R. B. 1959, ApJ, 130, 688 [NASA ADS] [CrossRef] [Google Scholar]
- Osorio, Y., Barklem, P. S., Lind, K., et al. 2015, A&A, 579, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pavlenko, Y. V., Jenkins, J. S., Jones, H. R. A., Ivanyuk, O., & Pinfield, D. J. 2012, MNRAS, 422, 542 [NASA ADS] [CrossRef] [Google Scholar]
- Percival, I. 1966, Nucl. Fusion, 6, 182 [CrossRef] [Google Scholar]
- Piskunov, N. E., Kupka, F., Ryabchikova, T. A., Weiss, W. W., & Jeffery, C. S. 1995, A&AS, 112, 525 [NASA ADS] [Google Scholar]
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 1992, Numerical Recipes in FORTRAN. The Art of Scientific Computing (Cambridge: Cambridge University Press) [Google Scholar]
- Ralchenko, Y., Kramida, A., Reader, J., & NIST ASD Team,. 2014, NIST Atomic Spectra Database (version 5.0), Available: http://physics.nist.gov/asd [Google Scholar]
- Ramírez, I., & Allende Prieto C. 2011, ApJ, 743, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Reddy, B. E., Lambert, D. L., & Allende Prieto C. 2006, MNRAS, 367, 1329 [NASA ADS] [CrossRef] [Google Scholar]
- Reiners, A., Mrotzek, N., Lemke, U., Hinrichs, J., & Reinsch, K. 2016, A&A, 587, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ryabchikova, T. A., Piskunov, N. E., Kupka, F., & Weiss, W. W. 1997, Balt. Astron., 6, 244 [NASA ADS] [Google Scholar]
- Saliba, G. J. 1985, Sol. Phys., 98, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Samson, A. M., & Berrington, K. A. 2001, At. Data Nucl. Data Tables, 77, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Scott, P., Grevesse, N., Asplund, M., et al. 2015, A&A, 573, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Seaton, M. J. 1962, Atomic and Molecular Processes, ed. D. R. Bates (New York: Academic Press), 375 [Google Scholar]
- Seaton, M. J., Yan, Y., Mihalas, D., & Pradhan, A. K. 1994, MNRAS, 266, 805 [NASA ADS] [CrossRef] [Google Scholar]
- Shabanova, L. N. 1963, Opt. Spectrosc., 15, 829 [Google Scholar]
- Smith, G. 1981, A&A, 103, 351 [NASA ADS] [Google Scholar]
- Smith, G. 1988, J. Phys. B At. Mol. Phys., 21, 2827 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, G., & Drake, J. J. 1987, A&A, 181, 103 [NASA ADS] [Google Scholar]
- Smith, G., & O’Neill, J. A. 1975, A&A, 38, 1 [NASA ADS] [Google Scholar]
- Smith, G., & Raggett, D. S. J. 1981, J. Phys. B At. Mol. Phys., 14, 4015 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, W. W., & Gallagher, A. 1966, Phys. Rev., 145, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Socas-Navarro, H., de la Cruz Rodríguez, J., Asensio Ramos, A., Trujillo Bueno, J., & Ruiz Cobo, B. 2015, A&A, 577, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spite, M., Andrievsky, S. M., Spite, F., et al. 2012, A&A, 541, A143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Steenbock, W., & Holweger, H. 1984, A&A, 130, 319 [NASA ADS] [Google Scholar]
- Strassmeier, K. G., Ilyin, I., & Steffen, M. 2018a, A&A, 612, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Strassmeier, K. G., Ilyin, I., & Weber, M. 2018b, A&A, 612, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Terlevich, E., Díaz, A. I., & Terlevich, R. 1989, Ap&SS, 157, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Theodosiou, C. E. 1989, Phys. Rev. A, 39, 4880 [NASA ADS] [CrossRef] [Google Scholar]
- van Regemorter, H. 1962, AJ, 136, 906 [Google Scholar]
- Vrinceanu, D. 2005, Phys. Rev. A, 72 [Google Scholar]
- Watanabe, T., & Steenbock, W. 1985, A&A, 149, 21 [NASA ADS] [Google Scholar]
- Welsh, B. Y., Lallement, R., Vergely, J.-L., & Raimond, S. 2010, A&A, 510, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wiese, W. L., Smith, M. W., & Miles, B. M. 1969, NSRDS-NBS (Washington, D.C.: US Department of Commerce, National Bureau of Standards) [Google Scholar]
- Wilson, J. C., Hearty, F., Skrutskie, M. F., et al. 2010, in Ground-based and Airborne Instrumentation for Astronomy III, Proc. SPIE, 7735, 77351C [NASA ADS] [CrossRef] [Google Scholar]
- Yu, Y., & Derevianko, A. 2018, At. Data Nucl. Data Tables, 119, 263 [NASA ADS] [CrossRef] [Google Scholar]
- Zatsarinny, O., Bartschat, K., Gedeon, S., Gedeon, V., & Lazur, V. 2006, Phys. Rev. A, 74, 052708 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Derived LTE/NLTE abundances from Ca I and Ca II lines using the all-lines and the line-by-line methods for each star.
Description of the transitions used in this work for comparison with observations.
All Figures
 |
Fig. 1 Grotrian diagram representing the Ca I (left panel) and Ca II (right panel) levels and radiative transitions (grey) used in our model atom. The horizontal black solid lines represent super levels. The dashed line in each diagram shows the ionisation limit. Only the lowest levels are labelled to ease visualisation. |
| In the text | |
 |
Fig. 2 Matrix with electron collisional rate coefficients at 5000 K taken from the extension of the calculations made in Zatsarinny et al. (2006) and used in this work. The colours represent the rate coefficients in a logarithmic scale. The crosses indicate one-electron transitions. Transitions involving the 4s.5g levels are not calculated and approximation formulas (valid only for one-electron transitions) are used. |
| In the text | |
 |
Fig. 3 Comparison of the observations in part of the overlapping region between the two atlases used for the Sun: Kurucz et al. (1984) for the visual region (solid black lines) and Livingston & Wallace (1991) for the IR (red dashed lines). The latter atlas has telluric lines removed and measures the disc centre intensity of the Sun. The wavelengths were shifted in order to match the observations. |
| In the text | |
 |
Fig. 4 Comparison of the observations of the Ca I 5590 Å line between popular atlases of the three studied stars. PEPSI atlases are from Strassmeier et al. (2018a,b). IAG atlas comes from Reiners et al. (2016), NOAO atlas for Arcturus comes from Hinkle et al. (2000) and McDonald data come from Allende Prieto et al. (2002). The atlases were wavelength shifted in order to match the air wavelength of the 5590 Å Ca I line. |
| In the text | |
 |
Fig. 5 Temperature structure of the two solar models used in this work. The MACKKL model includes the lower chromosphere. |
| In the text | |
 |
Fig. 6 Departure coefficients (b = nNLTE∕nLTE) of selected levels of Ca I and the ground level of Ca II using different electron collisional data. Line symbols represent different levels; in red are the departure coefficients obtained when the vR+A data are used for electron collisions (see text), and in black are the b coefficients obtained when updated electron collisional data are used. |
| In the text | |
 |
Fig. 7 Observed normalised flux spectra and comparison with our LTE/NLTE results. The spectra plots show the points used to calculate abundance and Vmac and the residuals with best fit in LTE and NLTE. The contours show the confidence regions corresponding to 1, 2, and 3σ (see Press et al. 1992). |
| In the text | |
 |
Fig. 8 Line-by-line Ca abundance determination in the three observed stars. Red and black symbols denote LTE and NLTE abundances, respectively; triangles correspond to Ca I and squares/asterisks to Ca II lines. The lines show the linear fit of the LTE (red) and NLTE (black) abundances. |
| In the text | |
 |
Fig. 9 Upper panel: comparison between observations (solid circles) and line profiles in LTE (dot-dash), NLTE using vR+A electron collisional data (dot-dash), and NLTE with updated electron collisional data of the solar Ca I 6439 Å line (A(Ca) = 6.25, Vmac = 3.0 m s−1). Lower panel: differences with observations. |
| In the text | |
 |
Fig. 10 Comparison of the mean of residuals ⟨r⟩ between observed and synthetic spectra after fitting each line separately (i.e. using the line-by-line method) between NLTE (abscissa) and LTE (ordinate) for the three stars studied here. The diagonal lines show the 1:1 relation between the two axes. |
| In the text | |
 |
Fig. 11 Centre-to-limb variation of the Ca lines in the [6160,6170] Å region and the 8662 Å Ca II triplet line. The atmospheric model used was MACKKL. In order to get the best fit for the observed intensity profile at μ = 1.0, calcium abundances and macroturbulent velocities were (A(Ca), vmacro) = (6.28 dex, 1.6 m s−1) for the LTE and (6.26 dex, 1.9 m s−1) for the NLTE synthetic profiles. The 8662 Å line produces an emission core in LTE due to the increase in temperature at τ approximately −4 in the MACKKL model; in order to avoid over-plotting, the emission cores at μ = 0.6 and 0.2 werecut. The Ca II triplet line was also modelled using the Kurucz solar model atmosphere. LTE-Kurucz profiles are the long dashed lines and NLTE-Kurucz profiles are the dot-dashed lines. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.