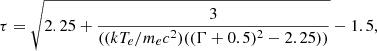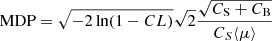| Issue |
A&A
Volume 623, March 2019
|
|
|---|---|---|
| Article Number | A12 | |
| Number of page(s) | 9 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201834454 | |
| Published online | 25 February 2019 | |
A deep X-ray view of the bare AGN Ark 120
VI. Geometry of the hot corona from spectroscopic and polarization signatures
1
Dipartimento di Matematica e Fisica, Università degli Studi Roma Tre, Via della Vasca Navale 84, 00146 Roma, Italy
e-mail: marinucci@fis.uniroma3.it
2
Aix-Marseille Université, CNRS, CNES, LAM (Laboratoire d’Astrophysique de Marseille) UMR 7326, 13388 Marseille, France
3
Astronomical Institute of the Czech Academy of Sciences, 14100 Prague, Czech Republic
4
Nicolaus Copernicus Astronomical Center, Polish Academy of Sciences, Bartycka 18, 00-716 Warsaw, Poland
5
Center for Space Science and Technology, University of Maryland Baltimore County, 1000 Hilltop Circle, Baltimore, MD 21250, USA
6
INAF-Osservatorio Astronomico di Brera, Via Bianchi 46, 23807 Merate (LC), Italy
7
Astrophysics Group, School of Physical and Geographical Sciences, Keele University, Keele, Staffordshire, ST5 5BG, UK
8
Université de Strasbourg, CNRS, Observatoire Astronomique de Strasbourg, UMR 7550, 67000 Strasbourg, France
9
Istituto Nazionale di Astrofisica (INAF) – Osservatorio Astrofisico di Arcetri, Largo Enrico Fermi 5, 50125 Firenze, Italy
10
INAF-Istituto di Astrofisica e Planetologie Spaziali, Via Fosso del Cavaliere, 00133 Roma, Italy
Received:
18
October
2018
Accepted:
16
November
2018
Context. The spectral shape of the hard X-ray continuum of Active Galactic Nuclei (AGN) can be ascribed to inverse Compton scattering of optical/UV seed photons from the accretion disc by a hot corona of electrons. This physical process produces a polarization signal which is strongly sensitive to the geometry of the scattering medium (i.e. the hot corona) and of the radiation field.
Aims. MoCA (Monte Carlo code for Comptonisation in Astrophysics) is a versatile code which allows for different geometries and configurations to be tested for Compton scattering in compact objects. A single photon approach is considered as well as polarisation and Klein–Nishina effects. In this work, we selected four different geometries for the scattering electrons cloud above the accretion disc, namely an extended slab, an extended spheroid and two compact spheroids.
Methods. We discuss the first application of the MoCA model to reproduce the hard X-ray primary continuum of the bare Seyfert 1 galaxy Ark 120, using different geometries for the hot corona above the accretion disc. The lack of extra-Galactic absorption along the line of sight makes it an excellent target for studying the accretion disc-corona system. We report on the spectral analysis of the simultaneous 2013 and 2014 XMM-Newton and NuSTAR observations of the source.
Results. A general agreement is found between the best fit values of the hot coronal parameters obtained with MoCA and the ones inferred using other Comptonisation codes from the literature. The expected polarization signal from the best fits with MoCA is then presented and discussed, in view of the launch in 2021 of the Imaging X-ray Polarimetry Explorer (IXPE).
Conclusions. We find that none of the tested geometries for the hot corona (extended slab and extended/compact spheroids) can be statistically preferred, based on spectroscopy solely. In the future, an IXPE observation less than 1 Ms long will clearly distinguish between an extended slab or a spherical hot corona.
Key words: black hole physics / polarization / galaxies: active / galaxies: Seyfert / galaxies: individual: Ark 120
© ESO 2019
1. Introduction
The spectral shape of the nuclear continuum of active galactic nuclei (AGN), in X-rays, can be well approximated with a cutoff power law, with a photon index in the range Γ = 1.6 − 2.2 (Bianchi et al. 2009; Sobolewska & Papadakis 2009). While this parameter is a function of the optical depth and temperature of the scattering medium, the high energy turnover of the power law mainly depends on the temperature (Shapiro et al. 1976; Rybicki & Lightman 1979; Sunyaev & Titarchuk 1980; Lightman & Zdziarski 1987; Beloborodov 1999; Petrucci et al. 2000, 2001). The current paradigm invokes the presence of a corona of hot electrons above the accretion disc, which efficiently scatter the ultraviolet radiation emitted by the accretion disc up to X-ray wavelenghts (the so called two-phase model: Haardt & Maraschi 1991; Haardt et al. 1994).
NuSTAR (Harrison et al. 2013) is the first satellite capable of focusing hard X-rays above 10 keV and up to 79 keV. With its broad spectral coverage, it has led to a number of works that have shown that optical depths and electron temperatures typically fall in the ranges τ = [0.1 − 4] and kTe = [10 − 500] keV, depending on the geometry and on the Comptonization model adopted (Fabian et al. 2015, 2017; Tortosa et al. 2018).
A second component has been also invoked to reproduce the soft X-ray excess of AGN (i.e. photons in the 0.5–2 keV band in excess of the extrapolation of the hard power-law component: Arnaud et al. 1985; Singh et al. 1985). These models assume a thermal Comptonisation in an optically thick (τ = 5 − 50) and warm (kTe = 0.1 − 1 keV) scattering plasma (Magdziarz et al. 1998; Porquet et al. 2004; Done et al. 2012; Jin et al. 2012; Petrucci et al. 2013, 2018; Różańska et al. 2015). In this work, however, we focus on Comptonisation from the hot corona only.
So far, X-ray spectroscopy has not been able to determine the geometry in any of the sources observed with NuSTAR and included in the catalogs mentioned above (simultaneously with XMM, Chandra, Suzaku, Swift). In fact, while the bet fit parameters may depend on the adopted geometry (Tortosa et al. 2018), the statistical quality of the fit is invariably the same, even for the best quality NuSTAR AGN spectra. On the other hand, Compton scattering will produce a polarization signal which is strongly dependent on the geometry of the scattering medium. The Imaging X-ray Polarimetry Explorer (IXPE; Weisskopf et al. 2016a,b) and eXTP (enhanced X-ray Timing and Polarimetry mission: Zhang et al. 2019) satellites will investigate the polarization properties of the hot coronae in the brightest, unobscured AGN. In particular, IXPE has been recently selected by NASA as a SMall EXplorer Mission (SMEX) for a launch in 2021 and it will be the first X-ray imaging polarimeter on orbit, operating in the 2–8 keV band.
In this context, a Comptonisation code which includes both special relativity (MoCA: a Monte Carlo code for Comptonisation in Astrophysics; Tamborra et al. 2018, Middei et al., in prep.) and general relativity effects (Tamborra et al., in prep.) as well as polarization has been recently released. Compared to different codes in the literature, such as COMPTT, COMPPS, NTHCOMP (Titarchuk 1994; Poutanen & Svensson 1996; Zdziarski et al. 1996; Życki et al. 1999), the energy-dependent Klein–Nishina cross section is taken into account (differently from Schnittman & Krolik 2010) and multiple geometries can be tested and investigated (similarly to Beheshtipour et al. 2017). Moreover, the Monte Carlo approach implies that no a priori limitations in the parameter space is present.
In this work, we constructed spectral models based on MOCA, and used it for fitting the 2013 and 2014 XMM and NuSTAR observations of the broad-line Seyfert 1 galaxy Ark 120, exploring different geometries of the hot corona. We will also use MOCA to predict the polarization signal expected in such geometries. The paper is organized as follows: in Sect. 2 we discuss the data reduction procedure and the implementation of the model, while in Sect. 3 we present the spectral analysis. The polarization signals are reported and discussed in Sect. 4. We summarize our results in Sect. 5.
Throughout the paper, we adopt the cosmological parameters H0 = 70 km s−1 Mpc−1, ΩΛ = 0.73 and Ωm = 0.27, i.e. the default ones in XSPEC 12.10.0 (Arnaud 1996). Errors correspond to the 90% confidence level for one interesting parameter (Δχ2 = 2.7), if not stated otherwise.
2. Observations and data reduction
2.1. XMM-Newton
Ark 120 has been the target of a deep XMM-Newton (Jansen et al. 2001) observation in 2014, starting on 2014 March 18 for a total elapsed time of ∼650 ks with the EPIC CCD cameras, the Pn (Strüder et al. 2001) and the two MOS (Turner et al. 2001), operated in small window and thin filter mode. In this work, we only focus on the third XMM orbit (observation 2014c in Porquet et al. 2019) since it is the only one simultaneous with NuSTAR. We also analyse data from the 2013 February 18 pointing (total elapsed time of 130 ks), also simultaneous with NuSTAR, applying the latest calibration files available on 2018 June. In 2014, the source was observed in a flux state which was a factor of ∼2 higher than in 2013. Data from the MOS detectors are not included in our analysis due to the high pile-up and lower statistics of the spectra. The extraction radii and the optimal time cuts for flaring particle background were computed with SAS 16 (Gabriel et al. 2004) via an iterative process which leads to a maximization of the Signal-to-Noise Ratio (SNR), similar to the approach described in Piconcelli et al. (2004). The resulting optimal extraction radii are 40 arcsec, net exposure times are 89 ks and 92 ks for the 2013 and 2014 observation, respectively. Background spectra were extracted from source-free circular regions with a radius of 50 arcsec. Spectra were then binned in order not to over-sample the instrumental resolution more than a factor of three and to have no less than 30 counts in each background-subtracted spectral channel. Since no significant spectral variability is observed within each observation, we used time averaged spectra (we refer the reader to Matt et al. 2014; Nardini et al. 2016; Lobban et al. 2018; Porquet et al. 2019, for further details).
2.2. NuSTAR
NuSTAR (Harrison et al. 2013) observed Ark 120 with its two coaligned X-ray telescopes with corresponding Focal Plane Module A (FPMA) and B (FPMB) simultaneously to XMM-Newton on 2013 February 18 and on 2014 March 22 for a total of 166 ks and 131 ks of elapsed time, respectively. The Level 1 data products were processed with the NuSTAR Data Analysis Software (NuSTARDAS) package (v. 1.8.0). Cleaned event files (level 2 data products) were produced and calibrated using standard filtering criteria with the NUPIPELINE task and the latest calibration files available in the NuSTAR calibration database (CALDB 20180419). Extraction radii for the source and background spectra were 30 arcsec and 50 arcsec and the net exposure times for the two observations were 80 ks and 65 ks, respectively. The two pairs of NuSTAR spectra were binned in order not to over-sample the instrumental resolution more than a factor of 2.5 and to have a SNR greater than 5σ in each spectral channel. A cross-calibration factor within 3 per cent between the two detectors is found. Broad band (between 3 and 79 keV) data are shown in Fig. 1 (top panel) and their residuals to a Γ = 1.85 power law model, with a 2–10 keV flux of 3 × 10−11 erg cm−2 s−1, indicate a clear spectral variation between the two pointings (bottom panel).
 |
Fig. 1. The simultaneous XMM-Newton and NuSTAR spectra and residuals to a power law model (in counts s−1 keV−1 cm−2 units) are shown, obtained on February 2013 and March 2014 for Ark 120. Dashed grey line indicate a Γ = 1.85 power law model, with a 2–10 keV flux of 3 × 10−11 erg cm−2 s−1. |
3. Data analysis
3.1. Building the model
The bare Seyfert galaxy Ark 120 (z = 0.0327 Osterbrock & Phillips 1977) is an excellent source for studying the accretion disc-corona environment, since no significant extra-Galactic absorption along the line of sight is present, both in the UV and in X-rays (Crenshaw et al. 1999; Vaughan et al. 2004; Reeves et al. 2016).
The source, throughout the years, has shown a variable emission complex in the 6–7 keV band with a broad relativistic Iron Kα component in the 2007 Suzaku spectrum (Nardini et al. 2011) which was not detected in the 2013 XMM+NuSTAR observation (Matt et al. 2014). The neutral core of the 6.4 keV Iron Kα fluorescence line was resolved in the 2014 Chandra High Energy Transmission Gratings spectrum and its Full Width at Half Maximum (FWHM) is consistent with being emitted in the optical Broad Line Region (FWHM =  km s−1: Nardini et al. 2016). Furthermore, the 2014 monitoring performed with Chandra, XMM and NuSTAR also led to the discovery of transient Fe K emission from the innermost regions of the accretion disc, both on the red and blue sides of the neutral 6.4 keV line. The full data set is analyzed and discussed in Porquet et al. (2019) and clear variations in the shape of the nuclear continuum were found with respect to the previous 2013 pointing. A steeper continuum was observed in the brighter state, accordingly to the well-known softer when brighter behavior (Shemmer et al. 2006; Risaliti et al. 2009; Ursini et al. 2016). The change in the slope of the primary emission and the detection of a high energy cutoff in the 2014 spectra are indicative of a variation of the scattering material configuration. We hereby investigate the geometry and the physical parameters of the hot corona, by using the Monte Carlo Comptonisation model MoCA. Even though the 2014 monitoring presented flux and spectral changes throughout the four XMM orbits (Lobban et al. 2018; Porquet et al. 2019), we only considered XMM data simultaneous with NuSTAR, to better characterize the shape of the primary continuum above 10 keV.
km s−1: Nardini et al. 2016). Furthermore, the 2014 monitoring performed with Chandra, XMM and NuSTAR also led to the discovery of transient Fe K emission from the innermost regions of the accretion disc, both on the red and blue sides of the neutral 6.4 keV line. The full data set is analyzed and discussed in Porquet et al. (2019) and clear variations in the shape of the nuclear continuum were found with respect to the previous 2013 pointing. A steeper continuum was observed in the brighter state, accordingly to the well-known softer when brighter behavior (Shemmer et al. 2006; Risaliti et al. 2009; Ursini et al. 2016). The change in the slope of the primary emission and the detection of a high energy cutoff in the 2014 spectra are indicative of a variation of the scattering material configuration. We hereby investigate the geometry and the physical parameters of the hot corona, by using the Monte Carlo Comptonisation model MoCA. Even though the 2014 monitoring presented flux and spectral changes throughout the four XMM orbits (Lobban et al. 2018; Porquet et al. 2019), we only considered XMM data simultaneous with NuSTAR, to better characterize the shape of the primary continuum above 10 keV.
MoCA is a versatile code which allows for different geometries and configurations (we refer the reader to Tamborra et al. 2018, for a more detailed description of the code). We selected two different geometries for the scattering electrons cloud above the accretion disc: an extended slab and a sphere. The accretion disc emits a multi-temperature black body from 6 up to 500 gravitational radii (rg = GM/c2) and both the slab and the sphere cover the whole disc. In all our simulations we considered a black hole mass Mbh = 1.5 × 108 M⊙ (estimated via reverberation mapping: Peterson et al. 2004), and an accretion rate LBol/LEdd = 10% (which is representative to the values found from the 2013 and 2014 optical to hard X-ray spectral fitting, i.e. 3–7% (Porquet et al. 2019). For simplicity, we used spectra integrated over the inclination angle and only Special Relativity effects are considered. We refer the reader to Tamborra et al. (in prep.) for further details on the inclusion of General Relativity effects (which are particularly relevant at radii r < 6rg) and on the (small) dependence of the emitted spectra on the inclination angle. For the extended slab we assumed a constant height H = 10 rg and we simulated spectra in the ranges kTe = 20 − 200 keV and τ = 0.1 − 2.5 adopting 5 keV and 0.1 steps for the temperature and optical depth, respectively. The angle-averaged spectrum is then recorded for each kTe − τ pair. The same procedure is adopted for the spherical geometry, in which we considered a hemisphere covering the disc with temperatures and optical depth in the ranges kTe = 20 − 200 keV and τ = 0.1 − 4.5, due to the different definition of the optical depth in the two geometries (in the sphere it is the radial one, thence equal to the effective one, while in the slab it is the vertical one, therefore smaller than the effective one). As a final step, we considered two scenarios in which the spherical hot corona is more compact, extending from 6 to 100 rg and from 6 to 20 rg (see Sect. 3.2.2). The latter is of the order of the coronal size envisaged via microlensing experiments (Reis & Miller 2013), coronal eclipses by clouds (Risaliti et al. 2011; Sanfrutos et al. 2013) or reverberation analyses (De Marco et al. 2013; Kara et al. 2016). XSPEC readable tables were generated between 0.1 and 700 keV for each configuration.
3.2. Spectral analysis
The baseline model adopted for fitting the simultaneous XMM/NuSTAR observations is the one discussed in (Porquet et al. 2019). It is composed of a primary cutoff power law, relativistic reflection from the accretion disc (modeled with RELXILL in XSPEC, García et al. 2014; Dauser et al. 2014, and references therein), three Gaussians fixed at 6.4 keV, 6.97 keV and 7.05 keV (see Nardini et al. 2016, for a more complete discussion on these components) and a warm comptonisation component to reproduce the soft excess (modeled with COMPTT: Titarchuk 1994, assuming a slab geometry). We used a fixed emissivity ϵ(r)∝r−3 and an inclination angle i = 30 degrees for the RELXILL component. The whole model is multiplied by a constant, to account for the cross-calibration between the three detectors, while Galactic absorption is modeled with TBABS, using a NH = 1.0 × 1021 cm−2 (Kalberla et al. 2005). In XSPEC, the model reads as follows:
CONST × TBABS × (CUTOFFPL + COMPTT + RELXILL + 3× ZGAUSS).
When applied to the 2013 and 2014 XMM/NuSTAR spectra we obtain decent fits, with χ2/d.o.f. = 569/516 and 555/499, respectively. The following parameters are left free to vary: photon index, high energy cutoff and normalization of the primary power law, kTe, τ and normalization of the COMPTT component, normalization for the Compton reflection and emission lines. No strong residuals are seen throughout the 0.3–79 keV band (Fig. 2, left and right top panels) and best fit values are in agreement with the ones already discussed in (Matt et al. 2014; Nardini et al. 2016; Porquet et al. 2019), including cross-calibration constants. For the COMPTT component used to reproduce the soft excess, we find 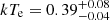 keV,
keV, 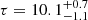 , N = 1.6 ± 0.15 and kTe = 0.42 ± 0.05 keV,
, N = 1.6 ± 0.15 and kTe = 0.42 ± 0.05 keV, 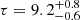 ,
, 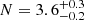 for the 2013 and 2014 data observations, respectively.
for the 2013 and 2014 data observations, respectively.
 |
Fig. 2. Residuals for the combined 2013 and 2014 XMM+NuSTAR observations are shown. See text for details about the four models applied. The only residuals present are near to 0.5 keV, which are likely associated to the OI K-shell absorption from our galaxy (see Reeves et al. 2016, for further details). |
In 2013, Ark 120 was in a flux state F = 2.3 ± 0.2 × 10−11 erg cm−2 s−1, calculated in the 2–10 keV band. Its primary continuum can be well reproduced with a power law with Γ = 1.79 ± 0.02 and Ec > 200 keV. On the other hand, on 2014 (March 22) the flux was a factor of ∼2 higher, F = 3.9 ± 0.1 × 10−11 erg cm−2 s−1 and the parameters of the nuclear continuum changed to Γ = 1.92 ± 0.02 and 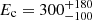 keV: such changes are clearly indicative of a variation of the hot coronal parameters. We therefore substituted the CUTOFFPL power law component with the Comptonisation model NTHCOMP (Zdziarski et al. 1996; Życki et al. 1999). We fixed the input seed photon temperature kTbb parameter to the COMPTT one (kTbb = 15 eV, inferred from the black hole mass and the mean accretion rate of the source) and left the photon index ΓNth, the coronal temperature kTe and the normalization free to vary. We obtain statistically equivalent fits to the ones in which a CUTOFFPL component is used, for both the 2013 and 2014 data sets (χ2/d.o.f. = 574/516 and χ2/d.o.f. = 560/499, respectively): best fit parameters are shown in Table 1. The inferred parameters from the 2013 and 2014 best fits (ΓNth = 1.80 ± 0.02, kTe > 40 keV and ΓNth = 1.94 ± 0.02,
keV: such changes are clearly indicative of a variation of the hot coronal parameters. We therefore substituted the CUTOFFPL power law component with the Comptonisation model NTHCOMP (Zdziarski et al. 1996; Życki et al. 1999). We fixed the input seed photon temperature kTbb parameter to the COMPTT one (kTbb = 15 eV, inferred from the black hole mass and the mean accretion rate of the source) and left the photon index ΓNth, the coronal temperature kTe and the normalization free to vary. We obtain statistically equivalent fits to the ones in which a CUTOFFPL component is used, for both the 2013 and 2014 data sets (χ2/d.o.f. = 574/516 and χ2/d.o.f. = 560/499, respectively): best fit parameters are shown in Table 1. The inferred parameters from the 2013 and 2014 best fits (ΓNth = 1.80 ± 0.02, kTe > 40 keV and ΓNth = 1.94 ± 0.02, 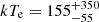 keV, respectively) can be translated into optical depths τ < 2.45 and τ ≃ 0.73, using the formula:
keV, respectively) can be translated into optical depths τ < 2.45 and τ ≃ 0.73, using the formula:
Hot coronal best fit parameters are reported, for the five models applied to the data.
obtained by inverting Eq. (A1) reported in Zdziarski et al. (1996).
At last, we substituted NTHCOMP with COMPTT, to directly compare best fit values in slab and spherical geometries with the ones obtained with MoCA. No statistically significant deviations can be found with respect to cutoff power law or NTHCOMP models; we report best fit values and reduced χ2 in Table 1, for 2013 and 2014 observations. Contour plots between kTe and τ for the two coronal configurations are shown in the top panels of Fig. 3.
 |
Fig. 3. Contour plots between kTe and τ for the slab (left panel), spherical (right panel) and compact spherical coronae (bottom panel) are shown, for the 2013 and 2014 best fits. For the 2013 data set yellow, orange and red contours indicate 99%, 90% and 68% confidence levels. For the 2014 data set cyan, light blue and dark blue contours indicate 99%, 90% and 68% confidence levels, respectively. We show, for the sake of visual comparison, the 99% c.l. contours adopting extended spherical coronae for the 2013 and 2014 observations in gray (bottom panel). |
3.2.1. Extended coronae
We then fitted the spectra using the MoCA tables. We removed the CUTOFFPL component and replaced it first with the MoCA generated table for the extended slab configuration (MOCA−SLAB model). Variable parameters for the primary continuum are the electron temperature kTe, the optical depth τ and the model normalization. We obtain statistically equivalent fits for the 2013 and 2014 observations (χ2/d.o.f. = 566/516 and 552/499 respectively) and best fit coronal parameters are reported in Table 1, while residuals are shown in Fig. 2. No statistically significant changes are found for the other parameters.
We then substituted the MOCA−SLAB component with the one generated adopting a geometry in which the scattering electrons are distributed as an extended sphere above the disc (MOCA−SPHERE model). We obtain statistically equivalent fits also in this case (χ2/d.o.f. = 561/516 and 551/499) and best fit parameters are reported in Table 1, while residuals are shown in Fig. 2. Again, no statistically significant changes are found for the other parameters. We conclude, therefore, that none of the two geometries for the hot corona can be preferred from the X-ray spectroscopic analysis.
We show, in Fig. 3, the contour plots between kTe and τ for the two geometries. Contours from lighter to darker colors indicate 99%, 90% and 68% confidence levels. It is interesting to note that, for a given geometry, the contour plots for the 2013 and 2014 observations do not overlap. This is not surprising given that a change in the slope of the primary continuum corresponds to changes in the coronal parameters. This is discussed in detail in Middei et al. (in prep.), where the relation between the photon index Γ and the Compton parameter obtained from MoCA simulations is presented.
3.2.2. Compact coronae
One of the proposed scenarios to explain the variable broad component of the Iron Kα in Ark 120 envisages a change in the spatial extension of the hot/warm coronae, which leaves the innermost regions of the accretion disc uncovered. The appearance of the broad, relativistic Iron Kα feature from the inner radii of the disc (if fitted with the RELLINE model in XSPEC 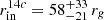 versus
versus 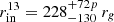 are obtained: Nardini et al. 2016) could be due to a smaller radius of the hot/warm coronae. This was tested in (Porquet et al. 2019) by using the OPTXCONV model (based on the OPTXAGNF model: Done et al. 2012, 2013; Jin et al. 2012) where we reported a radius of ∼73–110 rg in 2013 (where no relativistic component is detected, Matt et al. 2014) down to ∼12–17 rg in 2014. The model takes into account both the inner warm, thicker corona (to reproduce the soft excess) and the inner hot, thinner phase (for the hard power law emission), and the emission form the outer disc. The modeling took into account both disc inclination and relativistic effects. The variable parameters are mainly the spin of the black hole, the (warm and hot) corona radius and the accretion rate.
are obtained: Nardini et al. 2016) could be due to a smaller radius of the hot/warm coronae. This was tested in (Porquet et al. 2019) by using the OPTXCONV model (based on the OPTXAGNF model: Done et al. 2012, 2013; Jin et al. 2012) where we reported a radius of ∼73–110 rg in 2013 (where no relativistic component is detected, Matt et al. 2014) down to ∼12–17 rg in 2014. The model takes into account both the inner warm, thicker corona (to reproduce the soft excess) and the inner hot, thinner phase (for the hard power law emission), and the emission form the outer disc. The modeling took into account both disc inclination and relativistic effects. The variable parameters are mainly the spin of the black hole, the (warm and hot) corona radius and the accretion rate.
We therefore tried to fit the 2013 and 2014 data sets with tables generated adopting a spherical hot corona extended from 6 to 100 rg and from 6 up to 20 rg, respectively. We find that the reduced χ2 are comparable with the ones presented in Table 1 and we cannot prefer these solutions on statistical ground. It is also worth mentioning that the present version of MoCA does not include GR effects, which may be relevant especially for the most compact corona (see Tamborra, in prep. for a more complete discussion on the topic). Contour plots between kTe and τ are shown in the bottom panel of Fig. 3 and while no significant difference is found for the 2013 data set, we can spot a clear discrepancy for the 2014 observation, with respect to extended spherical coronae (see blue contours and gray solid contours for a visual comparison). This effect is further explained in the next section.
3.3. The geometry of the hot corona
The different configurations tested in the previous sections provide insights on the geometry of the hot corona in Ark 120. We find a good agreement between the best fit values of the coronal temperature and optical depth obtained with MoCA and the ones inferred using other Comptonisation codes from the literature (COMPTT, NTHCOMP). However, the top panels in Fig. 3 show that the shape of the contour plots obtained with MoCA are different from the COMPTT ones, indicating that different geometries of the corona lead to different kTe − τ planes. In MoCA, we assumed a slab with a fixed H/R = 0.02 and a sphere with radius r = 6 − 500 rg, fully covering the accretion disc. Compared to the COMPTT semi-infinite slab and sphere, a larger value of the input optical depth is needed to recover the same spectral shape, for a fixed electron temperature.
The change in normalization between the 2013 and 2014 MoCA best fits (N13 = 0.63 ± 0.01 × 10−2 and N14 = 1.30 ± 0.02 × 10−2 ph cm−2 s−1 keV−1 at 1 keV, respectively) can be explained in terms of a corona intercepting more seed photons, resulting in a higher luminosity for the 2014 observation, consistently with the UV fluxes reported in Lobban et al. (2018) for this object.
We also investigated a physical scenario in which the Comptonisation mechanism occurs in a very compact corona (r = 6 − 20 rg). For the 2014 data set (Fig. 3, bottom panel, lower contours), we see that compact coronae need higher optical depths for a given temperature to recover the same spectral shape (or equivalently higher electron temperatures are needed for a given optical depth). This effect is due to the effective number of scatterings that seed photons experience at a given radius. The input spectrum from the disc is assumed to be a multi-temperature black body and photons emitted from the innermost radii will hence be the most energetic ones, despite the geometry of the scattering medium. For values Mbh = 1.5 × 108 M⊙ and LBol/LEdd = 10%, the radial distribution of the seed photons will be therefore peaked at r ≃ 10 rg, with a negligible contribution from radii above r ≥ 100 rg. In MoCA, for spherical geometries, the input optical depth is the radial one but, since UV seed photons originate from the accretion disc, photons emitted at different radii will see an effective optical depth τe which will be different from the input optical depth τ. The effective optical depth of seed photons from the innermost regions decreases significantly in 6–20 rg coronae. From our calculations, in a kT = 100 keV and τ = 1 configuration, while photons emitted below 10 rg experience on average Ns ≃ 0.75 scatterings in the 6–500 rg and 6–100 rg cases, this number drops to Ns ≃ 0.62 for 6–20 rg coronae. This effect is further confirmed by comparing our simulated spectra for extended and compact coronae: we observe steeper continua (and hence lower τe) for 6–20 rg coronae. On average, the discrepancy between the photon indices is ΔΓ ≃ 0.1, as discussed in (Tamborra et al. 2018). Therefore we can conclude that thicker coronae are needed for a given temperature (or vice versa higher temperatures for a given τ) to recover the same spectral shape, in the case of 6–20 rg spherical coronae.
4. X-ray polarization
Compton scattering, as any scattering mechanism produces a linear polarization, which is strongly sensitive to the symmetry of the scattering medium (i.e. the hot corona) and of the radiation field. For the geometries considered here, we expect a polarization which is perpendicular to the plane of the disc (from now-on we will refer to it as vertical) with the slab showing a higher degree of polarization with respect to the sphere. The thermal emission from the disc is assumed to be polarized parallel to the disc plane (we will refer to it as horizontal) according to Chandrasekhar results for a pure electron scattering, optically thick atmospheres in plane-parallel approximation; the polarization degrees goes from zero for a face-on view of the disc, to almost 12% for an edge-on view (Chandrasekhar 1960).
We therefore chose the best fit coronal parameters for the 2013 and 2014 XMM-NuSTAR observations of Ark 120 and calculated the expected X-ray polarization as function of the inclination angle, integrated between 2 and 8 keV.
For the 2013 observations, we selected kTe = 110 keV − τ = 0.6 for the extended slab and kTe = 60 keV − τ = 3.0 for the extended spherical geometry (Fig. 4, top-left panel). These values correspond to the absolute minima of the fits (see Table 1). We also chose two more pairs of parameters, corresponding to the relative minima of the fits (see contour plots presented in Fig. 3). These additional pairs are kTe = 75 keV − τ = 1.1 and kTe = 85 keV − τ = 1.7 for slab spherical geometries, respectively (Fig. 4, top-right panel).
 |
Fig. 4. Polarization degree versus the cosine of the inclination angle μ are shown after integrating the signal in the IXPE operating band (2–8 keV), for the 2013 (top panels) and 2014 (bottom panels) cases and for both extended slab and spherical geometries. Left panels show simulations in which the input kTe and τ correspond to best fit values, while we took into account statistically equivalent parameters (i.e. corresponding to relative minima in the fits, see Fig. 3) in the right panels. |
We followed the same approach for the 2014 observations and selected kTe = 100 keV − τ = 0.5 for the extended slab and kTe = 120 keV − τ = 0.8 for the extended spherical geometry as absolute minima of the fits (Fig. 4, bottom-left panel). As secondary sets of parameters we simulated data using kTe = 57 keV − τ = 1.4 and kTe = 85 keV − τ = 1.4 for the slab and the sphere, respectively (Fig. 4, bottom-right panel).
4.1. Polarization angle
The polarization angle is always consistent with χ = π/2 for every considered configuration.
Compton scattering produces a vertical polarization, i.e. χ = π/2, in both geometries, with the angle measured with respect to the spin axis. Even though some photons are initially polarized horizontally, the flip in the polarization angle (seen in Schnittman & Krolik 2010, for instance) is not visible in the IXPE band where only photons which experienced multiple scattering are present and their polarization is already vertical.
4.2. Polarization degree
We show, in Fig. 4, the expected polarization degree versus the cosine of the inclination angle (μ = cosθ, with θ defined from the spin axis) in the four considered cases, assuming radiation integrated between 2 and 8 keV (corresponding to the IXPE operating energy band). Simulations for the 2013 and 2014 data sets are shown in the top and bottom panels, respectively. The expected signal arising from the slab configuration is plotted using a solid line while dashed lines are used for the spherical configurations. The polarization for the spherical corona is always lower than for the slab, in every simulated scenario, due to obvious symmetry reasons. For a given geometry we may also notice that thicker coronae will produce a larger polarization signal: the more the UV photons are Compton scattered, the more they will be polarized.
The maximum of the polarization degree is obtained towards high inclination angles (i.e. low values of μ). On the other hand, when the system is observed face-on, for μ = 1, it is perfectly symmetrical for both geometries and the polarization degree approaches zero in all scenarios, as expected. It is important to note that the polarization degree is not a monothonic function of μ, but has a maximum around μ ≃ 0.2, as already found by (Angel 1969, Fig. 2) for a τ = 2 scattering spheroid.
4.3. Polarization measurements with IXPE
To calculate the exposure time needed to constrain the coronal geometry with IXPE, we assumed a model composed of a power law with photon index Γ = 1.94 and a 2–8 keV flux of 3.3 × 10−11 erg cm−2 s−1. From Fig. 4 we can clearly see that the lowest values for the polarization degree are obtained in spherical coronae, ranging from 1% up to 4%. Much larger values are found in the slab geometry. The minimum polarization degree measurable at a certain confidence level (MDP, see Elsner et al. 2012, for details) is given by:
where CS are source counts, CB background counts, CL is the confidence level, and ⟨μ⟩ is the source-count-weighted modulation factor. In order to achieve an MDP of 2.5% at 99% c.l. in an IXPE observation of Ark 120, an exposure time texp ∼ 800 ks is needed1. The source is a bare Seyfert galaxy and its negligible intrinsic X-ray absorption (NH < 3.4 × 1019 cm−2: Reeves et al. 2016) suggests a low inclination for the accretion disc-corona system. In fact, an inclination angle i = 26° is measured for the host galaxy (Nordgren et al. 1995) but a misalignment between the X-ray obscuring material and the accretion disc cannot be excluded a priori (Lawrence & Elvis 2010). Different inclination angles of the accretion disc have been inferred via Iron Kα line spectroscopy (i = 35 ± 2 and 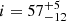 degrees: Porquet et al. 2019; Nardini et al. 2011, respectively) or using the OPTXCONV model which accounts for the warm and hot Comptonisation (i = 20 − 35 degrees, Porquet et al. 2019). These ranges in inclination angles translate into a global range of μ = 0.45 − 0.9 (see Marin 2016, for a complete list of measurements), which clearly allows us to measure a polarization signal and to distinguish between a slab or spherical geometry (see Fig. 4).
degrees: Porquet et al. 2019; Nardini et al. 2011, respectively) or using the OPTXCONV model which accounts for the warm and hot Comptonisation (i = 20 − 35 degrees, Porquet et al. 2019). These ranges in inclination angles translate into a global range of μ = 0.45 − 0.9 (see Marin 2016, for a complete list of measurements), which clearly allows us to measure a polarization signal and to distinguish between a slab or spherical geometry (see Fig. 4).
5. Conclusions
We presented the first application of the MOCA Comptonisation code to real X-ray data to model the hot corona for the bare Seyfert galaxy Ark 120. Our results can be summarized as follows.
-
The 2013 and 2014 simultaneous XMM and NuSTAR observations of Ark 120 have been analyzed and different models have been tested, to reproduce the X-ray shape of its nuclear continuum in order to characterize the hot corona. No statistically significant difference is found between a phenomenological model (cutoff power law), NTHCOMP, COMPTT and MOCA;
-
XSPEC readable tables based on MOCA have been generated for multiple geometries of the hot corona. We considered an extended slab above the accretion disc (r = 6 − 500 rg), an extended sphere (r = 6 − 500 rg) and two compact spheres (r = 6 − 20 rg and r = 6 − 100 rg). All the tested geometries for the hot coronae are statistically equivalent, based on spectroscopy solely, for both the 2013 and 2014 data sets. We found that thicker hot coronae are needed for a given temperature (or equivalently higher temperatures for a given τ) to recover the same spectral shape, in the case of 6–20 rg spherical coronae;
-
A general agreement is found between the best fit values of the hot coronal parameters obtained with MoCA and the ones inferred using other Comptonisation codes from the literature (COMPTT, NTHCOMP). However, the comparison between the best fit kTe-τ contour plots stress the importance of MoCA in modeling the geometry of the scattering material;
-
Best fit values from the spectral fits have been used to run simulations to calculate the polarization properties, when integrated in the IXPE energy band. A difference between the two geometries for the hot corona clearly emerges, due to the higher asymmetry of the extended slab compared to the extended sphere configuration;
-
We estimated that the two geometries for the hot corona can be distinguished with a texp ∼ 800 ks with IXPE, corresponding to a MDP99 = 2.5%.
The IXPE sensitivity calculator can be found at https://ixpe.msfc.nasa.gov/for_scientists/pimms/
Acknowledgments
We thank the anonymous referee for her/his comments. AM thanks Craig Gordon for useful suggestions about generating the MoCA XSPEC tables. AM, GM acknowledge financial support from the Italian Space Agency under grant ASI/INAF I/037/12/0-011/13. SB acknowledges financial support from the Italian Space Agency under grant ASI-INAF I/037/12/0. AM, GM, SB, RM, AT acknowledge financial support from ASI-INAF 2017-12-H.0. AL acknowledges support from STFC consolidated grant ST/M001040/1. FM would like to thank the Centre national d’ètudes spatiales (CNES) who funded this project through to the post-doctoral grant “Probing the geometry and physics of active galactic nuclei with ultraviolet and X-ray polarized radiative transfer”. EN acknowledges funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Skłlodowska-Curie grant agreement No. 664931.
References
- Angel, J. R. P. 1969, ApJ, 158, 219 [NASA ADS] [CrossRef] [Google Scholar]
- Arnaud, K. A. 1996, in Astronomical Data Analysis Software and Systems V, ASP Conf. Ser., 101, 17 [NASA ADS] [Google Scholar]
- Arnaud, K. A., Branduardi-Raymont, G., Culhane, J. L., et al. 1985, MNRAS, 217, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Beheshtipour, B., Krawczynski, H., & Malzac, J. 2017, ApJ, 850, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Beloborodov, A. M. 1999, in High Energy Processes in Accreting Black Holes, ASP Conf. Ser., 161, 295 [NASA ADS] [Google Scholar]
- Bianchi, S., Guainazzi, M., Matt, G., Fonseca Bonilla, N., & Ponti, G. 2009, A&A, 495, 421 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chandrasekhar, S. 1960, Radiative Transfer (New York: Dover) [Google Scholar]
- Crenshaw, D. M., Kraemer, S. B., Boggess, A., et al. 1999, ApJ, 516, 750 [NASA ADS] [CrossRef] [Google Scholar]
- Dauser, T., García, J., Parker, M. L., Fabian, A. C., & Wilms, J. 2014, MNRAS, 444, L100 [NASA ADS] [CrossRef] [Google Scholar]
- De Marco, B., Ponti, G., Cappi, M., et al. 2013, MNRAS, 431, 2441 [NASA ADS] [CrossRef] [Google Scholar]
- Done, C., Davis, S. W., Jin, C., Blaes, O., & Ward, M. 2012, MNRAS, 420, 1848 [NASA ADS] [CrossRef] [Google Scholar]
- Done, C., Jin, C., Middleton, M., & Ward, M. 2013, MNRAS, 434, 1955 [NASA ADS] [CrossRef] [Google Scholar]
- Elsner, R. F., O’Dell, S. L., & Weisskopf, M. C. 2012, in Space Telescopes and Instrumentation 2012: Ultraviolet to Gamma Ray, Proc. SPIE, 8443, 84434N [CrossRef] [Google Scholar]
- Fabian, A. C., Lohfink, A., Kara, E., et al. 2015, MNRAS, 451, 4375 [NASA ADS] [CrossRef] [Google Scholar]
- Fabian, A. C., Lohfink, A., Belmont, R., Malzac, J., & Coppi, P. 2017, MNRAS, 467, 2566 [NASA ADS] [CrossRef] [Google Scholar]
- Gabriel, C., Denby, M., Fyfe, D. J., et al. 2004, in Astronomical Data Analysis Software and Systems (ADASS) XIII, eds. F. Ochsenbein, M. G. Allen, D. Egret, & ASP Conf. Ser., 314, 759 [Google Scholar]
- García, J., Dauser, T., Lohfink, A., et al. 2014, ApJ, 782, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Haardt, F., & Maraschi, L. 1991, ApJ, 380, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Haardt, F., Maraschi, L., & Ghisellini, G. 1994, ApJ, 432, L95 [NASA ADS] [CrossRef] [Google Scholar]
- Harrison, F. A., Craig, W. W., Christensen, F. E., et al. 2013, ApJ, 770, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Jansen, F., Lumb, D., Altieri, B., et al. 2001, A&A, 365, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jin, C., Ward, M., Done, C., & Gelbord, J. 2012, MNRAS, 420, 1825 [NASA ADS] [CrossRef] [Google Scholar]
- Kalberla, P. M. W., Burton, W. B., Hartmann, D., et al. 2005, A&A, 440, 775 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kara, E., Alston, W. N., Fabian, A. C., et al. 2016, MNRAS, 462, 511 [Google Scholar]
- Lawrence, A., & Elvis, M. 2010, ApJ, 714, 561 [NASA ADS] [CrossRef] [Google Scholar]
- Lightman, A. P., & Zdziarski, A. A. 1987, ApJ, 319, 643 [NASA ADS] [CrossRef] [Google Scholar]
- Lobban, A. P., Porquet, D., Reeves, J. N., et al. 2018, MNRAS, 474, 3237 [NASA ADS] [CrossRef] [Google Scholar]
- Magdziarz, P., Blaes, O. M., Zdziarski, A. A., Johnson, W. N., & Smith, D. A. 1998, MNRAS, 301, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Marin, F. 2016, MNRAS, 460, 3679 [NASA ADS] [CrossRef] [Google Scholar]
- Matt, G., Marinucci, A., Guainazzi, M., et al. 2014, MNRAS, 439, 3016 [NASA ADS] [CrossRef] [Google Scholar]
- Nardini, E., Fabian, A. C., Reis, R. C., & Walton, D. J. 2011, MNRAS, 410, 1251 [NASA ADS] [CrossRef] [Google Scholar]
- Nardini, E., Porquet, D., Reeves, J. N., et al. 2016, ApJ, 832, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Nordgren, T. E., Helou, G., Chengalur, J. N., Terzian, Y., & Khachikian, E. 1995, ApJS, 99, 461 [NASA ADS] [CrossRef] [Google Scholar]
- Osterbrock, D. E., & Phillips, M. M. 1977, PASP, 89, 251 [NASA ADS] [CrossRef] [Google Scholar]
- Peterson, B. M., Ferrarese, L., Gilbert, K. M., et al. 2004, ApJ, 613,682 [NASA ADS] [CrossRef] [Google Scholar]
- Petrucci, P. O., Haardt, F., Maraschi, L., et al. 2000, ApJ, 540, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Petrucci, P. O., Haardt, F., Maraschi, L., et al. 2001, ApJ, 556, 716 [NASA ADS] [CrossRef] [Google Scholar]
- Petrucci, P.-O., Paltani, S., Malzac, J., et al. 2013, A&A, 549, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Petrucci, P.-O., Ursini, F., De Rosa, A., et al. 2018, A&A, 611, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Piconcelli, E., Jimenez-Bailón, E., Guainazzi, M., et al. 2004, MNRAS, 351, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Porquet, D., Reeves, J. N., O’Brien, P., & Brinkmann, W. 2004, A&A, 422, 85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Porquet, D., Done, C., Reeves, J. N., et al. 2019, A&A, 623, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Poutanen, J., & Svensson, R. 1996, ApJ, 470, 249 [NASA ADS] [CrossRef] [Google Scholar]
- Reeves, J. N., Porquet, D., Braito, V., et al. 2016, ApJ, 828, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Reis, R. C., & Miller, J. M. 2013, ApJ, 769, L7 [Google Scholar]
- Risaliti, G., Nardini, E., Elvis, M., Brenneman, L., & Salvati, M. 2011, MNRAS, 417, 178 [NASA ADS] [CrossRef] [Google Scholar]
- Risaliti, G., Young, M., & Elvis, M. 2009, ApJ, 700, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Różańska, A., Malzac, J., Belmont, R., Czerny, B., & Petrucci, P.-O. 2015, A&A, 580, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rybicki, G. B., & Lightman, A. P. 1979, Radiative Processes in Astrophysics (New York: Wiley-Interscience) [Google Scholar]
- Sanfrutos, M., Miniutti, G., Agís-González, B., et al. 2013, MNRAS, 436, 1588 [NASA ADS] [CrossRef] [Google Scholar]
- Schnittman, J. D., & Krolik, J. H. 2010, ApJ, 712, 908 [NASA ADS] [CrossRef] [Google Scholar]
- Shapiro, S. L., Lightman, A. P., & Eardley, D. M. 1976, ApJ, 204, 187 [NASA ADS] [CrossRef] [Google Scholar]
- Shemmer, O., Brandt, W. N., Netzer, H., Maiolino, R., & Kaspi, S. 2006, ApJ, 646, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Singh, K. P., Garmire, G. P., & Nousek, J. 1985, ApJ, 297, 633 [NASA ADS] [CrossRef] [Google Scholar]
- Sobolewska, M. A., & Papadakis, I. E. 2009, MNRAS, 399, 1597 [NASA ADS] [CrossRef] [Google Scholar]
- Strüder, L., Briel, U., Dennerl, K., et al. 2001, A&A, 365, L18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sunyaev, R. A., & Titarchuk, L. G. 1980, A&A, 86, 121 [NASA ADS] [Google Scholar]
- Tamborra, F., Matt, G., Bianchi, S., & Dovčiak, M. 2018, A&A, 619, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Titarchuk, L. 1994, ApJ, 434, 570 [NASA ADS] [CrossRef] [Google Scholar]
- Tortosa, A., Bianchi, S., Marinucci, A., Matt, G., & Petrucci, P. O. 2018, A&A, 614, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Turner, M. J. L., Abbey, A., Arnaud, M., et al. 2001, A&A, 365, L27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ursini, F., Petrucci, P.-O., Matt, G., et al. 2016, MNRAS, 463, 382 [NASA ADS] [CrossRef] [Google Scholar]
- Vaughan, S., Fabian, A. C., Ballantyne, D. R., et al. 2004, MNRAS, 351, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Weisskopf, M. C., Ramsey, B., O’Dell, S., et al. 2016a, in Space Telescopes and Instrumentation 2016: Ultraviolet to Gamma Ray, Proc. SPIE, 9905, 990517 [CrossRef] [Google Scholar]
- Weisskopf, M. C., Ramsey, B., O’Dell, S. L., et al. 2016b, Results Phys., 6, 1179 [NASA ADS] [CrossRef] [Google Scholar]
- Zdziarski, A. A., Johnson, W. N., & Magdziarz, P. 1996, MNRAS, 283, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, S., Santangelo, A., Feroci, M., et al. 2019, Sci. China Phys. Mech. & Astron, 62, 29502 [Google Scholar]
- Życki, P. T., Done, C., & Smith, D. A. 1999, MNRAS, 309, 561 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Hot coronal best fit parameters are reported, for the five models applied to the data.
All Figures
 |
Fig. 1. The simultaneous XMM-Newton and NuSTAR spectra and residuals to a power law model (in counts s−1 keV−1 cm−2 units) are shown, obtained on February 2013 and March 2014 for Ark 120. Dashed grey line indicate a Γ = 1.85 power law model, with a 2–10 keV flux of 3 × 10−11 erg cm−2 s−1. |
| In the text | |
 |
Fig. 2. Residuals for the combined 2013 and 2014 XMM+NuSTAR observations are shown. See text for details about the four models applied. The only residuals present are near to 0.5 keV, which are likely associated to the OI K-shell absorption from our galaxy (see Reeves et al. 2016, for further details). |
| In the text | |
 |
Fig. 3. Contour plots between kTe and τ for the slab (left panel), spherical (right panel) and compact spherical coronae (bottom panel) are shown, for the 2013 and 2014 best fits. For the 2013 data set yellow, orange and red contours indicate 99%, 90% and 68% confidence levels. For the 2014 data set cyan, light blue and dark blue contours indicate 99%, 90% and 68% confidence levels, respectively. We show, for the sake of visual comparison, the 99% c.l. contours adopting extended spherical coronae for the 2013 and 2014 observations in gray (bottom panel). |
| In the text | |
 |
Fig. 4. Polarization degree versus the cosine of the inclination angle μ are shown after integrating the signal in the IXPE operating band (2–8 keV), for the 2013 (top panels) and 2014 (bottom panels) cases and for both extended slab and spherical geometries. Left panels show simulations in which the input kTe and τ correspond to best fit values, while we took into account statistically equivalent parameters (i.e. corresponding to relative minima in the fits, see Fig. 3) in the right panels. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.