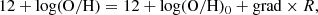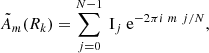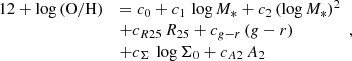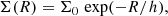| Issue |
A&A
Volume 623, March 2019
|
|
|---|---|---|
| Article Number | A7 | |
| Number of page(s) | 10 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201834364 | |
| Published online | 25 February 2019 | |
Characterizing the radial oxygen abundance distribution in disk galaxies⋆
1
Main Astronomical Observatory, National Academy of Sciences of Ukraine, 27 Akademika Zabolotnoho St., 03680 Kyiv, Ukraine
e-mail: zinchenko@mao.kiev.ua
2
Astronomisches Rechen-Institut, Zentrum für Astronomie der Universität Heidelberg, Mönchhofstr. 12–14, 69120 Heidelberg, Germany
3
Dark Cosmology Centre, Niels Bohr Institute, University of Copenhagen, Juliane Maries Vej 30, 2100 Copenhagen, Denmark
Received:
2
October
2018
Accepted:
13
January
2019
Context. The relation between the radial oxygen abundance distribution (gradient) and other parameters of a galaxy such as mass, Hubble type, and a bar strength, remains unclear although a large amount of observational data have been obtained in the past years.
Aims. We examine the possible dependence of the radial oxygen abundance distribution on non-axisymmetrical structures (bar/spirals) and other macroscopic parameters such as the mass, the optical radius R25, the color g − r, and the surface brightness of the galaxy. A sample of disk galaxies from the third data release of the Calar Alto Legacy Integral Field Area Survey (CALIFA DR3) is considered.
Methods. We adopted the Fourier amplitude A2 of the surface brightness as a quantitative characteristic of the strength of non-axisymmetric structures in a galactic disk, in addition to the commonly used morphologic division for A, AB, and B types based on the Hubble classification. To distinguish changes in local oxygen abundance caused by the non-axisymmetrical structures, the multiparametric mass–metallicity relation was constructed as a function of parameters such as the bar/spiral pattern strength, the disk size, color index g − r in the Sloan Digital Sky Survey (SDSS) bands, and central surface brightness of the disk. The gas-phase oxygen abundance gradient is determined by using the R calibration.
Results. We find that there is no significant impact of the non-axisymmetric structures such as a bar and/or spiral patterns on the local oxygen abundance and radial oxygen abundance gradient of disk galaxies. Galaxies with higher mass, however, exhibit flatter oxygen abundance gradients in units of dex/kpc, but this effect is significantly less prominent for the oxygen abundance gradients in units of dex/R25 and almost disappears when the inner parts are avoided (R > 0.25R25). We show that the oxygen abundance in the central part of the galaxy depends neither on the optical radius R25 nor on the color g − r or the surface brightness of the galaxy. Instead, outside the central part of the galaxy, the oxygen abundance increases with g − r value and central surface brightness of the disk.
Key words: galaxies: abundances / ISM: abundances / H II regions
Table 1 is also available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/623/A7
© ESO 2019
1. Introduction
It is known that the chemical abundances of heavy elements decrease with increasing galactocentric distance in the disks of our Galaxy and other nearby spiral galaxies (e.g., Mayor 1976; Searle 1971; Peimbert 1979; Shields & Searle 1978; Belfiore et al. 2017). This trend is usually referred to as the radial metallicity gradient (RMG). The oxygen abundance gradient in nearby galaxies, traced by H II regions, ranges from ∼0 dex kpc−1 to −0.1 dex kpc−1 (e.g., Vila-Costas & Edmunds 1992; Zaritsky et al. 1994; Sánchez et al. 2014; Pilyugin et al. 2014a). However, the origin of the gradient and its relation to other macroscopic parameters of galaxies are still open for discussion.
During the past decade, significant progress in the understanding of the main tendencies of chemical abundance distribution in galaxies became possible through integral field spectroscopy (IFS) data that were obtained in frameworks of large galaxy surveys. One such survey is the Calar Alto Legacy Integral Field Area Survey (CALIFA; Sánchez et al. 2012). Using oxygen abundance measurements in a large number of H II regions in more than 300 spiral galaxies from the CALIFA survey, Sánchez et al. (2014) showed that disk galaxies in the local Universe exhibit a common characteristic gradient in the oxygen abundance up to two effective disk radii, regardless of the galaxy parameters. The distribution of the abundance gradients is Gaussian around some mean value. Therefore, Sánchez et al. (2014) suggested that the scatter around the mean value could be a result of random fluctuations.
Sánchez et al. (2014) claimed that this result contradicts several previous observational studies that concluded that the slope of the gas-phase abundance gradient is related to other galactic properties, such as
-
morphology: the slopes of early-type spirals are more shallow than those of late-type galaxies (e.g., McCall et al. 1985; Vila-Costas & Edmunds 1992);
-
mass: the slopes of more massive spirals are more shallow than those of less massive galaxies (e.g., Zaritsky et al. 1994; Martin & Roy 1994; Garnett 1998);
-
presence of a bar: the slopes of barred galaxies are more shallow than than those of unbarred galaxies (e.g., Vila-Costas & Edmunds 1992; Zaritsky et al. 1994; Roy 1996);
-
interaction stage of the galaxies: evolved mergers present shallower slopes (e.g., Rich et al. 2012).
In contrast, many authors found no correlation between abundance gradient (expressed in dex/R25) and morphology (Zaritsky et al. 1994; Pilyugin et al. 2014a; Sánchez et al. 2014; Sánchez-Menguiano et al. 2016) and stellar mass (Ho et al. 2015; Sánchez-Menguiano et al. 2016, 2018). However, for the metallicity gradients expressed in dex/kpc, Ho et al. (2015) found that galaxies with lower mass tend to have steeper metallicity gradients on average.
Using the CALIFA survey, Sánchez-Blázquez et al. (2014) found no difference in the slope of the stellar-phase metallicity gradient for barred and unbarred galaxies. The same conclusion was made by Cheung et al. (2015), who analyzed stacked spectra from the Sloan Digital Sky Survey (SDSS).
Based on a sample of 550 nearby galaxies with integral field unit (IFU) data from the SDSS IV Mapping Nearby Galaxies at Apache Point Observatory survey (SDSS/MaNGA; Bundy et al. 2015; Blanton et al. 2017), it has recently been found that the radial metallicity gradient steepens when the stellar mass increases up to log(M/M⊙)=10.5, but flattens for galaxies with higher masses (Belfiore et al. 2017). However, using the same data from the SDSS-IV MaNGA survey, Lian et al. (2018) found that the stellar metallicity gradients tend to be mass dependent with steeper gradients in more massive galaxies, but they found no clear mass dependence for the gas metallicity gradient. Moreover, a recent analysis of IFU data suggests that galaxies can present a different behavior of the radial abundance gradient in the inner and outer parts (Sánchez et al. 2014; Sánchez-Menguiano et al. 2016, 2018; Belfiore et al. 2017).
According to the current observational picture presented above, despite the wide range of metallicity gradients exhibited by galaxies, only a few studies point out the connection between radial metallicity gradient and galaxy mass. Thus, there is no solid confirmation of the correlation between oxygen abundance gradient and galaxy parameters (with the exception of mergers).
On the other hand, theoretical simulations based on pure N-body galactic disk dynamics and self-consistent chemodynamical models produce an appreciable influence of non-axisymmetric structures (bar and spiral patterns) in the galactic disk, and interactions between galaxies. Several theoretical studies have suggested various mechanisms of gas and star mixing in barred galaxies (Athanassoula 1992; Sellwood & Binney 2002; Schönrich & Binney 2009; Minchev & Famaey 2010; Di Matteo et al. 2013; Minchev et al. 2013, 2014) that might lead to the flattening of the oxygen abundance distribution. This scenario is consistent with observational results (Ruiz-Lara et al. 2017) based on the analysis of the stellar content in a sample of CALIFA galaxies. Thus, the redistribution of heavy elements produced by the radial migration of stars and/or interstellar gas along the galactic disk is assumed to be the cause of a flattening of the metallicity gradient for the intermediate-age stellar populations and interstellar gas. However, Grand & Kawata (2016) demonstrated that corotating spiral arms do not change the radial metallicity gradient.
Zinchenko et al. (2016) analyzed the azimuthal variation of the oxygen abundance in CALIFA galaxies and found no significant asymmetry in the azimuthal abundance distribution. In this paper, we investigate the possible dependence of the oxygen abundance gradient in disk galaxies on a bar/spiral and other parameters of the galaxy, such as mass, size, color index, and surface brightness. We also study the mass–metallicity relation for the local oxygen abundance in the center and in intermediate and outer parts of the galaxy as a multivariable relation including size, color index, surface brightness, and the bar/spiral pattern strength.
2. Data
2.1. Sample
We used publicly available spectra from the integral field spectroscopic CALIFA survey data release 3 (DR3; Sánchez et al. 2016, 2012; Walcher et al. 2014) based on observations with the Potsdam Multi-Aperture Spectrophotometer (PMAS) and a specialized fiber-bundle, called PPAK (Pmas fiber PAcK), mounted on the Calar Alto 3.5-m telescope. CALIFA DR3 provides wide-field IFU data for 667 objects in total. The data for each galaxy are presented by two spectral datacubes that cover the spectral regions of 4300–7000 Å at a spectral resolution of R ∼ 850 (setup V500) and of 3700–5000 Å at R ∼ 1650 (setup V1200). Currently, there are 446 COMB datacubes that are a combination of V500 and V1200 datacubes and cover the spectral range of 3700–7000 Å. In this study we used COMB (a combination of V500+V1200) datacubes.
The galaxy inclination i and position angle of the major axis PA were estimated from the analysis of the surface brightness image in the r band of the SDSS. We applied the GALFIT code (Peng et al. 2002, 2010) to simultaenously fit the image of each galaxy with bulge+disk (Sersic+exponential profile) profiles. The position angle of the major axis and inclination of the exponential profile were adopted as the PA and i for all galaxies, with the exception of NGC 1070. Because the fit of the exponential profile for NGC 1070 is unreliable, the PA and i of the Sersic profile were adopted instead.
For further consideration, we selected galaxies with inclinations lower than 60°, which corresponds to a ratio of minor to major axis greater than ∼0.5. The optical isophotal radius R25 of a galaxy was determined from the analysis of the surface brightness profiles in the SDSS g and r bands converted into the Vega B band. We used the stellar masses derived from UV-to-near-infrared (NIR) photometry, morphological type, bar, and merger classification from the parameter tables described in Walcher et al. (2014). We adopted the distances from the NED database with flow corrections for Virgo, the Great Attractor, and the Shapley Supercluster infall. The adopted distances, morphological types, PA, i, stellar masses, R25, and g − r colors are shown in Table 1.
Adopted and derived properties of our target galaxies.
We selected only galaxies with no merger features, that is, galaxies that are classified as isolated. Galaxies with insufficient numbers of spaxels with measured oxygen abundance were excluded from our sample. Thus, our final sample contains 66 galaxies with a radial oxygen abundance gradient derived by at least 10 spaxels that are distributed in a significantly wide radial range. Figure 1 shows the correlation between the stellar mass and the optical isophotal radius for our sample of galaxies.
 |
Fig. 1. Comparison of stellar mass and optical radius R25 for our sample of galaxies. Unbarred (A), barred (B), and intermediate (AB) galaxies are shown with different colors and symbols. |
2.2. Emission line fluxes and abundance determination
The spectrum of each spaxel from the CALIFA DR3 datacubes was processed in the same way as described in Zinchenko et al. (2016). Briefly, the stellar background in all spaxels was fit using the public version of the STARLIGHT code (Cid Fernandes et al. 2005; Mateus et al. 2006; Asari et al. 2007) adapted for execution in the NorduGrid ARC1 environment of the Ukrainian National Grid. We used a set of 45 synthetic simple stellar population (SSP) spectra with metallicities Z = 0.004, 0.02, and 0.05, and 15 ages from 1 Myr up to 13 Gyr from the evolutionary synthesis models of Bruzual & Charlot (2003) and the reddening law of Cardelli et al. (1989) with RV = 3.1. The resulting stellar radiation contribution was subtracted from the measured spectrum in order to determine the nebular emission spectrum. For each spectrum, we measured the fluxes of the [O II]λ3727+λ3729, Hβ, [O III]λ4959, [O III]λ5007, [N II]λ6548, Hα, [N II]λ6584, [S II]λ6717, and [S II]λ6731 lines using our code ELF3D for emission line fitting. Each line was fit with a Gaussian profile. The measured line fluxes were corrected for interstellar reddening using the theoretical Hα to Hβ ratio (i.e., the standard value of Hα/Hβ = 2.86) and the analytical approximation of the Whitford interstellar reddening law from Izotov et al. (1994). When the measured value of Hα/Hβ was lower than 2.86, the reddening was set to zero.
The [O III]λ5007 and λ4959 lines originate from transitions from the same energy level, therefore their flux ratio is determined only by the transition probability ratio, which is very close to 3 (Storey & Zeippen 2000). The stronger line [O III]λ5007 is usually measured with higher precision than the weaker line [O III]λ4959. Therefore, the value of R3 is estimated as 1.33 [O III]λ5007, but not as a sum of the line fluxes. Similarly, the [N II]λ6584 and λ6548 lines also originate from transitions from the same energy level, and the transition probability ratio for these lines is again close to 3 (Storey & Zeippen 2000). The value of N2 is therefore estimated as 1.33 [N II]λ6584. Thus, the lines [O II] λλ 3727,3729, Hβ, [O III]λ5007, Hα, [N II]λ6584, [S II]λ6717, and [S II]λ6731 are used for the dereddening and the abundance determinations. The precision of the line flux is specified by the ratio of the flux to the flux error (parameter ϵ). We selected spectra where the parameter ϵ ≥ 4 for each of these lines. To select spaxels associated with star-forming regions, we applied BPT diagram log([O III]λ5007/Hβ) – log([N II]λλ6584/Hα) (Baldwin et al. 1981). To separate objects whose main ionization source are massive stars from those whose main ionization source are shocks of gas and/or active galactic nuclei (AGNs), we applied the criterion proposed by Kauffmann et al. (2003).
The CALIFA spectra, as well as the spectra of other surveys that use the IFU technique, can be contaminated by diffuse ionized gas (DIG; Haffner et al. 2009; Belfiore et al. 2015; Lacerda et al. 2018). This can lead to an increasing emission in low-ionization lines and therefore to biases in the chemical abundances derived by strong-line methods. However, Pilyugin et al. (2018) showed that the dividing line proposed by Kauffmann et al. (2003) can be applied to reject spectra with significant contamination by DIG.
To determine oxygen abundances, we used the new R calibration developed by Pilyugin & Grebel (2016). In comparison with previous calibrations, this calibration is applicable for the whole range of H II region metallicities and provides high-precision oxygen abundances with measurement errors smaller than 0.1 dex and a metallicity scale bounded to the direct Te method. Thus, the oxygen abundance was calculated for each spaxel using the R calibration.
3. Oxygen abundance gradient
We fit the radial oxygen abundance distribution in the disk using the following relation:
where 12 + log(O/H)0 is the oxygen abundance at R0 = 0, that is, the extrapolated value of the oxygen abundance in the galactic center, grad is the slope of the oxygen abundance gradient. It is known that the oxygen abundances in the inner and outer parts of some galaxies are systematically different from those expected from the overall abundance gradient (e.g., Belley & Roy 1992; Bresolin et al. 2009, 2012; Goddard et al. 2011; Rosales-Ortega et al. 2011; Werk et al. 2011; Patterson et al. 2012; Sánchez et al. 2012, 2014; Sánchez-Menguiano et al. 2016, 2018; Zinchenko et al. 2016). However, within an optical radius, these differences are relatively small, smaller than 0.05 dex, and a break in the slope of the radial oxygen abundance distribution can be found at any radius (Pilyugin et al. 2017). Thus, the oxygen abundance gradient was estimated in three ranges of galactocentric distances: within R25, in the inner R < 0.25R25, and outer 0.25R25 < R < R25 parts of the galaxy. It is presented in Table 12.
Figure 2 shows the oxygen abundance gradient for NGC 257. Circles represent the oxygen abundance in the individual spaxels. The black solid line is the best fit to spaxels within the optical radius R25 of the galaxy. Dashed red lines correspond to the best fit of the oxygen abundance gradient in the inner and outer parts of the galaxy. The radial gradient flattening is clearly seen in the inner part of the galaxy.
 |
Fig. 2. Oxygen abundance gradient for NGC 257. Circles represent the oxygen abundance in the individual spaxels. Vertical dashed lines represent 0.25 and 1.0 fraction of optical radius R25. The black solid line shows the best fit to all the data. Dashed red lines correspond to the best fit of the oxygen abundance gradient in the inner (R < 0.25R25) and outer (0.25R25 < R < R25) parts of the galaxy. The typical uncertainty of the oxygen abundance determination for the single spaxel is presented in the top right corner. |
Figure 3 shows the oxygen abundance gradient as a function of stellar mass. Black circles, red plus signs, and blue triangles represent unbarred (A), barred (B), and intermediate (AB) galaxies, respectively. Black dashed lines are the best fit for the subsample of unbarred galaxies, and red lines show this for the barred galaxies. Shaded areas represent the 1σ uncertainties of the fit. The left panels show the abundance gradient scaled to kiloparsecs, while the gradient in the right panels is scaled to R25. In all cases there is no significant difference between barred and unbarred galaxies.
 |
Fig. 3. Stellar mass – oxygen abundance gradient diagrams for the abundance gradient scaled to kpc (left columns) and R25 (right columns). Top panels: oxygen abundance gradient for galactocentric distances r < R25. Middle panels: oxygen abundance gradient for r < 0.25R25. Bottom panels: oxygen abundance gradient for 0.25 < r < R25. Unbarred (A), barred (B), and intermediate (AB) galaxies are shown with different colors and symbols. Black dashed lines are the best fit for the subsample of unbarred galaxies, and red lines show this for the barred galaxies. Shaded areas represent the 1σ uncertainties of the fit. |
Galaxies with higher mass exhibit flatter oxygen abundance gradients when the gradient is measured per kpc (left panels of the Fig. 3), in agreement with the result of the numerical simulation of Tissera et al. (2016). This effect is significantly less prominent for the oxygen abundance gradients scaled to R25 (right panels of the Fig. 3) and almost disappears for the gradient calculated in the outer region (bottom right panel). Our result confirms the conclusion of Ho et al. (2015), who attributed to the size effect the different dependence of the oxygen abundance gradient on the stellar mass for the oxygen abundance gradient normalized to kpc or R25. They noted that galaxies with steeper oxygen abundance gradients usually have a smaller optical radius. Thus, our result suggests that at the present epoch, the variation in oxygen abundance between the central and the outer parts of galaxies is similar for galaxies in the whole mass range, while the radial variation in absolute scale (e.g., per kpc) is larger for less massive galaxies.
Different approaches to quantify the strength of the bar based on the axis ratio and bar length (Martin 1995; Martinet & Friedli 1997; Chapelon et al. 1999; Aguerri 1999; Abraham & Merrifield 2000; Marinova & Jogee 2007), bar torque (Combes & Sanders 1981; Buta et al. 2003; Laurikainen & Salo 2002; Díaz-García et al. 2016), and Fourier analysis (Aguerri et al. 1998, 2000; Díaz-García et al. 2016; Garcia-Gómez et al. 2017), for instance, have been suggested and used in the literature. Following Díaz-García et al. (2016) and Saha & Naab (2013), to quantify the strength of the non-axisymmetric structures such as the bar and/or spiral patterns in the disk of a galaxy, we calculated the discrete Fourier transform of the surface brightness in the SDSS r band in the disk of each galaxy. After correcting for inclination, we divided the galactic disk into concentric rings and defined the Fourier amplitude coefficient in each ring. The mth complex Fourier coefficient is given by
where Ij is the surface brightness within the jth pixel in a given ring Rk. Am = Ãm/Ã0 are the normalized Fourier amplitudes. Ã0 refers to the axisymmetric surface brightness component (mean surface brightness at the given radius), and Ãm is an amplitude of the mth mode of the azimuthal variation of surface brightness. For the further analysis, we adopted a maximum value of the A2 Fourier amplitude for a galactocentric radius smaller than 0.5R25, which corresponds to the maximum length of a bar (Erwin 2005). These derived maxima of the A2 Fourier amplitudes for each galaxy are presented in Table 1. We did not consider Fourier amplitudes in the center of galaxies (R < 2 arcsec) either because they can be affected by the uncertainties in the position of the galactic center.
Figure 4 shows the oxygen abundance gradient as a function of the maximum value of the A2 Fourier amplitude. The dashed line is the linear fit of the data. We applied a two-sided p-value statistical test whose null hypothesis is that the slope of the grad versus A2 relation is zero. The p-values range from 0.30 to 0.86. We thus confirmed the null hypothesis of no correlation between oxygen abundance gradient and the A2 Fourier amplitude of the surface brightness in the SDSS r band.
 |
Fig. 4. Diagrams showing the A2 Fourier coefficient – oxygen abundance gradient for the abundance gradient scaled to kpc (left columns) and R25 (right columns). Top panels: oxygen abundance gradient for galactocentric distances r < R25. Middle panels: oxygen abundance gradient for r < 0.25R25. Bottom panels: oxygen abundance gradient for 0.25 < r < R25. |
4. Generalized mass–metallicity relation
The oxygen abundance in a galaxy can depend on the galaxy mass (Tremonti et al. 2004; Kewley & Ellison 2008; Thuan et al. 2010), the surface brightness (Vila-Costas & Edmunds 1992; Ryder 1995; Pilyugin et al. 2014b), the disk scale length (Pilyugin et al. 2014b; Zinchenko et al. 2015), the morphological type (Pilyugin et al. 2014b; Zinchenko et al. 2015), and the galactocentric radius (Peimbert 1979; Shields & Searle 1978; Sánchez et al. 2014; Zinchenko et al. 2016; Belfiore et al. 2017, among many others). Moreover, the dependence on the given parameter can be seen only at some range of galactocentric distances (Pilyugin et al. 2014b). We therefore considered the generalized mass–metallicity relation as a multiparameter function to distinguish the impact of size, color, disk surface brightness, and strength of bar/spirals on the oxygen abundance in the central, intermediate, and outer parts of the galaxy.
For a given galactocentric radius we applied the following parametric relation:
where M* is the stellar mass of the galaxy expressed in the mass of the Sun, R25 is the isophotal radius of a galaxy in kpc, g − r is the difference between the total magnitude of the galaxy in the SDSS g and r bands, Σ0 is the central surface brightness of the disk in the SDSS r band in units of L⊙/pc2, and A2 is the maximum value of the A2 Fourier coefficient. This relation was constructed for the three galactocentric radii of 0, 0.5R25, and R25. The oxygen abundance at a given radius was calculated using the fit of the abundance gradient. Abundances at the center of each galaxy were obtained from the inner region gradient fit (R < R25), while oxygen abundances at R = 0.5R25 and R = R25 were estimated using the outer gradient fit (0.25R25 < R < R25). The values of each coefficient for the three considered radii are listed in Table 2.
Coefficients of parametric mass–metallicity relation.
The disk surface brightness was obtained in the following way. We corrected the surface brightness of each pixel for Galactic foreground extinction using the given in the NASA Extragalactic Database (NED)3. We applied the Ar values from the recalibration by Schlafly & Finkbeiner (2011) of the Schlegel et al. (1998) infrared-based dust map. Then, we fit the radial surface brightness profile by an exponential profile
where Σ0 is the central disk surface brightness and h is the radial scale length. As the radial surface brightness profiles of many galaxies are affected by the bulge in the central part, we fit the surface brightness for the galactocentric distances 0.3R25 < R < R25. The surface brightness was converted into solar units for the further analysis. The magnitude of the Sun in the SDSS r band M⊙, r = 4.64 was taken from Blanton & Roweis (2007).
We estimated the probability distribution function (PDF) and the 95% confidence intervals for the cR25, cg − r, cΣ, and cA2 coefficients of the generalized mass–metallicity relation using a bootstrap method with 100 000 iterations (Fig. 5). We considered the generalized mass–metallicity relation for the local oxygen abundance in the center, at the half of the optical radius, and at the optical radius of a galaxy. For the central part of a galaxy, the zero value falls within the 95% confidence interval of the PDF for all parameters. This shows that the oxygen abundance in the central part of a galaxy depends neither on the optical radius R25 nor on the color g − r, Σ0, and A2 of the galaxy. However, outside the central part, the oxygen abundance increases with g − r and Σ0 at a confidence level of almost 95%. The right side columns of Fig. 5 show that there is no dependence of the generalized mass–metallicity relation on the A2 parameter because the zero value falls within the 95% confidence interval of the PDF at all radii.
 |
Fig. 5. Probability distribution function for the cR25, cg − r, cΣ, and cA2 coefficients of the generalized mass–metallicity relation in the center of galaxies (top panels), at R = 0.5R25 (middle panels), and R = R25 (bottom panels). The solid vertical line represents the zero value for each coefficient, and the dashed lines show the two-sided 95% confidence interval. |
Figure 6 shows the probability distribution function for the c1 (left column) and c2 (middle column) coefficients of the generalized mass–metallicity relation in the center of galaxies (top panels), at R = 0.5R25 (middle panels), and R = R25 (bottom panels). The solid vertical line represents the zero value for each coefficient. The coefficient c2 represents the nonlinearity of the generalized mass–metallicity relation, which is significant in the inner region of galaxies. The right column panels, which are 2D PDFs in c1 and c2 coordinate axes, represent the strong correlation between the c1 and c2 coefficients at all galactocentric radii. Because of this and the short mass range, the width of the PDF of c1 and c2 coefficients is quite large. For the outer part of the galaxy, the PDF centers for the c1 and c2 coefficients are close to zero. This might be thought to indicate that in the outer parts of the galaxies the oxygen abundance does not depend on the galaxy mass. To determine whether this is true, we examined the right bottom panel, which represents the correlation between c1 and c2 for the outer region of a disk. This panel contains the zoomed central part of the distribution. It is very unlikely that the c1 and c2 coefficients are both equal to zero simultaneously. This means that the oxygen abundance depends on the galaxy mass at the outer part of a galaxy as well.
 |
Fig. 6. Probability distribution function for the c1 (left column) and c2 (middle column) coefficients of the generalized mass–metallicity relation in the center of galaxies (top panels), at R = 0.5R25 (middle panels), and R = R25 (bottom panels). The solid vertical line represents the zero value for each coefficient. The right column represents the correlation between the c1 and c2 coefficients. |
We here limit our sample to face-on galaxies of large angular size in order to resolve the bar and spiral structure. In a future work we will investigate the nonlinearity of the generalized mass–metallicity relation in detail using a larger galaxy sample.
5. Discussion and summary
We investigated the possible dependence of the oxygen abundance gradient in disk galaxies on the presence of a bar/spiral and other parameters of the galaxy, such as mass, size, color index, and surface brightness. We also studied the generalized mass–metallicity relation for the oxygen abundance in the center, intermediate, and outer parts of the galaxy as a multivariable relation including size, color index, surface brightness, and the bar/spiral pattern strength. Our sample contains 66 galaxies from the CALIFA DR3 survey. We adopted the Fourier amplitude A2 of the surface brightness as the quantitative characteristic of the strength of non-axisymmetric structures in a galactic disk, in addition to a commonly used morphologic division into A, AB, and B types based on the Hubble classification.
We considered the generalized mass–metallicity relation in order to take into account a possible dependence of the local oxygen abundance and the strength of the non-axisymmetric structures in a disk. Our relation also takes into account the influence of the isophotal radius R25, the color index g − r in the SDSS bands, the central surface brightness of the disk Σ in the SDSS r band, and the bar/spiral strength, quantified as the maximum amplitude of the A2 Fourier coefficient. This approach allowed us to distinguish changes in local oxygen abundance that are caused by each parameter even when the oxygen abundance depends on many parameters simultaneously. This relation was constructed for the three galactocentric radii of 0, 0.5R25, and R25.
We find larger negative oxygen abundance gradients scaled to kpc for the galaxies with lower masses. However, this effect is significantly less prominent for the oxygen abundance gradients scaled to R25, as has been shown by previous observational (Ho et al. 2015) and theoretical (Prantzos & Boissier 2000) studies. The dependence of oxygen abundance gradient on the stellar mass almost disappears when the gradient is calculated for the outer part of the galaxy and scaled to R25.
We find neither a significant difference between the oxygen abundance gradient in unbarred and barred galaxies (Hubble types A an B) nor a dependence of the mass–local metallicity relation on the A2 parameter at any galactocentric radius. A standard deviation of the difference between oxygen abundances, observed and calculated with our generalized mass–metallicity relation, ranges from 0.04 dex at the center to 0.07 dex at the optical radius. Thus, our data suggest that there is no significant impact of the non-axisymmetric structures such as a bar and/or spiral patterns on the oxygen abundance and radial metallicity gradient of the spiral galaxies. The effect of the oxygen abundance distribution is smaller than ∼0.05 dex at any distance from the center of a galaxy. This conclusion agrees with the results on the stellar (Sánchez-Blázquez et al. 2014; Cheung et al. 2015) and gas-phase (Sánchez-Menguiano et al. 2016) metallicity gradients as well as with a few recent studies of the azimuthal variation in oxygen abundance (in the spiral arms and interarm medium) for the CALIFA galaxies. Sakhibov et al. (2018) showed that the enhancement of the oxygen abundance in the spiral arms as compared to the interarm regions is lower that 0.05 dex. Moreover, no significant changes in radial oxygen abundance gradient between the spiral arms and the interarm medium have been found. In addition, Sánchez-Menguiano et al. (2017) noted some differences in the azimuthal distribution of the oxygen abundance between the arm and interarm star-forming regions in barred and flocculent spirals. They suggested that this influence is not strong enough to affect the overall abundance distribution, which is confirmed by our results.
The absence of a correlation between the gas-phase oxygen abundance and the non-axisymmetric structures in galaxy disks suggests that at least for the oxygen, the processes of chemical enrichment of the interstellar medium are more efficient in producing the radial abundance gradient than the gas mixing.
We find that the local oxygen abundance in the outer part of the disk increased with the central surface brightness of the disk, while there is no such correlation for the central part of the galaxies. This result is consistent with the conclusion of Wu et al. (2015). They considered the averaged oxygen abundance in nearby galaxies with respect to its surface brightness and found that galaxies with lower surface brightness tend to have lower metallicity. The correlation between local oxygen abundance and surface brightness, in addition to the flattening of the radial metallicity gradient in the massive galaxies, can be considered as confirmation of the inside-out galaxy formation scenario (Kepner 1999; Pilkington et al. 2012). If the chemical evolution in the central part of the galaxy is almost completed, the dependence of the metallicity on the galaxy parameters should indeed be suppressed.
Our findings are briefly summarized below.
-
We showed that galaxies with higher stellar mass exhibit flatter oxygen abundance gradients. This correlation becomes more prominent for gradients expressed in units of dex/kpc and obtained for the central part of the galaxies (R < 0.25R25) and for the galactocentric distances in the range from 0 to R25.
-
There is no significant difference between the oxygen abundance gradient in unbarred and barred galaxies (Hubble types A and B). In addition, we did not find a dependence of the generalized mass–metallicity relation on the A2 parameter. Our data suggest that there is no significant impact of the non-axisymmetric structures such as a bar and/or spiral patterns on the local oxygen abundance in the disk of a galaxy or this impact is weaker than ∼0.05 dex. However, this correlation is significantly reduced when the abundance gradients are scaled to R25, and it almost disappears when the gradients are calculated for the outer part of the galaxy.
-
The local oxygen abundance does not depend on the optical radius R25 at any radius.
-
The local oxygen abundance increases with color index g − r of the galaxy outside the inner part.
-
The local oxygen abundance depends on the central surface brightness of the disk Σ0 only in the outer region of the galaxy. The correlation between local oxygen abundance and surface brightness in the outer region of galaxies, in addition to the flattening of the radial metallicity gradient in the massive galaxies, can be considered as confirmation of the inside-out galaxy formation scenario (Kepner 1999; Pilkington et al. 2012).
A detailed list of oxygen abundance gradients and errors for each galaxy is available at https://sites.google.com/view/igorzinchenko/main/califa
Acknowledgments
We are grateful to the referee for their constructive comments. I.A.Z. thanks the German Academic Exchange Service (DAAD) for financial support. I.A.Z. and L.S.P. acknowledge support within the framework of Sonderforschungsbereich (SFB 881) on “The Milky Way System” (especially subproject A5), which is funded by the German Research Foundation (DFG). L.S.P. and I.A.Z. thank the Astronomisches Rechen-Institut at the Universität Heidelberg, where this investigation was carried out, for the hospitality. I.A.Z. acknowledges the support by the Ukrainian National Grid program (project 400Kt) of the NAS of Ukraine. This study uses data provided by the Calar Alto Legacy Integral Field Area (CALIFA) survey (http://califa.caha.es/). Based on observations collected at the Centro Astronomico Hispano Aleman (CAHA) at Calar Alto, operated jointly by the Max-Planck-Institut fur Astronomie and the Instituto de Astrofisica de Andalucia (CSIC).
References
- Abraham, R. G., & Merrifield, M. R. 2000, AJ, 120, 2835 [NASA ADS] [CrossRef] [Google Scholar]
- Aguerri, J. A. L. 1999, A&A, 351, 43 [NASA ADS] [Google Scholar]
- Aguerri, J. A. L., Beckman, J. E., & Prieto, M. 1998, AJ, 116, 2136 [Google Scholar]
- Aguerri, J. A. L., Muñoz-Tuñón, C., Varela, A. M., & Prieto, M. 2000, A&A, 361, 841 [NASA ADS] [Google Scholar]
- Asari, N. V., Cid Fernandes, R., Stasińska, G., et al. 2007, MNRAS, 381, 263 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Athanassoula, E. 1992, MNRAS, 259, 345 [NASA ADS] [CrossRef] [Google Scholar]
- Baldwin, J. A., Phillips, M. M., & Terlevich, R. 1981, PASP, 93, 5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Belfiore, F., Maiolino, R., Bundy, K., et al. 2015, MNRAS, 449, 867 [NASA ADS] [CrossRef] [Google Scholar]
- Belfiore, F., Maiolino, R., Tremonti, C., et al. 2017, MNRAS, 469, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Belley, J., & Roy, J.-R. 1992, ApJS, 78, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Blanton, M. R., & Roweis, S. 2007, AJ, 133, 734 [NASA ADS] [CrossRef] [Google Scholar]
- Blanton, M. R., Bershady, M. A., Abolfathi, B., et al. 2017, AJ, 154, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Bresolin, F., Ryan-Weber, E., Kennicutt, R. C., & Goddard, Q. 2009, ApJ, 695, 580 [NASA ADS] [CrossRef] [Google Scholar]
- Bresolin, F., Kennicutt, R. C., & Ryan-Weber, E. 2012, ApJ, 750, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- Bundy, K., Bershady, M. A., Law, D. R., et al. 2015, ApJ, 798, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Buta, R., Block, D. L., & Knapen, J. H. 2003, AJ, 126, 1148 [NASA ADS] [CrossRef] [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Chapelon, S., Contini, T., & Davoust, E. 1999, A&A, 345, 81 [NASA ADS] [Google Scholar]
- Cheung, E., Conroy, C., Athanassoula, E., et al. 2015, ApJ, 807, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Cid Fernandes, R., Mateus, A., Sodré, L., Stasińska, G., & Gomes, J. M. 2005, MNRAS, 358, 363 [NASA ADS] [CrossRef] [Google Scholar]
- Combes, F., & Sanders, R. H. 1981, A&A, 96, 164 [NASA ADS] [Google Scholar]
- Díaz-García, S., Salo, H., Laurikainen, E., & Herrera-Endoqui, M. 2016, A&A, 587, A160 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Di Matteo, P., Haywood, M., Combes, F., Semelin, B., & Snaith, O. N. 2013, A&A, 553, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Erwin, P. 2005, MNRAS, 364, 283 [NASA ADS] [CrossRef] [Google Scholar]
- Garcia-Gómez, C., Athanassoula, E., Barberà, C., & Bosma, A. 2017, A&A, 601, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Garnett, D. R. 1998, Rev. Mex. Astron. Astrofis. Conf. Ser., 7, 58 [NASA ADS] [Google Scholar]
- Goddard, Q. E., Bresolin, F., Kennicutt, R. C., Ryan-Weber, E. V., & Rosales-Ortega, F. F. 2011, MNRAS, 412, 1246 [NASA ADS] [Google Scholar]
- Grand, R. J. J., & Kawata, D. 2016, Astron. Nachr., 337, 957 [NASA ADS] [CrossRef] [Google Scholar]
- Haffner, L. M., Dettmar, R.-J., Beckman, J. E., et al. 2009, Rev. Mod. Phys., 81, 969 [NASA ADS] [CrossRef] [Google Scholar]
- Ho, I.-T., Kudritzki, R.-P., Kewley, L. J., et al. 2015, MNRAS, 448, 2030 [NASA ADS] [CrossRef] [Google Scholar]
- Izotov, Y. I., Thuan, T. X., & Lipovetsky, V. A. 1994, ApJ, 435, 647 [NASA ADS] [CrossRef] [Google Scholar]
- Kauffmann, G., Heckman, T. M., Tremonti, C., et al. 2003, MNRAS, 346, 1055 [Google Scholar]
- Kepner, J. V. 1999, ApJ, 520, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Kewley, L. J., & Ellison, S. L. 2008, ApJ, 681, 1183 [NASA ADS] [CrossRef] [Google Scholar]
- Lacerda, E. A. D., Cid Fernandes, R., Couto, G. S., et al. 2018, MNRAS, 474, 3727 [NASA ADS] [CrossRef] [Google Scholar]
- Laurikainen, E., & Salo, H. 2002, MNRAS, 337, 1118 [NASA ADS] [CrossRef] [Google Scholar]
- Lian, J., Thomas, D., Maraston, C., et al. 2018, MNRAS, 476, 3883 [NASA ADS] [CrossRef] [Google Scholar]
- Marinova, I., & Jogee, S. 2007, ApJ, 659, 1176 [NASA ADS] [CrossRef] [Google Scholar]
- Martin, P. 1995, AJ, 109, 2428 [NASA ADS] [CrossRef] [Google Scholar]
- Martin, P., & Roy, J.-R. 1994, ApJ, 424, 599 [NASA ADS] [CrossRef] [Google Scholar]
- Martinet, L., & Friedli, D. 1997, A&A, 323, 363 [NASA ADS] [Google Scholar]
- Mateus, A., Sodré, L., Cid Fernandes, R., et al. 2006, MNRAS, 370, 721 [NASA ADS] [CrossRef] [Google Scholar]
- Mayor, M. 1976, in Abundance Effects in Classification, eds. B. Hauck, P. C. Keenan, & W. W. Morgan, IAU Symp., 72, 207 [NASA ADS] [CrossRef] [Google Scholar]
- McCall, M. L., Rybski, P. M., & Shields, G. A. 1985, ApJS, 57, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Minchev, I., & Famaey, B. 2010, ApJ, 722, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Minchev, I., Chiappini, C., & Martig, M. 2013, A&A, 558, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Minchev, I., Chiappini, C., & Martig, M. 2014, A&A, 572, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Patterson, M. T., Walterbos, R. A. M., Kennicutt, R. C., Chiappini, C., & Thilker, D. A. 2012, MNRAS, 422, 401 [NASA ADS] [CrossRef] [Google Scholar]
- Peimbert, M. 1979, in The Large-Scale Characteristics of the Galaxy, ed. W. B. Burton, IAU Symp., 84, 307 [NASA ADS] [CrossRef] [Google Scholar]
- Peng, C. Y., Ho, L. C., Impey, C. D., & Rix, H.-W. 2002, AJ, 124, 266 [NASA ADS] [CrossRef] [Google Scholar]
- Peng, C. Y., Ho, L. C., Impey, C. D., & Rix, H.-W. 2010, AJ, 139, 2097 [NASA ADS] [CrossRef] [Google Scholar]
- Pilkington, K., Few, C. G., Gibson, B. K., et al. 2012, A&A, 540, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pilyugin, L. S., & Grebel, E. K. 2016, MNRAS, 457, 3678 [NASA ADS] [CrossRef] [Google Scholar]
- Pilyugin, L. S., Grebel, E. K., & Kniazev, A. Y. 2014a, AJ, 147, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Pilyugin, L. S., Grebel, E. K., Zinchenko, I. A., & Kniazev, A. Y. 2014b, AJ, 148, 134 [NASA ADS] [CrossRef] [Google Scholar]
- Pilyugin, L. S., Grebel, E. K., Zinchenko, I. A., Nefedyev, Y. A., & Vílchez, J. M. 2017, A&A, 608, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pilyugin, L. S., Grebel, E. K., Zinchenko, I. A., et al. 2018, A&A, 613, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Prantzos, N., & Boissier, S. 2000, MNRAS, 313, 338 [NASA ADS] [CrossRef] [Google Scholar]
- Rich, J. A., Torrey, P., Kewley, L. J., Dopita, M. A., & Rupke, D. S. N. 2012, ApJ, 753, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Rosales-Ortega, F. F., Díaz, A. I., Kennicutt, R. C., & Sánchez, S. F. 2011, MNRAS, 415, 2439 [NASA ADS] [CrossRef] [Google Scholar]
- Roy, J. R. 1996, in IAU Colloq. 157: Barred Galaxies, eds. R. Buta, D. A. Crocker, & B. G. Elmegreen, ASP Conf. Ser., 91, 63 [NASA ADS] [Google Scholar]
- Ruiz-Lara, T., Pérez, I., Florido, E., et al. 2017, A&A, 604, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ryder, S. D. 1995, ApJ, 444, 610 [NASA ADS] [CrossRef] [Google Scholar]
- Saha, K., & Naab, T. 2013, MNRAS, 434, 1287 [NASA ADS] [CrossRef] [Google Scholar]
- Sakhibov, F., Zinchenko, I. A., Pilyugin, L. S., et al. 2018, MNRAS, 474, 1657 [Google Scholar]
- Sánchez, S. F., Kennicutt, R. C., Gil de Paz, A., et al. 2012, A&A, 538, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sánchez, S. F., Rosales-Ortega, F. F., Iglesias-Páramo, J., et al. 2014, A&A, 563, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sánchez, S. F., García-Benito, R., Zibetti, S., et al. 2016, A&A, 594, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sánchez-Blázquez, P., Rosales-Ortega, F. F., Méndez-Abreu, J., et al. 2014, A&A, 570, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sánchez-Menguiano, L., Sánchez, S. F., Pérez, I., et al. 2016, A&A, 587, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sánchez-Menguiano, L., Sánchez, S. F., Pérez, I., et al. 2017, A&A, 603, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sánchez-Menguiano, L., Sánchez, S. F., Pérez, I., et al. 2018, A&A, 609, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schlafly, E. F., & Finkbeiner, D. P. 2011, ApJ, 737, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Schönrich, R., & Binney, J. 2009, MNRAS, 396, 203 [NASA ADS] [CrossRef] [Google Scholar]
- Searle, L. 1971, ApJ, 168, 327 [NASA ADS] [CrossRef] [Google Scholar]
- Sellwood, J. A., & Binney, J. J. 2002, MNRAS, 336, 785 [NASA ADS] [CrossRef] [Google Scholar]
- Shields, G. A., & Searle, L. 1978, ApJ, 222, 821 [NASA ADS] [CrossRef] [Google Scholar]
- Storey, P. J., & Zeippen, C. J. 2000, MNRAS, 312, 813 [Google Scholar]
- Thuan, T. X., Pilyugin, L. S., & Zinchenko, I. A. 2010, ApJ, 712, 1029 [NASA ADS] [CrossRef] [Google Scholar]
- Tissera, P. B., Pedrosa, S. E., Sillero, E., & Vilchez, J. M. 2016, MNRAS, 456, 2982 [NASA ADS] [CrossRef] [Google Scholar]
- Tremonti, C. A., Heckman, T. M., Kauffmann, G., et al. 2004, ApJ, 613, 898 [NASA ADS] [CrossRef] [Google Scholar]
- Vila-Costas, M. B., & Edmunds, M. G. 1992, MNRAS, 259, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Walcher, C. J., Wisotzki, L., Bekeraité, S., et al. 2014, A&A, 569, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Werk, J. K., Putman, M. E., Meurer, G. R., & Santiago-Figueroa, N. 2011, ApJ, 735, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, P.-F., Kudritzki, R.-P., Tully, R. B., & Neill, J. D. 2015, ApJ, 810, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Zaritsky, D., Kennicutt, Jr., R. C., & Huchra, J. P. 1994, ApJ, 420, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Zinchenko, I. A., Kniazev, A. Y., Grebel, E. K., & Pilyugin, L. S. 2015, A&A, 582, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zinchenko, I. A., Pilyugin, L. S., Grebel, E. K., Sánchez, S. F., & Vílchez, J. M. 2016, MNRAS, 462, 2715 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1. Comparison of stellar mass and optical radius R25 for our sample of galaxies. Unbarred (A), barred (B), and intermediate (AB) galaxies are shown with different colors and symbols. |
| In the text | |
 |
Fig. 2. Oxygen abundance gradient for NGC 257. Circles represent the oxygen abundance in the individual spaxels. Vertical dashed lines represent 0.25 and 1.0 fraction of optical radius R25. The black solid line shows the best fit to all the data. Dashed red lines correspond to the best fit of the oxygen abundance gradient in the inner (R < 0.25R25) and outer (0.25R25 < R < R25) parts of the galaxy. The typical uncertainty of the oxygen abundance determination for the single spaxel is presented in the top right corner. |
| In the text | |
 |
Fig. 3. Stellar mass – oxygen abundance gradient diagrams for the abundance gradient scaled to kpc (left columns) and R25 (right columns). Top panels: oxygen abundance gradient for galactocentric distances r < R25. Middle panels: oxygen abundance gradient for r < 0.25R25. Bottom panels: oxygen abundance gradient for 0.25 < r < R25. Unbarred (A), barred (B), and intermediate (AB) galaxies are shown with different colors and symbols. Black dashed lines are the best fit for the subsample of unbarred galaxies, and red lines show this for the barred galaxies. Shaded areas represent the 1σ uncertainties of the fit. |
| In the text | |
 |
Fig. 4. Diagrams showing the A2 Fourier coefficient – oxygen abundance gradient for the abundance gradient scaled to kpc (left columns) and R25 (right columns). Top panels: oxygen abundance gradient for galactocentric distances r < R25. Middle panels: oxygen abundance gradient for r < 0.25R25. Bottom panels: oxygen abundance gradient for 0.25 < r < R25. |
| In the text | |
 |
Fig. 5. Probability distribution function for the cR25, cg − r, cΣ, and cA2 coefficients of the generalized mass–metallicity relation in the center of galaxies (top panels), at R = 0.5R25 (middle panels), and R = R25 (bottom panels). The solid vertical line represents the zero value for each coefficient, and the dashed lines show the two-sided 95% confidence interval. |
| In the text | |
 |
Fig. 6. Probability distribution function for the c1 (left column) and c2 (middle column) coefficients of the generalized mass–metallicity relation in the center of galaxies (top panels), at R = 0.5R25 (middle panels), and R = R25 (bottom panels). The solid vertical line represents the zero value for each coefficient. The right column represents the correlation between the c1 and c2 coefficients. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.