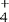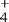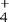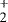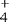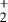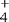| Issue |
A&A
Volume 623, March 2019
|
|
|---|---|---|
| Article Number | A18 | |
| Number of page(s) | 10 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201833761 | |
| Published online | 26 February 2019 | |
Monte Carlo calculations of the atmospheric sputtering yields on Titan
1
Space Science Institute, Macau University of Science and Technology,
Macau,
PR China
2
School of Atmospheric Sciences, Sun Yat-sen University,
Zhuhai,
Guangdong,
PR China
e-mail: cuijun7@mail.sysu.edu.cn
3
CAS Key Laboratory of Lunar and Deep Space Exploration, Chinese Academy of Sciences,
Beijing,
PR China
4
CAS Center for Excellence in Comparative Planetology, Chinese Academy of Sciences,
Hefei,
Anhui,
PR China
5
Mullard Space Science Laboratory, University College London,
Dorking,
UK
6
The Centre for Planetary Sciences at University College London/Birkbeck,
London,
UK
7
Department of Earth Sciences, National Taiwan Normal University,
Taipei,
Taiwan
Received:
3
July
2018
Accepted:
6
December
2018
Context. Sputtering serves as an important mechanism of atmospheric escape in the solar system.
Aims. This study is devoted to atmospheric sputtering on Titan, with a special focus on how the N2 and CH4 sputtering yields respond to varying ion incidence energy and angle, and varying ion mass.
Methods. A Monte Carlo model was constructed to track the energy degradation of incident ions and atmospheric recoils from which the sputtering yields were obtained. A large number of model runs were performed, taking into account three categories of incident ion with representative masses of 1, 16, and 28 Da, as well as two collision models both characterized by a strongly forward scattering angle distribution, but different in terms of the inclusion or exclusion of electronic excitation of ambient neutrals.
Results. Our model calculations reveal substantial increases in both the N2 and CH4 sputtering yields with increasing ion incidence energy and angle, and increasing ion mass. The energy distribution of escaping molecules is described reasonably well by a power law, with an enhanced high energy tail for more energetic incident ions and less massive atmospheric recoils. The CH4-to-N2 sputtering yield ratio is found to range from 10 to 20%, increasing with increasing incidence angle and also increasing with decreasing incidence energy. An approximate treatment of ion impact chemistry is also included in our model, predicting N2 sputtering yields on Titan that are in broad agreement with previous results.
Key words: planets and satellites: individual: Titan / planets and satellites: atmospheres
© ESO 2019
1 Introduction
Ambient plasma precipitating on the upper atmosphere of a planetary body induces a cascade of energy and momentum transfer events, a process usually referred to as atmospheric sputtering (Johnson 1994). The sputtered neutrals, when moving in the right direction, populate the region above the exobase of the parent body and lead to the expansion of the planetary corona; a significant portion of these sputtered neutrals have sufficient energy to overcome the gravitational potential and are lost to the interplanetary space. In general, sputtering serves as an important mechanism of atmospheric escape in the solar system (Johnson et al. 2008).
Atmospheric sputtering on Titan, the largest satellite of Saturn, is especially interesting because of its thick and permanent atmosphere primarily composed of N2 and CH4, and also because of its rich and complicated plasma environment which contains solar wind ions, magnetospheric ions, and locally produced pickup ions. Pre-Cassini model calculations predict a characteristic sputter-induced N2 escape rate of ~1024–1025 s−1 on Titan (Lammer & Bauer 1993; Shematovich et al. 2001, 2003; Michael et al. 2005). For comparison, the thermally driven escape rates were derived to be ~1028 s−1 for H2 and ~1027 for CH4 (Yelle et al. 2008; Strobel 2009; Cui et al. 2008, 2011, 2012), although the latter result is still under debate (Tucker & Johnson 2009; Bell et al. 2010, 2011; Schaufelberger et al. 2012). Meanwhile, the chemically driven non-thermal escape rates for both N2 and CH4 were predicted to be ~1024–1025 s−1 (Cravens et al. 1997; De La Haye et al. 2007). With the accumulation of the Cassini neutral and plasma data over the past decade, it is timely to perform a state-of-the-art evaluation of the sputter-induced N2 and CH4 escape rateson Titan. This would be useful for a rigorous determination of the relative importance of different escape mechanisms, and how the relative importance varies across Titan’s exobase and along Titan’s orbit around Saturn.
The crucial parameter for evaluating sputter-induced escape is the sputtering yield, defined as the average number of escaping atmospheric molecules produced per incident ion (Johnson 1994). Because of the random nature of ion-neutral collisions and the potentially large number of atmospheric recoils involved, the best approach for evaluating sputtering yields is via Monte Carlo calculations, which were also implemented in the early studies of sputter-induced escape on Titan (Shematovich et al. 2001, 2003; Michael et al. 2005). Before the escape rates could be calculated rigorously, the information on the variations of sputtering yields with the condition of ion incidence should be firmly established.
In the present study, a Monte Carlo model is developed to investigate both the N2 and CH4 sputtering yields on Titan, with a special emphasis placed on the dependence of the sputtering yields on the condition of ion incidence. The layout of the paper is as follows. The model setup including background neutral atmosphere, incident ion sources, and collision parameterization is described in detail in Sect. 2. The variations ofthe sputtering yields with the ion incidence energy and angle are presented in Sect. 3. In Sect. 4 we focus on the energy distributions of escaping molecules and how these distributions change in response to the varying condition of ion incidence. Discussions are presented in Sect. 5, where we compare our modeling results with those from previous works; we also evaluate the effect of the uncertainty in elastic scattering cross section. Finally, we end with concluding remarks in Sect. 6.
2 Model description
A test particle Monte Carlo model was constructed to simulate the energy degradation of incident ions and atmospheric recoils in Titan’s atmosphere. The background atmosphere, assumed to be plane parallel, was adopted from Strobel (2012) over the altitude range of 880–2000 km above Titan’s surface. The most abundant species of Titan’s atmosphere is N2, which has a mixing ratio of more than 98% at 880 km, but CH4 becomes increasingly important due to diffusive separation, starting to dominate over N2 at around 1800 km. Another important species, H2, is ignored here because H2 escape is known to be thermally driven (e.g., Cui et al. 2008; Tucker et al. 2013). Below 880 km, the mean free path for collision is sufficiently short that the energy of a typical atmospheric molecule is degraded rapidly to the local thermal energy over a length scale not exceeding 0.5 km, a situation consistent with local thermalization. At 2000 km, the collision probability drops to ~ 0.1%, and therefore Titan’s atmosphere above this altitude is not expected to have an appreciable influence on the derived sputtering yields. Both the horizontal variation of Titan’s atmosphere and its variation with Saturn local time are ignored since these variations are of minor importance compared to the variations in ion precipitation.
Recent Cassini measurements made with a number of instruments have revealed an extremely complicated plasma environment in the vicinity of Titan including both magnetospheric ions and pickup ions (e.g., Hartle et al. 2006; Szego et al. 2007; Sittler et al. 2010; Regoli et al. 2016a). It has been found that the major ion components of Saturn’s magnetosphere near Titan are H+, H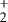 , and O+, whereas the major pickup ion components are H+, H
, and O+, whereas the major pickup ion components are H+, H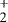 , N+ /CH
, N+ /CH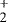 , CH
, CH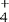 , and N
, and N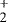 . In reality, heavy magnetospheric ions are more likely a combination of O+, OH+, and H2 O+, presumably contributed by H2O escape from Enceladus and other icy satellites (Jurac & Richardson 2005). Instead, heavy pickup ions are more likely dominated by HCNH+ and C2 H
. In reality, heavy magnetospheric ions are more likely a combination of O+, OH+, and H2 O+, presumably contributed by H2O escape from Enceladus and other icy satellites (Jurac & Richardson 2005). Instead, heavy pickup ions are more likely dominated by HCNH+ and C2 H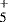 , the two most abundant species of Titan’s ionosphere (Cravens et al. 2005; Cui et al. 2009). These facts, however, should not greatly affect the numerical results presented here since our Monte Carlo calculations involve mass- and velocity-dependent collision processes only (see below). For simplicity, we grouped various incident ion components into three categories, one for low mass ions taking H+ as a proxy, another for intermediate mass ions taking CH
, the two most abundant species of Titan’s ionosphere (Cravens et al. 2005; Cui et al. 2009). These facts, however, should not greatly affect the numerical results presented here since our Monte Carlo calculations involve mass- and velocity-dependent collision processes only (see below). For simplicity, we grouped various incident ion components into three categories, one for low mass ions taking H+ as a proxy, another for intermediate mass ions taking CH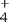 as a proxy, and a third for high mass ions taking N
as a proxy, and a third for high mass ions taking N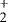 as a proxy. This categorization essentially incorporates the entire range of ions that are potentially important for atmospheric sputtering on Titan.
as a proxy. This categorization essentially incorporates the entire range of ions that are potentially important for atmospheric sputtering on Titan.
The collision model for elastic scattering is based on the Ziegler-Biersak-Littmark (ZBL) approximation (Ziegler & Biersack 1985), frequently used to parameterize the interaction potential between energetic incident ions and atmospheric neutrals at a minimum incidence energy of 10 eV (Johnson et al. 2000). The differential scattering cross section (DSCS) calculated numerically from the ZBL interaction potential is shown schematically in Fig. 1 for an incident CH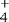 ion scattered by a target N2 molecule. The situations for three incidence energies are indicated. According to the figure, all DSCSs are beam-like and prefer forward scattering, and this trend increases with increasing ion incidence energy. The forward-to-backward scattering ratio is known to have an important influence on the simulated energy degradation process (Kallio & Barabash 2000).
ion scattered by a target N2 molecule. The situations for three incidence energies are indicated. According to the figure, all DSCSs are beam-like and prefer forward scattering, and this trend increases with increasing ion incidence energy. The forward-to-backward scattering ratio is known to have an important influence on the simulated energy degradation process (Kallio & Barabash 2000).
For a more sophisticated model, inelastic collisions such as electronic excitations are included along with the ZBL approximation for interaction potential. This was implemented via the formulism of Firsov (1959), which is only applicable at relative velocities much lower than the Bohr velocity. The Bohr velocities correspond to 23, 370, and 640 keV for the three categories of incident ions. For an incident CH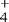 ion scattered by a target N2 molecule at an energy of 10 keV, the Firsov formulism predicts an energy loss of ~ 100 eV via inelasticprocesses at an impact distance of half of the Bohr radius, and this loss declines rapidly to ~ 3 eV at an impact distance of twice the Bohr radius. This model is called ZBL+Firsov in the rest of the paper. In contrast to some of the early studies (e.g., Michael et al. 2005), all chemical processes, such as ion impact ionization, dissociation, and charge exchange, are ignored for the moment, but a crude evaluation of the influence of these inelastic processes is presented in Sect. 5, where we compare our derived sputtering yields with previous results.
ion scattered by a target N2 molecule at an energy of 10 keV, the Firsov formulism predicts an energy loss of ~ 100 eV via inelasticprocesses at an impact distance of half of the Bohr radius, and this loss declines rapidly to ~ 3 eV at an impact distance of twice the Bohr radius. This model is called ZBL+Firsov in the rest of the paper. In contrast to some of the early studies (e.g., Michael et al. 2005), all chemical processes, such as ion impact ionization, dissociation, and charge exchange, are ignored for the moment, but a crude evaluation of the influence of these inelastic processes is presented in Sect. 5, where we compare our derived sputtering yields with previous results.
An ion at a given incidence energy is assumed to impact Titan’s upper atmosphere from above at a given direction of incidence. Following Johnson et al. (2000), a random number uniformly distributed between 0 and 1 was generated to determine the location of the next collision within the simulation box, according to
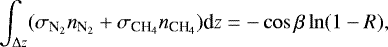 (1)
(1)
where 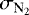 and
and 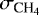 are the total cross sections for the elastic scattering of the incident ion by background N2 and CH4 molecules,
are the total cross sections for the elastic scattering of the incident ion by background N2 and CH4 molecules, 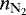 and
and 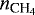 are the number densities in the ambient atmosphere, β is the anglebetween the ion velocity and the vertically downward direction, R is the random number, and Δz is the vertical length scale over which the integration is performed. Next, a second random number was generated to assign the collision target to either N2 or CH4 based on the ratio between the total cross sections of the two species. The relative velocity between the two colliding partners for determining the appropriate cross section is assumed to be identical to the velocity of the incident ion ignoring the random thermal velocity of the ambient neutral. This is a fair assumption as the incident ion was traced in our calculations to a lower limit energy (see below) well above the characteristic thermal energy of the ambient neutrals, typically at the level of 0.01 eV (e.g., Westlake et al. 2011; Snowden et al. 2013). The bulk wind velocity in the background atmosphere is even smaller than the thermal velocity (e.g., Müller-Wodarg et al. 2008) and can be safely ignored. Finally, a third random number was generated to determine the scattering angle following the angular distribution of ZBL cross section at the known ion incidence energy. This type of random sampling deserves some special caution due to the strong variation in DSCS at small incidence angles as depicted in Fig. 1. Analogous to Kallio & Barabash (2000), here the numerically obtained DSCS as a function of the scattering angle, θ, for a given incidence energy was fit empirically with a power law relation, and the random sampling could then be formulated as
are the number densities in the ambient atmosphere, β is the anglebetween the ion velocity and the vertically downward direction, R is the random number, and Δz is the vertical length scale over which the integration is performed. Next, a second random number was generated to assign the collision target to either N2 or CH4 based on the ratio between the total cross sections of the two species. The relative velocity between the two colliding partners for determining the appropriate cross section is assumed to be identical to the velocity of the incident ion ignoring the random thermal velocity of the ambient neutral. This is a fair assumption as the incident ion was traced in our calculations to a lower limit energy (see below) well above the characteristic thermal energy of the ambient neutrals, typically at the level of 0.01 eV (e.g., Westlake et al. 2011; Snowden et al. 2013). The bulk wind velocity in the background atmosphere is even smaller than the thermal velocity (e.g., Müller-Wodarg et al. 2008) and can be safely ignored. Finally, a third random number was generated to determine the scattering angle following the angular distribution of ZBL cross section at the known ion incidence energy. This type of random sampling deserves some special caution due to the strong variation in DSCS at small incidence angles as depicted in Fig. 1. Analogous to Kallio & Barabash (2000), here the numerically obtained DSCS as a function of the scattering angle, θ, for a given incidence energy was fit empirically with a power law relation, and the random sampling could then be formulated as
![\begin{equation*}\theta=[R(\theta_{\textrm{max}}^{\alpha}-\theta_{\textrm{min}}^{\alpha})+\theta_{\textrm{min}}^{\alpha}]^{1/\alpha}, \end{equation*}](/articles/aa/full_html/2019/03/aa33761-18/aa33761-18-eq16.png) (2)
(2)
where R is a random number uniformly distributed between 0 and 1, α is a constant exponent characterizing the best-fit power law relation and depending on the incidence energy. For an incidence energy of 1 keV, α is found to be − 1.4, which is fairly close to the exponent of − 1.5 for a similar power law fit to the forward scattering model of Kallio & Barabash (2000). In Eq. (2), the maximum scattering angle, θmax, is 180°, whereas the minimum scattering angle, θmin, is taken to be 1° to avoid an infinitely large cross section as the scattering angle approaches zero (Noël & Prölss 1993). The post-collision velocities of the colliding partners were then easily obtained with the aid of the momentum and energy conservation laws. For the ZBL+Firsov model, the inelastic energy loss was subtracted prior to each collision.
The procedure outlined above was repeated until the energy of an incident ion falls below the local escape energy along its energy degradation process, at which point it does not make a further contribution to escape. The ion is assumed to be fully thermalized, and thus no longer traced in the model, once it reaches the lower boundary ofour simulation box. As the ion reaches the upper boundary, it is assumed to be either reflected downward elastically or lost from Titan, provided that its energy is below or above the local escape energy, respectively. All N2 and CH4 recoils produced during the cascade of collisions were treated in the same way as the incident ion.
To evaluate the variations of the N2 and CH4 sputtering yields with different conditions of ion incidence, we considered a sequence of model runs, each characterized by a unique combination of ion incidence energy and angle. The incidence energy grid contains 21 energy levels logarithmically distributed from 10 to 100 keV, and for each energy level 14 incidence angles were pre-selected from 0° (normal incidence) to 85° with an interval of 10° below 40° and 5° above to characterize more accurately the rapid change in sputtering yield for conditions with large incidence angles (Johnson et al. 2000). The above scheme of parameterization, which characterizes nearly the full range of energetic particles accessible to the top of Titan’s atmosphere (e.g., Regoli et al. 2016b), yields a total number of 294 model runs for each category of incident ion.
The number of incident ions included in each model run varies logarithmically from 7940 for N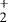 , 11 700 for CH
, 11 700 for CH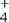 , and 23 300 for H+ at the lowest energy of 10 eV, to 200 for N
, and 23 300 for H+ at the lowest energy of 10 eV, to 200 for N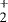 , 350 for CH
, 350 for CH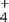 , and 600 for H+ at the highest energy of 100 keV. With such a choice, the total number of escaping CH4 molecules from Titan’s upper atmosphere remains above 400 under normal incidence for which the sputtering yield is expected to be minimized (Johnson et al. 2000), ensuring that statistically robust results with a typical uncertainty of no more than 5% be achieved for all model runs. The number of escaping N2 molecules should be substantially larger since the N2 column density is more than a factor of 3 higher than the CH4 column density above Titan’s exobase (De La Haye et al. 2007; Jiang et al. 2017).
, and 600 for H+ at the highest energy of 100 keV. With such a choice, the total number of escaping CH4 molecules from Titan’s upper atmosphere remains above 400 under normal incidence for which the sputtering yield is expected to be minimized (Johnson et al. 2000), ensuring that statistically robust results with a typical uncertainty of no more than 5% be achieved for all model runs. The number of escaping N2 molecules should be substantially larger since the N2 column density is more than a factor of 3 higher than the CH4 column density above Titan’s exobase (De La Haye et al. 2007; Jiang et al. 2017).
For illustrative purposes, we show in Fig. 2 several random examples for the stepwise trajectories of incident CH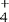 ions within Titan’s upper atmosphere, all starting at an energy of 50 keV under normal incidence. Three different cases are indicated in the upper panel. For each incident ion, the portion of its trajectory between two consecutive collisions is displayed as the projection to the local plane formed by the vertical direction and the direction of ion velocity, with the x-axis aligned with the projected ion trajectory on the horizontal plane.
ions within Titan’s upper atmosphere, all starting at an energy of 50 keV under normal incidence. Three different cases are indicated in the upper panel. For each incident ion, the portion of its trajectory between two consecutive collisions is displayed as the projection to the local plane formed by the vertical direction and the direction of ion velocity, with the x-axis aligned with the projected ion trajectory on the horizontal plane.
Our model calculations indicate that some of the incident ions are backscattered and escape at the top of the atmosphere. For the condition of incidence shown in Fig. 2, the backscattered CH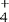 ions typically undergo 20 collisions before they leave the top of the simulation box.
ions typically undergo 20 collisions before they leave the top of the simulation box.
Throughout our calculations, the effect of the background magnetic field, typically at the level of several nT (e.g., Backes et al. 2005; Bertucci et al. 2008, 2009), is ignored for simplicity since the gyroradii of the incident ions could be estimated to exceed substantially their mean free paths due to elastic scattering by ambient neutrals. Taking incident CH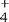 as an example, the mean free path ranges from 110 to 6500 km over the full incidence energy range of 10 to 100 keV, where we use for illustrative purposes a background N2 density of 1.7 × 107 cm−3 at 1500 km (Strobel 2012). For comparison, the CH
as an example, the mean free path ranges from 110 to 6500 km over the full incidence energy range of 10 to 100 keV, where we use for illustrative purposes a background N2 density of 1.7 × 107 cm−3 at 1500 km (Strobel 2012). For comparison, the CH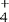 gyroradius is typically a factor of 5 larger, suggesting that the effect of ion gyromotion is of minor importance here. In addition, we note that the effect of the background magnetic field has not been included in previous modelings of Titan’s atmospheric sputtering (e.g., Shematovich et al. 2001, 2003; Michael et al. 2005), and a similar approximation adopted here facilitates a comparison of the derived sputtering yields between different studies in terms of the differentchoices of collision parameterization and of background atmosphere (see Sect. 5 for details).
gyroradius is typically a factor of 5 larger, suggesting that the effect of ion gyromotion is of minor importance here. In addition, we note that the effect of the background magnetic field has not been included in previous modelings of Titan’s atmospheric sputtering (e.g., Shematovich et al. 2001, 2003; Michael et al. 2005), and a similar approximation adopted here facilitates a comparison of the derived sputtering yields between different studies in terms of the differentchoices of collision parameterization and of background atmosphere (see Sect. 5 for details).
 |
Fig. 1 Differential scattering cross section calculated numerically from the ZBL interaction potential (Ziegler & Biersack 1985) for an incident CH |
 |
Fig. 2 Several random examples for the stepwise trajectories of incident CH |
3 Sputtering yields
We show in Fig. 3 the N2 and CH4 sputtering yields as a function of the incidence energy of the three categories of incident ions, all assuming normal incidence. The two different collision models, ZBL and ZBL+Firsov, are compared. Several interesting features are immediately seen in the figure. First, both the N2 and CH4 sputtering yields increase steadily with the increasing energy of incident ions, which is a natural result of the fact that more energetic ions tend to produce more atmospheric recoils along their energy degradation processes. Second, the sputtering yields increase with the ion mass, maximized for N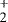 and minimized for H+, and this is explained by more efficient momentum transfer to atmospheric recoils for heavier incident ions. Third, the sputtering yields for ZBL are enhanced over ZBL+Firsov due to the extra energy spent in electronic excitation, but such an enhancement is suppressed for low energy incident ions because they are not able to excite atmospheric neutrals electronically.
and minimized for H+, and this is explained by more efficient momentum transfer to atmospheric recoils for heavier incident ions. Third, the sputtering yields for ZBL are enhanced over ZBL+Firsov due to the extra energy spent in electronic excitation, but such an enhancement is suppressed for low energy incident ions because they are not able to excite atmospheric neutrals electronically.
In Fig. 4 we show the sputtering yields as a function of the ion incidence angle for three representative incidence energies: 100 eV, 1 keV, and 10 keV. The curves for N2 and CH4 are displayed separately. Different collision models and different categories of incident ions give very similar variations, and only the ZBL+Firsov results for incident CH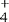 are presented. The figure shows clearly the expected tendency of enhanced sputtering yield at large incidence angles. This is easily interpreted by the fact that for a more slanted direction of ion incidence, the ion trajectories and the trajectories of atmospheric recoils tend to be restricted to the upper regions of Titan’s atmosphere where the density is lower and the probably for escape is higher.
are presented. The figure shows clearly the expected tendency of enhanced sputtering yield at large incidence angles. This is easily interpreted by the fact that for a more slanted direction of ion incidence, the ion trajectories and the trajectories of atmospheric recoils tend to be restricted to the upper regions of Titan’s atmosphere where the density is lower and the probably for escape is higher.
Two additional features can be seen in Fig. 4. First, the CH4 sputtering yield shows a more pronounced variation with incidence angle than the N2 sputtering yield, likely connected tothe increase in CH4 mixing ratiowith increasing altitude. Second, the variation of sputtering yield with incidence angle tends to be less pronounced for more energetic incident ions, which could be interpreted by the penetration of these ions into the deeper and denser regions of Titan’s atmosphere where escape is suppressed. To be more specific, we find that for an incident CH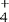 ion at 100 eV the N2 sputtering yield increases by a factor of 5.7 from normal incidence to a large incidence angle of 80°, whereas the CH4 sputtering yield increases by a factor of 7.4. Similarly, the N2 and CH4 sputtering yields increase by 5.2 and 6.8 over the same range of incidence angle, but for a more energetic incident CH
ion at 100 eV the N2 sputtering yield increases by a factor of 5.7 from normal incidence to a large incidence angle of 80°, whereas the CH4 sputtering yield increases by a factor of 7.4. Similarly, the N2 and CH4 sputtering yields increase by 5.2 and 6.8 over the same range of incidence angle, but for a more energetic incident CH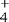 ion at 10 keV.
ion at 10 keV.
The sputtering of CH4 by incident ions is not included in previous modeling efforts (e.g., Shematovich et al. 2001, 2003; Michael et al. 2005). As stated in Sect. 1, the issue of CH4 escape on Titan is still under debate and it is crucial to carefully evaluate the relative contributions from a range of escaping mechanisms including atmospheric sputtering studied here (e.g., De La Haye et al. 2007; Yelle et al. 2008; Strobel 2009; Tucker & Johnson 2009; Bell et al. 2010, 2011; Cui et al. 2012; Schaufelberger et al. 2012; Jiang et al. 2017). For illustrative purposes, we show in Fig. 5 the ratio of the CH4 to the N2 sputtering yields as a function of the ion incidence energy, for normal incidence and for an incidence angle of 55°. The ZBL approximation is adopted for all the displayed model runs, and the incident ions are taken to be N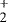 . The figure suggests reduced relative importance of CH4 sputtering at high incidence energies and small incidence angles, explained by a lower CH4 mixing ratio within the deeper regions of Titan’s atmosphere that are accessible by more energetic incident ions or ions with a more vertical direction of incidence. For comparison, the CH4 to N2 number density ratio is ~0.2 near the exobase (e.g., De La Haye et al. 2007; Jiang et al. 2017).
. The figure suggests reduced relative importance of CH4 sputtering at high incidence energies and small incidence angles, explained by a lower CH4 mixing ratio within the deeper regions of Titan’s atmosphere that are accessible by more energetic incident ions or ions with a more vertical direction of incidence. For comparison, the CH4 to N2 number density ratio is ~0.2 near the exobase (e.g., De La Haye et al. 2007; Jiang et al. 2017).
4 Energy and angular distributions of escaping molecules
It is instructive to investigate the energy distributions of escaping N2 and CH4 molecules and how they respond to the varying conditions of ion incidence. We focus here on the ZBL models for incident CH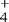 . A sequence of examples are compared in Fig. 6 for three different incidence energies of 100 eV, 1 keV, and 10 keV, but all assuming normal incidence. The energy distributions of escaping N2 and CH4 molecules are shown separately in the left and right panels, respectively. Since only escaping molecules were traced throughout our Monte Carlo calculations, each energy distribution shown in the figure starts, at the low energy end, from the local escape energies of 0.57 eV for N2 and 0.33 eV for CH4 referred to an altitude of 2000 km. In each panel, the probability distribution of escaping molecules declines almost monotonically with increasing energy, which is reasonably characterized by a power law as indicated by the thick solid line. The power law trend extends all the way from the local escape energy to a turnoff energy above which the distribution declines rapidly to zero. Such a rapid decline is essential to ensure that a finite number of escaping molecules are achieved for each model run. We note that for the highest energy bins displayed in Fig. 6, the uncertainty in energy distribution is relatively poor due to the small sample. For incident CH
. A sequence of examples are compared in Fig. 6 for three different incidence energies of 100 eV, 1 keV, and 10 keV, but all assuming normal incidence. The energy distributions of escaping N2 and CH4 molecules are shown separately in the left and right panels, respectively. Since only escaping molecules were traced throughout our Monte Carlo calculations, each energy distribution shown in the figure starts, at the low energy end, from the local escape energies of 0.57 eV for N2 and 0.33 eV for CH4 referred to an altitude of 2000 km. In each panel, the probability distribution of escaping molecules declines almost monotonically with increasing energy, which is reasonably characterized by a power law as indicated by the thick solid line. The power law trend extends all the way from the local escape energy to a turnoff energy above which the distribution declines rapidly to zero. Such a rapid decline is essential to ensure that a finite number of escaping molecules are achieved for each model run. We note that for the highest energy bins displayed in Fig. 6, the uncertainty in energy distribution is relatively poor due to the small sample. For incident CH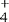 at 10 keV, the numbers of escaping CH4 molecules inthe last two energy bins are as small as 16 and 11, implying fairly large uncertainties of 25 and 30%, respectively. This perhaps accounts for the apparent absence of a clear turnoff in the respective CH4 energy distribution shown in the bottom right panel of Fig. 6.
at 10 keV, the numbers of escaping CH4 molecules inthe last two energy bins are as small as 16 and 11, implying fairly large uncertainties of 25 and 30%, respectively. This perhaps accounts for the apparent absence of a clear turnoff in the respective CH4 energy distribution shown in the bottom right panel of Fig. 6.
Figure 6 also reveals that the best-fit power index is less negative for a larger incidence energy, and also less negative for escaping CH4 than for escaping N2. These are expected results since the high energy tail of the distribution of escaping molecules tends to be more easily populated for cases with more efficient momentum transfer from the incident plasma flow to the ambient atmosphere, either when the ion projectiles are more energetic or when the neutral recoils are less massive. This trend is more clearly seen in Fig. 7 where the best-fit power index is plotted against the incidence energy for escaping N2 and for escaping CH4. The power index varies nearly monotonically from − 1.9 to − 0.4 over the incidence energy range from 10 eV to 100 keV for N2, and from − 0.9 to − 0.3 over the same incidence energy range for CH4, both assuming normal incidence. For comparison, the energy distribution of sputtered atmospheric recoils was proposed to roughly follow a power law trend with apower index of − 2 (Smith et al. 2004), but our numerical results indicate that such a power law only characterizes escaping N2 molecules with a very low incidence energy around 10 eV. For the typical range of ion incidence energy encountered in the vicinity of Titan (e.g., Dialynas et al. 2009; Thomsen et al. 2010; Garnier et al. 2010; Regoli et al. 2016a; Wilson et al. 2017), a less steeply declining energy distribution is expected for escaping molecules, with a power index of around − 0.6 for N2 and − 0.3 for CH4.
Similar variations in the energy distribution of escaping molecules could be observed in terms of the incidence angle, as demonstrated in Fig. 8 with the same drawing convention of Fig. 6 but for two representative incidence angles of 20° and 60°, both assuming an incidence energy of 1 keV. The distributions of escaping N2 and CH4 are shown separately in the left and right panels, respectively. The figure reveals that a more slanted direction of ion incidence favors the population of escaping molecules at the high energy tail, characterized by a less negative power index, even though such a trend is less prominent than the trend with incidence energy. For reference, we show in Fig. 9 the best-fit power index as a function of the incidence angle for a common incidence energy of 1 keV, with the same drawing convention of Fig. 7.
Finally, we mention without showing the details that a comparison between different collision models and different categories of incident ions suggests a very similar energy distribution for each of the escaping species, N2 or CH4. The Monte Carlo calculations of Michael et al. (2005) also reveal no significant difference in the energy distribution of escaping N2 molecules between cases with N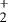 and N+ as incident ions (see their Fig. 1). However, following the above line of reasoning, we expect that the high energy tail of the N2 /CH4 distribution should be more easily populated by heavier incident ions due to more efficient momentum transfer to atmospheric recoils, thus leading to a less negative power exponent for incident N
and N+ as incident ions (see their Fig. 1). However, following the above line of reasoning, we expect that the high energy tail of the N2 /CH4 distribution should be more easily populated by heavier incident ions due to more efficient momentum transfer to atmospheric recoils, thus leading to a less negative power exponent for incident N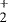 than for incident H+. This expected behavior appears too weak to be firmly established by our calculations.
than for incident H+. This expected behavior appears too weak to be firmly established by our calculations.
 |
Fig. 3 Variations in the N2
and CH4
sputtering yields with the ion incidence energy in Titan’s upper atmosphere based on our Monte Carlo calculations. Upper, middle, and lower panels: incident H+, CH |
 |
Fig. 4 Sputtering yield, normalized by the value obtained assuming normal incidence, as a function of the ion incidence angle, for three representative energies: 100 eV (squares), 1 keV (circles), and 10 keV (triangles). N2 and CH4
are displayed separately by the solid and open symbols, respectively. Different collision models and different categories of incident ions give very similar variations, and only the ZBL+Firsov results for incident CH |
 |
Fig. 5 Ratio of the CH4
to the N2
sputtering yields as a function of the ion incidence energy; shown are normal incidence (solid lines) and an incidence angle of 55°
(dashed lines). The ZBL approximation is adopted for all the displayed model runs, and the incident ions are taken to be N |
 |
Fig. 6 Several examples of the energy distribution of escaping molecules for three different incidence energies including 100 eV, 1 keV, and 10 keV, all assuming normal incidence. Distributions of escaping N2 and CH4 molecules are shown separately in the left and right panels, respectively. The probability distribution tends to decline near monotonically with increasing energy, which is reasonably well described by a power law as given by the thick solid line in each panel. Such a power law trend extends all the way from the local escape energy to a turnoff energy above which the distribution declines rapidly to zero. The best-fit power index is indicated in each panel for reference. |
 |
Fig. 7 The best-fit power index that characterizes the energy distribution of escaping molecules below the turnoff energy, triangles for escaping N2 and diamonds for escaping CH4. Normal incidence is assumed for all the displayed model runs. |
 |
Fig. 9 Best-fit power index characterizing the energy distribution of escaping molecules as a function of incidence angle below the turnoff energy for escaping N2 (triangles) and for escaping CH4 (diamonds). A common incidence energy of 1 keV is assumed for all the model runs shown. |
5 Discussion
To verify our modeling results, extensive comparisons were made with the results of Johnson et al. (2000), also based on Monte Carlo calculations but appropriate for a pure O atmosphere sputtered by incident O+ ions. For an incidence energy of 1 keV, Johnson et al. (2000) reported an O sputtering yield of 0.75, whereas we find an N2 sputtering yield of 3.3. Since both sputtering yields refer to the ZBL approximation and the condition of normal incidence, the difference between the two models must be connected to either the different escape energies, 0.57 eV in our model and 2 eV in the model of Johnson et al. (2000), or the different compositions of the background atmosphere, N2 in our model and O in theirs. The former is expected to be the dominant factor, as demonstrated by a test model run with the escape energy fixed at 2 eV giving an N2 sputtering yield of 0.9, now different from the Johnson et al. (2000) result by only 20%.
In terms of the trends of sputtering yield with the varying condition of ion incidence, a general consensus is reached between the two models in a qualitative manner, both predicting enhanced sputtering at high incidence energies and large incidence angles. However, quantitative differences are clearly present. For instance, Johnson et al. (2000) reported an increase in sputtering yield by a factor of 2.4 from 200 eV to 2 keV, whereas our model predicts a larger enhancement factor of 4.4, both assuming normal incidence. In contrast, the increase in sputtering yield for a common incidence energy of 1 keV is a factor of 3.2 from normal incidence to an incidence angle of 60° according to Johnson et al. (2000), which is close to the enhancement factor of 3.6 according to our calculations. Therefore, the variation of sputtering yield with incidence energy appears to be affected by the choice of the escape energy more substantially than the variation with incidence angle.
In their Monte Carlo modeling of atmospheric sputtering on Titan, Shematovich et al. (2001) considered N+ ions within Saturn’s magnetosphere near Titan, moving with a corotation energy of 2.9 keV and characterized by a number density of 0.2 cm−3. These values imply an incident N+ flux of 4 × 106 cm−2 s−1 at the top of Titan’s atmosphere from which they predicted a very low N2 escape flux of 3.2 × 105 cm−2 s−1 due to sputtering or equivalently an N2 sputtering yield of 0.08 only. This result led them to conclude that the total nitrogen escape on Titan is dominated by photodissociation (with an atomic N escape flux of 7 × 107 cm−2 s−1). For comparison, the N2 sputtering yield under the same condition of ion incidence and assuming ZBL interaction potential is 5.0 based on Fig. 3, revealing a difference of more than a factor of 60 between the two works.
One important factor that contributes to the above difference in sputtering yield is related to the chemical processes such as ion impact dissociation, ionization, and charge exchange, which are considered by Shematovich et al. (2001) but ignored here. For collisional dissociation of N2, the results of Johnson et al. (2002) below 1 keV are extrapolated to give a cross section of (0.4–1) × 10−16 cm2 for a range of impacting energetic particles, all at a representative incidence energy of 1.5 keV. The O+ −N2 charge exchange cross section is 2 × 10−16 cm2 at the same incidence energy adapted from Lindsay et al. (1998). The effect of ion impact ionization should be more prominent, as implied by a larger cross section of 8 × 10−16 cm2 at 1.5 keV for N2 ionization by impacting N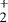 where the contributions from all ionization channels are summed (Luna et al. 2003). Comparing the above cross sections with the respective ZBL cross section of 1 × 10−15 cm2 at 1.5 keV, appropriate for the elastic scattering of both CH
where the contributions from all ionization channels are summed (Luna et al. 2003). Comparing the above cross sections with the respective ZBL cross section of 1 × 10−15 cm2 at 1.5 keV, appropriate for the elastic scattering of both CH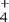 and N
and N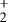 by N2, we adopted a simplified treatment of ion impact chemistry in that (1) ion impact dissociation is ignored as a first-order approximation, (2) ion impact ionization is included with a cross section equal to the respective ZBL cross section, and (3) charge exchange is included with the cross section of Lindsay et al. (1998) assumed to be valid for all charge exchange processes encountered here. For the second and third processes, a strongly forward scattering angle distribution was assumed (e.g., Lindsay et al. 1998). During ion impact ionization, the ionization energy of the ambient neutrals, N2 or CH4, was subtracted to ensure energy conservation, whereas during charge exchange, the incident ion was assumed to suffer negligible energy loss.
by N2, we adopted a simplified treatment of ion impact chemistry in that (1) ion impact dissociation is ignored as a first-order approximation, (2) ion impact ionization is included with a cross section equal to the respective ZBL cross section, and (3) charge exchange is included with the cross section of Lindsay et al. (1998) assumed to be valid for all charge exchange processes encountered here. For the second and third processes, a strongly forward scattering angle distribution was assumed (e.g., Lindsay et al. 1998). During ion impact ionization, the ionization energy of the ambient neutrals, N2 or CH4, was subtracted to ensure energy conservation, whereas during charge exchange, the incident ion was assumed to suffer negligible energy loss.
As expected, the inclusion of ion impact chemistry predicts substantially reduced N2 and CH4 sputtering yields compared to those presented in Sect. 3. This is mainly due to the removal of N2 /CH4 recoils from the simulation box as fragments such as N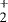 and N+, but also due to the extra energy loss accompanying ionization. The influence of charge exchange on the reduction of sputtering yield is of minor importance compared to the influence of ionization. For illustrative purposes, we show in Fig. 10 the ZBL+Firsov sputtering yields for incident CH
and N+, but also due to the extra energy loss accompanying ionization. The influence of charge exchange on the reduction of sputtering yield is of minor importance compared to the influence of ionization. For illustrative purposes, we show in Fig. 10 the ZBL+Firsov sputtering yields for incident CH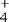 obtained with and without chemistry, both assuming normal incidence. Our calculations reveal that the N2 and CH4 sputtering yields are typically reduced by a factor of 4−7 over the full ranges of incidence energy and angle encountered here. Of special interest is a similar variation in sputtering yield found for the two models, with and without chemistry. This implies that the trends reported in Sect. 3 are probably robust irrespective of the detailed treatment of ion impact chemistry in the model.
obtained with and without chemistry, both assuming normal incidence. Our calculations reveal that the N2 and CH4 sputtering yields are typically reduced by a factor of 4−7 over the full ranges of incidence energy and angle encountered here. Of special interest is a similar variation in sputtering yield found for the two models, with and without chemistry. This implies that the trends reported in Sect. 3 are probably robust irrespective of the detailed treatment of ion impact chemistry in the model.
When ion impact ionization and charge exchange are included, the N2 sputtering yield for incident CH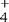 at 2.9 keV is found to be 0.93, much lower than the value of 5.0 quoted above without chemistry, but still higher than the Shematovich et al. (2001) result by a factor of 10. This difference, at least partly, arises from the different extent of the simulation box used for counting escaping molecules. In particular, the upper boundary in the model of Shematovich et al. (2001) is 1700 km with an N2 density of 3 × 106 cm−3, and the production of atmospheric N2 recoils above this altitude clearly makes a substantial contribution to escape (see their Fig. 3). This is to be compared with our upper boundary of 2000 km where the N2 density is only 7 × 104 cm−3 (Strobel 2012) and the production of atmospheric recoils at higher altitudes is negligible.
at 2.9 keV is found to be 0.93, much lower than the value of 5.0 quoted above without chemistry, but still higher than the Shematovich et al. (2001) result by a factor of 10. This difference, at least partly, arises from the different extent of the simulation box used for counting escaping molecules. In particular, the upper boundary in the model of Shematovich et al. (2001) is 1700 km with an N2 density of 3 × 106 cm−3, and the production of atmospheric N2 recoils above this altitude clearly makes a substantial contribution to escape (see their Fig. 3). This is to be compared with our upper boundary of 2000 km where the N2 density is only 7 × 104 cm−3 (Strobel 2012) and the production of atmospheric recoils at higher altitudes is negligible.
In a later study, Shematovich et al. (2003) used more realistic ion incident fluxes based on the hybrid model calculations of Brecht et al. (2000), including both magnetospheric N+ and pickup C2 H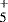 ions, and they found a substantially larger contribution of over 50% to the total nitrogen escape by sputtering. Their N2 sputtering yields are 0.23 and 0.59, respectively, for incident N+ and C2 H
ions, and they found a substantially larger contribution of over 50% to the total nitrogen escape by sputtering. Their N2 sputtering yields are 0.23 and 0.59, respectively, for incident N+ and C2 H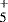 . The more recent Monte Carlo model of Michael et al. (2005), quite similar to that of Shematovich et al. (2003) but with 3-D calculations implemented, predicted comparable sputtering yields of 0.17 and 0.46. For comparison, using representative incidence energies of 750 eV for N+ and 1.5 keV for C2 H
. The more recent Monte Carlo model of Michael et al. (2005), quite similar to that of Shematovich et al. (2003) but with 3-D calculations implemented, predicted comparable sputtering yields of 0.17 and 0.46. For comparison, using representative incidence energies of 750 eV for N+ and 1.5 keV for C2 H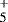 (see Fig. 1 in Shematovich et al. 2003), we obtain N2 sputtering yields of 2.6 and 4.4 without chemistry for the two categories of incident ion, under normal incidence and assuming ZBL. Therefore our values are higher by a factor of 10. However, if ion impact chemistry is taken into account following the simple procedure outlined above, the N2 sputtering yields are reduced to 0.48 and 0.85, respectively, which are consistent with the values of both Shematovich et al. (2003) and Michael et al. (2005) within a factor of 2.
(see Fig. 1 in Shematovich et al. 2003), we obtain N2 sputtering yields of 2.6 and 4.4 without chemistry for the two categories of incident ion, under normal incidence and assuming ZBL. Therefore our values are higher by a factor of 10. However, if ion impact chemistry is taken into account following the simple procedure outlined above, the N2 sputtering yields are reduced to 0.48 and 0.85, respectively, which are consistent with the values of both Shematovich et al. (2003) and Michael et al. (2005) within a factor of 2.
The absolute values of sputtering yield may also be affected by the uncertainty in ZBL cross section. Laboratory measurements of elastic scattering between the colliding partners involved in this study are available over limited ranges of incidence energy and scattering angle, but it is difficult to extrapolate existing measurements to the full parameter space required by our calculations. At a representative incidence energy of 1.5 keV, the measured cross section for CH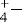 N2 elastic scattering (using O+ as a proxy) is 4 × 10−16 cm2 (Lindsay 2004), which is 40% of the cross section inferred from the ZBL interaction potential. To examine theeffect of absolute cross section, several test model runs were performed with the ZBL cross section of Ziegler & Biersack (1985) multiplied arbitrarily by 0.5, 2, and 4, all assuming incident CH
N2 elastic scattering (using O+ as a proxy) is 4 × 10−16 cm2 (Lindsay 2004), which is 40% of the cross section inferred from the ZBL interaction potential. To examine theeffect of absolute cross section, several test model runs were performed with the ZBL cross section of Ziegler & Biersack (1985) multiplied arbitrarily by 0.5, 2, and 4, all assuming incident CH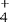 at 1.5 keV under normal incidence and all incorporating the simplified scheme of ion impact chemistry outlined above. These model runs predict N2 sputtering yields of 0.93, 0.80, and 0.67 to be compared with the value of 0.87 appropriate for the nominal ZBL collision model. It is interesting to note that the sputtering yield decreases with increasing cross section, opposite to the trend reported by Pospieszalska & Johnson (1996) for Io’s SO2 atmosphere impacted by O+ ions (see their Fig. 2). In practice, a larger cross section leads to an enhanced production of atmospheric recoils but at the same time also leads to a reduced probability for these recoils to escape. The actual dependence of sputtering yield on cross section thus reflects a contrast between the above two effects. It appears that for a thin atmosphere like that of Io the effect of enhanced production dominates, whereas for a thick atmosphere like that of Titan the effect of reduced escape probability dominates instead. To verify our speculation, an extra set of model runs was performed with the lower boundary raised to 1500 km. These model runs predict N2 sputtering yields of 0.032, 0.033, 0.036, and 0.040 for the cases with the ZBL cross section multiplied by 0.5, 1, 2, and 4, respectively, essentially reproducing the trend of Pospieszalska & Johnson (1996).
at 1.5 keV under normal incidence and all incorporating the simplified scheme of ion impact chemistry outlined above. These model runs predict N2 sputtering yields of 0.93, 0.80, and 0.67 to be compared with the value of 0.87 appropriate for the nominal ZBL collision model. It is interesting to note that the sputtering yield decreases with increasing cross section, opposite to the trend reported by Pospieszalska & Johnson (1996) for Io’s SO2 atmosphere impacted by O+ ions (see their Fig. 2). In practice, a larger cross section leads to an enhanced production of atmospheric recoils but at the same time also leads to a reduced probability for these recoils to escape. The actual dependence of sputtering yield on cross section thus reflects a contrast between the above two effects. It appears that for a thin atmosphere like that of Io the effect of enhanced production dominates, whereas for a thick atmosphere like that of Titan the effect of reduced escape probability dominates instead. To verify our speculation, an extra set of model runs was performed with the lower boundary raised to 1500 km. These model runs predict N2 sputtering yields of 0.032, 0.033, 0.036, and 0.040 for the cases with the ZBL cross section multiplied by 0.5, 1, 2, and 4, respectively, essentially reproducing the trend of Pospieszalska & Johnson (1996).
The above test model runs highlight the importance of the absolute value of cross section in modulating atmospheric sputtering, as already noticed by Fox & Hać (2014) in their Monte Carlo modeling of photochemical escape of atomic oxygen on Mars. According to their calculations, the range of absolute cross section used in existing models easily leads to derived escape rates that differ by an order of magnitude. We also caution that the scheme of ion impact chemistry implemented in our model is very crude and likely subject to significant uncertainties. For instance, we assume near equal impact ionization and elastic scattering cross sections which is fair around 1.5 keV (see above), whereas in reality the relative importance of ionization should decline as the ion projectile becomes less energetic. This suggests that the sputtering yields quoted above for the models with chemistry included tend to be underestimated, but it would be difficult to evaluate such an effect quantitatively unless the ionization cross section over the fully desired energy range is known. Despite the above considerations, we expect the variation of sputtering yield with the condition of ion incidence, as presented in Sect. 3, and the shape of the energy distribution of escaping molecules, as presented in Sect. 4, to remain almost unchanged, irrespective of the absolute value of cross section adopted and the detailed ion impact chemistry implemented.
 |
Fig. 10 ZBL+Firsov sputtering yields for incident CH |
6 Conclusion
Sputtering serves as an important mechanism of atmospheric escape in the solar system (Johnson et al. 2008), and this process is especially interesting on Titan due to its rich and complicated plasma environment which contains solar wind ions, magnetospheric ions, as well as local pickup ions (Arridge et al. 2011). The crucial parameter for evaluating sputter-induced escape is the sputtering yield, usually defined as the average number of escaping atmospheric molecules produced per incident ion (Johnson 1994).
The present study was devoted to a thorough investigation of the N2 and the CH4 sputtering yields on Titan, with a special focus on how these sputtering yields respond to the varying conditions of ion incidence. For this purpose, we constructed a Monte Carlo model that tracks, in a stochastic manner, the energy degradation of a large number of incident ions and atmospheric recoils within Titan’s upper atmosphere between 880 and 2000 km. Motivated by existing Cassini measurements of Saturn’s plasma environment in the vicinity of Titan (e.g., Thomsen et al. 2010; Regoli et al. 2016a; Wilson et al. 2017), we took into account three categories of incident ions with representative masses of 1, 16, and 28 Da, using H+, CH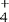 , and N
, and N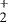 as proxies. Two collision models, ZBL and ZBL+Firsov, were tested, both characterized by a strongly forward scattering angle distribution, but one with electronic excitation taken into account and the other without. By counting the number of escaping molecules at the upper boundary, which was then divided by the total number of incident ions, the N2 and CH4 sputtering yields were favorably obtained.
as proxies. Two collision models, ZBL and ZBL+Firsov, were tested, both characterized by a strongly forward scattering angle distribution, but one with electronic excitation taken into account and the other without. By counting the number of escaping molecules at the upper boundary, which was then divided by the total number of incident ions, the N2 and CH4 sputtering yields were favorably obtained.
According to our Monte Carlo calculations, both the N2 and CH4 sputtering yields are enhanced for (1) higher incidence energy, which leads to the production of more atmospheric recoils; (2) larger incidence angle, which tends to restrict the trajectories of atmospheric recoils at higher altitudes where escape becomes easier; and (3) higher ion mass, which implies a more efficient momentum transfer from incident ions to atmospheric recoils. Our model results highlight the importance of scattering angle distribution.The CH4 to N2 sputtering yield ratio varies between 10 and 20%, increasing with increasing incidence angle, but decreasing with increasing energy. Both trends are compatible with the increase in CH4 mixing ratiowith increasing altitude.
We also examine the energy distribution of escaping molecules at the top of Titan’s atmosphere, which is found to be reasonably well described by a power law extending all the way from the local escape energy to a turnoff energy above which the distribution declines rapidly to zero. The best-fit power index is less negative for higher incidence energy, and also less negative for escaping CH4 than for escaping N2. These are expected results since the high energy tail of the distribution of escaping molecules tends to be more easily populated for cases with more efficient momentum transfer from the incident plasma flow to the ambient atmosphere, either when the incident ions are more energetic or when the atmospheric recoils are less massive. The power law fits that we obtain are generally less steep than the inverse square law assumed in some of the previous studies (e.g., Smith et al. 2004).
The sputtering yields reported here are compared to those found by Johnson et al. (2000), also based on Monte Carlo calculations but appropriate for a pure O atmosphere sputtered by incident O+ ions. The differences between the two models are largely due to the different choices of local escape energy. Meanwhile, early modeling works predicted N2 sputtering yields on Titan lower than our values by a large factor (Shematovich et al. 2001, 2003; Michael et al. 2005), which we speculate are related to the neglect of ion impact chemistry in our model. A crude treatment of chemistry is then implemented here, predicting N2 sputtering yields that are in broad agreement with previous results.
The collision parameterization adopted in this study is likely subject to significant uncertainties (e.g., Lindsay 2004), mainly due to the unavailability of the cross section data for the complete set of collision processes required by our calculations. This means that the absolute values of sputtering yield reported here should be quoted with caution. Even so, the predicted variation of sputtering yield with the condition of ion incidence and the shape of the energy distribution of escaping molecules are likely robust, irrespective of the detailed collision parameterization in terms of both elastic scattering and ion impact chemistry.
We recall that previous Monte Carlo calculations of Titan’s atmospheric sputtering focus exclusively on N2 and N (e.g., Shematovich et al. 2001, 2003; Michael et al. 2005), and note that the present study serves as the first attempt to evaluate sputter-induced CH4 escape on Titan. The sputtering yields derived here could be convolved with the differential intensity of incident ions to obtain the sputter-induced N2 and CH4 escape rates, and to determine the relative contributions of different ion sources, presumably varying both across Titan’s exobase and along Titan’s orbit around Saturn. These issues are left for a follow-up study based on realistic Cassini measurements of Titan’s highly variable plasma environment (e.g., Dialynas et al. 2009; Thomsen et al. 2010; Garnier et al. 2010; Regoli et al. 2016a; Wilson et al. 2017).
Acknowledgements
H.G. and J.C. are supported by the Science and Technology Development Fund of Macau SAR (FDCT) through grants 039/2013/A2 and 082/2015/A3. J.C. also acknowledges support from the National Science Foundation of China (NSFC) through grants 41525015 and 41774186. The authors are grateful to the anonymous referee for the constructive comments that have greatly improved the quality of the manuscript.
References
- Arridge, C. S., André, N., Bertucci, C. L., et al. 2011, Space Sci. Rev., 162, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Backes, H., Neubauer, F. M., Dougherty, M. K., et al. 2005, Science, 308, 992 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, J. M., Bougher, S. W., Waite, Jr. J. H., et al. 2010, J. Geophys. Res. Planets, 115, E12018 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, J. M., Bougher, S. W., Waite, Jr. J. H., et al. 2011, J. Geophys. Res. Planets, 116, E11002 [NASA ADS] [CrossRef] [Google Scholar]
- Bertucci, C., Achilleos, N., Dougherty, M. K., et al. 2008, Science, 321, 1475 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Bertucci, C., Sinclair, B., Achilleos, N., et al. 2009, Planet. Space Sci., 57, 1813 [NASA ADS] [CrossRef] [Google Scholar]
- Brecht, S. H., Luhmann, J. G., & Larson, D. J. 2000, J. Geophys. Res., 105, 13119 [NASA ADS] [CrossRef] [Google Scholar]
- Cravens, T. E., Keller, C. N., & Ray, B. 1997, Planet. Space Sci., 45, 889 [NASA ADS] [CrossRef] [Google Scholar]
- Cravens, T. E., Robertson, I. P., Clark, J., et al. 2005, Geophys. Res. Lett., 32, L12108 [NASA ADS] [CrossRef] [Google Scholar]
- Cui, J., Yelle, R. V., & Volk, K. 2008, J. Geophys. Res. Planets, 113, E10004 [Google Scholar]
- Cui, J., Galand, M., Yelle, R. V., et al. 2009, J. Geophys. Res. Space Phys., 114, A06310 [NASA ADS] [CrossRef] [Google Scholar]
- Cui, J., Yelle, R. V., Müller-Wodarg, I. C. F., Lavvas, P. P., & Galand, M. 2011, J. Geophys. Res. Space Phys., 116, A11324 [NASA ADS] [Google Scholar]
- Cui, J., Yelle, R. V., Strobel, D. F., et al. 2012, J. Geophys. Res. Planets, 117, E11006 [Google Scholar]
- De La Haye, V., Waite, J. H., Cravens, T. E., et al. 2007, Icarus, 191, 236 [NASA ADS] [CrossRef] [Google Scholar]
- Dialynas, K., Krimigis, S. M., Mitchell, D. G., et al. 2009, J. Geophys. Res. Space Phys., 114, A01212 [NASA ADS] [CrossRef] [Google Scholar]
- Firsov, O. B. 1959, Zh. Eksp. Teor. Fiz., 36, 1517 (Sov. Phys. JETP, Engl. Transl., 36, 1076, 1959) [Google Scholar]
- Fox, J. L., & Hać, A. B. 2014, Icarus, 228, 375 [NASA ADS] [CrossRef] [Google Scholar]
- Garnier, P., Dandouras, I., Toublanc, D., et al. 2010, Planet. Space Sci., 58, 1811 [NASA ADS] [CrossRef] [Google Scholar]
- Hartle, R. E., Sittler, E. C., Neubauer, F. M., et al. 2006, Geophys. Res. Lett., 33, L08201 [NASA ADS] [Google Scholar]
- Jiang, F., Cui, J., & Xu, J. 2017, AJ, 154, 271 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, R. E. 1994, Space Sci. Rev., 69, 215 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, R. E., Schnellenberger, D., & Wong, M. C. 2000, J. Geophys. Res., 105, 1659 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, R. E., Liu, M., & Tully, C. 2002, Planet. Space Sci., 50, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, R. E., Combi, M. R., Fox, J. L., et al. 2008, Space Sci. Rev., 139, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Jurac, S., & Richardson, J. D. 2005, J. Geophys. Res. Space Phys., 110, A09220 [NASA ADS] [CrossRef] [Google Scholar]
- Kallio, E., & Barabash, S. 2000, J. Geophys. Res., 105, 24973 [NASA ADS] [CrossRef] [Google Scholar]
- Lammer, H., & Bauer, S. J. 1993, Planet. Space Sci., 41, 657 [NASA ADS] [CrossRef] [Google Scholar]
- Lindsay, B. G. 2004, J. Geophys. Res. Space Phys., 109, A08305 [NASA ADS] [CrossRef] [Google Scholar]
- Lindsay, B. G., Merrill, R. L., Straub, H. C., Smith, K. A., & Stebbings, R. F. 1998, Phys. Rev. A, 57, 331 [NASA ADS] [CrossRef] [Google Scholar]
- Luna, H., Michael, M., Shah, M. B., et al. 2003, J. Geophys. Res. Planets, 108, 5033 [NASA ADS] [CrossRef] [Google Scholar]
- Michael, M., Johnson, R. E., Leblanc, F., et al. 2005, Icarus, 175, 263 [NASA ADS] [CrossRef] [Google Scholar]
- Müller-Wodarg, I. C. F., Yelle, R. V., Cui, J., & Waite, J. H. 2008, J. Geophys. Res. Planets, 113, E10005 [NASA ADS] [CrossRef] [Google Scholar]
- Noël, S., & Prölss, G. W. 1993, J. Geophys. Res., 98, 17317 [NASA ADS] [CrossRef] [Google Scholar]
- Pospieszalska, M. K., & Johnson, R. E. 1996, J. Geophys. Res., 101, 7565 [NASA ADS] [CrossRef] [Google Scholar]
- Regoli, L. H., Coates, A. J., Thomsen, M. F., et al. 2016a, J. Geophys. Res. Space Phys., 121, 8317 [NASA ADS] [CrossRef] [Google Scholar]
- Regoli, L. H., Roussos, E., Feyerabend, M., et al. 2016b, Planet. Space Sci., 130, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Schaufelberger, A., Wurz, P., Lammer, H., & Kulikov, Y. N. 2012, Planet. Space Sci., 61, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Shematovich, V. I., Tully, C., & Johnson, R. E. 2001, Adv. Space Res., 27, 1875 [NASA ADS] [CrossRef] [Google Scholar]
- Shematovich, V. I., Johnson, R. E., Michael, M., & Luhmann, J. G. 2003, J. Geophys. Res. Planets, 108, 5087 [Google Scholar]
- Sittler, E. C., Hartle, R. E., Johnson, R. E., et al. 2010, Planet. Space Sci., 58, 327 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, H. T., Johnson, R. E., & Shematovich, V. I. 2004, Geophys. Res. Lett., 31, L16804 [NASA ADS] [CrossRef] [Google Scholar]
- Snowden, D., Yelle, R. V., Cui, J., et al. 2013, Icarus, 226, 552 [NASA ADS] [CrossRef] [Google Scholar]
- Strobel, D. F. 2009, Icarus, 202, 632 [NASA ADS] [CrossRef] [Google Scholar]
- Strobel, D. F. 2012, Can. J. Phys., 90, 795 [NASA ADS] [CrossRef] [Google Scholar]
- Szego, K., Bebesi, Z., Bertucci, C., et al. 2007, Geophys. Res. Lett., 34, L24S03 [CrossRef] [Google Scholar]
- Thomsen, M. F., Reisenfeld, D. B., Delapp, D. M., et al. 2010, J. Geophys. Res. Space Phys., 115, A10220 [NASA ADS] [CrossRef] [Google Scholar]
- Tucker, O. J., & Johnson, R. E. 2009, Planet. Space Sci., 57, 1889 [NASA ADS] [CrossRef] [Google Scholar]
- Tucker, O. J., Johnson, R. E., Deighan, J. I., & Volkov, A. N. 2013, Icarus, 222, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Westlake, J. H., Bell, J. M., Waite, Jr., J. H., et al. 2011, J. Geophys. Res. Space Phys., 116, A03318 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, R. J., Bagenal, F., & Persoon, A. M. 2017, J. Geophys. Res. Space Phys., 122, 7256 [NASA ADS] [CrossRef] [Google Scholar]
- Yelle, R. V., Cui, J., & Müller-Wodarg, I. C. F. 2008, J. Geophys. Res. Planets, 113, E10003 [Google Scholar]
- Ziegler, J. F., & Biersack, J. P. 1985, The Stopping and Range of Ions in Matter (Berlin: Springer-Verlag), 93 [Google Scholar]
All Figures
 |
Fig. 1 Differential scattering cross section calculated numerically from the ZBL interaction potential (Ziegler & Biersack 1985) for an incident CH |
| In the text | |
 |
Fig. 2 Several random examples for the stepwise trajectories of incident CH |
| In the text | |
 |
Fig. 3 Variations in the N2
and CH4
sputtering yields with the ion incidence energy in Titan’s upper atmosphere based on our Monte Carlo calculations. Upper, middle, and lower panels: incident H+, CH |
| In the text | |
 |
Fig. 4 Sputtering yield, normalized by the value obtained assuming normal incidence, as a function of the ion incidence angle, for three representative energies: 100 eV (squares), 1 keV (circles), and 10 keV (triangles). N2 and CH4
are displayed separately by the solid and open symbols, respectively. Different collision models and different categories of incident ions give very similar variations, and only the ZBL+Firsov results for incident CH |
| In the text | |
 |
Fig. 5 Ratio of the CH4
to the N2
sputtering yields as a function of the ion incidence energy; shown are normal incidence (solid lines) and an incidence angle of 55°
(dashed lines). The ZBL approximation is adopted for all the displayed model runs, and the incident ions are taken to be N |
| In the text | |
 |
Fig. 6 Several examples of the energy distribution of escaping molecules for three different incidence energies including 100 eV, 1 keV, and 10 keV, all assuming normal incidence. Distributions of escaping N2 and CH4 molecules are shown separately in the left and right panels, respectively. The probability distribution tends to decline near monotonically with increasing energy, which is reasonably well described by a power law as given by the thick solid line in each panel. Such a power law trend extends all the way from the local escape energy to a turnoff energy above which the distribution declines rapidly to zero. The best-fit power index is indicated in each panel for reference. |
| In the text | |
 |
Fig. 7 The best-fit power index that characterizes the energy distribution of escaping molecules below the turnoff energy, triangles for escaping N2 and diamonds for escaping CH4. Normal incidence is assumed for all the displayed model runs. |
| In the text | |
 |
Fig. 8 Same as Fig. 6, but for different incidence angles with a common incidence energy of 1 keV. |
| In the text | |
 |
Fig. 9 Best-fit power index characterizing the energy distribution of escaping molecules as a function of incidence angle below the turnoff energy for escaping N2 (triangles) and for escaping CH4 (diamonds). A common incidence energy of 1 keV is assumed for all the model runs shown. |
| In the text | |
 |
Fig. 10 ZBL+Firsov sputtering yields for incident CH |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.