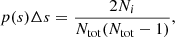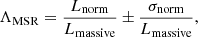| Issue |
A&A
Volume 623, March 2019
|
|
|---|---|---|
| Article Number | L8 | |
| Number of page(s) | 11 | |
| Section | Letters to the Editor | |
| DOI | https://doi.org/10.1051/0004-6361/201833687 | |
| Published online | 13 March 2019 | |
Letter to the Editor
Unveiling a cluster of protostellar disks around the massive protostar GGD 27 MM1
1
Institut de Ciències de l’Espai (ICE, CSIC), Can Magrans, s/n, 08193 Cerdanyola del Vallès, Catalonia, Spain
e-mail: busquet@ice.cat, girart@ice.cat
2
Institut d’Estudis Espacials de Catalunya (IEEC), 08034 Barcelona, Catalonia, Spain
3
Departament de Física Quàntica i Astrofísica, Institut de Ciències del Cosmos (ICC), Universitat de Barcelona (IEEC-UB), Martí i Franquès 1, 08028 Barcelona, Catalonia, Spain
4
Instituto Argentino de Radioastronomía, CCT-La Plata (CONICET), C.C.5, 1894 Villa Elisa, Argentina
5
Instituto de Radioastronomía y Astrofísica (IRyA), UNAM, Apdo. Postal 72-3 (Xangari), Morelia, Michoacán 58089, Mexico
6
Instituto de Astrofísica de Andalucía (IAA, CSIC), Glorieta de la Astronomía, s/n, 18008 Granada, Spain
7
Instituto de Astronomía, Universidad Nacional Autónoma de México (UNAM), Apartado Postal 70-264, DF 04510 Mexico, Mexico
Received:
21
June
2018
Accepted:
20
February
2019
Context. Most stars form in clusters and thus it is important to characterize the protostellar disk population in dense environments to assess whether the environment plays a role in the subsequent evolution. Specifically, it is critical to evaluate whether planet formation is altered with respect to more isolated stars formed in dark clouds.
Aims. We seek to investigate the properties of the protostellar disks in the GGD 27 cluster and compare these with those obtained from disks formed in nearby regions.
Methods. We used ALMA to observe the star-forming region GGD 27 at 1.14 mm with an unprecedented angular resolution, 40 mas (∼56 au), and sensitivity (∼0.002 M⊙).
Results. We detected a cluster of 25 continuum sources, most of which likely trace disks around Class 0/I protostars. Excluding the two most massive objects, disks masses are in the range 0.003–0.05 M⊙. The analysis of the cluster properties indicates that GGD 27 displays moderate subclustering. This result, combined with the dynamical timescale of the radio jet (∼104 years), suggests the youthfulness of the cluster. The lack of disk mass segregation signatures may support this as well. We found a clear paucity of disks with Rdisk > 100 au. The median value of the radius is 34 au; this value is smaller than the median of 92 au for Taurus but comparable to the value found in Ophiuchus and in the Orion Nebula Cluster. In GGD 27 there is no evidence of a distance-dependent disk mass distribution (i.e., disk mass depletion due to external photoevaporation), most likely due to the cluster youth.
There is a clear deficit of disks for distances <0.02 pc. Stars can only form larger and more massive disksfor distances >0.04 pc. This suggests that dynamical interactions far from the cluster center are weaker, although the small disks found could be the result of disk truncation. This work demonstrates the potential to characterize disks from low-mass young stellar objects in distant and massive (still deeply embedded) clustered environments.
Key words: stars: formation / accretion, accretion disks / ISM: individual objects: GGD 27 / ISM: individual objects: HH 80–81 / ISM: individual objects: IRAS 18162–2048
© ESO 2019
1. Introduction
One of the major challenges of modern astrophysics is the direct observation of protostellar disks, the progenitors of planetary systems in all stages of star formation, from extremely young protostars still deeply embedded in the natal dense envelope to more evolved pre-main sequence stars, at which point the envelope has dissipated and a young star (or stars) and a protoplanetary disk remain. The advent of new facilities such as the Atacama Large Millimeter/submillimeter Array (ALMA) and the Jansky Very Large Array (JVLA) have boosted the study of the formation and evolution of disks around young solar-type stars and started to unveil details of the planetary formation process (e.g., Andrews et al. 2016; Carrasco-González et al. 2016). Extensive surveys conducted mainly toward nearby and isolated low-mass star-forming regions, generally unaffected by their external environment, lead to major progress in the understanding of the disk properties and evolution (e.g., Andrews 2016). Although some fraction of the stellar population formed in an isolated mode such as in the Taurus-Auriga star-forming region, most stars, including our Sun, formed in clusters that are embedded within molecular clouds (e.g., Lada & Lada 2003; Adams 2010). In cluster environments, the high stellar density, protostellar outflow feedback, and ultraviolet (UV) radiation from the massive star(s) can influence the disk properties and evolution of low-mass cluster members such as in the Orion Nebula Cluster (ONC), where the extreme UV radiation field inhibits the potential to form planets close to the massive stars (Mann et al. 2014). To date, only a few publications reporting disks properties in clustered environments can be found in the literature for Orion (e.g., Mann et al. 2015; Eisner et al. 2016, 2018), the Upper Scorpius OB Association (e.g., Carpenter et al. 2014; Barenfeld et al. 2017), and the IC 348 cluster (e.g., Ruíz-Rodríguez et al. 2018). However, most of these studies focus on relatively evolved clusters. Characterizing the disk population in the earliest stages of star formation in cluster environments is essential to understand the initial conditions, formation process, and final properties of young planets.
GGD 27 is a reflection nebula at a distance of 1.4 kpc (Girart et al., in prep.)1. This source is illuminated mainly by a massive B0-type young stellar object (YSO), IRAS 18162−2048, which powers a long (14 pc), fast, and highly collimated radio jet associated with HH 80–81 (e.g., Martí et al. 1993; Masqué et al. 2012). The high-mass YSO driving the HH 80–81 jet is associated with the millimeter source MM1, a massive dusty disk surrounded by a warm and dense elongated molecular envelope (e.g., Girart et al. 2017, 2018). There is another site of massive star formation, the core MM2, located 7″ (∼10 000 au) northeast of MM1. These two massive protostellar sites are surrounded by a cluster of infrared and X-ray sources (e.g., Aspin et al. 1994; Pravdo et al. 2004, 2009; Qiu et al. 2008).
In this Letter we report the detection of a cluster of 1.14 mm continuum sources, most of which are previously unknown. The data is part of the polarimetric ALMA observations toward GGD 27 MM1 presented in Girart et al. (2018). A brief description of the observations is given in Sect. 2. The results are presented in Sect. 3. We analyze and discuss the properties of the cluster in comparison with previous works in other regions in Sect. 4.
2. Observations
The observations were performed in December 2015 in the C36-8/7 configuration at the central frequency of 263 GHz (1.14 mm). A detailed description is given in Girart et al. (2018). In order to highlight the emission of compact and weak sources within the field of view of  at 263 GHz, we performed maps with a robust weighting of 0.5 and excluded baselines shorter than 300 kλ. The robust weighting allows us to obtain a good compromise between sensitivity and angular resolution. The angular resolution achieved is 45.0 mas × 38.3 mas with a position angle of −62.4°. The exclusion of baselines shorter than 300 kλ allows us to have higher fidelity cleaned images (Girart et al. 2018). The images presented are corrected by the primary beam attenuation. The sensitivity is not uniform along the field of view. First, the correction of the primary beam attenuation makes the rms noise increase outward with respect to the phase center. Additionally, the presence of extended emission from the envelope around MM2, and especially around MM1, increases the rms noise nearby these sources. Thus, we adopted an 8σ threshold for source detection, where σ is the local rms noise measured within a radius of
at 263 GHz, we performed maps with a robust weighting of 0.5 and excluded baselines shorter than 300 kλ. The robust weighting allows us to obtain a good compromise between sensitivity and angular resolution. The angular resolution achieved is 45.0 mas × 38.3 mas with a position angle of −62.4°. The exclusion of baselines shorter than 300 kλ allows us to have higher fidelity cleaned images (Girart et al. 2018). The images presented are corrected by the primary beam attenuation. The sensitivity is not uniform along the field of view. First, the correction of the primary beam attenuation makes the rms noise increase outward with respect to the phase center. Additionally, the presence of extended emission from the envelope around MM2, and especially around MM1, increases the rms noise nearby these sources. Thus, we adopted an 8σ threshold for source detection, where σ is the local rms noise measured within a radius of  of the source and excluding its emission. Table A.1 shows the source name, position, peak intensity, flux density, brightness temperature, and counterpart identification. We include three additional tentative sources detected at 5σ, which are located in regions without signatures of extended emission.
of the source and excluding its emission. Table A.1 shows the source name, position, peak intensity, flux density, brightness temperature, and counterpart identification. We include three additional tentative sources detected at 5σ, which are located in regions without signatures of extended emission.
3. Results
Figure 1 shows the position of the 1.14 mm continuum sources detected with ALMA. We detected a cluster of 25 continuum sources, including the three previously know sites of massive star formation: MM1/ALMA 5, MM2(W)/ALMA 13, and MM2(W)/ALMA 17 (Fernández-López et al. 2011a; Girart et al. 2017, hereafter MM1, MM2(W), and MM2(E), respectively). The remaining 22 sources are new detections (Table A.1) and are distributed mainly north and southeast of MM1. In Fig. 2 we present close-up images of all ALMA detections, including the three tentatively detected sources. Most of the continuum sources are compact, and only two, ALMA 7 and ALMA 8, which are located close to MM1, present faint and extended emission.
 |
Fig. 1. Positions (indicated by crosses and labeled according to Table A.1) of the dust continuum sources detected in the GGD 27 region. Images of the individual sources are shown in Fig. 2. |
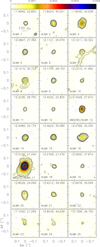 |
Fig. 2. Composite of the all sources detected in the field of view (except for MM1/ALMA 5). The images were corrected for the primary beam response. Black contours are −4, −3, 3, 4, 5, 8, 13, 20, 35, and 50 times the local rms noise of each image (Table A.1). White contours are 100, 150, 200, 250, and 300 times the local rms noise. Table A.1 lists their absolute positions. In each panel we labeled the second and arcsecond position of the center of the panel. The color scale is the same for all panels and it is shown at the top of the figure (units of Jy beam−1). The synthesized beam is shown in the bottom right corner of the first image. |
We assumed that the continuum emission arises from disks surrounding YSOs. This assumption is based on the derived sizes of a few 100 au or smaller (see below) and in the fact that no more than 1 mm extragalactic background is expected in the field of view (see Appendix B for a justification).
We obtained physical properties (masses, radius, inclination angle and position angle) for the detected disks. Appendix C describes the method used to derive these properties, which assumes that the intensity can be described with a power law of the radius. Table 1 shows the disk parameters inferred with this method. Except for the two massive disks, MM1 and MM2(E), the millimeter sources have disks masses in the range 0.003–0.05 M⊙ (Table 1)2, suggesting that these disks are associated with low-mass YSOs. For these low-mass YSOs, the median value of the disk radius is 34 au and only two YSOs have large disks (Rdisk ≳ 100 au). From Fig. 1 (see also Fig. D.1b) we can distinguish three possible multiple systems: the already known binary system formed by MM2(E) and MM2(W) whose separation is ∼1400 au, and two triple systems formed by MM1/ALMA 7/ALMA 8 and ALMA 14/ALMA 15/ALMA 16, separated by ∼1000 au and ∼1600 au, respectively.
Disk properties in the GGD 27 protostellar cluster.
4. Analysis and discussion
4.1. Clustering and mass segregation
In cluster environments, gravitational interactions group the most massive objects toward the center in a relatively short time and generates radial mass segregation and a smooth density distribution of sources that can be approached as a power law (e.g., Cartwright & Whitworth 2004; Allison et al. 2009). However, the clustering analysis done in Appendix D reveals a fractal type of subclustering with three possible subcenters separated by ∼0.04 pc: around MM1, MM2(E)-MM2(W), and the triple system ALMA 14–16. In addition, the GGD 27 cluster shows evidence for a lack of primordial mass segregation signatures in the disk population, but rather a very random distribution (see Fig. 3 where we present the mass segregation ratio (MSR) as a function of the NMST most massive disks and Appendix D.3.) Only the two most massive protostellar disks may have already relaxed toward the center of the cluster, since the relaxation time is inversely proportional to the protostellar system mass. This is in contrast to the Serpens South protocluster that shows evidence of primordial mass segregation (Plunkett et al. 2018). Despite the caveats and uncertainties of this analysis, all these facts combined (i.e., the low value of the 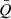 parameter, dynamical timescale of the radio jet (∼104 yr), and lack of mass segregation signatures) suggest that the cluster of disks is very young and probably associated with Class 0 and Class I low-mass protostars (see Appendix D.3 for further discussion). This is in agreement with the properties of the X-ray sources found in the region (Pravdo et al. 2009), who reported a cluster of Class I protostars in GGD 27. Interestingly, the two massive YSOs also appear to be in a very early stage of evolution. MM1 powers the HH 80–81 radio jet with a dynamical time of ∼104 yr (Masqué et al. 2012). MM2(E) is in an even earlier stage (Qiu & Zhang 2009; Fernández-López et al. 2011a; Girart et al. 2017). This suggests certain coevality of the low-mass cluster members with the two massive YSOs and therefore a smaller age dependence of the protostellar disk masses (see Appendix D.3). Our analysis indicates that the spatial distribution of the protostellar disk population does not depend on the disk mass.
parameter, dynamical timescale of the radio jet (∼104 yr), and lack of mass segregation signatures) suggest that the cluster of disks is very young and probably associated with Class 0 and Class I low-mass protostars (see Appendix D.3 for further discussion). This is in agreement with the properties of the X-ray sources found in the region (Pravdo et al. 2009), who reported a cluster of Class I protostars in GGD 27. Interestingly, the two massive YSOs also appear to be in a very early stage of evolution. MM1 powers the HH 80–81 radio jet with a dynamical time of ∼104 yr (Masqué et al. 2012). MM2(E) is in an even earlier stage (Qiu & Zhang 2009; Fernández-López et al. 2011a; Girart et al. 2017). This suggests certain coevality of the low-mass cluster members with the two massive YSOs and therefore a smaller age dependence of the protostellar disk masses (see Appendix D.3). Our analysis indicates that the spatial distribution of the protostellar disk population does not depend on the disk mass.
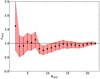 |
Fig. 3. Mass segregation ratio (ΛMSR; see Appendix D.3) as a function of the NMST (MST) most massive disks of GGD 27. ALMA 1 and ALMA 2, classified as Class II and Class III YSOs, respectively, are not included. The main deviation from a uniform behavior around unity is for NMST = 2, suggesting that the two most massive sources are closer to each other than the average distance between two random sources. The horizontal line at ΛMSR = 1 indicates the regime where sources show no evidence for mass segregation. |
4.2. Comparison with nearby regions
In this section, we investigated whether the disk properties of the GGD 27 cluster display similar/different features than those located in nearby regions. Figure 4a shows the 1.14 mm flux as a function of the radius of the disks for GGD 27, Taurus-Auriga (Guilloteau et al. 2011; Piétu et al. 2014), Ophiuchus (Cieza et al. 2019), and ONC (Eisner et al. 2018). We scaled the observed fluxes of GGD 27 to the distance of 140 pc and the fluxes of Taurus, Ophiuchus, and ONC disks to the wavelength of 1.14 mm assuming a spectral index α = 3. Given the different methods used in the literature to derive the disk radius (see Appendix C), we included disks whose radius has been measured with a power law3 or with a Gaussian fit, for which we used the relation C.4 of Appendix C to obtain the corresponding radii derived from a power-law fit. The 1.14 mm scaled flux-size relation shown in Fig 4a reveals that for a given flux, disks in GGD 27 cluster tend to be smaller than in Taurus-Auriga, with a clear deficit of disks with sizes Rdisk ≳ 100 au. Assuming the same conditions, i.e., excluding disks of all samples below our sensitivity limit (dotted line in Fig. 4a), we obtained that the median radius in GGD 27 is 34 au whereas the radii derived for Taurus and Ophiuchus disks are 92 au and 42 au, respectively. If we include the sample of Taurus-Auriga disks from Tripathi et al. (2017), whose size was measured with a different method (see Appendix C), we still found that disks in the GGD 27 cluster are smaller than in Taurus-Auriga. Recently, Maury et al. (2019) have shown that the youngest and more embedded Class 0 objects have relatively smaller disk (R < 60 au for 75% of their sample). This result is compatible with our hypothesis that disks in GGD 27 are associated with embedded YSOs. We also compared our results with ONC (Eisner et al. 2018) and obtained that the median radius of ONC disks is 44 au, similar to GGD 27 and Ophiuchus. Therefore, we do not find significant differences between disks formed in cluster environments, such as GGD 27 and ONC, and the Ophiuchus sample, which forms stars in isolation. Only disk population of Taurus-Auriga differs from the rest. This difference could be explained in terms of evolutionary effects or viscous evolution, since disks in Taurus are associated with Class II YSOs, while the sample of disks in Ophiuchus and GGD 27 contains objects in an earlier evolutionary stage. However, we cannot rule out other processes such as different initial conditions or intrinsically different viscous timescales. Further observations toward a larger sample of disks in different cluster environments are needed to fully investigate the effects of a cluster on the disk population.
 |
Fig. 4. Panel a: 1.14 mm flux (scaled to a distance of 140 pc) as a function of the radius for all disks detected in GGD 27 (black squares and triangles), Taurus-Auriga (red circles; Guilloteau et al. 2011; Piétu et al. 2014), Ophiuchus (gray circles; Cieza et al. 2019), and ONC (yellow squares; Eisner et al. 2018). The flux at 1.14 mm was extrapolated from the measurements at 1.3 mm for Taurus and Ophiuchus disks and from 850 μm for ONC disks using an spectral index of α = 3. The dotted line depicts the average mass sensitivity limit (8σ). We show, at the top, the median and its dispersion (1st and 3rd quartiles) for GGD 27 (black), Taurus (red), Ophiuchus (gray), and ONC (yellow) samples. The most massive disks MM1 and MM2(E) were removed from the plot. Panel b: disk masses in GGD 27 (black squares) and ONC (red circles) clusters as a function of their projected distance from the massive star IRAS 18162−2048 and θ1 Ori C (Mann et al. 2014), respectively. The dotted line depicts the average mass sensitivity limit while the dashed line indicates the higher 8σ limit close to MM1. Panel c: disk radii in GGD 27 as a function of their projected distance from the massive star. In all panels upper limits in Rdisk are indicated with triangles. |
Given the clustered nature of GGD 27 we might expect that its disk population could be affected mainly by two environmental factors: the high stellar density increases the probability of tidal/dynamical interactions, and second, the presence of a massive B star toward the cluster center may heat and photoevaporate disks of the surrounding low-mass cluster members. Observations and theoretical findings show that the mass-loss rate of disks due to external photoevaporation of the incident UV radiation field from the massive star depends on the distance of the disk to the central massive star (e.g., Hollenbach et al. 1994; Ansdell et al. 2017). Figure 4b presents the disks masses as a function of the projected distance from the most massive object in the GGD 27 cluster (i.e., IRAS 18162−2048, associated with MM1). Contrary to ONC, where there is a significant environmental impact with evidence of disk mass depletion at scales <0.03 pc (Mann et al. 2014; Eisner et al. 2018, see also Fig. 4b), in GGD 27 we found two massive disks (compared to ONC; ALMA 7 and ALMA 8) located close (< 0.005 pc) to the massive star, similar to the case of the NGC 2024 cluster (Mann et al. 2015). This could be explained because the GGD 27 cluster is younger than ONC, which is supported by the dynamical timescale of the radio jet (∼104 yr; Masqué et al. 2012) and the fact that the massive protostar has not yet developed a large HII region, or because the ionizing flux from GGD 27 (B0-type star) is much weaker than in ONC (O6-type star).
In Fig. 4c we show the radius of the disk as a function of the projected distance from the massive GGD 27 protostar. Interestingly, most of the disk population is located at distances >0.02 pc and only two disks are found in the immediate vicinity of the massive star, which could indicate that stars close to the massive star (i.e., close to the cluster center) may not be capable of forming disks. There is a clear lack of disks for distances between 0.006 pc and 0.02 pc, which is also observed in ONC but for smaller distances (see Fig. 4b). On the other hand, only for distances >0.04 pc disks appear larger and more massive than those located close to MM1 (Figs. 4b and c). This result could indicate that dynamical interactions far from the cluster center are weaker, indicating that larger disks can easily form, even though the small disks (Rdisk < 50 au) found at distances >0.02 pc could be the result of disk truncation due to interactions. However, a complete survey of the GGD 27 disk sample, which is currently probably observed in its high-mass end with a mass sensitivity of 0.002 M⊙, is needed. Such a survey would fully confirm both the absence of disk mass depletion and the deficit of disks close to the massive protostar since we cannot exclude the presence of faint and small disks.
In summary, the combination of sensitivity and spatial resolution leads us to the serendipitous discovery of a cluster of 25 continuum sources detected at 1.14 mm, most of which are previously unknown. These 1.14 mm sources trace the dust emission of disks with masses typically in the range 0.003–0.05 M⊙, surrounding Class 0 and Class I low-mass protostars. Excluding the most massive, which is associated with MM1, the median value of the disk radius is 34 au. This value is smaller than the median obtained for the Taurus disks but comparable to the results found in ONC and Ophiuchus and is consistent with the fact that disks in Taurus are associated with more evolved YSOs. The lack of disks close to the massive star GGD 27 MM1 suggests that in cluster environments protostars close to the massive star may not be able to maintain their disks for a long time. In the GGD 27 cluster we only find large (and relatively massive) disks (Rdisk > 100 au) at distances >0.04 pc from the massive star. On the other hand, disks in the GGD 27 cluster do not display evidence of external photoevaporation due to the massive star. However, observations with higher sensitivity are needed to fully support these results. This study shows the potential of ALMA to unveil a disk population at millimeter wavelengths, whose emission appears completely hidden in the near-infrared owing to the strong emission arising from the massive star. This will open a new window for ALMA to investigate the properties of protostellar disks in deeply embedded young cluster environments located at large distances.
Based on Gaia-DR2 astrometry of a sample of pre-main sequence stars identified using near-infrared imaging polarimetry data of GGD 27 (Kwon et al. 2016).
We note that the derived masses are most likely a lower limit since we assumed optically thin emission (see Appendix C).
We note that Guilloteau et al. (2011) and Piétu et al. (2014) adopted a power-law radial dust temperature while we assumed a constant temperature.
We consider all the sources reported in Table A.1 as cluster members, including the tentative detections ALMA 23 to ALMA 25.
Acknowledgments
We sincerely thank the referee for his/her valuable comments that helped to improve this paper. This paper makes use of the following ALMA data: ADS/JAO.ALMA#2015.1.00480.S. ALMA is a partnership of ESO (representing its member states), NSF (USA), and NINS (Japan), together with NRC (Canada), NSC and ASIAA (Taiwan), and KASI (Republic of Korea), in cooperation with the Republic of Chile. The Joint ALMA Observatory is operated by ESO, AUI/NRAO, and NAOJ. G.B., J.M.G., R.E., G.A., N.AL, M.O., and J.M.T. are supported by the MINECO (Spain) AYA2014-57369-C3 and AYA2017-84390-C2 grants (co-funded by FEDER). G.A. and M.O. acknowledge financial support from the State Agency for Research of the Spanish MCIU through the “Center of Excellence Severo Ochoa” award for the Instituto de Astrofísica de Andalucía (SEV-2017-0709). S.C. acknowledges support from DGAPA, UNAM and CONACyT, México.
References
- Adams, F. C. 2010, ARA&A, 48, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Allison, R. J., Goodwin, S. P., Parker, R. J., et al. 2009, MNRAS, 395, 1449 [Google Scholar]
- Andre, P., Ward-Thompson, D., & Barsony, M. 2000, Protostars and Planets IV, 59 [Google Scholar]
- Andrews, S. 2016, Resolving Planet Formation in the Era of ALMA and Extreme AO. Proceedings of the Conference held 16–20 May, 2016 in Santiago, Chile, 15, 15 [Google Scholar]
- Andrews, S. M., & Williams, J. P. 2005, ApJ, 631, 1134 [NASA ADS] [CrossRef] [Google Scholar]
- Andrews, S. M., Wilner, D. J., Hughes, A. M., Qi, C., & Dullemond, C. P. 2009, ApJ, 700, 1502 [NASA ADS] [CrossRef] [Google Scholar]
- Andrews, S. M., Wilner, D. J., Zhu, Z., et al. 2016, ApJ, 820, L40 [NASA ADS] [CrossRef] [Google Scholar]
- Ansdell, M., Williams, J. P., Manara, C. F., et al. 2017, AJ, 153, 240 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aspin, C., Puxley, P. J., Blanco, P. R., et al. 1994, A&A, 292, L9 [NASA ADS] [Google Scholar]
- Barenfeld, S. A., Carpenter, J. M., Sargent, A. I., Isella, A., & Ricci, L. 2017, ApJ, 851, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Beckwith, S. V. W., Sargent, A. I., Chini, R. S., & Guesten, R. 1990, AJ, 99, 924 [NASA ADS] [CrossRef] [Google Scholar]
- Carpenter, J. M., Ricci, L., & Isella, A. 2014, ApJ, 787, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Carrasco-González, C., Henning, T., Chandler, C. J., et al. 2016, ApJ, 821, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Cartwright, A., & Whitworth, A. P. 2004, MNRAS, 348, 589 [NASA ADS] [CrossRef] [Google Scholar]
- Cieza, L. A., Ruíz-Rodríguez, D., Hales, A., et al. 2019, MNRAS, 482, 698 [NASA ADS] [CrossRef] [Google Scholar]
- Dunham, M. M., Allen, L. E., Evans, II., N. J., et al. 2015, ApJS, 220, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Eisner, J. A., Bally, J. M., Ginsburg, A., & Sheehan, P. D. 2016, ApJ, 826, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Eisner, J. A., Arce, H. G., Ballering, N. P., et al. 2018, ApJ, 860, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Estalella, R. 2017, PASP, 129, 025003 [NASA ADS] [CrossRef] [Google Scholar]
- Fernández-López, M., Curiel, S., Girart, J. M., et al. 2011a, AJ, 141, 72 [NASA ADS] [CrossRef] [Google Scholar]
- Fernández-López, M., Girart, J. M., Curiel, S., et al. 2011b, Midwest Astrochemistry Meeting 2011, T05 [Google Scholar]
- Gavagnin, E., Bleuler, A., Rosdahl, J., & Teyssier, R. 2017, MNRAS, 472, 4155 [NASA ADS] [CrossRef] [Google Scholar]
- Girart, J. M., Estalella, R., Fernández-López, M., et al. 2017, ApJ, 847, 58 [NASA ADS] [CrossRef] [Google Scholar]
- Girart, J. M., Fernández-López, M., Li, Z.-Y., et al. 2018, ApJ, 856, L27 [CrossRef] [Google Scholar]
- Gomez, Y., Rodríguez, L. F., & Martí, J. 1995, ApJ, 453, 268 [NASA ADS] [CrossRef] [Google Scholar]
- Gómez, Y., Rodríguez, L. F., Girart, J. M., Garay, G., & Martí, J. 2003, ApJ, 597, 414 [NASA ADS] [CrossRef] [Google Scholar]
- Guilloteau, S., Dutrey, A., Piétu, V., & Boehler, Y. 2011, A&A, 529, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hatsukade, B., Kohno, K., Umehata, H., et al. 2016, PASJ, 68, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Hollenbach, D., Johnstone, D., Lizano, S., & Shu, F. 1994, ApJ, 428, 654 [NASA ADS] [CrossRef] [Google Scholar]
- Isella, A., Carpenter, J. M., & Sargent, A. I. 2010, ApJ, 714, 1746 [NASA ADS] [CrossRef] [Google Scholar]
- Kruskal, J. 1956, Proc. Am. Math. Soc., 7, 48 [Google Scholar]
- Kurtz, S., & Hofner, P. 2005, AJ, 130, 711 [NASA ADS] [CrossRef] [Google Scholar]
- Kurtz, S., Churchwell, E., & Wood, D. O. S. 1994, ApJS, 91, 659 [NASA ADS] [CrossRef] [Google Scholar]
- Kwon, J., Tamura, M., Hough, J. H., et al. 2016, ApJ, 824, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Lada, C. J., & Lada, E. A. 2003, ARA&A, 41, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Mann, R. K., Di Francesco, J., Johnstone, D., et al. 2014, ApJ, 784, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Mann, R. K., Andrews, S. M., Eisner, J. A., et al. 2015, ApJ, 802, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Martí, J., Rodríguez, L. F., & Reipurth, B. 1993, ApJ, 416, 208 [NASA ADS] [CrossRef] [Google Scholar]
- Martí, J., Rodríguez, L. F., & Torrelles, J. M. 1999, A&A, 345, L5 [NASA ADS] [Google Scholar]
- Masqué, J. M., Girart, J. M., Estalella, R., Rodríguez, L. F., & Beltrán, M. T. 2012, ApJ, 758, L10 [NASA ADS] [CrossRef] [Google Scholar]
- Maury, A. J., André, P., Testi, L., et al. 2019, A&A, 621, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Palau, A., Estalella, R., Girart, J. M., et al. 2014, ApJ, 785, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Parker, R. J. 2018, MNRAS, 476, 617 [Google Scholar]
- Pascucci, I., Testi, L., Herczeg, G. J., et al. 2016, ApJ, 831, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Piétu, V., Guilloteau, S., Di Folco, E., Dutrey, A., & Boehler, Y. 2014, A&A, 564, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Plunkett, A. L., Fernández-López, M., Arce, H. G., et al. 2018, A&A, 615, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pravdo, S. H., Tsuboi, Y., & Maeda, Y. 2004, ApJ, 605, 259 [NASA ADS] [CrossRef] [Google Scholar]
- Pravdo, S. H., Tsuboi, Y., Suzuki, Y., Thompson, T. J., & Rebull, L. 2009, ApJ, 690, 850 [NASA ADS] [CrossRef] [Google Scholar]
- Qiu, K., & Zhang, Q. 2009, ApJ, 702, L66 [NASA ADS] [CrossRef] [Google Scholar]
- Qiu, K., Zhang, Q., Megeath, S. T., et al. 2008, ApJ, 685, 1005 [NASA ADS] [CrossRef] [Google Scholar]
- Ruíz-Rodríguez, D., Cieza, L. A., Williams, J. P., et al. 2018, MNRAS, 1294 [Google Scholar]
- Tripathi, A., Andrews, S. M., Birnstiel, T., & Wilner, D. J. 2017, ApJ, 845, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Yamashita, T., Murata, Y., Kawabe, R., Kaifu, N., & Tamura, M. 1991, ApJ, 373, 560 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Table
Table A.1 lists the millimeter continuum sources detected in the GGD 27 region as explained in Sect. 2. We report the source coordinates, local rms measured in a region locally around each millimeter source (as explained in Sect. 2), peak intensity, flux density obtained by fitting a two-dimensional Gaussian function, and peak brightness temperature. We also report the counterpart identification at other wavelengths based on the work carried out by Pravdo et al. (2004, 2009), who cross-correlated the X-ray sources with sources from the 2MASS and USNO B1 catalogs and with Spitzer/IRAC detections, radio continuum studies from the literature, and high angular resolution (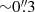 ) JVLA observations at 1 cm (project ID: VLA15A-132). Finally, we list the infrared spectral classification, when available, based on the work of Pravdo et al. (2009).
) JVLA observations at 1 cm (project ID: VLA15A-132). Finally, we list the infrared spectral classification, when available, based on the work of Pravdo et al. (2009).
Appendix B: Background sources
The analysis carried out in this paper assumes that the detected millimeter sources are tracing disks of dust around YSOs. This assumption is based on the small size of the sources, i.e., a few 100 au or less if they belong to the GGD 27 region. Alternatively, given the excellent sensitivity of ALMA, it could be feasible that some of these sources could be tracing dust emission from background extragalactic sources. To estimate how many of these could appear within the field of view, we used as a reference the deep 1.1 mm ALMA observations carried out by Hatsukade et al. (2016) over a 2 arcmin2 field. According to that work, for a flux density above than 0.2 mJy (i.e., above the 8σ threshold for a source detection), the number of sources per square degree is 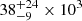 . Figure 1 shows a field of view of ∼0.16 arcmin2. That means that the number of extragalactic sources above the aforementioned flux level would be 2 ± 1. This represents an upper limit given that we considered the lowest rms of our ALMA image (see Table A.1). Therefore, we expect no more than one extragalactic source in our ALMA field of view.
. Figure 1 shows a field of view of ∼0.16 arcmin2. That means that the number of extragalactic sources above the aforementioned flux level would be 2 ± 1. This represents an upper limit given that we considered the lowest rms of our ALMA image (see Table A.1). Therefore, we expect no more than one extragalactic source in our ALMA field of view.
Appendix C: Disk masses and radii
We estimated the mass of gas and dust of the disk population of the GGD 27 protostellar cluster assuming that the 1.14 mm dust continuum emission is optically thin and the temperature distribution is uniform. We adopted a gas-to-dust ratio of 100 and the opacity law of Beckwith et al. (1990) with a dust opacity coefficient of κν = 2.63 cm−2 g−1 at 263 GHz and a spectral index β = 1. We assigned a dust temperature of 20 K to most of the millimeter sources in our sample based on the median temperature for the Taurus disks (Andrews & Williams 2005). We made the caveat that using Td = 10 K and Td = 30 K instead, the masses would be a factor of about 8/3 and 2/3 those obtained using Td = 20 K, respectively. The uncertainty in the masses due to an uncertainty in the dust opacity is a factor of two. For the two most massive sources, we adopted the more appropriate values of Td = 109 K for MM1 and Td = 35 K for MM2(E) and MM2(W) as found in Fernández-López et al. (2011a) and Qiu & Zhang (2009). The derived masses for MM1, especially for MM2(W) and MM2(E,) are smaller than that derived from the SMA with a larger beam (Fernández-López et al. 2011b). This is probably because of presence of extended emission from the core that is being filtered out by ALMA. It is important to mention that the derived masses are most likely a lower limit given the assumption of optically thin emission, which may not hold for all disks in GGD 27. For instance, Girart et al. (2018) found that the disk associated with ALMA 5/MM1 is optically thick.
In order to determine the characteristics of the disks, we modeled the emission of the disks seen at an inclination angle i (i = 0° for a face-on disk and i = 90° for an edge-on disk) with an intensity that is a power law of the radius (Iν ∝ r−q), up to a maximum radius Rdisk, convolved with a Gaussian beam with a half power beamwidth (HPBW) equal to that of the observation. The model depends on a maximum of eight parameters: the position of the disk center, (x0, y0); position angle of the disk axis, PA; disk inclination, i; disk radius, Rdisk; intensity power-law index, q; peak intensity, 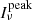 ; and background intensity,
; and background intensity, 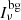 .
.
The fitting procedure was similar to that used in other fittings by Palau et al. (2014) and Estalella (2017). The fit was performed by sampling the space parameter of dimension up to eight using a Halton pseudo-random sequence, to find the minimum value of the rms fit residual. The details of the method and the derivation of the parameter uncertainties can be found in Estalella (2017).
The value of the power-law index resulted ill-determined for disks with a low signal-to noise ratio (S/N) or poorly angularly resolved. Thus, we decided to use the same value of q for all the disks, q = 1.1, except for ALMA 17. This value was derived from the fit to the disk with the highest S/N and well resolved by the observation, ALMA 3 (see Fig. 2). For ALMA 17 we fitted the radial intensity profile with the power-law index q as a free parameter, and obtained q = 1.46. In addition, we used a constant background intensity 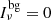 for all the disks, except for ALMA 7 and ALMA 8, where a cutoff of 0.20 mJy beam−1 and 0.15 mJy beam−1 was used, respectively. When the fit gave a value of the inclination consistent with a face-on disk, a second fit was performed forcing the inclination to be zero, and the position angle to be an arbitrary constant value. Thus, in general we fitted six parameters for inclined disks and four for face-on disks. Finally, when the error in the fitted radius was equal or larger than the value itself, we considered that the disk was unresolved and only an upper limit to Rdisk was given. Table 1 shows the disk parameters inferred by our model. It is important to point out that the disk radii were obtained using the ALMA image that excludes baselines shorter than 300 kλ. However, the derived disk sizes do not change significantly if all visibilities are included because they are always within the uncertainty of the two-dimensional Gaussian fit.
for all the disks, except for ALMA 7 and ALMA 8, where a cutoff of 0.20 mJy beam−1 and 0.15 mJy beam−1 was used, respectively. When the fit gave a value of the inclination consistent with a face-on disk, a second fit was performed forcing the inclination to be zero, and the position angle to be an arbitrary constant value. Thus, in general we fitted six parameters for inclined disks and four for face-on disks. Finally, when the error in the fitted radius was equal or larger than the value itself, we considered that the disk was unresolved and only an upper limit to Rdisk was given. Table 1 shows the disk parameters inferred by our model. It is important to point out that the disk radii were obtained using the ALMA image that excludes baselines shorter than 300 kλ. However, the derived disk sizes do not change significantly if all visibilities are included because they are always within the uncertainty of the two-dimensional Gaussian fit.
It is interesting to compare the radii derived from this model and the radii derived from a Gaussian fit to the intensity observed. A Gaussian fit can be understood as a fit that reproduces the moments up to order two of the observed intensity. We call RG the radius, i.e., the half width at half maximum, derived from the Gaussian fit
where we assume that the disk is centered at r = 0 (first order moment), Fν is the flux density (zeroth order moment), and the normalized second order moment in any direction of the Gaussian is
The model used in this paper assumes an intensity that is a power law of the radius, I = I0r−q up to a radius Rdisk. The normalized second-order moment of the power-law intensity can be easily computed and results in
ALMA 1.14 mm continuum sources toward GGD 27.
 |
Fig. C.1. Comparison between the disk radii obtained with a Gaussian fit and adopting a power law with an index of q = 1.1 for the sample of disks (Table 1). Red arrows indicate the upper limits. The solid lines shows the linear regression from the data, which indicates a relationship of RGauss = 0.48 ± 0.04 × RPower law. |
If we compare this result with the Gaussian fit, we find for the value of q found in this work, q = 1.1,
Thus, radii derived from a Gaussian fit are ∼2.2 times smaller than the radii derived from a power-law fit with a power-law index q = 1.1. Indeed, from our data the comparison between the measured radius adopting the aforementioned power law with respect to the radius derived from a Gaussian fit shows an excellent agreement with this result (see Fig. C.1). In three of the disks, ALMA 7, ALMA 11, and ALMA 13, the power-law fit gives only upper limits. In these case, we used the results of a Gaussian fit by applying the above correction factor.
The above two methods used to define disks radius are not the only approaches found in the literature. For cases in which the emission is well resolved, a surface density that follows a modified power with an exponential decay at larger radius: Σ(r)∝(r/R0)−γ exp(−(r/Rc)2 − γ) is also used (e.g., Andrews et al. 2009). In these cases the adopted disk radius is Rc, the “transition” radius between the power law and the exponential zones. On the other hand, in the compilation done by Tripathi et al. (2017), they use a different definition of radius, the so-called effective radius, Reff, which corresponds to the radius for which 68% of the total flux is located within this radius. We have compiled a list of sources where the disk radius has been derived from a simple power-law fit and also from either (or both) Rc and Reff (Guilloteau et al. 2011; Isella et al. 2010; Piétu et al. 2014; Tripathi et al. 2017). We found that for disks with a power-law index around 1, the radius obtained with a simple power law is on average about two times larger than the Rc and Reff, which is a similar result as that found with respect to a Gaussian fit.
Appendix D: Statistical analysis of the cluster
Although features such as clustering or gradients in the density of sources can be noticed by eye, some statistical tools have been developed to study the spatial distribution of the members of a given cluster. In this section we first determine (Appendices D.1 and D.2) whether the GGD 27 cluster of protostellar disks is centrally distributed or is clustered. To achieve this we follow the formalism of Cartwright & Whitworth (2004, hereafter CW2004) by using the minimum spanning tree (MST) and the distribution function of all the possible separations between the cluster members4. Second, we analyze (Appendix D.3) the mass segregation (see Allison et al. 2009). This analysis is based on the mass measured from dust continuum ALMA observations, which mainly arises from disks surrounding YSOs. We would like to point out that the infrared Spitzer and X-ray Chandra data show that there is a larger stellar population associated with the GGD 27 cluster (Qiu et al. 2008; Pravdo et al. 2004, 2009). However, we focused the following analysis toward the center of the cluster core (i.e., in a ∼0.15 pc region) close to the massive protostar GGD 27 MM1.
D.1. Distribution function
Following CW2004 we derived the distribution function, p(s), of the projected separations (s) between pairs of cluster stars. By counting the number of pairs Ni, we obtain the probability that the separation between whatever two stars of the cluster is in the interval (s, s + Δs). We used the normalized expression
where Ntot is the total number of stars in the cluster (25 in our ALMA observations of GGD 27). The value p(s) is the number of separations inside a range of width Δs, divided by the total number of separations in the cluster (25 ⋅ 24/2 = 300). We made 20 bins using Δs = 2RGGD27/20 = 2″, which provides an adequate sampling of the dataset. We note that the angular resolution is about 40 mas, and we defined the cluster radius RGGD27 = 20″ as the maximum separation between a star in the cluster and the average position of all the cluster stars.
Figure D.1a shows the distribution function p(s) of the separations measured for the protostellar disks of the GGD 27 cluster as a function of the separation s. CW2004 demonstrated that for clusters showing a smooth volume density profile, n ∝ r−α, the distribution function has only one maximum, while that of GGD 27 presents two peaks separated by 6″ (∼0.04 pc), indicative of subclustering and possible fractal structure. The first peak is located at a distance of 6″ or 0.04 pc, which approximately corresponds to the distance of three main groups in GGD 27: MM1 and ALMA 7-8 with ALMA 14-16, MM1 and ALMA 7-8 with MM2(W) and MM2(E), and MM2(W) and MM2(E) with ALMA 14-16. The dip between the two peaks corresponds to a separation of about 8.5″ (∼0.06 pc) and it is significant as long as the binning in the p(s) versus s plot is not larger than 2″ (∼0.01 pc), which is approximately one-third of the separation between the two peaks in that plot. The second peak in the plot corresponds to separations about 12″ (∼0.08 pc). We note that the decline for s > 1 is due to the ALMA primary beam. The sampling of separations is probably good enough up to this distance within our field of view, but note that these results can change if fainter sources are detected (through deeper observations) or a more spread out mosaic is carried out and new sources are detected outside of the current ALMA primary beam. Finally we estimate the mean separation between the GGD 27 disks (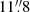 , about 0.08 pc) and normalize it to the cluster radius,
, about 0.08 pc) and normalize it to the cluster radius, 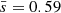 . We use
. We use 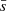 in the next section to derive the diagnostic parameter Q.
in the next section to derive the diagnostic parameter Q.
 |
Fig. D.1. Panel a: distribution function of separations between protostellar disks in the GGD 27 cluster. The quantity p(s) Δs is the probability that the projected separation between two randomly selected disks of the cluster is within s and s + Δs. Separations s are normalized to the cluster radius (20″) in the bottom axis, while the top axis extends up to twice this radius. The radius is determined as the distance from the average position of all the cluster members to its furthest protostellar disk. Dotted vertical lines mark the two peaks and the dip in the p(s) distribution. The right axis represents the number of pairs of stars within each separation bin Δs. Panel b: MST for the ALMA detections of the GGD 27 cluster. The positions of the cluster members are given with respect to the position of MM1 (ALMA 5) of Table A.1. MM1 and ALMA 14 are marked with colored stars. The gray cross marks the average position of the GGD 27 sources. |
D.2. Q parameter
The Q parameter was introduced by CW2004 to discern between clusters with a gradual decrement on the stellar density (centrally peaked clusters) and those showing a self-similar or subclustering appearance (fractal; see also Parker 2018). In order to use this formalism the MST of the cluster has to be constructed. The MST measures the shortest path length connecting all points in a given sample without including closed loops (Kruskal 1956). Figure D.1b presents the MST for the GGD 27 cluster. It shows two overdensities of sources around MM1 and ALMA 14 locations (colored stars), separated by 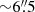 (0.05 pc), roughly matching the separations of the first peak in Fig. D.1a.
(0.05 pc), roughly matching the separations of the first peak in Fig. D.1a.
Following CW2004 and once the MST of the GGD 27 cluster has been built, we derived the normalized mean edge length, 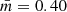 , defined as the sum of the MST paths linking all the stars divided by the normalization factor
, defined as the sum of the MST paths linking all the stars divided by the normalization factor 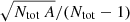 , where A is the cluster projected area. Having
, where A is the cluster projected area. Having 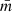 and
and 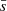 , we now obtain the value for the parameter
, we now obtain the value for the parameter 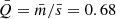 . This parameter serves as a diagnostic to distinguish between a cluster with a smooth overall radial density gradient of sources (
. This parameter serves as a diagnostic to distinguish between a cluster with a smooth overall radial density gradient of sources (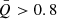 ) and a cluster with a multiscale fractal subclustering (
) and a cluster with a multiscale fractal subclustering (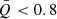 ). GGD 27 results to be of the second type, and moreover, given its
). GGD 27 results to be of the second type, and moreover, given its 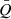 value we estimate that it has a notional fractal dimension D ≃ 2.2 (see Fig. 5 in CW2004), which stands for a moderate subclustering (D ranges between 1.5, for strong subclustering, and 3, for no subclustering). We note that by using this method it cannot be decided if a cluster is truly fractal in the sense that it replicates structures at different spatial scales (i.e., if it is hierarchically self-similar). Low values of
value we estimate that it has a notional fractal dimension D ≃ 2.2 (see Fig. 5 in CW2004), which stands for a moderate subclustering (D ranges between 1.5, for strong subclustering, and 3, for no subclustering). We note that by using this method it cannot be decided if a cluster is truly fractal in the sense that it replicates structures at different spatial scales (i.e., if it is hierarchically self-similar). Low values of 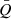 , such as that found in GGD 27, are expected in young clusters before any primordial subclustering washes out as the cluster acquires a radial density profile due to dynamical relaxation. Therefore, this supports the youthfulness of the GGD 27 cluster.
, such as that found in GGD 27, are expected in young clusters before any primordial subclustering washes out as the cluster acquires a radial density profile due to dynamical relaxation. Therefore, this supports the youthfulness of the GGD 27 cluster.
D.3. Mass segregation
For our second statistical analysis, we define the MSR (ΛMSR; Allison et al. 2009) as follows:
where Lmassive is the summation of the path-lengths in the MST of the N most massive sources. Lnorm is the average path-length of the MST of N sources picked randomly in the cluster. We take an average over 1000 random sets of N sources in the cluster to estimate Lnorm and derive its statistical deviation σnorm along the 1000 runs (Gavagnin et al. 2017). If ΛMSR is greater than unity, the path-length of the N most massive sources is shorter than the average path-length of N randomly chosen sources in the cluster, indicating a concentration of massive sources with respect to the random sample and hence a mass segregation.
To build up the plot in Fig. 3 we estimated ΛMSR for N = 2, …, 25. We removed ALMA 1 and ALMA 2 from this analysis since they are associated with a Class II and a Class III YSO, respectively (Pravdo et al. 2009, see also Table A.1). In addition, Pravdo et al. (2009) classified MM1 and ALMA 16 as Class I protostars. The remaining 21 ALMA dust continuum sources do not have an infrared counterpart and are not detected in X-rays (see Pravdo et al. 2009), suggesting that these disks are most likely associated with Class 0/I protostars. In addition, the very high extinction that may hidden X-ray sources only affects the northeastern region (see the NH3 emission map of Gómez et al. 2003). Thus, our analysis accounts only for the youngest objects of the GGD 27 cluster. Figure 3 shows a dominant ΛMSR value of about one, which means no mass segregation or random distribution regarding the protostellar disk masses. Only the two most massive protostellar disks, MM1 and MM2(E), which are located at the center of the gravitational potential of the cluster (e.g., see Gómez et al. 2003), appear segregated from the rest with a separation about 1.7 times shorter than the average distance between two sources picked up at random from the cluster. This result, together with the low value of the 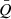 parameter, is in agreement with the expected youth of the cluster; older clusters are dynamically relaxed, implying that mass segregation has taken place already. Thus, it is probable that the disks detected are associated with protostars (Class 0 and Class I YSOs), since disks in Class II and Class III YSOs would be too faint to be detected with our sensitivity. For instance, Plunkett et al. (2018) have found that none of the Class II sources and most of the Flat spectrum YSOs identified with Spitzer by Dunham et al. (2015) in the Serpens South protocluster (located at a distance of 436 pc) is detected at millimeter wavelengths with ALMA with a sensitivity of 1.5 mJy beam−1. At the distance of GGD 27 this sensitivity would correspond to a flux density of 145 μJy, hence a Class II YSOs in GGD 27 would be well below our 3σ rms noise level. On the other hand, prestellar cores are too extended so they are completely filtered out by the interferometric observations. Thus, the age problem is minimal in our sample of millimeter sources, which may include disks from Class 0 and Class I protostars, and only two disks associated with a Class II (ALMA 1) and a Class III (ALMA 2) YSOs, which have been removed from the mass segregation analysis. However, we should make some caveats regarding the derived masses. The resulting mass estimates for the protostellar disks may not correlate with the masses of the protostars. While there is an observational trend between the disk mass and stellar mass (see e.g., Pascucci et al. 2016), the large scatter found prevented us from adopting this relation to derive the stellar mass. Nevertheless, the correlation between protostellar masses and protostellar disk masses can be roughly true for young Class 0 and Class I protostars, for which the derived mass contains most the mass of the whole system (Andre et al. 2000). Therefore we are confident that our analysis indicates that the spatial distribution of the protostellar disk population does not depend on the protostellar disk masses, and hence the derived masses reflect the lack of primordial mass segregation.
parameter, is in agreement with the expected youth of the cluster; older clusters are dynamically relaxed, implying that mass segregation has taken place already. Thus, it is probable that the disks detected are associated with protostars (Class 0 and Class I YSOs), since disks in Class II and Class III YSOs would be too faint to be detected with our sensitivity. For instance, Plunkett et al. (2018) have found that none of the Class II sources and most of the Flat spectrum YSOs identified with Spitzer by Dunham et al. (2015) in the Serpens South protocluster (located at a distance of 436 pc) is detected at millimeter wavelengths with ALMA with a sensitivity of 1.5 mJy beam−1. At the distance of GGD 27 this sensitivity would correspond to a flux density of 145 μJy, hence a Class II YSOs in GGD 27 would be well below our 3σ rms noise level. On the other hand, prestellar cores are too extended so they are completely filtered out by the interferometric observations. Thus, the age problem is minimal in our sample of millimeter sources, which may include disks from Class 0 and Class I protostars, and only two disks associated with a Class II (ALMA 1) and a Class III (ALMA 2) YSOs, which have been removed from the mass segregation analysis. However, we should make some caveats regarding the derived masses. The resulting mass estimates for the protostellar disks may not correlate with the masses of the protostars. While there is an observational trend between the disk mass and stellar mass (see e.g., Pascucci et al. 2016), the large scatter found prevented us from adopting this relation to derive the stellar mass. Nevertheless, the correlation between protostellar masses and protostellar disk masses can be roughly true for young Class 0 and Class I protostars, for which the derived mass contains most the mass of the whole system (Andre et al. 2000). Therefore we are confident that our analysis indicates that the spatial distribution of the protostellar disk population does not depend on the protostellar disk masses, and hence the derived masses reflect the lack of primordial mass segregation.
All Tables
All Figures
 |
Fig. 1. Positions (indicated by crosses and labeled according to Table A.1) of the dust continuum sources detected in the GGD 27 region. Images of the individual sources are shown in Fig. 2. |
| In the text | |
 |
Fig. 2. Composite of the all sources detected in the field of view (except for MM1/ALMA 5). The images were corrected for the primary beam response. Black contours are −4, −3, 3, 4, 5, 8, 13, 20, 35, and 50 times the local rms noise of each image (Table A.1). White contours are 100, 150, 200, 250, and 300 times the local rms noise. Table A.1 lists their absolute positions. In each panel we labeled the second and arcsecond position of the center of the panel. The color scale is the same for all panels and it is shown at the top of the figure (units of Jy beam−1). The synthesized beam is shown in the bottom right corner of the first image. |
| In the text | |
 |
Fig. 3. Mass segregation ratio (ΛMSR; see Appendix D.3) as a function of the NMST (MST) most massive disks of GGD 27. ALMA 1 and ALMA 2, classified as Class II and Class III YSOs, respectively, are not included. The main deviation from a uniform behavior around unity is for NMST = 2, suggesting that the two most massive sources are closer to each other than the average distance between two random sources. The horizontal line at ΛMSR = 1 indicates the regime where sources show no evidence for mass segregation. |
| In the text | |
 |
Fig. 4. Panel a: 1.14 mm flux (scaled to a distance of 140 pc) as a function of the radius for all disks detected in GGD 27 (black squares and triangles), Taurus-Auriga (red circles; Guilloteau et al. 2011; Piétu et al. 2014), Ophiuchus (gray circles; Cieza et al. 2019), and ONC (yellow squares; Eisner et al. 2018). The flux at 1.14 mm was extrapolated from the measurements at 1.3 mm for Taurus and Ophiuchus disks and from 850 μm for ONC disks using an spectral index of α = 3. The dotted line depicts the average mass sensitivity limit (8σ). We show, at the top, the median and its dispersion (1st and 3rd quartiles) for GGD 27 (black), Taurus (red), Ophiuchus (gray), and ONC (yellow) samples. The most massive disks MM1 and MM2(E) were removed from the plot. Panel b: disk masses in GGD 27 (black squares) and ONC (red circles) clusters as a function of their projected distance from the massive star IRAS 18162−2048 and θ1 Ori C (Mann et al. 2014), respectively. The dotted line depicts the average mass sensitivity limit while the dashed line indicates the higher 8σ limit close to MM1. Panel c: disk radii in GGD 27 as a function of their projected distance from the massive star. In all panels upper limits in Rdisk are indicated with triangles. |
| In the text | |
 |
Fig. C.1. Comparison between the disk radii obtained with a Gaussian fit and adopting a power law with an index of q = 1.1 for the sample of disks (Table 1). Red arrows indicate the upper limits. The solid lines shows the linear regression from the data, which indicates a relationship of RGauss = 0.48 ± 0.04 × RPower law. |
| In the text | |
 |
Fig. D.1. Panel a: distribution function of separations between protostellar disks in the GGD 27 cluster. The quantity p(s) Δs is the probability that the projected separation between two randomly selected disks of the cluster is within s and s + Δs. Separations s are normalized to the cluster radius (20″) in the bottom axis, while the top axis extends up to twice this radius. The radius is determined as the distance from the average position of all the cluster members to its furthest protostellar disk. Dotted vertical lines mark the two peaks and the dip in the p(s) distribution. The right axis represents the number of pairs of stars within each separation bin Δs. Panel b: MST for the ALMA detections of the GGD 27 cluster. The positions of the cluster members are given with respect to the position of MM1 (ALMA 5) of Table A.1. MM1 and ALMA 14 are marked with colored stars. The gray cross marks the average position of the GGD 27 sources. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



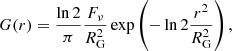
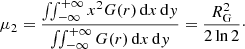
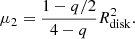
![$$ \begin{aligned} R_{\rm G}= \left[2\ln 2\frac{1-q/2}{4-q}\right]^{1/2}R_{\mathrm{disk} }= 0.46\,R_{\mathrm{disk} }. \end{aligned} $$](/articles/aa/full_html/2019/03/aa33687-18/aa33687-18-eq13.gif)