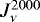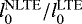EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 622 (February 2019) A&A, 622 (2019) A107 Full HTML
Free Access
Issue
A&A
Volume 622, February 2019
Article Number A107
Number of page(s) 7
Section Stellar atmospheres
DOI https://doi.org/10.1051/0004-6361/201834857
Published online 06 February 2019

© ESO 2019

1. Introduction

Spite & Spite (1982) reported in their pioneering work that the surface Li abundances of metal-poor late F and early G dwarfs in the halo were almost constant at A(Li) ~ 2.1 (logarithmic number abundances in the usual normalization of AH = 12.00) irrespective of metallicity. Although this value was considered at first to represent the initial Li composition created by Big-Bang nucleosynthesis (BBN), due to its remarkable constancy, it was later revealed to be considerably lower (by ~0.4–0.5 dex) than the cosmologically predicted primordial value, when the key parameter (baryon-to-photon ratio) for light-element production was established by analyzing the power spectrum of cosmic microwave background (CMB) based on the balloon-borne BOOMERANG experiment (de Bernardis et al. 2002) or the WMAP observation from space (Spergel et al. 2007). This so-called “cosmological Li problem” has attracted the attention of many astrophysicists, and a number of studies have been published on the subject. The historical aspect and the current status of this problem is summarized in the comprehensive review by Fields (2011), which includes most of the important references of that time.

Observationally, it has been almost established that the Li abundances spectroscopically determined for comparatively hot halo dwarfs near the turn-off point (corresponding to an effective temperature of 6500 K ≳ Teff ≳ 6000 K) are remarkably similarat ~2.1–2.2 (or higher by ~0.1–0.2 dex depending on the adopted Teff scale) with a considerably small dispersion over the metallicity range of − 3 ≲ [Fe/H] ≲ −1.5, often called the Spite plateau, though this plateau was revealed to show a slight [Fe/H]-dependent trend (decreasing tendency with a lowering of metallicity) that begins to breaks down (i.e., depletion with rather large dispersion) at the extremely metal-poor regime of [Fe/H] below approx. −3 (e.g., Meléndez et al. 2010; Sbordone et al. 2010; and references therein).

On the cosmological side, most people nowadays seem to believe that the primordial Li abundance due to BBN has been reliably settled at A(Li) = 2.64 ± 0.031 (Spergel et al. 2007), which is the value derived from the CMB observation by WMAP. Accordingly, based on the notion that the Spite plateau value is not primordial, various theoretical interpretations have been proposed to date to account for the reason why the observed lithium abundances of very old turn-off dwarf stars underwent appreciable changes from the original BBN value, for example solutions related to nuclear or particle physics, magnetic separation in the early universe, processes related to stellar physics suchas depletion in the pre-main sequence phase, or gravitational settling coupled with turbulent mixing (see references in Sect. 3 of Fields 2011 or in Sect. 1 of Fu et al. 2015). An in-depth discussion given by Asplund et al. (2006) is also informative.

Even so, it may be worthwhile to turn to the more fundamental question, “Are the observed Li abundances of Spite plateau stars truly reliable?” Actually, Kurucz (1995) once raised a critical remark that Li abundances derived by the conventional method could be considerably underestimated (by a factor of ~ 10) because classical 1D model atmospheres do not correctly describe the actual 3D inhomogeneous convective structure consisting of hot and cool convective cells and the Li I 6708 line is highly temperature-sensitive under the condition of almost all Li atoms being ionized. However, successive theoretical studies by different groups on the Li line formation in hydrodynamically inhomogeneous atmosphere showed that Kurucz (1995) claim was not correct because it was based on a too simplified, physically unrealistic modeling (Asplund et al. 1999, 2003; Cayrel & Steffen 2000). Accordingly, it is now generally believed that neither the 3D effect nor the non-local thermodynamical equilibrium (NLTE) effect can solve the Li discrepancy problem. This lead Asplund et al. (2006; Sect. 7.2) to state that “although the last word has not been said on the representation of the physics of the stellar atmospheres and the formation of the lithium lines, it would be extremely surprising if systematic errors in these areas were shown to resolve the lithium problem”.

However, our understanding of stellar atmospheres is far from complete; in particular, little is known about the upper atmospheric layers of metal-poor stars. In this respect, it should be noted that Takeda & Takada-Hidai (2011) reported the detection of the He I 10830 line in absorption in disk population I stars and in almost all population II stars in a wide range of metallicity down to [Fe/H] approximately − 3.7 as well, which suggests the existence of a high-temperature chromosphere2 because such a high-excitation line (χexc = 19.82 eV) cannot be observed in late-type stellar atmospheres with ever decreasing temperature towards the surface. Here, the behavior of line strengths is different for low-gravity giants (considerably large star-to-star dispersion) and high-gravity dwarfs (almost constant strength irrespective of metallicity over − 4 ≲ [Fe/H] ≲ −1) (cf. Fig. 3 therein). While the atmospheric heating for the former giants group may be due to some physical mechanism specific to unstable atmospheres (e.g., pulsation-induced shock) reflecting the low-density condition, the characteristic of the latter dwarfs group was rather unexpected because a rotation-induced dynamo mechanism would not work effectively in old stars where rotation should have been decelerated. So, this may suggest that rotation-independent “basal” chromospheric activity ubiquitously exists in all late-type dwarfs.

Whatever the physical process (acoustic wave, local dynamo, etc.) responsible for such a basal chromosphere may be, the important point is that very metal-poor halo dwarfs should have high-temperature layers (T ~ 104–105 K) in their upper atmospheres. If so, it is interesting to check whether the radiation emitted back from the hot chromosphere can have a significant influence on the formation of the Li I 6708 line (e.g., apparent weakening due to overionization) because the fraction of neutral lithium is so small (<0.1% in the photosphere of solar-type dwarfs) as to be very vulnerable to a slight change in the ionization balance. Could this idea shed any light on the Li-gap problem of Spite plateau stars?

This study was planned to examine this possibility by assuming a simple parameterized model. The points to be clarified are as follows:

  • Is it ever feasible to reproduce the Li abundance trend of the Spite plateau (i.e., systematic reduction by ~ 0.3–0.5 dex from the primordial value) under the influence of chromospheric back-radiation by an appropriate choice of parameters?

  • If so, what about the observational signature expected? Is it possible to find a way to verify such a model by actual observations?

2. Line formation under the existence of chromosphere

2.1. Modeling of chromospheric radiation

Since very little is known about the nature of chromospheres in old metal-poor stars, the following assumptions are made in this study in order to model the incident chromospheric radiation as simply as possible:

  • the chromosphere is modeled by a thin plane-parallel gaseous slab lying just above the normal model atmosphere;

  • this slab (homogeneous with frequency-independent opacity) is represented by two parameters (optical thickness τ0 and temperature T0), and emits only the thermal radiation with the source function expressed by the Planck function;

  • the structure of underlying the normal model atmosphere is not affected by the existence of such a high-temperature layer adjacent to the surface.

A schematic description of this model is depicted in Fig. 1. The chromospheric back radiation incident to the surface is expressed as Iν−(θ)=Bν(T0)[1−exp(−τ0/|cosθ|)]≃τ0Bν(T0)/|cosθ|   (for τ0≪1),\begin{eqnarray*} I^{-}_{\nu}(\theta) &=& B_{\nu}(T_{0})[1 - \exp(-\tau_{0}/|\cos\theta|)]\nonumber\\ &\simeq& \tau_{0} B_{\nu}(T_{0})/|\cos\theta| \;\;\; (\textrm{for} \; \tau_{0} \ll 1),\end{eqnarray*}(1)

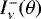where Iν−(θ)$I^{-}_{\nu}(\theta)$ is the chromospheric radiation (specific intensity) incident to the surface at an angle θ(> π∕2) relative to the outward normal and Bν is the Planck function.

thumbnail Fig. 1

Schematic description of the simple model chromosphere (uniform gaseous slab with temperature T0 and optical thickness τ0 lying just above the atmosphere) emitting thermal radiation incident at the surface.

2.2. NLTE calculation

Now that the incident chromospheric radiation 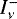Iν−$I^{-}_{\nu}$ has been specified, the next step is to carry out NLTE calculations (i.e., evaluation of the number population for each energy level of neutral lithium as functions of depth, by solving the coupled equations of statistical equilibrium and radiative transfer) in the same manner as usual, except that 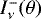Iν−(θ)$I^{-}_{\nu}(\theta)$ given by Eq. 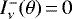(1) is used as the surface boundary condition instead of Iν−(θ) = 0$I^{-}_{\nu}(\theta)\,{=}\,0$.

As for the basic model atmospheres, the Kurucz (1993a) ATLAS9 models with Teff = 6250 K and log g = 4.0 (corresponding to the representative atmospheric parameters of Spite plateau stars) but with widely different metallicities ([Fe/H] ranging from 0 down to − 5 with a step of 1 dex) were adopted. Similarly, the Kurucz (1993b) opacity distribution function corresponding to the model metallicity was used to calculate the radiation field at each depth. For the microturbulence and input lithium abundance, a typical value of 1.5 km s−1 and the primordial value of A(Li) = 2.64 (see footnote 1) were assigned, respectively; see Takeda & Kawanomoto (2005, Sect. 3) and the references therein for the details of the adopted NLTE calculation procedures3.

Regarding the combination of (τ0, T0), which determines the incident chromospheric radiation (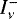Iν−$I^{-}_{\nu}$), it should be noted that τ0 simply scales the strength of 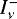Iν−$I^{-}_{\nu}$ (as ∝ τ0 since τ0 ≪1 should hold), while T0 controls both the strength and the energy distribution of 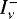Iν−$I^{-}_{\nu}$. This means that, as far as the UV photoionizing radiation field specifically important for Li ionization equilibrium is concerned, its strength can be adjusted by changing only T0 even if τ0 is fixed at an arbitrary value (tentatively assumed to be 10−3). Given this τ0, four logT values of 4.0, 4.3, 4.5, and 5.0 were eventually chosen after some test calculations. A summary of the adopted parameters for each model is presented in Table 1. We note that “STD” means the usual NLTE calculation done on the standard model without chromospheric irradiation.

Table 1

Summary of the adopted parameters for each model.

3. Discussion

3.1. Influence of chromospheric irradiation

Figure 2 shows the runs of radiation field Jν at 2000 Å (important for the photoionization of Li), the ratio of NLTE to LTE line opacity (≃ b1), and the ratio of line source function to Planck function (≃b2∕b1) as a function of depth, which were computed for each treatment of chromospheric radiation (characterized by T0) on the models of different metallicities ([Fe/H] = 0, − 2, and − 4). It is evident from Figs. 2a–c that Jν is progressively enhanced over Bν with increasing T0, as naturally expected. Although this tendency of Jν > Bν in UV has already been observed even in the STD model, inward irradiation of sufficiently strong 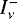Iν−$I^{-}_{\nu}$ at the surface can make Jν outweigh Bν by orders of magnitude. This indicates that the overionization effect, which is caused by an imbalance between the photoionization rate (determined by Jν) and the recombination rate (controlled by Bν because recombination is electron collision process), becomes more important as the chromospheric incident radiation is intensified. Figures 2d–f actually suggest that the NLTE line opacity of the Li I 6708 line (resonance line: transition from the ground level to the first excited level) is considerably reduced compared to the LTE line opacity (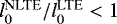l0NLTE/l0LTE<1$l_{0}^{\textrm{NLTE}}/l_{0}^{\textrm{LTE}} < 1$) because the ground level is depopulated as a result of overionization. This effect, being more significant with an increase in T0, acts in the direction of line weakening, and is the most important impact of chromospheric radiation upon the line strength. On the other hand, the influence of changing T0 upon the line source function is generally insignificant except for the strongest irradiation case (Figs. 2g–i).

The spectral distributions of the emergent flux (Hν) at the surface4 corresponding to each different T0 (computed for the [Fe/H] = − 2 model) are depicted in Fig. 3, where the distribution of assumed chromospheric radiation corresponding to each T0, τ0 Bν (T0)[= 10−3Bν(T0)], is also shown for comparison. We can see from this figure that the surface flux is manifestly enhanced in the ultraviolet (UV) region (below ≲3000 Å) in the chromospheric models in comparison with the STD model, while the change in the optical region (≳4000 Å) is insignificantly small (except for the T50 model). This means that the key to clarifying the existence and nature of a possible chromospheric layer is to observe the UV energy distribution.

thumbnail Fig. 2

Panels a–c: depth-dependence of Jν2000$J_{\nu}^{2000}$ (mean intensity at λ = 2000 Å) for each of the five models (STD, tm30T40, tm30T43, tm30T45, tm30T50); the local Planck function (Bν: dashed line) is also depicted for comparison. Panels d–f and g–i: runs of l0NLTE/l0LTE$l_{0}^{\textrm{NLTE}}/l_{0}^{\textrm{LTE}}$ (ratio of NLTE to LTE line opacity; ≃ b1) and SL ∕B (ratio of line source function to Planck function; ≃ b2∕b1) of the Li I 6708 line, respectively. The abscissa for each panel is the logarithm of continuum optical depth at 5000 Å.

3.2. Comparison with the observed trends

We are now ready to discuss the main topic of this study: can the observed trend of the Spite plateau be explained by the line-formation models under chromospheric irradiation?

By using the NLTE departure coefficients resulting from the calculations in Sect. 2.2, the NLTE equivalent widths of the Li I 6708 resonance doublet line (W) were computed for each of the models by using the Kurucz (1993a) WIDTH9 program5, while assuming the primordial lithium abundance as given (Agive = 2.64); see Table 3 of Takeda & Tajitsu (2017) for the atomic parameters of the Li I 6708 line adopted for this evaluation of W, where only lines of 7Li were included (6 Li ∕7Li = 0). Then, the computed W6 for each model was further analyzed in the usual manner by using the departure coefficient of the standard model (STD in Table 1)7 to inversely derive A, which is the apparent lithium abundance obtained by treating the chromosphere-affected equivalent width (computed for the given Agive) by the classical model without chromosphere. The resulting values of W and A for each of the models, which are summarized in Table 2, are plotted against [Fe/H] in Figs. 3a and b, respectively8.

Figure 3a reveals that the strength of Li I 6708 can be considerably decreased. The extent of reductionnaturally grows as the chromospheric radiation is enhanced, but the trend is not so much monotonic as exponential; i.e., while little change is observed in the T40 model, a decrease of a factor of ~ 2–3 is found in the T43 or T45 models, the T50 model even yielding a reduction as much as ~ 1∕10. More interesting is the metallicity dependence. In the STD model, W tends to show a marginal increase with a decrease in [Fe/H] (especially from [Fe/H] = 0 to − 1), which is due to a lowering of continuum opacity. However, a progressive decrease in W is observed with decreasing metallicity in the models including chromospheric radiation (except for T40) because the overionization caused by chromospheric irradiation penetrates deeper according to the increase of atmospheric transparency (i.e., decrease of opacity/metallicity). This situation is illustrated in Fig. 4, which shows the metallicity dependence of 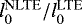l0NLTE/l0LTE$l_{0}^{\textrm{NLTE}}/l_{0}^{\textrm{LTE}}$ and SL ∕B (though the former influence is decisively important, while the latter is insignificant) in the deeper atmosphere including the line-forming region.

As a result of this behavior of W, the apparent Li abundances (A) inversely derived from W by using the standard model also show interesting characteristics in the context of the Li discrepancy problem in question (cf. Fig. 3b): A is found to be distinctly below the primordial value (2.64) by ~0.3–0.5 dex for the T43 or T45 models. Moreover, the slight [Fe/H]-dependent tendency (i.e., a gradual decrease of A toward lower [Fe/H]) seen in the chromosphere irradiation cases is worth noting. Our models can reproduce the extent of reduction, and also the metallicity dependence actually observed in Spite plateau stars in the range of − 4 ≲ [Fe/H] ≲ −1.5, as illustrated in Fig. 5 where the predicted A versus [Fe/H] relations for T43 and T45 models are compared with the observed data (taken from four representative studies).

Accordingly, the hypothesis of superficial weakening of the Li I 6708 line (due to substantial overionization of neutral lithium caused by extra UV radiation from the chromosphere), which was tentatively proposed as a solution to the cosmological Li problem of metal-poor turn-off stars, stands as a possibility and is worth further investigation.

Table 2

Computed equivalent widths and Li abundances.

thumbnail Fig. 3

Wavelength distribution of emergent surface flux Hν [ ≡ (1/2) ∫−1+1Iμμdμ$\int_{-1}^{+1} I_{\nu}\,\mu {\rm d}\mu$, where μ = cos θ] resulting from each model (solid lines). Wavelength distribution of chromospheric radiation [τ0Bν(T0) = 10−3 Bν(T0)] assumed for each model (dotted lines).
thumbnail Fig. 4

Panel a: NLTE equivalent widths of Li I 6708 line (W; computed for given primordial lithium abundance of 2.64 for each of the five models) plotted against [Fe/H]. Panel b: NLTE Li abundances (A; inversely obtained from each model’s W by using thestandard procedure of STD model) plotted against [Fe/H].
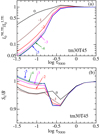thumbnail Fig. 5

Depth-dependence of the NLTE to LTE line opacity ratios (upper panel) and line source function to Planck function ratios (lower panel), which were computed for the tm30T45 models of different metallicities ([Fe/H] = 0, −1, −2, −3, −4, and −5).
thumbnail Fig. 6

Comparison of the predicted Li abundance vs. metallicity relations (lines) for two models (tm03T43 and tm03T45) with the observed data (symbols) of warm metal-poor dwarfs taken from Thorburn (1994; Teff > 6100 K; crosses), Ryan et al. (1999; open squares), Asplund et al. (2006; open circles), and Meléndez et al. (2010; Teff > 6100 K; filled squares). The horizontal dashed line indicates the primordial (CMB+BBN) Li abundance of 2.64.

3.3. The next step

This pilot study has shown that the characteristics of the Li abundances derived for metal-poor turn-off dwarfs, which show considerably small dispersion but are systematically lower than the primordial abundance established by observational cosmology, could be explained by the scenario of superficial abundance underestimation as a result of appreciable line weakening (due to overionization caused by chromospheric radiation). However, since the adopted two-parameter model is evidently too simple, some further considerations (even if speculative) may be due regarding the more realistic nature of possible overionization source and the feasibility of model verification from the observational side.

Regarding the radiation from the chromosphere, where the region below ≲2300 Å is the most important in the context of photoionizing neutral lithium atoms, the hypothesis of emitting only thermal radiation (continuum spectrum described by the Planck function) is probably unrealistic. The spectrum of chromospheric radiation must be more complex (including continuum emission as well as line emission) as a result of intricate physical processes in the high-temperature plasma. However, photoionization by strong UV emission lines might be less relevant for the present case involving nearly [Fe/H]-independent Li abundances in Spite plateau stars because the strengths of such photoionizing emission lines would significantly depend upon the metallicity. Instead, a metallicity-independent mechanism would be preferable for producing this radiation. In this context, it may be worth recalling that the detection of the He I 10830 line corroborated the existence of the chromosphere in very metal-poor stars, which was the motivation for this study (Sect. 1). For the case of the Sun, it is considered that the lower level of this He I 10830 transition (2s 3S) is mainly populated by photoionization of He I by extreme UV radiation (λ < 504 Å) from the solar corona, followed by recombination of He II to populate He I 2s 3S (e.g., Avrett et al. 1994). If this mechanism is assumed to be effective also for the formation of He I 10830 in population II dwarfs, emission of continuum radiation at λ< 2600 Å is expected as a result of the He II + e → He I 2s 3S recombination process [χion(He I) − χexc(He I 2s 3S) = 24.59 − 19.82 = 4.77 eV (corresponding to ~2600 Å], which may contribute to an efficient photoionization of neutral lithium (whose edge is at ~ 2300 Å).

However, constructing any reliable model of chromsphere (+corona) for simulating its radiation field is hardly possible for the present case of very metal-poor stars since observational information is seriously lacking. First of all, it is necessary to examine whether a UV photoionizing radiation strong enough to cause substantial overionization of Li exists, because spectral energy distributions of successful models (which can explain the observed trend of Spite plateau) show strong enhancement in the important UV region (~ 1000–3000 Å) as remarkedin Sect. 3.1 (see Fig. 3).

Unfortunately, such UV photometric observations have barely been done for very metal-poor halo dwarfs, for which a small number of available spectroscopic studies using the Hubble Space Telescope paid attention only to the core emission of strong lines indicative of chromospheric activity; e.g., Mg II doublet lines at ~ 2800 Å or Lyman α (Peterson & Schrijver 1997, 2001). Accordingly, checking the existence of significant UV excess in such comparatively warm turn-off dwarfs in the metal-deficient regime (− 4 ≲ [Fe/H] ≲ −1.5) would be a touchstone for deciding the validity of this hypothesis. In the case of the Sun, where a wealth of observational data is available, such UV excess is not seen. That is, the observed solar flux at 2000 ≲ λ ≲ 2500 Å is very low and that at λ ≲ 2000 Å is almost zero, and this is consistent with the theoretical flux predicted by the Kurucz (1993a) ATLAS9 solar model atmosphere (cf. Takeda et al. 2011, Fig. 11). Even so, we have no idea how the situation would come out for the case of very metal-poor stars, which may be markedly different from the Sun (i.e., metal-rich case where the UV flux is determined by overlapping opacities of numerous spectral lines).

As an alternative possibility, it might be worthwhile to examine the all-sky UV photometric survey data of GALEX9, which are available in two bands: far-UV (λeff = 1516 Å, ΔλFWHM = 269 Å) and near-UV (λeff = 2267 Å, ΔλFWHM = 616 Å). According to an estimation based on the results in Fig. 3, while fFUV is lower than fNUV by a factor of several tens for the case of the STD model, these two fluxes are almost comparable for the T43 or T45 models. Therefore, if both fluxes were detected at the reliable level and successful identification could be made, these data might be usable for checking the existence of UV excess.

In any case, it is undoubtedly important to observationally establish the UV energy distribution (and also the strength of He I 10830 line) for a number of Spite plateau stars, which would provide us with more insight to the physical nature of chromospheric layers in these stars and be able to confirm or disconfirm the interpretation proposed in this study.

Finally, if a special overionization due to extra chromospheric radiation were really operative to superficially reduce the Li abundances of plateau stars by ~0.4–0.5 dex, its influence should not be limited to lithium but should also reach other elements. For example, the Fe I/Fe II ionization equilibrium would be so affected that the abundances derived from Fe I lines in LTE are appreciably underestimated, whereas those from Fe II lines remain practically unaffected. While such an overionization is already expected in very metal-poor dwarfs even within the framework of traditional atmospheric models (by ~ 0.2–0.3 dex; e.g., Mashonkina et al. 2011), chromospheric irradiation would further exaggerate this effect. Although detailed NLTE calculations are necessary for quantitative estimation of this impact case by case, it may be expected from a simple analogy that the resonance lines of other neutral alkali elements with low ionization potential (such as Na I 5890/5896 or K I 7665/7699) would behave similarly to Li I 6708. Accordingly, it would be interesting to check whether any meaningful difference exists between the K abundances (unaffected by evolution-induced mixing) derived from very metal-poor Spite plateau stars and those from cooler red giants at the same metallicity.

4. Conclusion

Regarding what is known as the cosmological Li problem, which is the discrepancy between the lithium abundances of metal-poor turn-off dwarfs being nearly constant irrespective of metallicity (Spite plateau) and the primordial BBN value almost established from the CMB observations (e.g., WMAP), various explanations have been proposed, most of which suppose that the observed stellar Li abundance reflects the real composition in the atmosphere and would have been changed (i.e., decreased) from the initial value by some physical mechanism.

This study casts doubt on this general belief, and proposes that the problem might be on the technical side of abundance determination; i.e., the surface Li abundances of these stars might have been underestimated. This suspicion was motivated by the observational fact that hot chromosphere exists in metal-poor dwarfs, as evidenced by the detection of the He I 10830 line whose strength is almost constant irrespective of the metallicity. If so, chromospheric UV radiation might induce significant overionization of neutral lithium and considerable weakening of the Li I 6708 line, which could lead to an underestimation of the Li abundance if derived by the conventional method of analysis. The aim of this investigation was to examine this possibility. As to the modeling of chromospheric radiation, thermal radiation emitted by a uniform slab (characterized by optical thickness τ0 and temperature T0) was simply assumed. Incorporating this incident radiation in the surface boundary condition, NLTE calculations for neutral Li atoms were carried out with different combinations of (τ0, T0). In addition, based on the resulting NLTE departure coefficients, how the equivalent widths and the corresponding abundances are affected by these parameters were also investigated.

The results turned out rather satisfactory. If the parameters are adequately chosen, the equivalent width of Li I 6708 can be considerably reduced by a factor of ~2–3 due to the overionization effect caused by an enhanced UV radiation irradiated from the chromosphere, which eventually leads to an appreciable decrease in the apparent abundance by ~ 0.3–0.5 dex, being consistent with the discrepancy in question. Moreover, the observed slight metallicity-dependent slope of the plateau (i.e., Li abundance tends to slightly decrease with a decrease in [Fe/H]) can also be reproduced, because the overionization stemming from chromospheric irradiation penetrates deeper with an increase in atmospheric transparency (resulting from decreased metallicity).

Accordingly, the superficial underestimation of Li abundances, which results from an appreciable weakening of Li I 6708 line caused by considerable overionization due to external radiation from the chromosphere, may be a possible interpretation of the cosmological Li problem and is worth further investigation. However, since this calculation is based on a simple parameterized model, successful reproduction of the observed trend established by arbitrarily changing the parameters does not mean that this concept is justified. Therefore, in order to check the validity of this hypothesis, it is important to confirm the significant UV excess in these Spite plateau stars, which should be detected if significant overionization is actually present, though very few such UV spectrophotometric observations have been done to date for this class of very metal-poor stars.

References

  1. Asplund, M., Nordlund, Å., Trampedach, R., & Stein, R. F. 1999, A&A, 346, L17 [NASA ADS] [Google Scholar]
  2. Asplund, M., Carlsson, M., & Botnen, A. V. 2003, A&A, 399, L31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  3. Asplund, M., Lambert, D. L., Nissen, P. E., Primas, F., & Smith, V. V. 2006, ApJ, 644, 229 [NASA ADS] [CrossRef] [Google Scholar]
  4. Avrett, E. H., Fontenla, J. M., & Loeser, R. 1994, in Infrared Solar Physics, eds. D. M. Rabin, J. T. Jefferies, & C. Lindsey (Dordrecht: Kluwer), Proc. IAU Symp., 154, 35 [NASA ADS] [CrossRef] [Google Scholar]
  5. Cayrel, R., & Steffen, M. 2000, in The Light Elements and Their Evolution, Proc. IAU Symp. 198, eds. L. da Silva, M. Spite, & J. R. de Medeiros (San Francisco: Astron. Soc. Pacific), 437 [Google Scholar]
  6. Coc, A., Goriely, S., Xu, Y., Saimpert, M., & Vangioni, E. 2012, ApJ, 744, 158 [NASA ADS] [CrossRef] [Google Scholar]
  7. Coc, A., Uzan, J.-P., & Vangioni, E. 2014, Can Mirror Matter Solve the Cosmological Lithium Problem? AIP Conf. Ser., 1594, 12 [NASA ADS] [Google Scholar]
  8. de Bernardis, P., Ade, P. A. R., Bock, J. J., et al. 2002, ApJ, 564, 559 [NASA ADS] [CrossRef] [Google Scholar]
  9. Fields, B. D. 2011, Ann. Rev. Nucl. Part. Sci., 61, 47 [NASA ADS] [CrossRef] [Google Scholar]
  10. Fu, X., Bressan, A., Molaro, P., & Marigo, P. 2015, MNRAS, 452, 3256 [CrossRef] [Google Scholar]
  11. Kurucz, R. L. 1993a, Kurucz CD-ROM, No. 13 (Cambridge, MA: Harvard-Smithsonian Center for Astrophysics) [Google Scholar]
  12. Kurucz, R. L. 1993b, Kurucz CD-ROM, No. 14 (Cambridge, MA: Harvard-Smithsonian Center for Astrophysics) [Google Scholar]
  13. Kurucz, R. L. 1995, ApJ, 452, 102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Mashonkina, L., Gehren, T., Shi, J.-R., Korn, A. J., & Grupp, F. 2011, A&A, 528, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Meléndez, J., Casagrande, L., Ramírez, I., Asplund, M., & Schuster, W. J. 2010, A&A, 515, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Peterson, R. C., & Schrijver, C. J. 1997, ApJ, 480, L47 [NASA ADS] [CrossRef] [Google Scholar]
  17. Peterson, R. C., & Schrijver, C. J. 2001, in The 11th Cool Stars, Stellar Systems and The Sun,, eds. López, R. Rebolo, & M. R. Zapatero (San Francisco: ASP), ASP Conf. Ser. Vol. 223, 300 [NASA ADS] [Google Scholar]
  18. Ryan, S. G., Norris, J. E., & Beers, T. C. 1999, ApJ, 523, 654 [NASA ADS] [CrossRef] [Google Scholar]
  19. Sbordone, L., Bonifacio, P., Caffau, E., et al. 2010, A&A, 522, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  20. Spergel, D. N., Bean, R., Doré, O., et al. 2007, ApJS, 170, 377 [NASA ADS] [CrossRef] [Google Scholar]
  21. Spite, F., & Spite, M. 1982, A&A, 115, 357 [NASA ADS] [Google Scholar]
  22. Takeda, Y., & Kawanomoto, S. 2005, PASJ, 57, 45 [NASA ADS] [Google Scholar]
  23. Takeda, Y., & Tajitsu, A. 2017, PASJ, 69, 74 [NASA ADS] [Google Scholar]
  24. Takeda, Y., & Takada-Hidai, M. 2011, PASJ, 63, 547 [NASA ADS] [Google Scholar]
  25. Takeda, Y., Tajitsu, A., Honda, S., et al. 2011, PASJ, 63, 697 [NASA ADS] [Google Scholar]
  26. Thorburn, J. A. 1994, ApJ, 421, 318 [NASA ADS] [CrossRef] [Google Scholar]
1

The value of 2.64 is used as the primordial lithium abundance throughout this paper, although slightly higher values of ~2.7 reported by successive studies may be more adequate (cf. Coc et al. 2012, 2014).

2

In this paper, the term chromosphere is used broadly to indicate the high-temperature zone in the upper atmosphere (i.e., not the layer specifically similar to the solar chromosphere). As such, this word may also be regarded to represent the whole concept including chromosphere, transition layer, and corona in the solar analogy.

3

The reasonability of our NLTE calculation program may be assured by checking the consistency of computed NLTE corrections with those independently derived by previous studies using different codes; cf. Takeda & Kawanomoto (2005, Fig. 4) for G dwarfs and Takeda & Tajitsu (2017, Fig. 8) for G giants.

4

It should be noted that this Hν is the flux at the “surface” just below the chromospheric layer (indicated by the thick line in Fig. 1). In order to obtain the flux observed by an external observer, the radiation emitted by the thin chromosphere (dotted line in Fig. 3) has to be added.

5

This original program was considerably modified in order to handle the total equivalent width of multicomponent lines and to take into account the departure from LTE. While the NLTE effect was incorporated through the departure coefficients, we note that no special change was made to the surface boundary condition of radiative transfer equation in this WIDTH9 program (i.e., incident chromospheric radiation at the surface was not considered, which is insignificant; cf. footnote 6).

6

The remark given in footnote 4 also applies to this case. Calculations of equivalent widths by the WIDTH9 program are based on the emergent flux computed at the surface just below the chromosphere. Therefore, strictly speaking, the derived results (Table 2) do not correspond to those observed by an external observer, for which the radiation from the chromosphere should be added to the surface flux, resulting in a somewhat weaker equivalent width due to dilution. However, this effect is insignificantly small for T40, T43, and T45 (τ0Bν is less than ≲1∕10 of Hν at the wavelength of Li I 6708 line, though both are comparable for T50; see Fig. 3).

7

For the abundance derivation using the STD model, the difference between LTE and NLTE abundances (i.e., NLTE correction) is so small (a few hundredths of a dex at most) that both are almost the same in the practical sense.

8

In this paper, we focus only on the Li I 6708 line since almost all investigations have invoked this resonance line for Li abundance determinations. Even so, the weak subordinate line at ~ 6103.7 Å (χexc = 1.85 eV) can also be employed to derive the Li abundances of Spite plateau stars if the data quality is sufficiently high (e.g., Asplund et al. 2006). According to the calculations similarly done for this Li I 6104 line, it turned out that the abundance changes due to the overionization caused by chromospheric radiation are similar for both of the 6708 and 6104 lines, though the effect of abundance reduction is slightly weaker for the latter case; e.g., for the T43 model, (A6708, A6104) are (2.424, 2.476), (2.363, 2.423), and (2.337, 2.409) for [Fe/H] = − 1, − 2, and − 3, respectively.

All Tables

Table 1

Summary of the adopted parameters for each model.

In the text
Table 2

Computed equivalent widths and Li abundances.

In the text

All Figures

thumbnail Fig. 1

Schematic description of the simple model chromosphere (uniform gaseous slab with temperature T0 and optical thickness τ0 lying just above the atmosphere) emitting thermal radiation incident at the surface.
In the text
thumbnail Fig. 2

Panels a–c: depth-dependence of Jν2000$J_{\nu}^{2000}$ (mean intensity at λ = 2000 Å) for each of the five models (STD, tm30T40, tm30T43, tm30T45, tm30T50); the local Planck function (Bν: dashed line) is also depicted for comparison. Panels d–f and g–i: runs of l0NLTE/l0LTE$l_{0}^{\textrm{NLTE}}/l_{0}^{\textrm{LTE}}$ (ratio of NLTE to LTE line opacity; ≃ b1) and SL ∕B (ratio of line source function to Planck function; ≃ b2∕b1) of the Li I 6708 line, respectively. The abscissa for each panel is the logarithm of continuum optical depth at 5000 Å.
In the text
thumbnail Fig. 3

Wavelength distribution of emergent surface flux Hν [ ≡ (1/2) ∫−1+1Iμμdμ$\int_{-1}^{+1} I_{\nu}\,\mu {\rm d}\mu$, where μ = cos θ] resulting from each model (solid lines). Wavelength distribution of chromospheric radiation [τ0Bν(T0) = 10−3 Bν(T0)] assumed for each model (dotted lines).
In the text
thumbnail Fig. 4

Panel a: NLTE equivalent widths of Li I 6708 line (W; computed for given primordial lithium abundance of 2.64 for each of the five models) plotted against [Fe/H]. Panel b: NLTE Li abundances (A; inversely obtained from each model’s W by using thestandard procedure of STD model) plotted against [Fe/H].
In the text
thumbnail Fig. 5

Depth-dependence of the NLTE to LTE line opacity ratios (upper panel) and line source function to Planck function ratios (lower panel), which were computed for the tm30T45 models of different metallicities ([Fe/H] = 0, −1, −2, −3, −4, and −5).
In the text
thumbnail Fig. 6

Comparison of the predicted Li abundance vs. metallicity relations (lines) for two models (tm03T43 and tm03T45) with the observed data (symbols) of warm metal-poor dwarfs taken from Thorburn (1994; Teff > 6100 K; crosses), Ryan et al. (1999; open squares), Asplund et al. (2006; open circles), and Meléndez et al. (2010; Teff > 6100 K; filled squares). The horizontal dashed line indicates the primordial (CMB+BBN) Li abundance of 2.64.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.