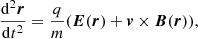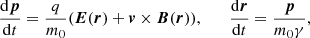| Issue |
A&A
Volume 622, February 2019
|
|
|---|---|---|
| Article Number | A207 | |
| Number of page(s) | 11 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201834284 | |
| Published online | 21 February 2019 | |
Proton acceleration at tearing coronal null-point current sheets
1
School of Science and Engineering, University of Dundee, UK
e-mail: r.pallister@dundee.ac.uk
2
Department of Mathematical Sciences, Durham University, UK
Received:
19
September
2018
Accepted:
19
December
2018
Context. Non-thermal particle acceleration in the solar corona is thought to constitute a substantial part of the energy budget of explosive events such as solar flares. One well-established mechanism of non-thermal acceleration is directly via fields in current sheets.
Aims. In this paper we study proton acceleration during “spine-fan reconnection” at a 3D magnetic null point. This type of reconnection has recently been implicated in some flares known as circular-ribbon flares. It has also recently been discovered that the reconnecting current sheet may undergo a non-linear tearing-type instability. This tearing leads to the formation of flux ropes and quasi-turbulent dynamics.
Methods. A predictor-corrector test particle code is used to model the trajectories of protons at different stages of sheet tearing: when the sheet is intact, just after the formation of the first major flux rope, and once the non-linear phase of the instability has become more fully developed. The fields for these proton trajectories were taken from snapshots of a 3D magnetohydrodynamics simulation treated as three static field geometries represented by interpolated grids. Acceleration in the intact current sheet is compared to earlier simulations of infinite static current sheets and then used as a control case with which to compare the later snapshots.
Results. Protons are found to be predominantly accelerated along the fan surface, especially in the absence of current sheet tearing. Most of the highest energy protons are accelerated in the main body of the current sheet, along the direction of strongest parallel electric field. A high energy tail is present in the kinetic energy distribution. After tearing commences, this direct acceleration no longer dominates and acceleration in the outflow regions makes a proportionally greater contribution. Sheet tearing appears overall to hinder the acceleration of protons in the fan plane, at least in the absence of time-dependent acceleration mechanisms. Some correlation is found between high energy protons and locations of flux ropes formed by the instability, but the nature of the link remains at present unclear.
Key words: acceleration of particles / magnetic reconnection / magnetohydrodynamics (MHD) / Sun: corona / plasmas / Sun: magnetic fields
© ESO 2018
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1. Introduction
Particle acceleration in the solar corona is driven by many mechanisms, both thermal and non-thermal. Non-thermal acceleration is of particular interest to us, as non-thermal electrons are thought to form the majority of ejected electrons in solar flare events (Lin & Hudson 1971). These effects of highly energetic particles are seen during solar flares by the hard X-ray (HXR) emission observed at footpoints on the surface of the photosphere (Fletcher et al. 2011). As such, by better understanding the mechanisms by which the highest energy particles of the corona are accelerated it is possible to better understand the field geometries in the corona during energetic events.
Magnetic reconnection is thought to be a mechanism for non-thermal acceleration. During magnetic reconnection, field lines break and reform into lower energy states. Reconnection occurs in the presence of current sheets, regions of high current density and strong electric fields (Parker 1983). Observations made by instruments such as RHESSI have established the role magnetic reconnection and the resultant current sheets play in acceleration during flares (Sui et al. 2004; Liu et al. 2013). The subsequent formation of current sheets and acceleration of particles during reconnection is therefore of great interest to those studying coronal acceleration. Reconnection has also been studied in non-astrophysical contexts. Notably, studies of laboratory plasmas in Tokamaks have been very informative when it comes to studying the formation and destabilisation of current sheets in plasmas; see Zweibel & Yamada (2009) for a review of magnetic reconnection in laboratory and astrophysical plasmas.
In three dimensions, magnetic reconnection can occur in current layers either at 3D null points or in their absence. In either case the field line evolution is characterised by a continuous field line slippage, rather than a one-to-one cut-and-paste of field line pairs (see Priest et al. 2003). Reconnection at 3D null points can occur in various different modes, including spine, fan, and spine-fan reconnection; see further discussion in Sect. 2.1.
Priest & Titov (1996) described magnetic reconnection about magnetic null points in 2, 2.5, and 3 dimensions for spine and fan reconnection. They describe how the plasma flow towards a magnetic null point is perpendicular to the magnetic field lines around it, and an electric field with a direction perpendicular to both. The reconnection occurs near the null point and drives plasma outflows perpendicular to the inflow directions.
Test particle simulations involve modelling the trajectories of a trace number of particles that are not numerous enough to significantly effect magnetohydrodynamics (MHD). However, there must be enough to get good statistics. Simulating such a large number of particles can be a computationally expensive process, and is therefore less suitable than MHD simulations for investigating bulk motions. Test particle simulations can be used alongside MHD simulations to build up a more complete picture of particle motion. There has been much existing work on test particle simulations near 2D, 2.5D, and 3D magnetic reconnection sites.
Early work was focussed on comparing the acceleration efficiency of the different reconnection types (Craig et al. 1997) or simulating full trajectories of particles in the vicinity of simple static 2D X-point reconnection zones (Ichi Mori et al. 1998; Heerikhuisen et al. 2002). Such simulations highlighted the varying behaviour and ejection patterns of protons and electrons in the same X-point geometry (Zharkova & Gordovskyy 2004, 2005). Later work expanded this to non-static 2.5D geometries containing simple infinite current sheets (Gordovskyy et al. 2010a,b), which demonstrated that the kinetic energy distributions of particles in such geometries were composed of a Maxwell-Boltzmann (thermal) component with a high energy non-thermal tail.
In this paper we use the test particle approach to study particle acceleration during 3D reconnection involving magnetic null points. Previous work in this area is described in the following section. These previous studies deal exclusively with reconnection in a single, smooth current layer about a 3D null. However, it was recently demonstrated by Wyper & Pontin (2014a) that these current layers are susceptible to a non-linear tearing (or “plasmoid”) instability at astrophysical values of the magnetic Reynolds number. The geometry formed by current sheet tearing is a highly dynamic and quasi-turbulent region containing many small-scale current sheet structures and many null points. Early work on tearing-mode instabilities (and indeed other current sheet instabilities) was performed by Furth et al. (1963). This work included discussion of the instability growth rates, and the conditions under which these instabilities arise. Later work by Chen & Morrison (1990) and Faganello et al. (2010) investigated the effect of a velocity shear on the instability growth rate.
In this study we introduce test particles into the 3D field geometry of the MHD simulations performed by Wyper & Pontin (2014a), with the aim being to determine the effect of the instability for non-thermal particle acceleration. While a number of studies have addressed the impact of current sheet fragmentation on particle acceleration in 2D (e.g. Gordovskyy et al. 2010b; Kowal 2012; Zhou et al. 2015, 2018a), this remains relatively unexplored in 3D. Liu et al. (2013) proposed that bi-directional outflows that occur at various stages of a flare could be caused by current sheet tearing, and that the outflow regions in such structures would be the main accelerator.
2. Previous models for reconnection and particle acceleration at 3D null points
2.1. Three-dimensional null-point reconnection models
Previous work addressing particle acceleration at 3D nulls has been based on various different models for the reconnection process. We therefore first summarise these different models. Priest & Titov (1996) proposed the first model of 3D null-point reconnection. Their model is ideal (zero resistivity), the magnetic field has zero current, and the solution is kinematic (solving the electromagnetic equations but not the plasma equations); see also Lau & Finn (1990). Priest & Titov (1996) realised that if a flow is imposed across the spine lines it leads to a singular electric field on the fan. These authors designated this “fan reconnection”, while an imposed flow across the fan leads to a singularity at the spine and “spine reconnection”. In contrast to these kinematic models, Craig and co-workers (Craig & Fabling 1996; Craig et al. 1997) found solutions to the full system of MHD equations for an incompressible plasma. These solutions allow for current layers localised either to the spine or the fan – these current layers extending to infinity by construction. Depending on whether the current is localised to the spine or fan, Craig & Fabling (1996) designated these solutions “spine reconnection” or “fan reconnection”, respectively. These solutions are sometimes described as exhibiting “reconnective annihilation”, since there is only an ideal plasma flow across the spine or fan, but not both (or in the corresponding 2D solution of Craig & Henton (1995), only across one separatrix).
Pontin et al. (2005) revisited the kinematic problem; in contrast to earlier studies they allowed for a non-zero current and a diffusion region around the null point. They realised that the flows across the spine and fan assumed by Priest & Titov (1996) cannot be decoupled, so that in fact the generic mode of reconnection has a “spine-fan” character when the diffusion region is fully localised. This type of reconnection occurs when the current vector at the null is orientated parallel to the fan surface. When the current vector is orientated parallel to the spine, a mode of reconnection characterised by rotational slippage of field lines around the spine occurs (Pontin et al. 2004), which is not relevant to the present study. The pure spine and fan reconnection solutions of Craig & Fabling (1996) are possible because the diffusion region (current layer) extends to infinity along either spine or fan. Indeed, it has been shown that the steady-state fan reconnection solution is dynamically accessible (Craig & Fabling 1998; Pontin et al. 2007a); however, the spine reconnection solutions appear not to be dynamically accessible (Titov et al. 2004; Pontin et al. 2007a). Moreover, in spite of the dynamic accessibility of the fan reconnection solutions, as soon as the assumption of incompressibility is relaxed, the current layer contracts to become localised around the null and spine-fan reconnection ensues (Pontin et al. 2007b,a).
As discussed below, dedicated particle acceleration studies have been performed based on the reconnection solutions of Priest & Titov (1996) and Craig & Fabling (1996). However, no dedicated study of particle acceleration in a spine-fan reconnection configuration has been performed (though see discussion of the work by Baumann et al. 2013 below). Thus, the first purpose of our study is to compare the acceleration of particles in a spine-fan reconnection process to that observed based on the earlier models of the reconnection process. We then analyse the effect of instabilities of the current sheet, as described above.
2.2. Particle acceleration at 3D nulls
Dalla & Browning (2005, 2006) performed test particle simulations based on the reconnection solutions of Priest & Titov (1996). Their spine reconnection solution was found to lead to acceleration of protons in symmetrical jets aligned with the spine axis. Additionally, the most efficient acceleration was found to occur in regions of strongest electric field strength in the core of the reconnection region. The population of ejected particles had a lower mean kinetic energy than the population of particles trapped by repeated magnetic reflection. Dalla & Browning also performed simulations on particles subjected to the fields from the fan reconnection solutions of Priest & Titov (1996). They concluded that fan reconnection appeared to be a less effective accelerator of particles overall, but found that the spatial distribution of protons ejected along the fan plane formed “ribbon-like” patterns. In both spine and fan reconnection, the energy distribution of the protons was composed of a Maxwell-Boltzmann (thermal) distribution and a high energy non-thermal tail, similar to later findings by Gordovskyy et al. (2010b,a).
Browning et al. (2010) simulated particle motion in the vicinity of a 3D magnetic null point, again focussing on the fields of the Priest & Titov (1996) solutions. They simulated the full motion of protons and used the guiding-centre (GC) approximation to model the motion of electrons. They determined that the greatest kinetic energy gain was found in particles initialised close to the spine and fan plane of the null-point geometry. The particles were initialised with Maxwellian kinetic energies, and over the course of the simulation deviated from this to form a significant high energy tail. They also replicated the existence of “trapped” particles, which undergo repeated magnetic reflection events without being ejected. They suggested that these particles may be a high energy source which could lead to HXR emission.
Stanier et al. (2012) performed full motion simulations of protons in the vicinity of 3D spine and fan reconnection, using the fields obtained from the solutions of Craig & Fabling (1996) and Craig et al. (1997). They found the incompressible fan-reconnection model to be a more effective accelerator of protons than the spine-reconnection model. Protons that pass through the current sheet were found to have the greatest kinetic energy gain. The kinetic energy gain over time has a similar shape to the aforementioned simulations by Browning et al. (2010).
As discussed above, in a compressible plasma the modes of null-point reconnection have been found to be somewhat different to the simplified models of Priest & Titov (1996) and Craig & Fabling (1996). Nonetheless, these models are an attractive option for studying particle acceleration, since they are mathematical solutions which can allow for a study scaling with parameters such as the plasma resistivity. By contrast, spine-fan reconnection has been observed in numerous simulations (e.g. Pontin et al. 2007b; Pariat et al. 2009; Edmondson et al. 2010; Wyper et al. 2016) and in laboratory experiments (Frank 1999; Gray et al. 2010) – however, no solution to the full set of MHD equations describing it exists. Therefore a test particle approach to studying acceleration must rely on extracting fields from numerical simulation grids. In the following (Sect. 4.1) we make a detailed such study. It is worth noting that one other effort has been made to study this problem. Baumann et al. (2013) performed an MHD simulation designed to mimic the magnetic field evolution during a “circular ribbon” flare. The magnetic field structure, extrapolated from a SOHO magnetogram, contained a null, and in their simulations the boundary motions (designed to mimic the observed photospheric flows) were found to lead to generation of a localised current layer at the null and spine-fan reconnection (see also Masson et al. 2009). Subsequently, they used a snapshot of this MHD simulation (over a sub-section of the spatial domain) to generate boundary conditions for a kinetic PIC (particle-in-cell) simulation of electron motions. As with the more idealised geometries, they identified a high energy non-thermal tail in the kinetic energy distribution, and found that the main accelerator in the domain was the strong electric field and current sheet across the fan plane. Accelerated particles were found to be localised mostly to the fan plane, consistent with earlier studies of fan reconnection.
Threlfall et al. (2016b) simulated GC approximated protons and electrons around reconnecting separator current layers. Separators are special magnetic field lines that connect pairs of magnetic null points and, like null points, they are thought to be associated with 3D reconnection. They found the greatest kinetic energy gain to be for particles accelerated along the fan planes.
3. Methods
3.1. Tearing null-point current sheets
Wyper & Pontin (2014a,b) returned to simulating the shear stressing of a 3D null point via boundary motions, previously addressed by for example Pontin et al. (2007b) and Galsgaard & Pontin (2011). Similar to Galsgaard & Pontin (2011), they maintained the driving flow until the system reached a quasi-steady reconnection configuration; however, with a larger magnetic Reynolds number than in previous studies they were able to identify the onset of a non-linear tearing-type instability of the current layer (see Fig. 1). We take these simulations as our basis for a particle acceleration study. The data comprise magnetic and electric field values on a rectangular grid of 450 × 2000 × 200 points over a domain x ∈ [−0.5, 0.5], y ∈ [−3.5, 3.5], z ∈ [−4, 4]. The resolution of the grid varies such that sizes of the grid cell close to the centre of the volume are smaller and the fields are therefore more detailed in this region. We note that in the initial state of the MHD simulation the null point is located at the origin, its spine coincides with the x-axis, and its fan separatrix surface coincides with the x = 0 plane (see Fig. 1). We also note that in this resistive MHD simulation, E = −υ × B + ηJ, and therefore E∥ = ηJ∥.
 |
Fig. 1. For each frame, top panel: 3D view of the MHD simulation domain, showing magnetic field lines and a volume rendering of |J|. Bottom panel: distribution of jz in the z = 0.0 plane. For t = 8 (panel a), t = 16 (panel b), t = 21 (panel c). The 3D images in panelsa and b are taken from Wyper & Pontin (2014a), and in panel c from Wyper & Pontin (2014b). |
This grid of field values produced by the simulations is used as a geometry within which to study particle motion. To investigate this particle motion in a fully self-consistent manner on MHD length-scales is prohibitively computationally expensive. Instead, to investigate how particle behaviour changes at different stages of tearing, we select several static snapshots from the MHD simulation, and employ a test-particle approach (see below). We follow our test particles in these static fields for a fixed time period. This time period is chosen as being equivalent to a time period shorter than one time unit in the MHD simulation. The three snapshots chosen from the MHD simulation are at t = 8 (when a monolithic current layer undergoes quasi-steady reconnection), t = 16 (just after instability onset, where the first major flux rope has formed, disrupting the current sheet) and t = 21 (some time after the onset of tearing). Figure 1 shows the relative current distribution at the z = 0 xy plane for each of these snapshots. We note that at t = 8 when reconnection is quasi-steady and the assumption that the electric and magnetic fields are steady on MHD timescales of less than one dimensionless time unit is a reasonably accurate approximation. As time goes on this approximation becomes gradually less accurate. Therefore we caution that time-dependent effects that could be significant for particle motion are neglected in this work; this is left for future study.
In order to obtain appropriate orders of magnitude for the electric and magnetic fields for the solar corona from the non-dimensional MHD simulations, scaling factors have been applied. These are loosely based on the observed circular-ribbon flare event described by Masson et al. (2009) and Baumann et al. (2013). Specifically, the chosen scaling factors are l0 = 106 m, T0 = 106 K, B0 = 10−4T = 1 G. Taking these factors for l0 and B0 and assuming a typical coronal temperature value T0, we can derive the Alfvén velocity scale and subsequently the E field scaling factor, E0 = 102 Vm−1. The uniform non-dimensional resistivity is η = 5 × 10−5. This is equivalent to an inverse Lundquist number S based on the Alfvén speed at the boundary; thus we have S = 2 × 104. The plasma beta based on the magnetic field strength at the driving boundary is β = 0.03 (and is infinite at the null). The resistive time based on the current sheet width is estimated to be between 50 and 100 s (or 105 s based on the domain scale).
It should be noted that owing to computational restrictions, the simulated value of the Lundquist number is of course many orders of magnitude smaller than the true coronal value (in common with all such simulations). The enhanced resistivity used in the simulations can be thought of as representing dissipation processes not captured in the simulations, such as turbulent fluctuations or plasma kinetic effects absent in the MHD approximation. While MHD is a good approximation for describing large-scale dynamics of coronal processes such as flares (e.g. Priest 2014), it may break down in the heart of the reconnecting flare current sheet. Finally, based on the above scaling factors, units of time in the MHD simulation correspond to τ ≈ 10 s, The particle simulations were run for a total time period of 0.3τ, i.e. 3 s.
3.2. Test particle motion
In the presence of a strong magnetic field, charged particles move in a helical motion, where gyrofrequencies and gyroradii are dependent on the magnetic field strength and velocity component perpendicular to the field. In the presence of a relatively constant magnetic field with a relatively weak electric field, the trajectories of particles can be modelled by simply tracing the centre of the helical motion. This is called the GC approximation.
The trajectories can be greatly affected by both changes in the magnetic field and the presence of a non-negligible electric field. Specifically, if the magnetic field changes significantly over the length scale of the particle gyroradius, this can introduce a drift in the trajectory. In the case in which simple helical motion cannot be assumed, the full motion of the particle must be simulated.
Charged particles are accelerated by electric and magnetic fields via the Lorentz force given in Eq. (1),
where E and B are the electric and magnetic fields, and the quantities q, m, r and υ = dr/dt are the charge, mass, position and velocity of the particle, respectively. We note that E here is derived from the MHD data via E = −y × B + ηJ, and that as discussed above the Lundquist number accessible in the MHD simulations is many orders of magnitude smaller than in the corona. We retain this enhanced value of η from the MHD simulations when generating E for self-consistency, as per previous studies (e.g. Gordovskyy et al. 2010a; Threlfall et al. 2016a, and references therein).
Since particles in our simulation may reach relativistic energies, it is necessary to use the relativistic version of Eq. (1). Thus the equations of motion we have solved are the relativistic Lorentz equations
where p is the particle momentum, m0 is the particle rest mass, γ2 = (1 − υ2/c2), c is the speed of light, and υ = |υ|.
The particles are assumed not to interact with one another, and no background population was included (the test particle approach). This means that the motions of the particles are governed only by the Lorentz equation above, and scattering is neglected. The mean free path of a proton based on the typical coronal dimensions taken in the previous section is of order λmfp ≈ 105 m. A typical value for the gyroradius of a thermal proton in or near the current sheet is rg ≈ 100 m.
A thermal proton moving in a straight-line trajectory travels a distance of approximately 3 × 105 m in the integration time. We note that this is comparable to the mean free path, so we would expect thermal particles to be scattered at some point during integration. By neglecting scattering terms, our model is a simplification. A more proper treatment would include a mechanism by which particles could be scattered in a background plasma (as in Gordovskyy et al. 2013; Borissov et al. 2017). One way to model scattering would be to include a drag term, resulting in momentum loss in the direction of motion but no change in direction. In regards to the results we would expect that this would not affect the spatial distribution of accelerated particles, but would reduce the kinetic energy of the population as a whole. Use of the test-particle approach in the solar atmosphere is discussed in more detail by Zharkova et al. (2011).
3.3. Particle trajectory code
The trajectories of the protons were modelled by solving the relativistic Lorentz Eq. (2) as a pair of differential equations. Particle-particle interactions were neglected. This was carried out using a fourth order predictor-corrector algorithm consisting of an Adams-Bashforth predictor and an Adams-Moulton corrector.
The simulation has a variable timestep, allowing each particle to vary its own timestep based on the difference between the predicted and corrected values of their positions and momenta. This difference is compared with a user-defined relative error to customise the balance between accuracy and runtime. The errors were calibrated by simulating the motion of particles and comparing with analytical results for particles in a simple infinite current sheet found by Speiser (1965). Based on this, a relative error of 10−9 for the trajectory simulations was chosen.
As described above, the MHD simulations provide electric and magnetic fields on a non-uniformly spaced rectangular grid. During our particle simulations, field values between the grid points were found using trilinear interpolation. The grid boundaries limit the spatial domain within which we can calculate particle trajectories. If a particle crosses the boundary of the domain it is linearly interpolated back to the point of exit, keeping its position and momentum static until the simulation ends.
3.4. Proton initial distribution
Owing to the high magnetic Reynolds number of the MHD simulations (and corresponding high spatial resolution), the reconnecting current sheet takes up only a tiny fraction of the simulation domain (see Fig. 1 and Wyper & Pontin 2014a). As such, a uniform or random distribution of initial particle positions gives an extremely poor resolution of the behaviour around the current layer. Additionally, since we are simulating protons over a limited timescale (see above), particles initialised outside of the current layer typically have insufficient time to drift into the current layer to be accelerated. As such, we concentrate on the behaviour of selected populations of particles that are initialised in or adjacent to the current layer. Specifically, protons were initialised within a parallelogram lying in the xy plane at several values of z: in particular at z = −0.2, 0.0, +0.2, +0.4, and +0.6. One hundred protons are placed along each dimension of the parallelogram, giving a total of 104 protons per parallelogram distribution. Each proton was initialised with a velocity selected at random from a Maxwellian distribution defined by the temperature scaling factor T0. This corresponds to an initial thermal energy distribution peaking at approximately 100 eV, or thermal velocity 1.0 in dimensionless code units. The speed of plasma inflow to the current sheet in the MHD simulations was found to be negligible (0.01 in dimensionless code units) compared with thermal velocities, therefore bulk plasma flow was neglected when initialising particle velocities.
The parallelograms within which particles are initialised were chosen to cover the current sheet in the particular plane; some overlap exists in the outflow regions. The current sheet axis makes a different angle in the xy plane for different values of z, and to account for this the parallelograms were sheared to ensure appropriate coverage of the current layer for different z values and different MHD snapshots. The initial spatial distribution for the the t = 8 snapshot is shown in Fig. 2.
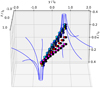 |
Fig. 2. Initial positions of protons in the t = 8 snapshot alongside the spine field lines. The parallelograms become increasingly sheared at larger z to account for the inclination of the sheet in the xy plane. The distributions shown are for z = −0.2 (cyan), z = 0.0 (green) z = +0.2 (yellow), z = +0.4 (red), and z = +0.6 (magenta). |
4. Results and discussion
4.1. Intact sheet (t = 8)
At MHD simulation output time t = 8, the current sheet has yet to tear: the sheet is close to planar, and the current is distributed relatively uniformly along its length, decaying smoothly away from the z = 0.0 symmetry plane; see Fig. 1a. There remains a single null point, located by symmetry at the origin. This is the time of the simulations at which the current distribution is most closely analogous to the simple infinite sheet used in the previous simulation work of Stanier et al. (2012). As such, it is interesting to compare our results for this snapshot with those of previous work.
We visualise the spatial distribution of accelerated particles in two principal ways: by plotting the final energy of the particles as a function of their final position and their initial position. First, Fig. 3a shows the latitude-longitude plot – centred on (x, y, z) = (0, 0, 0) – of the final positions of the particles initialised in the z = 0.0 plane. The (0, 0) coordinate in the plot corresponds to the positive z-axis in the MHD simulation domain. The plot shows a consistent band of particles in the centre, corresponding to a dominant motion in the +z direction, and the inclination matches that of the current sheet/fan surface. These final particle energies can also be plotted as a function of the initial particle position, as shown in Fig. 4c. It is clear from comparison of the current density distribution and the particle final energy distribution that the two are strongly correlated. As we mention below, the energy gain in the outflow regions relative to that in the current sheet plane is lower than it is in later snapshots. These observations indicate that the majority of the acceleration is direct from the strong parallel electric field present in the current layer.
 |
Fig. 3. Final position latitude (θ)-longitude (ϕ) plot for protons initialised at z = 0 for t = 8 (panel a), t = 16 (panel b), t = 21 (panel c). The origin point is defined by the direction of the +z axis at (x, y) = (0, 0) in Cartesian coordinates. The cyan crosses indicate the approximate location of the spine axis as it crosses the domain boundary. |
 |
Fig. 4. Final kinetic energies for thermal protons initialised in the parallelogram in the centre of the current sheet at z = 0.0 for t = 8 (panel c), t = 16 (panel d), t = 21 (panel e). The parallelogram is composed of 100 × 100 protons (in Cartesian coordinates in panel b) labelled on the axes. This shows the full energy gain plot in comparison to the current sheet shown in panel a, where Jz is the z-component of the current (also at z = 0.0). The plot is then skewed into a rectangle with a log scaling applied to the energy. The dimensions u and υ represent the particle number initialised along the long and short side of the parallelogram, respectively; (0, 0) represents the particle initialised at the top left and (100, 100) represents the particle initialised at the bottom right; see panel c. The corners [x, y] and dimensions of the parallelograms in code units are as follows (starting at the top left corner, going clockwise): panel c: ([−0.32, +0.72],[+0.32, −0.62],[+0.32, −0.72],[−0.32, +0.62]), length (in x) = 0.64, width (in y) = 0.1; panel d: ([−0.29, +1.45],[+0.29, −1.15],[+0.29, −1.45],[−0.29, +1.15]), length (in x) = 0.58, width (in y) = 0.3; and panel e: ([−0.26, +1.90],[+0.26, −1.30],[+0.26, −1.90],[−0.26, +1.30]), length (in x) = 0.52, width (in y) = 0.6. |
Our results indicate that the primary distribution of accelerated particles in this configuration is found in a band in the fan surface focussed in the direction of the current flow at the null. This is very much in keeping with the results of previous studies based on analytical solutions (Stanier et al. 2012) and PIC simulations (Baumann et al. 2013). We note however that there are some other locations at which high energy particles are found: in the z = 0.0 plane the dominant field component is along the length-wise axis in the xy-plane of the current sheet, so that some particles are guided towards the outflow regions and spine footpoints (see the accumulations of particles in Fig. 3a at ϕ = ±90°).
For particles initialised away from the central z = 0.0 plane in the +z direction (for all snapshots), the distribution retains the strong central band seen in Fig. 3a, but lacks high energy particles in the outflow regions. This appears to be because the fastest outflow and strongest associated fluctuations are present closest to the z = 0.0 plane; out of this plane the outflow tends to fan outwards along z, becoming progressively weaker (see e.g. Fig. 5 of Thurgood et al. 2017).
Figure 5a shows the kinetic energy distribution over time for all simulated particles (i.e. particles in all parallelograms in constant-z planes as shown in Fig. 2). The population was initialised with a Maxwellian energy distribution. As the simulation progresses, the Maxwellian shape begins to break down and a noticeable high energy tail forms. Both the deviation from the Maxwellian and the high energy tail are typical signs of significant non-thermal acceleration (Baumann et al. 2013).
 |
Fig. 5. Proton kinetic energy distributions at the start (purple), mid-point (blue), and end (green) of the simulations for snapshots t = 8 (panel a), t = 16 (panel b), t = 21 (panel c). |
4.2. Effect of sheet tearing (t = 16 and 21)
4.2.1. Final positions of accelerated particles
In order to compare the effect of the tearing instability on the acceleration of particles, we produced the same plots described above for the two later snapshots, after instability, t = 16 and 21. First we consider the latitude-longitude plots of the final positions of particles (Fig. 3). We observe that, in comparison to the t = 8 plot in Fig. 3a, the central band corresponding to acceleration in the positive-z direction is weaker for later MHD snapshots, thinning out significantly at t = 16 and barely noticeable in t = 21. Therefore the tearing within the current sheet appears to disrupt the systematic acceleration in the z-direction by the parallel electric field. This is perhaps to be expected, since the magnetic field line structure and current distribution become much less ordered, meaning persistent acceleration along a given direction is suppressed. While the peak current in the sheet increases (Wyper & Pontin 2014a), following tearing the current distribution develops many “holes” and in fact the peak current in the mid-plane decreases.
By contrast to the coherent acceleration along z in the heart of the current layer, the relative acceleration in the outflow regions increases for the later MHD snapshots. This shows that as the sheet tears and breaks down, acceleration in the +z direction becomes less significant than acceleration around the outflow regions.
As before, distributions initialised away from the centre z = 0.0 show a more consistent acceleration in the +z direction; this is probably due to the “guiding” field in that direction that grows with |z| – and fewer high energy particles at ϕ = ±90° as the initial distribution moves away from the turbulent outflow regions.
We should, however, note that there are a number of caveats to this. First, we considered only certain particle populations (see Sect. 3.4), and second these populations are not the same for the different snapshots. Broadly speaking the parallelograms of initial particle positions become less inclined for later snapshots, but also become broader, since a the sheet is broader, but also b it becomes less planar (see Fig. 1). It is not immediately clear how to circumvent these issues. In future work, however, we plan to implement a particle tracer that switches between following full-orbit and GC motion. The increased computational efficiency should allow many more particles to be simulated, and thus a more uniform and consistent sampling of particle initial positions to be implemented. A more thorough analysis may also require greater equivalence between the initial spatial distributions relative to their respective current sheets.
4.2.2. Initial position-energy gain maps
Figure 4 shows a series of “heat-maps” of particle final energy as a function of initial position for all three snapshots. These heat maps are plots of the log of the kinetic energy gain of each particle initialised in the z = 0.0 plane based on its starting position in the parallelogram, sheared into a rectangle as illustrated in the figure.
For the t = 8 plot, we can see a strong central band indicating that particles initialised in the current sheet are more greatly accelerated than those outside. This suggests that direct acceleration in the sheet itself is responsible for most of the acceleration in this snapshot, as discussed above. Both the t = 16 and t = 21 heat maps show a similar central band pattern. However, several features can be noted in the distributions that indicate that inhomogeneities in the magnetic field/current structure that develop within the current layer have direct implications for the acceleration of particles in this region. We compared the heat maps to the current diagrams for z = 0.0 shown in Fig. 1. In both heat maps, large disruptions in the centre of the band are associated with the flux ropes seen in the current diagrams. This is not surprising since the current density is depressed in these flux ropes compared to the adjacent sections of the current layer. Additionally, the t = 16 heat map shows a disruption part way along the band that does not appear to correlate with any feature observed in the current distribution. However, on closer inspection we find a small flux rope is in fact present there (perhaps recently formed): the disruption correlates with a quadrupolar structure seen in the electric field associated with this plasmoid (not shown). Energy gain plots for distributions initialised away from the centre show similar disruptions corresponding to the location of the flux rope at these values of z.
4.2.3. Kinetic energy distributions over time
Kinetic energy distributions were produced for the later snapshots in the same way as for t = 8. Figure 5 shows the development of the relative kinetic energy distributions for all three snapshots. It can be seen that as the sheet tears, the distribution deviates less from the initial Maxwellian and the high energy tails become much less significant. One possible conclusion is that non-thermal acceleration as a whole becomes less effective after sheet tearing. However, it is not clear whether this conclusion is justified, since the volume of space sampled by the initial particles is larger at later time (see the discussion above in Sect. 4.2.1 regarding the different sizes of the parallelograms). Moreover, it is to be expected that time-dependent acceleration mechanisms, ignored here, may become more significant after the tearing onset and the development of turbulence in the layer. One thing that is clear is that the outflow regions play a much more substantial role in accelerating particles at later times.
4.2.4. Particle impact distributions
Before concluding we consider one final way to visualise the pattern of particle acceleration. In particular, we plot “impact distributions” for each snapshot, i.e. plots showing the position and energies of particles when they pass through a particular plane. This is motivated by the fact that in the corona, we often observe accelerated particles indirectly through flare ribbons on the photosphere, and these ribbons show something like a particle impact distribution. Indeed, it has been speculated that the bright knots seen to run along flare ribbons may be associated with disruptions such as plasmoids in the reconnecting flare current layer (e.g. Brannon et al. 2015; Parker & Longcope 2017). Thus, impact distributions on several xy planes were made to examine the changes further out from the central z = 0.0 plane in the +z direction.
Figure 6a shows the impact distributions for planes in the t = 8 snapshot, superimposed on a magnetic connectivity plot. As expected, it can be seen that the higher energy protons almost universally align to the current sheet, which lies in the separatrix surface defining the connectivity boundary. There also appears to be a small bias of energetic particles towards the +y part of the sheet. In general, it shows the distribution out at z = +1.0 is closely aligned to the connectivity boundary.
 |
Fig. 6. Connectivity plots at z = +1.0 with impact distributions overlaid for t = 8 (panel a), t = 16 (panel b), t = 21 (panel c). The connectivity maps are produced by integrating a large number of field lines from a grid of points in the given plane, and colouring the corresponding point according to which boundary the field line intersects. The cyan regions are magnetically connected to the −x domain boundary and the magenta regions are connected the +x domain boundary. |
There is a different situation in Fig. 6b, which shows the equivalent impact distribution for t = 16. The figure shows that the highest energy particles moving in the +z direction seem to align to the locations of the flux ropes at particular xy planes. These flux ropes are identified as local regions where the connectivity plot exhibits a spiral pattern (sometimes very squashed). A similar effect can be seen in the impact distributions for t = 21, in Fig. 6c. This suggests that particles accelerated non-thermally in tearing current sheets tend to follow flux ropes. This does not, however, indicate how significant the flux ropes themselves are in the acceleration itself.
4.2.5. Proton trajectories along flux ropes
One interesting aspect of the above results is the apparently contradictory findings that a particle acceleration is locally suppressed in flux ropes formed in response to tearing, and yet that high energy particles appear to be found, in the end, in/around these flux ropes at least between z = 0.0 and z = +1.0. To understand this we specifically analysed the relationship between trajectories of high energy particles found in our simulations and field lines of the flux ropes. These flux ropes are obtained by seeding field lines in the weak current locations within the current layer, as in Wyper & Pontin (2014b).
Figure 7 shows the trajectories of the particles with the highest final energies for particles initialised in the planes z = −0.2, 0.0, +0.2, and +0.4. The figure shows that high energy particles that follow the flux ropes are not locally accelerated in or around the flux ropes, but rather gain energy prior to being “trapped” within, and subsequently guided by the flux ropes. All of the high energy particles found around the flux rope are initialised in the z = −0.2, +0.0, and +0.2 planes. However that these particles did not start within the flux ropes in general. Indeed, for the particles initialised at z = 0, +0.2 and to a lesser extent +0.4 (frames b, c and d) in particular, we note an anti-correlation between the flux rope field lines and the particle starting points. The main difference we see is that particles initialised further away from the centre are much less likely to encounter the flux ropes when energetic and they are not guided by the flux ropes. Other noteworthy features are the high energy particles in the outflow region of z = 0.0 in Fig. 7b, and what appears to be beams originating near the outflow regions at z = +0.2 in Fig. 7c.
 |
Fig. 7. Comparison of flux ropes (blue) and the trajectories of the 100 particles with the highest final kinetic energies initialised at z = −0.2 (panel a), z = 0.0 (panel b), z = +0.2 (panel c), z = +0.4 (panel d), for the t = 16 snapshot. |
5. Conclusions
In this paper we have addressed the acceleration of particles during spine-fan reconnection at a 3D magnetic null point, both before and after the onset of non-linear tearing within the reconnecting current layer. For the case of the intact current sheet (t = 8), the acceleration profile was found to be broadly consistent with simulations of acceleration in infinite current sheets based on incompressible MHD solutions (Craig & Fabling 1996; Stanier et al. 2012). The kinetic energy distribution also showed the characteristic shift from a Maxwellian distribution to one with a high energy tail.
Following onset of tearing within the current sheet (t = 16) the acceleration profile changes. There is less organised/consistent acceleration in the +z direction than for the intact sheet. The kinetic energy distribution better maintains a Maxwellian component as the simulation progresses, although the high energy tail is still obvious (at least for the populations considered in this work – see the caveats of the previous section).
Later in the MHD evolution, when the non-linear phase of the tearing instability is more fully developed (t = 21), the acceleration profile is more different still. The kinetic energy distribution also has a less prominent tail and the Maxwellian component is much more apparent. There is very little consistent proton acceleration in the +z direction. Instead, particle acceleration in the reconnection outflows make a substantial contribution – these outflows having become quasi-turbulent by this time.
The initial position - kinetic energy heat maps show that for the most part protons initialised in the current sheet or around the outflow regions gain the most kinetic energy. For the t = 16, 21 snapshots several features appear, corresponding to flux ropes and plasmoid structures in the sheet. Within these flux ropes the acceleration appears to be suppressed. However, particle impact distributions with planes of constant z indicate that higher energy particles appear to move outwards in the vicinity of major flux ropes, suggesting some correlation. This modifies the broad picture in which the particles mostly adhere to the current sheet, and thus impact at/around the connectivity boundaries. It will be interesting to explore further in future whether this can account for some of the time-dependent features observed, for example in flare ribbons.
It should be emphasised that there are a number of caveats to the above results regarding the effect of tearing onset. Foremost among these are the fact that we neglect time-dependent effects by considering static B and E fields and the fact that while the pre-tearing current layer is well resolved numerically, the post-tearing current sheet may not be. Moreover the limited resolution means that the post-tearing state does not show fully developed turbulence as would be expected at higher magnetic Reynolds number (see Wyper & Pontin 2014a,b, for further discussion). Regarding the potential importance of time-dependent effects, we can compare characteristic timescales between the particles and the MHD fields. One estimate of a characteristic “global” evolution timescale for the MHD simulation would be the ejection time of plasmoids from the current layer, taken as the outflow speed divided by the current sheet length, which turns out to be of order 20 s. However, there are many more rapid fluctuations in the fields within the current layer, on the timescale of seconds. As described above, we observe some particle acceleration to high energies over the 3 s timescale of the particle simulations: the typical dynamical timescale of a proton based on our scaling factors is approximately 1 s. However, many other particles remain “trapped”, particularly in the flux ropes, over these timescales. Thus, we might expect important time-dependent effects for some of these particles. One recent relevant study supporting this idea is the paper of Zhou et al. (2018b), who performed a large-scale kinetic (LSK) simulation (analogous to test particles) of electrons in an evolving 3D electromagnetic field geometry generated in a PIC simulation. They found that parallel electric fields tended to preferentially accelerate particles within flux ropes, concluding that the temporal evolution of the flux ropes was critical for the acceleration. It will be interesting in the future to investigate more closely the similarities and differences between their results and acceleration studies based on MHD studies such as ours.
Relaxing the assumption of a stationary field is one extension that could be performed; this would require interpolation over time as well as space to obtain B and E field values.
Our work has so far involved modelling the trajectories of protons. Electrons have a much greater charge-mass ratio than protons, which results in greater acceleration and potentially more distinctive patterns in the acceleration profiles. However this has a drawback from a simulation standpoint: in variable timestep codes larger accelerations generally result in much smaller timesteps, and therefore longer runtimes. Before we simulate electron trajectories some improvements to the code will be necessary.
To reduce the runtime of future simulations we will implement a GC code to dynamically switch to when necessary. A GC code will model only the centre of rotation for a particle moving in a helical trajectory. This is more efficient but requires regular helical motion, which can only be assumed in regions of relatively low electric field strength E and relatively constant B. These requirements will provide thresholds for the switching conditions.
Acknowledgments
We would like to thank Simon Candelerasi for his 3D field-line tracing Python script. R. P. acknowledges studentship funding from STFC through grant ST/N504026.
References
- Baumann, G., Galsgaard, K., & Nordlund, Å. 2013, Sol. Phys., 284, 467 [NASA ADS] [CrossRef] [Google Scholar]
- Borissov, A., Kontar, E. P., Threlfall, J., & Neukirch, T. 2017, A&A, 605, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brannon, S. R., Longcope, D. W., & Qiu, J. 2015, ApJ, 810, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Browning, P. K., Dalla, S., Peters, D., & Smith, J. 2010, A&A, 520, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chen, X. L., & Morrison, P. J. 1990, Phys. Fluids B Plasma Phys., 2, 495 [CrossRef] [MathSciNet] [Google Scholar]
- Craig, I. J. D., & Fabling, R. B. 1996, ApJ, 462, 969 [NASA ADS] [CrossRef] [Google Scholar]
- Craig, I. J. D., & Fabling, R. B. 1998, Phys. Plasmas, 5, 635 [NASA ADS] [CrossRef] [Google Scholar]
- Craig, I. J. D., & Henton, S. M. 1995, ApJ, 450, 280 [NASA ADS] [CrossRef] [Google Scholar]
- Craig, I. J. D., Fabling, R. B., & Watson, P. G. 1997, ApJ, 485, 383 [NASA ADS] [CrossRef] [Google Scholar]
- Dalla, S., & Browning, P. K. 2005, A&A, 436, 1103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dalla, S., & Browning, P. K. 2006, Astrophys. J. Lett., 640, L99 [Google Scholar]
- Edmondson, J. K., Antiochos, S. K., DeVore, C. R., Lynch, B. J., & Zurbuchen, T. H. 2010, ApJ, 714, 517 [NASA ADS] [CrossRef] [Google Scholar]
- Faganello, M., Pegoraro, F., Califano, F., & Marradi, L. 2010, Phys. Plasmas, 17, 062102 [NASA ADS] [CrossRef] [Google Scholar]
- Fletcher, L., Dennis, B. R., Hudson, H. S., et al. 2011, Space Sci. Rev., 159, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Frank, A. G. 1999, Plasma Phys. Control. Fusion, 41, A687 [NASA ADS] [CrossRef] [Google Scholar]
- Furth, H. P., Killeen, J., & Rosenbluth, M. N. 1963, Phys. Fluids, 6, 459 [NASA ADS] [CrossRef] [Google Scholar]
- Galsgaard, K., & Pontin, D. I. 2011, A&A, 529, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gordovskyy, M., Browning, P. K., & Vekstein, G. E. 2010a, A&A, 519, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gordovskyy, M., Browning, P., & Vekstein, G. E. 2010b, ApJ, 720, 1603 [NASA ADS] [CrossRef] [Google Scholar]
- Gordovskyy, M., Browning, P. K., Kontar, E. P., & Bian, N. H. 2013, Sol. Phys., 284, 489 [NASA ADS] [CrossRef] [Google Scholar]
- Gray, T., Lukin, V. S., Brown, M. R., & Cothran, C. D. 2010, Phys. Plasmas, 17, 102106 [NASA ADS] [CrossRef] [Google Scholar]
- Heerikhuisen, J., Litvinenko, Y. E., & Craig, I. J. D. 2002, ApJ, 566, 512 [NASA ADS] [CrossRef] [Google Scholar]
- Ichi Mori, K., Ichi Sakai, J., & Zhao, J. 1998, ApJ, 494, 430 [NASA ADS] [CrossRef] [Google Scholar]
- Kowal, G., & de Gouveia Dal Pino, E. M., Lazarian, A., 2012, Phys. Rev. Lett., 108, 241102 [NASA ADS] [CrossRef] [Google Scholar]
- Lau, Y. T., & Finn, J. M. 1990, ApJ, 350, 672 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, R. P., & Hudson, H. S. 1971, Sol. Phys., 17, 412 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, W., Chen, Q., & Petrosian, V. 2013, ApJ, 767, 168 [NASA ADS] [CrossRef] [Google Scholar]
- Masson, S., Pariat, E., Aulanier, G., & Schrijver, C. J. 2009, ApJ, 700, 559 [NASA ADS] [CrossRef] [Google Scholar]
- Pariat, E., Antiochos, S. K., & DeVore, C. R. 2009, ApJ, 691, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Parker, E. N. 1983, ApJ, 264, 635 [NASA ADS] [CrossRef] [Google Scholar]
- Parker, J., & Longcope, D. 2017, ApJ, 847, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Pontin, D. I., Hornig, G., & Priest, E. R. 2004, Geophys. Astrophys. Fluid Dyn., 98, 407 [NASA ADS] [CrossRef] [Google Scholar]
- Pontin, D. I., Hornig, G., & Priest, E. R. 2005, Geophys. Astrophys. Fluid Dyn., 99, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Pontin, D. I., Bhattacharjee, A., & Galsgaard, K. 2007a, Phys. Plasmas, 14, 052109 [NASA ADS] [CrossRef] [Google Scholar]
- Pontin, D. I., Bhattacharjee, A., & Galsgaard, K. 2007b, Phys. Plasmas, 14, 052106 [NASA ADS] [CrossRef] [Google Scholar]
- Priest, E. R. 2014, Magnetohydrodynamics of the Sun (Cambridge: Cambridge University Press), 74 [Google Scholar]
- Priest, E. R., & Titov, V. S. 1996, Phil. Trans. R. Soc. London A Math. Phys. Eng. Sci., 354, 2951 [NASA ADS] [CrossRef] [Google Scholar]
- Priest, E. R., Hornig, G., & Pontin, D. I. 2003, J. Geophys. Res. (Space Phys.), 108, 1285 [NASA ADS] [CrossRef] [Google Scholar]
- Speiser, T. W. 1965, J. Geophys. Res., 70, 4219 [NASA ADS] [CrossRef] [Google Scholar]
- Stanier, A., Browning, P., & Dalla, S. 2012, A&A, 542, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sui, L., Holman, G. D., & Dennis, B. R. 2004, ApJ, 612, 546 [NASA ADS] [CrossRef] [Google Scholar]
- Threlfall, J., Bourdin, P.-A., Neukirch, T., & Parnell, C. 2016a, A&A, 587, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Threlfall, J., Stevenson, J. E. H., Parnell, C. E., & Neukirch, T. 2016b, A&A, 585, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thurgood, J. O., Pontin, D. I., & McLaughlin, J. A. 2017, ApJ, 844, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Titov, V. S., Tassi, E., & Hornig, G. 2004, Phys. Plasmas, 11, 4662 [NASA ADS] [CrossRef] [Google Scholar]
- Wyper, P. F., & Pontin, D. I. 2014a, Phys. Plasmas, 21, 082114 [NASA ADS] [CrossRef] [Google Scholar]
- Wyper, P. F., & Pontin, D. I. 2014b, Phys. Plasmas, 21, 102102 [NASA ADS] [CrossRef] [Google Scholar]
- Wyper, P. F., DeVore, C. R., Karpen, J. T., & Lynch, B. J. 2016, ApJ, 827, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Zharkova, V. V., & Gordovskyy, M. 2004, ApJ, 604, 884 [NASA ADS] [CrossRef] [Google Scholar]
- Zharkova, V. V., & Gordovskyy, M. 2005, MNRAS, 356, 1107 [NASA ADS] [CrossRef] [Google Scholar]
- Zharkova, V. V., Arzner, K., Benz, A. O., et al. 2011, Space Sci. Rev., 159, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Zhou, X., Büchner, J., Bárta, M., Gan, W., & Liu, S. 2015, ApJ, 815, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Zhou, X., Büchner, J., Widmer, F., & Muñoz, P. A. 2018a, Phys. Plasmas, 25, 042904 [NASA ADS] [CrossRef] [Google Scholar]
- Zhou, M., El-Alaoui, M., Lapenta, G., et al. 2018b, J. Geophys. Res. Space Phys., 123, 8087 [NASA ADS] [CrossRef] [Google Scholar]
- Zweibel, E. G., & Yamada, M. 2009, ARA&A, 47, 291 [Google Scholar]
All Figures
 |
Fig. 1. For each frame, top panel: 3D view of the MHD simulation domain, showing magnetic field lines and a volume rendering of |J|. Bottom panel: distribution of jz in the z = 0.0 plane. For t = 8 (panel a), t = 16 (panel b), t = 21 (panel c). The 3D images in panelsa and b are taken from Wyper & Pontin (2014a), and in panel c from Wyper & Pontin (2014b). |
| In the text | |
 |
Fig. 2. Initial positions of protons in the t = 8 snapshot alongside the spine field lines. The parallelograms become increasingly sheared at larger z to account for the inclination of the sheet in the xy plane. The distributions shown are for z = −0.2 (cyan), z = 0.0 (green) z = +0.2 (yellow), z = +0.4 (red), and z = +0.6 (magenta). |
| In the text | |
 |
Fig. 3. Final position latitude (θ)-longitude (ϕ) plot for protons initialised at z = 0 for t = 8 (panel a), t = 16 (panel b), t = 21 (panel c). The origin point is defined by the direction of the +z axis at (x, y) = (0, 0) in Cartesian coordinates. The cyan crosses indicate the approximate location of the spine axis as it crosses the domain boundary. |
| In the text | |
 |
Fig. 4. Final kinetic energies for thermal protons initialised in the parallelogram in the centre of the current sheet at z = 0.0 for t = 8 (panel c), t = 16 (panel d), t = 21 (panel e). The parallelogram is composed of 100 × 100 protons (in Cartesian coordinates in panel b) labelled on the axes. This shows the full energy gain plot in comparison to the current sheet shown in panel a, where Jz is the z-component of the current (also at z = 0.0). The plot is then skewed into a rectangle with a log scaling applied to the energy. The dimensions u and υ represent the particle number initialised along the long and short side of the parallelogram, respectively; (0, 0) represents the particle initialised at the top left and (100, 100) represents the particle initialised at the bottom right; see panel c. The corners [x, y] and dimensions of the parallelograms in code units are as follows (starting at the top left corner, going clockwise): panel c: ([−0.32, +0.72],[+0.32, −0.62],[+0.32, −0.72],[−0.32, +0.62]), length (in x) = 0.64, width (in y) = 0.1; panel d: ([−0.29, +1.45],[+0.29, −1.15],[+0.29, −1.45],[−0.29, +1.15]), length (in x) = 0.58, width (in y) = 0.3; and panel e: ([−0.26, +1.90],[+0.26, −1.30],[+0.26, −1.90],[−0.26, +1.30]), length (in x) = 0.52, width (in y) = 0.6. |
| In the text | |
 |
Fig. 5. Proton kinetic energy distributions at the start (purple), mid-point (blue), and end (green) of the simulations for snapshots t = 8 (panel a), t = 16 (panel b), t = 21 (panel c). |
| In the text | |
 |
Fig. 6. Connectivity plots at z = +1.0 with impact distributions overlaid for t = 8 (panel a), t = 16 (panel b), t = 21 (panel c). The connectivity maps are produced by integrating a large number of field lines from a grid of points in the given plane, and colouring the corresponding point according to which boundary the field line intersects. The cyan regions are magnetically connected to the −x domain boundary and the magenta regions are connected the +x domain boundary. |
| In the text | |
 |
Fig. 7. Comparison of flux ropes (blue) and the trajectories of the 100 particles with the highest final kinetic energies initialised at z = −0.2 (panel a), z = 0.0 (panel b), z = +0.2 (panel c), z = +0.4 (panel d), for the t = 16 snapshot. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.