EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 622 (February 2019) A&A, 622 (2019) A185 Full HTML
Free Access
Issue
A&A
Volume 622, February 2019
Article Number A185
Number of page(s) 11
Section Interstellar and circumstellar matter
DOI https://doi.org/10.1051/0004-6361/201834276
Published online 20 February 2019

© ESO 2019

1. Introduction

Abundant carbon-chain molecules have been observed in the early stage of low-mass star forming regions which are known as lukewarm corinos. The mechanism for synthesizing carbon-chain molecules in these sources is known as warm carbon-chain chemistry (WCCC; Sakai et al. 2008), therefore the lukewarm corinos with abundant carbon-chain molecules are also called WCCC sources. L1527 in Taurus is confirmed to be the first WCCC source (Sakai et al. 2008), which contains the low-mass protostar IRAS 04368 + 2557 in the transitional phase from Class 0 to Class I (Andre et al. 2000; Hassel et al. 2008; Sakai et al. 2009a, 2010). So far 14 carbon-chain species with relatively high abundances have been observed towards L1527. IRAS 15398-3359 in Lupus, which is also identified as B228, is confirmed as the second WCCC source (Sakai et al. 2009b). This protostar is also in the transitional phase from Class 0 to Class I. Six carbon-chain species have been observed towards B228. Recently, abundant carbon-chain species as well as more saturated complex organic molecules (COMs) are observed towards L483 (Oya et al. 2017) in the Aquila Rift. This cloud contains the Class 0 protostar IRAS 18148-0440 (Fuller et al. 1995). Other possible WCCC sources include B1, L1448N (Sakai et al. 2009b; Hassel et al. 2011), and the L1251A molecular core around the Class 0 protostar L1251A IRS3 (Cordiner et al. 2011).

The discovery of abundant carbon-chain species in low-mass star forming regions is unexpected because these species are characteristics of dark clouds (Suzuki et al. 1992; Hassel et al. 2008; Sakai et al. 2008). Before abundant carbon-chain species were observed towards L1527, COMs have been observed towards low-mass star forming regions (Cazaux et al. 2003; Bottinelli et al. 2004, 2007; Jørgensen et al. 2005, 2012; Sakai et al. 2006; Maury et al. 2014; Taquet et al. 2015). These low-mass star-forming regions with COMs are known as hot corinos, which are warmer than the lukewarm corinos. The desorption of CH4 is the first step to synthesize carbon-chain species in the lukewarm corinos according to the WCCC mechanism (Sakai et al. 2008, 2009b; Lindberg et al. 2016). When the temperature arises to about 30 K, volatile species such as CH4 can sublime from the grain surface. The sublimated species participate in gas phase reactions to produce carbon-chain species. So far, carbon-chain species abundances predicted by chemical models for L1527 agree reasonably well with observations (Aikawa et al. 2008; Hassel et al. 2008, 2011). However, further modelling studies on WCCC are necessary because of the limitations of previous models.

First, some previous models use the rate equation (RE) approach in the numerical simulations which in some cases may be problematic. When the average population of reactive species on the grain surface is well below one, the RE approach can lead to large errors in the simulation results (Tielens & Charnley 1997). This problem is known as the finite size effect. Vasyunin et al. (2009) showed that the abundances of species predicted by the RE approach deviate much from that by the more rigorous macroscopic Monte Carlo (MC) approach if the temperature is within 20 and 50 K. Although previous WCCC model results at about 30 K agree with observations (Hassel et al. 2008), it is questionable whether the model results simulated with the more rigorous numerical approach still fit the observations well.

Second, a more serious problem with previous WCCC simulations is the way their models treat the surface chemistry. All volatile species such as CH4 and CO in the ice mantle of a dust grain are assumed to sublime when the temperature is higher than their sublimation temperatures in these models. However, laboratory experiments show that not all CO can desorb when the temperature is higher than the CO sublimation temperature (Sandford & Allamandola 1988; Collings et al. 2003). There is also observational evidence that CO might be trapped in the ice mantle. For instance, the abundance of CO in some prestellar cores is observed to be lower than its canonical value (Fuente et al. 2012), and one possible explanation is that CO is trapped in the ice mantle. As the sublimation of CH4 triggers the synthesis of carbon-chain species in the gas phase, the production of carbon-chain species may be less efficient if a fraction of CH4 molecules are locked in the ice mantle.

More advanced surface chemical models are necessary so that the trapped CH4 in the mantle at temperatures higher than 30 K is considered. All previous WCCC models have adopted the widely used two-phase model in which all surface species can participate in reactions including sublimation. In order to consider thetrapping effect, a more advanced model called the three-phase model was suggested by Hasegawa & Herbst (1993). This model distinguishes species on the grain surface active layers and species buried in the ice mantle. Species in the active layers are reactive while species in the ice mantle are chemically inert. As the temperature increases, only species in the active layers can sublime, thus the majority of solid species are trapped in the ice mantle. The original three-phase model was simulated using the RE approach, but recently, Vasyunin & Herbst (2013) performed more rigorous macroscopic MC simulations of the three-phase model. However, the assumption in the three-phase model that species in the bulk of ice are completely inert may not be correct. For example, it is estimated that the probability that photons are absorbed by one monolayer of ice is about 0.007 (Andersson & van Dishoeck 2008). Thus, photons can easily penetrate through about 150 monolayers of ice and photodissociate species deeply buried in the ice mantle. A few modified three-phase models that adopt a partially active bulk ice mantle are suggested (Garrod 2013a; Chang & Herbst 2014; Kalvāns et al. 2017; Lu et al. 2018). Moreover, in the model suggested by Lu et al. (2018), the exponential decay with depth of photolysis in the ice mantle is well mimicked.

In this work, we have investigated WCCC using the macroscopic MC method and the advanced surface chemical models. We are particularly interested in studying the carbon-chain species abundances predicted by different surface models. The models used in this work are the two-phase model, the three-phase model suggested by Vasyunin & Herbst (2013), and the new multi-phase models suggested by Lu et al. (2018).

In Sect. 2 we describe our chemical models and the physical model of lukewarm corinos. In Sect. 3 we present all model results. In Sect. 4 we compare the results with observations. In Sect. 5 we discuss the advantages and disadvantages of different models and present our conclusions.

2. Model

2.1. Chemical model

The new multi-phase model used in this work has been explained in detail by Lu et al. (2018). Here we only briefly explain the model in the following. The ice mantle on the grain surface is composed of surface active layers and a partially active bulk of ice. Species in the surface active layers can diffuse and participate in surface reactions including sublimation. There are two types of binding sites in the partially active bulk of ice, the normal sites and the interstitial sites. Species occupying normal sites are called normal species, while interstitial species occupy interstitial sites and are uniformly distributed in the partially active bulk of ice. Normal species are locked in the mantle, thus cannot sublime until the whole ice mantle sublimes, while interstitial species can diffuse in the bulk of ice and sublime at their sublimation temperatures. Interstitial species can be generated by the photolysis of species in the bulk of ice. Both the UV photons from the externalradiation and that induced by cosmic ray are considered in our chemical model. Photofragments of icy species can enter normal sites or interstitial sites. The probability for a photodissociation product at the Mth layer of ice to enter the interstitial site is 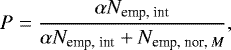P=αNemp,intαNemp,int+Nemp,nor,M,\begin{align*} P = \frac{\alpha N_{\textrm{{emp, int}}}}{\alpha N_{\textrm{{emp, int}}} +N_{\textrm{{emp, nor}, \it {M}}}},\end{align*}(1)

where Nemp, int is the average number of empty interstitial sites, Nemp, nor, M is the number of empty normal sites at the Mth layer, and α is a parameter depending on the difference of the binding energy of normal sites and interstitial sites. The larger the parameter α is, the more likely that photodissociation products occupy interstitial sites and, therefore, the more interstitial volatile species can sublime as the temperature increases. However, the parameter α is poorly known so far. Lu et al. (2018) argued that α should be no more than one, thus we set α to be 1, 0.5, and 0.01 in the new multi-phase models. Moreover, we also simulate a new multi-phase model in which all photodissociation products enter interstitial sites (α = + ∞) to maximize the population of interstitial species in the model. New multi-phase models adopting α = + ∞, 1, 0.5, and 0.01 are called new multi-phase model 0, 1, 2, and 3 in this work, respectively. We also simulated the two-phase model and the three-phase model suggested by Vasyunin & Herbst (2013), which is referred to as the basic multi-phase model in this work. The amounts of CH4 that can sublime at the CH4 sublimation temperature are different in these models. In the basic multi-phase model, CH4 molecules only in the active layers can sublime while all surface CH4 can desorb in the two-phase model. The amount of CH4 molecules that can sublime in the new multi-phase model is larger than that in the basic multi-phase model but less than that in the two-phase model, because CH4 molecules in the active layers and those occupying interstitial sites can sublime at the CH4 sublimation temperature in the new multi-phase models. Therefore, among all the models, carbon-chain species in the two-phase model should be the most abundant while the abundances of carbon-chain species predicted by the basic multi-phase model should be the lowest.

The macroscopic MC method is used to simulate the two-phase model, the basic multi-phase model and the new multi-phase models. Following Vasyunin et al. (2009), we isolate a cell of gas surrounding a dust particle. The total population of H nuclei is 1012 in the cell of gas if we set ρd = 3 g cm−3 and md∕g = 0.01 (Vasyunin et al. 2009). In this work, we report the fractional abundance of species, which is defined as the ratio of the population of the species to total population of H nuclei (1012) in the cell. If the population of a species is one, its fractional abundance is 10−12. This abundance is the minimum fractional abundance resolvable if we run a model only once. In order to reduce statistical fluctuation, we ran each model ten times to calculate the average fractional abundances, so the lowest fractional abundance resolvable is 10−13. Any fractional abundance lower than 10−13 is reported to be zero in this paper. In order to research the finite size effect, we also use the RE approach to simulate the two-phase model for comparison.

We performed the macroscopic MC simulations of the gas-grain chemical reaction network used by Hassel et al. (2008; hereafter HHG), which is based on the OSU2008 reaction network but with some changes, and found that even inthe two-phase model, carbon-chain species may be severely underproduced. The abundances of carbon-chain species in the two-phase model using a reaction network that includes all reactions in the OSU2008 and HHG agree with observations better than that using OSU2008 or HHG individually, therefore the combined reaction network is utilized in all models in this work. As a result, the gas-grain chemical reaction network includes 6462 reactions and 655 species. The competition mechanism is utilized to calculate the reaction rates for two surface reactions with barriers, CO + H → HCO and H2 CO + H → H3 CO (Chang & Herbst 2012). The reaction barriers of these two reactions are taken from Fuchs et al. (2009). Finally, the accretion of H2 consumes too much CPU time in the macroscopic MC simulations. However, it is found that H2 accretion is not important for the molecular evolution of dense clouds (Chang et al. 2017). Thus, H2 accretion is not includedin our chemical reaction network in order to reduce the computational cost. The bulk diffusion barrier for an interstitial species is set to be Eb2 = 0.7Ed (Lu et al. 2018), where Ed is the desorption energy of the same species in the active layers. All other parameters in the network are the same as that used by Hassel et al. (2008) and Semenov et al. (2010), which are shown in Table 1. We adopted the low initial metal abundances as shown in Table 2 (Hassel et al. 2008).

Table 1.

Model parameters.

Table 2.

Initial abundances (Hassel et al. 2008).

2.2. Physical model

We adoptedthe physical model used by Hassel et al. (2008), which is a homogeneous one-point model that includes two stages, a cold phase when the temperature of the molecular cloud is 10 K at the beginning and then a warm-up phase. In this model, the total hydrogen nucleus density is nH = 106 cm−3 in the central region of the prestellar core and the visual extinction AV = 10. The initial temperature is T = 10 K meanwhile the gas temperature and the grain temperature are in equilibrium all, the time for simplicity. The timescale of the cold phase tcold, when the temperature of the molecular cloud remains to be 10 K, is not well constrained. Hassel et al. (2008) argued through rate equation simulations that their two-phase model results are robust for the range 104 yr < tcold < 106 yr, thus they suggest a moderate value, tcold = 105 yr. However, we find that the results of the two-phase model simulated with the macroscopic MC method are dependent on tcold. Therefore, we simulate the two-phase model with the macroscopic MC method with different tcold and select a moderate value of tcold so that the predicted carbon-chain species abundances agree reasonably well with observations. Following Garrod & Herbst (2006) and Hassel et al. (2008, 2011), the temperature at the time tcold + Δt in the warm-up phase is 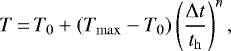T = T0+(Tmax−T0)(Δtth)n,\begin{align*} T{\,=\,}T_0&#x002B;(T_{\mathrm{max}}-T_0) \left( \frac{\UpDelta t}{t_{\mathrm{h}}} \right) ^n,\end{align*}(2)

where T0 is the initial temperature, 10 K, Tmax is the maximum temperature at the end of the warm-up phase that is adopted to be 200 K for the formation of hot cores or hot corinos, th is the heating timescale, and n is the order of the heating. According to Garrod & Herbst (2006) and Hassel et al. (2008, 2011), th = 2 × 105 yr is the timescale for intermediate star formation which is derived from the observed protostellar luminosity function (Molinari et al. 2000), and n = 2 for power law temperature profiles (Garrod & Herbst 2006). After the warm-up phase, the temperature remains constant.

Table 3.

Δt and the corresponding temperatures when the abundances of HC5N, HC7 N and HC9 N reach 10−12 in the two-phase model adopting different tcold values.

3. Results

In this section, we report the fractional abundances of carbon-chain species in different models. The finite size effect in the two-phase model is investigated in Sect. 3.1 through a comparison of the simulation results from the macroscopicMC method and the RE approach. The two-phase, the basic and the new multi-phase models are simulated with the macroscopic MC method, and the results from these models are compared in Sect. 3.2.

3.1. Finite size effect

The two-phase model is simulated with both the macroscopic MC method and the RE approach. The abundances of gas-phase HC5N, HC7N, and HC9N in the two-phase model calculated with the RE approach deviate much from that with the macroscopic MC method. Table 3 shows Δt in the warm-up phase and the corresponding temperatures when the abundance of HC5N, HC7N, and HC9N begins to be higher than 10−12 adopting different tcold. If tcold = 105 yr, the temperature has reached 33 K when the abundance of HC5N is over 10−12 in the simulation with the macroscopic MC method. The temperature can be even higher for HC7N and HC9N, which increases to 38 K and 57 K, respectively. The time at which the fractional abundance is higher than 10−12, tcold + Δt, becomes shorter so that the corresponding temperature is lower if the RE approach is used. For instance, the abundance of HC9N starts to be higher than 10−12 when the temperatureis 27 K if tcold = 105 yr. These differences arise from the fact that the macroscopic MC method takes into account the finite effect while the RE approach does not (Vasyunin et al. 2009). Our results agree with previous studies in that the discrepancies of some gas phase carbon-chain species abundances between the macroscopic MC method and the RE approach can be significant when T = 25 − 30 K (Vasyunin et al. 2009). Therefore, the finite size effect is important if tcold = 105 yr. On the other hand, the finite size effect becomes less important for longer tcold. If tcold = 3 × 105 yr, the temperatures of the core are about 21, 25, and 26 K, respectively, when the abundances of HC5N, HC7N, and HC9N are over 10−12 in the simulations with the macroscopic MC method. The RE approach predicts similar temperatures of the core, which are 23, 26, and 26 K, respectively. Moreover, in our simulations the temperatures are relatively robust if tcold > 3 × 105 yr. The reason for the decrease of the discrepancy between the RE and the macroscopic MC model results as tcold increases is that as the population of surface species increases, it becomes less likely that the average number of a surface species drops well below one, thus the finite size effect becomes less significant. In order for the abundances of carbon-chain species to be higher than 10−12 when the temperatures of the core are around 30 K in the MC models, tcold should be noshorter than 3 × 105 yr. Therefore, we set tcold to be 3 × 105 yr for all models in Sect. 3.2.

Figure 1 shows the evolutions of the abundances of selected gas-phase carbon-chain species in the two-phase model simulated with the RE approach and the macroscopic MC method. Different tcold is used to perform the simulations. In the two-phase model A, tcold is set to be 105 yr while in the two-phasemodel B, it is 3 × 105 yr. In an overview, the abundances of the selected carbon-chain species in the cold stage are much affected, regardless of tcold, by the numerical approach used in simulations. The finite size effect is not important at T = 10 K in our models, which agrees with Vasyunin et al. (2009). The maximum abundances in the cold stage can reach around 4.0 × 10−10, which are relatively low in the entire evolution of 107 yr. On the other hand, the abundances of carbon-chain species rise rapidly in the warm-up phase. The abundances can be more than two orders of magnitude than the peak values in the cold phase. Thus we can conclude that these carbon-chain species are synthesized rapidly during this period. Moreover, in the hot phase with T = 200 K, the abundances decrease from the peak values to 10−12. There are large differences between the results from the RE model and the macroscopic MC model in the warm-up phase when tcold = 105 yr. The maximum abundance of CH3CCH can be around 10−6 in the two-phase model A when the RE approach is utilized. However, the maximum abundance of CH3CCH drops by one order of magnitude in the same model when the macroscopic MC method is used. Moreover, it takes a shorter time for the abundances of carbon-chain species to decrease to 10−12 when the macroscopic MC method is utilized. In the RE calculations, the abundances of all selected carbon-chain species drop to 10−12 at around t ~ 5 × 106 yr while in the MC simulations, carbon-chain species drop earlier at around t ~ 2 × 106 yr. Thus, the finite size is important when tcold = 105 yr. On the other hand, the discrepancy between the RE model and the macroscopic MC model becomes smaller when longer tcold is adopted. For instance, the maximum abundance of CH3CCH in the two-phase model B simulated with the RE approach is only about a factor of three larger than that with the macroscopic MC method, compared with an order of magnitude in the case of a shorter tcold.

thumbnail Fig. 1.

Temporal evolution of the fractional abundances of selected carbon-chain species in the two-phase model simulated with the RE approach and the macroscopic MC method. RE represents the rate equation calculation and MC represents the macroscopic Monte Carlo simulation. The two-phase model adopts different tcold, tcold = 105 yr in the two-phase model A while tcold = 3 × 105 yr in the two-phase model B. The temporal evolution of the temperature T is also plotted in the figure.

3.2. Model results comparison

Hereafter, surface species are designated by the letter J. Surface species that can sublime at their sublimation temperatures before the whole ice mantle disappears are called sublimable species. In the two-phase model all surface species are sublimable species, while in the basic multi-phase model only species in the active layers are sublimable species. In the new multi-phase models, in addition to species in the active layers, interstitial species are also sublimable species. According to Sakai et al. (2008, 2009b), CH4 is the precursor for producing carbon-chain molecules, and CO is the precursor for producing complex organic molecules. Therefore, in order to investigate the synthesis of carbon-chain species in each model, it is important to research the abundances of sublimable JCH4 in each model. Figure 2 shows the temporal evolution of CH4, CO, total JCH4, sublimable JCH4, total JCO, and sublimable JCO in all models in the warm-up phase. The abundance of gas-phase CH4 in the two-phase model can reach 5.2 × 10−6 when T is slightly lower than 30 K, but its abundances in the new multi-phase model 0, 1, 2, and 3 can only reach around 3.0 × 10−7, which are about one order of magnitude lower than that in the two-phase model. The abundance of gaseous CH4 in the basic multi-phase model is even lower, around 1.0 × 10−7 when T is 30 K. On the other hand, the abundances of gaseous CH4 in all models are almost the same at 200 K when all species in the ice mantle sublime. The difference of gaseous CH4 abundance at 30 K originates from the different populations of sublimable JCH4 molecules in these models. Although the populations of total JCH4 in all models are approximately the same before these molecules start to sublime, the population of sublimable JCH4 molecules in the two-phase model is about one order of magnitude higher than that in the basic multi-phase model, while in the new multi-phase models, it is a factor of between two and three larger than that in the basic multi-phase model. The populations of sublimable JCH4 in the new multi-phase model 0–2 are approximately the same, while in the new multi-phase model 3 it is the lowest among all new multi-phase models. The same phenomenon occurs for CO. The abundance of gaseous CO in the two-phase model at 25 K is much higher than those in the basic and new multi-phase models, while gaseous CO abundances in the new multi-phase models are higher than that in the basic multi-phase model. Similarly, the abundance of sublimable JCO is the highest in the two-phase model and the lowest in the basic multi-phase model at temperatures below 25 K, and the abundances in the new multi-phase models are moderate.

Figure 3 shows the temporal evolutions of the abundances of selected gas-phase carbon-chain species in the two-phase, the basic multi-phase, and the new multi-phase models. We pay most attention to the time period when WCCC occurs at the temperature around 30 K (Hassel et al. 2008, 2011). The abundances of all selected gas-phase carbon-chain species in the new multi-phase models 0–2 are similar, which demonstrates that if α ≥0.5, the results of the new multi-phase models will not change much because the population of sublimable JCH4 hardly changes as discussed before. However, these abundances in the new multi-phase model 3 do deviate from that in the other new multi-phase models. At 30 K, the new multi-phase model 3 predicts slightly lower CH3CCH abundance and slightly higher C4H and C4 H2 abundances than the other new multi-phase models do. Since the abundance of gas-phase CH4 in the new multi-phase model 3 is lower than that in the other new multi-phase models at around 30 K, less CH3CCH are formed in the new multi-phase model 3. On the other hand, we can see that C4 H and C4 H2 abundances in the new multi-phase model 3 are slightly higher than those in the new multi-phase models 0–2. The discrepancy can be explained as follows. Interstitial O2 and O3 molecules can enter active layers upon warm-up and are hydrogenated to form OH and H2 O, which may enter gas phase via reactive desorption. Both gas-phase OH and H2 O can produce H3 O+ ions while the electron dissociative recombination of H3 O+ is the major destruction pathway for electrons in our models. Because the interstitial O2 and O3 abundances at 10 K in the new multi-phase model 3 are lower, the abundances of gas-phase OH and H2 O are lower at around 30 K in this model. Therefore, the new multi-phase model 3 predicts lower H3 O+ abundance and thus higher electron abundance at around 30 K. Moreover, electron dissociative recombination is important to produce C4 H and C4 H2. For instance, C4H and C4 H2 can be produced by reactions C4 H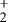2+$_2^{&#x002B;}$ + e− → C4 H + H and C4 H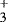3+$_3^{&#x002B;}$ + e− → C4 H2 + H, respectively. Thus, more C4H and C4 H2 are formed in the new multi-phase model 3 than those in the other new multi-phase models at around 30 K.

Overall, the carbon-chain species abundances predicted by the basic and the new multi-phase models are typically lower than that by the two-phase model at around 30 K when WCCC occurs because gas-phase CH4 in the two-phase model is much higher than that in the other models. The abundance of CH3CCH in the two-phase model at around 30 K is about two orders of magnitude higher than those in the basic and the new multi-phase models, while C4 H2 and HC5N produced in the basic and the new multi-phase models at around 30 K are about one order of magnitude less than those in the two-phase model. The abundances of C4H at 30 K do not vary much in different models and its abundance in the two-phase model is the highest. On the other hand, because O2 or O3 molecules that are buried in the bulk of ice cannot enter the active layers to be hydrogenated and form OH or H2 O upon warm-up in the basic multi-phase model, this model predicts lower H3 O+ abundance and higher electron abundance than the new multi-phase models do. Therefore, although the basic new multi-phase model predicts the lowest gaseous CH4 abundance at around 30 K, the carbon-chain species abundances predicted by the basic multi-phase model are not always the lowest. The abundances of C4H, C4 H2, and HC5N in the basic multi-phase model are approximately the same or even slightly higher than those in the new multi-phase models 0–2.

4. Comparison with observations

In order to compare the simulation results with the observations, we adopted the “mean confidence level” method as a quantitative standard (Garrod et al. 2007; Hassel et al. 2008). The confidence level κj represents the agreement between the abundance in the simulation Xj and the observation Xobs,j of species j, and κj is calculatedby 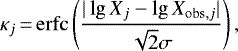κj = erfc(|lgXj−lgXobs,j|2σ),\begin{align*} \kappa_j{\,=\,}\mathrm{erfc} \left( \frac{|\lg X_j - \lg X_{\mathrm{obs,}j}|}{\sqrt{2}\sigma} \right),\end{align*}(3)

where erfc is the complementary error function, σ = 1 is the standard error. The value of κj is between 0 and 1. The agreement with the observations increases as κj approaches 1. We set σ = 1 because we assumed the uncertainty of the observations as one order of magnitude. Therefore, κj = 0.317 represents that the abundance of a species in a model is higher or lower by one order of magnitude than the observation. The average κ for all the observed species towards one astronomical source can be used to quantify the global agreement between the model results and the observations. Another parameter to quantify the global agreement is the number of fits, which is the number of species that fit the observations within one order of magnitude when the value of the average κ is the maximum. The time when the value of the average κ is the maximum, κmax is the optimum time tcold + Δtopt. We compared the model results with the observations and find out κmax, tcold + Δtopt, the number of fits, the temperature and the abundances of observed species at the time tcold + Δtopt.

Table 4 shows the results for the comparison of the model results and the observations towards L1527. Overall, the two-phase model results fit the observations towards L1527 the best while the basic multi-phase model works the worst. Comparing the results from the two-phase model simulated with the macroscopic MC approach with the observations, the peak value of κ is 0.616 when tcold + Δt = 3.604 × 105 yr and T = 27 K, and 23 of 26 species can fit the observations within one order of magnitude. However, κmax for the basic multi-phase model only reaches 0.398 when T = 32 K while the number of fits is just 14. The results from the new multi-phase models 0, 1, and 2 agree with the observations almost equally well but the new multi-phase model 3 performs slightly worse than the other new multi-phase models. For the new multi-phase models 0, 1, and 2, κmax is around 0.530 when T ~ 31–32 K while the number of fits is 21 or 20. However, κmax for the new multi-phase model 3 drops to about 0.510 and the number of fits is 19. In terms of fitting observations, the difference in the two-phase model results between the macroscopic MC method and the RE approach is not significant, because κmax and the number of fits are similar.

Tables 5 and 6 show the results for the comparison of the model results and the observations towards B228 and L483, respectively. The two-phase model still outperforms the basic and the new multi-phase models while κmax for the basic multi-phase model is still the lowest among all models. The two-phase model simulated with the RE approach fits the observationstowards L483 slightly better than that simulated with the macroscopic MC method, but fits the observations towards B228 slightly less well.

Gaseous CH4 abundances predicted by the basic and the new multi-phase models at tcold + Δtopt are around one order of magnitude lower than the observations towards L1527, while the two-phase model can reproduce the observed CH4 abundance pretty well. Because gaseous CH4 is the key molecule for the synthesis of carbon-chain species based on the WCCC mechanism, the abundances of carbon-chain species predicted by the basic and the new multi-phase models are typically lower than that by the two-phase model. However, the agreement between the model results and the observations varies depending on the carbon-chain species. The abundances of CH3CCH predicted by the basic multi-phase model are about two orders of magnitude lower than the observations towards L1527 and B228. The abundances of CH3CCH predicted by the new multi-phase models are about a factor of four larger than that in the basic multi-phase model, but they are still more than one order of magnitude lower than the observations. On the other hand, the abundances of C2 H and HC3N predicted by the basic and the new multi-phase models agree reasonably well with the observations towards all known sources. The two-phase model overproduces C4 H2 and C6 H2 by about two orders of magnitude. Although the abundances of these two species drop in the basic and the new multi-phase models, they are still more than one order of magnitude higher than the observations towards L1527 and B228. In addition to CH4 and carbon-chain species, another species that is severely underproduced by the basic and the new multi-phase models is CO. The observed CO abundances towards L1527 and L483 are four orders of magnitude higher than that predicted by the basic multi-phase model. The abundances of CO increase by two orders of magnitude in the new multi-phase models, but they are still two orders of magnitude lower than the observations.

thumbnail Fig. 2.

Temporal evolution of the fractional abundances of CH4, CO, total JCH4, sublimable JCH4, total JCO, and sublimable JCO in all models. The letter J represents species on the grain. The temperature is labelled on the top horizontal axis. For total JCH4 and JCO, the curves from all models except the two-phase model are almost the same.
thumbnail Fig. 3.

Temporal evolution of the fractional abundances of C4H, C4 H2, CH3 CCH, and HC5N in all models. The temperature is also labelled on the top horizontal axis.
Table 4.

Observed and simulated fractional abundances of L1527.

Table 5.

Observed and simulated fractional abundances of B228.

Table 6.

Observed and simulated fractional abundances of L483.

5. Discussions and conclusions

We investigated WCCC using the two-phase model, the basic and the new multi-phase models in this work. Because the macroscopic MC method was adopted in the simulations, we also paid attention to the significance of the finite size effect in the simulations. The results of the basic and the new multi-phase models are compared with that of the two-phase model. We find that gaseous CH4 abundance predicted by the basic multi-phase model is more than one order of magnitude lower than that predicted by the two-phase model when the temperature is around 30 K because most CH4 is frozen on grains. In addition to CH4 molecules in the active layers, interstitial CH4 can also sublime at 30 K in the new multi-phase models, thus the abundances of gaseous CH4 in the new multiphase models are around a factor of three larger than that in the basic multi-phase model. However, gaseous CH4 abundances in the new multi-phase models are still around one order of magnitude lower than that in the two-phase model. Because CH4 is important to synthesize carbon-chain species in the gas phase, the abundances of carbon-chain species in the two-phase model are the highest among all models. On the other hand, the increase of H3 O+ abundance can decrease the abundance of electrons. Meanwhile, electrons participate in the reactions of producing carbon-chain species. Therefore, carbon-chain species abundances in the basic multi-phase model at 30 K may be even higher than those in the new multi-phase models, because the H3 O+ abundance in the basic multi-phase model is the lowest among all models. In addition, the significance of the finite size effect depends on the duration of the cold stage. If tcold > 3 × 105 yr, the finite size effect is not important. However, if tcold < 3 × 105 yr, the difference in the results of the two-phase model between the RE approach and the macroscopic MC method is large.

Although the basic multi-phase model is more realistic than the two-phase model because icy species are distinguished, the abundances of species predicted by the basic multi-phase model agree worse with the observations than that by the two-phase model. The new multi-phase models do improve the agreement with the observations. However, a few species such as CH4 and CH3CCH are still severely underproduced by the new multi-phase models. We discuss the reasons for this below.

First, the UV radiation field in the cold stage may be stronger than that used in our simulations so that more interstitial species are formed, thus CH4 abundance may increase upon warm-up. Second, physical conditions can affect the chemical model results. For instance, we ran test simulations with the physical model used by Aikawa et al. (2008). We find that the abundances of gaseous CH4 and CO agree well with the observations towards L1527. However, overall the abundances of species predicted by all chemical models using this physical model agree worse with the observations. The reason may be that the pre-collapse duration in this physical model, 106 yr, may be too long. Finally, more rigorous lattice microscopic MC simulations show that abundant holes may exist in the ice mantle (Garrod 2013b). If there are abundant holes in the ice mantles on grain surfaces, more CH4 molecules inthe bulk of ice might diffuse into the active layers upon warm-up, thus more gaseous carbon-chain species may be produced. Therefore, WCCC may be used to test the validity of surface chemical models.

It is found that the population of species that can diffuse in the bulk of ice controls the efficiency of the synthesis of terrestrial COMs in the ice mantle (Lu et al. 2018). On the other hand, the population of solid CH4 that are mobile in the bulk of ice is also crucial for WCCC. Therefore, more studies on WCCC will also help to discover the formation of terrestrial COMs in various astronomical sources.

Acknowledgements

We thank our referee’s constructive comments to improve the quality of the article. The authors are grateful to Donghui Quan and Xia Zhang for the rate equation simulations. We also thank Eric Herbst, Ling Liao, Yang Lu, Longfei Chen, and Fujun Du for helpful discussions and valuable comments. We thank George E. Hassel for providing chemical reaction networks he used for WCCC simulations. We also thank Yuri Aikawa for providing the physical model she used for WCCC simulations. This work is supported by the National Key R&D Program of China (No. 2017YFA0402701). Q.C. acknowledges the support from the National Natural Science Foundation of China (NSFC) grant No. 11673054.

References

  1. Agúndez, M., Cernicharo, J., & Guélin, M. 2015, A&A, 577, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  2. Aikawa, Y., Wakelam, V., Garrod, R. T., & Herbst, E. 2008, ApJ, 674, 984 [NASA ADS] [CrossRef] [Google Scholar]
  3. Andersson, S., & van Dishoeck, E. F. 2008, A&A, 491, 907 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Andre, P., Ward-Thompson, D., & Barsony, M. 2000, Protostars and Planets IV (Tucson, AZ: University of Arizona Press), 59 [Google Scholar]
  5. Benson, P. J., Caselli, P., & Myers, P. C. 1998, ApJ, 506, 743 [NASA ADS] [CrossRef] [Google Scholar]
  6. Bottinelli, S., Ceccarelli, C., Neri, R., et al. 2004, ApJ, 617, L69 [NASA ADS] [CrossRef] [Google Scholar]
  7. Bottinelli, S., Ceccarelli, C., Williams, J. P., & Lefloch, B. 2007, A&A, 463, 601 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Cazaux, S., Tielens, A. G. G. M., Ceccarelli, C., et al. 2003, ApJ, 593, L51 [NASA ADS] [CrossRef] [Google Scholar]
  9. Chang, Q., & Herbst, E. 2012, ApJ, 759, 147 [NASA ADS] [CrossRef] [Google Scholar]
  10. Chang, Q., & Herbst, E. 2014, ApJ, 787, 135 [NASA ADS] [CrossRef] [Google Scholar]
  11. Chang, Q., Lu, Y., & Quan, D. 2017, ApJ, 851, 68 [NASA ADS] [CrossRef] [Google Scholar]
  12. Collings, M. P., Dever, J. W., Fraser, H. J., McCoustra, M. R. S., & Williams, D. A. 2003, ApJ, 583, 1058 [NASA ADS] [CrossRef] [Google Scholar]
  13. Cordiner, M. A., Charnley, S. B., Buckle, J. V., Walsh, C., & Millar, T. J. 2011, ApJ, 730, L18 [NASA ADS] [CrossRef] [Google Scholar]
  14. Fuchs, G. W., Cuppen, H. M., Ioppolo, S., et al. 2009, A&A, 505, 629 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Fuente, A., Caselli, P., McCoey, C., et al. 2012, A&A, 540, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Fuller, G. A., Lada, E. A., Masson, C. R., & Myers, P. C. 1995, ApJ, 453, 754 [NASA ADS] [CrossRef] [Google Scholar]
  17. Garrod, R. T. 2013a, ApJ, 765, 60 [Google Scholar]
  18. Garrod, R. T. 2013b, ApJ, 778, 158 [NASA ADS] [CrossRef] [Google Scholar]
  19. Garrod, R. T., & Herbst, E. 2006, A&A, 457, 927 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  20. Garrod, R. T., Wakelam, V., & Herbst, E. 2007, A&A, 467, 1103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. Hasegawa, T. I., & Herbst, E. 1993, MNRAS, 263, 589 [NASA ADS] [CrossRef] [Google Scholar]
  22. Hassel, G. E., Herbst, E., & Garrod, R. T. 2008, ApJ, 681, 1385 [NASA ADS] [CrossRef] [Google Scholar]
  23. Hassel, G. E., Harada, N., & Herbst, E. 2011, ApJ, 743, 182 [NASA ADS] [CrossRef] [Google Scholar]
  24. Hirota, T., Ohishi, M., & Yamamoto, S. 2009, ApJ, 699, 585 [NASA ADS] [CrossRef] [Google Scholar]
  25. Jørgensen, J. K., Schöier, F. L., & van Dishoeck, E. F. 2002, A&A, 389, 908 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Jørgensen, J. K., Schöier, F. L., & van Dishoeck, E. F. 2004, A&A, 416, 603 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  27. Jørgensen, J. K., Bourke, T. L., Myers, P. C., et al. 2005, ApJ, 632, 973 [NASA ADS] [CrossRef] [Google Scholar]
  28. Jørgensen, J. K., Favre, C., Bisschop, S. E., et al. 2012, ApJ, 757, L4 [NASA ADS] [CrossRef] [Google Scholar]
  29. Kalvāns, J., Shmeld, I., Kalnin, J. R., & Hocuk, S. 2017, MNRAS, 467, 1763 [NASA ADS] [Google Scholar]
  30. Lindberg, J. E., Charnley, S. B., & Cordiner, M. A. 2016, ApJ, 833, L14 [NASA ADS] [CrossRef] [Google Scholar]
  31. Lu, Y., Chang, Q., & Aikawa, Y. 2018, ApJ, 869, 165 [NASA ADS] [CrossRef] [Google Scholar]
  32. Maury, A. J., Belloche, A., André, P., et al. 2014, A&A, 563, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  33. Molinari, S., Brand, J., Cesaroni, R., & Palla, F. 2000, A&A, 355, 617 [NASA ADS] [Google Scholar]
  34. Oya, Y., Sakai, N., Watanabe, Y., et al. 2017, ApJ, 837, 174 [NASA ADS] [CrossRef] [Google Scholar]
  35. Sakai, N., Sakai, T., & Yamamoto, S. 2006, PASJ, 58, L15 [NASA ADS] [Google Scholar]
  36. Sakai, N., Sakai, T., Hirota, T., & Yamamoto, S. 2008, ApJ, 672, 371 [NASA ADS] [CrossRef] [Google Scholar]
  37. Sakai, N., Sakai, T., Hirota, T., & Yamamoto, S. 2009a, ApJ, 702, 1025 [NASA ADS] [CrossRef] [Google Scholar]
  38. Sakai, N., Sakai, T., Hirota, T., Burton, M., & Yamamoto, S. 2009b, ApJ, 697, 769 [NASA ADS] [CrossRef] [Google Scholar]
  39. Sakai, N., Sakai, T., Hirota, T., & Yamamoto, S. 2010, ApJ, 722, 1633 [NASA ADS] [CrossRef] [Google Scholar]
  40. Sakai, N., Shirley, Y. L., Sakai, T., et al. 2012, ApJ, 758, L4 [NASA ADS] [CrossRef] [Google Scholar]
  41. Sandford, S. A., & Allamandola, L. J. 1988, Icarus, 76, 201 [NASA ADS] [CrossRef] [Google Scholar]
  42. Semenov, D., Hersant, F., Wakelam, V., et al. 2010, A&A, 522, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  43. Suzuki, H., Yamamoto, S., Ohishi, M., et al. 1992, ApJ, 392, 551 [NASA ADS] [CrossRef] [Google Scholar]
  44. Tafalla, M., Myers, P. C., Mardones, D., & Bachiller, R. 2000, A&A, 359, 967 [NASA ADS] [Google Scholar]
  45. Taquet, V., López-Sepulcre, A., Ceccarelli, C., et al. 2015, ApJ, 804, 81 [NASA ADS] [CrossRef] [Google Scholar]
  46. Tielens, A. G. G. M., & Charnley, S. B. 1997, Origins of Life and Evolution of the Biosphere, 27, 23 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  47. Vasyunin, A. I., & Herbst, E. 2013, ApJ, 762, 86 [NASA ADS] [CrossRef] [Google Scholar]
  48. Vasyunin, A. I., Semenov, D. A., Wiebe, D. S., & Henning, T. 2009, ApJ, 691, 1459 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1.

Model parameters.

In the text
Table 2.

Initial abundances (Hassel et al. 2008).

In the text
Table 3.

Δt and the corresponding temperatures when the abundances of HC5N, HC7 N and HC9 N reach 10−12 in the two-phase model adopting different tcold values.

In the text
Table 4.

Observed and simulated fractional abundances of L1527.

In the text
Table 5.

Observed and simulated fractional abundances of B228.

In the text
Table 6.

Observed and simulated fractional abundances of L483.

In the text

All Figures

thumbnail Fig. 1.

Temporal evolution of the fractional abundances of selected carbon-chain species in the two-phase model simulated with the RE approach and the macroscopic MC method. RE represents the rate equation calculation and MC represents the macroscopic Monte Carlo simulation. The two-phase model adopts different tcold, tcold = 105 yr in the two-phase model A while tcold = 3 × 105 yr in the two-phase model B. The temporal evolution of the temperature T is also plotted in the figure.
In the text
thumbnail Fig. 2.

Temporal evolution of the fractional abundances of CH4, CO, total JCH4, sublimable JCH4, total JCO, and sublimable JCO in all models. The letter J represents species on the grain. The temperature is labelled on the top horizontal axis. For total JCH4 and JCO, the curves from all models except the two-phase model are almost the same.
In the text
thumbnail Fig. 3.

Temporal evolution of the fractional abundances of C4H, C4 H2, CH3 CCH, and HC5N in all models. The temperature is also labelled on the top horizontal axis.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.