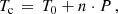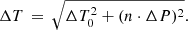| Issue |
A&A
Volume 622, February 2019
|
|
|---|---|---|
| Article Number | A81 | |
| Number of page(s) | 21 | |
| Section | Catalogs and data | |
| DOI | https://doi.org/10.1051/0004-6361/201834194 | |
| Published online | 31 January 2019 | |
Ephemeris refinement of 21 hot Jupiter exoplanets with high timing uncertainties⋆
1
Leibniz-Institut für Astrophysik Potsdam, An der Sternwarte 16, 14482 Potsdam, Germany
e-mail: mmallonn@aip.de
2
Stellar Astrophysics Centre, Department of Physics and Astronomy, Aarhus University, Ny Munkegade 120, 8000 Aarhus C, Denmark
3
Institut de Ciéncies de l’Espai (ICE, CSIC), Campus UAB, Carrer de Can Magrans s/n, 08193 Cerdanyola del Vallès, Spain
4
Institut d’Estudis Espacials de Catalunya (IEEC), C/Gran Capitá 2-4, Edif. Nexus 08034 Barcelona, Spain
5
Facultad de Ciencias Astronómicas y Geofísicas, Universidad Nacional de La Plata, Paseo del Bosque, B1900FWA La Plata, Argentina
6
Instituto de Astrofísica de La Plata (CCT-La Plata, CONICET-UNLP), Paseo del Bosque, B1900FWA La Plata, Argentina
7
Department of Astrophysical Sciences, Princeton University, 4 Ivy Lane, Princeton, NJ 08544, USA
8
Dept. of Physics, University of Warwick, Gibbet Hill Road, Coventry CV4 7AL, UK
9
Center of Astro-Engineering UC, Pontificia Universidad Católica de Chile, Av. Vicuña Mackenna 4860, 7820436 Macul, Santiago, Chile
10
Instituto de Astrofísica, Facultad de Física, Pontificia Universidad Católica de Chile, Av. Vicuña Mackenna 4860, 7820436 Macul, Santiago, Chile
11
Millennium Institute of Astrophysics, Av. Vicuña Mackenna 4860, 782-0436 Macul, Santiago, Chile
12
Observatoire des Baronnies provencales, Observatoire Astronomique, 05150 Moydans, France
13
Observatory Puig d’Agulles, Carrer Riera 1, 08759 Vallirana, Spain
14
Max-Planck-Institut für Astronomie, Königstuhl 17, 69117 Heidelberg, Germany
15
NASA Goddard Space Flight Center, Exoplanets and Stellar Astrophysics Laboratory, Greenbelt, MD 20771, USA
16
Emory University Department of Physics, 400 Dowman Drive, Suite N218, Atlanta, GA 30322, USA
17
Kavli Institute for Astrophysics and Space Research, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
18
Rarotonga Observatory, PO Box 876, Rarotonga, Cook Islands
19
La Vara, Valdes Observatory, 33784 Muñas de Arriba, Valdés, Asturias, Spain
20
Yunnan Observatories, Chinese Academy of Sciences, Kunming 650011, PR China
21
Key Laboratory for the Structure and Evolution of Celestial Objects, Chinese Academy of Sciences, Kunming 650216, PR China
22
University of Chinese Academy of Sciences, Beijing 100049, PR China
23
Observatori Astronòmic Albanyà, Camí de Bassegoda s/n, 17733 Albanyà, Spain
24
Observatoire Astronomique de Vaison, 84110 Vaison la Romaine, France
25
National Youth Space Center, 59567 Goheung, Jeollanam-do, South Korea
26
Space Research Institute, Austrian Academy of Sciences, Schmiedlstr. 6, 8042 Graz, Austria
27
Anunaki Observatory, Calle de los Llanos, 28410 Manzanares el Real, Spain
28
School of Physical Sciences, The Open University, Milton Keynes MK7 6AA, UK
29
Gruppo Astrofili Salese “Galileo Galilei”, Via G. Ferraris 1, 30036 Santa Maria di Sala (VE), Italy
30
Las Cumbres Observatory, 6740 Cortona Dr., Suite 102, Santa Barbara, CA 93117, USA
31
Special Astrophysical Observatory, Russian Academy of Sciences, Nizhnij Arkhyz 369167, Russia
32
Central Astronomical Observatory at Pulkovo of Russian Academy of Sciences, Pulkovskoje shosse d. 65, St., Petersburg 196140, Russia
Received:
8
November
2018
Accepted:
14
December
2018
Transit events of extrasolar planets offer a wealth of information for planetary characterization. However, for many known targets, the uncertainty of their predicted transit windows prohibits an accurate scheduling of follow-up observations. In this work, we refine the ephemerides of 21 hot Jupiter exoplanets with the largest timing uncertainties. We collected 120 professional and amateur transit light curves of the targets of interest, observed with a range of telescopes of 0.3 m–2.2 m, and analyzed them along with the timing information of the planets discovery papers. In the case of WASP-117b, we measured a timing deviation compared to the known ephemeris of about 3.5 h, and for HAT-P-29b and HAT-P-31b the deviation amounted to about 2 h and more. For all targets, the new ephemeris predicts transit timings with uncertainties of less than 6 min in the year 2018 and less than 13 min until 2025. Thus, our results allow for an accurate scheduling of follow-up observations in the next decade.
Key words: methods: observational / techniques: photometric / planets and satellites: fundamental parameters
Observational lightcurves are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/622/A81
© ESO 2019
1. Introduction
The transit of an extrasolar planet delivers a wealth of information. Time-series photometry of the event allows for the derivation of the orbital period, the orbital inclination, and the planet-star radius ratio (Charbonneau et al. 2000; Seager & Mallén-Ornelas 2003). If the host star is well characterized by high-resolution spectroscopy, a radial velocity curve by a spectroscopic time-series offers the mass of the transiting system (e.g., Bouchy et al. 2005). This mass in combination with the transit information yields the mean density of the planet. Transiting systems also provide information on their atmospheric composition through transmission spectroscopy, information on the thermal energy budget through emission spectroscopy, and allow for conclusions on their migration history through the measurement of the misalignment of stellar spin and planetary orbit in accordance with the Rossiter-McLaughlin effect (e.g., Wakeford et al. 2017; Arcangeli et al. 2018; Albrecht et al. 2012).
However, any follow-up observation of the transit events, either with photometry, low or high-resolution spectroscopy, or even with polarimetry, relies on reasonably accurate knowledge of the timing of the transit. This knowledge degrades over time because the timing uncertainty increases linearly with the number of transit epochs that have passed since the last observation. The large number of exoplanets discovered per year nowadays makes it more and more difficult to ensure parameter refinement studies for all targets. Therefore, there is a non-negligible number of systems for which the timing uncertainty has reached values of 30 min or more. This uncertainty is too high for follow-up observations with space-based or large ground-based telescopes, where observing time is very expensive and good coverage of out-of-transit observations cannot be guaranteed within a limited observing interval. The timing uncertainty can grow so much that the knowledge of when the transit happens is practically lost. Current examples are CoRoT-24b and c (Alonso et al. 2014).
The goal of this work is to refine the ephemeris information of hot Jupiter systems that exhibit large timing uncertainties to ensure the possibility of future follow-up observations. In Sect. 2, we describe our target selection, in Sect. 3 we provide details about the observations for this work, and in Sect. 4 we explain the data analysis. Section 5 provides the results, Sect. 6 gives a discussion, and in Sect. 7 we finish the paper by outlining our conclusions.
2. Target selection
We compiled a target list with the ephemeris information of hot Jupiter exoplanets from the NASA Exoplanet Archive (Akeson et al. 2013) and calculated the transit time uncertainty by mid 2018. We constrained our target selection to the planets discovered by ground-based surveys and include all planets named with the prefix WASP, HAT-P, HATS, XO, TrES, KELT, Qatar, and MASCARA. We noticed that several planets discovered by the space mission CoRoT, next to the aforementioned CoRoT-24 b and c, have a timing uncertainty above 30 min; examples are CoRoT-16b and 17b with three- and six-hour transit timing uncertainty. However, due to their relative faintness of about fifteenth magnitude in Johnson V, these targets are of limited value for detailed characterization and generally of less interest for follow-up observations. Hence, they are not included here. From the general formula of a planet ephemeris,
with T0 as the timing zero point, P as the orbital period, and n as the number of epochs passed since T0, we calculate the uncertainty of the calculated timing Tc according to the general rules of uncertainty propagation:
This equation does not take into account a potential covariance of T0 and P, however, for those of our targets with the largest timing uncertainties, ΔT is strongly dominated by the term n ⋅ ΔP and a potential covariance is of minor importance.
For the 267 targets in our list, the timing uncertainty by August 2018 ranges from 0.3 min to 172 min with a median of 4 min. For the 50 objects with the largest timing uncertainties, we verified that the used ephemeris values were still up to date by checking for each individual target the publications listed in The Extrasolar Planets Encyclopaedia (Schneider et al. 2011) under “Related Publications” and by checking all publications that cited the discovery paper of the target of interest.
At the time of target selection and data acquisition of this project, HAT-P-25b and HAT-P-38b were ranked position 11 and 8 in Table 1 with timing uncertainties of 23.7 and 24.6 min according to their discovery papers Quinn et al. (2012) and Sato et al. (2012). In the course of this work, the ephemerides of these planets were improved by Wang et al. (2018b) and Bruno et al. (2018). Both targets are still included here as a consistency check with the new values. For the three hot Jupiters Qatar-3b, -4b, and -5b, the orbital period uncertainty was not provided in their discovery paper Alsubai et al. (2017). These planets are included here for a new analysis because new results published at the Exoplanet Transit Database (ETD, Poddaný et al. 2010) indicate deviations from the currently known ephemerides for two of the three targets. We finish the ranking in Table 1 at an uncertainty of 11 min. This value is rather arbitrary, but we consider uncertainties smaller than this value to cause only minor problems in the scheduling of transit follow-up observations.
Ranking of hot Jupiter exoplanets according to their timing uncertainties as of August 2018.
The targets of our sample are very diverse in their planetary and stellar parameters, therefore they are of interest for a broad bandwidth of investigations: from investigations on radius inflation mechanisms of hot Jupiters (Qatar-4b and Kelt-8b have radii larger than 1.5 Jupiter radii) and tidal star-planet interactions (HAT-P-34b, Qatar-3b, Qatar-4b, and Qatar-5b have masses above 3 Jupiter masses), through studies on the formation history of the rare hot Jupiters with planetary companions (HAT-P-44b, HAT-P-45b, HAT-P-46b), to a search for mechanisms that excite the eccentricity of close-in gas giants (HAT-P-31b, HAT-P-34b, WASP-117b). Four host stars among the sample are peculiarly bright with V < 10.5 mag, simplifying any effort for follow-up. WASP-117b is one of the longest-period hot Jupiters and the orbit has been almost unchanged by tidal interaction during its lifetime (Lendl et al. 2014). Because of the large timing uncertainties of our targets, any effort for follow-up observations will greatly benefit from a prior ephemeris refinement.
3. Observations and data acquisition
Transit time-series photometry in the course of this work has been obtained with the 1.2-m STELLA telescope, the 0.8-m Joan Oró telescope (TJO) of the Montsec Astronomical Observatory, the 2.2-m telescope of the Calar Alto Observatory, the 2.15-m Jorge Sahade telescope (JST) of the Observatory Complejo Astronómico El Leoncito (CASLEO), the National Youth Space Center (NYSC) 1m telescope, the Chilean-Hungarian Automated Telescope (CHAT), a 1.0-m telescope of the Las Cumbres Observatory (LCO), and Yunnan.
STELLA and its wide-field imager WiFSIP (Strassmeier et al. 2004, 2010) observed 19 transits in total in the Sloan r′ filter. The original field of view of WiFSIP of 22′×22′ was reduced in all observations to 15′×15′ to shorten the read-out time. A mild defocus was always applied to spread the PSF to an artificial FWHM of about 3″.
Five transit light curves in Johnson V filter were obtained with the TJO and its main imager MEIA2. The instrument has a field of view of 12.3 × 12.3 arcmin and a resolution of 0.36 arcsec pixel−1. All TJO observations employed the Johnson V filter.
One transit light curve was observed with the Calar Alto 2.2 m telescope and its instrument CAFOS in imaging mode. The SITe CCD chip was binned by 2 × 2 pixels. Additionally, we applied a read-out window to reduce the read-out time. A mild defocus was applied.
We observed one primary transits of WASP-73b with the JST. The observations were carried out using an R filter and binning 1 × 1. To increase the size of the field of view to an unvignetted 9 arcmin radius, we employed a focal reducer.
Five transits were obtained with the NYSC 1 m telescope at Deukheung Optical Astronomy Observatory (DOAO) in South Korea with either a FLI PL-16803 CCD camera or a Princeton Instruments SOPHIA-2048B CCD. The telescope was slightly defocused during the observations, and we employed a Cousins R filter.
Two transit light curves were observed with the CHAT, which is a newly commissioned 0.7 telescope at Las Campanas Observatory, Chile, built by members of the HATSouth (Bakos et al. 2013) team, and dedicated to the follow-up of transiting exoplanets. A more detailed account of the CHAT facility will be published at a future date (Jordán et al., in prep.1). Data were obtained with a Finger Lakes Microline CCD camera equipped with a back-illuminated CCD and a Sloan i′ filter. The camera, which has a field of view of ≈21′×21′, was slightly defocused during the observations.
A light curve of WASP-117b transit was obtained in July 2017 at the LCO, which is a fully robotic network of telescopes (Brown et al. 2013), deployed around the globe in both hemispheres2. We used a 1.0-m telescope of the network at the South African Astrophysical Observatory (SAAO) and the Sinistro camera. The telescope was defocused by 3.0 mm.
One transit light curve was obtained with 1-m telescope of Yunnan Observatories, China, and its 2K × 2K CCD camera using the Cousins R filter. The instrument offers a field of view of 7.2′×7.2′ and a resolution of 0.2 arcsec pixel−1.
We complemented our data sample with a large number of amateur light curves, which we obtained from the ETD3 (Poddaný et al. 2010). We selected 85 light curves from this database by visual inspection. While the ETD offers an online fitting routine and provides the derived transit parameter, we downloaded the reduced light curves and re-analyzed them for their timing information homogeneously to the newly obtained light curves with professional telescopes (see Sect. 4). A summary of all 120 light curves and their properties is given in Table B.1.
Since the data of this paper were obtained by more than 30 different observatories, we did not attempt a homogeneous data reduction. The ETD observers uploaded reduced light curves to the online database and provided some details of the data reduction. The data reduction and light curve extraction of the professional observatories is briefly described in Appendix A.
All 120 light curves together with their transit fit (Sect. 4) are shown in Fig. B.1.
4. Light-curve analysis
In this work, we analyzed the photometric transit light curves with the publicly available software tool JKTEBOP (Southworth et al. 2004; Southworth 2008). Fit parameters were the orbital semi-major axis scaled by the stellar radius a/R⋆, the orbital inclination i, the planet-star radius ratio k, the midpoint of the transit T, the orbital period P, the eccentricity of the orbit e, the argument of periastron ω, and coefficients of the detrending function c0, 1, 2.
Many studies suggest that trends in small-telescope transit photometry of 1–2 mmag photometric precision is fit by simple detrending functions with very few coefficients (e.g., Juvan et al. 2018; Southworth et al. 2016; Mancini et al. 2016; Maciejewski et al. 2016). For STELLA/WiFSIP photometry, several studies used the Bayesian Information Criterion to show that first or second order polynomials over time form the best representation of trends or systematics in the light curves (e.g., Mallonn et al. 2015, 2016; Mackebrandt et al. 2017). Therefore, and for the reason that the ETD light curves are lacking the information of external parameters for a more complex detrending, we detrended all light curves of this work consistently by a simple second-order polynomial over time. For the vast majority of targets we present a multiplicity of light curves which warrants a consistency check.
Crucial for the final derivation of robust uncertainties on the transit timing measurement is a reliable estimation of the photometric uncertainties. We started with the values delivered by the different aperture photometry software tools, which generally include the photon noise of the target, ensemble of comparison stars and background. We ran an initial transit model fit, subtracted the best fit model from the data, and performed a 4-σ clipping on the residuals to remove outliers. As a second step, we ran another transit fit and multiplied the photometric uncertainties by a common factor that results in a reduced χ2 of unity for the fit. Additionally, we calculated the so-called β factor, a concept introduced by Gillon et al. (2006) and Winn et al. (2008) to include the contribution of correlated noise in the light curve analysis. It describes the evolution of the standard deviation σ of the light-curve residuals when they become binned in comparison to Poisson noise. In the presence of correlated noise, σ of the binned residuals is larger by the factor β than the binned uncorrelated (white) noise that decreases by the square root of the number of points per bin width. The value of β depends on the bin width, we use here the average of ten binning steps from half to twice the duration of ingress. We enlarged the photometric uncertainty finally by this factor β.
The dates of all light curves were converted to BJDTDB (Eastman et al. 2010). All individual transit light curves were now fit with i, a/R⋆, k, P, e, and ω fixed to literature values. In the case of HAT-P-29b, we used the updated parameter values of Wang et al. (2018a). The limb darkening coefficients of the quadratic law were fixed to theoretical values from Claret et al. (2012, 2013) according to their stellar parameters obtained from the planet discovery papers. ETD light curves taken with a Clear filter were fit with limb darkening coefficients according to Cousins R. The free-to-fit parameters for each individual light curve were T and c0, 1, 2. All individual transit mid-times are summarized in Table B.2.
The estimation of the transit parameter uncertainties was done in JKTEBOP with a Monte Carlo simulation (Southworth et al. 2005), and with a residual-permutation algorithm that takes correlated noise into account (Southworth 2008). The Monte Carlo simulation was run with 5000 steps. As final parameter uncertainties we adopted the larger value of both methods. The uncertainties of the fixed transit parameters were included in the final timing uncertainty by letting them vary during the error estimation within the 1-σ ranges of the literature values.
In the final step, we performed a joint fit of all light curves per target and included T0 with its uncertainty of the previous ephemeris of the discovery paper. Free-to-fit values were P and T0 of a new ephemeris and the detrending coefficients c0, 1, 2 per light curve. The epoch of T0 was chosen to minimize the covariance between T0 and P. In the cases of HAT-P-25b and HAT-P-38b, for which refined ephemerides were published in the course of our analysis, we included also the individual transit times that became available (see Table B.2). The new ephemerides of the 21 exoplanets of this work are summarized in Table 2. In Figs. B.2–B.4, we show the individual observed-minus-calculated timing deviations. For HAT-P-29b, Wang et al. (2018a) found the T0 provided in the discovery paper (Buchhave et al. 2011) to be affected by an overly small value of the transit duration. Therefore, we used the corrected timings from Wang et al. (2018a) in the joint fit. As a consequence, there is an offset between the displayed previous ephemeris and the corresponding corrected timing values (Fig. B.2, upper right panel) of the discovery paper.
Refined ephemerides resulting from this work.
We do not attempt a refinement of transit parameters in addition to the ephemerides because a significant fraction of the light curves used here either miss parts of the transit event or do not reach millimag-precision. However, the light curves are available at the Strasbourg astronomical Data Center (CDS) for further use.
5. Results
5.1. Ephemeris refinement of 21 exoplanets
We use the recently published, refined ephemeris values for HAT-P-25b and HAT-P-38b as a cross-check for the values derived in this work. For both planets, the periods deviate only by fractions of the 1-σ uncertainties compared to the refined values of Wang et al. (2018b) and Bruno et al. (2018). We were able to increase the precision of the orbital period estimation because we extended the covered time span by one more season. At a late stage in the preparation of this publication, a follow-up study for HAT-P-29b became available (Wang et al. 2018a). We also reached an agreement for the ephemeris within 1-σ for this latter work.
For all individual timings of this study over all targets, we calculate the reduced χ2 value to be about 1.1. This indicates a reasonable good match between the average deviation from the corresponding linear ephemeris and the measurement uncertainty. A 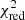 slightly larger than unity can be caused by starspots in the host-star photosphere that deform the shape of photometric transit curve (Oshagh et al. 2013; Holczer et al. 2015).
slightly larger than unity can be caused by starspots in the host-star photosphere that deform the shape of photometric transit curve (Oshagh et al. 2013; Holczer et al. 2015).
For the majority of the targets investigated in this work, the photometric quality of the light curves only allowed for a slight improvement on the precision of T0 compared to the discovery papers. However, including the timing measurement of these publications, our data expand the time interval of observed transit events for all targets significantly. Therefore, the uncertainty of the estimated orbital period P could be lowered by an order of magnitude for all targets. Objects worth emphasizing are WASP-117b, HAT-P-31b, and HAT-P-29b, for which we measured the predicted transit times to be off by more than 2 h. For WASP-117b, the actual deviation amounted to about 3.5 h. In the case of HAT-P-35b and WASP-73b, the difference between prediction and measurement was on the order of 1 hour. For HAT-P-29b, the measured timings deviated by 3.7σ from the ephemeris given in the discovery paper.
5.2. Comparison to the ETD online fit results
The Exoplanet Transit Database performs a transit fit to the uploaded light curves (Poddaný et al. 2010). The achieved best fit parameters are listed on the webpage and are regularly used in scientific publications (e.g., Southworth et al. 2016; Angerhausen et al. 2017; Lillo-Box et al. 2018). Our re-analyzed timing values of 85 ETD light curves allow for a cross check with these ETD results. We find that on average the absolute timing shows a deviation of only 20% of our 1-σ error bars; that is, there is no systematic offset. However, there is a significant scatter of the individual timing differences with a standard deviation of one when expressed in terms of our derived 1-σ uncertainties. In extreme cases, the deviations between our best-fit values and ETD derived parameters reached 4σ. We find that the ETD error bars are on average smaller by a factor of 1.7 than the corresponding values derived by the standard procedures used in this work. The ETD adopts the parameter uncertainties from a Levenberg–Marquardt optimization algorithm (Poddaný et al. 2010), which is believed to be unreliable in the presence of parameter correlations (see Southworth 2008, and references therein). Therefore, we recommend the re-analysis of ETD light curves instead of the usage of the transit parameters obtained by the online fitting tool.
6. Discussion
We use our sample of 21 newly determined ephemerides to check statistically if the differences between old and new ephmerides are in general agreement to the previous ephemeris uncertainties. When we express the measured-to-predicted timing deviation of all our 21 targets in units of their previously known timing uncertainties, we find a standard deviation for all targets of about 1.4 one-sigma uncertainties; that is, larger than unity. This indicates a trend of slightly underestimated uncertainties of the ephemerides. There may be various reasons for this depending on individual targets; for example, underestimated systematics in the data, systematic effects on the host star, like stellar activity, or transit timing variations (TTV).
We consider it to be possible that significant timing deviations from the predicted values originate from TTVs. Such variation could be caused by gravitational interactions of the observed hot Jupiter with unknown planetary companions (von Essen et al. 2018, and references therein). Hot Jupiter planets are known to mostly orbit their host star alone (Steffen et al. 2012). However in recent years a few exceptions to this general rule have been found, such as the planetary system of WASP-47 with one hot Jupiter accompanied by an interior and an exterior sub-Neptune (Becker et al. 2015; Neveu-VanMalle et al. 2016). Using all 3.5 years of Kepler spacecraft data, Huang et al. (2016) showed that these exceptions are very rare. For two of these systems, HAT-P-13 and WASP-47, the literature provides constraints on the TTV amplitude caused by the companions. In the case of HAT-P-13b, Fulton et al. (2011) ruled out periodic TTV of an amplitude larger than 144 s, while for WASP-47b, Becker et al. (2015) measured a TTV amplitude of 38 s. The planetary systems of the hot Jupiters WASP-53b and WASP-81b are uncommon in that they also each harbor an eccentric brown dwarf within a few astronomical units of the host star. Predicted TTVs of these hot Jupiters are below 1 min (Triaud et al. 2017).
Among our target list, there are three systems with RV candidate signals of Jupiter-mass companions within 1 AU, HAT-P-44, HAT-P-45, and HAT-P-46 (Hartman et al. 2014). Our newly derived ephemerides of HAT-P-45b and HAT-P-46b are in very good agreement with the ones previously published by Hartman et al. (2014). The individual data points from different seasons show no significant deviation from the linear ephemerides, and therefore we find no indications for significant effects of TTVs. On the other hand, the eight individual measurements of HAT-P-44b show a rather large reduced χ2 value of 2.3. Nevertheless, we find no TTV periodicity at the planet companion period of about 220 days. The newly derived value of the period deviates by about 25 min from the discovery paper. To compute an order of magnitude of the amplitude of TTVs of planet b caused by the outer perturber, we made use of TTVFast (Deck et al. 2014). Here we assumed coplanar orbits, a circular orbit for the perturber, and the masses and periods from Hartman et al. (2014). The derived TTV amplitude for planet HAT-P-44b is about 6 s, which is extremely challenging to measure for ground-based observatories. With increasing mutual inclination, the mass of the outer perturber would also increase due to the degeneracy of M with sin i, and so would the TTV amplitude (Payne & Ford 2011). However, we consider it to be likely that TTVs only have a marginal effect on the deviation of 25 min. It is more probable that this deviation is caused by the limited precision of the previous ephemeris, since it amounts to only 1.6σ, which we do not consider as significant.
An indicator for the potential existence of an outer perturber causing TTVs might also be a nonzero eccentricity of the hot Jupiter. Among our target list, there are four targets with an e significantly different from zero: WASP-117b, HAT-P-29b, HAT-P-31b, and HAT-P-34b. For all four targets, both the number of individual transit epochs and their individual precision is too low to allow for conclusions on TTVs with approximately one-minute amplitudes. We increase the precision of the period determination by an order of magnitude, and therefore our new ephemerides form the best available basis for future follow-up studies.
The target HAT-P-29b shows the most significant deviation of measured-to-predicted transit timings with a significance level of 3.7, a deviation very recently also described by Wang et al. (2018a). In this particular case, a likely explanation is the sensitivity of the used partial transit light curves to an overly small value of the transit duration derived in the discovery paper. For more details, we point the reader to the discussion supplied in Wang et al. (2018a).
7. Conclusion
We have refined the ephemerides of 21 exoplanets which previously had the largest timing uncertainties of ground-based detected hot Jupiters. We made use of a total of 120 transit light curves: 35 obtained from professional observatories and 85 from amateur observers. The bulk of our data might be considered as data of only moderate photometric quality, since more than half of our light curves have a point-to-point scatter larger than 3 mmag, or lack the ingress or egress part of the transit. However, the present work is a valuable example of where light curves of small-sized telescopes can still play a crucial role in modern science. All data were analyzed homogeneously, and resulted in an increased precision in the estimations of the orbital periods by one order of magnitude when combined with the transit-timing information of the discovery papers. Previous to our work, the timing uncertainty of the 21 analyzed objects ranged from 11 to 171 min. We were able to lower this to values ranging from 1 to 6 min, and thus to ensure a reasonable scheduling of follow-up studies at least until the year 2025, when the timing uncertainties will still be below 12 min for all our targets. Our new ephemerides might be affected to a certain extent by stellar activity and TTVs caused by unknown companions. The former constitutes a form of correlated noise in the data and is accounted for in the error estimation, while the latter is less likely because additional companions to hot Jupiters are extremely rare and cause TTV of low amplitude. In any case, we emphasize that even in the cases of ephemerides affected by astrophysical disturbances, our new ephemerides present the best available basis for future follow-up studies. Currently, the ground-based detected hot Jupiter with the largest timing uncertainty is KELT-10b with ΔTc ≈ 24 min (by August 2018). We note that especially due to the enormous effort of the observers of the Exoplanet Transit Database, there is currently no hot Jupiter known in the northern hemisphere discovered by ground-based surveys with a timing uncertainty larger than 14 min.
For updated information about the network, see: https://lco.global
Acknowledgments
E.H. acknowledges support by the Spanish Ministry of Economy and Competitiveness (MINECO) and the Fondo Europeo de Desarrollo Regional (FEDER) through grant ESP2016-80435-C2-1-R, as well as the support of the Generalitat de Catalunya/CERCA program. D. D. acknowledges support provided by NASA through Hubble Fellowship grant HST-HF2-51372.001-A awarded by the Space Telescope Science Institute, which is operated by the Association of Universities for Research in Astronomy, Inc., for NASA, under contract NAS5-26555. E.S. acknowledges support by the Russian Science Foundation grant No. 14-50-00043 for conducting international photometric observing campaign. I.S. acknowledges support by the Russian Foundation for Basic Research (project No. 17-02-00542). R.B. acknowledges support from FONDECYT Post-doctoral Fellowship Project No. 3180246. M.L. acknowledges support from the Austrian Research Promotion Agency (FFG) under project 859724 “GRAPPA”. S.-H.G. acknowledges the financial support from the National Natural Science Foundation of China (No.U1531121). L.C. recognizes funding from DLR – 50OR1804. Funding for the Stellar Astrophysics Centre is provided by The Danish National Research Foundation (Grant agreement no.: DNRF106). We thank the staff at the various participating observatories STELLA, CASLEO, Calar Alto, TJO, and others for their support. Partly based on data obtained with the STELLA robotic telescopes in Tenerife, an AIP facility jointly operated by AIP and IAC, on data acquired at Complejo Astronómico El Leoncito, operated under agreement between the Consejo Nacional de Investigaciones Científicas y Técnicas de la República Argentina and the National Universities of La Plata, Córdoba and San Juan, on observations collected at the Centro Astronómico Hispano Alemán (CAHA) at Calar Alto, operated jointly by the Max-Planck Institut für Astronomie and the Instituto de Astrofísica de Andalucía (CSIC), and on data obtained with the Joan Oró Telescope (TJO) of the Montsec Astronomical Observatory (OAdM), owned by the Generalitat de Catalunya and operated by the Institute for Space Studies of Catalonia (IEEC). This research has made use of the SIMBAD data base and VizieR catalog access tool, operated at CDS, Strasbourg, France, and of the NASA Astrophysics Data System (ADS).
References
- Akeson, R. L., Chen, X., Ciardi, D., et al. 2013, PASP, 125, 989 [NASA ADS] [CrossRef] [Google Scholar]
- Albrecht, S., Winn, J. N., Johnson, J. A., et al. 2012, ApJ, 757, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Alonso, R., Moutou, C., Endl, M., et al. 2014, A&A, 567, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alsubai, K., Mislis, D., Tsvetanov, Z. I., et al. 2017, AJ, 153, 200 [NASA ADS] [CrossRef] [Google Scholar]
- Angerhausen, D., Dreyer, C., Placek, B., et al. 2017, A&A, 608, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arcangeli, J., Désert, J.-M., Line, M. R., et al. 2018, ApJ, 855, L30 [NASA ADS] [CrossRef] [Google Scholar]
- Bakos, G. Á., Hartman, J. D., Torres, G., et al. 2012, AJ, 144, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Bakos, G. Á., Csubry, Z., Penev, K., et al. 2013, PASP, 125, 154 [NASA ADS] [CrossRef] [Google Scholar]
- Becker, J. C., Vanderburg, A., Adams, F. C., Rappaport, S. A., & Schwengeler, H. M. 2015, ApJ, 812, L18 [NASA ADS] [CrossRef] [Google Scholar]
- Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boisse, I., Hartman, J. D., Bakos, G. Á., et al. 2013, A&A, 558, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bouchy, F., Udry, S., Mayor, M., et al. 2005, A&A, 444, L15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brown, T. M., Baliber, N., Bianco, F. B., et al. 2013, PASP, 125, 1031 [NASA ADS] [CrossRef] [Google Scholar]
- Bruno, G., Lewis, N. K., Stevenson, K. B., et al. 2018, AJ, 155, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Buchhave, L. A., Bakos, G. Á., Hartman, J. D., et al. 2011, ApJ, 733, 116 [NASA ADS] [CrossRef] [Google Scholar]
- Charbonneau, D., Brown, T. M., Latham, D. W., & Mayor, M. 2000, ApJ, 529, L45 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Claret, A., Hauschildt, P. H., & Witte, S. 2012, A&A, 546, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Claret, A., Hauschildt, P. H., & Witte, S. 2013, A&A, 552, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Colome, J., & Ribas, I. 2006, IAU Special Session, 6, 11 [Google Scholar]
- Deck, K. M., Agol, E., Holman, M. J., & Nesvorný, D. 2014, ApJ, 787, 132 [CrossRef] [Google Scholar]
- Delrez, L., Van Grootel, V., Anderson, D. R., et al. 2014, A&A, 563, A143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eastman, J., Siverd, R., & Gaudi, B. S. 2010, PASP, 122, 935 [NASA ADS] [CrossRef] [Google Scholar]
- Faedi, F., Gómez Maqueo Chew, Y., Pollacco, D., et al. 2016, ArXiv e-prints [arXiv:1608.04225] [Google Scholar]
- Fulton, B. J., Shporer, A., Winn, J. N., et al. 2011, AJ, 142, 84 [NASA ADS] [CrossRef] [Google Scholar]
- Fulton, B. J., Collins, K. A., Gaudi, B. S., et al. 2015, ApJ, 810, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Gillon, M., Pont, F., Moutou, C., et al. 2006, A&A, 459, 249 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hartman, J. D., Bakos, G. Á., Torres, G., et al. 2014, AJ, 147, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Hartman, J. D., Bhatti, W., Bakos, G. Á., et al. 2015, AJ, 150, 168 [NASA ADS] [CrossRef] [Google Scholar]
- Hébrard, G., Collier Cameron, A., Brown, D. J. A., et al. 2013, A&A, 549, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hellier, C., Anderson, D. R., Cameron, A. C., et al. 2014, MNRAS, 440, 1982 [NASA ADS] [CrossRef] [Google Scholar]
- Holczer, T., Shporer, A., Mazeh, T., et al. 2015, ApJ, 807, 170 [NASA ADS] [CrossRef] [Google Scholar]
- Huang, C., Wu, Y., & Triaud, A. H. M. J. 2016, ApJ, 825, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Juvan, I. G., Lendl, M., Cubillos, P. E., et al. 2018, A&A, 610, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kipping, D. M., Hartman, J., Bakos, G. Á., et al. 2011, AJ, 142, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Kovács, G., Bakos, G. Á., Hartman, J. D., et al. 2010, ApJ, 724, 866 [NASA ADS] [CrossRef] [Google Scholar]
- Kuhn, R. B., Rodriguez, J. E., Collins, K. A., et al. 2016, MNRAS, 459, 4281 [NASA ADS] [CrossRef] [Google Scholar]
- Lendl, M., Triaud, A. H. M. J., Anderson, D. R., et al. 2014, A&A, 568, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lillo-Box, J., Leleu, A., Parviainen, H., et al. 2018, A&A, 618, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maciejewski, G., Dimitrov, D., Fernández, M., et al. 2016, A&A, 588, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mackebrandt, F., Mallonn, M., Ohlert, J. M., et al. 2017, A&A, 608, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mallonn, M., Nascimbeni, V., Weingrill, J., et al. 2015, A&A, 583, A138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mallonn, M., Bernt, I., Herrero, E., et al. 2016, MNRAS, 463, 604 [NASA ADS] [CrossRef] [Google Scholar]
- Mancini, L., Giordano, M., Mollière, P., et al. 2016, MNRAS, 461, 1053 [NASA ADS] [CrossRef] [Google Scholar]
- Neveu-VanMalle, M., Queloz, D., Anderson, D. R., et al. 2016, A&A, 586, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Oshagh, M., Santos, N. C., Boisse, I., et al. 2013, A&A, 556, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Payne, M. J., & Ford, E. B. 2011, ApJ, 729, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Pepper, J., Siverd, R. J., Beatty, T. G., et al. 2013, ApJ, 773, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Poddaný, S., Brát, L., & Pejcha, O. 2010, New Astron., 15, 297 [NASA ADS] [CrossRef] [Google Scholar]
- Quinn, S. N., Bakos, G. Á., Hartman, J., et al. 2012, ApJ, 745, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Rodriguez, J. E., Colón, K. D., Stassun, K. G., et al. 2016, AJ, 151, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Sato, B., Hartman, J. D., Bakos, G. Á., et al. 2012, PASJ, 64, 97 [NASA ADS] [Google Scholar]
- Schneider, J., Dedieu, C., Le Sidaner, P., Savalle, R., & Zolotukhin, I. 2011, A&A, 532, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Seager, S., & Mallén-Ornelas, G. 2003, ApJ, 585, 1038 [NASA ADS] [CrossRef] [Google Scholar]
- Shporer, A., Zhou, G., Fulton, B. J., et al. 2017, AJ, 154, 188 [NASA ADS] [CrossRef] [Google Scholar]
- Simpson, E. K., Faedi, F., Barros, S. C. C., et al. 2011, AJ, 141, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Southworth, J. 2008, MNRAS, 386, 1644 [NASA ADS] [CrossRef] [Google Scholar]
- Southworth, J., Maxted, P. F. L., & Smalley, B. 2004, MNRAS, 351, 1277 [NASA ADS] [CrossRef] [Google Scholar]
- Southworth, J., Smalley, B., Maxted, P. F. L., Claret, A., & Etzel, P. B. 2005, MNRAS, 363, 529 [NASA ADS] [CrossRef] [Google Scholar]
- Southworth, J., Tregloan-Reed, J., Andersen, M. I., et al. 2016, MNRAS, 457, 4205 [NASA ADS] [CrossRef] [Google Scholar]
- Steffen, J. H., Ragozzine, D., Fabrycky, D. C., et al. 2012, Proc. Natl. Acad. Sci., 109, 7982 [NASA ADS] [CrossRef] [Google Scholar]
- Strassmeier, K. G., Granzer, T., Weber, M., et al. 2004, Astron. Nachr., 325, 527 [NASA ADS] [CrossRef] [Google Scholar]
- Strassmeier, K. G., Granzer, T., Weber, M., et al. 2010, Adv. Astron., 2010, 970306 [Google Scholar]
- Triaud, A. H. M. J., Neveu-VanMalle, M., Lendl, M., et al. 2017, MNRAS, 467, 1714 [NASA ADS] [Google Scholar]
- von Essen, C., Ofir, A., Dreizler, S., et al. 2018, A&A, 615, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wakeford, H. R., Sing, D. K., Kataria, T., et al. 2017, Science, 356, 628 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, X.-B., Gu, S.-H., Collier Cameron, A., et al. 2014, AJ, 147, 92 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, S., Wang, X.-Y., Wang, Y.-H., et al. 2018a, AJ, 156, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, X.-Y., Wang, S., Hinse, T. C., et al. 2018b, PASP, 130, 064401 [NASA ADS] [CrossRef] [Google Scholar]
- Winn, J. N., Holman, M. J., Torres, G., et al. 2008, ApJ, 683, 1076 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Data reduction
The data reduction of the STELLA and CalarAlto data was done with a customized pipeline already used for previous transit light curve analyses (Mallonn et al. 2015, 2016; Mackebrandt et al. 2017). Aperture photometry was done with the publicly available software SExtractor (Bertin & Arnouts 1996). We selected the aperture size that minimized the scatter in the light curve residuals after subtraction of an initial transit model of literature transit parameters including a second-order polynomial over time for detrending. Using the same criterion of minimization of photometric scatter, our data reduction pipeline also automatically chose the best selection of comparison stars for differential photometry.
The TJO imaging frames were reduced using the ICAT reduction pipeline at the TJO (Colome & Ribas 2006) and aperture photometry was extracted using AstroImageJ.
The data reduction of the JST light curves was carried out using DIP2OL, which structure and use is fully explained in von Essen et al. (2018). Briefly, the first part of the pipeline is IRAF-based; it carries out the pre-reduction, the extraction of stellar fluxes, and the computation of photometric uncertainties in an automatized way. The second part of the pipeline is a python program that minimizes the scatter of the differential light curves by the most adequate combination of reference stars for the differential light curve, and an optimization of the aperture and the radius size where the sky counts are determined.
The four imaging time-series from the NYSC 1-m telescope were reduced by the IRAF ccdred package and aperture photometry was performed with SExtractor. Differential photometry was obtained by the usage of an ensemble of comparison stars.
The CHAT photometric images were reduced using a dedicated pipeline descendant of a pipeline created to obtain photometry using the Las Cumbres 1-m telescopes (Shporer et al. 2017; Espinoza et al., in prep.), which was also used for the LCO imaging time-series analyzed in this work.
The data reduction of the Yunnan Observatory data were reduced using the IRAF package, and systematic errors were removed from the resulting photometric data according to the procedures in Wang et al. (2014).
Appendix B: Figures and tables
 |
Fig. B.1. Detrended transit light curves in the same order as in Table B.1. Curves after the first are displaced vertically for clarity. Residuals from the fits are displayed in the right panel with the same vertical offset. |
 |
Fig. B.1. continued. |
 |
Fig. B.1. continued. |
 |
Fig. B.1. continued. |
 |
Fig. B.1. continued. |
 |
Fig. B.2. Observed minus calculated mid-transit times for HAT-P-25b, HAT-P-29b, HAT-P-31b, HAT-P-34b, HAT-P-35b, HAT-P-38b, HAT-P-42b, and HAT-P-43b. Measurements of this work in black, literature values included in our calculation in red. A black dashed line denotes the new ephemeris of this work with associated uncertainties in dotted lines. For comparison, the previous ephemeris of the discovery paper in blue. The offset between previous ephemeris and literature value for HAT-P-29b is caused by a timing offset corrected in Wang et al. (2018a); see text for details. |
 |
Fig. B.3. Continuation of Fig. B.2 for HAT-P-44b, HAT-P-45b, HAT-P-46b, HAT-P-52b, KELT-3b, KELT-8b, Qatar-3b, and Qatar-4b. We note that Qatar-3b and Qatar-4b lack an ephemeris uncertainty in their discovery paper. |
 |
Fig. B.4. Continuation of Fig. B.2 for Qatar-5b, WASP-37b, WASP-58b, WASP-73b, and WASP-117b. We note that Qatar-5b lacks an ephemeris uncertainty in its discovery paper. |
Overview about the transit observations of the investigated planets.
Observed transit times of the investigated planets.
All Tables
Ranking of hot Jupiter exoplanets according to their timing uncertainties as of August 2018.
All Figures
 |
Fig. B.1. Detrended transit light curves in the same order as in Table B.1. Curves after the first are displaced vertically for clarity. Residuals from the fits are displayed in the right panel with the same vertical offset. |
| In the text | |
 |
Fig. B.1. continued. |
| In the text | |
 |
Fig. B.1. continued. |
| In the text | |
 |
Fig. B.1. continued. |
| In the text | |
 |
Fig. B.1. continued. |
| In the text | |
 |
Fig. B.2. Observed minus calculated mid-transit times for HAT-P-25b, HAT-P-29b, HAT-P-31b, HAT-P-34b, HAT-P-35b, HAT-P-38b, HAT-P-42b, and HAT-P-43b. Measurements of this work in black, literature values included in our calculation in red. A black dashed line denotes the new ephemeris of this work with associated uncertainties in dotted lines. For comparison, the previous ephemeris of the discovery paper in blue. The offset between previous ephemeris and literature value for HAT-P-29b is caused by a timing offset corrected in Wang et al. (2018a); see text for details. |
| In the text | |
 |
Fig. B.3. Continuation of Fig. B.2 for HAT-P-44b, HAT-P-45b, HAT-P-46b, HAT-P-52b, KELT-3b, KELT-8b, Qatar-3b, and Qatar-4b. We note that Qatar-3b and Qatar-4b lack an ephemeris uncertainty in their discovery paper. |
| In the text | |
 |
Fig. B.4. Continuation of Fig. B.2 for Qatar-5b, WASP-37b, WASP-58b, WASP-73b, and WASP-117b. We note that Qatar-5b lacks an ephemeris uncertainty in its discovery paper. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.