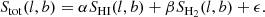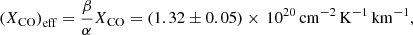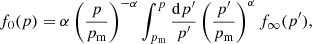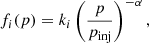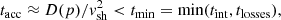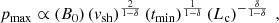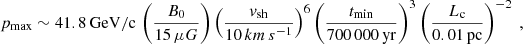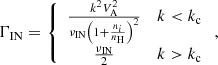| Issue |
A&A
Volume 622, February 2019
|
|
|---|---|---|
| Article Number | A57 | |
| Number of page(s) | 8 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201833651 | |
| Published online | 28 January 2019 | |
The Orion Region: Evidence of enhanced cosmic-ray density in a stellar wind forward shock interaction with a high density shell
1
INAF-IAPS, Via del Fosso del Cavaliere 100, 00133 Roma, Italy
e-mail: martina.cardillo@inaf.it
2
Dip. di Fisica, Univ. Tor Vergata, Via della Ricerca Scientifica 1, 00133 Roma, Italy
3
Gran Sasso Science Institute, Viale Francesco Crispi 7, 67100 L’Aquila, Italy
4
Astronomia, Accademia Nazionale dei Lincei, Via della Lungara 10, 00165 Roma, Italy
5
INAF – IASF Milano, Via E. Bassini 15, 20133 Milano, Italy
Received:
15
June
2018
Accepted:
19
December
2018
Context. In recent years, an in-depth γ-ray analysis of the Orion region has been carried out by the AGILE and Fermi/LAT (Large Area Telescope) teams with the aim of estimating the H2–CO conversion factor, XCO. The comparison of the data from both satellites with models of diffuse γ-ray Galactic emission unveiled an excess at (l, b)=[213.9, −19.5], in a region at a short angular distance from the OB star κ-Ori. Possible explanations of this excess are scattering of the so-called “dark gas”, non-linearity in the H2–CO relation, or cosmic-ray (CR) energization at the κ-Ori wind shock.
Aims. Concerning this last hypothesis, we want to verify whether cosmic-ray acceleration or re-acceleration could be triggered at the κ-Ori forward shock, which we suppose to be interacting with a star-forming shell detected in several wavebands and probably triggered by high energy particles.
Methods. Starting from the AGILE spectrum of the detected γ-ray excess, showed here for the first time, we developed a valid physical model for cosmic-ray energization, taking into account re-acceleration, acceleration, energy losses, and secondary electron contribution.
Results. Despite the characteristic low velocity of an OB star forward shock during its “snowplow” expansion phase, we find that the Orion γ-ray excess could be explained by re-acceleration of pre-existing cosmic rays in the interaction between the forward shock of κ-Ori and the CO-detected, star-forming shell swept-up by the star expansion. According to our calculations, a possible contribution from freshly accelerated particles is sub-dominant with respect the re-acceleration contribution. However, a simple adiabatic compression of the shell could also explain the detected γ-ray emission. Futher GeV and TeV observations of this region are highly recommended in order to correctly identify the real physical scenario.
Key words: acceleration of particles / radiation mechanisms: non-thermal / methods: data analysis / stars: winds / outflows / cosmic rays / gamma rays: ISM
© ESO 2019
1. Introduction
The Orion region and its surroundings (Bally et al. 2008, and references therein) is amongst the most studied Galactic region because it is the nearest star formation site known so far, and it is less affected by Galactic diffuse emission. It includes different structures: the stellar association Orion OB1, with about one hundred OB stars, and two giant molecular clouds (MCs), Orion A and Orion B (Pillitteri et al. 2016).
In recent years, an important survey by the X-ray satellite XMM-Newton in the Orion region has revealed the presence of several young stellar objects (YSO) in a high density shell overlapping the MC Orion A but probably unrelated to it (Pillitteri et al. 2016). This shell is shaped as a ring of 5–8 pc radius around κ-Ori, a blue super giant B0.5 Ia star at a distance of 240–280 pc from us, with an estimated age of 7 × 106 yr. Detections in the near- and far-IR, especially in the CO band, together with the analysis of new XMM-Newton data, show evidence that this shell is closer than the Orion A MC, at a distance compatible with that of κ-Ori. Consequently, the star formation process within it could have been triggered by the κ-Ori wind expansion that has swept up the shell, a hypothesis compatible with the estimated dynamical age of about 1.5 Myr (Wilson et al. 2005), which is lower by about one order of magnitude than the κ-Ori age.
At the highest energies, γ-ray emission from the Orion region was firstly detected by the COS-B (Cosmic ray Satellite, “option B”; Caraveo et al. 1980) and EGRET (Digel et al. 1995) satellites. Recent observations by Fermi/LAT (Ackermann et al. 2012) and AGILE (Marchili et al. 2018; hereafter M18) led to a more precise characterization of the diffuse emission from this region, allowing for a comparison with the expected flux from standard models. These take generally into account Bremsstrahlung and proton–proton (pp) emission related to the HI and H2 distributions, inverse-Compton scattering on the interstellar radiation field (ISRF), or CMB photons, an isotropic component due to the extragalactic emission and the contribution of point-like or extended known γ-ray sources. The analysis of Fermi/LAT and AGILE data shows significant emission exceeding the estimations of standard models, in a location overlapping the high-longitude part of the Orion A MC. A first attempt to explain this excess was done by adding a “dark gas” (gas not traced by HI and CO) contribution to diffuse γ-ray emission, following the approach introduced in Grenier et al. (2005). However, both Fermi/LAT and AGILE data analysis shows that this has only a marginal effect on the detected excess; therefore, another kind of physical mechanism is required to explain it. In Ackermann et al. (2012), in the light of some recent studies (see references within their paper), the authors hypothesized a non-linearity in the CO–H2 relation that implies a conversion factor, XCO, which is not constant. In M18, we introduced an alternative hypothesis. The AGILE-detected γ-ray excess seems to be in a good correlation with a star formation shell observed in the velocity maps from CO surveys and confirmed by X-ray observations of the XMM-Newton satellite, analysed in Pillitteri et al. (2016).
In this context, we considered the possibility of CR acceleration at the shock where the stellar wind collides with the interstellar medium (ISM; M18). Previous studies (e.g. Casse & Paul 1980; Voelk & Forman 1982; Cesarsky & Montmerle 1983; Ip 1995) suggested that the ideal location for CR acceleration is the strong termination shock (TS) of a stellar wind, because of its high velocity (order of 102 − 103 km s−1). We consider instead the possibility that CR energization occurs at the forward shock (FS) of κ-Ori, despite its relatively slow velocity (especially in the “snowplow” expansion phase, which describes well the present state of κ-Ori ; see Lamers et al. 1999). The detection in the CO of the high density star-forming shell around κ-Ori, partially overlapping the excess emission detected by AGILE, strongly supports our hypothesis.
In this paper, we discuss the AGILE γ-ray spectrum of the detected excess, assuming that it originates in the inner part of the star-forming shell described in Pillitteri et al. (2016). Following both acceleration and re-acceleration model described in Cardillo et al. (2016; hereafter Ca16), we try to explain the AGILE-detected emission in the context of CR re-acceleration and/or acceleration, taking into account all the known parameters and giving an estimation of the average density in that region. In Sect. 2, we summarize the results presented in M18, showing for the first time the AGILE spectral points. In Sect. 3, we give an overview of the model used in order to fit AGILE data in the context of CR re-acceleration and acceleration based on Ca16. In Sect. 4, we show our best results, and in Sect. 5 we analyse the physical consequences of all models and discuss different assumptions and parameters. The main points of the whole work are summarized in Sect. 6.
2. Orion γ-ray excess
In M18, we analysed AGILE data in the well-known Orion region with the aim of establishing a deeper understanding of the nature of its γ-ray emission. The large abundance of ISM suggests that diffuse γ-ray emission should be very abundant in that site. We focused on a region of interest (ROI) of 15 ° ×11° centred at (l, b)=[210.5, −15.5] (M18) and modelled γ-ray diffuse emission in different steps. In the first, we considered the Galactic contribution due to pp-interactions and Bremsstrahlung emissivity per Hydrogen atom (HI and H2), and to inverse compton (IC) emissivity from the ISRF, removing distance and energy dependences through spatial and energetic integration. Then, we included the extra-galactic contribution as an isotropic component, neglecting the contribution from point sources because the AGILE-GRID source catalogue does not contain any object inside the ROI. Finally, we fitted the AGILE total γ-ray flux Stot as a linear combination of the contributions due to HI (SHI), H2 (SH2), and the whole isotropic component (IC and extragalactic contributions, added up in the variable ϵ):
In this equation, α and β represent the γ-ray emissivity due to pp and Bremsstrahlung emission, therefore, if we have computed in the correct way the spatial distribution of HI and H2, these coefficients should be equal (M18). A difference in their values would be due to the uncertainty in the column density estimators. We can provide an estimation of the effective CO–H2 conversion factor, (XCO)eff, which is correlated with the real conversion factor through α and β ratio
taking into account possible uncertainties in the column density estimation. The value obtained is in very good agreement with previous measurements by EGRET (Diegel et al. 1999) and Fermi/LAT (Ackermann et al. 2012). Moreover, the AGILE residual map shows a further confirmation of the Fermi result: we found a γ-ray excess accounted for neither by atomic and/or molecular hydrogen nor by the extragalactic component; this excess is centred at (l, b)=[213.9, −19.5] and perfectly overlaps an excess found in Ackermann et al. (2012). It is arc-shaped and seems to belong to a ring centred on the position of the B0.5 Ia star κ-Ori, about 4 pc away from it. Ackermann et al. (2012) try to explain the detected γ-ray excess with the presence of “dark gas”, a gas component not traced by HI or CO but possibly by thermal IR emission (Grenier et al. 2005). After introducing this “dark gas” contribution to the emission, which they computed following a template based on reddening map of IRAS (InfraRed Astronomical Satellite) and COBE (COsmic Background Explorer; Schlegel et al. 1998), the diffuse emission model of the whole Orion region provides a better description of the observed flux; the improvement, however, is much more significant for outer regions than for Orion A. A better modelling of the Orion A γ-ray excess is achieved by assuming a non-linear behaviour of the CO−H2 relation, which implies a variable conversion factor. This hypothesis is in line with several works developed in the last years (see Ackermann et al. 2012, and references therein), according to which, in sites with high star formation rates, the ratio between the two molecules is variable and depends on environmental parameters.
AGILE extended likelihood analysis estimates a flux of (11 ± 2)×10−8 ph cm−2 s−1 with a significance of 5.2σ. In our previous work, we considered three different templates for the computation of the “dark gas” contribution (for details see M18), amongst which also the one used in Ackermann et al. (2012). The best-fit template for “dark gas” appeared to be the reddening map derived from the Pan-STARRS1 (Panoramic Survey Telescope & Rapid Response System) stellar photometry in Schlafly & Finkbeiner (2014); we used it as an estimate of the “dark gas” contribution to the total flux computation in Eq. (1). As in Ackermann et al. (2012), the new model improves the description of the observed diffuse emission; the “dark gas” template, however, seems to account for only ∼25% of the γ-ray excess detected in the high-longitude part of Orion A.
Looking for an alternative explanation, we considered the results of Pillitteri et al. (2016). Analysing data obtained from a XMM-Newton X-ray survey, they associated an arc-shaped emission detected in the IR, X-ray, and CO bands to a star formation region that they locate at a distance between 5 and 8 pc from κ-Ori. Looking at Fig. 1, it is evident that the AGILE γ-ray emission arises in the inner part of this shell, partially overlapping the CO emission, likely in correspondence with the interaction of the FS of κ-Ori ’s strong stellar wind with the high density shell.
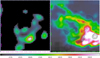 |
Fig. 1. Left panel: ring of γ-ray excess detected by AGILE. Right panel: CO map (Dame et al. 2001), which reveals the star formation shell discussed by Pillitteri et al. (2016); the contour levels from γ-ray data are shown in black. The figure is from M18. |
Given the striking similarities in shape and position between the γ-ray emission and the star formation shell in Pillitteri et al. (2016), we formulated a possible explanation of the γ-ray excess in the context of in situ CR acceleration and re-acceleration. Moreover, the AGILE extended source analysis of the excess gives a very hard spectral index, 1.7 ± 0.2, which could support a diffusive shock acceleration (DSA) process (Blasi 2004), even if only a detailed theoretical model can give the real range of the parent proton population spectral index.
In Fig. 2, we show the γ-ray spectrum of the AGILE detected excess. The spectral points are obtained by analysing the AGILE data between November 2009 and March 2017, corresponding to AGILE spinning mode data-taking. We carried out an extended-source analysis by assuming, as template for γ-ray emission, a uniform disc centred on (l, b)=[214.4, −18.5] with a 1° radius (the same used in M18). In order to perform a spectral analysis, the circle has been convoluted with the AGILE point spread function (PSF) in each energy band. For this study, we used the Build 23 AGILE software on the consolidated data archive, and the I0025 response matrices. According to the spectral energy distribution estimated with AGILE, this γ-ray excess could be the first evidence of accelerated/re-accelerated CR presence in correspondence with a strong stellar wind of a single OB star.
 |
Fig. 2. AGILE γ-ray spectrum obtained with an extended source likelihood analysis centred on (l, b) = [214.4, −18.5] with a 1° radius convoluted with AGILE PSF (M18). The blue line shows the best-fit power-law function, with index 1.7. |
3. Model overview
The energetics of an OB star with an average wind terminal velocity Vw ∼ 2 × 103 km s−1 and a mass loss rate between 10−7 − 10−5 M⊙ yr−1 is between 1050 and 1051 erg, of the same order of the total supernova (SN) explosion energy (Lamers et al. 1999; Casse & Paul 1980; Cesarsky & Montmerle 1983). The possibility of particle acceleration in correspondence with the TS of strong stellar winds was proposed in order to explain γ-ray emission detected by the Cos-B satellite from the ρ-Oph cloud (Casse & Paul 1980; Voelk & Forman 1982; Cesarsky & Montmerle 1983), and confirmed in recent years by the observations of γ-ray sources associated to young stellar clusters (see H.E.S.S. Collaboration 2011, for instance). However, AGILE detected γ-ray excess only in the south-west side of the κ-Ori expanding wind. Even if this asymmetric γ-ray emission could be explained in terms of TS energization because of the presence of the CO shell only in that region, the FS interacts with it before the TS. Consequently we considered particle energization in correspondence with the interaction of the FS with the dense molecular shell. The OB star κ-Ori is now in its “snowplow” phase (Lamers et al. 1999) and, consequently, the FS velocity should be of the order of a few tens of km s−1. However, considering that the upstream is a cold (T < 100 K) dense shell, the Mach number of the shock is of the order of 10 and we can consider the FS still a strong shock. Moreover, the estimated average density n0 = 30 cm−3 is large enough to trigger the formation of a radiative thin shell in the interaction location, which provides a very high compressed density and, consequently, enhances the γ-ray emission (see Eq. (1) in Blandford & Cowie 1982).
The scenario we propose to explain the cosmic-ray energization is similar to the typical one found in a supernova remnant (SNR) shock, for example in the W44 SNR (Giuliani et al. 2011; Cardillo et al. 2014, 2016; Ackermann et al. 2013). Consequently, we model this emission following the approach described in Ca16; we take into account both re-acceleration and acceleration contributions from protons, helium, and electrons (primaries and secondaries) with their radiation losses. In M18, we estimated for our ROI a γ-ray flux Fγ = 11 ± 10−8 ph cm−2 s−1, corresponding to a γ-ray luminosity between 100 and 3000 MeV, Lγ = 5.2 × 1031 erg s−1. Assuming that all the γ-ray luminosity is produced by pp interaction π0 decay, we can estimate a total CR energy of WCR ∼ 4 × 1045 erg (see for instance Aharonian et al. 2018). In the following, we summarize the main points of this model and the related physical issues.
The effect of re-acceleration is to harden the spectrum of Galactic particles with a spectrum steeper than f(p)∝p−α, where α is the DSA spectral index related to the compression ratio, that is, the ratio between upstream velocity (ahead of the shock) and downstream velocity (behind the shock), 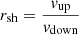 . In the strong shock approximation (Amato 2014),
. In the strong shock approximation (Amato 2014), 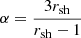 . The re-accelerated particle spectrum is obtained with the equation
. The re-accelerated particle spectrum is obtained with the equation
where p is the particle momentum and pm represents a minimum momentum in the Galactic CR spectrum, in this case equal to 1 MeV, consistent with the lowest energy of the Voyager probe’s spectral data, which is a few MeV. The distribution function f∞(p′) describes the Galactic CR spectrum for different kinds of particles (protons, electrons, and helium nuclei) that we modelled according to the local interstellar (LIS) spectrum measured by Voyager 1 at low energies (E ≳ 1 MeV n−1; Webber & McDonald 2013), and PAMELA (Payload for Antimatter Matter Exploration and Light-nuclei Astrophysics; Adriani et al. 2011) and AMS-02 (Alpha Magnetic Spectrometer) data (Aguilar et al. 2014, 2015a,b) at higher energies.
The distribution of possible freshly accelerated CRs (both hadrons and leptons) is described by the conservative power-law spectrum directly provided by DSA theory,
where index i reads p for protons and e for electrons. The normalization factor ki is obtained considering that CR pressure is a fraction ξCR of ram pressure of the shock, 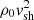 , where ξCR is the CR acceleration efficiency, ρ0 is the initial density mass (in our model we have assumed a totally ionized medium at the shock), and vsh is the shock velocity. The normalization of electron distribution, ke, is then fixed by assuming a standard CR electron/proton ratio in a strong shock, kep ≈ 10−2. Finally, pinj is the injection momentum. As in the case of SNR shocks, even at the FS of strong stellar wind the injection mechanism is not well known (Casse & Paul 1980); consequently, we used the same convention used in Caprioli & Spitkovsky (2014), which provides
, where ξCR is the CR acceleration efficiency, ρ0 is the initial density mass (in our model we have assumed a totally ionized medium at the shock), and vsh is the shock velocity. The normalization of electron distribution, ke, is then fixed by assuming a standard CR electron/proton ratio in a strong shock, kep ≈ 10−2. Finally, pinj is the injection momentum. As in the case of SNR shocks, even at the FS of strong stellar wind the injection mechanism is not well known (Casse & Paul 1980); consequently, we used the same convention used in Caprioli & Spitkovsky (2014), which provides 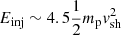 . In order to obtain the observed spectrum, we need to consider energy losses affecting the re-accelerated spectrum (see Eq. (15) in Ca16). Protons are affected by ionization losses (at lower energies) and pp-interaction losses (at higher energies) whereas primary and secondary electrons are affected mainly by Bremsstrahlung, Synchrotron, and IC losses (at higher energies) and ionization losses (at lower energies).
. In order to obtain the observed spectrum, we need to consider energy losses affecting the re-accelerated spectrum (see Eq. (15) in Ca16). Protons are affected by ionization losses (at lower energies) and pp-interaction losses (at higher energies) whereas primary and secondary electrons are affected mainly by Bremsstrahlung, Synchrotron, and IC losses (at higher energies) and ionization losses (at lower energies).
To be effective, the energization mechanism at the shock must take place in a time shorter than the minimum value between loss time tloss and interaction time tint:
where 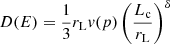 is the diffusion coefficient, strictly related to the particle Larmor radius,
is the diffusion coefficient, strictly related to the particle Larmor radius, 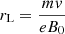 , to particle velocity v(p), to the perturbation spectrum and, consequently, to the correlation length of magnetic field perturbations, Lc. From this condition, we obtain the following relation for the maximum momentum reachable by particles:
, to particle velocity v(p), to the perturbation spectrum and, consequently, to the correlation length of magnetic field perturbations, Lc. From this condition, we obtain the following relation for the maximum momentum reachable by particles:
where the magnetic power spectrum index, δ, depends on the turbulence model considered.
4. Results
In this section we illustrate our results in terms of re-acceleration and the possible contribution of acceleration. Our main assumption is that the medium in correspondence with the shock is totally ionized. So far, no radio emission was detected from our ROI, implying that our model has to account for a low synchrotron flux. Also at TeV energies, there is no γ-ray detection; our computation should therefore return a negligible amount of high energy emission. The number of degrees of freedom of the system can be reduced by considering the known parameters of κ-Ori: its age, tage ∼ 7 × 106 yr (Pillitteri et al. 2016); its distance, d ∼ 280 pc (Pillitteri et al. 2016); and the radius of the surrounding ring of diffuse emission, R ∼ 6 pc. This radius is an intermediate value between the one estimated for the γ-ray emission in M18 and the one estimated for the CO shell (Pillitteri et al. 2016), because we are considering their interaction region as the location of energization. Considering the age of κ-Ori, we can deduce that this OB star is now in its “snowplow” expansion phase and, consequently, the FS velocity has to be of about 10 km s−1 (Lamers et al. 1999; Pillitteri et al. 2016).
To estimate the average particle density corresponding to the γ-ray excess region, we used HI and H2 column densities from, respectively, the Leiden/Argentine/Bonn (LAB) 21-cm survey (Kalberla et al. 2005; Hartmann & Burton 1997) and the CO survey described in Dame et al. (2001). The latter was then converted into H2 abundance using the XCO conversion factor found in M18. These column densities have been translated into volumetric particle densities by assuming an extension of the region parallel to the line of sight similar to the perpendicular one. The value that we obtained is n0 ∼ 30 cm−3. Since the estimated density value for the ROI is higher than the ISM one, a large range of correlation length and initial magnetic field values can be taken into account. We know that, in the ISM, Lc ∼ 100 pc but in high density medium it can be very small, down to Lc = 0.1 − 0.01 pc (Houde et al. 2009). The initial magnetic field, 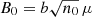 G, depends on the parameter
G, depends on the parameter 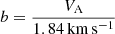 , where VA is the Alfveń velocity, and it is equal to 1 in the ISM but can vary between 0.3 and 3 in a high density medium.
, where VA is the Alfveń velocity, and it is equal to 1 in the ISM but can vary between 0.3 and 3 in a high density medium.
From Pillitteri et al. (2016), we know that the dynamical age of the star formation shell is lower than the κ-Ori age. This piece of information is used to constrain the interaction time (which refers to the starting time of γ-ray emission production and, therefore, of the energization process) to a value of tint ∼ 0.1tage. Since the emissivity has to be integrated over the emission volume, another basic parameter for our model is the filling factor fV: assuming a uniform emissivity, the volume of the κ-Ori shell covered by γ-ray emission is 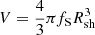 , where Rsh is the shock radius. We fix fV at 20% of the κ-Ori wind shell volume, which seems a reasonable assumption given the extension of the detected γ-ray emission.
, where Rsh is the shock radius. We fix fV at 20% of the κ-Ori wind shell volume, which seems a reasonable assumption given the extension of the detected γ-ray emission.
Finally, in order to compute the maximum momentum of the system, we need to consider a specific turbulence spectrum; we used the more conservative Kolmogorov spectrum that provides 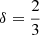 . In this way, we obtain the explicit equation for the maximum momentum
. In this way, we obtain the explicit equation for the maximum momentum
where the normalization values are of the order of the ones used (or estimated) in our best model. Looking at the numerical value of this equation, it is clear that we expect a cut-off at low energies, excluding the possibility of TeV emission from this region.
The last but not the least important issue is our assumption of the presence of a thin compressed radiative shell in correspondence with the interaction region. The physics of the FS (Lamers et al. 1999) and the presence of the CO shell support the existence of this cooling shell that is the fundamental ingredient for the “crushed cloud” model of Blandford & Cowie (1982), providing a further compression that enhances the final density, and, consequently, the γ-ray emission (details in Ca16). However, we will see that the high interaction time counteracts the increment in the γ-ray flux because of the large amount of energy losses.
4.1. Re-acceleration
Our best model is based on the assumption that only re-acceleration of pre-existing cosmic rays is present. Diffuse CR protons, He-nuclei, and electrons in the ISM are re-accelerated at the shock between the κ-Ori wind and the near star formation region.
Keeping fixed n0 = 30 cm−3, vsh = 12 km s−1, and fV = 20%, we tuned interaction time, magnetic field parameter b, and correlation length values in order to fit the spectral normalization. Using tint = 0.08tage = 5.6 × 105 years, b = 2 (corresponding to B0 = 11 μG), and Lc = 0.01 pc, we fit the AGILE spectral points remarkably well, obtaining a compressed density nm = 170 cm−3, a compressed magnetic field 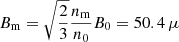 G, and EM = 22.3 GeV n−1 (once again, He nuclei are considered too). In this model, we used the more conservative momentum spectral index used in the linear DSA, α = 4, which leads to a compression ratio rsh = 4. However, a cut-off at such a low energy, together with loss-limited energization, implies a certain degree of covariance in the spectral index values. In fact, models developed with a spectral index in the range 3.5 < α < 5 turn out to be equally physically consistent, with only small variations of the other parameters involved. In Fig. 3 we show the spectral energy distribution (SED) resulting from our best-fit re-acceleration model.
G, and EM = 22.3 GeV n−1 (once again, He nuclei are considered too). In this model, we used the more conservative momentum spectral index used in the linear DSA, α = 4, which leads to a compression ratio rsh = 4. However, a cut-off at such a low energy, together with loss-limited energization, implies a certain degree of covariance in the spectral index values. In fact, models developed with a spectral index in the range 3.5 < α < 5 turn out to be equally physically consistent, with only small variations of the other parameters involved. In Fig. 3 we show the spectral energy distribution (SED) resulting from our best-fit re-acceleration model.
 |
Fig. 3. AGILE (red) γ-ray points plotted with γ-ray emission from pion decay (blue line), from primary Bremsstrahlung (cyan dashed line), from secondary Bremsstrahlung (magenta dashed line), and total emission (black line). |
Most of the contribution to γ-ray emission comes from pion decay; the flux decrement at a few GeV is directly correlated with the particle energy cut-off at about EM ∼ 23 GeV n−1. A particle cut-off at these energies is in agreement with no detection of the Orion region at the TeV energy band. Secondary electrons, produced in inelastic pp-collisions from the decay of charged pions, dominate over primary electrons because of high density and energy losses influence, giving a contribution at E < 200 MeV through Bremsstrahlung emission. Energy losses are also the reason for very low synchrotron emission (E2f(E) < 10−14 TeV cm−2 s−1, not shown in Fig. 3). Our prediction concerning radio emission is in agreement with the lack of radio detection in the ROI.
We want to stress that the contribution of “crushed cloud” adiabatic compression is not really necessary in order to explain the γ-ray emission detected by AGILE. Using the same parameters, we also have a good fit with only re-accelerated particles with different final values because of the lack of adiabatic compression: nm = 120 cm−3, a compressed magnetic field Bm = 35.8 μG, and EM = 51.4 GeV n−1 (we also consider He nuclei). This result is important because the diffusion length inside the thin shell in a time tint, is 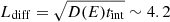 pc, which is a value lower than the shock radius Rsh, but likely greater than the interaction region scale. This means that it could be very difficult to confine re-accelerated particles inside the radiative shell for the time tint and compress them adiabatically. In such a scenario, we verified that the downstream re-accelerated particles alone could make a sufficient contribution to account for the Orion region γ-ray excess.
pc, which is a value lower than the shock radius Rsh, but likely greater than the interaction region scale. This means that it could be very difficult to confine re-accelerated particles inside the radiative shell for the time tint and compress them adiabatically. In such a scenario, we verified that the downstream re-accelerated particles alone could make a sufficient contribution to account for the Orion region γ-ray excess.
4.2. Acceleration contribution
We showed that the contribution of re-accelerated particles (with or without the adiabatic compression) is sufficient to fully explain the γ-ray excess seen by AGILE with reasonable physical parameters. However, we tested the hypothesis of a possible further contribution from freshly accelerated particles.
Keeping the physical parameters of our best re-acceleration model, we calculated an upper limit to the acceleration efficiency ξCR such that the total γ-ray emission, due to both re-acceleration and acceleration, is compatible with the AGILE spectrum. The value we found, ξCR ∼ 6%, shows that a contribution from freshly accelerated CRs, although plausible, would anyway be marginal compared to the one from GCR re-acceleration, as shown in Fig. 4.
 |
Fig. 4. AGILE (red) γ-ray points plotted with the total γ-ray emission produced by re-acceleration (brown line) and acceleration (grey line, ξCR = 20%) described with parameters of our best model. The black line is the sum of the two contributions. |
The grey line in Fig. 4 represents the total contribution from acceleration emission process, primary and secondary Bremsstrahlung, and pion emission. Given the low velocity of the κ-Ori FS and the long interaction time, the low contribution from accelerated particles is not surprising. Galactic CRs are present everywhere in the Galaxy and, if there are energization conditions, for instance, at the SNR shocks or at the stellar wind shocks, they are always re-accelerated. The present case resembles that of the middle-aged SNR W44 (see Ca16), for which the γ-ray flux is explained in terms of a dominant re-acceleration process. A dominant contribution from freshly accelerated particles, instead, can be found in young objects, such as young SNRs or stellar wind TS; these are characterized by shocks with very high velocities (order of 103 km s−1), for which strong γ-ray fluxes can be achieved with reasonable values of CR efficiency.
4.3. Compression only
One of the main assumptions of our model is that the radiative shell is totally ionized. This condition allows the development of a strong turbulence that energizes CR particles. However, since the presence of neutrals could efficiently dampen the turbulence (Chevalier 1999; Bykov et al. 2000), we computed a lower limit for their density found by the condition that the ion-neutral damping time is longer than the interaction time. Following Ptuskin & Zirakashvili (2003), the ion-neutral damping is
where νIN = 8.4 × 10−9 s−1 (T/104 K)0.4nH is the ion-neutral collision frequency, with T the temperature, and nH the density of neutrals in units of cm−3. The critical wave number separating the two regimes is kc = (νIN/VA)(ni/nH), which corresponds to perturbations of wavelength resonant with particles of energy Ec ≈ 1.7 × 105 GeV in the regime of density and magnetic field strength we are considering. Consequently, we consider the ion-neutral damping rate for E < Ec as corresponding to k < kc, and by requiring that ΓIN < 1/tint we obtain a lower limit for the neutral fraction, nH < 1.3 × 10−5 cm−3, which is a very stringent condition. Even considering the self-generated turbulence (Cardillo et al. 2016), we cannot enhance this lower limit; consequently, we try to explain the AGILE-detected γ-ray emission using only adiabatic compression, without any energization. This model is shown in Fig. 5.
The parameters of this model are the same as our re-acceleration one but here the interaction time is set to be of the order of tint = 10−4tage = 700 yr. This lower value can be understood because a lower interaction time leads to lower energy losses and a higher γ-ray emission. However, the available time is too short for intense secondary electron production and secondary Bremsstrahlung contribution is totally negligible. We can say that, even in case of turbulence damping, an adiabatic compression could explain the AGILE γ-ray emission with the condition that the κ-Ori shock and the CO shell have only been interacting for 103 yr. A rough estimation of the shell cooling time from the cooling time curve in Draine (2011), using the density value of our model, gives τcool ∼ 102 yr < tint, confirming the plausibility of the only-compression scenario. Moreover, in this model, the diffusion length issue inside the radiative shell discussed in Sect. 4.1 is automatically solved. In the re-acceleration model, the presence of a compressed shell implies a diffusion length that is too high; assuming instead a purely adiabatic compression, the lower value of the interaction time provides a value Ldiff ∼ 0.01 pc, implying a higher chance of confining and compressing particles adiabatically.
5. Discussion
It is generally assumed (Casse & Paul 1980; Voelk & Forman 1982; Cesarsky & Montmerle 1983) that CR acceleration due to strong stellar winds takes place in the TS. However, the asymmetry in the AGILE- and Fermi/LAT-detected γ-ray emission from the Orion region is not easily understandable in this scenario; a wind TS expands symmetrically into the stellar wind, having the same upstream everywhere in the wind bubble. Therefore, we associated the high energy emission to the interaction of the slower FS with the CO shell described in Pillitteri et al. (2016), which approximately coincides with the AGILE emission region. A more precise measurement of the κ-Ori FS velocity is very important. Small variations of its value have a strong impact on the model: velocities of about 5 km s−1 or lower would make the proposed mechanism of CR energization virtually impossible, because both the maximum momentum and normalization become too low. Given the sensitivity of the model to the shock velocity, we decided to fix this parameter to a value consistent with the FS physics and that provides a validity range physically consistent for all the other parameters.
From Pillitteri et al. (2016) we know that κ-Ori started to sweep up the shell about 1.5 Myr ago; this implies that the interaction time cannot be much lower than the age of κ-Ori (7 Myr). Assuming an interaction time lower than tint = 0.08tage by an order of magnitude, particles do not have the necessary time to be re-accelerated and they can only be compressed, providing a γ-ray emission that cannot fit the AGILE data. If we hypothesized, instead, that the interaction time is of the same order of the age of κ-Ori, energy loss processes would dissipate very large amounts of energy, leading to a γ-ray flux much lower than the one observed.
Analysing the behaviour of our model as the density changes, we found that the presence of a thin radiative shell is not a fundamental condition in order to have the correct amount of γ-ray flux. Indeed, excluding the only adiabatic compression, we obtain an equally consistent model. This can be explained by the fact that an emission due to a compressed density that is too high, when associated to a long interaction time, leads to large energy losses with a consequent flux suppression. On the other hand, if the initial density is too low, there are not enough target particles to justify the γ-ray emission observed by AGILE.
On the other hand, we also analysed a scenario in which our assumption of totally ionized shocked material is not real, which implies perturbation damping due to ion-neutral collisions and, consequently, the lack of an effective re-acceleration. We showed that, even with only adiabatic compression within the thin shell, Galactic CRs are energized in a sufficient way to explain the γ-ray detected emission.
Another important parameter, very difficult to estimate, is the coherence length, which we assumed to be of the order of its estimated minimum value in a high density medium (Houde et al. 2009). If we hypothesize that its value is higher by an order of magnitude, that is, Lc = 0.1 pc, AGILE data can be fitted only by significant modifications of the other model free parameters. In particular, an increase of both shock velocity (about 18 km s−1) and filling factor (fV ∼ 25%) would be needed to compensate for a decrement in the maximum momentum and an increase in the acceleration time (Ca16). Such values, however, seem to be unrealistic in the context described here.
We already mentioned in our previous work that the extended source data analysis leads to a hard photon spectral index, 1.7 ± 0.2. However, in a DSA context the final photon spectral index is the result of the parent proton population distribution spectrum being affected by different processes, such as re-acceleration, energy losses, and diffusion. Consequently, the photon spectral index obtained by a best-fit analysis cannot give stringent constraints on the original proton distribution. In our model, the injection proton index is strictly correlated with the compression ratio of the shock; we found equally consistent models for a large range of its values, [2.5–7], corresponding (in a strong shock) to a range for the momentum spectral index between 5 and 3.5. This large range is due to the very low high energy cut-off which provides a suppression of the photon flux before we can observe different spectral behaviour due to different proton spectral indices.
Regardless of the combination of parameters used, in our work we can draw two important conclusions. Firstly, even using different realistic values for all relevant parameters, we cannot obtain a maximum momentum higher than about 50 GeV n−1, definitely ruling out high energy emission, in agreement with the absence of detections at TeV energies. Moreover, any model seems to provide a radio emission above 10−14 TeV cm−2 s−1, in agreement with the lack of radio detection in our ROI. Another important conclusion we reached is that Galactic CR re-acceleration can fully explain the AGILE and Fermi/LAT γ-ray excess detected in the Orion region. Freshly accelerated particles only provide a marginal contribution, if any.
6. Summary and conclusions
Because of the large amount of ISM it hosts, the Orion region is a very important target for the study of diffuse γ-ray emission in our Galaxy. In recent years, the Fermi/LAT (Ackermann et al. 2012) and AGILE (Marchili et al. 2018) satellites allowed us to map this emission in a more precise way and to model it according to a “standard model” that includes pp and Bremsstrahlung emission from atomic and molecular hydrogen (HI and H2), isotropic emission from inverse Compton scattering in the ISRF, point-source emission, and extragalactic isotropic emission. An in-depth analysis of both the Fermi/LAT and the AGILE data reveals a significant γ-ray excess, which cannot be explained by “dark gas” contributions (Grenier et al. 2005).
In Ackermann et al. (2012) this γ-ray excess is explained with a non-linearity in the CO–H2 relation. Here we try to model it in the context of CR energization in the strong stellar wind from the OB star κ-Ori. CR acceleration in the TS of an OB star is a mechanism that is considered a reasonable alternative to acceleration in SNR shocks (Casse & Paul 1980; Voelk & Forman 1982; Cesarsky & Montmerle 1983). We developed here an alternative scenario in which particle energization takes place in correspondence with the interaction region between the slow FS of κ-Ori and a dense star formation region, shaped in a dense shell detected in IR and CO maps. It surrounds the detected γ-ray emission and includes many OB stars, analysed in the X-ray band by Pillitteri et al. (2016). It is likely that this dense shell was swept-up during the κ-Ori stellar wind expansion.
This scenario is very similar to the standard one found in the SNR/MC interaction context. Consequently, in order to model the AGILE γ-ray excess, we followed the re-acceleration and acceleration model described in Cardillo et al. (2016), considering Galactic CR spectra (for protons, Helium, and electrons) measured from Voyager and PAMELA, primary and secondary electron contributions, and energy losses. The main constraint in our model is the shock velocity. The OB star κ-Ori is now in its “snowplow” expansion phase (Lamers et al. 1999) and the FS is very slow, with a velocity of about 10 km s−1. Only the combination of a high density target with a quite long interaction time can give the necessary conditions to allow CR energization in such a slow shock.
We estimate the average density in correspondence with the emission region to be of the order of n0 = 30 cm−3. The physics of the FS (Lamers et al. 1999), together with the interaction with a MC, leads to the formation of a thin compressed radiative shell according to Blandford & Cowie (1982), implying a further compression of the medium. The interaction time has to be very high, because we know that the star formation shell has been swept-up by the κ-Ori shell for about 106 yr. For this reason, energy losses give the highest contribution in the estimation of the maximum momentum. These considerations allowed us to constrain magnetic field and correlation length values, fixing an emitting volume filling factor of about 20%.
Taking into account the constraints on the FS velocity and on the interaction time, we obtained a solid re-acceleration model, showing how the AGILE γ-ray excess can be explained by first order Fermi re-acceleration of particles at the shock between κ-Ori wind and the star formation shell. Radio emission provided by this model is very low, in agreement with observations, and secondary Bremsstrahlung emission dominates the primary one, mainly because of energy losses. IC contribution is totally negligible.
Unfortunately, our analysis can give very little information about the parent proton spectral distribution. The best model that we found provides a very low cut-off energy, EM ∼ 23 GeV n−1, implying that we cannot distinguish between different spectral behaviours due to a proton spectral index that is high or steep. We obtain a good fit of the AGILE data with a spectral index in a range between 3.5 and 5.
In spite of possible variations in some of the assumed parameters and the ambiguity of others, we can fix some important constraints. Even if a contribution from freshly accelerated particles is present, it is always marginal with respect to the re-acceleration one and this is mainly due to the very low FS velocity. Moreover, our re-acceleration model provides negligible γ-ray emission beyond energies of about EM ∼ 50 GeV n−1, and a radio flux lower than about 10−14 TeV cm−2 s−1, in agreement with the lack of TeV and radio detection in the ROI. The AGILE γ-ray excess from the Orion region could be the first detection of a FS stellar wind.
Moreover, we showed that, even relaxing our hypothesis of a completely ionized medium and, consequently, considering a possible inhibition of re-acceleration due to ion-neutral collisions, we can explain the AGILE γ-ray detection from the Orion region invoking only adiabatic compression, without re-acceleration. In this case, a lower interaction time, tint = 700 yr, is required. For a more precise characterization of the emitting region, multi-wavelength analysis of the Orion region, focused on the γ-ray excess detected by AGILE and Fermi/LAT, is required.
Acknowledgments
We wish to thank the anonymous referee for the useful comments which significantly improved the paper.
References
- Ackermann, M., Ajello, M., Allafort, A., et al. 2012, ApJ, 756, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Ackermann, M., Ajello, M., Allafort, A., et al. 2013, Science, 339, 807 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Adriani, O., Barbarino, G. C., Bazilevskaya, G. A., et al. 2011, Science, 332, 69 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Aguilar, M., Aisa, D., Alvino, A., et al. 2014, Phys. Rev. Lett., 113, 121102 [Google Scholar]
- Aguilar, M., Aisa, D., Alvino, A., et al. 2015a, Phys. Rev. Lett., 114, 171103 [CrossRef] [PubMed] [Google Scholar]
- Aguilar, M., Aisa, D., Alvino, A., et al. 2015b, Phys. Rev. Lett., 115, 211101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Aharonian, F., Yang, R., & de Ona Wilhelmi, E. 2018, ArXiv e-prints [arXiv:1804.02331] [Google Scholar]
- Amato, E. 2014, IJMPD, 23, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Bally, J. 2008, in Overview of the Orion Complex, ed. R. Reipurth, 459 [Google Scholar]
- Blandford, R. D., & Cowie, L. L. 1982, ApJ, 260, 625 [NASA ADS] [CrossRef] [Google Scholar]
- Blasi, P. 2004, Astrop. Phys., 21, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Bykov, A. M., Chevalier, R. A., Ellison, D. C., & Uvarov, Y. A. 2000, ApJ, 538, 203 [NASA ADS] [CrossRef] [Google Scholar]
- Caprioli, D., & Spitkovsky, A. 2014, ApJ, 783, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Caraveo, P. A., Bennett, K., Bignami, G. F., et al. 1980, A&A, 91, L3 [NASA ADS] [Google Scholar]
- Cardillo, M., Tavani, M., Giuliani, A., et al. 2014, A&A, 565, 74 [Google Scholar]
- Cardillo, M., Amato, E., & Blasi, P. 2016, A&A, 595, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Casse, M., & Paul, J. A. 1980, ApJ, 237, 243 [Google Scholar]
- Cesarsky, C. J., & Montmerle, T. 1983, SSRV, 36, 173 [Google Scholar]
- Chevalier, R. A. 1999, ApJ, 511, 798 [NASA ADS] [CrossRef] [Google Scholar]
- Crowther, P. A., Lennon, D. J., & Walborn, N. R. 2006, A&A, 446, 279 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dame, T. M., Hartmann, D., & Thaddeus, P. 2001, ApJ, 547, 792 [NASA ADS] [CrossRef] [Google Scholar]
- Digel, S. W., Hunter, S. D., & Mukherjee, R. 1995, ApJ, 441, 270 [NASA ADS] [CrossRef] [Google Scholar]
- Diegel, S. W., Aprile, E., Hunter, S. D., et al. 1999, ApJ, 520, 196 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T. 2011, Physics of the Interstellar and Intergalactic Medium (Princeton, NJ: Princeton University Press) [Google Scholar]
- Giuliani, A., Cardillo, M., Tavani, M., et al. 2011, ApJ, 742, 30 [Google Scholar]
- Grenier, I. A., Casandjian, J.-M., & Terrier, R. 2005, Science, 307, 1292 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Hartmann, D., & Burton, W. B. 1997, Atlas of Galactic Neutral Hydrogen (Cambridge: Cambridge University Press), 243 [Google Scholar]
- H.E.S.S. Collaboration (Abramowski, A., et al.) 2011, A&A, 525, A46 [Google Scholar]
- Houde, M., Vaillancourt, J. E., Hildebrand, R. H., et al. 2009, ApJ, 706, 1504 [NASA ADS] [CrossRef] [Google Scholar]
- Ip, W.-H. 1995, A&A, 300, 283 [NASA ADS] [Google Scholar]
- Kalberla, P. M. W., Burton, W. B., Hartmann, D., et al. 2005, A&A, 440, 775 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lamers, H. J., Cassinelli, J. P., & Cassinelli, J. 1999, Introduction to Stellar Winds (Cambridge: Cambridge University Press) [CrossRef] [Google Scholar]
- Marchili, N., Piano, G., Cardillo, M., et al. 2018, A&A, 615, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pillitteri, I., Wolk, S. J., & Megeath, S. T. 2016, ApJ, 820, L28 [NASA ADS] [CrossRef] [Google Scholar]
- Ptuskin, V. S., & Zirakashvili, V. N. 2003, A&A, 403, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schlafly, E. F., Finkbeiner, D. P., et al. 2014, ApJ, 789, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Voelk, H. J., & Forman, M. 1982, ApJ, 253, 188 [NASA ADS] [CrossRef] [Google Scholar]
- Webber, W. R., & McDonald, F. B. 2013, Geophys. Res. Lett., 40, 665 [Google Scholar]
- Wilson, B. A., Dame, T. M., Masheder, M. R. W., & Thaddeus, P. 2005, A&A, 430, 523 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zirakashvili, V. N., & Ptuskin, V. S. 2017, ApJ, 98, 21 [Google Scholar]
All Figures
 |
Fig. 1. Left panel: ring of γ-ray excess detected by AGILE. Right panel: CO map (Dame et al. 2001), which reveals the star formation shell discussed by Pillitteri et al. (2016); the contour levels from γ-ray data are shown in black. The figure is from M18. |
| In the text | |
 |
Fig. 2. AGILE γ-ray spectrum obtained with an extended source likelihood analysis centred on (l, b) = [214.4, −18.5] with a 1° radius convoluted with AGILE PSF (M18). The blue line shows the best-fit power-law function, with index 1.7. |
| In the text | |
 |
Fig. 3. AGILE (red) γ-ray points plotted with γ-ray emission from pion decay (blue line), from primary Bremsstrahlung (cyan dashed line), from secondary Bremsstrahlung (magenta dashed line), and total emission (black line). |
| In the text | |
 |
Fig. 4. AGILE (red) γ-ray points plotted with the total γ-ray emission produced by re-acceleration (brown line) and acceleration (grey line, ξCR = 20%) described with parameters of our best model. The black line is the sum of the two contributions. |
| In the text | |
 |
Fig. 5. Same data and model curves as Fig. 3, assuming that only adiabatic compression is present. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.