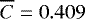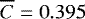| Issue |
A&A
Volume 622, February 2019
|
|
|---|---|---|
| Article Number | A95 | |
| Number of page(s) | 22 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201833342 | |
| Published online | 12 February 2019 | |
Long-term orbital and rotational motions of Ceres and Vesta
ASD/IMCCE, Observatoire de Paris, PSL Université, Sorbonne Université,
77 avenue Denfert-Rochereau,
75014
Paris,
France
e-mail: timothee.vaillant@obspm.fr
Received:
2
May
2018
Accepted:
24
July
2018
Context. The dwarf planet Ceres and the asteroid Vesta have been studied by the Dawn space mission. They are the two heaviest bodies of the main asteroid belt and have different characteristics. Notably, Vesta appears to be dry and inactive with two large basins at its south pole. Ceres is an ice-rich body with signs of cryovolcanic activity.
Aims. The aim of this paper is to determine the obliquity variations of Ceres and Vesta and to study their rotational stability.
Methods. The orbital and rotational motions have been integrated by symplectic integration. The rotational stability has been studied by integrating secular equations and by computing the diffusion of the precession frequency.
Results. The obliquity variations of Ceres over [−20 : 0] Myr are between 2° and 20° and the obliquity variations of Vesta are between 21° and 45°. The two giant impacts suffered by Vesta modified the precession constant and could have put Vesta closer to the resonance with the orbital frequency 2s6 − sV. Given the uncertainty on the polar moment of inertia, the present Vesta could be in this resonance where the obliquity variations can vary between 17° and 48°.
Conclusions. Although Ceres and Vesta have precession frequencies close to the secular orbital frequencies of the inner planets, their long-term rotations are relatively stable. The perturbations of Jupiter and Saturn dominate the secular orbital dynamics of Ceres and Vesta and the perturbations of the inner planets are much weaker. The secular resonances with the inner planets also have smaller widths and do not overlap, contrary to the case of the inner planets.
Key words: celestial mechanics / minor planets, asteroids: individual: Vesta / minor planets, asteroids: individual: Ceres / planets and satellites: dynamical evolution and stability
© ESO 2019
1. Introduction
Ceres and Vesta are the two heaviest bodies of the main asteroid belt. They have been studied by the Dawn space mission which has determined their shapes, gravity fields, surface compositions, spin rates, and orientations (Russell et al. 2012, 2016). However, the precession frequency of their spin axes has not be determined and there are still uncertainties about their internal structures (e.g., Park et al. 2014, 2016; Ermakov et al. 2014, 2017a; Konopliv et al. 2018). No satellites have been detected from observations with the Hubble Space Telescope and the Dawn space mission around these bodies (McFadden et al. 2012, 2015; DeMario et al. 2016).
The long-term rotation of the bodies in the solar system can be studied with the secular equations (Kinoshita 1977; Laskar 1986; Laskar & Robutel 1993) or with a symplectic integration of the orbital and rotational motions (Touma & Wisdom 1994). Secular equations are averaged over the mean longitude and over the proper rotation, which is generally fast for the bodies of the solar system, and their integration is much faster. They were used by Laskar et al. (1993a) and Laskar & Robutel (1993) to study the stability of the planets in the solar system.
The method of Laskar & Robutel (1993) has been applied by Skoglöv et al. (1996) to study the stability of the rotation and the variations of the obliquity for Ceres and nine asteroids including Vesta. At this time, however, the initial conditions for the spin axes were not determined precisely and the knowledge of the internal structure was not sufficient to constrain the precession frequencies. Skoglöv et al. (1996) assumed that the bodies are homogeneous and concluded that their long-term rotations are relatively stable. By using secular equations and a secular model for the orbital motion, Bills & Scott (2017) determined the obliquity variations of Ceres. Ermakov et al. (2017b) obtained the obliquity variations of Ceres for different polar moments of inertia by realizing the symplectic integration of the rotational and orbital motions.
Asteroid impacts and close encounters can influence the long-term rotation of bodies in the main asteroid belt. Vesta has suffered two giants impacts (Marchi et al. 2012; Schenk et al. 2012) that have significantly modified its shape and its spin rate (Fu et al. 2014; Ermakov et al. 2014). Laskar et al. (2011a) obtained an orbital solution of Ceres and Vesta, called La2010, which takes into account mutual interactions between bodies of the main asteroid belt, and Laskar et al. (2011b) showed that close encounters in the solution La2010 are the cause of the chaotic nature of the orbits of Ceres and Vesta. These close encounters can affect their long-term rotation.
For Ceres, the obliquity drives the ice distribution on and under the surface. Ceres possesses cold trap regions that do not receive sunlight during a full orbit. This prevents the sublimation of the ice, which can accumulate (Platz et al. 2016). The surface area of these coldtraps depends on the value of the obliquity. Ermakov et al. (2017b) determined that the obliquity of Ceres varies between 2° and 20° and that the cold trap areas for an obliquity of 20° correspond to bright crater floor deposits that are likely water ice deposits. Platz et al. (2016) determined that one bright deposit near a shadowed crater is water ice. In addition, the Dawn mission gave evidence of the presence of ice under the surface of Ceres from the nuclear spectroscopy instrument (Prettyman et al. 2017) and from the morphology of the terrains (Schmidt et al. 2017). The ice distribution and the burial depth with respect to the latitude depend on the history of the obliquity (Schorghofer 2008, 2016). For Vesta, studies of the long-term evolution of the obliquity were not performed with the initial conditions of the spin axis and the physical characteristics determined by the Dawn space mission.
The main purpose of this article is to investigate the long-term evolution of the rotational motions of Ceres and Vesta. First, we explore the obliquity variations of these bodies for a range of possible precession constants obtained from the data of the Dawn mission. Then, the stability of their spin axes is studied.
In this paper for the orbital motion we consider the solutions La2011 and La2010 (Laskar et al. 2011a), which do not include the rotation of Ceres and Vesta. To compute the obliquity variations, we follow the symplectic method of Farago et al. (2009) by averaging the fast proper rotation. This method avoids integrating the fast rotation and allows us to use a large step to reduce the computation time. We call the long-term rotational solution obtained Ceres2017. The orbital and rotational equations are integrated simultaneously in a symplectic way and the effects of the rotation on the orbital motions are considered. We consider the close encounters of Ceres and Vesta with the bodies of the main asteroid belt used in Laskar et al. (2011b) and estimate with a statistical approach their effects on the long-term rotation of Ceres and Vesta. In order to determine the secular frequencies and identify the possible secular resonances on the orbital and rotational motions, the solutions are studied by the method of the frequency map analysis (Laskar 1988, 1990, 1993, 2003; Laskar et al. 1992). Moreover, to study the effects of the close secular orbital resonances, we compute a secular Hamiltonian from the method of Laskar & Robutel (1995). We obtain a secular model, which reproduces the secular evolution of the solution La2011 and allows us to investigate the effects of the secular resonances.
The stability of the spin axes is studied by using secular equations with a secular orbital solution obtained from the frequency analysis of the solution La2011. We verify beforehand that they allow us to reproduce the obliquity variations computed by the symplectic method and have the same stability properties. We study the stability of the rotation in the vicinity of the range of possible precession constants to identify the secular resonances between the orbital and rotational motions. Vesta has suffered two giant impacts that have changed its shape and its spin rate (Fu et al. 2014; Ermakov et al. 2014) and also its precession constant. We investigate whether this possible evolution of precession constant changed the stability properties. Following the method of Laskar & Robutel (1993), we finally realize a stability map of the spin axes of Ceres and Vesta.
In Sect. 2, we present the methods used in this paper to obtain the long-term rotation. In Sect. 3, we estimate the precession constants deduced from Dawn space mission and their possible variations during the history of Ceres and Vesta. In Sect. 4, we analyze the long-term solutions obtained for the orbital and rotational motions. In Sect. 5, we study the effects of the orbital secular resonances with a secular Hamiltonian model. In Sect. 6, we study the stability of the rotation axes from the secular equations of the rotation.
2. Methods for the integration of the rotation
The spin rates of Ceres and Vesta are relatively fast (see Sect. 3). We thus average the fast rotation using the method of Farago et al. (2009) in order to integrate in a symplectic way the angular momentum of a rigid body.
When we need many integrations with different initial conditions or parameters, we use the secular equations from Boué & Laskar (2006) in order to speed up the computation.
2.1. Symplectic integration of the angular momentum
We consider a planetary system of n + 1 bodies with a central body 0 and n planetary bodies, where the body of index 1 is a rigid body and the other planetary bodies point masses. We note the vectors in bold. The Hamiltonian H of the system is (Boué & Laskar 2006)
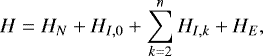 (1)
(1)
with HN the Hamiltonian of n + 1 point masses. The Hamiltonian HE of the free rigid body is
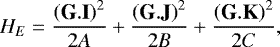 (2)
(2)
where (I,J,K) is the basis associated with the principal axes of moments of inertia respectively A, B, C, where A ≤ B ≤ C, and G the angular momentum of the rigid body. The Hamiltonians HI,0 and HI,k are, respectively, the interactions without the point mass interactions of the central body 0 and of the planetary body k with the rigid body 1 and are obtained with a development in Legendre polynomials (Boué & Laskar 2006)
![\begin{align*} H_{I,0} = & {-}\frac{\mathcal{G}m_{0}}{2r_{1}^{3}}\left[\left(B+C-2A\right)\left(\frac{\textbf{r}_{1}.\textbf{I}}{r_{1}}\right)^{2}+\left(A+C-2B\right)\left(\frac{\textbf{r}_{1}.\textbf{J}}{r_{1}}\right)^{2} \right. \nonumber\\[3pt] & \left. +\left(A+B-2C\right)\left(\frac{\textbf{r}_{1}.\textbf{K}}{r_{1}}\right)^{2}\right],\\[3pt] H_{I,k} = & {-}\frac{\mathcal{G}m_{k}}{2r_{1,k}^{3}}\left[\left(B+C-2A\right)\left(\frac{\textbf{r}_{1,k}.\textbf{I}}{r_{1,k}}\right)^{2}+\left(A+C-2B\right)\left(\frac{\textbf{r}_{1,k}.\textbf{J}}{r_{1,k}}\right)^{2} \right. \nonumber\\[3pt] & \left. +\left(A+B-2C\right)\left(\frac{\textbf{r}_{1,k}.\textbf{K}}{r_{1,k}}\right)^{2}\right], \end{align*}](/articles/aa/full_html/2019/02/aa33342-18/aa33342-18-eq3.png)
with (rk,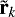 ) the heliocentric position and the conjugate momemtum of the body k, mk the mass of the body k, r1,k = r1 −rk, r1 and r1,k the norms of r1 and r1,k, and
) the heliocentric position and the conjugate momemtum of the body k, mk the mass of the body k, r1,k = r1 −rk, r1 and r1,k the norms of r1 and r1,k, and 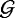 the gravitational constant. By averaging over the fast Andoyer angles g, the angle of proper rotation, and l, the angle of precession of the polar axis K around the angular momentum G (Boué & Laskar 2006), HE becomes constant and the averaged total Hamiltonian
the gravitational constant. By averaging over the fast Andoyer angles g, the angle of proper rotation, and l, the angle of precession of the polar axis K around the angular momentum G (Boué & Laskar 2006), HE becomes constant and the averaged total Hamiltonian 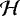 is
is
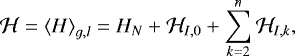 (5)
(5)
J the Andoyer angle between w and K, and G the norm of the angular momentum G.
The Hamiltonian 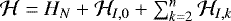 can be split into several parts. The Hamiltonian HN of n point masses can be integrated with the existing symplectic integrators (e.g., Wisdom & Holman 1991; Laskar & Robutel 2001; Farrés et al. 2013).
can be split into several parts. The Hamiltonian HN of n point masses can be integrated with the existing symplectic integrators (e.g., Wisdom & Holman 1991; Laskar & Robutel 2001; Farrés et al. 2013).
For a planetary system where a planet is located much closer to the central star than the other planets, Farago et al. (2009) averaged its fast orbital motion to obtain a Hamiltonian of interaction between the orbital angular momentum of the closest planet and the other more distant planets. Because the Hamiltonians 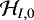 and
and 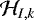 are analogous to this Hamiltonian, we can use the symplectic method developed by Farago et al. (2009) for this case. We detail explicitly how this method can be applied here.
are analogous to this Hamiltonian, we can use the symplectic method developed by Farago et al. (2009) for this case. We detail explicitly how this method can be applied here.
The Hamiltonian 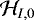 gives the equations of the motion (Boué & Laskar 2006)
gives the equations of the motion (Boué & Laskar 2006)
![\begin{equation*} \left\{ \begin{array}{@{}l@{\hskip3pt}l@{\hskip3pt}l} \dot{\textbf{r}}_{1} &=& \textbf{0}, \\ \dot{\tilde{\textbf{r}}}_{1} &=& -\nabla_{\textbf{r}_{1}} \mathcal{H}_{I,0} \\[3pt] & =&-\frac{3\mathcal{C}_{1}m_{0}}{r_{1}^{5}}\left(\left(1-5\left(\frac{\textbf{r}_{1}.\textbf{w}}{r_{1}}\right)^{2}\right) \textbf{r}_1+2\left(\textbf{r}_{1}.\textbf{w}\right)\textbf{w}\right),\\[6pt] \dot{\textbf{w}} &=& \frac{1}{G}\nabla_{\textbf{w}} \mathcal{H}_{I,0} \times\textbf{w} = \frac{6\mathcal{C}_{1}m_{0}}{Gr_{1}^{5}}\left(\textbf{r}_{1}.\textbf{w}\right)\textbf{r}_{1}\times\textbf{w}. \end{array}\right. \end{equation*}](/articles/aa/full_html/2019/02/aa33342-18/aa33342-18-eq15.png) (10)
(10)
Here r1 is conserved and because of 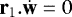 , r1.w is also constant. With the angular frequency
, r1.w is also constant. With the angular frequency 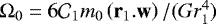 as in Farago et al. (2009), the solution for w is
as in Farago et al. (2009), the solution for w is
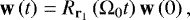 (11)
(11)
where 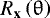 is the rotation matrix of angle θ around the vector x. The solution for
is the rotation matrix of angle θ around the vector x. The solution for 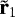 is (Farago et al. 2009)
is (Farago et al. 2009)
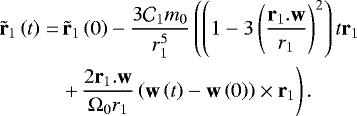 (12)
(12)
We have then an exact solution for the Hamiltonian 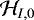 .
.
The equations of motion for the Hamiltonian 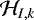 are similar. However, this Hamiltonian modifies the variables of the body k. The equations are then
are similar. However, this Hamiltonian modifies the variables of the body k. The equations are then
![\begin{equation*}\left\{ \begin{array}{@{}l@{\hskip3pt}l@{\hskip3pt}l} \dot{\textbf{r}}_{1} &=& \textbf{0}, \\ \dot{\tilde{\textbf{r}}}_{1} &= & -\frac{3\mathcal{C}_{1}m_{k}}{r_{1,k}^{5}}\left(\left(1-5\left(\frac{\textbf{r}_{1,k}.\textbf{w}}{r_{1,k}}\right)^{2}\right)\textbf{r}_{1,k}+2\left(\textbf{r}_{1,k}.\textbf{w}\right)\textbf{w}\right), \\ \dot{\textbf{r}}_{k} &=& \textbf{0},\\ \dot{\tilde{\textbf{r}}}_{k} &= & \frac{3\mathcal{C}_{1}m_{k}}{r_{1,k}^{5}}\left(\left(1-5\left(\frac{\textbf{r}_{1,k}.\textbf{w}}{r_{1,k}}\right)^{2}\right)\textbf{r}_{1,k}+2\left(\textbf{r}_{1,k}.\textbf{w}\right)\textbf{w}\right), \\[6pt] \dot{\textbf{w}} &=& \frac{6\mathcal{C}_{1}m_{k}}{Gr_{1,k}^{5}}\left(\textbf{r}_{1,k}.\textbf{w}\right)\textbf{r}_{1,k}\times \textbf{w}, \end{array}\right. \end{equation*}](/articles/aa/full_html/2019/02/aa33342-18/aa33342-18-eq24.png) (13)
(13)
with the angular frequency 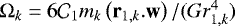 .
.
The symplectic scheme for the total Hamiltonian is (Farago et al. 2009)
 (15)
(15)
where LX represents the Lie derivative ofa Hamiltonian X. This schemegives a symplectic solution for the long-term evolution of the angular momentum of the rigid body.
It is possible to neglect the effects of the rotation on the orbital motion by keeping 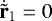 and
and 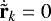 in Eqs. (10) and (13). This allows us to obtain multiple solutions for the long-term rotation with different initial conditions for the angular momentum by computing only one orbital evolution. In this case, the total energy is still conserved, but it is not the case for the total angular momentum.
in Eqs. (10) and (13). This allows us to obtain multiple solutions for the long-term rotation with different initial conditions for the angular momentum by computing only one orbital evolution. In this case, the total energy is still conserved, but it is not the case for the total angular momentum.
By averaging over the fast rotation of Ceres and Vesta, this method is used in Sect. 4 to obtain the long-term evolution of the angular momenta of Ceres and Vesta where the torques are exerted by the Sun and the planets.
2.2. Secular equations for the angular momentum
In order to speed up the computation, we average the Hamiltonian (Eq. (5)) over the mean longitude of the rigid body. By considering only the torque exerted by the Sun, we obtain the secular Hamiltonian for the rotation axis (Boué & Laskar 2006)
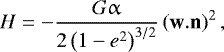 (16)
(16)
with G = Cω for the spin rate ω. The motion of the angular momentum is forced by a secular orbital solution, from which the normal to the orbit n and the eccentricity e are computed. The precession constant α can be written
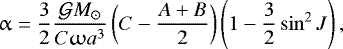 (17)
(17)
with a the semi-major axis and M⊙ the mass of the Sun. The moments of inertia can be normalized by
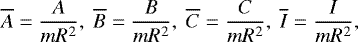 (18)
(18)
with I = (A + B + C)∕3 the mean moment of inertia, m the mass of the solid body, and R the reference radius used for the determination of the gravity field. The gravitational flattening J2 depends on the normalized moments of inertia with
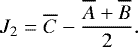 (19)
(19)
The precession constant can then be written
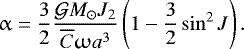 (20)
(20)
The secular equation for the angular momentum w is then (e.g., Colombo 1966; Boué & Laskar 2006)
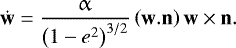 (21)
(21)
The angle between the normal to the orbit, n, and the angular momentum, w, is the obliquity ϵ.
Equation (21) is used in Sect. 6 to study the stability of the spin axes of Ceres and Vesta.
3. Precession constants and initial conditions
To determine the quantity 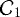 (Eq. (9)) and the precession constant α (Eq. (20)), the polar moment of inertia C, the spin rate ω, the gravitational flattening J2, and the Andoyer angle J are necessary.
(Eq. (9)) and the precession constant α (Eq. (20)), the polar moment of inertia C, the spin rate ω, the gravitational flattening J2, and the Andoyer angle J are necessary.
3.1. Estimation of the Andoyer angle J
The Andoyer angle J is the angle between the angular momentum G and the polar axis K.
The Dawn space mission determined the principal axes of Ceres and Vesta and measured the gravitational field in these frames. To obtain the precision of the determination of the principal axes, we estimate the angle γ between the polar axis and its determination by Dawn with the expression
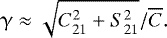 (22)
(22)
The spherical harmonic gravity coefficients of second degree and first-order C21 and S21 were determined with their uncertainties by Dawn for Ceres (Park et al. 2016) and Vesta (Konopliv et al. 2014). Because C21 and S21 are smaller than their uncertainties and than the other coefficients of second degree for both bodies, Park et al. (2016) and Konopliv et al. (2014) deduce that this angle is negligible. By replacing C21 and S21 by their uncertainties in Eq. (22) and 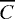 by the values of Sects. 3.2.2 and 3.3.2, the angle γ is about 7 × 10−5° and 1 × 10−6°, respectively,for Ceres and Vesta.
by the values of Sects. 3.2.2 and 3.3.2, the angle γ is about 7 × 10−5° and 1 × 10−6°, respectively,for Ceres and Vesta.
Using the basis (I, J, K) associated with the principal axes of moments of inertia, the rotational vector Ω can be expressed as
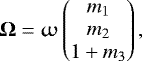 (23)
(23)
where m1 and m2 describe the polar motion and m3 the length of day variations, which were estimated by Rambaux et al. (2011) and Rambaux (2013), respectively, for Ceres and Vesta. The amplitude of the polar motion is about 0.4 mas for Ceres and 0.8 mas for Vesta. Rambaux et al. (2011) assumed that Ceres is axisymmetric and obtained an amplitude of about 8 × 10−4 mas for m3. Rambaux (2013) considered a triaxial shape for Vesta and obtained an amplitude for m3 of about 0.1 mas. The angle between the rotational vector Ω and the polar axis is about 1 × 10−7° for Ceres and 2 × 10−7° for Vesta and the polar motion is then negligible.
The rotational vector can also be approximated by Ω = ωK and G verifies G = CωK. Therefore, we can neglect sin2J in Eq. (20) and the precession constant becomes
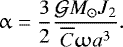 (24)
(24)
3.2. Precession constant of Ceres
3.2.1. Physical parameters
From the Dawn data, Park et al. (2016) determined J2
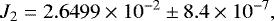 (25)
(25)
Park et al. (2016) also refined the spin rate to
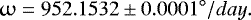 (27)
(27)
3.2.2. Polar moment of inertia
The polar moment of inertia can be estimated from a model of internal structure. Park et al. (2016) proposed a set of internal models withtwo layers by numerically integrating Clairaut’s equations of hydrostatic equilibrium. The mantle of density 2460–2900 kg m−3 has a composition similar to those of different types of chondrites and the outer shell of density 1680–1950 kg m−3 is a blend of volatiles, silicates, and salts. Ermakov et al. (2017a) used the gravity field and the shape obtained by the Dawn space mission and took into account the effect of the isostasy to constrain the internal structure of Ceres. Their favored model has a crust density of 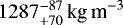 , a crust thickness of
, a crust thickness of 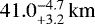 , a mantle density of
, a mantle density of 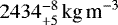 , and a mantle radius of
, and a mantle radius of 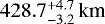 .
.
In Fig. 1, the purple curve represents the numerical solutions of Clairaut’s equations which reproduce the observed gravitational flattening J2 (Park et al. 2016). In Fig. 1, the normalized mean moment of inertia 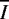 is computed by assuming a spherical shape, as in Eq. (1) of Rambaux et al. (2011). For a mantle density of 2460–2900 kg m−3, we have
is computed by assuming a spherical shape, as in Eq. (1) of Rambaux et al. (2011). For a mantle density of 2460–2900 kg m−3, we have 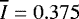 . The normalized polar moment of inertia
. The normalized polar moment of inertia 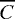 can be deduced by
can be deduced by
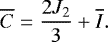 (28)
(28)
With Eq. (25) and 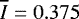 , we found
, we found 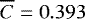 1.
1.
The gravitational flattening possesses a nonhydrostatic component 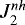 , which causes an uncertainty on
, which causes an uncertainty on 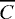 . Park et al. (2016) estimated
. Park et al. (2016) estimated  with
with
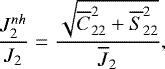 (29)
(29)
for the normalized spherical harmonic gravity coefficients of second degree and second-order 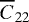 and
and 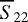 and
and 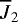 the normalized value of J2. By deriving the Radau–Darwin relation (e.g., Rambaux et al. 2015; Ermakov et al. 2017a), we obtain the uncertainty
the normalized value of J2. By deriving the Radau–Darwin relation (e.g., Rambaux et al. 2015; Ermakov et al. 2017a), we obtain the uncertainty 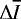 on
on 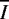
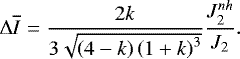 (30)
(30)
The fluid Love number k verifies k = 3J2∕q (Ermakov et al. 2017a) with 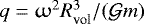 , Rvol the volume-equivalent radius, and m the mass. For Rvol = 469.7 km (Ermakov et al. 2017a), Eq. (30) gives the uncertainty
, Rvol the volume-equivalent radius, and m the mass. For Rvol = 469.7 km (Ermakov et al. 2017a), Eq. (30) gives the uncertainty 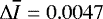 . With Eq. (28), we have
. With Eq. (28), we have 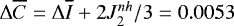 . We keep
. We keep 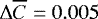 as in Ermakov et al. (2017b).
as in Ermakov et al. (2017b).
For the integration of the obliquity, we choose 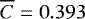 and 0.005 for its uncertainty. The interval of uncertainty on
and 0.005 for its uncertainty. The interval of uncertainty on 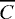 is then [0.388 : 0.398]. Ermakov et al. (2017b) obtained the value
is then [0.388 : 0.398]. Ermakov et al. (2017b) obtained the value 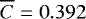 for a radius of R = 469.7 km, which corresponds to
for a radius of R = 469.7 km, which corresponds to 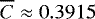 for R = 470 km. The value
for R = 470 km. The value 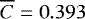 is then consistent with the value of Ermakov et al. (2017b) given the uncertainties.
is then consistent with the value of Ermakov et al. (2017b) given the uncertainties.
 |
Fig. 1. Normalized mean moment of inertia |
3.2.3. Precession constant
We take a constant semi-major axis to compute the precession constant. We use the average of the semi-major axis of the solution La2011 on [−25 : 5] Myr, which is about a ≈ 2.767 AU. On this interval, the semi-major axis can move away to Δa = 0.005 AU from this value. From Eq. (24) and previous values and uncertainties, we deduce the precession constant
 (31)
(31)
3.2.4. Early Ceres
Mao & McKinnon (2018) estimated that Ceres should spin about 7 ± 4% faster to be in hydrostatic equilibrium with the observed present shape. They supposed that Ceres had been in hydrostatic equilibrium in the past and had then slowed down due to some phenomenon like significant asteroid impacts. They obtained for this higher spin rate an internal structure of normalized mean moment of inertia 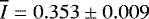 for a reference radius R = 470 km. With Eq. (28), it corresponds to a normalized polar moment of inertia
for a reference radius R = 470 km. With Eq. (28), it corresponds to a normalized polar moment of inertia 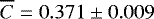 . The corresponding precession constant is
. The corresponding precession constant is
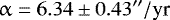 (32)
(32)
with the value of the semi-major axis of the section 3.2.3. With the present spin rate and considering a normalized polar moment of inertia of 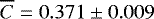 , the precession constant of the present Ceres would be
, the precession constant of the present Ceres would be
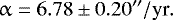 (33)
(33)
3.3. Precession constant of Vesta
3.3.1. Physical parameters
From the Dawn data, Konopliv et al. (2014) gave the normalized value for J2
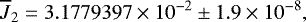 (34)
(34)
It corresponds to about 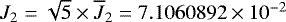 . The rotation rate has been refined by Konopliv et al. (2014) with
. The rotation rate has been refined by Konopliv et al. (2014) with
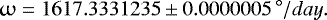 (36)
(36)
3.3.2. Polar moment of inertia
The polar moment of inertia C of Vesta could not be obtained from the observation of the precession and nutation of its pole (Konopliv et al. 2014). Following Rambaux (2013), we determine C from an internal model composed of ellipsoidallayers of semi-axes ai, bi, and ci, and uniform densities ρi, where ai, bi, and ci are, respectively,the major, intermediate, and minor semi-axes. For a three-layer model constituted of a crust (1), a mantle (2), and a core (3), C is
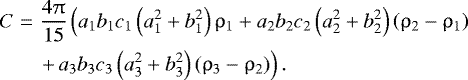 (37)
(37)
Ermakov et al. (2014) and Park et al. (2014) proposed internal models from the gravity field and the shape model of Gaskell (2012). Ermakov et al. (2014) determined the interface between the crust and the mantle. The densities and the reference ellipsoids used by Ermakov et al. (2014) to compare their model are in Table 1. For these parameters, Eq. (37) gives 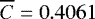 . If we use instead of the biaxial crust in Table 1, the triaxial best-fit ellipsoid of Ermakov et al. (2014) determined from the shape model of Gaskell (2012) with a = 284.895, b = 277.431, and c = 226.838 km, we obtain
. If we use instead of the biaxial crust in Table 1, the triaxial best-fit ellipsoid of Ermakov et al. (2014) determined from the shape model of Gaskell (2012) with a = 284.895, b = 277.431, and c = 226.838 km, we obtain 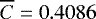 .
.
Park et al. (2014) proposed three-layer and two-layer models (Table 1). For the form of the crust, we use the best-fit ellipsoid of Konopliv et al. (2014) instead of the shape of Gaskell (2012). Equation (37) gives the approximate values 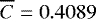 for the three-layer model and
for the three-layer model and 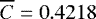 for the two-layer model.
for the two-layer model.
We keep 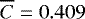 obtained for the three-layer model of Park et al. (2014) with the uncertainty 0.013, given from the uncertainty interval [0.406: 0.422].
obtained for the three-layer model of Park et al. (2014) with the uncertainty 0.013, given from the uncertainty interval [0.406: 0.422].
Densities and semi-principal axes for different models of internal structure of Vesta.
3.3.3. Precession constant
As we did for Ceres, we consider a mean value for the semi-major axis. With a ≈ 2.361 AU and Δ a = 0.002 AU, Eq. (24) gives
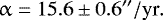 (38)
(38)
3.3.4. Early Vesta
The southern hemisphere of Vesta has a large depression with two basins, Veneneia and Rheasilvia, created by two giant impacts (Marchi et al. 2012; Schenk et al. 2012). Fu et al. (2014) fitted the regions of the northern hemisphere not affected by the giant impacts with an ellipsoid of principal axes of dimensions a = 280.6, b = 274.6 and c = 236.8 km. By extrapolating this shape to the two hemispheres of the early Vesta supposed hydrostatic, Fu et al. (2014) obtained a paleorotation period of 5.02 h and Ermakov et al. (2014) a paleorotation period between 4.83 h and 4.93 h for, respectively, the most and least differentiated internal structures.
By replacing the shape of the previous models by the supposed shape of the early Vesta determined by Fu et al. (2014), Eq. (37) gives 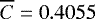 for the three-layer model of Ermakov et al. (2014), and
for the three-layer model of Ermakov et al. (2014), and 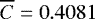 and
and 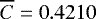 , respectively, for the three-layer and two-layer models of Park et al. (2014). We choose
, respectively, for the three-layer and two-layer models of Park et al. (2014). We choose 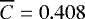 with an uncertainty of 0.013. The corresponding gravitational flattening is J2 = 0.0559 ± 0.0003, where the uncertainty is given from the gravitational flattenings of the three different models of internal structure. We choose the paleorotation period of 5.02 h of Fu et al. (2014). We use the value of the semi-major axis of Sect. 3.3.3, and Eq. (24) gives the precession constant for the early Vesta
with an uncertainty of 0.013. The corresponding gravitational flattening is J2 = 0.0559 ± 0.0003, where the uncertainty is given from the gravitational flattenings of the three different models of internal structure. We choose the paleorotation period of 5.02 h of Fu et al. (2014). We use the value of the semi-major axis of Sect. 3.3.3, and Eq. (24) gives the precession constant for the early Vesta
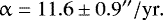 (39)
(39)
3.4. Initial conditions
The Dawn space mission refined the orientation of the rotation axes of Ceres and Vesta. We use the coordinates given under the form right ascension/declination in the ICRF frame for the epoch J2000 by Park et al. (2016) for Ceres and by Konopliv et al. (2014) for Vesta listed in Table 2. From these coordinates and their uncertainties, we obtain the obliquities ϵC and ϵV of, respectively, Ceres and Vesta at the epoch J2000

Right ascension (RA) and declination (Dec) of Ceres (Park et al. 2016) and Vesta (Konopliv et al. 2014) at the epoch J2000 in the ICRF frame.
4. Orbital and rotational solutions obtained with the symplectic integration
This section is dedicated to the long-term solutions La2011 for the orbital motion and Ceres2017 for the rotational motion, which is obtained with the symplectic integration of the angular momentum described in Sect. 2.1. The time origin of the solutions is the epoch J2000.
We analyze the solutions with the method of the frequency map analysis (Laskar 1988, 1990, 1993, 2003; Laskar et al. 1992), which decomposes a discrete temporal function in a quasi-periodic approximation. The precision of the obtained frequencies is estimated by performing a frequency analysis of the solution rebuilt from the frequency decomposition with a temporal offset (Laskar 1990). The differences between the frequencies of the two decompositions give an estimate of the accuracy on the determination of the frequencies.
4.1. Perturbations on the rotation axis
We investigate and estimate some effects that can affect the long-term rotation in addition to the torques exerted by the Sun and the planets.
4.1.1. Tidal dissipation
The torque exerted on a celestial body for the solar tides is (Mignard 1979)
![\begin{equation*} \mathbf{\Gamma} = 3\frac{k_{2}\mathcal{G}M_{\odot}^2R^5}{Cr^8}\mathrm{\Delta} t\left[ \left(\mathbf{r}.\mathbf{G}\right)\mathbf{r}-r^2\mathbf{G}+C\mathbf{r}\times\mathbf{v}\right], \end{equation*}](/articles/aa/full_html/2019/02/aa33342-18/aa33342-18-eq97.png) (42)
(42)
with Δt the time delay between the stress exerted by the Sun and the response of the body, k2 the Love number, R the radius of the body, r and v the heliocentric position and velocity of the body, and r the norm of r. For a circular and equatorial orbit, Mignard (1979) writes
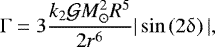 (43)
(43)
with δ = (ω − n) Δt the phase lag and n the mean motion. The phase lag δ is related to the effective specific tidal dissipation function Q by 1∕Q = tan(2δ) (MacDonald 1964).
Because of the dependence in r−6, the torque decreases strongly with the distance to the Sun. Laskar et al. (2004a) concluded that the tidal dissipation in the long-term rotation of Mars has an effect on the obliquity inferior to 0.002° in 10 Myr. We estimate this torque for Ceres and Vesta and compare these values with that for Mars in Table 3. The values of k2 and Q used for theestimation of the torque are those used by Rambaux et al. (2011) for Ceres and by Bills & Nimmo (2011) for Vesta. The ratio of the torque on the rotation angular momentum is, respectively, about 1000 and 10 000 times weaker for Ceres and Vesta than for Mars, for which the effect can already be considered weak (Laskar et al. 2004a). Therefore, the solar tidal dissipation for Ceres and Vesta was not considered.
Estimation of the solar tidal torque Γ∕(Cω) on Mars, Ceres, and Vesta.
4.1.2. Close encounters
In the long-term solution La2010 (Laskar et al. 2011a), the five bodies of the asteroid belt (1) Ceres, (2) Pallas, (4) Vesta, (7) Iris, and (324) Bamberga are considered planets and there are mutual gravitational interactions between them. Laskar et al. (2011a) considered these bodies because Ceres, Vesta, and Pallas are the three main bodies of the main asteroid belt and becauseIris and Bamberga significantly influence the orbital motion of Mars. Laskar et al. (2011b) studied the close encounters between these bodies and showed that they are responsible for their chaotic behavior. If a body comes close to Ceres or Vesta, it can exert a significant torque during the encounter. The effects of close encounters on the rotation axes of the giant planets have been studied by Lee et al. (2007). For a body of mass m with no satellites, the maximum difference ∥Δw∥ between the angular momentum before an encounter with a perturbing body of mass mpert and the angular momentum after is (Lee et al. 2007)
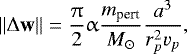 (44)
(44)
with α the precession constant (Eq. (24)), a the semi-major axis, and rp and 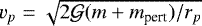 , respectively, the distance and the relative speed between the two bodies at the closest distance. We can write this formula as
, respectively, the distance and the relative speed between the two bodies at the closest distance. We can write this formula as
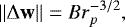 (45)
(45)
The values of the coefficient B have been computed in Table 4 for close encounters considered in Laskar et al. (2011b). Therefore, a close encounter changes the orientation of the rotation axis at the most of the angle
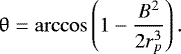 (47)
(47)
Laskar et al. (2011b) studied the probability of close encounters between the five bodies of the asteroid belt considered in the solution La2010 (Laskar et al. 2011a) and determined that the probability density ρ(rp) per unit of time of an encounter with a distance rp at the closest approach can be fitted by a linear function of rp for rp ≤ 1 × 10−3 AU
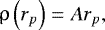 (48)
(48)
Here Nc is the collision probability per unit of time between two bodies of radii R1 and R2. Table 4 gives the radii, the collision probability Nc extracted from Table 3 in Laskar et al. (2011b), and the deduced coefficient A between each considered pair on 1 Gyr for the five bodies considered in Laskar et al. (2011b).
We suppose that each close encounter moves the angular momentum in a random direction. The motion of the rotation axis is described by a random walk on a sphere of distribution (Perrin 1928; Roberts & Ursell 1960)
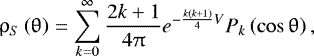 (50)
(50)
with the variance V, 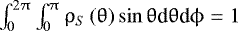 , and Pk the Legendre polynomial of order k. For a random walk of N steps with a large value of N, where each step causes a small change β in the orientation, the variance V is (Roberts & Ursell 1960)
, and Pk the Legendre polynomial of order k. For a random walk of N steps with a large value of N, where each step causes a small change β in the orientation, the variance V is (Roberts & Ursell 1960)
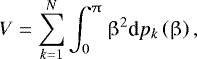 (51)
(51)
with 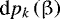 the probability to have a change of angle β for the step k. For Ceres, we consider the close encounters with the bodies considered in Laskar et al. (2011b) for which we have the probability of close encounters and we can write
the probability to have a change of angle β for the step k. For Ceres, we consider the close encounters with the bodies considered in Laskar et al. (2011b) for which we have the probability of close encounters and we can write
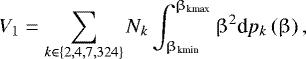 (52)
(52)
with k the number of the body for which we consider the close encounter with Ceres, βkmin the minimum change of orientation at the distance 1 × 10−3 AU, βkmax the maximum change of orientation for a grazing encounter at the distance R1 + Rk, Nk the number of close encounters, and 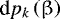 the probability distribution to have the change β for a close encounter with the body k. As
the probability distribution to have the change β for a close encounter with the body k. As 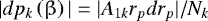 , the variance V1 verifies
, the variance V1 verifies
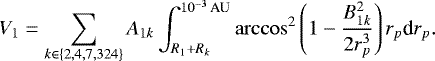 (53)
(53)
We compute the standard deviation of the distribution of the rotation axis of Ceres on 1 Gyr under the effects of the close encounters with the bodies (2) Pallas, (4) Vesta, (7) Iris, and (324) Bamberga with the formula
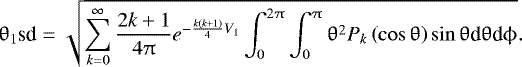 (54)
(54)
We obtain with the intermediary quantities in Table 4 about
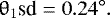 (55)
(55)
We realize a similar computation for Vesta in Table 4 to obtain
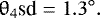 (56)
(56)
The time interval [−100 : 0] Myr is smaller than 1 Gyr and the effects of close encounters are then weaker on this interval. Moreover, these standard deviations are computed for close encounters, which cause a maximum effect on the rotation axis.
Although their effects are weak, we consider for the long-term integration of the rotation the torques exerted on the angular momenta of Ceres and Vesta by the five bodies of the main asteroid belt considered in Laskar et al. (2011b).
Radii R used by Laskar et al. (2011b) to compute the collision probabilities Nc between Ceres and Vesta and some bodies.
4.2. Orbital motion La2011
The orbital solution La2011 is computed on [−250 : 250] Myr in a frame associated with the invariable plane (Laskar et al. 2011a). Two successive rotations allow us to pass from this frame to the ICRF as explained in Appendix A. The variables z = eexp(iϖ) and ζ = sin(i/2)exp(iΩ) are computed from the noncanonical elliptical elements (a, λ, e, ϖ, i, Ω), where a is the semi-major axis, λ the mean longitude, e the eccentricity, ϖ the longitude of the perihelion, i the inclination with respect to the invariable plane, and Ω the longitude of the ascending node. These elements are computed from the heliocentric positions and velocities.
As made for the solution La2004 of Laskar et al. (2004b), we perform a frequency analysis of the quantities zi and ζi on [−20 : 0] Myr for the four inner planets and on [−50 : 0] Myr for the four giant planets and Pluto to obtain the proper perihelion precession frequencies gi and ascending node precession frequencies si in Table 5.
The evolutions of the eccentricity and the inclination are represented for Ceres and Vesta on [−1 : 0] Myr, respectively, in Figs. 2 and 3. For Ceres, the eccentricity oscillates between 0.0629 and 0.169 and the inclination between 8.77 and 10.6° on [−20 : 0] Myr. For Vesta, the eccentricity varies between 0.0392 and 0.160 and the inclination between 5.21 and 7.56° on [−20 : 0] Myr. The amplitudes of the variations have the same order of magnitude for Ceres and Vesta on [−250 : 250] Myr.
For Ceres and Vesta, we perform a frequency analysis of z and ζ on the time interval [−25 : 5] Myr. We consider the 50 secular terms with the highest amplitudes which have a frequency in the interval [−300 : 300]′′/yr in Tables B.1 and B.2. The frequency decompositions of Tables B.1 and B.2 allow us to obtain a secular solution, which reproduces the secular evolution of the solution La2011 on [−20 : 0] Myr in Figs. 4 and 5, where the differences with the solution La2011 correspond to the short-period terms excluded from the secular solution. It is not the case for those obtained with a frequency analysis on the time interval [−20 : 0] Myr.
These frequency decompositions are used in Sect. 6 to compute the orbital quantities in Eq. (21) needed for the secular integration of the rotation. The terms of weak amplitude can play a role in the long-term rotation in the case of secular resonances. For instance, the passage through the resonance with the frequency s6 + g5 − g6 is responsible for a decrease in the obliquity of about 0.4° for the Earth (Laskar et al. 1993b, 2004b). Therefore, we add to the frequency decompositions of the variable ζ for Ceres the 100 following terms in the interval [−45 : 60]′′/yr and for Vesta the 100 following terms in the interval [−34:60]′′/yr. These boundaries have been chosen such that they select the frequencies, which can play a role in the long-term rotation without all the terms close to the principal frequencies s.
For Ceres, the proper secular frequencies are gC = 54.2525 ± 0.0006′′∕yr and sC = −59.254 ± 0.002′′∕yr with the respectively associated periods 23.888 kyr and 21.872 kyr. The first 50 secular terms of the frequency decompositions do not include proper frequencies of the inner planets. Their perturbations on the orbital motions are then much weaker than those of the giant planets. We observe the proximity of the frequencies 2g6 − g5 ≈ 52.23′′∕yr and 2g6 − g7 ≈ 53.40′′∕yr with gC. Resonances with these two frequencies could affect the orbital motion of Ceres.
For Vesta, the proper secular frequencies are gV = 36.895 ± 0.003′′∕yr and sV = −39.609 ± 0.003′′∕yr with respectively associated periods 35.13 kyr and 32.72 kyr. The proper frequencies of the inner planets are not present except perhaps for the frequency − 17.74′′∕yr, which could correspond to the node frequency of Mars s4. Vesta has a shorter semi-major axis, and the planetary perturbations of Mars are then more important than for Ceres, which could explain the presence of this frequency with a higher amplitude.
As in Laskar (1990), we estimate the size of the chaotic zones and perform a frequency analysis of the solution La2011 on sliding intervals of 30 Myr over [−250 : 250] Myr with a 5 Myr step size. The evolutions of the proper frequencies of Ceres and Vesta are respectively in Figs. 6 and 7. The values of frequencies gC and sC vary respectively in about [54.225 : 54.261]′′/yr and [−59.263 : −59.209]′′/yr, and gV and sV respectively in about [36.809 : 36.939]′′/yr and [−40.011 : −39.514]′′/yr . The secular frequencies vary because of the chaotic diffusion, which is then higher for Vesta than for Ceres. The frequency sV has the highest diffusion with a decrease of about 0.50′′∕yr on [115 : 220] Myr.
Principal secular frequencies of the solution La2011 gi, si determined on [−20 : 0] Myr for the four inner planets and on [−50 : 0] Myr for the four giant planets and Pluto.
 |
Fig. 2. Eccentricity (panel a) and inclination (panel b) of Ceres for the solution La2011. |
 |
Fig. 3. Eccentricity (panel a) and inclination (panel b) of Vesta for the solution La2011. |
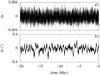 |
Fig. 4. Difference for Ceres in eccentricity (panel a) and inclination (panel b) between the solution La2011 and the secular solution. |
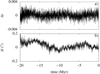 |
Fig. 5. Difference for Vesta in eccentricity (panel a) and inclination (panel b) between the solution La2011 and the secular solution. |
 |
Fig. 6. Secular frequencies gC (panel a) and sC (panel b) of Ceres on [−250 : 250] Myr computed with a step of 5 Myr with the frequency map analysis on an interval of 30 Myr. The error bars are given by the precision of the frequency map analysis. |
 |
Fig. 7. Secular frequencies gV (panel a) and sV (panel b) of Vesta on [−250 : 250] Myr, computed with a step of 5 Myr with the frequency map analysis on an interval of 30 Myr. The error bars are given by the precision of the frequency map analysis. |
4.3. Rotational motion Ceres2017
The solution La2011 does not include the integration of the rotation axes of Ceres and Vesta. We compute then the solution Ceres2017 where the spin axes of Ceres and Vesta are integrated with the symplectic method presented in Sect. 2.1. We consider the interactions between the orbital and rotational motions and the torques exerted by the Sun and the planets on Ceres and Vesta. As they are in La2011, Ceres, Vesta, Pallas, Iris, and Bamberga are considered planets and exert a torque on Ceres and Vesta. We use the same initial condition for the orbital motion as in La2011. To integrate the long-term rotation, we use the parameters listed in Table 6 and the initial conditions for the rotation axis in Table 2. The integration is realized on [−100 : 100] Myr in extended precision with a time step of 0.005 yr. We use the integrator  developed for perturbed Hamiltonians by Laskar & Robutel (2001). A symmetric composition of this integrator with the method of Suzuki (1990) allows one to obtain a higher order integrator, as indicated in Laskar & Robutel (2001).
developed for perturbed Hamiltonians by Laskar & Robutel (2001). A symmetric composition of this integrator with the method of Suzuki (1990) allows one to obtain a higher order integrator, as indicated in Laskar & Robutel (2001).
The differences between La2011 and Ceres2017 for the eccentricity and inclination of Ceres and Vesta oscillate around zero. The amplitudes on [−20 : 0] Myr are about 0.008 and 0.1° for the eccentricity and the inclination of Ceres and about 0.02 and 0.2° for Vesta. These differences have similar amplitudes to those observed for a small change (1 × 10−10 rad) of the initial mean longitude λ of Ceres and Vesta. Therefore, they come from the chaotic behavior for the orbital motions of Ceres and Vesta (Laskar et al. 2011b) and are thus not significant.
The evolution of the obliquity is represented on the time intervals [−100 : 0] kyr , [−1 : 0] Myr , and [−20 : 0] Myr in Figs. 8 and 9, respectively, for Ceres and Vesta. For Ceres, we obtain similar results to Bills & Scott (2017) and Ermakov et al. (2017b) with oscillations between about 2.06° and 19.6° on [−20 : 0] Myr. For Vesta, we observe oscillations between 21.4° and 44.1°. The amplitudes of the oscillations of the obliquities of Ceres and Vesta are similar on [−100 : 100] Myr.
We perform the frequency analysis of the solution Ceres2017 on the time interval [−20 : 0] Myr. The frequency decompositions of the quantity wx + iwy, where wx and wy are the coordinates in the invariant frame of the component parallel to the invariable plane of the normalized angular momentum, are in Tables B.3 and B.4, respectively, for Ceres and Vesta. For Ceres, the precession frequency of the rotation axis is then fC = −6.1588 ± 0.0002′′∕yr, which corresponds to a precession period of about 210.43 kyr and is consistent with the precession period of 210 kyr determined by Ermakov et al. (2017b). For Vesta, the precession frequency of the rotation axis is fV = −12.882 ± 0.002′′∕yr, which corresponds to a period of precession of about 100.61 kyr.
Skoglöv et al. (1996) noticed that bodies like Ceres and Vesta, which have a high inclination and a precession frequency of the ascending node higher than the precession frequency of the rotation axis, could have strong variations in the obliquity. Indeed, the obliquity is given by
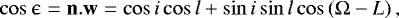 (57)
(57)
with (l, L) the inclination and the longitude of the ascending node of the equatorial plane and (i, Ω) those of the orbital plane in the frame of the invariable plane. Then the precession of the ascending node causes obliquity variations if the inclination of the orbital plane is not null. The inclination of the orbit plane with respect to the initial equatorial plane is represented by a red curve in Figs. 8 and 9, respectively, for Ceres and Vesta. For Ceres, a large part of the amplitude of the obliquity is caused by the precession of the ascending node, which creates oscillations between 2.1° and 17.1° on [−100 : 0] kyr. For Vesta, the contribution is less important.
We have integrated for the time interval [−100 : 0] Myr the rotationof Ceres and Vesta for different normalized polar moments of inertia, respectively, in the intervals [0.380 : 0.406] and [0.390 : 0.430]. For Ceres, all the different normalized polar moments of inertia give solutions for the obliquity with oscillations of similar amplitude (Fig. 10), as noticed by Ermakov et al. (2017b). The mean differences come from the precession frequency, which depends on the normalized polar moment of inertia. A small difference on the precession frequency causes a phase difference, which growswhen the time increases. For Vesta, the obliquity solutions of the different normalized polar moments of inertia have all oscillations of similar amplitude (Fig. 11) except for the solution obtained for 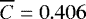 . Because of a secular resonance with the orbital frequency 2s6 − sV (see Sect. 6.2.2), the obliquity can decrease to 18.9° on [−20 : 0] Myr for
. Because of a secular resonance with the orbital frequency 2s6 − sV (see Sect. 6.2.2), the obliquity can decrease to 18.9° on [−20 : 0] Myr for 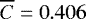 .
.
Physical characteristics of Ceres and Vesta used for the computation of the long-term rotation.
 |
Fig. 8. Obliquity of Ceres on [−100 : 0] kyr(panel a), [−1 : 0] Myr (panel b), and [−20 : 0] Myr (panel c). In panel a the obliquity caused only by the change in orientation of the orbit is represented by the red curve. |
 |
Fig. 9. Obliquity of Vesta on [−100 : 0] kyr (panel a), [−1 : 0] Myr (panel b), and [−20 : 0] Myr (panel c). Inpanel a the obliquity caused only by the change in orientation of the orbit is represented by the red curve. |
 |
Fig. 10. Maximum, mean, and minimum obliquities, respectively, in red, black, and blue for Ceres on [−20 : 0] Myr with respectto the normalized polar moment of inertia. |
 |
Fig. 11. Maximum, mean, and minimum obliquities, respectively, in red, black, and blue for Vesta on [−20 : 0] Myr with respectto the normalized polar moment of inertia. |
5. Secular model for the orbital motion
In Sect. 4.2, we have observed the proximity of Ceres with the resonances of the frequencies 2g6 − g5 ≈ 52.23′′∕yr and 2g6 − g7 ≈ 53.40′′∕yr. If Ceres is close to these two resonances and if these resonances overlap, it could affect its orbital motion and therefore the rotational motion. We have especially seen in Sect. 4.3 that the values of the inclination have direct consequences on the variations ofthe obliquity. Moreover, as noted by Laskar & Robutel (1993), the chaotic behavior of the orbital motion can widen by diffusion the possible chaotic zones of the rotation axis.
A secular model can be obtained from the secular Hamiltonian of Ceres and Vesta to get secular equations, which are integrated much faster than full equations. From the development of the secular Hamiltonian of Laskar & Robutel (1995), we build a secular model of Ceres and Vesta perturbed only by Jupiter and Saturn, which allows us to identify the important terms of the planetary perturbations and to study the close secular resonances.
5.1. Hamiltonian secular model
Laskar & Robutel (1995) computed the development of the Hamiltonian of the planetary perturbations. We consider the case of a body only perturbed by Jupiter and Saturn. From Laskar & Robutel (1995), the Hamiltonian is
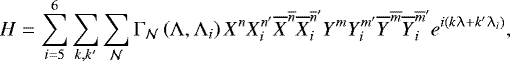 (58)
(58)
with 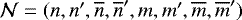 and the coefficients ΓN(Λ,Λi), which depend only on the ratio of the semi-major axes. The Poincaré rectangular canonical coordinates (Λ,λ,x,
and the coefficients ΓN(Λ,Λi), which depend only on the ratio of the semi-major axes. The Poincaré rectangular canonical coordinates (Λ,λ,x, 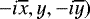 are defined by
are defined by
![\begin{align*} &\Lambda=\upbeta\sqrt{\mu a},\\[6pt] &x=\sqrt{\Lambda\left(1-\sqrt{1-e^{2}} \right)}e^{i\upvarpi},\\[6pt] &y=\sqrt{\Lambda\sqrt{1-e^{2}} \left(1-\cos i \right)}e^{i\Omega}, \end{align*}](/articles/aa/full_html/2019/02/aa33342-18/aa33342-18-eq161.png)
with β = mM⊙∕(m + M⊙),
μ = G(m + M⊙) and m the mass of the perturbed body. The variables X and Y are given by 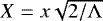 and
and 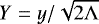 (Laskar & Robutel 1995). We select the terms verifying the secular inequality (0,0) for (k,k′) to obtain the secular part of the Hamiltonian (Eq. (58)) and we consider the case of a massless perturbed body.
(Laskar & Robutel 1995). We select the terms verifying the secular inequality (0,0) for (k,k′) to obtain the secular part of the Hamiltonian (Eq. (58)) and we consider the case of a massless perturbed body.
The secular interaction Hamiltonian has been computed for the order 1 in mass and the degree 4 in eccentricity and inclination. We perform a frequency analysis of the solution La2011 on [−20 : 0] Myr and conserve only the main secular terms to create a secular solution of Jupiter and Saturn, which we inject in the Hamiltonian. The Hamiltonian depends then only on timeand on X, Y. The equations ofthe motion are
![\begin{align}&\frac{\textrm{d}X}{\textrm{d}t}=-\frac{2i}{\Lambda}\frac{\partial H}{\partial \overline{X}},\\[5pt] &\frac{\textrm{d}Y}{\textrm{d}t}=-\frac{i}{2\Lambda}\frac{\partial H}{\partial \overline{Y}}. \end{align}](/articles/aa/full_html/2019/02/aa33342-18/aa33342-18-eq168.png)
5.2. Adjustment of the secular model
Equations (62) and (63) are integrated with a step size of 100 yr with a numerical integrator Runge–Kutta 8(7) on [−20 : 0] Myr. The obtained solution allows us to reproduce the amplitudes of the oscillations of the eccentricity and the inclination of the solution La2011. However, there are differences in the proper frequencies g and s with the solution La2011. These differences of frequency cause phase differences between the perihelion and ascending node longitudes, which grow approximately linearly with time. The secular model does not allow us then to reproduce the solution La2011 (Figs. 12 and 13). To increase the precision of the secular model, it is possible to increase the order of the secular Hamiltonian, but this only allows us to partly reduce the differences in the frequencies.
As was done by Laskar (1990), we adjust the secular frequencies of the model. The differences in the perihelion and ascending node longitudes between the solution La2011 and the secular model are fitted by the affine functions 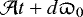 and
and 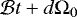 . The frequencies of the secular model are adjusted by applying the following procedure to obtain the Hamiltonian H′
. The frequencies of the secular model are adjusted by applying the following procedure to obtain the Hamiltonian H′
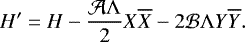 (64)
(64)
The initial conditions for the perihelion longitudes and ascending node longitudes are also respectively corrected by the quantities d ϖ0 and d Ω0. The initial conditions for the eccentricity and the inclination are also slightly corrected. We iterate this procedure until we obtain a difference between the solution La2011 and the secular model, which has a mean close to zero for the four quantities e, i, ϖ, and Ω. The adjustment of the frequencies is then about 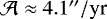 and
and 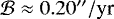 for Ceres and
for Ceres and 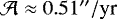 and
and 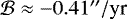 for Vesta. The differences for the eccentricity and the inclination between the two solutions then oscillate around zero and correspond to short-period terms, which are not reproduced by the secular Hamiltonian (Figs. 12 and 13). On [−20 : 0] Myr, the maximum differences in absolute value between the solution La2011 and the adjusted secular model are then 0.0082 and 0.23° for the eccentricity and the inclination of Ceres and 0.013 and 0.65° for the eccentricity and the inclination of Vesta.
for Vesta. The differences for the eccentricity and the inclination between the two solutions then oscillate around zero and correspond to short-period terms, which are not reproduced by the secular Hamiltonian (Figs. 12 and 13). On [−20 : 0] Myr, the maximum differences in absolute value between the solution La2011 and the adjusted secular model are then 0.0082 and 0.23° for the eccentricity and the inclination of Ceres and 0.013 and 0.65° for the eccentricity and the inclination of Vesta.
This Hamiltonian model with the adjustment of the frequencies g and s allows us to reproduce the variations in the eccentricity and the inclination of Ceres and Vesta on [−20 : 0] Myr. Therefore, the long-term orbital dynamics of Ceres and Vesta is given for the most part by the planetary perturbations of Jupiter and Saturn, as noticed by Skoglöv et al. (1996) for Ceres and Vesta and Ermakov et al. (2017b) for Ceres.
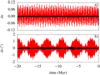 |
Fig. 12. Difference in eccentricity (panel a) and inclination (panel b) for Ceres between the solution La2011 and the Hamiltoniansecular model with adjustment of the frequencies in black, and without in red. |
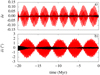 |
Fig. 13. Difference in eccentricity (panel a) and inclination (panel b) for Vesta between the solution La2011 and the Hamiltoniansecular model with adjustment of the frequencies in black, and without in red. |
5.3. Study of the close resonances
This model allows us to study the resonances close to Ceres and Vesta. The integration of the secular Hamiltonian is about 104 faster than the complete integration and allows us to proceed to many integrations with different parameters 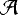 and
and 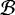 near the values used for the models to see the effects of the close secular resonances. For each value of these parameters, Eqs. (62) and (63) are integrated on [−20 : 0] Myr and the secular frequencies g and s are determined with the frequency analysis.
near the values used for the models to see the effects of the close secular resonances. For each value of these parameters, Eqs. (62) and (63) are integrated on [−20 : 0] Myr and the secular frequencies g and s are determined with the frequency analysis.
For Ceres, the evolutions of the eccentricity, the inclination, and the frequency gC are in Fig. 14 for ![$\mathcal{A}\in \left[0:6\right]{}^{\prime\prime}/\textrm{yr}$](/articles/aa/full_html/2019/02/aa33342-18/aa33342-18-eq182.png) . The resonance with the frequency 2g6 − g5 ≈ 52.23′′∕yr, present in the secular motion of Jupiter and Saturn, acts for about
gC ∈ [51.32 : 53.16]′′/yr. The maximum and minimum eccentricities vary, respectively, from 0.18 to 0.27 and from 0.04 to 0.0002. The maximum inclination rises from 10.6 to 11.1°, which would increase the variations in the obliquity, as noticed in Sect. 4.3. For about gC ∈ [53.21 : 53.60]′′/yr
, there is a resonance with the frequency 2g6 − g7 ≈ 53.40′′ ∕yr present in the secular motion of Jupiter and Saturn, and the maximum eccentricity increases from 0.17 to 0.19. Therefore, the resonance with the frequency 2g6 − g7 has a weaker chaotic nature than that with 2g6 − g5. In Sect.4.2, we have given the interval [54.225 : 54.261]′′/yr as an estimation of the variation in the frequency gC because of the chaotic diffusion on [−250 : 250] Myr. Therefore, the chaotic diffusion of Ceres is too weak to put Ceres in resonance with the frequencies 2g6 − g5 and 2g6 − g7 on [−250 : 250] Myr. The frequency g7 + 2g6 − 2g5 ≈ 51.06′′∕yr in the motion of Jupiter and Saturn causes a resonance with weaker but observable effects on the eccentricity for gC ∈ [50.97 : 51.20]′′/yr. In the secular model of the motions of Jupiter and Saturn, we find the frequency 3g6 − 2g5 + s6 − s7 ≈ 52.87′′∕yr with a smaller amplitude and it is then difficult to distinguish its effects from those of the resonance with the frequency 2g6 − g5. The evolutions of the eccentricity, the inclination, and the frequency sC are in Fig. 15 for
. The resonance with the frequency 2g6 − g5 ≈ 52.23′′∕yr, present in the secular motion of Jupiter and Saturn, acts for about
gC ∈ [51.32 : 53.16]′′/yr. The maximum and minimum eccentricities vary, respectively, from 0.18 to 0.27 and from 0.04 to 0.0002. The maximum inclination rises from 10.6 to 11.1°, which would increase the variations in the obliquity, as noticed in Sect. 4.3. For about gC ∈ [53.21 : 53.60]′′/yr
, there is a resonance with the frequency 2g6 − g7 ≈ 53.40′′ ∕yr present in the secular motion of Jupiter and Saturn, and the maximum eccentricity increases from 0.17 to 0.19. Therefore, the resonance with the frequency 2g6 − g7 has a weaker chaotic nature than that with 2g6 − g5. In Sect.4.2, we have given the interval [54.225 : 54.261]′′/yr as an estimation of the variation in the frequency gC because of the chaotic diffusion on [−250 : 250] Myr. Therefore, the chaotic diffusion of Ceres is too weak to put Ceres in resonance with the frequencies 2g6 − g5 and 2g6 − g7 on [−250 : 250] Myr. The frequency g7 + 2g6 − 2g5 ≈ 51.06′′∕yr in the motion of Jupiter and Saturn causes a resonance with weaker but observable effects on the eccentricity for gC ∈ [50.97 : 51.20]′′/yr. In the secular model of the motions of Jupiter and Saturn, we find the frequency 3g6 − 2g5 + s6 − s7 ≈ 52.87′′∕yr with a smaller amplitude and it is then difficult to distinguish its effects from those of the resonance with the frequency 2g6 − g5. The evolutions of the eccentricity, the inclination, and the frequency sC are in Fig. 15 for ![$\mathcal{B}\in\left[-3{:}3\right]{}^{\prime\prime}/\textrm{yr}$](/articles/aa/full_html/2019/02/aa33342-18/aa33342-18-eq189.png) and have slight irregularities for sC ∈ [−59.95 : −59.73]′′/yr. This frequency interval does not correspond to a term used for the secular motion of Jupiter and Saturn.
and have slight irregularities for sC ∈ [−59.95 : −59.73]′′/yr. This frequency interval does not correspond to a term used for the secular motion of Jupiter and Saturn.
For Vesta, the evolutions of the eccentricity, the inclination, and the frequency gV are in Fig. 16 for ![$\mathcal{A}\in\left[-3\textrm{:}3\right]{}^{\prime\prime}/\textrm{yr}$](/articles/aa/full_html/2019/02/aa33342-18/aa33342-18-eq191.png) . For gV ∈ [34.56 : 35.25]′′/yr , there is a resonance with the frequency 2g5 − s6 ≈ 34.86′′∕yr where the maximum eccentricity increases from 0.17 to 0.19 and the maximum inclination from 7.5 to 8.0°. For gV ∈ [38.86 : 39.12]′′/yr, the maximum inclination increases from 7.6 to 7.7°. This area does not correspond to terms used for the secular motion of Jupiter and Saturn. The evolutions of the eccentricity, the inclination, and the frequency sV are in Fig. 17 for
. For gV ∈ [34.56 : 35.25]′′/yr , there is a resonance with the frequency 2g5 − s6 ≈ 34.86′′∕yr where the maximum eccentricity increases from 0.17 to 0.19 and the maximum inclination from 7.5 to 8.0°. For gV ∈ [38.86 : 39.12]′′/yr, the maximum inclination increases from 7.6 to 7.7°. This area does not correspond to terms used for the secular motion of Jupiter and Saturn. The evolutions of the eccentricity, the inclination, and the frequency sV are in Fig. 17 for ![$\mathcal{B}\in\left[-3\textrm{:}3\right]{}^{\prime\prime}/\textrm{yr}$](/articles/aa/full_html/2019/02/aa33342-18/aa33342-18-eq194.png) . For sV∈[−41.71:−41.49]′′/yr, the inclination can increase from 7.3 to 7.4°. This resonance does not match any term used for the secular motion of Jupiter and Saturn.
. For sV∈[−41.71:−41.49]′′/yr, the inclination can increase from 7.3 to 7.4°. This resonance does not match any term used for the secular motion of Jupiter and Saturn.
 |
Fig. 14. Eccentricity (panel a), inclination (panel b), and frequency gC (panel c) with respect to |
 |
Fig. 15. Eccentricity (panel a), inclination (panel b), and frequency sC (panel c) with respect to |
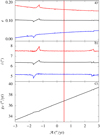 |
Fig. 16. Eccentricity (panel a), inclination (panel b), and frequency gV (panel c) with respect to |
 |
Fig. 17. Eccentricity (panel a), inclination (panel b), and frequency sV (panel c) with respect to |
6. Stability of the rotation axes
In this section, we are interested in the study of the long-term stability of the rotation axis. Like in Laskar et al. (1993a) and Laskar & Robutel (1993), the stability of the rotation axis can be estimated using frequency analysis. We determine the precession frequency f1 on the interval [−20 : 0] Myr and the precession frequency f2 on the interval [−40 : −20] Myr. The quantity σ = |(f1 − f2)∕f1| gives an estimate of the diffusion of the precession frequency (Laskar 1993; Dumas & Laskar 1993). For an integrable system, this quantity must stay null. For a weakly perturbed system, this quantity is small, but increases if the system becomes chaotic.
6.1. Secular solution for the obliquity
We integrate the secular equation (Eq. (21)) with an Adams integrator and a step size of 100 yr. The normal to the orbit n and the eccentricity e are computed from the secular orbital solution obtained from the secular frequency decompositions in Sect. 4.2. We use the initial conditions for the rotation axis of Table 2. The secular solutions for the obliquities are compared to the nonsecular ones for Ceres and Vesta in Fig. 18 for the time interval [−20 : 0] Myr. The secular computation of the obliquity, which is about 1 million times faster, allows us then to reproduce correctly the evolution of the obliquity.
The secular orbital solution has initial conditions different from those of solution La2011 because we have removed the short-period variations in Figs. 4 and 5. This modifies the initial obliquities of Ceres and Vesta of about 0.02° for Ceres and −0.05° for Vesta, and could explain the differences observed in Fig. 18.
We integrate on [−40 : 0] Myr the rotation axis with the symplectic method of the Sect. 2.1 and the secular equation (Eq. (21)). For both integrations, the initial obliquities vary from 0° to 100° with a step of 0.5°. The diffusion of the precession frequency is represented in Fig. 19 with respect to the initial obliquity. For Ceres, the diffusion is quite similar with close amplitude and evolution and the areas with a strong increase in σ allow us to recognize resonances with the orbital frequencies for the two cases. For Vesta, the diffusion σ is higher for the secular solution. However, the areas with high values of the diffusion σ correspond. The secular and nonsecular solutions of the obliquity thus have close stability properties.
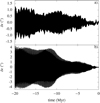 |
Fig. 18. Difference between the solution Ceres2017 and the secular solution for the obliquity of Ceres (a) and of Vesta (b) on [−20 : 0] Myr. |
 |
Fig. 19. Diffusion of the precession frequency with respect to the initial obliquity for the complete solution (in black) and for the secular solution (in red) for Ceres (a) and Vesta (b). |
6.2. Study of the close resonances
We integrate the secular equation (Eq. (21)) on [−40 : 0] Myr for different precession constants in an interval with a step of 0.01′′∕yr to determine the effects of the resonances.
6.2.1. Ceres
The precession frequency, its diffusion, and the variations in the obliquity are represented for Ceres in Fig. 20 with respect to the precession constant in the interval [0.01 : 12]′′/yr. We observe areas with strong variations in the diffusion, specified in Table 7, which correspond to resonances with orbital frequencies. Most of these frequencies are already present in the frequency decompositions of the variables z and ζ used for the construction of the secular solution. The quantities n and e, which appear in the secular equation (Eq. (21)) and which are used to obtain the angular momentum w, are computed from the secular solution of the variables z and ζ, and can include additional frequencies. To identify the remaining frequencies in Table 7, we then perform a frequency analysis of the quantities nx + iny and (nx + iny)/(1 − e2)3/2, where nx and ny are the coordinates in the invariant frame of the component parallel to the invariable plane of the normal to the orbit n. We find no trace of the remaining frequencies in the first 4000 terms of the frequency analysis of nx + iny. In the first 4000 terms of the frequency analysis of (nx + iny)/(1 − e2)3/2, we find the missing frequencies of the areas identified in Table 7. The variations in the eccentricity are then responsible for the apparition of additional secular resonances between the orbital and the rotational motions.
We note in particular the appearance of the resonance with the frequency sC + 2(gC − g6) + (g5 − g7) ≈−6.07′′∕yr, which is included in the interval of uncertainty of the precession constant. Therefore, Ceres could be in resonance with this frequency. However, this effect on the obliquity is very limited. In the vicinity of the interval of uncertainty, we observe a narrow area with a small decrease up to 1° of the minimum obliquity because of the resonance with the frequency sC + (3gC − 4g6 + g7) ≈−6.39′′∕yr. More distant resonances have stronger effects on the obliquity of Ceres. The resonance with the frequency sC + (gC − g5) ≈−9.26′′∕yr causes variations in the obliquity in the interval between 0° and almost 40° and that with s7 ≈−2.99′′∕yr variations between 0° and almost 30°. Ceres is closer to a less important resonance with sC + 2(gC − g6) ≈−7.24′′∕yr, where there are variations inthe obliquity between 0° and 26°. However Ceres should have a precession constant between about 7.15 and 7.85′′∕yr to be inside this resonance.
In Fig. 20, we see the diffusion for the precession constants computed with a rotation rate that is 7% higher (Mao & McKinnon 2018), as discussed in Sect. 3.2.4. If the early Ceres were in hydrostatic equilibrium, as supposed by Mao & McKinnon (2018), it could be in resonance with the frequencies s1 ≈−5.61′′∕yr, sC + 2(gC − g6) + (g5 − g7) ≈−6.07′′∕yr and sC + (3gC − 4g6 + g7) ≈−6.39′′∕yr, which have weak effects on the obliquity as seen in Fig. 20 and the amplitudes of the oscillations of the obliquity would be similar. The events or phenomena, which would have changed its rotation rate, would not have significantly changed the interval of variation in the obliquity.
As discussed in Sect. 3.2.4, if the early Ceres were in hydrosatic equilibrium and the shape and the internal structure had not changed as supposed by Mao & McKinnon (2018), the present Ceres would have a precession constant in the interval [6.58 : 6.98]′′/yr for a normalized polar moment of inertia of 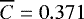 . With these precession constants, Ceres could be in resonance with the frequency sC + (3gC − 4g6 + g7) ≈ −6.39′′∕yr (Table 7) with no significant changes in the obliquity.
. With these precession constants, Ceres could be in resonance with the frequency sC + (3gC − 4g6 + g7) ≈ −6.39′′∕yr (Table 7) with no significant changes in the obliquity.
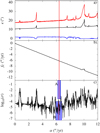 |
Fig. 20. Obliquity (panel a), precession frequency (panel b), and diffusion of the precession frequency (panel c) for Ceres on [−40 : 0] Myr with respect to the precession constant. In panel a the maximum, mean, and minimum obliquities are, respectively, in red, black, and blue. In panel c, the rectangle A represents the precession constants for |
6.2.2. Vesta
The precession frequency, its diffusion, and the variations in the obliquity are represented for Vesta in Fig. 21 with respect to the precession constant in the interval [10 : 22]′′/yr. The frequencies of the resonances are in Table 8. We identify the frequencies 2s6 − sV ≈−13.09′′∕yr, sV − g5 + g6 ≈−15.62′′∕yr, and − 17.74′′∕yr, which are among the frequencies of the secular model. As for Ceres, we perform a frequency analysis of the quantities nx + iny and (nx + iny)/(1 − e2)3/2 to identify the remaining frequencies. We do not find them in the frequency analysis of nx + iny, but in the frequency analysis of (nx + iny)/(1 − e2)3/2 we find the frequencies − 9.09′′∕yr, s7 − (gV − g6) ≈−11.65′′∕yr, sV + (g6 − g7) ≈−14.46′′∕yr, which can correspond to the areas identified in Table 8. As for Ceres, the variations of the eccentricity are responsible for the appearance of some resonances. The interval of frequency [−11.16 : −10.93]′′/yr in Table 8 does not correspond to any term of the frequency analysis.
The resonance which has the most important effect in the vicinity of Vesta is that with the frequency −17.74′′∕yr. If the maximum obliquity increases by about 3°, the minimum obliquity decreases by about 10°. The domain of the resonance with the frequency 2s6 − sV ≈ −13.09′′∕yr is included in the uncertainty interval for the precession constant. We have observed in Sect. 4.3 that for the value 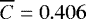 of the normalized polar moment of inertia, the minimum obliquity decreases compared to the evolution of the obliquity for the other normalized polar moments of inertia. We can see here that it is an effect of the resonance with the frequency 2s6 − sV. In this resonance, the minimum obliquity can decrease to 17.6° and the maximum obliquity can increase to 47.7°.
of the normalized polar moment of inertia, the minimum obliquity decreases compared to the evolution of the obliquity for the other normalized polar moments of inertia. We can see here that it is an effect of the resonance with the frequency 2s6 − sV. In this resonance, the minimum obliquity can decrease to 17.6° and the maximum obliquity can increase to 47.7°.
In Fig. 21, we observe the diffusion for the precession constants computed with the paleorotation rate of the early Vesta determined by Fu et al. (2014) and the physical parameters discussed in Sect. 3.3.4. The two giant impacts could then have put Vesta closer to the resonance with the frequency 2s6 − sV, which involves the crossing of two small resonances and could also have slightly increased the interval of variation of the obliquity.
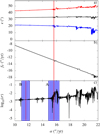 |
Fig. 21. Obliquity (panel a), precession frequency (panel b), and diffusion of the precession frequency (panel c) for Vesta on [−40 : 0] Myr with respect to the precession constant. In panel a the maximum, mean, and minimum obliquities are, respectively, in red, black, and blue. In panel c the rectangle A represents the precession constants for |
6.3. Global stability of the rotation axis
As in Laskar et al. (1993a) and in Laskar & Robutel (1993), we look for the long-term stability of the rotation axis. We integrate the rotation axis on [−40 : 0] Myr with the secular equation (Eq. (21)) on a grid of 24120 points for initial obliquities from 0° to 100° with a step of 0.5° and for precession constants from 0.5 to 60′′∕yr with a step of 0.5′′∕yr.
The precession frequency corresponds in the frequency analysis to the frequency with the largest amplitude. However, in the case of an important resonance, the frequency with the largest amplitude can correspond to the resonance frequency. We also consider as precession frequency the one with the largest amplitude, for which the difference with the frequencies s and s6 is larger than 5 × 10−3′′/yr.
6.3.1. Ceres
In Fig. 22, we see the value of the quantity log10 (σ), the maximum amplitude of the obliquity on [−40 : 0] Myr, which corresponds to the difference between the minimum and maximum obliquities on [−40 : 0] Myr and the precession frequency of Ceres obtained by frequency analysis on [−20 : 0] Myr. The position of Ceres for the epoch J2000 is indicated with a white circle.
Ceres is in a quite stable zone and is far from the most chaotic zones, which correspond to the resonance with the frequencies sC, s6 and sC + (gC − g6). The motion of its rotation axis is relatively stable although Ceres has a precession frequency fC = − 6.1588 ′ ′ ∕yr (Table B.3) close to the node precession frequencies of the inner planets, Mercury s1 = − 5.61′ ′ ∕yr and Venus s2 = − 7.06′′ ∕yr (Table 5). The secular orbital motion of Ceres is almost entirely determined by the planetary perturbations of Jupiter and Saturn (Sect. 5.2), and the amplitudes of frequencies of the inner planets are small in the motion of the ascending node of Ceres. Therefore, the width of these resonances is small and they do not overlap, contrary to the case of the inner planets (Laskar & Robutel 1993).
The resonances with the frequencies s7 and s8 have more important effects than those with the inner planets. These resonances can increase the amplitude of the obliquity of several degrees. With the present precession constant, we see that the resonance with s7 can affect the rotation axis of Ceres only if Ceres has an initial obliquity of about 70° and the resonance with s8 can affect Ceres if the initial obliquity is about 90°. The resonance with the frequency s6 has large amplitudes of the obliquity, but does not correspond to that of the most chaotic zone except when it overlaps with the resonance at the frequency sC+(gC−g6). As for the case of the planets, as noted by Laskar & Robutel (1993), the resonance with the frequency s6 is isolated.
The most important nearby resonance is with the frequency sC+(gC − g5) ≈ − 9.24 ′ ′/yr, which has asignificant effect on the amplitude of the obliquity. For an initial obliquity between 0° and 10°, the amplitude of the obliquity passes from about 20° to 40°. However, this resonance has a limited width of about 1′′∕yr and it has no influence on Ceres.
 |
Fig. 22. Stability of the rotation axis (panels a and d), amplitude of the obliquity on [−40 : 0] Myr (panels b and e), precession frequency on [−20 : 0] Myr (panels c and f), respectively, for Ceres and Vesta with respect to the initial obliquity and the precession constant for a grid of 24120 points. The white circles represent Ceres and Vesta for the epoch J2000. The color scale of the diffusion is represented on [−6 : −1], although log10 (σ) takes values outside this interval. Panels a and d: red points correspond to log10 (σ) ≥ −1 and black points to log10(σ) ≤ −6. Panels d–f: white squares represent Vesta before the two giant impacts. |
6.3.2. Vesta
The diffusion log10 (σ), the maximum amplitude of the obliquity, and the precession frequency are represented for Vesta in Fig. 22. Vesta for the epoch J2000 is indicated with a white circle.
Vesta is at the boundary of a relatively stable region. Vesta is far from the chaotic zone created by the resonances with the frequencies sV and s6 and is close to the resonance with the orbital frequency 2s6 − sV. The most important resonance in the vicinity is the one with the frequency − 17.74′′∕yr, which could correspond to the frequency s4. In this resonance, the amplitude of the obliquity passes about from 30° to 40°. Because of this limited width, it has no influence on Vesta. The effect of the resonances with the frequencies s7 and s8 are less important than for Ceres. The resonance with s7 increases the amplitude of the obliquity only by a few degrees. As for Ceres, the resonance with the frequency sV+(gV−g5)≈−6.97′′/yr still has an important effect on the amplitude of the obliquity, which increases from about 20° to 30° in the resonance.
Like Ceres, Vesta has a precession frequency fV = −12.882′′∕yr (Table B.3) close to the node precession frequencies of the inner planets, the Earth s3 = −18.848′′∕yr, and Mars s4 = −17.751′′∕yr (Table 5), but their perturbations on the orbit of Vesta are too weak to have significant consequences on the stability of the rotation axis for the present Vesta.
The early Vesta is represented in Fig. 22 by a white square for the precession constant computed from the supposed rotational parameters before the two giant impacts. The early Vesta would also be in a more stable region. As seen in Sect. 6.2.2, the two giant impacts could have put Vesta closer to the resonance with the orbital frequency 2s6 − sV.
7. Conclusion
We applied the method of Farago et al. (2009) to realize a symplectic integration of the rotation axes only averaged over the fast proper rotation. The obliquity variations of Ceres have been obtained between 2° and 20° for the last 20 Myr in agreement with the results of Bills & Scott (2017) and Ermakov et al. (2017b). If we use for Ceres the value of the normalized polar moment of inertia 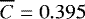 (Eq. (18)), which takes into account the nonspherical form of Ceres, we obtain obliquity variations in the same interval and the frequency precession decreases in absolute value of about 0.5% with respect to the value obtained for
(Eq. (18)), which takes into account the nonspherical form of Ceres, we obtain obliquity variations in the same interval and the frequency precession decreases in absolute value of about 0.5% with respect to the value obtained for 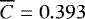 . For Vesta, the obliquity variations are between 21° and 45° for the last 20 Myr. As noted by Skoglöv et al. (1996), these large variations in the obliquity are due to the significant inclinations of Ceres and Vesta with respect to the invariable plane.
. For Vesta, the obliquity variations are between 21° and 45° for the last 20 Myr. As noted by Skoglöv et al. (1996), these large variations in the obliquity are due to the significant inclinations of Ceres and Vesta with respect to the invariable plane.
The secular orbital model in Sect. 5 has allowed us to show that the chaotic diffusion of the secular frequency gC of Ceres does not seem sufficiently important to put Ceres in a secular orbital resonance with the frequencies 2g6 − g5 and 2g6 − g7. For Vesta, the chaotic diffusion of the secular frequencies is more important especially for sV. This model has also allowed us to show that a secular model of Ceres and Vesta only perturbed by Jupiter and Saturn could entirely reproduce their secular orbital motions. The secular orbital dynamics of Ceres and Vesta is then dominated by the perturbations of Jupiter and Saturn, as noted by Skoglöv et al. (1996) for Ceres and Vesta and confirmed by Ermakov et al. (2017b) for Ceres.
Ceres and Vesta have precession frequencies close to the secular orbital frequencies of the terrestrial planets, as is the case for Mars. The precession frequency of Ceres is close to secular orbital frequencies of Mercury and Venus and that of Vesta to secular orbital frequencies of the Earth and Mars. However, their long-term rotations are relatively stable. They are in an orbital region where the perturbations of Jupiter and Saturn dominate the secular orbital dynamics and the perturbations of the inner planets are relatively weak. The secular resonances with the inner planets have smaller widths and do not overlap, contrary to the case of the inner planets.
This is an illustration that the stability of the long-term rotation depends strongly on the orbital motion. For Ceres and Vesta, there is a chaotic zonewith large oscillations of the obliquity as for the inner planets, but it is caused by the overlapping of resonances due to their proper secular frequencies with other resonances due to the perturbations of Jupiter and Saturn. We also note for Ceres and Vesta that the evolution of the eccentricity is responsible for the appearance of secular resonances for the spin axis. However, their effects on the obliquity and the stability are modest.
The twogiant impacts suffered by Vesta modified the precession constant and could have put Vesta closer to the resonance with the orbital frequency 2s6 − sV. Given the uncertainty on the polar moment of inertia, the present Vesta could be in resonance with the frequency 2s6 − sV, where the obliquity can decreaseto about 17° and increaseto about 48°.
Acknowledgements
T.V. thanks Nathan Hara for the fruitful discussions and references about the random walk on a sphere. The authors thank Anton Ermakov for the useful comments on this work.
Appendix A: Passage from the invariable plane frame to the ICRF
We consider a vector x in the frameassociated with the invariable plane. The coordinates in the ICRF become
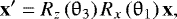 (A.1)
(A.1)
with Rx the rotation of axis (1, 0, 0) and Rz the rotation of axis (0, 0, 1). The angles θ1 and θ3 are given by
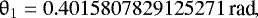 (A.2)
(A.2)
being about θ1 ≈ 23.01° and
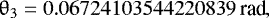 (A.3)
(A.3)
being about θ3 ≈ 3.85°.
Appendix B: Frequency decompositions
First 50 terms of the frequency decomposition 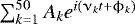 of z (a) and ζ (b) for Ceres on [−25 : 5] Myr.
of z (a) and ζ (b) for Ceres on [−25 : 5] Myr.
First 50 terms of the frequency decomposition 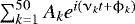 of z (a) and ζ (b) for Vesta on [−25 : 5] Myr.
of z (a) and ζ (b) for Vesta on [−25 : 5] Myr.
First 50 terms of the frequency decomposition 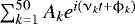 of wx +iwy for Ceres on [−20 : 0]Myr.
of wx +iwy for Ceres on [−20 : 0]Myr.
First 50 terms of the frequency decomposition 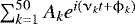 of wx +iwy for Vesta on [−20 : 0] Myr.
of wx +iwy for Vesta on [−20 : 0] Myr.
References
- Bills, B. G., & Nimmo, F. 2011, Icarus, 213, 496 [NASA ADS] [CrossRef] [Google Scholar]
- Bills, B. G., & Scott, B. R. 2017, Icarus, 284, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Boué, G., & Laskar, J. 2006, Icarus, 185, 312 [NASA ADS] [CrossRef] [Google Scholar]
- Colombo, G. 1966, AJ, 71, 891 [NASA ADS] [CrossRef] [Google Scholar]
- DeMario, B. E., Schmidt, B. E., Mutchler, M. J., et al. 2016, Icarus, 280, 308 [NASA ADS] [CrossRef] [Google Scholar]
- Dumas, H. S., & Laskar, J. 1993, Phys. Rev. Lett., 70, 2975 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Ermakov, A. I., Zuber, M. T., Smith, D. E., et al. 2014, Icarus, 240, 146 [NASA ADS] [CrossRef] [Google Scholar]
- Ermakov, A. I., Fu, R. R., Castillo-Rogez, J. C., et al. 2017a, J. Geophys. Res., 122, 2267 [Google Scholar]
- Ermakov, A. I., Mazarico, E., Schröder, S., et al. 2017b, Geophys. Res. Lett., 44, 2652 [NASA ADS] [CrossRef] [Google Scholar]
- Farago, F., Laskar, J., & Couetdic, J. 2009, Celest. Mech. Dyn. Astron., 104, 291 [NASA ADS] [CrossRef] [Google Scholar]
- Farrés, A., Laskar, J., Blanes, S., et al. 2013, Celest. Mech. Dyn. Astron., 116, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Fu, R. R., Hager, B. H., Ermakov, A. I., & Zuber, M. T. 2014, Icarus, 240, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Gaskell, R. W. 2012, AAS/Division for Planetary Sciences Meeting Abstracts, 44, 209 [Google Scholar]
- Kinoshita, H. 1977, Celest. Mech., 15, 277 [Google Scholar]
- Konopliv, A. S., Yoder, C. F., Standish, E. M., Yuan, D.-N., & Sjogren, W. L. 2006, Icarus, 182, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Konopliv, A. S., Asmar, S. W., Park, R. S., et al. 2014, Icarus, 240, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Konopliv, A. S., Park, R. S., Vaughan, A. T., et al. 2018, Icarus, 299, 411 [NASA ADS] [CrossRef] [Google Scholar]
- Laskar, J. 1986, A&A, 157, 59 [NASA ADS] [Google Scholar]
- Laskar, J. 1988, A&A, 198, 341 [NASA ADS] [Google Scholar]
- Laskar, J. 1990, Icarus, 88, 266 [NASA ADS] [CrossRef] [Google Scholar]
- Laskar, J. 1993, Physica D, 67, 257 [Google Scholar]
- Laskar, J. 2003, ArXiv Mathematics e-prints [math/0305364] [Google Scholar]
- Laskar, J., & Robutel, P. 1993, Nature, 361, 608 [NASA ADS] [CrossRef] [Google Scholar]
- Laskar, J., Froeschlé, C., & Celletti, A. 1992, Physica D, 56, 253 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Laskar, J., Joutel, F., & Robutel, P. 1993a, Nature, 361, 615 [Google Scholar]
- Laskar, J., Joutel, F., & Boudin, F. 1993b, A&A, 270, 522 [NASA ADS] [Google Scholar]
- Laskar, J., & Robutel, P. 1995, Celest. Mech. Dyn. Astron., 62, 193 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Laskar, J., & Robutel, P. 2001, Celest. Mech. Dyn. Astron., 80, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Laskar, J., Correia, A., Gastineau, M., et al. 2004a, Icarus, 170, 343 [NASA ADS] [CrossRef] [Google Scholar]
- Laskar, J., Robutel, P., Joutel, F., et al. 2004b, A&A, 428, 261 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Laskar, J., Fienga, A., Gastineau, M., & Manche, H. 2011a, A&A, 532, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Laskar, J., Gastineau, M., Delisle, J.-B., Farrés, A., & Fienga, A. 2011b, A&A, 532, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lee, M. H., Peale, S., Pfahl, E., & Ward, W. R. 2007, Icarus, 190, 103 [NASA ADS] [CrossRef] [Google Scholar]
- MacDonald, G. J. 1964, Rev. Geophys., 2, 467 [NASA ADS] [CrossRef] [Google Scholar]
- Mao, X., & McKinnon, W. B. 2018, Icarus, 299, 430 [NASA ADS] [CrossRef] [Google Scholar]
- Marchi, S., McSween, H. Y., O’Brien, D. P., et al. 2012, Science, 336, 690 [NASA ADS] [CrossRef] [Google Scholar]
- McFadden, L. A., Bastien, F. A., Mutchler, M., et al. 2012, Icarus 220, 305 [NASA ADS] [CrossRef] [Google Scholar]
- McFadden, L. A., Skillman, D. R., Memarsadeghi, N., et al. 2015, Icarus, 257, 207 [NASA ADS] [CrossRef] [Google Scholar]
- Mignard, F. 1979, Moon Planets, 20, 301 [NASA ADS] [CrossRef] [Google Scholar]
- Park, R. S., Konopliv, A. S., Asmar, S. W., et al. 2014, Icarus, 240, 118 [NASA ADS] [CrossRef] [Google Scholar]
- Park, R. S., Konopliv, A. S., Bills, B. G., et al. 2016, Nature, 537, 515 [NASA ADS] [CrossRef] [Google Scholar]
- Perrin, F. 1928, Ann. Sci. Ec. Norm. Sup. Troisième Série, 45, 1 [Google Scholar]
- Platz, T., Nathues, A., Schorghofer, N., et al. 2016, Nat. Astron., 1, 0007 [CrossRef] [Google Scholar]
- Prettyman, T. H., Yamashita, N., Toplis, M. J., et al. 2017, Science, 355, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Rambaux, N. 2013, A&A, 556, A151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rambaux, N., Castillo-Rogez, J., Dehant, V., & Kuchynka, P. 2011, A&A, 535, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rambaux, N., Chambat, F., & Castillo-Rogez, J. C. 2015, A&A, 584, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roberts, P. H., & Ursell, H. D. 1960, Philos. Trans. R. Soc. Lond. A Math. Phys. Eng. Sci., 252, 317 [NASA ADS] [CrossRef] [Google Scholar]
- Russell, C. T., Raymond, C. A., Coradini, A., et al. 2012, Science, 336, 684 [NASA ADS] [CrossRef] [Google Scholar]
- Russell, C. T., Raymond, C. A., Ammannito, E., et al. 2016, Science, 353, 1008 [NASA ADS] [CrossRef] [Google Scholar]
- Schenk, P., O’Brien, D. P., Marchi, S., et al. 2012, Science, 336, 694 [NASA ADS] [CrossRef] [Google Scholar]
- Schmidt, B. E., Hughson, K. H. G., Chilton, H. T., et al. 2017, Nat. Geosci., 10, 338 [NASA ADS] [CrossRef] [Google Scholar]
- Schorghofer, N. 2008, ApJ, 682, 697 [NASA ADS] [CrossRef] [Google Scholar]
- Schorghofer, N. 2016, Icarus, 276, 88 [NASA ADS] [CrossRef] [Google Scholar]
- Skoglöv, E., Magnusson, P., & Dahlgren, M. 1996, Planet. Space Sci., 44, 1177 [NASA ADS] [CrossRef] [Google Scholar]
- Suzuki, M. 1990, Phys. Lett. A, 146, 319 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Touma, J., & Wisdom, J. 1994, AJ, 107, 1189 [NASA ADS] [CrossRef] [Google Scholar]
- Wisdom, J., & Holman, M. 1991, AJ, 102, 1528 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Densities and semi-principal axes for different models of internal structure of Vesta.
Right ascension (RA) and declination (Dec) of Ceres (Park et al. 2016) and Vesta (Konopliv et al. 2014) at the epoch J2000 in the ICRF frame.
Radii R used by Laskar et al. (2011b) to compute the collision probabilities Nc between Ceres and Vesta and some bodies.
Principal secular frequencies of the solution La2011 gi, si determined on [−20 : 0] Myr for the four inner planets and on [−50 : 0] Myr for the four giant planets and Pluto.
Physical characteristics of Ceres and Vesta used for the computation of the long-term rotation.
First 50 terms of the frequency decomposition 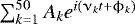 of z (a) and ζ (b) for Ceres on [−25 : 5] Myr.
of z (a) and ζ (b) for Ceres on [−25 : 5] Myr.
First 50 terms of the frequency decomposition 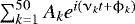 of z (a) and ζ (b) for Vesta on [−25 : 5] Myr.
of z (a) and ζ (b) for Vesta on [−25 : 5] Myr.
First 50 terms of the frequency decomposition 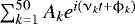 of wx +iwy for Ceres on [−20 : 0]Myr.
of wx +iwy for Ceres on [−20 : 0]Myr.
First 50 terms of the frequency decomposition 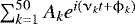 of wx +iwy for Vesta on [−20 : 0] Myr.
of wx +iwy for Vesta on [−20 : 0] Myr.
All Figures
 |
Fig. 1. Normalized mean moment of inertia |
| In the text | |
 |
Fig. 2. Eccentricity (panel a) and inclination (panel b) of Ceres for the solution La2011. |
| In the text | |
 |
Fig. 3. Eccentricity (panel a) and inclination (panel b) of Vesta for the solution La2011. |
| In the text | |
 |
Fig. 4. Difference for Ceres in eccentricity (panel a) and inclination (panel b) between the solution La2011 and the secular solution. |
| In the text | |
 |
Fig. 5. Difference for Vesta in eccentricity (panel a) and inclination (panel b) between the solution La2011 and the secular solution. |
| In the text | |
 |
Fig. 6. Secular frequencies gC (panel a) and sC (panel b) of Ceres on [−250 : 250] Myr computed with a step of 5 Myr with the frequency map analysis on an interval of 30 Myr. The error bars are given by the precision of the frequency map analysis. |
| In the text | |
 |
Fig. 7. Secular frequencies gV (panel a) and sV (panel b) of Vesta on [−250 : 250] Myr, computed with a step of 5 Myr with the frequency map analysis on an interval of 30 Myr. The error bars are given by the precision of the frequency map analysis. |
| In the text | |
 |
Fig. 8. Obliquity of Ceres on [−100 : 0] kyr(panel a), [−1 : 0] Myr (panel b), and [−20 : 0] Myr (panel c). In panel a the obliquity caused only by the change in orientation of the orbit is represented by the red curve. |
| In the text | |
 |
Fig. 9. Obliquity of Vesta on [−100 : 0] kyr (panel a), [−1 : 0] Myr (panel b), and [−20 : 0] Myr (panel c). Inpanel a the obliquity caused only by the change in orientation of the orbit is represented by the red curve. |
| In the text | |
 |
Fig. 10. Maximum, mean, and minimum obliquities, respectively, in red, black, and blue for Ceres on [−20 : 0] Myr with respectto the normalized polar moment of inertia. |
| In the text | |
 |
Fig. 11. Maximum, mean, and minimum obliquities, respectively, in red, black, and blue for Vesta on [−20 : 0] Myr with respectto the normalized polar moment of inertia. |
| In the text | |
 |
Fig. 12. Difference in eccentricity (panel a) and inclination (panel b) for Ceres between the solution La2011 and the Hamiltoniansecular model with adjustment of the frequencies in black, and without in red. |
| In the text | |
 |
Fig. 13. Difference in eccentricity (panel a) and inclination (panel b) for Vesta between the solution La2011 and the Hamiltoniansecular model with adjustment of the frequencies in black, and without in red. |
| In the text | |
 |
Fig. 14. Eccentricity (panel a), inclination (panel b), and frequency gC (panel c) with respect to |
| In the text | |
 |
Fig. 15. Eccentricity (panel a), inclination (panel b), and frequency sC (panel c) with respect to |
| In the text | |
 |
Fig. 16. Eccentricity (panel a), inclination (panel b), and frequency gV (panel c) with respect to |
| In the text | |
 |
Fig. 17. Eccentricity (panel a), inclination (panel b), and frequency sV (panel c) with respect to |
| In the text | |
 |
Fig. 18. Difference between the solution Ceres2017 and the secular solution for the obliquity of Ceres (a) and of Vesta (b) on [−20 : 0] Myr. |
| In the text | |
 |
Fig. 19. Diffusion of the precession frequency with respect to the initial obliquity for the complete solution (in black) and for the secular solution (in red) for Ceres (a) and Vesta (b). |
| In the text | |
 |
Fig. 20. Obliquity (panel a), precession frequency (panel b), and diffusion of the precession frequency (panel c) for Ceres on [−40 : 0] Myr with respect to the precession constant. In panel a the maximum, mean, and minimum obliquities are, respectively, in red, black, and blue. In panel c, the rectangle A represents the precession constants for |
| In the text | |
 |
Fig. 21. Obliquity (panel a), precession frequency (panel b), and diffusion of the precession frequency (panel c) for Vesta on [−40 : 0] Myr with respect to the precession constant. In panel a the maximum, mean, and minimum obliquities are, respectively, in red, black, and blue. In panel c the rectangle A represents the precession constants for |
| In the text | |
 |
Fig. 22. Stability of the rotation axis (panels a and d), amplitude of the obliquity on [−40 : 0] Myr (panels b and e), precession frequency on [−20 : 0] Myr (panels c and f), respectively, for Ceres and Vesta with respect to the initial obliquity and the precession constant for a grid of 24120 points. The white circles represent Ceres and Vesta for the epoch J2000. The color scale of the diffusion is represented on [−6 : −1], although log10 (σ) takes values outside this interval. Panels a and d: red points correspond to log10 (σ) ≥ −1 and black points to log10(σ) ≤ −6. Panels d–f: white squares represent Vesta before the two giant impacts. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![\begin{align}\mathcal{H}_{I,0}&=\left\langle H_{I,0} \right\rangle_{g,l}=-\frac{\mathcal{C}_{1}m_{0}}{r_{1}^{3}}\left(1-3\left(\frac{\textbf{r}_{1}.\textbf{w}}{r_{1}}\right)^{2}\right),\\[3pt] \mathcal{H}_{I,k}&=\left\langle H_{I,k} \right\rangle_{g,l}=-\frac{\mathcal{C}_{1}m_{k}}{r_{1,k}^{3}}\left(1-3\left(\frac{\textbf{r}_{1,k}.\textbf{w}}{r_{1,k}}\right)^{2}\right),\end{align}](/articles/aa/full_html/2019/02/aa33342-18/aa33342-18-eq8.png)
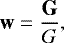
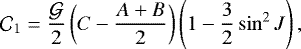
![\begin{equation*} \left\{ \begin{array}{@{}l@{\hskip3pt}l@{\hskip3pt}l} \tilde{\textbf{r}}_{1}\left(t\right)&=&\tilde{\textbf{r}}_{1}\left(0\right)-\frac{3\mathcal{C}_{1}m_{k}}{r_{1,k}^{5}}\left(\left(1-3\left(\frac{\textbf{r}_{1,k}.\textbf{w}}{r_{1,k}}\right)^{2}\right)t\textbf{r}_{1,k} \right. \\[4pt] &&\!\left.+\,\frac{2\textbf{r}_{1,k}.\textbf{w}}{\Omega_{k} r_{1,k}}\left(\textbf{w}\left(t\right)-\textbf{w}\left(0\right)\right)\times\textbf{r}_{1,k}\right), \\[4pt] \tilde{\textbf{r}}_{k}\left(t\right) &= & \tilde{\textbf{r}}_{k}\left(0\right)+\frac{3\mathcal{C}_{1}m_{k}}{r_{1,k}^{5}}\left(\left(1-3\left(\frac{\textbf{r}_{1,k}.\textbf{w}}{r_{1,k}}\right)^{2}\right)t\textbf{r}_{1,k} \right. \\[4pt] &&\!\left.+\,\frac{2\textbf{r}_{1,k}.\textbf{w}}{\mathrm\Omega_{k} r_{1,k}}\left(\textbf{w}\left(t\right)-\textbf{w}\left(0\right)\right)\times\textbf{r}_{1,k}\right), \\[4pt] \textbf{w}\left(t\right) &=& R_{\textbf{r}_{1,k}}\left(\mathrm\Omega_{k}t\right)\textbf{w}\left(0\right), \end{array}\right. \end{equation*}](/articles/aa/full_html/2019/02/aa33342-18/aa33342-18-eq25.png)
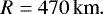

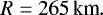
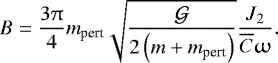
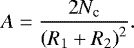
![$\overline{C}\in[0.380:0.406]$](/articles/aa/full_html/2019/02/aa33342-18/aa33342-18-eq248.png)
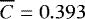
![$\overline{C}\in[0.390:0.430]$](/articles/aa/full_html/2019/02/aa33342-18/aa33342-18-eq252.png)