| Issue |
A&A
Volume 621, January 2019
|
|
|---|---|---|
| Article Number | A75 | |
| Number of page(s) | 21 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201833380 | |
| Published online | 10 January 2019 | |
Formation of cometary O2 ice and related ice species on grain surfaces in the midplane of the pre-solar nebula
1
Leiden Observatory, Leiden University,
PO Box 9513,
2300 RA Leiden,
The Netherlands
e-mail: eistrup@strw.leidenuniv.nl
2
School of Physics and Astronomy, University of Leeds,
Leeds LS2 9JT,
UK
e-mail: c.walsh1@leeds.ac.uk
Received:
7
May
2018
Accepted:
20
July
2018
Context. Detection of abundant O2 at 1–10% relative to H2O ice in the comae of comets 1P/Halley and 67P/Churyumov-Gerasimenko has motivated attempts to explain the origin of the high O2 ice abundance. Recent chemical modelling of the outer, colder regions of a protoplanetary disk midplane has shown production of O2 ice at the same abundance as that measured in the comet.
Aims. We aim to carry out a thorough investigation to constrain the conditions under which O2 ice could have been produced through kinetic chemistry in the pre-solar nebula midplane.
Methods. We have utilised an updated chemical kinetics code to evolve chemistry under pre-solar nebula midplane conditions. Four different chemical starting conditions and the effects of various chemical parameters have been tested.
Results. Using the fiducial network, and for either reset conditions (atomic initial abundances) or atomic oxygen only conditions, the abundance level of O2 ice measured in the comets can be reproduced at an intermediate time, after 0.1–2 Myr of evolution, depending on ionisation level. When including O3 chemistry, the abundance of O2 ice is much lower than the cometary abundance (by several orders of magnitude). We find that H2O2 and O3 ices are abundantly produced (at around the level of O2 ice) in disagreement with their respective abundances or upper limits from observations of comet 67P. Upon closer investigation of the parameter space, and varying parameters for grain–surface chemistry, it is found that for temperatures 15–25 K, densities of 109−1010 cm−3, and a barrier for quantum tunnelling set to 2 Å, the measured level of O2 ice can be reproduced with the new chemical network, including an updated binding energy for atomic oxygen (1660 K). However, the abundances of H2O2 and O3 ices still disagree with the observations. A larger activation energy for the O + O2 → O3 reaction (Eact > 1000 K) helps to reproduce the non-detection of O3 ice in the comet, as well as reproducing the observed abundances of H2O2 and O2 ices. The only other case in which the O2 ice matches the observed abundance, and O3 and H2O2 ice are lower, is the case when starting with an appreciable amount of oxygen locked in O2.
Conclusions. The parameter space investigation revealed a sweet spot for production of O2 ice at an abundance matching those in 67P and 1P, and O3 and H2O2 ice abundances matching those in 67P. This means that there is a radial region in the pre-solar nebula from 120–150 AU, within which O2 could have been produced in situ via ice chemistry on grain surfaces. However, it is apparent that there is a high degree of sensitivity of the chemistry to the assumed chemical parameters (e.g. binding energy, activation barrier width, and quantum tunnelling barrier). Hence, because the more likely scenario starting with a percentage of elemental oxygen locked in O2 also reproduces the O2 ice abundance in 67P at early stages, this supports previous suggestions that the cometary O2 ice could have a primordial origin.
Key words: molecular processes / methods: numerical / comets: general / comets: individual: 1P/Halley / comets: individual: 67P/Churyumov-Gerasimenko / protoplanetary disks
© ESO 2019
1 Introduction
The detection of abundant molecular oxygen at 1-10% (average 3.8 ± 0.85%) relative to H2O ice in the coma of comet 67P/Churyumov-Gerasimenko (hereinafter 67P: Bieler et al. 2015) came as a surprise, as it was the first detection of O2 in a comet. This was not expected because O2 ice has been found to be efficiently converted to H2O ice in laboratory studies under interstellar conditions (e.g. Ioppolo et al. 2008). Subsequent to this detection, a re-analysis of Comet 1P/Halley data from the Giotto mission (Rubin et al. 2015) indicates a similar O2/H2O ice ratio (3.8 ± 1.7%), suggesting that indeed O2 ice may be a common ice species in solar system comets. These detections have thus prompted speculation as to the chemical origin of the O2 ice. Taquet et al. (2016) modelled the chemical evolution of material from the pre-stellar core stage to the midplane of the formed protoplanetary disk, and found that O2 ice can be produced at the early stages and survive the transport to the disk midplane. Mousis et al. (2016) found that if O2 ice is formed from radiolysis of H2O ice through the reaction 2iH2O 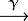 2iH2 + iO2 (where “i” denotes a molecule in the ice form), then this likely did not happen during the pre-solar nebula (PSN) disk phase, but rather in the parent cloud, thus supporting the findings of Taquet et al. (2016). Dulieu et al. (2017) performed laboratory experiments to investigate if dismutation of H2O2 ice (2iH2O2 → 2iH2O + iO2) on the cometary surface could be the origin of the O2 detection. However, this explanation requires a high initial abundance of H2O2 ice relative to H2O ice (twice the detected abundance of O2, or ~ 7%), and a high efficiency for the conversion of H2O2 to O2 in order to match the low detected level of H2O2 relative to O2Of ~ 6 × 10−4. O3 ice, a molecule chemically related to O2, H2O2 and H2O, was not detected in the coma of comet 67P, and has an upper limit of 10−6 with respect to H2O ice. We note here that molecular oxygen is also produced when CO2 ice is exposed to far-UV radiation (see, e.g., Martín-Doménech et al. 2015). However, although this may be a viable chemical route to O2 ice, it does not explain the strong association between the production rates for H2O and O2 seen for comet 67P (Bieler et al. 2015). On the other hand, experiments investigating chemistry in CO2 ice irradiated with 5 keV ions (H+ and He+) and electrons (Ennis et al. 2011; Jones et al. 2014) favour the production of ozone (O3) over molecular oxygen (O2). These experiments mimic the conditions that ices are exposed to in the outer solar system, and upon cosmic ray impact.
2iH2 + iO2 (where “i” denotes a molecule in the ice form), then this likely did not happen during the pre-solar nebula (PSN) disk phase, but rather in the parent cloud, thus supporting the findings of Taquet et al. (2016). Dulieu et al. (2017) performed laboratory experiments to investigate if dismutation of H2O2 ice (2iH2O2 → 2iH2O + iO2) on the cometary surface could be the origin of the O2 detection. However, this explanation requires a high initial abundance of H2O2 ice relative to H2O ice (twice the detected abundance of O2, or ~ 7%), and a high efficiency for the conversion of H2O2 to O2 in order to match the low detected level of H2O2 relative to O2Of ~ 6 × 10−4. O3 ice, a molecule chemically related to O2, H2O2 and H2O, was not detected in the coma of comet 67P, and has an upper limit of 10−6 with respect to H2O ice. We note here that molecular oxygen is also produced when CO2 ice is exposed to far-UV radiation (see, e.g., Martín-Doménech et al. 2015). However, although this may be a viable chemical route to O2 ice, it does not explain the strong association between the production rates for H2O and O2 seen for comet 67P (Bieler et al. 2015). On the other hand, experiments investigating chemistry in CO2 ice irradiated with 5 keV ions (H+ and He+) and electrons (Ennis et al. 2011; Jones et al. 2014) favour the production of ozone (O3) over molecular oxygen (O2). These experiments mimic the conditions that ices are exposed to in the outer solar system, and upon cosmic ray impact.
In Eistrup et al. (2016; hereafter Paper I), we find through chemical kinetic modelling of protoplanetary disk midplanes that O2 ice could be produced to match the measured cometary abundance by 1 Myr, if the chemical starting conditions were purely atomised and the ionisation level was low (~10−19 s−1). Purely atomised starting conditions reflect the assumption that an energetic stellar outburst or accretion heating close to the star could have fully dissociated all volatiles in the midplane, and low ionisation means that the only ionisation source in the midplane is the decay of short-lived radionuclides. This latter scenario assumes that a magnetic field could have shielded the midplane from cosmic rays (as proposed by Cleeves et al. 2013). This finding sparked interest into whether or not the chemical origin of the O2 ice could bechemical processing of the icy material in the PSN disk midplane. Most recently, Mousis et al. (2018) explored the possibility that turbulent transport of icy grains between the disk midplane and the upper layers of the disk exposed the grains to a stronger cosmic-ray flux, thus chemically processing H2O ice to produce O2 ice via radiolysis. They find that on a 10 Myr timescale O2 ice in the midplane remains underproduced by up to two orders of magnitude relative to the abundances observed in the comets. Eistrup et al. (2018) also found that this abundance for O2 ice be reached on similarly long timescales.
Based on the promising results in Paper I, in this work we have investigated the conditions under which O2 ice in the PSN midplane could have been chemically produced in situ to reach the observed abundance level in the comets. This work differs from that in Mousis et al. (2018) in that a full chemical kinetics network was used that follows the chemical connection between H2O, O2, and related ice species. A more suitable disk model for the PSN was used, and a more thorough investigation of the O2 kinetic ice chemistry was conducted. Initial chemical abundances, physical conditions, parameters for grain–surface chemistry, as well as the inclusion of O3 in the chemical network were all tested to see the effect on the O2 ice production and abundance.
2 Methods
In orderto investigate the chemical evolution in the PSN midplane, the physical disk model for the PSN from Hayashi (1981) was utilised. This disk model estimates the structure and mass of the PSN, assuming the total current mass of the planets in the solar system to be distributed as dust and gas in a protoplanetary disk in equilibrium. The mass of this nebula is MMMSN = 0.08 M⊙, based on integrating the PSN surface density structure from Aikawa et al. (1997)1 from 0.1–1000 AU. This provides temperature and density profiles for the disk midplane, as well as the surface density profile. The latter is used to calculate the attenuation of cosmic rays (herefrom CRs) impinging on the disk, thereby estimating the contribution of CRs to the disk midplane ionisation, as was discussed in detail in Paper I. The disk structure is static in time, which was shown in Eistrup et al. (2018) to not cause a significantly different chemical evolution from an evolving disk structure, apart from the inward shifting of molecular icelines in response to decreasing temperature with time.
In Fig. 1a this PSN midplane temperature and density structure is plotted from 0.1–1000 AU. The temperature decreases by two orders of magnitude from ~900 K to 9 K from the inner to the outer disk, and the density drops from 1018 to 106 cm−3. The dynamic ranges, especially in density, are thus larger than what was used in Paper I. However, this disk also extends out to 1000 AU, instead of the 30 AU seen in Paper I. This is because this PSN disk midplane is significantly warmer and more massive than the disk structure in Paper I (0.08 versus 0.01 M⊙), thus the relevant temperatureregime for O2 ice chemistry (10–30 K) is found outside 100 AU here.
2.1 Ionisation levels
In Paper I, we confirm that ionisation is an important driver of chemistry in disk midplanes (see, e.g., Aikawa et al. 1997; Walsh et al. 2015). It is also found that abundant O2 ice was produced at low ionisation (only radionuclide decay, and no contribution from cosmic rays). Therefore, three different levels of ionisation are explored here: a low level (Level 1, SLRs only), a high level (Level 2, the fiducial level which includes galactic cosmic rays), and an extra high level (Level 3, which includes enhanced cosmic rays), see Fig. 1b. The two former levels assume the same contributions to the midplane ionisation as was the case for the low and high levels in Paper I: ionisation Level 1 includes only the contribution from short-lived radionuclides (SLRs) in the midplane. Ionisation Level 2 includes in addition CRs impinging on the disk, using the canonical cosmic ray ionisation rate for the local ISM (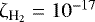 s−1). Ionisation Level 3 assumes a CR ionisation contribution 10 times higher than for ionisation Level 2, based on estimates from e.g. van Dishoeck & Black (1986), Dalgarno (2006), and Indriolo et al. (2015) that the galactic cosmic ray rate ζGCR could be in the range ζH = 10−17 − 10−16 s−1 in diffuse clouds. We explore this enhanced CR scenario because O2 ice has been found to be efficiently synthesised in experiments studying H2O ice radiolysis in relation to solar system icy bodies (see, e.g., lab work by Teolis et al. 2017, and others). For Levels 1 and 2, the ionisation ranges between 10−18 and 10−17 s−1 throughout the disk, whereas for Level 3, ~10−16 s−1 is reached at radii larger than 10 AU. In the inner disk inside ~2 AU, all three ionisation levels are the same, because the surface densities here (>600 g cm−2) attenuate the impinging CRs, so that only the SLRs contribute. In the outer, more diffuse disk, the contribution from CRs impinging on the disk becomes more dominant, thus leading to three markedly different ionisation levels.
s−1). Ionisation Level 3 assumes a CR ionisation contribution 10 times higher than for ionisation Level 2, based on estimates from e.g. van Dishoeck & Black (1986), Dalgarno (2006), and Indriolo et al. (2015) that the galactic cosmic ray rate ζGCR could be in the range ζH = 10−17 − 10−16 s−1 in diffuse clouds. We explore this enhanced CR scenario because O2 ice has been found to be efficiently synthesised in experiments studying H2O ice radiolysis in relation to solar system icy bodies (see, e.g., lab work by Teolis et al. 2017, and others). For Levels 1 and 2, the ionisation ranges between 10−18 and 10−17 s−1 throughout the disk, whereas for Level 3, ~10−16 s−1 is reached at radii larger than 10 AU. In the inner disk inside ~2 AU, all three ionisation levels are the same, because the surface densities here (>600 g cm−2) attenuate the impinging CRs, so that only the SLRs contribute. In the outer, more diffuse disk, the contribution from CRs impinging on the disk becomes more dominant, thus leading to three markedly different ionisation levels.
2.2 Chemical network
The chemical model used here includes gas-phase chemistry, gas–grain interactions and grain–surface chemistry. The gas-phase chemistry is from the latest release of the UMIST Database for Astrochemistry (McElroy et al. 2013) termed RATE12. The rates for gas–grain interactions and grain–surface chemistry are calculated as described in Walsh et al. (2015, and references therein). A gas to dust mass ratio of 100 is adopted. This setup is similar to the “full chemistry” setup from Paper I. The adopted grain size is 0.1 μm.
Four scenarios of initial chemical abundances are explored: the first two are cloud inheritance (hereafter the “inheritance” scenario) and chemical reset (hereafter the “reset” scenario). In the inheritance scenario the initial abundances are molecular (but no O2 initially), and assumed inherited from the parent molecular cloud. In the reset scenario, the initial abundances are atomic, because all molecules are assumed dissociated prior to arrival in the disk midplane, due to exposure to a sufficiently strong accretion shock en route into the disk, or accretion heating very close to the star leading to high temperatures. The reset scenario is of particular interest for this paper because in Paper I, we see that for this scenario that the O2 ice to H2O ice ratio was similar to that found in comets 67P and 1P (Bieler et al. 2015; Rubin et al. 2015). Table A.1 lists the initial atomic and molecular abundances used in these two scenarios. Tables 1 and 2 list the relevant binding energies for species, and activation barriers for reactions applicable to the O2 chemistry, respectively. Radiolysis of H2O ice through the reaction 2iH2O 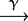 2iH2 + iO2 and dismutation of H2O2 ice through the reaction 2iH2O2 → 2iH2O + iO2 are not explicitly included in the network. For the inheritance scenario, in this chemical network, atomic oxygen can be produced in situ in the ice mantles via the cosmic-ray induced photodissociation of H2O ice and other abundant oxygen-bearing molecules therein (e.g. CO2 ice).
2iH2 + iO2 and dismutation of H2O2 ice through the reaction 2iH2O2 → 2iH2O + iO2 are not explicitly included in the network. For the inheritance scenario, in this chemical network, atomic oxygen can be produced in situ in the ice mantles via the cosmic-ray induced photodissociation of H2O ice and other abundant oxygen-bearing molecules therein (e.g. CO2 ice).
The third and fourth scenarios for the initial chemical abundances are more simple: first, the “water”-scenario, which assumes initial abundances of gas-phase H, He, H2 and H2O. The intention with this scenario is to investigate if O2 ice can be produced through processing of H2O ice. Second, the “atomic oxygen”-scenario, which assumes gas-phase H, He, H2, and O as initial abundances. Here it is investigated whether or not O2 ice production from atoms depends on the presence of elements other than oxygen. Eistrup et al. (2018) showed that H2 S ice on the grain surfaces acts as a catalyst for the conversion of adsorbed oxygen atoms into O2 ice. Whether or not the sulphur-bearing species are essential for the production of O2 ice can be tested in these two scenarios, because they exclude sulphur, and only include a source of oxygen in the form of oxygen atoms or H2O.
Lastly, we have explored whether the observed cometary O2 ice abundance can be maintained if the PSN started out with a percentage (5%) of elemental oxygen locked up in primordial O2, as suggested by Taquet et al. (2016).
 |
Fig. 1 Panel a: midplane temperature and density profiles for the pre-solar nebula. Panel b: ionisation levels utilised in the models. Level 1: SLRs only. Level 2: SLRs + fiducial CRs. Level 3: SLRs + enhanced CRs. |
Binding energies Ebin[K] for relevant species.
3 Results
In this section the chemical evolution of various species in the PSN are presented in a number of figures. Due to the focus on O2 ice in this paper, the attention will be on species that are chemically related to O2 ice (a schematic overview of these species can be found in Cuppen et al. 2010).
 |
Fig. 2 Radial abundance profiles for the inheritance scenario at multiple evolutionary time steps. Top to bottom panels: H2O, O2, and H2O2. Left to right panels: increasing ionisation levels. For O2 and H2O2, the limits detected in comet 67P are indicated as yellow and red shaded areas, respectively. The chemical network utilised does not include O3 chemistry. |
Activation energies Eact [K] for relevant grain–surface reactions.
3.1 PSN abundance evolution
3.1.1 Inheritance scenario
Figure 2 features abundances as a function of midplane radius for different evolutionary times up to 10 Myr for the inheritance scenario. H2O ice is plotted with respect to Hnuc abundance, whereas O2 and H2O2 ice are plotted with respect to H2O ice. This is done to match the convention used in the reporting of cometary abundances. The model details are listed in each panel, alongwith colour-coding indicating evolution times. In the middle and lower panels, the respective observed limits for O2 and H2O2 ices are marked with orange and red shaded regions, respectively. The orange shading for O2 ice marks the limits to the mean O2 ice abundance observed in comet 67P (3.8 ± 0.85 × 10−2 with respect to H2O ice), and the red shading marks the limits for H2O2 ice (6 ± 0.7 × 10−4 wrt O2 ice, thus 2.34 ± 0.8 × 10−5 wrt H2O ice; Bieler et al. 2015). We note that in 67P variations in O2Over H2O ice were seen spanning 1–10%.
An evolution time of 10 Myr is chosen because this is assumed to be the maximum lifetime of a gaseous protoplanetary disk, and based on the results from Eistrup et al. (2018), the outer icy disk midplane should have reached steady state by this time. Since the focus in this work is the outer, icy PSN disk midplane, the radial range starts at 50 AU, which lies inside the O2 iceline (~ 120 AU at ~29 K).
For ionisation Level 1 in Fig. 2a, H2O ice stays abundant throughout the evolution. For higher ionisations, the H2O ice abundance decreases with time inside, and increases with time outside ~ 120 AU. This radius marks the O2 iceline. Panels d–f show the evolution of O2 ice for the different ionisation levels. The profiles for O2 ice for ionisation Levels 1 and 2 peak at similar abundance levels of 2–3 × 10−3 with respect to H2O ice, which is an order of magnitude lower than the observed abundance. We see that for higher levels of ionisation, this abundance is reached faster, with ionisation Level 1 producing of order 10−3 with respect to H2O ice by only 10 Myr.
We see that for H2O2 ice abundance profiles featured in panels g to i they evolve in a similar way to O2 (we note the same y-axis range as for O2 ice), and reach peak abundances at ~120 AU by 10 Myr, that are a factor of between two and three lower than those for O2 ice. This abundance level is 30–100 times higher than that observed for H2O2 ice in comet 67P. For all ionisation levels, there are narrow radial regions where the H2O2 ice abundance matches the observed levels over a time range defined by the ionisation level (e.g. between 70 and 80 AU ionisation Level 3 at all times). However, at these points the O2 ice abundance does not match that observed. For the inheritance scenario, it is thus seen that O2 ice is underproduced by at least an order of magnitude, and H2O2 is overproduced by up to two orders of magnitude.
3.1.2 Reset scenario
The abundance evolution profiles for the reset scenario are shown in Fig. 3. For O2 ice in panels d to f we see that a high abundance (10−2−10−1 with respect to H2O ice) is reached for both ionisation Levels 1 and 2, with each reproducing the observed abundance for a large radial range covering 150–300 AU. For ionisation Level 1 the O2 ice abundance matching the observation is maintained up to 2 Myr. Until 1 Myr between 150–220 AU, the modelled abundance lies above the observations (>5 × 10−2 with respect to H2O ice). For Level 2 the abundance level matching the observed values happens between 5 × 104−105 yr in the range 150–200 AU, but subsequently drops to reach 2–3 × 10−3 with respect to H2O ice by 10 Myr. This was also the abundance level reached for O2 ice by 10 Myr for the inheritance scenario. For ionisation Level 3, the abundance is below the observed level by 5 × 104 yr of evolution already, and by 10 Myr it also has reached the level of 2–3 × 10−3 with respect to H2O ice. For ionisation Level 1, the abundance remains higher than 2–3 × 10−3 with respect to H2O ice throughout the evolution, indicating that, for both inheritance and reset, at this ionisation level, 10 Myr of chemical evolution is not enough to bring the O2 ice abundance to what appears to be its steady-state level according to the results from the inheritance scenario in Fig. 2 (for a description of disk midplane chemical steady state, see Eistrup et al. 2018).
We see H2O2 ice in Fig. 3, panels g–i, to evolve significantly over time. For all ionisation levels, H2O2 ice is produced over time with the timescale dependent on ionisation level. The fastest production is seen for Level 3, where the peak abundance of >10−2 with respect to H2O ice is reached already by 105 yr. On the other hand, it takes 0.5 Myr and 3 Myr to reach a similar abundance for Levels 2 and 1, respectively. The H2O2 ice is subsequently destroyed after reaching its peak. For ionisation Levels 2 and 3, a steady-state abundance of order 10−3 with respect to H2O ice is reached at radii ~100–120 AU. Beyondthis radius it has disappeared by 10 Myr.
 |
Fig. 3 Radial abundance profiles for the reset scenario at multiple evolutionary time steps. Top to bottom panels are H2O, O2 and H2O2 ices. Left to right panels are increasing ionisation levels. For O2 and H2O2 the limits detected in comet 67P are indicated as yellow and red shaded areas, respectively. The chemical network utilised does not include O3 chemistry. |
3.1.3 Water and atomic oxygen starting conditions
Models were also run starting with simpler sets of initial abundances, either with all oxygen already present in H2O (water scenario) or all free (atomic oxygen scenario), in addition to H and He. This was to test the formation of O2 ice solely from processing of H2O ice, and theformation via assembly from free oxygen atoms, in the absence of other chemistry. It was found that the water scenario did not, at any point in time or radius, reproduce O2 ice to the abundance seen in the comets. The maximum abundance was <10−7 with respect to H2O ice, regardless of ionisation level. This is shown in Fig. A.1, where the gas and ice abundances of O, O2, H2O, and H2O2 are plotted as a function of radius by 10 Myr of evolution.
The atomic oxygen scenario, on the other hand, can reproduce the observed abundance of O2 ice by 10 Myr, as is seen in panel a of Fig. 4. This panel of Fig. 4 shows the abundances of H2O, O, O3 and H2O2 with respect to Hnuc as a function of radius, by 10 Myr of evolution. The radial range (80–300 AU) for this reproduction is similar to the range in the reset scenario, but in the atomic oxygen scenario H2O2 ice is found to be more efficiently formed than O2 ice. This scenario is revisited later in the paper.
 |
Fig. 4 Abundances by 10 Myr evolution in the oxygen-only scenario, for ionisation Level 1. Panel a: without O3 chemistry included. Panel b: with O3 chemistry included. |
3.2 Including ozone ice chemistry
The chemical network utilised so far has not included O3. This is because it has not been considered to be an important player in ISM chemistry, as it is formed primarily in the gas phase via a three-body mechanism. However, data exist on O3 ice chemistry, as outlined in, for example, Cuppen et al. (2010) and Lamberts et al. (2013). The production pathway to O3 ice is
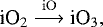 (1)
(1)
with a fiducial barrier of 500 K, and the destruction pathway is
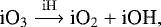 (2)
(2)
which has no barrier. Hence, it is expected that the pathway to O3 ice via O2 ice may impact on the O2 ice abundance, and will be dependent on the both the availability of free oxygen atoms on the ice, and the efficiency of hydrogenation.
Figure 5 presents the evolving abundances of H2O ice, O2 ice, H2O2 ice, and O3 ice as a function of radius for the inheritance scenario, thus now including O3 ice chemistry. These panels are directly comparable with those in Fig. 2. The abundance evolution of O3 ice is shown in the bottom row. The abundance evolution seen for O2 ice in panels d–f and for H2O2 ice in panels g–i are similar to the trends in Fig. 2 for the chemistry without O3. However, the abundances reached by 10 Myr with O3 chemistry are lower than those without: both O2 ice and H2O2 ice abundances peak at ~5 × 10−4 with respect to H2O ice, thus a factor of two lower for H2O2 ice and a factor of five lower for O2 ice when compared with the scenario that does not include O3 chemistry. The peak O2 ice abundance is almost two orders of magnitude lower than the observed value, and the peak of the H2O2 ice is about 20 times higher than the observed value.
For O3 ice in panels j–l, we see a steady build-up over time. We note that the range on the y-axis range is different for O3 ice than for H2O2 and O2 ices. The O3 ice reaches maximum abundance fastest at ionisationLevel 3 (~10−4 with respect to H2O ice), thus a factor of five lower than that reached for H2O2 ice and O2 ice, yet twoorders of magnitude higher than the observed upper limit at 10−6 with respect to H2O ice for O3 ice in comet 67P. Only at larger radii (between 150 and 270 AU, depending on evolution time) do the O3 and H2O2 ice abundances fall within the observed limits, although O2 ice does not. All three ice species thus show similarities in their evolution, and order-of-magnitude similarities in their peak abundances. The observed large differences between their respective abundances (O3:H2O2:O2 ≲ 1:23.5:39 200) are not reproduced by these models.
For the reset scenario, including O3 chemistry, Fig. 6 shows a higher abundance level of O2, H2O2 and O3 ices than for the inheritance scenario. At ionisation Level 1, O2 and H2O2 ices peak at ~10−2 with respect to H2O ice at ~ 150 AU between 0.5–1 Myr evolution, but subsequently drop by about an order of magnitude by 10 Myr. For ionisation Levels 2 and 3, abundance levels for both species of ~ 10−2 with respect to H2O ice are only achieved by 5 × 104 yr, and the peak abundances by 10 Myr are at 1–2 × 10−4 with respect to H2O ice, thus neither matching the observed values of H2O2 ice nor of O2 ice. At no point in time or radius does the reset scenario including O3 chemistry reproduce the observed mean abundance of O2 ice. However, for ionisation Levels 1 and 2 the abundance between 150–200 AU reaches above 1% of H2O ice, which is within the observed range in comet 67P (1–10%).
The O3 abundance for the reset scenario at ionisation Level 1 starts out high at 1− 3 × 10−2 with respect to H2O ice between 100 and 200 AU up to 5 × 105 yr ⋅ s seen in Fig. 6. We note that the higher ratios reached within 70 AU is due to generally low absolute ice abundances (see panels a–c in Fig. 6). For ionisation Levels 2 and 3, these high abundances reduce over time leading to a peak of at a few times 10−5 with respect to H2O ice by 10 Myr between 100–120 AU. The maximum abundance achieved by 10 Myr is an order of magnitude higher than the observed upper limit. Only in the wings of the abundance profiles do the models reproduce this upper limit for the entire radial range, depending on evolution time and ionisation level.
The scenarios that begin with only H2O or elemental oxygen were also investigated after the inclusion of O3 chemistry. However, neither of them reproduced a significant amount of O2 ice. The abundances by 10 Myr are shown for the oxygen-only scenario in Fig. 4b. Upon inclusion of O3 chemistry, the peak abundance of O2 ice from panel a (without O3) drops by at least four orders of magnitude to <10−9 with respectto H2O ice in panel b. Starting with atomic oxygen only therefore does not reproduce the observed abundance. For the water scenario, there is also no O2 ice. An overview of gas and ice abundances of H2O, O2, O3, and H2O2 as a function of radius by 10 Myr of evolution for the inheritance, reset, water and oxygen scenarios is shown in Fig. A.2. In none of the tested cases including O3 chemistry is the O2 ice abundance reproduced to match the levels observed in the comets.
 |
Fig. 5 Radial abundance profiles for the inheritance scenario at multiple evolutionary time steps. Top to bottom panels: H2O, O2, H2O2, and O3 ices. Left to right panels: increasing ionisation levels. For O2, H2O2, and O3 the limits, and upper limit, detected in comet 67P, are indicated as yellow, red and grey shaded areas, respectively. The chemical network utilised includes O3 chemistry. |
 |
Fig. 6 Radial abundance profiles for the reset scenario at multiple evolutionary time steps. Top to bottom panels: H2O, O2 and H2O2 and O3 ices. Left to right panels: increasing ionisation levels. For O2, H2O2, and O3 limits, and upper limit, detected in comet 67P, are indicated as yellow, red, and grey shaded areas, respectively. The chemical network utilised includes O3 chemistry. |
3.3 Exploring the sensitivity of the abundances to assumed grain–surface parameters
The underproduction of O2 ice and overproduction of H2O2 and O3 ices may be a result of the adsorption and reaction parameters assumed for the network of reactions involving oxygen and hydrogen. If, for example, the reaction iO2 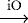 iO3 is too efficient on the grain surfaces, this could lead to over- and under-production of O3 and O2 ices, respectively. This reaction is dependent on the adsorption of atomic oxygen, for which the utilised binding energy here is Ebin = 800 K. This is based on estimates from Tielens & Allamandola (1987). However, recent experimental work by He et al. (2015) experimentally determined a binding energy of Ebin = 1660 K, thus more than doubling the former value. This higher binding energy should act to keep oxygen atoms from desorbing at higher temperatures, thereby facilitating each step in the reaction pathway leading from iO
iO3 is too efficient on the grain surfaces, this could lead to over- and under-production of O3 and O2 ices, respectively. This reaction is dependent on the adsorption of atomic oxygen, for which the utilised binding energy here is Ebin = 800 K. This is based on estimates from Tielens & Allamandola (1987). However, recent experimental work by He et al. (2015) experimentally determined a binding energy of Ebin = 1660 K, thus more than doubling the former value. This higher binding energy should act to keep oxygen atoms from desorbing at higher temperatures, thereby facilitating each step in the reaction pathway leading from iO 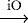 iO2
iO2 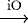 iO3. On the other hand, at low temperature the mobility of atomic oxygen will be reduced. This latter case could possibly lead to a decreased production of O3 ice.
iO3. On the other hand, at low temperature the mobility of atomic oxygen will be reduced. This latter case could possibly lead to a decreased production of O3 ice.
In this subsection, the sensitivity of the chemistry to several parameters is explored for single-point models (i.e. single n, T) which cover the temperature and density ranges in the PSN midplane where O2 ice production is expected, based on the model results described thus far. The first parameter explored is the barrier width for quantum tunnelling bqt which is set to either 1 or 2 Å representing the limits to the range of values usually assumed for bqt when modelling grain–surface chemistry, see Cuppen et al. (2017), and references therein. The second parameter is the ratio of the diffusion energy to the molecular binding energy Ediff∕Ebin, which is taken to be either 0.3 or 0.5 (see Ruffle & Herbst 2000; Garrod & Herbst 2006, and references therein). This amounts to four combinations of the two reaction parameters. The values of each parameter associated with a given model setup is given in each panel. The values for the grain–surface chemistry used in Eistrup et al. (2016, 2018), are bqt = 1 Å and Ediff∕Ebin = 0.5. Onlythe reset scenario is studied here because this is the case for which maximal O2 ice formation is seen.
3.3.1 Abundance mosaics
Figures A.3, 7, A.4, and A.5 show the abundances of H2O ice with respect to Hnuc, and O2 ice, O3 ice and H2O2 ice with respect to H2O ice, again, maintaining the convention used by the comet community. From top to bottom span evolution times from 5 × 104 yr up to 107 yr. In each panel in the figures, a mosaic of colour-indicated abundances shows the results across different combinations of midplane temperature (ranging from 10 to 30 K on the y-axis), and densities (ranging from 108 to 1010 cm−3 on the x-axis). The ionisation level is kept constant at ζ = 10−17 s−1, approximately the same as ionisation Level 2 from Fig. 1 in the outer disk midplane. This ionisation level was seen in Fig. 3 (model without O3) to match the observed O2 ice abundance early in the evolution (up to 0.1 Myr).
From left to right in each of Figs. A.3 and A.4, two grain–surface reactions parameters are changed. The first one is the barrier width for quantum tunnelling bqt which is either 1 Å (Columns one and two, in each figure) or 2 Å (Columns three and four, in each figure). The second parameter is the ratio of diffusion energy to molecular binding energy Ediff∕Ebin, which can be either 0.3 (Columns one and three, in each figure) or 0.5 (Columns two and four, in each figure). This amount to four combinations of the two reaction parameters, thus the four columns of mosaics in each figure. The values of each parameter associated with a given model setup is given in each panel.
The range of evolution time steps is chosen to cover both the evolutionary stage at which O2 ice was abundant in Fig. 3 (5 × 104 yr, for ionisation Level 2, ~10−17 s−1), as well as the later stages of disk evolution. The colours in the mosaic are chosen to enable distinguishing between abundance levels that change per order-of-magnitude, with dark red (top colour in colourbar) representing the highest abundance, and dark blue (bottom colour in colourbar) representing the lowest. The range of abundance levels in each figure is chosen to cover the full range of abundances produced for each species in the models. By showing the abundance evolutions in this way model results matching the observed abundances of, for example, O2 ice (1–10% of H2O ice) shows as orange (second highest colour in colourbar) in Fig. 7.
For H2O ice in Fig. A.3 it is seen that for Columns one and two (bqt = 1 Å) the abundance level largely remains within the initial order of magnitude of 10−4 with respect to H2O ice. For Columns three and four (bqt = 2 Å), some change is seen: especially for the third column (Ediff∕Ebin = 0.3), the abundance is an order of magnitude lower for temperatures 25–30 K than for 10–20 K, and the abundance increases with time at 20 K. Turning to Fig. 7 for O2 ice, limited production is seen for Columns one and two, with an early peak abundance between 10−4−10−3 with respect to H2O ice at 25 K for n = 108−109 cm−3 by 5 × 104 yr. More interesting still are Columns three and four: until 0.5 Myr, abundances of 10−2 − 1 with respect to H2O ice are reached for temperatures 15–25 K for all densities. Thus, the O2 ice abundance lies above or reproduces the observed values. For these cases, by >1 Myr, the produced O2 ice is destroyed and reaches 10−5−10−3 with respect to H2O ice by 10 Myr.
Having narrowed in on this parameter range (early evolutionary times, and bqt = 2 Å), it can now be checked if H2O2 and O3 ices can match the observed levels for the same model parameters. Figure A.4 shows the same suite of plots for O3 ice. The results in Columns three and four up to 0.5 Myr evolution show that O3 ice is abundantly produced, at a similar or higher level than O2 ice, thus not matching the observed upper limit (darkest shade of blue, <10−6 with respect to H2O ice). The subsequent destruction by >1 Myr does not bring the abundance level much further down, and the O3 ice abundance is generally similar to that for O2 ice. O3 ice only matches the observed upper limit for T = 10 K.
In Fig. A.5, H2O2 ice is abundantly produced for bqt = 2 Åand Ediff∕Ebin = 0.3. For 25 K it is consistently at a level of 10−1 − 1 with respectto H2O ice during the entire evolution. For 20 K it is also abundant, although 1–2 orders of magnitude lower than that found at 25 K, and it is less abundant than O2 ice until ~0.5 Myr by between one and two orders of magnitude. At later times, for 20–25 K, H2O2 ice becomes 1–3 orders of magnitude more abundant than O2 ice. For Ediff∕Ebin = 0.5 it is produced at levels 10−6−10−3 with respect to H2O ice, depending on density.
 |
Fig. 7 Abundances (given as colours) for O2 ice as function of midplane density (x-axes), and temperature (y-axes) at different evolutionary steps for the reset scenario. From left to right panels: abundances from model runs with different parameters for grain–surface reactions: Cols. 1 and 2: bqt = 1 Å, Cols. 3 and 4: bqt = 1 Å, Cols. 1 and 3: with Ediff∕Ebin = 0.3, and Cols. 2 and 4: with Ediff∕Ebin = 0.5. From top to bottom panels: different evolutionary times, from 0.05 Myr (top) to 10 Myr (bottom). To the right of each plot is a colourbar, indicating the abundance level with respect to H2O ice for each colour. The chemical network utilised includes O3 chemistry. Orange matches cometary O2 abundances. |
3.3.2 Abundance evolutions for selected parameter sets
In Sect. 3.3.1 the colour mosaics revealed a promising set of physical and chemical parameters that supported the production of O2 ice in situ under conditions suitable for the PSN: bqt = 2 Å (rather than the fiducial value of 1 Å), T = 15–25 K, n =109− 1010 cm−3 and evolution times up to 0.5 Myr. The ratio of diffusion-to-binding energy for ice species appeared to play a minor role, with both values of 0.3 and 0.5 facilitating O2 ice production.
In Fig. 8 evolving abundances are plotted for O2, O3, H2O2, and O2H ices with respect to H2O ice, for the three different temperatures and two densities outlined above, and with Ediff∕Ebin = 0.3. Details about each plot can be found in the labels. Each panel includes shaded regions indicating the observed abundances for O2 ice (yellow), H2O2 ice (red), and upper limit for O3 ice (grey).
For all six panels, it is seen that O2 ice is within the measured abundance values, at least for a period during evolution. In all cases an initial production is seen, with the abundances of O2 ice across model setups peaking at 30–40% with respect to H2O ice between ~5 × 104−5 × 105 yr, with the highest abundances reached at 20 K. For temperatures at 15–20 K, the O2 ice abundances are generally higher than for T = 25 K. By ~ 3 × 105–106 yr, depending on model setup, the O2 ice abundance drops at least two orders of magnitude below maximum. Hence, the observed abundance of O2 ice can be reproduced in all six setups, but only at early times.
Regarding ice species besides O2, Fig. 8 shows that O3 is the most abundant of the plotted species, at least until 105 yr. At early evolutionary stages, O3 ice is even more abundant than H2O ice. This is because the calculations are started with free oxygen atoms (reset scenario). This high level is not seen in the measurements of comet 67P, in which an upper limit of 10−6 with respect to H2O ice was reported.
Likewise for H2O2 ice, it is mostly produced at a high abundance (>10−3 with respect to H2O ice) in these models. At 25 K after ~0.5 Myr of evolution, H2O2 ice is the most abundant of the plotted species. At no point in time in any of the plots does the abundance of H2O2 ice match the levels observed (red shaded region): for 15 K it is at least an order of magnitude too low, and between 20 and 25 K it is overproduced by between a factor of three and two orders of magnitude.
For a ratio of diffusion-to-binding energy of 0.5, similar plots are shown in Fig. 9. Between 20 and 25 K there are evolutionary times when O2 ice is reproduced to match the observations. However the highest abundance reached is at 20 K. For T = 15 K, no reproduction of the observed abundances of neither O2 ice nor H2O2 ice is seen, and O3 ice is (next to H2O ice) the dominant carrier of elemental oxygen. At T = 25 K for n = 109 cm−3, the abundance of H2O2 ice matches that measured in the comet both by ~0.03 Myr and by ~3 Myr, and by 0.03 Myr the O2 ice abundance is only ~ 2 times lower than the observed abundance. Along the same lines, for T = 25 K and n = 109 cm−3 by ~ 0.4 Myr O2 ice matches the observed abundance, and H2O2 ice is only approximately twice as high as the observed level. This indicates that something close to a match with the observed abundances between both O2 and H2O2 ice abundances with respect to H2O ice is reached at 25 K. However, all the models still vastly overproduce the O3 ice abundance compared with the measurements.
This parameter space investigation has shown that there are sweet spots, both for the physical and chemical setup, where O2 ice can be produced to match the measurements on comet 67P, even after expanding the grain–surface chemical network to include O3 ice chemistry. However, the low measured abundance of O3 ice remains unexplained by the models.
A possible way to adjust the models to lower the O3 ice production could be to increase the reaction barrier for the iO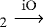 iO3 reaction, where the default barrier is at Eact = 500 K. Because the abundance levels of O2 ice and H2O2 ice in panel c of Fig. 9 (T = 25 K, Ediff∕Ebin = 0.5, n =10−9 cm−3, bqt = 2 Å and ζ = 10−17 s−1) featured evolutionary stages when they were simultaneously in proximity to the observed levels, this model setup is now tested with three different values for the activation energy for the iO2
iO3 reaction, where the default barrier is at Eact = 500 K. Because the abundance levels of O2 ice and H2O2 ice in panel c of Fig. 9 (T = 25 K, Ediff∕Ebin = 0.5, n =10−9 cm−3, bqt = 2 Å and ζ = 10−17 s−1) featured evolutionary stages when they were simultaneously in proximity to the observed levels, this model setup is now tested with three different values for the activation energy for the iO2 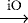 iO3 reaction. In addition to the fiducial 500 K, also 1000 K and 2000 K activation energies are tested. We note that these are likely too high relative to what is known from laboratory work where O3 is seen to form readily at low temperatures (Lamberts et al. 2013). However, given that O3 ice is not seen to be efficiently produced in space including comets, the hypothetical situation with a higher barrier is explored, as a means to mitigate as of yet unknown chemical pathways away from O3 ice. To compare theeffects of these changes, the same tests of activation energies were performed for the setup in panel b in the same figure (T = 20 K, keeping all other parameters the same).
iO3 reaction. In addition to the fiducial 500 K, also 1000 K and 2000 K activation energies are tested. We note that these are likely too high relative to what is known from laboratory work where O3 is seen to form readily at low temperatures (Lamberts et al. 2013). However, given that O3 ice is not seen to be efficiently produced in space including comets, the hypothetical situation with a higher barrier is explored, as a means to mitigate as of yet unknown chemical pathways away from O3 ice. To compare theeffects of these changes, the same tests of activation energies were performed for the setup in panel b in the same figure (T = 20 K, keeping all other parameters the same).
In panels a and b of Fig. 10, abundances for O2, O3, and H2O2 ices are plotted as a function of time, with solid, dashed and dotted profiles representing activation energies for the O3 ice production reaction of 500 K, 1000 K and 2000 K, respectively. In panel a only the abundance of O2 ice is found to match the observed level. However, in panel b, at 25 K, it is seen that for at Eact = 2000 K, O2 ice and H2O2 ice are both reproduced to within the observed values between 0.8–1 Myr evolution. For the same evolutionary timescale, O3 ice is much lower in abundance (~10−16 with respectto H2O ice), thus also agreeing with the upper limit for the cometary abundance. This is therefore a sweet spot in the physical and chemical parameter space, in which the observed abundances of all three species are reproduced. We note that the ionisation level for this sweet spot includes the contributions from both SLRs and CRs, whereas it was found in Paper I that O2 ice be reproduced only without CRs. However, the framework here is different from that in Paper I, as O3 chemistry and the updated binding energy for atomic oxygen have been included. We note that the anomalously high activation required for O + O2 is likely masking as of yet unknown routes in the O3 chemistry.
 |
Fig. 8 Evolving abundances as function of time for the reset scenario for six different combinations of temperature (15, 20, or 25 K), density (109 or 1010 cm−3) and molecular diffusion-to-binding energy ratio of 0.3. The barrier width for quantum tunnelling is bqt = 2 Å. Theorange shaded regions indicate the limits to the measured abundance of O2 ice in the coma of comet 67P. The red shaded regions indicate the limits to the measured abundance of H2O2, and the top of the grey shaded region marks the upper limit to the measured abundance of O3 ice in comet 67P. The chemical network utilised includes O3 chemistry. |
 |
Fig. 9 Evolving abundances as function of time for the reset scenario for six different combinations of temperature (15, 20, or 25 K), density (109 or 1010 cm−3) and molecular diffusion-to-binding energy ratio of 0.5. The barrier width for quantum tunnelling is bqt = 2 Å. Theorange shaded regions indicate the limits to the measured abundance of O2 ice in the coma of comet 67P. The red shaded regions indicate the limits to the measured abundance of H2O2, and the top of the grey shaded region marks the upper limit to the measured abundance of O3 ice in comet 67P. The chemical network utilised includes O3 chemistry. |
 |
Fig. 10 Evolving abundances for O2 ice, H2O2 ice and O3 ice for three different activation energies for the reaction iO + iO2. Panel a is for T = 20 K. Panel b is for T = 25 K. The barrier width for quantum tunnelling is bqt = 2 Å, and the molecular diffusion-to-binding energy is 0.5. |
3.4 Including a primordial source of O2 ice
Here, the results from the scenario starting with 5% of atomic oxygen locked in O2 is tested, exploring the theory for the primordial origin of O2 ice, as suggested by Taquet et al. (2016) and Mousis et al. (2016). This is a modification of the inheritance scenario so that remaining oxygen is already locked in molecules (mostly H2O, CO, and CO2, see the inheritance scenario abundances in Table A.1). In Fig. 11 evolving abundance profiles for this scenario are shown, for temperatures between 15 and 25 K from left to right, and densities between 109 and 1010 cm−3 from top to bottom. The ionisation rate is at ζ = 10−17 s−1, the ratio of diffusion-to-binding energy is 0.5, and the barrier width for quantum tunnelling is 2 Å. The activation energy for the O + O2 reaction is the fiducial value of 500 K.
We see in panels a, b, d, and e, of Fig. 11, that an early abundance level of O2 ice at or above the observed mean is maintained until a few times 104 yr for temperatures between 15 and 20 K. At 25 K, the abundance of O2 ice is lower early on, and in particular for n =109 cm−3 the abundance is <10−2 with respect to H2O ice, which is outside the observed range. Simultaneously with O2 ice matching the observed abundance in some cases, the abundance of O3 ice is one to two orders of magnitude lower than O2 ice by 3× 103 yr for all cases except in panel c. Between a few times 104 yr and 10 Myr, the O2 ice abundance decreases by more than two orders of magnitude compared with the initial abundance, and from ~ 105 yr, O3 ice is the dominant oxygen carrier of the plotted species. Hence, this scenario can reproduce the observed abundance of O2 at early stages, and with lower abundances of H2O2 and O3 ices, although abundances for the latter two species are still higher than measured.
 |
Fig. 11 Evolving abundances as function of time for the inheritance scenario, plus 5% extra elemental oxygen as O2, for six different combinations of temperature (15, 20, or 25 K), density (109 or 1010 cm−3), and molecular diffusion-to-binding energy ratio of 0.5. The barrier width for quantum tunnelling is bqt = 2 Å. Theorange shaded regions indicate the limits to the measured abundance of O2 ice in the coma of comet 67P. The red shaded regions indicate the limits to the measured abundance of H2O2, and the top of the grey shaded region marks the upper limit to the measured abundance of O3 ice in comet 67P. |
4 Discussion
The abundance of O2 ice in comet 67P has motivated much work as to its origin. Rubin et al. (2015), Mousis et al. (2016, 2018), Taquet et al. (2016), and Dulieu et al. (2017) have all attempted to explain the O2 level from a point of view of possible chemical origins. Mousis et al. (2016) and Rubin et al. (2015) approached the problem by investigating chemical processing of either H2O ice or H2O2 ice into O2 ice. Mousis et al. (2018) attempted an explanation with a scenario in which ice-covered grains were transported from the midplane to the upper layers of the disk. Here, the grains undergo photochemical processing producing O2 ice, which is then cycled back to the disk midplane. It is noted that Mousis et al. (2018) only consider the O2 ice abundances, not H2O2 Or O3 ices. On the other hand, Taquet et al. (2016) approached it from a broader point of view considering primordial production pathways in the parent cloud, and utilising extensive chemical networks and subsequently tracking the primordially produced O2 ice to the disk midplane. While those works all conclude that a primordial origin and subsequent retention of O2 ice was the most likely, Paper I concluded that starting from a fully atomised disk midplane, there is an evolutionary phase during which a range of radii in the outer icy midplane (outside the O2 iceline) will reasonably reproduce the measured O2 /H2O ice ratio level.
The investigation here has taken the step further from Paper I: exploring the physical and chemical parameter space that may facilitate the production of O2 ice in situ in the PSN, and simultaneously tracing the abundances of the chemically related species H2O2, O3, and O2 H, as well as using a more massive disk model more appropriate for the PSN.
4.1 Chemical starting conditions
The chemical starting conditions’ effects on the O2 ice production were explored. It is clear that only an atomised start can facilitate the production, although models starting with a percentage of elemental oxygen in O2 did retain this O2 ice for a short period of evolution. The presence of atoms other than oxygen (such as sulphur), however, has no large impact on the production of O2 ice. That means that oxygen-only and hydrogenated oxygen species lock up the majority of the available elemental oxygen.
4.2 Dependence on ionisation levels
The ionisation levels have been shown to facilitate different chemical evolution of abundances. The chemical timescales are shorter for higher ionisation levels. Ionisation Level 1 only reproduced the observed O2 abundance for models without O3, and ionisation Levels 2 and 3 cause similar evolutionary trends, meaning that Level 3 does not facilitate any more O2 ice production than Level 2. We note that the sweet spot for reproduction of O2, H2O2 and O3 ices to within the observed abundances was found for a ionisation level of ζ = 10−17 s−1, which is the local ISM value for dense clouds. This ionisation resembles ionisation Level 2 at 100–130 AU in the PSN disk midplane (see Fig. 1, panel b), which is also the radial range covering the temperature and density of the sweet spot, which is just outside the O2 iceline.
4.3 Changing Ebin for atomic oxygen, and inclusion of O3
We introduced O3 and included it in the chemical network with production through iO2 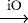 iO3 (activation energy of 500 K), and destruction through barrierless hydrogenation. After this change, the binding energy Ebin for oxygen atoms was increased from 800 to 1660 K, as measured by He et al. (2015). This change was expected to make oxygen atoms less volatile, thus having them reside on the grain surfaces at higher temperatures than before. This was expected to aid the production of O2 and O3 ices through the pathwayiO
iO3 (activation energy of 500 K), and destruction through barrierless hydrogenation. After this change, the binding energy Ebin for oxygen atoms was increased from 800 to 1660 K, as measured by He et al. (2015). This change was expected to make oxygen atoms less volatile, thus having them reside on the grain surfaces at higher temperatures than before. This was expected to aid the production of O2 and O3 ices through the pathwayiO 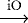 iO2
iO2 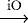 iO3.
iO3.
The expansion to include O3 chemistry induces verydifferent behaviours of O2, O3, and the chemically related H2O2. Still assuming the PSN midplane, and ionisation Level 1, O2 ice is not reproduced to match the observed cometary abundances.
The updated binding energy for atomic oxygen also had an effect, as the parameter space investigation revealed O2 ice production matching the observed value, even when including O3 chemistry. This change made the oxygen atoms less volatile, thus adsorbing to the grain at higher temperatures.
4.4 Narrowing down on O2 ice production
With the lower produced level of O2 ice after inclusion of O3 chemistry the question remained if O2 ice, in any case, can be produced to within the measured levels. Besides updating Ebin for atomic oxygen, two parameters for grain–surface chemistry, which had been kept constant thus far were now varied: the barrier width for quantum tunnelling, and the ratio of diffusion-to-binding energy of icy molecules. Adjusting these parameters, in particular the barrier width for quantum tunnelling, appears to have important impacts on the production level of O2 ice. Increasing the barrier for quantum tunnelling from 1 to 2 Å, for temperatures ranging between 15–25 K, and densities 109 –1010 cm−3, results in O2 ice produced to within the mean measured level in comet 67P. Increasing the barrier width from 1 to 2 Å lowers the mobility of H and H2On the grain surfaces. This means that O + O reactions proceed more efficiently than hydrogenation of O, O2, and O3 ice, which in turn leads to higher abundances of O2 and O3 ices for a bqt of 2 Å. Generally, with this wider tunnelling barrier, the measured mean abundance of O2 ice can be reproduced relatively early in the evolution, from 0.05–0.5 Myr. At 25 K the corresponding level of H2O2 ice was close to its observed value. O3 ice, however, remains more abundant than O2 ice. Early in the evolution, O3 ice is even more abundant than H2O ice, but this is explained by O3 ice being a precursor to H2O ice in the reaction pathway:
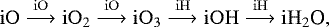 (3)
(3)
due to the availability of free oxygen. Indeed, in Fig. 8, showing the time evolution of species, O3 is the dominant oxygen carrier at early times, and H2O at later times. Exceptions to this are the cases of a low ratio of diffusion-to-binding energy of 0.3, and temperatures of 25 K (panels c and f in Fig. 8), where H2O2 dominates at later times. In those cases, a lower diffusion energy and higher temperature means a higher mobility of icy molecules on the grain surface. This leads to OH (the product of O3 + H) reacting with O2 ice (precursor to O3 ice and product of the hydrogenation of O3 ice), thereby lowering the abundance of O3 ice, and increasing the abundance of first O2H ice, and subsequently H2O2 ice via the reaction pathway 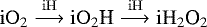 .
.
4.5 Activation energy for O3 ice production pathway
A crucial element in modelling chemical evolution is the assumed activation energies for reactions. Especially for grain–surface chemistry, these energies remain somewhat uncertain, due to the difficulty of estimating them through production rates in the lab. In this work, the fiducial activation energy for the reaction iO + iO2 → iO3 was Eact = 500 K (Lamberts et al. 2013), resulting in model O3 ice at a higher abundance than its parent species, O2 ice. This means that the modelled abundance of O3 ice is several orders of magnitude higher than the upper limit determined in comet 67P (see Figs. 8 and 9).
Testing out higher activation energies for the production of O3 ice (thereby impeding the O + O2 reaction) revealed that for Eact = 2000 K, the production of O3 ice was sufficiently impeded to bring the abundance below the limit observed in the comet. This test simultaneously showed a match between both the abundances of O2 ice and H2O2 ice and the cometary abundances at 25 K between 0.8 and 1 Myr evolution for an ionisation level of ζ = 10−17 s−1, starting from the reset scenario. Thus, a sweet spot in the parameter space, where all three species match observed abundances, was found. However, it should be emphasised that such a high barrier is not supported in previous analyses of laboratory experiments. An upper limit for the activation energy of O + O2Of Eact = 150 K on amorphous silicate surfaces was derived from experimental results by Minissale et al. (2014). Lamberts et al. (2013) required an activation energy of Eact = 500 K in order to reproduce experimental results from Ioppolo et al. (2010) of O3 production on thick ices, and in agreement with this result, Taquet et al. (2016) were able to reproduce the low abundances O3 and O2 H on ice mantles in dark clouds using an activation energy of Eact = 300 K.
In this work O3 remains overproduced for these levels of activation energies, even when increasing it to Eact = 1000 K. Only using an artificially high energy of Eact = 2000 K for the O + O2 reaction lowered the abundance of O3 ice to the observed level. This could suggest that as-yet unknown reactions may be missing from the network: reactions involving either O2 Or O that do not lead to O3 (so O and O2 get locked up in other molecules than O3) and/or new routes for destruction of O3 ice.
4.6 Location of O2 ice production sweet spot in PSN disk midplane
Taking the sweet spot for matching abundances of O2 ice, H2O2 ice, and O3 ice, it is interesting to look at where in the PSN disk midplane the physical conditions for this match may be satisfied. A close look at Fig. 1a shows that indeed in the radial range ~ 100–130 AU are found a temperature of ~25 K and a density of 109−1010 cm−3. Thus, for the sweet-spot O2 ice production scenario, this would be the predicted radial range for formation of both comets 1P and 67P, and a formation timescale by 0.8–1 Myr, given the model assumptions. This radial range is two to three times larger than the orbit of the present day Kuiper belt (30–50 AU).
4.7 Primordial origin of O2 ice
One scenario does, however, predict early presence of O2 ice to within the observed level, and H2O2 ice and O3 ice orders of magnitude lower than that of O2 ice. This is the scenario starting with an initial abundance of O2Of ~ 5% with respect to the total elemental oxygen abundance, which was inspired by the results of Taquet et al. (2016) assuming that the O2 is inherited from the parent cloud. Given early formation of the comets (by thousands to tens of thousands of years after formation of the PSN midplane), this scenario remains likely for the formation of the ices, and the fiducial values of bqt = 1 Å and Eact= 500 K for the O + O2 reaction in the ice. This scenario agrees with the findings of Taquet et al. (2016).
5 Conclusion
Since the somewhat unexpected detection of abundant O2 ice in the coma of comet 67P, several studies have attempted to explain the origin of the O2. Building on the results from Paper I, this work has investigated the possibility of in situ formation of O2 ice on grains in the midplane of the PSN disk midplane.
While a high abundance of O2 ice, matching that observed in comet 67P, is reproduced outside the O2 ice in the PSN disk midplane at intermediate evolutionary stages when assuming the initial chemistry to be reset, the same production is not seen after including O3 ice chemistry into the chemical network. For the fiducial choice of parameters for grain–surface chemistry, and an activation energy of 500 K for the O + O2 → O3 reaction on the grains, O3 ice is, in most cases, found to be the dominant oxygen-carrier next to H2O ice, and O2 ice was orders of magnitude too low in abundance compared to the abundance observed in comet 67P.
In order to test the sensitivity of the production of O2, O3, and H2O2 ices to the assumed parameters for grain–surface chemistry, in particular the barrier width for quantum tunnelling bqt and the ratio of diffusion-to-binding energy of icemolecules Ediff∕Ebin, a parameterspace investigation was conducted. Several temperatures and densities were also tested, and the reset scenario assumed for initial abundances. This led to a sweet-spot set of parameters being revealed: bqt = 2 Å, Ediff∕Ebin = 0.3−0.5 T = 15–25 K and n = 109−1010 cm−3 which facilitated O2 reproduction matching the observed level. However, the abundances of O3 and H2O2 ices were still in disagreement with the observed values by orders of magnitude.
As a last adjustment of the chemistry intended to lower the O3 ice abundance, the activation energy for production of O3 ice from the association of O and O2 ices was increased in order to mitigate possible unknown chemical pathways away from O3. For an activation energy of Eact = 2000 K, Ediff∕Ebin = 0.5, and the remaining physical and chemical conditions as given above, the abundances of O2 ice, H2O2 ice, and the upper limit for O3 ice in the comet were all reproduced. This matches a formation location in the PSN disk midplane between 120 and 150 AU, just outside the O2 iceline. However, this high activation energy for O3 ice production is not supported by laboratory estimates, and thus more laboratory work is needed to determine potential missing chemical pathways for O3 ice chemistry.
A model that starts out with a percentage of elemental oxygen locked in O2 and thus assuming a primordial origin of O2, also reproduced the observed abundance of O2 ice at early stages of evolution, without increasing Eact for the O + O2 reaction. Here, the O3 and H2O2 ice abundances were below the O2 ice abundance, but not matching the observed abundance levels. However, since the observed abundances of all three ices species are only reproduced in this work in the case for a set of rather extreme choices for the chemical parameters, the most plausible explanation for the origin of the cometary O2 ice remains the primordial, as originally proposed by Taquet et al. (2016).
Acknowledgements
The authors thank Ewine van Dishoeck and Arthur Bosman for many useful discussions and comments that helped the investigation and improved the quality of the manuscript. The authors also thank an anonymous referee for their review of this work. Astrochemistry in Leiden is supported by the European Union A-ERC grant 291141 CHEMPLAN and the Netherlands Research School for Astronomy (NOVA). C.W. also acknowledges the Netherlands Organisation for Scientific Research (NWO, grant 639.041.335) and the University of Leeds for financial support.
Appendix A Additional table and figures
Figure A.1 shows the gas and ice abundances of O, O2, H2O, and H2O2 as a function of radius by 10 Myr of evolution, for the chemical network without O3 chemistry. Figure A.2 shows the gas and ice abundances of O2, H2O and H2O2 and O3 as a function of radius by 10 Myr of evolution, for the chemical network including O3.
Initial abundances (with respect to Hnuc) for atomic (reset scenario) and molecular (inheritance scenario) setups.
 |
Fig. A.1 Abundances by 10 Myr evolution. From top to bottom panels: inheritance scenario, reset scenario, water scenario, and oxygen scenario. From left to right panels: changing ionisation levels. The chemical network utilised does not include O3 chemistry. |
 |
Fig. A.2 Abundances by 10 Myr evolution. From top to bottom panels: inheritance scenario, reset scenario, water scenario, and oxygenscenario. From left to right panels: changing ionisation levels. The chemical network utilised includes O3 chemistry. |
 |
Fig. A.3 Abundances (given as colours) for H2O ice as function of midplane density (x-axes), and temperature (y-axes) at different evolutionary steps for the reset scenario. From left to right panels: abundances from model runs with different parameters for grain–surface reactions: Cols. 1 and 2: bqt = 1 Å, Cols. 3 and 4: bqt = 1 Å, Cols. 1 and 3: with Ediff∕Ebin = 0.3, and Cols. 2 and 4: with Ediff∕Ebin = 0.5. From top to bottom panels: different evolutionary times, from 0.05 Myr (top) to 10 Myr (bottom). To the right of each plot is a colourbar, indicating the abundance level with respect to Hnuc for each colour. The chemical network utilised includes O3 chemistry. |
 |
Fig. A.4 Abundances (given as colours) for O3 ice as function of midplane density (x-axes), and temperature (y-axes) at different evolutionary steps for the reset scenario. From left to right panels: abundances from model runs with different parameters for grain–surface reactions: Cols. 1 and 2: bqt = 1 Å, Cols. 3 and 4: bqt = 1 Å, Cols. 1 and 3: with Ediff∕Ebin = 0.3, and Cols. 2 and 4: with Ediff∕Ebin = 0.5. From top to bottom panels: different evolutionary times, from 0.05 Myr (top) to 10 Myr (bottom). To the right of each plot is a colourbar, indicating the abundance level with respect to H2O ice for each colour. The chemical network utilised includes O3 chemistry. Darkest hue of blue matches the upper limit for cometary O3 abundances. |
 |
Fig. A.5 Abundances (given as colours) for H2O2 ice as function of midplane density (x-axes), and temperature (y-axes) at different evolutionary steps for the reset scenario. From left to right panels: abundances from model runs with different parameters for grain–surface reactions: Cols. 1 and 2: bqt = 1 Å, Cols. 3and 4: bqt = 1 Å, Cols. 1 and 3: with Ediff∕Ebin = 0.3, and Cols. 2 and 4: with Ediff∕Ebin= 0.5. From top to bottom panels: different evolutionary times, from 0.05 Myr (top) to 10 Myr (bottom). To the right of each plot is a colourbar, indicating the abundance level with respect to H2O ice for each colour. The chemical network utilised includes O3 chemistry. Lightest hue of blue matches the cometary H2O2 abundances. |
References
- Aikawa, Y., Umebayashi, T., Nakano, T., & Miyama, S. M. 1997, ApJ, 486, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Bieler, A., Altwegg, K., Balsiger, H., et al. 2015, Nature, 526, 678 [Google Scholar]
- Brown, W. A., & Bolina, A. S. 2007, MNRAS, 374, 1006 [NASA ADS] [CrossRef] [Google Scholar]
- Cazaux, S., & Tielens, A. G. G. M. 2002, ApJ, 575, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Cleeves, L. I., Adams, F. C., & Bergin, E. A. 2013, ApJ, 772, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Cuppen, H. M., Ioppolo, S., Romanzin, C., & Linnartz, H. 2010, Phys. Chem. Chem. Phys., 12, 12077 [NASA ADS] [CrossRef] [Google Scholar]
- Cuppen, H. M., Walsh, C., Lamberts, T., et al. 2017, Space Sci. Rev., 212, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Dalgarno, A. 2006, Proc. Natl. Acad. Sci. USA, 103, 12269 [NASA ADS] [CrossRef] [Google Scholar]
- Dulieu, F., Minissale, M., & Bockelée-Morvan, D. 2017, A&A, 597, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eistrup, C., Walsh, C., & van Dishoeck E. F. 2016, A&A, 595, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eistrup, C., Walsh, C., & van Dishoeck E. F. 2018, A&A, 613, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ennis, C. P., Bennett, C. J., & Kaiser, R. I. 2011, Phys. Chem. Chem. Phys., 13, 9469 [CrossRef] [Google Scholar]
- Garrod, R. T., & Herbst, E. 2006, A&A, 457, 927 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hayashi, C. 1981, Prog. Theor. Phys. Suppl., 70, 35 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- He, J., Shi, J., Hopkins, T., Vidali, G., & Kaufman, M. J. 2015, ApJ, 801, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Indriolo, N., Neufeld, D. A., Gerin, M., et al. 2015, ApJ, 800, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Ioppolo, S., Cuppen, H. M., Romanzin, C., van Dishoeck, E. F., & Linnartz, H. 2008, ApJ, 686, 1474 [NASA ADS] [CrossRef] [Google Scholar]
- Ioppolo, S., Cuppen, H. M., Romanzin, C., van Dishoeck, E. F., & Linnartz, H. 2010, Phys. Chem. Chem. Phys., 12, 12065 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, B. M., Kaiser, R. I., & Strazzulla, G. 2014, ApJ, 781, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Lamberts, T., Cuppen, H. M., Ioppolo, S., & Linnartz, H. 2013, Phys. Chem. Chem. Phys., 15, 8287 [CrossRef] [Google Scholar]
- Martín-Doménech, R., Manzano-Santamaría, J., Muñoz Caro, G. M., et al. 2015, A&A, 584, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McElroy, D., Walsh, C., Markwick, A. J., et al. 2013, A&A, 550, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Minissale, M., Congiu, E., & Dulieu, F. 2014, J. Chem. Phys., 140, 074705 [NASA ADS] [CrossRef] [Google Scholar]
- Mousis, O., Ronnet, T., Brugger, B., et al. 2016, ApJ, 823, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Mousis, O., Ronnet, T., Lunine, J. I., et al. 2018, ApJ, 858, 66 [NASA ADS] [CrossRef] [Google Scholar]
- Penteado, E. M., Walsh, C., & Cuppen, H. M. 2017, ApJ, 844, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Rubin, M., Altwegg, K., van Dishoeck, E. F., & Schwehm, G. 2015, ApJ, 815, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Ruffle, D. P., & Herbst, E. 2000, MNRAS, 319, 837 [NASA ADS] [CrossRef] [Google Scholar]
- Taquet, V., Furuya, K., Walsh, C., & van Dishoeck E. F. 2016, MNRAS, 462, S99 [NASA ADS] [CrossRef] [Google Scholar]
- Teolis, B. D., Plainaki, C., Cassidy, T. A., & Raut, U. 2017, J. Geophys. Res., 122, 1996 [CrossRef] [Google Scholar]
- Tielens, A. G. G. M., & Allamandola, L. J. 1987, Astrophys. Space Sci. Lib., 134, 397 [Google Scholar]
- van Dishoeck, E. F., & Black, J. H. 1986, in Interstellar Processes: Abstracts of Contributed Papers, eds. D. J. Hollenbach & H. A. Thronson, Jr. [Google Scholar]
- Walsh, C., Nomura, H., & van Dishoeck E. 2015, A&A, 582, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Initial abundances (with respect to Hnuc) for atomic (reset scenario) and molecular (inheritance scenario) setups.
All Figures
 |
Fig. 1 Panel a: midplane temperature and density profiles for the pre-solar nebula. Panel b: ionisation levels utilised in the models. Level 1: SLRs only. Level 2: SLRs + fiducial CRs. Level 3: SLRs + enhanced CRs. |
| In the text | |
 |
Fig. 2 Radial abundance profiles for the inheritance scenario at multiple evolutionary time steps. Top to bottom panels: H2O, O2, and H2O2. Left to right panels: increasing ionisation levels. For O2 and H2O2, the limits detected in comet 67P are indicated as yellow and red shaded areas, respectively. The chemical network utilised does not include O3 chemistry. |
| In the text | |
 |
Fig. 3 Radial abundance profiles for the reset scenario at multiple evolutionary time steps. Top to bottom panels are H2O, O2 and H2O2 ices. Left to right panels are increasing ionisation levels. For O2 and H2O2 the limits detected in comet 67P are indicated as yellow and red shaded areas, respectively. The chemical network utilised does not include O3 chemistry. |
| In the text | |
 |
Fig. 4 Abundances by 10 Myr evolution in the oxygen-only scenario, for ionisation Level 1. Panel a: without O3 chemistry included. Panel b: with O3 chemistry included. |
| In the text | |
 |
Fig. 5 Radial abundance profiles for the inheritance scenario at multiple evolutionary time steps. Top to bottom panels: H2O, O2, H2O2, and O3 ices. Left to right panels: increasing ionisation levels. For O2, H2O2, and O3 the limits, and upper limit, detected in comet 67P, are indicated as yellow, red and grey shaded areas, respectively. The chemical network utilised includes O3 chemistry. |
| In the text | |
 |
Fig. 6 Radial abundance profiles for the reset scenario at multiple evolutionary time steps. Top to bottom panels: H2O, O2 and H2O2 and O3 ices. Left to right panels: increasing ionisation levels. For O2, H2O2, and O3 limits, and upper limit, detected in comet 67P, are indicated as yellow, red, and grey shaded areas, respectively. The chemical network utilised includes O3 chemistry. |
| In the text | |
 |
Fig. 7 Abundances (given as colours) for O2 ice as function of midplane density (x-axes), and temperature (y-axes) at different evolutionary steps for the reset scenario. From left to right panels: abundances from model runs with different parameters for grain–surface reactions: Cols. 1 and 2: bqt = 1 Å, Cols. 3 and 4: bqt = 1 Å, Cols. 1 and 3: with Ediff∕Ebin = 0.3, and Cols. 2 and 4: with Ediff∕Ebin = 0.5. From top to bottom panels: different evolutionary times, from 0.05 Myr (top) to 10 Myr (bottom). To the right of each plot is a colourbar, indicating the abundance level with respect to H2O ice for each colour. The chemical network utilised includes O3 chemistry. Orange matches cometary O2 abundances. |
| In the text | |
 |
Fig. 8 Evolving abundances as function of time for the reset scenario for six different combinations of temperature (15, 20, or 25 K), density (109 or 1010 cm−3) and molecular diffusion-to-binding energy ratio of 0.3. The barrier width for quantum tunnelling is bqt = 2 Å. Theorange shaded regions indicate the limits to the measured abundance of O2 ice in the coma of comet 67P. The red shaded regions indicate the limits to the measured abundance of H2O2, and the top of the grey shaded region marks the upper limit to the measured abundance of O3 ice in comet 67P. The chemical network utilised includes O3 chemistry. |
| In the text | |
 |
Fig. 9 Evolving abundances as function of time for the reset scenario for six different combinations of temperature (15, 20, or 25 K), density (109 or 1010 cm−3) and molecular diffusion-to-binding energy ratio of 0.5. The barrier width for quantum tunnelling is bqt = 2 Å. Theorange shaded regions indicate the limits to the measured abundance of O2 ice in the coma of comet 67P. The red shaded regions indicate the limits to the measured abundance of H2O2, and the top of the grey shaded region marks the upper limit to the measured abundance of O3 ice in comet 67P. The chemical network utilised includes O3 chemistry. |
| In the text | |
 |
Fig. 10 Evolving abundances for O2 ice, H2O2 ice and O3 ice for three different activation energies for the reaction iO + iO2. Panel a is for T = 20 K. Panel b is for T = 25 K. The barrier width for quantum tunnelling is bqt = 2 Å, and the molecular diffusion-to-binding energy is 0.5. |
| In the text | |
 |
Fig. 11 Evolving abundances as function of time for the inheritance scenario, plus 5% extra elemental oxygen as O2, for six different combinations of temperature (15, 20, or 25 K), density (109 or 1010 cm−3), and molecular diffusion-to-binding energy ratio of 0.5. The barrier width for quantum tunnelling is bqt = 2 Å. Theorange shaded regions indicate the limits to the measured abundance of O2 ice in the coma of comet 67P. The red shaded regions indicate the limits to the measured abundance of H2O2, and the top of the grey shaded region marks the upper limit to the measured abundance of O3 ice in comet 67P. |
| In the text | |
 |
Fig. A.1 Abundances by 10 Myr evolution. From top to bottom panels: inheritance scenario, reset scenario, water scenario, and oxygen scenario. From left to right panels: changing ionisation levels. The chemical network utilised does not include O3 chemistry. |
| In the text | |
 |
Fig. A.2 Abundances by 10 Myr evolution. From top to bottom panels: inheritance scenario, reset scenario, water scenario, and oxygenscenario. From left to right panels: changing ionisation levels. The chemical network utilised includes O3 chemistry. |
| In the text | |
 |
Fig. A.3 Abundances (given as colours) for H2O ice as function of midplane density (x-axes), and temperature (y-axes) at different evolutionary steps for the reset scenario. From left to right panels: abundances from model runs with different parameters for grain–surface reactions: Cols. 1 and 2: bqt = 1 Å, Cols. 3 and 4: bqt = 1 Å, Cols. 1 and 3: with Ediff∕Ebin = 0.3, and Cols. 2 and 4: with Ediff∕Ebin = 0.5. From top to bottom panels: different evolutionary times, from 0.05 Myr (top) to 10 Myr (bottom). To the right of each plot is a colourbar, indicating the abundance level with respect to Hnuc for each colour. The chemical network utilised includes O3 chemistry. |
| In the text | |
 |
Fig. A.4 Abundances (given as colours) for O3 ice as function of midplane density (x-axes), and temperature (y-axes) at different evolutionary steps for the reset scenario. From left to right panels: abundances from model runs with different parameters for grain–surface reactions: Cols. 1 and 2: bqt = 1 Å, Cols. 3 and 4: bqt = 1 Å, Cols. 1 and 3: with Ediff∕Ebin = 0.3, and Cols. 2 and 4: with Ediff∕Ebin = 0.5. From top to bottom panels: different evolutionary times, from 0.05 Myr (top) to 10 Myr (bottom). To the right of each plot is a colourbar, indicating the abundance level with respect to H2O ice for each colour. The chemical network utilised includes O3 chemistry. Darkest hue of blue matches the upper limit for cometary O3 abundances. |
| In the text | |
 |
Fig. A.5 Abundances (given as colours) for H2O2 ice as function of midplane density (x-axes), and temperature (y-axes) at different evolutionary steps for the reset scenario. From left to right panels: abundances from model runs with different parameters for grain–surface reactions: Cols. 1 and 2: bqt = 1 Å, Cols. 3and 4: bqt = 1 Å, Cols. 1 and 3: with Ediff∕Ebin = 0.3, and Cols. 2 and 4: with Ediff∕Ebin= 0.5. From top to bottom panels: different evolutionary times, from 0.05 Myr (top) to 10 Myr (bottom). To the right of each plot is a colourbar, indicating the abundance level with respect to H2O ice for each colour. The chemical network utilised includes O3 chemistry. Lightest hue of blue matches the cometary H2O2 abundances. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.