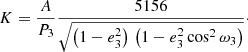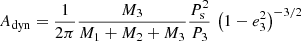| Issue |
A&A
Volume 620, December 2018
|
|
|---|---|---|
| Article Number | A72 | |
| Number of page(s) | 7 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201833708 | |
| Published online | 30 November 2018 | |
Possible substellar companions in low-mass eclipsing binaries: GU Bootis and YY Geminorum
1
Astronomical Institute, Faculty of Mathematics and Physics, Charles University, V Holešovičkách 2, 180 00
Praha 8, Czech Republic
e-mail: wolf@cesnet.cz
2
Astronomical Institute, Academy of Sciences, Fričova 298, 251 65
Ondřejov, Czech Republic
3
Institute of Physics, Faculty of Philosophy and Science, Silesian University in Opava, Bezručovo nám. 13, 746 01
Opava, Czech Republic
4
Variable Star and Exoplanet Section of the Czech Astronomical Society, Czech Republic
5
Observatory Valašské Meziříčí, Vsetínská 78, 757 01
Valašské Meziříčí, Czech Republic
6
Observatory Prostějov, Kolářovy sady 3348, 796 01
Prostějov, Czech Republic
7
Faculty of Civil Engineering, University of Technology, Brno, Czech Republic
8
Observatory Mladá Boleslav, 294 04
Dolní Bousov, Czech Republic
9
Observatory Úpice, U Lipek 160, 542 32
Úpice, Czech Republic
Received:
25
June
2018
Accepted:
22
September
2018
We present the next results of our long-term observational project to analyze the variations in the orbital periods of low-mass eclipsing binaries. About 70 new precise mid-eclipse times recorded with a CCD were obtained for two eclipsing binaries with short orbital periods: GU Boo (P = 0.d49) and YY Gem (0.d81). Observed-minus-calculated diagrams of the stars were analyzed using all reliable timings, and new parameters of the light-time effect were obtained. We derived for the first time or improved the short orbital periods of possible third bodies of 11 and 54 years for these low-mass binaries, respectively. We calculated that the minimum masses of the third components are close to 50 MJup, which corresponds to the mass of brown dwarfs. The multiplicity of these systems also plays an important role in the precise determination of their physical parameters.
Key words: (stars:) binaries: eclipsing / stars: late-type / stars: individual: GU Bootis / stars: individual: YY Geminorum / stars: fundamental parameters
© ESO 2018
1. Introduction
Low-mass stars and their multiple systems play an important role in stellar astrophysics. The origin of low-mass stars and brown dwarfs is still an unresolved question in star formation theory. Moreover, observations of low-mass stars show a discrepancy between estimated and modeled parameters, where the models give 5–10% smaller radii than observations (Chabrier & Baraffe 2000; Morales et al. 2010; Mann et al. 2015). The identification and characterization of low-mass multiples is also highly relevant to exoplanet studies.
Searching for substellar companions to short-period low-mass eclipsing binaries (LMB) sheds more light on the formation and evolution of planets and brown dwarfs. Because of the small size of the binary components, the eclipse times of this type of binary system can be determined with high precision, and very small amplitude variations in the orbital period can be detected by analyzing the observed-minus-calculated (O–C) diagram. This makes them very promising targets to search for circumbinary brown dwarfs or giant planets by analyzing the light-time effect (LITE). To date, several substellar companions to LMBs have been discovered using this efficient method (Lee et al. 2009; Hinse et al. 2012; Pribulla et al. 2012). Moreover, low-mass stars frequently exhibit phenomena associated with magnetic activity, such as flares and star spots.
We here report on a long-term mid-eclipse time campaign of two selected LMBs. These systems are all relatively well-known low-mass objects in the northern hemisphere. Their orbital periods are up to 20 h, and spectroscopic observations have been published for both LMBs. This paper is a continuation of our previous period study of LMB presented in Wolf et al. (2016).
2. Observations of mid-eclipses
Long-term photometric observations for accumulating the mid-eclipse times are necessary when the O–C method is used to analyze the period variation. Short-period and detached LMBs with deep and symmetric eclipses enable us to obtain individual minimum times of eclipses with high accuracy. Moreover, this observing program is suitable for small amateur telescopes connected with modern detectors.
Since 2006, we have accumulated nearly 104 photometric observations during primary and secondary eclipses and derived about 80 precise times of minimum light for both systems. New CCD photometry was obtained mostly at the Ondřejov Observatory, Czech Republic, using the 0.65 m (f/3.6) reflecting telescope with the CCD cameras Apogee AP7p or the Moravian Instruments G2-3200 and VRI photometric filters. The next precise CCD photometry was carried out at the Valašské Meziříčí Observatory, Czech Republic, using the 0.3 m Celestron Ultima telescope with the CCD camera SBIG ST-7 or G2-1600 and VRI filters, and with the Jan Šindel Telescope (JST) reflector (0.40 m f/5) and G2-1600 CCD camera with a set of VR bandpass filters operated at the observing house of the Astronomical Society in Hradec Králové. Additional measurements were obtained at the Prostějov and Mladá Boleslav observatories, where a 0.2 m Newtonian telescope and the CCD camera Atik 320E and MII G2-8300 without filter were used, respectively.
A standard calibration (dark frame, flat field) was applied to the observed CCD frames. APHOT, a synthetic aperture photometry and astrometry software, was routinely used for data obtained at Ondřejov observatory. C-MUNIPACK1 was used to reduce our CCD time series obtained at Valašské Meziříčí, Hradec Králové, Mladá Boleslav and Prostějov. Differential photometry was performed using suitable comparison stars.
The computers at the telescope are synchronized using the time-server provided by tick.usno.navy.mil every two minutes. These corrections are usually on the order of 10−3 s. The new times of primary and secondary minima and their errors were generally determined by fitting the light curve by Gaussians or polynomials of the third or fourth order; we used the least-squares method. All new times are given in Tables A.1 and 3. The columns are self-explaining. If necessary, the times for the mid-eclipses are the averages of times obtained in two or three bandpasses.
All of the new timings we used in this analysis were first converted into barycentric Julian date dynamical time (BJD_TBD) using the time utilities of the Ohio State University2 (Eastman et al. 2010). Our new timings were combined with previously published times of minima, and where appropriate, the historic times were converted into BJD_TBD before analyses.
All new precise CCD times of minima were used with a weight of 10 in our computation. Some of our less precise measurements were weighted by a factor of 5, while the earlier visual times or times determined form sky surveys were given a weight of 1 or 0 because of the large scatter in these data. We found this traditional weighting scheme more reliable than using sometimes overestimated formal errors of individual mid-eclipse times obtained from different telescopes and light curves. We tested the stability of the results with respect to our somewhat arbitrarily chosen weighting scheme. The results show some dependence on the weighting, but this is mainly related to the less ideal distribution of available observations. For this reason, the results must be considered preliminary.
3. Period variations
An unseen circumbinary body can be detected by observing the timings of the mid-eclipse times of the eclipsing binary. The presence of an additional body causes a change in the relative distance of the eclipsing pair to the observer depending on the motion of the third body around the common barycenter of the system. As a result, the eclipses present delays or advances in the timings of minimum light. This well-known light-time effect (LITE) was introduced by Irwin (1952, 1959), who also gave a graphical fitting procedure for determining the elements of the light-time orbit. Later, the LITE was improved by Mayer (1990). See also Sterken (2005) for a short review on the application of O–C diagrams in the analysis of period variations of different variable stars. If the orbital period of the third star is short (usually up to one year), then additional dynamical perturbations of the inner orbit can occur that also create changes in the mid-eclipse times (see Borkovits et al. 2011, 2016). The precise mid-eclipse time estimation enable us to find small apparent period changes and derive the physical parameters of the next orbiting bodies that are of a substellar size and mass.
We propose LITE in both systems studied by means of an O–C diagram analysis. For an accurate calculation, the method originally described by Irwin (1952) and later extended by Mayer (1990) was applied. The least-squares method was used. Seven independent variables (T0, Ps, P3, e3, A, ω3, and T3) are determined in this procedure, where Ps is the orbital period of the binary, P3 is the orbital period of the third body, A is the semiamplitude of LITE, e3 represents the eccentricity of the outer orbit, and T3 is the periastron passage time of the third body. The zero epoch is given by T0, and the corresponding position of the periastron is represented by ω3.
3.1. GU Boo
The detached eclipsing binary GU Boo (also NSVS 7820507, GSC 02566-00776, Vmax = 13m.11, Sp. M0/1.5, Gaia parallax 6.146 ± 0.015 mas) is a relatively well-known northern low-mass binary and double-lined system with a short orbital period (P = 0.49 d). It was discovered as a variable object by Diethelm (2001) in the Robotic Optical Transient Search Experiment database (ROTSE I, Akerlof et al. 2000). Later, López-Morales & Ribas (2005) derived the first precise absolute dimensions and physical parameters. They identified this system as a low-mass binary composed of two similar stars of about 0.6 M⊙. The following linear light elements were derived by these authors:
von Braun et al. (2008) presented a set of Spitzer 24 micron MIPS time series and confirmed the previously derived system parameters from optical studies. The effect of star spots on accurate radius determination was measured by Windmiller et al. (2010), who also confirmed the previous results of López-Morales & Ribas (2005) at the level ∼2%.
The additional measurements were obtained at Úpice observatory (0.2 m telescope without filter) and Prostějov observatory, where a 0.4 m telescope and the V filter were used. The flare activity on this LMB was also captured during the monitoring of the secondary eclipse at Prostějov observatory on June 14, 2017 (see Fig 1). The brightness in V band has suddenly increased by 0.37 mag in BJD 2457919.4073.
 |
Fig. 1. V light curve of the secondary eclipse of GU Boo obtained in Prostějov observatory on June 14, 2017. The flare is clearly visible on the descending branch of the light curve on BJD 2457919.4073. |
The next timing of GU Boo was derived from the ASAS database (Pojmanski 2002) with lower precision. The Bootes-2 telescope3 in Spain (0.6 m RC telescope and CCD camera Andor iXon, Jelinek et al. 2016) was also used for the photometry of this object. All mid-eclipse times are listed in Table A.1, where epochs are calculated from the ephemeris given in Table 2. The data from Brát et al. (2009, 2011), Diethelm (2009, 2011, 2012), Zasche et al. (2011), and Hubscher (2017) were also included. A total of 125 times of minimum light were taken into our analysis, with 57 secondary eclipses among them. Several published times of amateur observers were omitted due to large scatter of these less precise data. The O–C diagram is shown in Fig. 2, the computed LITE parameters and their internal errors of the least-squares fit are given in Table 2. It also lists the period ratio 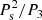 , which indicates possible dynamical interactions between the orbits that could be observed. a12 is the semi-axis of the eclipsing-pair orbit around the common center of mass with the third body. The reduced chi-square value,
, which indicates possible dynamical interactions between the orbits that could be observed. a12 is the semi-axis of the eclipsing-pair orbit around the common center of mass with the third body. The reduced chi-square value, 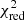 , is also calculated. The nonlinear prediction, corresponding to the fitted parameters, is plotted as a continuous blue curve.
, is also calculated. The nonlinear prediction, corresponding to the fitted parameters, is plotted as a continuous blue curve.
New times of minimum light for GU Boo.
 |
Fig. 2. Current O–C diagram for the eclipse times of GU Boo. The sinusoidal curve represents the LITE with a period of 11.1 years. The individual primary and secondary minima are denoted by circles and triangles, respectively. Larger symbols correspond to the CCD measurements, which were given higher weights in the calculations. |
3.2. YY Gem
The detached eclipsing binary YY Geminorum (also Castor C, Gliese 278C, BD+32 1582, ADS 6175C, HD 60179C, Vmax = 9m.27, Sp. dM1e, Gaia parallax 66.23 ± 0.05 mas and the distance 15.1 pc) is a frequently studied low-mass and double-lined spectroscopic binary and a member of the nearby Castor multiple stellar system. It contains two nearly identical components with a well-known flare activity. It was discovered spectroscopically in 1916 by Adams & Joy (1917); later, van Gent (1926) discovered eclipses and presented the first photographic light curve. YY Gem has been extensively studied in the past. The very precise absolute dimensions were obtained by Torres & Ribas (2002), M = 0.5992 ± 0.0047 M⊙, R = 0.6191 ± 0.0057 R⊙ and Teff = 3820 ± 100 K) for two practically identical components. See also the investigation history of the Castor multiple system presented in that paper. Qian et al. (2002) later found that the orbital period shows a secular decrease with a rate ∼10−10 day yr−1. They conclude that the system is undergoing secular mass and angular momentum loss through a magnetic stellar wind. They also presented the improved light elements
Recently, a multiwavelength study of YY Gem was presented by Butler et al. (2015). They included broad-band optical, near-infrared, ultraviolet, and radio data to determine the physical parameters and transient spots located near quadrature longitudes. New observations of eclipses were obtained at Mladá Boleslav and Prostějov observatories, where a 0.2 m Newtonian telescopes, Atik 320E, and the MII G2-8300 CCD camera were used, respectively. All mid-eclipse times of YY Gem given in Torres & Ribas (2002, their Table 3) as well as in Agerer & Hubscher (1999, 2002), Tas et al. (2004), Hubscher et al. (2009a,b, 2012), Hubscher (2011), Hubscher & Lehman (2015), Hubscher (2016), Zasche et al. (2014), and new timings published on the O–C Gateway of the Variable Star and Exoplanet Section, Czech Astronomical Society4, were included in our calculation with different weights. A total of 194 times of minimum light were used in our analysis, including 87 secondary eclipses. Many older visual mid-eclipse times were omitted due to the large scatter of these points. The computed LITE parameters are given in Table 2, the complete O–C diagram is shown in Fig. 3.
LITE parameters for selected LMBs (with errors of the last digit in parentheses).
New times of minimum light for YY Gem.
 |
Fig. 3. O–C graph for YY Gem. See legend to Fig. 2. The sinusoidal curve represents the LITE with a period of about 55 yr and an amplitude of 5 min. |
4. Discussion
The detection of the LITE in LMBs enables us to test the stellar multiplicity in low-mass stars and also prove current models of stellar evolution. The derived parameters of the third-body orbit allow us to determine the mass function f(M)
where P3 is the period of the third body (in years) and Mi are the component masses. The systemic radial velocity of the eclipsing pair has an amplitude (in km s−1) of
Assuming a coplanar orbit (i3 ∼ 90°), we can obtain a lower limit for the mass of the third component M3, min. These values for the third body of individual systems were calculated by iteration and are collected in Table 4. The amplitude of the dynamical contribution of the third body Adyn is given approximately by (Borkovits et al. 2016)
Physical properties of the selected LMBs and parameters of their third bodies (with errors of the last digit in parentheses).
and is also given in Table 4. The value of Adyn is on the order of seconds and is comparable with the precision of individual mid-eclipse time estimation.
Another possible mechanism for cyclical period variation is a magnetic activity cycle for systems with a late-type secondary star (Applegate 1992). However, the newly derived LITE periods for GU Boo (∼11 yr) are too short for the magnetic cycle when compared with a mean value of about 40–50 yr in Algols and RS CVn binaries (Lanza & Rodono 1999). This mechanism can contribute significantly to the observed period changes in YY Gem.
The reduced chi-square value, 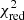 , is satisfactory for GU Boo. This value is substantially higher than unity for YY Gem, caused very probably by the large scatter of older mid-eclipse times. For both LMBs we expect the brown dwarfs that are well below the mass limit of 0.075 M⊙ as the unseen third body orbiting the eclipsing pair. Moreover, the Castor stellar system could be at least septuple.
, is satisfactory for GU Boo. This value is substantially higher than unity for YY Gem, caused very probably by the large scatter of older mid-eclipse times. For both LMBs we expect the brown dwarfs that are well below the mass limit of 0.075 M⊙ as the unseen third body orbiting the eclipsing pair. Moreover, the Castor stellar system could be at least septuple.
Additional timing variations with small amplitudes might be produced by the asymmetries of the eclipse light curves through stellar activity, such as star spots or small flares. The effect of star spots on the O–C diagrams was studied by Kalimeris et al. (2002). They found that star spots modulate the O–C values and can introduce high-frequency and low-amplitude disturbances of less than 0.01 d. These variations are caused by the change in the surface density and center of light over the visible hemisphere. Barros et al. (2013) showed that observed transit time variations in the hot-Jupiter WASP-10b system are also due to spot occultation features. Recently, Korda et al. (2017) tested the spot variability on the light curve of low-mass binaries and found a difference in mid-eclipse times of about 95 s.
It is possible that circumbinary companions may be detected to transit these binary systems, especially if their orbital plane is closely aligned with the orbital plane of the binary system. Our predicted circumbinary companions have orbital periods measured in years and orbital distances in au, giving them a low probability of detecting a transit.
On the other hand, the probable brown dwarf could be confirmed spectroscopically using modern precise spectrographs connected to medium-size telescopes. The derived amplitudes of the systemic radial velocity of both LMB are on the order of hundreds of m/s (Table 4). For YY Gem the previous measurements of radial velocity were obtained by Torres & Ribas (2002) in the phase of the third-body orbital period near 0.8. Their result γ = 0.54 ± 0.26 km s−1 is close to the value γ = 1.97 ± 0.24 km s−1 obtained by Ségransan et al. (2000) in practically the same phase. In 2019, we start at phase 0.2 of the long third-body orbit, which promises that we may be able to discover a detectable change in the systemic velocity of the binary. The previous radial-velocity curve of GU Boo was obtained in the phase 0.675 of the third-body orbital period (López-Morales & Ribas 2005) and resulted in γ = −24.57 ± 0.36 km s−1. After 2019, we can measure in phase up to 0.1, thus it will be also possible to determine a change in the γ-velocity with a precision on the order of several hundreds of m/s.
5. Conclusions
Our analysis of O–C diagrams has led to the identification of the next two probable triples in the known low-mass eclipsing binaries. The sinusoidal term in the orbital period is interpreted as the LITE being caused by a third body as the more likely scenario, most probably brown dwarfs of a similar mass about 50 MJup. In both systems the whole third-body orbital period is now practically covered by the precise mid-eclipse times.
Our results contribute to this class of rare triple systems in our Galaxy (Tokovinin 2004; Raghavan et al. 2010). The sample of well-known LMB needs to be increased, and observations of additional systems would be very useful.
Acknowledgments
This research was supported by the Research Program MSM0021620860 Physical Study of objects and processes in the Solar System and in Astrophysics of the Ministry of Education of the Czech Republic and partially by the Czech Science Foundation, grant P209/10/0715, and in its final stage by the grant GA15-02112S. K.H. was supported by the project RVO: 67985815. The authors would also like to thank Lenka Kotková, Ondřejov observatory, Marek Chrastina and Dalibor Hanžl, Masaryk University Brno, for their important contribution to photometric observations. The following internet-based resources were used in research for this paper: the SIMBAD database and the VizieR service operated at CDS, Strasbourg, France; the NASA’s Astrophysics Data System Bibliographic Services. This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement. This research is part of an ongoing collaboration between professional astronomers and the Czech Astronomical Society, Variable Star and Exoplanet Section. We gratefully acknowledge very useful suggestions by the referee.
References
- Adams, W. S., & Joy, A. H. 1917, ApJ, 46, 313 [NASA ADS] [CrossRef] [Google Scholar]
- Agerer, F., & Hubscher, J. 1999, IBVS No. 4711 [Google Scholar]
- Agerer, F., & Hubscher, J. 2002, IBVS No. 5296 [Google Scholar]
- Akerlof, C., Amrose, S., Balsano, R., et al. 2000, AJ, 119, 1901 [NASA ADS] [CrossRef] [Google Scholar]
- Applegate, J. H. 1992, ApJ, 385, 621 [NASA ADS] [CrossRef] [Google Scholar]
- Baraffe, I., Chabrier, G., Allard, F., & Hauschild, P. H. 1998, A&A, 337, 403 [NASA ADS] [Google Scholar]
- Barros, S. C. C., Boué, G., Gibson, N. P., et al. 2013, MNRAS, 430, 3032 [NASA ADS] [CrossRef] [Google Scholar]
- Borkovits, T., Csizmadia, Sz, Forgacs-Dajka, E., et al. 2011, A&A, 528, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Borkovits, T., Hajdu, T., Sztakovics, J., et al. 2016, MNRAS, 455, 4136 [NASA ADS] [CrossRef] [Google Scholar]
- Brát, L., Zejda, M. & Svoboda, P. 2007, OEJV, 74 [Google Scholar]
- Brát, L., Trnka, J., Lehký, M., et al. 2009, OEJV, 107 [Google Scholar]
- Brát, L., Trnka, J., Šmelcer, L., et al. 2011, OEJV, 137 [Google Scholar]
- Butler, C. J., Erkan, N., Budding, E., et al. 2015, MNRAS, 446, 4205 [NASA ADS] [CrossRef] [Google Scholar]
- Chabrier, G., & Baraffe, I. 2000, ARA&A, 38, 337 [NASA ADS] [CrossRef] [Google Scholar]
- Diethelm, R. 2001, IBVS No. 5060 [Google Scholar]
- Diethelm, R. 2009, IBVS No. 5894 [Google Scholar]
- Diethelm, R. 2010, IBVS No. 5920 [Google Scholar]
- Diethelm, R. 2011, IBVS No. 5992 [Google Scholar]
- Diethelm, R. 2012, IBVS No. 6029 [Google Scholar]
- Diethelm, R. 2013, IBVS No. 6063 [Google Scholar]
- Eastman, J., Siverd, R., & Gaudi, B. S. 2010, PASP, 122, 935 [NASA ADS] [CrossRef] [Google Scholar]
- Hinse, T. C., Lee, J. W., Gozdziewski, K., et al. 2012, MNRAS, 420, 3609 [NASA ADS] [CrossRef] [Google Scholar]
- Hoňková, K., Juryšek, J., Lehký, M., et al. 2013, OEJV, 160, 1 [Google Scholar]
- Hoňková, K., Juryšek, J., Lehký, M., et al. 2015, OEJV, 168 [Google Scholar]
- Hubscher, J. 2011, IBVS No. 5984 [Google Scholar]
- Hubscher, J. 2016, IBVS No. 6157 [Google Scholar]
- Hubscher, J. 2017, IBVS No. 6149 [Google Scholar]
- Hubscher, J., & Lehman 2015, IBVS No. 6149 [Google Scholar]
- Hubscher, J., Lehmann, P. B., & Walter, F. 2012, IBVS No. 6010 [Google Scholar]
- Hubscher, J., Steinbach, H. M., & Walter, F. 2009a, IBVS No. 5874 [Google Scholar]
- Hubscher, J., Steinbach, H. M., & Walter, F. 2009b, IBVS No. 5889 [Google Scholar]
- Irwin, J. B. 1952, ApJ, 116, 211 [NASA ADS] [CrossRef] [Google Scholar]
- Irwin, J. B. 1959, AJ, 64, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Jelinek, M., Castro-Tirado, A. J., Cunniffe, R., et al. 2016, Adv. Astron., 1928465 [Google Scholar]
- Juryšek, J., Hoňková, K., Šmelcer, L., et al. 2017, OEJV, 179 [Google Scholar]
- Kalimeris, A., Rovithis-Livaniou, H., & Rovithis, P. 2002, A&A, 387, 969 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Korda, D., Zasche, P., Wolf, M., et al. 2017, AJ, 154, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Lanza, A. F., & Rodono, M. 1999, A&A, 349, 887 [NASA ADS] [Google Scholar]
- Lee, J. W., Kim, S. L., Kim, C. H., et al. 2009, AJ, 137, 3181 [NASA ADS] [CrossRef] [Google Scholar]
- López-Morales, M., & Ribas, I. 2005, ApJ, 631, 1120 [NASA ADS] [CrossRef] [Google Scholar]
- Mann, A. W., Feiden, G. A., Gaidos, E., et al. 2015, ApJ, 804, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Mayer, P. 1990, Bull. Astr. Inst. Czech., 41, 231 [Google Scholar]
- Morales, J. C., Gallardo, J., Ribas, I., et al. 2010, ApJ, 718, 502 [NASA ADS] [CrossRef] [Google Scholar]
- Paschke, A. 2014, OEJV, 162 [Google Scholar]
- Pojmanski, G. 2002, AcA, 52, 397 [Google Scholar]
- Pribulla, T., Vaňko, M., Ammler-von Eiff, M., et al. 2012, Astron. Nachr., 333, 754 [NASA ADS] [CrossRef] [Google Scholar]
- Qian, S., Liu, D., Tan, W., et al. 2002, AJ, 124, 1060 [NASA ADS] [CrossRef] [Google Scholar]
- Raghavan, D., McAlister, H. A., Henry, T. J., et al. 2010, ApJS, 190, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Riaz, R., Vanaverbeke, S., & Schleicher, D. R. G. 2018, MNRAS, 478, 5460 [NASA ADS] [CrossRef] [Google Scholar]
- Ségransan, D., Delfosse, X., Forveille, T., et al. 2000, A&A, 364, 665 [Google Scholar]
- Sterken, C. 2005, in The Light-Time Effect in Astrophysics, Proc of ASP Conf Series, 335 [Google Scholar]
- Tas, G., Sipahi, E., Dal, H. A., et al. 2004, IBVS No. 5548 [Google Scholar]
- Tokovinin, A. 2004, Rev. Mex. Astron. Astrofis. Conf. Ser., 21, 7 [NASA ADS] [Google Scholar]
- Torres, G., & Ribas, I. 2002, ApJ, 567, 1140 [NASA ADS] [CrossRef] [Google Scholar]
- von Braun, K., van Belle, G. T., Ciardi, D. R., et al. 2008, ApJ, 677, 545 [NASA ADS] [CrossRef] [Google Scholar]
- van Gent, H. 1926, BAN, 3, 121 [NASA ADS] [Google Scholar]
- Windmiller, G., Orosz, J. A., & Etzel, P. B. 2010, ApJ, 712, 1003 [NASA ADS] [CrossRef] [Google Scholar]
- Wolf, M., Zasche, P., Kučáková, H., et al. 2016, A&A, 587, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zasche, P., Uhlař, R., Kučáková, H., et al. 2011, IBVS No. 6007 [Google Scholar]
- Zasche, P., Uhlař, R., Kučáková, H., et al. 2014, IBVS No. 6114 [Google Scholar]
Appendix A: Tables of mid-eclipse times
Minima timings of GU Boo.
All Tables
LITE parameters for selected LMBs (with errors of the last digit in parentheses).
Physical properties of the selected LMBs and parameters of their third bodies (with errors of the last digit in parentheses).
All Figures
 |
Fig. 1. V light curve of the secondary eclipse of GU Boo obtained in Prostějov observatory on June 14, 2017. The flare is clearly visible on the descending branch of the light curve on BJD 2457919.4073. |
| In the text | |
 |
Fig. 2. Current O–C diagram for the eclipse times of GU Boo. The sinusoidal curve represents the LITE with a period of 11.1 years. The individual primary and secondary minima are denoted by circles and triangles, respectively. Larger symbols correspond to the CCD measurements, which were given higher weights in the calculations. |
| In the text | |
 |
Fig. 3. O–C graph for YY Gem. See legend to Fig. 2. The sinusoidal curve represents the LITE with a period of about 55 yr and an amplitude of 5 min. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.




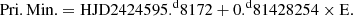
![$$ \begin{aligned} f(M) = \frac{M_3^3 \sin ^3 i_3}{(M_1+M_2+M_3)^2} = \frac{1}{P^2_3} \, \left[ \frac{173.15 \, A}{\sqrt{1 - e_3^2 \cos ^2 \omega _3}} \right] ^3, \end{aligned} $$](/articles/aa/full_html/2018/12/aa33708-18/aa33708-18-eq7.gif)