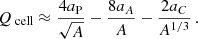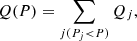| Issue |
A&A
Volume 620, December 2018
|
|
|---|---|---|
| Article Number | A105 | |
| Number of page(s) | 19 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201833605 | |
| Published online | 04 December 2018 | |
Crustal heating in accreting neutron stars from the nuclear energy-density functional theory
I. Proton shell effects and neutron-matter constraint
1
Grand Accélérateur National d’Ions Lourds (GANIL), CEA/DRF – CNRS/IN2P3, Boulevard Henri Becquerel, 14076 Caen, France
e-mail: anthea.fantina@ganil.fr
2
Institut d’Astronomie et d’Astrophysique, CP-226, Université Libre de Bruxelles, 1050 Brussels, Belgium
3
N. Copernicus Astronomical Center, Polish Academy of Sciences, Bartycka 18, 00-716 Warszawa, Poland
e-mail: jlz@camk.edu.pl
4
Dépt. de Physique, Université de Montréal, Montréal, Québec H3C 3J7, Canada
Received:
10
June
2018
Accepted:
3
October
2018
Context. X-ray observations of soft X-ray transients in quiescence suggest the existence of heat sources in the crust of accreted neutron stars. Heat is thought to be released by electroweak and nuclear processes triggered by the burying of ashes of X-ray bursts.
Aims. The heating in the crust of accreting neutron stars is studied using a fully quantum approach taking consistently into account nuclear shell effects.
Methods. To this end, we have followed the evolution of ashes made of 56Fe employing the nuclear energy-density functional theory. Both the outer and inner crusts are described using the same functional, thus ensuring a unified and thermodynamically consistent treatment. To assess the role of accretion on the structure of the crust, we have employed the set of accurately calibrated Brussels–Montreal functionals BSk19, BSk20, and BSk21, for which the equations of state of nonaccreted neutron stars have been already calculated. These energy-density functionals were fitted to the same set of nuclear masses but were simultaneously adjusted to realistic neutron-matter equations of state with different degrees of stiffness at suprasaturation densities. For comparison, we have also considered the SLy4 functional.
Results. Due to nuclear shell effects, the interior of fully accreted crust is found to be much less stratified than in previous studies. In particular, large regions of the inner crust contain clusters with the magic number Z = 14. The heat deposited in the outer crust is tightly constrained by experimental atomic mass data. The shallow heating we obtain does not exceed 0.2 MeV per accreted nucleon and is therefore not enough to explain the cooling of some soft X-ray transients. The total heat released in the crust is very sensitive to details of the nuclear structure and is predicted to lie in the range from 1.5 MeV to 1.7 MeV per accreted nucleon.
Conclusions. The evolution of an accreted matter element and therefore the location of heat sources are governed to a large extent by the existence of nuclear shell closures. Ignoring these effects in the inner crust, the total heat falls to ∼0.6 MeV per accreted nucleon.
Key words: dense matter / equation of state / stars: neutron / accretion / accretion disks / nuclear reactions / nucleosynthesis / abundances
© ESO 2018
1. Introduction
The crust of a neutron star (NS) contributes only about one percent to the stellar mass. However, it is essential for many astrophysical phenomena associated with NSs, such as pulsar glitches, X-ray bursts, and repetitive gamma-ray flares in magnetars. From the dense-matter theory point of view, the description of the crust of a NS, with its density below the normal nuclear density, seems much less challenging than the core. Still, the properties of the crust beyond the onset of neutron drip can only be studied theoretically, because such an environment cannot be reproduced in terrestrial laboratories (for a review of the physics of NS crusts, see e.g. Chamel & Haensel 2008).
A standard assumption concerning the crust of a non-accreting (isolated) NS is that it is made of “cold-catalysed matter”, that is electrically charge neutral matter at zero temperature in its absolute ground state (Harrison et al. 1958, 1965). The composition of any crustal layer at pressure P is thus obtained from the (absolute) minimum of the Gibbs free energy per nucleon g. This minimum energy state is, by construction, independent of the evolutionary cooling path from the hot initial state in the aftermath of gravitational core-collapse supernova, when the temperature T in the NS interior reaches T9 = T/109 K ≈ 50−100. The actual crust formation scenario deserves some more detailed explanations, in particular in terms of the nuclear processes occurring in the cooling hot dense plasma of the outer layers of a NS. The plasma consists of a large set of atomic nuclei (A, Z) with mass number A and atomic number Z in a bath of light particles α, free neutrons and protons, n and p, and photons γ. As long as T9 ≳ 10, the matter composition stays in nuclear statistical equilibrium due to the high rates of photodisintegrations (dissolving nuclei into n, p, and α) and radiative captures of n, p, and α (making nuclei growing in A and Z), as described in Clayton (1968), Rolfs & Rodney (1988), and Haensel et al. (2007). However, the rates of these reactions drop with decreasing T (Clayton 1968; Rolfs & Rodney 1988). When the outer layer of a NS cools below T9 = 4−5, its nuclear composition freezes because the nuclear reaction channels relevant for maintaining nuclear statistical equilibrium (photodissociation, photoabsorption) are closed (see e.g. Bisnovatyi-Kogan 2001, and references therein). Furthermore, for T9 ≲ 3, nuclear shell effects and nucleon superfluidity become important (Haensel et al. 2007), and further contribute to freeze the nuclear composition of the crust, which may deviate from that of the minimum energy state (Bisnovatyi-Kogan & Chechetkin 1979; Bisnovatyi-Kogan 2001). Moreover, the composition of the crust could be later altered by the accretion of matter from a stellar companion in a close binary system. The crust of a NS can thus be a reservoir of nuclear energy, which could be released under favourable conditions (Bisnovatyi-Kogan & Chechetkin 1973, 1974, 1979; Bisnovatyi-Kogan et al. 1976; Haensel & Zdunik 1990a; Blaes et al. 1990).
The energy release in non-equilibrium layers of NS crusts dev-iating from the minimum energy state was originally proposed as the potential source of heat powering the thermal X-ray radiation of isolated NSs (Bisnovatyi-Kogan & Chechetkin 1973, 1974; Bisnovatyi-Kogan et al. 1976). Later, the instabilities in non-equilibrium crustal shells were considered as being at the origin of Galactic gamma-ray bursts (Bisnovatyi-Kogan & Chechetkin 1979; Blaes et al. 1990). The models employed in these pioneering studies for describing the inner crust, where most of the heat release takes place, were very simplified, and therefore the predicted distributions and strengths of the nuclear energy sources were very approximate. Systematic calculations of the steady energy release in an accreting NS crust were carried out by Haensel & Zdunik (1990a), hereafter HZ), based on the compressible liquid-drop model (CLDM) of Mackie & Baym (1977), hereafter MB). The results of Haensel & Zdunik (1990a) were applied to the modelling of the thermal structure of accreting NSs by Miralda-Escudé et al. (1990).
The interest in the nuclear processes taking place in the crust of accreting NSs grew in the late 1990s when it was shown that the associated heating could be relevant for interpreting the measured surface temperatures of soft X-ray transients (SXTs) in quiescence (Bildsten & Brown 1997; Brown et al. 1998). Because the main heat sources predicted by HZ were concentrated in the crustal layers ∼300−400 m below the stellar surface, the heat deposition mechanism was thus called “deep crustal heating” (DCH). The heat is released during accretion stages (days–weeks). Accretion (bursting, or active) stages are characterised by X-ray bursts (typically a minute long) separated by about an hour needed to accumulate a new envelope of nuclear fuel for the next burst. The active periods are separated by much longer periods of quiescence with no bursts, and very little accretion or no accretion at all. For SXTs in quiescence, the thermal radiation from the NS surface can be observed and the effective surface temperature can be inferred. The crustal heating during active stages is driven by the compression of the deep layers of NS crust, implying electron captures inducing neutronisation and neutron emission, and, above ∼1012 g cm−3, also possibly the pycnonuclear fusion of nuclear clusters1. After ∼105 yr, a quasiequilibrium quiescent state is reached with an observable (isotropic) surface photon luminosity 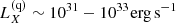 . An additional heating Qtot of the deep layers of the crust during active periods, by some 1.5 MeV per accreted nucleon (nicely consistent with HZ), together with data referring to the overall time-averaged accretion rate for a given SXT, reproduce most of the measured values of
. An additional heating Qtot of the deep layers of the crust during active periods, by some 1.5 MeV per accreted nucleon (nicely consistent with HZ), together with data referring to the overall time-averaged accretion rate for a given SXT, reproduce most of the measured values of 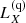 for two dozen of SXTs, with some remarkable ex-ceptions (Beznogov & Yakovlev 2015, and references therein).
for two dozen of SXTs, with some remarkable ex-ceptions (Beznogov & Yakovlev 2015, and references therein).
The HZ model was improved and extended in subsequent works on crustal heating in the framework of the CLDM. Haensel & Zdunik (2003) showed, using the MB model, that Qtot is only weakly dependent on the composition of the X-ray burst ashes. Gupta et al. (2007) considered a network of nuclear reactions in a hot multi-component plasma of nuclei taking into account excited states, but their study was restricted to the outer crust only. Nuclear masses were obtained from the finite-range droplet model of Möller et al. (1995), whereas the pressure of free neutrons was calculated using the MB model. The equation of state (EoS) of electrons (including electron-ion electrostatic corrections) was taken from Timmes & Swesty (2000). Haensel & Zdunik (2008) later showed that the one-component plasma approximation at T = 0, as implemented in the MB model, leads to a similar estimate for the cumulated heat Q( ρ) (total crustal heating per one accreted nucleon integrated up to density ρ) as that obtained by Gupta et al. (2007), provided neutrino losses are ignored thus mimicking in this way the effect of the de-excitation of the final states of the daughter nuclei in the electron captures. Gupta et al. (2008) followed the evolution of accreted material down to the shallowest layers of the inner crust at densities ∼1012 g cm−3 including neutron captures and dissociations. Steiner (2012) later calculated crustal heating in a multi-component plasma in quasistatistical equilibrium, using a set of CLDMs that include an empirical nuclear shell correction. The total heat released Qtot was found to be significantly higher than that calculated in previous studies. More recently, Schatz et al. (2014) studied the role of β− decay in the crust reactions and showed that the Urca process can occur in some layers. In a very recent paper Lau et al. (2018) applied the same crust model as Gupta et al. (2007); Schatz et al. (2014), but they considered various compositions of initial ashes, and a large network of reactions including electron captures, β− decays, neutron captures and dissociations as well as the first pycnocnuclear reactions. They found a total heating Qtot ∼ 2 MeV per accreted nucleon quite independent of the initial composition of ashes. However, they could not extend their calculations beyond 2 × 1012 g cm−3 because their model of nuclei (Möller et al. 1995) does not take into account the effect of the surrounding neutron liquid in the inner crust.
The calculations of Qtot in the models of HZ, Haensel & Zdunik (2003, 2008) and Steiner (2012) reviewed above were based on the assumption that the whole original crust is replaced by accreted matter, down to the crust-core interface. However, this may not be the case if the total accretion time onto a NS in a low-mass X-ray binary (LMXB) is too short compared to the NS age, and/or the time averaged accretion rate is too low, especially for some faint X-ray transients (Wijnands et al. 2013). These NSs could thus have an hybrid crust made of accreted material on top of the compressed original crust (Wijnands et al. 2013). Gupta et al. (2007, 2008), Schatz et al. (2014), and Lau et al. (2018) did not follow the compression of accreted materials at densities well above the onset of neutron drip due to the limitations of their model of the inner crust. The possibility of partially accreted crusts has not been fully explored yet.
The aim of this paper is to reexamine crustal heating in accre-ted NS crusts, and in particular to clarify the role of nuclear shell effects on the location of the heat sources as well as on the total heat released. To this end, we follow a more microscopic approach based on the self-consistent nuclear energy-density functional (EDF) theory (Bender et al. 2003; Stone & Reinhard 2007). Unlike the works of Gupta et al. (2007), Steiner (2012), and Lau et al. (2018), we adopt the one-component plasma approximation, which was shown to be accurate enough for the calculation of the cumulated heat. The Brussels–Montreal EDFs BSk19, BSk20, and BSk21 that we employ here have been fitted to the same wealth of nuclear data and to different neutron-matter EoSs based on many-body methods using realistic nuclear forces. Moreover, unified EoSs of catalysed matter have already been calculated for these EDFs (Pearson et al. 2011, 2012; Fantina et al. 2013; Potekhin et al. 2013) thus allowing for a direct comparison between nonaccreted and accreted NS crusts. However, in order to better assess the sensitivity of our predictions with respect to nuclear physics uncertainties, we shall also consider the SLy4 EDF (Chabanat et al. 1998) that underlies the popular SLy unified EoS (Douchin & Haensel 2001).
The plan of the paper is as follows. In Sect. 2 we review the astrophysical scenarios of formation of NS crusts, the difficulties, and the limitations of the calculation of crustal heating. Our microscopic model of accreted crust is presented in Sect. 3. The evolution of an element of crust matter and its composition as a function of the matter density are described in Sect. 4. In Sect. 5, the distribution of crustal heating sources is studied for various approximations for the energy of the Wigner–Seitz (WS) cell and the importance of the shell correction to the energy is illustrated. We also illustrate there the importance of using EDFs that are consistent with up-to-date nuclear constraints, both of theoretical microscopic origin, and semi-empirical ones. Discussion, including a comparison with previous calculations, and interpretation of generic features of our results are presented in Sect. 6.
2. Formation of accreted crust
2.1. Fully accreted crust vs. partially accreted crust
Let us consider the evolution of the crust starting from the very beginning of the mass transfer stage in LMXB. The history of a SXT is a succession of two intermittent stages: periods when matter from the accretion disk falls onto the NS (ta), interceded by quiescence periods tq ≫ ta with no or very little accretion onto the NS. Active periods are characterised by observations of X-ray bursts. This is explained as follows. During an active period, matter is being accreted onto the NS surface, at some rate Ṁa, which can be calculated from the X-ray luminosity of the NS surface between X-ray bursts. Typically for SXTs, Ṁa ∼ 10−10−10−9 M⊙ yr−1. Accreted matter is hydrogen rich and settles on the NS surface, forming an envelope with a hydrogen burning shell at ∼105 g cm−3. Below the hydrogen burning shell, helium is accumulating and ignites after reaching critical conditions for runaway thermonuclear burning. A thermonuclear explosion burns all the overlying envelope within a second, leading to the brightening of the NS surface corresponding to an X-ray burst of isotropic luminosity ∼1038 erg s−1, which is decaying and softening its spectrum on a timescale of a minute. The thermonuclear burning of the envelope produces a layer of nuclear ashes, composed of iron peak nuclides and heavier elements. The next X-ray burst is preceded by an accretion stage lasting from hours to days, and this sequence of X-ray bursts separated by nuclear fuel cumulation periods is continued during ta (typically weeks–months). During quiescent periods, the accretion rate is so low or just zero that in spite of tq ≫ ta an amount of thermonuclear fuel which can be cumulated (if any) is not sufficient to trigger even a single burst. The overall time averaged accretion rate is
Here, accretion rates refer to the baryon (rest) mass of the matter, and time is measured by a distant observer.
The accretion of a baryon mass ΔMa = ta⟨Ṁ⟩ implies the replacement of the “old” outer layer of baryon mass ≈ΔMa by accreted and possibly processed material. Let us denote the initial baryon mass of the crust by 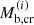 . After time t, the top layer of the crust will be replaced by a mass t⟨Ṁ⟩ of accreted matter. The same amount of baryon mass of the original crust will be pushed into the liquid core, and converted into a homogeneous plasma phase in a timescale
. After time t, the top layer of the crust will be replaced by a mass t⟨Ṁ⟩ of accreted matter. The same amount of baryon mass of the original crust will be pushed into the liquid core, and converted into a homogeneous plasma phase in a timescale 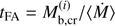 . However, as long as t < tFA, only the outer parts of the original crust will be replaced by accreted material. We shall refer to these two situations as fully accreted crust and partially accreted crust respectively. Possibility of partially accreted crusts in SXTs, with particular emphasis on the observational aspects, was considered by Wijnands et al. (2013).
. However, as long as t < tFA, only the outer parts of the original crust will be replaced by accreted material. We shall refer to these two situations as fully accreted crust and partially accreted crust respectively. Possibility of partially accreted crusts in SXTs, with particular emphasis on the observational aspects, was considered by Wijnands et al. (2013).
2.2. Timescales
For t ≫ tq the accreted crust mass is given by
The replacement of the original outer crust by accreted matter requires the accretion of 10−4.6 M⊙ (see Fig. 36 in Chamel & Haensel 2008), which takes
where ⟨Ṁ⟩−10 = ⟨Ṁ⟩/10−10 M⊙ yr−1. After toc, the outer crust exhibits a quasistatic structure with a steady heating during the active stages.
However, the most powerful crustal heating comes from the inner layer of the crust at densities between 1011.5 g cm−3 and 1013 g cm−3. To replace this crucial layer, the accretion of 10−3.6 M⊙ is needed (see Fig. 36 in Chamel & Haensel 2008). This takes
Basically, tDCH is the time needed to obtain a nearly full crustal heating. After tDCH, the partially accreted crust heating regime is left, and crustal heating is well approximated by a fully accreted crust model. This stems from the fact that the integrated heat Q( ρ) saturates at 1013 g cm−3 (e.g. Haensel & Zdunik 2008, see also Sect. 5).
It should be mentioned that the time needed for the formation of a fully accreted crust at the same mean accretion rate is much longer, tFA ≈ 40tDCH = 108 yr/⟨Ṁ⟩−10.
2.3. Astrophysical context
Let us consider ten SXTs for which ⟨Ṁ⟩ has been estimated via the analysis of the X-ray data spanning over the timelines from 10.7 yr to 35 yr (Table 2 in Heinke et al. 2007 and Table 2 in Heinke et al. 2009; we refer to these references for additional informations). These ten SXTs are: Aql X-1, 4U 1608−522, MXB 1659−29, Terzan 5, NGC 6440 X-1, RX J1709−2639, SAX J11808.4−3658, (Heinke et al. 2007) and IGR 00291+5934, XTE J1814−338, XTE J1751−305 (Heinke et al. 2009). The estimated values of the present time averaged accretion rate ⟨Ṁ⟩pr range from 2.5 × 10−12 M⊙ yr−1 for IGR 00291+5934 (Heinke et al. 2009) up to 3.6 × 10−10 M⊙ yr−1 for 4U 1608−522 (Heinke et al. 2007).
A typical expected lifetime of a SXT in LMXB is of order 108−109 yr (de Loore & Doom 1993; Tauris & van den Heuvel 2006). This leads to conclusion that SXTs with ⟨Ṁ⟩ ≳ 10 −10 M⊙ yr−1 could reach the stage of nearly full crustal heating. Assuming ⟨Ṁ⟩ = ⟨Ṁ⟩pr, this refers to Aql X-1, 4U 1608−522, MXB 1659−29, NGC 6440 X-1, RX J1709−2639, and Terzan 5. On the other hand, SXTs with ⟨Ṁ⟩ ≲ 10−12 M⊙ yr−1 could not reach full power of the crustal heating in their partially accreted crusts. Assuming ⟨Ṁ⟩ = ⟨Ṁ⟩pr, this would be the case of IGR 00291+5934, SAX J11808.4−3658, XTE J1751−305, and XTE J1814−338. Observational aspects stemming from the possibility of partially accreted crusts in SXTs were studied by Wijnands et al. (2013), who also tested the DCH model of SXTs in quiescence using the lowest luminosity sources.
Actually, our assumption of ⟨Ṁ⟩ = ⟨Ṁ⟩pr is difficult to justify. Higher accretion rates in the past leading to fully accreted crust cannot be excluded. In view of this uncertainty, a different method for the evaluation of the accreted mass would be helpful. It could be based on the scenario of the spin-up by accretion (e.g. Tauris et al. 2012). For the further remarks on this point we refer to Sect. 6.
In the following, we calculate the full crustal heating.
3. Microscopic model of accreted crust
The crust of an accreting NS is covered by an envelope, whose composition depends on the NS history and can be strongly time dependent (in X-ray bursters). The envelope is crucial for the spectrum of photons emitted by NS, and for the transport of heat between the NS core and surface (Potekhin 2003). In the present paper the bottom density of the envelope will be fixed at 108 g cm−3, and by the NS crust we will mean the layers with density higher than this value.
3.1. Main assumptions
Under the conditions generally prevailing in accreting NS crusts, namely T9 < 1 (see e.g. Chamel & Haensel 2008; Lau et al. 2018 consider 5 × 108 K, similarly as in Gupta et al. 2008), the thermal contributions to the thermodynamic potentials can be neglected. Each crustal layer will be assumed to contain structures made of only one type of nuclides with proton number Z and mass number A. For simplicity, we further suppose that the crust consists of an ordered solid, as suggested by the analysis of the SXT data (see e.g. Chamel & Haensel 2008). The structure of each layer is therefore fully determined by the composition of a single spherical WS cell. As in Haensel & Zdunik (2008), we shall only consider ground-state transitions and we shall neglect neutrino losses. These approximations will be used throughout this paper.
In hydrostatic equilibrium, the pressure P throughout the star must vary continuously; therefore, the suitable thermodynamic potential for determining the equilibrium structure of the crust is the Gibbs free energy per nucleon g(A, Z, P).
3.2. Evolution of an element of accreted matter
The determination of the composition of the accreted crust and the sources of crustal heating follows the same approach as in Haensel & Zdunik (2008). Let us consider the evolution of some matter element, composed of nuclei (A, Z) compressed by accretion. Before the onset of pycnonuclear reactions, the mass number A remains unchanged as the pressure increases. On the other hand, the proton number Z can change due to the capture of an electron (simultaneous multiple electron captures are very unlikely and are therefore not considered): the nucleus (A, Z) transforms into a nucleus (A, Z − 1) with proton number Z − 1 and mass number A with the emission of an electron neutrino. This reaction occurs as soon as the pressure reaches a threshold value Pβ such that g(A, Z, Pβ) = g(A, Z − 1, Pβ). Very accurate analytical formulas for Pβ and the corresponding threshold density ρβ were obtained by Chamel & Fantina (2015, 2016a). The electron capture will generally be almost immediately followed by further electron captures on the daughter nucleus (A, Z − 1). This chain of reactions stops at Z0 defined by g(A, Z0, Pβ) < g(A, Z0−1, Pβ), which corresponds to a local minimum of the Gibbs free energy per nucleon at pressure P. The global minimum of g (obtained by relaxing the condition of fixed A) defines the state of cold catalysed matter in complete thermodynamical equilibrium. As discussed by Haensel & Zdunik (2008), the heat effectively deposited in matter per one WS cell for the chain of reactions (A, Z) → (A, Z0) is approximately given by
With increasing pressure, nuclei become progressively more neutron-rich due to electron captures. At some point, the nucleus (A, Z) may become unstable against the capture of electrons accompanied by the emission of free neutrons. The nucleus (A, Z) will thus transform into a nucleus (A − ΔN, Z − 1) with proton number Z − 1 and mass number A − ΔN with the emission of ΔN neutrons and an electron neutrino. As previously discussed by Chamel et al. (2015), the mean-nucleus approach leads to a discontinuous variation of the neutron density and of the neutron chemical potential due to the sudden appearance of ΔN free neutrons in each WS cell. Such unphysical jumps can also be seen in the results obtained by Steiner (2012) from a multi-component CLDM (see his Figs. 3 and 4). Considering that only an infinitesimal small fraction of nuclei (A, Z) are initially converted into (A − ΔN, Z − 1), Chamel et al. (2015) showed that the onset of neutron emission actually occurs at lower density and pressure than those predicted by the mean-nucleus treatment. We shall follow the same approach here. In this way, the neutron-drip transition is guaranteed to be continuous, as found in full reaction network calculations (Gupta et al. 2008,Lau et al. 2018).
The number ΔN of emitted neutrons may be larger than one depending on the composition of the X-ray burst ashes and on the nuclear mass model employed (Chamel et al. 2015; Fantina et al. 2016). The neutron-drip transition delimits the boundary between the outer crust and the inner crust, where neutron–proton clusters coexist with a neutron liquid and a gas of electrons. Electron captures (with neutron emission and absorption), pycnonuclear reactions, and crustal heat in the inner crust are determined as in the outer crust, except that A is now replaced by the total number Acell of nucleons in the WS cell.
As the matter element sinks deeper inside the star and undergoes further electron captures thus decreasing Z, the Coulomb barrier between nuclei may become low enough, and the energy of the zero-point vibrations around the lattice sites high enough to trigger pycnonuclear reactions, where nuclei (A, Z) fuse by penetrating the Coulomb barrier into nuclei (2A, 2Z). However, in view of the large uncertainties in the rates of these reactions (see e.g. Yakovlev et al. 2006b), we simply assume that these processes occur whenever Z reaches the minimum value Zmin = 8. We checked this assumption. For this value of Z, the timescale for first pycnonuclear O–O fusion at 1.2 × 1012 g cm−3 is estimated as τpyc(Z = 8)∼0.1 s ≪ τDCH, whereas for Si–Si, predicted to be produced in the O–O fusion and subsequent electron captures, τpyc(Z = 14)∼1030 s ≫ τDCH. However, further compression of Si layer induces electron captures on Si nuclei and neutron emissions, leading again to Z = 8 and O–O pycnonuclear fusion (see Tables A.1–A.3). We used formulae for the pycnonuclear fusion rate derived in the classical paper of Salpeter & Van Horn (1969), as adapted for accreting NS by Sato (1979). The formula for the astrophysical S-factor, was taken from Sato (1979). We checked that using up-to-date theoretically calculated S-factors in Afanasjev et al. (2012) does not essentially change our results, because of the dominating dependence of the fusion rate on Z. We neglected thermal enhancement of the fusion rate, studied in Yakovlev et al. (2006a), because for our processes the Coulomb barrier is significantly higher (Si–Si and O–O instead of C–C and O–C in Yakovlev et al. 2006a) and the density is much larger (1012 g cm−3 instead of 1010 g cm−3 in Yakovlev et al. 2006a).
Our treatment of accreted crust relies on the EDF theory. For the sake of comparison, we shall also consider an improved version of the MB model employed previously by HZ.
3.3. Nuclear energy-density functional theory
Our models of accreting NS crusts are based on the nuclear EDF theory (Bender et al. 2003; Stone & Reinhard 2007). This theory, which has proved to be very successful for describing the properties of finite nuclei such as those encountered in the outer crust of a NS, also allows for a consistent treatment of the inner crust, where neutron–proton clusters coexist with a neutron liquid. Moreover, the EDF theory can be applied to homogeneous nuclear matter thus providing a unified description of all regions of a NS. The structure, the composition and the EoS of nonaccreted NSs was determined in this way (see Pearson et al. 2011, 2012) under the assumption of cold catalysed matter. Analytical representations of these EoSs were obtained by Potekhin et al. (2013). Using the same Brussels–Montreal EDFs labelled BSk19, BSk20 and BSk21 respectively, we shall now study the properties of accreting NS crusts.
The Brussels–Montreal EDFs that we consider here are based on generalised Skyrme effective nucleon–nucleon interactions (Chamel et al. 2009; Goriely et al. 2010), supplemented with a microscopic contact pairing interaction (Chamel 2010). These EDFs were fitted to the 2149 measured masses of nuclei with neutron and proton numbers, N and Z ≥ 8 respectively, given in the 2003 atomic mass evaluation (AME; Audi et al. 2003), with a root-mean square (rms) deviation as low as 0.58 MeV for the three functionals, and an optimal fit to charge radii. The masses of bound nuclei were obtained by adding to the Hartree–Fock–Bogoliubov (HFB) energy a phenomenological Wigner term and correction term for the collective energy. The precise fit to the mass data thus makes the functionals well-suited for the description of the nuclei found in the outer crust of a NS. The symmetry coefficient was set at J = 30 MeV for the three functionals (see e.g. Goriely et al. 2010; Tsang et al. 2012; Tews et al. 2017, for a more thorough discussion of experimental and theoretical estimates of J). This value of the symmetry energy was later found to yield the best fit to nuclear masses for the EDFs in Goriely et al. (2013), and is also supported by NS observations (Pearson et al. 2014). Furthermore, (i) the incompressibility Kv of symmetric nuclear matter at saturation was required to fall in the experimental range 240 ± 10 MeV (Colò et al. 2004), (ii) the ratio of the isoscalar effective mass to bare nucleon mass in symmetric nuclear matter at saturation was set to the realistic value of 0.8 (see the discussion by Goriely et al. 2003), (iii) the isovector effective mass was found to be smaller than the isoscalar effective mass, in agreement with both experiments and many-body calculations (see Goriely et al. 2010, for a detailed discussion), (iv) a qualitatively realistic distribution of the potential energy among the four spin-isospin channels in nuclear matter was obtained, and (v) spurious spin and spin-isospin instabilities in nuclear matter that generally plague older Skyrme functionals have been eliminated for all densities prevailing in NSs by extending the Skyrme functional (Chamel et al. 2009; Chamel & Goriely 2010). The Brussels–Montreal EDFs BSk19, BSk20 and BSk21 were also constrained to reproduce various properties of homogeneous nuclear matter as obtained from many-body calculations using realistic two- and three-nucleon interactions. In particular, these EDFs were fitted to three different neutron-matter EoSs, reflecting the current lack of knowledge of the high-density behaviour of dense matter. BSk19 was adjusted to the “soft” EoS of neutron matter of Friedman & Pandharipande (1981) obtained from the realistic Urbana v14 nucleon–nucleon force with the three-body force TNI, BSk20 was fitted to the EoS of Akmal et al. (1998) labelled “A18 + δυ + UIX”, whereas BSk21 was constrained to reproduce the “stiff” EoS labelled “V18” from Li & Schulze (2008). These EoSs are compatible with the constraints inferred from more recent calculations based on auxiliary field diffusion Monte Carlo method and chiral effective field theory (Fantina et al. 2014). With these features, the EDFs BSk19, BSk20, and BSk21 are well-suited for describing the crust of accreting NSs. We note that at densities relevant for NS crusts, all three models yield very similar neutron-matter EoSs (see Sect. 5.4).
For comparison, we shall also consider the SLy4 EDF (Chabanat et al. 1998), which was employed by Douchin & Haensel (2001) to compute the EoS of the inner crust and core of nonaccreted NS within a CLDM. The SLy4 EDF was also adopted by Steiner (2012) for the calculations of accreted NS crusts. Contrary to the Brussels–Montreal EDFs, the SLy4 EDF was not fitted to a particular realistic neutron-matter EoS, but was only constrained to yield a “reasonable reproduction” of the EoS of Wiringa et al. (1988) up to a density of 1.6 fm−3. Moreover, the SLy4 EDF was fitted to only five atomic masses (40, 48Ca, 56Ni, 132Sn, and 208Pb) from a modified version of AME 1995 (Audi et al. 1997). By including N = Z nuclei in the fit without adding a Wigner term, the SLy4 functional overestimates the symmetry coefficient. The rms deviation from the 2003 AME data (Audi et al. 2003; considering only even–even nuclei) is about 5.1 MeV (Dobaczewski et al. 2004), about an order of magnitude larger than for the Brussels–Montreal models. Although the Rs and Gs EDFs (Friedrich & Reinhard 1986) were considered by Steiner (2012), we will not include them here since these EDFs yield unrealistic neutron-matter EoS, as we shall discuss in Sect. 5.4.
The EDF theory is implemented using different methods in the outer and inner crusts, as explained in the following sections.
3.4. Outer crust
The properties of the outer crust are calculated in the framework of the standard model of Baym et al. (1971). This model assumes that the outer crust is made of fully ionised atoms arranged in a body-centred cubic lattice neutralised by a degenerate electron gas. We follow the same approach as in Pearson et al. (2011), except that we now include electron charge polarisation effects using Eqs. (6) and (8) from Chamel & Fantina (2016a).
The only microscopic inputs of this model are the nuclear masses M′(A, Z), which were obtained from the available experimental atomic masses M(A, Z) after subtracting out the binding energy of atomic electrons using Eq. (A4) of Lunney et al. (2003). For the masses that have not yet been measured, we used the Brussels–Montreal HFB atomic mass tables from the BRUSLIB database (Xu et al. 2013). Because the SLy4 mass table of Dobaczewski et al. (2004) contain only even–even nuclei, we have employed the full SLy4 mass table recalculated for the purpose of this work within the HFB method, using the same framework as described in the original paper.
The improvements of this model compared to the previous works of Haensel & Zdunik (1990a,b, 2003, 2008) and Steiner (2012) are twofold: (i) the use of more recent atomic mass measurements, and (ii) the use of much more microscopic and more precise nuclear models to predict experimentally unknown nuclear masses. In particular, experimental nuclear masses are taken from the 2016 AME (Wang et al. 2017), whereas Haensel & Zdunik (1990a,b, 2003, 2008) used data from the 1971 AME (Wapstra & Gove 1971). Nuclear shell effects, which were not included in the MB model employed by Haensel & Zdunik (1990a,b, 2003, 2008), are now calculated microscopically. Moreover, the CLDM of Haensel & Zdunik (1990a,b, 2003, 2008) assumes that nucleons are uniformly distributed within the nucleus with a sharp surface. For the HFB mass tables employed in the present work, the nucleon distributions were calculated fully self-consistently and quantum-mechanically using the EDF theory. Not surprisingly, the MB model reproduced rather poorly the nuclear mass data available at that time, with a rms deviation of 2.6 MeV for 1126 masses of heavy nuclei with A ≥ 40. Steiner (2012) developed a series of CLDMs fitted to the 2003 AME data (Audi et al. 2003) with a rms error of 1.2 MeV. The relatively low rms error compared to typical CLDM was achieved by introducing phenomenological shell corrections. The Brussels–Montreal HFB nuclear mass models employed in this work were fitted to the 2149 measured masses of nuclei with N and Z ≥ 8 given in the 2003 AME (Audi et al. 2003) with a rms deviation lying below 0.6 MeV. These models also yield an equally good fit to the 2408 experimental masses of nuclei with Z, N ≥ 8 from the 2016 AME (Wang et al. 2017). For comparison, the HFB mass table based on SLy4 and the same pairing force as BSk19-21 that we calculated yields a rather poor fit to the same data, with a rms deviation of 3.961 MeV, and a relatively bad description of the closed shell nuclei with respect to open-shell ones due to the low value of 0.69 for the isoscalar effective mass.
3.5. Neutron-drip transition
The onset of neutron emission by nuclei is determined as discussed by Chamel et al. (2015), thus ensuring the thermodynamic consistency across the boundary between the outer and inner crusts. In particular, the neutron chemical potential varies continuously across the transition contrary to the results shown in Figs. 3 and 4 in Steiner (2012). Very accurate analytical formulas for the neutron-drip pressure and density can be found in Chamel & Fantina (2016a).
As shown by Chamel et al. (2015), the atomic number Z of the dripping nucleus is given by the highest number of protons lying below that of the ashes for which the ΔN-neutron separation energy is negative, or equivalently
The daughter nucleus may undergo further electron captures and neutron emissions.
3.6. Inner crust
Because neutrons are highly degenerate, they contribute to the pressure and can substantially affect the mass of the clusters. However, fully self-consistent calculations of the inner crust within the EDF theory are computationally extremely costly. For this reason, we have implemented a computationally high-speed approximation based on the 4th order Extended Thomas-Fermi (ETF) development with proton shell corrections added perturbatively via the Strutinsky integral theorem (Onsi et al. 2008; Pearson et al. 2012). Neutron shell corrections, which were shown to be much smaller than proton shell corrections (Oyamatsu & Yamada 1994), are neglected. The validity of this Extended Thomas-Fermi with Strutinsky Integral (ETFSI) method has been discussed by Pearson et al. (2012). We have employed the same EDFs as those underlying the HFB nuclear mass models used for the outer crust, thus ensuing a consistent description of the outer and inner parts of the crust.
Although neutrons and protons may arrange themselves into so called nuclear “pastas”, these configurations, if they exist, are only expected to be found near the crust-core interface (see e.g. Sect. 3.3 in Chamel & Haensel 2008, for a brief review). Therefore, nuclear clusters are assumed to be spherical and the Coulomb energy is calculated using the WS approximation. In order to further reduce the computation time, the nucleon density distributions in the WS cell are parameterised as follows (q = n, p for neutrons, protons respectively):
where r is the radial distance from the centre of the spherical cell, nBq is the background density while the second term accounts for the presence of inhomogeneities, with the dimensionless function fq(r) given by
R being the radius of the WS cell. The expression of fq(r) ensures that density derivatives vanish at the surface of the cell, thus providing a smooth matching of the nucleon distributions between adjacent cells.
In the absence of pycnonuclear reactions, Acell remains unchanged with increasing pressure whereas Z can decrease if electrons are captured. The configuration of a matter element at any pressure P can thus be determined by minimising the baryon chemical potential g with respect to all the parameters of the WS cell keeping Acell fixed. However, this procedure would be computationally very costly. Instead, we first minimised the internal energy e per nucleon at constant average baryon number density n, and for given values of the proton number Z and nucleon number Acell (details can be found in Pearson et al. 2012). In a second stage, we calculated the corresponding pressure P and the Gibbs free energy per nucleon g. We repeated this calculation for different values of n and Z. In this way, we evaluated g as a function of Z and P for the given value of Acell.
Neutrons resulting from electron captures by nuclear clusters may be either bound or unbound. Contrary to the CLDM used by Haensel & Zdunik (1990a,b, 2003, 2008), and Steiner (2012), we do not need to consider these two cases separately since both neutrons in clusters and free neutrons are treated consistently in the EDF theory. The number ΔN of emitted neutrons can thus take any real positive value. For the sake of comparison, it is convenient to introduce the neutron-cluster number N defined as
Since all protons are bound, the number of nucleons in clusters is therefore A = Z + N. Another improvement compared to the work of Haensel & Zdunik (1990a,b, 2003, 2008) is the inclusion of proton shell effects. As mentioned earlier, these effects were considered by Steiner (2012) but using an empirical parameterisation, whereas shell effects are consistently and quantum mechanically calculated here.
For comparison, we also calculate the properties of accreted NS crusts making use of the experimental data from AME 1971 and the MB model, as in the earlier studies of Haensel & Zdunik (1990a,b, 2003, 2008). However, our approach is slightly different from that followed in Haensel & Zdunik (1990a,b, 2003, 2008). To be consistent with the ETFSI calculations, the equilibrium configuration at each pressure P and for given proton number Z is now determined by minimising g(Acell, Z, P) without imposing any constraint on the number of neutrons in the clusters or in the neutron gas (except of course the requirement of a fixed baryon number Acell in the WS cell). In this way, neutron emissions and absorptions by clusters are taken into account. Because of the separate treatment of clusters and gas, the number N of neutrons in clusters is constrained to take integer value.
4. Structure and composition of accreted crust
The internal constitution of the crust of a NS is of utmost importance for studying transport properties, which in turn can affect the cooling of the star, the evolution of the magnetic field or the seismic activity (Chamel & Haensel 2008). Using the microscopic models described in Sect. 3, we have determined the composition of accreted NS crusts considering X-ray burst ashes made of 56Fe.
4.1. Outer crust
The variations of the proton number Z and neutron number N with increasing pressure are shown in Fig. 1. The value of Z systematically decreases with increasing depth due to electron captures, as discussed in Sect. 3. The HFB models with different EDFs and the MB model predict the same composition for the outer crust, but a different stratification. The first two shallowest layers are completely determined by measured masses, and the associated transition densities and pressures are therefore the same for all models. The boundaries of the densest layers are found to be model dependent due to the lack of experimental data.
 |
Fig. 1. Proton number Z and neutron number N of nuclei in the outer crust of an accreted NS for X-ray burst ashes made of 56Fe. Results are shown for the model of Mackie & Baym (1977), hereafter MB) and for HFB nuclear mass models using different EDFs: BSk19, BSk20 and BSk21 from Goriely et al. (2010) and SLy4 from Chabanat et al. (1998). |
At high enough densities, electron captures by 56Ar are predicted by all models to emit free neutrons, thus marking the bottom of the outer crust. With the approach proposed by Chamel et al. (2015), the transition is found to be very smooth, in agreement with nuclear network calculations (Gupta et al. 2008; Lau et al. 2018). However, the neutron-drip density and pressure are found to depend on the details of the nuclear mass model employed, as previously analysed by Fantina et al. (2016). The properties of accreted NS crust at the neutron-drip transition are summarised in Table 12. The values for the neutron-drip density and pressure are found to differ very little (less than 1%) from those obtained in a strictly mean-nucleus treatment except for the model of MB, as previously shown by Chamel et al. (2015). Very accurate analytical formulas for the pressure at the transition between two adjacent strata as well as the average baryon number densities of each layer can be found in Chamel & Fantina (2016b).
Neutron-drip transition in the crust of accreting NSs, as predicted by different nuclear mass models for 56Fe ashes.
4.2. Inner crust
The composition obtained with the EDF theory is substantially different from that predicted by the MB model in the inner part of the crust, as shown in Fig. 2. In particular, the ETFSI model with the BSk19 EDF predicts that a large part of the inner crust is made of Z = 14 clusters, whereas the MB model leads to a highly stratified crust with a high number of layers each of which contains a different type of cluster with Z ranging from 10 to 18. Similar differences can be seen on the variations of the neutron number. In the EDF theory, nuclear clusters are thus found to be more stable against electron captures and pycnonuclear reactions than in the MB model. In the absence of electron captures and pycnonuclear reactions, the compression of a matter element is accompanied by a slight increase of the neutron number caused by the external neutron gas pressure which “pushes” back neutrons into the clusters. The discrepancies between the EDF theory and the MB model can be attributed to the inclusion of nuclear shell effects in the EDF theory. In particular, the occurrence of crustal regions made of silicon isotopes supports the predictions of Dutta et al. (2004) that Z = 14 is a magic proton number in a dense stellar environment. As a matter of fact, the neutron-rich nucleus 42Si (with Z = 14 and N = 28) appears as doubly magic (Fridmann et al. 2005). It has been recently suggested that 48Si (with Z = 14 and N = 34) could also be doubly magic (Li et al. 2016, 2018). The existence of the magic neutron number N = 34 was experimentally confirmed, especially from measurements of 54Ca (Steppenbeck et al. 2013). Quite remarkably, our ETFSI calculations predict the existence of 48Si in some layers despite our neglect of neutron-shell corrections. The appearance of N = 34 in the extremely neutron-rich environment of the inner crust of accreted NSs might be driven by nuclear symmetry effects, and the existence of the proton magic number Z = 14. To better illustrate the role of nuclear shell effects, we have performed calculations in the ETF approximation with no shell corrections. The resulting composition is strikingly different from that obtained in the full ETFSI treatment, as shown in Fig. 2. In the absence of nuclear shell effects, a compressed matter element undergoes successive electron captures until the proton number becomes low enough for pycnonuclear reactions to occur. As expected, the ETF approximation leads to similar variations of Z with pressure as those found with the MB model. As shown in Fig. 3, all four EDFs considered here predict similar compositions.
 |
Fig. 2. Proton number Z and neutron number N of nuclear clusters in the inner crust of an accreted NS for X-ray burst ashes made of 56Fe. Pycnonuclear reactions are marked by asterisks. Results are shown for the model of MB, and for the model based on the BSk19 EDF comparing two different treatments: ETFSI vs. ETF (no shell correction). |
 |
Fig. 3. Proton number Z and neutron number N of nuclear clusters in the inner crust of an accreted NS for X-ray burst ashes made of 56Fe. Pycnonuclear reactions are marked by asterisks. Results are shown for the ETFSI models based on the EDFs BSk19, BSk20, BSk21, and SLy4. |
4.3. Accreted vs. catalysed crusts
Although both accreted and catalysed crusts contain 56Fe in their outer part, the composition of their inner layers are remarkably different. As discussed in Sect. 3, the proton number Z in accreted crust systematically decreases with increasing depth due to electron captures unless pycnonuclear reactions occur. But even in this case, the daughter nucleus is generally highly unstable against electron captures so that Z remains lower than 26 in all regions of the crust. In contrast, the catalysed crust was found to be made of much heavier elements with Z ≥ 26 within the EDF theory (Pearson et al. 2011, 2012).
In spite of the radically different constitution of accreted and catalysed crusts, in both cases matter becomes progressively more neutron rich with increasing pressure due to gravitational settling (see e.g. Chamel & Fantina 2016b for a generic argument based on Le Chatelier’s principle; see also De Blasio 2000). The properties of catalysed NS crust at the neutron-drip transition are summarised in Table 2, where we have listed, for the different models, the Z and N of the dripping nucleus, the mass–energy density, and the corresponding pressure. For the EDF models HFB-19, HFB-20, HFB-21, and SLy4, the latters have been calculated as described in Chamel & Fantina (2016a) by solving numerically their Eqs. (13) and (14) and including the electron exchange and polarisation corrections. As shown in Figs. 4 and 5, the proton fraction Z/Acell, the fraction A/Acell of nucleons contained in nuclei, and the Gibbs free energy per nucleon g follow the same trend in both accreted and catalysed crusts. This can be understood as follows. Although the values of Z and A arise from a detailed balance between surface and Coulomb effects (see e.g. Chamel & Haensel 2008), the ratios yp ≡ Z/Acell and x ≡ A/Acell can be roughly estimated considering the coexistence of two distinct homogeneous phases: a dense nuclear matter phase representing clusters (nuclei in the outer crust) and a dilute neutron gas. Electrons are uniformly distributed, and therefore permeate the two phases. It should be remarked that the errors induced by this simple description decrease with increasing pressure as matter become progressively more homogeneous. The composition of catalysed crust at any given pressure P is obtained by minimising g. In accreted crusts, matter is not in full thermodynamic equilibrium. The composition is determined from a constrained minimisation of g with Acell fixed to the mass number of the ashes of X-ray bursts, and Z can only be reduced unless pycnonuclear reactions are allowed. However, in the bulk approximation, the Gibbs free energy per nucleon does not depend on Z, A, and Acell separately but only on the ratios Z/Acell and A/Acell, which can be treated as continuous variables at this level of approximation. Consequently, not only yp(P) and x(P), but also g are the same for both accreted and catalysed crusts.
Neutron-drip transition in the crust of catalysed NSs, as predicted by different nuclear mass models.
 |
Fig. 4. Proton fraction (top panel) and fraction of nucleons in nuclei (bottom panel) for accreting NS crust and catalysed NS crust (for the model based on the BSk19 EDF, thin solid line). Results are shown for the model of MB, and for the model based on the BSk19 EDF comparing two different treatments for the inner crust: ETFSI vs. ETF (no shell correction). For the ETF model in the top panel, results are shown only for the inner crust. |
 |
Fig. 5. Gibbs free energy per nucleon g in accreting NS crust and catalysed NS crust (thin bottom lines). Top panel: predictions from the model of MB and from the model based on the BSk19 EDF comparing two different treatments for the inner crust: ETFSI vs. ETF (no shell correction). Bottom panel: predictions from models based on differents EDFs. See text for details. |
The most remarkable differences between accreted and catalysed crusts concern the variation of the Gibbs free energy per nucleon with pressure, which is discontinuous in the former case and continuous in the latter case, as shown in Fig. 5. Jumps in g correspond to the heat Qcell released by electron captures and/or pycnonuclear reactions, see Eq. (5). In turn, Qcell is very sensitive to the fine details of the nuclear structure, and therefore to the nuclear model employed. In particular, Qcell is determined to a large extent by nuclear shell effects, as can be seen in Fig. 5 from the comparison of the ETFSI and ETF results. By definition, no heat can be further extracted from catalysed matter. Therefore, g increases continuously with pressure in catalysed crust, and is lower than the values obtained for accreted crusts. However, the differences become negligibly small at high pressures, as shown in Fig. 5.
5. Crustal heating
5.1. Outer crust
The heat sources, as obtained from different nuclear mass models, are indicated in Figs. 6 and 7. In the shallowest two layers of the outer crust, all models yield similar predictions since electrons are captured by nuclei whose masses are experimentally known. On the other hand, large discrepancies can be observed at higher densities between the different models. As discussed in Sect. 3.3, the EDFs BSk19, BSk20, and BSk21 were all fitted to the atomic mass data from AME 2003 (Audi et al. 2003), whereas SLy4 was fitted to a few atomic masses from AME 1995. To assess the reliability of the different models, we have compared their predictions for the atomic mass excess of 56Sc, which has been only recently measured. As can be seen in Table 3, the largest deviation between experimental and theoretical values is found for SLy4. The Brussels–Montreal EDFs considered here yield predictions closer to the experimental value, the best (worse) agreement being achieved with HFB-21 (HFB-19) consistently with the previous analysis of Chamel et al. (2011). To evaluate the impact of theoretical nuclear masses on the heat released, we have repeated the outer-crust calculations considering data from the older AME 2003 (Audi et al. 2003) and AME 2012 (Audi et al. 2012). As shown in Table 4, the most robust predictions are given by HFB-21. On the contrary, the heat obtained with HFB SLy4 is increased by about a factor of two including the newly measured mass of 56Sc. For this model, the transitions from Z = 22 to Z = 21, and from Z = 21 to Z = 20 both occur in quasiequilibrium with no heat released.
 |
Fig. 6. Heat sources in the outer crust of accreting NS. Comparison between the model of MB and the HFB mass model using the BSk20 EDF. |
 |
Fig. 7. Heat sources in the outer crust of accreting NS. Comparison between the HFB mass models using the BSk19, BSk20, and BSk21 EDFs. The first two reactions are fully determined by experimental measurements, and are the same for all HFB models. |
Experimental atomic mass excess (in MeV) of 56Sc from AME 2016 (Wang et al. 2017), as compared to the prediction from different models.
Total heat per accreted nucleon (in MeV) deposited in the outer crust of an accreting NS, for X-ray burst ashes made of 56Fe using experimental atomic masses supplemented with theoretical predictions from HFB models based on different EDFs (BSk19-21, SLy4).
As summarised in Table 5, the MB model yields intermediate values for the total heat. The most remarkable difference between the HFB and the MB models lies in the individual heat sources, which are very sensitive to the nuclear structure. Indeed, approximating the Gibbs free energy per nucleon by (Baym et al. 1971)
the heat released by the capture of two electrons by the nuclei (A, Z) is given by
Total heat per accreted nucleon (in MeV) deposited in the outer and inner crust of an accreting NS, for X-ray burst ashes made of 56Fe for different nuclear models: microscopic models based on different EDFs (BSk19-21, SLy4) compared to the liquid drop model of Mackie & Baym (MB).
From this equation, Qcell is expected to be comparatively smaller for nuclei near shell closure. This is confirmed by the HFB models with the accurately calibrated Brussels–Montreal EDFs: they predict a smaller heat released in the densest region of the outer crust, where electron captures involve nuclei with proton magic number Z = 20. On the contrary, the HFB model with SLy4 leads to the largest heat source for the transition from Z = 22 to Z = 20, thus reflecting an improper description of the nuclear shell closure.
In contrast to HFB models, the heat sources obtained from the MB model are roughly the same for all reactions. The MB model relies on the liquid-drop picture of the nucleus ignoring the underlying nuclear shell structure. It is based on a refined version of the semi-empirical mass formula of von Weizsäcker (1935), and Bethe (1936)
where the binding energy B(A, Z) is expressed as
The first term in Eq. (13) accounts for the bulk energy of symmetric nuclear matter, the second for the surface energy of the nucleus, the third for the Coulomb energy, the fourth for the symmetry energy, and the last for the “pairing” energy. In the MB model, the coefficients are not constant but depend on the mean neutron and proton densities inside the nucleus. Ignoring these refinements here, using Eqs. (11) and (13), we find that the heat released during the capture of two electrons by nuclei (A, Z) is independent of Z, and is approximately given by
In reality, the heat released is weakly dependent on Z because of the interactions between electrons and ions that we have neglected in Eq. (11). This analysis shows that the heat released is independent of volume and surface terms in the mass formula (13), but mainly arises from “pairing”. However, this contribution is partially cancelled by the symmetry energy term, and to a lesser extent by the Coulomb term. Indeed, it is energetically favourable for a nucleus with an odd number of protons to transform into a nucleus with an even number of protons because of pairing. On the other hand, this can only be realised through the capture of an electron. However this process, which implies the conversion of the unpaired proton into a neutron, costs symmetry energy thus reducing the heat released. In other words, high values of the symmetry energy coefficient aA would lead to the release of a small quantity of heat, and vice versa. Using values of the coefficients from the MB model with A = 56, we find that the total heat released by the four electron captures in the outer crust is about 0.11 MeV. This value differs from that indicated in Table 5 due to the inclusion of density-dependent coefficients.
5.2. Inner crust
The heat sources in the inner crust of accreting NS, as predicted by different models, are indicated in Figs. 8 and 9. Most of the heat is released through electron captures as well as neutron emissions and absorptions associated with pycnonuclear reactions. The number of pycnonuclear reactions is the same (3) for all models in the range of densities shown in Figs. 8 and 9. However, the amount of heat released by these processes is found to be twice as small for the MB model (∼0.67 MeV) as compared to the ETFSI models (∼1.4 MeV). These discrepancies can be explained by the inclusion of nuclear shell effects in the ETFSI approach. Indeed, the ETF approximation leads to comparable heat release from pycnonuclear reactions (∼0.64 MeV) as the MB model. Without any nuclear shell corrections, pycnonuclear reactions are actually the only source of heat since electron captures and neutron emissions occur in quasi-equilibrium.
 |
Fig. 8. Heat sources in the inner crust of accreting NS. Comparison between the model of MB and the EDF theory using BSk19 for two different treatments: ETFSI and ETF. Pycnonuclear reactions correspond to the three largest peaks for each model. See text for details. |
 |
Fig. 9. Heat sources in the inner crust of accreting NS. Comparison between the ETFSI models based on the EDFs BSk19, BSk20, BSk21, and SLy4. See text for details. |
The integrated heat, defined by
is presented in Figs. 10 and 11. The total heat deposited in the crust is indicated in Table 5. For the ETFSI models, the results are quite similar for all four EDFs. In particular, the differences between SLy4 and BSk19-21 are less pronounced than in the outer crust. Most of the heat is released from pycnonuclear reactions involving transitions from Z = 16 to Z = 14. The close agreement between the different EDFs reflects the fact that the nuclear closure at Z = 14 is a robust prediction from HFB calculations.
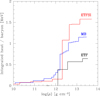 |
Fig. 10. Integrated heat in the crust of accreting NS. Comparison between the model of MB and the EDF theory using BSk19 for two different treatments: ETFSI and ETF. See text for details. For the ETF model, results are shown only for the inner crust. |
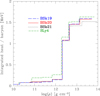 |
Fig. 11. Integrated heat in the crust of accreting NS. Comparison between the ETFSI models based on the EDFs SLy4, BSk19, BSk20, and BSk21. See text for details. |
The total heat obtained for SLy4 is significantly lower than the value of 2.5 MeV found by Steiner (2012) for the same EDF within a liquid-drop picture and considering pure ashes made of 56Ni. The discrepancy cannot be simply explained by the conversion of 56Ni into 56Fe, since the associated heat released is estimated as 0.04 MeV from Eq. (11) using the data of Audi et al. (2003). The large heat predicted by Steiner (2012) must thus lie in the different treatment of crustal matter. In particular, the SLy4 EDF enters into the calculations of Steiner (2012) only through the bulk nuclear energy of matter. The surface and Coulomb energies were calculated phenomenologically. More importantly, the added empirical corrections for pairing and shell effects fail to reproduce some magic numbers, especially for very neutron-rich nuclei, such as the neutron number N = 34 (see also the discussion in Sect. 4.2). However, the total heat deposited in the crust is very sensitive to nuclear shell effects. As illustrated in Fig. 10, the heat is indeed considerably reduced, by about a factor of three, in pure ETF calculations without any shell correction. The MB model yields an intermediate value of 1.16 MeV due to the inclusion of pairing effects. This amount of the total deposited heat is substantially lower than the value of 1.85 MeV found by Haensel & Zdunik (2008). The discrepancy arises from the more realistic treatment of the neutron emissions and absorptions by clusters in this work, as discussed in Sect. 3.6. In particular, in previous works of Haensel & Zdunik (1990a,b, 2003, 2008) neutrons produced by electron captures were confined in the clusters, thus introducing artificial shell effects. The role of nuclear shell effects is more closely analysed in the next section.
5.3. Importance of nuclear shell effects
The importance of nuclear shell effects for the evolution of an accreted matter element and deep crustal heating is illustrated in Fig. 12. The variation of the Gibbs free energy per nucleon as a function of Z is shown for three different values of the pressure P1 < P2 < P3 for the ETFSI model based on the EDF BSk20 (the other EDFs yielding qualitatively similar results) and for the MB model.
 |
Fig. 12. Gibbs free energy per nucleon for accreted NS crust (renormalised to that of catalysed matter) for nuclear clusters with different Z, as predicted by the model of MB (lower panel) and the ETFSI model with the BSk20 EDF (upper panel). With increasing pressure (P1 < P2 < P3), the energetically preferred value for Z decreases. For BSk20 (P1, P2, P3)=(0.82, 1.22, 2.6)⋅1030 erg cm−3, for MB (bottom panel) (P1, P2, P3)=(1.03, 1.28, 1.54)×1030 erg cm−3. Solid dots represent stable clusters at given pressure whereas circles denote the parent clusters for the last reactions just before the given pressure is reached. |
At pressures P ≲ P1 = 8.2 × 1029 erg cm−3, the accreted material obtained from the ETFSI model consists of 56Ar (Z = 18), corresponding to the global minimum of g. At P = P1, the minimum of g shifts to Z = 17: 56Ar nuclei capture one electron and transform into 56Cl. A similar situation occurs as the pressure attains P = 9.3 × 1029 erg cm−3, 56Cl being converted into 56S. With further compression, 56S nuclei become unstable against electron captures at pressure P ≃ P2 = 1.22 × 1030 erg cm−3 (the local minimum of g at Z = 16 disappears) and the matter element evolves to the local minimum of g corresponding to Z = 14 with the release of heat equal to the relative depth of this minimum. Since Z = 14 is a magic number, this local minimum persists over a large range of pressures, up to P3 = 2.6 × 1030 erg cm−3. As a consequence, nuclei 56Si undergo a chain of six electron captures accompanied by neutron emissions. These reactions are highly exothermic.
The evolution of an accreted matter element is radically different for the MB model. With the inclusion of pairing effects, the local minima of g correspond to even values of Z. As a consequence, the matter element undergo many more electron captures. For instance, 56Ar nuclei present at pressure P1 = 1.03 × 1030 erg cm−3 become unstable at pressure P2 = 1.07 × 1030 erg cm−3, and transform into 56S. Similarly, 56S nuclei are converted into 56Si at pressure P3 = 1.46 × 1030 erg cm−3. The changes of pressure between two successive reactions are much smaller for the MB model than in the ETFSI approach. In the example discussed above, the pressure difference P3 − P2 is about five times smaller in the MB model than in the ETFSI model. This means that in the ETFSI model five times larger amount of mass (or five times longer time for given accretion rate) is needed for a matter element to be compressed to the density at which the third reaction takes place. On the other hand, the heat released is larger by a similar factor (five to six) so that the total heat deposited in the crust is of the same order as predicted by the MB model.
5.4. Importance of realistic neutron-matter equation of state
As can be seen in Fig. 9, most of the heat is deposited in the intermediate regions of the crust from pycnonuclear reactions followed by a chain of electron captures, neutron emissions and absorptions. In turn, the presence of free neutrons modifies the properties of the clusters, and thereby their stability against further electron captures. As a matter of fact, the surrounding neutrons are crucial for the stability of the clusters, which would otherwise disintegrate. The neutron-matter stiffness was shown to have a strong influence on the composition of the inner crust of a nonaccreted NS (Goriely et al. 2005), and it is expected to play a similarly important role for accreted NSs. All the EDFs considered in this work are consistent with realistic neutron-matter EoSs, as shown in Fig. 13. On the contrary, the Gs and Rs EDFs (Friedrich & Reinhard 1986) considered by Steiner (2012) are incompatible with microscopic calculations at the low densities relevant for NS crusts. This may explain the large amounts of heat found with these EDFs, namely 4.3 MeV/nucleon and 4.8 MeV/nucleon respectively.
 |
Fig. 13. Equation of state of pure neutron matter, as predicted by different EDFs (lines). For comparison, the microscopic calculations of Friedman & Pandharipande (1981, FP) and Akmal et al. (1998, APR) based on realistic nucleon–nucleon interactions are shown by symbols. The shaded areas are the constraints inferred from the ab-initio calculations of Drischler et al. (2016) and Lynn et al. (2016). |
6. Discussion and conclusions
We have studied heating in the crust of accreting NSs following a more realistic approach than previous studies based on a liquid drop picture. In particular, we have applied the EDF theory, in which nuclear shell effects are naturally incorporated. We have described both the outer and inner crusts with the same functional, thus ensuring a unified and thermodynamically consistent treatment. To assess the impact of the neutron-matter constraint, we have employed the set of Brussels–Montreal functionals BSk19, BSk20, and BSk21 (Goriely et al. 2010). These functionals were fitted to all atomic mass data of nuclei with Z, N ≥ 8 and to different realistic neutron-matter EoSs and spanning different degrees of stiffness. For comparison, we have also considered the SLy4 functional (Chabanat et al. 1998). All these functionals have been already employed to determine the EoS of cold catalysed NSs.
For the outer crust, we have made use of experimental data from the latest AME 2016 (Wang et al. 2017) whenever available supplemented with theoretical nuclear masses obtained from the HFB method. For the inner crust, we have adopted the 4th order ETF approach with proton shell corrections added perturbatively via the Strutinsky integral theorem. This ETFSI method, which was previously applied for catalysed matter (Onsi et al. 2008; Pearson et al. 2012), is a computationally fast implementation of the HF method.
We have followed the evolution of an accreted matter element, considering ashes of X-ray bursts made of 56Fe to compare with previous calculations from HZ. As they sink into deeper layers, nuclei undergo a series of electron captures. The first two reactions are completely determined by experimental atomic masses, and all models thus predict the same heat sources. On the contrary, the location of the sources and the amount of heat deposited in the denser region is model dependent. In particular, the HFB calculations using SLy4 predict a much larger heat release for the transition from Z = 22 to Z = 20 than the other HFB models. This result, however, is the manifestation of an improper description of nuclear shell closure. For this reason, SLy4 leads to a significantly larger integrated heat than the other functionals. In contrast to HFB models, the heat obtained from the MB model is roughly the same for all reactions due to the lack of nuclear shell effects. In any case, the total heat deposited in the outer crust does not exceed 0.2 MeV per accreted nucleon. Therefore, the origin of shallow heating required to explain the cooling of some SXTs remains unknown (see e.g. Parikh et al. 2017, and references therein). At high enough densities, electron captures are accompanied by neutron emissions thus marking the transition to the inner crust. Very accurate analytical formulas for the neutron-drip density and pressure are given in Chamel & Fantina (2016a). Due to the constraints imposed on the possible reactions, all models give the same stratification of the outer crust. However, the position of the boundary between adjacent layers depends on the model employed.
In the inner crust, most of the heat is released in electron captures, neutron emissions and absorptions induced by pycnonuclear reactions, whereby the proton number of the clusters changes from Z = 16 to the magic number Z = 14. Because the shell closure at Z = 14 is a robust prediction of EDF calculations, all functionals give similar amount of the total heat deposited in the inner crust. For the same reason, clusters with Z = 14 are present in large regions of the inner crust. On the contrary, the MB model leads to a highly stratified crust. The composition of accreted crust is found to be radically different from that of catalysed crust. In contrast to catalysed crust, Z is found to be everywhere smaller than 26 in accreted crust, and clusters are much lighter. However, the ratios Z/A and A/Acell are similar, and less sensitive to fine details of the nuclear structure.
The total heat deposited in the crust, as predicted by the EDF theory, lies in the range from 1.5 MeV to 1.7 MeV per accreted nucleon. For comparison, ETF calculations in the inner crust (with no shell effects) yield much lower values ∼0.6 MeV, thus highlighting the importance of nuclear shell effects. The MB model adopted here leads to an intermediate value of 1.2 MeV due to the inclusion of pairing effects. This result is substantially lower than that previously obtained by HZ. The discrepancy arises from the more realistic treatment of the neutron emissions and absorptions by clusters in this work. The total crustal heating we have found is much lower than that predicted by Steiner (2012) within the liquid-drop picture. Steiner (2012) attributed the large amount of heat – up to 4.8 MeV per accreted nucleon depending on the adopted functional – to different behaviour of the symmetry energy. Our analysis suggests that the discrepancy could rather stem from an empirical parameterisation of nuclear shell effects and the use by Steiner (2012) of the functionals Rs and Gs (Friedrich & Reinhard 1986) that yield unrealistic neutron-matter EoS. The role of the symmetry energy should be further examined.
The values we find for the crustal heat are somewhat smaller than those obtained in the recent nuclear network calculations of Lau et al. (2018), and our main heating sources are located deeper. These differences could be attributed to the inclusion by Lau et al. (2018) of transitions to excited states and superthreshold electron capture cascades beyond neutron drip. However, the amounts of cumulated heat predicted by the two approaches appear to be in good agreement at densities 1.6 × 1012 g cm3 corresponding to the shallow region of the inner crust. The deviations observed at higher densities where free neutrons are very abundant may thus also come from our consistent description of the NS crust, and in particular the inclusion of the medium modification of nuclear shell effects within the microscopic EDF theory.
In the present paper we calculated the heating from a fully accreted crust. In our discussion of particular SXTs that could have a fully accreted crust (see Sect. 2.3), we used arguments based on the present accretion rate averaged over 10–35 years of observations. Actually, some of the SXTs are also observed as accreting X-ray pulsars (Wijnands et al. 2017). Such SXTs are being spinning-up by accretion. Relations between the present spin period and the accreted mass during recycling of millisecond pulsars are available (Tauris et al. 2012). Preliminary estimates indicate that SXTs with rotation period less than 5 ms are likely to have a have fully accreted crust. The possibility of partially accreted crust in the SXTs, considered by Wijnands et al. (2013) needs to be further studied.
Values in Table 1 slightly differ from those in Table V in Chamel et al. (2015); at variance with the latter work we now include electron exchange and polarisation corrections.
Acknowledgments
We are particularly grateful to J. Margueron for valuable discussions. Remarks and comments on the manuscript by R. Wijnands, which resulted in correcting the text, are acknowledged. We also thank A.Y. Potekhin and A.I. Chugunov for the critical reading of the manuscript and for their inspiring and motivating questions and comments. This work was financially supported by F.R.S-FNRS (Belgium), NSERC (Canada), and the European Cooperation in Science and Technology (COST) actions MP1304 and CA16214. N. C. acknowledges the support of the Fonds de la Recherche Scientifique – FNRS (Belgium) under grant n° CDR-J.0187.16 and CDR-J.0115.18. This work was partially supported by the Polish National Science Centre (NCN) grant no. 2013/11/B/ST9/04528.
References
- Afanasjev, A. V., Beard, M., Chugunov, A. I., Wiescher, M., & Yakovlev, D. G. 2012, Phys. Rev. C, 85, 054615 [NASA ADS] [CrossRef] [Google Scholar]
- Akmal, A., Pandharipande, V. R., & Ravenhall, D. G. 1998, Phys. Rev. C, 58, 1804 [NASA ADS] [CrossRef] [Google Scholar]
- Ainsworth, T. L., Wambach, J., & Pines, D. 1989, Phys. Lett. B, 222, 173 [NASA ADS] [CrossRef] [Google Scholar]
- Audi, G., Bersillon, O., Blachot, J., & Wapstra, A. H. 1997, Nucl. Phys. A, 624, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Audi, G., Wapstra, A. H., & Thibault, C. 2003, Nucl. Phys. A, 729, 337 [NASA ADS] [CrossRef] [Google Scholar]
- Audi, G., Wang, M., Wapstra, A. H., Kondev, F. G., MacCormick, M., Xu, X., & Pfeiffer, B. 2012, Chin. Phys. C, 36, 1287 [Google Scholar]
- Baumann, P., Huck, A., Klotz, G., et al. 1989, Phys. Lett. B, 228, 458 [NASA ADS] [CrossRef] [Google Scholar]
- Baym, G., & Pethick, C. 1991, Landau Fermi-liquid Theory. Concepts and Applications (New York: Wiley) [CrossRef] [Google Scholar]
- Baym, G., Pethick, C., & Sutherland, P. 1971, ApJ, 170, 299 [Google Scholar]
- Bender, M., Rutz, K., Reinhard, P.-G., & Maruhn, J. A. 2000, Eur. Phys. J. A, 8, 59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bender, M., Heenen, P.-H., & Reinhard, P.-G. 2003, Reviews of Modern Physics, 75, 121 [Google Scholar]
- Bethe, H. A. 1936, Rev. Mod. Phys., 8, 139 [CrossRef] [Google Scholar]
- Beznogov, M. V., & Yakovlev, D. G. 2015, MNRAS, 447, 1598 [Google Scholar]
- Bildsten, L., & Brown, E. F. 1997, ApJ, 477, 897 [NASA ADS] [CrossRef] [Google Scholar]
- Bisnovatyi-Kogan, G. S. 2001, Stellar Physics 1. Fundamental Concepts and Stellar Equilibrium (Berlin: Springer) sect.1.4.6 [Google Scholar]
- Bisnovatyi-Kogan, G. S., & Chechetkin, V. M. 1973, JETP Lett., 17, 437 [NASA ADS] [Google Scholar]
- Bisnovatyi-Kogan, G. S., & Chechetkin, V. M. 1974, Astrophys. Space Sci., 26, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Bisnovatyi-Kogan, G. S., & Chechetkin, V. M. 1979, Sov. Phys. Usp., 22, 89 [Google Scholar]
- Bisnovatyi-Kogan, G. S., Kulikov, Yu N, & Chechetkin, V. M. 1976, Sov. Astron., 20, 552 [NASA ADS] [Google Scholar]
- Blaes, O., Blandford, R., Madau, P., & Koonin, S. 1990, ApJ, 363, 612 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, E. F., Bildsten, L., & Rutledge, R. E. 1998, ApJ, 504, L95 [Google Scholar]
- Chabanat, E., Bonche, P., Haensel, P., Meyer, J., & Schaeffer, R. 1998, Nucl. Phys. A, 635, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Chamel, N. 2010, Phys. Rev. C, 82, 061307 [NASA ADS] [CrossRef] [Google Scholar]
- Chamel, N., & Fantina, A. F. 2016a, Phys. Rev. D, 93, 063001 [NASA ADS] [CrossRef] [Google Scholar]
- Chamel, N., & Fantina, A. F. 2016b, Phys. Rev. C, 94, 065802 [NASA ADS] [CrossRef] [Google Scholar]
- Chamel, N., & Fantina, A. F. 2015, Phys. Rev. D, 92, 023008 [NASA ADS] [CrossRef] [Google Scholar]
- Chamel, N., & Goriely, S. 2010, Phys. Rev. C, 82, 045804 [NASA ADS] [CrossRef] [Google Scholar]
- Chamel, N., & Haensel, P. 2008, Liv. Rev. Relat., 11, 10 [Google Scholar]
- Chamel, N., Naimi, S., Khan, E., & Margueron, J. 2007, Phys. Rev. C, 75, 055806 [NASA ADS] [CrossRef] [Google Scholar]
- Chamel, N., Goriely, S., & Pearson, J. M. 2009, Phys. Rev. C, 80, 065804 [NASA ADS] [CrossRef] [Google Scholar]
- Chamel, N., Fantina, A. F., Pearson, J. M., & Goriely, S. 2011, Phys. Rev. C, 84, 062802(R) [NASA ADS] [CrossRef] [Google Scholar]
- Chamel, N., Fantina, A. F., & Zdunik, J.- L., Haensel, P., 2015, Phys. Rev. C, 91, 055803 [NASA ADS] [CrossRef] [Google Scholar]
- Clayton, D. E. 1968, Principles of Stellar Evolution and Nucleosynthesis (Chicago: The University of Chicago Press) sects.7-1,7–2 [Google Scholar]
- Colò, G., van Giai, N., Meyer, J., Bennaceur, K., & Bonche, P. 2004, Phys. Rev. C, 70, 024307 [NASA ADS] [CrossRef] [Google Scholar]
- Coldwell-Horsfall, R. A., & Maradudin, A. A. 1960, J. Math. Phys., 1, 395 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- De Blasio, F. V. 2000, A&A, 353, 1129 [NASA ADS] [Google Scholar]
- Dobaczewski, J., Stoitsov, M. V., & Nazarewicz, W. 2004, Am. Inst. Phys. Conf. Ser., 726, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Douchin, F., & Haensel, P. 2001, A&A, 380, 151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Drischler, C., Carbone, A., Hebeler, K., & Schwenk, A. 2016, Phys. Rev. C, 94, 054307 [NASA ADS] [CrossRef] [Google Scholar]
- Dutta, A. K., Onsi, M., & Pearson, J. M. 2004, Phys. Rev. C, 69, 052801(R) [NASA ADS] [CrossRef] [Google Scholar]
- Fantina, A. F., Chamel, N., Pearson, J. M., & Goriely, S. 2013, A&A, 559, A128 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fantina, A. F., Chamel, N., Pearson, J. M., & Goriely, S. 2014, EPJ Web Conf., 66, 07005 [CrossRef] [Google Scholar]
- Fantina, A. F., Chamel, N., Mutafchieva, Y. D., et al. 2016, Phys. Rev. C, 93, 015801 [NASA ADS] [CrossRef] [Google Scholar]
- Friedman, B., & Pandharipande, V. R. 1981, Nucl. Phys. A, 361, 502 [NASA ADS] [CrossRef] [Google Scholar]
- Fridmann, J., Wiedenhover, I., Gade, A., et al. 2005, Nature, 435, 922 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Friedrich, J., & Reinhard, P.-G. 1986, Phys. Rev. C, 33, 335 [NASA ADS] [CrossRef] [Google Scholar]
- Goriely, S., Samyn, M., Bender, M., & Pearson, J. M. 2003, Phys. Rev. C, 68, 054325 [NASA ADS] [CrossRef] [Google Scholar]
- Goriely, S., Samyn, M., Pearson, J. M., & Onsi, M. 2005, Nucl. Phys. A, 750, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Goriely, S., Chamel, N., & Pearson, J. M. 2010, Phys. Rev. C, 82, 035804 [NASA ADS] [CrossRef] [Google Scholar]
- Goriely, S., Chamel, N., & Pearson, J. M. 2013, Phys. Rev. C, 88, 024308 [NASA ADS] [CrossRef] [Google Scholar]
- Gupta, S., Brown, E. F., Schatz, H., Moeller, P., & Kratz, K.-L. 2007, ApJ, 662, 1188 [NASA ADS] [CrossRef] [Google Scholar]
- Gupta, S., Kawano, T., & Möller, P. 2008, Phys. Rev. Lett., 101, 231101 [NASA ADS] [CrossRef] [Google Scholar]
- Haensel, P., & Pichon, B. 1994, A&A, 283, 313 [NASA ADS] [Google Scholar]
- Haensel, P., & Zdunik, J. L. 1990a, A&A, 227, 431 [NASA ADS] [Google Scholar]
- Haensel, P., & Zdunik, J. L. 1990b, A&A, 229, 117 [NASA ADS] [Google Scholar]
- Haensel, P., & Zdunik, J. L. 2003, A&A, 404, L33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haensel, P., & Zdunik, J. L. 2008, A&A, 480, 459 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haensel, P., Potekhin, A. Y., & Yakovlev, D. G. 2007, Neutron Stars 1. Equation of State and Structure (New York: Springer) sect.3.1 [Google Scholar]
- Harrison, B. K., Wakano, M., & Wheeler, J. A. 1958, La structure et évolution de l’univers (Brussels: R. Stoops), 124 [Google Scholar]
- Harrison, B. K., Wakano, M., Thorne, K. S., & Wheeler, J. A. 1965, Gravitation Theory and Gravitational Collapse (Chicago: University of Chicago Press) [Google Scholar]
- Heinke, C. O., Jonker, P. G., Wijnands, R., & Tamm, R. E. 2007, ApJ, 660, 1424 [NASA ADS] [CrossRef] [Google Scholar]
- Heinke, C. O., Jonker, P. G., Wijnands, R., Deloye, C. J., & Tamm, R. E. 2009, ApJ, 691, 1035 [NASA ADS] [CrossRef] [Google Scholar]
- Lattimer, J. M. 2012, Ann. Rev. Nucl. Part. Sci., 62, 485 [NASA ADS] [CrossRef] [Google Scholar]
- Lau, R., Beard, M., Gupta, S. S., et al. 2018, ApJ, 859, 62 [Google Scholar]
- Li, J. J., Margueron, J., Long, W. H., & Van Giai, N. 2016, Phys. Lett. B, 753, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Li, J. J., Long, W. H., Margueron, J., & Van Giai, N. 2018, ArXiv e-prints [arXiv:1807.10000v1] [Google Scholar]
- Li, Z. H., & Schulze, H.-J. 2008, Phys. Rev. C, 78, 028801 [NASA ADS] [CrossRef] [Google Scholar]
- de Loore, C. W. H., & Doom, C. 1993, Structure and Evolution of Single and Binary Stars (Dordrecht: Kluwer Academic Publishers) [Google Scholar]
- Lunney, D., Pearson, J. M., & Thibault, C. 2003, Rev. Mod. Phys., 75, 1021 [NASA ADS] [CrossRef] [Google Scholar]
- Lynn, J. E., Tews, I., Carlson, J., et al. 2016, Phys. Rev. Lett., 116, 062501 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Mackie, F. D., & Baym, G. 1977, Nucl. Phys. A, 285, 332 [NASA ADS] [CrossRef] [Google Scholar]
- Madland, D. G., & Nix, J. R. 1988, Nucl. Phys. A, 476, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Miralda-Escudé, J., Haensel, P., & Paczynski, B. 1990, ApJ, 362, 572 [NASA ADS] [CrossRef] [Google Scholar]
- Möller, P., Nix, J. R., Myers, W. D., & Swiatecki, W. J. 1995, At. Data Nucl. Data Tables, 59, 185 [Google Scholar]
- Onsi, M., Dutta, A. K., Chatri, H., et al. 2008, Phys. Rev. C, 77, 065805 [Google Scholar]
- Oyamatsu, K., & Yamada, M. 1994, Nucl. Phys. A, 578, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Parikh, A. S., Homan, J., Wijnands, R., et al. 2017, ApJ, 851, L28 [NASA ADS] [CrossRef] [Google Scholar]
- Pearson, J. M., Goriely, S., & Chamel, N. 2011, Phys. Rev. C, 83, 065810 [NASA ADS] [CrossRef] [Google Scholar]
- Pearson, J. M., Chamel, N., Goriely, S., & Ducoin, C. 2012, Phys. Rev. C, 85, 065803 [NASA ADS] [CrossRef] [Google Scholar]
- Pearson, J. M., Chamel, N., Fantina, A. F., & Goriely, S. 2014, Eur. Phys. J. A, 50, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Potekhin, A. Y., Yakovlev, D. G., Chabrier, G., et al. 2003, ApJ, 594, 404 [NASA ADS] [CrossRef] [Google Scholar]
- Potekhin, A. Y., Fantina, A. F., Chamel, N., Pearson, J. M., & Goriely, S. 2013, A&A, 560, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rolfs, C. E., & Rodney, W. S. 1988, Cauldrons in the Cosmos. Nuclear Astrophysics (Chicago: The University of Chicago Press) sect.8.2 [Google Scholar]
- Salpeter, E. E., & Van Horn, H. M. 1969, ApJ, 155, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Sato, K. 1979, Prog. Theor. Phys., 62, 957 [NASA ADS] [CrossRef] [Google Scholar]
- Schatz, H., Gupta, S., Möller, P., et al. 2014, Nature, 505, 62 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Steiner, A. W. 2012, Phys. Rev. C, 85, 055804 [NASA ADS] [CrossRef] [Google Scholar]
- Steppenbeck, D., Takeuchi, S., Aoi, N., et al. 2013, Nature, 502, 207 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Stone, J. R., & Reinhard, P.-G. 2007, Prog. Part. Nucl. Phys., 58, 587 [NASA ADS] [CrossRef] [Google Scholar]
- Tauris, T. M., & van den Heuvel, E. P. J. 2006, Compact Stellar X-ray Sources (Cambridge: Cambridge University Press), 623 [CrossRef] [Google Scholar]
- Tauris, T. M., Langer, N., & Kramer, M. 2012, MNRAS, 425, 1601 [NASA ADS] [CrossRef] [Google Scholar]
- Tews, I., Lattimer, J. M., Ohnishi, A., & Kolomeitsev, E. E. 2017, ApJ, 848, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Timmes, F. X., & Swesty, F. D. 2000, ApJS, 126, 501 [NASA ADS] [CrossRef] [Google Scholar]
- Tsang, M. B., Stone, J. R., Camera, F., et al. 2012, Phys. Rev. C, 86, 015803 [NASA ADS] [CrossRef] [Google Scholar]
- von Weizsäcker, C. F. 1935, Z. Phys., 96, 431 [CrossRef] [Google Scholar]
- Wang, M., Audi, G., Kondev, F. G., Huang, W. J., Naimi, S., & Xu, X. 2017, Chin. Phys. C, 41, 030002 [Google Scholar]
- Wapstra, A. H., & Gove, N. B. 1971, Atomic Data and Nuclear Data Tables, 9, 267 [NASA ADS] [CrossRef] [Google Scholar]
- Wijnands, R., Degenaar, N., & Page, D. 2013, MNRAS, 432, 2366 [NASA ADS] [CrossRef] [Google Scholar]
- Wijnands, R., Degenaar, N., & Page, D. 2017, Journal of Astrophysics and Astronomy, 38, 49 [Google Scholar]
- Wiringa, R. B., Fiks, V., & Fabrocini, A. 1988, Phys. Rev. C, 38, 1010 [NASA ADS] [CrossRef] [Google Scholar]
- Xu, Y. I., Goriely, S., Jorissen, A., Chen, G., & Arnould, M. 2013, A&A, 549, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yakovlev, D. G., Gasques, L. R., Afanasjev, A. V., Beard, M., & Wiescher, M. 2006a, Phys. Rev. C, 74, 035803 [NASA ADS] [CrossRef] [Google Scholar]
- Yakovlev, D. G., Gasques, L. R., & Wiescher, M. 2006b, MNRAS, 371, 1322 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Additional Tables
The tables contain the properties of the reactions in the crust of accreting NSs for the considered EDFs BSk19, BSk20, BSk21, and SLy4, as well as for the MB model. We assume that the ashes of X-ray bursts consist of pure 56Fe. For the EDFs models the atomic number of clusters in the inner crust is only approximate (rounded), since in our approach nucleons inside clusters and free nucleons are not treated separately. For the same reason the number ΔN of emitted neutrons is not specified. The pressure and density at which the reactions take place are denoted by P and ρ, respectively. The relative density jump Δρ/ρj and the deposited heat (per one accreted nucleon) qj associated with the process j are presented in the fifth and seventh column respectively. Xn = 1 −A/Acell is the fraction of free neutrons among nucleons, and μe is the electron Fermi energy, both in the layer just above the reaction layer. Pycnonuclear reactions, which lead to the doubled Acell, are marked by horizontal lines.
Non-equilibrium processes in the crust of an accreting NS assuming that the ashes of X-ray bursts consist of pure 56Fe using the EDF BSk21 (HFB method in the outer crust, ETFSI method in the inner crust).
Non-equilibrium processes in the crust of an accreting NS assuming that the ashes of X-ray bursts consist of pure 56Fe using the EDF BSk20 (HFB method in the outer crust, ETFSI method in the inner crust).
Non-equilibrium processes in the crust of an accreting NS assuming that the ashes of X-ray bursts consist of pure 56Fe using the EDF BSk19 (HFB method in the outer crust, ETFSI method in the inner crust).
Non-equilibrium processes in the inner crust of an accreting NS assuming that the ashes of X-ray bursts consist of pure 56Fe. ETF model with EDF BSk19.
Non-equilibrium processes in the crust of an accreting NS assuming that the ashes of X-ray bursts consist of pure 56Fe using the EDF SLy4 (HFB method in the outer crust, ETFSI method in the inner crust).
Non-equilibrium processes in the crust of an accreting NS assuming that the ashes of X-ray bursts consist of pure 56Fe using the Mackie-Baym model adapted to the scheme presented in this paper.
All Tables
Neutron-drip transition in the crust of accreting NSs, as predicted by different nuclear mass models for 56Fe ashes.
Neutron-drip transition in the crust of catalysed NSs, as predicted by different nuclear mass models.
Experimental atomic mass excess (in MeV) of 56Sc from AME 2016 (Wang et al. 2017), as compared to the prediction from different models.
Total heat per accreted nucleon (in MeV) deposited in the outer crust of an accreting NS, for X-ray burst ashes made of 56Fe using experimental atomic masses supplemented with theoretical predictions from HFB models based on different EDFs (BSk19-21, SLy4).
Total heat per accreted nucleon (in MeV) deposited in the outer and inner crust of an accreting NS, for X-ray burst ashes made of 56Fe for different nuclear models: microscopic models based on different EDFs (BSk19-21, SLy4) compared to the liquid drop model of Mackie & Baym (MB).
Non-equilibrium processes in the crust of an accreting NS assuming that the ashes of X-ray bursts consist of pure 56Fe using the EDF BSk21 (HFB method in the outer crust, ETFSI method in the inner crust).
Non-equilibrium processes in the crust of an accreting NS assuming that the ashes of X-ray bursts consist of pure 56Fe using the EDF BSk20 (HFB method in the outer crust, ETFSI method in the inner crust).
Non-equilibrium processes in the crust of an accreting NS assuming that the ashes of X-ray bursts consist of pure 56Fe using the EDF BSk19 (HFB method in the outer crust, ETFSI method in the inner crust).
Non-equilibrium processes in the inner crust of an accreting NS assuming that the ashes of X-ray bursts consist of pure 56Fe. ETF model with EDF BSk19.
Non-equilibrium processes in the crust of an accreting NS assuming that the ashes of X-ray bursts consist of pure 56Fe using the EDF SLy4 (HFB method in the outer crust, ETFSI method in the inner crust).
Non-equilibrium processes in the crust of an accreting NS assuming that the ashes of X-ray bursts consist of pure 56Fe using the Mackie-Baym model adapted to the scheme presented in this paper.
All Figures
 |
Fig. 1. Proton number Z and neutron number N of nuclei in the outer crust of an accreted NS for X-ray burst ashes made of 56Fe. Results are shown for the model of Mackie & Baym (1977), hereafter MB) and for HFB nuclear mass models using different EDFs: BSk19, BSk20 and BSk21 from Goriely et al. (2010) and SLy4 from Chabanat et al. (1998). |
| In the text | |
 |
Fig. 2. Proton number Z and neutron number N of nuclear clusters in the inner crust of an accreted NS for X-ray burst ashes made of 56Fe. Pycnonuclear reactions are marked by asterisks. Results are shown for the model of MB, and for the model based on the BSk19 EDF comparing two different treatments: ETFSI vs. ETF (no shell correction). |
| In the text | |
 |
Fig. 3. Proton number Z and neutron number N of nuclear clusters in the inner crust of an accreted NS for X-ray burst ashes made of 56Fe. Pycnonuclear reactions are marked by asterisks. Results are shown for the ETFSI models based on the EDFs BSk19, BSk20, BSk21, and SLy4. |
| In the text | |
 |
Fig. 4. Proton fraction (top panel) and fraction of nucleons in nuclei (bottom panel) for accreting NS crust and catalysed NS crust (for the model based on the BSk19 EDF, thin solid line). Results are shown for the model of MB, and for the model based on the BSk19 EDF comparing two different treatments for the inner crust: ETFSI vs. ETF (no shell correction). For the ETF model in the top panel, results are shown only for the inner crust. |
| In the text | |
 |
Fig. 5. Gibbs free energy per nucleon g in accreting NS crust and catalysed NS crust (thin bottom lines). Top panel: predictions from the model of MB and from the model based on the BSk19 EDF comparing two different treatments for the inner crust: ETFSI vs. ETF (no shell correction). Bottom panel: predictions from models based on differents EDFs. See text for details. |
| In the text | |
 |
Fig. 6. Heat sources in the outer crust of accreting NS. Comparison between the model of MB and the HFB mass model using the BSk20 EDF. |
| In the text | |
 |
Fig. 7. Heat sources in the outer crust of accreting NS. Comparison between the HFB mass models using the BSk19, BSk20, and BSk21 EDFs. The first two reactions are fully determined by experimental measurements, and are the same for all HFB models. |
| In the text | |
 |
Fig. 8. Heat sources in the inner crust of accreting NS. Comparison between the model of MB and the EDF theory using BSk19 for two different treatments: ETFSI and ETF. Pycnonuclear reactions correspond to the three largest peaks for each model. See text for details. |
| In the text | |
 |
Fig. 9. Heat sources in the inner crust of accreting NS. Comparison between the ETFSI models based on the EDFs BSk19, BSk20, BSk21, and SLy4. See text for details. |
| In the text | |
 |
Fig. 10. Integrated heat in the crust of accreting NS. Comparison between the model of MB and the EDF theory using BSk19 for two different treatments: ETFSI and ETF. See text for details. For the ETF model, results are shown only for the inner crust. |
| In the text | |
 |
Fig. 11. Integrated heat in the crust of accreting NS. Comparison between the ETFSI models based on the EDFs SLy4, BSk19, BSk20, and BSk21. See text for details. |
| In the text | |
 |
Fig. 12. Gibbs free energy per nucleon for accreted NS crust (renormalised to that of catalysed matter) for nuclear clusters with different Z, as predicted by the model of MB (lower panel) and the ETFSI model with the BSk20 EDF (upper panel). With increasing pressure (P1 < P2 < P3), the energetically preferred value for Z decreases. For BSk20 (P1, P2, P3)=(0.82, 1.22, 2.6)⋅1030 erg cm−3, for MB (bottom panel) (P1, P2, P3)=(1.03, 1.28, 1.54)×1030 erg cm−3. Solid dots represent stable clusters at given pressure whereas circles denote the parent clusters for the last reactions just before the given pressure is reached. |
| In the text | |
 |
Fig. 13. Equation of state of pure neutron matter, as predicted by different EDFs (lines). For comparison, the microscopic calculations of Friedman & Pandharipande (1981, FP) and Akmal et al. (1998, APR) based on realistic nucleon–nucleon interactions are shown by symbols. The shaded areas are the constraints inferred from the ab-initio calculations of Drischler et al. (2016) and Lynn et al. (2016). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



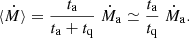
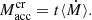
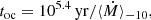
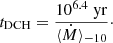
![$$ \begin{aligned} Q_\text{ cell}\approx \left[g(A,Z,P_\beta )-g(A,Z_0,P_\beta )\right] A. \end{aligned} $$](/articles/aa/full_html/2018/12/aa33605-18/aa33605-18-eq9.gif)
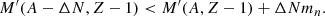
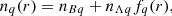
![$$ \begin{aligned} f_q(r) = \frac{1}{1 + \exp \left[ \Big (\frac{C_q - R}{r - R}\Big )^2 - 1\right] \exp \Big (\frac{r-C_q}{a_q}\Big ) }, \end{aligned} $$](/articles/aa/full_html/2018/12/aa33605-18/aa33605-18-eq12.gif)
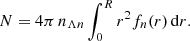
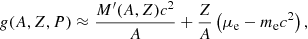
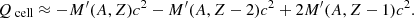
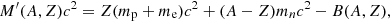
![$$ \begin{aligned}&B(A,Z)=a_V A - a_S A^{2/3} - a_C \frac{Z^2}{A^{1/3}}- a_A\frac{(A-2Z)^2}{A}\nonumber \\&\qquad \;+\frac{(-1)^Z}{2}\biggl [1+(-1)^A\biggr ]\frac{a_{\rm P}}{\sqrt{A}}\cdot \end{aligned} $$](/articles/aa/full_html/2018/12/aa33605-18/aa33605-18-eq17.gif)