| Issue |
A&A
Volume 620, December 2018
|
|
|---|---|---|
| Article Number | A32 | |
| Number of page(s) | 10 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201833546 | |
| Published online | 23 November 2018 | |
Far-infrared emission of massive stars★
1
European Southern Observatory,
Karl-Schwarzschild-Str. 2,
85748 Garching b. München,
Germany
e-mail: Ralf.Siebenmorgen@eso.org
2
Institue of Astronomy and Astrophyscis, Academia Sinica,
11F of AS/NTU Astronomy-Mathematics Building, No. 1, Sec. 4, Roosevelt Rd, Taipei 10617, Taiwan
3
Center for Astronomy, Nicolaus Copernicus University, Grudzia̧dzka 5, Pl-87-100 Toruń, and Rzeszów University,
al. T. Rejtana 16c,
35-959 Rzeszów, Poland
Received:
1
June
2018
Accepted:
4
September
2018
We present results of the analysis of a sample of 22 stars of spectral types from O7 to B5 and luminosity classes I–V for which spectra from the Infrared Spectrograph (IRS) of Spitzer are available. The IRS spectra of these stars are examined for signs of excess infrared (IR) emission by comparison with stellar atmospheric spectra. We find that the spectra of half of the studied stars are dominated by excess emission in the far-IR, including all six super- and bright giants. In order to examine the origin of the far-IR excess, we supplement the Spitzer data with optical high-resolution echelle spectroscopy (λ∕Δλ ~ 105), near-IR high-contrast coronagraphic imaging taken with the SPHERE instrument at VLT with a spatial resolution of 0.′′05, and WISE and Herschel photometry. In the optical region, we detect various absorption and emission lines (H α, C III, and N III) irrespective of the far-IR excess. Pfund α and Humphrey α lines are observed at the same time as the far-IR excess. These lines are stronger in stars with far-IR excess than in stars without excess. A scattered-light disk in the central r ≲ 2.5′′ region of the far-IR excess stars HD 149404, HD 151804, and HD 154368 can be excluded from H band imaging down to a 1σ contrast of F(r)∕F∗~ 10−6. The far-IR excess is fit either by a free–free component from ionized gas as for the winds of hot stars or a large (1 pc) circumstellar dust shell. The putative dust envelopes required to explain the excess have a visual extinction as low as a few hundred μ-mag.
Key words: infrared: stars / dust, extinction / stars: early-type / infrared: ISM
Optical high-resolution spectra are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/620/A32
© ESO 2018
1 Introduction
Thanks to the sensitivity of recent space missions, particularly the Spitzer and Herschel space telescope, infrared (IR) excess emission has been revealed for a large number of stars in a variety of environments. In low-mass stars, IR excess emission is commonly attributed to the presence of circumstellar dust, which absorbs stellar radiation and re-radiates it in the IR. This includes protoplanetary disks and AGB shells as well as debris disks. In more massive main sequence stars, excess emission is commonly attributed to thermal free–free emission in a hot, dense ionised wind (Hartmann & Cassinelli 1977). This produces a continuum of emission from the IR to the radio with a distinctive power-law spectral index fν ∝ ν0.7 (Barlow 1979). A particular case are Be-stars emitting copious free–free radiation (Rivinius et al. 2013 for a recent review). However, in the IR it is difficult to distinguish free–free from optically thin dust emission. The presence or absence of dust could hold important information regarding sources of interstellar dust, particularly in high-redshift galaxies, and the formation and evolution of massive stars.
We present a sample of massive stars for which Spitzer/IRS (Houck et al. 2004) 5–35 μm spectra are available. These mid- to far-IR spectra1 are used to search for excess emission over the expected photospheric flux, which we seek to correctly attribute to wind and/or dust emission. In Sect. 2 we outline our sample selection and the data available for the stars. Section 3 discusses the modeling of the excesses as either wind or dust emission including the possible origins of the grains. Section 4 summarises our conclusions.
2 Observations
2.1 Sample
We select a sample of targets that forms a subsample of the Voshchinnikov & Henning (2010) sample of 196 OB stars, which were originally selected for knowledge of the dust phase abundances of O, Mg, Fe and Si in the interstellar medium (ISM). The available data was extended in Voshchinnikov et al. (2012) by collating fractional polarisation measurements. In the optical region it is shown that the wavelength dependence of polarisation towards these stars follows a Serkowski curve (Bagnulo et al. 2017). The polarisation cannot therefore be due to scattering on dust or free electrons and must come from dichroic absorption by aligned dust particles. Further, it is assumed that the dichroism appears along the sightline towards the star in the diffuse ISM (Siebenmorgen et al. 2018), and ignoring any connection with the circumstellar environment of the stars. Voshchinnikov et al. (2012) study the role of the elements in the grain alignment that results in polarisation. Table 1 lists the relevant details of our sample, taken from the aforementioned papers, and references to the spectral types of the star.
Details of sample stars.
2.2 Archival data
Our selection of stars is based on the availability of archival IRS (Houck et al. 2004) spectra, giving us a total of 22 stars. These data were complimented with optical (UBVRI) and near-IR (JHK) photometry obtained from Vizier/CDS and the 2MASS point-source catalogue (Cutri et al. 2003; Skrutskie et al. 2006). Where possible, further archival IR data were collected including those from the Infrared Array Camera (Fazio et al. 2004) of Spitzer, AKARI (Ishihara et al. 2010), the Infrared Astronomical Satellite (IRAS, Neugebauer et al. 1984; Joint Iras Science 1994), the Wide-Field Infrared Survey Explorer (WISE, Cutri et al. 2012) photometry, and Infrared Space Observatory (ISO) spectra from the Short Wavelength Spectrometer (SWS, Sloan et al. 2003). In most cases only upper limits are available. Unfortunately it has not been possible to locate higher quality data at wavelengths longer than 40 μm from the Multi-Band Imaging Photometer (MIPS) of Spitzer. However, point-source photometry of the Photodetector Array Camera and Spectrometer (PACS) of Herschel (Marton et al. 2017) is available at 70, 100, and 160 μm for HD 24912, HD 149404, HD 149757, HD 151804, and HD 210839.
2.3 Detection of excess far-IR emission
The photospheric flux of the sources is determined by taking a black-body spectrum appropriate to the spectral type of the star, giving a satisfactory fit to the 2MASS, WISE, and UBVRI photometry accounting for distance and foreground extinction. In the optical region the reddening correction is important. We take for each sightline the extinction curve and foreground extinction as given by Valencic et al. (2004); Fitzpatrick (2004), Fitzpatrick & Massa (2007), and Gordon et al. (2009). We compare this estimate of the photospheric flux with stellar atmosphere models taken from the Castelli & Kurucz (2004) atlas for the stellar type given in Table 1. The stellar atmosphere models are identical to black bodies at wavelengths ≥ 0.8 μm and in the optical continuum when reddened by additional 0.1 mag. Given the precision of IR photometry we believe the uncertainties on photospheric parameters to be less than 10%. Temperatures for the black body spectra were based on the Heap et al. (2006) calibration of O-star properties, and this was also used as a starting point for the luminosities. Figure 1 shows the IRS spectra and the contribution of the photospheres. The photospheric contribution thus determined was subtracted from the IRS spectrum to identify excess emission. The precision of our estimate of the emission by the photosphere is exemplified in Fig. 5. Apparently our single stellar temperature fits the optical/IR photometry well. The model provides a reasonable estimate of the far-IR emission of the photosphere, even for multiple-component systems such as HD 149404.
For 12 of the 22 sources, the fractional excess (FIRS−Fbb)∕Fbb ≥ 0.1 over a large portion of the IRS wavelength coverage, and for two stars, HD 149757 and HD 165024, the detected excess is marginal (Fig. 1). Ten of the stars are not considered host excess emission. Given the high signal-to-noise ratio (S/N) of our IRS spectra with absolute flux uncertainties of a few percent, this lower limit is somewhat conservative but allows for reasonable (< 10%) uncertainty in the photospheric parameters. The excess becomes clearly visible at wavelengths λ ≳ 10 μm and in Fig. 1 can be seen to be most pronounced at the longest wavelengths, such that we refer to it as far-IR excess.
 |
Fig. 1 Infrared (5–35 μm) SEDs of sources. The yellow shaded region shows the photospheric contribution, while the yellow line shows the IRS spectrum. The magenta shaded region in between highlights the excess. Photometry for HD 151804 are shown as grey circles due to the restricted wavelength coverage of IRS. |
2.4 High-resolution spectroscopy
For our sample, we collate high-resolution optical spectra observed over the past 25 yr. We have used ESO telescopes with instruments UVES/VLT offering a resolving power of R = λ∕Δλ ~ 80 000−110 000, HARPS (R = 115 000) at the 3.6 m, and FEROS (R = 48 000) at the ESO/MPG 2.2 m. We also used spectrographs at other observatories such as ELODIE (R = 42 000) at the 1.93 m Observatoire de Haute-Provence, GRAMS (R = 40 000) at the 1 m of the Russian Special Astrophysical Observatory at Northern Caucasus, Sandiford (R = 64 000) at the 2.1 m Otto Struve telescope, BOES (R = 30 000−90 000) at the 1.8 m Bohyunsan Optical Astronomy Observatory in Korea, and MAESTRO (R = 40 000−120 000) at the 2 m telescope of the Terskol Observatory at Northern Caucasus.
In Table 2 we list for each star the spectrograph used together with the observing date. We derive distance to the stars from Gaia DR2 parallaxes (Gaia Collaboration 2018), Ca II (Megier et al. 2009), and from the spectral and luminosity class (Sp/L). We note that there is often a large scatter of up to a factor of two in the distance estimates (Krełowski 2018). We comment on the presence or absence of the H α at 6563 Å, C III at 5596 Å, and N III at 4641 Å lines and specify the strength of the Pfund α (n = 6 → 5) near 7.5 μm and Humphrey α (n = 7 → 6) transitions near 12.3 μm (Kramida et al. 2018), as measured in the Spitzer/IRS spectrum. Pfund and Humphrey, C III and N III lines are detected in emission. Spectral classification of the stars is based on our optical HR spectra and reported in Table 1. Our classifications generally agree with those derived by Bowen et al. (2008), Jenkins (2009), Rauw et al. (2015); Skiff (2013); Sota et al. (2011, 2014).
Free–free radiation is emitted wherever there is ionised gas. The presence of hydrogen lines can also be a transient phenomenon and prototypical examples are Be-stars. The transient nature of the H α emission in our sample is best demonstrated by HD 149757. The star is a rapid rotator and frequently classified as O9.5. We confirm the more recent O9.2IV classification by Sota et al. (2014), whereas Levenhagen & Leister (2006) classified the star as Be-star (type B0Ve). Their classification is based on a spectrum taken in April 2000 at the ESO 1.2m. We have taken multiple high resolution spectra between May 1993 and March 2010 (Fig. 3). With the exception of a spectrum taken in 2006 where we observed weak H α emission in the wings of the absorption line, H α emission is not detected in any of these spectra of HD 149757. The Spitzer IRS spectrum taken in September 2008 displays Pfund α and Humphrey α in emission.
We present a second example underscoring the transient nature of the lines and show high-resolution FEROS and UVES spectra of HD 149404 in Fig. 2. The He I lines at 4471 and 5876 Å observed with FEROS demonstrate that HD 149404 is a binary. One of the components shows the C IV 5812 Å line and is therefore an O type star while the second does not show the C IV 5812 Å line and is a B type star. The combined spectrum is apparently variable.
We detect H α emission in ~60% (7 out of 12) of the far-IR excess stars and in only 14% (1 out of 7) of the non-far-IR excess stars. Therefore, we cannot firmly conclude from optical recombination lines whether a far-IR excess is present or not. Interestingly, the non-far-IR excess star HD 47839 displays C III and N III but no hydrogen lines despite it being classified as a Be-star.
Spitzer/IRS offers the unique capability of observing hydrogen lines simultaneously with the far-IR emission. This is of great advantage because of the transient nature of the lines. The strongest H recombination lines observed in the IRS domain are the Pfund α (n = 6 → 5) and Humphrey α (n = 7 → 6) transitions near 7.5 and 12.3 μm, respectively. Pf α lines are stronger than Hu α lines. We find that there is no strong correlation between the detection of these lines and the presence of a far-IR excess. Although from inspection of Table 2 a clear trend can be reported: the line intensities are typically an order of magnitude stronger in stars with far-IR excess than in stars without far-IR excess. The detection rate of the lines is ~ 84% (10 out of 12) for IR-excess stars whereas Pf α is detected only in 50% and Hu α in 33% for stars without IR excess.
Spectral lines for stars with and without far–IR excess.
2.5 High-contrast imaging
The IRS spectra reveal a high detection rate of excess far-IR emission over the predicted photospheric component for 12 out of the 22 massive stars (55%). We aim to resolve a dust component in a possible disk-like structure in scattered starlight using SPHERE, the extreme-adaptive-optics instrument at the VLT (Beuzit et al. 2008). The detection of scattered-light disks around massive stars would have presented interesting historical parallels to the detection of dusty disks around low-mass stars, such as β Pic, which was first identified in the IR using IRAS before being confirmed by scattered-light imaging (Smith & Terrile 1984).
We performed near-IR (H band) high-contrast coronagraphic imaging observations of three stars that show excess far-IR emission: HD 149404, HD 151804, and HD 154368, together with HD 147225 as a reference star. We used the IRDIS sub-instrument of SPHERE (Beuzit et al. 2008) on April 19 and June 19, 2015. The targets were observed for approximately 45 min in the broad H band filter with a detector integration time of 0.84 s and a pixel scale of 12.27 mas. All exposures are flat-field corrected and background subtracted, their bad pixels are removed, and the detector dithering is corrected. Before adding the exposures, a subpixel shift algorithm is used to centre the images over time, and then the IRDIS detector channels are averaged. The procedure is performed on the science and reference star. The latter was used for point spread function (PSF) subtraction applying the algorithm described by Lafreniere et al. (2008). Finally, we compute the contrast given as the flux ratio F(r)∕F∗ of science target and stellar halo as estimated from the PSF. The contrast is a function of distance r (separation)from the star.
We do not observe any significant structures above the noise of the stellar halo that one could claim as scattered-light disk detection. A 1σ noise limit of the contrast curve is computed. It is given for each pixel separation as standard deviation in annuli with one-pixel width centred on the PSF core. Further details of the observing set-up and data reduction are given by Banas (2017) and Scicluna et al. (2017). The upper limits of the contrast curves of the three stars are displayed in Fig. 4. At ~ 2′′ separation from the star, our data reaches a 1σ contrast of 2 × 10−7, demonstrating the unparalleled imaging contrast that can be achieved with SPHERE/IRDIS.
 |
Fig. 2 High-resolution spectra (top panel) of HD 149404 taken with FEROS in 2005 (red) and UVES in 2009 (green). Bottom panel: velocity dispersion. One notices an additional component observed in the HeI 5876 Å line, likely originated in a companion star, while in C IV such a second component is absent. |
 |
Fig. 3 High-resolution spectra of HD 149757 between observing epochs from 1993 to 2009. H α emission is detected only in the 2006 spectrum; we note the wings of the absorption profile. |
3 Discussion
After the detection of the far-IR excess in 12 out of 22 OB stars, we explore the possible origin; we discuss the impact of background sources, the Be phenomenon, and emission from a faint dust halo around the sources. Spectral energy distribution (SED) models of the stars are best constrained when Spitzer spectra are available together with Herschel photometry. This is the case for five stars with far-IR excess that are listed in Table 3 (Col. 1) together with their stellar temperature (Col. 2), luminosity (Col. 3), and mass (Col. 4). To quantify the strength of the excess far-IR emission, we compute the ratio of the observed and photospheric luminosity in the IRS 5− 35 μm spectral range (Col. 5).
3.1 Background source
To identify possible contamination by dusty background sources, we fit a single-temperature modified black body, fν ∝ ν2Bν(T), to the continuum excess using MPFIT (Markwardt 2009). The reduced-χ2 values are all ≫1, indicating that a single black body is not adequate for fitting these spectra. Given the high temperatures of the best fits (150–290 K) it is also clear that a cool background source is not able to explain the excess.
3.2 Be-stars
Be-stars show a B-type stellar spectrum in combination with Balmer line emission, and an IR excess is often observed. The IR excess of Be stars is due to free–free emission from an ionized purely gaseous circumstellar disk and does not come from a wind or synchrotron component (Rivinius et al. 2013). For dense disks, the excess starts to dominate the photospheric emission at near- to mid-IR wavelengths (Vieira et al. 2017). The slope of the IR excess depends on the density profile of the disk, and is close to a power-law νγ with 0.6 ≲ γ ≲ 2 (Klement et al. 2017). The Be phenomenon may be a period in the life of a “normal” B star (Galazutdinov & Krełowski 2006).
We searched various catalogues and publications listing Be-stars (Fabregat et al. 1996; Rivinius et al. 2006; Wisniewski et al. 2007; Catanzaro 2013; Draper et al. 2014; Chojnowski et al. 2015; Lin et al. 2015) and find three stars in our sample that were classified as Be-type stars. There is HD 47839 that does not display a far-IR excess, HD 149757 (ζ Oph) that occasionally shows Be-type outbursts (Vogt & Penrod 1983; Kambe et al. 1997, Fig. 3), and HD 206773 that has a strong far-IR excess with a rising wavelength dependency at ≳ 25 μm (Fig. 1). The occurrence of three likely Be-stars in our sample of 22 stars is in line with the estimate that about 17% of B-type stars are Be-stars (Zorec & Briot 1997). However, we detect a far-IR excess in 12out of 22 sources at a much higher detection rate. Fully ionized optically thick disk models of Be-stars are presented by Carciofi & Bjorkman (2006). They predict excess emission for disks inclinations ≤ 60° emerging at short wavelengths (≲1 μm) and for edge-on view (90°) in the mid-IR at ~10 μm. The excess that we are observing develops in the far-IR at wavelengths ≳ 10 μm (Fig. 1). It is unlikely that all our far-IR excess stars are yet unclassified Be-stars with their disks viewed nearly edge-on. Therefore, the Be-star phenomenon is unlikely to be the dominant origin of the far-IR excess.
Characteristics of far-IR excess sources with available Spitzer/IRS and Herschel photometry.
 |
Fig. 4 SPHERE/IRDIS upper limits (3σ) of the contrast F(r)∕F∗ (black) as a function of separation r from the stars. A dust model fitting the upper limit of the contrast of HD 149404 (magenta line) is shown together with the applied dust density distribution ∝ ρ(r)∕ρ0 (green dotted line). |
3.3 Wind models
It has been shown (Barlow 1979) that a dense ionised medium generates free–free emission at wavelengths from radio to IR. A simple Fff∝ ν0.7 dependence has been shown to fit well over six orders of magnitude in frequency from the IR to the radio (Klement et al. 2017). It is apparent for the strongest radio-emitters (e.g. HD 210839) that an IR free–free component is present. In order to investigate this effect we located relevant radio data for our targets where available. For those stars with no radio data, it is possible to estimate a theoretical mass-loss rate Ṁ (Vink et al. 2001), as a function of the mass, luminosity, temperature and metallicity of the source2. As a result, it is necessary to determine masses for our sample of stars. To do so, we compare the luminosity and temperature to the Geneva evolutionary tracks (Ekström et al. 2012) for solar metallicity to find a best fitting mass. Multiple systems should be excluded from such an analysis. The mass-loss rates thus derived are then used to predict a 3.6 cm flux for the wind Fwind. The flux estimate is based on
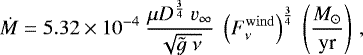 (1)
(1)
where D is the distance, v∞ the wind thermal velocity, and 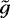 is the Gaunt factor assuming an effective wind temperature Twind ~ 0.6 T* (Carciofi & Bjorkman 2006). In the model by Vink et al. (2001) it is assumed that the wind is composed entirely of ionised hydrogen, and so the mean ionic weight μ = 0.5 in units of proton mass. The derived mass-loss rates are given in Table 3 (Col. 6) together with the 3.6 cm flux Fwind (Col. 8). We extrapolate the fit to the IR data by the free–free component to a 3.6 cm flux Fff (Col. 7), which using Eq. (1) gives a mass-loss rate Ṁff specified in Col. 7. Whenever available we give the observed 3.6 cm flux Fobs in Col. 9.
is the Gaunt factor assuming an effective wind temperature Twind ~ 0.6 T* (Carciofi & Bjorkman 2006). In the model by Vink et al. (2001) it is assumed that the wind is composed entirely of ionised hydrogen, and so the mean ionic weight μ = 0.5 in units of proton mass. The derived mass-loss rates are given in Table 3 (Col. 6) together with the 3.6 cm flux Fwind (Col. 8). We extrapolate the fit to the IR data by the free–free component to a 3.6 cm flux Fff (Col. 7), which using Eq. (1) gives a mass-loss rate Ṁff specified in Col. 7. Whenever available we give the observed 3.6 cm flux Fobs in Col. 9.
In Fig. 5 (left panels) the free–free component Fff is shown using a blue dotted line, and the total flux F∗ + Fff using a green full line. We find that the free–free component can always be adjusted so that IR data are matched. The SEDs of HD 149757 and HD 210839 are well fit when assuming that the free–free flux is given by the wind models (Fff = Fwind) while such a model underestimates IR data of the other sources. However, the required 3.6 cm free–free flux is much stronger (factor ~ 2) than the observed fluxes of HD 24912 and HD 210839 by Puls et al. (2006) and HD 151804 by Lamers & Leitherer (1993).
 |
Fig. 5 SED of massive stars. The total emission is fit by adding to the photosphere (yellow) either free–free (left blue dotted lines) or dust emission in apertures as labelled (right red-brown lines). Data (black) are from optical catalogues as available at VizieR/CDS, 2MASS, WISE, Spitzer/IRS, and Herschel/PACS with 1σ error bars and 3σ upper limits. |
3.4 Circumstellar dust models
As a single dust temperature cannot reproduce the observed emission, we require a distribution of dust near the source with a range of temperatures and masses: a circumstellar envelope. The data for each source were modelled assuming spherical symmetry using a code described in Krügel (2008) with dust heated by a central star. The code solves the radiative transfer equation by ray tracing, with the source placed at the centre of the cloud. We solve the radiative transfer equation
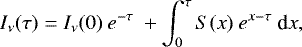 (2)
(2)
where Iν is the intensity, Bν(T) is the Planck function, P(T) is the temperature distribution for stochastically heated grains (Siebenmorgen et al. 1992), Kabs is the absorption, Ksca the scattering, Kext the extinction cross-sections, g is the scattering anisotropy parameter, and τ is the optical depth. By multiplying the scattering cross-section by 1 − g we are able to account for anisotropic scattering by effectively dividing the scattering into a purely isotropic component and a forward scattered component (Scicluna & Siebenmorgen 2015). The boundary conditions are provided by the external radiation field and the stellar flux. The input stellar spectrum is treated as a black body of given temperature and integrated luminosity truncated at Ly α, which is then processed by the dust distribution. It is not necessary to treat an interstellar radiation field as the luminosity of the stars is so great that they dominate the local radiation field (Mathis et al. 1983). Krügel (2008) gives the interstellar radiation field a mean value of 0.04 erg s−1 cm−2, while for a star of luminosity 104 L⊙ the radiation field at 1 pc is 0.32 erg s−1 cm−2, an order of magnitude larger. The orbital separations of the multiple stars included in the sample are small compared to the expected dust inner radius, so we model them as a single point source.
The dust model consists of sub-micron sized grains of amorphous carbon and/or silicates, as well as stochastically heated particles in the form of PAHs and nanometre-scale graphite and silicate particles (Siebenmorgen et al. 2014). We apply dust parameters for single-cloud sightlines given by Siebenmorgen et al. (2018). The radiative transfer is solved iteratively, and dust emission and temperatures are solved self-consistently. The geometry of the envelopes is characterised by an inner and outer dust radius, and a dust density distribution ρ(r). The model allows the computation of SEDs within apertures of the circumstellar envelope of different angular sizes.
We demonstrate the models using the strong far-IR excess source HD 149404 for which a SPHERE contrast curve and Herschel photometry are available. Its photosphere is approximated by a single temperature of 33 000 K, which is reddened by AV = 2.2 mag, and a Fitzpatrick (2004) and Gordon et al. (2009) extinction curve with RV = 3.65. As shown in Fig. 5, the photosphere model fits the optical (UBVR), 2MASS, and WISE photometry despite the variability of this multi-component system (Fig. 2). The lower panel of Fig. 2 shows an additional component in the HeI 5876 Å line representing the fainter O-type companion star, while such a second component is absent in the C IV 5812 Å line. WISE photometry at 12 and 22 μm is consistentwith the Spitzer IRS spectrum.
We take the SPHERE contrast curve to constrain the innermost 0.05′′−2.5′′ region of the dust shell (Fig. 4). The IR data are fit assuming a constant dust density in a shallow dust envelope in the range 0.011 < r ≤ 1 (pc) of AV = 300 μmag. We also compute a second model in which the dust content in the inner region (≤ 2275 AU) is increased by multi-component power laws until the 3σ upper limit of the contrast curve is matched. This gives an upper limit of the total amount of warm (≳ 250 K) dust of ≲ 10−10 M⊙. The density distribution in the inner region is shown as green and the contrast curve of that model is shown with a magenta line in Fig. 4. The low amount of warm dust does not contribute to the SED in the IRS spectral range. For HD 24912, HD 149757, and HD 151804, we keep the same structure of the circumstellar dust shell and set ρ(r)= ρ0 to be constant for 0.011 < r ≤ 1 (pc) and otherwise there is no dust. For HD 210839, our highest-luminosity far-IR excess star, we increased the inner radius to 0.026 pc so that the model does not show the SiO dust bands. At the inner radius, the dust temperature is about 300 K. Nano-sized particles are photo-dissociated up to distances of ~ 6 × 1016 cm from the star. The models are consistent with the non-detection of PAH features or oxygen-rich dust bands (silicates) in the IRS spectra. The dust emission spectrum is insensitive to the adopted effective temperature of the OB stars. The computed dust emission spectra are identical when stars of the same luminosity and of spectral shapes ranging between 30 000 and 40 000 K are considered. Therefore, we only allow ρ0 to vary as a free parameter when fitting the far-IR data. The corresponding extinction AV, CS and dust mass MD are listed in Table 3. Spectral energy distribution models are shown for different observing apertures of the circumstellar dust shells in the right panels of Fig. 5. A similar quality fit is achieved for the SEDs using either the free–free or dust model, and so a preference for one or the other model was not decided upon. At the spatial resolution of ALMA the extended dust halo model predicts submillimetre fluxes that are orders of magnitude fainter than the point-like emission that is estimated by the free–free model. Therefore, the nature of the far-IR excess can be tested by future ALMA observations in the submillimetre continuum. A similar argument holds for observations in the radio, however there is the underlying assumption that one can extrapolate the power law of the free–free component over many orders of magnitude in frequency.
3.5 Dust formation
The observed far-IR excess may be due to free–free or dust emission, and for the latter, one wonders how grains may sustain the harsh environment of the OB stars. For A stars, the blow-out radius or the dust grain radius below which all grains experience greater radiation pressure forces than gravitational is several micrometres (Beust 2010). The blow-out radius is proportional to L* ∕M* implying that it is between 1 and 2 orders of magnitude larger for OB stars. This means that sub-micrometre sized grains should be rapidly removed and only much larger particles would remain in the stellar environment. Another important effect to consider is Poynting–Robertson drag, which causes dust grains to lose angular momentum and spiral toward the star (Draine 2011). Once again, this effect is stronger for smaller grains around more luminous stars and would cause grains between 0.1 and 1 mm to spiral in from the inner radius of our models on timescales of 106 −107 yr. Therefore, this dust population is not long-lived and must be replenished from some source. A replenishment similar to collisional cascades observed by debris-disk emission (Su et al. 2013) is unlikely because of the non-detection of a scattered-light disk in the high-contrast imaging observations with SPHERE of at least three of our far-IR excess stars.
One possible cause for stars to have both dust and wind emission is that dust formation takes place in the winds. This is most likely occurring in multiple-systems where the wind collisional region between the two components is likely to reach extremely high densities, allowing the condensation of dust particles, as in, for example, the WC7+O5 binary WR140 (Williams 2008). From our data set, we cannot rule out the presence of lower luminosity companions that are also able to drive a wind, particularly for the most luminous stars. A further suggestion for those stars that have left the main sequence is that they could have undergone phases – for example, as a red supergiant – where a cooler photosphere may have driven a dusty wind which is now being cleared. If either of these scenarios is accurate, it would provide an efficient way for a stellar population to produce large quantities of dust before the appearance of red supergiants, supernovae, and AGB stars, which may help to explain the observations of anomalously high dust content of high-redshift galaxies (Omont et al. 2001). All of these scenarios would be expected to produce highly inhomogeneous dust distributions, allowing for identification with resolved high-sensitivity thermal/submillimetre imaging. A disturbed large-scale thermal structure appears in some of our sources and one example is provided by the Spitzer/MIPS 24 μm image of HD 206773 shown in Fig. 6. Colliding wind binaries would produce a dense dusty region between the two stars, while the other two scenarios would produce clumpy circumstellar shells. Finally, we wish to stress the faintness of the dusty parsec-scaled halos, with a total optical depth as low as ≲ 10−4 and dust masses below that of Jupiter.
3.6 Influence on ISM extinction or polarisation
The Voshchinnikov sample of stars is frequently used to study dust in the diffuse ISM (Hincelin et al. 2011; Boyarchuk et al. 2016; Zhukovska et al. 2016; Shchekinov et al. 2017), Siebenmorgen et al. 2018). All of the stars lie on sightlines with visual extinction of less than 2.5 mag, colour excess of a few tenths of a magnitude (Table 1), and polarisation of a few percent,which is assumed to be of interstellar origin. The observed polarisation curves follow the Serkowski-law which is explained by dichroic absorption by aligned dust grains and not by scattering on dust or free electrons (Voshchinnikov 2012). We are therefore able to confirm that for our subsample of 22 stars the polarisation originates in the ISM and not in the faint dusty halo around the stars. Even for the far-IR excess stars there is not sufficient circumstellar dust material available that could significantly contribute: their dust envelopes are too optically thin to influence the observed reddening. The shallow circumstellar dust halo also has no influence on the observed polarisation, whether caused by absorption or by scattering.
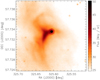 |
Fig. 6 Spitzer/MIPS 24 μm image of HD 206773. Right ascension and declination is in degrees, the colour bar shows flux in MJy sr−1. We note thelarge-scale background structure to the west. |
4 Conclusion
By comparing models with high-sensitivity Spitzer/IRS spectra we have found excess far-IR emission in 55% of a sample of 22 massive stars that are, with one exception, not known to be Be-stars and not connected to clouds. The excess becomes apparent at wavelengths ≳10 μm and is more pronounced in the far-IR. Black-body fits rule out the possibility of background source contribution to the excess. We successfully applied wind and dust models to account for the detected far-IR excess. Distinguishing or quantifying the contribution between these scenarios requires high-sensitivity resolved imaging observations at submillimetre wavelengths.
Spitzer/IRS offers the great advantage of observing mid-IR fine structure lines simultaneously with the far-IR continuum. This is important because of the transient nature of the excitation, as we demonstrate here. In stars with far-IR excess we detect Pf α in 10 out of 12 sources while for non-far-IR excess stars the detection rate drops down to 50% Pf α and 33% in Hu α, and where the line intensities become an order of magnitude weaker.
By means of echelle high-resolution spectroscopy we detect (or not) optical lines in H α, C III and N III irrespective of the presence of a far-IR excess. However, the detection rate of H α is higher (60%) for far-IR excess stars than it is for non-far-IR excess stars (~ 14%). We monitored HD 149757 between 1993 and 2010 and find weak H α emission in only one spectrum taken in 2006. For the Be-star HD 47839 we do not detect H α emission in a spectrum taken in 1996.
For far-IR excess, which is due to dust emission, the bulk material is located at parsec scales around the star in an extremely optically thin (AV, CS < 500 μm) circumstellar halo. The circumstellar dust halos are too faint to contribute to the observed extinction and dichroic polarisation observed along the sightline towards these sources. However, any significant dust population related to stars of such high luminosity may require continuous replenishment to be long-lived. Coronagraphic high-contrast imaging with SPHERE/IRDIS for three of these stars rules out the possibility that they host debris-disk-like populations of large rocky bodies whose collisions might provide a reservoir of material. Alternatively, the dust may be formed in situ in the wind or as a result of wind–wind interactions, possibly providing a channel for dust formation at high-redshift. The existence of such dust may be detectable in a 24 μm Spitzer image.
Acknowledgements
We thank Robert Klement for discussions on Be-stars, T.D. Banas for supporting us in the SPHERE data reduction, and B. Altieri for help on the Herschel photometry. We are grateful to Nikolai Voshchinnikov for helpful comments and suggestions. This research is based on data obtained from the ESO Science Archive Facility and in particular on observations collected under ESO programme 095.C-0158(A). This research has made use of the SIMBAD database, operated at CDS, Strasbourg, France. This work is based in part on observations made with the Spitzer Space Telescope, which is operated by the Jet Propulsion Laboratory, California Institute of Technology under a contract with NASA. This research is based on observations with AKARI, a JAXA project with the participation of ESA. This publication makes use of data products from the Two Micron All Sky Survey, which is a joint project of the University of Massachusetts and the Infrared Processing and Analysis Center/California Institute of Technology, funded by the National Aeronautics and Space Administration and the National Science Foundation. This publication makes use of data products from the Wide-field Infrared Survey Explorer, which is a joint project of the University of California, Los Angeles, and the Jet Propulsion Laboratory/California Institute of Technology, funded by the National Aeronautics and Space Administration.
References
- Bagnulo, S., Cox, N. J. L., Cikota, A., et al. 2017, A&A, 608, A146 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Banas, T. D. 2017, Master Thesis, Ludwig Maximilian University, München [Google Scholar]
- Barlow, M. J. 1979, in Mass Loss and Evolution of O-T Stars, eds. P. S. Conti & C. W. H. De Loore, IAU Symp., 83, 119 [NASA ADS] [Google Scholar]
- Benaglia, P., Vink, J. S., Martí, J., et al. 2007, A&A, 467, 1265 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beust, H. 2010, EAS Pub. Ser., 41, 219 [CrossRef] [Google Scholar]
- Beuzit, J. L., Feldt, M., Dohlen, K., et al. 2008, Proc. SPIE, 7014, 701418 [CrossRef] [Google Scholar]
- Bowen, D. L., Jenkins, E. B., Tripp, T. M., et al. 2008, ApJS, 176, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Boyarchuk, A. A., Shustov, B. M., Savanov, I. S., et al. 2016, Astron. Rep. 60, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Carciofi, A. C., & Bjorkman, J. E. 2006, ApJ, 639, 1081 [NASA ADS] [CrossRef] [Google Scholar]
- Castelli, F., & Kurucz, R. L. 2003, IAU Symp., 210P, A20C [Google Scholar]
- Castelli, F., & Kurucz, R. L. 2004, ArXiv e-prints [arXiv:astro-ph/0405087] [Google Scholar]
- Catanzaro, G. 2013, A&A, 550, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chojnowski, S. D., Whelan, D. G., Wisniewski, J. P., et al. 2015, Cat, 51490007C [Google Scholar]
- Cutri, R. M., Skrutskie, M. F., van Dyk, S., et al. 2003, VizieR Online Data Catalog: II/246 [Google Scholar]
- Cutri, R. M., Wright, E. L., Conrow, T., et al. 2012, VizieR Online Data Catalog: II/311 [Google Scholar]
- Draine, B. T. 2011, Physics of the Interstellar and Intergalactic Medium (Princeton: Princeton University Press) [Google Scholar]
- Draper, Z. H., Wisniewski, J. P., Bjorkman, K. S., et al. 2014, ApJ, 786, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Ekström, S., Georgy, C., Eggenberger, P., et al. 2012, A&A, 537, A146 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fabregat, J., Torrejon, J. M., Reig, P., et al. 1996, A&AS, 119, 271 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fazio, G. G., Hora, J. L., Allen, L. E., et al. 2004, ApJS, 154, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Fitzpatrick, E. L. 2004, in Astrophysics of Dust, eds. A. N. Witt, G. C. Clayton, & B. T. Draine, ASP Conf. Ser., 309, 33 [NASA ADS] [Google Scholar]
- Fitzpatrick, E. L., & Massa, D. 2007, ApJ, 663, 320 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Brown, A.G.A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Galazutdinov, G. A., & Krełowski, J. 2006, ApJ, 637, 342 [NASA ADS] [CrossRef] [Google Scholar]
- Gordon, K. D., Cartledge, S., & Clayton, G. C. 2009, ApJ, 705, 1320 [NASA ADS] [CrossRef] [Google Scholar]
- Hall, J. S. 1958, Publications of the U.S. Naval Observatory Second Series, 17, 275 [NASA ADS] [Google Scholar]
- Hartmann, L., & Cassinelli, J. P. 1977, ApJ, 215, 155 [NASA ADS] [CrossRef] [Google Scholar]
- Heap, S. R., Lanz, T., & Hubeny, I. 2006, ApJ, 638, 409 [NASA ADS] [CrossRef] [Google Scholar]
- Hincelin, U., Wakelam, V., Hersant, F., et al. 2011, A&A, 530A, 61 [Google Scholar]
- Houck, J. R., Roellig, T. L., van Cleve, J., et al. 2004, ApJS, 154, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Ishihara, D., Onaka, T., Kataza, H., et al. 2010, VizieR Online Data Catalog: II/297 [Google Scholar]
- Jenkins, E. B. 2009, ApJ, 700, 1299 [NASA ADS] [CrossRef] [Google Scholar]
- Joint Iras Science, W. G. 1994, VizieR Online Data Catalog: II/125 [Google Scholar]
- Kambe, E., Hirata, R., Ando, H., et al. 1997, ApJ, 481, 406 [NASA ADS] [CrossRef] [Google Scholar]
- Klement, R., Carciofi, A. C., Rivinius, T., et al. 2017, A&A, 601, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kramida, A., Ralchenko, Y., Reader, J., and N. A. Team 2018, NIST Atomic Spectra Database (ver. 5.5.2). Available at https://physics.nist.gov/asd (Accessed: 2018, January 25), National Institute of Standards and Technology, Gaithersburg, MD [Google Scholar]
- Krełowski, J., Strobel, A., Vješnica, S., et al. 2018, MNRAS, 476, 4987 [NASA ADS] [CrossRef] [Google Scholar]
- Krügel, E. 2008, An introduction to the physics of interstellar dust (Bristol: IoP) [Google Scholar]
- Lafreniere, D., Marois, C., Doyon, R., et al. 2008, ApJ, 660, 770 [Google Scholar]
- Lamers, H. J. G. L. M., & Leitherer, C. 1993, ApJ, 412, 771 [NASA ADS] [CrossRef] [Google Scholar]
- Levenhagen, R. S., & Leister, N. V. 2006, MNRAS, 371, 252 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, C.-C., Hou, J.-L., Chen, L., et al. 2015, yCatp, 040001504L [Google Scholar]
- Markwardt, C. B. 2009, in Astronomical Data Analysis Software and Systems XVIII, eds. D. A. Bohlender, D. Durand, & P. Dowler, ASP Conf. Ser., 411, 251 [NASA ADS] [Google Scholar]
- Martins, F., Schaerer, D., Hillier, D. J., et al. 2005, A&A, 441, 735 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marton, G., Calzoletti, L. P., Garcia, A. M., et al. 2017, ArXiv e-prints [arXiv:1705.05693] [Google Scholar]
- Mathis, J. S., Mezger, P. G., & Panagia, N. 1983, A&A, 128, 212 [NASA ADS] [Google Scholar]
- Megier, A., Strobel, A., Galazutdinov, G. A., & Krełowski, J. 2009, A&A, 507, 833 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Neugebauer, G., Habing, H. J., van Duinen, R., et al. 1984, ApJ, 278, L1 [Google Scholar]
- Omont, A., Cox, P., Bertoldi, F., et al. 2001, A&A, 374, 371 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Puls, J., Markova, N., Scuderi, S., et al. 2006, A&A, 454, 625 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rauw, G., Herve, A., Naze, Y., et al. 2015, A&A, 580, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rivinius, T., Stefl, S., & Baade, D. 2006, A&A, 459, 137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rivinius, T., Carciofi, A. C., & Martayan, C. 2013, A&ARv, 21, 69 [Google Scholar]
- Scicluna, P., & Siebenmorgen, R. 2015, A&A, 584, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scicluna, P., Siebenmorgen, R., & Blommaert, J. 2017, IAU, 329, 1666 [Google Scholar]
- Shchekinov, Y. A., Lukash, V. N., Mikheeva, E. V., et al. 2017, PhyU 60, 961S [NASA ADS] [Google Scholar]
- Siebenmorgen,R., Krügel, E., & Mathis, J. S. 1992, A&A, 266, 501 [NASA ADS] [Google Scholar]
- Siebenmorgen,R., Krügel, E., & Laureijs, R. J. 2001, A&A, 377, 735 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Siebenmorgen,R., Voshchinnikov, N. V., & Bagnulo, S. 2014, A&A, 561, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Siebenmorgen, R., Voshchinnikov, N. V., Bagnulo, S., et al. 2018, A&A, 611, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Skiff, B. A. 2013, yCat, 1, 2023 [NASA ADS] [Google Scholar]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Sloan, G. C., Kraemer, K. E., Price, S. D., & Shipman, R. F. 2003, ApJS, 147, 379 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, B. A., & Terrile, R. J. 1984, Science, 226, 1421 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Sota, A. M., Apellániz, J., Walborn, N. R., et al. 2011, ApJS, 193, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Sota, A. M., Apellániz, J., Morrell, N. I., et al. 2014, ApJS, 211, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Su, K. Y. L., Rieke, G. H., Malhotra, R., et al. 2013, ApJ, 763, 118 [NASA ADS] [CrossRef] [Google Scholar]
- Valencic, L. A., Clayton, G. C., & Gordon, K. D. 2004, ApJ, 616, 912 [NASA ADS] [CrossRef] [Google Scholar]
- van Loon, J. T., & Oliveira, J. M. 2003, A&A, 405, L33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vieira, R. G., Carciofi, A. C., Bjorkman, J. E., et al. 2017, MNRAS, 464, 3071 [NASA ADS] [CrossRef] [Google Scholar]
- Vink, J. S., de Koter, A., & Lamers, H. J. G. L. M. 2001, A&A, 369, 574 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vogt. S., & Penrod, G. D. 1983, ApJ, 275, 661 [NASA ADS] [CrossRef] [Google Scholar]
- Voshchinnikov, N. V. 2012, J. Quant. Spectr. Rad. Transf., 113, 2334 [Google Scholar]
- Voshchinnikov, N. V., & Henning, T. 2010, A&A, 517, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Voshchinnikov, N. V., Henning, T., Prokopjeva, M. S., & Das, H. K. 2012, A&A, 541, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Williams, P. M. 2008, Rev. Mex. Astron. Astrofis., 27, 71 [Google Scholar]
- Wisniewski, J. P., Bjorkman, K. S., Magalhaes, A. M., et al. 2007, ApJ, 671, 2040 [NASA ADS] [CrossRef] [Google Scholar]
- Wright, C. M., D. Duy, T., & Lawson, W. 2016, MNRAS, 457, 1593 [NASA ADS] [CrossRef] [Google Scholar]
- Zhukovska, S., Dobbs, C., Jenkins, E. B., & Klessen, R. S. 2016, ApJ, 831, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Zorec, J., & Briot, D. 1997, A&A, 318, 443 [NASA ADS] [Google Scholar]
Using a routine from http://star.arm.ac.uk/~jsv/Mdot.pro.
All Tables
Characteristics of far-IR excess sources with available Spitzer/IRS and Herschel photometry.
All Figures
 |
Fig. 1 Infrared (5–35 μm) SEDs of sources. The yellow shaded region shows the photospheric contribution, while the yellow line shows the IRS spectrum. The magenta shaded region in between highlights the excess. Photometry for HD 151804 are shown as grey circles due to the restricted wavelength coverage of IRS. |
| In the text | |
 |
Fig. 2 High-resolution spectra (top panel) of HD 149404 taken with FEROS in 2005 (red) and UVES in 2009 (green). Bottom panel: velocity dispersion. One notices an additional component observed in the HeI 5876 Å line, likely originated in a companion star, while in C IV such a second component is absent. |
| In the text | |
 |
Fig. 3 High-resolution spectra of HD 149757 between observing epochs from 1993 to 2009. H α emission is detected only in the 2006 spectrum; we note the wings of the absorption profile. |
| In the text | |
 |
Fig. 4 SPHERE/IRDIS upper limits (3σ) of the contrast F(r)∕F∗ (black) as a function of separation r from the stars. A dust model fitting the upper limit of the contrast of HD 149404 (magenta line) is shown together with the applied dust density distribution ∝ ρ(r)∕ρ0 (green dotted line). |
| In the text | |
 |
Fig. 5 SED of massive stars. The total emission is fit by adding to the photosphere (yellow) either free–free (left blue dotted lines) or dust emission in apertures as labelled (right red-brown lines). Data (black) are from optical catalogues as available at VizieR/CDS, 2MASS, WISE, Spitzer/IRS, and Herschel/PACS with 1σ error bars and 3σ upper limits. |
| In the text | |
 |
Fig. 6 Spitzer/MIPS 24 μm image of HD 206773. Right ascension and declination is in degrees, the colour bar shows flux in MJy sr−1. We note thelarge-scale background structure to the west. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



