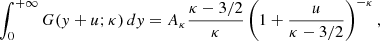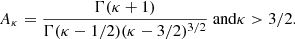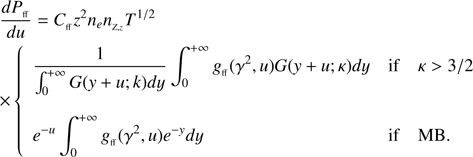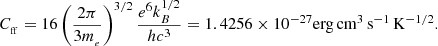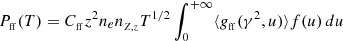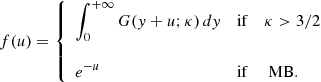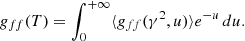| Issue |
A&A
Volume 620, December 2018
|
|
|---|---|---|
| Article Number | C1 | |
| Number of page(s) | 4 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201526104e | |
| Published online | 30 November 2018 | |
Temperature-averaged and total free-free Gaunt factors for κ and Maxwellian distributions of electrons⋆ (Corrigendum)
1 Department of Mathematics, University of Évora, R. Romão Ramalho 59, 7000 Évora, Portugal
e-mail: mavillez@galaxy.lca.uevora.pt
2 Zentrum für Astronomie und Astrophysik, Technische Universität Berlin, Hardenbergstrasse 36, 10623 Berlin, Germany
Key words: atomic processes / radiation mechanisms: general / ISM: general / galaxies: ISM / errata, adenda
The set of tables is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/620/C1
1. Introduction
A missing normalization coefficient in Eqs. (11) and (12) of de Avillez & Breitschwerdt (2015) affected the results shown in Figs. 3 and 4 and discussed in Sect. 3 of that earlier publication. Here, we present the corrected version of the equations and the corresponding results discussed in Sect. 3 and shown in Figs. 3 and 4 of that paper. In addition we provide supplementary material in the form of tables covering a larger parameter space than the one previously used. These tables are available at the CDS.
2. Temperature-averaged and total Gaunt factor
During the interaction of an electron with the Coulomb field of an ion of ionic state z and atomic number Z the amount of free-free energy emitted per unit time and unit volume is given by
with z denoting the ionic state of an ion with atomic number Z and number density nZ, z, ne is the electron number density, h is the Planck constant, c is the speed of light, e is the electron charge in Coulombs, me is the electron mass, kB is the Boltzmann constant, T is the temperature, and ⟨gff(γ2, u)⟩ is the temperature averaged Gaunt factor given by (see, e.g., de Avillez & Breitschwerdt 2017)
where f is the electron distribution function, u = hν/kBT (ν is the frequency of the emitted photon), γ2 = z2Ry/kBT (Ry is the Rydberg constant), and Ne is a normalization coefficient defined such ⟨gf f(γ2, u)⟩ = 1 when gf f(γ2, u)=1. For the κ and Maxwell-Boltzmann (MB) electron distribution functions Ne is given by
with
and
which becomes e−u when κ → ∞ (Fig. 1). In these expressions
Therefore, Eq. (11) in de Avillez & Breitschwerdt (2015) must be rewritten as
where
The total free-free power associated with an ion (Z, z) given by
with
The integral in the RHS of (8) is the total free-free Gaunt factor. When κ → ∞ the Integral in (9) tends to e−u and total Gaunt factor for the MB distribution of electrons as defined by Karzas & Latter (1961) is recovered
The top panel of Fig. 2 and the panels in Fig. 3 display the variation with γ2 of the temperature-averaged Gaunt factor, ⟨gf f(γ2, u)⟩, for different values of u ∈ [10−4, 104] for the MB and κ = 2, ...,1200 distributions. The bottom panel of Fig. 2 highlights in a magnified image of the region γ2 ∈ [10−2, 106] the distribution with γ2 of ⟨gf f(γ2, u)⟩ for different values of u.
It is clear that as κ increases the temperature-averaged κ distributed Gaunt factors approach those calculated with the MB distribution. However, the speed (with κ variation) of this approach depends on the values of u. For u < 10 this approach is faster than for u ≥ 10 (compare top panel of Fig. 2 and the two panels in Fig. 3). For values as high as κ = 1200 there is still no overlap between the κ and Maxwellian values of ⟨gf f(γ2, u)⟩ for u > 102 and γ2 < 10 (Fig. 3). This is a consequence of the slow approach to e−u of the integral 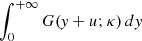 for u ≥ 10 in comparison to u < 10 (Fig. 1).
for u ≥ 10 in comparison to u < 10 (Fig. 1).
 |
Fig. 1. Variation of Integral (5) with κ as function of u. The solid black line represents e−u which is overlapped by the integral as κ → ∞. |
 |
Fig. 2. Temperature-averaged Gaunt factors calculated for κ = 2, 3, 5 and MB (black line in both panels) distributions of electrons for the range 10−5 ≤ γ2 ≤ 1010 (top panel) and a magnification of the region γ2 ∈ [10−2, 106] and ⟨gf f(γ2, u)⟩ ∈ [0.9, 1.5] (bottom panel). |
 |
Fig. 3. Temperature-averaged Gaunt factors calculated for κ = 10, 15, 25, and 50 (left panel), 100, 500, 1000, and 1200 (right panel) and MB (black line in both panels) distributions of electrons for the range 10−5 ≤ γ2 ≤ 1010. We note the slow approach ⟨gf f(γ2, u)⟩ to the Maxwellian values for u > 10 and γ2 < 10 for large values of the κ parameter. |
Figure 4 displays the total free-free Gaunt factor, ⟨gf f(γ2)⟩, calculated for the MB and κ = 2, 3, 5, 10, 15, and 25 distributions. For larger κ the ⟨gf f(γ2)⟩ almost overlap with the Maxwellian value as shown in the magnification of the regions ⟨gf f(γ2)⟩ ∈ [ − 1.0, 0.8] and ⟨gf f(γ2)⟩ ∈ [1.38, 1.45] (top panel of Fig. 5), and ⟨gf f(γ2)⟩ ∈ [6, 10] and ⟨gf f(γ2)⟩ ∈ [0.995, 1.005] (bottom panel of same Figure). It turns out that even for κ parameters as high as 1000 there is still a slight difference between ⟨gf f(γ2)⟩ calculated for the κ and MB distributions.
 |
Fig. 4. Total free-free Gaunt factor calculated for κ(2, 3, 5, 10, 15, and 25) and MB distributions. |
 |
Fig. 5. Magnification of the total free-free Gaunt factor in two regions in γ2 and in the ⟨gf f(γ2)⟩ profile shown in Fig. 4 but for κ = 50, 100, 500, and 1000. The solid black line refers to the Maxwellian value. |
3. Tables
Supplementary material is available at the CDS with a set of tables referring to the temperature-averaged Gaunt factor versus γ2 and different u, and a table for the total Gaunt factor versus γ2 for results obtained with the κ = 2, 3, 5, 10, 15, 25, 50, 100, and 500 and MB electron distributions. The parameter space comprises γ2 ∈ [10−5, 1010] and u ∈ [10−12, 1011].
Acknowledgments
This research was supported by the project Enabling Green E-science for the SKA Research Infrastructure (ENGAGE SKA), reference POCI-01-0145-FEDER-022217, funded by COMPETE 2020 & FCT, Portugal.
References
- de Avillez, M. A., & Breitschwerdt, D. 2015, A&A, 580, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Avillez, M. A. & Breitschwerdt, D. 2017, ApJS, 232, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Karzas, W. J. & Latter, R. 1961, ApJS, 6, 167 [NASA ADS] [CrossRef] [Google Scholar]
© ESO 2018
All Figures
 |
Fig. 1. Variation of Integral (5) with κ as function of u. The solid black line represents e−u which is overlapped by the integral as κ → ∞. |
| In the text | |
 |
Fig. 2. Temperature-averaged Gaunt factors calculated for κ = 2, 3, 5 and MB (black line in both panels) distributions of electrons for the range 10−5 ≤ γ2 ≤ 1010 (top panel) and a magnification of the region γ2 ∈ [10−2, 106] and ⟨gf f(γ2, u)⟩ ∈ [0.9, 1.5] (bottom panel). |
| In the text | |
 |
Fig. 3. Temperature-averaged Gaunt factors calculated for κ = 10, 15, 25, and 50 (left panel), 100, 500, 1000, and 1200 (right panel) and MB (black line in both panels) distributions of electrons for the range 10−5 ≤ γ2 ≤ 1010. We note the slow approach ⟨gf f(γ2, u)⟩ to the Maxwellian values for u > 10 and γ2 < 10 for large values of the κ parameter. |
| In the text | |
 |
Fig. 4. Total free-free Gaunt factor calculated for κ(2, 3, 5, 10, 15, and 25) and MB distributions. |
| In the text | |
 |
Fig. 5. Magnification of the total free-free Gaunt factor in two regions in γ2 and in the ⟨gf f(γ2)⟩ profile shown in Fig. 4 but for κ = 50, 100, 500, and 1000. The solid black line refers to the Maxwellian value. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



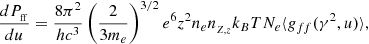
![$$ \begin{array}{*{20}{l}}{\begin{array}{*{20}{l}}{\langle {g_{ff}}({\gamma ^2},u)\rangle = \frac{{{{({k_B}T)}^{1/2}}}}{{{N_e}}}}\\{ \times \int_0^{ + \infty } {\frac{1}{{{{(y + u)}^{1/2}}}}} f[(y + u){k_B}T]{g_{ff}}\left( {{_i} = \frac{{y + u}}{{{\gamma ^2}}},{_f} = \frac{y}{{{\gamma ^2}}}} \right)dy}\end{array}}\end{array}\ $$](/articles/aa/full_html/2018/12/aa26104e-15/aa26104e-15-eq2.gif)
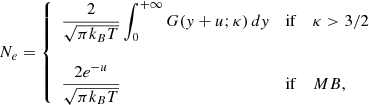
![$$ \begin{aligned} G(x;\kappa )=\frac{A_{\kappa }}{\displaystyle \left[1+\frac{x}{\kappa -3/2}\right]^{\kappa +1}}, \end{aligned} $$](/articles/aa/full_html/2018/12/aa26104e-15/aa26104e-15-eq4.gif)