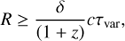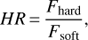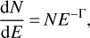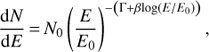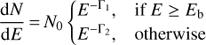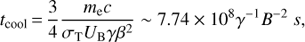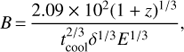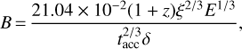| Issue |
A&A
Volume 619, November 2018
|
|
|---|---|---|
| Article Number | A93 | |
| Number of page(s) | 19 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201833628 | |
| Published online | 12 November 2018 | |
Hard X-ray properties of NuSTAR blazars
1
Astronomical Observatory, Jagiellonian University, ul. Orla 171, 30-244 Kraków, Poland
e-mail: gopal@oa.uj.edu.pl
2
Taras Shevchenko National University of Kyiv, Akademika Hlushkova Ave 4b, 02000 Kyiv, Ukraine
Received:
13
June
2018
Accepted:
8
August
2018
Context. Investigation of the hard X-ray emission properties of blazars is key to the understanding of the central engine of the sources and associated jet process. In particular, simultaneous spectral and timing analyses of the intraday hard X-ray observations provide us a means to peer into the compact innermost blazar regions that are not accessible to our current instruments.
Aims. The primary objective of the work is to associate the observed hard X-ray variability properties in blazars with their flux and spectral states, thereby, based on the correlation among these states, extract the details about the emission regions and processes occurring near the central engine.
Methods. We carried out timing, spectral, and cross-correlation analysis of 31 NuSTAR observations of 13 blazars. We investigated the spectral shapes of the sources using single power-law, broken power-law, and log-parabola models. We also studied the co-relation between the soft and hard emission using z-transformed discrete correlation function. In addition, we attempted to constrain the smallest emission regions using minimum variability timescales derived from the light curves.
Results. We found that, for most of the sources, the hard X-ray emission can be well represented by the log-parabola model and that the spectral slopes for different blazar subclasses are consistent with the so-called blazar sequence. We also report the steepest spectra (Γ ∼ 3) in the BL Lacertae PKS 2155–304 and the hardest spectra (Γ ∼ 1.4) in the flat-spectrum radio quasar PKS 2149–306. In addition, we noted a close connection between the flux and spectral slope within the source subclass in the sense that high flux and/or flux states tend to be harder in spectra. In BL Lacertae objects, assuming particle acceleration by diffusive shocks and synchrotron cooling as the dominant processes governing the observed flux variability, we constrain the magnetic field of the emission region to be a few Gauss; whereas in flat-spectrum radio quasars, using external Compton models, we estimate the energy of the lower end of the injected electrons to be a few Lorentz factors.
Key words: accretion / accretion disks / radiation mechanisms: non-thermal / galaxies: active / BL Lacertae objects: general
© ESO 2018
1. Introduction
Blazars, a subclass of active galactic nuclei (AGN), are radio-loud sources with their relativistic jets closely aligned to the line of sight. The Doppler boosted nonthermal emission is highly variable over a wide range of spatial and temporal frequencies. The broadband spectral energy distribution (SED) of blazars features two distinct spectral peaks. The lower peak, usually observed between radio and X-ray wavelengths, is widely accepted to be result of synchrotron emission by energetic particles; however, the origin of a high energy component, mostly peaking between UV and γ-ray, is still debated. There are two widely discussed models based on the origin of seed photons. According to the synchrotron self-Compton (SSC) model (e.g., Maraschi et al. 1992; Mastichiadis & Kirk 2002), the same population of the electrons emitting synchrotron radiation up-scatters the softer photon to high energy, whereas in the external Compton (EC) model the seed photons for the Compton up-scattering are provided by the various components of an AGN, such as accretion disk (AD; Dermer & Schlickeiser 1993), broad-line region (BLR; Sikora 1994), and dusty torus (DT; Błażejowski et al. 2000).
Blazars consists of further two subclasses: flat-spectrum radio quasars (FSRQ) and BL Lacertae (BL Lac) sources. The more luminous sources, FSRQs, show emission lines over the continuum and their synchrotron peak is in the lower frequency. As the sources are found to have abundant seed photons due to the AD, BLR, and DT, the high energy emission is most likely due to the EC process as opposed to SSC (Ghisellini et al. 2011). BL Lac objects constitute less powerful subclass that has weak or no emission lines over the continuum and the synchrotron peak in these objects lies in the UV to X-rays bands. BL Lacs represent an extreme class of sources with an excess of high energy emission (hard X-rays to TeV emission) resulting from the synchrotron and inverse-Compton (IC) processes. However, their apparent low luminosity could be due to lack of strong circumnuclear photon fields and relatively low accretion rates. Blazar sources can have further subdivision based on the frequency of the synchrotron peak (νs): high synchrotron peaked blazars (HSP; νs > 1015 Hz), intermediate synchrotron peaked blazars (ISP; 1014 < νs < 1015 Hz), and low synchrotron peaked blazars (LSP; νs < 1014 Hz; see Abdo et al. 2010). In the unifying scheme known as blazar sequence, the bolometric luminosity decreases as we move from FSRQ to HSP but γ-ray emission increases (Fossati et al. 1998; Ghisellini et al. 2017). This means that while FSRQs are γ-ray dominated, in HSP sources synchrotron and γ-ray emission become comparable. In other words, with the increase in their bolometric luminosities, blazars become redder and Compton dominant as the ratio of the luminosities at the Compton peak to the synchrotron peak frequency increases.
Blazar continuum emission is characterized by broadband emission, which is variable on diverse timescales. The variability timescales can be long term (years to decades), short term (weeks to months) and intraday/night (minutes to hours). Long-term variability most likely arises owing to variable accretion rates; short-term flaring episodes lasting a few weeks could be due to the shock waves propagating down the jets; and the low-amplitude rapid variability known as intraday variability might arise owing to the turbulent flow of the plasma in the innermost regions of the jets (e.g., Bhatta et al. 2013; Cawthorne 2006; Lister & Homan 2005; Hughes et al. 1998; Marscher & Travis 1996). In general, the variability shown by AGNs appears predominantly aperiodic in nature, although quasi-periodic oscillations on various timescales have been detected for a number of sources (see Bhatta 2017; Bhatta et al. 2016b; Zola et al. 2016)
Blazar variability in X-ray bands has been extensively studied using numerous instruments over the past several decades. In a study including a large sample of BL Lac sources observed with Einstein Observatory Imaging Proportional Counter (IPC), the source spectra were well described by single power-law model with spectral slope indexes (αX) in the range of 0.1–0.5 (Worrall & Wilkes 1990). The soft X-ray study of a sample of radio-selected BL Lacs (RBL; Urry et al. 1996) and X-ray-selected BL Lac objects (XBL; Perlman et al. 1996) using ROSAT Position Sensitive Proportional Counter (PSPC) showed that the 0.2–2.0 keV spectra of the sources could be well described mostly by single power law with αX between 0.5 and 2.3. The single power-law and the broken power-law models were successfully used to describe the X-ray spectra from various instruments such as Advanced Satellite for Cosmology and Astrophysics (ASCA; e.g., Kubo et al. 1998), BeppoSAX (Wolter et al. 1998; Padovani et al. 2002), European X-ray Observatory Satellite (EXOSAT; e.g., Sambruna et al. 1994), and the ROentgen SATellite (ROSAT; e.g., Perlman et al. 1996; Urry et al. 1996). In the ASCA spectra of four FSRQs, Sambruna et al. (2000) found steep (ΓX ∼ 2 − 2.5) soft X-ray (0.2–2.4 keV) photon indexes similar to those observed in synchrotron-dominated BL Lac objects; and the spectra were found to be consistent with power-law models. However, the ASCA spectra were observed to be flatter than their ROSAT spectra. Similarly, in some cases continuously curved, log-parabola models provided better representation for the X-ray spectral distribution of some sources (Donato et al. 2005). Also, Massaro et al. (2004a, b) found the log-parabola as the best model for the characterization of X-ray spectra of Mrk 421 and Mrk 501 in their multiple flux states. Spectral curvature has also been detected in the XMM-Newton spectra of a number of X-ray bright BL Lac objects from the Einstein Slew Survey (see Perlman et al. 2005) and several BeppoSAX blazars (see Donato et al. 2005). Using Swift/XRT spectra of a sample of TeV blazars, Wierzcholska & Wagner (2016b) decomposed the synchrotron and IC components. Furthermore, in a few sources a linear relation between the flux and hardness ratio, also called the “harder-when-brighter” trend, has been reported by Zhang et al. (2005, 2006). Similarly, soft and hard lags were observed during the correlation study between the emission in various X-ray bands (e.g., Fossati et al. 2000b; Zhang et al. 2006). In addition, hysteresis loops in the spectral index and flux intensity plane have been reported (e.g., Ravasio et al. 2004; Falcone et al. 2004; Brinkmann et al. 2005). To sum up, these studies over the decades have suggested that the sources exhibit high amplitude rapid variability on diverse timescales ranging from a few hours to a few months and that the nature of X-ray blazar spectra in various energy bands behave in variable and complex fashions.
General information about the studied blazar sources.
Recently, several sources have been observed in the hard X-ray regime by Nuclear Spectroscopic Telescope Array (NuSTAR), mostly to complement the contemporaneous multifrequency observing campaigns. Madsen et al. (2015) described the NuSTAR spectra of the blazar 3C 273 by an exponentially cutoff power-law with a weak reflection component from cold, dense material; the spectra revealed an evidence of a weak neutral iron line as well. In the NuSTAR observations of the FSRQ 3C 279, Hayashida et al. (2015) observed a spectral softening by ΔΓX ≈ 0.4 at ∼4 keV between the two observation epochs. Blazar S5 0836+71 was found to be highly variable in hard X-ray during the broadband study by Paliya (2015). Similarly, Furniss et al. (2015) found that the combined Swift and NuSTAR of the blazar Mrk 501, during both a low and high flux state, could be well fitted by a log-parabolic spectrum. In the combined NuSTAR and Swift/XRT spectra of S5 0716+714, Wierzcholska & Siejkowski (2016a) reported a break energy at ∼8 keV revealing both low and high energy components. In their study of the two high red-shifted blazars, S5 0014+81 and B0222+185, Sbarrato et al. (2016) concluded that the two sources harbored the most luminous AD and the most powerful jet, respectively, placing these sources at the extreme end of the disk-jet relation for γ-ray blazars. Rani et al. (2017) observed rapid hard X-ray variability on hour timescales in a few blazar sources. Similarly, Pandey et al. (2017) reported the instances of intraday variability in the NuSTAR light curves of a number of TeV blazars, and also noticed a general harder-when-brighter trend.
In this paper, we conduct a thorough analysis of all the blazar sources from the NuSTAR data archive by carrying out timing, spectral, and cross-correlation analyses to study the nature of the variability properties of blazars in the hard X-ray regime. Our work is mainly motivated to understand the physical process in the blazars by exploring the possible relation of variability properties, particularly variability and the minimum variability timescale, with the mean flux and spectral state of the sample sources, and thereby shed light into the innermost regions of blazars hidden from our direct view. We organize our presentations in the following way: in Sect. 2, the observation and the data processing of 31 NuSTAR observations of 13 blazar sources are discussed. We present our timing, spectral, and cross-correlation study on the light curves and the spectra in Sect. 3. In Sect. 4, we report several interesting observational features such as rapid flux and spectra variability, a connection between higher flux and harder spectra, and hard and soft lags, and we discuss the observed features in the light of current blazar models. Finally we summarize our conclusions in Sect. 5.
2. Observations and data reduction
2.1. Source sample
We selected the sample sources from the NuSTAR archive that were classified as blazar sources. Moreover, only the observations with observation period greater than ten kiloseconds (ks) and carrying the issue flag 0 were included in the study. The name, class, position and redshift of the sources are listed in Table 1. The source sample consists of seven FSRQs, two ISPs, and four HSPs1, which are also TeV blazars. The redshift of the sources has a diverse range from the nearest (z = 0.0334; Mrk 501) to the farthest source (z = 3.366; S5 0014+81).
2.2. NuSTAR Observations
Nuclear Spectroscopic Telescope Array (NuSTAR) is a sensitive hard X-ray (3–79 keV) instrument with two focal plane modules: FPMA and FPMB. The observatory operates within the bandpass with spectral resolution of ∼1 keV. The field of view of each telescope is ∼13′ and the half-power diameter of an image of a point source is ∼1′ (see Harrison et al. 2013). The raw data products were processed using NuSTAR Data Analysis Software (NuSTARDAS) package version 1.3.1. We reduced and analyzed the observations via HEASOFT2 version 6.21 and CALDB version 2017-06-14. By using the standard nupipeline script, calibrated and cleaned event files were produced. Source flux and spectra were extracted from a region of 30′′ radius centered around the source location, and the background was extracted from a 70′′ radius region relatively close to the source but also far enough to be free from contamination by the source. The light curves were generated with a time bin of 15 min. Similarly, the spectra were re-binned with the task grppha to have at least 30 counts per channel.
Observational data and variability properties of the NuSTAR blazar sources.
3. Analysis
The NuSTAR observations of the blazar sources discussed in this paper along with their observation ID and observation dates are listed in Table 2. The light curve of the source 3C 279 (Obs. ID: 60002020002), displaying modulations in the hard X-ray emission, is presented in the top panel of Fig. 1. To see the spectral states of the individual flux points, the plot symbols are color-coded according to the hardness ratio (defined below). The light curves for the other observations are presented similarly in Appendix A. Timing, spectral, and cross-correlation analyses are performed to examine the hard X-ray variability properties of the sample sources; these analyses are discussed below.
3.1. Flux variability
Most of the observations for the sample sources are found to be rapidly variable within the observation period. The observed variability is quantified by defining two measures. Variability amplitude (VA) measuring the peak-to-peak flux oscillations is given as
where Fmax and Fmin are the maximum and minimum flux in counts/sec. This kind of variability measure, derived only from the extreme fluxes, may not represent the overall variability. In such a case, fractional variability (FV; see Vaughan et al. 2003; Bhatta & Webb 2018), which considers all the fluxes in the light curve, may be a more suitable measure to represent the observed variability. Following Burbidge et al. (1974), the minimum timescale of such variability is determined using the expression
where Δt is the time interval between flux measurements (see also Hagen-Thorn et al. 2008). To compute the uncertainty in τvar, we followed the general error propagation rule, i.e., for a general function y = f(x1, x2, ..xn) with the corresponding uncertainties Δx1, Δx2, ..Δxn in x1, x2, ..xn, respectively, uncertainty in y can be expressed as (similar to Eq. (3.14) in Bevington & Robinson 2003)
Thus using Eq. (3), uncertainty in τvar are estimated as
where F1 and F2 are the count rates used to estimate the minimum variability timescales, and ΔF1 and ΔF2 their corresponding uncertainties.
All these quantities characterizing flux variability in the sources, i.e., FV, VA, and minimum variability timescales for the source sample are listed in Cols. 6, 7, and 8, respectively, of Table 2.
Now, using the causality argument, the minimum variability timescale τvar can be used to estimate the upper limit for the minimum size of the emission region (R) as given by
where δ, Doppler factor, is defined as δ = (Γ(1−βcosθ))−1 and for the velocity β = v/c the bulk Lorentz factor can be written as 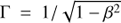 . It is assumed that the emission originates from the innermost regions of the blazar jets, which move with high speeds along the path that makes an angle, θ, with the line of sight. For a moderate value of δ = 10, the distribution of the emission region sizes are shown in Fig. 2.
. It is assumed that the emission originates from the innermost regions of the blazar jets, which move with high speeds along the path that makes an angle, θ, with the line of sight. For a moderate value of δ = 10, the distribution of the emission region sizes are shown in Fig. 2.
3.2. Spectral analysis: Hardness ratio and spectral fitting
To study the spectral variability of the X-ray emission from the sources, the source light curves are produced in two energy bands: a soft band between 3 and 10 keV and a hard band between 10 and 79 keV. Then we define hardness ratio (HR) as
where Fhard and Fsoft are the flux in count rates in the hard (10–79 keV) and soft (3–10 keV) bands, respectively. The HR is a commonly used model-independent method to study spectral variations over time and flux states. In this work, we particularly examine the relation between flux and HRs over the observation period to constrain the underlying physics. The middle panel of Fig. 1 shows the flux-HR plot for the source Mrk 501 (Obs. ID: 6000202400), with clearly visible harder-when-brighter trend. To look for possible hysteresis loops in the flux-HR plane, the symbols are color-coded according to the time.
 |
Fig. 1. Hard X-ray NuSTAR observations of blazar sources showing light curve and flux-HR relation, ZDCF, and spectral fit from top to bottom for the sources 3C 279, Mrk 501, 3C 279, and S5 0716+714, respectively. The color bars in light curve and the flux-HR plots represent the HR and time, respectively. Similar plots for other sources are shown in Appendix A. |
 |
Fig. 2. Distribution of the emission region sizes in the NuSTAR blazars derived from their minimum variability timescales. |
Spectral analyses of the NuSTAR blazars were carried out by the spectral fitting the source spectra using xspec (Arnaud 1996) models and using the χ2 minimization statistics. The spectra from the instruments FPMA and FPMB were simultaneously fitted in xspec. To account for any possible subtle differences between the instruments, an intercalibration constant was included in the spectral models. The values of the constant, ranging from 0.97 to 1.04, indicate that there are no major differences between the observations obtained by the two instruments. To ascertain the best representation of the spectral behavior, we fit each spectrum using three spectral models: power law (PL), log-parabola (LP) and broken power law (BPL). The power-law model can be given as
where N, E, and Γ are normalization, photon energy, and photon index, respectively. Similarly, the log-parabola model that has a continuous break is given by
where N0 and E0 are the normalization and reference energy fixed to 10 keV, and Γ and β are the photon index and the curvature parameter, respectively (see Massaro et al. 2004a). Finally, the broken power law is expressed as
where Γ1 and Γ2 represent the high and low energy photon indexes and N0 and Eb are the normalization and break energy, respectively. To account for the galactic absorption tbabs (Tuebingen–Boulder ISM absorption model; Wilms et al. 2000) is multiplied with these models, while the hydrogen column density are taken from Kalberla et al. (2005).
Of the three models, we chose the best-fit spectral model after performing F-test3. In particular the significance of LP and BPL was estimated against PL (null hypothesis) and the model was accepted as a better fit if the probability under the null hypothesis was equal or smaller than 0.1 – equivalently, a significance equal or greater than 90%. If not, PL was considered to be the best representation. Further, between two models, i.e., LP and BPL, the model with higher significance (or lower probability value) was chosen to be the best model. Based on such criteria, out of 31 observation spectra, 7, 17, and 7 spectra were found to be best represented by PL, LP, and BPL spectral models, respectively. The fitting parameters for all the observations are listed in Table 3. Spectral fitting for the source S5 0716+714 is presented in the bottom panel of Fig. 1 and similar figures for the rest of the observations are presented in Appendix A. The distribution of the photon indexes, resulting from the best-fit models, over the mean flux in count rates is shown in Fig. 6.
Spectral fitting of the NuSTAR blazars.
continued.
3.3. Discrete correlation function
Cross-correlation study between emission in different energy bands offers insights that can shed light into the ongoing processes at the emission sites, for instance, the dominant radiative processes involved and distribution of the emitting particles (see, e.g., Zhang 2002). We analyzed the correlation between the NuSTAR blazar light curves in the soft energy (3–10 keV) and hard energy (10–79 keV) using z-transformed discrete correlation function (ZDCF) along with the likelihood of the ZDCF peaks and the associated uncertainties as described in Alexander (20134; see also Bhatta & Webb 2018). The ZDCFs between the lower energy (LE) and higher energy (HE) light curves for the source 3C 279 (Obs. ID 60002020002) are shown in the bottom panel of Fig. 1, and similar plots for the rest of the observations discussed in the paper are presented in Appendix A; the results are also tabulated in Table 4. In the figure, we see that in most cases we do not find a strong correlation between low and high energy emission at the zero lag, and in a few cases hints of hard and soft lags can be seen. It should be pointed out that between two similar DCF values at the different lags, the value closer to zero lag would be statistically more significant as the number of observations that go into the calculation of DCF value decreases with the increase in the lead/lag.
4. Results
The results of all of the above analyses on the individual sources along with their brief introduction are presented below.
Discrete cross-correlation function between the low (3–10 keV) and high energy (10–79 keV) emission of the NuSTAR blazars.
4.1. S5 0014+81
FSRQ S5 0014+81, detected by multiple X-ray instruments, possesses the most luminous AD among blazars (see Sbarrato et al. 2016, and references therein). Also, of the sources discussed in this paper, it is the most distant source at the redshift of 3.366. The high-redshift blazar reveals contributions due to thermal emission from the AD in its optical continuum (Ghisellini et al. 2010a). We looked into two NuSTAR observations separated by one month. The first observation (Obs. ID: 60001098002) shows one of the largest variability with FV ∼ 30% and rapid (τvar = 0.91 ± 0.93 ks) minimum variability timescale within 46 ks observation period, while the second observation shows a moderate variability (FV ∼ 14%) within 39 ks. No obvious trend in flux-HR plane could be observed. While in the first observation, we do not see any significant correlation between the low and high energy emission, in the second observation we found a hint of soft lag of ∼0.9 ks with ZDCF coefficient ∼0.34 and likelihood (LH) = 0.62. The spectra for the first observation is fitted with BPL with a break at ∼20 keV energy, whereas the power-law model with ΓX ∼ 1.7 is fitted well for the second observation.
4.2. B0222+185
Blazar B0222+185 has been widely studied by X-ray instruments, for example, Swift/BAT (Ajello et al. 2012; Baumgartner et al. 2013). In the hard X-ray study, it was found to be one the most powerful blazars ever observed (Sbarrato et al. 2016); the optical flux showed evidence for the thermal emission from the AD (Ghisellini et al. 2010a). It is one of the most distant sources (z = 2.69) discussed in this work. We studied two NuSTAR observations spanning 61 and 70 ks. In the light curves, the flux points appear to be scattered showing no coherent variability pattern. Similarly, no clear trend in the flux-HR plane can be observed. The correlation between the soft and hard emission shows a sign of hard lag of ∼9.0 ks and ∼2 ks with ZDCF ∼0.48 and ∼0.53. However the larger associated errors and small values of LH make them inconclusive. The first observation is fitted with LP with β ∼ 0.2 and the second observation is well fitted with BPL with Eb ∼ 6.5 keV.
4.3. HB 0836+710
Source HB 0836+710 is a high-redshift blazar, extensively studied in multiband emission (see Akyuz et al. 2013, and reference therein). The source is identified with a prominent kpc-scale radio jet (Hummel et al. 1992). The optical-UV spectrum is dominated by thermal emission from the AD (Ghisellini et al. 2010a) and the γ-ray emission region is found to be located ∼35 pc away from the central engine (Jorstad et al. 2013). In the two NuSTAR observations that we examined, the source shows rapid variability with the minimum variability timescales as small as 2.53 ± 0.91 ks. The second observation shows a systematic modulation of flux-HR plane. However, the ZDCF values ∼0.31 and ∼0.30 at the zero lag show that there is not much correlation between the low and high energy emission. For the first and second observations BPL and LP models are fitted, respectively.
4.4. 3C 273
3C 273 is the nearest bright quasar with a large-scale visible jet. Because it is highly variable across nearly all energies, the source has been the subject of numerous broadband observation campaigns (e.g., Soldi et al. 2008; Abdo et al. 2010). In the optical-UV band there is a bright excess, commonly called blue bump, possibly a signature of thermal reprocessing from the AD (Paltani et al. 1998). We examined two NuSTAR observations (Obs. ID 10202020002 and 10302020002) exactly one year apart. In the first observation, we find moderate (FV ∼ 10%) but rapid variability (τvar = 8.81 ± 3.34 ks). We observe that the flux is stable and HR changes randomly, whereas in the second observation the source became more variable with FV ∼ 15% and rapid (τvar = 1.24 ± 1.70 ks) in flux and HR. In the first observation, we find a good correlation (ZDCF = 0.45 and LH = 0.44) between the high and the low energy emission at zero lag. In the second epoch, although not very significant (ZDCF = 0.46 and LH = 0.45), we see a possible soft lag of ∼4.8 ks. The spectra for both of the observations are well fitted with LP with β ∼ 0.1.
4.5. 3C 279
Blazar 3C 279 is a FSRQ source profusely emitting in hard X-ray and γ-rays. The source, highly variable across a wide range of spectral bands (see Hayashida et al. 2015, and the references therein), is one of a handful of sources detected above 100 GeV (MAGIC Collaboration 2008). The source reveals a compact, milliarcsecond-scale radio core ejecting radio knots with a bulk Lorentz factor, Γ = 15.5 ± 2.5, along the direction making an angle, θobs = 2.1 ± 1.1°, to the line of sight (Jorstad et al. 2005, 2004). Our study concerning two NuSTAR observations shows that the source displays moderate variability in hour-like timescales (τvar = 2.31 ± 1.26 ks and 5.61 ± 3.99 ks), the correlation between soft and hard emission shows a hard lag by a few ks, particularly distinguished (ZDCF ∼ 0.79 and LH = 0.45) in the second observation (Obs. ID: 60002020004). We cannot see any clear trend in flux-HR plane. Of the three spectral models, the first observation is fitted with BPL model with Eb ∼ 30 keV and the second is well represented by LP with a small β ∼ 0.07.
4.6. PKS 1441+25
PKS 1441+25, a TeV blazar, has been detected in very high energy (VHE) γ-rays by VERITAS and MAGIC (see Abeysekara et al. 2015). The source shows rapid variability when flux doubled within a few hours and it also exhibits one of the most rapid (τvar = 1.24 ± 0.62 ks) and largest variability (FV ∼ 26%) observed within the observation period of 72 ks. We do not see a simple correlation between the flux and HR, and there is no apparent correlation (ZDCF ∼0.00) between the low and high energy emission at the zero lag. The spectrum is fitted well with a PL model with photon index ∼2.
4.7. PKS 2149–306
PKS 2149-306 is a X-ray bright FSRQ often marked by dramatic flux and spectral variability as observed by most of the X-ray telescopes (see D’Ammando & Orienti 2016, and references therein). In both of the NuSTAR observation we studied, the source shows significant variability (FV∼10%) in the timescale of a few hours. In the first observation, we see a hint of a soft lag near 1.8 ks with ZDCF = 0.47 and LH = 0.72 and a harder-when-brighter trend, whereas in the second there is not much correlation between the low and high energy emission and a complex flux HR relation is observed. For both the observations, the source spectra are fitted with BPL and PL with the flattest photon indexes of ∼1.5.
4.8. 1ES 0229+200
BL Lac 1ES 0229+200 is one of the important TeV sources that has been used to study the properties of the extragalactic background light and intergalactic magnetic field through its very high energy emission (Aliu et al. 2014, and references therein). We examined the 38 ks long NuSTAR observation for its hard X-ray properties. The source displays a significant (FV ∼ 13%) and rapid (τvar = 2.35 ± 1.23 ks) variability. The flux does not appear to be correlated with the HR. The source spectra are best fitted using LP model with photon index, ΓX ∼ 2.
4.9. S5 0716+714
S5 0716+714 is one of the best-studied sources across broad bands. The TeV source is widely famous for its variability with almost 100% duty cycle (see Bhatta et al. 2016a, and the references therein). In the NuSTAR observation we studied, the source shows rapid variability; the flux nearly doubled within the observation period of 32 ks. In addition, significant average flux variability (FV ∼ 15%) with 2.79 ± 1.43 ks minimum variability timescale is noticed. We do not detect any obvious HR-flux relation, however the correlation between the high and low energy emission reveals a possible hard lag of ∼3.00 ks with ZDCF value ∼0.5 however with a small LH, 0.13. The spectrum is fitted using LP model with ΓX ∼ 1.9 and a negative curvature, β ∼ −0.33.
4.10. Mrk 501
Mrk 501, which shines bright in X-ray, is one of the most favored targets for multifrequency observations (see Furniss et al. 2015, and references therein). We studied four NuSTAR observations between April and July 2013. The light curve of the first observation (Obs. ID: 60002024002) shows low variability (FV∼ 5%) and no clear trend in HR variability. In the second observation (Obs. ID: 60002024004), the overall flux follows a rising trend for ∼47 ks and later declines during the remaining 8 ks; the source displays significant variability with FV ∼17%. The harder-when-brighter behavior is clearly visible in the flux-HR plane as shown in Fig. 1 (middle panel). During the third observation (60002024006) the source is nearly twice as bright as in the other observations but has decreased variability (FV ∼ 5%). The last data set for Mrk 501 (60002024008) shows the source getting fainter with random flux-HR trend. Similarly, we found that of the four observations, the correlation between LE and HE light curves were significant for Obs ID 60002024004 and 60002024008, whereas for the other two observations we do not find any clear lead/lag. The spectra are fitted well with different power-law models for different observations, the ΓX ranging from 2.1 − 2.3 (refer to Table 3).
4.11. 1ES 1959+650
BL Lac 1ES 1959+650, a HSP (Giebels et al. 2002) and a TeV blazar (see Holder et al. 2003), was first detected in X-rays by Elvis et al. (1992). We analyzed data for the two observations 60002055002 and 60002055004. In the first observation, we see the flux rising by the factor ∼2, displaying the harder-when-brighter trend. Although the FV does not differ significantly from the first observation, in the second epoch the light curve is relatively stable and does not display a well-defined trend in the flux-HR plane. The ZDCF analysis shows that LE and HE light curves have a relatively strong correlation around zero lag. For both of the observations, LP model with ΓX ∼2.3 and 2.6 best describes the source spectra.
4.12. PKS 2155–304
PKS 2155–304 is one of the brightest HSP blazars and has been widely studied in X-ray bands (see Madejski et al. 2016, and references therein). The source is known to frequently exhibit rapid variability in the X-ray bands on hourly timescales (e.g., Rani et al. 2017; Tanihata et al. 2001; Zhang et al. 1999). We analyzed nine NuSTAR observations between July 2012 and October 2013, and found that the source displayed several interesting features including large FV (∼27%) and the most rapid variability with smallest minimum variability timescale 0.30 ± 0.12 ks. In addition, in three of the observations, the flux changes by twice within a few hours. However, the flux-HR relation does not show any obvious trend. The ZDCF analysis does not reveal any clear lead/lag between LE and HE light curves (refer to Table 4). The spectra for different observations are fitted separately with all three models, i.e., PL, LP, and BPL models, while the photon indexes range between ∼2.5 and 3.0. We note that with ΓX ∼ 3.0 the source displays one of the steepest spectra usually found in any BL Lac objects.
4.13. BL Lac
BL Lac is a prototype source of the class with the same name. The source has been observed by several multiwavelength campaigns (see Bhatta & Webb 2018, and the references therein). The 42 ks long NuSTAR observation that we examined shows large (FV ∼ 25%) and rapid (τvar = 1.88 ± 0.96 ks) variability. However, the HR does not appear to be correlated with the flux. We observe a relatively smaller correlation (∼0.30) between the high and low energy emission at the zero lag. The source spectra is best-fitted with PL model with ΓX ∼ 1.85.
5. Discussion
In this section, we attempt to explain the results of the above analyses in the light of the existing blazar models.
5.1. Rapid hard X-ray variability
Hard X-ray observations offer a direct access to the heart of an AGN revealing important processes occurring at the innermost regions of the central engine. The variable hard X-ray emission in AGN is considered to originate at the corona, which is a compact region above the AD. Hard X-ray emission from most of the AGNs mainly consists of three components: soft-access, neutral iron line, and the Compton hump. In Seyfert I type galaxies, these components are distinctly observed in their spectra (e.g., see Walton et al. 2014). However, in case of blazars, as the Doppler boosted jet emission is dominant over the coronal emission, the spectra exhibits pure power-law shapes devoid of emission or absorption features. Hard X-ray variability in blazars over various timescales could be resulted by the up-scattering of the soft photon fields located at various geometrical components of an AGN including AD, jets, DT, and BLR. Consequently, any modulation in the photon field, high energy electron population, and magnetic field in situ can produce hard X-ray variability, which can propagate along the jets. In addition, the distribution of the emission region sizes, as presented in Fig. 2, points out that such variability originates in compact (∼1012 cm) volumes of the sources.
Thus estimated sizes of the emission regions are smaller than the gravitational radius of an AGN with a typical black hole mass of 109 M⊙ ∼ 1.5 × 1012 cm. This suggests the observed short timescale modulations could either be ascribed to changes occurring at a fraction of the entire black hole region or the fluctuations could reflect small-scale instabilities intrinsic to the jet (see Begelman et al. 2008). In the relativistic turbulence scenario by Narayan & Piran (2012), magnetohydrodynamic turbulence in the jet can lead to compact substructures that move relativistically in random directions. Alternatively, very high bulk Lorentz factors (e.g., Γ ∼ 100) associated with the emitting regions can make the size of these regions appear comparable to rg. It is possible to achieve a such high Γs with the jets-in-a-jet model in which magnetic reconnection (e.g., Giannios et al. 2009) or turbulence (e.g., Narayan & Piran 2012) can produce relativistic outflows the bulk jet frame.
The rapid flux variations could also be explained as the emission from the shocked regions in the blazar jets viewed close to line of sight (e.g., Marscher & Gear 1985; Spada et al. 2001; Joshi & Böttcher 2011). The nonthermal emission modulations can also be attributed to various instabilities in the jet such as turbulence behind the shocks (see Bhatta et al. 2013; Marscher 2014).
 |
Fig. 3. Relation between the magnetic field and the particle acceleration and synchrotron cooling timescales in the observed frame for the moderate values of Doppler factors. |
In HSPs, the hard X-ray emission is probably due to the high energy tail of the synchrotron emission from large-scale jets. The variable emission then can be related to the particle acceleration and synchrotron emission by the electrons of the highest energy. In such a scenario, the variability timescales can be directly linked with particle acceleration and cooling timescales. To estimate the synchrotron cooling timescale, i.e., cooling due to synchrotron emission, we define tcool = (energy of an electron)/(synchrotron power loss) = γmec2/Psyn. This gives
where we use β ∼ 1 considering ultra-relativistic electrons. We note that such energy dependent cooling timescale can produce more rapid variability at hard X-ray energies than at soft X-ray energies. If we assume that the cooling takes place mainly because of the synchrotron process and that the most of the synchrotron emission is emitted in the NuSTAR energy band (∼15 keV; logarithmic mean of the NuSTAR range), then following Zhang (2002), magnetic field corresponding to the cooling timescales can be given as
where E is the energy of the observed photons expressed in keV, and B and δ are the magnetic field and Doppler factor of the emitting region, respectively. Similarly, assuming the particle acceleration due to diffusive shock acceleration (e.g., Blandford & Eichler 1987), magnetic field corresponding to the particle acceleration timescales can be given as
where ξ is the acceleration parameter conveniently expressed in the fiducial scale of 105 (for details see Zhang 2002) indicating the acceleration rate of electrons. For moderate δ and z = 0.1, the curves showing the relation between the magnetic field and the acceleration and synchrotron cooling timescales within the NuSTAR band, are presented in Fig. 3. It is interesting to note that for a reasonable ξ = 0.2 × 105, the cooling curves closely follow the acceleration curves. From these curves, it can be inferred that for the given variability timescales of a few hours as seen in the source (refer to Table 2 last column), a reasonable value of the magnetic field could be in the order of a few Gauss. Once we constrain the magnetic field, we can also estimate the energy of the high-tail synchrotron emitting electrons. Assuming most of the emission is concentrated near the maximum synchrotron frequency νs (in Hz), it can be expressed as
Using B = 1 G, the Lorentz factor for the highest energy electrons can be estimated as γmax ∼ 9.8 × 105; such a high value of γmax is particularly consistent with the fact that most of the BL Lacs discussed in the paper are TeV blazars.
 |
Fig. 4. Fractional variability of NuSTAR light curves plotted against the photon power-law index for the corresponding observations for FSRQs (black) and BL Lacs (red). The green, black, and red dashed lines represent the linear fit to all the sources, only FSRQs, and only BL Lacs, respectively. |
 |
Fig. 5. Correlation between minimum variability timescales of the NuSTAR blazar sources and their mean fluxes. The green dashed line represents the linear best fit to the data. |
In powerful FSRQs, the hard X-ray could result from a number of processes such as synchrotron radiation of pair cascades powered by ultra-relativistic protons, synchrotron radiation by ultra-relativistic protons, and IC scattering of the external soft photons (see Sikora et al. 2009, and references therein). In the more likely EC scenario, the IC cooling timescale, depending on the energy density of the external photon field and electron energy, can be written as
Now, the external photon field can be attributed to hot DT, BLR, or even the AD. As a more realistic example, assuming that HDR with monotonic photon field energy hν0 ∼ 0.1 eV (in infrared range; see Kataoka et al. 2008) poses for the Uext, and that the most of the IC emission lies within the NuSTAR band, the energy of the injected electrons in the source rest frame can be estimated using ν ∼ γ2ν0, where ν0 and ν are the frequencies of the soft and up-scattered emission, respectively. Moreover, to account for the fact that the emission zone is moving with a Doppler factor δ, the relation can be written as ν ∼ γ2δ2ν0. Now using hν0 = 0.1 eV for HDR and 10 eV for BLR (see Nalewajko et al. 2012), the energy of the lower tail of the high energy particles (γmin) turns out to be ∼40 and 4 Lorentz factors, respectively. It is preferable to have lower γmin because the jet power is very sensitive to the minimum energy of the emitting electrons. A large γmin (typically, ≳100) would drastically reduce the kinetic jet power and can make it even smaller than the radiative power. All the kinetic power of the jet would then be consumed by the radiation making the jet weaker and eventually stop. In such a case, we would not expect to see the Mpc scale radio jets, which is against the observations (for relevant discussion refer to Ghisellini et al. 2010b).
 |
Fig. 6. Distribution of the NuSTAR power-law photon indexes over the mean fluxes for FSRQ (black), ISP (red), and HSP (green). The dashed lines represent the corresponding linear best fits. |
Figure 4, presenting the distribution of the FV over the photon indexes ΓX, suggests that the sources tend to be more variable in their steeper spectral states. The strength of the correlation between the quantities are measured by Spearman rank correlation coefficient (ρ). The correlation looks more pronounced in FSRQs (black symbols) as indicated by the higher value of ρ = 0.84 with p-value = 3 × 10−4 compare to ρ = 0.59 with p-value = 0.01 for HSPs (red symbols). When all the sources (green symbols) are included the correlation becomes moderate with ρ = 0.60 and p-value = 2 × 10−4. The best linear fit for FSRQ only, HSP only, and all the sources are shown by black, red, and green dashed lines, respectively.
In combination with the close relation between high flux and harder photon index seen in Fig. 6 (discussed more in Sect. 5.3), this indicates that the observed overall variability could be dominantly contributed by the softer photons. The idea also seems to be reflected in Fig. 5 showing a correlation between mean flux and minimum variability timescale (ρ = 0.60 with p-value = 1.88 × 10−7), which indicates more rapid minimum variability timescales for fainter flux states. Such a rapid variability associated with a low-flux level could be linked to small-scale substructures resulting from turbulence at the innermost blazar regions (e.g., Narayan & Piran 2012; Bhatta et al. 2013; Marscher 2014) in contrast to the processes involving a large injection (e.g., due to shocks) or release (e.g., due to magnetic reconnection) of energy over a large volume, which processes are capable of producing big flares in the light curves (e.g., Hayashida et al. 2015). As also seen in Fig. 4, the relation (the steeper the spectrum the more variable) between FV and ΓX in BL Lacs does not look as distinct as in the FSRQs, as suggested by the relatively poor linear fit (dashed red line). It is possible that the relation might have been diluted in BL Lacs owing to the rapid synchrotron cooling timescales for the particles at the high energy end of the power-law distribution. Such a cooling process would contributing to the photons at the high energy end of the spectrum and thereby make the spectrum hard.
Alternatively, the hard X-ray variability exhibited by the sources can be related to extrinsic effects, for example, a rapid swing in the angle of the emission regions about the line of sight. A small deflection in viewing angle and/or bulk Lorentz factor leading to change in Doppler factor can also result in a large flux variations in the order of the VAs displayed by the sources as listed in the sixth column of Table 2. (for detailed discussion refer to Ghisellini et al. 1997; Bhatta 2017).
5.2. Flux hardness ratio relation
We explored the relation between the flux and HR in the source by plotting one against another. However, we did not observe any obvious correlation between the flux and HR that could be applied to all the observation. We could only observe clear evidence of harder-when-brighter within the observation period in one case (see Fig. 1, second panel). We also looked for signs of hysteresis loops in the flux-HR plane. However, no such loops could be found.
In blazars, the nature of the correlation between the flux and spectral state is somewhat uncertain so far. In the optical band, a bluer-when-brighter tendency is more associated with BL Lacs in the intraday timescales, whereas a redder-when-brighter trend seems to be frequently observed in FSRQs. In γ-ray regime blazars were also found to behave in the similar fashion, i.e., in some cases the spectrum hardens with the source intensity and in other cases the spectrum softens with the flux enhancements (see Bhatta 2017, for the discussion). The bluer-when-brighter trend seen in the NuSTAR observation of Mrk 501 (Fig. 1, second panel) could be due to local enhancements of the magnetic field in the jets leading to elevated synchrotron emission with an excess of hard photons.
5.3. Spectral shapes and photon index distribution
Figure 6 shows the distribution of the photon indexes of the best-fit models over the mean fluxes. The distribution clearly distinguishes the photon indexes for FSRQs and HSPs. It can be seen that the spectral indexes αX (αX = ΓX − 1) for the HSPs are steep, ranging from ∼2–1 and those for the FSRQs range from ∼1–0.3. These results are consistent with previous similar works (e.g., Donato et al. 2005; Tramacere et al. 2007). Although, there are only two ISPs, their αXs in appropriate place in the figures between the ΓXs for HSPs and FSRQs. The results are consistent with the standard blazar paradigm, so-called blazar sequence, in which in the high energy regime the FSRQs with large Compton dominance (Padovani et al. 1997) exhibit harder spectra in comparison to the BL Lacs (in present case TeV blazars). A similar distinction between FSRQs and BL Lacs, based their ΓX in the Swift X-ray range and Γγ in the Fermi/LAT γ-ray range, was observed by Sambruna et al. (2010). The BL Lacs in general are dim possibly because of the sub-Eddington accretion rates and they are usually identified with flatter spectra in the hard X-ray/γ-region. Figure 6 also suggests a close connection between the flux and spectral slope within the source class in the sense that high flux and/or flux states tend to be of harder spectra, i.e., ρ = −0.67, p-value = 0.019 (FSRQ), ρ = −0.74, and p-value = 0.001 (HSP). This might indicate that high flux and/or flux states are most likely linked to small-scale instantaneous changes in the mass accretion rate and disk efficiency, which could be modulated by disk instabilities (e.g., Mangalam & Wiita 1993) from the formation of hot spots. Thus hard X-ray flux modulations seen in the sources are possibly triggered at the innermost regions of the central engine.
5.4. Correlation between low and high energy emission
As we examined the correlation between the low and high energy emission by the sources, there does not seem to be a single behavior that can be generalized for all the observations. Instead, all kinds of relation are observed: In some cases there is a strong correlation between the emission in the two energy bands, whereas in some cases they appear completely uncorrelated as indicated by their low ZDCF values at all lags. Similarly, we also observed possible signatures of hard and soft lags. However, owing to the Poisson noise-like behavior of the variability, it is hard to bey conclusive. The apparent uncorrelated energy bands might be the result of emission from completely unrelated population of the particles or reflection from the uncorrelated regions of varying sizes (similar to Tanihata et al. 2000). On the other hand, the hard and soft lags can be interpreted within the framework of the particle injection and synchrotron cooling at the emission sites (see Kirk et al. 1998; Zhang 2002). In such a frame work, depending upon whether the cooling or particle acceleration mechanism dominates the variability processes, soft and hard lag can be expected, respectively (for details see Zhang 2002).
6. Conclusions
We analyzed the 31 NuSTAR observation for 13 blazars including 7 FSRQs, 4 HSPs, and 2 ISPs. The source displayed high amplitude rapid variability within a timescale of a few hours; the minimum variability timescales range from 0.3 to 18.8 ks, whereas the FV ranges from ∼5–38 %. On one occasion, the relation between the HR and flux could be dubbed as a harder-when-brighter trend, but in general the relation between the flux and HR seemed more complex. Similarly, we did not detect any trend in the correlation between the hard and soft energy emission that could be generalized for all the observations. We also found hints of the presence of soft and hard lags by a few hours. However the low values of the associated likelihood render the results inconclusive. For most of the observations, the log-parabolic model revealing spectral curvature seems to be the best representation of the NuSTAR blazar spectra, although some of the source spectra were better fitted with single power-law and broken power-law models. Moreover, the distribution of the spectral slopes appear consistent with the current blazar paradigm in which the HSPs possess the steepest and FSRQs have the flattest spectral slope. In addition, we detected close connection between the photon indexes and mean flux states that could been seen within the blazar subclasses. We also noted that the sources tend to be more variable in their steeper spectral states. However, the last feature should be explored further involving a larger sample of blazars.
The software is publicly available at http://www.weizmann.ac.il/particle/tal/research-activities/software
Acknowledgments
We are thankful to the anonymous reviewer for his/her constructive comments that helped improve the quality of the paper significantly. GB acknowledges the financial support by the Polish National Science Centre through the grants UMO-2017/26/D/ST9/01178 and DEC- 2012/04/A/ST9/00083. We would also like to thank Prof. Michał Ostrowski and ᴌukasz Stawarz for their useful comments and suggestions during the work. This paper made use of data from the NuSTAR mission, a project led by the California Institute of Technology, managed by the Jet Propulsion Laboratory, funded by the National Aeronautics and Space Administration. We thank the NuSTAR Operations, Software and Calibration teams for support with the execution and analysis of these observations. This research made use of the NuSTAR Data Analysis Software (NuSTARDAS) jointly developed by the ASI Science Data Center (ASDC, Italy), and the California Institute of Technology (USA).
References
- Abeysekara, A. U., Archambault, S., Archer, A., et al. 2015, ApJ, 815, L22 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010, ApJS, 188, 405 [NASA ADS] [CrossRef] [Google Scholar]
- Aharonian, F. A. 2000, New Astron., 5, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Ajello, M., Alexander, D. M., Greiner, J., et al. 2012, ApJ, 749, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Akyuz, A., Thompson, D. J., Donato, D., et al. 2013, A&A, 556, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aleksić, J., Ansoldi, S., Antonelli, L. A., et al. 2015, A&A, 576, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alexander, T. 2013, ArXiv e-prints [arXiv: 1302.1508] [Google Scholar]
- Aliu, E., Archambault, S., Arlen, T., et al. 2014, ApJ, 782, 13 [Google Scholar]
- Arnaud, K. A. 1996, ASP Conf. Ser., 101, 17 [Google Scholar]
- Baumgartner, W. H., Tueller, J., Markwardt, C. B., et al. 2013, ApJS, 207, 19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Begelman, M. C., Fabian, A. C., & Rees, M. J. 2008, MNRAS, 384, L1 [Google Scholar]
- Bevington, P. R., & Robinson, D. K. 2003, in Data Reduction and Error Analysis for the Physical Sciences, 3rd ed. (Boston, MA: McGraw-Hill) [Google Scholar]
- Bhatta, G. 2017, ApJ, 487, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Bhatta, G., & Webb, J. 2018, Galaxies, 6, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Bhatta, G., Webb, J. R., Hollingsworth, H., et al. 2013, A&A, 558, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bhatta, G., Stawarz, Ł., Ostrowski, M., et al. 2016a, ApJ, 831, 92 [NASA ADS] [CrossRef] [Google Scholar]
- Bhatta, G., Zola, S., Stawarz, Ł., et al. 2016b, ApJ, 832, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Błażejowski, M., Sikora, M., Moderski, R., & Madejski, G. M. 2000, ApJ, 545, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Blandford, R., & Eichler, D. 1987, Phys. Rep., 154, 1 [Google Scholar]
- Böttcher, M., & Els, P. 2016, ApJ, 821, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Brinkmann, W., Papadakis, I. E., Raeth, C., Mimica, P., & Haberl, F. 2005, A&A, 443, 397 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Burbidge, G. R., Jones, T. W., & Odell, S. L. 1974, ApJ, 193, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Camenzind, M., & Krockenberger, M. 1992, A&A, 255, 59 [NASA ADS] [Google Scholar]
- Cawthorne, T. V. 2006, MNRAS, 367, 851 [NASA ADS] [CrossRef] [Google Scholar]
- D’Ammando, F., & Orienti, M. 2016, MNRAS, 455, 1881 [NASA ADS] [CrossRef] [Google Scholar]
- Dermer, C. D., & Schlickeiser, R. 1993, ApJ, 416, 458 [NASA ADS] [CrossRef] [Google Scholar]
- Donato, D., Sambruna, R. M., & Gliozzi, M. 2005, A&A, 433, 1163 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Edelson, R. A., & Krolik, J. H. 1988, ApJ, 333, 646 [NASA ADS] [CrossRef] [Google Scholar]
- Edelson, R., Vaughan, S., Malkan, M., et al. 2014, ApJ, 795, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Elvis, M., Plummer, D., Schachter, J., & Fabbiano, G. 1992, ApJS, 80, 257 [NASA ADS] [CrossRef] [Google Scholar]
- Falcone, A. D., Cui, W., & Finley, J. P. 2004, ApJ, 601, 165 [NASA ADS] [CrossRef] [Google Scholar]
- Fossati, G., Maraschi, L., Celotti, A., Comastri, A., & Ghisellini, G. 1998, MNRAS, 299, 433 [NASA ADS] [CrossRef] [Google Scholar]
- Fossati, G., Celotti, A., Chiaberge, M., et al. 2000a, ApJ, 541, 166 [NASA ADS] [CrossRef] [Google Scholar]
- Fossati, G., Celotti, A., Chiaberge, M., et al. 2000b, ApJ, 541, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Furniss, A., Noda, K., Boggs, S., et al. 2015, ApJ, 812, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Ghisellini, G., Villata, M., & Raiteri 1997, A&A, 327, 61 [NASA ADS] [Google Scholar]
- Ghisellini, G., Della Ceca, R., Volonteri, M., et al. 2010a, MNRAS, 405, 387 [NASA ADS] [Google Scholar]
- Ghisellini, G., Tavecchio, F., Foschini, L., et al. 2010b, MNRAS, 402, 497 [NASA ADS] [CrossRef] [Google Scholar]
- Ghisellini, G., Tavecchio, F., Foschini, L., & Ghirlanda, G. 2011, MNRAS, 414, 2674 [NASA ADS] [CrossRef] [Google Scholar]
- Ghisellini, G., Righi, C., Costamante, L., & Tavecchio, F. 2017, MNRAS, 469, 255 [NASA ADS] [CrossRef] [Google Scholar]
- Giannios, D., Uzdensky, D. A., & Begelman, M. C. 2009, MNRAS, 395, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Giebels, B., Bloom, E. D., Focke, W., et al. 2002, ApJ, 571, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Giommi, P., Massaro, E., Chiappetti, L., et al. 1999, A&A, 351, 59 [NASA ADS] [Google Scholar]
- Hagen-Thorn, V. A., Larionov, V. M., Jorstad, S. G., et al. 2008, ApJ, 672, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Harrison, F. A., Craig, W. W., Christensen, F. E., et al. 2013, ApJ, 770, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Hayashida, M., Nalewajko, K., Madejski, G. M., et al. 2015, ApJ, 807, 79 [Google Scholar]
- Holder, J., Bond, I. H., Boyle, P. J., et al. 2003, ApJ, 583, L9 [Google Scholar]
- Homan, D. C., Attridge, J. M., & Wardle, J. F. C. 2001, ApJ, 556, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Hughes, P. A., Aller, H. D., & Aller, M. F. 1998, ApJ, 503, 662 [NASA ADS] [CrossRef] [Google Scholar]
- Hummel, C. A., Muxlow, T. W. B., Krichbaum, T. P., et al. 1992, A&A, 266, 93 [NASA ADS] [Google Scholar]
- Impey, C. D., & Neugebauer, G. 1988, AJ, 95, 307 [NASA ADS] [CrossRef] [Google Scholar]
- Jorstad, S. G., Marscher, A. P., Lister, M. L., et al. 2004, AJ, 127, 3115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jorstad, S. G., Marscher, A. P., Lister, M. L., et al. 2005, AJ, 130, 1418 [NASA ADS] [CrossRef] [Google Scholar]
- Jorstad, S., Marscher, A., Larionov, V., et al. 2013, Eur. Phys. J. Web Conf., 61, 04003 [CrossRef] [Google Scholar]
- Joshi, M., & Böttcher, M. 2011, ApJ, 727, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Kalberla, P. M. W., Burton, W. B., Hartmann, D., et al. 2005, A&A, 440, 775 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kataoka, J., Madejski, G., Sikora, M., et al. 2008, ApJ, 672, 787 [NASA ADS] [CrossRef] [Google Scholar]
- Kirk, J., Reiger, F. M., & Mastichiadis, A. 1998, A&A, 333, 452 [NASA ADS] [Google Scholar]
- Kubo, H., Takahashi, T., Madejski, G., et al. 1998, ApJ, 504, 693 [NASA ADS] [CrossRef] [Google Scholar]
- Lister, M. L., & Homan, D. C. 2005, AJ, 130, 1389 [NASA ADS] [CrossRef] [Google Scholar]
- Madejski, G. M., Nalewajko, K., Madsen, K. K., et al. 2016, ApJ, 831, 142 [NASA ADS] [CrossRef] [Google Scholar]
- Madsen, K. K., Fürst, F., Walton, D. J., et al. 2015, ApJ, 812, 14 [NASA ADS] [CrossRef] [Google Scholar]
- MAGIC Collaboration (Albert, J., et al.) 2008, Science, 320, 1752 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Mangalam, A. V., & Wiita, P. J. 1993, ApJ, 406, 420 [NASA ADS] [CrossRef] [Google Scholar]
- Maraschi, L., Ghisellini, G., & Celotti, A. 1992, ApJ, 397, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Marscher, A. P. 2014, ApJ, 780, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Marscher, A. P., & Gear, W. K. 1985, ApJ, 298, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Marscher, A. P., & Travis, J. P. 1996, A&AS, 120, 537 [NASA ADS] [Google Scholar]
- Massaro, E., Perri, M., Giommi, P., & Nesci, R. 2004a, A&A, 413, 489 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Massaro, E., Perri, M., Giommi, P., Nesci, R., & Verrecchia, F. 2004b, A&A, 422, 103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Massaro, E., Tramacere, A., Perri, M., Giommi, P., & Tosti, G. 2006, A&A, 448, 861 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Massaro, F., Giommi, P., Tosti, G., et al. 2008, A&A, 489, 1047 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mastichiadis, A., & Kirk, J. G. 2002, PASA, 19, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Nalewajko, K., Begelman, M. C., Cerutti, B., Uzdensky, D. A., & Sikora, M. 2012, MNRAS, 425, 2519 [NASA ADS] [CrossRef] [Google Scholar]
- Narayan, R., & Piran, T. 2012, MNRAS, 420, 604 [NASA ADS] [CrossRef] [Google Scholar]
- Padovani, P., Giommi, P., & Fiore, F. 1997, MNRAS, 284, 569 [NASA ADS] [CrossRef] [Google Scholar]
- Padovani, P., Costamante, L., Ghisellini, G., Giommi, P., & Perlman, E. 2002, ApJ, 581, 895 [NASA ADS] [CrossRef] [Google Scholar]
- Paliya, V. S. 2015, ApJ, 804, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Paltani, S., Courvoisier, T. J.-L., & Walter, R. 1998, A&A, 340, 47 [NASA ADS] [Google Scholar]
- Pandey, A., Gupta, A. C., & Wiita, P. J. 2017, ApJ, 841, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Perlman, E. S., Stocke, J. T., Wang, Q. D., & Morris, S. L. 1996, ApJ, 456, 451 [NASA ADS] [CrossRef] [Google Scholar]
- Perlman, E. S., Madejski, G., Georganopoulos, M., et al. 2005, ApJ, 625, 727 [NASA ADS] [CrossRef] [Google Scholar]
- Peterson, B. M. 1997, An introduction to active galactic nuclei (Cambridge: New York Cambridge University Press), 238 [Google Scholar]
- Raiteri, C. M., Villata, M., D’Ammando, F., et al. 2013, MNRAS, 436, 1530 [NASA ADS] [CrossRef] [Google Scholar]
- Rani, P., Stalin, C. S., & Rakshit, S. 2017, MNRAS, 466, 3309 [NASA ADS] [CrossRef] [Google Scholar]
- Ravasio, M., Tagliaferri, G., Ghisellini, G., et al. 2002, A&A, 383, 763 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ravasio, M., Tagliaferri, G., Ghisellini, G., & Tavecchio, F. 2004, A&A, 424, 841 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sambruna, R. M., Barr, P., Giommi, P., et al. 1994, ApJ, 434, 468 [NASA ADS] [CrossRef] [Google Scholar]
- Sambruna, R. M., Chou, L. L., & Urry, C. M. 2000, ApJ, 533, 650 [NASA ADS] [CrossRef] [Google Scholar]
- Sambruna, R. M., Tavecchio, F., Ghisellini, G., et al. 2007, ApJ, 669, 884 [NASA ADS] [CrossRef] [Google Scholar]
- Sambruna, R. M., Donato, D., Ajello, M., et al. 2010, ApJ, 710, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Sbarrato, T., Ghisellini, G., Tagliaferri, G., et al. 2016, MNRAS, 462, 1542 [NASA ADS] [CrossRef] [Google Scholar]
- Sikora, M. 1994, ApJS, 90, 923 [NASA ADS] [CrossRef] [Google Scholar]
- Sikora, M., & Begelman, M. C. 2013, ApJ, 764, L24 [NASA ADS] [CrossRef] [Google Scholar]
- Sikora, M., Stawarz, Ł., Moderski, R., Nalewajko, K., & Madejski, G. M. 2009, ApJ, 704, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Soldi, S., Türler, M., Paltani, S., et al. 2008, A&A, 486, 411 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spada, M., Ghisellini, G., Lazzati, D., & Celotti, A. 2001, MNRAS, 325, 1559 [NASA ADS] [CrossRef] [Google Scholar]
- Tanihata, C., Takahashi, T., Kataoka, J., et al. 2000, ApJ, 543, 124 [NASA ADS] [CrossRef] [Google Scholar]
- Tanihata, C., Urry, C. M., Takahashi, T., et al. 2001, ApJ, 563, 569 [NASA ADS] [CrossRef] [Google Scholar]
- Tramacere, A., Giommi, P., Massaro, E., et al. 2007, A&A, 467, 501 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Urry, C. M., Sambruna, R. M., Worrall, D. M., et al. 1996, ApJ, 463, 424 [NASA ADS] [CrossRef] [Google Scholar]
- Vaughan, S., Edelson, R., Warwick, R. S., & Uttley, P. 2003, MNRAS, 345, 1271 [NASA ADS] [CrossRef] [Google Scholar]
- Wagner, S. J., & Witzel, A. 1995, ARA&A, 33, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Walton, D. J., Risaliti, G., Harrison, F. A., et al. 2014, ApJ, 788, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Welsh, W. F. 1999, PASP, 111, 1347 [NASA ADS] [CrossRef] [Google Scholar]
- Wierzcholska, A., & Siejkowski, H. 2016a, MNRAS, 458, 2350 [NASA ADS] [CrossRef] [Google Scholar]
- Wierzcholska, A., & Wagner, S. J. 2016b, MNRAS, 458, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Wilms, J., Allen, A., & McCray, R. 2000, ApJ, 542, 914 [NASA ADS] [CrossRef] [Google Scholar]
- Wolter, A., Comastri, A., Ghisellini, G., et al. 1998, A&A, 335, 899 [NASA ADS] [Google Scholar]
- Worrall, D. M., & Wilkes, B. J. 1990, ApJ, 360, 396 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, Y. H. 2002, MNRAS, 337, 609 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, Y. H., Celotti, A., Treves, A., et al. 1999, ApJ, 527, 719 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, Y. H., Treves, A., Celotti, A., Qin, Y. P., & Bai, J. M. 2005, ApJ, 629, 686 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, Y. H., Bai, J. M., Zhang, S. N., et al. 2006, ApJ, 651, 782 [NASA ADS] [CrossRef] [Google Scholar]
- Zola, S., Valtonen, M., Bhatta, G., et al. 2016, Galaxies, 4, 41 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A Light curves, HR plots, and spectral fits of NuSTAR blazars
 |
Fig. A.1. In each row: light curve, flux-HR relation, ZDCF, and spectral fit from left to right respectively, for the NuSTAR blazar observations listed in the Table 2. The color bars in the light curve and flux-HR plots represent the HR and time, respectively. |
 |
Fig. A.1. continued. |
 |
Fig. A.1. continued. |
 |
Fig. A.1. continued. |
 |
Fig. A.1. continued. |
 |
Fig. A.1. continued. |
All Tables
Discrete cross-correlation function between the low (3–10 keV) and high energy (10–79 keV) emission of the NuSTAR blazars.
All Figures
 |
Fig. 1. Hard X-ray NuSTAR observations of blazar sources showing light curve and flux-HR relation, ZDCF, and spectral fit from top to bottom for the sources 3C 279, Mrk 501, 3C 279, and S5 0716+714, respectively. The color bars in light curve and the flux-HR plots represent the HR and time, respectively. Similar plots for other sources are shown in Appendix A. |
| In the text | |
 |
Fig. 2. Distribution of the emission region sizes in the NuSTAR blazars derived from their minimum variability timescales. |
| In the text | |
 |
Fig. 3. Relation between the magnetic field and the particle acceleration and synchrotron cooling timescales in the observed frame for the moderate values of Doppler factors. |
| In the text | |
 |
Fig. 4. Fractional variability of NuSTAR light curves plotted against the photon power-law index for the corresponding observations for FSRQs (black) and BL Lacs (red). The green, black, and red dashed lines represent the linear fit to all the sources, only FSRQs, and only BL Lacs, respectively. |
| In the text | |
 |
Fig. 5. Correlation between minimum variability timescales of the NuSTAR blazar sources and their mean fluxes. The green dashed line represents the linear best fit to the data. |
| In the text | |
 |
Fig. 6. Distribution of the NuSTAR power-law photon indexes over the mean fluxes for FSRQ (black), ISP (red), and HSP (green). The dashed lines represent the corresponding linear best fits. |
| In the text | |
 |
Fig. A.1. In each row: light curve, flux-HR relation, ZDCF, and spectral fit from left to right respectively, for the NuSTAR blazar observations listed in the Table 2. The color bars in the light curve and flux-HR plots represent the HR and time, respectively. |
| In the text | |
 |
Fig. A.1. continued. |
| In the text | |
 |
Fig. A.1. continued. |
| In the text | |
 |
Fig. A.1. continued. |
| In the text | |
 |
Fig. A.1. continued. |
| In the text | |
 |
Fig. A.1. continued. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



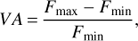
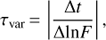
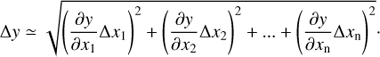
![$$ \begin{aligned} \Delta \tau _\mathrm{var} \simeq \sqrt{\frac{F_{1}^{2} \Delta {F}_{2}^{2} +F_{2}^{2} \Delta F_{1}^{2}}{F_{1}^{2}F_{2}^{2}\left(\mathrm{ln} \left[ F_{1}/F_{2} \right]\right)^{4}}}\ \Delta t, \end{aligned} $$](/articles/aa/full_html/2018/11/aa33628-18/aa33628-18-eq4.gif)