| Issue |
A&A
Volume 619, November 2018
|
|
|---|---|---|
| Article Number | A156 | |
| Number of page(s) | 14 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201833582 | |
| Published online | 20 November 2018 | |
Monitoring of the activity and composition of comets 41P/Tuttle–Giacobini–Kresak and 45P/Honda–Mrkos–Pajdusakova
1
Space Sciences, Technologies and Astrophysics Research (STAR) Institute, University of Liège,
Liège, Belgium
e-mail: youssef.moulane@doct.uliege.be
2
Oukaimeden Observatory, High Energy Physics and Astrophysics Laboratory, Cadi Ayyad University, Marrakech, Morocco
3
European Southern Observatory,
Alonso de Cordova 3107,
Vitacura, Santiago, Chile
Received:
6
June
2018
Accepted:
11
September
2018
We report on photometry and imaging of the Jupiter family comets 41P/Tuttle–Giacobini–Kresak and 45P/Honda–Mrkos–Pajdusakova with the TRAPPIST-North (TRAnsiting Planets and PlanetesImals Small Telescope) telescope. We observed 41P on 34 nights from February 16 to July 27, 2017, pre- and post-perihelion (rh = 1.04 au), and collected data for comet 45P after perihelion (rh = 0.53 au) from February 10 to March 30, 2017. We computed the production rates of the daughter species OH, NH, CN, C3 and C2 and we measured the dust proxy, Afρ, for both comets. The peak of water-production rate of 41P was (3.46 ± 0.20) × 1027 molecules s−1 on April 3, 2017, when the comet was at 1.05 au from the Sun. We have shown that the activity of 41P is decreasing by about 30–40% from one apparition to the next. We measured a mean water-production rate for 45P of (1.43 ± 0.62) × 1027 molecules s−1 during a month after perihelion. Our results show that these Jupiter family comets had low gas and dust activity and no outburst was detected. Relative abundances, expressed as ratios of production rates and the Afρ parameter with respect to OH and to CN, were compared to those measured in other comets. We found that 41P and 45P have a typical composition in terms of carbon-bearing species. The study of coma features exhibited by the CN gas species allowed the measurement of the rotation period of 41P, showing a surprisingly large increase of the rotation period from (30 ± 5) h at the end of March to (50 ± 10) h at the end of April, 2017, in agreement with recent observations by other teams.
Key words: comets: individual: 45P/Honda / Mrkos / Pajdusakova / comets: individual: 41P/Tuttle / Giacobini / Kresak / comets: general / techniques: photometric
© ESO 2018
1 Introduction
Comets are among the best preserved specimens of the primitive solar nebula. This status gives them a unique role in our efforts to understand the origins of the solar system. The success of the Rosetta mission to the Jupiter family comet (JFC) 67P/Churyumov-Gerasimenko (hereafter 67P) is changing our knowledge of comets (Marty et al. 2017). At the same time it shows that ground-based observations are also important for the completion of in situ data as they provide information on a larger scale of the coma and for a greater number of comets, which is necessary to extrapolate the results of the entire comet population. The link between the composition of comets and their dynamical history must still be clarified.
The comet 41P/Tuttle–Giacobini–Kresák (hereafter 41P) is a JFC discovered by Horace Parnell Tuttle on May 3, 1858, and re-discovered independently by Michel Giacobini and L’ubor Kresák in 1907 and 1951, respectively. The comet had two close encounters with Jupiter in 1975 and 1988 that have altered its orbit slightly. Its perihelion distance is now 1.05 au and its orbital period 5.42 yr1.
The comet 41P is famous for major outbursts that makes it highly variable in brightness. During its 1973 apparition, 41P briefly reached magnitude 4 after a major outburst (Kresak & Kresakova 1974). The apparition of the comet in late 2000 and early 2001 was not expected to be one of the best, with a magnitude of about 12 by early January 2001. During that period, 41P was observed by the Solar and Heliospheric Observatory (SOHO). The water-production rate was (5.20 ± 0.07) × 1028 molecules s−1 at perihelion (rh = 1.05 au, January 6, 2001). This rate was derived by modelling the observed distribution of atomic hydrogen in the cometary coma (Combi 2017). In its 2006 apparition, the water-production rate obtained from SOHO decreased to (1.60 ± 0.08) × 1028 molecules s−1 at perihelion (rh = 1.05 au). The last perihelion of the comet was on November 12, 2011, but it was not observed because it was on the far side of the Sun. The heliocentric light curve of Tancredi et al. (2000) indicates that 41P has a small nucleus. Lamy et al. (2004) estimate the nucleus radius to be about 0.7 km, but even this may only be an upper limit. The radius of 41P is less than 70% of all measured radii of JFCs (Fernández et al. 2013), so 41P can be considered as a small comet.
The comet 45P/Honda–Mrkos–Pajdusakova (hereafter 45P) is a short-period comet that also belongs to the Jupiter family. It was discovered on December 3, 1948, by Minoru Honda, Antonín Mrkos, and Ludmila Pajdušáková. Since then, it has been observed on every apparition except for its 1959 and 1985 passages, when it was too close to the Sun. Over the last few apparitions, it was close to Jupiter in 1935 and in 1983. Its perihelion distance is now 0.53 au and its orbital period 5.25 yr.
The recent apparitions of 45P were in 2006 when the comet was on the far side of the Sun around the time of perihelion. The last apparition was in 2011 when it was well positioned for pre-perihelion observations. At this time, the comet approached the Earth within 0.06 au on August 15, 2011. Its perihelion was on September 28, 2011, and the comet reached a peak of magnitude of 7.5. The water-production rate obtained from SOHO observatory was around 9 × 1028 molecules s−1 when the comet was 0.54 au from the Sun and at 0.87 au from the Earth (Combi 2017). For the nucleus size of 45P, Lowry et al. (2003) obtained a mean value of rn = 0.34 ± 0.01 km from observations performed on two consecutive days during the passage in June 1999, using the Hubble Space Telescope. The snapshot observation of Lamy et al. (1999) gives a much larger value of rn = 1.34 ± 0.55 km, but the large error bar means that rn could be as small as 0.8 km. Using radar observations, Lejoly & Howell (2017) estimated the effective radius of 45P’s nucleus to be in the range of 1.2–1.3 km with a rotation period of about 7.5 h.
In this work, we present the monitoring of the activity and composition for various gas species and the dust of 41P over 5 months and of 45P over 40 days after perihelion with the TRAPPIST-North telescope. In Sect. 2, we report on our observation strategy and the tools used in the data reduction. In Sect. 3, we follow the evolution of the activity of the different daughter molecules considered in this work, and the dust properties obtained from A(θ)fρ parameter over a wide range of heliocentric distances, and on both sides of perihelion for 41P. Sect. 4 contains an explanation of the comparison of the coma morphology exhibited by various gas species allowing us to determine the rotation period of comet 41P. Finally, in Sect. 5, we summarise our results for both comets.
2 Observations and data reduction
TRAPPIST-North (TRAnsiting Planets and PlanetesImals Small Telescope) is a 60 cm robotic telescope that was installed in May, 2016, at the Oukaimeden Observatory at 2750 m of altitude in the Atlas mountains of Morocco (Benkhaldoun 2018). TRAPPIST-North (TN) is a twin of TRAPPIST-South (TS) which was installed at the ESO La Silla Observatory in 2010 (Jehin et al. 2011). TRAPPIST telescopes are dedicated to the detection and characterisation of exoplanets and the study of comets and other small bodies of the solar system. With TN we can now also observe comets in the northern hemisphere and with TS we can access almost the whole sky on a regular basis. With the two telescopes, we can follow comets over a large part of their orbits. The telescope is equipped with a thermo-electrically cooled 2K × 2K Andor IKONL CCD camera with a 20′ × 20′ field of view. We bin the pixels two by two giving a resulting plate scale of 1.3′′ pixel−1. We observe bright comets (typically V < 12) with HB narrow-band filters isolating the emission bands of OH[310 nm], NH[336 nm], CN[385 nm], C3 [405 nm], and C2 [515 nm] daughter species as well as emission free dust continuum in three regions covering the optical range BC [445 nm], GC [525 nm], and RC [715 nm]. These narrow-band filters are interference filters, whose design was carefully thought to maximize the fraction of the emission bands encompassed while minimizing the continuum contamination for the gas filters. The continuum filters have to be large enough to provide significant signal but avoid gas contamination at the same time. The final HB filter set was the result of these considerations (Farnham et al. 2000). Images are also taken with broadband B, V, Rc, and Ic Johnson-Cousin filters (Bessell 1990). All these filters are the same as those used for TRAPPIST-South observations.
We have obtained 600 images of comet 41P with TN over 5 months from February 16, when the comet was at 1.27 au from the Sun and at 0.29 au from the Earth, until July 27, 2017, when the comet was at 1.69 au. Its perihelion was on April 12 at 1.0 au and the comet was at its closest distance to Earth on April 1 at only 0.14 au. We also observed 41P with TS before perihelion on February 25 and on March 8, 2017, with narrow- and broadband filters. In the OH, NH, and RC filters, no signal was detected. Exposure times range from 60 to 240 s forthe broad-band filters, and from 300 to 1200 s for the narrow-band filters. Most Rc, CN, and C2 images wereobtained in sets of 4–12 images per night whereas most images in other filters were obtained as single images.
We started to collect data for 45P as soon as the comet was visible from Morocco, on February 10. It was about one month after perihelion and at a distance of 0.97 au from the Sun and at its closest distance to Earth, only 0.08 au. With a perihelion at 0.53 au, the comet had a small solar elongation (<30°) around perihelion. Most ground-based telescopes are not able to observe this close to the Sun, which leads to a lack of data for this comet at perihelion. During most of our observations, the comet coma was huge and filling most of the field of view as it was very close to Earth. The comet was rising fast and it was soon visible all night. Comet 45P faded rapidly and NH was not detected during our observations. We continued to observe 45P about twice a week until the end of March when the comet was at 1.62 au. The comet was also observed with TS on February 25 and on March 8, 20–21, 2017, with narrow- and broadband filters. No signal was detected in the OH and NH filters. The exposure time ranged from 60 to 240 s for the broadband filters, and from 300 to 1200 s for the narrow-band filters.
Standard procedures were used to calibrate the data by creation of master bias, flat, and dark frames. The bias and dark subtraction, as well as the flat-field correction are done using IRAF (Image Reduction and Analysis Facility). The absolute flux calibration was made using standard stars observed during the same period. The next step was the removal of the sky background coming mainly from atmospheric activity and moon contamination, which are variable and depend on the wavelength. The subtraction of the sky background has to be done with great care for extended objects. We used the procedure developed in previous papers (Opitom et al. 2015a,b, 2016). After the determination of the comet centre using the Imcntr IRAF task, we derived median radial brightness profiles from the gas (and dust) images. Then, we removed the dust contamination from the gas radial profiles using images of comets in the BC filter, because it is less contaminated by cometary gas emission than the other dust filters (Farnham et al. 2000).
The fluorescence efficiency of each molecule, also called g-factor, is used to convert the flux to column density. The g-factor represents the number of photons per second scattered by a single atom or molecule exposed to the unattenuated sunlight (Swamy 2010).
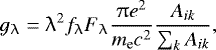 (1)
(1)
where Fλ is the solar flux per unit of wavelength and fλ is the oscillator strength. Aik are the Einstein coefficients. The term 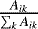 represents the fraction of photons emitted from the energy level i to the energy level k relative to all the photons emitted from the energy level i. Factors e and me are the charge and mass of an electron, respectively. The fluorescence efficiency values for the different gas filters are taken from Schleicher’s website2. The C2 g-factors have a single value for the Δυ = 0 band sequence with a band head near 5160 Å, and it is scaled by
represents the fraction of photons emitted from the energy level i to the energy level k relative to all the photons emitted from the energy level i. Factors e and me are the charge and mass of an electron, respectively. The fluorescence efficiency values for the different gas filters are taken from Schleicher’s website2. The C2 g-factors have a single value for the Δυ = 0 band sequence with a band head near 5160 Å, and it is scaled by  (A’Hearn et al. 1984). The C3 g-factor has a single value for the C3 band complex which peaks near 4030 Å and extends from 3300 to 4400 Å. The C3 fluorescence efficiencies are scaled by
(A’Hearn et al. 1984). The C3 g-factor has a single value for the C3 band complex which peaks near 4030 Å and extends from 3300 to 4400 Å. The C3 fluorescence efficiencies are scaled by  and are taken from A’Hearn (1982). The CN and NH fluorescence efficiencies vary with both the heliocentric velocity and distance (because of the strong change in the number of rotational levels populated with heliocentric distance). The CN and NH g-factors are taken from Schleicher (2010) and from Meier et al. (1998), respectively. The OH g-factor value of the 0-0 band centred near 3090 Å varies with the heliocentric velocity and also depends on whether or not the lambda-doublet ground state is quenched; scaled by
and are taken from A’Hearn (1982). The CN and NH fluorescence efficiencies vary with both the heliocentric velocity and distance (because of the strong change in the number of rotational levels populated with heliocentric distance). The CN and NH g-factors are taken from Schleicher (2010) and from Meier et al. (1998), respectively. The OH g-factor value of the 0-0 band centred near 3090 Å varies with the heliocentric velocity and also depends on whether or not the lambda-doublet ground state is quenched; scaled by 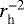 (Schleicher & A’Hearn 1988).
(Schleicher & A’Hearn 1988).
In order to derive the production rates, we have converted the flux for different gas species (OH, NH, CN, C3 and C2) to column densities and have adjusted their profiles with a Haser model (Haser 1957). This rather simple model is based on a number of assumptions. Outgassing is assumed to be isotropic and the gas streams from the nucleus with a constant radial velocity. Parent molecules coming off the nucleus are decaying by photo dissociation to produce the observed daughter molecules. Table 1 shows the scale lengths and lifetimes of different daughter and parent molecules at1 au from the Sun (A’Hearn et al. 1995) that we used to adjust the radial profiles to the Haser model. The Vectorial model introduced by Festou (1981a, b) is physically more realistic; it considers the existence of collisions in the inner coma producing a non-radial motion of the molecules and becomes less pronounced when the cometocentric distance increases. Furthermore, the release of energy when daughter molecules are produced may result in an additional non-radial motion throughout the entire cometary coma. It is noted that a vectorial model appears to be required to represent the density distribution of some radicals in a comet. But the Vectorial model has more free parameters, which are usually poorly determined and may be a major source of uncertainty in the determination of gas-production rates. Most authors are still using the Haser model to derive the production rates. In this work, we decided to use this model to compute the production rates in order to compare our results with others. Figure 1 shows the comparison of Vectorial and Haser models for a similar OH production rate (Q(OH) = 2.21 × 1027 molecules s−1 computed from a fit at 10 000 km from the nucleus when 41P was at 1.12 au from the Sun and at 0.17 au from Earth). The Vectorial model column density can be retrieved online3. In order to derive the OH column density profile from the Vectorial model website, we set different parameters. We used the same scale lengths and lifetimes for the Haser model given in Table 1. We set the velocities of the parent and daughter molecules at 1 km s−1 for a heliocentric distance of 1 au. The program internally adjusts the parent molecule velocity with the factor of 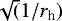 , while the model considered that the daughter molecule velocity is independent of the heliocentric distance and no scaling for distance is made.
, while the model considered that the daughter molecule velocity is independent of the heliocentric distance and no scaling for distance is made.
In order to estimate the dust production, we derived the Afρ parameter, a quantity introduced by A’Hearn et al. (1984), from the dust profiles using the narrow-band BC, GC, and RC filters and the broadband Rc filter. In the cometary coma, the brightness of the continuum is affected by the dependence on the solar phase angle of the scattering of sunlight by cometary grains. In all cases, there is a strong increase in the forward direction of scattering, and a much smaller peak at small backscattering angles. In practice these effects can reach up to a factor of three over a range of phase angles between 0° and 110°, and much more at higher phase angles (Schleicher et al. 1998). An early phase function for cometary dust was constructed by Divine (1981), which appears to provide a reasonable match to comet observations between phase angles of ~15° and 70°. But this phase function is too shallow at smaller phase angles (Ney & Merrill 1976; Hanner & Newburn 1989; Schleicher et al. 1998), and does not increase sufficiently fast at large phase angles (Marcus 2007). In this work, the A(θ)fρ values were corrected from the phase angle effect according to the phase function normalized at θ = 0° given by Schleicher (2010)4.
Scale lengths and life times of molecules at 1 au scaled by 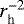 (A’Hearn et al. 1995).
(A’Hearn et al. 1995).
 |
Fig. 1 Comparison of the OH column density profile of 41P from the Vectorial and the Haser models for a production rate of 2.21 × 1027 molecules s−1 obtained on March 14, 2017. |
3 Narrow-band photometry
In this section, we present the narrow-band photometry with a description of the activity and composition evolution of 41P before and after perihelion and 45P after perihelion.
We adjust the Haser model (Haser 1957) on the observed radial profiles for the gas filter images. Since the comets presented in this work have been observed over a wide range of heliocentric and geocentric distances, we decided to make the adjustment at a physical distance around 10 000 km from the nucleus, to derive the gas production rates. In most cases, the signal-to-noise ratio (S/N) is still high at this cometocentric distance, and the influence of the seeing effect is limited to the first few pixels and the dust contamination is low. In the dust filter images, the S/N is very weak at large cometocentric distance. We then decided to measure the Afρ values at 5000 km from the nucleus.
OH, NH, CN, C2, and C3 production rates and A(θ = 0°)fρ parameter for comet 41P/Tuttle–Giacobini–Kresák.
3.1 Comet 41P/Tuttle–Giacobini–Kresak
The derived production rates for each gas species and A(θ)fρ values for the green, blue, and red continua are given in Table 2 with their errors. We started to detect CN, C2, and C3 species at the beginning of the second half of February, 2017 (rh = 1.27 au), when the OH and NH species were detected for the first time on March 11 and March 26, respectively. The gas production rates relatively increase towards the perihelion. We continued to monitor 41P until the perihelion when the comet was at 1.05 au from the Sun. The OH, NH, CN, C2 and C3 production rates did not vary much between March 26 and May 27, 2017. We also monitored 41P after perihelion, the CN and C2 were detected until July 20, when the comet was at 1.63 au from the Sun, and C3 was not detected after June 22 (rh = 1.39 au). The CN, C2, and C3 production rates start to decrease from May 27 until the end of monitoring. Hydroxyl (OH) was detected until May 24 (rh = 1.18 au) with a production rate of (1.57 ± 0.08) × 1027 and NH reached (1.91 ± 0.10) × 1025 molecules s−1 on April 27. Figure 2 shows the production rates for all gas species in logarithmic scale as a function of time to perihelion. The OH, CN, C3, and C2 production rates from TN are in agreement with the few measurements obtained with TS at the beginning of the monitoring.
In order to estimate the dust activity, we observed 41P with the BC, RC, and GC continuum filters in addition to the ones regularly performed with the broadband Rc filter. The values of the A(θ)fρ parameter corrected from the phase angle are shown in Fig. 3 in a logarithmic scale as a function of time from perihelion. The present paper focuses on the analysis of the activity and the gas composition. The analysis of the dust coma of 41P has been done in Pozuelos et al. (2018). These latter authors performed Monte Carlo simulations to characterise the dust environment as a function of the heliocentric distance using the model described in Moreno et al. (2012). The total amount of dust produced was roughly 7.5 × 108 kg, with a peak of activity of 110 kg s−1 a few days before perihelion. They concluded that 41P is a dust-poor comet compared to other JFCs.
Figure 4 presents the comparison of the water-production rates of 41P at different apparitions as a function of time to perihelion. The water-production rates, corresponding to the apparition in 2001 (black circles) and 2006 (red squares), were derived from the hydrogen Lyman-α emission observed with the SWAN instrument onboard the SOHO spacecraft. For the SWAN data, 1σ stochastic errors are shown; systematic uncertainties are at the 30% level (Combi et al. 2006, 2011). Bodewits et al. (2018) used recent Swift/UVOT observations of OH emission to determine the water-production rate in 2017 (green triangles). These values are in good agreement with our TRAPPIST water-production rates. Using our data, we computed vectorial-equivalent water-production rates (blue diamonds) from our Haser-model OH production rates using Q(H2O) = 1.361 ×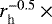 Q(OH) given in Cochran & Schleicher (1993). The water-production rate peaked around (183 ± 0.26) × 1027 molecules s−1 on December 21, 2000, when the comet was at 1.07 au from the Sun and (22.2 ± 0.67) × 1027 molecules s−1 on May 15, 2006, when 41P was at 1.10 au from the Sun (Combi 2017). As shown in Fig. 4, two outbursts have been detected at optical wavelengths as peaks 33 and 15 days before perihelion in 2001 (Kronk 2017; Combi 2017). However, no outburst was detected during the 2017 perihelion passage. From the data shown in Fig. 4, we conclude that there was a ~3.5 × decrease in water outgassing between 2001 and 2006, for two continuous orbits (~5 yr), and a ~5 × decrease between 2006 and 2017, an interval of two orbits. This implies a relatively consistent drop of about 30–40% from one apparition to the next. Generally, the distribution of active surface areas of comets correlate with the smaller nuclei (A’Hearn et al. 1995). As 41P has a small nucleus, Bodewits et al. (2018) claims that more than 50% of the surface of 41P could be active, while studies show that less than 3% of the surface of most comets is active (A’Hearn et al. 1995). We note that the water-production rates are coming from different techniques and observations at different wavelengths, which means the comparison of the results should be taken with caution.
Q(OH) given in Cochran & Schleicher (1993). The water-production rate peaked around (183 ± 0.26) × 1027 molecules s−1 on December 21, 2000, when the comet was at 1.07 au from the Sun and (22.2 ± 0.67) × 1027 molecules s−1 on May 15, 2006, when 41P was at 1.10 au from the Sun (Combi 2017). As shown in Fig. 4, two outbursts have been detected at optical wavelengths as peaks 33 and 15 days before perihelion in 2001 (Kronk 2017; Combi 2017). However, no outburst was detected during the 2017 perihelion passage. From the data shown in Fig. 4, we conclude that there was a ~3.5 × decrease in water outgassing between 2001 and 2006, for two continuous orbits (~5 yr), and a ~5 × decrease between 2006 and 2017, an interval of two orbits. This implies a relatively consistent drop of about 30–40% from one apparition to the next. Generally, the distribution of active surface areas of comets correlate with the smaller nuclei (A’Hearn et al. 1995). As 41P has a small nucleus, Bodewits et al. (2018) claims that more than 50% of the surface of 41P could be active, while studies show that less than 3% of the surface of most comets is active (A’Hearn et al. 1995). We note that the water-production rates are coming from different techniques and observations at different wavelengths, which means the comparison of the results should be taken with caution.
 |
Fig. 2 Production rates of comet 41P for each observed molecular species as a function of time to perihelion. The TN data are represented with filled symbols and TS data with open symbols. The values and their uncertainties are given in Table 2. |
 |
Fig. 3 The A(θ = 0°)fρ parameter of comet 41P for the narrow-band filters (BC, RC and GC) and for the broadband filter Rc as a function of time to perihelion. We normalized the A(θ)fρ values at 0° phase angle. The TN data are represented with filled symbols and TS data with open symbols. The values and their uncertainties are given in Table 2. |
3.2 Comet 45P/Honda–Mrkos–Pajdušáková
The mean OH, CN, C2, and C3 production rates that we obtain for 45P during our observations were (1.07 ± 0.46) × 1027, (1.77 ± 0.05) × 1024, (1.93 ± 0.06) × 1024, and (0.65 ± 0.04) × 1024 molecules s−1, respectively. While NH was not detected, the OH, CN, C2, and C3 production rates and Afρ in the broad- and narrow-band filters are given with their uncertainties in Table 3. The evolution of comet 45P gas and dust activity as functions of time to perihelion are summarised in Figs. 5 and 6, respectively. As shown in Fig. 5, the gas species production rates decrease after perihelion (from 0.97 to 1.62 au from the Sun). The lack of data for this comet prevents us from computing the production-rate slopes, but the gas-production rates still show a dependence on heliocentric distance. The A(θ)fρ parameter, corrected from the phase angle effect, shows a peak of 33 cm in the Rc filter around 50 days after perihelion. Subsequently, the A(0)fρ starts to decrease with heliocentric distance. 45P phase angle changes from 110° to 20° during the entire observing period. The TRAPPIST-North and -South results are again in agreement.
Comet 45P was observed by numerous observers at different wavelengths to detect the parent molecules (H2 O, NH3, HCN, and C2 H2). DiSanti et al. (2017) reported various molecule production rates of 45P on 6–8 January, 2017 (rh = 0.55 au, one week after perihelion), using the high-spectral-resolution cross-dispersed facility, iSHELL, at the NASA Infrared Telescope Facility in Maunakea. The authors obtained a mean value of the water-production rate of 1.5 × 1028 molecules s−1 noting a decrease during these two days. We have a mean water-production rate of 1.5 × 1027 molecules s−1. Possible reasons for this discrepancy could be the different size of the field of view and also the technique used to derive the water-production rate. Moreover, DiSanti et al. (2017) had observed 45P around the perihelion, while we started to observe this comet 40 days after perihelion. Using radar observations made on February 9, 2017, Lejoly & Howell (2017) detected a skirt of material around the nucleus of the comet, indicating that there is a large population of centimetre-sized grains being emitted from the comet.
Comet 45P has been observed in the past. During its passage in July 1990, it was observed with the Lowell Observatory when the comet was at 1.15 au from the Sun and 0.36 au from the Earth. The production rates obtained for five gas species were: Q(OH) = 6.16 × 1026, Q(NH) = 3.80 × 1024, Q(CN) = 8.12 × 1023, Q(C2) = 9.12 × 1022, Q(C3) = 1.38 × 1024 molecules s−1 and the Afρ parameter was 11 cm measured at 5000 km from the nucleus. At this time, the water-production rate was about 8 × 1026 molecules s−1 (Randall et al. 1992; Osip et al. 1992; A’Hearn et al. 1995). The comparison of these results with our mean production rate values of 45P in 2017 shows that OH and CN production rates increased by a factor 2 and C2 increased by 20, while the production rate of C3 decreased by 2. We conclude that 45P developed its activity between the passage in 1999 and that is 2017.
3.3 Production rates ratios and comparison to other comets
A’Hearn et al. (1995) presented a chemical classification for 85 comets observed between 1976 and 1992 using production rate ratios with respect to CN and OH. In order to compare 41P and 45P to this taxonomy, we computed those ratios for all the gas species. Our results show that 41P and 45P are “typical” comets of the JF. Typical comets are defined in A’Hearn et al. (1995) as those with log[Q(C2)/Q(CN)] ≥−0.18, which was updated by Schleicher (2006) to log[Q(C2)/Q(CN)] ≥−0.11. The mean value of this quantity during our monitoring of 41P and 45P is 0.06 ± 0.003 and 0.04 ± 0.003, respectively, in agreement with the mean value given in A’Hearn et al. (1995) and Schleicher (2008) for JFCs (see Table 4). Preliminary results from the Near-Infrared Spectrograph indicate that 41P has typical C2H2 and HCN abundances compared to other JFCs, while the C2H6 abundance is similar to that of nearly isotropic comets (NICs), but is enriched compared to other JFCs (McKay et al. 2018).
The logarithm of the production rate ratios with respect to CN and to OH as well as ratios of A(0)fρ-to-Q(OH) and A(0)fρ-to-Q(CN) for comet 41P are shown in Fig. 7. Generally, the ratios do not vary significantly on both sides of perihelion, but they vary significantly more with respect to OH than with respect to CN. The C2 -to-CN production rate ratio (Fig. 7d) stays nearly constant with perihelion distance.
Determining a mean value for the dust-to-gas ratio is problematic for several reasons, such as the dependence of Afρ on aperture size, heliocentric distance, and phase angle. In this work, we have computed the Afρ values in the coma at 5000 km from the nucleus and we corrected it for the phase angle effect at θ = 0°. The mean values for log[A(0)fρ/Q(CN)] and log[A(0)fρ/Q(OH)] are −23.00 ± 0.06 and −25.46 ± 0.03 cm s molecules−1, respectively, for comet 41P, and −22.88 ± 0.12 and −25.66 ± 0.11 for comet 45P. As shown in Fig. 7e and j, the evolution of the dust-to-gas ratios of 41P is symmetric on both sides of perihelion. The relatively low dust-to-gas ratios for 41P and 45P is consistent with the trend of an increasing dust-to-gas ratio as a function of the perihelion distance found by A’Hearn et al. (1995; see Fig. 4), which they assume to be associated with thermal processing of nuclei surfaces.
Figure 8 represents the logarithm of the ratio of the C2 to OH production rates against the logarithm of the ratio of CN to OH, using a mean value for 41P and 45P compared to JFCs and long-period comets observed with the TS telescope between 2010 and 2016 (Opitom 2016), and also compared to typical and depleted comets given in A’Hearn et al. (1995). Most comets observed with TRAPPIST, including 41P and 45P, are typical and lie on a diagonal trend, except for comet 168P/Hergenrother which is depleted in carbon chain species.
OH, CN, C2, and C3 production rates and the A(θ = 0°)fρ parameter for comet 45P/Honda–Mrkos–Pajdusakova.
 |
Fig. 4 Logarithm of the water-production rate for different apparitions of comet 41P in 2001, 2006 and 2017 as a function of time to perihelion. Combi (2017) derived the production rates from hydrogen Lyman-α emission observed by the SWAN instrument onboard SOHO in 2001 (black circles) and 2006 (red squares). Our water-production rates (blue diamonds) were derived from the OH production rates using the relationship given in Cochran & Schleicher (1993). The water-production rates given in Bodewits et al. (2018) are derived from the Swift/UVOT observations of OH emissions (green triangles) and are in good agreement with the TRAPPIST ones. |
 |
Fig. 5 Logarithm of the production rates of 45P for each observed molecular species as a function of time to perihelion. The TN data are represented with filled symbols and TS data with open symbols. The values and their uncertainties are given in Table 3. |
 |
Fig. 6 The A(θ = 0°)fρ parameter of comet 45P for the narrow-band filters (BC, RC, and GC) and for the broadband filter Rc as a function of time to perihelion. We normalized the A(θ)fρ values at 0° phase angle. The TN data are represented with filled symbols and TS data with open symbols. The values and their uncertainties are given in Table 3. |
 |
Fig. 7 Logarithm of the ratio of C2 to OH production rates as a function of the logarithm of the ratio of CN to OH for comets 41P (triangle right) and 45P (triangle left) compared to JFCs (filled circles) and long-period comets (open circles) observed with TS between 2010 and 2016 (Opitom 2016), and also with typical (filled squares) and depleted comets (open squares) given in A’Hearn et al. (1995). |
Mean of the logarithm of production rates and A(0)fρ ratios with respect to OH, and for C2 with respect to CN for 41P and 45P compared to the mean values presented in A’Hearn et al. (1995) and Schleicher (2008).
 |
Fig. 8 Logarithm of the production rates and A(θ = 0°)fρ ratios with respect to CN and to OH as a function of the logarithm of the heliocentric distance of comet 41P. Pre-perihelion values are represented with filled symbols and post-perihelion values with open symbols. The log(Afρ/Q) ratio is expressed in cm second per molecule. |
4 Coma morphology
In this section, we discuss the morphology of the coma of 41P, which showed an important activity on both sides of perihelion. Comet 45P does not show any interesting jet activity because it was far away from the Sun when we started to monitor it.
The coma is dominated by the overall brightness distribution, and many individual features are not easily recognisable. This makes analysing enhanced cometary images difficult, as important structural information is contained both near the coma centre and in the dimmer outer regions. The study of coma morphology can give us information about the rotation period, active areas, and homogeneity of the nucleus. This section is dedicated to the morphological features of gaseous species and broadband Rc continuum images, using a simple rotational filter which takes the difference between two oppositely rotated copies of the image. This technique requires an angle by which the image is rotated clockwise and counterclockwise prior to calculating the difference. We tested several rotation angles, and they always revealed the same features. Finally we adopted a 40° angle, which provided the highest contrast images. The technique presented here is very sensitive to the centring of the nucleus, which we can set as the centroid of the profile or put manually.
Figure 9 shows an example of CN, C3, C2, and Rc features on March 31, 2017. Even though it is slightly contaminated by the gas, we decided to use the broadband dust filter (Rc) to show the dust features in our data because the S/N is too small in the narrow-band dust filter images for such processing. These images were obtained one week before perihelion. Usually, we acquired one or two C2 and C3 images per night, while we acquired more than six images for CN. Over most of the nights we saw CN and C2 with sufficient S/N to detect variations of the jet positions in the coma caused by a variation of the viewing geometry. We started to detect the CN features at the beginning of March but we only saw one main jet, due to the low S/N of the images at that time. At the end of March, and as shown in Fig. 9, we were able to see a second jet more clearly with the relative intensity and position of the jets varying with rotation. This allowed us to measure the rotation period of 41P’s nucleus (see Sect. 4). This is more or less the same feature thatwe saw in April with an additional variation of jet position and brightness over the night. The C3 and C2 features are weaker than CN; they both display two short jets in opposite directions with different brightness compared to CN. These features are also weaker than the dust jet (frame Rc), and are not detected in every image during our observations. The OH and NH features are not detected in our data set, due to the lower S/N in these bands. The Rc image shows an enhancement of the coma in the dust tail direction.
41P rotation period
The changes of orientation and morphology of the features is not necessarily a direct representation of the rotation period of the nucleus. The coma morphology depends on the shape, activity, and rotational state of the nucleus of the comet, but can also be influenced by the orientation of the active regions on the nucleus, changing viewing geometry and seasonal changes in activity (Belton et al. 1991; Jewitt 1997; Davidsson 2001; Keller et al. 2015). However, observing repeating changes in the morphology of the coma is still one of the best ways to determine the rotation period of a comet nucleus from ground-based observations (Samarasinha et al. 2004; Samarasinha & Larson 2014).
We enhanced the CN narrow-band images of 41P using a simple rotational filter, as described in the previous section. Often, CN images are used to investigate the gas coma features because those images have a better S/N and are less contaminated by the underlying dust continuum. This technique has been used to measure the rotationperiod of several comet nuclei such as 1P/Halley (A’Hearn et al. 1986), C/2004 Q2 Machholz (Farnham et al. 2007), 8P/Tuttle (Waniak et al. 2009), and C/2012 F6 Lemmon which was observed with TS (Opitom et al. 2015a).
The first two series of CN images were obtained during the nights of March 3 and 7, 2017, but it is hard to distinguish the jets in the coma because of the faint signal.Following these, we have no further long series until March 31, when we took a series of 16 images with exposure time of 600 s spanning over 8 h. We enhanced the images using the method described above. Figure 10 shows an example of the CN coma features obtained. Two jets labelled J1 and J2 are clearly detected like partial spirals in a counterclockwise rotation. The jets are rotating, with a position angle difference of 90° between the first andthe last image of the series. Dividing the measured position angle difference by the time between the measurements, and considering that the jet is moving at the same rate throughout the entire rotation, we obtain a rotation period of about (30 ± 5) h. The last long series is on April 27. We collected 25 images in the CN filter over 5 h. Figure 11 shows two examples of CN-enhanced images for this date. Two jets are detected (J2 brighter than J1) moving slowly in a counterclockwise rotation. The change of the jets’ position angle is 40° over 5 h which gives a rotation period of (50 ± 10) h. In conclusion, with these two long series that we obtained during one month, we found a change in the rotation period of about 20 h with an average increase of 0.68 h per day.
Several authors reported on the rotation period of the nucleus of 41P. Farnham et al. (2017) reported a rotation period of 19.75–20.05 h during March 6–9 using images of CN coma features taken with the Large Monolithic Imager on Lowell Observatory’s 4.3 m Discovery Channel Telescope (DCT). Using the Lowell Observatory’s 31′′ telescope and the same method, Knight et al. (2017) reported a change of the rotation period from 24 to 27 h during the period of March 19–27. Using the aperture photometry technique, Bodewits et al. (2018) found that the rotation period was changing from 46 to 60 h, with an average increase of 0.40–0.67 h per day, during the period of May 7–9 using Swift/UVOT data (Gehrels et al. 2004). Schleicher et al. (2017) measured a rotation period of approximately 48 h on April 28. The rotation period of 41P therefore more than doubled between March and May 2017, increasing from 20 to 50 h. Our measurements are in agreement with these data. Figure 12 shows the evolution of the rotation period of 41P’s nucleus as a function of time to perihelion. Bodewits et al. (2018) extrapolated the rotation period of the comet in time to investigate the past and future behaviour assuming that the activity level and torques, as well as the water-production rates and orientation of spin axis did not change significantly in the past. The authors found that before 2006 the comet could have been rotating with a period of only about 5 h, which is near the fragmentation limit. In the future they assume that the rotation period could exceed 100 h. They hypothesise that the rapid rotation might be linked to the bright outburst that occurred during the perihelion passage in 2001. This is the fastest rate of change ever measured for a comet nucleus. Pozuelos et al. (2018) found a complex ejection pattern which started as full isotropic, switched to anisotropic about 1.21–1.11 au inbound (February 24–March 14, 2017), and then switched again to full isotropic around 1.3–1.45 au outbound. During the anisotropic ejection, they found that two strong active areas took over the dust emission, ejecting at least 90% of particles. The same authors related this result with the spin down found by Bodewits et al. (2018), in the sense that those active areas could act as brakes. All of this may suggest the nucleus rapidly changes its rotation period as a result of changes in cometary activity and the strong active areas.
Several JFCs have also shown variation of their rotation periods. The best example is 103P/Hartley 2, the target of NASA’s EPOXI mission, which has a nucleus of 0.57 km in diameter and a rotation period of 17 h (A’Hearn et al. 2011). This comet showed a variation of its rotation period of 2 h in the three months around perihelion (October 28, 2010) during its return in 2010 (A’Hearn et al. 2011; Knight & Schleicher 2011; Belton et al. 2013; Samarasinha & Mueller 2013). However, 103P had a peak water-production rate three times higher than 41P (Jehin et al. 2010; Knight & Schleicher 2011). In this context, we can also mention 9P/Tempel 1 (Prot = 41 h), whose rotation was shown to decrease by 0.2 h over a period of 50 days (A’Hearn et al. 1995; Manfroid et al. 2007; Belton et al. 2011; Samarasinha & Mueller 2013). The target of ESA’s Rosetta spacecraft, 67P (Prot = 12 h) shows a decrease of ~0.4 h over 10 smonths after its perihelion passage (Mottola et al. 2014; Keller et al. 2015). Non-periodic comets have also shown changes in their rotation such as C/2001 K5 (LINEAR; Drahus & Waniak 2006) and C/1990 K1 (Levy; Schleicher et al. 1991; Feldman et al. 1992). Many have shown a rotation period change, even though the amplitude in the case of 41P is rather unusual.
 |
Fig. 9 Gas and dust coma morphology of 41P on March 31, 2017. Each image is centred on the nucleus and enhanced by a simple rotational filter. The filter name is indicated at the top of each frame. All images are oriented with north down and east left with the direction of the Sun as indicated in the Rc frame. The field of view of each image is 5.8′ × 5.9′, which covers36 600 × 37 800 km. |
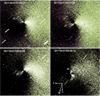 |
Fig. 10 CN coma morphology of 41P on March 31, 2017 (before perihelion). Each image is centred on the nucleus, and has been enhanced by a simple rotational filter. The date (in UT) is indicated at the top of each frame. In all images north is down and east to the left with the direction of the Sun indicated in the bottom right frame. The field of view of each image is 8.5′ × 9.8′, which covers53 120 × 26 520 km. |
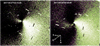 |
Fig. 11 CN coma morphology of 41P on April 27, 2017 (after perihelion). The images are enhanced by a simple rotational filter. The date (in UT) is indicated at the top of each frame. In all images north is down and east to the left with the direction of the Sun as indicated in the right frame. The field of view of each image is 8.4′ × 7.6′, which covers67 500 × 62 800 km. |
 |
Fig. 12 Rotation period evolution of comet 41P as a function of time to perihelion. The DCT value (black circle) is from Farnham et al. (2017). The Lowell values (green triangles) are from Knight et al. (2017). The triangle down value is from Schleicher et al. (2017). The Swift value (blue diamond) is from Bodewits et al. (2018). The error bar on the Swift observation indicates the range of possible solutions due to the uncertainty in the change of activity as a function of heliocentric distance. |
5 Summary
We have presented the results of the photometric monitoring and imaging of the JFCs, 41P, and 45P, over a five-month period with TRAPPIST-North telescope. Production rates of OH, NH, CN, C2, and C3 were computed as well as the A(θ)fρ parameter on both sides of perihelion for comet 41P and after perihelion for comet 45P. Both comets are dust-poor in comparison with other JFCs. They have a “typical” composition regarding their Q(C2)/Q(CN) and Q(C3)/Q(CN) ratios. We have shown that the activity of 41P is decreasing by about 30–40% from one apparition to the next. We analysed the coma features of 41P in CN, C2, and C3 filters as well as those of the dust continuum windows using a simple rotational filter. We detected variations of the coma morphology during long series of observations performed over individual nights, due to the rotation of the nucleus. This allowed us to determine the rotation period of 41P, which increased from (30 ± 5) h at the end of March to (50 ± 10) h at the endof April, when the comet was closer to the Sun. Our results confirm the strong braking of 41P rotation presented in the literature (Knight et al. 2017; Bodewits et al. 2018).
Acknowledgments
TRAPPIST-North is a project funded by the University of Liège, in collaboration with Cadi Ayyad University of Marrakech (Morocco). TRAPPIST-South is a project funded by the Belgian Fonds (National) de la Recherche Scientifique (F.R.S.-FNRS) under grant FRFC 2.5.594.09.F, with the participation of the Swiss National Science Foundation(FNS/SNSF). Y.M. acknowledges the support of Erasmus+ International Credit Mobility. E.J. is FNRS Senior Research Associates. F.J.P. is a Marie Curie Cofund fellow, cofunded by European Union and University of Liège. M.G. is FNRS Research Associate and J.M. is Honorary Research Director of the FNRS. We thank NASA, David Schleicher, and the Lowell Observatory for the loan of a set of HB comet filters.
References
- A’Hearn, M. F. 1982, in Comet Discoveries, Statistics, and Observational Selection, ed. L. L. Wilkening, IAU Colloq., 61, 433 [NASA ADS] [Google Scholar]
- A’Hearn, M. F., Schleicher, D. G., Millis, R. L., Feldman, P. D., & Thompson, D. T. 1984, AJ, 89, 579 [NASA ADS] [CrossRef] [Google Scholar]
- A’Hearn, M. F., Hoban, S., Birch, P. V., et al. 1986, Nature, 324, 649 [NASA ADS] [CrossRef] [Google Scholar]
- A’Hearn, M. F., Millis, R. C., Schleicher, D. O., Osip, D. J., & Birch, P. V. 1995, Icarus, 118, 223 [NASA ADS] [CrossRef] [Google Scholar]
- A’Hearn, M. F., Belton, M. J., Delamere, W. A., et al. 2011, Science, 332, 1396 [NASA ADS] [CrossRef] [Google Scholar]
- Belton, M. J., Julian, W. H., Anderson, A. J., & Mueller, B. E. 1991, Icarus, 93, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Belton, M. J. S., Meech, K. J., Chesley, S., et al. 2011, Icarus, 213, 345 [NASA ADS] [CrossRef] [Google Scholar]
- Belton, M. J. S., Thomas, P., Li, J.-Y., et al. 2013, Icarus, 222, 595 [NASA ADS] [CrossRef] [Google Scholar]
- Benkhaldoun, Z. 2018, Nat. Astron., 2, 352 [NASA ADS] [CrossRef] [Google Scholar]
- Bessell, M. S. 1990, PASP, 102, 1181 [NASA ADS] [CrossRef] [Google Scholar]
- Bodewits, D., Farnham, T. L., Kelley, M. S. P., & Knight, M. M. 2018, Nature, 553, 186 [NASA ADS] [CrossRef] [Google Scholar]
- Cochran, A. L., & Schleicher, D. G. 1993, Icarus, 105, 235 [Google Scholar]
- Combi, M. 2017, NASA Planetary Data System [Google Scholar]
- Combi, M. R., Makinen, J. T., Henry, N. J., Bertaux, J. L., & Quemerais, E. 2006, BASS, 38, 535 [Google Scholar]
- Combi, M. R., Bertaux, J.-L., Quémerais, E., Ferron, S., & Mäkinen, J. T. T. 2011, ApJ, 734, L6 [CrossRef] [Google Scholar]
- Davidsson, B. J. 2001, Icarus, 149, 375 [NASA ADS] [CrossRef] [Google Scholar]
- DiSanti, M. A., Bonev, B. P., Russo, N. D., et al. 2017, AJ, 154, 246 [NASA ADS] [CrossRef] [Google Scholar]
- Divine, N. 1981, in The Comet Halley Dust and Gas Environment, eds. B. Battrick, & E. Swallow, ESA Special Publication, 174 [Google Scholar]
- Drahus, M., & Waniak, W. 2006, Icarus, 185, 544 [NASA ADS] [CrossRef] [Google Scholar]
- Farnham, T. L., Schleicher, D. G., & A’Hearn, M. F. 2000, Icarus, 147, 180 [NASA ADS] [CrossRef] [Google Scholar]
- Farnham, T. L., Samarasinha, N. H., Mueller, B. E. A., & Knight, M. M. 2007, AJ, 133, 2001 [NASA ADS] [CrossRef] [Google Scholar]
- Farnham, T. L., Knight, M., Eisner, N., Schleicher, D., & Thirouin, A. 2017, Central Bureau Electronic Telegrams, 4375 [Google Scholar]
- Feldman, P. D., Budzien, S. A., Festou, M. C., A’Hearn, M. F., & Tozzi, G. P. 1992, Icarus, 95, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Fernández, Y., Kelley, M., Lamy, P., et al. 2013, Icarus, 226, 1138 [NASA ADS] [CrossRef] [Google Scholar]
- Festou, M. C. 1981a, A&A, 95, 69 [NASA ADS] [Google Scholar]
- Festou, M. C. 1981b, A&A, 96, 52 [NASA ADS] [Google Scholar]
- Gehrels, N., Chincarini, G., Giommi, P., et al. 2004, ApJ, 611, 1005 [NASA ADS] [CrossRef] [Google Scholar]
- Hanner, M. S., & Newburn, R. L. 1989, AJ, 97, 254 [NASA ADS] [CrossRef] [Google Scholar]
- Haser, L. 1957, Bull. Soc. Roy. Sci. Liége, 43, 740 [Google Scholar]
- Jehin, E., Manfroid, J., Hutsemekers, D., Gillon, M., & Magain, P. 2010, Central Bureau Electronic Telegrams, 2589 [Google Scholar]
- Jehin, E., Gillon, M., Queloz, D., et al. 2011, The Messenger, 145, 2 [NASA ADS] [Google Scholar]
- Jewitt, D. 1997, Earth Moon Planets, 79, 35 [Google Scholar]
- Keller, H., Mottola, S., Skorov, Y., & Jorda, L. 2015, A&A, 579, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Knight, M. M., & Schleicher, D. G. 2011, AJ, 141, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Knight, M., Eisner, N., Schleicher, D., & Thirouin, A. 2017, Central Bureau Electronic Telegrams, 4377 [Google Scholar]
- Kresak, L., & Kresakova, M. 1974, Bull. Astr. Inst. Czechosl., 25, 336 [NASA ADS] [Google Scholar]
- Kronk, G. W. 2017, Cometography (Cambridge: Cambridge University Press) [CrossRef] [Google Scholar]
- Lamy, P. L., Toth, I., A’Hearn, M. F., & Weaver, H. A. 1999, Icarus, 140, 424 [NASA ADS] [CrossRef] [Google Scholar]
- Lamy, P. L., Toth, I., Fernandez, Y. R., & Weaver, H. A. 2004, in Comets II, ed. M. C. Festou, H. U. Keller, & H. A. Weaver (Tucson, AZ: University of Arizona Press), 745, 223 [Google Scholar]
- Lejoly, M., & Howell, N. 2017, Central Bureau Electronic Telegrams, 4357 [Google Scholar]
- Lowry, S. C., Fitzsimmons, A., & Collander-Brown, S. 2003, A&A, 397, 329 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Manfroid, J., Hutsemékers, D., Jehin, E., et al. 2007, Icarus, 191, 348 [CrossRef] [Google Scholar]
- Marcus, J. N. 2007, Int. Comet Q., 29, 39 [Google Scholar]
- Marty, B., Altwegg, K., Balsiger, H., et al. 2017, Science, 356, 1069 [NASA ADS] [CrossRef] [Google Scholar]
- McKay, A., DiSanti, M., Cochran, A., et al. 2018, American Astronomical Society Meeting Abstracts, 231, 144 [Google Scholar]
- Meier, R., Wellnitz, D., Kim, S. J., & A’Hearn, M. F. 1998, Icarus, 136, 268 [NASA ADS] [CrossRef] [Google Scholar]
- Moreno, F., Pozuelos, F., Aceituno, F., et al. 2012, ApJ, 752, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Mottola, S., Lowry, S., Snodgrass, C., et al. 2014, A&A, 569, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ney, E. P., & Merrill, K. M. 1976, Science, 194, 1051 [NASA ADS] [CrossRef] [Google Scholar]
- Opitom, C. 2016, Ph.D. Thesis, Université de Liège, Liège, Belgium [Google Scholar]
- Opitom, C., Jehin, E., Manfroid, J., et al. 2015a, A&A, 574, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Opitom, C., Jehin, E., Manfroid, J., et al. 2015b, A&A, 584, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Opitom, C., Guilbert-Lepoutre, A., Jehin, E., et al. 2016, A&A, 589, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Osip, D. J., Schleicher, D. G., Millis, R. L., Hearn, M. F. A., & Birch, P. V. 1992, in Asteroids, Comets, Meteors 1991, ed. A. W. Harris & E. Bowell (Houston, TX: Lunar and Planetary Institute) [Google Scholar]
- Pozuelos, F. J., Jehin, E., Moulane, Y., et al. 2018, A&A, 615, A154 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Randall, C. E., Schleicher, D. G., Ballou, R. G., & Osip, D. J. 1992, BAAS, 24, 1002 [NASA ADS] [Google Scholar]
- Samarasinha, N. H., & Mueller, B. E. 2013, ApJ, 775, L10 [NASA ADS] [CrossRef] [Google Scholar]
- Samarasinha, N. H., & Larson, S. M. 2014, Icarus, 239, 168 [NASA ADS] [CrossRef] [Google Scholar]
- Samarasinha, N. H., Mueller, B. E., Belton, M. J., & Jorda, L. 2004, Comets II (Cambridge, UK: Cambridge University Press), 281 [Google Scholar]
- Schleicher, D. G. 2006, Icarus, 181, 442 [CrossRef] [Google Scholar]
- Schleicher, D. G. 2008, AJ, 136, 2204 [Google Scholar]
- Schleicher, D. G. 2010, AJ, 140, 973 [NASA ADS] [CrossRef] [Google Scholar]
- Schleicher, D. G., & A’Hearn, M. F. 1988, ApJ, 331, 1058 [Google Scholar]
- Schleicher, D. G., Millis, R. L., Osip, D. J., & Birch, P. V. 1991, Icarus, 94, 511 [NASA ADS] [CrossRef] [Google Scholar]
- Schleicher, D. G., Millis, R. L., & Birch, P. V. 1998, Icarus, 132, 397 [NASA ADS] [CrossRef] [Google Scholar]
- Schleicher, D. G., Eisner, N., Knight, M. M., & Thirouin, A. 2017, AAS/Div. Planet. Sci. Meet. Abstr., 49, 305 [Google Scholar]
- Swamy, K. S. K. 2010, Physics of Comets, 3rd edn. (Singapore: World Scientific) [CrossRef] [Google Scholar]
- Tancredi, G., Fernández, J. A., Rickman, H., & Licandro, J. 2000, A&AS, 146, 73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Waniak, W., Borisov, G., Drahus, M., et al. 2009, Earth Moon Planets, 105, 327 [NASA ADS] [CrossRef] [Google Scholar]
JPL small bodies data browser: https://ssd.jpl.nasa.gov/sbdb.cgi#top
Comet fluorescence efficiency: http://asteroid.lowell.edu/comet/gfactor.html
Vectorial model: http://www.boulder.swri.edu/wvm-2011/
Phase function for comets: http://asteroid.lowell.edu/comet/dustphase.html
All Tables
Scale lengths and life times of molecules at 1 au scaled by 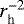 (A’Hearn et al. 1995).
(A’Hearn et al. 1995).
OH, NH, CN, C2, and C3 production rates and A(θ = 0°)fρ parameter for comet 41P/Tuttle–Giacobini–Kresák.
OH, CN, C2, and C3 production rates and the A(θ = 0°)fρ parameter for comet 45P/Honda–Mrkos–Pajdusakova.
Mean of the logarithm of production rates and A(0)fρ ratios with respect to OH, and for C2 with respect to CN for 41P and 45P compared to the mean values presented in A’Hearn et al. (1995) and Schleicher (2008).
All Figures
 |
Fig. 1 Comparison of the OH column density profile of 41P from the Vectorial and the Haser models for a production rate of 2.21 × 1027 molecules s−1 obtained on March 14, 2017. |
| In the text | |
 |
Fig. 2 Production rates of comet 41P for each observed molecular species as a function of time to perihelion. The TN data are represented with filled symbols and TS data with open symbols. The values and their uncertainties are given in Table 2. |
| In the text | |
 |
Fig. 3 The A(θ = 0°)fρ parameter of comet 41P for the narrow-band filters (BC, RC and GC) and for the broadband filter Rc as a function of time to perihelion. We normalized the A(θ)fρ values at 0° phase angle. The TN data are represented with filled symbols and TS data with open symbols. The values and their uncertainties are given in Table 2. |
| In the text | |
 |
Fig. 4 Logarithm of the water-production rate for different apparitions of comet 41P in 2001, 2006 and 2017 as a function of time to perihelion. Combi (2017) derived the production rates from hydrogen Lyman-α emission observed by the SWAN instrument onboard SOHO in 2001 (black circles) and 2006 (red squares). Our water-production rates (blue diamonds) were derived from the OH production rates using the relationship given in Cochran & Schleicher (1993). The water-production rates given in Bodewits et al. (2018) are derived from the Swift/UVOT observations of OH emissions (green triangles) and are in good agreement with the TRAPPIST ones. |
| In the text | |
 |
Fig. 5 Logarithm of the production rates of 45P for each observed molecular species as a function of time to perihelion. The TN data are represented with filled symbols and TS data with open symbols. The values and their uncertainties are given in Table 3. |
| In the text | |
 |
Fig. 6 The A(θ = 0°)fρ parameter of comet 45P for the narrow-band filters (BC, RC, and GC) and for the broadband filter Rc as a function of time to perihelion. We normalized the A(θ)fρ values at 0° phase angle. The TN data are represented with filled symbols and TS data with open symbols. The values and their uncertainties are given in Table 3. |
| In the text | |
 |
Fig. 7 Logarithm of the ratio of C2 to OH production rates as a function of the logarithm of the ratio of CN to OH for comets 41P (triangle right) and 45P (triangle left) compared to JFCs (filled circles) and long-period comets (open circles) observed with TS between 2010 and 2016 (Opitom 2016), and also with typical (filled squares) and depleted comets (open squares) given in A’Hearn et al. (1995). |
| In the text | |
 |
Fig. 8 Logarithm of the production rates and A(θ = 0°)fρ ratios with respect to CN and to OH as a function of the logarithm of the heliocentric distance of comet 41P. Pre-perihelion values are represented with filled symbols and post-perihelion values with open symbols. The log(Afρ/Q) ratio is expressed in cm second per molecule. |
| In the text | |
 |
Fig. 9 Gas and dust coma morphology of 41P on March 31, 2017. Each image is centred on the nucleus and enhanced by a simple rotational filter. The filter name is indicated at the top of each frame. All images are oriented with north down and east left with the direction of the Sun as indicated in the Rc frame. The field of view of each image is 5.8′ × 5.9′, which covers36 600 × 37 800 km. |
| In the text | |
 |
Fig. 10 CN coma morphology of 41P on March 31, 2017 (before perihelion). Each image is centred on the nucleus, and has been enhanced by a simple rotational filter. The date (in UT) is indicated at the top of each frame. In all images north is down and east to the left with the direction of the Sun indicated in the bottom right frame. The field of view of each image is 8.5′ × 9.8′, which covers53 120 × 26 520 km. |
| In the text | |
 |
Fig. 11 CN coma morphology of 41P on April 27, 2017 (after perihelion). The images are enhanced by a simple rotational filter. The date (in UT) is indicated at the top of each frame. In all images north is down and east to the left with the direction of the Sun as indicated in the right frame. The field of view of each image is 8.4′ × 7.6′, which covers67 500 × 62 800 km. |
| In the text | |
 |
Fig. 12 Rotation period evolution of comet 41P as a function of time to perihelion. The DCT value (black circle) is from Farnham et al. (2017). The Lowell values (green triangles) are from Knight et al. (2017). The triangle down value is from Schleicher et al. (2017). The Swift value (blue diamond) is from Bodewits et al. (2018). The error bar on the Swift observation indicates the range of possible solutions due to the uncertainty in the change of activity as a function of heliocentric distance. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


