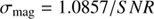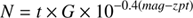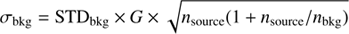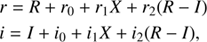| Issue |
A&A
Volume 619, November 2018
|
|
|---|---|---|
| Article Number | A141 | |
| Number of page(s) | 14 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/201833499 | |
| Published online | 16 November 2018 | |
NELIOTA: The wide-field, high-cadence, lunar monitoring system at the prime focus of the Kryoneri telescope
1
Institute for Astronomy, Astrophysics, Space Applications & Remote Sensing, National Observatory of Athens, P. Penteli, 15236
Athens, Greece
e-mail: xilouris@noa.gr
2
Department of Physics, University of Crete, 71003
Heraklion, Greece
3
DFM Engineering, Inc., 1035 Delaware Avenue, Longmont, CO, 80501
USA
4
Scientific Support Office, Directorate of Science, European Space Research and Technology Centre (ESA/ESTEC), 2201 AZ
Noordwijk, The Netherlands
5
Chair of Astronautics, Technical University of Munich, 85748
Garching, Germany
6
European Space Astronomy Centre (ESA/ESAC), Camino bajo del Castillo, s/n, Urbanizacion Villafranca del Castillo, Villanueva de la Cañada, 28692
Madrid, Spain
7
Department of Physics, Aristotle University of Thessaloniki, 54124
Thessaloniki, Greece
8
Section of Astrophysics, Astronomy and Mechanics, Department of Physics, University of Athens, Zografos, 15783
Athens, Greece
Received:
25
May
2018
Accepted:
31
August
2018
We present the technical specifications and first results of the ESA-funded, lunar monitoring project “NELIOTA” (NEO Lunar Impacts and Optical TrAnsients) at the National Observatory of Athens, which aims to determine the size-frequency distribution of small near-Earth objects (NEOs) via detection of impact flashes on the surface of the Moon. For the purposes of this project a twin camera instrument was specially designed and installed at the 1.2 m Kryoneri telescope utilizing the fast-frame capabilities of scientific Complementary Metal-Oxide Semiconductor detectors (sCMOS). The system provides a wide field-of-view (17.0′ × 14.4′) and simultaneous observations in two photometric bands (R and I), reaching limiting magnitudes of 18.7 mag in 10 s in both bands at a 2.5 signal-to-noise ratio (S/N) level. This makes it a unique instrument that can be used for the detection of NEO impacts on the Moon, as well as for any astronomy projects that demand high-cadence multicolor observations. The wide field-of-view ensures that a large portion of the Moon is observed, while the simultaneous, high-cadence, monitoring in two photometric bands makes possible the determination of the temperatures of the impacts on the Moon’s surface and the validation of the impact flashes from a single site. Considering the varying background level on the Moon’s surface we demonstrate that the NELIOTA system can detect NEO impact flashes at a 2.5 S/N level of ∼12.4 mag in the I-band and R-band for observations made at low lunar phases (∼0.1). We report 31 NEO impact flashes detected during the first year of the NELIOTA campaign. The faintest flash was at 11.24 mag in the R-band (about two magnitudes fainter than ever observed before) at lunar phase 0.32. Our observations suggest a detection rate of 1.96 × 10−7 events km−2 h−1.
Key words: instrumentation: detectors / techniques: miscellaneous / telescopes / Moon / surveys
© ESO 2018
1. Introduction
Lunar monitoring provides a promising method for determining the size-frequency distribution (SFD; Ivanov et al. 2002; Werner et al. 2002; Harris & D’Abramo 2015) of small near-Earth objects (NEOs) via the detection of NEO impact flashes on the Moon (see Bouley et al. 2012; Suggs et al. 2014, and references therein). Determining the SFD for objects in the decimeter to meter range is important for evaluating the danger of small NEOs impacting Earth, in light of the recent Chelyabinsk event (Brown et al. 2013), as well as the risk to artificial satellites and future man-made stations on the Moon. The Lunar Reconnaissance Orbiter (LRO) provides an indirect measurement of the SFD, by determining the cratering rate on the Moon via temporal imaging (Speyerer et al. 2016). So far, two new craters have been associated with observed impact flashes (Suggs et al. 2014; Robinson et al. 2015; Madiedo et al. 2014, 2018), demonstrating the potential of the synergy between lunar monitoring from the ground and space.
The estimation of the NEO size from lunar monitoring observations depends on the assumed value of the luminous efficiency ηλ, which is defined as the ratio of the measured luminous energy emitted at a particular wavelength λ to the total kinetic energy of the meteoroid. It therefore implies the knowledge of the impactor velocity, which cannot be accurately known for sporadic meteoroids. The luminous efficiency is best constrained for meteoroids originating from specific, well-studied, meteor showers (Ortiz et al. 2000). Bellot Rubio et al. (2000) obtain values of η ∼ 2 × 10−3 from lunar Leonids, while Moser et al. (2011) report values between 1.2 × 10−3 and 1.6 × 10−3 from lunar impacts involving Geminid, Lyrid, and Taurid meteoroids. Results of numerical simulations (Nemtchinov et al. 1998) predict η to range from a lower limit of 10−6 − 10−5 to an upper limit of 10−3, whereas impact simulations modeling the high velocity of the Leonids yield values of η on the order of 10−3 to 2 × 10−2 (Artem’eva et al. 2001). In any case, it is evident that lunar impact observations during meteor showers are valuable for constraining the value of η. Suggs et al. (2014) report estimated sizes of their observed impactors – originating from non-sporadic meteoroids – to be in the order of centimeters.
Ground-based lunar monitoring typically employs modest-sized aperture (∼30 cm) telescopes, which survey on the order of ∼106 km2 of the lunar surface at a time. The advantage this method offers over monitoring meteors in the Earth’s atmosphere using all-sky cameras, is that the monitored surface area is larger by two orders of magnitude. Several groups have therefore undertaken lunar monitoring surveys for NEO flashes (e.g., Madiedo et al. 2014; Ortiz et al. 2015; Rembold & Ryan 2015; Ait Moulay Larbi 2015). Ground-based surveys routinely use two or more telescopes often located at different sites in order to distinguish noise, seeing variations, cosmic rays, and satellite glints from real impact events. A lunar impact event is confirmed when a simultaneous detection has been made independently by two telescopes.
The “NEO Lunar Impacts and Optical TrAnsients” (NELIOTA) Project1 is an activity launched by ESA at the National Observatory of Athens (NOA) in 2015. It aims to contribute to the SFD of small NEOs, by developing a system that will perform a 22-month lunar monitoring campaign. NELIOTA brings three innovative aspects to the field of lunar monitoring: (1) a single telescope with a twin camera system, which detects and confirms events, (2) the twin cameras simultaneously monitor the Moon in two photometric bands, allowing for a temperature determination of each flash and the evolution of the flash, in case of flashes detected on multiple-frames (Bonanos et al. 2018), and (3) a large aperture telescope, which, in principle, can detect fainter impact flashes than the modest-sized aperture telescopes typically used. The limitation to the faintness of observed lunar impacts arises from the variable brightness of the lunar background (i.e., earthshine; Goode et al. 2001), in combination with the wavelength observed and the frame rate of the observations.
The selection of telescope and cameras were made to satisfy the main project requirements: (1) to monitor the Moon at ≥20 frames per second, (2) detect lunar impacts down to 12th magnitude, (3) have the ability to distinguish false positives (e.g., cosmic rays, foreground glints) from real flashes, and (4) to guarantee availability of the telescope for continuous usage that is better than 95%.
To address the specific needs of the NELIOTA project the 1.2 m Kryoneri telescope2 of NOA was upgraded in 2016, commissioning a prime focus, high-speed, twin-camera Lunar imager. The project has deployed a hardware system for recording and processing images. We have also developed a software system, which controls both the telescope and the cameras, processes the images and automatically detects candidate NEO lunar impact flashes. The impact events are verified, characterized, and made available to the scientific community and the general public via the NELIOTA website3 within 24 h of discovery. NELIOTA completed its commissioning phase in early 2017 and began a 22 month observing campaign in February 2017 in search of NEO impact flashes on the Moon. The 1.2 m Kryoneri telescope is capable of detecting flashes that are much fainter than all current, smaller-aperture, lunar monitoring telescopes. NELIOTA is therefore expected to characterize the size-frequency distribution of NEOs weighting as little as a few grams.
Bonanos et al. (2018) present the first scientific results of the project. Specifically, it is the first refereed publication of temperature measurements of impact flashes although observations allowing for such measurements had already been obtained (Madiedo et al. 2018). This paper presents a detailed description of the NELIOTA system and its components. Section 2 presents the upgraded 1.2 m Kryoneri telescope and its new optical design, while the Lunar imager camera system is detailed in Sect. 3. The NELIOTA system is presented in Sect. 4, while a brief description of the system’s software is given in Sect. 5. The instrument’s performance is evaluated in Sect. 6 with the results of the first year of the NELIOTA campaign presented in Sect. 7. Finally, a summary of the NELIOTA system and its first results are given in Sect. 8.
2. The 1.2 m Kryoneri telescope
The 1.2 m Kryoneri telescope was selected (after a trade-off analysis) as the optimal facility of NOA for the NELIOTA project. It was built by Grubb-Parsons and commissioned in 1975. The telescope is situated at Kryoneri Observatory (37° 58′ 19″ north, 22° 37′ 07″ east), in the district of Corinth in the northern Peloponnese, Greece, at the top of mount Kyllini, at an altitude of 930 m, close to Kryoneri village.
During approximately its first 40 years of operation, the telescope’s optical system consisted of a paraboloidal primary mirror of 1.2 m diameter and f/3 focal ratio and a hyperboloidal secondary mirror (31 cm). Both mirrors are made of Zerodur. This configuration produced a final focal ratio of f/13 at Cassegrain focus. The main scientific instrument in the last years has been a 2.5′ × 2.5′ charge-coupled device (CCD) camera Apogee Ap47p with a set of UBVRI filters.
2.1. Telescope retrofit
The NELIOTA science objectives imposed strict requirements on the optical design in order to provide: (i) the capacity to image simultaneously in two bands, (ii) a large FOV (∼20′) and (iii) seeing-limited image quality (with ∼1.5″ being a typical site seeing at Kryoneri Observatory (typical dome seeing ∼2.5″), yielding a scale of ∼0.4″ pixel−1).
In 2016, the telescope underwent an extensive upgrade by DFM Engineering Inc.4, within the NELIOTA project. The electro-mechanical upgrade included replacement of the telescope servo-motors and associated hardware (including new encoder systems), and deployment of a new system for dome opening and rotation as well as motorized primary mirror doors. A computerized telescope control system (TCS), developed by DFM, replaced the legacy console and allowed moving the observation control out of the telescope housing area. A new, GPS-based time server (Meinberg, LanTime M200/GPS) has been installed and is used by the TCS and other systems in the Observatory.
Furthermore, and according to the requirement for lunar observations, the optics of the telescope were modified to operate with instruments at the prime focus, bringing the telescope back to its primary mirror f/3 focal ratio and providing an unvignetted field-of-view (FOV) of ∼1.4°. A twin imaging system, the Kryoneri Prime Focus Instrument (KPFI), designed and developed by DFM Engineering Inc., is now in use, sampling 17.0′ × 14.4′ of the total corrected FOV at the prime focus of the telescope, providing simultaneous high-cadence observations in two bands. With such a FOV, a significant fraction of the non-sunlit part of the Moon, the only “usuable”, for our purposes, can be monitored to detect faint flashes coming from NEO impacts. A direct imaging optical configuration, using a separate CCD detector, was also added to the design to allow use of the full FOV. This was made possible through a computer controlled camera slider plate mechanism allowing for two operating modes, either using the twin imaging system (the “lunar imager” hereafter) or the direct imaging configuration (the “direct imager” hereafter).
2.2. The new Kryoneri prime focus instrument (KPFI)
Several optical elements were needed to overcome the challenge of placing an instrument at the prime focus of the 1.2 m Kryoneri telescope. The existing parabolic primary mirror (f/3) of the telescope was used along with a set of field corrector lenses in order to focus the beam in the prime focus. In total, three corrector lenses were used (see layout in Fig. 1 and characteristics in Table 1). The first and second field corrector elements (labeled as field corrector lens #1 and #2 in Fig. 1) are common for the two imaging modes. This configuration produces a f/3.1 focal ratio for the direct imager providing a maximum usable FOV of ∼1.4°. A third corrector lens (labeled as field corrector lens #3 in Fig. 1), followed by a dichroic beam splitter were placed in the optical path of the Lunar imager producing a focal ratio of f/2.8 in both channels. In front of each detector a lens pair is placed in order to provide the necessary focal reduction and the same effective focal length in each channel. A set of Johnson-Cousins R- and I-band filters is used so that calibrated photometric measurements can be made. The choice of this set of filters also assures direct comparison with other NEO studies already conducted (e.g., Suggs et al. 2014). Figure 2 presents the filter response functions and the dichroic beam splitter transmission curves.
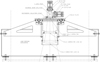 |
Fig. 1. Section view of the Kryoneri Prime Focus Instrument (KPFI) optical layout. The position of the field corrector lenses #1, #2, and #3, the dichroic beam splitter, as well as the lens pair elements in front of the Lunar imaging detectors and the R- and I-band filters are shown. The focus plate and the instrument selector stage are also indicated (Credit: DFM Engineering Inc.). |
Basic characteristics of the optical elements.
 |
Fig. 2. KPFI filters (red solid line for the R-band and green solid line for the I-band) and dichroic beam splitter transmission curves (dashed and dashed-dotted lines) combined with the QE response of the Lunar imaging detectors (blue solid line). Filter curves reflect the Johnson R- and I-band. The dichroic is centered at 730 nm with a > 90% throughput. |
Field corrector lenses #1 and #2 were placed inside a cylindrical baffle in order to reduce any scattered light. The cylinder is topped with a structural plate that attaches to the spyder vanes. The focus stage (allowing for a focus travel of 13.3 mm) is situated above the structural plate, and above the focus stage is the camera selector stage. The camera selector stage is motorized and remotely controlled, facilitating selection between the two imaging modes.
The dichroic beam splitter was positioned 95.25 mm from the Lunar imaging detectors (see Fig. 1). The specifications of the dichroic were constrained by the beam size and wavelength distribution. The dichroic element consists of two 75 mm prisms. Prism diagonals were coated to make a dichroic beam splitter that reflects 730 nm and shorter light (R-band) and allows light from 730 nm and longer wavelengths to pass through (I-band). The prisms are aligned to within 3′. Appropriate anti-reflective coatings were applied to the faces of the prisms. To avoid vignetting, we specified a minimum clear aperture of 100.0 × 142.0 ± 0.5 mm. The reflected beam has a range of 530 − 730 nm with a throughput of > 90%, and the transmitted beam has a range of 730 − 950 nm, with an identical throughput to its counterpart (see Fig. 2).
3. Lunar Imager camera system
Systems designed, so far, for monitoring lunar impact events mostly use black-and-white CCD video cameras. These are rather small size detectors (about 700 × 500 pixels) operating at 25–30 frames per second rate producing interlaced eight-bit frames. In this way, the effective rate is doubled, but a half frame (including either the odd or the even rows) is recorded after each exposure. For the NELIOTA project large size scientific Complementary Metal-Oxide Semiconductors (sCMOS) detectors are used.
The twin imaging system for NELIOTA includes a pair of identical detectors (Zyla 5.5 sCMOS) providing simultaneous observations in two photometric bands. These detectors were selected since they satisfy the project requirements for a fast-frame rate, high sensitivity and resolution, and a light and compact design (as they were in the prime focus, they had to be small enough in size in order not to cause vignetting of light from the source). To our knowledge, this makes NELIOTA the first astronomical system to use sCMOS detectors at a fast-frame rate. The active chip is 22 mm in diagonal with 2560 × 2160 square pixels (5.5 Megapixels), each 6.48 μm in size. With the NELIOTA setup (see Table 2) these cameras provide images at a rate of 30 frames per second, offering interframe gaps as small as a sub-microsecond. Their quantum efficiency is 60−50% in the R-band and 30−20% in the I-band. Andor’s Zyla 5.5 sCMOS offers a high-accuracy hardware-generated time-stamp on each frame, essential for providing high precision time measurements of the detected lunar impact events. For NELIOTA observations a 2×2 binning configuration and a 30 frames per second rate has been chosen to optimize the transfer rate of the obtained data. This configuration provides a pixel size of 0.8 arcsec pixel−1, well under the typical seeing measured on site, a FOV of 17.0′ × 14.4′ (see Fig. 3), and also well sampled frames in the time domain.
Specifications of the Andor Zyla 5.5 sCMOS camera for the NELIOTA project with a 2 × 2 binning configuration.
 |
Fig. 3. I-band image of the Moon observed with the NELIOTA system illustrating the available FOV, which is 17.0′ × 14.4′. |
The sCMOS sensor has a highly parallel read-out architecture. Each of the 2560 columns possess a separate amplifier and analog to digital converter, at both the top and bottom of the column. While all columns are read out in parallel, the read-out direction of each column is split in the center into the signal from the top and bottom halves. There are two different pixel read-out rates, slow read at 200 MHz (100 MHz × 2 sensor halves) and fast read at 560 MHz (280 MHz × 2 sensor halves), at either 12-bit or 16-bit mode, each with three different Gain settings and two different read-out modes (Global and Rolling shutter). The mode selected for the NELIOTA project is the fast read-out rate of 2 × 280 MHz, using the Gain settings of Low noise & High well capacity (16-bit) and the Global shutter. The latter offers the capability of all pixels being exposed simultaneously and allows for easier synchronization of the two cameras. The specifications of the cameras are summarized in Table 2. An extensive evaluation of sCMOS cameras for astronomical purposes can be found in Qiu et al. (2013).
4. NELIOTA system
The NELIOTA system is able to plan and ensure acquisition of the necessary data (Moon observations, calibration stars, flat-field, and dark frames), to manage the data recording to high capacity storage systems, to process the stored datasets and, finally, to detect possible impact events. The system organizes and stores the detected events in the archive and, finally, provides useful information about the events on the dedicated NELIOTA web-based interface1.
The NELIOTA system is organized as a sequence of four functional domains, namely, “observation”, “detection”, “archiving”, “information”, each of them controlling particular subsystems and assuring that the necessary information is shared among them (see Fig. 4). The observation domain controls the external hardware (telescope, cameras, GPS, and meteorological station) and monitors their status, ensuring that the desired observing plan is executed and that the raw (uncalibrated) frames and metadata are stored in real time. The detection domain provides post-observation data processing of the raw frames and applications of the impact detection algorithm (see Sect. 5.2). As a result of this process, candidate impact flashes are automatically detected and calibrated. They are then automatically forwarded to and treated within the archiving domain, where they are stored in a database-driven archive, and further evaluation and validation by expert scientists is performed. Finally, the information domain ensures web-based publishing of all the relevant information about the validated impact events and provides the general public with access to the NELIOTA results. In addition to this, registered users have indirect, read-only, access (downloads) to the detected event files through the archiving system service, allowing for independent analysis of the datasets. In particular, the registered user can download a data cube (in FITS format) of the detected event accompanied by the seven frames of the observation before the beginning of the event and after the end of the event so that a direct comparison of the local background can be made. For each observing run the detected events (if any) are published in the NELIOTA database3 within 24 h from the beginning of the observation.
 |
Fig. 4. NELIOTA system architecture and communication block diagram. The four software modules (observation, detection, archiving and information), the basic hardware telescope (TEL), camera system (CAM), time server (GPS), meteorological station (MET), high-performance storage (ODSTO), archiving storage (ARCSTO) and their interfaces (IF), as well as the human-machine-interfaces (HMI) are shown. |
4.1. Design and implementation
Each domain includes a top-level software component which controls particular hardware subsystems through a dedicated machine-to-machine interface and/or processes the data flow as necessary. These operations are controlled and monitored through a graphical user interface (GUI). Particular technologies have been used for the software development and implementation of the processing algorithms. With the exception of the information module, all others are developed in Java 8 SDK5 platform with its widget toolkit JFC/Swing applied for creating the GUIs. The Eclipse6 integrated development environment (IDE) has been used to write, to test and to package the three Java-based modules as JAR-executables.
The observation component is developed almost exclusively in Java, with a small interface in C++ to control, through a TCP socket, the two sCMOS cameras utilizing the supplier’s library (Andor-SDK3). The telescope is controlled through a TCP/IP link to the Telescope Control System (DFM’s WinTCS), exploiting the system’s remote control commands. The GPS (ntp-service) and the weather station services are passively accessed through corresponding NELIOTA system interfaces. The GUI utilizes two 4K ultra-HD monitors, one used for the operations control and for the monitoring of the status of the NELIOTA system, and the other for real-time display of the acquired frames. The observation system software is packaged in a executable JAR file.
The detection system is fully developed in Java and implements the algorithm for automated detection of the candidate impact events (see Sect. 5.2), their characterization and location on the Moon as well as the re-formatting of the raw frames into FITS format. An interface based on a FTP-client then transfers the detected event files to the remote archiving system.
The archiving system (also written in Java) includes an interface to the FTP-server that allows the data of the candidate impact events to be transfered to the data-base driven archive (Microsoft SQL Server). Its GUI provides the appropriate tools so that the expert scientist can visually inspect the data and validate the detected events. Furthermore, the archiving system utilizes a Windows Service and a Web Service for interfacing with the information domain. Through this interface the bulk of information of the new events are being transfered in a proper format, ready to be published on the web. The archive also, indirectly services user-requests to the information system for events, supplying the latter with properly packaged event records for further downloading. The executable JAR is activated as a non-stop service.
The information system’s top-level component is a website which implements its functionality as an ASP.net7 web application based on the model-view controller (MVC) architectural pattern. Most components are written in C#. The application registers itself on a Microsoft IIS server to listen for public user requests to provide html-pages and to service downloads. It is the only domain to which public users have limited access. The system implements a Windows service to manage downloading requests and a Web service to obtain the necessary content from the archiving system.
4.2. NELIOTA system deployment
The functional requirements set above for the NELIOTA system (Sect. 4) impose special characteristics to the hardware in order (1) to assure synchronized operation of the telescope and the two cameras, (2) to achieve high performance storage capabilities in terms of speed, capacity, security and hardware-failure safe operations, (3) for storage virtualization, and (4) for high-performance data processing resources. For practical reasons that have to do with the location of Kryoneri Observatory, the NELIOTA system had to be split into two subsystems in order to be most efficient. One of the subsystems is physically present at Kryoneri Observatory and the other is hosted at the computer center of IAASARS/NOA located in the northern suburbs of Athens, with the two of them connected through a private 11 Gbps RF-link. The observation and detection systems are deployed at the Kryoneri site on a cluster of two nodes, both using a common external high-performance storage array of a total of 38.4 TB through a dedicated switch (Table 3). The storage subsystem is linked through 8 × 1 Gb copper connections to the switch, while the two servers are connected to this switch by their optical SFP ports. These connections form a dedicated ring, in other words, an isolated high-speed iSCSI network for data transfer between the servers and the storage.
Specifications of the NELIOTA hardware systems at the Kryoneri site.
A second ring is implemented as a typical communication network for device management, routing configuration and remote access to devices for healthy operation monitoring. The main service provided within this ring is the control of the telescope as well as the dome of the building housing the telescope via the dedicated telescope control system (TCS, see Sect. 2.1) and through a dedicated TCP/IP network. The two cameras are connected to the observation server via optical links exploiting in full the USB 3.0 capability of each camera (see Sect. 3). The server passively accesses the remote meteorological system gathering environmental information. Both servers, like the TCS, are time-synchronized through the ntp-protocol by the local, GPS-based, server (Sect. 2.1). Both the observations and detection systems are mirrored on the two nodes, so in the case of a failure, only the reconnection of the camera USB links from one node to the other is needed for resuming the observation. The NELIOTA physical data system at Kryoneri is presented in Fig. 5.
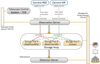 |
Fig. 5. Configuration of the NELIOTA physical data system at the Kryoneri site. |
The NELIOTA archiving and information systems are deployed in the IAASARS/NOA node on two virtual servers. The two servers are almost identical apart from the size of the dedicated memory and storage (Table 4). The hardware of the server system has been implemented on the Virtual Machines Cluster of the Network Information Center (NIC) of the National Observatory of Athens.
Specifications of the NELIOTA virtual server hardware systems.
4.3. Data acquisition
The built system configuration achieves a throughput of 5 Gbps/camera (camera to storage array). The two controllers of the storage array have been programed to operate in parallel and independently manipulate the two cameras, routing the related data streams to the storage array (red and green solid lines in Fig. 5). Following this concept the storage array is divided into two parts (storage pools “A” and “B” organized in RAID-5 parity) and each controller directs the related stream to a separate set of physical hard disks. In addition, each controller operates as a backup of the other one ensuring the maintenance of operation in cases of hardware failure (dashed lines in Fig. 5). On the other hand, a storage pool “C” has been created with RAID-1 parity in order to secure the data with the candidate events, produced by the detection system.
Based on the observation setup with the two cameras each acquiring 30 frames per second with a 2 × 2 binning, the produced data rate is almost 1.4 Gbps and hence, the required storage capacity is about 612 GB h−1. It has been estimated that no more than 2.5–3.0 TB storage for raw data is required per one observing cycle of NELIOTA. Having in mind the requirements for observing conditions (see Sect. 5.1), the capacity of the storage allows to keep observed raw frames for at least two months. On the other hand, the storage pool “C” capacity provides enough storage to hold detected event records for a few years of NELIOTA operation.
5. NELIOTA software
A dedicated software system has been developed in order to control the telescope, schedule observations, reduce individual frames, and perform automatic detection of the impact events. In addition, an entry in our web-based, user-friendly database is automatically created when a new event is detected (within 24 h of the event observation). The software (presented in detail elsewhere; Fytsilis et al. in prep.) has been developed in JAVA using ECLIPSE IDE and JAVA RE8 and is running on a Windows server. It provides a computer interface between all individual components of the NELIOTA system.
5.1. Telescope- and camera-control software
The NELIOTA observations are scheduled and performed using the observation planner and acquisition functions of the software. The observation planner produces an observing plan for each night according to the visibility of the Moon and the observability of the photometric calibrators. The observations are performed in the non-sunlit part of the Moon when the illuminated fraction is between ∼10 − 45% (i.e., from waxing crescent to the first quarter and from the last quarter to the waning crescent phase). An elevation limit of 20° above horizon is set due to the dome clearance. The Moon is observed at a frame rate of 30 frames per second for a 15 min interval or “chunk” before this dataset is stored on the server. A selection of photometric calibrator stars from Landolt (1992) is made by the planner according to their proximity to the Moon and observed in between lunar observing chunks. The exposure time of the calibrators ranges from 0.05 to 4 s depending on their apparent magnitude. In the case of an impact event the calibrator observed closest in time to the event is selected to conduct the photometric analysis. Ancillary observations (flat-field and dark frames) are obtained on each night. Sky flat-field frames are observed during twilight with exposure times set automatically by the software (typically ranging between 0.04 and 2 s) in order to make the best use of the dynamical range of the detectors. Dark frames are obtained before and after the end of lunar observations. The NELIOTA software commands the telescope through the TCS interface, while the cameras are controlled by using the software development kit (SDK) version 3.11 provided by Andor.
5.2. Impact detection software
Due to the large amount of data collected, a pipeline has been developed in order to detect candidate impact events, which are later evaluated by an expert scientist. The pipeline is based on two successive steps: (i) calibration of the raw data, and (ii) application of the detection algorithm.
At the observed rate of 30 frames per second the actual on-source integration time is 0.023 s followed by a read-out time of 0.010 s. Events that are detected in a single frame are considered to have a duration of 0.033 s (upper limit), while for the events that are detected in more than one frames, the total duration is calculated by summing the integration and read-out times of the successive frames until the end of the event.
Calibration of the observed frames is done in a standard way by performing a dark current subtraction using the median-combined dark frames and also flat-field corrections using the median-combined sky flat-frames observed. The calibrated lunar frames are then background subtracted to remove the inhomogeneous surface of the Moon and earthshine. To calculate the background Bt for each individual frame It observed at time t, an adaptive background is created by combining all individual frames of the Moon observed until t − 1 (the frame observed before the one at time t). These frames are weighted in time as Bt = α × It − 1 + (1 − α) × Bt − 1 with α having values in the range (0, 1) depending on the degree of importance of the most recent frames. The value that we use in the NELIOTA setup is α = 0.35. This ensures that at the observed rate of 30 frames-per-second, the main contribution in the background comes from the most recent observations (closer to time t), which reduces the effects of seeing as well as possible telescope tracking deviations, but it produces a robust estimate of the global background.
The background subtracted image of interest Dt = It − Bt is then subjected to a threshold detection process using a high and a low threshold value. The high threshold value is primarily used to define pixels with large deviations from the local background, while a low value is subsequently used to better define these deviations by looking at the fainter levels. When a candidate event is flagged, the connected components are extracted so that the event can be treated as a single object and its extent can be defined. With this criterion, objects that are smaller than a minimum size (ten pixels) are considered to be noise and are thus rejected. Objects that are large enough are then considered as candidate events and are recorded. This same procedure is then repeated for the subsequent frame (t + 1) with the exception that in the calculation of the new background, the area extracted by the connected component analysis is not considered. This secures detection of the same event in subsequent frames as the event fades.
For each candidate event that is detected by the software, visual inspection is performed to validate it. The twin camera system can easily rule out cosmic rays since they only appear in one of the two frames. Other artifacts, such as satellites or airplanes crossing the field-of-view, can also be easily identified and ruled out using their elongated trajectory. Once an event is validated, photometric calibration is performed by an expert scientist. The photometric calibrator closest (in time and angular distance) to the observation of the event is then used to derive the photometric zero-point and thus calculate the apparent magnitude of the event. Events that are only detected in the I-band resembling flashes are also stored and flagged as “suspected”.
The location of the flashes on the Moon is derived in a semi-automatic way using a dedicated tool of the NELIOTA detection software and a high detailed image of the Moon from the Virtual Moon Atlas 6.0 (VMA6)8 software. Using the options available for the latter (i.e., date, time observing site, libration) it is feasible to export a highly detailed image of the Moon as seen from the observing site at the exact time when the flash is detected. The localization tool stacks the images contained in the data cube of each event (see Sect. 4) in order to produce a higher contrast image of the Moon in which the lunar features can easily be spotted. Subsequently, the user imports the detailed image produced by the VMA6 and identifies at least three lunar features (e.g., small craters) by selecting them in both the VMA6 image and the stacked image. After the successful cross match, the software exports the initial VMA6 image in which the location of the flash is marked. The exact selenographic coordinates can then be extracted. The error in the location determination, taking into account the typical seeing values for the site and also the error in corss matching features on the Moon between the observations and the VMA6 map, is roughly estimated to be 6.5″ (∼0.5° in selenographic coordinates). All the information described above is made available on the NELIOTA website1 within 24 h after the observation.
6. Instrument performance
6.1. Noise characterization
We have performed observations of the open cluster NGC 1960 (RA2000: 05h36m17s, Dec2000: +34° 08′ 27″) in order to assess the instrument performance in terms of depth and instrument photonic noise. The open cluster was observed simultaneously in the two bands on the night of March 11th, 2018 with exposure times of 10, 1, and 0.023 s (the last being the fixed exposure time setting for the NELIOTA observations) and four different airmasses (X = 1.027, 1.138, 1.598, 2.397). For the photometry we used the phot task in IRAF9. The photometry was performed within an aperture of three pixels radius, corresponding to 2.4″, while the sky background was measured in an annulus centered at each star with an inner radius of ten pixels and an outer radius of 15 pixels. In each 10 s exposure we used 20 relatively bright and isolated stars in the field to calculate the aperture corrections needed for an aperture of ten pixels in order to account for the stellar light missing in the smaller, 3 pixel, aperture used in the photometry of the cluster. The mean sky background standard deviation (STDbkg) was measured to be 12, 14, and 38 counts in 0.023, 1, and 10 s, respectively, in the I-band and 12, 13, and 30 counts in 0.023, 1, and 10 s, respectively, in the R-band. The uncertainty on the brightness of the source (σmag) was then calculated as
with the signal-to-noise ratio (SNR) defined as
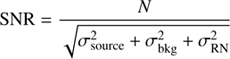 (2)(see, e.g., Everett & Howell 2001). Here, N is the source flux in electrons, σsource the source shot noise, σbkg the background noise and σRN the read-out noise. In particular,
(2)(see, e.g., Everett & Howell 2001). Here, N is the source flux in electrons, σsource the source shot noise, σbkg the background noise and σRN the read-out noise. In particular,
with t being the exposure time (in s), mag, the magnitude of the source and z
p
t the zero point in the magnitude scale (see below for the computed values in the R- and I-bands (r0 and i0 respectively)). The source shot noise is defined as 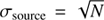 , the background noise as
, the background noise as
and the read-out noise as  . In this case G = 0.4 e− per A/D count, and R
N = 5.1 e− (see Table 2 for the specifications of the detectors), while nsource is the number of pixels inside the photometry aperture (radius of 3 pixels) and nbkg the number of pixels inside the background annulus (inner radius of 10 pixels and outter radius of 15 pixels). Given the values above, nsource/nbkg = 0.072. For each exposure setting, several isolated and well detected stars were chosen as photometric calibrators for the rest of the stars in the cluster. In particular, 5, 20, and 26 such stars were selected for the 0.023, 1, and 10 s exposures with their reference magnitudes obtained from Jeffries et al. (2013). The above procedure resulted in the determination of the zero points in the magnitude scale (r0, i0), of atmospheric extinction coefficients (r1, i1) and of the color terms (r2, i2) in the following photometric equations:
. In this case G = 0.4 e− per A/D count, and R
N = 5.1 e− (see Table 2 for the specifications of the detectors), while nsource is the number of pixels inside the photometry aperture (radius of 3 pixels) and nbkg the number of pixels inside the background annulus (inner radius of 10 pixels and outter radius of 15 pixels). Given the values above, nsource/nbkg = 0.072. For each exposure setting, several isolated and well detected stars were chosen as photometric calibrators for the rest of the stars in the cluster. In particular, 5, 20, and 26 such stars were selected for the 0.023, 1, and 10 s exposures with their reference magnitudes obtained from Jeffries et al. (2013). The above procedure resulted in the determination of the zero points in the magnitude scale (r0, i0), of atmospheric extinction coefficients (r1, i1) and of the color terms (r2, i2) in the following photometric equations:
where r and i are the instrumental magnitudes of the stars, R and I the reference magnitudes, and X the airmasses (common for both bands) at the time of the observation of the cluster. In our photometric calibration run we found r0 = 23.01 mag, i0 = 23.07 mag, r1 = 0.11 mag/airmass, i1 = 0.06 mag/airmass, r2 = 0.30 mag and i2 = 0.06 mag. The inverted transformation equations were then used to calibrate the instrumental magnitudes and their associated uncertainties of 25 stars in the 0.023 s exposure, 325 stars in the 1 s exposure and 650 stars in the 10 s observations common in the I- and R-bands.
The results are shown in Fig. 6 with the I-band observations in the left panel and the R-band observations in the right panel (see the caption of Fig. 6 for the explanation of different symbols and lines). For both bands the 0.023 s, the 1 s and the 10 s observations are shown along with the theoretical predictions imposed by Eq. (1). What is evident is that the model predictions follow nicely the measured instrumental magnitudes and associated errors. Using the model, the magnitudes reached at these exposure times (at a certain noise level) can be derived. We find that observations through KPFI of stellar-like objects on a dark night in the I-band can reach up to 13.05 mag, 17.07 mag and 18.76 mag in 0.023, 1 and 10 s, respectively, at a 0.4 × σmag level (corresponding to 0.25 S/N detections). At 0.1 × σmag level (S/N = 10) the magnitudes reached are 11.43, 15.45 and 17.21 in 0.023, 1, and 10 s, respectively. R-band observations can reach up to 12.81 mag, 16.82 mag and 18.74 mag in 0.023, 1, and 10 s, respectively, at a 0.4 × σmag level, while the magnitudes that can be reached at a 0.1 × σmag level are 11.19, 15.21 and 17.18 in 0.023, 1, and 10 s, respectively.
 |
Fig. 6. Instrument performance for the two channels (I- and R-band; left and right panels respectively). In each panel the measured magnitudes of stars in the open cluster NGC 1960 are plotted against their measured uncertainty (σmag) for three different exposure settings (10 s (circles), 1 s (asteriscs) and 0.023 s (crosses)). The curves passing through the photometric measurements are the model predictions of Eq. (1) providing information on the magnitude level that can be reached at a certain σmag level (see text for more details). The horizontal line in each panel indicate the 0.1 mag noise level. |
Additionally to the sources of uncertainties discussed above there is another kind of noise which becomes significant at short exposures (like in this case) and can dominate the error in the measurements especially at large airmasses. This is the scintillation noise (σscint) which depends on many parameters, mainly on the stability of the atmosphere on the night of oservation. As a first attempt to explore this effect we followed the description described in Suggs et al. (2014) by performing observations of a photometric standard star (SA 113-475, RA2000: 21h41m51s, Dec2000: +00° 39′ 05″; Landolt 1992) on the night of 7 July, 2018. We have observed this star in both bands at four different airmasses (X=1.26, 1.7, 2.2, 2.75) with an exposure time of 23 msec and for 30 times per airmass. The results of the aperture photometry that we performed, using the phot task in IRAF9, are shown in the top panel of Fig. 7 with the instrumental magnitudes (small circles) in both R- and I-bands (red and blue symbols respectively) plotted against the airmass. The large circle in each airmass group of points is the corresponding mean value of the measured counts in magnitudes. It is evident that there is a signifficant scatter in brightness, mainly due to scintillation, around the mean value which gets larger with airmass. This is shown more clearly in the bottom panel of Fig. 7 with the scintillation noise (σscint), calculated as the standard deviation of the observations in each airmass group, plotted against the airmass. The standard deviation was calculated as the 1-sigma variation of the measured fluxes (in counts). Linear fits to the data give an estimate of the actual effect of scintillation with airmass. In particular, we find that in the R-band σscint changes as 0.034 + 0.026 X with airmass and in the I-band this relation becomes −0.011 + 0.037 X. We can see that at large airmasses this can be the dominant source of uncertainty reaching up to ∼0.1 mag. In the NELIOTA observations that will follow we consider a combined photometric and scintillation error in the form of
 |
Fig. 7. Scintillation noise (σscint) as a function of airmass. The top panel shows the scatter of the instrumental R- and I-band brightness of a photometric starndard star (SA 113-475) observed with an exposure time of 23 msec at four different airmasses (X = 1.26, 1.7, 2.2, 2.75; small circles) along with the mean values at each airmass (large circles). In the bottom panel the standard deviation of the brightness of the source, in each airmass, is plotted against the airmass with the linear fits to the data provided (see the text for more details). |
although, in a subsequent paper (Liakos et al., in prep.), we plan to carry out a more thorough analysis in a subsequent paper in which we take into account various seeing conditions and a range of brightnesses so that more realistic measurements of the scintillation noise can be obtained.
6.2. Field distortion
Despite the simple design of the KPFI, the passage of light through the optical elements will cause some distortion. The knowledge of the level of distortion in the two channels of the KPFI is of great importance for NELIOTA science since it could introduce uncertainties in the determination of the exact position of the NEO impact. We observed the dense stellar field of the open cluster NGC 6811 (RA2000: 19h37m17s, Dec2000: +46° 23′ 18″), on the night of October 13th, 2017, at 10 s exposure, in order to produce the distortion maps in the R- and I-bands. This was done by calculating the astrometric differences of the stars in the field using the ccmap task in IRAF7 that provides the plate solution using a list of matched pixel and celestial coordinates, the latter obtained from Janes et al. (2013). A total of 30 bright stars located throughout the field were used in both bands to compute the plane solution by fitting third-order polynomials in both the x- and y-axis. The maps are presented in Fig. 8 for the I-band (left panel) and for the R-band (right panel). The arrows indicate the expected position of the star (beginning of the arrow) and the observed position (end of arrow). For displaying purposes the arrows are artificially enlarged by a factor of 50 with a scale indicator (four enlarged pixels) shown in the upper left part of each plot. It is evident that the distortion is very small in the center of the field, while it increases toward the edges. The rms of the fit was found to be 60 mas in the I-band and 55 mas in the R-band. Nevertheless, the maximum distortion is on the order of the pixel scale and, in any case, less than the seeing effects, therefore it does not affect the localization of NELIOTA flashes (accurate to 6.5″ on the Moon; see Sect. 7).
 |
Fig. 8. Field distortion map of the I-band (left panel) and the R-band (right panel) frames. Each arrow shows the expected position on the sky (beginning of arrow) and the measured position (end of arrow). For displaying purposes the arrows are artificially enlarged by a factor of 50 with a scale indicator (four enlarged pixels) shown in the upper left part of each plot. |
7. NELIOTA observations
During the first year of the NELIOTA campaign, February 201710–February 2018, 31 NEO impacts on the Moon have been successfully detected and recorded, at a frame rate of 30 fps, simultaneously in two photometric bands (R and I; Table 5). About half of them fade out very fast [within the duration of one single frame (33 msec)], while for the rest we were able to follow their brightness variation with time (see Table 5). An example of such a multiframe event is shown in Fig. 9. In this time sequence the light variation of the event observed at 04:35:09.967 UT on 14th December, 2017 (event ID 30) is shown in the four I-band frames in which it was detected. For comparison the frame just before the event occurred and right after the event finished are also presented. The time at the beginning of the exposure in each frame is also given in each panel (t = 0 msec corresponds to the frame where the event was initially detected). In one case (event ID 21) the event was captured during its rise with the I-band brightness measured in the first frame (8.49 ± 0.04 mag) being slightly lower than its peak brightness detected in the second frame (8.37 ± 0.04 mag). Similar detections have been reported by others (Suggs et al. 2014) with the video frames showing faint flashes followed by brighter ones. Photometry of the detected flashes was performed using standard aperture photometry routines, with a detailed description given elsewhere (Liakos et al., in prep.) with the uncertainties in brightness calculated as in Eq. (5). The first science results of the campaign, including determination of the temperatures developed during the impact events, are presented in Bonanos et al. (2018).
Basic parameters of the impact flashes observed with the 1.2 m Kryoneri telescope as part of the NELIOTA project.
 |
Fig. 9. Time sequence of the I-band brightness of the impact detected by the NELIOTA system at 04:35:09.967 UT on December 14th, 2017 (event ID 30). The magenta contours show the 500 ADUs level, corresponding to approximately S/N of 2 detection threshold. The leftmost and rightmost panels are the frames before and after the event and are also displayed for comparison purposes. The time of the beginning of the exposure of each frame is also indicated in each panel (with the start of the event occurring at t = 0 msec). The size of each panel is 110 × 85 arcsec. |
The spatial distribution of the detected impacts on the Moon’s surface is presented in Fig. 10. In this figure the location of the 31 validated impacts on the lunar surface is indicated with the 27 being sporadic events (yellow symbols) and the remaining four (green symbols) related to the Geminid shower observed during December 2017 (flashes with IDs 27-30 in Table 5). Apart from the validated events (observed both in the I- and R-bands) 17 more flashes have been detected only in the I-band (not shown in Fig. 10).
 |
Fig. 10. Positions of impacts on the Moon observed during the first year of the NELIOTA campaign. A total of 31 “validated” events have been recorded so far with 27 being sporadic (yellow points) and four possibly originating from the Geminid stream observed during the period of 12–14 December 2017 (green points). The index associated with each impact corresponds to the flash ID (1st column in Table 5). During this period a total of 17 flashes (not shown here) were classified as “suspected” since they were only detected in the I-band. |
The distribution of the brightness of the flashes detected during the first year of the campaign is given in Fig. 11 for the detections in the I-band (left panel) and the detections in the R-band (right panel). For the multiframe events we plotted the peak magnitudes which in all cases, except the I-band measurements of event ID 21, were measured in the frame where the event was first detected. Something that is directly evident from these histograms is that flashes are always fainter in the R-band with respect to the I-band. An average R-I color index for all the flashes detected by NELIOTA is 1.02 ± 0.05 mag. For comparison, in Fig. 11 we have also included the R-band magnitude distribution of the events detected by Suggs et al. (2014). This shows that the NELIOTA setup was successful in detecting fainter flashes (about two magnitudes fainter than was done before). The primary reason for this is the larger aperture telescope that is now being used but also the higher efficiency detectors that are implemented in the NELIOTA system. Since these fainter flashes are more frequent (see, e.g., Suggs et al. 2014) the NELIOTA system is more sensitive in detecting those, compared to brighter flashes already detected by other experiments. The difference in the number statistics between the two samples (Suggs et al. 2014 and NELIOTA) comes from the fact that the first one accounts for a five-year campaign compared to the one year operation of NELIOTA.
 |
Fig. 11. Distribution of the peak magnitudes of the validated events in the I-band (left panel) and in the R-band (right panel). For comparison we have plotted the distribution of the events observed by Suggs et al. (2014) in the R-band (black-line histogram in the right panel). It is evident that the NELIOTA campaign is detecting flashes about two magnitudes fainter than what was previously detected by Suggs et al. (2014), a result of the use of a larger aperture telescope (see text for details). The difference in the number of the events is mainly due to the different campaign periods (one year of NELIOTA observations versus five years of observations in Suggs et al. 2014). |
Taking into account the total number of impacts (31), total exposure time during which these events were collected (54 h of Moon observations), and the average surface observed per night, we estimate a detection rate of 1.96 × 10−7 events km−2 h−1. This is about a factor of two higher than what has been reported before (1.03 × 10−7 events km−2 h−1 (Suggs et al. 2014) and 1.09 × 10−7 events km−2 h−1 Rembold & Ryan 2015). This is a direct result of the use of a larger aperture telescope (compared to previous campaigns) allowing for the detection of fainter events (see Fig. 11), which are more frequent (see, e.g., Drolshagen et al. 2017 and references therein).
7.1. Expected limiting magnitudes
In our attempt to quantify the expected performance of the NELIOTA system, we explored how the analysis performed on stellar photometry (Sect. 6.1) can be applied to predict the limiting magnitudes of the impact flashes that the NELIOTA system can reach. One parameter that greately affects the detection of such flashes is the background noise (σbkg; see Eq. (2)) which in the case of the Moon, in contrast to the uniform sky background observed in stellar objects, varies significantly depending on the lunar phase. As the noise of the background (σbkg) scales with the square root of the brightness of the background, in this case the illumination of the Moon, we expect that σbkg obtains its smallest values on observations obtained when the side of the Moon visible from the earth is illuminated the least. For NELIOTA scheduling this corresponds to phase ∼0.1. Even in this case, since the Moon is not uniformly illuminated, σbkg is expected to vary throughout its surface (gradually becoming brighter from the limb to the center). In order to explore the effect of σbkg on the impact flash detections, we calculate the standard deviation (STDbkg) in 352, randomly selected, regions throughout the Moon’s surface, in both bands (R and I). The background was measured within an aperture of a radius of 11 pixels, which roughly corresponds to an area similar to the one used to calculate the local background of the stars in the cluster. We used the observations performed on 1 March, 2017 (exposure time of 23 msec) that corresponds to the lowest lunar phase (0.118) at which observations have been obtained. The measured values for STDbkg are shown in the two histograms in Fig. 12 corresponding to the I-band (left panel) and R-band (right panel). We find that the values of STDbkg range from ∼30 to 50 counts in the I-band, with the most frequent value at ∼35 counts and from ∼22 to 37 counts in the R-band, with the most frequent value at ∼25 counts.
 |
Fig. 12. Background standard deviation (STDbkg) distributions in I- and R-band (left and right panels respectively) for observations made in lunar phase of 0.118 on 1 March, 2017. Each measurement comes from an aperture of radius of 11 pixels with 352 such regions randomly selected throughout the Moon’s surface observed. |
In order to estimate the NELIOTA detection limit we plotted in Fig. 13 the observed magnitudes and their calculated uncertainties for both the impact flashes and the stars (see Fig. 6) at the fixed NELIOTA exposure time of 0.023 s. In both bands the observed impact flashes at a given uncertainty level are brighter than their respective stellar analogs, a result, mainly due to the significant increase in σbkg compared to the sky background as discussed above. Furthermore, the scatter in brightness of the impact flashes at a given uncertainty is, mainly, due to the variation in σbkg, which, as mentioned earlier, greatly depends on the lunar phase. In Fig. 13, we have also plotted the model predictions (Eq. (1)) for the stars (the solid line; also seen in Fig. 6), corresponding to a STDbkg value of 12 counts (see Sect. 6.1). Adjusting Eq. (2) for different background noise levels we can then plot the model for the range of STDbkg values observed for ∼0.1 lunar phases. We have done so by plotting the minimum (dashed lines) and maximum (dotted lines) observed values of STDbkg (30 and 50 counts in the I-band and 22 and 37 for the R-band). For the I-band we find that the NELIOTA detections at the S/N = 2.5 threshold may vary from 11.90 mag to 12.39 mag depending on the measured STDbkg (as shown in Fig. 12). The 10 S/N detections range between 10.35 mag and 10.83 mag. Similarly, in the R-band, the S/N = 2.5 detections range between 11.95 mag and 12.41 mag, while the S/N = 10 detections range between 10.39 mag and 10.83 mag.
 |
Fig. 13. Measured magnitudes versus the associated magnitude uncertainty (σmag) for both stars and lunar impact flashes in the I- and R-bands (left and right, respectively). In both panels the stellar measurements are presented as stars, while the validated impact flashes are shown as circles. For the I-band the suspected impact events (cyan crosses) are also shown. For the stars, the predicted model (Eq. (1)) is also presented (solid line; see Fig. 6). The dashed and dotted lines in each panel indicate the model prediction when the minimum and maximum value, respectively, of the background noise (STDbkg) are considered for the case of the observations of 1 March, 2017 with the lower lunar phase ∼0.1 (Fig. 12) observed. |
7.2. Detection completeness
We furthermore explored the detection completeness as a funtion of the brightness of the impact flash in the R-band. To achieve this we created mock impact-flashes of certain brightnesses on a real observation of the Moon (in both R- and I-band images) and subsequently identified the flashes with S/N above 2.5 (σmag < 0.4). A constrain of an average color index of R−I=1, as indicated by our sample (see Sect. 7) was applied. In more detail, we used the observation of the lowest observed lunar phase of March 1st, 2017 (see above) and placed 50 mock flashes in random places over the surface of the Moon using the task mkobjects in IRAF9. Each flash was made to resemble point like Gaussian distributions of FWHM of 2.4″, the mean seeing value of all the nights with NELIOTA observations and were grouped in bins of 0.2 mags in brightness ranging from 9.4 to 13.4 mag in the R-band. The produced image of the impact flashes on the Moon was then background subtracted with the procedure described in Sect. 5.2 and used as input to the phot task in IRAF9 in order to count the detections showing a S/N greater than 2.5. The completeness was then formed as the ratio of the mock flashes fulfilling the above criteria to the initial number of flashes created (50). The results of this procedure are presented in Fig. 14 with the detection completeness presented as a function of R-band brightness. The drop in the source completeness begins at 10.4 mag (0.98) and it gets practically zero (0.02) at 12.4 mag, well in accordance with our previous analysis for the limiting magnitudes (Fig. 13), with a 50% detection completeness at 11.4 mag. In a subsequent paper we plan for a more detailed analysis on the NELIOTA detection completeness taking into account all the parameters that influence such calculations (e.g., seeing, source morphology, variable background level, and variable color index) in order to properly define the intrinsic luminosity function of relatively faint Lunar impact flashes.
 |
Fig. 14. Detection completeness as a function of the brightness of the impact flashes in the R-band. For each magnitude bin of 0.2 mag in the R-band 50 mock flashes were placed in random positions throughout a real observation of the Moon (in both the R- and I-band images) with a color index of R-I=1 mag. The completeness is then computed by forming the ratio of the ones detected with S/N above 2.5 (σmag < 0.4), in both R- and I-bands, to the total number created (50). |
8. Conclusions
We present the design and performance of KPFI, a wide-field, high-cadence, twin lunar monitoring system at the prime focus of the 1.2 m Kryoneri telescope that is used for the NELIOTA project. The project aims at detecting faint flashes on the Moon’s surface produced by impacts of NEOs. The optical design, the detectors, the control system as well as the dedicated software for the detection of the NEO impacts are discussed, while the instrument performance and highlights of the first scientific results are shown. The novelty of the NELIOTA system is the use of a large aperture telescope (larger than ever used before for this purpose) and the high-cadence achieved by two detectors observing simultaneously at a rate of 30 frames-per-second in two optical bands (R and I). The noise model predicts that the NELIOTA system can detect NEO impact flashes at a S/N = 2.5 level of 12.39 mag in the I-band and 12.41 mag in the R-band for observations made at low lunar phase (∼0.1). During the first year of operation, 31 such NEO impacts on the Moon’s surface were observed with the faintest flash being 11.24 mag in the R-band (about two magnitudes fainter than ever previously observed) translated into a detection rate of 1.96 × 10−7 events km−2 h−1. The ability to monitor the impact flashes in two bands at the same time provides significant constraints on the temperatures produced during the impact.
The wide-field, high-cadence and simultaneous multicolor abilities of KPFI make it a unique instrument that can be used by the community for a variety of astronomy projects such as occultations (e.g., Sicardy et al., in prep.), exoplanet transit light curves, monitoring of early supernova light curves (e.g., Bonanos & Boumis 2016), as well as transient follow up (e.g., Wyrzykowski et al. 2017) and other NEO science. We encourage the reader to visit the dedicated NELIOTA website1 for further information.
Acknowledgments
The authors wish to thank the anonymous referee for constructive comments that helped improving the paper. We are also grateful to A. Georgakakis for stimulating discussions, to J.M. Madiedo for comments on the manuscript and to E. Palaiologou for useful guidance on the field distortion calculations. The authors gratefully acknowledge financial support by the European Space Agency under the NELIOTA program, contract No. 4000112943. This work has made use of data from the European Space Agency NELIOTA project, obtained with the 1.2 m Kryoneri telescope, which is operated by IAASARS, National Observatory of Athens, Greece.
References
- Ait Moulay Larbi, M., Daassou, A., Baratoux, D., et al. 2015, Earth Moon and Planets, 115, 1 [Google Scholar]
- Artem’eva, N. A., Kosarev, I. B., Nemtchinov, I. V., Trubetskaya, I. A., & Shuvalov, V. V. 2001, Sol. Syst. Res., 35, 177 [NASA ADS] [CrossRef] [Google Scholar]
- Bellot Rubio, L. R., Ortiz, J. L., & Sada, P. V. 2000, ApJ, 542, L65 [NASA ADS] [CrossRef] [Google Scholar]
- Bonanos, A. Z., & Boumis, P. 2016, A&A, 585, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonanos, A. Z., Avdellidou, C., Liakos, A., et al. 2018, A&A, 612, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bouley, S., Baratoux, D., Vaubaillon, J., et al. 2012, Icarus, 218, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, P. G., Assink, J. D., Astiz, L., et al. 2013, Nature, 503, 238 [NASA ADS] [Google Scholar]
- Drolshagen, G., Koschny, D., Drolshagen, S., Kretschmer, J., & Poppe, B. 2017, Planet. Space Sci., 143, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Everett, M. E., & Howell, S. B. 2001, PASP, 113, 1428 [NASA ADS] [CrossRef] [Google Scholar]
- Goode, P. R., Qiu, J., Yurchyshyn, V., et al. 2001, Geophys. Res. Lett., 28, 1671 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, A. W., & D’Abramo, G. 2015, Icarus, 257, 302 [NASA ADS] [CrossRef] [Google Scholar]
- Ivanov, B. A., Neukum, G., Bottke, Jr., W. F., & Hartmann, W. K. 2002, in The Comparison of Size-Frequency Distributions of Impact Craters and Asteroids and the Planetary Cratering Rate, eds. W. F. Bottke, Jr.,A. Cellino,P. Paolicchi, & R. P. Binzel, 89 [Google Scholar]
- Janes, K., Barnes, S. A., Meibom, S., & Hoq, S. 2013, AJ, 145, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Jeffries, R. D., Naylor, T., Mayne, N. J., Bell, C. P. M., & Littlefair, S. P. 2013, MNRAS, 434, 2438 [NASA ADS] [CrossRef] [Google Scholar]
- Landolt, A. U. 1992, AJ, 104, 340 [NASA ADS] [CrossRef] [Google Scholar]
- Madiedo, J. M., & Ortiz, J. L. 2018, in Lunar Impact Event: The 11 September 2013, ed. B. Cudnik (Cham: Springer International Publishing), 1 [Google Scholar]
- Madiedo, J. M., Ortiz, J. L., Morales, N., & Cabrera-Caño, J. 2014, MNRAS, 439, 2364 [NASA ADS] [CrossRef] [Google Scholar]
- Madiedo, J. M., Ortiz, J. L., & Morales, N. 2018, MNRAS, 480, 5010 [Google Scholar]
- Moser, D. E., Suggs, R. M., & Swift, W. R. 2011, in Meteoroids: The Smallest Solar System Bodies, eds. W. J. Cooke, D. E. Moser, B. F. Hardin, & D. Janches, 142 [Google Scholar]
- Nemtchinov, I. V., Shuvalov, V. V., Artem’eva, N. A., et al. 1998, Sol. Syst. Res., 32, 99 [NASA ADS] [Google Scholar]
- Ortiz, J. L., Sada, P. V., Bellot Rubio, L. R., et al. 2000, Nature, 405, 921 [NASA ADS] [CrossRef] [Google Scholar]
- Ortiz, J. L., Madiedo, J. M., Morales, N., Santos-Sanz, P., & Aceituno, F. J. 2015, MNRAS, 454, 344 [NASA ADS] [CrossRef] [Google Scholar]
- Qiu, P., Mao, Y.-N., Lu, X.-M., Xiang, E., & Jiang, X.-J. 2013, Res. Astron. Astrophys., 13, 615 [NASA ADS] [CrossRef] [Google Scholar]
- Rembold, J. J., & Ryan, E. V. 2015, Planet. Space Sci., 117, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Robinson, M. S., Boyd, A. K., Denevi, B. W., et al. 2015, Icarus, 252, 229 [NASA ADS] [CrossRef] [Google Scholar]
- Speyerer, E. J., Povilaitis, R. Z., Robinson, M. S., Thomas, P. C., & Wagner, R. V. 2016, Nature, 538, 215 [NASA ADS] [CrossRef] [Google Scholar]
- Suggs, R. M., Moser, D. E., Cooke, W. J., & Suggs, R. J. 2014, Icarus, 238, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Werner, S. C., Harris, A. W., Neukum, G., & Ivanov, B. A. 2002, Icarus, 156, 287 [NASA ADS] [CrossRef] [Google Scholar]
- Wyrzykowski, L., Mroz, P., & Rybicki, K. 2017, ATel, 10341 [Google Scholar]
All Tables
Specifications of the Andor Zyla 5.5 sCMOS camera for the NELIOTA project with a 2 × 2 binning configuration.
Basic parameters of the impact flashes observed with the 1.2 m Kryoneri telescope as part of the NELIOTA project.
All Figures
 |
Fig. 1. Section view of the Kryoneri Prime Focus Instrument (KPFI) optical layout. The position of the field corrector lenses #1, #2, and #3, the dichroic beam splitter, as well as the lens pair elements in front of the Lunar imaging detectors and the R- and I-band filters are shown. The focus plate and the instrument selector stage are also indicated (Credit: DFM Engineering Inc.). |
| In the text | |
 |
Fig. 2. KPFI filters (red solid line for the R-band and green solid line for the I-band) and dichroic beam splitter transmission curves (dashed and dashed-dotted lines) combined with the QE response of the Lunar imaging detectors (blue solid line). Filter curves reflect the Johnson R- and I-band. The dichroic is centered at 730 nm with a > 90% throughput. |
| In the text | |
 |
Fig. 3. I-band image of the Moon observed with the NELIOTA system illustrating the available FOV, which is 17.0′ × 14.4′. |
| In the text | |
 |
Fig. 4. NELIOTA system architecture and communication block diagram. The four software modules (observation, detection, archiving and information), the basic hardware telescope (TEL), camera system (CAM), time server (GPS), meteorological station (MET), high-performance storage (ODSTO), archiving storage (ARCSTO) and their interfaces (IF), as well as the human-machine-interfaces (HMI) are shown. |
| In the text | |
 |
Fig. 5. Configuration of the NELIOTA physical data system at the Kryoneri site. |
| In the text | |
 |
Fig. 6. Instrument performance for the two channels (I- and R-band; left and right panels respectively). In each panel the measured magnitudes of stars in the open cluster NGC 1960 are plotted against their measured uncertainty (σmag) for three different exposure settings (10 s (circles), 1 s (asteriscs) and 0.023 s (crosses)). The curves passing through the photometric measurements are the model predictions of Eq. (1) providing information on the magnitude level that can be reached at a certain σmag level (see text for more details). The horizontal line in each panel indicate the 0.1 mag noise level. |
| In the text | |
 |
Fig. 7. Scintillation noise (σscint) as a function of airmass. The top panel shows the scatter of the instrumental R- and I-band brightness of a photometric starndard star (SA 113-475) observed with an exposure time of 23 msec at four different airmasses (X = 1.26, 1.7, 2.2, 2.75; small circles) along with the mean values at each airmass (large circles). In the bottom panel the standard deviation of the brightness of the source, in each airmass, is plotted against the airmass with the linear fits to the data provided (see the text for more details). |
| In the text | |
 |
Fig. 8. Field distortion map of the I-band (left panel) and the R-band (right panel) frames. Each arrow shows the expected position on the sky (beginning of arrow) and the measured position (end of arrow). For displaying purposes the arrows are artificially enlarged by a factor of 50 with a scale indicator (four enlarged pixels) shown in the upper left part of each plot. |
| In the text | |
 |
Fig. 9. Time sequence of the I-band brightness of the impact detected by the NELIOTA system at 04:35:09.967 UT on December 14th, 2017 (event ID 30). The magenta contours show the 500 ADUs level, corresponding to approximately S/N of 2 detection threshold. The leftmost and rightmost panels are the frames before and after the event and are also displayed for comparison purposes. The time of the beginning of the exposure of each frame is also indicated in each panel (with the start of the event occurring at t = 0 msec). The size of each panel is 110 × 85 arcsec. |
| In the text | |
 |
Fig. 10. Positions of impacts on the Moon observed during the first year of the NELIOTA campaign. A total of 31 “validated” events have been recorded so far with 27 being sporadic (yellow points) and four possibly originating from the Geminid stream observed during the period of 12–14 December 2017 (green points). The index associated with each impact corresponds to the flash ID (1st column in Table 5). During this period a total of 17 flashes (not shown here) were classified as “suspected” since they were only detected in the I-band. |
| In the text | |
 |
Fig. 11. Distribution of the peak magnitudes of the validated events in the I-band (left panel) and in the R-band (right panel). For comparison we have plotted the distribution of the events observed by Suggs et al. (2014) in the R-band (black-line histogram in the right panel). It is evident that the NELIOTA campaign is detecting flashes about two magnitudes fainter than what was previously detected by Suggs et al. (2014), a result of the use of a larger aperture telescope (see text for details). The difference in the number of the events is mainly due to the different campaign periods (one year of NELIOTA observations versus five years of observations in Suggs et al. 2014). |
| In the text | |
 |
Fig. 12. Background standard deviation (STDbkg) distributions in I- and R-band (left and right panels respectively) for observations made in lunar phase of 0.118 on 1 March, 2017. Each measurement comes from an aperture of radius of 11 pixels with 352 such regions randomly selected throughout the Moon’s surface observed. |
| In the text | |
 |
Fig. 13. Measured magnitudes versus the associated magnitude uncertainty (σmag) for both stars and lunar impact flashes in the I- and R-bands (left and right, respectively). In both panels the stellar measurements are presented as stars, while the validated impact flashes are shown as circles. For the I-band the suspected impact events (cyan crosses) are also shown. For the stars, the predicted model (Eq. (1)) is also presented (solid line; see Fig. 6). The dashed and dotted lines in each panel indicate the model prediction when the minimum and maximum value, respectively, of the background noise (STDbkg) are considered for the case of the observations of 1 March, 2017 with the lower lunar phase ∼0.1 (Fig. 12) observed. |
| In the text | |
 |
Fig. 14. Detection completeness as a function of the brightness of the impact flashes in the R-band. For each magnitude bin of 0.2 mag in the R-band 50 mock flashes were placed in random positions throughout a real observation of the Moon (in both the R- and I-band images) with a color index of R-I=1 mag. The completeness is then computed by forming the ratio of the ones detected with S/N above 2.5 (σmag < 0.4), in both R- and I-bands, to the total number created (50). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.