| Issue |
A&A
Volume 619, November 2018
|
|
|---|---|---|
| Article Number | A78 | |
| Number of page(s) | 7 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201833465 | |
| Published online | 09 November 2018 | |
Gaia DR2 reveals a very massive runaway star ejected from R136
1
ESA, European Space Astronomy Centre, Apdo. de Correos 78, Villanueva de la Cañada, 28691, Madrid, Spain
e-mail: danny.lennon@sciops.esa.int
2
UK Astronomy Technology Centre, Royal Observatory Edinburgh, Blackford Hill, Edinburgh, EH9 3HJ, UK
3
Space Telescope Science Institute, 3700 San Martin Drive, Baltimore, MD 21218, USA
4
Department of Physics and Astronomy, Johns Hopkins University, 3400 North Charles Street, Baltimore, MD 21218, USA
5
Instituto de Astrofísica de Canarias, 38200, La Laguna, Tenerife, Spain
6
Departamento de Astrofísica, Universidad de La Laguna, 38205 La Laguna, Tenerife, Spain
7
Anton Pannekoek Institute for Astronomy, University of Amsterdam, Science Park 904, 1098 XH Amsterdam, The Netherlands
8
Institute of Astrophysics, KU Leuven, Celestijnlaan 200D, 3001 Leuven, Belgium
9
INAF – Osservatorio Astronomico di Padova, Vicolo dell’Osservatorio 5, 35122 Padova, Italy
10
Department of Physics and Astronomy, Hicks Building, Hounsfield Road, University of Sheffield, Sheffield S3 7RH, UK
11
Argelander-Institüt für Astronomie, Universität Bonn, Auf dem Hügel 71, 53121 Bonn, Germany
12
Vitrociset Belgium for ESA, European Space Astronomy Centre, Apdo. de Correos 78, 28691 Villanueva de la Cañada, Madrid, Spain
13
Department of Physics, University of Oxford, Denys Wilkinson Building, Keble Road, Oxford OX1 3RH, UK
Received:
21
May
2018
Accepted:
21
July
2018
A previous spectroscopic study identified the very massive O2 III star VFTS 16 in the Tarantula Nebula as a runaway star based on its peculiar line-of-sight velocity. We use the Gaia DR2 catalog to measure the relative proper motion of VFTS 16 and nearby bright stars to test if this star might have been ejected from the central cluster, R136, via dynamical ejection. We find that the position angle and magnitude of the relative proper motion (0.338±0.046 mas yr−1, or approximately 80±11 km s−1) of VFTS 16 are consistent with ejection from R136 approximately 1.5±0.2 Myr ago, very soon after the cluster was formed. There is some tension with the presumed age of VFTS 16 that, from published stellar parameters, cannot be greater than 0.9+0.3−0.2 Myr. Older ages for this star would appear to be prohibited due to the absence of He I lines in its optical spectrum, since this sets a firm lower limit on its effective temperature. The dynamical constraints may imply an unusual evolutionary history for this object, perhaps indicating it is a merger product. Gaia DR2 also confirms that another very massive star in the Tarantula Nebula, VFTS 72 (alias BI 253; O2 III-V(n)((f*)), is also a runaway on the basis of its proper motion as measured by Gaia. While its tangential proper motion (0.392±0.062 mas yr−1 or 93±15 km s−1) would be consistent with dynamical ejection from R136 approximately 1 Myr ago, its position angle is discrepant with this direction at the 2σ level. From their Gaia DR2 proper motions we conclude that the two ∼100 M⊙ O2 stars, VFTS 16 and VFTS 72, are fast runaway stars, with space velocities of around 100 km s−1 relative to R136 and the local massive star population. The dynamics of VFTS 16 are consistent with it having been ejected from R136, and this star therefore sets a robust lower limit on the age of the central cluster of ∼1.3 Myr.
Key words: stars: kinematics and dynamics / stars: massive / proper motions / Magellanic Clouds
© ESO 2018
1. Introduction
The presence of very massive (M ≳ 100 M⊙) isolated stars within ∼100 parsec of extremely young massive clusters such as R136 and Westerlund 2 (Walborn et al. 2002; Evans et al. 2010; Roman-Lopes et al. 2011) is interpreted as evidence that the dynamical ejection scenario (DES; Poveda et al. 1967) is an effective mechanism for ejecting some of the most massive stars from their birthplaces. The competing channel of ejection by the binary supernova ejection scenario (BES; Blaauw 1961) may be excluded since, with ages of less than about 2 Myr (Sabbi et al. 2012; Crowther et al. 2016; Zeidler et al. 2015), these clusters are unlikely to have produced a core-collapse SN, an event even less likely when these stars were ejected. While it has been suggested that some isolated massive stars may form from small molecular clouds (Parker & Goodwin 2007; Bressert et al. 2012; Lamb et al. 2016), the peculiar line of sight (LOS) velocities of some of the most massive stars indicate that they are runaway stars and strong candidates for dynamical ejection. In fact,N-body simulations of dynamical ejection from star clusters (Banerjee et al. 2012; Perets & Šubr 2012; Oh & Kroupa 2016) have had some success in explaining the presence of the isolated very massive stars around clusters like R136, as has the model in which a single very massive wide binary, a “bully binary”, scatters massive stars out of their host cluster after a single interaction (Fujii & Portegies Zwart 2011).
The proto-typical example of such an object, presented by Evans et al. (2010), is the star VFTS 16, a ∼100 M⊙ O2 III star on the periphery of 30 Doradus within the Tarantula Nebula of the Large Magellanic Cloud. This star is ∼120 pc in projection from the central cluster R136 and data from the VLT-FLAMES Tarantula Survey (VFTS; Evans et al. 2011) shows that it has a LOS radial velocity which is discrepant by −85 km s−1 compared to the central cluster, R136, while multiplicity is ruled out by the survey’s multi-epoch data. In the absence of any measured proper motion for VFTS 16, Evans et al. (2010) proposed R136 as the parent cluster based on the star’s main-sequence lifetime, assuming a transverse velocity comparable to its peculiar radial velocity, and given the youth and mass of R136. They further argued that VFTS 16 may be one of the clearest cases for ejection of a very massive star by dynamical interaction from a young massive cluster, with Banerjee et al. (2012) presenting an N-body simulation in support of this idea.
In this paper we present the Gaia DR2 proper motion for VFTS16, and demonstrate that its magnitude and direction are fully consistent with R136 as its point of origin, reinforcing the idea that the star has indeed been ejected from the cluster. In Sect. 2 we present the Gaia data and analysis details upon which our conclusions are based, while in Sect. 3 we discuss their potential significance.
2. Analysis of Gaia DR2 data
2.1. Defining the local reference frame of R136
Using the Gaia Data Release 2 (DR2) catalog (Lindegren et al. 2018) we extracted all sources within 0.2 degrees of R136 after first screening out stars fainter than G = 17.0m, corresponding to the approximate faint limit of the VFTS (given the significant extinction of OB stars in this field we have that G ≈ V). This sample was cross-matched with VFTS sources and other known massive stars before filtering out foreground stars using their parallax measurements, and measured radial velocities (also from VFTS).
 |
Fig. 1. Left panel (red points): fast sample of stars (202 sources) with assumed spurious tangential velocities greater than 100 km s−1. Right panel (blue points): slow sample of stars (625 sources) with tangential velocities less than 100 km s−1. The fast sample, 24% of the total, are clearly clumped within regions of high stellar density and/or strong nebulosity. |
We noticed that the resulting sample of 827 sources had considerable numbers of stars with very high tangential velocities relative to their surroundings, up to 250 km s−1 in some cases. These high velocities are clearly spurious as we know from spectroscopy that the LOS relative velocities should be less than ∼100 km s−1. Dividing our sample into fast (202 sources, or 24% of the filtered sample) and slow (625 sources) subgroups, with the divide being arbitrarily chosen to be a tangential velocity of 100 km s−1, we noted a clear difference in distributions with the fast subgroup being more strongly concentrated in areas of high stellar density and/or strong nebulosity, such as in the centre of the field near R136 itself (i.e. NGC 2070), as shown in Fig. 1. This distribution, with the fastest moving stars more strongly clumped, is also the opposite of what one expects if these proper motions were real. We also see some apparently fast moving stars in more isolated environments, however spot checking these it appears they are often either blended sources (OB stars) or late-type LMC field stars.
As discussed by Arenou et al. (2018) the presence of close companions may contribute to delivering spurious astrometric solutions and indeed we confirmed that in some cases, using existing multi-colour HST imaging of our field from the Hubble Tarantula Treasury Project (HTTP; Sabbi et al. 2013), stars with very high proper motions were indeed blended sources. While Arenou et al. (2018) discuss potential filtering approaches, we found that most of the sources in our sample with spuriously high proper motions were removed by excluding those sources with proper motion errors greater than 0.1 mas yr−1 in both co-ordinates. Filtering our original Gaia sample with this constraint produced a subsample of 682 sources. This subsample was found to have mean proper motion components of pmRA = 1.72 and pmDec = 0.67 mas yr−1. Restricting the sample to the central 153 stars within 0.05 degrees of R136 (thus including NGC 2060), on the other hand, resulted in only slightly different values of pmRA = 1.74 and pmDec = 0.70 mas yr−1, with standard deviations of 0.13 and 0.20 mas yr−1 respectively (the error in the means being 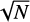 smaller; 0.01 and 0.02 mas yr−1 respectively). Since we are primarily interested in testing the hypothesis that VFTS16 was ejected from the central R136 cluster, we have converted all absolute proper motions to proper motions relative to this region by subtracting the mean motion of the central stars from the sample.
smaller; 0.01 and 0.02 mas yr−1 respectively). Since we are primarily interested in testing the hypothesis that VFTS16 was ejected from the central R136 cluster, we have converted all absolute proper motions to proper motions relative to this region by subtracting the mean motion of the central stars from the sample.
2.2. The relative proper motions of the O-type stars
We cross-matched the resulting catalog against the O-type stars taken from the VFTS catalog (Evans et al. 2011) and obtained matches for 193 sources. However it was found that the proper motion diagram of this sample still had a significant number of outliers, therefore we applied a further, stricter, filter by excluding all sources with proper motions errors greater than 0.07 mas yr−1 in both ordinates, resulting in a final selection of 79 sources. While this procedure undoubtedly removes many bona fide measurements, our primary objective is to set the context for VFTS 16, with errors of approximately 0.05 mas yr−1, and for that purpose the procedure is sufficient. This is illustrated in Fig. 2 where one can see that due to the rapid increase in the dispersion of the proper motion measurements for stars with errors greater than ∼0.07 mas yr−1, it would be impossible to unambiguously distinguish between genuine runaway candidates and outliers if we include these stars in a proper motion diagram. Moreover, from Fig. B.2 of Lindegren et al. (2018), 0.07 mas yr−1 is the median value of the formal uncertainty of the proper motion for all sources in the Gaia catalog at the approximate median magnitude of our O-star sample (G ∼ 15.3).
In Fig. 3a we display the resulting proper motion diagram, where one can see that we now have only a small number (5) of clear outliers, with relative proper motions in excess of 0.3 mas yr−1. The distribution of the bulk of the stars appears to be offset to negative velocities with respect to the origin (i.e. R136). However checking the distributions of these stars it is clear that this is due to the large number of O-type stars in NGC 2060 (see Fig. 4) that have on average a bulk velocity with respect to R136/NGC 2060 of approximately −0.06 mas yr−1 in RA, or 15 km s−1, and about +0.02 mas yr−1 in Dec or about 5 km s−1.
We made a final manual review of outliers in this diagram to check for crowded stars, or stars contaminated with strong nebular emission. Three of these objects; the O2III-V((f*)) spectroscopic binary VFTS 512 (and an X-ray source), the O6.5 Iafc+O6 Iaf binary VFTS 527 (alias R 139 and also an X-ray source) and the O2 III(f*) star VFTS 599, are in the crowded inner region of NGC 2070 where we detect many spuriously large proper motions. We suspect some, or all, of these three measurements may not be reliable and defer discussion of these objects pending further analysis of the impact of crowding and/or strong nebulosity on the Gaia astrometry.
In contrast we confirm that VFTS16 is isolated, and resides in a region of very low stellar density, consistent with its runaway status from Evans et al. (2010). Its Gaia parameters indicate that the source was well observed (having visibility_periods_used=17), indicating high astrometric quality with very low DR2 uncertainties. This is also confirmed by the astrometric_sigma5d_max (being 0.055 mas) which represents the semi-major axis of the position error ellipse and is therefore useful for filtering out cases where one of the five parameters, or some linear combination of several parameters, was particularly ill-determined (Lindegren et al. 2018).
 |
Fig. 2. Comparison of relative proper motion versus the magnitude of the semi-major axis of the error ellipse of the proper motion for all 193 O-stars in our core sample, with the filled symbols representing those stars with errors less than 0.07 mas yr−1 in both proper motion ordinates. Ignoring outliers, it is apparent that the dispersion of proper motions begins to increase significantly above 0.07 mas yr−1 (vertical dashed line). For illustration the horizontal dashed line represents a velocity of 50 km s−1 at the distance of the LMC. Labels are the VFTS identification numbers for those stars discussed in the text. |
VFTS 72 is also an obvious outlier and we confirm that this is also isolated in the HST images. As discussed by Evans et al. (2010) this O2 III-V(n)((f*)) star was also suggested as a potential runaway star in 30 Doradus (Walborn et al. 2002), however its LOS velocity of 273 km s−1 is both very close to the mean O-star velocity of 270 km s−1, and shows no significant variation (Sana et al. 2013). We therefore confirm it as a runaway based on its proper motion with respect to R136. Similarly to VFTS 16, its Gaia DR2 parameters indicate that VFTS 72 has an astrometric quality that is very high (a visibility_periods_used of 16 and an astrometric_sigma5d_max of 0.067).
 |
Fig. 3. Relative proper motions (0.1 mas yr−1 ≈ 25 km s−1) for the 79 O-type VFTS stars in 30 Doradus that have proper motion errors less than 0.07 mas yr−1. VFTS 16 and 72 are labelled (marked with +), as are three additional outliers (marked with ×) that are discussed briefly in the text. Panel a: standard proper motion diagram with the error ellipses indicated for these 5 stars, though for clarity the ellipses for the full sample are omitted. The inner dashed ellipse denotes the velocity dispersion of the local reference frame around R136/NGC 2070 sample discussed in Sect. 2.2. Panel: polar plot of the radial and tangential components relative to the direction from R136, concentric circles denoting relative proper motions of 0.1, 0.2 and 0.4 mas yr−1. In this diagram the positive x-axis, 0°, denotes a direction radially outward from R136, with positive angles indicating that the tangential component is counterclockwise with respect to the position angle of the star relative to R136. |
For each star the PM case for runaway status is statistically significant. The joint probability of a PM as large as observed (or larger) and an angular alignment as well as observed (or better) jointly occurring by chance, for a PM distribution with the RMS values in Fig. 3a, is less than 1%. Given that we have studied a sample of 79 stars in Fig. 3, the probability a finding a single 1%-unlikely PM event is non-negligible. However, the fact that for both these stars there is independent evidence for runaway status already in the literature, as discussed in this paper, strongly suggests that these are not just chance alignments in the normal tail of the PM distribution.
Platais et al. (2018) have also presented proper motions for stars in 30 Doradus and the Tarantula Nebula based on two epochs of HST observations. However VFTS 16 was not included in that catalogue because the star is saturated in all exposures, and VFTS 72 was outside the field covered by the catalogue (though the star was observed in some exposures of the subsequent HTTP survey). However a new method to determine the proper motions of saturated stars in HST images (Anderson 2018, priv. comm.) does suggest a proper motion for VFTS 16 that is consistent with the Gaia DR2 measurement, lending added confidence to the main result of the present paper.
For visualisation, we also decomposed the proper motions of the sample stars into radial and tangential proper motions relative to R136. Figure 3b shows the resulting scatter diagram. A star that is moving rapidly and purely radially away from R136 would appear near the x-axis to the far right of the plot. Indeed, VFTS 16 and VFTS 72 are found in this area, confirming their status as candidate runaway stars. We do note that one of the other rapidly moving stars, VFTS 512, also has a nearly radially directed motion. Therefore its measured DR2 proper motion could possibly be correct, and indicative of runaway status. When we relax our conservative sample cut on the proper motion errors of 0.07 mas yr−1, several more stars appear near VFTS 16 and VFTS 72 in our polar plot of proper motions, namely VFTS 80, 460, 481, 627, 722, 753 and VFTS 231, 830 respectively. However from Fig. 2 one can see that their nature is somewhat ambiguous and, in the absence of a better understanding of the DR2 systematic uncertainties discussed in Sect. 2.1 (and illustrated in Fig. 1), we refrain from interpreting the motions of these stars here. For example our most extreme outlier in proper motion from Fig. 2 is VFTS 141, however close inspection of HST images of this star confirm it to be a very close visual binary and hence we consider this measurement unreliable. Nevertheless, it is possible that with additional analyses or future Gaia data releases, some of them may prove to be true runaways. Hereafter, we focus exclusively on the cases of VFTS 16 and VFTS 72.
Properties for both of these stars are collected in Table 1, where we convert proper motion to velocity assuming a distance to the LMC of 50.1 ± 2.5 kpc, corresponding to a distance modulus of m−M = 18.50 ± 0.1 (Freedman et al. 2001). We note that the distance uncertainty also implies a ∼5% systematic uncertainty in predicted and derived velocities.
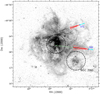 |
Fig. 4. Proper motions of VFTS 16 and 72 relative to the cluster R136, that resides within the centre of the association NGC 2070. The lengths of the arrows are scaled to their tangential proper motions. Red arrows indicate the projections of these stars’ proper motions backwards in time, scaled to their ages, and their approximate opening angles, from Table 1. The green arrow denotes the denotes the distance the star would cover to R136. The other major grouping of O-type stars in this region, NGC 2060, is also indicated. |
3. Discussion
Evans et al. (2010) argued that VFTS 16 was a candidate for dynamical ejection from R136 based on various of pieces of circumstantial evidence; it is a LOS runaway and it is very massive and so young that R136 is the only potential launch site, even when accounting for plausible rejuvenation of the runaway star, provided its high peculiar LOS velocity (−78 km s−1) would be matched by its tangential velocity. The case for VFTS 72 being a runaway was first put forward by Walborn et al. (2002) and was based primarily on the discussion of this star’s relative isolation in the field near 30 Doradus, albeit from VFTS we have that this star’s radial velocity is not anomalous (Sana et al. 2013), and exhibits little sign of variability. In the above we have determined that VFTS 16 and VFTS 72 are indeed runaway stars in the tangential plane, with relative tangential speeds of 80 and 93 km s−1 respectively.
In the following we discuss the consistency of the various timescales of interest for each star, namely, their flight times to R136, their ages (for now assuming single star evolution), and the age of the central R136 cluster. For the age of the cluster we adopt the value proposed by Crowther et al. (2016) of 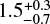 Myr as this is based on HST/STIS spectroscopy of the most massive stars within the central parsec of the cluster.
Myr as this is based on HST/STIS spectroscopy of the most massive stars within the central parsec of the cluster.
In Table 1 we present the flight time to R136, t R136, simply dividing the angular distance to the cluster, d R136, by the tangential proper motion. This is of course only correct if the proper motions align exactly along the position angle to the central cluster, which is a good approximation for VFTS 16 but not for VFTS 72, as shown in Fig. 4, and in Table 1. In addition these values do not take account of possible deceleration as the star leaves the cluster, and as such should be interpreted as upper limits (though the effect is small). Nevertheless, considering VFTS 16 we find that the position angle of its velocity vector with respect to R136 is ∼+3°, with an opening angle of ∼17°, which is consistent within the uncertainties. Also from Table 1 we have tR136 ∼ 1.5 Myr, to be compared with the age estimate provided by Schneider et al. (2018) of 0.7 ± 0.1 Myr. Clearly the latter value is in tension with the flight time though we will return to this issue below. For now we note that tR136 is in good agreement with the age of R136 of 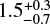 Myr, also noting that this timing implies that ejection would have to have occurred very early in the lifetime of the cluster. The case of VFTS 72 is a little different. Its position angle is 20° from alignment with the central cluster, a discrepancy of ∼2σ. Schneider et al. (2018) determined the age of VFTS 72 as
Myr, also noting that this timing implies that ejection would have to have occurred very early in the lifetime of the cluster. The case of VFTS 72 is a little different. Its position angle is 20° from alignment with the central cluster, a discrepancy of ∼2σ. Schneider et al. (2018) determined the age of VFTS 72 as 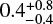 Myr, somewhat smaller than tR136, but consistent within the uncertainties.
Myr, somewhat smaller than tR136, but consistent within the uncertainties.
Fujii & Portegies Zwart (2011) presented a DES model, the “bully binary” model, for the ejection of massive stars from dense young clusters, focusing on R136 as an important test case and in fact proposing that VFTS 16 is one of the ejected stars predicted by their model. In this model, a very massive wide binary that formed during the collapse of a young star cluster acts as a scattering source due to its high collision cross section. The scattered stars may attain velocities well in excess of the cluster escape velocity, and Fujii & Portegies Zwart (2011) predict that a cluster like R136 should have produced ∼5 runaways with velocities greater than 30 km s−1, and with masses greater than 8 M⊙. While there are promising properties of the bully binary model to explain runaways around massive clusters, a potential problem with this model is that it has difficulty producing very massive runaways with space velocities as high as VFTS 16 (112 km s−1) because in this model it is assumed the runaway is ejected after a single interaction with the bully binary. Models that allow for multiple interactions with multiple binaries do predict faster runaways (Oh & Kroupa 2016; Perets & Šubr 2012) though the fraction of runaways produced with velocities greater than ∼100 km s−1 is typically very small, a few percent or less. In a similar N-body simulation taylored specifically to R136, Banerjee et al. (2012) demonstrate that two of their four simulations of R136 each produce a single runaway with properties similar to VFTS 16 within the first Myr. If VFTS 72 would also be a DES runaway, that would begin to strain the predicted numbers of such very massive and fast runaways by roughly a factor of 2–4 (see also Renzo et al. 2018b, for a further candidate). However given the caveats expressed in Sect. 2.2 that will affect the completeness of our sample, in particular the difficulty in determining proper motions of stars close to R136, it is not useful at the present time to make statistical comparisons.
As mentioned above, the inferred age of VFTS 16 (0.7 ± 0.1 Myr) is significantly less that its flight time (1.50 ± 0.21 Myr) and also just consistent with the age of R136 (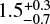 Myr) within the errors. It is tempting to argue that VFTS 16 star might be a merger product of an ejected binary (see Oh et al. 2014 for a simulation of how the very massive binary R144 may be a DES runaway from R136). Indeed stellar mergers may lead to rejuvenated stellar products (Schneider et al. 2016; de Mink et al. 2014) and thus provide a potential channel to explain the age versus flight time discrepancy. However VFTS 16 has a rather low vsini of 112 km s−1, and a surface nitrogen abundance that implies an initial rotational velocity not much larger than that (see Fig. 5). While its properties do not naturally suggest that it is a merger product, it is worth recalling that the massive runaway stars predicted by Banerjee et al. (2012) are, in fact, mergers.
Myr) within the errors. It is tempting to argue that VFTS 16 star might be a merger product of an ejected binary (see Oh et al. 2014 for a simulation of how the very massive binary R144 may be a DES runaway from R136). Indeed stellar mergers may lead to rejuvenated stellar products (Schneider et al. 2016; de Mink et al. 2014) and thus provide a potential channel to explain the age versus flight time discrepancy. However VFTS 16 has a rather low vsini of 112 km s−1, and a surface nitrogen abundance that implies an initial rotational velocity not much larger than that (see Fig. 5). While its properties do not naturally suggest that it is a merger product, it is worth recalling that the massive runaway stars predicted by Banerjee et al. (2012) are, in fact, mergers.
The ages in Table 1 are from Schneider et al. (2018) and are based on the FASTWIND analysis of the VFTS optical data from Ramírez-Agudelo et al. (2017) and Sabín-Sanjulián et al. (2017) for VFTS 16 and VFTS 72 respectively, and make use of the evolutionary tracks of Köhler et al. (2015) for LMC metallicity. In the case of VFTS 16 the small uncertainty in the age is driven primarily by the adoption of a 1σ formal error (68% confidence limit) in the effective temperature, 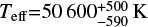 . We note that Ramírez-Agudelo et al. (2017) quote the 95% confidence intervals of
. We note that Ramírez-Agudelo et al. (2017) quote the 95% confidence intervals of 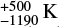 in Teff for this star, while Bestenlehner et al. (2014) derived a higher Teff for VFTS 16 of 53 100 K using CMFGEN, quoting an error of 0.02 dex, or approximately 2500 K. Analogous comments apply to VFTS 72. It has been analysed a number of times using FASTWIND and CMFGEN with Teff values ranging from 50 000 K to 55 000 K (Mokiem et al. 2007; Doran & Crowther 2011; Rivero González et al. 2012; Bestenlehner et al. 2014; Sabín-Sanjulián et al. 2017).
in Teff for this star, while Bestenlehner et al. (2014) derived a higher Teff for VFTS 16 of 53 100 K using CMFGEN, quoting an error of 0.02 dex, or approximately 2500 K. Analogous comments apply to VFTS 72. It has been analysed a number of times using FASTWIND and CMFGEN with Teff values ranging from 50 000 K to 55 000 K (Mokiem et al. 2007; Doran & Crowther 2011; Rivero González et al. 2012; Bestenlehner et al. 2014; Sabín-Sanjulián et al. 2017).
 |
Fig. 5. Illustration of the positions of VFTS 16 and 72 in the surface nitrogen enrichment versus effective temperature diagram, superimposed on the evolutionary tracks of Köhler et al. (2015) for LMC metallicity (in blue). The tracks are labelled with their initial rotational velocity, with time-steps indicated along with surface helium abundance. Since O2 dwarfs and giants typically have Teff≳ 50 000 K one can see that for such a star to have an age of ∼1.5 Myr it would be significantly more nitrogen rich than is derived for VFTS 16, and it should be helium rich (also not inferred from the observations). For comparison we also show tracks (in red) from Choi et al. (2016), as discussed in Sect. 3. |
To examine the sensitivity of the age of VFTS 16 to systematics in the determination of Teff we assumed a larger uncertainty of 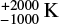 in the effective temperature and, using BONNSAI1 (Schneider et al. 2014, 2017), we derive an age of
in the effective temperature and, using BONNSAI1 (Schneider et al. 2014, 2017), we derive an age of 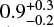 Myr. It is difficult to argue for an age greater than this as the upper bound is quite robust. As discussed by Walborn et al. (2002), in their paper defining the O2 spectral type, these stars are characterised primarily by the lack of He I lines in the optical. Consequently the lower bound on Teff, and the upper bound on the age, is provided by the presence of a weak He I 4471 line in the models, and its absence in the observations. Lowering the temperature below 50 000–49 000 K gives rise to He I in the models that is not detected in the data. Turning to VFTS 72 we consider
Myr. It is difficult to argue for an age greater than this as the upper bound is quite robust. As discussed by Walborn et al. (2002), in their paper defining the O2 spectral type, these stars are characterised primarily by the lack of He I lines in the optical. Consequently the lower bound on Teff, and the upper bound on the age, is provided by the presence of a weak He I 4471 line in the models, and its absence in the observations. Lowering the temperature below 50 000–49 000 K gives rise to He I in the models that is not detected in the data. Turning to VFTS 72 we consider 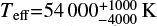 as a compromise between published parameters. We also adopt a nitrogen abundance of 8.2 ± 0.3 dex derived from the same VFTS data and methods described in Sabín-Sanjulián et al. (2017), and with these modified parameters we derive an age of
as a compromise between published parameters. We also adopt a nitrogen abundance of 8.2 ± 0.3 dex derived from the same VFTS data and methods described in Sabín-Sanjulián et al. (2017), and with these modified parameters we derive an age of 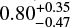 Myr, consistent with the results of Schneider et al. (2018). We illustrate the sensitivity of the ages to the stellar parameters and evolutionary tracks in Fig. 5 (the nitrogen abundance for VFTS 72 is from Grin et al. 2017). Summarising this part of the discussion, even allowing for the range of published effective temperatures of these stars, it is difficult to reconcile the age of VFTS 16 with the flight time of the star from R136.
Myr, consistent with the results of Schneider et al. (2018). We illustrate the sensitivity of the ages to the stellar parameters and evolutionary tracks in Fig. 5 (the nitrogen abundance for VFTS 72 is from Grin et al. 2017). Summarising this part of the discussion, even allowing for the range of published effective temperatures of these stars, it is difficult to reconcile the age of VFTS 16 with the flight time of the star from R136.
In order to assess the sensitivity of the age discrepancy on the underlying stellar evolution models, we reviewed the literature and found that a 100 M⊙ model including rotation for half-solar metallicity is provided by Choi et al. (2016). However, their model rotates initially very fast (vrot,initial/v crit = 0.4, or vrot,initial ≃ 450 km s−1), and reaches CNO-equilibrium abundances at the surface very quickly, evolving from the ZAMS (Teff ≃ 54 000 K) only to hotter surface temperatures (solid red track in Fig. 5). The use of solar scaled initial abundances by Choi et al. (2016) limits the surface nitrogen enrichment to a factor of order 10, while both observations and models using LMC initial abundances suggest consistently a maximum enrichment factor of the order of 30 in LMC massive stars (Hunter et al. 2009). To mimic this, we have doubled the N-enrichment in the track of Choi et al. (2016; dotted red track in Fig. 5). Using this enhanced abundance, their model reaches the level of nitrogen enhancement as observed in VFTS16 after about 0.3 Myr. At an age of 1.5 Myr, its surface has reached CNO equilibrium, and the model has left the plot area to the left in Fig. 5.
Thus, in agreement with the results from Köhler et al. (2015), models of fast rotators can not represent VFTS16. This is confirmed by the rotating (vrot,initial/vcrit = 0.4) LMC models shown by Crowther et al. (2010). While nitrogen enhancement is not discussed in detail in their paper, at an age of 1.5 Myr all their models are strongly helium-enriched, which implies CNO- equilibrium surface abundances (Grin et al. 2017).
Thus, the interpretation of VFTS 16 in terms of single star models requires moderate initial rotational velocities, in the range vrot,initial ≃ 150. . .200 km s−1. Except for those of Köhler et al. (2015), corresponding models are not available in the literature. However, as studied by Sanyal et al. (2015), the effective temperature evolution of the models by Köhler et al. (2015) is affected by envelope inflation, as they are very close to the Eddington limit. They showed that the degree of envelope inflation, and thus the effective temperature at a given time, depends on the efficiency of energy transport in the subsurface convection zones of these models. At an age of 1.5 Myr, the radii of the models of Köhler et al. shown in Fig. 5 are inflated by about 20%, implying that corresponding non-inflated models would be about 5000 K hotter. While there is empirical and theoretical evidence for the inflation phenomenon (Petrovic et al. 2006; Gräfener et al. 2012), its extent is uncertain. The models of Köhler et al. (2015) could therefore underestimate the effective temperatures, and we can not exclude the possibility that VFTS 16 is an evolved single star with an age of 1.5 Myr.
Nor can we exclude the possibility that either star might be a BES runaway, though clearly this is more relevant to VFTS 72 whose proper motion direction is approximately 2σ away from its position angle with respect to R136. Whereas population synthesis studies mostly predict smaller kinematic velocities then those we derived for our two stars (Eldridge et al. 2011; Renzo et al. 2018a), the fastest BES runaways may come from binaries which undergo common envelope evolution (see for example Boubert et al. 2017) which is essentially unconstrained at very high mass. In any case, the age problem of both stars is even more severe in the BES scenario, since they would necessarily have to be older than the shortest stellar life time of about 2 Myr (Köhler et al. 2015). This remains true even when considering a potential rejuvenation of a BES runaway due to mass accretion, since the stellar life times at very high mass depend only weakly on the stellar mass. We therefore consider a BES origin for both stars as unlikely, most strongly so for VFTS 16, for which also the weak nitrogen enrichment argues against an accretion history.
Properties of the candidate runaway O2 stars.
4. Conclusions
Consideration of the Gaia DR2 proper motions of O-type stars in the region of the Tarantula Nebula provides strong support for the hypothesis proposed by Evans et al. (2010) that the ∼100 M⊙ runaway star VFTS 16 was ejected from the central cluster R136 by the mechanism of dynamical interaction with extremely massive binaries in the cluster.
We have also discovered that another isolated ∼100 M⊙ star in the region, VFTS 72, is also a proper motion runaway, as previously suspected by Walborn et al. (2002) on the basis of its relative isolation (it has a typical LOS velocity for its environment). The origin of VFTS 72 is unclear as its direction of motion is ∼2σ away from R136.
While the uncertainties on the inferred evolutionary ages of these two stars are significant, they are systematically lower than their dynamical ages assuming both stars have been ejected from R136, or close to that cluster. As such, both stars, and VFTS 16 in particular, are useful constraints on stellar evolution models of very massive stars.
Finally, assuming VFTS 16 was ejected from R136, the dynamics of this star set a robust lower limit on the age of the cluster of ∼1.3 Myr.
Acknowledgments
This work has made use of data from the ESA space mission Gaia (http://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, http://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement. DJL thanks Alex Bombrun and Jose Hernandez of the ESAC Gaia Science Operations Centre, and Nate Bastian, for many useful discussions. SdM has received funding under the European Unions Horizon 2020 research and innovation programme from the European Research. AH and S. S.-D. acknowledge financial support from the Spanish Ministry of Economy and Competitiveness (MINECO) through grants AYA2015-68012-C2-1 and Severo Ochoa SEV-2015-0548, and grant ProID2017010115 from the Gobierno de Canarias. This research made use of Simbad and Vizier provided by CDS, Strasbourg; ESASky, developed by the ESAC Science Data Centre (ESDC); and TOPCAT. We also thank the HSTPROMO (High-resolution Space Telescope PROper MOtion) Collaboration at STScI for the sharing of their ideas and software. Finally, our colleague Nolan Walborn, who passed away earlier this year, was a strong advocate of the idea that the two stars discussed here were likely ejected from R136. He would have welcomed Fig. 4 with his usual enthusiasm!
References
- Arenou, F., Luri, X., Babusiaux, C., et al. 2018, A&A, 616, A17 [Google Scholar]
- Blaauw, A. 1961, Bull. Astron. Inst. Netherlands, 15, 265 [NASA ADS] [Google Scholar]
- Banerjee, S., Kroupa, P., & Oh, S. 2012, ApJ, 746, 15 [Google Scholar]
- Bestenlehner, J. M., Gräfener, G., Vink, J. S., et al. 2014, A&A, 570, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boubert, D., Erkal, D., Evans, N. W., & Izzard, R. G. 2017, MNRAS, 469, 2151 [NASA ADS] [CrossRef] [Google Scholar]
- Bressert, E., Bastian, N., Evans, C. J., et al. 2012, A&A, 542, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Choi, J., Dotter, A., Conroy, C., et al. 2016, ApJ, 823, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Crowther, P. A., Schnurr, O., Hirschi, R., et al. 2010, MNRAS, 408, 731 [NASA ADS] [CrossRef] [Google Scholar]
- Crowther, P. A., Caballero-Nieves, S. M., Bostroem, K. A., et al. 2016, MNRAS, 458, 624 [NASA ADS] [CrossRef] [Google Scholar]
- de Mink, S. E., Sana, H., Langer, N., Izzard, R. G., & Schneider, F. R. N. 2014, ApJ, 782, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Doran, E. I., & Crowther, P. A. 2011, Bull. Soc. Roy. Sci. Liège, 80, 129 [NASA ADS] [Google Scholar]
- Eldridge, J. J., Langer, N., & Tout, C. A. 2011, MNRAS, 414, 3501 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, C. J., Walborn, N. R., Crowther, P. A., et al. 2010, ApJ, 715, L74 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, C. J., Taylor, W. D., Hénault-Brunet, V., et al. 2011, A&A, 530, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Freedman, W. L., Madore, B. F., Gibson, B. K., et al. 2001, ApJ, 553, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Fujii, M. S., & Portegies Zwart, S. 2011, Science, 334, 1380 [NASA ADS] [CrossRef] [Google Scholar]
- Gräfener, G., Owocki, S. P., & Vink, J. S. 2012, A&A, 538, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grin, N. J., Ramírez-Agudelo, O. H., de Koter, A., et al. 2017, A&A, 600, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hénault-Brunet, V., Evans, C. J., Sana, H., et al. 2012, A&A, 546, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hunter, I., Brott, I., Langer, N., et al. 2009, A&A, 496, 841 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Köhler, K., Langer, N., de Koter, A., et al. 2015, A&A, 573, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lamb, J. B., Oey, M. S., Segura-Cox, D. M., et al. 2016, ApJ, 817, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Lindegren, L., Lammers, U., Bastian, U., et al. 2016, A&A, 595, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lindegren, L., Hernández, J., Bombrun, A., et al. 2018, A&A, 616, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mokiem, M. R., de Koter, A., Vink, J. S., et al. 2007, A&A, 473, 603 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Oh, S., & Kroupa, P. 2016, A&A, 590, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Oh, S., Kroupa, P., & Banerjee, S. 2014, MNRAS, 437, 4000 [NASA ADS] [CrossRef] [Google Scholar]
- Parker, R. J., & Goodwin, S. P. 2007, MNRAS, 380, 1271 [NASA ADS] [CrossRef] [Google Scholar]
- Perets, H. B., & Šubr, L. 2012, ApJ, 751, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Petrovic, J., Pols, O., & Langer, N. 2006, A&A, 450, 219 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Platais, I., Lennon, D. J., van der Marel, R. P., et al. 2018, AJ, 156, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Poveda, A., Ruiz, J., & Allen, C. 1967, Boletin de los Observatorios Tonantzintla y Tacubaya, 4, 86 [Google Scholar]
- Ramírez-Agudelo, O. H., Simón-Díaz, S., Sana, H., et al. 2013, A&A, 560, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ramírez-Agudelo, O. H., Sana, H., de Koter, A., et al. 2017, A&A, 600, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Renzo, M., Zapartas, E., de Mink, S. E., et al. 2018a, ArXiv e-prints [arXiv:1804.09164] [Google Scholar]
- Renzo, M., de Mink, S. E., Lennon, D. J., et al. 2018b, MNRAS, accepted [arXiv:1810.05650] [Google Scholar]
- Rivero González, J. G., Puls, J., Massey, P., & Najarro, F. 2012, A&A, 543, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roman-Lopes, A., Barba, R. H., & Morrell, N. I. 2011, MNRAS, 416, 501 [NASA ADS] [Google Scholar]
- Sabbi, E., Lennon, D. J., Gieles, M., et al. 2012, ApJ, 754, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Sabbi, E., Anderson, J., Lennon, D. J., et al. 2013, AJ, 146, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Sabín-Sanjulián, C., Simón-Díaz, S., Herrero, A., et al. 2017, A&A, 601, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sana, H., de Koter, A., de Mink, S. E., et al. 2013, A&A, 550, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sanyal, D., Grassitelli, L., Langer, N., & Bestenlehner, J. M. 2015, A&A, 580, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schneider, F. R. N., Langer, N., de Koter, A., et al. 2014, A&A, 570, A66 [Google Scholar]
- Schneider, F. R. N., Podsiadlowski, P., Langer, N., Castro, N., & Fossati, L. 2016, MNRAS, 457, 2355 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, F. R. N., Castro, N., Fossati, L., Langer, N., & de Koter, A. 2017, A&A, 598, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schneider, F. R. N., Sana, H., Evans, C. J., et al. 2018, Science, 359, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Walborn, N. R., Howarth, I. D., Lennon, D. J., et al. 2002, AJ, 123, 2754 [NASA ADS] [CrossRef] [Google Scholar]
- Walborn, N. R., Sana, H., Simón-Díaz, S., et al. 2014, A&A, 564, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zeidler, P., Sabbi, E., Nota, A., et al. 2015, AJ, 150, 78 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1. Left panel (red points): fast sample of stars (202 sources) with assumed spurious tangential velocities greater than 100 km s−1. Right panel (blue points): slow sample of stars (625 sources) with tangential velocities less than 100 km s−1. The fast sample, 24% of the total, are clearly clumped within regions of high stellar density and/or strong nebulosity. |
| In the text | |
 |
Fig. 2. Comparison of relative proper motion versus the magnitude of the semi-major axis of the error ellipse of the proper motion for all 193 O-stars in our core sample, with the filled symbols representing those stars with errors less than 0.07 mas yr−1 in both proper motion ordinates. Ignoring outliers, it is apparent that the dispersion of proper motions begins to increase significantly above 0.07 mas yr−1 (vertical dashed line). For illustration the horizontal dashed line represents a velocity of 50 km s−1 at the distance of the LMC. Labels are the VFTS identification numbers for those stars discussed in the text. |
| In the text | |
 |
Fig. 3. Relative proper motions (0.1 mas yr−1 ≈ 25 km s−1) for the 79 O-type VFTS stars in 30 Doradus that have proper motion errors less than 0.07 mas yr−1. VFTS 16 and 72 are labelled (marked with +), as are three additional outliers (marked with ×) that are discussed briefly in the text. Panel a: standard proper motion diagram with the error ellipses indicated for these 5 stars, though for clarity the ellipses for the full sample are omitted. The inner dashed ellipse denotes the velocity dispersion of the local reference frame around R136/NGC 2070 sample discussed in Sect. 2.2. Panel: polar plot of the radial and tangential components relative to the direction from R136, concentric circles denoting relative proper motions of 0.1, 0.2 and 0.4 mas yr−1. In this diagram the positive x-axis, 0°, denotes a direction radially outward from R136, with positive angles indicating that the tangential component is counterclockwise with respect to the position angle of the star relative to R136. |
| In the text | |
 |
Fig. 4. Proper motions of VFTS 16 and 72 relative to the cluster R136, that resides within the centre of the association NGC 2070. The lengths of the arrows are scaled to their tangential proper motions. Red arrows indicate the projections of these stars’ proper motions backwards in time, scaled to their ages, and their approximate opening angles, from Table 1. The green arrow denotes the denotes the distance the star would cover to R136. The other major grouping of O-type stars in this region, NGC 2060, is also indicated. |
| In the text | |
 |
Fig. 5. Illustration of the positions of VFTS 16 and 72 in the surface nitrogen enrichment versus effective temperature diagram, superimposed on the evolutionary tracks of Köhler et al. (2015) for LMC metallicity (in blue). The tracks are labelled with their initial rotational velocity, with time-steps indicated along with surface helium abundance. Since O2 dwarfs and giants typically have Teff≳ 50 000 K one can see that for such a star to have an age of ∼1.5 Myr it would be significantly more nitrogen rich than is derived for VFTS 16, and it should be helium rich (also not inferred from the observations). For comparison we also show tracks (in red) from Choi et al. (2016), as discussed in Sect. 3. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


