| Issue |
A&A
Volume 619, November 2018
|
|
|---|---|---|
| Article Number | A76 | |
| Number of page(s) | 13 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201833434 | |
| Published online | 13 November 2018 | |
A unique distant submillimeter galaxy with an X-ray-obscured radio-luminous active galactic nucleus
1 Department of Physics, Anhui Normal University Wuhu Anhui 241000 PR China
xwshu@mail.ahnu.edu.cn
2 CAS Key Laboratory for Researches in Galaxies and Cosmology, Department of Astronomy, University of Science and Technology of China Hefei Anhui 230026 PR China
3 School of Astronomy and Space Science, University of Science and Technology of China Hefei 230026 PR China
4 Max Planck Institute for Astronomy Königstuhl 17 69117 Heidelberg Germany
5 Laboratoire AIM-Paris-Saclay, CEA/DSM/Irfu – CNRS – Université Paris Diderot, CEA-Saclay 91191 Gif-sur-Yvette France
6 Institute of Astronomy, The University of Tokyo, 2-21-1 Osawa, Mitaka Tokyo 181-0015 Japan
7 Yunnan Observatories, Chinese Academy of Sciences Kunming 650011 PR China
8 Academia Sinica Institute of Astronomy and Astrophysics PO Box 23-141 Taipei 10617 Taiwan
9 Max-Planck-Institut für extraterrestrische Physik Giessenbachstrasse 1 85748 Garching, bei München Germany
10 Purple Mountain Observatory, Chinese Academy of Sciences Nanjing 210008 PR China
11 The Australian National University, Mt Stromlo Observatory Cotter Rd Weston Creek ACT 2611 Australia
Received:
16
May
2018
Accepted:
25
August
2018
Aims. We present a multiwavelength study of an atypical submillimeter galaxy, GH500.30, in the GOODS-North field, with the aim to understand its physical properties of stellar and dust emission, as well as the central active galactic nucleus (AGN) activity. Although it is shown that the source is likely an extremely dusty galaxy at high redshift, its exact position of submillimeter emission is unknown.
Methods. We use NOEMA observation at 1.2 mm with subarcsecond resolution to resolve the dust emission, and precisely localize the counterparts at other wavelengths, which allows us to better constrain its stellar and dust spectral energy distribution (SED) as well as redshift. We carry out the new near-infrared (NIR) photometry of GH500.30 observed with HST, and perform panchromatic SED modelling from ultraviolet (UV)/optical to submillimeter. We derive the photometric redshift using both NIR and far-infrared (FIR) SED modeling, and place constraints on the stellar and dust properties such as stellar mass, age, dust attenuation, IR luminosity, and star-formation rate (SFR). The AGN properties are inferred from the X-ray spectral analysis and radio observations, and its contribution to the total IR luminosity is estimated from the broadband SED fittings using MAGPHYS.
Results. With the new NOEMA interferometric imaging, we confirm that the source is a unique dusty galaxy. It has no obvious counterpart in the optical and even NIR images observed with HST at λ ≲ 1.4 μm. Photometric-redshift analyses from both stellar and dust SED suggest it to likely be at z ≳ 4, though a lower redshift at z ≳ 3.1 cannot be fully ruled out (at 90% confidence interval). Explaining its unusual optical-to-NIR properties requires an old stellar population (∼0.67 Gyr), coexisting with a very dusty ongoing starburst component. The latter is contributing to the FIR emission, with its rest-frame UV and optical light being largely obscured along our line of sight. If the observed fluxes at the rest-frame optical/NIR wavelengths were mainly contributed by old stars, a total stellar mass of ∼3.5 × 1011 M⊙ would be obtained. An X-ray spectral analysis suggests that this galaxy harbors a heavily obscured AGN with NH = 3.3+2.0−1.7 × 1023 cm−2 and an intrinsic 2–10 keV luminosity of Lx ∼ 2.6 × 1044 erg s−1, which places this object among distant type 2 quasars. The radio emission of the source is extremely bright, which is an order of magnitude higher than the star-formation-powered emission, making it one of the most distant radio-luminous dusty galaxies.
Conclusions. The combined characteristics of the galaxy suggest that the source appears to have been caught in a rare but critical transition stage in the evolution of submillimeter galaxies, where we are witnessing the birth of a young AGN and possibly the earliest stage of its jet formation and feedback.
Key words: galaxies: starburst / galaxies: high-redshift / galaxies: active / submillimeter: galaxies / X-rays: galaxies
© ESO 2018
1. Introduction
Over the last decade, far-infrared (FIR) and submillimeter (submm) surveys have revolutionized our understanding of galaxy formation and evolution by uncovering a new population of heavily dust-obscured starburst systems at high redshifts (e.g., Chapman 2005; Michałowski et al. 2010; Casey et al. 2014). These dusty submillimeter galaxies (SMGs) are found to have very high FIR luminosities of LFIR ∼ 1012 − 1013 L⊙, indicative of extreme star formation rates (SFRs) of hundreds to thousands of solar masses per year. While the bulk of this population has been found to lie at z ∼ 2, recent blank-field surveys (e.g., by Herschel and South Pole Telescope) have started to reveal the high-redshift (z ≳ 4) tail of the SMG distribution (Vieira et al. 2013; Dowell et al. 2014; Ivison et al. 2016). These are thought to be progenitors of present-day massive ellipticals (e.g., Swinbank et al. 2006), and provide critical physical conditions for the formation of luminous quasars at high redshifts coppin et al. 2008. However, details about their evolutionary process are still poorly known.
Submillimeter galaxies are known to show red optical to near-infrared (NIR) color and to not emit strongly in the rest-frame ultraviolet (UV; e.g. Yun et al. 2008), mainly due to the huge dust extinction produced by ongoing starbursts and/or evolved stellar population if at high redshift. Two illustrative examples are given by the bright SMGs GN10 and HDF850.1 in the Great Observatories Origins Deep Survey (GOODS) North field, both of which have no detectable optical or NIR counterparts in extremely deep imaging (Wang et al. 2007; Cowie et al. 2009), and now have been confirmed to be at z = 4.05 (Daddi et al. 2009a) and z = 5.2 (Walter et al. 2012), respectively, based on molecular CO emission lines. The two galaxies are instead detected significantly at mid-infrared (MIR) wavelengths λ ≳ 3.6 μm with the Spitzer/IRAC, yielding extremely red colors of H-[4.5 μm] > 4.0.
An outstanding issue relevant to the dusty starburst galaxies at high redshift is the early growth of the central supermassive black holes (SMBHs). The volume density and redshift distribution of SMGs similar to those of quasars suggest that the two populations are possibly evolutionarily linked (Chapman 2005). Multiwavelength diagnostics, particularly those at X-rays, indicate that a substantial fraction (20%–50%) of bright SMGs have an active galactic nucleus (AGN) at their center (Alexander et al. 2003a, 2005; Borys et al. 2005; Laird et al. 2010; Wang et al. 2013). Follow-up studies have found that the BH masses for SMGs appear to be systematically smaller than those found in quasars (Alexander et al. 2008b), implying that they are likely at an early phase of the BH growth.
While the detections and identifications of SMGs at z ≳ 4 are rapidly increasing (e.g., Capak et al. 2008; Coppin et al. 2008; Daddi et al. 2009b; Dowell et al. 2014; Ivison et al. 2016), the incidence and properties of AGNs (often heavily obscured) in these high-redshift systems have yet to be properly explored. Only a few z ≳ 4 SMGs with an X-ray AGN have been identified, in which the X-ray data are usually too poor to ensure meaningful spectral fitting and hence effectively constrain the amount of gas obscuring the nucleus (e.g., Wang et al. 2013). One notable example is the V-band dropout galaxy LESS J033229.4-275619 at z = 4.76 (Vanzella et al. 2006). This object was detected as a bright SMG (Coppin et al. 2009), and the 4Ms Chandra Deep Field-South observations (Xue et al. 2011) revealed the presence of a Compton-thick AGN with an X-ray luminosity of LX ∼ 2.5 × 1044 erg s−1 (Gilli et al. 2011, 2014), making it one of the most distant type 2 quasars discovered so far. Objects like LESS J033229.4-275619 are therefore ideal laboratories to study the co-evolution of BHs with their host galaxies.
In this paper, we describe the multiwavelength properties of an unusual FIR bright galaxy, GH500.30 (RA = 12:37:13.86; Dec = 62:18:26.2), which is undetected in most optical and even NIR bands with HST in the GOODS-North field, likely an extremely dusty galaxy at high redshift of z ≳ 4. The source is not only extreme for its faintness from optical to NIR, but the X-ray and radio properties are exceptional. For instance, it is extremely bright in the radio for a SMG, with a 1.4 GHz flux density of ∼630 μJy, and has a radio excess of an order of magnitude more than the star-formation powered emission, indicating that it maybe one of the most distant radio-luminous SMGs in the early Universe. We note that some results from X-ray observations of the source have been presented by Laird et al. (2010) for a sample of bright SMGs. However, Laird et al. (2010) did not perform a detailed analysis of the multiwavelength spectral energy distribution (SED), and in particular quoted a rough estimate of photometric redshift (z = 2.6) from only IRAC colors, which may be incorrect and may therefore bias our understanding of the physical properties of the source. In addition, their reference for the high submillimeter flux at 850 μm is found to be incorrect in later observations (see Sect. 2). We will provide a revised view on the true nature of this unique SMG, in particular in light of the new NOEMA data which allow for precise localization of submillimeter emission and hence unambiguous identification of its counterparts at other bands. Throughout this paper, we assume a cosmology with H0 = 70 km s−1 Mpc−1, ΩM = 0.27, Ω∧ = 0.73.
2. Data and analysis
2.1. Optical to mid-infrared data
The optical to MIR data we used for photometric analysis are drawn from a -band selected multiwavelength catalog (Ks = 24.3 mag, ID = 73108, Yang et al. 2014) supplemented by the new HST data from the 3D-HST program (Skelton et al. 2014). The 3D-HST data release1 provides calibrated ground-based and HST images, as well as multiwavelength photometric catalogs for five CANDELS fields. The photometric catalog for each field was constructed based on the sources detected in the combined image of three HST /WFC3 NIR bands (F125W, F140W, and F160W). Matching with the coordinate of the Ks-band source for GH500.30 (12:37:13.86; +62:18:26.43), we did not find a counterpart in the 3D-HST photometric catalog suggesting non-detections in the three WFC3/IR bands (F125W, F140W and F160W) down to a 5σ depth of ∼26.2 mag. We attempted to perform manual photometry at the position of the -band source in a circular aperture of radius using the Python photometry routine developed by ourselves to determine whether there is any low-level flux recorded. The background and flux errors were estimated in an annulus area with inner and outer radii of and, respectively. We found only a marginal detection of 26.6 ± 0.3 mag in the H-band (∼ 1.6 μm), and the source is not detected (< 1σ) in any other HST optical and NIR wavelengths (i.e., F435W, F606W, F775W, F850LP, F125W, and F140W). We provide the HST measurements (and 1σ upper limits) in Table 1.
Photometric data of GH500.30.
2.2. FIR and submillimeter data
We take advantage of the FIR data from deep Herschel observations as a part of the GOODS-Herschel program. A detailed description of the observations is given in Elbaz et al. (2011). Since GH500.30 is well separated in the MIPS 24 μm, PACS 100 μm, and PACS 160 μm images, the photometry at these passbands is directly taken from the GOODS-Herschel catalog. Source confusion is a severe issue in the Herschel/SPIRE data where the spatial resolution is poor (θbeam ∼ 20−40″), which makes it difficult to identify the correct counterparts and measure fluxes for individual Herschel sources. As we demonstrated in Shu et al. (2016), some candidate Herschel sources at z ≳ 2 have no measured 500 μm fluxes in the catalog of the GOODS-Herschel data release, which is likely due to the effect of source blending. This is for the case of GH500.30, for which the non-detection in the 500 μm in the catalog is likely due to the incorrect association of its flux with the neighboring galaxy (RA = 12:37:16.83; Dec = 62:18:24.16) at z = 0.84. Therefore, the Herschel/SPIRE flux densities for the source were derived independently from our PSF-fittings with GALFIT (Peng et al. 2002). We used a very similar source extraction and photometry method to the one described in Elbaz et al. (2011), but placed constraints on the 500 μm flux density of the nearby source to be less than the predicted one from SED fittings. We fitted the 24, 100, and 160 μm photometry with a library of CE01 templates to obtain a best-fit SED, using which we predicted the 500 μm flux of ∼ 5 mJy for the nearby contaminating source. The Herschel/SPIRE fluxes from our GALFIT fittings are listed in Table 1. We note that our measurements are consistent with the super-deblended fluxes in the photometry catalog of Liu et al. (2018, ID 3532) where S500 μm = 8.5 ± 0.4 mJy, S350 μm = 11.2 ± 0.8mJy, and S500 μm = 10.7 ± 1.0mJy are found. Although there are a few nearby sources within a radius of seen in the NIR images (Fig. 1) that might contribute to the 500 μm flux, our NOEMA observation at subarcsecond resolution (see below) revealed no other sources close to GH500.30 (with a 3σ upper limit on 1.2 mm flux of ∼ 0.5 mJy, Fig. 1), indicating that the flux contamination from these neighboring sources on the FIR fluxes is negligible.
 |
Fig. 1. Postage-stamp images of GH500.30 from multiwavelength observations. From left to right and top to bottom: HST/ACS (F435+F606+F775+F850LP), HST/WFC3 (F125W+F140W+F160W), CFHT Ks, IRAC [3.6 μm], MIPS 24 μm, PACS 100 μm and 160 μm, SPIRE 250 μm, 350 μm and 500 μm, SCUBA2 850 μm, NOEMA 1.2 mm, VLA 1.4 GHz, and Chandra 0.5–8 keV. Each panel has a size of 20″ × 20″. The detailed photometry is listed in Table 1. |
The source was also detected in the SCUBA2 850 μm with S850 μm = 4.5 ± 0.8mJy (CDFN28, Barger et al. 2014), and AzTEC 1.1 mm with S1.1mm = 2.4 ± 1.1mJy (AzGN26, Perera et al. 2008) and is found to have similar 850 μm flux in the recent SCUBA2 Cosmology Legacy Survey data release (Geach et al. 2017). We note that the source was reported to have much larger 850 μm flux (S850 μm = 10.9 ± 2.9mJy) based on the old SCUBA data (Wall et al. 2008), which is likely attributed to the large contribution from noise artifact, as it lies at the edge of the map where the noise fluctuations are significant.
Recently, GH500.30 has been observed with NOEMA as a part of the program aiming at accurately measuring the FIR SED for a sample of Herschel selected galaxies at z > 3 (Liu et al., in prep.). The observations of GH500.30 were done in the winter of 2016 with 8 antennae in track-sharing mode with other Herschel sources in the sample. The on-source time for GH500.30 is ∼1 h. The synthesized beam is θmaj × θmin ∼ 1.06″ × 0.63″ and the continuum of this source is well detected (spatially unresolved) at the phase center which is predefined as its IRAC position. With the NOEMA data, we obtained an accurate position for the submillimeter source (12:37:13.879; +62:18:26.296) and flux at 1.2 mm (S1.2mm = 2.24 ± 0.16) mJy through uv-plane point-source fittings with the GILDAS2 uv_fit tool. The statistical positional error can be estimated as 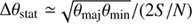 (where θmaj and θmin are the major and minor axes of the beam; e.g., Younger et al. 2007). Given the source’s signal-to-noise ratio (S/N) of ∼ 14, we estimated the positional error at Δθstat ∼ 0.03″. Therefore, the high angular resolution and positional accuracy of the NOEMA data are good enough for us to precisely localize the source position and identify correct counterparts at other bands without confusion problems. For example, the synthesized beam size of ∼1″ at 1.2 mm is comparable with (or better than) the resolution at Ks-band (FWHM ∼ 0.8″) and IRAC (FWHM ∼ 2″). This confirms that the SMG has no optical counterparts in the deep HST imaging.
(where θmaj and θmin are the major and minor axes of the beam; e.g., Younger et al. 2007). Given the source’s signal-to-noise ratio (S/N) of ∼ 14, we estimated the positional error at Δθstat ∼ 0.03″. Therefore, the high angular resolution and positional accuracy of the NOEMA data are good enough for us to precisely localize the source position and identify correct counterparts at other bands without confusion problems. For example, the synthesized beam size of ∼1″ at 1.2 mm is comparable with (or better than) the resolution at Ks-band (FWHM ∼ 0.8″) and IRAC (FWHM ∼ 2″). This confirms that the SMG has no optical counterparts in the deep HST imaging.
2.3. X-ray data
A total exposure of ∼2 Ms has been accumulated on the Chandra Deep Field North (CDFN) as a result of 20 individual observations with Chandra ACIS-I (Alexander et al. 2003b), which is the second deepest X-ray survey ever (see, e.g., Xue et al. 2017 for a review), behind the 7 Ms CDFS (Luo et al. 2017). X-ray data products including event files for each observation and also for the merged data set are publicly available3. The galaxy GH500.30 was clearly detected in the 2 Ms CDFN catalog (XID = 374, Alexander et al. 2003b) with the soft X-ray flux of F0.5−2 keV = 4.71 × 10−16 erg cm−2 s−1 and the hard X-ray flux of F2−8 keV = 1.19 × 10−15 erg cm−2 s−1. In this paper, we used the new CDFN products with the improved data reduction by Xue et al. (2016), which includes a flexible and reliable two-stage source-detection approach, better background estimate, and optimal extractions of X-ray photometry. We note that the separation between the -band and X-ray centroid is ∼0.27″, which is well within the 1σ X-ray source positional uncertainty (∼0.47″).
We obtained 235 ± 17 net counts in the 0.3–7 keV band, corresponding to a 13.8σ detection. We checked the photometry of five periods separately and found no significant source variability in both soft and hard bands. A detailed X-ray spectral analysis will be presented in Sect. 4.1.
2.4. Radio data
The radio flux density at 1.4 GHz (S1.4 GHz = 626 ± 5 μJy) was taken from Barger et al. (2014), which was also listed in the source catalog of the latest VLA observations of the GOODS-North field (Owen 2018). The latest VLA imaging reaches an rms noise in the field center of 2.2 μJy with a resolution of 1.6″. The source is also detected at 5.5 GHz with VLA at a sub-arcsec resolution, with a flux S5.5 GHz = 270.1 ± 7.1 μJy (Guidetti et al. 2017). A compact radio core emission at 1.6 GHz has been detected with the new VLBI observations at a resolution of ∼5 mas (Radcliffe et al. 2016), which yields a flux of S1.6 GHz = 252.5 ± 10.1 μJy. The radio position is coincident with the position found in the submillimeter imaging obtained at the NOEMA.
3. SED and redshift constraints
We used the position of the submillimeter source obtained with NOEMA to identify its counterparts at other bands; namely, X-ray, optical to MIR, FIR and radio. There are no obvious counterparts in the optical and even NIR observed with HST at the position of the submillimeter source. The flux densities and/or upper limits from optical to radio wavelengths are given in Table 1. The postage-stamp images of HST optical and NIR, CFHT, Spitzer/IRAC and MIPS, Herschel PACS and SPIRE, SCUBA2 850 μm, NOEMA 1.2 mm, VLA 1.4 GHz, and Chandra X-ray are presented in Fig. 4. The weak detections in the optical and NIR reveal an extraordinarily red SED in the NIR. For example, the marginal detection at the 1.6 μm by HST implies a S4.5 μm/S1.6 μm flux ratio greater than 70, corresponding to an extremely red color of H-[4.5 μm] > 4.6. We note that it is unlikely that this red color is due to the Lyman break which would otherwise imply a redshift z > 16. Galaxies with red H and IRAC colors are identified to be massive dusty galaxies at either z ∼ 2.5 or z ∼ 4.4 (Wang et al. 2016), but most of them have H-[4.5 μm] colors in the range of 2 < H-[4.5 μm]<3.
It is extremely difficult to measure the redshift of GH500.30 through conventional optical and NIR spectroscopy because of its faintness in the optical and NIR. Here we estimate the photometric redshift (photo-z) by fitting the photometric data points with a suit of SED templates to gain further insights into its nature.
3.1. Photometric redshift from near-infrared data
Since the GH500.30 has extremely red H-[4.5 μm] color indicating unusually high dust extinction (e.g., Huang et al. 2011), the standard templates used by most photo-z codes may not be enough to represent the observed SED of the source. We use Bayesian SED modeling code–BayeSED (Han & Han 2012, 2014) to self-consistently estimate the photometric redshift and infer the physical properties of the galaxy. By employing efficient machine learning methods, such as the artificial neural network (ANN) algorithm, K-Nearest Neighbors (KNN) searching, and the Bayesian inference tool–MultiNest, BayeSED allows a continuous stochastic sampling of the parameter space and provides the posterior probability distribution function of all modeling parameters. This allows us to easily recognize the degeneracies between parameters and to reasonably estimate the parameter uncertainties. We note that the BayeSED code has been extensively tested for both mock and real galaxy catalogs in (Han & Han 2014), and found to show consistent results with the traditional grid-based SED-fitting code FAST (Kriek et al. 2009).
We have used Bruzual & Charlot (2003, BC03) stellar population synthesis models with solar metallicity, assuming the Chabrier (2003) initial mass function (IMF) form in the range 0.1–100 M⊙. We adopted an exponentially declining star-formation history (SFH) with e-folding times in the range of τ = 0.1 − 10Gyr. For our photometric redshift calculations we adopted uniform priors on log(age/yr) in the range of [7.0, 10.1], and a very wide range of dust extinction of mag assuming the standard Calzetti attenuation curve. As another prior, the age of a galaxy is restricted to be less than the age of the universe at that redshift of the galaxy.
We fitted the model templates to the U-band to IRAC 8 μm photometry (including 1σ upper limits) listed in Table 1 to investigate which redshift and how much dust extinction can make the red SED of the GH500.30. Although the source is not detected in most optical and NIR bands, the upper limits suggest a very red SED at λ < 2 μm (Fig. 2) and therefore still provide useful constraints. We assigned zero fluxes to the non-detections and corresponding 1σ errors as the flux uncertainties. The best-fit (maximum likelihood) template from BayeSED yields a redshift at z = 4.19 ± 1.12 and a modest extinction of Av = 2.89 ± 1.8. Such a model template is similar to those obtained in Huang et al. (2011) for a sample of dusty galaxies with similarly red H-[4.5 μm] colors. We note that using the EAZY photo-z package (Brammer et al. 2008) with empirically observed SEDs yields a consistent but slightly higher redshift at z = 4.56 (1σ confidence range 4.21–5.03).
 |
Fig. 2. Optical to MIR SED for GH500.30 (upper panel). The filled circles show the observed photometry, while the downward arrows indicate 1σ upper limits. The red curve shows the best-fit (maximum likelihood) SED based on BayeSED modeling, whilst the black curve represents the best-fit SED from FAST. We also plot the fit with an extremely dusty template (AV = 9:8 and zphot = 0:64) for comparison (gray curve). The HST H-band image is shown in the inset left panel. Insert right panel shows the χ2 contours of redshift vs. dust extinction (AV) from the FAST SED fittings. Lower panel: data to model ratios for the BayeSED fitting at z = 4:19 (black solid circles) and for the FAST SED fitting at z = 0:64 (gray solid circles). Only detected fluxes above 1 μm are shown. |
For a consistency check, we also used FAST to perform SED fittings to the U-band to IRAC 8 μm photometry. We assumed the solar metallicity and exponentially declining SFH with e-folding times in the range τ = 0.1 − 10Gyr. We adopted the standard Calzetti law with a very wide range of dust extinction of 0 < Av < 10. The best-fit template from FAST yields a redshift at z = 4.18 with a modest extinction of Av = 2.9, which are in good agreement with the fitting results from the BayeSED. The best-fit SED templates are shown in Fig. 2.
One uncertainty in the above photo-z analysis is the degeneracy between the redshift and dust extinction in the SED fittings. As we show in Fig. 2, if we allow very large extinctions, the red SED of GH500.30 can be reproduced by a highly reddened galaxy (Av ∼ 10) at z < 1. However, we argue that this possibility of an extremely dusty low-z galaxy can be ruled out given its significant FIR to submillimeter emission. Furthermore, SED fittings to submillimeter-selected galaxies generally give Av ∼ 0 − 5 (Yun et al. 2012; da Cunha et al. 2015). For example, the stellar population analysis for the GN 10, which is a known dusty galaxy at z = 4.05, yields Av ∼ 3 (Daddi et al. 2009a). This value is very similar to that obtained from our best-fit (maximum likelihood) template for the GH500.30. Figure 3 shows the posterior probability distributions on the redshift, dust extinction and the stellar mass from the BayeSED fittings. Although degeneracies in stellar population modeling parameters do exist, the Bayesian analysis suggests that significant dust extinction (i.e., Av > 7) is unlikely.
 |
Fig. 3. Joint one- and two-dimensional posterior probability distributions (normalized to unit area) of redshift, dust extinction, and stellar mass for GH500.30. The color coding represents confidence levels. The joint 90 and 95% confidence contours are shown in black. |
Another uncertainty is the existence of an AGN, which may have effects on the NIR photometric analyses. The galaxy GH500.30 shows a featureless power-law continuum in the IRAC bands, with the brightest being the 8 μm; if due to the stellar emission, this would imply that the rest-frame 1.6 μm bump is beyond the 5.8 μm channel, or z ≳ 3.5. However, the IRAC emission can also be due to a reddened and obscured AGN, as indicated by a slight excess emission at 8 μm compared with the best-fit SED template (Fig. 2). Yun et al. (2008) proposed that a young dusty starburst at high redshift is able to generate similar red IRAC colors as obscured AGNs. The galaxy GH500.30 appears to fall into the red power-law region in the IRAC color-color diagram of Yun et al. (2008), where AGNs and young and extremely dusty starbursts at z > 3 overlap. Although it is difficult to disentangle the relative contribution of the two causing the IRAC power-law spectral slope, we compared the S500 μm/S24 μm flux ratio to Mrk 231, a local FIR luminous Compton-thick AGN. For a fair comparison we redshifted the SED of Mrk 231 to z = 4.19 (the best-fit photometric redshift for GH500.30) to derive the S500 μm/S24 μm ratio. We found the S500 μm/S24 μm flux ratio of GH500.30 is a factor of 3.9 higher than that in Mrk 231, indicating that the source may have low levels of the warm dust emission due to an AGN. In fact, we estimated that an AGN may contribute at an approximately 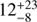 % level to the rest-frame MIR continuum emission (Sect. 4.3). We note that by using only a library of pure AGN- or hybrid AGN-galaxy templates4, we obtained a best-fit photometric redshift at
% level to the rest-frame MIR continuum emission (Sect. 4.3). We note that by using only a library of pure AGN- or hybrid AGN-galaxy templates4, we obtained a best-fit photometric redshift at 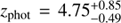 , a value consistent with that estimated assuming stellar templates within errors. Yang et al. (2014) obtained a similar best-fit redshift of
, a value consistent with that estimated assuming stellar templates within errors. Yang et al. (2014) obtained a similar best-fit redshift of 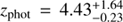 by using an optimal combination of galaxy and AGN templates. We therefore conclude that the existence of an AGN has a small effect on the photo-z estimation of GH500.30. In fact, the AGN’s emission at the rest-frame UV/optical is likely heavily attenuated considering the strong absorption inferred from the X-ray observations (Sect. 4.1).
by using an optimal combination of galaxy and AGN templates. We therefore conclude that the existence of an AGN has a small effect on the photo-z estimation of GH500.30. In fact, the AGN’s emission at the rest-frame UV/optical is likely heavily attenuated considering the strong absorption inferred from the X-ray observations (Sect. 4.1).
3.2. Photometric redshift from far-infrared SED
An independent estimate of the redshift for GH500.30 can be performed from its FIR emission, because the mid-to-far-IR emission has a generally well-defined peak at the rest-frame 50–200 μm. There have been a number of previous studies exploring the use of the FIR-radio relation to constrain the redshifts of SMGs (e.g., Carilli & Yun 1999; Wang et al. 2009; Barger et al. 2012), which would be helpful when a galaxy suffers from extremely heavy extinction in the rest-frame optical/NIR bands. The main uncertainty of this method is the dust temperature which is still poorly constrained for high-z SMGs.
We use the available photometry in Table 1 at 24 μm, 100 μm, 160 μm, 250 μm, 350 μm, 500 μm, 850 μm, 1.1 mm and 20 cm (Fig. 4), and compare them to a suite of 105 template SEDs from the Chary & Elbaz (2001) library (CE01 hereafter), as a function of redshift. The CE01 templates are sorted by IR luminosities from Log Log LIR/L⊙ = 8.41 to Log LIR/L⊙ = 13.55, with dust temperatures becoming warmer with increasing luminosity. We calculate the χ2 values between the observed flux densities of GH500.30 and predictions for each SED model of given luminosity as a function of redshift. We choose a redshift grid from z = 0.1 to z = 8 in steps of δz = 0.1. We note that an AGN contributes significantly to the radio emission, higher than the predicted value from any SED template by a factor of more than 20. Such radio excess could bias the best-fit redshift. We are therefore excluding the radio data in our FIR SED fits. Figure 4 (bottom) shows the χ2 values for each of best-fit SED model as a function of redshift (thin curve). The best-fitting redshift is zphot = 3.1 and the 90% confidence interval is 2.51 < z < 4.35, which agrees with the NIR photometric redshift within the errors (Sect. 3.1). We note that this analysis allows us to reject the possibility of a highly reddened low-redshift galaxy (i.e., at z ∼ 0.6).
 |
Fig. 4. Top panel: FIR to radio SED of GH500.30 (open squares). The black curve shows the best-fit SED among all 105 CE01 templates. The best-fits with Mrk 231, Arp 220 and M82 SED are shown in red, green and blue curves, respectively. The fill squares are observed Spitzer/IRAC fluxes. Bottom panel: χ2vs. redshift. The black curve represents the results from the best-fit CE01 SED at each redshift, and the color-coded curves are for the Mrk 231, Arp 220 and M82 SED. The horizontal dashed line shows the 90% confidence interval for the redshift. The lower panel at the bottom shows the IR luminosities from CE01 templates that allow for the minimum χ2 at each redshift. The vertical gray curve represents the best-fit redshift (z = 4.19) from the optical-to-NIR SED. |
As mentioned above, the dust temperature can bias the redshift estimation from the FIR to radio SED fittings. For instance, SED templates with lower dust temperature can decrease the best-fit redshift. This can be seen in Fig. 4 (bottom) which shows the best-fit FIR luminosity that gives the least χ2 value at each redshift. Since the CE01 templates are sorted such that the dust temperatures become warmer with increasing luminosity, the lower FIR luminosity inferred at z < 2 is suggestive of lower dust temperature for the best-fit template. For comparison, we also estimated the redshift of GH500.30 by fitting the well-studied SEDs of local galaxy Mrk 231 (an obscured AGN with warm dust), Arp 220 (luminous starburst with cool dust), and M82 (low-luminosity starburst with warm dust). The 24 μm flux is excluded in the SED fittings, as it can bias the fit statistics. The best-fit comes from Mrk 231 at z = 4.9, whilst the fit with the Arp 220 template yields a relatively low redshift of z = 3.7. This is perhaps not too surprising since the Arp 220 SED has a colder dust temperature. The best fit of the CE01 templates yielding a lower redshift at z = 3.1 is perhaps due to the very wide range of SED models. Generally speaking, the CE01 models provide good fits in the z ∼ 2.5−4.5 range at a 90% confidence level.
Our analysis suggests that the result of the FIR redshift for GH500.30 highly depends on its dust temperature which cannot be determined independently. In addition, as shown in Fig. 4 (upper panel), the best-fit CE01 SED at z = 3.1 overpredicts the observed fluxes at <10 μm. This may be due to the poor calibrations of the optical/NIR part of the CE01 templates, and/or heterogeneous dust extinction from a more complicated dust distribution (e.g., Daddi et al. 2009a).
Therefore, we favor the NIR redshift of z = 4.19 for GH500.30 in this paper, though we cannot fully rule out a lower redshift of z ∼ 3.1 from the FIR SED fittings. We note that Liu et al. (2018) obtained a redshift of z = 3.988 by independent FIR SED fittings in which the Magdis et al. (2012) library of main sequence and starburst galaxies was used as a template.
3.3. Ultraviolet to far-infrared broadband SED fittings
It should be noted that the NIR and FIR SED analyses presented above were modeling the stellar and dust emission properties separately, and do not take into account the AGN component. Now, we employ the MAGPHYS code (da Cunha et al. 2008, 2015) to model the UV-optical to submillimeter broadband SED in a more consistent way. MAGPHYS is built on a global energy balance between stellar and dust emissions: the UV/optical emission from stellar continuum is absorbed by dust grains in star-forming regions, which re-radiate the absorbed energy in the MIR to FIR wavelengths. Here we used the latest version of MAGPHYS that includes the contribution by AGN emission to the SEDs (de Cunha et al., in prep.). This allows us to disentangle the AGN emission from the broadband SED. The AGN emission is modeled using a set of empirical templates from Richards et al. (2006), Polletta et al. (2007), Prieto et al. (2010), and Mullaney et al. (2011), which span a wide range of representative AGN SEDs including type 2 AGNs, type 1 AGNs and quasars as shown in Chang et al. (2017). The contribution of the AGN template to the total IR luminosity is defined as 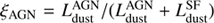 , which is allowed to vary between 0 and 1 for each of the templates.
, which is allowed to vary between 0 and 1 for each of the templates.
Since MAGPHYS was designed to perform SED fittings with known redshifts, we fixed the redshift at zphot = 4.19 for GH500.30. The result of the MAGPHYS SED fitting is shown in Fig. 5 (left panel), which reproduces the broadband SED of GH500.30 well, with 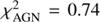 . The SED fitting appears to tightly constrain the AGN fraction based on the detection of MIR photometric point at the 24 μm (which differentiates between AGNs and star-forming galaxies). The posterior probability distribution suggests that the AGN component contributes at most ∼ 30% to the total IR luminosity, with ∼18% being the most probable level of contribution. The SED fitting assuming the source at zphot = 3.1 is also plotted in Fig. 5 (right panel), which yields an even smaller best-fitted AGN fraction of ∼1%. The dust and stellar properties inferred from the MAGPHYS fittings will be discussed in the following section.
. The SED fitting appears to tightly constrain the AGN fraction based on the detection of MIR photometric point at the 24 μm (which differentiates between AGNs and star-forming galaxies). The posterior probability distribution suggests that the AGN component contributes at most ∼ 30% to the total IR luminosity, with ∼18% being the most probable level of contribution. The SED fitting assuming the source at zphot = 3.1 is also plotted in Fig. 5 (right panel), which yields an even smaller best-fitted AGN fraction of ∼1%. The dust and stellar properties inferred from the MAGPHYS fittings will be discussed in the following section.
 |
Fig. 5. SED fittings to the broadband UV to submillimeter data with MAGPHYS at z = 4.19 (left panel) and z = 3.1 (right panel). The thick orange line represents the AGN component, with contributions that are estimated at 18% and 1% to the total IR SED, respectively. The red solid circles are the photometric data and the black lines are the best-fitting model. The corresponding data to model ratios are shown in the middle panels. The blue line represents the (unattenuated) star formation component. The attenuated stellar emission and the reproduced dust emission are shown with the green line. The posterior probability distribution of best-fitting parameters are shown in the lower panels. The dashed lines are the median values and the dotted lines are the best-fitting values. |
4. Properties of GH500.30
4.1. A heavily obscured AGN in GH500.30
Here we investigate the detailed properties of the X-ray source presented in Sect. 2. Although some results from X-ray spectral fitting have been shown by Laird et al. (2010), they assumed a much lower redshift of z = 2.6 for the source, which may result in different spectral parameters from ours. We emphasize that the analysis presented in this paper is more robust, because it is based on new constraints on the redshift and updated X-ray data reduction. The spectral data were grouped to have at least 1 count per bin and the C-statistics was adopted for minimization. Spectral fittings were performed in the 0.5–7 keV band using the XSPEC (Version 12.6). All statistical errors provided hereafter correspond to 90% confidence for one interesting parameter (Δχ2 = 2.706). Throughout the model fittings, the Galactic column density was considered and fixed at 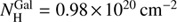 (Kalberla et al. 2005). We performed the spectral fitting with a simple absorbed power-law (wabs*(zwabs*zpowerlaw)), assuming z = 4.19. The best-fitting parameters are
(Kalberla et al. 2005). We performed the spectral fitting with a simple absorbed power-law (wabs*(zwabs*zpowerlaw)), assuming z = 4.19. The best-fitting parameters are 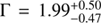 and
and 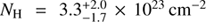 , with C = 162.5 for 163 degrees of freedom. Such a Γ is typical in X-ray bright Seyfert galaxies (e.g., Tozzi et al. 2006). The measured indicates that the source is heavily absorbed but not Compton-thick. The 99% confidence contour of the vs. Γ shown in Fig. 6 implies an upper limit of NH < 1024 cm−2. No prominent iron Kα line is observed at 1.233 keV (i.e., rest-frame 6.4 keV based on the photo-z). We therefore obtained an upper limit on the rest-frame equivalent width of the line of ∼760 eV. This best-fitting model gives the observed X-ray fluxes of f0.5−2 keV = 4.8 × 10−16 erg cm−2 s−1 and f2−10 keV = 1.5 × 10−15 erg cm−2 s−1. As can be see in Fig. 6 (a) and (b), a positive excess in the fit residuals was present around 1.5 keV. Therefore, we added a redshifted Gaussian emission component to test whether or not it is significant. The addition of this component improves the fit moderately with for two extra free parameters (Fig. 6 c). If assuming it to be the Fe Kα line at 6.4 keV, the best-fit yields a redshift of
, with C = 162.5 for 163 degrees of freedom. Such a Γ is typical in X-ray bright Seyfert galaxies (e.g., Tozzi et al. 2006). The measured indicates that the source is heavily absorbed but not Compton-thick. The 99% confidence contour of the vs. Γ shown in Fig. 6 implies an upper limit of NH < 1024 cm−2. No prominent iron Kα line is observed at 1.233 keV (i.e., rest-frame 6.4 keV based on the photo-z). We therefore obtained an upper limit on the rest-frame equivalent width of the line of ∼760 eV. This best-fitting model gives the observed X-ray fluxes of f0.5−2 keV = 4.8 × 10−16 erg cm−2 s−1 and f2−10 keV = 1.5 × 10−15 erg cm−2 s−1. As can be see in Fig. 6 (a) and (b), a positive excess in the fit residuals was present around 1.5 keV. Therefore, we added a redshifted Gaussian emission component to test whether or not it is significant. The addition of this component improves the fit moderately with for two extra free parameters (Fig. 6 c). If assuming it to be the Fe Kα line at 6.4 keV, the best-fit yields a redshift of 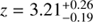 , and a rest-frame equivalent width of the line
, and a rest-frame equivalent width of the line 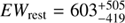 eV. The significance of the line detection was at <99% confidence level for two parameters (i.e., redshift and normalization). If it is real, the best-fit value of redshift is consistent with that obtained from the FIR SED fittings (z = 3.1, Sect. 3.2). However, due to the limited spectral resolution and statistics of the Chandra data, the possibility for the presence of a line emission at Eobs ∼ 1.52 keV is still low. If we fix the redshift at z = 3.1 in the spectral fittings without a Gaussian line, the residuals vanish as well (Fig. 6 d), suggesting that the line feature is likely not real.
eV. The significance of the line detection was at <99% confidence level for two parameters (i.e., redshift and normalization). If it is real, the best-fit value of redshift is consistent with that obtained from the FIR SED fittings (z = 3.1, Sect. 3.2). However, due to the limited spectral resolution and statistics of the Chandra data, the possibility for the presence of a line emission at Eobs ∼ 1.52 keV is still low. If we fix the redshift at z = 3.1 in the spectral fittings without a Gaussian line, the residuals vanish as well (Fig. 6 d), suggesting that the line feature is likely not real.
 |
Fig. 6. Chandra X-ray spectrum for GH500.30. The red solid line is the best-fit model (wabs*zwabs*zpowerlaw in XSPEC), with the data to model ratio shown in panel b. The inset panel shows the χ2 contours of the photon index Γ vs. column density at the 68%, 90% and 99% confidence levels (from the inside out). Panel c: data/model residuals after including a Gaussian line at Eobs = 1.52keV. Panel d: data/model residuals by fixing redshift at z = 3.1. |
The absorption-corrected luminosity in the rest frame 2–10 keV, which can be estimated as 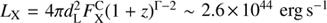 and 1.6 × 1044 erg s−1, for a source at z = 4.19 and z = 3.1, respectively, places GH500.30 at the low end of the X-ray luminosity range for type-2 quasars. Therefore it is likely that GH500.30 hosts a heavily obscured AGN (but not Compton thick), which is one of the X-ray luminous objects found among the SMG population (Alexander et al. 2005; Wang et al. 2013). However, we note that the uncertainties in redshift and the geometry of the obscuring material might affect the derivation of the intrinsic luminosity.
and 1.6 × 1044 erg s−1, for a source at z = 4.19 and z = 3.1, respectively, places GH500.30 at the low end of the X-ray luminosity range for type-2 quasars. Therefore it is likely that GH500.30 hosts a heavily obscured AGN (but not Compton thick), which is one of the X-ray luminous objects found among the SMG population (Alexander et al. 2005; Wang et al. 2013). However, we note that the uncertainties in redshift and the geometry of the obscuring material might affect the derivation of the intrinsic luminosity.
We investigated whether the uncertainty in redshift could affect the estimation of the amount of absorption from spectral fittings. We run simulations in XSPEC using the wabs*(zwabs*zpow) model by fixing Γ = 1.8 and varying NH to construct hardness ratio tracks as a function of redshift (e.g., Wang et al. 2013). The results are shown in Fig. 7. The value constrained in this way is not distinguished from the one derived from spectral fitting, suggesting that the GH500.30 is heavily obscured, with NH < 1023 cm−2 if at z > 3. We note that the intrinsic luminosity could be considerably greater than the observed luminosity if the obscuration is much higher.
 |
Fig. 7. Hardness ratio between the 2–8 keV (hard) and 0.5–2 keV (soft) bands (i.e., X-ray hardness) as a function of redshift. The dashed lines are simulated tracks for an absorbed power-law with photon index fixed at 1.8. The red star is the X-ray hardness for GH500.30. For comparison, we also plot in gray dots the hardness ratios for SMGs in Wang et al. (2013), which include the most distant Compton-thick AGN, LESS J033229.4-275619 at z = 4.76 (red circle). |
4.2. Infrared luminosity and star formation rate
Given the large X-ray luminosity, the bolometric output from the central AGN in GH500.30 can heat up the interstellar dust and this may contribute to a substantial fraction of the FIR luminosity of the host galaxy. We derived the FIR luminosity of GH500.30 by fitting the data at wavelengths greater than 24 μm with a suit of CE01 templates assuming the galaxy is located at z = 4.19, and integrating the best-fit SED between rest-frame 8 μm and 1000 μm. The inferred total IR luminosity is 8.4 × 1012 L⊙. Using the SEDs of local galaxies (M82, Arp 220 and Mrk 231) as templates yields consistent luminosities in the range (7.8 − 8.6) × 1012 L⊙. The unabsorbed X-ray to FIR luminosity ratio of GH500.30 is LX/LFIR = 0.008. This value is very similar to that found by Alexander et al. (2005) (median LX/LFIR = 0.004), but is an order of magnitude smaller than those found in quasars (LX/LFIR ∼ 0.05; Elvis et al. 1994; Alexander et al. 2005). The reason why the luminosity ratio is so much smaller than those in quasars is the extreme FIR luminosity of the source. This suggests that the large FIR luminosity of GH500.30 is not mainly powered by the AGN, but should be attributed to intense star formation activities. This is consistent with the estimate that the AGN contributes at most ∼ 30% of the total IR luminosity from the MAGPHYS SED fittings (Sect. 3.3).
The SFR for GH500.30 can be estimated with the relation SFR = 1.7 × 10−10 LIR/L⊙ (e.g., Kennicutt 1998). Subtracting the 30% AGN contribution from the total IR luminosity, we obtained a SFR of 1001 M⊙ yr−1 with a Salpeter IMF and 623 M⊙ yr−1 if assuming a Chabrier IMF. We note that MAGPHYS gives similarly high dust luminosity (8.0 × 1012 L⊙) produced by the star formation activities. This suggests the source to be among the most extreme star-forming galaxies seen in the early universe (e.g., Casey et al. 2014 and references therein).
4.3. Stellar population
As shown in Fig. 2, the NIR SED of GH500.30 is nearly a power law in the IRAC bands but shows a clear spectral break between 1.6 and 3.6 μm. This cannot be fully explained by a normal extinction curve. The best-fit template from the BayeSED modeling is at z = 4.19 with the Calzetti extinction of Av = 2.89. In this scenario, the red H-[4.5 μm] color is mainly due to the redshifted 4000 Å Balmer break at z > 4, which is a signature of existence of older stellar population. The stellar population model from BayeSED agrees with this interpretation: the best-fit template has an age of 0.67 Gyr (maximum likelihood value), which is about half the age of the universe at z = 4.19. On the other hand, GH500.30 has a very strong FIR emission, very similar to GN10 (Wang et al. 2009), implying an intensive ongoing starburst and the formation of a young galaxy. There seems to be a two-component SED model to reconcile the old stellar population and very dusty star-forming component seen in the FIR, but the current data are insufficient for further decomposing the two components in GH500.30. It is possible that the star-forming component is extremely dusty, such that its rest-frame UV and optical light being largely obscured along our line of sight, and the NIR SED in the IRAC bands is dominated by an older stellar population with a moderate extinction of Av < 3. We note that the optical/NIR and IRAC data cannot constrain the stellar age well because of its degeneracy with the dust attenuation. By marginalizing a wider range of SFRs, the MAGPHYS SED fittings yield a stellar age of ∼ 0.4 Gyr with a higher Av = 4.1. The galaxy GH500.30 is not resolved by the NOEMA (beam size of ∼1.06”). We overlaid the NOEMA contours on the NIR Ks-band image, and found an offset of ∼0.2” between the NOEMA and Ks-band centroid. The latter image is also found to show a clear extension to the northwest (Fig. 8). This suggests that the dusty star forming region may be different from that producing MIR emission. However, though the NOEMA’s positional accuracy is high (∼0.03”), the astrometric accuracy of observations at Ks-band is not as good. Wang et al. (2010) have shown that typical astrometric uncertainty at Ks-band for a source with S/N > 20 and FWHM < 1.2” is ∼0.05”. Given the relatively low S/N of GH500.30 detected at Ks-band, we estimated a positional error of ∼0.2”. Such an offset should therefore be considered as tentative. We note that recent high-resolution submillimeter and/or radio observations have confirmed that some SMGs indeed show significant spatial offsets between the positions of dust emission and the UV/optical emission (e.g., Schinnerer et al. 2008; Chen et al. 2015; Hatsukade et al. 2015; Elbaz et al. 2018).
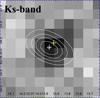 |
Fig. 8. NOEMA contours (white) overlaid on the Ks-band image. The white and yellow cross represents the NOEMA 1.2 mm (beam size of ∼1.06″ × 0.63″) and Ks-band centroid, respectively. The image has a size of 3″ × 3″. |
We argue that the AGN component is not a major contribution in the MIR. Using the intrinsic, absorption-corrected X-ray luminosity from Sect. 4.1, we can estimate the rest-frame 6 μm luminosity due to the AGN, and compare it with the total 6 μm luminosity measured in the MIR. Assuming that the X-ray-to-MIR luminosity relationship for local AGNs (Lutz et al. 2004) holds at high redshift, the intrinsic 2–10 keV luminosity suggests a 6μm luminosity of 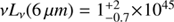 erg s−1 for the AGN. We derived total 6 μm luminosity from the 24 μm flux (the MIR spectral slope of α=1.8, Sv ∝ v−∝ is used for the small K-correction, Coppin et al. 2010), and found vLv(6 μm) = 8.6 × 1045 erg s−1. Taking into account the dispersion of the X-ray to MIR luminosity relation, the AGN may contribute ∼ 4 – 35% of the observed 24 μm emission, consistent with the inferred fraction of AGN contribution to the total IR luminosity from the MAGPHYS fittings (Sect. 3.3). As shown in Fig. 5, assuming the 24 μm flux is completely due to the AGN, the extrapolation of the best-fitting AGN SED to the IRAC bands yields a contribution to the IRAC fluxes of less than 10%. We note that Riechers et al. (2014) recently presented a measurement of ∼ 30–60% AGN contribution to the MIR continuum emission in GN20, an X-ray detected bright SMG at z = 4.05, from the Spitzer/IRS spectral decomposition5. In Fig. 9, a comparison between the NIR SED of GN20 and the GH500.30 (scaled to the 24 μm flux) is shown. This comparison suggests that the presence of an obscured AGN in GH500.30 is likely, but its contribution to the MIR emission is not as much as in GN 20. For comparison, we also plot the SED of the extremely dusty SMG GN 10 (Wang et al. 2009). Because of the strong dust extinction, the AGN contribution to the IRAC flux densities in GN10 is even smaller, which is consistent with its non-detection in the X-rays.
erg s−1 for the AGN. We derived total 6 μm luminosity from the 24 μm flux (the MIR spectral slope of α=1.8, Sv ∝ v−∝ is used for the small K-correction, Coppin et al. 2010), and found vLv(6 μm) = 8.6 × 1045 erg s−1. Taking into account the dispersion of the X-ray to MIR luminosity relation, the AGN may contribute ∼ 4 – 35% of the observed 24 μm emission, consistent with the inferred fraction of AGN contribution to the total IR luminosity from the MAGPHYS fittings (Sect. 3.3). As shown in Fig. 5, assuming the 24 μm flux is completely due to the AGN, the extrapolation of the best-fitting AGN SED to the IRAC bands yields a contribution to the IRAC fluxes of less than 10%. We note that Riechers et al. (2014) recently presented a measurement of ∼ 30–60% AGN contribution to the MIR continuum emission in GN20, an X-ray detected bright SMG at z = 4.05, from the Spitzer/IRS spectral decomposition5. In Fig. 9, a comparison between the NIR SED of GN20 and the GH500.30 (scaled to the 24 μm flux) is shown. This comparison suggests that the presence of an obscured AGN in GH500.30 is likely, but its contribution to the MIR emission is not as much as in GN 20. For comparison, we also plot the SED of the extremely dusty SMG GN 10 (Wang et al. 2009). Because of the strong dust extinction, the AGN contribution to the IRAC flux densities in GN10 is even smaller, which is consistent with its non-detection in the X-rays.
 |
Fig. 9. NIR SED of GH500.30 at λ > 1 μm (filled squares) for GH500.30, compared to SEDs of another two bright SMGs at z = 4, GN 20 (circles) and GN 10 (triangles). The flux densities are scaled to the 24 μm flux of GH500.30. |
Having established that the observed IRAC fluxes are dominated by old stars, we can estimate the stellar mass for GH500.30. The best-fit SED model from the BC03 stellar population yields a stellar mass of Mstar = 3.5 × 1011 M⊙. We note that the MAGPHYS SED fittings yielded an even higher stellar mass of 8.9 × 1011 M⊙, which may be due to higher dust attenuation Av inferred, as there is a degeneracy between the two (Fig. 3). This mass is similar to those for typical SMGs at z ≳ 4 (e.g., Huang et al. 2014; Michałowski et al. 2012; Smolčić et al. 2015), but is larger than that of coeval UV-selected star-forming galaxies which have stellar masses of ∼1010 – 1010.5 M⊙ (e.g., Stark et al. 2007, 2009). For comparison, Borys et al. (2005) have studied stellar components of 13 SMGs in the GOODS-North field, and found stellar masses of ∼1011 – 1012 M⊙ and a mean stellar mass of ∼2 × 1011 M⊙. Although the posterior probability distribution on Av is weakly constrained (Fig. 3), the maximum likelihood value of Av from the best-fitting model is also comparable to those found in SMGs with rest-frame optical spectroscopy observations by Swinbank et al. (2004, Av = 3.0 ± 1.0), Borys et al. (2005, Av = 1.7 ± 0.2), and Takata et al. (2006, Av = 2.9 ± 0.5). To summarize, GH500.30 appears to be a massive galaxy with an old stellar population (∼0.4−0.6 Gyr) and moderate dust extinction of Av ∼ 3 – 4, which may be spatially offset from the extremely dusty starburst region. Given its extreme faintness at wavelengths λ < 2μm, massive galaxies like GH500.30 at z ≳ 4 may be missed in deep optical and even NIR surveys with HST (Wang et al. 2016).
5. Discussion
The galaxy GH500.30 shares many properties with GN 10, one of the bright SMGs in the GOODS-North field confirmed at z = 4.05. Both sources are incredibly faint at all optical to NIR wavelengths at λ ≲ 2 μm, with extremely red colors of H-[4.5 μm] ≳ 4, indicating the existence of an older stellar population if found to be due to a strong, redshifted 4000 Å Balmer break. One unique property of GH500.30 is its significant detection in the X-rays and radio, suggesting the presence of an AGN. The full-band ∼250 net counts ensure meaningful X-ray spectral fitting, and hence put strong constrains on the absorption of 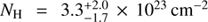 . This is one of the most distant heavily obscured AGNs confirmed by direct X-ray spectral analysis. The most distant Compton-thick AGN discovered so far is LESS J033229.4-275619 (Gilli et al. 2011), which is also a submillimeter bright dusty starburst galaxy. However, unlike GH500.30, its rest-frame UV/optical light is only partially obscured along our line of sight, suggesting less dust extinction or a different dust distribution in the star-forming region. In addition, no significant radio emission due to the AGN is detected in LESS J033229.4-275619.
. This is one of the most distant heavily obscured AGNs confirmed by direct X-ray spectral analysis. The most distant Compton-thick AGN discovered so far is LESS J033229.4-275619 (Gilli et al. 2011), which is also a submillimeter bright dusty starburst galaxy. However, unlike GH500.30, its rest-frame UV/optical light is only partially obscured along our line of sight, suggesting less dust extinction or a different dust distribution in the star-forming region. In addition, no significant radio emission due to the AGN is detected in LESS J033229.4-275619.
5.1. Can GH500.30 -like objects fit into the evolutionary sequence?
The formation and co-evolution of AGNs and stellar populations are focuses of a large amount of current research. It is believed that the starburst and the growth of SMBHs are generally triggered by major mergers of gas-rich galaxies (see e.g., Hopkins et al. 2008, and references therein). Intense starburst rapidly enshrouds a forming galaxy in cold dust which emits at submillimeter wavelengths. This is followed by an increase in fueling of the SMBH, triggering an AGN and generating X-ray and radio emission. Finally, AGN feedback affects star formation in the host galaxy by removing the dust and gas, leaving a quiescent massive galaxy (e.g., Sanders et al. 1988; Hopkins et al. 2006; Narayanan et al. 2010). In this scenario, GH500.30 may be in the early transition phase from a starburst SMG to an obscured quasar where a radio-mode feedback is in place, making it a powerful probe of evolutionary models.
GH500.30 appears to be a luminous massive starburst, forming stars at a rate of ∼ 1000M⊙ yr-1, with properties representative of SMGs at z ∼ 2−4. The presence of an AGN has been suggested for approximately 25% of the SMG population at z ∼ 2 (Alexander et al. 2005; Wang et al. 2013). Assuming that all bright SMGs go through a subsequent AGN phase, the inferred AGN fraction may represent a “duty cycle” for BH accretion. The current total lifetime estimates from modeling SMGs are ∼ 100−300 Myr (e.g., Swinbank et al. 2006), and thus the AGN-dominated phase caught by the X-ray/radio would be occurring during the last ∼ 25−75 Myr of an SMG lifetime. These relative lifetimes and duty cycle are consistent with the merger simulations of Hopkins et al. (2008). It is therefore possible that the BH accretion in GH500.30 is at a transition phase to an obscured quasar, or a protoquasar phase where the BH is growing more rapidly than in typical quasars and is still not completely buried in the central dust and gas-rich region at the approximately parsec scale, as in the dusty torus (e.g., Alexander et al. 2005; Kawakatu & Wada 2009; Tamura et al. 2010). Tentative evidence for this has been found in typical SMGs where the BH-to-galaxy mass ratio is found to be lower than in z ∼ 2 quasars (Alexander et al. 2008b; Coppin et al. 2008). One puzzling property of GH500.30 is that while strong AGN emission is observed in the X-rays and radio, it does not contribute significantly to the MIR fluxes (Sect. 4.3). This may be because the AGN is attenuated by dust on a larger scale in the host (from starburst) rather than a torus component which may have not yet fully formed in GH500.30.
5.2. Young powerful radio jet in a transitional submillimeter galaxy
Another unique property of GH500.30 is its extremely strong radio emission. The rest-frame 1.4 GHz monochromatic luminosity is 6.6 × 1025 W Hz-1, and the ratio of rest-frame 1.4 GHz to rest-frame 4400 Å (observed Ks ) flux densities is ∼ 580, which qualifies GH500.30 as radio loud (Stern et al. 2000). To derive the rest-frame 1.4 GHz flux, we used a typical radio slope of Sv ∼ v−0.7 (e.g., Thomson et al. 2014) for the K-correction assuming the source at z = 4.19. However, because the observed -band flux is dominated by stellar population and the AGN optical emission is heavily attenuated, we should treat this estimation with caution. Alternatively, the radio loudness can be measured from the ratio of the flux densities between 5 GHz and the X-ray, RX = vLv(5GHz)/LX, where 5 GHz luminosity is in the rest-frame and LX is the intrinsic luminosity in the 2–10 keV band. We obtained a logRX value of −2.29, placing GH500.30 as a radio-loud object where radio-loud is defined as logRX > −4.5 (Terashima & Wilson 2003). Using the rest-frame FIR luminosity from the best-fit SED template, we obtain qIR = 1.04 which is defined as the logarithmic ratio of the rest-frame 8–1000 μm flux and the 1.4 GHz flux density. This is twenty times more radio loud than the normal value of 2.4 ± 0.24 for FIR-selected star-forming galaxies (Ivison 2010). For comparison, the ratio between the FIR and radio emission in GH500.30 is much less than most of the radio excess sources studied with Herschel in the GOODS-North field (Fig. 10 a). The detection of a radio-luminous AGN at such a high redshift (z ≳ 4) is rare, but may provide us new insights into the earliest stages of jet formation and AGN evolution.
 |
Fig. 10. Upper panel: rest-frame FIR (42.5–122.5 μm) vs. radio 1.4 GHz luminosity for GH500.30 (red star, assuming at z = 4.19 and z = 3.1, respectively). Radio-excess sources from Del Moro et al. (2013) are plotted as filled circles for comparison. The solid line corresponds to q = 2.21 (average for “radio-normal” sources) and the dotted line correspond to q = 1.68, for the selection limit for radio-excess sources. Lower panel: radio slope based on the observations at 1.4 GHz and 5.5 GHz. The 1.6 GHz flux obtained from the high-resolution VLBI observation is shown for comparison. The light-red shaded region shows the 1.4 GHz radio flux expected from the star-formation process, which is derived by extrapolating the best-fitting SED model to 1.4 GHz (Fig. 4). |
A compact radio core emission has been observed for GH500.30 with VLBI at ∼5 ymas scale (Radcliffe et al. 2016), corresponding to a linear size less than 1 kpc at the source redshift. This is similar to those of compact steep-spectrum (CSS) radio sources, a class of AGNs mostly composed of young radio galaxies (O’Dea 1998). As shown in Fig. 10 b, the VLBI observation resolves out ∼70% of the radio flux observed with VLA at a resolution of 1.6”. We note that most of the emission that is invisible to high-resolution VLBA imaging tends to be the extended component of the jet emission, such as lobes on larger scales, rather than the star-forming process. The latter is estimated to represent only ∼5% of the total radio flux observed by VLA. Therefore, strong interactions between the jet and the dense nuclear ISM are anticipated in GH500.30, which may signify the earlier stage of the feedback from AGN jet mechanical energy. Based on the VLA observations at 1.4 GHz and 5.5 GHz, we obtained a steep radio slope of α ∼ −0.62, consistent with those CSS sources. However, such a measurement of radio slope is not robust, because the resolution is different between the two frequencies (by a factor of ∼3). Future high-resolution observations with VLBI at other frequencies will be helpful to better characterize the radio slope, yielding more accurate constraints on the physical properties of the AGN radio emission, that is, a young powerful jet in its earliest formation stage.
Theoretically, the formation of jets is thought to be related to the BH and accretion process (e.g., Celotti & Blandford 2001; Meier 2003; Ballantyne 2007). Greene et al. (2006 and references therein) more generally suggested that radio loudness (formation of radio jets) is anticorrelated with accretion rate (their Fig. 3) in a sample of Seyfert galaxies and PG quasars, albeit with large scatter. This strengthens the similar situation in microquasars (BH X-ray binaries) where jets are found at the low accretion state (Fender et al. 2004; Fender & Gallo 2014). Whether this trend still holds for high-redshift, highly accreting quasars has yet to be explored. Given the possibly high efficiency of BH accretion (η > 0.1), as suggested in SMGs in general, GH500.30 presents a strong case where jet, at least mildly relativistic, can be produced in high-η systems. This is important for addressing basic questions as to how jets are formed. Although the situation is far from clear, there are some suggestions that radio–loud AGNs are associated with rapidly spinning BHs that are ultimately spun-up by major BH-BH mergers (Wilson & Colbert 1995; Chiaberge & Marconi 2011; Chiaberge et al. 2015). This is consistent with the major “merger” evolutionary scenario for the formation of SMGs (like GH500.30) that starts with the collision of gas-rich disk galaxies (e.g., Hopkins et al. 2008), seemingly hinting at a possibly important role of BH spin in the making of relativistic jets.
It is interesting to compare the properties of GH500.30 to the AGN-dominated Hot Dust Obscured Galaxies (HotDOGs) which are proposed as tracers of an exceptional rapid and dusty phase of quasar/host galaxy co-evolution (e.g., Wu et al. 2012; Piconcelli et al. 2015; Assef et al. 2015). Recent X-ray observations of a few HotDOGs confirm their harboring of highly buried AGNs (Stern et al. 2014; Piconcelli et al. 2015), with absorption column density NH > 1023 cm−2. The bolometric luminosities of many HotDOGs exceed 1013 L⊙, suggesting them to be among the most luminous objects in the universe, which are likely maintained by SMBHs with MBH ∼ 109 M⊙ accreting near the Eddington limit (e.g., Tsai et al. 2015). The prototype HotDOG, WISE J1814+3412, has shown radio emission exceeding the amount expected from the FIR-radio correlation by a factor of approximately ten (Eisenhardt et al. 2012), indicative of a radio-loud AGN. Further high-resolution radio observations of HotDOGs show that their radio properties are consistent with young radio AGNs (Lonsdale et al. 2015; Frey et al. 2016). If most of the radio emission is indeed due to AGN jets, and considering their extreme luminosities and Eddington ratios (λ ≳ 1), HotDOGs seem not to fit the simple picture for jet formation (Fender et al. 2004), as we inferred for GH500.30. However, unlike GH500.30, HotDOGs may represent a late phase of the AGN-SMG evolution, with similar cold-dust components to SMGs (Wu et al. 2012; Jones et al. 2015) but more massive SMBHs.
6. Conclusions
Our analyses of multiwavelength observations reveal many unusual properties of GH500.30. The SED is well constrained at wavelengths λ > 2μm thanks to the NOEMA interferometer observations, with significant detections by Spitzer/IRAC and MIPS wavelengths, and by Herschel, SCUBA2, AzTEC, and VLA from FIR to centimeter wavelengths. This galaxy is also detected at the X-ray by Chandra with high significance (>10σ), allowing for a direct spectral analysis. However, its flux drops out at shorter wavelengths, displaying a steeply declining spectrum in NIR. We analyzed the photometric redshifts of GH500.30, using both the NIR and FIR photometric SED fittings, yielding a consistent result that the source is likely to be at z ≳ 4; though a lower redshift at z ≳ 3.1 cannot be fully ruled out.
Explaining the observed properties of the source requires a two-component SED model with an old stellar population dominating the optical-to-NIR SED and a very dusty ongoing starburst (SFR ∼ 1000 M⊙ yr-1) contributing to the FIR emission that is barely visible in the rest-frame UV/optical. The optical-to-NIR SED fitting suggests a modest dust extinction (Av ∼ 2.9 mag) of starlight from a stellar component with a mass of Mstar = 3.5 × 1011 M⊙ (assuming at z = 4.19), which may be spatially offset from the starburst region. Modeling of the X-ray spectrum of GH500.30 suggests that it harbors a heavily obscured AGN with 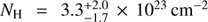 , and a 2–10 keV luminosity of LX = 2.6 × 1044 erg s−1, which is in the range of type 2 quasars. The radio emission of the source is extremely bright, which is an order of magnitude more than the star-formation powered emission, making it one of the most distant radio-luminous SMGs known so far.
, and a 2–10 keV luminosity of LX = 2.6 × 1044 erg s−1, which is in the range of type 2 quasars. The radio emission of the source is extremely bright, which is an order of magnitude more than the star-formation powered emission, making it one of the most distant radio-luminous SMGs known so far.
In view of the combination of observed characteristics of the galaxy, we conclude that the source appears to have been caught in a rare but critical early transition stage from a submillimeter galaxy to a dust-obscured quasar. The high redshift of GH500.30, if confirmed, will have important implications for the early growth of a massive BH and its host galaxy, as well as the formation of jet in the early universe. However, its extreme faintness at λ < 2μm hampers any optical and NIR spectroscopic observations. Blind searches of CO molecular emission line(s) with NOEMA, VLA and LMT are required, and may be the only way to spectroscopically identify its redshift.
The templates were used to derive photometric redshifts for bright X-ray sources in the COSMOS field (Salvato et al. 2009).
Tan et al. (2014) have shown that the IRAC fluxes from 4.5 μm to 8 μm exceed the best-fit stellar SED for GN20, which is likely due to the contribution by an AGN (Riechers et al. 2014). Such an excess IRAC emission was not found in the best-fitting stellar SED for GH500.30 (Fig. 2), suggesting a relatively weak AGN contribution.
Acknowledgments
This work is supported by the Chinese NSF through grant 11573001 and 11822301, National Basic Research Program 2015CB857005, the Sino-French LIA-Origin joint exchange program and Anhui Provincial NSF (1608085QA06). Y.Q.X. acknowledges support from the 973 Program (2015CB857004), NSFC-11473026, NSFC-11421303, and the CAS Frontier Science Key Research Program (QYZDJ-SSW-SLH006). D.L. acknowledges funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No. 694343). Y.H. acknowledges support from NSFC-11773063.
References
- Alexander, D. M., Bauer, F. E., Brandt, W. N., et al. 2003a, AJ, 125, 383 [NASA ADS] [CrossRef] [Google Scholar]
- Alexander, D. M., Bauer, F. E., Brandt, W. N., et al. 2003b, AJ, 126, 539 [NASA ADS] [CrossRef] [Google Scholar]
- Alexander, D. M., Bauer, F. E., Chapman, S. C., et al. 2005, ApJ, 632, 736 [NASA ADS] [CrossRef] [Google Scholar]
- Alexander, D. M.,Chary, R.-R.,Pope, A., et al. 2008a, ApJ, 687, 835 [NASA ADS] [CrossRef] [Google Scholar]
- Alexander, D. M., Brandt, W. N.,Smail, I., et al. 2008b, AJ, 135, 1968 [NASA ADS] [CrossRef] [Google Scholar]
- Assef, R. J., Eisenhardt, P. R. M.,Stern, D., et al. 2015, ApJ, 804, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Ballantyne, D. R. 2007, Mod. Phys. Lett. A., 22, 2397 [NASA ADS] [CrossRef] [Google Scholar]
- Barger, A. J.,Wang, W.-H., Cowie, L. L., et al. 2012, ApJ, 761, 89 [Google Scholar]
- Barger, A. J., Cowie, L. L.,Chen, C.-C., et al. 2014, ApJ, 784, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Borys, C., Smail, I., Chapman, S. C., et al. 2005, ApJ, 635, 853 [NASA ADS] [CrossRef] [Google Scholar]
- Brammer, G. B., van Dokkum, P. G., & Coppi, P. 2008, ApJ, 686, 1503 [NASA ADS] [CrossRef] [Google Scholar]
- Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- Capak, P., Carilli, C. L.,Lee, N., et al. 2008, ApJ, 681, L53 [Google Scholar]
- Carilli, C. L., & Yun, M. S. 1999, ApJ, 513, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Casey, C. M.,Narayanan, D., & Cooray, A. 2014, Phys. Rep., 541, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Celotti, A., & Blandford, R. D. 2001, Black Holes in Binaries and Galactic Nuclei, eds. L. Kaper, E. P. J. V. D. Heuvel, & P. A. Woudt, 206 [Google Scholar]
- Chabrier, G. 2003, PASP, 115, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Chang, Y.-Y., Le Floc’h, E.,Juneau, S., et al. 2017, ApJS, 233, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Chapman, S. C., Blain, A. W.,Smail, I., & Ivison, R. J. 2005, ApJ, 622, 772 [NASA ADS] [CrossRef] [Google Scholar]
- Chary, R., & Elbaz, D. 2001, ApJ, 556, 562 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, C.-C.,Smail, I., Swinbank, A. M., et al. 2015, ApJ, 799, 194 [NASA ADS] [CrossRef] [Google Scholar]
- Chiaberge, M., & Marconi, A. 2011, MNRAS, 416, 917 [NASA ADS] [CrossRef] [Google Scholar]
- Chiaberge, M., Gilli, R., Lotz, J. M., & Norman, C. 2015, ApJ, 806, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Coppin, K. E. K., Swinbank, A. M.,Neri, R., et al. 2008, MNRAS, 389, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Coppin, K. E. K.,Smail, I., Alexander, D. M., et al. 2009, MNRAS, 395, 1905 [NASA ADS] [CrossRef] [Google Scholar]
- Coppin, K., Pope, A., Menéndez-Delmestre, K., et al. 2010, ApJ, 713, 503 [NASA ADS] [CrossRef] [Google Scholar]
- Cowie, L. L., Barger, A. J.,Wang, W.-H., & Williams, J. P. 2009, ApJ, 697, L122 [NASA ADS] [CrossRef] [Google Scholar]
- da Cunha, E.,Charlot, S., & Elbaz, D. 2008, MNRAS, 388, 1595 [NASA ADS] [CrossRef] [Google Scholar]
- da Cunha, E.,Walter, F., Smail, I. R., et al. 2015, ApJ, 806, 110 [NASA ADS] [CrossRef] [Google Scholar]
- Daddi, E., Dannerbauer, H.,Krips, M., et al. 2009a, ApJ, 695, L176 [NASA ADS] [CrossRef] [Google Scholar]
- Daddi, E., Dannerbauer, H.,Stern, D., et al. 2009b, ApJ, 694, 1517 [Google Scholar]
- Del Moro, A., Alexander, D. M., Mullaney, J. R., et al. 2013, A&A, 549, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dowell, C. D.,Conley, A.,Glenn, J., et al. 2014, ApJ, 780, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Elbaz, D., Dickinson, M., Hwang, H. S., et al. 2011, A&A, 533, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Elbaz, D., Leiton, R.,Nagar, N., et al. 2018, A&A, 616, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eisenhardt, P. R. M.,Wu, J.,Tsai, C.-W., et al. 2012, ApJ, 755, 173 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Elvis, M., Wilkes, B. J., McDowell, J. C., et al. 1994, ApJS, 95, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Fender, R., & Gallo, E. 2014, Space Sci. Rev., 183, 323 [NASA ADS] [CrossRef] [Google Scholar]
- Fender, R. P., Belloni, T. M., & Gallo, E. 2004, MNRAS, 355, 1105 [NASA ADS] [CrossRef] [Google Scholar]
- Frey, S., Paragi, Z., Gabányi, K. É., & An, T. 2016, MNRAS, 455, 2058 [NASA ADS] [CrossRef] [Google Scholar]
- Geach, J. E., Dunlop, J. S.,Halpern, M., et al. 2017, MNRAS, 465, 1789 [NASA ADS] [CrossRef] [Google Scholar]
- Gilli, R., Su, J.,Norman, C., et al. 2011, ApJ, 730, L28 [NASA ADS] [CrossRef] [Google Scholar]
- Gilli, R., Norman, C.,Vignali, C., et al. 2014, A&A, 562, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Greene, J. E., Ho, L. C., & Ulvestad, J. S. 2006, ApJ, 636, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Greve, T. R.,Pope, A.,Scott, D., et al. 2008, MNRAS, 389, 1489 [NASA ADS] [CrossRef] [Google Scholar]
- Guidetti, D., Bondi, M.,Prandoni, I., et al. 2017, MNRAS, 471, 210 [NASA ADS] [CrossRef] [Google Scholar]
- Han, Y., & Han, Z. 2012, ApJ, 749, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Han, Y., & Han, Z. 2014, ApJS, 215, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Hatsukade, B., Ohta, K.,Yabe, K., et al. 2015, ApJ, 810, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Huang, J.-S., Zheng, X. Z.,Rigopoulou, D., et al. 2011, ApJ, 742, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Huang, J.-S.,Rigopoulou, D.,Magdis, G., et al. 2014, ApJ, 784, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, P. F.,Hernquist, L., Cox, T. J., et al. 2006, ApJS, 163, 1 [Google Scholar]
- Hopkins, P. F.,Hernquist, L., Cox, T. J., & Kereš, D. 2008, ApJS, 175, 356 [NASA ADS] [CrossRef] [Google Scholar]
- Ivison, R. J.,Magnelli, B.,Ibar, E., et al. 2010, A&A, 518, L31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ivison, R. J., Lewis, A. J. R.,Weiss, A., et al. 2016, ApJ, 832, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, S. F., Blain, A. W.,Lonsdale, C., et al. 2015, MNRAS, 448, 3325 [NASA ADS] [CrossRef] [Google Scholar]
- Kalberla, P. M. W., Burton, W. B.,Hartmann, D., et al. 2005, A&A, 440, 775 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kauffmann, G., Heckman, T. M., & Best, P. N. 2008, MNRAS, 384, 953 [NASA ADS] [CrossRef] [Google Scholar]
- Kawakatu, N., & Wada, K. 2009, ApJ, 706, 676 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, R. C., Jr 1998, ARA&A, 36, 189 [Google Scholar]
- Kriek, M., van Dokkum, P. G., Labbé, I., et al. 2009, ApJ, 700, 221 [NASA ADS] [CrossRef] [Google Scholar]
- Laird, E. S.,Nandra, K.,Pope, A., & Scott, D. 2010, MNRAS, 401, 2763 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, D., Daddi, E.,Dickinson, M., et al. 2018, ApJ, 853, 172 [NASA ADS] [CrossRef] [Google Scholar]
- Lonsdale, C. J.,Lacy, M., Kimball, A. E., et al. 2015, ApJ, 813, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Luo, B., Brandt, W. N., Xue, Y. Q., et al. 2017, ApJS, 228, 2 [Google Scholar]
- Lutz, D., Maiolino, R., Spoon, H. W. W., & Moorwood, A. F. M. 2004, A&A, 418, 465 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Magdis, G. E.,Daddi, E., Béthermin, M., et al. 2012, ApJ, 760, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Meier, D. L. 2003, New Astron. Rev., 47, 667 [NASA ADS] [CrossRef] [Google Scholar]
- Michałowski, M., Hjorth, J., & Watson, D. 2010, A&A, 514, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Michałowski, M. J., Dunlop, J. S., Ivison, R. J., et al. 2012, MNRAS, 426, 1845 [NASA ADS] [CrossRef] [Google Scholar]
- Morrison, G. E., Owen, F. N.,Dickinson, M., Ivison, R. J., & Ibar, E. 2010, ApJS, 188, 178 [NASA ADS] [CrossRef] [Google Scholar]
- Mullaney, J. R., Alexander, D. M., Goulding, A. D., & Hickox, R. C. 2011, MNRAS, 414, 1082 [NASA ADS] [CrossRef] [Google Scholar]
- Narayanan, D., Dey, A., Hayward, C. C., et al. 2010, MNRAS, 407, 1701 [NASA ADS] [CrossRef] [Google Scholar]
- O’Dea, C. P. 1998, PASP, 110, 493 [NASA ADS] [CrossRef] [Google Scholar]
- Owen, F. N. 2018, ApJS, 235, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Peng, C. Y., Ho, L. C., Impey, C. D., & Rix, H.-W. 2002, AJ, 124, 266 [NASA ADS] [CrossRef] [Google Scholar]
- Perera, T. A., Chapin, E. L., Austermann, J. E., et al. 2008, MNRAS, 391, 1227 [NASA ADS] [CrossRef] [Google Scholar]
- Piconcelli, E., Vignali, C.,Bianchi, S., et al. 2015, A&A, 574, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Polletta, M., Tajer, M.,Maraschi, L., et al. 2007, ApJ, 663, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Pope, A., Chary, R.-R., Alexander, D. M., et al. 2008, ApJ, 675, 1171 [Google Scholar]
- Prieto, M. A.,Reunanen, J., Tristram, K. R. W., et al. 2010, MNRAS, 402, 724 [NASA ADS] [CrossRef] [Google Scholar]
- Radcliffe, J. F., Garrett, M. A., Beswick, R. J., et al. 2016, A&A, 587, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Richards, G. T.,Lacy, M., Storrie-Lombardi, L. J., et al. 2006, ApJS, 166, 470 [NASA ADS] [CrossRef] [Google Scholar]
- Riechers, D. A.,Pope, A.,Daddi, E., et al. 2014, ApJ, 786, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Sanders, D. B., Soifer, B. T., Elias, J. H., et al. 1988, ApJ, 325, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Salvato, M., Hasinger, G.,Ilbert, O., et al. 2009, ApJ, 690, 1250 [CrossRef] [Google Scholar]
- Schinnerer, E., Carilli, C. L.,Capak, P., et al. 2008, ApJ, 689, L5 [Google Scholar]
- Shu, X. W.,Elbaz, D.,Bourne, N., et al. 2016, ApJS, 222, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Skelton, R. E., Whitaker, K. E., Momcheva, I. G., et al. 2014, ApJS, 214, 24 [Google Scholar]
- Smolčić, V.,Karim, A.,Miettinen, O., et al. 2015, A&A, 576, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stark, D. P., Bunker, A. J., Ellis, R. S., Eyles, L. P., & Lacy, M. 2007, ApJ, 659, 84 [NASA ADS] [CrossRef] [Google Scholar]
- Stark, D. P., Ellis, R. S.,Bunker, A., et al. 2009, ApJ, 697, 1493 [NASA ADS] [CrossRef] [Google Scholar]
- Stern, D., Djorgovski, S. G., Perley, R. A., de Carvalho, R. R., & Wall, J. V. 2000, AJ, 119, 1526 [NASA ADS] [CrossRef] [Google Scholar]
- Stern, D., Lansbury, G. B., Assef, R. J., et al. 2014, ApJ, 794, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Swinbank, A. M.,Smail, I., Chapman, S. C., et al. 2004, ApJ, 617, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Swinbank, A. M., Chapman, S. C.,Smail, I., et al. 2006, MNRAS, 371, 465 [NASA ADS] [CrossRef] [Google Scholar]
- Takata, T., Sekiguchi, K.,Smail, I., et al. 2006, ApJ, 651, 713 [NASA ADS] [CrossRef] [Google Scholar]
- Tamura, Y., Iono, D., Wilner, D. J., et al. 2010, ApJ, 724, 1270 [NASA ADS] [CrossRef] [Google Scholar]
- Tan, Q., Daddi, E.,Magdis, G., et al. 2014, A&A, 569, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Terashima, Y. & Wilson, A. S. 2003, ApJ, 583, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Thomson, A. P., Ivison, R. J., Simpson, J. M., et al. 2014, MNRAS, 442, 577 [NASA ADS] [CrossRef] [Google Scholar]
- Tozzi, P., Gilli, R.,Mainieri, V., et al. 2006, A&A, 451, 457 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tsai, C.-W., Eisenhardt, P. R. M.,Wu, J., et al. 2015, ApJ, 805, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Vanzella, E., Cristiani, S.,Dickinson, M., et al. 2006, A&A, 454, 423 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vieira, J. D., Marrone, D. P., Chapman, S. C., et al. 2013, Nature, 495, 344 [NASA ADS] [CrossRef] [Google Scholar]
- Wall, J. V.,Pope, A., & Scott, D. 2008, MNRAS, 383, 435 [NASA ADS] [CrossRef] [Google Scholar]
- Walter, F., Decarli, R.,Carilli, C., et al. 2012, Nature, 486, 233 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, W.-H., Cowie, L. L., van Saders, J., Barger, A. J., & Williams, J. P. 2007, ApJ, 670, L89 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, W.-H., Barger, A. J., & Cowie, L. L. 2009, ApJ, 690, 319 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, W.-H., Cowie, L. L., Barger, A. J., Keenan, R. C., & Ting, H.-C. 2010, ApJS, 187, 251 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, S. X., Brandt, W. N.,Luo, B., et al. 2013, ApJ, 778, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, T., Elbaz, D.,Schreiber, C., et al. 2016, ApJ, 816, 84 [Google Scholar]
- Wilson, A. S., & Colbert, E. J. M. 1995, ApJ, 438, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, J., Tsai, C.-W.,Sayers, J., et al. 2012, ApJ, 756, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Xue, Y. Q. 2017, New Astron. Rev., 79, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Xue, Y. Q.,Luo, B., Brandt, W. N., et al. 2011, ApJS, 195, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Xue, Y. Q.,Luo, B., Brandt, W. N., et al. 2016, ApJS, 224, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, G., Xue, Y. Q.,Luo, B., et al. 2014, ApJS, 215, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Younger, J. D., Fazio, G. G.,Huang, J.-S., et al. 2007, ApJ, 671, 1531 [Google Scholar]
- Yun, M. S.,Aretxaga, I., Ashby, M. L. N., et al. 2008, MNRAS, 389, 333 [NASA ADS] [CrossRef] [Google Scholar]
- Yun, M. S., Scott, K. S.,Guo, Y., et al. 2012, MNRAS, 420, 957 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1. Postage-stamp images of GH500.30 from multiwavelength observations. From left to right and top to bottom: HST/ACS (F435+F606+F775+F850LP), HST/WFC3 (F125W+F140W+F160W), CFHT Ks, IRAC [3.6 μm], MIPS 24 μm, PACS 100 μm and 160 μm, SPIRE 250 μm, 350 μm and 500 μm, SCUBA2 850 μm, NOEMA 1.2 mm, VLA 1.4 GHz, and Chandra 0.5–8 keV. Each panel has a size of 20″ × 20″. The detailed photometry is listed in Table 1. |
| In the text | |
 |
Fig. 2. Optical to MIR SED for GH500.30 (upper panel). The filled circles show the observed photometry, while the downward arrows indicate 1σ upper limits. The red curve shows the best-fit (maximum likelihood) SED based on BayeSED modeling, whilst the black curve represents the best-fit SED from FAST. We also plot the fit with an extremely dusty template (AV = 9:8 and zphot = 0:64) for comparison (gray curve). The HST H-band image is shown in the inset left panel. Insert right panel shows the χ2 contours of redshift vs. dust extinction (AV) from the FAST SED fittings. Lower panel: data to model ratios for the BayeSED fitting at z = 4:19 (black solid circles) and for the FAST SED fitting at z = 0:64 (gray solid circles). Only detected fluxes above 1 μm are shown. |
| In the text | |
 |
Fig. 3. Joint one- and two-dimensional posterior probability distributions (normalized to unit area) of redshift, dust extinction, and stellar mass for GH500.30. The color coding represents confidence levels. The joint 90 and 95% confidence contours are shown in black. |
| In the text | |
 |
Fig. 4. Top panel: FIR to radio SED of GH500.30 (open squares). The black curve shows the best-fit SED among all 105 CE01 templates. The best-fits with Mrk 231, Arp 220 and M82 SED are shown in red, green and blue curves, respectively. The fill squares are observed Spitzer/IRAC fluxes. Bottom panel: χ2vs. redshift. The black curve represents the results from the best-fit CE01 SED at each redshift, and the color-coded curves are for the Mrk 231, Arp 220 and M82 SED. The horizontal dashed line shows the 90% confidence interval for the redshift. The lower panel at the bottom shows the IR luminosities from CE01 templates that allow for the minimum χ2 at each redshift. The vertical gray curve represents the best-fit redshift (z = 4.19) from the optical-to-NIR SED. |
| In the text | |
 |
Fig. 5. SED fittings to the broadband UV to submillimeter data with MAGPHYS at z = 4.19 (left panel) and z = 3.1 (right panel). The thick orange line represents the AGN component, with contributions that are estimated at 18% and 1% to the total IR SED, respectively. The red solid circles are the photometric data and the black lines are the best-fitting model. The corresponding data to model ratios are shown in the middle panels. The blue line represents the (unattenuated) star formation component. The attenuated stellar emission and the reproduced dust emission are shown with the green line. The posterior probability distribution of best-fitting parameters are shown in the lower panels. The dashed lines are the median values and the dotted lines are the best-fitting values. |
| In the text | |
 |
Fig. 6. Chandra X-ray spectrum for GH500.30. The red solid line is the best-fit model (wabs*zwabs*zpowerlaw in XSPEC), with the data to model ratio shown in panel b. The inset panel shows the χ2 contours of the photon index Γ vs. column density at the 68%, 90% and 99% confidence levels (from the inside out). Panel c: data/model residuals after including a Gaussian line at Eobs = 1.52keV. Panel d: data/model residuals by fixing redshift at z = 3.1. |
| In the text | |
 |
Fig. 7. Hardness ratio between the 2–8 keV (hard) and 0.5–2 keV (soft) bands (i.e., X-ray hardness) as a function of redshift. The dashed lines are simulated tracks for an absorbed power-law with photon index fixed at 1.8. The red star is the X-ray hardness for GH500.30. For comparison, we also plot in gray dots the hardness ratios for SMGs in Wang et al. (2013), which include the most distant Compton-thick AGN, LESS J033229.4-275619 at z = 4.76 (red circle). |
| In the text | |
 |
Fig. 8. NOEMA contours (white) overlaid on the Ks-band image. The white and yellow cross represents the NOEMA 1.2 mm (beam size of ∼1.06″ × 0.63″) and Ks-band centroid, respectively. The image has a size of 3″ × 3″. |
| In the text | |
 |
Fig. 9. NIR SED of GH500.30 at λ > 1 μm (filled squares) for GH500.30, compared to SEDs of another two bright SMGs at z = 4, GN 20 (circles) and GN 10 (triangles). The flux densities are scaled to the 24 μm flux of GH500.30. |
| In the text | |
 |
Fig. 10. Upper panel: rest-frame FIR (42.5–122.5 μm) vs. radio 1.4 GHz luminosity for GH500.30 (red star, assuming at z = 4.19 and z = 3.1, respectively). Radio-excess sources from Del Moro et al. (2013) are plotted as filled circles for comparison. The solid line corresponds to q = 2.21 (average for “radio-normal” sources) and the dotted line correspond to q = 1.68, for the selection limit for radio-excess sources. Lower panel: radio slope based on the observations at 1.4 GHz and 5.5 GHz. The 1.6 GHz flux obtained from the high-resolution VLBI observation is shown for comparison. The light-red shaded region shows the 1.4 GHz radio flux expected from the star-formation process, which is derived by extrapolating the best-fitting SED model to 1.4 GHz (Fig. 4). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


