| Issue |
A&A
Volume 619, November 2018
|
|
|---|---|---|
| Article Number | A121 | |
| Number of page(s) | 8 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201833422 | |
| Published online | 15 November 2018 | |
Two-dimensional simulations of mixing in classical novae: The effect of white dwarf composition and mass⋆
1
Physics Division, Oak Ridge National Laboratory, TN 37831-6354, PO Box 2008 Oak Ridge, USA
e-mail: novaj@ornl.gov
2
Departament de Física, EEBE, Universitat Politècnica de Catalunya, c/Eduard Maristany 10, 08930 Barcelona, Spain
3
Institut d’Estudis Espacials de Catalunya, c/Gran Capità 2-4, Ed. Nexus-201, 08034 Barcelona, Spain
4
Dipartimento di Física “Enrico Fermi”, Università di Pisa and INFN, Sezione di Pisa, Largo B. Pontecorvo 3, 56127 Pisa, Italy
Received:
14
May
2018
Accepted:
25
July
2018
Context. Classical novae are explosive phenomena that take place in stellar binary systems. They are powered by mass transfer from a low-mass main sequence star onto either a CO or ONe white dwarf. The material accumulates for 104–105 yr until ignition under degenerate conditions, resulting in a thermonuclear runaway. The nuclear energy released produces peak temperatures of ∼0.1–0.4 GK. During these events, 10−7−10−3 M⊙ enriched in intermediate-mass elements, with respect to solar abundances, are ejected into the interstellar medium. However, the origin of the large metallicity enhancements and the inhomogeneous distribution of chemical species observed in high-resolution spectra of ejected nova shells is not fully understood.
Aims. Recent multidimensional simulations have demonstrated that Kelvin-Helmholtz instabilities that operate at the core-envelope interface can naturally produce self-enrichment of the accreted envelope with material from the underlying white dwarf at levels that agree with observations. However, such multidimensional simulations have been performed for a small number of cases and much of the parameter space remains unexplored.
Methods. We investigated the dredge-up, driven by Kelvin-Helmholtz instabilities, for white dwarf masses in the range 0.8–1.25 M⊙ and different core compositions, that is, CO-rich and ONe-rich substrates. We present a set of five numerical simulations performed in two dimensions aimed at analyzing the possible impact of the white dwarf mass, and composition, on the metallicity enhancement and explosion characteristics.
Results. At the time we stop the simulations, we observe greater mixing (∼30% higher when measured in the same conditions) and more energetic outbursts for ONe-rich substrates than for CO-rich substrates and more massive white dwarfs.
Key words: novae, cataclysmic variables / nuclear reactions, nucleosynthesis, abundances / hydrodynamics / instabilities / convection / turbulence
The movies associated to Fig. 1 are available at https://www.aanda.org
© ESO 2018
1. Introduction
Classical novae are stellar explosions powered by thermonuclear runaways (TNR) on the surface of a white dwarf after an accretion episode of hydrogen-rich matter from the companion star at typical rates of ∼10−10–10−9 M⊙ yr−1. The TNR drives peak temperatures of ∼ (1−4) × 108 K. Between 10−7 and 10−3 M⊙ are ejected with peak velocities that achieve several thousand km s−1. The suite of nuclear processes that operate in the envelope results in nonsolar isotopic abundance ratios in the ejecta (Gehrz et al. 1998; Downen et al. 2013; Kelly et al. 2013). Classical novae are spectroscopically classified as neon novae and non-neon novae. Neon novae are characterized by the presence of intense Ne lines and are thought to take place on ONe white dwarfs; non-neon novae are absent of Ne lines and take place on CO white dwarfs. Novae contribute to the production of Galactic 15N, 17O, and 13C (Starrfield et al. 2008, 2016; José & Hernanz 1998; José 2016). Other species, such as 31P, 32S, and 35Cl can also be produced in the most massive ONe novae, since the pressure achieved at the base of the accreted envelope is higher in these novae. In ONe novae, this translates into higher peak temperatures and nuclear processing that extends toward heavier isotopes, beyond the CNO region (José 2016; José & Shore 2008).
While the matter accreted from the companion onto the white dwarf has approximately solar composition (Z ∼ 0.02), the ejecta does not. The metallicity enhancements inferred from observations reveal values in a wide range from slightly above solar to Z ∼ 0.801 for the more massive ONe novae (see Vanlandingham et al. 1997 and Gehrz et al. 1998, and references therein). Owing to the moderately low peak temperatures achieved during the outburst, nuclear processing in the accreted envelope alone is unlikely to account for the high metallicities inferred from observations. Instead, mixing at the core-envelope interface (CEI) is a more reliable alternative to explain the metallicity enhancement in the ejecta. One-dimensional, spherical symmetric models often assume mixing, at a constant rate, between the material transferred from the companion and the outermost layers of the underlying white dwarf, whose composition reflects its previous evolutionary history. Such mixing is, however, most likely time dependent. For the 1D simulations, several mixing mechanisms have been proposed, such as diffusive mixing (Prialnik & Kovetz 1984; Kovetz & Prialnik 1985; Fujimoto & Iben 1992; Iben et al. 1991, 1992) and shear mixing (Durisen 1977; Kippenhahn & Thomas 1978; MacDonald 1983; Livio & Truran 1987; Fujimoto 1988; Sparks & Kutter 1987; Kutter & Sparks 1987, 1989). Yet none can reproduce the full range of metallicity enhancements inferred from observations (Livio & Truran 1990). Aside from the difficulties faced by 1D models in the search for a feasible mixing mechanism, spherically symmetric simulations cannot explore how the ignition begins and how the deflagration spreads throughout the accreted envelope (Shara 1982). Therefore, multidimensional hydrodynamical calculations are required to shed more light on the unexplained features of classical nova explosions, in particular, the role of fluid instabilities for the CNO enhancement.
Recent studies in 2D and 3D simulations (see Glasner et al. 2012; Casanova et al. 2016, and references therein) confirmed that Kelvin-Helmholtz instabilities at the CEI can dredge up material from the underlying white dwarf and efficiently enrich the accreted envelope to levels in agreement with observations. While most of the multidimensional nova studies performed to date have focused on mixing with CO-rich substrates, two independent efforts have analyzed the effect of various compositions on the underlying white dwarf (Glasner et al. 2012, 2014; Casanova et al. 2016). The 2D models by Glasner et al. (2012, 2014) assumed mass-accretion of solar composition onto a 1.147 M⊙ white dwarf with a maximum resolution of 1.4 × 1.4 km2 in spherical-polar coordinates. The authors found that Kelvin-Helmholtz instabilities can enrich the accreted envelope with material from the underlying white dwarf, independent of the nature of the chemical substrate (CO, pure He, pure 16O, and pure 24Mg), but the study did not consider a realistic composition of an ONe white dwarf. The 3D work in Cartesian coordinates by Casanova et al. (2016) employed instead an ONe-rich substrate model based on Ritossa et al. (1996), assuming accretion of solar composition onto a 1.25 M⊙ ONe white dwarf with a maximum resolution of 1.56 × 1.56 × 1.56 km3. The authors found larger metallicity enhancements and longer durations of TNR for ONe-rich substrates, but further analysis of the influence of the core composition for various white dwarf masses is needed. In this paper, we present a 2D study of mixing at the CEI during nova outbursts with self-consistent models to explore the effect of the white dwarf mass and composition and with the aim of understanding the impact of white dwarf gravity for a given chemical composition.
2. Input physics and initial setup
We used the 1D implicit Lagrangian hydrodynamic code SHIVA to simulate the accretion of solar composition material (Z = 0.02) onto the white dwarf at a rate of 2 × 10−10 M⊙ yr−1 (José & Hernanz 1998; José 2016). We assumed cold accretion with no premixing, at a constant rate. For this study, we computed three models of CO-rich and two models of ONe-rich substrates with different white dwarf masses: 0.8 M⊙ CO, 1.0 M⊙ CO, 1.15 M⊙ CO, 1.15 M⊙ ONe, and 1.25 M⊙ ONe. For CO-rich substrate models, the composition of the underlying white dwarf is X(12C) = X(16O) = 0.5. For ONe-rich substrate models, we adopted the composition of the outer white dwarf layers from Ritossa et al. (1996): X(16O) = 0.511, X(20Ne) = 0.313, X(23Na) = 0.0644, X(24Mg) = 0.0548, X(25Mg) = 0.0158, X(27Al) = 0.0108, X(12C) = 0.00916, X(26Mg) = 0.00989, X(21Ne) = 0.00598, and X(22Ne) = 0.00431.
The structures were mapped onto a 2D Cartesian grid when the CEI temperature reached T = 0.1 GK, and the subsequent evolution was followed with the multidimensional parallelized explicit Eulerian FLASH code. The FLASH code is based on the piecewise parabolic interpolation of physical quantities to solve the hydrodynamic equations that describe the stellar plasma. This code has a timestep limited by the Courant-Friedrichs-Lewy condition and uses adaptive mesh refinement to resolve critical features along the computational domain (Fryxell et al. 2000). Thermal diffusion is implemented by adding the heat flux in the energy equation, which is calculated using a Rossland mean opacity that includes radiative and conductive contributions (Timmes 2000). The physical description of the fluid is closed by the Helmholtz equation of state, which is suitable for degenerate stellar matter and includes contributions from ions treated as an ideal gas, radiation as a blackbody, and degenerate electrons and positrons described with a noninteracting Fermi gas (Timmes & Arnett 2000; Timmes & Swesty 2000). The FLASH code uses dissipation algorithms, as described in Colella & Woodward (1984), such as a flattening procedure and a monotonicity constraint (rather than artificial viscosity) to control oscillations near discontinuities; this feature is shared with the MUSCL scheme of van Leer (van Leer 1979). The calculations were performed on the MareNostrum supercomputer (Barcelona Supercomputing Center).
The 2D computational domain for the CO nova models is 800 × 800 km2, initially comprising 128 unevenly spaced radial layers, and 1024 equally spaced grid points along the horizontal axis. For the ONe nova models, the 2D computational domain is 800 × 400 km2 and has 96 unevenly spaced radial zones and 1024 equally spaced zones along the horizontal axis. The initial spacing is determined by the refinement criterion used by the FLASH code, which tends to refine the regions characterized by rapidly changing physical variables (i.e., the CEI rather than other regions of the accreted envelope). The critical mass and extent of the accreted envelopes depend sensitively on the properties of the underlying white dwarf. The envelope is more massive and larger for CO-rich than for the more massive ONe-rich white dwarfs, although the latter reach higher densities because of the white dwarf mass-radius relation (Starrfield et al. 1998; José & Hernanz 1998; Yaron et al. 2005; José 2016). A maximum resolution of 0.78 × 0.78 km2 was adopted to capture the mixing process operating at the CEI in all the simulations reported in this paper. Initially, the structure was forced to be in hydrostatic equilibrium throughout the envelope. This condition is reinforced with a reflecting boundary condition at the bottom (i.e., the sign of the velocity is reversed), and an outflow condition at the top, which allows matter to escape. Periodic lateral boundary conditions were adopted (Zingale et al. 2002; Casanova et al. 2010, 2011a,b, 2016).
We employed a reduced nuclear network containing 13 chemical species (1H, 4He, 12,13C, 13,14,15N, 14,15,16,17O, and 17,18F) linked through 18 nuclear reactions, mainly p-captures and β+-disintegrations, to compute the energetics of CO-rich novae (Casanova et al. 2010, 2011a,b). For ONe-rich novae, we employed an extended nuclear network containing 31 chemical species (1H, 4He, 12,13C, 13,14,15N, 14,15,16,17O, 17,18F, 20,21Ne, 21,22,23Na, 22,23,24,25,26Mg, 24,25,26g,26m,27Al, and 26,27,28Si), since the main nuclear processing extends beyond the CNO cycle in this type of novae (Casanova et al. 2016). The reaction rates were taken from STARLIB nuclear reaction library (Iliadis et al. 2010).
3. Results
We initiated the simulations by introducing a top-hat temperature perturbation (5%) operating only at the first timestep in a 1 km wide region located near the CEI. The location of the perturbation is the same for the five computed models. Previous work (Casanova et al. 2011a) has shown that the outcome is insensitive to the nature of the perturbation. The perturbation disrupts the initial equilibrium configuration and creates fluctuations at the interface that spawn strong buoyant fingers. In Fig. 1, panel a shows the development of these primary fluctuations at t = 54 s for the 1.0 M⊙ CO model. Panels b–f in Fig. 1 show the progress of the convective front at the time it is located at 4 pressure scale heights above the CEI, for the different models reported in this work. The scale pressure height, at the times indicated in Fig. 1, is calculated as Hp = kT/mg, where k is the Boltzmann constant, T is the temperature, m is the molecular mass, and g is the value of the gravity. The two 1.15 M⊙ models have the same gravity, but once mixing operates, the values of T and m differ, resulting in different values of Hp. Four pressure scale heights correspond to 627.2 km, 284.6 km, 146.9 km, 110.5 km, and 66.4 km above the CEI for models 0.8 M⊙ CO, 1.0 M⊙ CO, 1.15 M⊙ CO, 1.15 M⊙ ONe, and 1.25 M⊙ ONe, respectively. Shear flows develop at the interface and trigger strong Kelvin-Helmholtz instabilities that efficiently dredge-up core material and enrich the envelope in metals. The convective front progresses subsonically upward almost uniformly, such that the event proceeds almost in spherical symmetry. That explains the success of 1D calculations in describing the main characteristics of classical nova explosions (Starrfield et al. 1998; Kovetz & Prialnik 1997; Yaron et al. 2005; José & Hernanz 1998).
 |
Fig. 1. Panel a shows the growth of the primary fluid instabilities at t = 54 s, in terms of 12C mass fraction and in logarithmic scale, for model 1.0 M⊙ CO white dwarf. The other panels show snapshots of the convective front when it is at a distance of 4 pressure scale heights above the CEI for models 0.8 M⊙ CO (panel b), 1.0 M⊙ CO (panel c), 1.15 M⊙ CO (panel d), 1.15 M⊙ ONe (panel e), and 1.25 M⊙ ONe (panel f). The snapshots are shown in terms of 12C mass fraction for CO-rich substrates, and in terms of 20Ne mass fraction for ONe-rich substrates, both in logarithmic scale. The times are t = 326s, t = 149s, t = 66s, t = 194s, and t = 133s, respectively. The reflection condition is imposed in the lower boundary, which is located 50 km below the CEI for all the simulations. See movies available online. |
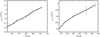 |
Fig. 2. Propagation of the convective front throughout the accreted envelope as a function of time for models 1.0 M⊙ CO (panel a) and 1.25 M⊙ ONe (panel b). |
The advance of the convective front is limited by the abundance stratification and temperature gradient within the accreted envelope. Consequently, matter burns layer by layer depending on the composition and temperature that characterizes each stratum, and the front moves upward almost uniformly. Figure 2 demonstrates the advance of the convective front as a function of time until the convective front has nearly reached the upper boundary at t = 310s and t = 657s for models 1.0 M⊙ CO and 1.25 M⊙ ONe, respectively. As burning proceeds, convection becomes more disordered2 and the 2D convective cells continue growing in size, occupying almost the entire domain length. As opposed to the 3D case (Casanova et al. 2011b, 2016), conservation of vorticity in 2D forces eddies to grow in an inverse vorticity cascade with a distribution that deviates from the Kolmogorov spectrum (Pope 2000; Lesieur 2008; Shore 2007). In a 3D framework, the fluid shows a more chaotic pattern, where filaments originating at the CEI tend to break into smaller structures while being engulfed at the upper parts of the envelope. The formation of long-lived eddies of multiple sizes is a signature of the intermittent behavior of turbulence. Movies showing the development of the Kelvin-Helmoltz instabilities and the progress of the convective front for models 1.0 M⊙ CO and 1.25 M⊙ ONe are available online3. We note that the movie of the 1.25 M⊙ ONe shows a Landau-like bifurcation at ∼100 s (Landau & Lifshitz 1987). This bifurcation appears when nonlinear modes become strong enough that the fluid becomes unstable and develops an oscillatory transition into a more tangled regime. In Fig. 3, we show the total velocity histograms at the end of the simulation for model 1.0 M⊙ CO at t = 310 s (mean velocity = 1.06 × 107 cm s−1 and dispersion = 6.74 × 106 cm s−1), and model 1.25 M⊙ ONe at t = 657 s (mean velocity = 1.87 × 106 cm s−1 and dispersion = 1.48 × 106 cm s−1). Model 1.0 M⊙ CO presents a more developed turbulent regime that translates into a distribution that is approximately Gaussian with higher mean velocity and a lower dispersion. The 1.25 M⊙ ONe model instead presents a distribution with a larger dispersion and lower velocities, indicating that turbulence is less developed. The same trend is found in the cumulant distribution functions of the Mach number for these models (see Fig. 4). Mean values of the Mach numbers and their corresponding variances are 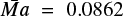 and σ2 = 0.0002 for model 1.0 M⊙ CO, and
and σ2 = 0.0002 for model 1.0 M⊙ CO, and 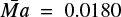 and σ2 = 0.0024 for model 1.25 M⊙ ONe. The inhomogenous distribution with an extended tail is distinctly non-Gaussian, indicating that these quantities present a signature of the intermittent behavior of the turbulence (Casanova et al. 2011b).
and σ2 = 0.0024 for model 1.25 M⊙ ONe. The inhomogenous distribution with an extended tail is distinctly non-Gaussian, indicating that these quantities present a signature of the intermittent behavior of the turbulence (Casanova et al. 2011b).
When the convective front reached 4 pressure scale heights above the interface, we obtain reference parameters for the five computed models. In Table 1, we list the main characteristics at this time: white dwarf substrate (Nova), size of the computational domain (Size), mass of the white dwarf (Mwd), the value of the gravity at the CEI (g), rise time of the initial buoyant fingering (tinst)4, value of the pressure scale height (Hp), distance above the CEI at which the convective front is at (d), final computed time at which the convective front is at 4 pressure scale heights above the CEI (tHp), mean metallicity throughout the accreted envelope (Z), and base temperature (Tbase). The initial temperature perturbation diffuses rapidly and creates hot spots that burn faster and transfer energy to the surrounding material, which becomes buoyant. The initial buoyant fingering appears sooner in the simulations for ONe-rich substrates and for more massive white dwarfs owing to higher density values in the accreted envelope and steeper density gradients which, in turn, translate into a higher pressure at the base (see tinst in Table 1, and panel a in Fig. 5; José 2016). The buoyant fingering time for the ONe models and the formation of small convective eddies in the innermost layers of the envelope is delayed relative to the CO models. For instance, in the 1.25 M⊙ ONe model, it takes ∼35 s for the initial buoyant fingering to develop convection, while it only takes ∼20 s in the 1.0 M⊙ CO model (see movies). Rising plumes contain hot gas that is replaced by material from the cold upper layers and effective circulation initiates at the innermost layers of the accreted envelope. However, when this occurs depends on the ignition timescale. For solar material5, ignition is driven by the reaction 12C + p, which is faster than other channels, such as 16O + p or 20Ne + p (José et al. 2016). Hence, ignition and the establishment of superadiabatic gradients required for convection occur earlier in CO-rich substrates6. In ONe-rich substrates, the amount of 12C that can be excavated from the core by Kelvin-Helmholtz instabilities is small compared to CO-rich substrates (X(C12) = 0.00916 and X(C12) = 0.5, respectively), which results in a longer dredge-up episode, and therefore, a higher degree of mixing (Casanova et al. 2016). The timescale of the explosion, as well as the completeness of convection, is consequently longer in ONe-rich substrates, requiring more than 600 s to reach the upper boundary, as opposed to ∼300 s in CO-rich substrates (see movies)7. We also note that the convective front propagates faster in CO-rich substrates (see Fig. 2). In Fig. 5, panel b shows a comparison of the evolution of the metallicity between models 1.15 M⊙ CO and 1.15 M⊙ ONe at the time the convective front reached 4 pressure scale heights. The mean metallicities are indeed higher at the time we stop the simulations, ∼30%, in ONe-rich substrates (Z = 0.0330 ± 0.0045 in CO-rich substrates versus Z = 0.0530 ± 0.0003 in ONe-rich substrates). We observe a much more homogeneous metallicity enhancement for ONe models; we note the smaller dispersion that these models present in panel b of Fig. 5. Mixing is less uniform in CO-rich substrates because a larger amount of 12C can be dredged up from the core. Therefore, burning proceeds faster, resulting in a more developed turbulent regime, which in turn, translates into a more inhomogeneous filamentary behavior. The trend observed in the final metallicities is also found in spherical (1D) models José & Hernanz 1998.
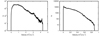 |
Fig. 3. Velocity histograms for models 1.0 M⊙ CO at t = 310s (panel a) and 1.25 M⊙ ONe at t = 657s (panel b). The discontinuities in the velocity are due to different stages of the turbulent mixing during the burning advance. |
 |
Fig. 4. Cumulant distribution function of the Mach number for models 1.0 M⊙ CO at t = 310s (panel a) and 1.25 M⊙ ONe at t = 657 s (panel b). The cumulant distribution shows the probability that the Mach number is equal or below a certain value. |
 |
Fig. 5. Panel a: initial density profiles for the five computed models. Panel b: comparison of the time evolution of the mean metallicity throughout the envelope for models 1.15 M⊙ CO and 1.15 M⊙ ONe until the convective front reaches 4 pressure scale heights above the CEI. |
It is worth mentioning that the burning front for these models is the boundary of the convecting region. Its advance is the consequence of the time development of the nuclear source and the nonlinear process of thermally buoyant motions inducing dynamical instabilities. We cannot capture the fully developed stage because of the relatively short duration of the simulations, relatively limited size of the computational domain, and restriction of all motions to two dimensions. But notwithstanding these limitations the models suffice to make some firm statements. There is a cascade, to the extent that a broad spectrum of motion and density clearly develops, such that the models lead to a broad hierarchy of mixing with large coherent structures persisting that differ in chemical composition.
In Fig. 6, we show the evolution of the metallicity throughout the envelope with time for CO-rich (panel a) and ONe-rich substrates (panel b) until the convective front reaches 4 pressure scale heights. Since the base density and peak temperatures are higher for more massive white dwarfs, the reaction rates increase, which translates into substantial nuclear processing that involves heavier elements. More massive white dwarfs result in a higher metallicity enhancement. For instance, in CO-rich substrates, the final metallicities at the time we stop the simulations are Z = 0.0268 for 0.8 M⊙, Z = 0.0772 for 1.0 M⊙, and Z = 0.2651 for 1.15 M⊙. In ONe-rich substrates, we obtain Z = 0.0866 for 1.15 M⊙, and Z = 0.1174 for 1.25 M⊙. These final mean metallicities are higher than those reported in Table 1 because they are measured at the time the convective front almost reached the upper boundary (∼650 km above the CEI for CO models, and ∼250 km for ONe models)8.
Peak temperatures are determined by the pressure achieved at the base of the envelope before ignition. Accordingly, more massive white dwarfs reach higher pressures and higher peak temperatures; see radial temperature profiles, measured at the time the convective front reached the upper boundary, in panels a and b of Fig. 7. The base temperatures in Fig. 7 are higher than those reported in Table 1 because these are measured at the end of the simulation. At the time we stop the simulations, base temperatures still keep rising, but we expect them to level off when detachment results. The maximum temperatures (the peak value is not yet reached) are lower in ONe-rich substrates at the time we stop the simulations, although we would also expect them to be higher for ONe models than for CO models at the time of detachment (José & Hernanz 1998). In ONe-rich substrates, the nuclear activity extends beyond the CNO mass region, shifting toward the MgAl and NeNa regions where heavier isotopes are produced; see the development of fluid instabilities in terms of 18F and 22Na mass fractions depending on the adopted underlying white dwarf in Fig. 8. In Fig. 9 we show the evolution of the 15O abundance for models 1.0 M⊙ CO (panel a) and 1.25 M⊙ ONe (panel b). The dispersion found in ONe models is again smaller than for CO models, indicating a more uniform enhancement.
 |
Fig. 6. Evolution of the mean metallicity with time in CO-rich (panel a) and ONe-rich (panel b) substrates at 4 pressure scale heights above the CEI, respectively. More massive white dwarfs result in larger metallicity enhancements. |
 |
Fig. 7. Averaged radial temperature profile in CO-rich (panel a) and ONe-rich (panel b) substrates at the time the convective front almost reaches the upper boundary, 650 km and 250 km above the CEI, respectively. Base temperatures are higher in more massive white dwarfs because of higher pressures at the base of the envelope. |
 |
Fig. 8. Development of the initial fluid instabilities at the CEI at t = 310s, in terms of 18F mass fraction and in logarithmic scale, for model 1.0 M⊙ CO (panel a), and at t = 657s, in terms of 22Na mass fraction and in logarithmic scale, for model 1.25 M⊙ ONe (panel b). Identical plots are obtained for the other chemical species. |
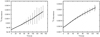 |
Fig. 9. Evolution of the mean 15O abundance with time throughout the envelope until the convective front reaches 4 pressure scale heights, for models 1.0 M⊙ CO (panel a) and 1.25 M⊙ ONe (panel b). |
Main characteristics of the computed models.
4. Discussion
In this paper, we have explored the viability of Kelvin-Helmholtz instabilities operating at the CEI as a mechanism for self-enrichment of the accreted envelope with material from the underlying white dwarf, using various substrates and white dwarf masses. While this was partially investigated by Glasner et al. (2012) in the framework of CO, pure He, pure 16O, and pure 24Mg substrates, our work adopts a more realistic composition for an ONe-rich substrate and extends the analysis for a range of white dwarf masses. All the initial models have been self-consistently computed (in 1D), and hence, the adopted envelope masses are also more realistic. The 2D simulations reported in this paper show that ONe-rich substrates produce a longer dredge-up episode and higher resulting metallicities within the accreted envelope. Finally, we also find more mixing and more energetic explosions for more massive white dwarfs.
A detailed analysis of the development of turbulence in 2D and 3D frameworks in classical nova explosions and characterization of its intermittent behavior is currently underway. It is worth noting that the convective pattern found in our simulations is an unavoidable consequence of the assumed 2D configuration, forcing the fluid motion to behave differently than in 3D convection (Shore 2007; Meakin & Arnett 2007). In 2D, the convective cells are forced to merge into large convective eddies with a size comparable to the envelope height. Nevertheless, the levels of metallicity enhancements and the essential explosion properties are recovered in a 2D framework, since fully 3D simulations differ qualitatively, but not quantitatively, from 2D simulations (Casanova et al. 2011b).
The different envelope size in our 2D simulations, although imposed by the properties of the underlying white dwarf, makes it hard to quantify the final envelope metallicities. The metallicity values reported in this work represent lower limits since the simulations were stopped when the convective front reaches the top of the computational domain and much before the expected detachment of the layers occurs. Extended models are necessary to simulate the entire nova outburst from mixing to the final expansion of the envelope and to quantify rigorously the dredge-up and investigate the progress of the explosion and subsequent ejection. Since our goal is to investigate the mixing mechanism during the TNR, we start the simulations from 1D models that assume no premixing. However, forcing the initial 1D model to be in hydrostatic equilibrium after mapping into 2D imposes a restriction on the portion of the envelope that can be computed, since the density dramatically decreases and produces numerical underflows. A procedure to expand the initial models under hydrostatic equilibrium was explored by Zingale et al. (2002). These authors stopped placing the initial model into hydrostatic equilibrium when a certain density cutoff was reached and added a portion of matter with very low constant density on top of it. This method was found to have a negligible impact on their results. We plan to investigate a similar procedure to extend the initial models in future calculations
A final aspect needs further discussion. In our 1D solar accretion models, the envelope is fully convective when the base temperature is ∼9 × 107 K. A realistic comparison between CO and ONe models should be made when the rates for proton capture on 12C and 20Ne are similar. At the time we map our models (base temperatures of 108 K), the proton capture rate on 12C is much faster than that on 20Ne. Therefore, CO models should be mapped at earlier times to be consistent with ONe models, regarding the length of the mixing process. Previous studies in 2D (Glasner et al. 1997, 2007) investigated how mapping the initial 1D models at lower temperatures (∼7 × 107 K) influences the overall mixing. However, the authors found minor impact on the results.
Movies
Movies of Fig. 1 Access here
Movies of Fig. 1 Access here
Movies of Fig. 1 Access here
Movies of Fig. 1 Access here
For example, V1370 Aql 1982 (Snijders et al. 1987; Andreä et al. 1994), although it is worth mentioning that these studies used ionization correction methods.
Based on the prescription by Spitzer (1962) as implemented in the FLASH code, typical values of the Reynolds and Prandtl numbers are ∼1019 and ∼10−7, respectively.
See, however, Shen & Bildsten (2009) for ignition conditions in C-poor envelopes.
Acknowledgments
Part of the software used in this work was developed by the DOE-supposed ASC/Alliances Center for Astrophysical Thermonuclear Flashes at the University of Chicago. This work has been partially supported by the Spanish MINECO grant AYA2017-86274-P, by the E.U. FEDER funds, by the AGAUR/Generalitat de Catalunya grant SGR-661/2017, and by the US Department of Energy, Office of Science, Office of Nuclear Physics. We also acknowledge the Barcelona Supercomputing Center for a generous allocation of time at the MareNostrum supercomputer. This article benefited from discussions within the ChETEC COST Action (CA16117).
References
- Andreä, J., Dreschel, H., & Starrfield, S. 1994, A&A, 291, 869 [NASA ADS] [Google Scholar]
- Casanova, J., José, J., García-Berro, E., Calder, A., & Shore, S. N. 2010, A&A, 513, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Casanova, J., José, J., García-Berro, E., Calder, A., & Shore, S. N. 2011a, A&A, 527, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Casanova, J., José, J., García-Berro, E., Calder, A., & Shore, S. N. 2011b, Nature, 478, 490 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Casanova, J., José, J., García-Berro, E., & Shore, S. N. 2016, A&A, 595, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Colella, P., & Woodward, P. R. 1984, J. Comput. Phys., 54, 174 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Downen, L. N., Iliadis, C., José, J., & Starrfield, S. 2013, ApJ, 762, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Durisen, R. H. 1977, ApJ, 213, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Fryxell, B., Olson, K., Ricker, P., et al. 2000, ApJ, 399, 646 [Google Scholar]
- Fujimoto, M. Y. 1988, A&A, 198, 163 [NASA ADS] [Google Scholar]
- Fujimoto, M., & Iben, I. Jr., 1992, ApJ, 399, 646 [NASA ADS] [CrossRef] [Google Scholar]
- Gehrz, R. D., Truran, J. W., Williams, R. E., & Starrfield, S. 1998, PASP, 110, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Glasner, S. A., Livne, E., & Truran, J. W. 1997, ApJ, 475, 754 [NASA ADS] [CrossRef] [Google Scholar]
- Glasner, S. A., Livne, E., & Truran, J. W. 2007, ApJ, 665, 1321 [NASA ADS] [CrossRef] [Google Scholar]
- Glasner, S. A., Livne, E., & Truran, J. W. 2012, MNRAS, 427, 2411 [NASA ADS] [CrossRef] [Google Scholar]
- Glasner, S. A.Livne, E., & Truran, J. W. 2014, in Stella Novae: Past and Future Decades, eds. P. A. Woudt, & V. A. R. M. Ribeiro, ASP Conf. Ser., 490, 295 [NASA ADS] [Google Scholar]
- Iben, I., Jr., Fujimoto, M. Y., & MacDonald, J. 1991, ApJ, 375, L27 [NASA ADS] [CrossRef] [Google Scholar]
- Iben, I., Jr., Fujimoto, M. Y., & MacDonald, J. 1992, ApJ, 388, 521 [NASA ADS] [CrossRef] [Google Scholar]
- Iliadis, C., Longland, R., Champagne, A. E., Coc, A., & Fitzgerald, R. 2010, Nucl. Phys. A, 841, 31 [NASA ADS] [CrossRef] [Google Scholar]
- José, J. 2016, in Stellar Explosions: Hydrodynamics and Nucleosynthesis (Boca Raton: CRC/Taylor and Francis) [CrossRef] [Google Scholar]
- José, J., & Hernanz, M. 1998, ApJ, 494, 680 [NASA ADS] [CrossRef] [Google Scholar]
- Jose, J., & Shore, N. S. 2008, in Classical Novae, 2nd edn., eds. M. F. Bode, & A. Evans (Cambridge: Cambridge Univ. Press), 77 [Google Scholar]
- José, J., Halabi, G. M., & El Eid, M. F. 2016, A&A, 593, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kelly, K. J., Iliadis, C., Downen, L., José, J., & Champagne, A. 2013, ApJ, 777, 130K [NASA ADS] [CrossRef] [Google Scholar]
- Kippenhahn, R., & Thomas, H. 1978, A&A, 63, 265 [NASA ADS] [Google Scholar]
- Kovetz, A., & Prialnik, D. 1985, ApJ, 291, 812 [NASA ADS] [CrossRef] [Google Scholar]
- Kovetz, A., & Prialnik, D. 1997, ApJ, 477, 356 [NASA ADS] [CrossRef] [Google Scholar]
- Kutter, G. S., & Sparks, W. M. 1987, ApJ, 321, 386 [NASA ADS] [CrossRef] [Google Scholar]
- Kutter, G. S., & Sparks, W. M. 1989, ApJ, 340, 985 [NASA ADS] [CrossRef] [Google Scholar]
- Landau, L. D., & Lifshitz, E. M. 1987, in Fluid Mechanics, 2nd edn. (Butterworth-Heinemann) [Google Scholar]
- Lesieur, M. 2008, in Turbulence in Fluids, New Trends in Turbulence (Springer) [CrossRef] [Google Scholar]
- Livio, M., & Truran, J. W. 1987, ApJ, 318, 316 [NASA ADS] [CrossRef] [Google Scholar]
- Livio, M., & Truran, J. W. 1990, Proc. 5th Florida Workshop in Nonlinear Astronomy, 617, 126 [Google Scholar]
- MacDonald, J. 1983, ApJ, 273, 289 [NASA ADS] [CrossRef] [Google Scholar]
- Meakin, C. A., & Arnett, D. 2007, ApJ, 667, 448 [NASA ADS] [CrossRef] [Google Scholar]
- Pope, S. B. 2000, in Turbulent Flows (Cambridge: Cambridge Univ. Press) [CrossRef] [Google Scholar]
- Prialnik, D., & Kovetz, A. 1984, ApJ, 281, 367 [NASA ADS] [CrossRef] [Google Scholar]
- Ritossa, C., García-Berro, E., & Iben, I., Jr. 1996, ApJ, 460, 489 [NASA ADS] [CrossRef] [Google Scholar]
- Shara, M. M. 1982, ApJ, 261, 649 [NASA ADS] [CrossRef] [Google Scholar]
- Shen, K., & Bildsten, L. 2009, ApJ, 281, 367 [Google Scholar]
- Shore, S. N. 2007, in Astrophysical Hydrodynamics: An Introduction (Darmstadt: Wiley/VHC) [CrossRef] [Google Scholar]
- Shore, S. N., Livio, M., & van den Heuval, E. P. J. 1994, in Interacting binaries. Saas-Fee Advanced Course 22: Interacting Binaries (Berlin: Springer) [CrossRef] [Google Scholar]
- Snijders, M. A. J., Batt, T. J., Roche, P. F., et al. 1987, MNRAS, 228, 329 [NASA ADS] [CrossRef] [Google Scholar]
- Sparks, W. M., & Kutter, G. S. 1987, ApJ, 321, 394 [NASA ADS] [CrossRef] [Google Scholar]
- Spitzer, L. 1962, in Physics of Fully Ionized Gases (New York: Wiley/Interscience) [Google Scholar]
- Starrfield, S., Truran, J. W., Wiescher, M., & Sparks, W. 1998, MNRAS, 296, 502 [NASA ADS] [CrossRef] [Google Scholar]
- Starrfield, S., Iliadis, C., & Hix, W. R. 2008, in Classical Novae, 2nd edn., eds. Bode M. F., & Evans A., (Cambridge: Cambridge Univ. Press), 77 [Google Scholar]
- Starrfield, S., Iliadis, C., & Hix, R. W. 2016, PASP, 28, 963 [Google Scholar]
- Timmes, F. X. 2000, ApJ, 528, 913 [NASA ADS] [CrossRef] [Google Scholar]
- Timmes, F. X., & Arnett, D. 2000, ApJS, 125, 277 [Google Scholar]
- Timmes, F. X., & Swesty, F. D. 2000, ApJS, 126, 501 [NASA ADS] [CrossRef] [Google Scholar]
- Vanlandingham, K., Starrfield, S., & Shore, S. N. 1997, MNRAS, 290, 87 [NASA ADS] [CrossRef] [Google Scholar]
- van Leer, B. 1979, J. Comput. Phys., 32, 101 [Google Scholar]
- Yaron, O., Prialnik, D., Shara, M. M., & Kovetz, A. 2005, ApJ, 623, 398 [NASA ADS] [CrossRef] [Google Scholar]
- Zingale, M., Dursi, L. J., Zuhone, J., et al. 2002, ApJS, 143, 539 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1. Panel a shows the growth of the primary fluid instabilities at t = 54 s, in terms of 12C mass fraction and in logarithmic scale, for model 1.0 M⊙ CO white dwarf. The other panels show snapshots of the convective front when it is at a distance of 4 pressure scale heights above the CEI for models 0.8 M⊙ CO (panel b), 1.0 M⊙ CO (panel c), 1.15 M⊙ CO (panel d), 1.15 M⊙ ONe (panel e), and 1.25 M⊙ ONe (panel f). The snapshots are shown in terms of 12C mass fraction for CO-rich substrates, and in terms of 20Ne mass fraction for ONe-rich substrates, both in logarithmic scale. The times are t = 326s, t = 149s, t = 66s, t = 194s, and t = 133s, respectively. The reflection condition is imposed in the lower boundary, which is located 50 km below the CEI for all the simulations. See movies available online. |
| In the text | |
 |
Fig. 2. Propagation of the convective front throughout the accreted envelope as a function of time for models 1.0 M⊙ CO (panel a) and 1.25 M⊙ ONe (panel b). |
| In the text | |
 |
Fig. 3. Velocity histograms for models 1.0 M⊙ CO at t = 310s (panel a) and 1.25 M⊙ ONe at t = 657s (panel b). The discontinuities in the velocity are due to different stages of the turbulent mixing during the burning advance. |
| In the text | |
 |
Fig. 4. Cumulant distribution function of the Mach number for models 1.0 M⊙ CO at t = 310s (panel a) and 1.25 M⊙ ONe at t = 657 s (panel b). The cumulant distribution shows the probability that the Mach number is equal or below a certain value. |
| In the text | |
 |
Fig. 5. Panel a: initial density profiles for the five computed models. Panel b: comparison of the time evolution of the mean metallicity throughout the envelope for models 1.15 M⊙ CO and 1.15 M⊙ ONe until the convective front reaches 4 pressure scale heights above the CEI. |
| In the text | |
 |
Fig. 6. Evolution of the mean metallicity with time in CO-rich (panel a) and ONe-rich (panel b) substrates at 4 pressure scale heights above the CEI, respectively. More massive white dwarfs result in larger metallicity enhancements. |
| In the text | |
 |
Fig. 7. Averaged radial temperature profile in CO-rich (panel a) and ONe-rich (panel b) substrates at the time the convective front almost reaches the upper boundary, 650 km and 250 km above the CEI, respectively. Base temperatures are higher in more massive white dwarfs because of higher pressures at the base of the envelope. |
| In the text | |
 |
Fig. 8. Development of the initial fluid instabilities at the CEI at t = 310s, in terms of 18F mass fraction and in logarithmic scale, for model 1.0 M⊙ CO (panel a), and at t = 657s, in terms of 22Na mass fraction and in logarithmic scale, for model 1.25 M⊙ ONe (panel b). Identical plots are obtained for the other chemical species. |
| In the text | |
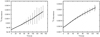 |
Fig. 9. Evolution of the mean 15O abundance with time throughout the envelope until the convective front reaches 4 pressure scale heights, for models 1.0 M⊙ CO (panel a) and 1.25 M⊙ ONe (panel b). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


